c数值分析c17-5
素陶粒混凝土c7.5与c15的区别

素陶粒混凝土c7.5与c15的区别
素陶粒混凝土C7.5与C15在多个方面存在区别,以下是详细的解释:
1.强度:C7.5表示混凝土的抗压强度为7.5兆帕,而C15则代表混凝土的抗压强度为
15兆帕。
因此,在强度方面,C15混凝土的强度明显高于C7.5混凝土。
2.用途:由于C7.5混凝土的强度较低,它通常用于对强度要求不高的场合,如垫层、
找平层等。
而C15混凝土则常用于需要一定强度的结构或构件,如基础、梁板等。
3.材料组成:素陶粒混凝土,又称轻质混凝土(Light Weight Concrete,简称LC),
主要使用轻质的陶粒作为骨料进行拌合。
这种混凝土具有较高的强度和较低的密度,适用于需要减轻结构自重、抗震等特殊要求的场合。
不过,具体的材料组成比例和添加剂的使用可能会因强度等级(C7.5或C15)的不同而有所差异。
4.其他性能:除了强度外,素陶粒混凝土还具有保温、隔热、耐火等优异性能。
这些
性能可能会因混凝土的强度等级和具体配比的不同而有所变化。
5.生产与成本:由于C15混凝土的强度要求较高,其生产过程中可能需要更多的水泥
和其他添加剂,以及更严格的工艺控制。
因此,C15混凝土的生产成本通常会比C7.5混凝土高。
总的来说,素陶粒混凝土C7.5与C15在强度、用途、材料组成、其他性能以及生产
与成本等方面都存在明显的区别。
在选择使用时,应根据具体工程的需求和条件进行综合考虑。
c17的用途碳

c17的用途碳C17的用途碳C17碳是一种重要的有机化合物,具有广泛的用途。
下面将介绍C17碳的用途。
1. 医药C17碳是许多药物的活性成分之一。
例如,C17碳可以用于制备一些镇痛药物和抗癌药物。
此外,C17碳还可以用于生产激素类药物,如口服避孕药等。
2. 食品添加剂C17碳可以用作食品添加剂,主要是作为增稠剂、乳化剂和稳定剂。
例如,C17碳可以用于制备蛋糕、糖果、奶油等食品。
此外,C17碳还可以用于制备口香糖和润滑油等。
3. 化妆品C17碳可以用于制备化妆品,主要是作为乳化剂、稳定剂和增稠剂。
例如,C17碳可以用于制备面霜、洗发水、沐浴露等。
此外,C17碳还可以用于制备口红、眼影等化妆品。
4. 塑料C17碳可以用于生产塑料,主要是作为增塑剂和稳定剂。
例如,C17碳可以用于制备聚氯乙烯(PVC)塑料。
此外,C17碳还可以用于制备塑料制品,如水管、电线套管等。
5. 涂料C17碳可以用于制备涂料,主要是作为增稠剂和稳定剂。
例如,C17碳可以用于制备油漆、涂料等。
此外,C17碳还可以用于制备涂料辅助材料,如涂料添加剂等。
6. 纤维C17碳可以用于生产纤维,主要是作为润滑剂和防静电剂。
例如,C17碳可以用于制备合成纤维和人造毛绒织物。
此外,C17碳还可以用于制备纺织品添加剂、染料添加剂等。
7. 燃料C17碳可以用于生产燃料,主要是作为汽油和柴油的添加剂。
例如,C17碳可以用于制备高辛烷值汽油和低硫柴油。
此外,C17碳还可以用于制备航空燃料添加剂等。
C17碳具有广泛的用途,不仅可以用于医药、食品添加剂、化妆品、塑料、涂料、纤维、燃料等领域,还可以用于其他领域。
因此,C17碳在现代工业中具有重要的地位,对于推动经济发展和提高生活质量起到了积极的作用。
细胞色素C的含量测定

细胞色素C的含量测定
林范天
【期刊名称】《中国医院药学杂志》
【年(卷),期】1985()2
【摘要】细胞色素C我国药典是采用分光光度法作含量测定,由于还原型的细胞色素C在550nm处有尖锐的吸收峰,所以狭缝的宽度和波长对吸收度都有很大的影响。
【总页数】3页(P25-27)
【作者】林范天
【作者单位】武汉市药品检验所
【正文语种】中文
【中图分类】TS2
【相关文献】
1.马心细胞色素C含量测定的几种方法比较
2.大鼠急性脑干损伤致死后脑干组织细胞色素C含量的测定
3.甲状腺癌患者细胞色素C含量测定的临床意义
4.GC法测定复方细胞色素C滴眼液中丁二酸钠含量
5.大鼠肝微粒中5种细胞色素P-450的特异性底物含量的高效液相色谱法同时测定
因版权原因,仅展示原文概要,查看原文内容请购买。
c同位素分析

c同位素分析以“C同位素分析”为标题,写一篇3000字的中文文章C同位素分析是一种通过分析物质中C同位素组成,以确定物质成分及原料来源来支撑定量生态学研究的方法,也是研究生物群落结构特征及其变化的一种重要手段。
它是一种独特的工具,可以揭示营养的来源、群落的食物网络特征、物种的食性、捕食者的捕食过程、以及生态网络的调节作用等。
C同位素分析是利用气相色谱-质谱联用设备,以放射性稳定同位素C-12、C-13的质量比做指标,对无机和有机物质中的碳按其生物同位素丰度分析的方法,从而进行识别和定量分析。
C-13定位素在碳物质中的丰度水平是由物质的来源决定的,主要有生物还原和来自工业分配,工业分配的C-13丰度偏低,而生物还原的C-13丰度一般较高,因此,还原的碳源的C-13定位素比值普遍较低,而来自有机物的碳则具有较高的C-13定位素比值。
C同位素分析可以分析物质来源,如有机碳物质来源于植物或动物,而石油、天然气等无机碳物质则来自非生物源。
在分析食物网络中,C同位素分析可以确定消费者在食物链中的位置,从而帮助研究物种特征、个体数目及其饱食度等信息,进而提高营养学研究的准确性。
C同位素分析也可以用于追踪污染物的原料来源。
C同位素分析可以将污染物来源分辨为有机或无机物质,从而比较定位素的比值,以识别污染来源。
此外,C同位素分析可以用于鉴别生物体的季节性变化,以及研究生态系统中物质的健康状态和变化趋势。
例如,碳同位素可以用来确定森林生物群落的碳循环过程,从而了解森林的能量来源和消耗,研究森林碳汇的效应,并进一步推断森林处于保护状态或被破坏状态。
C同位素分析在实际应用中仍然有很多不足,这主要是由于C同位素分析需要购买特殊的设备和贵重的试剂,而且,C同位素分析的过程比较繁琐复杂,分析结果不够准确。
因此,要提高C同位素分析的实用性,还需要更多研究来完善该技术。
总而言之,C同位素分析是一种重要的生态学研究技术,它可以用于物质来源的分析,同时可以分析食物网络的结构,为森林碳汇的研究及污染物的追踪提供定量的信息,然而,其实用性还存在许多不足,需要进一步的改进。
维生素C含量的测定
实验十一、维生素C 含量的测定一、实验目的1、掌握碘标准溶液的配制方法与标定原理。
2、掌握直接碘量法测定维生素C 的原理、方法及其操作。
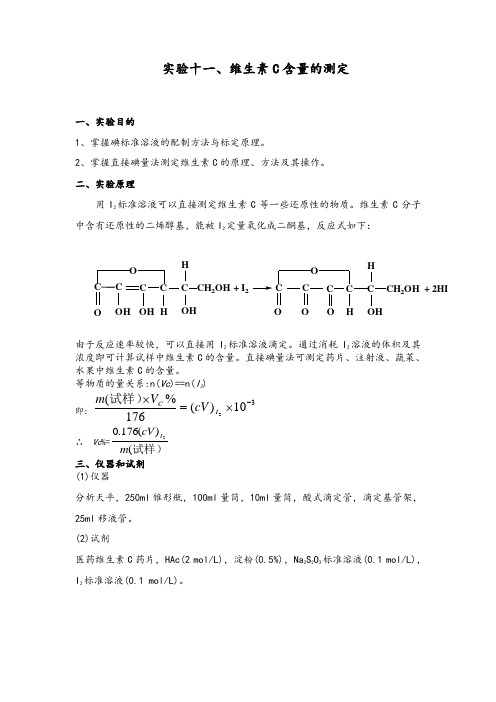
二、实验原理用I 2标准溶液可以直接测定维生素C 等一些还原性的物质。
维生素C 分子中含有还原性的二烯醇基,能被I 2定量氧化成二酮基,反应式如下:C OCCC CCH 2OH OOH OHHOH H+ I 2C OC C C C CH 2OH OOHHH OO + 2HI由于反应速率较快,可以直接用I 2标准溶液滴定。
通过消耗I 2溶液的体积及其浓度即可计算试样中维生素C 的含量。
直接碘量法可测定药片、注射液、蔬菜、水果中维生素C 的含量。
等物质的量关系:n(Vc )==n(I 2)即:310)(176%(2-⨯=⨯I C cV V m 试样)∴ Vc %=试样)()(176.02m cV I三、仪器和试剂 (1)仪器分析天平,250ml 锥形瓶,100ml 量筒,10ml 量筒,酸式滴定管,滴定基管架,25ml 移液管。
(2)试剂医药维生素C 药片,HAc(2 mol/L),淀粉(0.5%),Na 2S 2O 3标准溶液(0.1 mol/L),I 2标准溶液(0.1 mol/L)。
三、实验步骤1. 0.05 mol ·L -1 I 2标准溶液的配制与标定将3.3g I 2与5g KI 置于研钵中,在通风柜中加入少量水(切不可多加!)研磨,待I 2全部溶解后,将溶液转入棕色瓶中,加水稀释至250mL ,摇匀。
用移液管移取25.00mL Na 2S 2O 3 标准溶液于250mL 锥形瓶中,加50mL 水、5mL0.5%淀粉溶液,用I 2标准溶液滴定至稳定的蓝色,30s 内不褪色即为终点。
平行标定三次。
2. 维生素C 含量的测定准确称取约0.2g 维生素C 片(研成粉末即用),置于250mL 锥形瓶中,加入新煮沸过并冷却的蒸馏水100mL 、10mL 2mol ·L-1 HAc 和5mL0.5%淀粉指定剂,立即用I 2标准溶液滴定至溶液显稳定的蓝色, 30s 内不褪色即为终点。
c++入门基础PPT

汇报人:可编辑 2023-12-24
目录
• C简介 • C基础语法 • C面向对象编程 • C标准库 • C进阶概念 • C实践项目
01
C简介
C的发展历程
1983年
Bjarne Stroustrup在Bell Labs开始开发C
1985年
C的第一个版本发布
1998年
C标准委员会发布了C98标准
与while语句类似,先执行一次代 码块再判断条件。
if语句
用于根据条件选择执行不同的代 码块。
for语句
用于重复执行一段代码一定次数 ,或者根据循环变量的变化来执 行。
函数
函数定义
包括函数名、参数列表和函数体。
函数调用
通过函数名和参数列表来调用函数。
函数返回值
函数执行完毕后返回一个值。
03
C面向对象编程
异常处理是C提供的一种机制,用于捕获和处理程序中出现的异常。通过try、catch和 throw语句,可以在程序中添加异常处理逻辑,以避免程序因异常而崩溃或出现不可预
测的行为。
04
C标准库
标准库的组成
语言核心库
提供基本的输入输出、 内存管理、字符串处理
等功能。
算法库
提供各种算法函数,如 排序、查找、数值计算
数组类型
用于存储同一类型的多个 数据。
结构体类型
用于组合多个不同类型的 数据。
数据类型
联合体类型
用于在同一块内存中存储多个不同类型的数据。
枚举类型
用于定义一组命名的常量。
运算符
关系运算符
包括==、!=、>、 <等,用于比较两个 值的大小关系。
IF钢碳含量的过程控制_卿家胜

2011 年 6 月 第 27 卷 第 3 期
炼钢 St eelmaking
Jun. 2011 Vol. 27 No. 3 15
1. 3 过铸过程钢中增碳分析
对中间包和结晶器浇铸过程的前、中、后分别 取样, 碳含量的变化情况见表 4 所示。
由表 4 可见, 中间包浇铸过程钢水中碳含量 有所增加, w ( C) = 0. 000 3 % ~ 0. 000 4 % , 主 要是因为中包覆盖剂使用的主料、辅料和耐火砖 中的部分碳进入钢水; 结晶器浇铸过程 w ( C) = 0. 000 3 % ~ 0. 000 5 % , 这主要来源于保护渣和 耐火砖中的碳。
第3期
卿家胜, 等: IF 钢碳含量的过程控制
17
炉号
1 04 644 1 04 645 1 04 646
RH 出站
0. 001 4 0. 001 5 0. 001 5
表 4 RH 出站至铸坯的 w( C) 变化情况
中间 包浇铸过程
w( C) / %
结晶器浇铸过程
前期
中期
后期
前期
中期
后期
0. 001 6
16
炼钢
第 27 卷
车用钢不但对钢质量的要求日益提高, 对钢中碳 含量也提出了更高的要求, 特别是超深冲用钢, 要 求钢中 w ( C) < 30 10- 6 [ 4-6] 。从表 1 可知, 目前 国内外 IF 钢的碳质量分数最低可以控制到 10 10- 6 , 攀枝花钢铁( 集团) 公司( 以下简称攀钢) 现 阶段生产的 IF 钢成品碳质量分数在 30 10- 6 左 右, 距世界先进水平还有一定的差距。
c85710化学成分

c85710化学成分
【原创版】
目录
1.引言
2.碳 (C)
3.氢 (H)
4.氧 (O)
5.氮 (N)
6.硫 (S)
7.磷 (P)
8.结论
正文
化学成分是指一个物质中所含有的各种化学元素及其含量。
c85710 是一种化合物,其化学成分主要包括碳 (C)、氢 (H)、氧 (O)、氮 (N)、硫 (S) 和磷 (P) 等元素。
首先,让我们来看一下 c85710 中的碳 (C) 元素。
碳元素是有机物的基本构成元素,它在 c85710 中的含量直接影响到该化合物的物理和化学性质。
接下来是氢 (H) 元素。
氢元素通常与碳元素结合,形成有机物的基本结构单元。
在 c85710 中,氢元素的含量同样重要。
再来看看氧 (O) 元素。
氧元素在有机物中通常以羟基 (-OH) 的形式存在,对于 c85710 的化学性质和生物活性有着重要影响。
此外,c85710 中还含有一定量的氮 (N) 元素。
氮元素在有机物中可以形成胺基 (-NH2) 或亚胺基 (-NH-),从而影响该化合物的化学性质和
生物活性。
硫 (S) 元素和磷 (P) 元素在 c85710 中的含量较低,但它们同样对 c85710 的物理和化学性质有着重要影响。
综上所述,c85710 的化学成分主要包括碳 (C)、氢 (H)、氧 (O)、氮 (N)、硫 (S) 和磷 (P) 等元素,这些元素的含量和比例决定了
c85710 的物理和化学性质,以及其生物活性。
十七碳烯酸(C17-1)检测

十七碳烯酸(C17:1)检测
顺-10-十七碳烯酸(cis-10-heptadecenoicacid,17:1)是一种脂肪酸,存在于大鼠、猪肉、香蕉、大肠埃希菌等动植物、微生物中,是反刍动物脂肪中含量较少的组成部分,具有生物活性。
迪信泰检测平台采用高效液相色谱(HPLC)、液质联用(LC-MS)、气质联用(GC-MS)和生化法,可高效、精准的检测十七碳烯酸的含量变化。
此外,我们还提供其他脂肪酸检测服务,以满足您的不同需求。
HPLC、LC-MS和GC-MS测定十七碳烯酸样本要求:
1. 请确保样本量大于0.2g或者0.2mL。
周期:2~3周
项目结束后迪信泰检测平台将会提供详细中英文双语技术报告,报告包括:
1. 实验步骤(中英文)
2. 相关质谱参数(中英文)
3. 质谱图片
4. 原始数据
5. 十七碳烯酸含量信息。
数值分析上机(C++版)

数值分析论文NUMERICAL ANALYSIS(THESIS)题目数值分析论文学生指导教师鸿雁学院专业班级2016年12月目录一二分法与牛顿迭代法1二拉格朗日插值法6三最小二乘法10四复合辛普森求积公式15五改进欧拉公式18六列主元消去法21七不动点迭代法26一二分法与牛顿迭代法一问题简介在有气体参加的恒容反应体系里,反应体系的总压会随着反应的进行而改变。
通过反应的平衡常数可以求出反应后气体的总量,而气体分子的分压与其所占比率是成正比的。
这类问题中关键是要求出反应后各分子的分压,各分子分压之和即为总压,其实质即为求方程的根。
例如:在298K下,化学反应2OF2=O2+2F2的平衡常数为0.410atm,如在298K下将OF2通入容器,当t=0时为1atm,问最后总压是多少?计算精度为10-3。
二数学模型假设是理想气体,可知2OF2=O2+2F2设氧的分压为p,平衡时有1-2p p p平衡时有整理得4p3-1640p2+164p-0410=0函数关系式为三算法选择与算法过程由计算得f(0.2)=-0.1156,f(0.3)=0.0424因此,有根区间为[0.2,0.3]用求单根的二分法计算时:可令a=0.2,b=0.3;最后计算得氧气分压:p=0.274609atm,总压为:P=3p+(1-2p)=1.274609atm用牛顿迭代法计算时:令则迭代公式为:令进行迭代,最后计算得氧气分压为:p=0.274901,则总压为:P=3p+(1-2p)=1.274901二分法的计算算法:#include <iostream>#include<math.h>using namespace std;double a=0.2,b=0.3,e=0.001,n;double f(float c){n=4*c*c*c-1.6400000*c*c+1.64*c-0.410;return n;}void main(){double c,m,p,a=0.2,b=0.3;for(p=a;b-a>=0.001;){c=(a+b)/2;m=f(c);if(m<0){a=c;}else if(m>0){b=c;}else{p=c;break;}p=(a+b)/2;}cout<<"\n a="<<a<<endl;cout<<"\n b="<<b<<endl;}牛顿迭代法的算法:#include<iostream>#include<string>#include<cmath>using namespace std;double f(double x){double m,n;m=4*x*x*x-1.640*x*x+1.64*x-0.410;n=12*x*x-3.280*x+1.64;return x-m/n;}void newton(double x,double d){double a=x;double b=f(a);int k; //记录循环的次数for(k=1;fabs(a-b)>d;k++){a=b;b=f(a);if(k>100){cout<<"迭代失败,该函数可能不收敛!"<<endl;}}cout<<"\n b="<<b<<endl;cout<<"\n k="<<k<<endl;return;}int main(){cout<<"请输入初始值x0和要求得结果的精度:";double x,d;cin>>x>>d;newton(x,d);return 0;}四数值实验过程二分法通过VC6.0程序运行的结果如下图所示:牛顿迭代法通过VC6.0的计算结果如下:五相关数值分析和实际应用分析由二分法程序输出结果可得:a=0.274219,b=0.275。
毕业论文ppt

滴定时易受其他还原性物质的干扰,试剂价格昂贵,操 作繁琐,测定速度慢,1次只能测定1个样品, 不能实现连 续测定。2,4-二硝基苯肼法具有操作简便快速,准确度高 快速不需要特殊仪器的特点。同时2种方法的试验结果相 差较大,在相对允许的误差范围内, 2,6-二氯酚靛酚滴定 法更适合测紫薯中Vc的含量。
V—滴定样液时消耗染料的体积,mL;
V0—滴定空白时消耗染料的体积,mL。
2021/4/6
8
2,4-二硝基苯肼比色法
用活性炭把样品中的还原型抗坏血酸氧化为 脱氢型抗坏血酸,继续氧化为二酮古乐糖酸。二酮 古乐糖酸与2,4-二硝基苯肼偶联生成红色的脎。 根据脎在硫酸溶液中的含量与总抗坏血酸含量成正 比进行比色测定。
Vc标准使用液
2021/4/6
12
容量瓶编号: 1 2 3 4 5 6 7
Vc标准使用液 5.00
10.00
20.00 30.00 40.00 50.00 60.00
1%硫脲定容
二硝基苯肼1.00mL
37土0.5 ℃恒温水浴3h
冰水冷却,滴加5.00mL85%硫酸
取出,室温置30min 500nm,1cm比色皿测A
1. 样品的制备 2. 样品的测定 3. 2,6-二氯酚靛酚溶液的标定
2021/4/6
7
5.计算
维生素C含量(mg/100g样品)
X={[(V-V0) ×T]/M}×100
式中:X—样品中的Vc的含量,mg/100g;
T—1mL染料溶液相当于Vc标准溶液的量,mg;
M—滴定时所取的滤液中含有样品的质量,g;
C描述的高精度数值计算

C描述的高精度数值计算
夏仁强
【期刊名称】《毕节学院学报》
【年(卷),期】2006(024)004
【摘要】从数据结构+算法的角度系统地给出的高精度数值计算的程序,可以突破计算机对数值表示范围的限制,从而使其具有任意位高精度数值的加、减、乘、除等强大的数值计算的功能.
【总页数】5页(P56-60)
【作者】夏仁强
【作者单位】毕节学院计算机科学系,贵州,毕节,551700
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.非定常Euler方程数值计算中高精度格式应用 [J], 赵云飞;刘绪;涂国华;刘伟;毛枚良
2.约束空间爆炸冲击波高精度数值计算及实验验证 [J], 徐维铮;孔祥韶;郑成;吴卫国
3.爆炸波高精度数值计算程序开发及应用 [J], 徐维铮;吴卫国
4.在Cap—cyclide坐标中Wangerin函数Nm^n(v)的高精度数值计算 [J], 黄华;恰汗·合孜尔;宋艳萍;努尔古丽·艾力
5.爆炸与冲击问题的高精度模拟与大规模数值计算研究 [J], 宁建国;马天宝;王成
因版权原因,仅展示原文概要,查看原文内容请购买。
cxcl5分子量

cxcl5分子量CXCL5分子量简介CXCL5(C-X-C motif chemokine ligand 5),也被称为ENA-78(epithelialcell-derived neutrophil attractant 78),是一种趋化因子,它可以刺激白细胞移动到炎症区域。
CXCL5属于CXC,又称Cys-X-Cys,这个类别的趋化因子,这意味着分子中有两个半胱氨酸(Cys)之间有一个任意氨基酸(X)。
CXCL5是由上皮细胞产生的,在许多炎症和感染的过程中发挥着重要作用。
CXCL5的分子量约为12.5千道尔顿(kDa)。
在水中,它是单体,由70个氨基酸组成。
CXCL5的化学式为C307H503N91O95S8。
CXCL5的分子量相当小,因此它可以通过细胞壁渗透到细胞内,并通过受体结合激活信号通路。
CXCL5的结构特点CXCL5作为趋化因子,它具有许多与其他趋化因子类似的特征。
它是一个蛋白质,由一个单体结构组成,它的结构也与其他CXC趋化因子相似。
CXCL5的结构包括四个高度保守的半胱氨酸残基,这四个半胱氨酸残基形成了两个二硫键,这些二硫键是这个蛋白质分子稳定性的重要因素。
此外,CXCL5分子结构中,还有一些其他保守的氨基酸序列,这些序列的存在可以对分子的最终折叠结构产生重要的影响。
它具有典型的四个螺旋环形结构,其中两个周围的半胱氨酸氨基酸残基之间的二硫键形成了一个小的结构域。
CXCL5是一种趋化因子,它在许多炎症和感染的过程中发挥着重要作用。
它可以引起各种细胞的移动,包括单核细胞、粒细胞和NK细胞。
在肺炎球菌感染中,CXCL5也可以促进中性粒细胞的迁移。
在肺炎球菌感染结束后,CXCL5的水平仍然升高,说明CXCL5可能对细胞内坏死和死亡起重要作用。
此外,CXCL5也参与了许多其他炎症性疾病的发展,如关节炎、斑块组织形成和乳腺癌。
因此,通过研究CXCL5参与的各种炎症过程,可以为这些疾病的治疗提供帮助。
c2075

c2075C2075: 一款高性能计算卡的综合评测引言C2075是一款由NVIDIA推出的高性能计算卡,专为科学、工程和技术领域的专业计算任务而设计。
本文将对C2075进行综合评测,并从性能、功耗、应用领域等方面进行分析。
希望本文可以为对C2075感兴趣的读者提供有价值的信息。
一、基本介绍C2075采用了NVIDIA的Fermi架构,拥有448个CUDA核心和6GB GDDR5显存。
它的GPU时钟频率为575MHz,内存时钟频率为778MHz,采用384位内存接口,带宽高达144GB/s。
C2075支持CUDA和OpenCL,并且具有良好的可编程性和灵活性。
二、性能评测1. 浮点运算性能C2075的浮点运算性能是其最引人注目的特点之一。
通过CUDA核心的大规模并行计算,C2075可以实现高达1.03 TFLOPS的双精度浮点性能和515 GFLOPS的单精度浮点性能。
这使得C2075在科学计算和工程仿真等领域中具有强大的计算能力。
2. 内存性能C2075的6GB GDDR5显存和高带宽内存接口可以提供卓越的内存性能。
在大规模数据处理任务中,C2075能够以每秒144GB的速度读写数据,从而大大提高了计算效率。
此外,C2075还支持ECC 内存,可以提供更高的数据可靠性。
3. 吞吐量和带宽C2075通过高效的内存访问和并行计算能力,可以实现很高的吞吐量和带宽。
它的存储带宽达到了每秒144GB,这对于处理大规模数据集和复杂计算任务非常重要。
吞吐量的提高使得C2075能够更快地完成计算任务,提高工作效率。
三、功耗和散热1. 功耗评估C2075在提供卓越性能的同时也需要相应的功耗支持。
根据NVIDIA的官方数据,C2075的最大功耗为225W。
在实际使用中,功耗受到任务的性质和计算负载的影响。
因此,在选择C2075时,需要考虑到系统的电源和散热能力。
2. 散热设计由于C2075的高功耗,良好的散热设计非常重要。
直接碘量法测定维生素C含量

一.实验目的之阿布丰王创作时间:二O 二一年七月二十九日1.掌握碘标准溶液的配制和标定方法; 2.了解直接碘量法测定维生素C 的原理和方法. 二.实验原理维生素C (Vc )又称抗坏血酸,分子式686O H C ,分子量1mol •176.1232/g -.Vc具有还原性,可被2I 定量氧化,因而可用2I 标准溶液直接滴定.其滴定反应式为:.由于Vc 的还原性很强,较易被溶液和空气中的氧氧化,在碱性介质中这种氧化作用更强,因此滴定宜在酸性介质中进行,以减少副反应的发生.考虑到-I 在强酸性溶液中也易被氧化,故一般选在pH=3~4的弱酸性溶液中进行滴定.三.主要试剂1.2I 溶液(约1L •0.05mol-):称取2I 和5g KI ,置于研钵中,加少量水,在通风橱中研磨.待2I 全部溶解后,将溶液转入棕色试剂瓶中,加水稀释至250mL,充沛摇匀,放阴暗处保管.2.322O S Na 标准溶液(1L •0.1127mol -) 3.HAc (1L •2mol -) 4.淀粉溶液 5.维生素C 片剂 6.KI 溶液 四.实验步伐1.2I 溶液的标定322O S Na 标准溶液于250mL 锥形瓶中,加40mL 蒸馏水,4mL 淀粉溶液,然后用2I 溶液滴定至溶液呈浅蓝色,30s 内不褪色即为终点.平行标定3份,计算12L •)/mol (I -c . 2.维生素C 片剂中Vc 含量的测定准确称取2片维生素C 药片,置于250mL 锥形瓶中,加入100mL 新煮沸过并冷却的蒸馏水,10mLHAc 溶液和5mL 淀粉溶液,立即用2I 标准溶液滴定至呈现稳定的浅蓝色,且在30s 内不褪色即为终点,记下消耗的)/mL (I 2V .平行滴定3份,计算试样中的Vc 的质量分数. 五.数据记录与处置 1.I 溶液的标定2.维生素C 片剂中Vc 含量的测定六.实验总结标定得)L •04825(mol .0)(I 12-=c ,测得%52.84)Vc (=ω. 七.分析讨论1.KI I 2-溶液呈深棕色,在滴定管中较难分辨凹液面,但液面最高点较清楚,所以常读取液面最高点,读时应调节眼睛的位置,使之与液面最高点前后在同一水平位置上.2.使用碘量法时,应该用碘量瓶,防止2I 、322O S Na 、Vc 被氧化,影响实验结果的准确性.3.由于实验中不能防止地摇动锥形瓶,因此空气中的氧会将Vc 氧化,使结果偏低.八.思考题1.溶解2I 时,加入过量KI 的作用是什么?答:查得,碘在水中的溶解度为O)00gH g/(02.021.因此,溶解度很低.加入过量的KI ,可增加2I 在水中的溶解度,反应式如下:2.维生素C 固体试样溶解时为何要加入新煮沸并冷却的蒸馏水?答:Vc 有强还原性,为防止水中溶解的氧氧化Vc,因此要将蒸馏水煮沸,以除去水中溶解的氧;为防止Vc 的结构被破坏,因此要将煮沸的蒸馏水冷却.3.碘量法的误差来源有哪些?应采用哪些办法减少误差?答:(1)读数误差,由于碘标准溶液颜色较深,溶液凹液面难以分辨;但液面最高点较清楚,所以常读数液面最高点,读时应调节眼睛的位置,使之与液面最高点前后在同一水平位置上.(2)反应物容易被空气中的氧氧化;滴定过程中用碘量瓶,而不用锥形瓶,防止剧烈地摇动.。
c数值分析c6-12

6.12Hypergeometric Functions 271Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5)Copyright (C) 1988-1992 by Cambridge University Press.Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).CITED REFERENCES AND FURTHER READING:Erd´elyi,A.,Magnus,W.,Oberhettinger,F .,and T ricomi,F .G.1953,Higher T ranscendentalFunctions ,Vol.II,(New Y ork:McGraw-Hill).[1]Gradshteyn,I.S.,and Ryzhik,I.W.1980,T able of Integrals,Series,and Products (New Y ork:Academic Press).[2]Carlson,B.C.1977,SIAM Journal on Mathematical Analysis ,vol.8,pp.231–242.[3]Carlson,B.C.1987,Mathematics of Computation ,vol.49,pp.595–606[4];1988,op.cit.,vol.51,pp.267–280[5];1989,op.cit.,vol.53,pp.327–333[6];1991,op.cit.,vol.56,pp.267–280.[7]Bulirsch,R.1965,Numerische Mathematik ,vol.7,pp.78–90;1965,op.cit.,vol.7,pp.353–354;1969,op.cit.,vol.13,pp.305–315.[8]Carlson,B.C.1979,Numerische Mathematik ,vol.33,pp.1–16.[9]Carlson,B.C.,and Notis,E.M.1981,ACM T ransactions on Mathematical Software ,vol.7,pp.398–403.[10]Carlson,B.C.1978,SIAM Journal on Mathematical Analysis ,vol.9,p.524–528.[11]Abramowitz,M.,and Stegun,I.A.1964,Handbook of Mathematical Functions ,Applied Mathe-matics Series,Volume 55(Washington:National Bureau of Standards;reprinted 1968by Dover Publications,New Y ork),Chapter 17.[12]Mathews,J.,and Walker,R.L.1970,Mathematical Methods of Physics ,2nd ed.(Reading,MA:W.A.Benjamin/Addison-Wesley),pp.78–79.6.12Hypergeometric FunctionsAs was discussed in §5.14,a fast,general routine for the the complex hyperge-ometric function 2F 1(a,b,c ;z ),is difficult or impossible.The function is defined as the analytic continuation of the hypergeometric series,2F 1(a,b,c ;z )=1+ab c z 1!+a (a +1)b (b +1)c (c +1)z 22!+···+a (a +1)...(a +j −1)b (b +1)...(b +j −1)z j+···(6.12.1)This series converges only within the unit circle |z |<1(see [1]),but one’s interest in the function is not confined to this region.Section 5.14discussed the method of evaluating this function by direct path integration in the complex plane.We here merely list the routines that result.Implementation of the function hypgeo is straightforward,and is described by comments in the program.The machinery associated with Chapter 16’s routine for integrating differential equations,odeint ,is only minimally intrusive,and need not even be completely understood:use of odeint requires one zeroed global variable,one function call,and a prescribed format for the derivative routine hypdrv .The function hypgeo will fail,of course,for values of z too close to the singularity at 1.(If you need to approach this singularity,or the one at ∞,use the “linear transformation formulas”in §15.3of [1].)Away from z =1,and for moderate values of a,b,c ,it is often remarkable how few steps are required to integrate the equations.A half-dozen is typical.272Chapter 6.Special FunctionsSample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5)Copyright (C) 1988-1992 by Cambridge University Press.Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).#include <math.h>#include "complex.h"#include "nrutil.h"#define EPS 1.0e-6Accuracy parameter.fcomplex aa,bb,cc,z0,dz;Communicates with hypdrv .int kmax,kount;Used by odeint .float *xp,**yp,dxsav;fcomplex hypgeo(fcomplex a,fcomplex b,fcomplex c,fcomplex z)Complex hypergeometric function 2F 1for complex a,b,c ,and z ,by direct integration of the hypergeometric equation in the complex plane.The branch cut is taken to lie along the real axis,Re z >1.{void bsstep(float y[],float dydx[],int nv,float *xx,float htry,float eps,float yscal[],float *hdid,float *hnext,void (*derivs)(float,float [],float []));void hypdrv(float s,float yy[],float dyyds[]);void hypser(fcomplex a,fcomplex b,fcomplex c,fcomplex z,fcomplex *series,fcomplex *deriv);void odeint(float ystart[],int nvar,float x1,float x2,float eps,float h1,float hmin,int *nok,int *nbad,void (*derivs)(float,float [],float []),void (*rkqs)(float [],float [],int,float *,float,float,float [],float *,float *,void (*)(float,float [],float [])));int nbad,nok;fcomplex ans,y[3];float *yy;kmax=0;if (z.r*z.r+z.i*z.i <=0.25){Use series...hypser(a,b,c,z,&ans,&y[2]);return ans;}else if (z.r <0.0)z0=Complex(-0.5,0.0);...or pick a starting point for the path integration.else if (z.r <=1.0)z0=Complex(0.5,0.0);else z0=Complex(0.0,z.i >=0.0?0.5:-0.5);aa=a;Load the global variables to pass pa-rameters “over the head”of odeint to hypdrv .bb=b;cc=c;dz=Csub(z,z0);hypser(aa,bb,cc,z0,&y[1],&y[2]);Get starting function and derivative.yy=vector(1,4);yy[1]=y[1].r;yy[2]=y[1].i;yy[3]=y[2].r;yy[4]=y[2].i;odeint(yy,4,0.0,1.0,EPS,0.1,0.0001,&nok,&nbad,hypdrv,bsstep);The arguments to odeint are the vector of independent variables,its length,the starting and ending values of the dependent variable,the accuracy parameter,an initial guess for stepsize,a minimum stepsize,the (returned)number of good and bad steps taken,and the names of the derivative routine and the (here Bulirsch-Stoer)stepping routine.y[1]=Complex(yy[1],yy[2]);free_vector(yy,1,4);return y[1];}6.12Hypergeometric Functions 273Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5)Copyright (C) 1988-1992 by Cambridge University Press.Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).#include "complex.h"#define ONE Complex(1.0,0.0)void hypser(fcomplex a,fcomplex b,fcomplex c,fcomplex z,fcomplex *series,fcomplex *deriv)Returns the hypergeometric series 2F 1and its derivative,iterating to machine accuracy.For |z |≤1/2convergence is quite rapid.{void nrerror(char error_text[]);int n;fcomplex aa,bb,cc,fac,temp;deriv->r=0.0;deriv->i=0.0;fac=Complex(1.0,0.0);temp=fac;aa=a;bb=b;cc=c;for (n=1;n<=1000;n++){fac=Cmul(fac,Cdiv(Cmul(aa,bb),cc));deriv->r+=fac.r;deriv->i+=fac.i;fac=Cmul(fac,RCmul(1.0/n,z));*series=Cadd(temp,fac);if (series->r ==temp.r &&series->i ==temp.i)return;temp=*series;aa=Cadd(aa,ONE);bb=Cadd(bb,ONE);cc=Cadd(cc,ONE);}nrerror("convergence failure in hypser");}#include "complex.h"#define ONE Complex(1.0,0.0)extern fcomplex aa,bb,cc,z0,dz;Defined in hypgeo .void hypdrv(float s,float yy[],float dyyds[])Computes derivatives for the hypergeometric equation,see text equation (5.14.4).{fcomplex z,y[3],dyds[3];y[1]=Complex(yy[1],yy[2]);y[2]=Complex(yy[3],yy[4]);z=Cadd(z0,RCmul(s,dz));dyds[1]=Cmul(y[2],dz);dyds[2]=Cmul(Csub(Cmul(Cmul(aa,bb),y[1]),Cmul(Csub(cc,Cmul(Cadd(Cadd(aa,bb),ONE),z)),y[2])),Cdiv(dz,Cmul(z,Csub(ONE,z))));dyyds[1]=dyds[1].r;dyyds[2]=dyds[1].i;dyyds[3]=dyds[2].r;dyyds[4]=dyds[2].i;}CITED REFERENCES AND FURTHER READING:Abramowitz,M.,and Stegun,I.A.1964,Handbook of Mathematical Functions ,Applied Mathe-matics Series,Volume 55(Washington:National Bureau of Standards;reprinted 1968by Dover Publications,New Y ork).[1]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17.5Automated Allocation of Mesh Points 783Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5)Copyright (C) 1988-1992 by Cambridge University Press.Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).17.5Automated Allocation of Mesh PointsIn relaxation problems,you have to choose values for the independent variable at the mesh points.This is called allocating the grid or mesh.The usual procedure is to pick a plausible set of values and,if it works,to be content.If it doesn’t work,increasing the number of points usually cures the problem.If we know ahead of time where our solutions will be rapidly varying,we can put more grid points there and less elsewhere.Alternatively,we can solve the problem first on a uniform mesh and then examine the solution to see where we should add more points.We then repeat the solution with the improved grid.The object of the exercise is to allocate points in such a way as to represent the solution accurately.It is also possible to automate the allocation of mesh points,so that it is done “dynamically”during the relaxation process.This powerful technique not only improves the accuracy of the relaxation method,but also (as we will see in the next section)allows internal singularities to be handled in quite a neat way.Here we learn how to accomplish the automatic allocation.We want to focus attention on the independent variable x ,and consider two alternative reparametrizations of it.The first,we term q ;this is just the coordinate corresponding to the mesh points themselves,so that q =1at k =1,q =2at k =2,and so on.Between any two mesh points we have ∆q =1.In the change of independent variable in the ODEs from x to q ,d ydx =g (17.5.1)becomes d y dq =g dxdq (17.5.2)In terms of q ,equation (17.5.2)as an FDE might be written y k −y k −1−12 g dx dq k + g dx dqk −1=0(17.5.3)or some related version.Note that dx/dq should accompany g .The transformation between x and q depends only on the Jacobian dx/dq .Its reciprocal dq/dx is proportional to the density of mesh points.Now,given the function y (x ),or its approximation at the current stage of relaxation,we are supposed to have some idea of how we want to specify the density of mesh points.For example,we might want dq/dx to be larger where y is changing rapidly,or near to the boundaries,or both.In fact,we can probably make up a formula for what we would like dq/dx to be proportional to.The problem is that we do not know the proportionality constant.That is,the formula that we might invent would not have the correct integral over the whole range of x so as to make q vary from 1to M ,according to its definition.To solve this problem we introduce a second reparametrization Q (q ),where Q is a new independent variable.The relation between Q and q is taken to be linear ,so that a mesh spacing formula for dQ/dx differs only in its unknown proportionality constant.A linear relation impliesd 2Qdq 2=0(17.5.4)or,expressed in the usual manner as coupled first-order equations,dQ (x )dq =ψdψdq =0(17.5.5)where ψis a new intermediate variable.We add these two equations to the set of ODEs being solved.Completing the prescription,we add a third ODE that is just our desired mesh-density function,namelyφ(x )=dQdx =dQ dq dqdx (17.5.6)784Chapter 17.T wo Point Boundary Value ProblemsSample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5)Copyright (C) 1988-1992 by Cambridge University Press.Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copying of machine-readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website or call 1-800-872-7423 (North America only),or send email to directcustserv@ (outside North America).where φ(x )is chosen by us.Written in terms of the mesh variable q ,this equation is dxdq =ψφ(x )(17.5.7)Notice that φ(x )should be chosen to be positive definite,so that the density of mesh points is everywhere positive.Otherwise (17.5.7)can have a zero in its denominator.To use automated mesh spacing,you add the three ODEs (17.5.5)and (17.5.7)to your set of equations,i.e.,to the array y[j][k].Now x becomes a dependent variable!Q and ψalso become new dependent variables.Normally,evaluating φrequires little extra work since it will be composed from pieces of the g ’s that exist anyway.The automated procedure allows one to investigate quickly how the numerical results might be affected by various strategies for mesh spacing.(A special case occurs if the desired mesh spacing function Q can be found analytically,i.e.,dQ/dx is directly integrable.Then,you need to add only two equations,those in 17.5.5,and two new variables x,ψ.)As an example of a typical strategy for implementing this scheme,consider a system with one dependent variable y (x ).We could setdQ =dx ∆+|d ln y |(17.5.8)orφ(x )=dQ dx =1∆+ dy/dx yδ(17.5.9)where ∆and δare constants that we choose.The first term would give a uniform spacing in x if it alone were present.The second term forces more grid points to be used where y is changing rapidly.The constants act to make every logarithmic change in y of an amount δabout as “attractive”to a grid point as a change in x of amount ∆.You adjust the constants according to taste.Other strategies are possible,such as a logarithmic spacing in x ,replacing dx in the first term with d ln x .CITED REFERENCES AND FURTHER READING:Eggleton,P .P .1971,Monthly Notices of the Royal Astronomical Society ,vol.151,pp.351–364.Kippenhan,R.,Weigert,A.,and Hofmeister,E.1968,in Methods in Computational Physics ,vol.7(New Y ork:Academic Press),pp.129ff.17.6Handling Internal Boundary Conditionsor Singular PointsSingularities can occur in the interiors of two point boundary value problems.Typically,there is a point x s at which a derivative must be evaluated by an expression of the formS (x s )=N (x s ,y )D (x s ,y )(17.6.1)where the denominator D (xs ,y )=0.In physical problems with finite answers,singularpoints usually come with their own cure:Where D →0,there the physical solution y mustbe such as to make N →0simultaneously,in such a way that the ratio takes on a meaningful value.This constraint on the solution y is often called a regularity condition .The condition that D (x s ,y )satisfy some special constraint at xs is entirely analogous to an extra boundary condition,an algebraic relation among the dependent variables that must hold at a point.We discussed a related situation earlier,in §17.2,when we described the “fitting point method”to handle the task of integrating equations with singular behavior at the boundaries.In those problems you are unable to integrate from one side of the domain to the other.。
