19.1.2函数的图像()

合集下载

人教版八年级数学下册第十九章19.1.2函数的图象(第一课时)函数的图象

为什么没有 “0”？
解:(1)列表取自变量的一些值, 并求出对应的函数值,填入表中.
y
新知探究
6
5
4
3
2
1
解:(1)列表
-5 -4 -3 -2 -1 o -1
(2)描点分别以表中对应的x、y为 -2
横纵坐标,在坐标系中描出对应的 -3
点.
-4
-5
(3)连线用光滑的曲线把这些点 -6
依次连接起来.
2
填写下表，再描点、连线）
的图象.（先
x … -3 -2 -1 0
y
…
3 2
-1
1 2
0
2.点P（2，5）不在（填“在”或 “不在”）函数y=2x的图象上.
12
1
1
2
y
3
2
1
3…
3 2
…
-4 -3 -2 -1O-1 -2 -3
12345 x
3.下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔, 然后散步走回家，图中x表示时间，y表示张强离家的距离.
思考：对于某个函数，给定一个自变 b 量的值x，确定唯一的函数值y，由此能否确定一个点(x，y)呢?
(a，b) a
函数图象的意义问题：请画出下面问题中能直观地反映函数变化规
律的图形：正方形面积 S 与边长 x 之间的函数解析式为 S=x2．
思考：（1）这个函数的自变量取值范围是什么？ x ＞0
第十九章一次函数 19.1.2 函数的图象
第1课时函数的图象
学习目标
【学习目标】 1.知道函数图象上的点的横坐标与纵坐标的意义. 2.能从函数图象上读取信息. 【学习重点】从函数图象上读取信息. 【学习难点】函数图象上的点的横坐标与纵坐标的意义.

人教版八年级数学下册19.1.2《函数的图像》课件

如点(2，4)表示x=2时 S=4。
八年级数学
第十一九章函数的图象
函数的图象
你记住了吗？
对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象。
上图中的曲线即为函数 s x2 (x＞0)的图象．
函数图象可以数形结合地研究函数，给我们带来便利。
y
2.5
y=x+0.5
从函数图象可以看出，
直线从左到右上升，
1.5
即当x由小到大时，
y=x+0.5随之增大．
0.5
-1
O -0.5
12x
自己动手画一画画出函数（2）y 6 x 0 的图象
x
（2）y 6 x 0
列表：
x
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
S/m
S/m
s1
s2
X/s
O
O
s1 s2
S/m X/s
O
S/m
s1
s1
s2
s2
X/s
X/s
O
A
B
C
D
回归问题
问题：观察下图，你能大致描述男女孩平均身高在平均身高之上还是之下？你能估计自己18岁时的身高吗？
八年级数学
第十一九章函数的图象
一个思想————数学结合思想两个关系———应用函数图象研究实际问题时，注意自变量与函数的对应关系
S=x2
…
(x>0) 0 0.25 1 2.25 4 6.25 9
如果我们在直角坐标系中，将你所填表格中的自变量x及对应的函数值S当作一个点的横坐标与纵坐标，即可在坐标系中得到一些点。

19.1.2函数的图像PPT演示课件

间？
x/min
12
应用
例2 下图反映的过程是小明从家去食堂吃早餐，
接着去图书馆读报，然后回家．其中x 表示时间，y 表
示小明离家的距离，小明家、食堂、图书馆在同一直线
上．
y/km
0.8 0.6
O
8
25 28
根据图象回答下列问题：
（2）小明在食堂吃早餐用了多少时间？
58
68
x/min
13
应用
例2 下图反映的过程是小明从家去食堂吃早餐，
19.1.2函数的图象(1)
1.一辆汽车的油箱中现有汽油50升，如果不再加油，那么油箱中的油量y（升）随行驶里程x（公里）的增加而减少，平均耗油量为0.1升/公里。
（1）写出表示y与x的函数关系的式子。（2）指出自变量x的取值范围（3）汽车行驶200公里时，油箱中还有多少油？
2
2.求下列函数中自变量的取值范围
上．
y/km
0.8 0.6
O
8
25 28
58
68
根据图象回答下列问题：
（5）图书馆离小明家多远？小明从图书馆回家的平均
速度是多少？
x/min
16
练习1：
300
y(米)
(1)小强让爷爷先上多少米？
60米
(2)山顶高多少米？谁先爬上山顶？
山顶离山脚的距离有300米，小强先爬上山顶．
240
180
爷爷
120
按照横坐标从小到大的顺序把描出的点用平滑曲线依次连接起来
11
应用
例2. 下图反映的过程是小明从家去食堂吃早餐，
接着去图书馆读报，然后回家．其中x 表示时间，y 表
示小明离家的距离，小明家、食堂、图书馆在同一直线

2021年人教版数学八年级下册学案 19.1.2《函数的图象》(含答案)

19.1.2 函数的图象第1课时函数的图象学习目标①知道函数图象的意义.②学会用列表、描点、连线画函数图象．③学会观察、分析函数图象信息．④能利用函数的图象解决实际问题重点难点：函数图象的画法；观察、分析、概括图象中的信息．学习过程一、自主学习（阅读教材并完成下列活动）【活动1】思考：如图是某人体检时的心电图，图上点的横坐标x表示时间，纵坐标y表示心脏部位的生物电流，y与x之间的函数关系能用式子表达吗？显然有些函数问题用函数关系式表示出来，然而可以通过来直观反映．【活动2】正方形的边长x与面积S的函数关系式为；在这个函数中，自变量是、它的取值范围是，是的函数，请根据这个函数关x 0 0.5 1 2 3 ……S ……思考与探究：如果把自变量的值当作横坐标，函数S的值作为纵坐标，组成一对有序实数对（x、S），这样的实数对有多少对？请在下面的直角坐标系中描出这些点，你有什么发现？二、探究新知识①一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的、坐标，那么坐标平面内由这些点组成的图形，就是这个函数的。

②画函数图象的一般步骤是：、、。

③在坐标平面内，若点P（x,y）向右上方移动，则y随x的增大而；若点P（x,y）向右下方移动，则y随x的增大而。

第2课时函数的表示方法学习目标①进一步理解函数及其图像的意义.②学会根据自变量的值求函数值；或根据函数值求自变量的值，掌握函数的表示方法.③熟练掌握求函数中自变量的取值范围的方法.重点难点：①怎样根据自变量的值求函数值；②怎样求函数自变量的取值范围；③根据函数图象解决实际问题.学习过程一、自主学习（阅读教材）【活动1】分析并解决下列列问题:1．用解析法表示函数关系优点： . 缺点： . 2．用列表表示函数关系优点： . 缺点： . 3．用图象法表示函数关系优点： . 缺点： . 【活动2】请用原来所学的知识完成下列填空：1、若错误!未找到引用源。

有意义，则x的取值范围是 .2、若错误!未找到引用源。

19.1.2函数的图像(正式稿)

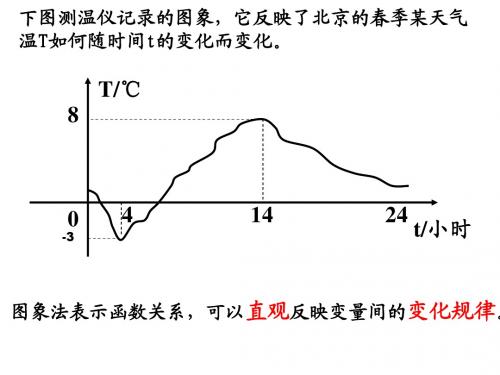
1、列表 2、描点
3、连线
列出自变量与函数的对应值表。注意：自变量的值（满足取值范围），并取值要适当，以便画图.
建立直角坐标系，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点按照横坐标从小到大的顺序把描出的点用平滑曲线依次连接起来
注：函数图象可能是曲线，也可能是直线，也可能是线段或射线，函数图象的形状取决于函数关系和自变量的取值范围。
【反思归纳】函数的三种表示法通常是相互关联，可以相互转化(特殊的函数除外): (1)由函数解析式可以得到这个函数的列表及图象; (2)由函数的图象可以得到其解析式及函数的对应值表格; (3)由函数的表格可以得到函数的解析式及图象.
（1）函数图象上的点的横纵坐标分别表示什么？（2）画函数图象时，怎样体现函数的自变量取值范围？
（1）判断下列各点是否在函数 y =x+ 0.5的图象上？ ①（-4，-4.5）； ②（4，4.5）． 6 （2）判断下列各点是否在函数 y = （x＞0）的图象上？ x ①（2，3）；②（4，2）．
2、函数 y=-2x-6的图象上,若点B(a,a+1)在这个函数图象上,则a=________.
s/米
2.周末小明一家乘出租车前往离家8千米的公园，出租车的收费标准如下：
里程收费/元
t/秒
3千米以下（含3千米）
3千米以上，增加1千米
5.00
1.00
（1）写出出租车行驶的里程数x（千米）与费用y（元）之间的函数关系。（2）小明带了10元钱，够不够付到公园的车费，为什么？
3. 已知某一函数的图象如图所示，根据图象回答下列问题：（1）确定自变量的取值范围；（2）求当x=-4，-2，4时y的值是多少？（3）求当y=0，4时x的值是多少？（4）当x取何值时y的值最大？当x取何值时y的值最小？ (5)当x的值在什么范围内时y随x的增大而增大？当x的值在什么范围内时y•随x的增大而减小？

人教版八年级数学下册第十九章 19.1.2 函数的图像课件(3课时,共69张PPT)

（3）如果水位的变化规律不变，按上述函数预测，再持续2小时，水位的高度： __y_=_0_.3_×__7_+_3_=_5_._1_(m__)_____. 此时函数图象（线段AB）向 ___________延伸到对应的位置，这时水位高度约为___5_.1_m______米.
由例可以看出，函数的不同表示法之间可以__转__化_______.
值范围是： X取全体实数；第一步：从的取值范围中选取一些简洁的数值，算出的对应值，填写在表格里；
x … －3 －2 －1 0 1 2 …
y … -2.5 -1.5 -0.5 0.51.52.5 …
知识点用描点法画函数图象第二步：根据表中数值描点（ x ,y）；
y=x+0.5
• • • • • •
1、如果A、B两人在一次百米赛跑中，路程（米）与赛跑的时间t（秒）的关系
如图所示则下列说法正确的是（ C）
A. A比B先出发； B. A、B两人的速度相同； C. A先到达终点； D. B比A跑的路程多.
2、用列表法与解析式法表示n边形的内角和m（单位：度）关于边数的n函数.
解：列表法：
边数n 3 4 5 …
内角和 m/度 180 360 540
…
解析法：m=(n-2)×180 °,n≥3
大而减小，当x＞0时，y随x的增大而增大。
画函数图象的一般步骤：
列表、描点、连线，这种画函数图象的方法称为描点法。
函数图象的三种表示法
1、描点法画函数图象的一般步骤：（1）_列__表__，（2）_描__点__，（3）_连__线___. 2、表示函数的三种方法分别为：
__解_析__式__法__、___列_表__法__ 、_图__象_法__ .

人教版八年级数学下册19.1.2《函数的图象(1)》习题含答案

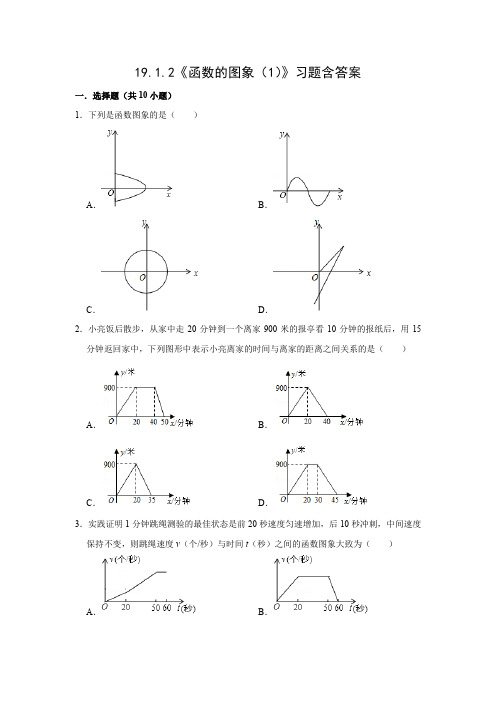
19.1.2《函数的图象（1）》习题含答案一．选择题（共10小题）1．下列是函数图象的是（）A．B．C．D．2．小亮饭后散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小亮离家的时间与离家的距离之间关系的是（）A．B．C．D．3．实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（）A．B．C．D．4．今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用时间为t（分钟），所走路程为s（米），s与t之间的函数关系如图所示，则下列说法中，错误的是（）A．小明中途休息用了20分钟B．小明在上述过程中所走路程为7200米C．小明休息前爬山的速度为每分钟60米D．小明休息前后爬山的平均速度相等5．如图所示的游泳池内蓄满了水，现打开深水区底部的出水口匀速放水，在这个过程中，可以近似地刻画出泳池水面高度h与放水时间t之间的变化情况的是（）A．B．C．D．6．某同学放学回家，在路上遇到一个同学，一块去同学家玩了会儿，然后独自回家．下列图象能表示这位同学所剩路程与时间变化关系的是（）A．B．C．D．7．一列火车匀速通过隧道（隧道长大于火车的长），火车在隧道内的长度y与火车进入隧道的时间x之间的关系用图象表示正确的是（）A．B．C．D．8．某天小明骑自行车上学，途中因自行车发生故障，修车耽误一段时间后继续骑行，按时赶到了学校．如图描述了他上学情景，下列说法中错误的是（）A．用了5分钟来修车B．自行车发生故障时离家距离为1000米C．学校离家的距离为2000米D．到达学校时骑行时间为20分钟9．如图，一只蚂蚁沿台阶A1→A2→A3→A4→A5匀速爬行，蚂蚁爬行的高度h随时间t变化的图象大致是（）A．B．C．D．10．甲、乙两名同学骑自行车从A地出发沿同一条路前往B地，他们离A地的距离s（km）与甲离开A地的时间t（h）之间的函数关系的图象如图所示，根据图象提供的信息，有下列说法：①甲、乙同学都骑行了18km②甲、乙同学同时到达B地③甲停留前、后的骑行速度相同④乙的骑行速度是12km/h其中正确的说法是（）A．①③B．①④C．②④D．②③二．填空题（共3小题）11．如图是某市某天的气温T（℃）随时间t（时）变化的图象，则由图象可知，该天最高气温与最低气温之差为℃．12．甲、乙两人分别从A、B两地相向而行，y与x的函数关系如图，其中x表示乙行走的时间（时），y表示两人与A地的距离（千米），甲的速度比乙每小时快千米．13．小明从家跑步到学校，接着马上原路步行回家．如图是小明离家的路程y（米）与时间t（分）的关系图象，则小明回家的速度是每分钟步行米．14．某天早晨，小王从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是小王从家到学校这一过程中所走的路程s（米）与时间t（分）之间的关系．（1）小王从家到学校的路程共米，从家出发到学校，小明共用了分钟；（2）小王吃早餐用了分钟；（3）小王吃早餐以前和吃完早餐后的平均速度分别是多少米/分钟？15．如图是甲、乙两人从同一地点出发后，路程随时间变化的图象．（1）在此变化过程中，是自变量；（2）甲的速度乙的速度；（填“大于”、“等于”、或“小于”）（3）甲出发后与乙相遇；（4）甲比乙先走小时；（5）9时甲在乙的（填“前面”、“后面”、“相同位置”）；（6）路程为150千米，甲行驶了小时，乙行驶了小时．19.1.2《函数的图象（1）》习题答案一．选择题（共10小题）1．【分析】根据函数的概念（当x取一值时，y有唯一与它对应的值）解答即可．【解答】解：A、当x取一值时，y没有唯一与它对应的值，y不是x的函数，故本选项不合题意；B、当x取一值时，y有唯一与它对应的值，y是x的函数，故本选项符合题意；C、当x取一值时，y没有唯一与它对应的值，y不是x的函数，故本选项不合题意；D、当x取一值时，y没有唯一与它对应的值，y不是x的函数，故本选项不合题意；故选：B．2．【分析】从小亮散步的时间段看，分为0﹣20分钟散步，20﹣30分钟看报，30﹣45分钟返回家，按时间段把函数图象分为三段．【解答】解：依题意，0﹣20分钟散步，离家路程增加到900米，20﹣30分钟看报，离家路程不变，30﹣45分钟返回家，离家路程减少为0米．故选：D．3．【分析】根据前20秒匀加速进行，20秒至50秒保持跳绳速度不变，后10秒继续匀加速进行，得出速度y随时间x的增加的变化情况，即可求出答案．【解答】解：随着时间的变化，前20秒匀加速进行，所以此时跳绳速度y随时间x的增加而增加，再根据20秒至50秒保持跳绳速度不变，所以此时跳绳速度y随时间x的增加而不变，再根据后10秒继续匀加速进行，所以此时跳绳速度y随时间x的增加而增加，故选：C．4．【分析】根据函数图象可知，小明40分钟爬山2400米，40～60分钟休息，60～100分钟爬山（4800﹣2400）米，爬山的总路程为4800米，根据路程、速度、时间之间的关系进行解答即可．【解答】解：A、小明中途休息的时间是：60﹣40＝20分钟，故本选项正确；B、小明在上述过程中所走路程为4800米，故本选项错误；C、小明休息前爬山的速度为＝60（米/分钟），故本选项正确；D、因为小明休息后爬山的速度是＝60（米/分钟），所以小明休息前后爬山的平均速度相等，故本选项正确；故选：B．5．【分析】根据题意和图形，可以得到浅水区和深水区h随t的变化情况，从而可以解答本题．【解答】解：由题意可得，在浅水区，h随t的增大而减小，h下降的速度比较慢，在深水区，h随t的增大而减小，h下降的速度比较快，故选：C．6．【分析】根据题意可以写出各段过程中，所剩路程与时间的关系，从而可以解答本题．【解答】解：由题意可得，这位同学从学校出发到与同学相遇前这一过程中，所剩路程随着时间的增加而减小，这位同学与同学相遇到在同学家玩这一过程中，所剩路程随着时间的增加不变，这位同学离开同学家到回到家的这一过程中，所剩路程随着时间的增加而减小，故选：C．7．【分析】根据题意可以写出火车行驶的各个阶段中y与x的函数关系，从而可以解答本题．【解答】解：由题意可得，火车头刚进入隧道到火车尾刚进入隧道的这一过程中，y随x的增大而增大，火车尾刚进入隧道到火车头刚要驶离隧道的这一过车中，y随x的增加不发生变化，火车头刚出隧道到火车尾刚驶离隧道这一过程中，y随x的增大而减小，故选：A．8．【分析】根据图象分析，从纵坐标可以看出，在离家1000米处停留了15﹣10＝5分钟，20分钟时，离家2000米到学校．根据这些信息即可判断．【解答】解：根据图象分析，从纵坐标可以看出，在离家1000米处停留了15﹣10＝5分钟，故A正确，此时离家2000﹣1000＝1000米．故B正确，20分钟时，离家2000米到学校．故C正确，到达学校骑行的时间为：20﹣5＝15分钟，故D错误故选：D．9．【分析】根据图形，可以分析出各段过程中，h随t的增加如何变化，从而可以解答本题．【解答】解：由图可得，蚂蚁沿台阶从A1→A2的过程中，h随t的增加不发生变化，蚂蚁沿台阶从A2→A3的过程中，h随t的增加在变小，蚂蚁沿台阶从A3→A4的过程中，h随t的增加不发生变化，蚂蚁沿台阶从A4→A5的过程中，h随t的增加变小直到为零，故选：A．10．【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确，从而可以解答本题．【解答】解：由图象可得，甲、乙同学都骑行了18km，故①正确，甲比乙先到达B地，故②错误，甲停留前的速度为：10÷0.5＝20km/h，甲停留后的速度为：（18﹣10）÷（1.5﹣1）＝16km/h，故③错误，乙的骑行速度为：18÷（2﹣0.5）＝12km/h，故④正确，故选：B．二．填空题（共3小题）11．【分析】根据观察函数图象的纵坐标，可得最高气温、最低气温，根据有理数的减法，可得温差．【解答】解：如图：，由纵坐标看出最高气温是10℃，最低气温是﹣2℃，该天最高气温与最低气温之差为10﹣（﹣2）＝12℃．故答案为：1212．【分析】根据“速度＝路程÷时间”分别求得甲、乙的速度，然后求其差．【解答】解：根据图示知，甲的速度是：8÷（5﹣1）＝2（千米/小时），乙的速度是：8÷5＝1.6（千米/小时）．则：2﹣1.6＝0.4（千米/小时）．故答案是：0.4．13．【分析】总路程÷回家用的时间，即可求解．【解答】解：小明回家用了15﹣5＝10分钟，总路程为500，故小明回家的速度为：500÷10＝50（米/分），故答案为50．三．解答题（共13小题）14．【分析】（1）看图象即可求解；（2）小王吃早餐时，s的值为常数，即可求解；（3）确定该时段学生走的距离和时间，即可求解．【解答】解：（1）从图象看，小王从家到学校的路程共1000米，从家出发到学校，小明共用了25分钟；故答案为1000，25；（2）小王吃早餐时，s的值为常数，故从10分钟到20分钟，共10分钟，故答案为：10；（3）小王吃早餐以前的平均速度为：500÷10＝50米/分钟；小王吃早餐后的平均速度为：（1000﹣500）÷5＝100米/分钟．15．【分析】（1）根据自变量与因变量的含义得到时间是自变量，路程是因变量；（2）甲走6行驶100千米，乙走3小时行驶了100千米，则可得到它们的速度的大小；（3）6时两图象相交，说明他们相遇；（4）甲比乙先走3小时；（5）观察图象得到t＝9时，乙的图象在甲的上方，即乙行驶的路程远些；（6）路程为150千米，甲行驶了9时，根据乙的速度可得乙行驶的时间．【解答】解：（1）函数图象反映路程随时间变化的图象，则t是自变量，s为因变量；（2）甲的速度＝千米/小时，所以甲的速度小于乙的速度；（3）6时表示他们相遇，即乙追赶上了甲；（4）甲比乙先走3小时；（5）t＝9时，乙的图象在甲的上方，即乙行驶的路程远些，所以9时甲在乙的后面；（6）路程为150千米，甲行驶了9时，乙行驶的时间为：150÷（100÷3）＝4.5（小时）．故答案为：（1）t；（2）小于；（3）6时；（4）3；（5）后面；（6）9；4.5．。

人教版七年级数学下册课件：19.1.2函数的图象(共31张ppt)

解：①列表（自变量x取一切实数）
x…
…
y…
…
例3（1）、画出函数y=x+0.5的图象
解：①列表（自变量x取一切实数）
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5-0.5 0.5 1.5 2.5 3.5 …
②描点
y 5
③连线
4 3
2
1
y=x+0.5
从该函数图象可以看出哪些
AB
O0
15 25 37
55
E
80 x/分
问题2：小明给菜地浇水用了多少（出时2，）小间由明横给？坐菜标地看浇
y/千米
水用了10分。（25-10）
解：由横坐标看出，小明给菜地浇水用了10分钟。
2
C
D
AB
1.1
O0
15 25 37
55
E
80 x/分
问题3：菜地离玉米地多远？小明从菜地走到玉米地用了多少时间？
探索归纳：
一、由函数图象的定义可知： (1)函数图象上的点一定满足函数解析式。
(2)满足函数解析式的点的一定在函数图象上。即：函数图象上的点与函数解析式的每一对对应值
是一一对应的。
二、判断点在函数图象上的方法：
将这个点的坐标(x, y)代入函数解析式中，若满足函数解析式，那么点就在函数的图象上；如果不满足函数解析式，那么点就不在函数的图象上。
y/千米
C
D
2
AB
1.1
O
0
15 25
37
55
E
80 x/分
问题1：菜地离小明家多远？小明走到菜地
用了多少时间？

人教版八年级数学下册19.1.2函数的图像1ppt课件

（A） A比B先出发（B） A、B两人的速度相同（C） A先到达终点（D） B比A跑的路程多
2.某人早上进行登山活动，从山脚到山顶休息一会儿又沿原路返回，若用横轴表示时间t，纵轴表示与山脚距离h，那么下列四个图中反映全程h与t的关系图是（）
D
3．小芳今天到学校参加初中毕业会考，从家里出发走10分到离家500米的地方吃早餐，吃早餐用了20分；再用10分赶到离家 1000米的学校参加考试．下列图象中，能反映这一过程的是（）．
b.乙在途中停留了０.５h；
c.甲和乙两人同时到达目的地；
d.甲乙两人途中没有相遇过．
根据图象信息，以上说法正确的是
（）
s/km
20
乙
甲
A.1个
O 0.5 1
t/h
2 2.5
C.３个
Ｂ B.２个 D.４个
龟兔赛跑
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉, 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已经来不及了,乌龟先到达了终点………现在用和分别表示乌龟、兔子所走的路程，t为时间，则下列图象中，能够表示S 和t之间的函数关系式的是（）
如点(2，4)表示x=2时S=4。
1.函数图象定义：
一般来说，对于一个函数,如果把自变量和函数的每一对对应值分别作为点的横坐标和纵坐标,那么在坐标平面内由这些点组成的图形，叫做这个函数的图象. 画函数图象的步骤：
1.列表
2.描点
3.连线
活动一
下图是自动测温仪记录的图象，它反映了北京的春季某天气温T如何随时间t 的变化而变化。你从图象中得到了哪些信息?
x＞ 0 （2）怎样获得组成函数图象的点？
先确定点的坐标．（3）怎样确定满足函数关系的点的坐标？

19.1.2函数图像(2)-画函数图像

函数的图象（1）知识技术目标1.掌握用描点法画出函数的图象；2.认识函数图像的性质 .过程性目标1.经过学生自己着手，领悟用描点法画函数的图象的步骤.2.结合画出的图形，教会学生看解析图形的性质，重点看什么。

授课过程一、复习引入问题 1 上节课的内容：函数的定义；定义域，值域；表达方式有三种：列表法，图形法，解析式法问题 2 提问：画函数图像的步骤是？列表——描点——连线二、研究归纳教师举例： p74 练习 1（ 1）y x2 x0每个步骤都要有注意的地方。

1.列表：列表给出自变量与函数的一些对应值；2.描点：以表中对应值为坐标，在坐标平面内描出相应的点；理论上点越多越好，不能够少于 5 个点，一般取 7 个点3.连线：依照自变量由小到大的序次，把所描各点用圆滑的曲线连结起来．描出的点越多，图象越精确．有时不能够把所有的点都描出，就用圆滑的曲线连结画出的点，从而获取函数的近似的图象．三、实践应用课堂让学生着手画三个函数图像：①y x 2②y 1 ③y 2x 1 x四、交流反思我们看图像看的是什么？1、定义域、值域2、对称性3、与坐标轴交点个数4、函数的单调性师生共同谈论：y x 2 图像定义域： x 可取任意实数，y ＞0；对称轴是 y 轴；与坐标轴交于（ 0,0 ）为什么 y ＞0，为什么以 y 轴为对称轴？； x<0 时， y 随着 x 的增大而减小， x>0 时， y 随着 x 的增大而增大。

师生共同谈论：y1 图像的定义域： x 0 ， y 0 ；对称轴是 x 轴， y 轴， x=y ，x=-y ；与坐标轴没有交点 x为什么会有以上特色呢？x<0 时， y 随着 x 的增大而减小， x>0,y 随着 x 的增大而减小。

师生共同谈论：y2x 1 图像的定义域： x可取任意实数， y可取任意实数；与坐标轴交于两点，与x轴交于（1，0），与y轴交于（0，-1）；y随着x的增大而增大2。