河北省武安三中2013届高三上学期第四次月考数学文试题 Word版含答案

合集下载

2016-2017学年河北省邯郸市武安三中高三(上)第一次月考数学试卷+(文科)(解析版)

2016-2017学年河北省邯郸市武安三中高三（上）第一次月考数学试卷（文科）一、选择题：（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填涂在答题卡上．）1．（5分）已知集合P={2，3，4，5，6}，Q={3，5，7}，若M=P∩Q，则M的子集个数为（）A．5 B．4 C．3 D．22．（5分）已知集合A={x|x2﹣2x﹣3≤0}，B={x|y=ln（2﹣x）}，则A∩B=（）A．（1，3）B．（1，3]C．[﹣1，2）D．（﹣1，2）3．（5分）已知命题p：∀x∈R，sinx≤1，则（）A．￢p：∂x0∈R，sinx0≥1 B．￢p：∀x∈R，sinx≥1C．￢p：∂x0∈R，sinx0＞1 D．￢p：∀x∈R，sinx＞14．（5分）已知函数f（x）满足f（2x）=x，则f（3）=（）A．log23 B．log32 C．ln2 D．ln35．（5分）如果函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，2]上单调递减，那么实数a的取值范围是（）A．a≤﹣2 B．a≥﹣2 C．a≤﹣1 D．a≥16．（5分）已知函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，则函数y=f（x）+2图象恒过点的坐标为（）A．（1，0）B．（0，1）C．（1，2）D．（0，3）7．（5分）已知方程|2x﹣1|=a有两个不等实根，则实数a的取值范围是（）A．（﹣∞，0）B．（1，2）C．（0，+∞）D．（0，1）8．（5分）下列函数中，在其定义域内既是奇函数又是单调递增的函数是（）A．y=﹣B．y=3﹣x﹣3x C．y=x|x|D．y=x3﹣x9．（5分）三个数0.76，60.7，log0.76的大小关系为（）A．0.76＜log0.76＜60.7B．0.76＜60.7＜log0.76C．log0.76＜60.7＜0.76D．log0.76＜0.76＜60.710．（5分）函数f（x）=零点的取值范围是（）A． B．C．D．11．（5分）已知函数f（x）=x3﹣3ax+，若函数y=f（x）的极小值为0，则a的值为（）A．B．﹣C．D．﹣12．（5分）已知函数y=f（x）是定义在R上的奇函数，且当x∈（﹣∞，0）时不等式f（x）+xf′（x）＜0成立，若a=3f（3），b=﹣2f（﹣2），c=f（1），则a，b，c的大小关系是（）A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b二、填空题（本大题共4个小题，每小题5分，共20分，在每小题给出横线上填上正确结果）13．（5分）若不等式|x﹣1|＜a成立的充分条件是0＜x＜4，则实数a的取值范围是．14．（5分）若幂函数f（x）=（m2﹣3m+3）•x的图象不过原点，则m的值为．15．（5分）函数f（x）=lnx的图象在点x=1处的切线方程是．16．（5分）已知f（x）=x3+2xf′（1），则f′（1）=．三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（10分）已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}，若A⊆∁R B，求实数m的取值范围．18．（12分）设p：2x2﹣x﹣1≤0，q：x2﹣（2a﹣1）x+a（a﹣1）≤0，若非q是非p的必要不充分条件，求实数a的取值范围．19．（12分）设f（x）是定义在[﹣3，3]上的偶函数，当0≤x≤3时，f（x）单调递减，若f（1﹣2m）＜f（m）成立，求m的取值范围．20．（12分）已知函数f（x）=lg（+a）为奇函数．（I）求实数a的值；（II）求不等式f（x）＞0的解集．21．（12分）记函数f（x）=的定义域为A，g（x）=lg[（x﹣a﹣1）（2a﹣x）]（a＜1）的定义域为B．（1）求A；（2）若B⊆A，求实数a的取值范围．22．（12分）函数f（x）=lnx﹣ax2﹣2x．（Ⅰ）当a=3时，求f（x）的单调区间；（Ⅱ）若∀a∈（﹣1，+∞），∂x∈（1，e），有f（x）﹣b＜0，求实数b的取值范围．2016-2017学年河北省邯郸市武安三中高三（上）第一次月考数学试卷（文科）参考答案与试题解析一、选择题：（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填涂在答题卡上．）1．（5分）（2016•漳州模拟）已知集合P={2，3，4，5，6}，Q={3，5，7}，若M=P∩Q，则M的子集个数为（）A．5 B．4 C．3 D．2【分析】求出P与Q的交集确定出M，即可求出M子集的个数．【解答】解：∵P={2，3，4，5，6}，Q={3，5，7}，∴M=P∩Q={3，5}，则M的子集个数为22=4．故选：B．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）（2016•大庆校级二模）已知集合A={x|x2﹣2x﹣3≤0}，B={x|y=ln（2﹣x）}，则A∩B=（）A．（1，3）B．（1，3]C．[﹣1，2）D．（﹣1，2）【分析】化简集合A、B，求出A∩B即可．【解答】解：∵集合A={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3}=[﹣1，3]，B={x|y=ln（2﹣x）}={x|2﹣x＞0}={x|x＜2}=（﹣∞，2）；∴A∩B=[﹣1，2）．故选：C．【点评】本题考查了集合的化简与运算问题，是基础题目．3．（5分）（2015秋•曲沃县校级期末）已知命题p：∀x∈R，sinx≤1，则（）A．￢p：∂x0∈R，sinx0≥1 B．￢p：∀x∈R，sinx≥1C．￢p：∂x0∈R，sinx0＞1 D．￢p：∀x∈R，sinx＞1【分析】利用“￢p”即可得出．【解答】解：∵命题p：∀x∈R，sinx≤1，∴￢p：∂x0∈R，sinx0＞1．故选：C．【点评】本题考查了“非命题”的意义，考查了推理能力，属于基础题．4．（5分）（2016•漳州模拟）已知函数f（x）满足f（2x）=x，则f（3）=（）A．log23 B．log32 C．ln2 D．ln3【分析】用换元法，设2x=t，则x=log2t，求出解析式f（t），计算f（3）的值即可．【解答】解：设2x=t，∴x=log2t，∴f（t）=log2t，即f（x）=log2x；∴f（3）=log23．故选：A．【点评】本题考查了利用换元法求函数解析式以及利用解析式求函数值的应用问题，是基础题目．5．（5分）（2015秋•贵阳校级期中）如果函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，2]上单调递减，那么实数a的取值范围是（）A．a≤﹣2 B．a≥﹣2 C．a≤﹣1 D．a≥1【分析】求出二次函数的对称轴，根据单调区间与对称轴之间的关系建立条件，即可求出a的取值范围．【解答】解：∵函数f（x）=x2+2（a﹣1）x+2∴二次函数的对称轴为x==1﹣a，抛物线开口向上，∴函数在（﹣∞，1﹣a]上单调递减，要使f（x）在区间（﹣∞，2]上单调递减，则对称轴1﹣a≥2，解得a≤﹣1．故选：C．【点评】本题主要考查二次函数的图象和性质，根据二次函数单调性与对称轴之间的关系是解决本题的关键．6．（5分）（2015秋•贵阳校级期中）已知函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，则函数y=f （x）+2图象恒过点的坐标为（）A．（1，0）B．（0，1）C．（1，2）D．（0，3）【分析】根据对数函数的反函数是指数函数，写出f（x）的解析式，再求函数y=f（x）+2图象恒过点的坐标．【解答】解：∵函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，∴f（x）=a x，它的图象恒过点（0，1），∴函数y=f（x）+2的图象恒过点（0，3）．故选：D．【点评】本题考查了指数函数与对数函数的图象与性质的应用问题，是基础题目．7．（5分）（2014秋•余姚市校级期中）已知方程|2x﹣1|=a有两个不等实根，则实数a的取值范围是（）A．（﹣∞，0）B．（1，2）C．（0，+∞）D．（0，1）【分析】若关于x的方程|2x﹣1|=a有两个不等实数根，则函数y=|2x﹣1|的图象与y=a有两个交点，画出函数y=|2x﹣1|的图象，数形结合可得实数a的取值范围．【解答】解：若关于x的方程|2x﹣1|=a有两个不等实数根，则y=|2x﹣1|的图象与y=a有两个交点，函数y=|2x﹣1|的图象如下图所示：由图可得，当a∈（0，1）时，函数y=|2x﹣1|的图象与y=a有两个交点，故实数a的取值范围是（0，1），故选：D【点评】本题主要考查方程个数的判断，将方程转化为函数，利用函数图象的交点个数，即可判断方程根的个数，利用数形结合是解决此类问题的基本方法．8．（5分）（2016•太原二模）下列函数中，在其定义域内既是奇函数又是单调递增的函数是（）A．y=﹣B．y=3﹣x﹣3x C．y=x|x|D．y=x3﹣x【分析】先求出函数的定义域，再验证f（﹣x）和f（x）的关系判断奇偶性，最后利用基本初等函数判定单调性．【解答】解：对于A，y=的定义域为{x|x≠0}，是奇函数，但在定义域上不单调，不满足条件；对于B，y=3﹣x﹣3x的定义域为R，奇函数，是定义域上单调减函数，不满足条件；对于C，y=x|x|的定义域为R，满足f（﹣x）=﹣f（x），是奇函数，是定义域R上的单调增函数，满足题意；对于D，f（x）=x3﹣x的定义域为R，满足f（﹣x）=﹣f（x），是奇函数，在R上不是单调函数，不满足条件．故选：C．【点评】本题考查了函数的奇偶性和单调性的应用问题，解题时应先考虑定义域，再判定奇偶性与单调性，是基础题目．9．（5分）（2011•湖北校级模拟）三个数0.76，60.7，log0.76的大小关系为（）A．0.76＜log0.76＜60.7B．0.76＜60.7＜log0.76C．log0.76＜60.7＜0.76D．log0.76＜0.76＜60.7【分析】由对数函数的图象和性质，可得到log0.76＜0，再指数函数的图象和性质，可得0.76＜1，60.7＞1从而得到结论．【解答】解：由对数函数y=log0.7x的图象和性质可知：log0.76＜0由指数函数y=0.7x，y=6x的图象和性质可知0.76＜1，60.7＞1∴log0.76＜0.76＜60.7故选D【点评】本题主要考查指数函数，对数函数的图象和性质，在比较大小中往往转化为函数的单调性或图象分面来解决．10．（5分）（2014秋•路南区校级期中）函数f（x）=零点的取值范围是（）A． B．C．D．【分析】直接求出x=0，，，，1的函数值，即可判断零点所在的区间．【解答】解：因为f（0）=1，f（）=＞0f（）=＞0f（）=＜0，f（1）=﹣．所以，函数f（x）=零点的取值范围是：．故选C．【点评】本题考查函数的零点存在定理的应用，注意函数值与0的比较，指数函数以及幂函数的基本性质的应用．11．（5分）（2016•包头二模）已知函数f（x）=x3﹣3ax+，若函数y=f（x）的极小值为0，则a的值为（）A．B．﹣C．D．﹣【分析】求导，分类当a≤0，无极值，a＞0，根据函数的单调性求得当x=时，取极小值，即f（）=a﹣3a+=0，即可求得a的值．【解答】解：f（x）=x3﹣3ax+，f′（x）=3x2﹣3a，当a≤0，f′（x）≥0，恒成立，函数y=f（x）无极值，当a＞0，令f′（x）=0，解得：x=，当f′（x）＞0，解得x＞，当f′（x）＜0，解得0＜x＜，∴函数在（0，）单调递减，在（，+∞）单调递增，∴x=时，取极小值，∴f（）=a﹣3a+=0，解得：a=，故选：A．【点评】本题考查利用导数研究函数的单调性及极值，考查运算能力，属于基础题．12．（5分）（2016春•曲阜市校级期中）已知函数y=f（x）是定义在R上的奇函数，且当x∈（﹣∞，0）时不等式f（x）+xf′（x）＜0成立，若a=3f（3），b=﹣2f（﹣2），c=f（1），则a，b，c的大小关系是（）A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b【分析】构造函数F（x）=xf（x），求导数，判断单调性求解．【解答】解：令函数F（x）=xf（x），则F′（x）=f（x）+xf′（x）∵f（x）+xf′（x）＜0，∴F（x）=xf（x），x∈（﹣∞，0）单调递减，∵y=f（x）是定义在R上的奇函数，∴F（x）=xf（x），在（﹣∞，0）上为减函数，可知F（x）=xf（x），（0，+∞）上为增函数∵a=3•f（3），b=﹣2f（﹣2），c=f（1），∴a=F（﹣3），b=F（﹣2），c=F（﹣1）∴F（﹣3）＞F（﹣2）＞F（﹣1），即a＞b＞c．故选：A．【点评】本题考查复合函数的求导，导数在单调性中的应用，考查学生分析解决问题的能力，属于中档题．二、填空题（本大题共4个小题，每小题5分，共20分，在每小题给出横线上填上正确结果）13．（5分）（2015•潍坊校级模拟）若不等式|x﹣1|＜a成立的充分条件是0＜x＜4，则实数a的取值范围是[3，+∞）．【分析】先求出不等式|x﹣1|＜a的解集为集合B，再根据条件可知{x|0＜x＜4}⊂B，建立关于a的不等式组，解之从而确定a的取值范围．【解答】解：|x﹣1|＜a⇒1﹣a＜x＜a+1由题意可知﹣≤x＜0 0＜x＜4是1﹣a＜x＜a+1成立的充分不必要条件∴解得a≥3∴实数a的取值范围是[3，+∞）故答案为：[3，+∞）【点评】本题考查充分不必要条件的应用，解题时要注意含绝对值不等式的解法和应用，属于基础题．14．（5分）（2016•武汉校级模拟）若幂函数f（x）=（m2﹣3m+3）•x的图象不过原点，则m的值为m=1或m=2．【分析】由幂函数的图象不过原点，知，由此能求出实数m 的值．【解答】解：∵幂函数的图象不过原点，∴，解得m=1或m=2．故答案为：m=1或m=2．【点评】本题考查幂函数的性质和应用，解题时要认真审题，仔细解答．15．（5分）（2012秋•增城市期末）函数f（x）=lnx的图象在点x=1处的切线方程是y=x﹣1．【分析】先x=1代入解析式求出切点的坐标，再求出函数的导数后代入求出f′（1），即为所求的切线斜率，再代入点斜式进行整理即可．【解答】解：把x=1代入f（x）=lnx得，f（1）=ln1=0，∴切点的坐标为：（1，0），由f′（x）=（lnx）′=，得在点x=1处的切线斜率k=f′（1）=1，∴在点x=1处的切线方程为：y=x﹣1，故答案为：y=x﹣1．【点评】本题考查了导数的几何意义和直线点斜式方程，关键求出某点处切线的斜率即该点处的导数值，还有切点的坐标，利用切点在曲线上和切线上．16．（5分）（2016秋•武安市校级月考）已知f（x）=x3+2xf′（1），则f′（1）=﹣3．【分析】求函数的导数，令x=0即可得到结论．【解答】解：函数的导数f′（x）=3x2+2f′（1），令x=1，则f′（1）=3+2f′（1），解得f′（1）=﹣3，故答案为：﹣3【点评】本题主要考查到导数的计算，利用导数公式进行求解是解决本题的关键．三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（10分）（2016秋•武安市校级月考）已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}，若A⊆∁R B，求实数m的取值范围．【分析】根据一元二次不等式的解法，对A，B集合中的不等式进行因式分解，从而解出集合A，B，再根据A⊆C R B，利用子集的定义和补集的定义，列出不等式进行求解．【解答】解：由已知得：A={x|﹣1≤x≤3}，B={x|m﹣2≤x≤m+2}．∴C R B={x|x＜m﹣2，或x＞m+2}∵A⊆C R B，∴m﹣2＞3，或m+2＜﹣1，∴m＞5，或m＜﹣3．【点评】此题主要考查集合的定义及集合的交集及补集运算，一元二次不等式的解法及集合间的交、并、补运算是高考中的常考内容，要认真掌握．18．（12分）（2016秋•武安市校级月考）设p：2x2﹣x﹣1≤0，q：x2﹣（2a﹣1）x+a（a﹣1）≤0，若非q 是非p的必要不充分条件，求实数a的取值范围．【分析】分别化简p，q，利用非q是非p的必要不充分条件，即q是p的充分不必要条件，即可得出．【解答】解：由2x2﹣x﹣1≤0得．记P=．由x2﹣（2a﹣1）x+a（a﹣1）≤0得a﹣1≤x≤a．记Q=[a﹣1，a]．因为非q是非p的必要不充分条件，即q是p的充分不必要条件，得：Q是P的真子集，a﹣1≥﹣，且a≤1，得．【点评】本题考查了简易逻辑的判定方法、集合之间的关系，考查了推理能力与计算能力，属于中档题．19．（12分）（2015秋•鞍山校级期末）设f（x）是定义在[﹣3，3]上的偶函数，当0≤x≤3时，f（x）单调递减，若f（1﹣2m）＜f（m）成立，求m的取值范围．【分析】根据函数奇偶性和单调性的关系将不等式进行转化，建立不等式关系进行求解即可．【解答】解：∵f（x）是定义在[﹣3，3]上的偶函数，∴f（1﹣2m）＜f（m）等价为f（|1﹣2m|）＜f（|m|），∵当0≤x≤3时，f（x）单调递减，∴，∴，∴，解得．【点评】本题主要考查不等式的求解，根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键．20．（12分）（2015秋•大庆校级期末）已知函数f（x）=lg（+a）为奇函数．（I）求实数a的值；（II）求不等式f（x）＞0的解集．【分析】（I）利用f（0）=lg（2+a）=0，求实数a的值；（II）不等式f（x）＞0可化为不等式lg（﹣1）＞0，即可求不等式f（x）＞0的解集．【解答】解：（I）∵函数f（x）=lg（+a）为奇函数，∴f（0）=lg（2+a）=0，∴a=﹣1；（II）不等式f（x）＞0可化为不等式lg（﹣1）＞0，∴﹣1＞1，∴＞0，∴﹣10＜x＜0，∴不等式f（x）＞0的解集为{x|﹣10＜x＜0}．【点评】本题考查奇函数的性质，考查解不等式的能力，正确求出a是关键．21．（12分）（2012•信阳一模）记函数f（x）=的定义域为A，g（x）=lg[（x﹣a﹣1）（2a﹣x）]（a＜1）的定义域为B．（1）求A；（2）若B⊆A，求实数a的取值范围．【分析】（1）令被开方数大于等于零，列出不等式进行求解，最后需要用集合或区间的形式表示出来；（2）先根据真数大于零，求出函数g（x）的定义域，再由B⊆A和a＜1求出a的范围．【解答】解：（1）由2﹣≥0，得≥0，解得，x＜﹣1或x≥1，即A=（﹣∞，﹣1）∪[1，+∞），（2）由（x﹣a﹣1）（2a﹣x）＞0，得（x﹣a﹣1）（x﹣2a）＜0，∵a＜1，∴a+1＞2a．∴B=（2a，a+1），∵B⊆A，∴2a≥1或a+1≤﹣1，即a≥或a≤﹣2，∵a＜1，∴≤a＜1或a≤﹣2，故当B⊆A时，实数a的取值范围是（﹣∞，﹣2]∪[，1）．【点评】本题是有关集合和函数的综合题，涉及了集合子集的运算，函数定义域求法的法则，如：被开方数大于等于零、对数的真数大于零、分母不为零等等．22．（12分）（2016春•桂林校级期中）函数f（x）=lnx﹣ax2﹣2x．（Ⅰ）当a=3时，求f（x）的单调区间；（Ⅱ）若∀a∈（﹣1，+∞），∂x∈（1，e），有f（x）﹣b＜0，求实数b的取值范围．【分析】（Ⅰ）当a=3时，求得f（x）的解析式，令f′（x）＞0，求得函数的单调递增区间，f′（x）＜0，求得f（x）的单调递减区间；（2）将原不等式转化成b＞f（x）的最小值，由函数性质可知h（a）=﹣ax2﹣2x+lnx在（﹣1，+∞）上是减函数，可知b≥x2﹣2x+lnx，构造辅助函数g（x）=x2﹣2x+lnx，求导，根据函数的单调性，求得g （x）的最小值，即可求得实数b的取值范围．【解答】解：（Ⅰ）由当a=3时，f（x）=lnx﹣x2﹣2x．求导f′（x）=﹣（x＞0），令f′（x）=0，解得：x=，∴x∈（0，）时，f′（x）＞0，f（x）单调递增，x∈（，+∞）时，f′（x）＜0，f（x）单调递减，∴f（x）的单调递增区间（0，），单调递减区间为（，+∞）；..…（6分）（Ⅱ）由∀a∈（﹣1，+∞），lnx﹣ax2﹣2x＜b恒成立，则b＞f（x）的最小值，…（7分）由函数h（a）=lnx﹣ax2﹣2x=﹣ax2﹣2x+lnx在（﹣1，+∞）上是减函数，∴h（a）＜h（﹣1）=x2﹣2x+lnx，∴b≥x2﹣2x+lnx，..…（8分）由∂x∈（1，e），使不等式b≥x2﹣2x+lnx成立，∴．…（10分）令g（x）=x2﹣2x+lnx，求导g′（x）=x﹣2﹣≥0，∴函数g（x）在（1，e）上是增函数，于是，故，即b的取值范围是…（12分）【点评】本题考查导数知识的运用，考查利用函数的导数研究函数单调性及极值，考查存在性问题的研究，考查转化思想，属于中档题．2017年1月8日。

河北省武安市第三中学高三数学上学期第一次月考试题

武安三中高三年级第一次月考（理数）考试范围：集合与简易逻辑，函数，极坐标与参数方程考试时间：120分钟一、选择题（本大题共12小题，每小题5分，共60分）1、已知全集{}1,2,3,4U =,集合{}{}1,2,2,3A B ==,则()U C A B =U （） A ．{}2 B ．{}3 C ．{}2,3 D ．{}2,3,42、已知集合{}{}21,2,|43S T x x x ==<-,则S T =I （） A ．{}1 B ．{}2 C ．1 D ．23、设20.320.3,2,log 0.3,,,a b c a b c ===则的大小关系为（）A ．c a b <<B ．c b a <<C ．a b c <<D ．a c b << 4、命题“2,x R x ∃∈是无理数”的否定是（） A ．2,x R x ∃∉不是无理数 B ．2,x R x ∃∈不是无理数 C ．2,x R x ∀∉不是无理数 D ．2,x R x ∀∈不是无理数5、若函数()f x 定义域为R ，则“函数()f x 是奇函数”是“(0)0f =”的（） A ．必要不充分条件 B ．充分不必要条件 C ．充要条件 D ．既不充分也不必要6、下列函数中，在其定义域内既是奇函数又单调递增的函数是 A ．1y x=-B ．33x x y -=-C ．y x x =D ．3y x x =- 7、点M 的直角坐标)1,3(-化成极坐标为（）A.)65,2(π B.)32,2(π C.)35,2(π D.)611,2(π 8、曲线的极坐标方程θρsin 4=化为直角坐标方程为（）A.4)2(22=++y x B.4)2(22=-+y xC.4)2(22=+-y x D.4)2(22=++y x9、函数y ＝xxa x（0＜a ＜1）的图象的大致形状是（）10、函数34)(-+=x e x f x的零点所在的区间（）A.)0,41(-B.)410(，C.)21,41(D.)43,21( 11、已知函数()f x 关于直线2x =-对称，且周期为2，当[3,2]x ∈--时，2()(2)f x x =+，则5()2f =（）A ．0B ．14 C ．116D ．1 12、设()f x 是奇函数，且在(0,)+∞内是增函数，又(3)0f -=，则()0x f x ⋅<的解集是（） A ．{}|303x x x -<<>或 B ．{}|303x x x <-<<或 C ．{}|33x x x <->或 D ．{}|3003x x x -<<<<或二、填空题（本大题共4小题，每小题5分，共20分）13、已知{1,2,3,4}A ⊆，且A 中至少有一个偶数，则这样的A 有______个．14、参数方程4125x t y t =+⎧⎨=--⎩（t 为参数）化为普通方程为____________________．15、已知函数142log ,1()24,1xx x f x x +>⎧⎪=⎨⎪+≤⎩，则1(())2f f = 。

2013届高三上册数学文科期中考试卷(含答案)

2013届高三上册数学文科期中考试卷(含答案)包三十三中2012-2013学年第一学期期中Ⅱ考试高三年级数学（文科）试卷命题：杨翠梅审题：教科室2012.11.14本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

本卷满分150分，考试时间120分钟。

第Ⅰ卷一.选择题：本卷共12小题，每题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.函数的定义域是（）A．B．C．D．2.下列函数中，既是奇函数又是增函数的为（）A.B.C.D.3.已知直线的倾斜角为，则=（）A.B.C.D.4.曲线在点P(1，12)处的切线与y轴交点的纵坐标是()A.-9B.-3C.9D.155.公比为的等比数列的各项都是正数，且，则（）A.B.C.D.6.已知变量满足约束条件，则目标函数的取值范围是()A.B.C.D.7.设平面与平面相交于直线，直线在平面内，直线在平面内，且，则“”是“”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件8.某几何体的三视图如图所示，它的体积为（）A．12πB.45πC.57πD.81π9.△ABC中，AB边的高为CD，若，则（）A.B.C.D.10.已知，(0，π)，则=（）A.1B.C.D.111.设是椭圆的左、右焦点，为直线上一点，是底角为的等腰三角形，则的离心率为（）A.B.C.D.12.函数则()A.在单调递增，其图象关于直线对称B.在单调递增，其图象关于直线对称C.在单调递减，其图象关于直线对称D.在单调递减，其图象关于直线对称第Ⅱ卷二.填空题：本大题共4个小题，每小题5分，共20分，把答案填在题中横线上.13.已知是等差数列，，表示的前项和，则使得达到最大值的是_______.14.如图，已知正三棱柱的各条棱长都相等，是侧棱的中点，则异面直线所成的角的大小是15.在中，.若以为焦点的椭圆经过点，则该椭圆的离心率_______.16.不等式对任意实数恒成立，则实数的取值范围是_______.三.解答题：本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤.17.在中，角的对边分别是.已知，⑴求的值；⑵若，求边的值.18.已知为圆：的两条相互垂直的弦，垂足为，求四边形的面积的最大值.19.如图，四棱锥的底面是正方形，，点E在棱PB上.⑴求证：平面；⑵当，且E为PB的中点时，求AE与平面PDB所成的角的大小.20.等差数列中，且成等比数列，求数列前20项的和．21.设椭圆的右焦点为，过的直线与椭圆相交于两点，直线的倾斜角为，.⑴求椭圆的离心率；⑵如果，求椭圆的方程.22.设函数，曲线在点处的切线方程为．⑴求的解析式；⑵证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值．包三十三中2012-2013学年第一学期期中Ⅱ考试高三年级数学（文科）参考答案123456789101112CDBCBAACDACD13.2014.15.16.17.解⑴：由已知得由，得，即，两边平方得5分⑵由>0,得即由，得由，得则.由余弦定理得所以10分18.设分别是到的距离，则，当且仅当时上式取等号，即时上式取等号.19.⑴∵四边形ABCD是正方形，∴AC⊥BD，∵，∴PD⊥AC，∴AC⊥平面PDB，平面.6分⑵设AC∩BD=O，连接OE，由⑴知AC⊥平面PDB于O，∴∠AEO为AE与平面PDB所的角，∴O，E分别为DB、PB的中点，∴OE//PD，，又∵，∴OE⊥底面ABCD，OE⊥AO，在Rt△AOE中，，∴，即AE与平面PDB所成的角的大小为.12分20.解：设数列的公差为，则，，．3分由成等比数列得，即，整理得，解得或．7分当时，．9分当时，，于是．12分21.解：设，由题意知＜0，＞0.（Ⅰ）直线的方程为，其中.联立得解得因为，所以.即得离心率.……6分（Ⅱ）因为，所以.由得.所以，得a=3，.椭圆C的方程为.……12分22.解：⑴方程可化为．当时，．2分又，于是解得故．6分⑵设为曲线上任一点，由知曲线在点处的切线方程为，即．令得，从而得切线与直线的交点坐标为．令得，从而得切线与直线的交点坐标为．10分所以点处的切线与直线，所围成的三角形面积为．故曲线上任一点处的切线与直线，所围成的三角形的面积为定值，此定值为．12分。

2020-2021学年河北省邯郸市武安三中高三(上)第一次月考数学(文科)试题Word版含解析

2020-2021学年河北省邯郸市武安三中高三（上）第一次月考数学（文科）试题一、选择题：（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填涂在答题卡上．）1．（5分）已知集合P={2，3，4，5，6}，Q={3，5，7}，若M=P∩Q，则M的子集个数为（）A．5 B．4 C．3 D．22．（5分）已知集合A={x|x2﹣2x﹣3≤0}，B={x|y=ln（2﹣x）}，则A∩B=（）A．（1，3）B．（1，3] C．[﹣1，2）D．（﹣1，2）3．（5分）已知命题p：∀x∈R，sinx≤1，则（）A．￢p：∃x0∈R，sinx0≥1 B．￢p：∀x∈R，sinx≥1C．￢p：∃x0∈R，sinx0＞1 D．￢p：∀x∈R，sinx＞14．（5分）已知函数f（x）满足f（2x）=x，则f（3）=（）A．log23 B．log32 C．ln2 D．ln35．（5分）如果函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，2]上单调递减，那么实数a的取值范围是（）A．a≤﹣2 B．a≥﹣2 C．a≤﹣1 D．a≥16．（5分）已知函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，则函数y=f（x）+2图象恒过点的坐标为（）A．（1，0）B．（0，1）C．（1，2）D．（0，3）7．（5分）已知方程|2x﹣1|=a有两个不等实根，则实数a的取值范围是（）A．（﹣∞，0）B．（1，2）C．（0，+∞）D．（0，1）8．（5分）下列函数中，在其定义域内既是奇函数又是单调递增的函数是（）A．y=﹣B．y=3﹣x﹣3x C．y=x|x| D．y=x3﹣x9．（5分）三个数0.76，60.7，log0.76的大小关系为（）A．0.76＜log0.76＜60.7 B．0.76＜60.7＜log0.76C．log0.76＜60.7＜0.76 D．log0.76＜0.76＜60.710．（5分）函数f（x）=零点的取值范围是（）A． B．C．D．11．（5分）已知函数f（x）=x3﹣3ax+，若函数y=f（x）的极小值为0，则a的值为（）A．B．﹣ C．D．﹣12．（5分）已知函数y=f（x）是定义在R上的奇函数，且当x∈（﹣∞，0）时不等式f（x）+xf′（x）＜0成立，若a=3f（3），b=﹣2f（﹣2），c=f（1），则a，b，c的大小关系是（）A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b二、填空题（本大题共4个小题，每小题5分，共20分，在每小题给出横线上填上正确结果）13．（5分）若不等式|x﹣1|＜a成立的充分条件是0＜x＜4，则实数a的取值范围是．14．（5分）若幂函数f（x）=（m2﹣3m+3）•x的图象不过原点，则m的值为．15．（5分）函数f（x）=lnx的图象在点x=1处的切线方程是．16．（5分）已知f（x）=x3+2xf′（1），则f′（1）= ．三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（10分）已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}，若A⊆∁R B，求实数m的取值范围．18．（12分）设p：2x2﹣x﹣1≤0，q：x2﹣（2a﹣1）x+a（a﹣1）≤0，若非q是非p的必要不充分条件，求实数a的取值范围．19．（12分）设f（x）是定义在[﹣3，3]上的偶函数，当0≤x≤3时，f（x）单调递减，若f（1﹣2m）＜f （m）成立，求m的取值范围．20．（12分）已知函数f（x）=lg（+a）为奇函数．（I）求实数a的值；（II）求不等式f（x）＞0的解集．21．（12分）记函数f（x）=的定义域为A，g（x）=lg[（x﹣a﹣1）（2a﹣x）]（a＜1）的定义域为B．（1）求A；（2）若B⊆A，求实数a的取值范围．22．（12分）函数f（x）=lnx﹣ax2﹣2x．（Ⅰ）当a=3时，求f（x）的单调区间；（Ⅱ）若∀a∈（﹣1，+∞），∃x∈（1，e），有f（x）﹣b＜0，求实数b的取值范围．2020-2021学年河北省邯郸市武安三中高三（上）第一次月考数学（文科）试题参考答案一、选择题：（本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填涂在答题卡上．）1．（5分）已知集合P={2，3，4，5，6}，Q={3，5，7}，若M=P∩Q，则M的子集个数为（）A．5 B．4 C．3 D．2【分析】求出P与Q的交集确定出M，即可求出M子集的个数．【解答】解：∵P={2，3，4，5，6}，Q={3，5，7}，∴M=P∩Q={3，5}，则M的子集个数为22=4．故选：B．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）已知集合A={x|x2﹣2x﹣3≤0}，B={x|y=ln（2﹣x）}，则A∩B=（）A．（1，3）B．（1，3] C．[﹣1，2）D．（﹣1，2）【分析】化简集合A、B，求出A∩B即可．【解答】解：∵集合A={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3}=[﹣1，3]，B={x|y=ln（2﹣x）}={x|2﹣x＞0}={x|x＜2}=（﹣∞，2）；∴A∩B=[﹣1，2）．故选：C．【点评】本题考查了集合的化简与运算问题，是基础题目．3．（5分）已知命题p：∀x∈R，sinx≤1，则（）A．￢p：∃x0∈R，sinx0≥1 B．￢p：∀x∈R，sinx≥1C．￢p：∃x0∈R，sinx0＞1 D．￢p：∀x∈R，sinx＞1【分析】利用“￢p”即可得出．【解答】解：∵命题p：∀x∈R，sinx≤1，∴￢p：∃x0∈R，sinx0＞1．故选：C．【点评】本题考查了“非命题”的意义，考查了推理能力，属于基础题．4．（5分）已知函数f（x）满足f（2x）=x，则f（3）=（）A．log23 B．log32 C．ln2 D．ln3【分析】用换元法，设2x=t，则x=log2t，求出解析式f（t），计算f（3）的值即可．【解答】解：设2x=t，∴x=log2t，∴f（t）=log2t，即f（x）=log2x；∴f（3）=log23．故选：A．【点评】本题考查了利用换元法求函数解析式以及利用解析式求函数值的应用问题，是基础题目．5．（5分）如果函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，2]上单调递减，那么实数a的取值范围是（）A．a≤﹣2 B．a≥﹣2 C．a≤﹣1 D．a≥1【分析】求出二次函数的对称轴，根据单调区间与对称轴之间的关系建立条件，即可求出a的取值范围．【解答】解：∵函数f（x）=x2+2（a﹣1）x+2∴二次函数的对称轴为x==1﹣a，抛物线开口向上，∴函数在（﹣∞，1﹣a]上单调递减，要使f（x）在区间（﹣∞，2]上单调递减，则对称轴1﹣a≥2，解得a≤﹣1．故选：C．【点评】本题主要考查二次函数的图象和性质，根据二次函数单调性与对称轴之间的关系是解决本题的关键．6．（5分）已知函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，则函数y=f（x）+2图象恒过点的坐标为（）A．（1，0）B．（0，1）C．（1，2）D．（0，3）【分析】根据对数函数的反函数是指数函数，写出f（x）的解析式，再求函数y=f（x）+2图象恒过点的坐标．【解答】解：∵函数f（x）是函数y=log a x（a＞0且a≠1）的反函数，∴f（x）=a x，它的图象恒过点（0，1），∴函数y=f（x）+2的图象恒过点（0，3）．故选：D．【点评】本题考查了指数函数与对数函数的图象与性质的应用问题，是基础题目．7．（5分）已知方程|2x﹣1|=a有两个不等实根，则实数a的取值范围是（）A．（﹣∞，0）B．（1，2）C．（0，+∞）D．（0，1）【分析】若关于x的方程|2x﹣1|=a有两个不等实数根，则函数y=|2x﹣1|的图象与y=a有两个交点，画出函数y=|2x﹣1|的图象，数形结合可得实数a的取值范围．【解答】解：若关于x的方程|2x﹣1|=a有两个不等实数根，则y=|2x﹣1|的图象与y=a有两个交点，函数y=|2x﹣1|的图象如下图所示：由图可得，当a∈（0，1）时，函数y=|2x﹣1|的图象与y=a有两个交点，故实数a的取值范围是（0，1），故选：D【点评】本题主要考查方程个数的判断，将方程转化为函数，利用函数图象的交点个数，即可判断方程根的个数，利用数形结合是解决此类问题的基本方法．8．（5分）下列函数中，在其定义域内既是奇函数又是单调递增的函数是（）A．y=﹣B．y=3﹣x﹣3x C．y=x|x| D．y=x3﹣x【分析】先求出函数的定义域，再验证f（﹣x）和f（x）的关系判断奇偶性，最后利用基本初等函数判定单调性．【解答】解：对于A，y=的定义域为{x|x≠0}，是奇函数，但在定义域上不单调，不满足条件；对于B，y=3﹣x﹣3x的定义域为R，奇函数，是定义域上单调减函数，不满足条件；对于C，y=x|x|的定义域为R，满足f（﹣x）=﹣f（x），是奇函数，是定义域R上的单调增函数，满足题意；对于D，f（x）=x3﹣x的定义域为R，满足f（﹣x）=﹣f（x），是奇函数，在R上不是单调函数，不满足条件．故选：C．【点评】本题考查了函数的奇偶性和单调性的应用问题，解题时应先考虑定义域，再判定奇偶性与单调性，是基础题目．9．（5分）三个数0.76，60.7，log0.76的大小关系为（）A．0.76＜log0.76＜60.7 B．0.76＜60.7＜log0.76C．log0.76＜60.7＜0.76 D．log0.76＜0.76＜60.7【分析】由对数函数的图象和性质，可得到log0.76＜0，再指数函数的图象和性质，可得0.76＜1，60.7＞1从而得到结论．【解答】解：由对数函数y=log0.7x的图象和性质可知：log0.76＜0由指数函数y=0.7x，y=6x的图象和性质可知0.76＜1，60.7＞1∴log0.76＜0.76＜60.7故选D【点评】本题主要考查指数函数，对数函数的图象和性质，在比较大小中往往转化为函数的单调性或图象分面来解决．10．（5分）函数f（x）=零点的取值范围是（）A． B．C．D．【分析】直接求出x=0，，，，1的函数值，即可判断零点所在的区间．【解答】解：因为f（0）=1，f（）=＞0f（）=＞0f（）=＜0，f（1）=﹣．所以，函数f（x）=零点的取值范围是：．故选C．【点评】本题考查函数的零点存在定理的应用，注意函数值与0的比较，指数函数以及幂函数的基本性质的应用．11．（5分）已知函数f（x）=x3﹣3ax+，若函数y=f（x）的极小值为0，则a的值为（）A．B．﹣ C．D．﹣【分析】求导，分类当a≤0，无极值，a＞0，根据函数的单调性求得当x=时，取极小值，即f（）=a﹣3a+=0，即可求得a的值．【解答】解：f（x）=x3﹣3ax+，f′（x）=3x2﹣3a，当a≤0，f′（x）≥0，恒成立，函数y=f（x）无极值，当a＞0，令f′（x）=0，解得：x=，当f′（x）＞0，解得x＞，当f′（x）＜0，解得0＜x＜，∴函数在（0，）单调递减，在（，+∞）单调递增，∴x=时，取极小值，∴f（）=a﹣3a+=0，解得：a=，故选：A．【点评】本题考查利用导数研究函数的单调性及极值，考查运算能力，属于基础题．12．（5分）已知函数y=f（x）是定义在R上的奇函数，且当x∈（﹣∞，0）时不等式f（x）+xf′（x）＜0成立，若a=3f（3），b=﹣2f（﹣2），c=f（1），则a，b，c的大小关系是（）A．a＞b＞c B．c＞b＞a C．c＞a＞b D．a＞c＞b【分析】构造函数F（x）=xf（x），求导数，判断单调性求解．【解答】解：令函数F（x）=xf（x），则F′（x）=f（x）+xf′（x）∵f（x）+xf′（x）＜0，∴F（x）=xf（x），x∈（﹣∞，0）单调递减，∵y=f（x）是定义在R上的奇函数，∴F（x）=xf（x），在（﹣∞，0）上为减函数，可知F（x）=xf（x），（0，+∞）上为增函数∵a=3•f（3），b=﹣2f（﹣2），c=f（1），∴a=F（﹣3），b=F（﹣2），c=F（﹣1）∴F（﹣3）＞F（﹣2）＞F（﹣1），即a＞b＞c．故选：A．【点评】本题考查复合函数的求导，导数在单调性中的应用，考查学生分析解决问题的能力，属于中档题．二、填空题（本大题共4个小题，每小题5分，共20分，在每小题给出横线上填上正确结果）13．（5分）若不等式|x﹣1|＜a成立的充分条件是0＜x＜4，则实数a的取值范围是[3，+∞）．【分析】先求出不等式|x﹣1|＜a的解集为集合B，再根据条件可知{x|0＜x＜4}⊂B，建立关于a的不等式组，解之从而确定 a的取值范围．【解答】解：|x﹣1|＜a⇒1﹣a＜x＜a+1由题意可知﹣≤x＜0 0＜x＜4是1﹣a＜x＜a+1成立的充分不必要条件∴解得a≥3∴实数a的取值范围是[3，+∞）故答案为：[3，+∞）【点评】本题考查充分不必要条件的应用，解题时要注意含绝对值不等式的解法和应用，属于基础题．14．（5分）若幂函数f（x）=（m2﹣3m+3）•x的图象不过原点，则m的值为m=1或m=2 ．【分析】由幂函数的图象不过原点，知，由此能求出实数m的值．【解答】解：∵幂函数的图象不过原点，∴，解得m=1或m=2．故答案为：m=1或m=2．【点评】本题考查幂函数的性质和应用，解题时要认真审题，仔细解答．15．（5分）函数f（x）=lnx的图象在点x=1处的切线方程是y=x﹣1 ．【分析】先x=1代入解析式求出切点的坐标，再求出函数的导数后代入求出f′（1），即为所求的切线斜率，再代入点斜式进行整理即可．【解答】解：把x=1代入f（x）=lnx得，f（1）=ln1=0，∴切点的坐标为：（1，0），由f′（x）=（lnx）′=，得在点x=1处的切线斜率k=f′（1）=1，∴在点x=1处的切线方程为：y=x﹣1，故答案为：y=x﹣1．【点评】本题考查了导数的几何意义和直线点斜式方程，关键求出某点处切线的斜率即该点处的导数值，还有切点的坐标，利用切点在曲线上和切线上．16．（5分）已知f（x）=x3+2xf′（1），则f′（1）= ﹣3 ．【分析】求函数的导数，令x=0即可得到结论．【解答】解：函数的导数f′（x）=3x2+2f′（1），令x=1，则f′（1）=3+2f′（1），解得f′（1）=﹣3，故答案为：﹣3【点评】本题主要考查到导数的计算，利用导数公式进行求解是解决本题的关键．三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（10分）已知集合A={x|x2﹣2x﹣3≤0，x∈R}，B={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}，若A⊆∁R B，求实数m的取值范围．【分析】根据一元二次不等式的解法，对A，B集合中的不等式进行因式分解，从而解出集合A，B，再根据A⊆C R B，利用子集的定义和补集的定义，列出不等式进行求解．【解答】解：由已知得：A={x|﹣1≤x≤3}，B={x|m﹣2≤x≤m+2}．∴C R B={x|x＜m﹣2，或x＞m+2}∵A⊆C R B，∴m﹣2＞3，或m+2＜﹣1，∴m＞5，或m＜﹣3．【点评】此题主要考查集合的定义及集合的交集及补集运算，一元二次不等式的解法及集合间的交、并、补运算是高考中的常考内容，要认真掌握．18．（12分）设p：2x2﹣x﹣1≤0，q：x2﹣（2a﹣1）x+a（a﹣1）≤0，若非q是非p的必要不充分条件，求实数a的取值范围．【分析】分别化简p，q，利用非q是非p的必要不充分条件，即q是p的充分不必要条件，即可得出．【解答】解：由2x2﹣x﹣1≤0得．记P=．由x2﹣（2a﹣1）x+a（a﹣1）≤0得a﹣1≤x≤a．记Q=[a﹣1，a]．因为非q是非p的必要不充分条件，即q是p的充分不必要条件，得：Q是P的真子集，a﹣1≥﹣，且a≤1，得．【点评】本题考查了简易逻辑的判定方法、集合之间的关系，考查了推理能力与计算能力，属于中档题．19．（12分）设f（x）是定义在[﹣3，3]上的偶函数，当0≤x≤3时，f（x）单调递减，若f（1﹣2m）＜f （m）成立，求m的取值范围．【分析】根据函数奇偶性和单调性的关系将不等式进行转化，建立不等式关系进行求解即可．【解答】解：∵f（x）是定义在[﹣3，3]上的偶函数，∴f（1﹣2m）＜f（m）等价为f（|1﹣2m|）＜f（|m|），∵当0≤x≤3时，f（x）单调递减，∴，∴，∴，解得．【点评】本题主要考查不等式的求解，根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键．20．（12分）已知函数f（x）=lg（+a）为奇函数．（I）求实数a的值；（II）求不等式f（x）＞0的解集．【分析】（I）利用f（0）=lg（2+a）=0，求实数a的值；（II）不等式f（x）＞0可化为不等式lg（﹣1）＞0，即可求不等式f（x）＞0的解集．【解答】解：（I）∵函数f（x）=lg（+a）为奇函数，∴f（0）=lg（2+a）=0，∴a=﹣1；（II）不等式f（x）＞0可化为不等式lg（﹣1）＞0，∴﹣1＞1，∴＞0，∴﹣10＜x＜0，∴不等式f（x）＞0的解集为{x|﹣10＜x＜0}．【点评】本题考查奇函数的性质，考查解不等式的能力，正确求出a是关键．21．（12分）记函数f（x）=的定义域为A，g（x）=lg[（x﹣a﹣1）（2a﹣x）]（a＜1）的定义域为B．（1）求A；（2）若B⊆A，求实数a的取值范围．【分析】（1）令被开方数大于等于零，列出不等式进行求解，最后需要用集合或区间的形式表示出来；（2）先根据真数大于零，求出函数g（x）的定义域，再由B⊆A和a＜1求出a的范围．【解答】解：（1）由2﹣≥0，得≥0，解得，x＜﹣1或x≥1，即A=（﹣∞，﹣1）∪[1，+∞），（2）由（x﹣a﹣1）（2a﹣x）＞0，得（x﹣a﹣1）（x﹣2a）＜0，∵a＜1，∴a+1＞2a．∴B=（2a，a+1），∵B⊆A，∴2a≥1或a+1≤﹣1，即a≥或a≤﹣2，∵a＜1，∴≤a＜1或a≤﹣2，故当B⊆A时，实数a的取值范围是（﹣∞，﹣2]∪[，1）．【点评】本题是有关集合和函数的综合题，涉及了集合子集的运算，函数定义域求法的法则，如：被开方数大于等于零、对数的真数大于零、分母不为零等等．22．（12分）函数f（x）=lnx﹣ax2﹣2x．（Ⅰ）当a=3时，求f（x）的单调区间；（Ⅱ）若∀a∈（﹣1，+∞），∃x∈（1，e），有f（x）﹣b＜0，求实数b的取值范围．【分析】（Ⅰ）当a=3时，求得f（x）的解析式，令f′（x）＞0，求得函数的单调递增区间，f′（x）＜0，求得f（x）的单调递减区间；（2）将原不等式转化成b＞f（x）的最小值，由函数性质可知h（a）=﹣ax2﹣2x+lnx在（﹣1，+∞）上是减函数，可知b≥x2﹣2x+lnx，构造辅助函数g（x）=x2﹣2x+lnx，求导，根据函数的单调性，求得g （x）的最小值，即可求得实数b的取值范围．【解答】解：（Ⅰ）由当a=3时，f（x）=lnx﹣x2﹣2x．求导f′（x）=﹣（x＞0），令f′（x）=0，解得：x=，∴x∈（0，）时，f′（x）＞0，f（x）单调递增，x∈（，+∞）时，f′（x）＜0，f（x）单调递减，∴f（x）的单调递增区间（0，），单调递减区间为（，+∞）；..…（6分）（Ⅱ）由∀a∈（﹣1，+∞），lnx﹣ax2﹣2x＜b恒成立，则b＞f（x）的最小值，…（7分）由函数h（a）=lnx﹣ax2﹣2x=﹣ax2﹣2x+lnx在（﹣1，+∞）上是减函数，∴h（a）＜h（﹣1）=x2﹣2x+lnx，∴b≥x2﹣2x+lnx，..…（8分）由∃x∈（1，e），使不等式b≥x2﹣2x+lnx成立，∴．…（10分）令g（x）=x2﹣2x+lnx，求导g′（x）=x﹣2﹣≥0，∴函数g（x）在（1，e）上是增函数，于是，故，即b的取值范围是…（12分）【点评】本题考查导数知识的运用，考查利用函数的导数研究函数单调性及极值，考查存在性问题的研究，考查转化思想，属于中档题．。

河北省武安县高三数学上学期第四次月考试题文

武安市第三中学第四次月考文科数学试卷卷Ⅰ(选择题共60分)一．选择题（共12小题，每小题5分，计60分。

在每小题给出的四个选项中，只有一个选项正确）1、已知集合错误!未找到引用源。

，错误!未找到引用源。

则错误!未找到引用源。

( )A.错误!未找到引用源。

B.错误!未找到引用源。

C.错误!未找到引用源。

D.错误!未找到引用源。

2、已知i 是虚数单位，则复数错误!未找到引用源。

的虚部等于（）A.错误!未找到引用源。

B. 错误!未找到引用源。

C. 错误!未找到引用源。

D. 13、已知向量错误!未找到引用源。

，错误!未找到引用源。

，则错误!未找到引用源。

的最大值为（）A.1B. 错误!未找到引用源。

C.3D.94、在等差数列错误!未找到引用源。

中，前n 项的和为错误!未找到引用源。

，若错误!未找到引用源。

，则错误!未找到引用源。

（）A.54B.45C.36D.275、下列四个命题中的真命题为（） A. 错误!未找到引用源。

R ,使得错误!未找到引用源。

；B. 错误!未找到引用源。

R ,总有错误!未找到引用源。

；C. 错误!未找到引用源。

R , 错误!未找到引用源。

R ,错误!未找到引用源。

D. 错误!未找到引用源。

R , 错误!未找到引用源。

R ,错误!未找到引用源。

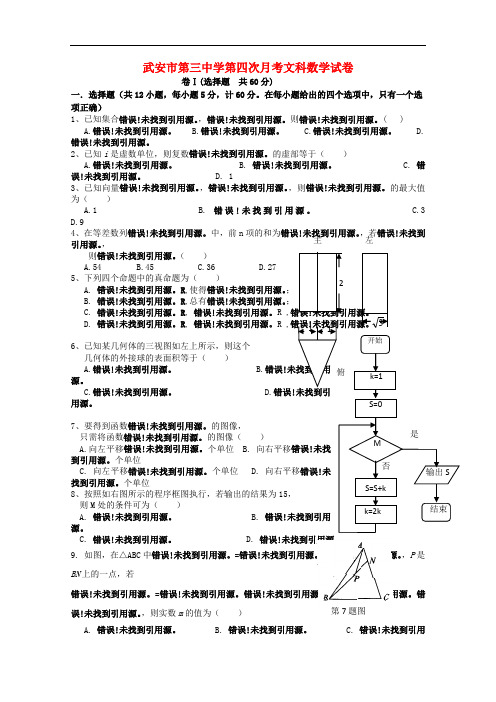
6、已知某几何体的三视图如左上所示，则这个几何体的外接球的表面积等于（）A.错误!未找到引用源。

B.错误!未找到引用源。

C.错误!未找到引用源。

D.错误!用源。

7、要得到函数错误!未找到引用源。

的图像，只需将函数错误!未找到引用源。

的图像（） A.向左平移错误!未找到引用源。

个单位 B. 向右平移错误!未找到引用源。

个单位 C. 向左平移错误!未找到引用源。

个单位 D. 向右平移错误!未找到引用源。

个单位 8、按照如右图所示的程序框图执行，若输出的结果为15，则M 处的条件可为（） A. 错误!未找到引用源。

B. 错误!未找到引用源。

2013-2014学年河北省衡水中学高三(上)第四次调考数学试卷(文科)

○…………外…………○…………装…………○…………订…………○…………线…………○……… 学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○……… 绝密★启用前 2013-2014学年河北省衡水中学高三（上）第四次调考数学试卷（文科）试卷副标题考试范围：xxx ；考试时间：120分钟；命题人：xxx 题号一二三四总分得分第I 卷（选择题）请点击修改第I 卷的文字说明评卷人得分一、选择题 1. 集合A={x∈Z|≤2x ≤2}，B={y|y=cosx ，x∈A}，则A∩B=（） A ．{1} B ．{0} C ．{0，1} D ．{-1，0，1} 2. 已知复数z 满足z=（i 为虚数单位），则复数所对应的点所在象限为（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3. 函数f （x ）=2lnx+x 2-bx+a （b ＞0，a∈R）在点（b ，f （b ））处的切线斜率的最小值是（） A ． B ．2 C ． D ．1 4. 若抛物线y 2=2px （p ＞0）上一点到焦点和抛物线对称轴的距离分别为10和6，则抛物线方程为（） A ．y 2=4x B ．y 2=36x C ．y 2=4x 或y 2=36x D ．y 2=8x 或y 2=32x 5. 已知数列{a n }，{b n }满足a 1=b 1=1，，则数列的前10项的和为（） A ． B ． C ． D ． 6. 如图，在正方体ABCD-A 1B 1C 1D 1中，M ，N 分别是BC 1，CD 1的中点，则下列说法错误的是（） A ．MN 与CC 1垂直 B ．MN 与AC 垂直 C ．MN 与BD 平行 D ．MN 与A 1B 1平行 7. 已知函数，则函数y=f （x ）的大致图象为（） A ． B ． C ． D ． 8. 已知某几何体的三视图如图所示，则该几何体的表面积等于（）A ．B ．160C ．64+32D ．88+8 9. 函数f （x ）=2sin （ωx+φ）（ω＞0）的部分图象如图，其中M （m ，0），N （n ，2），P （π，0），且mn ＜0，则f （x ）在下列哪个区间中是单调的（） A ．（0，） B ．（，） C ．（，） D ．（，π） 10. 点P 是双曲线（a ＞0，b ＞0）左支上的一点，其右焦点为F （c ，0），若M 为线段FP 的中点，且M 到坐标原点的距离为，则双曲线的离心率e 范围是（） A ．（1，8] B ． C ． D ．（2，3] 11. 两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线l 1：2x-y+a=0，l 2：2x-y+a 2+1=0和圆：x 2+y 2+2x-4=0相切，则a 的取值范围是（） A ．a ＞7或a ＜-3 B ． C ．-3≤a≤一或≤a≤7 D ．a≥7或a≤-3○…………外…………○…………装…………○…………订…………○…………线…………○………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※ ○…………内…………○…………装…………○…………订…………○…………线…………○……… 12. 在平面直角坐标系中，定义d （P ，Q ）=|x 1-x 2|+|y 1-y 2|为两点P （x 1，y 1），Q （x 2，y 2）之间的“折线距离”．在这个定义下，给出下列命题： ①到原点的“折线距离”等于1的点的集合是一个正方形； ②到原点的“折线距离”等于1的点的集合是一个圆； ③到M （-1，0），N （1，0）两点的“折线距离”相等的点的轨迹方程是x=0； ④到M （-1，0），N （1，0）两点的“折线距离”差的绝对值为1的点的集合是两条平行线．其中正确的命题有（） A ．1个 B ．2 个 C ．3 个 D ．4个第II 卷（非选择题）请点击修改第II 卷的文字说明评卷人得分二、填空题 1. 若直线y=2x 上存在点（x ，y ）满足约束条件，则实数m 的取值范围__________． 2. 设△ABC 的三个内角A 、B 、C 所对的边长依次为a 、b 、c ，若△ABC 的面积为S ，且S=a 2-（b-c ）2，则=__________． 3. 如图，已知球O 是棱长为1的正方体ABCD-A 1B 1C 1D 1的内切球，则平面ACD 1截球O 的截面面积为__________． 4. 直线l 过椭圆的左焦点F ，且与椭圆相交于P 、Q 两点，M 为PQ 的中点，O 为原点．若△FMO 是以OF 为底边的等腰三角形，则直线l 的方程为__________．评卷人得分三、其它1. 如图，AB 是圆O 的直径，C ，D 是圆O 上两点，AC 与BD 相交于点E ，GC ，GD 是圆O 的切线，点F 在DG 的延长线上，且DG=GF ．求证：（1）D 、E 、C 、F 四点共圆；（2）GE⊥AB．评卷人得分四、解答题1. 在△ABC 中，角A 、B 、C 所对的边为a 、b 、c ，且满足cos2A-cos2B=（1）求角B 的值；（2）若且b≤a，求的取值范围．2. 已知数列{a n }满足：a 1=20，a 2=7，a n+2-a n =-2（n∈N*）．（Ⅰ）求a 3，a 4，并求数列{a n }通项公式；（Ⅱ）记数列{a n }前2n 项和为S 2n ，当S 2n 取最大值时，求n 的值．3. （v0图4•郑州一模）右图所示的几何体AB0DF0中，△AB0，△DF0都是等边三角形，且所在平面平行，四边形B00D 是边长为v 的正方形，且所在平面垂直于平面AB0．○…………外…………○…………装…………○…………订…………○…………线…………○……… 学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○……… （Ⅰ）求几何体AB0DF0的体积；（Ⅱ）证明：平面AD0∥平面B0F ． 4. 如图，已知抛物线C ：y 2=2px 和⊙M：（x-4）2+y 2=1，过抛物线C 上一点H （x 0，y 0）（y 0≥1）作两条直线与⊙M 相切于A 、两点，分别交抛物线为E 、F 两点，圆心点M 到抛物线准线的距离为．（Ⅰ）求抛物线C 的方程；（Ⅱ）当∠AHB 的角平分线垂直x 轴时，求直线EF 的斜率；（Ⅲ）若直线AB 在y 轴上的截距为t ，求t 的最小值． 5. 已知函数f （x ）=lnx ，g （x ）=f （x ）+ax 2-3x ，函数g （x ）的图象在点（1，g （x ））处的切线平行于x 轴．（1）求a 的值；（2）求函数g （x ）的极小值；（3）设斜率为k 的直线与函数f （x ）的图象交于两点A （x 1，y 1），B （x 2，y 2），（x 1＜x 2），证明：＜k ＜． 6. 已知函数f （x ）=|x-1|．（1）解不等式f （x ）+f （x+4）≥8；（2）若|a|＜1，|b|＜1，且a≠0，求证：f （ab ）＞|a|f （）．参考答案一、选择题1．【答案】A【解析】试题分析：先化简集合A，再求集合B，利用交集运算求出结果．试题解析：∵集合A={x∈Z|≤2x≤2}={-1，0，1}B={y|y=cosx，x∈A}，∴B={cos1，1}∴A∩B={1}故选：A．2．【答案】A【解析】试题分析：由运算法则化简复数z，进而可得，可得其对应的点的坐标，可得答案．试题解析：化简可得z=====8-i，∴复数=8+i，对应的点为（8，1）在第一象限，故选：A3．【答案】A【解析】试题分析：根据题意和求导公式求出导数，求出切线的斜率为，再由基本不等式求出的范围，再求出斜率的最小值即可．试题解析：由题意得，f′（x）=+2x-b，∴在点（b，f（b））处的切线斜率是：k=f′（b）=，∵b＞0，∴f′（b）=≥，当且仅当时取等号，∴在点（b，f（b））处的切线斜率的最小值是，故选A．4．【答案】C【解析】试题分析：由抛物线上点P到的对称轴的距离6，设P的坐标为（x0，±6）．根据点P坐标适合抛物线方程及点P到焦点的距离为10，联列方程组，解之可得p与x0的值，从而得到本题的答案．试题解析：∵抛物线y2=2px（p＞0）上一点到的对称轴的距离6，∴设该点为P，则P的坐标为（x0，±6）∵P到抛物线的焦点F（，0）的距离为10∴由抛物线的定义，得x0+=10 (1)∵点P是抛物线上的点，∴2px0=36 (2)由（1）（2）联立，解得p=2，x0=2或p=18，x0=1则抛物线方程为y2=4x或y2=36x．故选：C．5．【答案】D【解析】由题意可得，所以数列{a n}是等差数列，且公差是2，{b n}是等比数列，且公比是2．又因为a1=1，所以a n=a1+（n-1）d=2n-1．所以=b1•22n-2=22n-2．设c n=，所以c n=22n-2，所以，所以数列{c n}是等比数列，且公比为4，首项为1．由等比数列的前n项和的公式得：其前10 项的和为．故选D．6．【答案】D【解析】试题分析：先利用三角形中位线定理证明MN∥BD，再利用线面垂直的判定定理定义证明MN与CC1垂直，由异面直线所成的角的定义证明MN与AC垂直，故排除A、B、C选D试题解析：如图：连接C1D，BD，在三角形C1DB中，MN∥BD，故C正确；∵CC1⊥平面ABCD，∴CC1⊥BD，∴MN与CC1垂直，故A正确；∵AC⊥BD，MN∥BD，∴MN与AC垂直，B正确；∵A1B1与BD异面，MN∥BD，∴MN与A1B1不可能平行，D错误故选D7．【答案】B【解析】试题分析：由函数不是奇函数图象不关于原点对称，排除A、C，由x＞0时，函数值恒正，排除D．试题解析：函数y=f（x）是一个非奇非偶函数，图象不关于原点对称，故排除选项A、C，又当x=-1时，函数值等于0，故排除D，故选 B．8．【答案】C【解析】由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥组成，三棱柱的底面是一个直角边长为4的直角三角形，高为8，即AD=DE=4，AB=8，FH=4，∴CF=，AE=，∴该几何体的表面积为==64+，故选：C．9．【答案】B【解析】试题分析：由题意得到三角函数的周期满足π＜T＜，然后取周期接近π和接近分别排除选项D、A、C，从而得到正确选项．试题解析：∵mn＜0，∴m，n异号，由图可知：m＜0，n＞0．又P（π，0），∴T＞π且，则π＜T＜．当周期无限接近π时，图中的最低点自左向右无限接近，∴f（x）在上先减后增不单调，排除D；当周期接近又小于时，图中最高点N的横坐标大于0小于，f（x）在上先增后减不单调，排除A；图中的最低点的横坐标大于小于，f（x）在上先减后增不单调，排除C．∴正确的答案为B．故选：B．10．【答案】B【解析】试题分析：直接利用双曲线的定义，结合三角形的中位线定理，推出a，b，c 的关系，求出双曲线的离心率．试题解析：设双曲线的左焦点为F1，因为点P是双曲线（a＞0，b＞0）左支上的一点，其右焦点为F（c，0），若M为线段FP的中点，且M到坐标原点的距离为，由三角形中位线定理可知：OM=PF1，PF1=PF-2a，PF≥a+c．所以，1．故选B．11．【答案】C【解析】试题分析：当两平行直线和圆相交时，由求得a 的范围，当两平行直线和圆相离时，由求得 a的取值范围．再把以上所求得的a的范围取并集后，再取此并集的补集，即得所求．试题解析：当两平行直线和圆相交时，有，解得-＜a ＜．当两平行直线和圆相离时，有，解得 a＜-3 或a＞7．故当两平行直线和圆相切时，把以上两种情况下求得的a的范围取并集后，再取此并集的补集，即得所求．故所求的a的取值范围是-3≤a≤一或≤a≤7，故选：C．12．【答案】C【解析】试题分析：先根据折线距离的定义分别表示出所求的集合，然后根据集合中绝对值的性质进行判定即可．试题解析：到原点的“折线距离”等于1的点的集合{（x，y）||x|+|y|=1}，是一个正方形，故①正确，②错误；到M（-1，0），N（1，0）两点的“折线距离”相等点的集合是{（x，y）||x+1|+|y|=|x-1|+|y|}，由|x+1|=|x-1|，解得x=0，∴到M（-1，0），N（1，0）两点的“折线距离”相等的点的轨迹方程是x=0，即③正确；到M（-1，0），N（1，0）两点的“折线距离”差的绝对值为1的点的集合{（x，y）||x+1|+|y|-|x-1|-|y|=±1}={（x，y）||x+1|-|x-1|=±1}，集合是两条平行线，故④正确；综上知，正确的命题为①③④，共3个．故选：C．二、填空题1．【答案】（-∞，1]【解析】由题意，由，可求得交点坐标为（1，2）要使直线y=2x上存在点（x，y）满足约束条件，如图所示．可得m≤1则实数m的取值范围（-∞，1]．故答案为：（-∞，1]．2．【答案】4【解析】∵△ABC的面积为S，且S=a2-（b-c）2=a2-b2-c2+2bc=bc•sinA，∴由余弦定理可得-2bc•cosA+2bc=bc•sinA，∴4-4cosA=sinA，∴==4，故答案为 4．3．【答案】【解析】试题分析：根据正方体和球的结构特征，判断出平面ACD1是正三角形，求出它的边长，再通过图求出它的内切圆的半径，最后求出内切圆的面积试题解析：根据题意知，平面ACD1是边长为的正三角形，且球与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点，故所求截面的面积是该正三角形的内切圆的面积，则由图得，△ACD1内切圆的半径是×tan30°=，则所求的截面圆的面积是π××=．故答案为：．4．【答案】【解析】试题分析：由椭圆的方程求出椭圆的左焦点，由题意可知直线l的斜率存在且不等于0，写出直线l的方程，和椭圆方程联立后利用根与系数关系得到PQ中点M的横坐标，再由△FMO是以OF为底边的等腰三角形得到M的横坐标，两数相等求出k的值，则直线l的方程可求．试题解析：由，得a2=2，b2=1，所以c2=a2-b2=2-1=1．则c=1，则左焦点F（-1，0）．由题意可知，直线l的斜率存在且不等于0，则直线l的方程为y=kx+k．设l与椭圆相交于P（x1，y1）、Q（x2，y2），联立，得：（2k2+1）x2+4k2x+2k2-2=0．所以．则PQ的中点M的横坐标为．因为△FMO是以OF为底边的等腰三角形，所以．解得：．所以直线l的方程为．故答案为．三、其它1．【答案】见答案解析【解析】试题分析：（Ⅰ）如图，连接OC，OD，则OC⊥CG，OD⊥DG，可得四点O，D，G，C共圆．设∠CAB=∠1，∠DBA=∠2，∠ACO=∠3，可得∠COB=2∠1，∠DOA=2∠2．于是∠DGC=180°-∠DOC=2（∠1+∠2）．利用切线长定理可得DG=CG，而DG=GF，可得GF=GC．从而可得∠F=∠1+∠2．可得∠DEC+∠F=180°，即可证明．（Ⅱ）延长GE交AB于H．由GD=GC=GF，可得点G是经过D，E，C，F四点的圆的圆心．可得GE=GC，∠GCE=∠GEC．又∠GCE+∠3=90°，∠1=∠3，可得∠AEH+∠1=90°，进而得出证明．试题解析：（Ⅰ）如图，连接OC，OD，则OC⊥CG，OD⊥DG，∴四点O，D，G，C共圆．设∠CAB=∠1，∠DBA=∠2，∠ACO=∠3，∠COB=2∠1，∠DOA=2∠2．∴∠DGC=180°-∠DOC=2（∠1+∠2）．∵DG=GF，DG=CG．∴GF=GC．∴∠GCF=∠F．∵∠DGC=2∠F，∴∠F=∠1+∠2．又∵∠DEC=∠AEB=180°-（∠1+∠2），∴∠DEC+∠F=180°，∴D，E，C，F四点共圆．（Ⅱ）延长GE交AB于H．∵GD=GC=GF，∴点G是经过D，E，C，F四点的圆的圆心．∴GE=GC，∴∠GCE=∠GEC．又∵∠GCE+∠3=90°，∠1=∠3，∴∠GEC+∠3=90°，∴∠AEH+∠1=90°，∴∠EHA=90°，即GE⊥AB．四、解答题1．【答案】见答案解析【解析】试题分析：（1）由条件利用三角恒等变换化简可得2-2sin2A-2cos2B=-2sin2A，求得cos2B 的值，可得cosB的值，从而求得B的值．（2）由b=≤a，可得B=60°．再由正弦定理可得．试题解析：（1）在△ABC中，∵cos2A-cos2B==2（cosA+sinA）（cosA-sinA）=2（cos2A-sin2A）=cos2A-sin2A=-2sin2A．又因为 cos2A-cos2B=1-2sin2A-（2cos2B-1）=2-2sin2A-2cos2B，∴2-2sin2A-2cos2B=-2sin2A，∴cos2B=，∴cosB=±，∴B=或．（2）∵b=≤a，∴B=，由正弦====2，得a=2sinA，c=2sinC，故a-c=2sinA-sinC=2sinA-sin（-A）=sinA-cosA=sin（A-），因为b≤a，所以≤A＜，≤A-＜，所以a-c=sin（A-）∈[，）．2．【答案】见答案解析【解析】试题分析：（I）由a1=20，a2=7，a n+2-a n=-2，分布令n=1，2即可求解a3，a4，由题意可得数列{a n}奇数项、偶数项分布是以-2为公差的等差数列，结合等差数列的通项公式，分n为奇数，n为偶数两种情况可求a n，（II）由s2n=a1+a2+…+a2n=（a1+a3+…+a2n-1）+（a2+…+a2n），分组利用等差数列的求和公式可求试题解析：（I）∵a1=20，a2=7，a n+2-a n=-2∴a3=18，a4=5由题意可得数列{a n}奇数项、偶数项分布是以-2为公差的等差数列当n为奇数时，=21-n当n为偶数时，=9-n∴a n=（II）s2n=a1+a2+…+a2n=（a1+a3+…+a2n-1）+（a2+…+a2n）==-2n2+29n结合二次函数的性质可知，当n=7时最大3．【答案】见答案解析【解析】（Ⅰ）取BC的中点O，cD的中点G，连接AO，OF，FG，AG．因为△ABC，△DFc都是等边三角形，故有AO⊥BC，且平面BCcD⊥平面ABC，所以AO⊥平面BCcD，同理FG⊥平面BCcD，因为，o边形BCcD是边长为2的正方形，所以，．…（6分）（Ⅱ）由（Ⅰ）知AO∥FG，AO=FG，所以o边形AOFG为平行o边形，故AG∥OF，又Dc∥BC，所以，平面ADc∥平面BCF．…（62分）4．【答案】见答案解析【解析】（Ⅰ）∵点M到抛物线准线的距离为=，∴，∴抛物线C的方程为y2=x．（2分）（Ⅱ）法一：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴k HE=-k HF，设E（x1，y1），F（x2，y2），∴，∴，∴y1+y2=-2y H=-4．（5分）∴．（7分）法二：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴∠AHB=60°，可得，，∴直线HA的方程为，联立方程组，得，∵∴，．（5分）同理可得，，∴．（7分）（Ⅲ）法一：设A（x1，y1），B（x2，y2），∵，∴，∴直线HA的方程为（4-x1）x-y1y+4x1-15=0，同理，直线HB的方程为（4-x2）x-y2y+4x2-15=0，∴，，（9分）∴直线AB的方程为，令x=0，可得，∵，∴t关于y0的函数在[1，+∞）上单调递增，∴当y0=1时，t min=-11．（12分）法二：设点H（m2，m）（m≥1），HM2=m4-7m2+16，HA2=m4-7m2+15．以H为圆心，HA为半径的圆方程为（x-m2）2+（y-m）2=m4-7m2+15，①⊙M方程：（x-4）2+y2=1．②①-②得：直线AB的方程为（2x-m2-4）（4-m2）-（2y-m）m=m4-7m2+14．（9分）当x=0时，直线AB在y轴上的截距（m≥1），∵，∴t关于m的函数在[1，+∞）上单调递增，∴当m=1时，t min=-11．（12分）5．【答案】见答案解析【解析】试题分析：（1）求导函数，利用由函数g（x）的图象在点（1，g（x））处的切线平行于x轴，可得：g′（1）=0，即可求a的值；（2）确定函数的单调性，即可求函数g（x）的极小值；（3）表示出直线的斜率，再构造函数，研究函数的单调性，即可证明结论．试题解析：（1）依题意得g（x）=lnx+ax2-3x，则．由函数g（x）的图象在点（1，g（x））处的切线平行于x轴得：g′（1）=1+2a-3=0∴a=1；（2）函数g（x）的定义域为（0，+∞）．由（1）得令g′（x）=0得x=或x=1．∴函数故（x）在（0，），（1，+∞）上单调递增，在（，1）单调递减．故函数g（x）的极小值为g（1）=-2；（3）证明：依题意得=，∴lnx2-kx2=lnx1-kx1，令h（x）=lnx-kx，则h′（x）=，由h′（x）=0得，当x＞时，h′（x）＜0，当0＜x＜时，h′（x）＞0，∴h（x）在（0，）单调递增，在（，+∞）单调递减，又h（x1）=h（x2），∴，即＜k＜．．6．【答案】见答案解析【解析】试题分析：（Ⅰ）根据f（x）+f（x+4）=|x-1|+|x+3|=，分类讨论求得不等式f（x）+f（x+4）≥8的解集．（Ⅱ）要证的不等式即|ab-1|＞|a-b|，根据|a|＜1，|b|＜1，可得|ab-1|2-|a-b|2＞0，从而得到所证不等式成立．试题解析：（Ⅰ）f（x）+f（x+4）=|x-1|+|x+3|=，当x＜-3时，由-2x-2≥8，解得x≤-5；当-3≤x≤1时，f（x）≤8不成立；当x＞1时，由2x+2≥8，解得x≥3．所以，不等式f（x）≤4的解集为{x|x≤-5，或x≥3}．（Ⅱ）f（ab）＞|a|f（），即|ab-1|＞|a-b|．因为|a|＜1，|b|＜1，所以|ab-1|2-|a-b|2=（a2b2-2ab+1）-（a2-2ab+b2）=（a2-1）（b2-1）＞0，所以|ab-1|＞|a-b|，故所证不等式成立．。

河北省武安县高三数学上学期第四次月考试题文

第四次月考文科数学试卷卷Ⅰ(选择题共60分)一．选择题（共12小题，每小题5分，计60分。

在每小题给出的四个选项中，只有一个选项正确）1、已知集合}1|1||{<-=x x M ，)}32(log |{22++==x x y y N 则=N M ( ) A.}21||{<≤x x B.}20||{<<x x C.}21||{<<x x D.φ2、已知i 是虚数单位，则复数ii -+1)1(2的虚部等于（）A.1-B. i -C. iD. 13、已知向量)sin ,(cos θθ=a ，)1,3(=b ，则||b a -的最大值为（） A.1 B. 3 C.3 D.94、在等差数列}{n a 中，前n 项的和为n S ，若11862a a +=，则=9S （） A.54 B.45 C.36 D.27 5、下列四个命题中的真命题为（） A. ∈∃x R ,使得5.1cos sin =+x x ； B. ∈∀x R ,总有0322≥--x x ； C. ∈∀x R , ∈∃y R ,x y <2 D. ∈∃x R , ∈∀y R ,y x y =⋅6、已知某几何体的三视图如左上所示，则这个几何体的外接球的表面积等于（）A.π37 B.π328C.π8D.π167、要得到函数)23cos(x y -=π的图像，只需将函数x y 2sin =的图像（）A.向左平移12π个单位 B. 向右平移12π个单位 C. 向左平移6π个单位 D. 向右平移6π个单位8、按照如右图所示的程序框图执行，若输出的结果为15则M 处的条件可为（）A. 8≥kB. 8<kC. 16<kD. 16≥k 9. 如图，在△ABC 中AN =41NC ，P 是BN 上的一点，若 AP =m +112AC ，则实数m 的值为（） A. 119 B. 112 C. 113 D. 111 10、过抛物线)0(22>=p px y 的焦点F 作直线交抛物线于A 、 B 两点，O 为抛物线的顶点，主左第7题图则△ABO 是一个 ( )A.等边三角形B.直角三角形C.不等边锐角三角形D.钝角三角形11、已知函数x x f lg )(=,若b a <<0,且)()(b f a f =则b a 2+的取值范围是（）A.)+∞B.)+∞C.(3,)+∞D.[3,)+∞12、已知函数⎩⎨⎧>+-≤-=0,1)1(0),1(log )(2x x f x x x f ，则=)2011(f （） A.2012 B.2011 C.2010 D.2009第II 卷二、填空题:本大题共4小题，每小题5分，共20分．13已知抛物线的准线方程是14x =-，则它的标准方程是__________.14、已知实数y x ,满足⎪⎪⎩⎪⎪⎨⎧≤+≥≤-42211y x x y x ，则y x 3-的最大值为________________.15、已知双曲线)0,(12222>=-b a by a x 的右焦点F ，若过F 且倾斜角为600的直线l 与双曲线的右支有且只有1个交点，则此双曲线的离心率e 的范围是_________________.16、已知直线)(R m mx y ∈=与函数312(),02()11,02x x f x x x ⎧-≤⎪⎪=⎨⎪+>⎪⎩的图象恰有三个不同的公共点，则实数m 的取值范围是 __________ .三、解答题：(大题共6个小题满分70分，17题10分，其余各题均12分．) 17.（本小题满分10分）已知数列{}n a 的前n 项和为n S ，且*41()n n S a n =+∈N ．（1）求1a ，2a ；（2）设3log ||n n b a =，求数列{}n b 的通项公式．18. （本小题满分12分）已知函数)(1sin 2cos sin 2)(2R x x x x x f ∈+-=．（1）求函数)(x f 的最小正周期和单调递增区间；（2）若在ABC ∆中，角C B A ,,的对边分别为c b a ,,，3=a ，A 为锐角，且32)8(=+πA f ，求ABC ∆面积S 的最大值．19.（本小题满分12分）某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题.（1）求全班人数及分数在[80,90)之间的频数；（2）若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率.20.（本小题满分12分）如图已知E 、F 分别是棱长为1的正方体ABCD —A 1B 1C 1D 1的棱A 1A 、CC 1的中点。

河北省邯郸市2013届高三四校联考数学(文)试题

成安一中、临漳一中、涉县一中、永年二中高三年级四校联考数学试卷（文科）（分数150分时间120分钟）一、选择题：（60分，每题5分）1.已知{{},sin ,P Q y y R θθ=-==∈，则=P Q （）A.∅B. {}0C. {}1,0-D. {-2．若复数i a a a z )3()32(2++-+=为纯虚数(i 为虚数单位)，则实数a 的值是( ) A ．3- B ．3-或1 C ．3 或1- D ．13．已知22:(1)1;:,10,p a q x R ax ax -≤∀∈-+≥则p 是q 成立的（） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知向量(1,1),(2,),a b x ==若a b +与a b -平行，则实数x 的值是( )A ．－2B ．0C ．1D ．25．已知等比数列{}n a 的公比q 为正数，且3452,a a a +=则q 的值为( )A ．32B ．2C ．52D ．36.函数cos(2)3y x π=+的图象可以由cos y x =的图象( ) A 、右移6π个单位，再每点的纵坐标不变，横坐标变为原来的2倍; B 、左移6π个单位，再每点的纵坐标不变，横坐标变为原来的12倍; C 、每点的纵坐标不变，横坐标变为原来的12倍，再左移3π个单位; D 、左移3π个单位，再每点的纵坐标不变，横坐标变为原来的12倍.7( ) A 、（1,2） B 、（e ，3） C 、（2，e ） D 、（e ，+∞）8.函数21()x f x e -=的部分图象大致是 ( )9．设变量x ，y 满足约束条件：3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩.则目标函数z=2x+3y 的最小值为( )A 6B 7C 8D 2310．下列选项叙述错误的是 ( )A.命题“若1x ≠，则2320x x -+≠”的逆否命题是“若2320x x -+=，则1x =”B.若命题P ：2,10x R x x ∀∈++≠，则P ⌝：2,10x R x x ∃∈++=C.若p q ∨为真命题，则p ，q 均为真命题D. “2x >”是“2320x x -+>”的充分不必要条件11.） A、函数的最小正周期为B 、函数的图象关于直线C 、函数的图象是由的图象向左平移D 12．下面能得出△ABC 为锐角三角形的条件是（）A ．51cos sin =+A AB ．0<⋅BC AB C ．︒===30,33,3B c bD ．0tan tan tan >++C B A 二、填空题：（共计20分，每题5分）13．已知曲线y ＝3x 2＋2x 在点(1，5)处的切线与直线2ax －y －6＝0平行，则a ＝14．已知函数1()()sin 2x f x x =-，则()f x 在[]0,2π上零点的个数为 2cos2y x =()f x ()f x 2π()f x15. 若α是锐角，且1sin(),cos 63παα-=则的值是 16、数列}{n a 满足12 (01),1 (1).n n n n n a a a a a +≤≤⎧=⎨->⎩且167a =,则2010a = 三、解答题：(共计70分)17. (10分)已知函数f (x )=cos 2x +sin x cos x (x ∈R )(1)求f (8π3)的值；(2)求f (x )的单调递增区间 18.（12分）设2()(8),f x ax b x a ab =+---不等式()0f x >的解集是（－3，2）.（1）求()f x ；（2）当函数f （x ）的定义域是[0，1]时，求函数()f x 的值域.19．(12分)已知向量a 、b 、c 是同一平面内的三个向量，其中a ＝(1,2)．(1)若|c |＝25，且a ∥c ，求c 的坐标；(2)若|b |＝52，且a ＋2b 与2a －b 垂直，求a 与b 的夹角θ. 20.（12分）在锐角ABC ∆中，已知角C B 、、A 所对的边分别为c b a ,,且)tan tan 1(33tan tan B A B A +=-，若ab b a c -+=222 （1）求角C B 、、A 的大小(2)若边6=c ，求边b 的值21 （12分）已知}{n a 为等差数列，且12,84231=+=+a a a a .（1）求数列}{n a 的通项公式；（2）}{n a 的前n 项和为n S ，若21,,+k k S a a 成等比数列，求正整数k 的值 22．（12分）已知函数f(x)= x 2+alnx.（1）当a=-2时，求函数f(x)的单调区间和极值；（2）若g(x)= f(x)+2x在[1,+∞)上是单调增函数，求实数a 的取值范围.2013届高三11月联考数学（文）试题答案一、选择题1---12CDADB DCCBC DD二、填空题 13. 4 14.2 15.61-62 16.3/7 三．解答题（共70分）17.解：（1）21)42sin(222sin 2122cos 1)(++=++=πx x x x f 2121)443sin(22)83(=++=πππf （2）由Z k k x k ∈+≤+≤-,224222πππππ Z k k x k ∈+≤≤-,883ππππ 所以增区间为：Z k k k ∈⎥⎦⎤⎢⎣⎡+-,8,83ππππ 18．解不等式()0f x >的解集是（－3，2）于是方程()0f x =的解是－3，2(3)0f -=。

2017年河北省邯郸市武安三中高三上学期期中数学试卷含解析答案(文科)

2016-2017学年河北省邯郸市武安三中高三（上）期中数学试卷（文科）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的，将正确的选项填涂在答题卡上）1．（5分）已知集合M={x|（x+2）（x﹣1）＜0}，N={x|x+1＜0}，则M∩N=（）A．（﹣1，1）B．（﹣2，1）C．（﹣2，﹣1）D．（1，2）2．（5分）已知复数z满足（i是虚数单位），则z的共轭复数为（）A． B． C． D．3．（5分）已知复数z=﹣3i，则|z|等于（）A．2 B．C．D．4．（5分）下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（）A．y=lnx B．y=cosx C．y=﹣x2D．5．（5分）定义在R上的函数f（x）是奇函数又是以2为周期的周期函数，则f （1）+f（4）+f（7）等于（）A．﹣1 B．0 C．1 D．46．（5分）若函数f（x）=2x+b﹣1（b∈R）的图象不经过第二象限，则有（）A．b≥1 B．b≤1 C．b≥0 D．b≤07．（5分）设a=log0.70.8，b=log1.20.8，c=1.20.7，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a8．（5分）若=，则tan2α=（）A．﹣ B．C．﹣ D．9．（5分）已知α+β=，则（1+tanα）（1+tanβ）的值是（）A．﹣1 B．1 C．2 D．410．（5分）函数y=x+lnx2的大致图象为（）A．B．C．D．11．（5分）已知点P在曲线y=上，a为曲线在点P处的倾斜角，则a的取值范围是（）A．[0，）B．[，） C．（，]D．[，π）12．（5分）已知函数（a＞0），有下列四个命题：①f（x）的值域是（﹣∞，0）∪（0，+∞）；②f（x）是奇函数；③f（x）在（﹣∞，0）∪（0，+∞）上单调递增；④方程|f（x）|=a总有四个不同的解，其中正确的是（）A．仅②④B．仅②③C．仅①②D．仅③④二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．（5分）若幂函数f（x）的图象过点，则f（9）=．14．（5分）函数y=tan（2x+）的定义域是．15．（5分）函数y=sin2x+cos2x的最小正周期为，最大值为．16．（5分）在锐角△ABC中，b=，c=3，B=30°，则a等于．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（10分）设复数z=m2﹣2m﹣3+（m2+3m+2）i，试求实数m取何值时，（1）z是实数；（2）z是纯虚数；（3）z对应的点位于复平面的第二象限．18．（12分）已知α∈（，π），且sin+cos=（1）求cosα的值（2）若sin（α﹣β）=﹣，β∈（，π），求cosβ的值．19．（12分）已知a、b、c是△ABC中∠A、∠B、∠C的对边，，b=6，．（1）求c；（2）求的值．20．（12分）已知函数f（x）=+x在x=1处的切线方程为2x﹣y+b=0．（Ⅰ）求实数a，b的值；（Ⅱ）若函数g（x）=f（x）+x2﹣kx，且g（x）是其定义域上的增函数，求实数k的取值范围．21．（12分）已知函数f（x）=sin2x+sinxcosx﹣（1）若x∈[0，]，求函数f（x）的取值范围；（2）已知a，b，c分别为△ABC内角A、B、C的对边，其中A为锐角，a=2，c=4且f（A）=1，求A，b和△ABC的面积S．22．（12分）已知函数f（x）=（2﹣a）lnx++2ax（a≥0）（1）当a=0时，求f（x）的极值；（2）当a＜0时，讨论f（x）的单调性；（3）若对于任意的x1，x2∈[1，3]，a∈（﹣∞，﹣2）都有|f（x1）﹣f（x2）|＜（m+ln3）a﹣2ln3，求实数m的取值范围．2016-2017学年河北省邯郸市武安三中高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的，将正确的选项填涂在答题卡上）1．（5分）已知集合M={x|（x+2）（x﹣1）＜0}，N={x|x+1＜0}，则M∩N=（）A．（﹣1，1）B．（﹣2，1）C．（﹣2，﹣1）D．（1，2）【解答】解：∵集合M={x|（x+2）（x﹣1）＜0}，∴M={x|﹣2＜x＜1}，∵N={x|x+1＜0}，∴N={x|x＜﹣1}，∴M∩N={x|﹣2＜x＜﹣1}故选：C．2．（5分）已知复数z满足（i是虚数单位），则z的共轭复数为（）A． B． C． D．【解答】解：∵复数z满足，∴z===∴复数的共轭复数是故选：B．3．（5分）已知复数z=﹣3i，则|z|等于（）A．2 B．C．D．【解答】解：复数z=﹣3i，则|z|=||=|1﹣i|=．故选：D．4．（5分）下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（）A．y=lnx B．y=cosx C．y=﹣x2D．【解答】解：A．y=lnx的图象不关于y轴对称，不是偶函数，∴该选项错误；B．y=cosx在（0，+∞）上没有单调性，∴该选项错误；C．y=﹣x2是偶函数，且在（0，+∞）上单调递减，∴该选项正确；D.的图象不关于y轴对称，不是偶函数，∴该选项错误．故选：C．5．（5分）定义在R上的函数f（x）是奇函数又是以2为周期的周期函数，则f （1）+f（4）+f（7）等于（）A．﹣1 B．0 C．1 D．4【解答】解：据题意f（7）=f（﹣1+8）=﹣f（1），∴f（1）+f（7）=0，又f（4）=f（0）=0，∴f（1）+f（4）+f（7）=0．故选：B．6．（5分）若函数f（x）=2x+b﹣1（b∈R）的图象不经过第二象限，则有（）A．b≥1 B．b≤1 C．b≥0 D．b≤0【解答】解：因为y=2x，当x＜0时，y∈（0，1）．所以，函数f（x）=2x+b﹣1（b∈R）的图象不经过第二象限，则有b﹣1≤﹣1，解得b≤0．故选：D．7．（5分）设a=log0.70.8，b=log1.20.8，c=1.20.7，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a【解答】解：∵0＜a=log0.70.8＜log0.70.7=1，b=log1.20.8＜0，c=1.20.7＞1，∴c＞a＞b．故选：C．8．（5分）若=，则tan2α=（）A．﹣ B．C．﹣ D．【解答】解：∵==，∴tanα=﹣3，则tan2α===．故选：B．9．（5分）已知α+β=，则（1+tanα）（1+tanβ）的值是（）A．﹣1 B．1 C．2 D．4【解答】解：由α+β=，得到tan（α+β）=tan=1，所以tan（α+β）==1，即tanα+tanβ=1﹣tanαtanβ，则（1+tanα）（1+tanβ）=1+tanα+tanβ+tanαtanβ=2．故选：C．10．（5分）函数y=x+lnx2的大致图象为（）A．B．C．D．【解答】解：由函数有意义可得x2＞0，∴f（x）的定义域为{x|x≠0}，排除A；y′=1+，∴当x＞0或x＜﹣2时，y′＞0，当﹣2＜x＜0时，y′＜0．∴f（x）在（﹣∞，﹣2）上单调递增，在（﹣2，0）上单调递减，在（0，+∞）上单调递增，排除B，D．故选：C．11．（5分）已知点P在曲线y=上，a为曲线在点P处的倾斜角，则a的取值范围是（）A．[0，）B．[，） C．（，]D．[，π）【解答】解：因为y=上的导数为y′=﹣=﹣，∵e x+e﹣x≥2=2，∴e x+e﹣x+2≥4，∴y′∈[﹣1，0）即tanα∈[﹣1，0），∵0≤α＜π∴π≤α＜π．即α的取值范围是[π，π）．故选：D．12．（5分）已知函数（a＞0），有下列四个命题：①f（x）的值域是（﹣∞，0）∪（0，+∞）；②f（x）是奇函数；③f（x）在（﹣∞，0）∪（0，+∞）上单调递增；④方程|f（x）|=a总有四个不同的解，其中正确的是（）A．仅②④B．仅②③C．仅①②D．仅③④【解答】解：①当a=x=1时f（x）=0，所以f（x）的值域是（﹣∞，0）∪（0，+∞），错误；②f（﹣x）=﹣x+，而f（x）=x﹣，所以f（﹣x）+f（x）=﹣x++x﹣=0得到函数为奇函数，正确；③因为f′（x）=1+，由a＞0得到f′（x）＞1＞0，所以函数单调递增，区间不能用并集符号，错误；④|f（x）|=a得到f（x）=±a即x﹣=±a，x＞0，x＜0各有两解，则方程有四个解，正确．故选：A．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．（5分）若幂函数f（x）的图象过点，则f（9）=．【解答】解：设幂函数f（x）=xα，∵幂函数y=f（x）的图象过点（），∴，解得．∴f（x）=，∴f（9）==，故答案为：．14．（5分）函数y=tan（2x+）的定义域是{x|x≠+，k∈Z} ．【解答】解：由y=tanx的定义域为{x|x≠kπ+，k∈Z}，令2x+≠kπ+，则x≠+，则定义域为{x|x≠+，k∈Z}，故答案为：{x|x≠+，k∈Z}．15．（5分）函数y=sin2x+cos2x的最小正周期为π，最大值为．【解答】解：∵y=sin2x+cos2x=sin2x+cos2x+=sin（2x+）+，∴函数y=sin2x+cos2x的最小正周期T=，∴=1=．故答案为：π，．16．（5分）在锐角△ABC中，b=，c=3，B=30°，则a等于．【解答】解：由余弦定理可得：b2=a2+c2﹣2accosB，∴=a2+32﹣6acos30°，化为：a2﹣3a+6=0，解得a=2或．当a=时，C=180°﹣2×30°=120°，不满足条件，舍去．∴．故答案为：2．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．（10分）设复数z=m2﹣2m﹣3+（m2+3m+2）i，试求实数m取何值时，（1）z是实数；（2）z是纯虚数；（3）z对应的点位于复平面的第二象限．【解答】解：（1）由m2+3m+2=0，解得m=﹣1或﹣2．∴m=﹣1或﹣2时，z是实数；（2）由，解得m=3，∴m=3时，z是纯虚数．（3）由，解得﹣1＜m＜3，∴当﹣1＜m＜3，z对应的点位于复平面的第二象限．18．（12分）已知α∈（，π），且sin+cos=（1）求cosα的值（2）若sin（α﹣β）=﹣，β∈（，π），求cosβ的值．【解答】解：（1）∵α∈（，π），且sin+cos=，两边平方可得：1+sinα=，∴sinα=，可得：cosα=﹣=﹣．（2）∵由（1）可得：sin α=，cosα=﹣．∵＜α＜π，＜β＜π，∴﹣＜α﹣β＜，又sin（α﹣β）=﹣，得cos（α﹣β）=，∴cos β=cos[α﹣（α﹣β）]=cosαcos（α﹣β）+sinαs in（α﹣β）=﹣×+×（﹣）=﹣．19．（12分）已知a、b、c是△ABC中∠A、∠B、∠C的对边，，b=6，．（1）求c；（2）求的值．【解答】解：（1）在△ABC中，由余弦定理得，a2=b2+c2﹣2bccosA，即48=36+c2﹣2×c×6×（﹣），整理得：c2+4c﹣12=0，即（c+6）（c﹣2）=0，解得：c=2或c=﹣6（舍去），则c=2；（2）由cosA=﹣＜0，得A为钝角，∴sinA==，在△ABC中，由正弦定理，得=，则sinB===，∵B为锐角，∴cosB==，∴cos2B=1﹣2sin2B=﹣，sin2B=2sinBcosB=，则cos（2B﹣）=（cos2B+sin2B）=×（﹣+）=．20．（12分）已知函数f（x）=+x在x=1处的切线方程为2x﹣y+b=0．（Ⅰ）求实数a，b的值；（Ⅱ）若函数g（x）=f（x）+x2﹣kx，且g（x）是其定义域上的增函数，求实数k的取值范围．【解答】解：（Ⅰ）∵f（x）=+x，∴f′（x）=+1，∵f（x）在x=1处的切线方程为2x﹣y+b=0，∴+1=2，2﹣1+b=0，∴a=1，b=﹣1；（Ⅱ）f（x）=lnx+x，g（x）=x2﹣kx+lnx+x，∴g′（x）=x﹣k++1，∵g（x）在其定义域（0，+∞）上是增函数，∴g′（x）≥0在其定义域上恒成立，∴x﹣k++1≥0在其定义域上恒成立，∴k≤x++1在其定义域上恒成立，而x++1≥2+1=3，当且仅当x=1时“=”成立，∴k≤3．21．（12分）已知函数f（x）=sin2x+sinxcosx﹣（1）若x∈[0，]，求函数f（x）的取值范围；（2）已知a，b，c分别为△ABC内角A、B、C的对边，其中A为锐角，a=2，c=4且f（A）=1，求A，b和△ABC的面积S．【解答】解：（1）∵f（x）=sin2x+sin xcosx﹣=sin2x cos2x=sin2x cos2x=sin（2x﹣），又x∈[0，]，则2x﹣∈[，]，∴f（x）∈[﹣，1]，（2）f（A）=sin（2A﹣）=1，∵A∈（0，），2A﹣∈（，），∴2A﹣）=，A=，∵根据余弦定理：a2=b2+c2﹣2bccosA，得出：b=2，所以S=sinA=sin60°=2，22．（12分）已知函数f（x）=（2﹣a）lnx++2ax（a≥0）（1）当a=0时，求f（x）的极值；（2）当a＜0时，讨论f（x）的单调性；（3）若对于任意的x1，x2∈[1，3]，a∈（﹣∞，﹣2）都有|f（x1）﹣f（x2）|＜（m+ln3）a﹣2ln3，求实数m的取值范围．【解答】解：（1）依题意知f（x）的定义域为（0，+∞），当a=0时，f（x）=2lnx+，f′（x）=，令f′（x）=0，解得x=，当0＜x＜时，f′（x）＜0；当x≥时，f′（x）＞0又∵f（）=2ln+2=2﹣2ln2∴f（x）的极小值为2﹣2ln2，无极大值．（2）f′（x）=﹣+2a=，当a＜﹣2时，﹣＜，令f′（x）＜0 得0＜x＜﹣或x＞，令f′（x）＞0 得﹣＜x＜；当﹣2＜a＜0时，得﹣＞，令f′（x）＜0 得0＜x＜或x＞﹣，令f′（x）＞0 得＜x＜﹣；当a=﹣2时，f′（x）=﹣≤0，综上所述，当a＜﹣2时f（x），的递减区间为（0，﹣）和（，+∞），递增区间为（﹣，）；当a=﹣2时，f（x）在（0，+∞）单调递减；当﹣2＜a ＜0时，f （x ）的递减区间为（0，）和（﹣，+∞），递增区间为（，﹣）．（3）由（Ⅱ）可知，当a ∈（﹣∞，﹣2）时，f （x ）在区间[1，3]上单调递减，当x=1时，f （x ）取最大值；当x=3时，f （x ）取最小值；|f （x 1）﹣f （x 2）|≤f （1）﹣f （3）=（1+2a ）﹣[（2﹣a ）ln3++6a ]=﹣4a +（a ﹣2）ln3，∵（m +ln3）a ﹣ln3＞|f （x 1）﹣f （x 2）|恒成立， ∴（m +ln3）a ﹣2ln3＞﹣4a +（a ﹣2）ln3 整理得ma ＞﹣4a ， ∵a ＜0，∴m ＜﹣4恒成立，∵﹣3＜a ＜﹣2，∴﹣＜﹣4＜﹣，∴m ≤﹣．赠送—高中数学知识点【2.1.1】指数与指数幂的运算（1）根式的概念①如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n n a n 是偶数时，正数a 的正的n n a 表示，负的n 次方根用符号n a -0的n 次方根是0；负数a 没有n 次方根．n a n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：()n n a a =；当n 为奇数时，nn a a =；当n 为偶数时，(0)|| (0) nna a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m na a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈【2.1.2】指数函数及其性质（4）指数函数〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a a MM N N-= ③数乘：log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质。

2013秋高三上册数学第一次摸底考试文科试题(含答案)

2013秋高三上册数学第一次摸底考试文科试题(含答案)河北省邯郸市武安三中2014届高三（上）第一次摸底数学试卷（文科）一、选择题：本大题共12小题。

每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的一项。

1．已知集合,集合,,则（）A．B．C．D．2．已知i是虚数单位,则(2+i)(3+i)=（）A．5-5iB．7-5iC．5+5iD．7+5i3．集合A={2,3},B={1,2,3},从A,B中各取任意一个数,则这两数之和等于4的概率是（）A．B．C．D．4．双曲线的顶点到其渐近线的距离等于（）A．B．C．1D．5．命题“对任意,都有”的否定为（）A．对任意,使得B．不存在,使得C．存在,都有D．存在,都有6．已知数列满足（）A．B．C．D．7．执行如图所示的程序框图,若输入（）A．B．C．D．8．直线被圆截得的弦长为（）A．1B．2C．4D．9．函数的图象大致为（）10．设的内角所对边的长分别为,若,则角=（）A．B．C．D．11．一几何体的三视图如右所示,则该几何体的体积为（）A．200+9πB．200+18πC．140+9πD．140+18π12．设函数.若实数a,b满足,则(A)(B)(C)(D)第Ⅱ卷本卷包括必考题和选考题两个部分。

第（13）题-第（21）题为必考题，每个考生都必须作答。

第（22）题-第（24）题为选考题，考生根据要求作答。

二．填空题：本大题共四小题，每小题5分。

13．若非零向量满足,则夹角的余弦值为_______.14．若满足约束条件则____________.15．已知一个正方体的所有顶点在一个球面上.若球的体积为,则正方体的棱长为______.16．函数的图像向右平移个单位后，与函数的图像重合，则___________.三.解答题：解答应写出文字说明，证明过程或演算步骤。

17．（本小题满分12分）等差数列中,(I)求的通项公式;(II)设18（本小题满分共12分）某小组共有五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:ABCDE身高1.691.731.751.791.82体重指标19.225.118.523.320.9(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在18.5,23.9)中的概率19.（本小题满分12分）如图,四棱锥的底面是边长为2的菱形,.已知. (Ⅰ)证明:(Ⅱ)若为的中点,求三菱锥的体积.20．（本小题满分共12分）已知函数(I)求(II)若21．(本小题满分12分)椭圆C:=1(a>b>0)的离心率，a+b=3(1)求椭圆C的方程；(2)如图，A,B,D是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线DP交x轴于点N直线AD交BP于点M，设BP的斜率为k，MN的斜率为m，证明2m-k为定值。

河北省邯郸市武安西交中学高三数学文月考试题含解析

河北省邯郸市武安西交中学高三数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 下列命题：（1）若“，则”的逆命题；（2）“全等三角形面积相等”的否命题；（3）“若，则的解集为R”的逆否命题；（4）“若为有理数，则为无理数”。

其中正确的命题是（）A.（3）（4）B.（1）（3）C.（1）（2）D.（2）（4）参考答案：A略2. 方程lgx=8﹣2x的根x∈（k，k+1），k∈Z，则k=（）A．2 B．3 C．4 D．5参考答案：B【考点】函数的零点与方程根的关系．【专题】计算题．【分析】令f（x）=lgx+2x﹣8则可知函数f（x）在（0，+∞）单调递增，且函数在（0，+∞）连续，检验只要满足f（k）f（k+1）＜0即可【解答】解：令f（x）=lgx+2x﹣8则可知函数f（x）在（0，+∞）单调递增，且函数在（0，+∞）连续∵f（1）=﹣6＜0，f（2）=lg2﹣4＜0，f（3）=lg3﹣2＜0，f（4）=lg4＞0∴f（3）f（4）＜0由函数的零点判定定理可得，函数的零点区间（3，4）∴k=3故选：B【点评】本题主要考查了函数的零点判定定理的应用，属于基础性试题3. 抛物线与直线相交于A、B两点，点P是抛物线C上不同A、B的一点，若直线PA、PB分别与直线相交于点Q、R，O为坐标原点，则的值是A. 20B. 16C. 12D. 与点P位置有关的一个实数参考答案：A4. 一个空间几何体的三视图如图，则该几何体的体积为A．B．0C．D．参考答案：D5. 某工厂今年年初贷款a万元，年利率为r（按复利计算），从今年末起，每年年末偿还固定数量金额，5年内还清，则每年应还金额为（）万元．A．B．C．D．参考答案：B【考点】有理数指数幂的化简求值．【分析】假设每年偿还x元，由题意可得a（1+r）5=x（1+r）4+x（1+r）3+…+x（1+r）+x，利用等比数列的前n项和公式即可得出．【解答】解：假设每年偿还x元，由题意可得a（1+r）5=x（1+r）4+x（1+r）3+…+x（1+r）+x，化为a（1+r）5=x?，解得x=．故选：B．6. 已知双曲线与抛物线有一个公共的焦点，且两曲线的一个交点为，若，则双曲线的离心率为( )A．B． C．D．参考答案：A7. 函数的零点个数为（）A．个 B．个 C．个 D．个参考答案：C略8. 已知集合,，集合为A.B． C. D.参考答案：A略9. 设、是两条不同的直线，、是两个不同的平面，下列命题中正确的是（）A．若，，则B．若，，则C．若，，则D．若，，，则参考答案：D略10. 在如图所示的正方形中随机投掷10000个点，则落入阴影外部（曲线C为正态分布的密度曲线）的点的个数的估计值为（）A．3413 B．1193 C．2718 D．6587附：若,则，参考答案：D【知识点】正态分布几何概型【试题解析】由题知：阴影的面积为所以落入阴影的点的个数为：个，所以落入阴影外部的点的个数的估计值为：10000-3413=6587个。

河北省邯郸市武安西交中学高三数学文月考试卷含解析

河北省邯郸市武安西交中学高三数学文月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知，定义域为，任意，点组成的图形为正方形，则实数的值为(▲)A．B．C．D．参考答案：D略2. 若平面向量与的夹角是，且，则的坐标为A．B．C．D．参考答案：A3. 双曲线与抛物线的准线交于A，B两点，，则双曲线的离心率为（）A． B．2 C． D．4参考答案：A略4. 已知奇函数在时的图象如图所示,则不等式的解集为( ) A.(1,2) B.(－2,－1) C. (－2,－1)∪(1,2) D.(－1,1)参考答案：C5. 一个几何体的三视图及其尺寸(单位：cm) ，如右图所示，则该几何体的体积为( )．A.144B.C． D．64参考答案：D略6. 一个几何体的三视图如图所示，其中正视图和侧视图相同，其上部分是半圆，下部分是边长为2的正方形；俯视图是边长为2的正方形及其外接圆．则该几何体的体积为（）A．4+ B．4+C．8+D．8+参考答案：C【考点】由三视图求面积、体积．【分析】首先由几何体还原几何体，是下面是底面为正方体，上面是半径为的半球，由此计算体积．【解答】解：由几何体的三视图得到几何体为组合体，下面是底面为正方体，上面是半径为的半球，所以几何体的体积为2×2×2+=8+故选C．【点评】本题考查了组合体的三视图以及体积的计算；关键是明确几何体的形状，由体积公式计算．7. 设a=（a1，a2）,b=（b1,b2）．定义一种向量积．已知，点P（x,y）在y=sinx的图象上运动,点Q在y=f（x）的图象上运动，且满足（其中O为坐标原点），则y=f（x）的最大值A及最小正周期T分别为（）A．2, B．2,4 C． D．参考答案：C设Q（x,y），P（x0，y0），则由得,代入得，则y=f（x）的最大值A及最小正周期T分别为,故选C．8. 若函数有三个零点，则实数的取值范围是A. B. C. D.参考答案：A设，则，令，得，由图象易知，又当时，，且时，；当时，为增函数，且时，，因此函数有三个零点时，，故选A.9. 已知，满足且目标函数的最大值为7，最小值为１，则（）Ａ．-２Ｂ．２Ｃ．１Ｄ．-１参考答案：A10. 已知是第二象限角，且sin(，则tan2的值为( )A． B． C． D．参考答案：【知识点】二倍角的正切． C6【答案解析】C 解析：由sin（π+α）=﹣sinα=﹣，得到sinα=，又α是第二象限角，所以cosα=﹣=﹣，tanα=﹣，则tan2α===﹣．故选C【思路点拨】根据诱导公式由已知的等式求出sinα的值，然后由α是第二象限角得到cosα小于0，利用同角三角函数间的基本关系即可求出cosα的值，进而求出tanα的值，把所求的式子利用二倍角的正切函数公式化简后，把tanα的值代入即可求出值．二、填空题:本大题共7小题,每小题4分,共28分11. 若log a 4b=－1，则a+b 的最小值为。

河北省武安市第三中学高三数学上学期第一次月考试题

武安三中高三第一次月考文科数学试题（时间120分钟，满分150分）注意事项：1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上3.考试范围：集合与常用逻辑用语，函数，导数。

第Ⅰ卷（客观题共60 分）一、选择题：(本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填涂在答题卡上．)1.若集合}65432{，，，，=P ，}753{，，=Q ，若Q P M I =，则M 的子集个数为（）A ．5B ．4C ．3D ．22.已知集合2{|230}A x x x =--≤，{|ln(2)}B x y x ==-，则A B =I （）A ．(1,3)B ．(1,3]C ．[1,2)-D ．(1,2)-3.已知命题:p x ∀∈R ，sin 1x ≤，则（）A.R x p ∈∀⌝0:，1sin 0≥xB. :p x ⌝∀∈R ，sin 1x >C. :p x ⌝∃∉R ，sin 1x >D.R x p ∈∃⌝0:，1sin 0>x 4.已知函数)(x f 满足x f x=)2(，则=)3(f （）A ．3log 2B ．2log 3C ．2lnD ．3ln5.如果函数f （x ）=x 2+2（a ﹣1）x+2在区间（﹣∞，2]上单调递减，那么实数a 的取值范围是（）A ．a≤﹣2B ．a≥﹣2C ．a ≤﹣1D ．a≥16.已知函数f （x ）是函数y=log a x （a ＞0且a≠1）的反函数，则函数y=f （x ）+2图象恒过点的坐标为（）A ．（1，0）B ．（0，1）C ．（1，2）D ．（0，3） 7.已知方程a x =-12有两个不等实根，则实数a 的取值范围是( )A ．()0,∞-B ．()2,1C ．()+∞,0D ．()1,08. 下列函数中，在其定义域内既是奇函数又单调递增的函数是( )A ．1y x =-B ．33x x y -=-C ．y x x =D ．3y x x =- 9.三个数60.7，0.76，0.7log 6的大小关系为（）A. 60.70.70.7log 66<<B. 60.70.70.76log 6<<C ．0.760.7log 660.7<< D. 60.70.7log 60.76<<10.函数131()()2x f x x =-的零点所在的区间为（） A. 1(0,)6 B. 11(,)63 C. 11(,)32 D. 1(,1)211.已知函数()3134f x x ax =-+，若函数()y f x =的极小值为0，则a 的值为（） A ．14 B ．12- C ．34 D ．34- 12.已知函数=y )(x f 是定义在R 上的奇函数，且当)0,(-∞∈x 时不等式()()0f x xf x '+<成立，若3(3)a f =，2(2),b f =--(1)c f =，则c b a ,,的大小关系是（）A ．c b a >>B ．a b c >>C ．c a b >>D ．b c a >>第Ⅱ卷（主观题共90分）二、填空题（本大题共4个小题，每小题5分，共20分，在每小题给出横线上填上正确结果）13. 若不等式1x a -<成立的充分条件是04x <<，则实数a 的取值范围是．14.若幂函数()()22233--⋅+-=m m x m m x f 的图像不过原点，则m 的值为 .15.函数ln y x x =的图象在点1x =处的切线方程_____________．16.已知3()2'(1)f x x xf =+，则'(1)f =________三、解答题：(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．)17．(10分)已知集合A ＝{x |x 2－2x －3≤0，x ∈R}，B ＝{x |x 2－2mx ＋m 2－4≤0，x ∈R ，m ∈R}．若A ⊆∁R B ，求实数m 的取值范围．18．（12分）设p ：2x 2－x －1≤0，q ：x 2－(2a －1)x ＋a(a －1)≤0，若非q 是非p 的必要不充分条件，求实数a 的取值范围.19.（12分）设()f x 是定义在[3,3]-上的偶函数，当03x ≤≤时，()f x 单调递减，若(12)()f m f m -<成立，求m 的取值范围．20.（12分）已知函数⎪⎭⎫⎝⎛++=a x x f 1020lg )(为奇函数，（Ⅰ）求实数a 的值；（Ⅱ）求不等式0)(>x f 的解集。

河北省武安三中2013届高三上学期第四次月考理科综合试题.pdf

当物资的速度方向与水平方向成θ时，物资的水平位移x与竖直位移y的关系为（不计空气阻力）
A．x=ytanθ B．x=2ytanθ C．x=D．x=17．一光滑圆环竖直放置，可绕竖直轴MN转动(如图示)，环半
径R=20cm，在环上套一个质量为m的小球，当环绕MN以=10rad/s的角速度匀速转动时，小球与环心连线与MN
(1)实验电路如图所示，请在图中虚线框内填入所选电压表的字母代号;
(2)该同学测量出路端电压U和干路电流I，作出U-I图线如图2所示，由图线可知，该电池的短路电流为
_______mA，电动势为_______V,内阻为_______kΩ;
24.（14分）如图所示，物体A、B质量分别为mA、mB，用轻质弹簧相连接，弹簧的劲度系数为k，c为一固定挡板
Ca2+＋HCO3-＋OH-＝CaCO3↓＋H2O
二、选择题：本题共8小题，每小题6分。在每小题给出的四个选项中，有的只有一项符合题目要求，有的有多项符
合题目要求。全部选对的得6分，选对但不全的得3分，有选错的得0分。
14. 许多物理学家为物理学的发展做出了巨大贡献，下列表述中正确的是
A．亚里士多德首先提出了力是改变物体运动状态的原因
B．Na2SO3溶液使酸性KMnO4溶液褪色：5SO32-＋6H+＋2MnO4-＝5SO42-＋2Mn2+＋3H2O
C．在含有等物质的量的Fe(NO3)2和KI组成的混合溶液中滴入稀盐酸：
3Fe2+＋4H+＋NO3-＝3Fe3+＋NO↑＋2H2O
D．等物质的量浓度、等体积的Ca(HCO3)2溶液与氢氧化钠溶液相混合：
B．aL甲烷和乙烷混合气体中的分子数为NA
C．5.6 g铁与足量氯气或硫蒸气反应转移的电子数为0.3 NA

河北省武安市第三中学等校2024届高三上学期期中联考数学试题

河北省武安市第三中学等校2024届高三上学期期中联考数学试题一、单选题1．若集合 {}215M x x =->，{}N |15N x x *=∈-<<，则()M N =R I ð（）A ．{}0,1,2,3B ．{}1,2,3C ．{}0,1,2D ．{}1,22．已知i 为虚数单位，若复数2i1iz +=-，则z =（）A ．32B C ．52D3．已知()f x 是定义在R 上的奇函数，当0x <时，()e 2xf x -=-，则()ln 2f =（）A ．1-B ．0C ．1D ．24．在等差数列{}n a 中，n S 为前n 项和，若10823a a =-，则11S =（） A ．11B ．19C ．25D ．335．函数()cos 33xf x x =+-的图象大致是（）A ．B ．C ．D ．6．如图所示的三棱锥A-BCD 中，令AB a u u u r r=，AC b =u u u r r ，AD c =u u u r r ，且M ，G 分别是BC ，CD 的中点，则MG AG +u u u u r u u u r等于（）A ．1122-++r r ra b c B ．12a b c ++r r rC ．12a b c -++r r rD ．1122a b c -+-r r r7．一枚质地均匀的正方体骰子，其六个面分别刻有1，2，3，4，5，6六个数字，投掷这枚骰子两次，A 表示事件“第一次向上一面的数字是1”，B 表示事件“第二次向上一面的数字是2”，C 表示事件“两次向上一面的数字之和是7”，D 表示事件“两次向上一面的数字之和是8”，则（）A ．C 与D 相互独立B ．A 与D 相互独立C ．B 与D 相互独立 D ．A 与C 相互独立8．已知π3αβ-=，tan tan αβ-=cos()αβ+的值为（） A ．12B ．13C ．14-D ．16-二、多选题9．某产品售后服务中心选取了10个工作日，分别记录了每个工作日接到的客户服务电话的数量（单位：次）：67 57 37 40 46 62 31 47 31 30 则这组数据的（） A ．众数是31 B ．中位数是40 C ．极差是37D ．10%分位数是30.510．已知函数()()cos f x A x ωϕ=+（0A >，0ω>，π2ϕ<）的部分图象如图所示，则（）A ．()f x 的最小正周期为πB ．π3ϕ=C ．将曲线()y f x =向右平移π12个单位长度后得到的图象关于y 轴对称D ．若()f x 在区间(),a a -上单调递增，则π06a <≤11．如图，在四棱锥P ABCD -中，PD ⊥底面ABCD ，四边形ABCD 是边长为1的菱形，且120ADC ∠=︒，PD AD =，则（）A ．()1DA DC DP +⋅=u u u r u u u r u u u rB ．()12DP DB BC +⋅=-u u u r u u u r u u u rC ．12PA CP ⋅=u u u r u u u r D ．12AB BP ⋅=-u u u r u u u r 12．已知函数()f x 是定义在()(),00,∞-+∞U 上的奇函数，且当0x >时，()ln f x x =.对于数列{}()1,2,3,4n x n =及数列(){}()1,2,3,4n f x n =，若1234x x x x <<<，下列说法正确的是（）A ．存在数列{}n x ，使得{}n x 与(){}n f x 都为等比数列B ．存在数列{}n x ，使得{}n x 与(){}n f x 都为等差数列C ．存在数列{}n x ，使得{}n x 为等比数列，且(){}n f x 为等差数列D ．存在数列{}n x ，使得{}n x 为等差数列，且(){}n f x 为等比数列三、填空题13．已知向量()2,a t =r ，()3,1b t =-r ，若a b ∥r r，则a =r . 14．写出同时满足如下三个条件的一个函数解析式()f x =． ①()f x 为偶函数；②()f x 的定义域为R ；③()f x 的值域为[]0,115．已知正实数a ，b 满足221a b +=，则114422a b a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值为． 16．如图，在正四棱台1111ABCD A B C D -中，O ，1O 分别是正方形ABCD ，1111D C B A 的中心.若以1O 为球心，11O A 为半径的球与平面ABCD 相切，且O 是该四棱台的外接球的球心，则该四棱台的体积与其外接球的体积之比为.四、解答题17．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知cos A =(1)若b =2c =，求a 的值；(2)若22a bc=B ，C 的大小.18．已知函数()(0)x xf x a k a a -=-⋅>是奇函数，且()312f =.(1)求,a k 的值；(2)若[]1,2x ∀∈，不等式()()20f x mf x +≥恒成立，求m 的取值范围. 19．已知函数()()()21f x x x a =+-，其中1a ≥-. (1)讨论()f x 的单调性；(2)当1a >-时，设1x ，2x 分别为()f x 的极大值点和极小值点，且点()()11,A x f x ，()()22,B x f x ，若直线AB 在y 轴上的截距大于()413a +，求a 的取值范围.20．在数列{}n a ，{}n b 中，已知14a =，12b =，且12n n a b +=，12n n b a +=+. (1)证明：数列{}214n a -+是等比数列； (2)求数列{}n b 的前2n 项的和2n S .21．如图，在五面体111ABC A B C -中，AB AC ⊥，1CC ⊥平面ABC ，11AA BB ∥.已知2AB AC ==，13AA =，1111A B AC =，且11BB CC <.(1)证明：1AA ⊥平面ABC ；(2)求平面111A B C 与平面11AAC 的夹角的余弦值的取值范围. 22．已知函数()()21ln 12f x x x a x =--+． (1)讨论函数()f x 的单调性；(2)当0a >时，若m 为函数()f x 的正零点，证明：m >。

河北省武安三中2013届高三上学期第四次月考数学 文 试题 Word版含答案

2016-2017学年河北省邯郸市武安三中高三(上)第一次月考数学试卷+(文科)(解析版)

河北省武安市第三中学高三数学上学期第一次月考试题

2013届高三上册数学文科期中考试卷(含答案)

2020-2021学年河北省邯郸市武安三中高三(上)第一次月考数学(文科)试题Word版含解析

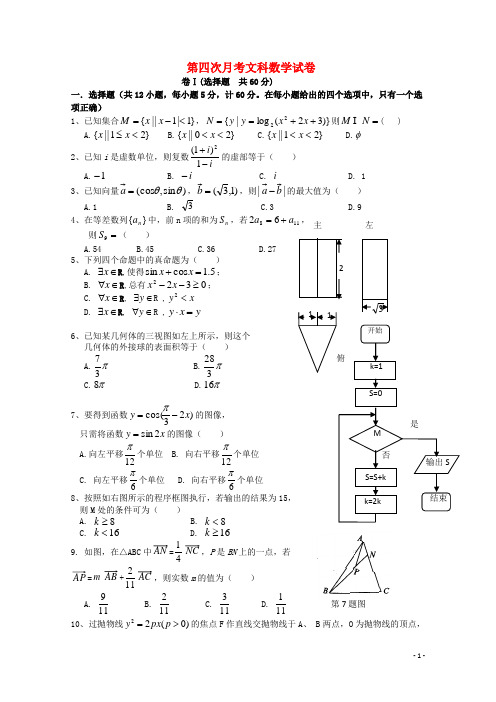
河北省武安县高三数学上学期第四次月考试题 文

2013-2014学年河北省衡水中学高三(上)第四次调考数学试卷(文科)

河北省武安县高三数学上学期第四次月考试题文

河北省邯郸市2013届高三四校联考数学(文)试题

2017年河北省邯郸市武安三中高三上学期期中数学试卷含解析答案(文科)

2013秋高三上册数学第一次摸底考试文科试题(含答案)

河北省邯郸市武安西交中学高三数学文月考试题含解析

河北省邯郸市武安西交中学高三数学文月考试卷含解析

河北省武安市第三中学高三数学上学期第一次月考试题

河北省武安三中2013届高三上学期第四次月考理科综合试题.pdf

河北省武安市第三中学等校2024届高三上学期期中联考数学试题

河北省武安三中2013届高三上学期第四次月考数学文试题 Word版含答案

河北省武安县高三数学上学期第四次月考试题文