QC小组绘制直方图的注意事项

合集下载

QC七大手法--(直方图2)讲义

品管七大手法
直方圖的制作實戰區
直方圖制作
第一步:搜集數據并記錄
首先制作查檢表,用于記錄數據. 搜集數據時應注意: 事先利用層別法進行分組,可得到事倍成半的功效.
樣本數量應大于30PCS
直方圖制作
第二步:找出數據中的最大值(MAX)與最小值(MIN)及全距(R)
例:某廠之成品尺寸規格為145+15,今按隨機抽樣方式抽取60個樣本
例題: 第一組:(121-1/2) ～﹝(120-1/2)+4﹞=120.5 ～124.5 第二組:124.5 ～128.5 第三組:128.5～132.5 第四組:132.5～136.5 第五組:136.5～140.5 第六組:140.5～144.5 第七組:144.5～148.5
直方圖制作
第六步:求組中點
(2) 橫軸與縱軸各取適當的單位長度. 再將各
組界標在橫軸上, 各組界為等距離.
次
數
(3) 以各組內之次數為高, 組距為底; 并畫成矩形,
則完成直方圖.
(4) 在圖的右上角記入數據履歷(如數據數, 平均值, 標準差), 并劃出規格之上, 下限.
(5) 記入必要事項: 品名, 工程名, 日期, 作者等.
直方圖制作
第七步:及數據分配次數
²Õ ¸¹
²Õ ¬É
²Õ ¤ ÂI
º¹ °O
1
120.5 ã¡ 124.5 122.5 \
2
124.5 ¡ã 128.5 126.5 \\
3
128.5¡ã 132.5 130.5 \\\\ \\\\ \\
4
132.5¡ã 136.5 134.5 \\\\ \\\\ \\\\ \\\
1. 公式計算:K=1+3.32logn

QC七大手法-直方图

QC七大手法-直方图一、什么是QC七大手法QC（Quality Control）七大手法是一种常用于解决质量问题和提高产品质量的方法。

它包含了七种常用的统计学手法，分别是：直方图、控制图、散点图、因果图、帕累托图、箱线图和流程图。

这些手法可以帮助我们分析和解决质量问题，以达到质量改进的目的。

本文将重点介绍其中一种手法——直方图。

二、直方图的基本概念直方图是一种用于显示数据分布情况的图表。

它通过将数据划分为一系列间隔，然后统计每个间隔内数据出现的频率，最终通过矩形条来呈现数据的分布情况。

直方图通常用于展示连续变量或离散变量的频率分布，可以帮助我们了解数据的分布规律和集中趋势。

三、绘制直方图的步骤1. 数据收集首先，我们需要收集相关的数据。

这些数据可以是产品的尺寸数据、质量数据或其他与质量有关的数据。

2. 数据整理在绘制直方图之前，我们需要对数据进行整理和分类。

将数据按照一定的规则进行分组，并记录每组数据的频数。

3. 确定间隔和组数在进行数据分组时，我们需要确定数据的间隔和组数。

间隔一般是根据数据的最大值和最小值来确定的，组数可以根据实际情况进行调整。

4. 绘制直方图绘制直方图可以使用各类数据分析软件、编程语言或绘图工具。

在绘图时，我们需要将每组数据的频数表示为相应的矩形条，并将矩形条按照一定的间隔排列。

5. 添加标题和注解为了使直方图更具可读性，我们可以添加标题和注解。

标题可以简要描述直方图的目的和内容，注解可以解释数据的分布情况和统计指标。

6. 分析直方图通过观察直方图，我们可以了解数据的分布情况和集中趋势。

例如，我们可以通过直方图来判断数据是正态分布、偏态分布还是离散分布。

同时，我们还可以通过直方图来确定数据的中位数、均值和标准差等统计指标。

四、直方图在QC中的应用直方图在QC中有广泛的应用，可以帮助我们分析和解决质量问题。

以下是直方图在QC中的一些常见应用场景：1. 检测质量问题通过绘制产品尺寸、质量或其他相关数据的直方图，我们可以快速发现质量问题。

品管(QC)七大手法之直方图

直方图的制作
❖ 製作步驟:
1.蒐集數據並且記錄在紙上。
2.找出全體數據中之最大值（L）與最小值（S）
3.定全距（R）＝最大值（L）－最小值（S）
4.決定組數
1.史特吉斯公式組數：K＝1＋3.32log n
ห้องสมุดไป่ตู้
n＝數據個數 2.組數決定參考表(經驗法則)
數據數目 50～100 100～250 250 以上
目录 1.直方图定义 2.直方图功用与用途 3.直方图的分类 4.直方图的案例
直方图定义
定义：
將所蒐集的數據、特性值或結果值，在橫軸上適當地區分成幾個相等區間，並將各區間內測定值所出現的次數累加起來，用柱形畫出的圖形.
直方图功用与用途
❖使用目的:
1.測知製程能力. 2.測知數據的真偽. 3.測知分配型態. 4.計算產品不良率. 5.調查是否混入兩個以上的不同群體. 6. 藉以訂定規格界限. 7. 規格與標準值比較. 8. 設計管制界限是否可用於製程管制
型態
對策
先加以層別，再重新製作直方圖。
直方图的型態、形成原因與對策:
型號 3
型別高原型
特徵
中間部分特別高
作業系統狀況
不同平均值的分配混合在一起所致。
型態
對策
先加以層別，再重新製作直方圖。
型號 4
型別絕壁型
特徵一端不見
作業系統狀況
‧當全部數據或製程本身全部都被檢查過。 ‧下限規格以外的數據被剔除。
組數 6～10 7～12 10～20
直方图的制作
5.定組距（H）＝R／K＝全距／組數 6.求各組上、下組界
第一組下組界＝最小值－最小測定值／2 第一組上組界＝下組界＋組距（以此類推） 7.決定組的中心點。（上組界＋下組界）／2＝組的中心點 8.製作次數分配表。 9.製作直方圖。 10.填上主題、規格、平均值、數據來源、日期等資料.

QC七大手法--直方图

5. 雙峰型
形狀: 有二個高峰出現.
說明: 此為兩種分配相混合形成的.
(1) 兩臺機器所生產之產品混在一起. (2) 亦可能來自兩種不同廠商或原料. (3) 不同的操作人員所造成.
四. 直方圖常見型態
6. 離島型
形狀: 在左端或右端形成小島.
說明: (1) 測定有錯誤.
(2) 工程調節錯誤. (3) 使用不同原料造成. 一定有羿常原因存在, 只要去除, 即可制出合乎規格的產品.
【品管中心培訓教材】
教材編號 : QC001-1
Quality
版
本 : 1.0
知識就是力量
核準: 審核: 編寫：
前言

現場工作人員經常要面對一大堆的數據, 這些數據非常的多. 它們到底可以提供我們什么情報呢?

用直方圖將數據加以整理,制程能力及品質散布的狀態即呈現在眼前. 我) 檢驗員對定值有偏好現象.
(2) 或有假造數據. (3) 測量儀器不夠精密. (4) 組數寬度不是倍數時, 亦有此狀.
四. 直方圖常見型態
3. 偏態型
圖形: 高處偏向一邊, 另一邊低, 拖長尾巴.
為偏態分配, 分偏右型, 偏左型.
偏左型
說明: 尾巴拖長時, 應檢討技術上是否能接
受, 工具磨損或松動時, 也有此情形發生.
按次數分配如下:
個數
6 5 4 3 2 1
2 1 3 2 1 1 SL
u
SU 6
4
3 4 5 6 7 8 9 10
尺寸
由上圖與規格比較, 超過規格的有5個Tray, 而總數為20pcs, 因此不良率為2.5%
五.直方圖的應用
3. 調查是否有混入兩個以上不同群體.

QC七大手法直方图介绍

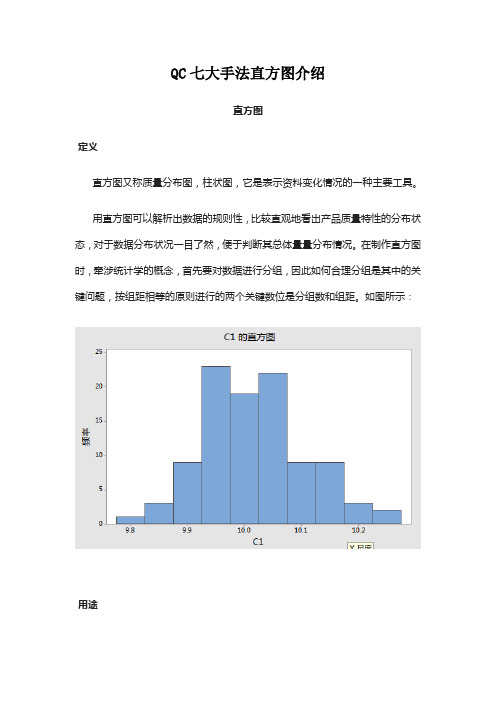
QC七大手法直方图介绍直方图定义直方图又称质量分布图，柱状图，它是表示资料变化情况的一种主要工具。

用直方图可以解析出数据的规则性，比较直观地看出产品质量特性的分布状态，对于数据分布状况一目了然，便于判断其总体量量分布情况。

在制作直方图时，牵涉统计学的概念，首先要对数据进行分组，因此如何合理分组是其中的关键问题，按组距相等的原则进行的两个关键数位是分组数和组距。

如图所示：用途作直方图的目的就是通过观察图的形状，判断生产过程是否稳定，预测生产过程的质量。

具体来说，作直方图的目的有：判断一批已加工完毕的产品；验证工序的稳定性；为计算工序能力搜集有关数据。

直方图将数据根据差异进行分类，特点是明察秋毫地掌握差异画法1)集中和记录数据，求出其最大值和最小值。

数据的数量应在100 个以上，在数量不多的情况下，至少也应在50 个以上。

我们把分成组的个数称为组数，每一个组的两个端点的差称为组距。

2)将数据分成若干组，并做好记号。

分组的数量在5－12 之间较为适宜。

3)计算组距的宽度。

用最大值和最小值之差去除组数，求出组距的宽度。

4)计算各组的界限位。

各组的界限位可以从第一组开始依次计算，第一组的下界为最小值减去最小测定单位的一半，第一组的上界为其下界值加上组距。

第二组的下界限位为第一组的上界限值，第二组的下界限值加上组距，就是第二组的上界限位，依此类推。

5)统计各组数据出现频数，作频数分布表。

6)作直方图。

以组距为底长，以频数为高，作各组的矩形图。

1.4 直方图在应用上应注意事项1)直方图可根据山形图案分布形状来分析2)产品规格分布图案可与目标，标准规格作比较，有多大的差异3)是否必要再进一步层别化4)确认直方图是否具有合适的比例5)直方图最好和其它图如控制图等结合使用，因为直方图无法显示过程随时间的变异直方图分析正常型正常型是指过程处于稳定的图型，它的形状是中间高、两边低，左右近似对称；近似是指直方图多少有点参差不齐，主要看整体形状孤岛型在直方图旁边有孤立的小岛出现，当这种情况出现时过程中有异常原因。

QC七工具之直方图

QC七工具之直方图直方图（Histogram）是频数直方图的简称，它用一系列宽度相等、高度不等的长方形表示数据的图。

长方形的宽度表示数据范围的间隔，长方形的高度表示在给定间隔内的数据数。

直方图的作用是：显示质量波动的状态；直观地传递有关过程质量状况的信息；掌握过程的状况，确定在什么地方集中力量进行质量改进工作。

图一正常型直方图图一显示的就是一家电阻公司收集了一个批次的产品阻值数据，并以此为基础绘制而成的一张直方图。

观察和分析直方图时应着眼于整个图形的形状。

在正常型的直方图里，中部有一个山峰，左右两边逐渐降低，近似对称。

这时，可以大致判定流程处于稳定状态，图一所示的直方图就属于这种状态。

应用直方图时，应当注意以下事项：1.当出现非正常型直方图，如偏向型直方图、双峰型直方图、孤岛型直方图等时，往往提示流程存在着严重的变异源，需要我们进一步调查原因。

2．即使直方图的形状呈正常形态，也不能马上断定工序合乎要求，还需要将此图与规格界限进行比较，以分析判断工序满足公差要求的程度。

3．不要孤立地分别使用直方图，如果能够将同一过程中多个变量的直方图整合到一起观察和分析，常常会有意想不到的效果。

接下来的三个小案例就是借助JMP软件对以上介绍的直方图原理的活学活用。

图二显示的就是一种双峰型直方图，之所以会出现两个山峰，是由于数据来自不同的总体，如把两个工人、两批原材料或两台设备生产的产品混在一起造成的。

JMP软件可以把这两个不同总体的分布拟合形状和分布参数（如Location参数“平均值”和Dispersion参数“标准差”）都辨别和估算出来。

图三显示的则是一张标记了上公差USL、下公差LSL和目标值Target的直方图，同时辅以包含Cp、Cpk、缺陷百分比Percent、百万分之缺陷数PPM和西格玛质量水平Sigma Quality等过程能力指数的表格，清楚地说明虽然该流程处于稳定状态，但是流程的能力还没有达到理想要求，应当设法采取措施，减少流程波动。

QC手法应用(直方图)

ห้องสมุดไป่ตู้68% 16% 1σ
99.73% 13.5%
3σ
1.7PPM
99.999966% 1.7PPM 6σ
平均值与标准偏差的关系
• X 1 68.26% • X 2 95.44% • X 3 99.73 % • X 4 99.9937% ~6300PPM • X 5 99.999943% ~57PPM • X 6 99.99999976% ~ 3.4PPB
项目改善教育训练教材
QC手法应用之四 (直方图法)
问题的产生
目前状态
预想状态未知
好奇与求知
现有状态
理想状态已知
与目标不符
日常状态
特殊状态异常
与常态不符
问题的分类
一般性问题
用经验法则来解决
偶发性问题(可能运用机智与决断仅此一次)
新型问题
必须深思熟虑,以建立新政策
业务方面的问题管理方面的问题
制作直方图的步骤
(L)，最小值(S)，找出全距(R) R＝L－S
(M)M ≒ n 求出組距 (h ) 組距 (h)＝ M R＝ LM S
组数与样本之关系
样本数 50以下 50～100 100～250 250以上
组数 5～７ 6～10 7～12 10～20
直方图的型态
直方图的应用
加强工作教导、修编手册与程序、改善工作环境与条件
4
具问题意识、发现问题的能力、系统思考的能力
策略方面的问题预测变化的能力、信息搜集力、判断力、创造力、综合力
直方图
就其分析资料所成的次数分配表在平面坐标上第一象限，沿横轴以各资料组，组界为分界，组距为底边，以各组次数为高度，在每一组距上画上一矩形，如此所绘成的图形称之。

QC七大手法---直方图1汇编

9
Light Master Technology（Ning Bo）INC.
◆组数K：对于所研究的数据进行分组，所分组的个数就是该直方 ± í
Êý ¾Ý ¸ö Êý £¨n£©
× é Êý £¨k©£
50ÒÔ ÄÚ
5~7
50-100
6~10
100-250
7~12
Light Master Technology（Ning Bo）INC.
Property of Light Master Corporation
一、直方图的定义
Light Master Technology（Ning Bo）INC.
直方图又称品质分布图，它是根据生产过程中收集来的品质数据分布情况，画成的以组距为底边、以次数为高度的一系列连接起来的直方型排列的图。
250ÒÔ ÉÏ
10~12
◆组距h：组距表示的是所分成组的跨度区间，在图上体现的则是柱
子的宽度，且所有的组距都是相等的。
h=R/K
◆方差V：方差（又称分散）：偏差平方和的平均值
v (x1 x)2 (x2 x)2 ... (xn x)2 /(n 1)
◆标准差σ(S)：各数据偏离平均数的距离的平均数
14 12 10
8 6 4 2
303 306 309 312 315 318 321
表示特性值(尺寸、重量、时间等计量值）频度分布的柱状图。由此图可计算出该特性值分布的平均值、标准偏差、工序能力指数等参数。
Property of Light Master Corporation
5
二、直方图的用途
Property of Light Master Corporation

QC直方图应用控制图常见的错误

职业资格：项目管理师、二级建造师、招标师
讲授课程：采购管理、投资项目管理、精益管理、
QC小组活动、科技创新等
目录
一
控制图的概念
二
控制图的作用
三
常见的错误
一、控制图的概念
控制图
又叫管理图、休哈特图，是用于区分由异常原因（系统原因）引起的波动或是由过程固有的随机原因引起的波动的一种工具。
控制图图例
三、常见的错误
2、用控制图进行要因确认 “应招尽招”
示例
原因分析阶段，使用控制图进行要因确认，较为常见。
三、常见的错误
3、不对控制图的排列缺陷进行分析判断 “应招尽招”
控制图异常的8个判定准则
三、常见的错误
3、不对控制图的排列缺陷进行分析判断 “应招尽招”
控制图异常的8个判定准则
三、常见的错误
（3）当“5M1E”发生变化时，未及时调整控制线。
（4）画法不规范或不完整。
谢谢不足之处，制图常见的错误
安徽省烟草公司合肥市公司周存根
授课人简介：
周存根，男，汉族，1982年1月生，中共党员， 2002年退出现役（义务兵），2007年毕业于安徽师范大学经济学专业获得经济学学士学位，同年进入烟草行业。2013年毕业于安徽师范大学伦理学专业获得哲学硕士学位，现为合肥市烟草公司办公室投资兼资产管理员。
二、控制图的作用
1、用于诊断
分析生产过程是否处于统计控制状态（稳定状态）；
2、用于控制
确定合适需要对过程进行调整，以控制生产过程，保持相应的稳定状态；
3、用于确认确认某一生产过程是否得到了改进。
三、常见的错误
1、过程不稳定时用控制图 “应招尽招”

QC(旧)七大手法之五——直方图(histogram)

QC （旧）七大手法之五——直方图（histogram ）第一小节直方图的观察分析一．定义众所周知在相同的条件下制造出来的产品，其质量特性也不完全相同，但也不会相差太大，总是在一定范围内波动，而且这种波动有一定的规律性，直方图就是直观而形象地把质量分布规律用图形表示出来的统计工具。

直方图（histogram ）是频数直方图的简称，又叫质量分布图、矩形图、柱形图、柱状图、频数图。

是指通过对生产过程中产品质量的分布状态的描绘与分析，来判断生产过程质量的一种常用方法，它是工序质量控制统计方法中的主要工具之一(另一工序质量控制工具就是控制图)。

直方图是一种几何图表，它是根据从生产过程中收集到的质量数据（通常不能少于50个，最少不能少于30个数据）分布情况，画成以组距为底边、以频数为高度的一系列连接起来的直方形矩形图。

十六世纪末十七世纪初英格兰人普莱菲和德国地理学者科洛玛是使用直方图的先驱者。

直方图的分类：直方图根据使用的各组数据是频数还是频率分为频数直方图与频率直方图；在表示分布时又分为一般直方图和累计直方图两种。

直方图的基本形式（格式）：说明：横坐标表示产品的质量特性值（如尺寸、重量等计量值），在横坐标上划分了若干个间距相等的区间（即矩形的宽度表示数据范围的间隔）。

纵坐标表示在n 个数据中，落在各个区间里的频数（即反复出现在该区间的次数）（即高度表示在给定的间隔内数据出现的频数即数目）。

一个个直方形，其宽度取决于区间的宽度，其高度取决于该区间的频数（频数常用f 表示），n 表示样本大小(即样本量)，X 表示样本中全体数据的平均值（表示分布中心），S 表示样本的标准偏差（S 表示质量特性离散程度，有的也称标准差）。

直方图适用于对于大量计量值数据进行整理加工，找出其统计规律，也就是分析数据的形态，以便对其整体的分布特征进行推断（即通过变化的高度形态表示数据的分布情况）。

直方图是从总体中随机抽取样本，对从样本中获得的数据进行整理后，用一系列等宽的矩形来表示数据。

QC七大手法之直方图教育训练讲义

QC七大手法之直方圖教育訓練講義一、何謂直方圖？將所彙集的數據、特性值或結果值，用一定的範圍在橫軸上加以分成幾個相等的區間，將各區間內的測定值所出現的次數累積起來的面積用柱型畫出的圖形。

二、目的直方圖可以了解產品在規格標準之下分布的型態、製程的中心值與差異的大小等情形。

三、實施步驟1彙集數據並且紀錄在紙上彙集數據時對於抽樣分佈必須特別注意，不可指取某些部份樣品，應就全部均勻的加以抽查。

數據的彙集最好在50~100組之間。

2.找出數據中最大值與最小值將最大值與最小值分別找出，紀錄在每行底列，再根據底列的數據找出全體的最大值與最小值。

3.計算全距（R）R＝最大值－最小值4.決定組數與組距組數就是直方圖柱型數量，組數的計算是根據數量的多寡來決定。

可由數據分組數參考表（表1），即可決定組數。

表1另外也可以用公式計算。

公式：組數（K）＝1＋3.23log n組距的計算方式：組距＝全距÷組數為了方便計算平均數與標準差，組距通常是2、5或10的倍數。

5.決定各組的上組界與下組界組界的決定由最小一組的下組界為基準以下列公式求出：最小一組的下組界＝全部數據的最小值－量測值最小位數（一般是1）×0.5 最小一組的上組界＝最小一組的下組界＋組距最小二組的下組界＝最小一組的上組界如此各組依此類推，計算到最大一組的上組界。

6.決定組的中心點計算方式：（上組界＋下組界）÷2 ＝組的中心點1.製作次數分配表將所有的數據依照數值的大小記入各組的組界內，然後計算各組界的次數。

2.製作直方圖以橫軸表示測量值的變化，縱軸表示次數，橫軸與縱軸取出適當的長度標上記號，然後將各組的組界分別標示在橫軸上，各組次數的多少則用柱型畫在各組距上，柱與柱之間不能有間隙，如此就完成直方圖。

可在空白處填上主題、規格、平均值、數據來源、日期等資料。

一、注意事項1.直方圖可根據山型圖案分佈形狀來觀察製品工程是否正常。

2.產品規格分佈圖案可與目標、標準規格做比較，看看是否差異過大。

QC小组活动应注意的问题

QC小组活动应注意的问题本文依照QC小组活动PDCA循环各步骤，具体阐述在每一步骤活动时的关键细节把握。

从活动步骤具体实施、工具使用、成果发表各个层面进行分析总结。

标签：QC小组；活动步骤；工具使用；成果发表；问题QC小组是企业员工围绕企业经营战略、方针目标和现场存在的问题，以改进质量、降低消耗、提高人的素质和提高效益等为目的组织起来的，运用管理理论和方法开展活动的小组。

多年来的实践证明，QC小组活动是企业一项基础性的管理工作，是企业持续改进，不断完善，不断自我超越与创新的有效手段，是企业提高市场竞争力的有效途径。

通过近几年开展QC小组活动实践和参加国家、省、集团公司组织的QC小组活动成果发布，揣摩了一些QC活动经验。

现结合个人切身感受，总结在开展QC活动的时应注意的一些事项：1 课题选择：1.1 课题选择应“小、实、活、新”。

“小、实、活、新”是QC小组开展活动的特点，小课题一般是施工现场急需解决的问题，员工对现状比较清楚，成立小组开展活动，也比较容易解决。

如果课题选大了，所需达到的目标就多，就会涉及更多人员，花费时间长，超过小组能力范围，不宜成功，即便勉强完成活动目标，评审时也会使人怀疑其真实性、科学性。

也可以选择一些新颖的课题，新技术、新工艺作为QC攻关的对象，活动效果比较显著。

课题的名称要精炼油，不宜太长，直接针对需要解决的问题。

注意不要将对策加在课题名称里，因为在活动初期选择课题期间并没有制定出对策。

1.2 选题理由应直观明了。

选题理由切不可含糊不清，缺乏依据，选题理由必须充分、明了、实事求是，不可用宏观的口号式方针。

最好使用图表形式，这样可以更直观的说明情况。

2 现状调查：2.1 调查结论要明确，要有说服力。

现状调查的主要目的是找出主要问题，主要问题最多不能超过两个，这是为以后的原因分析埋下伏笔。

另外，若想要调查结论具有说服力，数据的搜集整理是重点，调查要从现象的各个相关面展开，只有使用充足的数据才能说明事实，不可只凭小组讨论的表面现象得出结论。

QC小组-绘制直方图的注意事项

14
8 35.5～40.5 38 / / / / / / / / / /
10
9 40.5～45.5 43 / / /
3
3.直方图旳绘制
6、按数据值百分比画横坐标。 7、按频数值百分比画纵坐标，以观察值数目或百分数表达。（摘自《质量管理小组理论与措施》（2023年版）第183页
（6）按数据值百分比画横坐标。在横坐标上以每组相应旳组距为底。（7）按频数值百分比画纵坐标。以该组旳频数为高。
10
5
0
重量(cg)
0 0.5
5.5
10.5
15.5
20.5
25.5
35.5 30.5
45.5 40.5
50.5
成品重量直方图
4.直方图绘制旳注意事项
1
数据搜集是作直方图旳第一步，其数据一般应不小于50个。数据太少所作出旳直方图不能确切地反应分析旳形态，计算出旳原则偏差s精度也会降低诸多。
长方形旳宽度表达数据旳间隔长方形旳高度表达在给定间隔内旳数据值
2.直方图旳作用
（1）显示质量波动旳状态；（2）较直观地传递有关过程质量情况旳信息；（3）根据质量数据波动情况，掌握过程旳能力情况和受控状态，从而拟定在什么
地方集中力量进行质量改善工作。
(a)
(b)
(c)
(d)
(e)
常见旳直方图形态
例题：以某厂生产旳产品重量为例，对直方图旳应用程序加以阐明。该产品旳重量规范要求为1000＋50 克。
（1）搜集数据
某产品重量数据表
测量单位（g）
43 28 27 26 33 29 18 24 32 14
34 22 30 29 22 24 22 28 48

QC小组绘制直方图的注意事项课件

38 / / / / / / / / / /
9学习交4流04.55P.P5～T
43 / / /
8
10 45.5～ 48 / / /
3.直方图的绘制
6、按数据值比例画横坐标。 7、按频数值比例画纵坐标，以观测值数目或百分数表示。（摘自《质量管理小组理论与方法》（2013年版）第183页
（6）按数据值比例画横坐标。在横坐标上以每组对应的组距为（7）按频数值比例画纵坐标。以该组的频数为高。
数据记录表No：————
频数分布表
—— 年 ——月——日 N
组
组界
组中
号小→大
值
1 0.5～5.5 3 /
频数统计
2 0.5～10.5 8 / / /
3
10.5～ 15.5
13 / / / / / /
4
15.5～ 20.5
18 / / / / / / / / / / / / / /
5
20.5～ 25.5
学习交流PPT
7
3.直方图的绘制
5、编制频数分布表。把各组的上下界限值分别填入频数分布表内，并把数据表中的各个数据“对号入座”地列入相应的组，统计落入各组的数据个数，即各组频数（f ）。（摘自《质量管理小组理论与方法》（2013年版）第183页
（5）编制频数分布表。把各组的上下限值分别填入频数分布表内，据表中的各个数据列入相应的组，“对号入座”地列入相应的组，并各组频数（f）（见下表）
绘制直方图的注意事项
学习交流PPT
1
目录 CONTEN
TS
01 直方图的概念 02 直方图的作用 03 直方图的绘制 04 直方图绘制注意事项 05 用Minitab绘制直方图

品质管理QC七大手法之六直方图

10 8 6 4 2 0
6.高原型
不同平均值的分配混合在一起,应层别之后再作直方图
10 9 8 7 6 5 4 3 2 1 0
与规格值或标准值作比较
1.符合规格
A.理想型:制品良好,能力足够.制程能力在规格界限内,且平均值与规格中心一致,平均值加减4倍标准偏差为规格界限,制程稍有变大或变小都不会超过规格值是一种最理想的直方图.
层别作解析
第六章
一.何谓直方图?
直方图
直方图就是将所收集的数据.特性或结果值,用一定的范围在横轴上加以区分成几个相等的区间,将各区间内的测定值所出现的次数累积起来的面积用柱形画出的图形.
第六章
二.直方图的制作步骤:
直方图
1..
2.找出数据中的最大值与最小值. 3.计算全距. 4.决定组数与组距. 5.决定各组的上组界与下组界. 6.决定组的中心点. 7.制作次数分配表. 8.制作直方图.
100~250 250个以上
组数 6~10
7~12 10~20
3.组距
组距=全距/组数组距一般取5,10或2的倍数
4.决定各组之上下组界
最小一组的下组界=最小值-测定值之最小位数/2
测定值的最小位数确定方法:如数据为整数,取1;如数据为小数,取小数所精确到的最后一位 (0.1;0.01;0.001……) 最小一组的上组界=下组界+组距
2.决定组数组数过少,虽可得到相当简单的表格, 但却失去次数分配的本质;组数过多,虽然表列详尽,但无法达到简化的目
的.(异常值应先除去再分组).
分组不宜过多,也不宜过少,一般用数学家史特吉斯提出的公式计算组数,其公式如下: K=1+3.32 LgN

品质管理QC七种(大)手法工具--直方图

品质管理QC 七种(大)手法工具--直方图质量的偏差是无法回避的，判断质量的偏差是否由于偶然原因引起的，有必要对质量偏差状况进行实际测量和采集数据。

下表为某一制品的100个对象，测量其长度，得到以下数据：从如此罗列的数据表是不能知道制品长度的偏差状态的。

为了把握长度的偏差状态，有必要将其数据表换写成能读取偏差状态的频数表。

直方图是将数据存在的区域分成几个区间，各区间里分布的数据的出现次数做成频数表，以柱形的高度来表示各区间的所属次数，能够清楚地知道偏差的状态。

一、直方图的作法手顺1：收集数据作成直方图，采集数据的数是50—250，通常情况下100左右为佳。

手顺2：求出数据中的最大值和最小值具体的作法：可以先找出各行（各列）中的最大值和最小值，然后在这些值中找出最大值和最小值。

行的最大值作记号 ●，最小值作记号▲，然后找出●记号中的最大值，▲记号中的最小值。

X max ＝199， Xmin ＝170手顺3：求出最大值和最小值的差（即数据波动的范围）范围 R ＝Xmax-Xmin ＝199－170 ＝29手顺4：决定假定区间数假定区间数＝n如果n 不为整数，则按四舍五入法计算手顺5：求出测定单位（测定值的最小刻度）即所有数据间差的最小值。

本例中测定单位为1mm 。

手顺6：决定区间的幅度区间的幅度h=nmaxmax 假定区间数数据最小值数据最大值X X因测定单位为1mm ，所以是1的整数倍，离2.9最近的值是3。

手顺7：求出区间的境界值区间的境界值规定在测定单位的1／2之处。

这是因为区间的境界值和数据值相同，就不清楚其数据值应放在上区间或下区间。

（1）由以下公式求出第一区间的下境界值：第一区间的下侧界限值=数据最小值—2测定单位=170—21=169.5（2）因为级的幅度=3，所以：第一区间的上限境界值=第一区间的下限境界值+区间的幅度=169.5+3=172.5（3）以此类推，按照这样的顺序求出第二、三……区间的上下限境界值，直到最终区间的上限境界值超过数据最大值（199），即数据最大值被包括在最终区间内。

Qc七大手法之直方图

Xi - X0 μ=
, X0=次数最多一组的组中点
组距(h)
Xi=各组组中点
⑼众数(M) 次数分配中出现次数最多组的值。
第八章直方图 117
例：
不合格数
3
5
7
9
10
11
次数
11
15
18
24
13
16
次数最多为 24，不合格数是 9，故众数为 9。
⑽组中点(m)
一组数据中最大值与最小值的平均值，
（上组界+下组界）÷ 2=组中点
118 品管七大手法
例:某厂成品尺寸规格为 130 至 160mm，今按随机抽样方式抽取 60 个样本，其测定值如附表，试制作直方图。
138 142 148 145 140 141 139 140 141 138 138 139 144 138 139 136 137 137 131 127 138 137 137 133 140 130 136 128 138 132 145 141 135 131 136 131 134 136 137 133 134 132 135 134 132 134 121 129 137 132 130 135 135 134 136 131 131 139 136 135
步骤 2：找出数据中的最大值(L)与最小值(S) 先从各行（或列）求出最大值，最小值，再予比较。最大值用“□”框起来，最小值用“○”框起来
得知：
EX: No.1 No.2 No.3 No.4 No.5 No.6 138 142 148 145 140 141 139 140 141 138 138 139 144 138 139 136 137 137 131 127 138 137 137 133 140 130 136 128 138 132 145 141 135 131 136 131 134 136 137 133 134 132 135 134 132 134 121 129 137 132 130 135 135 134 136 131 131 139 136 135

《QC七大手法直方图》

8 下限
7 6 5 4 3 2 1 0
上限
编辑课件
C.表示製程之生產完全沒有依照規格去考慮,或規格訂得不合理,根本無法達到規格.
7 下限
6 5 4 3 2 1 0
上限
编辑课件
實例1
某電纜廠有兩臺生產設備,最近,經常有不符合規格值(135~210g)異常產品發生,今就A,B兩臺設備分別測定 50批產品,請解析並回答下列回題: 1.作全距數據的直方圖. 2.作A,B兩臺設備之層別圖 3.敘述由直方圖所得的情報
次數
SL=135
20
SU=210
18
16
15
14
13
12
10
8
7
7
6
4
42
2
1
1
0 122.5 130.5 138.5 146.5 154.5 162.5 170.5 178.5 186.5 194.5 202.5 210.5
組中點
编辑课件
4.結論
項目
全體
A設備
B設備
形狀
稍偏左
正常
稍偏左
分佈中心與規格中全部在規格界分佈中習與
编辑课件
五.與規格值或標準值作比較
1.符合規格 A.理想型:制品良好,能力足夠.制程能力在規格界限
內,且平均值與規格中心一致,平均值加減4倍標準差為規格界限,制程稍有變大或變小都不會超過規格值是一種最理想的直方圖.
8 7 6 5 4 3 2 1 0
编辑课件
B.一側無餘裕:制品偏向一邊,而另一邊有餘裕很多,若製程再變大(或變小),很可能會有不良發生,必須設法使製程中心值與規格中心值吻合才好.
1.求全距 2.決定組數