八年级数学《1.1 分式--分式的值》教学课件(1)

合集下载

人教版八年级上册数学《分式的基本性质》分式PPT教学课件(第1课时)

同类题检测：平板推题
1.下列分式中，是最简分式的是
(填序号)．
x3 （1）
3x
；（2）x＋y 2x
；（3） c
c 2＋7c
；（4）xx2＋＋yy2
；（5）xx2＋＋yy2 .
2.下列约分正确的是( ) A． 2(b c) 2 a 3(b c) a 3
B.
(a b)2 (b a)2
1
C.
的分子分母中各项的系数都化为整数，
4
结果为
。
自学释疑、拓展提升
知识点二：分式的约分自学问题：分式约分的关键是约去公因式，对于分子分母是多项式的需
要先进行因式分解后再约去公分母；约分进行式子变形时，易忽略分子与分母的符号变化。学生典型问题展示：展示《15.1.2分式的基本性质（1）课前自测》中第5、6题的正确率，以及做错的学生的错题选项；学案上知识点二学生中存在问题图片展示。问题解决：问题1：观察教材129页例2（1）中的两个分式，在变形前后的分子、分母有什么变化？类比分数的相应变形，你联想到什么？归纳总结：根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分
A．x<0 B.x>0 C.x≠0 D.x≠0且x≠－2
2.下列等式：①
(a b) a b
c
c
x y ;② x
x y x
a b a b
;③ c
c
;④
m n m n
m
m
中,成立的是（）
A．①②
B．③④
C．①③a
D．②④
0.4b
3.不改变分式的值，将分式
2 0.6a 3 b
课前检测和学案整体完成情况较好的学生：图片展示（课前自主学习整体完成优秀展示）

新人教版-八年级(初二)数学上册-分式章节-分式的化简求值(1).讲义教师版

内容基本要求略高要求较高要求分式的概念了解分式的概念，能确定分式有意义的条件能确定使分式的值为零的条件分式的性质理解分式的基本性质，并能进行简单的变型能用分式的性质进行通分和约分分式的运算理解分式的加、减、乘、除运算法则会进行简单的分式加、减、乘、除运算，会运用适当的方法解决与分式有关的问题一、比例的性质： ⑴ 比例的基本性质：a cad bc b d=⇔=，比例的两外项之积等于两内项之积. ⑵ 更比性（交换比例的内项或外项）： ( ) ( ) ( )a bc d a c d cb d b a d bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩交换内项交换外项同时交换内外项⑶ 反比性（把比例的前项、后项交换）：a c b db d a c=⇒=⑷ 合比性：a c a b c d b d b d ±±=⇒=，推广：a c a kb c kdb d b d±±=⇒=（k 为任意实数） ⑸ 等比性：如果....a c m b d n ===，那么......a c m ab d n b+++=+++（...0b d n +++≠）二、基本运算分式的乘法：a c a cb d b d⋅⋅=⋅分式的除法：a c a d a db d bc b c⋅÷=⨯=⋅乘方：()n nn nn a a aa a aa ab b bb b bb b ⋅=⋅=⋅个个n 个＝(n 为正整数) 整数指数幂运算性质：⑴m n m n a a a +⋅=(m 、n 为整数) ⑵()m n mn a a =(m 、n 为整数) ⑶()n n n ab a b =(n 为整数)知识点睛中考要求分式的化简求值（1）⑷m n m n a a a -÷=(0a ≠，m 、n 为整数) 负整指数幂：一般地，当n 是正整数时，1n n a a-=(0a ≠)，即n a -(0a ≠)是n a 的倒数分式的加减法法则：同分母分式相加减，分母不变，把分子相加减，a b a bc c c+±=异分母分式相加减，先通分，变为同分母的分式再加减，a c ad bc ad bcb d bd bd bd±±=±=分式的混合运算的运算顺序：先算乘方，再算乘除，后算加减，如有括号，括号内先算．结果以最简形式存在.一、化简后直接代入求值【例1】先化简再求值：2111x x x---，其中2x = 【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，湖南郴州【解析】原式()()111x x x x x =---()111x x x x-==-当2x =时，原式112x ==【答案】12【例2】已知：2221()111a a a a a a a ---÷⋅-++，其中3a =【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】【解析】222221(1)()4111(1)a a a a a a a a a ---+÷⋅=-=--++-【答案】4-【巩固】先化简，再求值：22144(1)1a a a a a-+-÷--，其中1a =- 【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，安徽省中考例题精讲【解析】()2221144211122a a a a a a a a a a a a --+-⎛⎫-÷=⋅= ⎪----⎝⎭- 当1a =-时，原式112123a a -===---【答案】13【例3】先化简，再求值：211(1)(2)11x x x -÷+-+-，其中x =【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，湖北省十堰市中考试题【解析】原式()()()111121x x x x x +-=⋅+-+-+ ()()12x x x =-+-22x =-当x 时，原式224=-=．【答案】4【例4】先化简，后求值：22121(1)24x x x x -++÷--，其中5x =-．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，广东省肇庆市中考试题【解析】22121(1)24x x x x -++÷--=221(1)2(2)(2)x x x x x -+-÷-+- =21(2)(2)2(1)x x x x x -+-⋅-- =21x x +- 当5-=x 时，原式21x x =+-521512+-=-=-. 【答案】12【巩固】先化简，再计算：231124a a a +⎛⎫+÷ ⎪--⎝⎭，其中3a =．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，湖南省岳阳市中考试题【解析】原式2223221a a a a a a +--⎛⎫=+⨯⎪--+⎝⎭()()22121a a a a a +-+=⨯-+ 2a =+【答案】2a +【例5】当12x =-时，求代数式22226124111x x x x x x x x ⎛⎫++-+-+÷ ⎪--+⎝⎭的值【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】【解析】原式2224(1)1(1)(1)2413x x x x x x x x x x -++=⨯==+--+- 【答案】13【例6】先化简分式22222936931a a a a a a a a a ---÷-+-+-，然后在0，1，2，3中选一个你认为合适的a 值，代入求值．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，广东省深圳市中考试题【解析】原式()()()()223332313a a a a a a a a a a a a +-+-=⋅-=+=--+ 当0123a =，，，时，原式0246=，，，【答案】0，2，4，6【巩固】先化简：22222a b ab b a a ab a⎛⎫-+÷+ ⎪-⎝⎭，当1b =-时，再从22a -<<的范围内选取一个合适的整数a 代入求值．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，贵州省贵阳市中考试题【解析】原式()()()()22221a b a b a ab b a b a a a b a a a ba b +-+++=÷=⋅=-++在22a -<<中，a 可取的整数为101-，，，而当1b =-时，①若1a =-，分式222a b a ab--无意义；②若0a =，分式22ab b a +无意义；③若1a =，分式1a b+无意义．所以a 在规定的范围内取整数，原式均无意义（或所求值不存在）【答案】a 在规定的范围内取整数，原式均无意义（或所求值不存在）【巩固】已知212242xA B C x x x ===--+，，将它们组合成()A B C -÷或A B C -÷的形式，请你从中任选一种进行计算，先化简，再求值其中3=x ．【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】2010年，河南省中考试题【解析】选一：()()()21221242222x x x A B C x x x x x x x +⎛⎫-÷=-÷=⨯= ⎪--++--⎝⎭ 当3x =时，原式1132==- 选二：()21212124222x A B C x x x x x x x -÷=-÷=-=--+--，当3x =时，原式13=【答案】选一：当3x =时，原式1132==- 选二：当3x =时，原式13=【例7】先化简，再求值:224125(2)2[2()](34)(2)a a a a a a a a +++÷--÷-+，其中4a =【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】【解析】原式2224(3)5(2)(2)[2](34)(2)a a a a a a a a +++=÷--÷-+4(3)(2)(2)5(34)(2)2a a a a a a +-+-=÷-++ 4(3)2(34)(2)(3)(3)a a a a a a ++=⋅-+-+4(34)(3)a a =-- 当4a =时，原式441(34)(3)(344)(43)2a a ===--⨯--本题含分式乘方、加、减、乘、除混合运算；与分式四则混合运算类似，分式的四则混合运算的顺序是:先算乘方，再算乘除，后算加减，如有括号，括号内先算．【答案】12【例8】已知22a b ==a bb a-的值．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，湖北荆门市中考试题【解析】∵22a b =+=∴4a b +=，a b -=，1ab =而a b b a -22()()a b a b a b ab ab -+-==∴a b b a -=()()a b a b ab+-==【答案】【例9】先化简，再求值：()()x yy x y x x y -++，其中11x y ==，．【考点】化简后直接代入求值【难度】2星【题型】解答【关键词】2010年，湖南湘潭市中考试题【解析】原式()()22x y xy x y xy x y =-++ ()22x y xy x y -=+()()()x y x y xy x y -+=+x y xy-=当 11x y ==，时，11221x yxy--=== 【答案】2【例10】化简，再求值：11-a b b a ⎛⎫+ ⎪+⎝⎭ab a b ÷+.其中1a =, b =. 【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】2010年，黄石市中考试题【解析】原式()()()()()2b a a b a b a b b a ab a b b++-+=⋅=-+-∵1a b ==，∴原式1b ==，∴=【巩固】先化简，再求值：22112b a b a b a ab b⎛⎫-÷ ⎪-+-+⎝⎭，其中11a b ==-【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】2010年，宣武一模试题【解析】原式()()()()()()22a b a b a b a b a b a b b a b+----=⋅=-++当11a b ==-==【答案】【例11】先化简，再求值：22211x yx y x y x y ⎛⎫+÷ ⎪-+-⎝⎭，其中11x y ==，【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】2010年，广西桂林中考试题【解析】原式2222222x y x y x yx y x y x y ⎛⎫+-=+÷ ⎪---⎝⎭ 22222x y x y x y x y x y++--=⨯- 222x x y xy==当11x y ==，原式22131xy====-【答案】1【例12】求代数式()()22222222222a b c a b c ab ac a a ab ab a b a b -----+⋅÷-++-的值，其中1a =，12b =-，23c =- 【考点】化简后直接代入求值【难度】3星【题型】解答【关键词】【解析】()()22222222222a b ca b c ab ac a a ab ab a b a b -----+⋅÷-++-()()()()2a b c a a b c a b c a b a b a a b a b c a b c a b -+-+--+-=⋅⋅-+--++a b ca b --=+． ∴当1a =，12b =-，23c =-时，原式12123112++=-1313263=⨯=．【答案】133二、条件等式化简求值1. 直接换元求值【例13】已知：2244a b ab +=（0ab ≠），求22225369a b a b ba b a ab b a b--÷-++++的值．【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】2010年，石景山二模【解析】由2244a b ab +=得2b a =原式2a ba b-=+当2b a =时，原式42a aa a-=+1=-【答案】1-【例14】已知：34x y =，求2222222x y xy y x xy y x xy -+÷-+-的值【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】【解析】2222222()()()32()()4x y xy y x y x y y x y x x xy y x xy x y x x y y -++-+÷=÷==-+--- 【答案】34【巩固】已知x y z ，，满足235x y z z x ==-+，则52x yy z-+的值为（） A.1 B.13C.13-D.12【考点】直接换元求值（分式）【难度】4星【题型】选择【关键词】2007年，全国初中数学联赛试题【解析】B ；由235x y z z x ==-+得332y x z x ==，，∴55312333x y x x y z x x --==++ 【答案】13【例15】已知12=x y ，求2222222-⋅+-++-x x y y x xy y x y x y 的值．【考点】直接换元求值（分式）【难度】2星【题型】解答【关键词】2010年，海淀一模【解析】y x y y x y x y xy x x-++-⋅+-2222222 22()()2()x x y x y yx y x y x y -+=⋅++--22()x y x y x y =+--2()()x y x y +=-．当21=y x 时，x y 2=. 原式2(2)6(2)x x x x +==--.【答案】6-【例16】已知221547280x xy y -+=，求xy的值. 【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】【解析】221547280x xy y -+=，∴(37)(54)0x y x y ++=，∴370x y +=或540x y +=，由题意可知:0y ≠，73x y =-或45x y =-. 【答案】45-【巩固】已知22690x xy y -+=，求代数式 2235(2)4x yx y x y+⋅+-的值. 【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】2010年，海淀二模【解析】22690x xy y -+=，2(3)0x y -=．∴ 3x y =． ∴原式35(2)(2)(2)x yx y x y x y +=⋅++-352x yx y +=-3(3)52(3)y yy y+=-145=．【答案】145【例17】已知x =，求351x x x ++的值．【考点】条件等式化简求值【难度】4星【题型】解答【关键词】降次，整体置换【解析】21x -=21x x =+，0x ≠．则()233245555111x x x x x x x x x x x++++=====【例18】已知123a b c a c ==++，求ca b+的值．【考点】直接换元求值（分式）【难度】4星【题型】解答【关键词】第8届，华罗庚金杯复赛【解析】23b c a a c a +=⎧⎨+=⎩22b c a c a +=⎧⇒⎨=⎩02b c a =⎧⇒⎨=⎩，所以220c aa b a ==++．【答案】2【例19】已知22(3)0x y a b -+-=，求32223322232332a x ab y b xya x ab y b xy++++的值．【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】第9届，华罗庚金杯总决赛1试【解析】由已知可得：2y x =，3a b =，故原式7297=. 【答案】7297【巩固】已知2232a b ab -=，0a >，0b >，求证：252a b a b +=- 【考点】直接换元求值（分式）【难度】4星【题型】解答【关键词】【解析】由已知可得22230a ab b --=，则(3)()0a b a b -+=，所以3a b =或a b =-∵0a >,0b >，∴3a b =，则23255322a hb b b a b b b b ++===-- 【答案】52【巩固】已知分式1x y xy+-的值是m ，如果用x ，y 的相反数代入这个分式，那么所得的值为n ，则m 、n 是什么关系？【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】【解析】由题可知：()()()1.1x y m xy x y n x y +⎧=⎪-⎪⎨-+-⎪=⎪---⎩，①② 由②得：11x y x y n m xy xy--+==-=---． ∴m n =-，∴0m n +=．所以m n ，的关系为互为相反数．【答案】m n ，的关系为互为相反数【例20】已知：233mx y +=，且()22201nx y x y -=≠≠-，．试用x y ，表示m n．【考点】直接换元求值（分式）【难度】4星【题型】解答【关键词】【解析】∵0x ≠，∴由233mx y +=，得：()()231133y y y m x x +--==．由222nx y -=，得：222122y y n x x ++==． ∵1y ≠-，∴0n ≠， ∴()()()231121y y y m n x x +-+=÷()()()231121y y x x y +-=⋅+()312x y -=．【答案】()312x y -【例21】已知：230a b c -+=，3260a b c --=，且0abc ≠，求3332223273a b c ab bc a c-++-的值. 【考点】直接换元求值（分式）【难度】4星【题型】解答【关键词】【解析】由题意可知：2303260a b c a b c -+=⎧⎨--=⎩，解得43a c b c =⎧⎨=⎩，333322233215173453a b c c ab bc a c c -+-==-+- 【答案】13-【巩固】已知方程组:230230x y z x y z -+=⎧⎨-+=⎩(0xyz ≠)，求：::x y z 【考点】直接换元求值（分式）【难度】3星【题型】解答【关键词】【解析】把z 看作已知数，解关于x 、y 的方程组，解得5y z =，7x z =，所以::7:5:1x y z =.【答案】::7:5:1x y z =【例22】设自然数x 、y 、m 、n 满足条件58x y m y m n ===，求的x y m n +++最小值．【考点】直接换元求值（分式）【难度】5星【题型】解答【关键词】黄冈市初中数学竞赛【解析】58x y =，58y m =，85m y =，864525n m y ==，从而y 是825200⨯=的倍数，当200y = 586412520032051211578525x y m n y y y y +++=+++=+++= 【答案】1157【例23】设有理数a b c ，，都不为0，且0a b c ++=，则222222222111b c a c a b a b c +++-+-+-的值为___________。

八年级数学上册第1章分式全章教学课件湘教版

1
3 4
6
8
9 ；
12
2
6 18
3
9
1.
3
分式的分子、分母都乘同一个不为0的数，分式的值不变；
分式的分子、分母都除以它们的公约数，分式的值不变。
对于分式是否也有类似于分数的性质？如果有，分式的分子、分母应当都乘或除以一个什么式子？
有类似分数的性质.分式的分子、分母应当乘同一个非零整式。
2x 3
求下列条件下分式 x 5 的值：
x6
(1)x=3；
(2)x=-0.4.
1.分式也是代数式，求分式的值就是将字母的值代入分式进行计算求值；
2.求分式的值要注意符号，结果是分式的要约分化成最简分数 .
解： (1) 当x=3时， x 5 3 5 2 . x6 36 9
(2) 当x=-0.4时， x 5 0.4 5 5.4 27 . x 6 0.4 6 5.6 28
当x取什么值时，分式
x2 2x 3
的值
(1)不存在； (2)等于0？
(1)分式的值不存在，就是分式无意义，此时分式的分母等于0；
(1)分式的值等于0，必须分子等于0时，同时满足分母不等于0 .
解： (1) 当分母2x-3=0，即x= 3 时，分子的 2
值不存在.
(2) 当分子x-2=0，即x=2时，分母2x-3≠0，分式 x 2 的值等于0.
分式的分子、分母都除以它们的一个公因式，所得分式与原分式相等。
你能用公式表示分式除以分子、分母的一个公因式的性质吗？
f mk m . g nk n
下列等式是否成立？为什么？
成立.把分式的分子、分母都乘-1，即可由每个等式的左边得出右边。

人教版八年级上册数学精品教学课件第1课时分式方程及其解法3

8
8
x 2 2x 15 x 2 16x 48
x2
x2x159
x2
16x
48
2
经检验, x 9 是原方程的根
2
11 1 1 x 3 x 4 x 5 x 12
1 1 11 x 3 x 12 x 5 x 4
2x 9 0
x
2x
3x
9 12
x
2x 9
5x
4
x 9 2
x2 9x 36 x2 9x 9
经检验, x 9 是 2
原方程的根
例3 ：解方程 y 4 y 5 y 7 y 8 y5 y6 y8 y9
点拨：此方程的特点是：各分式的分子与分母的次数相
同，这样一般可将各分式拆成：整式+分式的形式。
解：1 1 1 1 1 1 1 1
y 5
y6
y 8
y9
1
1
1
y 1 y 2y01yy12y1,y2102yyy1121y,y220 20
下面的过程请同学们自己完成相信你们能行
以下各方程能利用换元法进行换元吗？
x x2 1
x2 1 x
5 2
能 y 1 5 y2
( x )2 5( x ) 3 能 y2 5y 3
x 1
x 1
x2 x2
1 1
3(x2 1) x2 1
2x
0
不能
小结
有些分式方程用常规方法-----------去分母，是很复杂，甚至无法求解，有时要采取其他的方法
①采取局部通分法,会使解法很简单.这种解法称为 ——通分法
②各分式的分子、分母的次数相同，且相差一定的数，可将各分式拆成几项的和。这种解法称为 —— 拆项法

北师大版数学八年级下册《第五章分式与分式方程 1 认识分式第1课时分式的概念》教学课件

第五章分式与分式方程 1 认识分式
第1课时分式的概念
北师版八年级下册
新课导入
面对日益严重的土地沙漠化问题，某县决定在
一定期限内固沙造林2400hm2，实际每月固沙造林
的面积比原计划多30hm2 ，结果提前完成原计划的
任务.如果设原计划每月固沙造林xhm2，那么
（1）原计划完成造林任务需要多少月？ 2 4 0 0
b a x
上面问题中出现了代数式 2 4 0 0 ， 2 4 0 0 ，
35a 45b ， b
x
x + 30
，它们有什么共同特征？
ab a x
观察下列两组式子，它们都是整式吗？它们有什么特点？（1）a，-3x2y3，5x-1，x2+xy+y2 （2） 2 ，y，a ，c
m-n x 9a-1 ab
x2
A. ±2
B.2 C. -2
D.4
分析分式的值为零，即分子为零且分母不为零. 根据题意，得x2-4=0且x-2≠0，解得x=-2.
3.有下列式子：①x； ②y2； ③5； ④x2 .
3 y x2
其中是分式的有（ B ）
A. 1个
B.2个 C. 3个
D.4个
课后小结
一般地，.只要分母不等于零，分式就有意义；
（2）有关求分式有意义、无意义的条件的问题，常转化为不等式的问题.
分式的值为零的条件
分式的值为零的条件：分子为零，分母不为零. 用式子表示：B A=0A=0且B0 例当x为何值时，分式 x 2 9 的值为零.
x3
[分析] 分式的值为零分分子母= 00xx239 解出x的值.
解依题意，得
x 2 9 = 0 ①

湘教版数学八年级上册《1.1 分式》教学设计

湘教版数学八年级上册《1.1 分式》教学设计一. 教材分析湘教版数学八年级上册《1.1 分式》是学生在学习了有理数、实数等知识后，进一步对数学概念和数学表达式的深入学习。

本节课主要介绍了分式的概念、分式的性质、分式的运算等。

教材通过丰富的例题和练习题，帮助学生掌握分式的基本知识，培养学生解决实际问题的能力。

二. 学情分析学生在七年级时已经学习了有理数、实数等知识，对数学概念和数学表达式有一定的理解。

但是，对于分式的概念和性质，学生可能还比较陌生，需要通过实例和练习来逐步理解和掌握。

此外，学生可能对于分式的运算规则和技巧还不够熟练，需要通过大量的练习来提高。

三. 教学目标1.理解分式的概念，掌握分式的性质。

2.学会分式的基本运算，提高解决实际问题的能力。

3.培养学生的逻辑思维能力和团队合作能力。

四. 教学重难点1.分式的概念和性质的理解。

2.分式的运算规则和技巧的掌握。

五. 教学方法1.采用问题驱动的教学方法，引导学生通过思考和讨论来理解分式的概念和性质。

2.使用实例和练习题，让学生通过动手操作和思考来掌握分式的运算规则和技巧。

3.采用小组合作的学习方式，培养学生的团队合作能力和逻辑思维能力。

六. 教学准备1.教材和教学参考书。

2.投影仪和幻灯片。

3.练习题和答案。

七. 教学过程1.导入（5分钟）通过向学生提出实际问题，引发学生对分式的思考，进而导入本节课的主题。

示例问题：某商品的原价是100元，现在打8折出售，求打折后的价格。

2.呈现（10分钟）通过幻灯片向学生介绍分式的概念和性质。

分式的概念：分式是形如a/b的表达式，其中a和b是整式，b不为0。

分式的性质：分式的分子和分母都可以乘以（或除以）同一个非零整式，分式的值不变。

3.操练（10分钟）让学生通过动手操作，解决一些简单的分式问题，巩固对分式的理解。

练习题：求分式的值。

1.1/2 + 2/32.3/4 - 1/23.1/3 × 4/54.巩固（10分钟）让学生通过解决实际问题，运用分式的知识。

人教八年级数学上册《分式的加减第1课时：分式的加减法法则》精品教学课件

2
p
1
3q
-
2
1 p-3q
.
解：(1)
2
p
1
3q
2
1 p-3q
=
(2
p
2 p-3q 3q)(2 p-3q)
(2
p
2 p 3q 3q)(2 p-3q)
2 p-3q 2 p 3q (2 p 3q)(2 p-3q)
(2 p
4p 3q)(2 p-3q)
通分
创设情境探究新知应用新知巩固新知课堂小结布置作业
1
8 a2 4
8(a2 4) 8(a2 1) (a2 1)(a2 4) (a2 1)(a2 4)
8(a2 4) 8(a2 1)
(a2 1)(a2 4)
8(a2 4 a2+1) (a2 1)(a2 4)
(a2
24 1)(a 2
4)
.
创设情境探究新知应用新知巩固新知课堂小结布置作业
3q2 p
3q
3q
2p
6q
3q2 p
3q
创设情境探究新知应用新知巩固新知课堂小结布置作业
归纳
异分母分式相加减的一般步骤：（1）通分：将异分母分式转化为同分母分式；（2）加减：写成分母不变、分子相加减的形式；（3）合并：若分子有括号，则先去括号、再合并同类项；（4）约分：分子、分母约分，将结果化成最简分式或整式.
1+ 1 两队共同工作一天完成这项工程的__n___n___3_.
创设情境探究新知应用新知巩固新知课堂小结布置作业
思考
问题2：2019年、2020年、2021年某地的森林面积 (单位：km2) 分别是S1，S2，S3，2021年与2020年相比，森林面积增长率提高了多少？

湘教版八年级上册数学精品教学课件第1章分式可化为一元一次方程的分式方程第2课时分式方程的应用

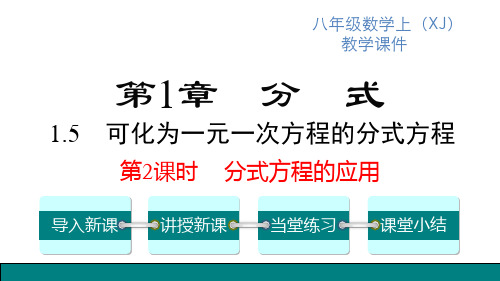
们同时到达，已知汽车的速度是自行车的 3 倍，求两车
的速度.
解：设自行车的速度为 x 千米/时，那么汽车的速度是
3x 千米/时，依题意得：
15 15 2 . 3x x 3
解得 x＝15.
经检验，x＝15 是原方程的根. 由 x＝15 得 3x＝45.
答：自行车的速度是15千米/时，汽车的速度是45千米/时.
因此 x = 2200 是原方程的根，且符合题意.
答：该款空调补贴前的售价为每台 2200 元.
2. 一轮船往返于 A、B 两地之间，顺水比逆水快 1 小时到
达.已知 A、B 两地相距 80 千米，水流速度是 2 千米/时，
求轮船在静水中的速度.
解：设船在静水中的速度为 x 千米/时,根据题意得
80 80 1. x2 x2
答：面包车的速度为 100 km/h，小轿车的速度为 90 km/h.
做一做 1.小轿车发现跟丢时，面包车行驶了 200 km，小轿车行驶了 180 km，小轿车为了追上面包车，他就马上提速，他们约定好在 300 公里的地方碰头，他们正好同时到达，请问小轿车提速多少 km/h？
0
180 200
甲的工1作效(1率 1是) 13
，根据题意得 1 1 1，即
3
2 x2
1 1 2 2x
1.
方程两边同乘 2x，得 x 1 2x.
解得 x = 1.
检验：当 x = 1 时，2x≠0. 所以，原分式方程的解为 x = 1. 由上可知，若乙队单独施工 1 个月可以完成全部
任务，而甲队单独施工需 3 个月才可以完成全部任务，所以乙队的施工速度快.
车行驶了 200 km 时，发现小轿车只行驶了 180 km，若面包车的行驶速度比小轿车快 10 km/h，请问面包车、小轿车的速度分别为多少？

湘教版数学八年级上册：1.1分式(共44张PPT)

1.分式的定义：
类似地，一个整式f 除以一个非零整式 g
（g 中含有字母），所得的商
f g
叫作分
式，其中f 是分式的分子，g 是分式的分母
，g≠0.
如：式子理解：
S x
，xa ++ by
a ，__6_-0__4__ 都是分式.
①分式就是表示两个整式_相__除__的式子，其
中分母含有字__母__. ②分式与整式的区别是_看_分__母__是__否__含_有__字__母_
（2 ） _____________ 5x2
（3）
x
5x 2-3
x
=（
x
5
-3
）
x2 +xy
（4）____________
x+y
x __________ = 1 （）
3.根据分式的基本性质确定分子与分母的符号变化
（1）
1--aa2
=（
a2 -1
a
）
4x 5
-4x w （） ____________
则它的宽为___Sx____m；
2. 如果两块面积分别为x公顷，y公顷的稻
田，分别产稻谷a kg，b kg，那么这两
块稻田平均每公顷产稻谷__xa_++__by___kg.
分式
本节课的学习目标
1.类比分数的定义理解掌握分式的定义； 2.知道分式有意义的条件是什么； 3.知道分式的值等于0的条件是什么；
4.分数 2 与 4 有什么区别？ 5 10
其中 2 称为_最__简__分数； 4 中的分
5
10
子与分母有公__因__数__2_，可以约去公__因__数__2

《分式》PPT教学课件(第1课时)

a b2 a b2
1
b a4 a b4 a b2 .
注意判断一个分式是不是最简分式，要严格按照定义来判断，就是看分子、分母有没有公因式.分子或分母是多项式时，要先把分子、分母因式分解.
三分式的求值
分式的求值对一些较复杂的分式求值，应先约分化简，再代入具体数据求值.常用方法有整体代入法，倒数法，换元法和配方法等.
课堂小结
❖分式的概念 ①分子分母都是整式； ②分母中必含有字母. ❖分母中字母的取值不能使分母值为零，否则分式无意义. ❖当分子为零且分母不为零时，分式值为零. ❖分式的基本性质
课后作业
见《学练优》本课时练习
第十二章分式和分式方程
分式
第2课时
学习目标
1.理解约分和最简分式的意义.（难点） 2.根据定义找出分式中分子与分母的公因式，并会约分. 3.理解分式求值的意义，学会根据已知条件求分式值.(重点）
1
;
2
a b
b a
2 4
;
3
x2
y 8x 8
.
解析：最简分式： x2 y2 ; x2 2x 1 .
y2 2x2 8x 8
不是最简分式：
m2 2m 1 m2
1
;
a b
b a
2 4
.
m2 2m 1 m 12 m 1;
1 m2
m 1m 1 m 1
分式的特点分式的特征是: ①分子、分母都是整式；
②分母中含有字母 .
二分式有（无）意义及分式值为0
观察与思考
探究求下列分式的值：
x … -2 -1
0
1
2…
x x-2 …
1 2
1 3

名师课堂湘教版八年级数学上册课件1.1第1课时分式

=
v-v0
t
整数整数分数
整式(A) 整式(B) 分式(AB )
判断：下面的式子哪些是分式？
2 bs
4 5b c
3000 2 300 a 7
5 5x 7
VS S 32
x2 xy y2 2x 1
2x2 1 5
3x2 1
分式:
A思考：
B1、分式的分母有什么条件限制？
当B=0时，分式 A 无意义.
A
当B≠0时B，分式
BA B
有意义.
2、当
A B
=0时分子和分母应满足什
么条件？
当A=0而 B≠0时，分式 B A的值为零.
例1
当x取何值时，分式
x2 2x 3Leabharlann 的值（1）不存在；
（2）等于0？
解：（1）当分母2x-3=0，即x= 3 时，分子的值
为
3

2

0
，因此当x=
1.1 分式
第1课时分式
问题 :一艘轮船在静水中的最大航速是20千米/ 时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等.江水的流速是多少?
如果设江水的流速为u千米/时.
最大船速顺流航行100千米所用时间=以最大航速逆流航行60千米所用的时间
100
20 u
60 20 u
阅读课本2页到3页，回答下面的问题
10 1.长方形的面积为10cm²,长为7cm.宽应为___7___cm;长方
S 形的面积为S,长为a,宽应为__a____;
S
?
a
2.把体积为200cm³的水倒入底面积为

新湘教版八年级数学上第1章分式小结与复习ppt公开课优质教学课件

能多铺设20米，且甲工程
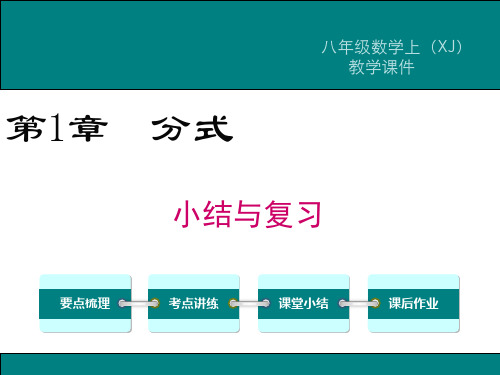
队铺设350米所用的天数与乙工程队铺设250米所用的天数相同．问甲、乙两个工程队每天各能铺设多少米？
解：设乙工程队每天能铺设x米；
则甲工程队每天能铺设（x+20）米，依题意，得 350 250 ，解得x=50，
x 20 x
经检验，x=50是原方程的解，且符合题意．
分
式
分式的运算及化简求值
分式方程的定义分式
分式方程
分式方程的解法及增根求值问题步骤
分式方程的应用类型
一审二设三列四解五检六写，尤其不要忘了验根
行程问题、工程问题、销售问题等
课后作业
见本章小结与复习
2 2 2
解：由
x 2 ，得 x 2 y ， y 3 3
把x2y 3
x2 y 2 xy y 2 2 2 2 x 2 xy y 2 x 2 xy ( x y )( x y ) 2 x( x y ) 2 ( x y) y( x y) 2x . 4 y y
分式值为 0 的条件:
f=0且 g ≠0
3.分式的基本性质
分式的分子与分母都乘同一个非零整式，所得分式与原分式相等.
f f f ·h 即对于分式，有 g g ·h g
( h 0 ).
分式的符号法则:
f f f f f , . g g g g g
二、分式的运算 1.分式的乘除法法则分式的乘法
1 1 2 2 又因为 x 4 ( x 2 ) 2 x x 1 2 [( x ) 2]2 2 x (25 2) 2 2 527.
考点三分式方程的解法
例3 解下列分式方程：

初中数学人教版八年级上册《15.分式方程》课件(1)

谢谢大家
解：方程两边同时乘以(x-m)(x-n),
可得(x+m)(x-m)+(x+n)(x-n)=2(x-m)(x-n),
即是 x2 - m2 x2 - n2 2x2 - 2(m n)x 2m,n 整理得：2(m n)x (m n)2 ，
因为 m ≠n，所以m+n≠0，解得：x m n ，
5k
解得k≠-3.
②x存在，则 3 k 有意义，即k≠-5. 5k
所以k的取值范围是k≠-3且k≠-5.
3 k ≠，1 5k
含字母的分式方程
含字母的分式方程的概念
解含字母的分式方程的一般步骤
若关于x的分式方程 2 - 1- kx 1 无解，求k的值. x-2 2-x
解析：分式方程无解分为两种情况： ①分式方程化为整式方程后，求出整式方程的解使得最简公分母为0； ②分式方程化为的整式方程无解. 根据两种情况分类讨论，确定 k 的值即可.
分式方程
解关于x的分式方程： x m x n 2(m n.) x-n x-m
解析：原方程是关于x的分式方程，则x表示未知数，m、n表示已知数，将字母m、n看作是常数，按照解一般分式方程的步骤即可. 注意：原分式方程含有常数项，在去分母的时候要将常数项也乘以最简公分母.
解关于x的分式方程： x m x n 2(m n.) x-n x-m
x
2
3
.
解：方程两边同时乘以2x(x+3)，得x+3=4x，解得：x=1. 检验：当x=1时，2x(x+3)=8≠0，所以原分式方程的解是 x=1.
解分式方程： 2 x -1
4 x2 -1
.
解：方程两边同时乘以(x+1)(x-1)，得2(x+1)=4，解得：x=1. 检验：当x=1时，(x+1)(x-1)=0，所以x=1不是原分式方程的解，则原分式方程无解.

人教版八年级数学上册15.分式的加减(第1课时)

_____s_3__s_2___s2___s1.
s2
s1
从上面的问题可知，为讨论数量关系，有时需要进行分式的加减运算．这就是我们这节课将要学习的内容。
速度比拼：计算： (1) 2 1 55
(2) 1 2 55
类比分(数3)的12加减法13，分式的加减法法(则4是) 12：
1 3
同分母分式相加减，分母不变，分子相加减；
问题1：甲工程队完成一项工程需n天, 乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?
1
答乙:工甲程工队程一队天一完天成完这成项这工项程工的程_的______n______1____________,, 两队共同工作一天完成这项工程的 n 3
_________(_1_____1__.) n n3
例 4 计算：
先找出最简公分母，再正确通分，
5 6a2b
2 3ab2
3 4abc
转化为同分母的分式相加减。
解：原式=
10bc 12a2b2c
8ac 12a2b2c
9ab 12a2b2c
10bc 8ac 12a2b2c
9ab
例5、先化简，再求值:其中x=3
x2 1 x 1
,
x2 2x 2x x2
3
3a2b ab2
5
8
a2b ab2
一个整体，先用括号括
起来！
解：原式= (5a2b 3) (3a2b 5) (8 a2b) ab2
5a2b 3 3a2b 5 8 a2b
=
a 2b = ab2
ab2
注意：结果要化为最简分式！
a
=b
例 3 计算：解:

北师版初中数学八年级下册精品教学课件第五章分式与分式方程 1认识分式第1课时

分式与分式方程
1
认识分式
第1课时
快乐预习·感知
1.一般地,用A,B表示两个整式,A÷B就可以表示成
含有
的

字母 ,那么称为分式,其中A称为分式的

分母 .对于任意一个分式,分母都不能为零
分式必须具备4个条件:①A,B为
有字母 ;④B≠ 0
整式 ;②形式:
的形式,如果B中
分子
,B称为分式
A.1
B.-1
C.±1
D.不为1的数
).
答案:B
返回首页
-2
3.若分式
的值等于0,则x的值是(
+3
).
答案:A
1
4.若分式 3- 有意义,则x的取值范围是
.
答案:x≠3
返回首页
返回首页
本
课
结
束
.

Байду номын сангаас
;③B中含
.
返回首页

2.对于分式 ,分式有无意义的条件:当B ≠0 时,分式有意义;当B =0
分式无意义;分式的值为0的条件:当B
≠0 ,且A =0
时,
时,分式的值为0.
返回首页
轻松尝试·应用
1.下列式子是分式的是(

A.
2

B.
+1
).

C. +y
2

D.
π
答案:B
||-1
2.若分式 -1 的值等于0,则x的值是(