6月月考

合集下载

2024四川省成都市第七中学高一下学期6月月考化学试题及答案

成都七中2023-2024学年度下期6月考试化学试卷（考试时间：75分钟；试卷满分：100分）可能用到的相对原子质量：H-1 C-12 N-14 O-16 Mg-24 Al-27一、单项选择题（本题共14小题，每题3分，共42分）1. 我国科技自立自强。

近年来，取得了重大进展。

下列有关科技成果说法正确的是A ．“异域深海，宝藏无穷”——自主开采的可燃冰燃烧时，环境温度升高，体系温度降低B ．“科技冬奥，温暖护航”——发热服饰材料中的石墨烯与C 60互为同分异构体C ．“高产水稻，喜获丰收”——高产水稻中的淀粉属于天然有机高分子D ．“浩渺太空，无限征途”——飞船返回舱“外衣”中的合成树脂属于新型无机非金属材料A ．某灶具使用煤气做燃料，改用天然气后其进风口应改大B ．乙烯、乙醇都能使酸性KMnO 4褪色，但反应类型不同C ．聚乙烯分子的单体为—CH 2—CH 2—D ．动物油脂经氢化后可生产人造奶油4. 化学离不开实验。

下列实验操作正确的是A B C DA ．制备并收集乙酸乙酯B ．测定一定质量镁铝合金中金属铝的含量C ．配制0.10 mol ·L －1 NaOH 溶液D ．制备NH 35. 宏观辨识与微观探析是化学学科核心素养之一。

下列反应方程式书写错误的是A ．Cu 与浓硝酸反应：Cu ＋2NO -3＋4H ＋＝Cu 2＋＋2NO 2↑＋2H 2OB ．以石英砂为原料制粗硅：SiO 2＋C =====高温Si ＋CO 2↑C ．用足量Na 2CO 3溶液吸收NO 2尾气：2NO 2＋2CO 2-3＋H 2O ＝NO -3＋NO -2＋2HCO -3D ．汽车发动机中产生NO 尾气：N 2＋O 2=====高温2NO10. 一定温度下，向恒容密闭容器中投入E 和M 发生如下反应：E(g)+M(g)====① F(g)⇌③②G(g)。

已知反应初始c 0(E)＝c 0(M)＝0.10 mol ·L -1，部分物质的浓度(c )随时间(t )的变化关系如图所示，t 2后反应体系达到平衡状态。

四川省成都市第七中学2023-2024学年高一下学期6月月考英语试题(含答案)

成都七中2023—2024学年度高一（下）6月阶段性考试英语注意事项：1．答题前，务必将自己的姓名、考号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

答非选择题时，必须使用0.5毫米黑色笔迹的签字笔，将答案书写在答题卡规定的位置上。

所有题目必须在答题卡上作答，在试题卷上答题无效。

3．考试结束后，只将答题卡交回。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．What is the man busy with?A．A visit.B．A project.C．A video.2．What do the speakers plan to do tomorrow?A．Go camping.B．Do some shopping.C．Find a blanket.3．Where are the speakers going to?A．A station.B．Another country.C．Their hometown.4．What does the woman think of Jimmy?A．Silent.B．Caring.C．Hard—working.5．What are the speakers talking about?A．The new laws.B．A healthy lifestyle.C．Profitable industries.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

2024四川省成都市第七中学高一下学期6月月考政治试题及答案

2023—2024学年度下期高2026届6月阶段性考试政治试卷考试时间：60分钟满分：100分一、选择题，本题共16小题，每小题3分。

在下列每小题的四个选项中，只有一个最符合题目要求。

1．2024年4月，中共中央办公厅印发了《关于在全党开展党纪学习教育的通知》。

《通知》指出，为深入学习贯彻修订后的《中国共产党纪律处分条例》，经党中央同意，自4月至7月，在全党开展党纪学习教育。

党纪学习教（）①是推动全面从严治党向纵深发展的重要举措②必须坚持以严的基调全面加强党的组织建设③体现了全面从严治党要以党的纪律建设为统领④彰显了党推进自我革命的坚定决心和坚强意志A．①③B．①④C．②③D．②④2．二十届中央纪委三次全会给2024年度反腐工作划了重点：把严惩政商勾连的腐败作为攻坚战重中之重；深化整治金融、国企、能源、烟草、医药、基建工程和招投标等领域腐败问题……这表明（）①坚持自我革命是中国共产党的鲜明品格②我国加强重点领域防治腐败制度体系建设③党坚持刀刃向内，保持惩治腐败高压态势④党加强廉政教育，维护人民群众根本利益A．③④B．②④C．①③D．①②3．为助力山海协作工程的实施，浙江省政协组织协调省级各民主党派、相关专委会等，联动开展调研，推行网络议政，积极建言资政，念好“山海经”走好“共富路”。

这体现了人民政协（）①认真履行政治协商、参政议政的职能②通过民主决策广泛凝聚社会共识③助推国家重大方针和政策的贯彻落实④是国家治理体系的重要组成部分A．①②B．①④C．②③D．③④4．某物业党支部立足商户占比高、人员结构复杂、利益诉求多元的社区实际，坚持以社区党委为“轴心”，链接社区红色阵地资源、商家联盟资源、服务管理资源，搭建合作共赢平台。

定期开展民情社情分析研判，采用“线上线下提、网格党支部汇、共同协商议、协同联动办、全程跟踪督、办理结果示、党员群众评”七步工作法，有效破解治理堵点、痛点。

该做法（）①擦亮了“红色物业”党建品牌，将党建引领优势转化为基层治理效能②扩大了社区的社会服务职能，推动了物业服务与社会治理融合发展③丰富了基层自治的组织形式，是开展基层民主实践活动的重要探索④完善了协同治理的工作方式，汇集社区发展资源提升基层治理能力A．①②B．①④C．②③ D．③④5．社区工作者是指在社区从事党建、治理、服务工作的全日制专职人员，主要包括社区党组织成员、社区居民委员会成员中的专职人员和社区专职工作人员。

山东省临沂市第三中学北校区2023-2024学年高一下学期6月月考数学试题

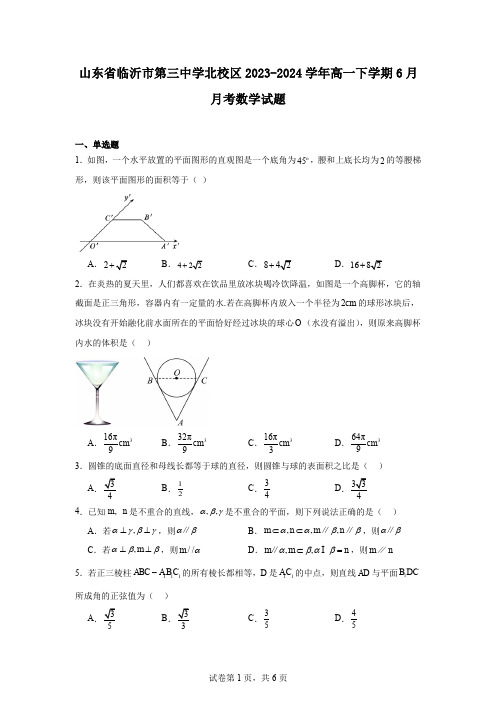
山东省临沂市第三中学北校区2023-2024学年高一下学期6月月考数学试题一、单选题1．如图，一个水平放置的平面图形的直观图是一个底角为45o ，腰和上底长均为2的等腰梯形，则该平面图形的面积等于（）A ．2B ．4+C ．8+D ．16+2．在炎热的夏天里，人们都喜欢在饮品里放冰块喝冷饮降温，如图是一个高脚杯，它的轴截面是正三角形，容器内有一定量的水.若在高脚杯内放入一个半径为2cm 的球形冰块后，冰块没有开始融化前水面所在的平面恰好经过冰块的球心O （水没有溢出），则原来高脚杯内水的体积是（）A ．316πcm 9B ．332πcm 9C ．316πcm 3D ．364πcm 93．圆锥的底面直径和母线长都等于球的直径，则圆锥与球的表面积之比是（）A B ．12C ．34D 4．已知m ，n 是不重合的直线，,,αβγ是不重合的平面，则下列说法正确的是（） A ．若,αγβγ⊥⊥，则αβ∥ B ．,,,m n m n ααββ⊂⊂∥∥，则αβ∥ C ．若,m αββ⊥⊥，则//m αD ．,,⊂=I ∥m m n αβαβ，则m n ∥5．若正三棱柱111ABC A B C -的所有棱长都相等，D 是11AC 的中点，则直线AD 与平面1B DC 所成角的正弦值为（）A B C ．35D ．456．如图，111A B C ABC -是直三棱柱，090BCA ∠=，点1D 、1F 分别是11A B 、11AC 的中点，若1BC CA CC ==，则1BD 与1AF 所成角的余弦值是A ．3010B ．12C ．D ．15107．长方､堑堵､阳马､鳖臑这些名词出自中国古代数学名著《九章算术·商功》，其中阳马和鳖臑是我国古代对一些特殊锥体的称呼.取一长方，如图长方体1111ABCD A B C D -，按平面11ABC D 斜切一分为二，得到两个一模一样的三棱柱，称该三棱柱为堑堵，再沿堑堵的一顶点与相对的棱剖开，得四棱锥和三棱锥各一个，其中与矩形为底另有一棱与底面垂直的三棱锥1D ABCD -称为阳马，余下的三棱锥11D BCC -是由四个直角三角形组成的四面体称为鳖臑，已知长方体1111ABCD A B C D -中2AB =，3BC =，14AA =，按以上操作得到阳马，则阳马的最长棱长为（）A ．B ．5CD ．8．已知正方体1111ABCD A B C D -的棱长为2,EF ､分别是棱1AA ､11A D 的中点，点P 为底面四边形ABCD 内（包括边界）的一动点，若直线1D P 与平面BEF 无公共点，则点P 的轨迹长度为（）A ．2BCD ．二、多选题9．在正方体1111ABCD A B C D -中，下述正确的是（） A ．AC // 平面11A BC B ．AD ⊥平面11A BC C ．111AC AD ⊥D ．平面11A BC ⊥平面11BB D D10．如图，在四面体ABCD 中，点,,,P Q M N 分别是棱,,,AB BC CD AD 的中点，截面PQMN 是正方形，则下列结论正确的为（）A ．//AC 截面PQMNB ．异面直线PM 与BD 所成的角为60︒C ．AC BD ⊥ D ．BD ⊥平面ACD11．如图，在边长为2的正方形ABCD 中，E ，F 分别是BC ，CD 的中点，G 是EF 的中点，将ABE V ，ADF △分别沿AE ，AF 折起，使B ，D 两点重合于H ，下列说法正确的是（）A ．若把CEF △沿EF 继续折起，C 与H 恰好重合B ．AH EF ⊥C ．四面体A HEF -D ．点H 在面AEF 上的射影为AEF △的重心三、填空题12．平面α⊥平面β，l αβ=I ，n β⊂，n l ⊥，直线m α⊥（m ，n 是两条不同的直线），则直线m 与n 的位置关系是.13．如图，D ，E ，F 分别是边长为4的正三角形三边,,CA AB BC 的中点，将ADE V ，BEF △，CFD △分别沿,,DE EF FD 向上翻折至与平面DEF 均成直二面角，得到几何体ABC DEF -．则二面角C AB E --的余弦值为；几何体ABC DEF -的外接球表面积为．142的正三棱锥P -ABC 中，E ，F 分别为AB ，BC 的中点，M ，N 分别为PE 和平面P AF 上的动点，则BM MN +的最小值为．四、解答题15．如图，在三棱锥P ABC -中，PA ⊥底面ABC ，AC BC ⊥，M ，N 分别是BC ，PC 的中点．(1)求证：//MN n 平面PAB ； (2)求证：BC AN ⊥．16．如图，平面ABCD ⊥平面DBNM ，且四边形ABCD 与四边形DBNM 是正方形．(1)求证：平面ACN ⊥平面DBMN ； (2)若2AB =，求三棱锥D MAC -的体积．17．如图，在三棱锥-P ABC 中，PC ⊥平面ABC ，（1）若CD PB ⊥，AB BC ⊥.求证：CD PA ⊥；（2）若E ，F 分别在棱AC ，PA 上，且AE EC =，3PF AF =，问在棱PB 上是否存在一点D ，使得//CD 平面BEF .若存在，则求出PDDB的值；若不存在.请说明理由.-中，底面ABCD为菱形PA⊥底面ABCD，E是PC上的一点，18．如图四棱锥P ABCD=，PC⊥平面BED，2PE EC2PA=，（1）求AC的长；（2）若平面APB⊥平面CPB，试求PB与平面PDC所成角的正弦值．19．如图，在直角梯形ABCD中，AB//DC，∠ABC=90°，AB=2DC=2BC，E为AB的中点，沿DE将△ADE折起，使得点A到点P位置，且PE⊥EB，M为PB的中点，N是BC上的动点(与点B，C不重合).（1）求证：平面EMN⊥平面PBC；（2）是否存在点N，使得二面角B﹣EN﹣M N点位置；若不存在，说明理由.。

六年级下学期6月月考语文试题(原卷+答案与解释)2023-2024学年第二学期部编版

2023-2024学年六年级下学期6月月考语文试题一、积累运用。

（34分）1．下列词语中带点字的注音完全正确的一组是（）。

A．学弈．(yì) 鸿鹄．(hú) 脸颊．(jiá) 见微知著．(zhù)B．汝．(rù)辈埋．(mán)怨年庚．(gēng) 赴．(pù)汤蹈火C．蝎．(xiē)子琴弦．(xuán) 花圃．(pú) 戛．(gá)然而止D．承载．(zài) 弗．(fÓ)若测量．(liáng) 锲．(qì)而不舍2．下列词语书写完全正确的一组是（）。

A．辩论争辨司空见惯尾尾动听B．机械柔和声泪俱下桃李满门C．领域砂锅全神惯注朝西相处D．维恐盐酸身临其镜迫不急待3．下列各组加点字的意思相同的一项是（）。

A．今乃．掉尾而斗。

乃．破琴绝弦。

B．故．园无此声。

见两小儿辩斗，问其故．。

C．一人虽．听之。

虽．与之俱学。

D．为．设果，果有杨梅。

为．是其智弗若与？4．下列名句与“见微知著”意思不相似的一项是（）。

A．见一叶而知深秋，窥一斑而见全豹。

B．一花一世界，一叶一菩提。

C．月晕而风，础润而雨。

D．绳锯木断，水滴石穿。

5．下面的说法不属于良好的学习习惯的一项是（）。

A．我现在每天都读课外书，大多是读名著，阅读品味也在提高。

B．我每次完成习作后都不修改，也不让别人修改。

C．我边读书边思考，用旁批或笔记把心得写下来。

D．碰到不懂的问题，我会向老师或者同学请教。

6．对引用名言的好处表述正确的一项是（）。

A．使文章辞藻华丽，吸引读者。

B．压缩语言，节省文字空间。

C．使表达的观点更有说服力。

D．开门见山，直接表明作者的观点。

7．下列句子没有语病的一项是（）。

A．我永远不会忘记，老师耐心地纠正并指出我的问题。

B．《聪明在于学习，天才在于积累》是华罗庚先生在北京大学所做的演讲。

C．看了同学们在毕业晚会表演的精彩节目，使我赞叹不已。

安徽省宿州市泗县2023-2024学年七年级下学期6月月考数学试卷(含答案)

七年级数学注意事项：1．你拿到的试卷满分为150分，考试时间为120分钟。

2．本试卷包括“试题卷”和“答题卷”两部分。

“试题卷”共4页，“答题卷”共6页。

3．请务必在“答题卷”上答题，在“试题卷”上答题是无效的。

4．考试结束后，请将“试题卷”和“答题卷”一并交回。

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的．1．下列图形中，不是轴对称图形的是（）A．B．C．D．2．下列运算错误的是（）A．B．C．D．3．若三角形三个内角度数之比为，则这个三角形一定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰直角三角形4．如图，与关于直线对称，交于点，则下列说法不一定正确的是（）A．B．C．D．5．如图，点，在上，，，添加：①；②；③；④四个条件中的一个，能使的是（）A．①或③B．①或④C．②或④D．②或③6．的补角是它余角的3倍，则的度数为（）A．B．C．D．7．下列图形，符合龟兔赛跑的故事情节的是（）A．B．C．D．8．如图所示的风格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则的度数为（）A．B．C．D．9．如图，在中，，分别以点，为圆心，以长为半径画弧，两弧交于点，连接．下列结论错误的是（）A．B．C．D．是的垂直平分线10．如图，是中边上的中线．若，，则的取值范围是（）A．B．C．D．二、填空题（本大题共4小题，每小题5分，满分20分）11．如图，桥梁拉杆和桥面构成三角形的结构，根据的数学道理是________．12．如图，，，，则________．13．如图，点在的平分线上，于点，于点，则下列结论：①；②；③与的面积相等；④，其中正确的有________．（填序号）14．如图，若正方形与正方形的面积之差是6，则________．三、（本大题共2小题，每小题8分，满分16分）15．数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务，善思小组想到了以下方案：如图，用螺丝钉将两根小棒，的中点固定，测得，之间的距离为，于是得出锥形瓶内部底面的内径是，试说明此方案的数学依据．16．如图，在中，，．通过观察尺规作图的痕迹，求图中的度数．四、（本大题共2小题，每小题8分，满分16分）17．如图，，，，求的度数．18．如图，点在的边上，，，．若，，求的长．五、（本大题共2小题，每小题10分，满分20分）19．已知，求整数的值．（提示：分类考虑）20．如图，在的网格图中，每小格均为边长是1的正方形，给出直线及格点，其中的顶点均在网格线的交点上．（1）画出格点关于直线对称的；（2）在上求作点，使的周长最小．（不写作法，保留作图痕迹）六、（本题满分12分）21．如图，在四边形中，，，点为边上的一点，且平分，平分．求证：（1）；（2）点为的中点．七、（本题满分12分）22．某剧院观众席的座位呈扇形分布，且按下列方式设置：排数1234…座位数50535659…（1）按照上表所示的规律，当每增加1时，如何变化？（2）写出座位数与排数之间的关系式；（3）按照上表所示的规律，某一排可能有90个座位吗？说说你的理由．八、（本题满分14分）23．如图，在中，，，．点从点出发，沿折线以每秒2个单位长度的速度向终点运动，点从点出发沿折线以每秒6个单位长度的速度向终点运动，，两点同时出发．分别过，两点作于点，于点．设点的运动时间为．（1）当，两点相遇时，求的值；（2）在整个运动过程中，求，的长；（用含的代数式表示）（3）当与全等时，求的值．参考答案一、1．D 2．C 3．B 4．D 5．D 6．A 7．C 8．B 9．D 10．B10．[提示]如答图，过点作，与的延长线交于点．∵，∴，．又∵是中边上的中线，∴．∴（AAS）．∴，．∵，，∴，即．∴．故选B．二、11．三角形的稳定性12．6 13．①②③④14．314．[提示]设正方形的边长为，正方形的边长为．∵正方形与正方形的面积之差是6，∴．∵，∴．三、15．解：由题意，得，．∵与是对顶角，∴．∴（SAS）．∴．即锥形瓶内部底面的内径是．8分16．解：由图中尺规作图痕迹可知垂直平分，平分．∵垂直平分，∴．∴．又∵，∴．∵平分，∴．8分四、17．解：∵，，∴．∴．∵，∴．∵，∴．∴．8分18．解：∵，∴．在和中，∵∴（ASA）．∴，．∴．8分五、19．解：当，即时，，∴．3分当，，即且时，，∴．6分当，即时，，∴．9分综上，整数的值为0或．10分20．（1）如图所示．5分（2）点的位置如图所示．10分六、21．证明：（1）∵平分，平分，∴，．∵，∴．∴．∴．∴，即．6分（2）如答图，过点作于点．∵，，∴，．∵平分，平分，，∴，．∴，即点为的中点．12分七、22．解：（1）由表中数据，知当每增加1时，增加3．3分（2）由题意，得．7分（3）某一排不可能有90个座位．8分理由：由题意当时，代入，得，解得．∵不是整数，∴某一排不可能有90个座位．12分八、23．解：（1）由题意，得，解得．∴当，两点相遇时，的值为．3分（2）由题意可知，点运动的路线长为，当时，．当时，．5分由题意可知，点运动的路线长为，当时，．当时，．7分（3）当点运动到点时，；当点运动到点时，．当点在上，点在上时，∵，∴．∵，，∴．∴．∴．当时，（AAS）．∴，解得．9分当点在上，点在上时，当点，重合时，．∴．即，解得．11分当点在上时，点到终点与点重合，．∴．即，解得．13分综上，当与全等时，的值为或或．14分。

2024北京一六六中高一6月月考英语

2024北京一六六中高一6月月考英语（时长：90分钟）班级：______姓名：______考查目标知识：必修二Unit3、至必修三Unit4词汇、语法能力：阅读能力、写作能力第一部分：完型填空（共10题；每小题1.5分，满分15分）阅读下面短文，掌握其大意，从每题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

Anger Is a Gift“Mom, where are you? I’ve been waiting for 10 minutes.” I shouted into the phone.“Honey, sorry. I left the office a bit late and the 1 caused really bad traffic, but I…”I hung up. Conversations like this happen every week. Being a teen is 2 enough, and my parents often make me feel less important than their work.In second grade, I broke my arm on the slide. When the school nurse called my mom, she was too 3 to answer. When the phone call reached my father, he sighed（叹息） and said, “I’m in the middle of research.” I sat in the nurse’s office for hours, before my parents finally 4 to take me to hospital.I wished my parents could keep me company. To make my parents take me seriously, I screamed. I tried to establish my own authority by ignoring their schedule. My mom did everything possible to solve the problem, but nothing 5 until she met that adviser.One day after I shut my door in her face, my mom didn’t complain or cry. Instead, she knocked and said, “I have something to tell you.” I opened the door. “Today I met a really good adviser. He said that every time your daughter is angry, she is just saying: I 6 you.”It dawned on me that my anger was merely a mask for me to 7 my loneliness and disappointment. But facing one’s 8 need is the first step towards being happier. This concept not only helped things between my parents and me but also enabled me to handle conflicts and emotions. I started to pay attention to other people’s 9 When an angry customer approached me at my volunteering job, he was saying, “I need more service.” When a homeless person shouted to me in a parking lot, he was simply saying, “I need food and help.”I am now able to see through the fog of anger and see the real face and heart of other people.Five minutes after I hung up on her, my mom’s car finally appeared through the fog. She rolled down her window and said, “Let’s go to a hotpot place, shall we?” I 10 , “OK, but promise me you won’t be late again.”l．A．rain B．snow C．fog D．wind2．A．hard B．unusual C．interesting D．exciting3．A．upset B．scared C．nervous D．busy4．A．passed by B．drove away C．showed up D．gave in5．A．appeared B．mattered C．happened D．worked6．A．hate B．need C．believe D．understand7．A．avoid B．relieve C．show D．hide8．A．unsatisfied B．typical C．increasing D．physical9．A．behavior B．anger C．reaction D．satisfaction10．A．whispered B．complained C．smiled D．hesitated第二部分：阅读理解（共两节，30分）第一节（共10题；每小题2，满分20分）阅读下列短文，从每题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

山东省枣庄市第三中学2023-2024学年高二6月月考英语试题

山东省枣庄市第三中学2023-2024学年高二6月月考英语试题一、听力选择题1．What is the weather like?A．Cloudy.B．Sunny.C．Rainy.2．What is the woman doing?A．Asking for help.B．Giving suggestions.C．Sharing an experience. 3．Who is Karen?A．A teacher.B．An artist.C．A bank clerk.4．Where does the conversation probably take place?A．At a hotel.B．At a supermarket.C．At a travel agency. 5．What is the conversation mainly about?A．Insects.B．A book.C．The planet.听下面一段较长对话，回答以下小题。

6．What do we know about the platform?A．It’s aimed at improving spoken English.B．It provides Chinese reading materials.C．It offers reading services to all ages.7．What does the man tell Jennifer in the end?A．How to access the platform.B．Whether to pay for the service.C．When to sign up for the course.听下面一段较长对话，回答以下小题。

8．Why does Susan talk to Mike?A．To tell him about an event about crops.B．To collect some information.C．To extend an invitation.9．What does Mike think of the event?A．Interesting.B．Boring.C．Average. 10．When will the event end?A．At 8:00 am.B．At 11:00 am.C．At 3:00 pm.听下面一段较长对话，回答以下小题。

四川省成都市第七中学2023-2024学年高一下学期6月月考物理试卷(含答案)

四川省成都市第七中学2023-2024学年高一下学期6月月考物理试卷一、选择题（1-7小题，每题只有一个选项符合题意，每题3分；8-12小题，每题有两个或两个以上的选项符合题意，选对得4分，选对不全得2分，选错或不选得0分，共41分）1．在探索宇宙奥秘的历史长河中，下列描述中正确的是（）A．万有引力定律描述的是一种只在大质量天体之间存在的引力B．天文学家第谷通过观测行星的运动，记录了大量数据并总结出行星运动的定律C．牛顿通过实验验证了万有引力定律D．“地心说”认为地球是静止不动的，太阳和其他行星都绕地球运动2．某热爱运动的同学质量为55kg，在做俯卧撑运动的过程中可将他的身体视为一根直棒。

已知重心在c点，其垂线与脚、两手连线中点间的距离oa、ob分别为1.0m和0.5m。

若他在1分钟内做了36个俯卧撑，每次肩部上升的距离均为0.5m，则他在1分钟内克服重力做功和相应的功率约为（）A．3300J，55W B．4950J，82.5WC．6600J，110W D．9900J，165W3．北斗卫星导航系统由地球同步静止轨道卫星、与同步静止轨道卫星具有相同周期的地球同步倾斜轨道卫星，以及比它们轨道低一些的中轨道卫星组成。

假设它们均为圆轨道卫星，根据以上信息，下列说法正确的有（）A．可以发射一颗中轨道卫星，使其轨道平面和成都所处纬线圈平面重合B．可以发射一颗倾斜地球同步轨道卫星，每天同一时间经过北京上空C．所有同步卫星绕地球运动的速率大于中轨道卫星绕地球运动的速率D．中轨道卫星与同步轨道卫星相比，中轨道卫星所具有的周期较大4．实际问题中，有很多情况是变力在对物体做功。

我们需要通过各种方法来求解力所做的功。

如图，对于甲、乙、丙、丁四种情况下求解某个力所做的功，下列说法正确的是（）A．甲图中若F大小不变，物块从A到C过程中力F做的为W=F⋅|AC|B．乙图中，全过程中F做的总功为72JC．丙图中，绳长为R，若空气阻力f大小不变，小球从A运动到B过程中空气阻力做的功W=1πRf2 D．图丁中，F始终保持水平，无论是F缓慢将小球从P拉到Q，还是F为恒力将小球从P拉到Q，F做的功都是W=Fl sinθ5．原地纵跳摸高是常见的体能测试项目。

贵阳市第一中学2023-2024学年高二下学期第四次月考暨6月月考数学试卷+答案

高二数学试卷本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，第I 卷第1页至第2页，第Ⅱ卷第3页至第4页.考试结束后，请将答题卡交回.满分150分，考试用时120分钟.第I 卷（选择题，共58分）注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名､准考证号､考场号､座位号在答题卡上填写清楚，2.每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效一､单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知命题π:,tan 03p x x x $>->，则命题p 的否定是（）A. π,tan 03x x x "£-> B. π,tan 03x x x ">-£C. π,tan 03x x x $£-> D. π,tan 03x x x $>-£2.曲线sin cos y x x =+在π2x =处切线倾斜角为（）A.0B.π4C.π2D.3π43.我国古代数学著作《九章算术》中有如下问题：“今有牛､马､羊食人苗，苗主责之粟五斗，羊主曰：“我羊食半马.”马主曰：“我马食半牛.”问：“马主出几何？”意思是“现有羊､马､牛三畜，吃了人家田里的禾苗，禾苗主人要求三位主人共赔偿5斗粟.羊主人说：“我的羊所吃禾苗数是马吃的一半，”马主人说：“我的马所吃数是牛吃的一半.”问马主人应赔偿多少更合理？（）A 57斗 B.56斗 C. 107斗 D.53斗4.()6(2)x y x y +-的展开式中52x y 的系数是（）A 48 B.-48C.72D.-725.小王去秦始皇兵马俑博物馆游玩，买了8个不同的兵马俑纪念品，其中将军俑3个，骑兵俑3个，跪射俑2个，将这8个纪念品排成一排，要求同种类型相邻，则不同的排法共有（）种.A.48B.72C.216D.432的..6. 已知在ABC V 中，角,,A B C 所对的边分别为,,a b c .内角,,A B C 为等差数列，若AC边上的中线长为ABC Vb 的值为（）A. 2B. 3C. 4D. 57. 已知点P 在函数()2ln 2f x x x =-+图象上，点Q 在直线:30l x y -+=上，记2||M PQ =，则（）A. 当M 取最小值时，点Q 的横坐标为1-B. 当M 取最小时，点Q 的横坐标为1C. 当M 取最小值时，点Q 的横坐标为12D. 当M 取最小时，点Q 的横坐标为12-8. 已知()232ln3ln41,,e 4ea b c -===，则（）A. a b c << B. a c b <<C. b a c<< D. b c a<<二､多项选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项是符合题目要求的.全部选对的得6分，部分选对的得部分分，有选错的得0分）9. 下列说法正确的是（）A. 设已知随机变量,X Y 满足()31,5Y X E Y =-=，则()2E X =B. 若110,5X B æö~ç÷èø，则()2D X =C. 若()22,X N s:，设()10.6P X ³=，则()30.4P X ³=D. 若事件,A B 相互独立且()01P B <<，则()()()P A B P A B P A ==∣∣10. 已知函数()e ln xf x a x =+，下列说法中正确的是（）A. 对于任意0a >，函数()f x 在定义域上是单调递减函数B. 对于任意0a <，函数()f x 存在最小值C. 存在0a >，使得对于任意()0,x Î+¥都有()0f x >恒成立D. 存在0a <，使得()f x 在定义域上有两个零点的11. 已知,A B 为两个随机事件，,A B 分别为其对立事件，则下列说法正确的是（）A. 若()()11,34P A P B ==，则()712P A B È=B. 若()()()121,,|552P A P B P B A ===，则()3|8P B A =C. 若()()()137,|,|3416P A P A B P B A ===，则()14P B =D. 若()()()133,|,|248P A P A B P A B ===，则()13P B =第II 卷（非选择题，共92分）注意事项：第II 卷用黑色碳素笔在答题卡上各题的答题区域内作答，在试题卷上作答无效.三､填空题（本大题共3小题，每小题5分，共15分）12. 某社团有3名女生､4名男生，随机选3名同学出来参加某个活动，用X 表示选到男生的人数，则1X ³的概率是__________.13. 若10121001210(1)(1)(1)x a a x a x a x =+++++++L ，则13579a a a a a ++++=______.（用数字作答）14. 已知定义在R 上的函数()f x 满足：()()()6235e ,22e xf f x f x =--¢<，则不等式()22ln 2ln f x x x x £-的解集为__________.四､解答题（共77分.解答应写出文字说明，证明过程或演算步骤）15. 在某次数学竞赛的初赛中，参赛选手需要从4道“圆锥曲线”和3道“函数与导数”共7道不同的试题中依次抽取2道进行作答，抽出的题目不再放回.（1）求选手甲第1次抽到“圆锥曲线”试题且第2次抽到“函数与导数”试题的概率；（2）求选手甲第2次抽到“函数与导数”试题的概率；（3）求选手甲第2次抽到“函数与导数”试题的条件下，第1次抽到“圆锥曲线”试题的概率.16. 如图，在三棱柱111ABC A B C -中，底面ABC 是边长为6的正三角形，O 是ABC V 的重心，1111,60,C CA C CB C CO AA ÐÐÐ===o .（1）证明：1C O ^平面ABC ；（2）求二面角1A CC B --的正弦值.17. 中国国际大数据产业博览会（简称“数博会”）从2015年在贵阳开办，至今已过9年.某校机器人社团为了解贵阳市市民对历年“数博会”科技成果的关注情况，在贵阳市随机抽取了1000名市民进行问卷调查，问卷调查的成绩x 近似服从正态分布()277,N s，且()77800.3P x ££=.（1）估计抽取市民中问卷成绩在80分以上市民人数；（2）若本次问卷调查得分超过80分，则认为该市民对“数博会”的关注度较高，现从贵阳市随机抽取3名市民，记对“数博会”关注度较高的市民人数为随机变量X ，求X 的分布列和数学期望.18. 已知圆：22430x y x +-+=的圆心为椭圆2222:1(0)x y C a b a b+=>>的右焦点F ，且椭圆C 的离心.（1）求椭圆C 的标准方程；（2）过点F 且不与x 轴重合的直线l 交椭圆C 于,A B 两点，N 为AB 的中点，O 为坐标原点，分别过,A B 作椭圆C 的切线，两切线相交于点M .（i ）求证：,,O M N 三点共线；（ii ）当l 不与x 轴垂直时，求AB FMFN×的最小值.19. 设()f x ¢是函数()f x 的导函数，若()f x ¢可导，则称函数()f x ¢的导函数为()f x 的二阶导函数，记为()f x ¢¢.若()f x ¢¢有变号零点0x x =，则称点()()00,x f x 为曲线()y f x =的“拐点”.（1）研究发现，任意三次函数()()320ax bx d a f x cx =+++¹，曲线()y f x =都有“拐点”，且该“拐点”也是函数()y f x =的图象的对称中心.已知函数()3224f x x bx x d =+-+的图象的对称中心为()1,3，求函数()f x 的解析式，并讨论()f x的单调性；的（2）已知函数()132221112e1(0)623mx g x mx x x m m m m -=+-+-->.（i ）求曲线()y g x =的“拐点”；（ii ）若()()()12122g x g x x x +=-¹，求证：122x x m+<.高二数学试卷本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，第I 卷第1页至第2页，第Ⅱ卷第3页至第4页.考试结束后，请将答题卡交回.满分150分，考试用时120分钟.第I 卷（选择题，共58分）注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名､准考证号､考场号､座位号在答题卡上填写清楚，2.每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效一､单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知命题π:,tan 03p x x x $>->，则命题p 的否定是（）A. π,tan 03x x x "£-> B. π,tan 03x x x ">-£C. π,tan 03x x x $£-> D. π,tan 03x x x $>-£【答案】B 【解析】【分析】根据全称命题与存在性命题的关系，准确改写，即可求解.【详解】由题意，根据全称命题与存在性命题的关系，可得：命题π:,tan 03p x x x $>->的否定是π,tan 03x x x ">-£.故选：B.2. 曲线sin cos y x x =+在π2x =处切线的倾斜角为（）A. 0B.π4C.π2D.3π4【答案】D 【解析】【分析】利用导数的几何意义求解.【详解】解：因为cos sin y x x -¢=，所以曲线在π2x =处的切线的斜率为1k =-，结合直线倾斜角范围及斜率与倾斜角关系知：切线倾斜角为3π4，故选：D.3. 我国古代数学著作《九章算术》中有如下问题：“今有牛､马､羊食人苗，苗主责之粟五斗，羊主曰：“我羊食半马.”马主曰：“我马食半牛.”问：“马主出几何？”意思是“现有羊､马､牛三畜，吃了人家田里的禾苗，禾苗主人要求三位主人共赔偿5斗粟.羊主人说：“我的羊所吃禾苗数是马吃的一半，”马主人说：“我的马所吃数是牛吃的一半.”问马主人应赔偿多少更合理？（）A.57斗 B.56斗 C.107斗 D.53斗【答案】C 【解析】【分析】设羊主人应赔偿1a 斗，则马主人应赔偿12a 斗，牛主人应赔偿14a 斗，根据题意，列出方程，即可求解.【详解】设羊主人应赔偿1a 斗，则马主人应赔偿12a 斗，牛主人应赔偿14a 斗，由题意得11112475a a a a ++==，所以157a =，所以马主人应赔偿11027a =斗.故选：C.4. ()6(2)x y x y +-的展开式中52x y 的系数是（）A. 48B. -48C. 72D. -72【答案】A 【解析】【分析】根据题意，利用二项式定理得展开式，结合多项式展开式的形式，即可求解.【详解】由题意，多项式()6(2)x y x y +-的展开式中，52x y 的系数等于221166C (2)C (2)48-+-=.故选：A.5. 小王去秦始皇兵马俑博物馆游玩，买了8个不同的兵马俑纪念品，其中将军俑3个，骑兵俑3个，跪射俑2个，将这8个纪念品排成一排，要求同种类型相邻，则不同的排法共有（）种.A. 48 B. 72 C. 216 D. 432【答案】D 【解析】【分析】利用相邻问题中的捆绑法可求出结果.【详解】先将3个将军俑捆在一起当一个元素使用，有33A 6=种捆法，将3个骑兵俑捆在一起当一个元素使用，有33A 6=种捆法，将2个跪射俑捆在一起当一个元素使用，有22A 2=种捆法，再将所得3个元素作全排，有33A 6=种排法，所以不同的排法共有33233323A A A A 432=种.故选：D.6. 已知在ABC V 中，角,,A B C 所对的边分别为,,a b c .内角,,A B C 为等差数列，若AC 边上的中线长为ABC V b 的值为（）A. 2B. 3C. 4D. 5【答案】A 【解析】【分析】首先求出B ，根据平行四边形法则得2BM BA BC =+uuuu r uuu r uuu r，两边平方得到一个关于a ，c 的方程，再根据面积公式得到a ，c 的另一个方程，最后由余弦定理计算出b .【详解】因为内角,,A B C 成等差数列，所以3πA B C B ++==,即π3B =，设AC 中点为M ，所以2BM BA BC =+uuuu r uuu r uuu r，由题意，BM =，所以22()4||12BA BC BM +==uuu r uuu r uuuu r ，即2212a c ac ++=，又因为1sin 2ABC S ac B ===△4ac =，228a c +=，由余弦定理，2222cos 4b a c ac B =+-=，所以2b =.故选：A.7. 已知点P 在函数()2ln 2f x x x =-+的图象上，点Q 在直线:30l x y -+=上，记2||M PQ =，则（）A. 当M 取最小值时，点Q 的横坐标为1-B. 当M 取最小时，点Q 的横坐标为1C. 当M 取最小值时，点Q 的横坐标为12D. 当M 取最小时，点Q 的横坐标为12-【答案】D 【解析】【分析】利用导数研究函数()f x 的单调性，作出函数的图象，然后利用数形结合知函数()2ln 2f x x x =-+在P 点处的切线平行于直线l ，然后利用导数的几何意义求得切点坐标，再利用垂直关系求得直线PQ 方程，与直线:30l x y -+=联立求解交点即可.【详解】()2ln 2f x x x =-+，则()221x f x x x-=-=¢，令()0f x ¢>得02x <<，令()0f x ¢<得2x >，所以函数()f x 在()0,2上单调递增，在()2,¥+上单调递减，作出函数函数()2ln 2f x x x =-+的图象，如图：由题意，当M 最小时，函数()2ln 2f x x x =-+在P 点处的切线平行于直线l ，过P 点作直线l 的垂线，垂足即为点Q .设P 的坐标为()000,2ln 2x x x -+，因为()21f x x¢=-，所以()00211f x x -¢==，解得01x =，即P 点的坐标为()1,1，所以过P 点，且与直线l 垂直的直线方程为20x y +-=，联立方程20,30,x y x y +-=ìí-+=î解得Q 的坐标为15,22æö-ç÷èø.故选：D.8. 已知()232ln3ln41,,e 4ea b c -===，则（）A. a b c << B. a c b <<C. b a c << D. b c a<<【答案】C 【解析】【分析】令函数()ln xf x x=，利用导数求得函数()f x 在()0,e 上单调递增，结合对数的运算性质和函数的单调性，即可求解.【详解】令函数()ln xf x x =，可得()21ln (0)x f x x x -=>¢，所以函数()f x 在()0,e 上单调递增，又因为()()222e ln e ln4ln21lne 3,2,e e 342e e 3a fb fc f æö========ç÷èø，因为2e 2e 3<<，所以()()2e 2(e 3f f f <<，即b a c <<.故选：C.二､多项选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项是符合题目要求的.全部选对的得6分，部分选对的得部分分，有选错的得0分）9. 下列说法正确的是（）A. 设已知随机变量,X Y 满足()31,5Y X E Y =-=，则()2E X =B. 若110,5X B æö~ç÷èø，则()2D X =C. 若()22,X N s:，设()10.6P X ³=，则()30.4P X ³=D. 若事件,A B 相互独立且()01P B <<，则()()()P A B P A B P A ==∣∣【答案】ACD 【解析】【分析】根据期望的性质，可判定A 正确；结合二项分布方差的公式，可判定B 错误；根据正态分布曲线的对称性，可得判定C 正确；根据条件概率的计算公式，可判定D 正确.【详解】对于A 中，由()()31E Y E X =-，所以()()123E Y E X +==，所以A 正确；对于B 中，由110,5X B æö~ç÷èø，所以()14810555D X =´´=，所以B 错误；对于C 中，由()22,X N s:，所以()()()31110.4P X P X P X ³=£=-³=，所以C 正确；对于D 中，因为,A B 相互独立，所以()()()(|)()()()P AB P A P B P A B P A P B P B ===，且()()()()()()(|()()()1()P AB P A P AB P A P A P B P A B P A P B P B P B --====-，所以D 正确.故选：ACD.10. 已知函数()e ln xf x a x =+，下列说法中正确的是（）A. 对于任意0a >，函数()f x 在定义域上是单调递减函数B. 对于任意0a <，函数()f x 存在最小值C. 存在0a >，使得对于任意()0,x Î+¥都有()0f x >恒成立D. 存在0a <，使得()f x 在定义域上有两个零点【答案】BD 【解析】【分析】A.利用导数法判断；C.由0,0a x >®时，()f x ¥®-判断；B.利用导数法判断；D.利用导数法判断.【详解】因为()e ln xf x a x =+，所以()e (0)xaf x x x+¢=>.当0a >时，()e 0xaf x x=¢+>，函数()f x 在()0,¥+上单调递增，A 错误；又因为当0,0a x >®时，()f x ¥®-，C 错误；当0a <时，显然()e xaf x x=¢+在()0,¥+上单调递增，且当0x ®时，()f x ¥¢®-，当x ®+¥时，()f x ¥¢®+，所以存在()00,x ¥Î+，使得函数()f x 在()00,x 上单调递减，在()0,x ¥+上单调递增，所以函数()f x 有最小值，B 正确；又因为当0a <时，当0x ®时，()f x ¥®+，当x ®+¥时，()f x ¥®+，所以只需函数()f x 的最小值小于0，函数()f x 就有两个零点，D 正确，故选：BD.11. 已知,A B 为两个随机事件，,A B 分别为其对立事件，则下列说法正确的是（）A. 若()()11,34P A P B ==，则()712P A B È=B. 若()()()121,,|552P A P B P B A ===，则()3|8P B A =C. 若()()()137,|,|3416P A P A B P B A ===，则()14P B =D. 若()()()133,|,|248P A P A B P A B ===，则()13P B =【答案】BCD 【解析】【分析】根据事件和概率加法公式，全概率，条件概率的概率公式以及独立事件与对立事件的概率公式，对四个选项进行逐一的分析判断即可．【详解】对于A ，()()()()P A B P A P B P AB =+-U ，故A 错误；对于B ，因为()()11,|52P A P B A ==，所以()()()1|10P AB P A P B A =×=，所以()()()()()()213510|11815P AB P B P AB P B A P A P A --====--，故B 正确；对于C ，因为()()()137,|,|3416P A P A B P B A ===，所以()()()()()()()37|,|448P AB P B P A B P B P AB P A P B A ====，所以()()()P AB P AB P A +=，解得()14P B =，故C 正确；对于D ，因为()12P A =，所以()12P A =，又因为()()()()()()()()()333|,|1488P AB P B P A B P B P AB P B P A B P B P B =====-éùëû，所以()()()()()()333314888P AB P AB P B P B P B P A +=+-=+=éùëû，解得()13P B =，故D 正确.故选：BCD.第II 卷（非选择题，共92分）注意事项：第II 卷用黑色碳素笔在答题卡上各题的答题区域内作答，在试题卷上作答无效.三､填空题（本大题共3小题，每小题5分，共15分）12. 某社团有3名女生､4名男生，随机选3名同学出来参加某个活动，用X 表示选到男生的人数，则1X ³的概率是__________.【答案】3435【解析】【分析】根据题意，得到随机变量X 的可能取值为0,1,2,3，结合()()110P X P X ³=-=，即可求解.【详解】由题意，某社团有3名女生､4名男生，随机选3名同学出来参加某个活动，随机变量男生人数X 的可能取值为0,1,2,3，则()()3337C 341101C 35P X P X ³=-==-=.故答案为：3435.13. 若10121001210(1)(1)(1)x a a x a x a x =+++++++L ，则13579a a a a a ++++=______.（用数字作答）【答案】512-【解析】【分析】利用赋值法，分别令0x =，令2x =-，代入求解即可.【详解】令0x =，可得012100a a a a ++++=L ；令2x =-，可得01239101024a a a a a a -+--+=L ；两式相减除以2，得13579512a a a a a ++++=-.故答案为：512-14. 已知定义在R 上的函数()f x 满足：()()()6235e ,22e xf f x f x =--¢<，则不等式()22ln 2ln f x x x x £-的解集为__________.【答案】(30,e ùû【解析】【分析】令()()22e x f x g x x =+，利用导数求得()g x 为增函数，把不等式转化为()ln ln 2ln 1exf x x +£，得到()()ln 3g x g £，列出不等式组，即可求解.【详解】令()()22e x f x g x x =+，则()()()2222e 0exxf x f xg x -+¢=>¢，所以()g x 增函数，不等式()22ln 2ln f x x x x £-可变形为()2ln ln 2ln 1exf x x +£，因为()()6336561ef g =+=-+=，所以不等式()2ln ln 2ln 1e x f x x +£等价于()()ln 3g x g £，所以ln 30x x £ìí>î，解得30e x <£，所以不等式()22ln 2ln f x x x x £-的解集为(30,e ùû.故答案为：(30,e ùû.四､解答题（共77分.解答应写出文字说明，证明过程或演算步骤）15. 在某次数学竞赛的初赛中，参赛选手需要从4道“圆锥曲线”和3道“函数与导数”共7道不同的试题中依次抽取2道进行作答，抽出的题目不再放回.（1）求选手甲第1次抽到“圆锥曲线”试题且第2次抽到“函数与导数”试题的概率；（2）求选手甲第2次抽到“函数与导数”试题的概率；（3）求选手甲第2次抽到“函数与导数”试题的条件下，第1次抽到“圆锥曲线”试题的概率.【答案】（1）27（2）37（3）23【解析】【分析】（1）法一：结合排列组合数运算利用古典概型概率公式求解即可；法二：利用条件概率公式求解即可.（2）利用全概率概率公式求解即可.（3）利用条件概率公式求解即可.【小问1详解】记“选手甲第1次抽到“圆锥曲线”试题”为事件A ，“选手甲第2次抽到“函数与导数”试题”为事件B ，法一：()114327C C 432A 767P AB ´===´.是法二：由概率乘法公式可得()()()432767P AB P A P B A ==´=.【小问2详解】由全概率公式可得()()()()()4332376767P B P A P BA P A PB A =+=´+´=∣∣.【小问3详解】由条件概率公式可得()()()227337P AB P A B P B ===.16. 如图，在三棱柱111ABC A B C -中，底面ABC 是边长为6正三角形，O 是ABC V的重心，1111,60,C CA C CB C CO AA ÐÐÐ===o .（1）证明：1C O ^平面ABC ；（2）求二面角1A CC B --的正弦值.【答案】（1）证明见解析（2）1213.【解析】【分析】（1）利用全等思想来证明等腰，然后可得中线就是垂线，从而可证明线面垂直到线线垂直，再证明线面垂直即可；（2）利用空间向量法来求解二面角的余弦值，再求出正弦值即可.【小问1详解】证明：如图，连接CO 并延长交AB 于点D ，连接111,,C A CBC D ，的在1C CA △与1C CB △中，111,,CA CB C CA C CB C C ÐÐ==为公共边，11C CA C CB \@V V ，11C A C B \=，1AB C D \^，又1,CD C D D CD Ç=Ì平面11,C CD C D Ì平面1C CD ，AB \^平面1C CD ，又1C O Ì平面1C CD ，1AB C O \^.正ABC V 的边长为6，CD \=，CO \=又11160CC AA C CO ==Ð=o ，在1C CO △中，由余弦定理可得，16C O ==，22211||C O CO CC \+=，1C O CO \^.又,AB CO D AB Ç=Ì平面,ABC CO Ì平面ABC ，1C O \^平面ABC .【小问2详解】如图，过D 作Dz ^面ABC ，建立空间直角坐标系D xyz -，则()()()()13,0,0,3,0,0,,A B C C -，故()()1,0,AC CC ==-uuu r uuuu r，()BC =-uuu r设平面1ACC 的法向量()1,,n x y z =ur ，则306z ì=ïí-+=ïî，令3x =，解得1y z ==-，则()13,1n =-ur.设平面1BCC 的法向量()2,,n x y z =uu r ，则060z ì-=ïí-+=ïî，令3x =，解得1y z ==，则O 是V ABC 的重心，\D 是AB 的中点，又底面ABC 是正三角形，\AB ^CD .()2n =uu r.设二面角1A CC B --的大小为q93151313--==，()0,q p ÎQ ,12sin 13q \==，即二面角1A CC B --的正弦值为1213.17. 中国国际大数据产业博览会（简称“数博会”）从2015年在贵阳开办，至今已过9年.某校机器人社团为了解贵阳市市民对历年“数博会”科技成果的关注情况，在贵阳市随机抽取了1000名市民进行问卷调查，问卷调查的成绩x 近似服从正态分布()277,N s，且()77800.3P x ££=.（1）估计抽取市民中问卷成绩在80分以上的市民人数；（2）若本次问卷调查得分超过80分，则认为该市民对“数博会”的关注度较高，现从贵阳市随机抽取3名市民，记对“数博会”关注度较高的市民人数为随机变量X ，求X 的分布列和数学期望.【答案】（1）200人. （2）分布列见解析，0.6【解析】【分析】（1）由变量x 近似服从正态分布()277,N s ，求得(80)0.2P x >=，进而得到问卷成绩在80分以上的市民人数；（2）根据题意，得到随机变变量()3,0.2X B :，结合对立重复试验的概率公式，求得相应的概率，列出分布列，求得数学期望.【小问1详解】解：因为随机变量x 近似服从正态分布()277,N s，且()77800.3P x ££=，所以()(80)0.577800.2P P x x >=-££=，所以10000.2200´=，所以估计抽取市民中问卷成绩在80分以上的市民人数为200人.【小问2详解】解：由题意，贵阳市市民对“数博会”关注度较高的概率为0.2，且()3,0.2X B :，所以随机变量X 的分布列为()33C 0.20.8,0,1,2,3kkkP X k k -==´=，所以随机变量X 的分布列为：X 0123P 0.5120.38400960.008所以随机变量X 的均值为()30.20.6E X =´=.18. 已知圆：22430x y x +-+=的圆心为椭圆2222:1(0)x y C a b a b+=>>的右焦点F ，且椭圆C 的离心.（1）求椭圆C 的标准方程；（2）过点F 且不与x 轴重合的直线l 交椭圆C 于,A B 两点，N 为AB 的中点，O 为坐标原点，分别过,A B 作椭圆C 的切线，两切线相交于点M .（i ）求证：,,O M N 三点共线；（ii ）当l 不与x 轴垂直时，求AB FMFN×的最小值.【答案】（1）2215x y +=（2）（i ）证明见解析；（ii 【解析】【分析】（1）根据焦点坐标和离心率求得2c =，2c =，即可求解椭圆方程；（2）（i ）分l 斜率不存在和存在两种情况讨论，当l 斜率存在时，设出方程与椭圆方程联立，韦达定理求出N 的坐标，利用判别式法求出切线方程，进而求得M 的坐标为()2112122112215,y y x x x y x y x y x y æö--ç÷--èø，即可证明三点共线；（ii ）利用距离公式和弦长公式分别求出,,AB FM FN ，即可求解.【小问1详解】由圆：22430x y x +-+=即()2221x y -+=可得：圆心()2,0F ，所以2c =，ca=，所以a =，所以2221b a c =-=，所以椭圆标准方程为2215x y +=..【小问2详解】（i ）①当l 斜率不存在时，l x ^轴，由椭圆的对称性可知，,M N 均在x 轴上，所以,,O M N 三点共线.②当l 斜率存在时，设l 的方程为()()20y k x k =-¹，且()()1122,,,A x y B x y ，联立方程组()222,1,5y k x x y ì=-ïí+=ïî可得：()()222251202050k x k x k +-+-=，则2212122220205,5151k k x x x x k k -+==++，点N 的坐标为222102,5151k k k k æö-ç÷++èø，所以ON 所在的直线的方程为15y x k=-，先证：椭圆22221(0)x y a b a b+=>>上一点()00,x y 处的切线方程为00221x x y y a b +=，当切线斜率存在时，设过点()00,x y 的切线方程为y kx m =+，联立方程22221x y a by kx m ì+=ïíï=+î，整理得()22222222220b a k x kma x a m a b +++-=，由Δ0=可得()()()222222222240kma b a k a ma b -+-=，所以22220a k mb -+=由韦达定理可知2202222kma b x a k -+=，即20x m ka =-，把20x m ka =-代入y kx m =+中，得2b m y =，所以220200b x b y kx m a y y =+=-+，化简得00221x x y ya b+=．当切线斜率不存在时，过()00,x y 的切线方程为x a =±，满足上式．综上，椭圆上一点()00,x y 的切线方程为00221x x y ya b +=.所以椭圆C 在,A B 处的切线方程为12121,155x x x xy y y y +=+=，联立方程组11221,51,5x xy y x x y y ì+=ïïíï+=ïî解得点M 的坐标为()2112122112215,y y x x x y x y x y x y æö--ç÷--èø，()()12122112212112211555OMON x x x y x y x x k k y y y y k x y x y ---===-=---，故,,O M N 三点共线.（ii ）由（i）可知，2AB x =-=，又,,F A B 三点共线，所以21210022y y x x --=--，所以()1221212x y x y y y -=-，即点M 化简得51,22k æö-ç÷，=，即1k =时，等号成立.所以AB FM FN×的最小值为【点睛】关键点睛：解决第二问的关键是证明过椭椭圆22221(0)x y a b a b+=>>上一点()00,x y 处的切线方程为00221x x y ya b+=，属较难题.19. 设()f x ¢是函数()f x 的导函数，若()f x ¢可导，则称函数()f x ¢的导函数为()f x 的二阶导函数，记为()f x ¢¢.若()f x ¢¢有变号零点0x x =，则称点()()00,x f x 为曲线()y f x =的“拐点”.（1）研究发现，任意三次函数()()320ax bx d a f x cx =+++¹，曲线()y f x =都有“拐点”，且该“拐点”也是函数()y f x =的图象的对称中心.已知函数()3224f x x bx x d =+-+的图象的对称中心为()1,3，求函数()f x 的解析式，并讨论()f x 的单调性；（2）已知函数()132221112e1(0)623mx g x mx x x m m m m -=+-+-->.（i ）求曲线()y g x =的“拐点”；（ii ）若()()()12122g x g x x x +=-¹，求证：122x x m +<【答案】（1）()3232429f x x x x =--+，函数()f x 在(),2-¥-上单调递增，在()2,4-上单调递减，在()4,+¥上单调递增.（2）（i ）1,1m æö-ç÷èø；（ii ）证明见解析【解析】【分析】（1）根据“拐点”的定义，对函数()y f x =求导列式求解3,29b d =-=，利用导数研究函数()f x 的单调性即可求解，（2）（ⅰ）根据“拐点”的定义，对函数()g x 求导，利用二阶导函数的异号零点得出结果；（ⅱ）由（i ）可得函数()g x 在R 上单调递增，将要证的不等式转化为()1122g x g x m æö+->-ç÷èø，构造函数()()2h x g x g x m æö=+-ç÷èø，利用导数研究函数的单调性，再根据函数()h x 的单调性得到关于12,x x 的不等式，即可证明.【小问1详解】()3224f x x bx x d =+-+Q ，()23224f x x bx \=+-¢，()62f x x b \=+¢¢，又函数()3224f x x bx x d =+-+的图象的对称中心为()1,3，即拐点为()1,3，()()11243,1620,f b d f b ¢¢ì=+-+=ï\í=+=ïî解得3,29b d =-=，()3232429f x x x x \=--+，()()()23624342f x x x x x \=--=-+¢，.Q 函数()f x ¢在(),2¥--上为正，在()2,4-上为负，在()4,¥+上为正，\函数()f x 在(),2¥--上单调递增，在()2,4-上单调递减，在()4,¥+上单调递增.【小问2详解】（i ）()132221112e 1623mx g x mx x x m m m -=+-+--Q ，()12111e 222mx g x mx x m m-\=+-+¢，()1e 2mx g x mx -¢¢\=+-.显然，()1e 2mx g x mx -=+¢-¢在R 上单调递增，且011e 20g m m m æö=+´-=ç¢÷èø¢，1x m\=是()g x ¢¢的变号零点，又0232211111112e 11623g m m mm m m m m æö=+´-+´--=-ç÷èø，\曲线()y g x =的拐点是1,1m æö-ç÷èø.（ii ）由（i ）可得，当1,x m ¥æöÎ-ç÷èø时，()()0,g x g x ¢¢¢<单调递减；当1,x m ¥æöÎ+ç÷èø时，()()0,g x g x ¢¢¢>单调递增；()02111111e 2022g x g m m mm m m æö\³=+´-´+÷¢=çèø¢，\函数()g x 在R 上单调递增，不妨设121x x m <<.要证122x x m +<，即证212x x m <-，即证()212g x g x m æö<-ç÷èø，又()()122g x g x +=-，即证()1122g x g x m æö--<-ç÷èø，即证()1122g x g x m æö+->-ç÷èø令()()2h x g x g x m æö=+-ç÷èø，则()()2h x g x g x m ¢æö=--ç÷è¢ø¢，()()()21122e 2e 2m x mx m h x g x g x mx m x m m æö-ç÷-èøéùæöæö\=+-=+-++--êúç÷ç÷èøèøêúë¢¢¢¢û¢¢.11111e e 2e 20e mx mx mx mx ----=+-=+-³，\函数()()2h x g x g x m ¢æö=--ç÷è¢ø¢在R 上单调递增，又11210h g g m m m m æöæöæö=--¢=ç÷ç÷ç÷èøèøèø¢¢，\函数()()2h x g x g x m æö=+-ç÷èø在1,m ¥æö-ç÷èø上单调递减，在1,m ¥æö+ç÷èø上单调递增.()()111211212h x g x g x h g g m m m m m æöæöæöæö\=+->=+-=-ç÷ç÷ç÷ç÷èøèøèøèø得证，即122x x m +<成立.【点睛】方法点睛：处理此类双变量问题有两个策略：一是转化，即从已知条件入手，寻找双变量所满足的不等式，并把含双变量的不等式转化为含单变量的不等式；二是巧妙构造函数，再借用导数判断函数的单调性，从而求解.。

安徽省池州市贵池区池州市第一中学2022-2023学年高二下学期6月月考数学试题

1号卷• A10联盟高二年级（2021级）下学期6月学情调研考试数学试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分.满分150分.考试时间120分钟.第I 卷（选择题共60分）一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）,廿化人A = <!x|x 2 +16< 10x 1.若集合 I -B = \x\x> 5,则A<j B=()A. {x|x>2 C. {x|5vxv8}D.B. 2 < x < 52.若曲线y = x 2-lnx 的一条切线的斜率是-1,则切点的横坐标为（)r ^2Vx. -------2B ・I A. 1 D. °3.通用技术结业课程上，老师带领大家设计一个圆台状的器皿材料的厚度忽略不计，该器皿下底面半径为3cm,上底面半径为18cm,容积为1935右7©113 ,则该器皿的高为（)A. 5a /§chi C. 150cm D.20^/§cm B. 12j§cm 4.棣莫佛公式p(cos6 + isi 〃0)]〃="(cos 〃0 + isin 〃O )(i 为虚数单位,是由法国数学家棣莫r >0 ),佛发现的.根据棣莫佛公式，复数z =5n . . 5兀 ——+ ism ——12 124的虚部为)1 A.——81B.—8V38D.Vx.----------85.若直线/u 平面1,直线mu 平面”，则“111（3"的一个必要不充分条件是（)A. a // [3 B. I,所共面 C. m//a D.I,所无交点6.音乐与数学在某些领域息息相关，比如在音乐中可以用正弦函数来表示单音，用正弦函数相叠加表示和弦.已知某和弦可表示为函数/（x ） = sinx-2sin2x,则川）在［-兀,兀］上的图像大致为（）7.正多边形具有对称美的特点，很多建筑设计都围绕着这一特点展开.已知某公园的平面设计图如图所示，^ABC 是边长为2的等边三角形，四边形庞，AGFC, BCHI 都是正方形，则A. 4-20B. -4-20C. 2-4a /3D. -2-"n ]8. 18世纪数学家欧拉在研究调和级数时得到了这样的成果：当〃很大时，Y- = lnn+r (〃为常数).i=i i40000 ]4 60000 ] 6 90000 ] 9基于上述事实，已知1= Z 匚一=，b= Z 匚—三，c= S 匚一成，则"，b ，c 的大小关系为z=30001 1 3 z=50001 1 5 z=70001 1 '()A. a> obB. c> a>bC. a>b>cD. b> c> a 二、选择题(本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.)9.将函数/(x) = 2sinf3x-^的图像的横坐标伸长为原来的2倍后，再向左平移;个单位长度，得到函数g ⑴的图像，则()A. g(x)的周期为亏B. g （7l ） = -V2C.g"+；］=g（T）D.g（x）在-；,0上单调递减10.某中学共有1000名学生，其中初中生600人，身高的平均数为160,方差为100,高中生400人，身高的平均数为170,方差为200,则下列说法正确的是（）A.该中学所有学生身高的平均数为164B.该中学所有学生身高的平均数为162C.该中学所有学生身高方差为162D.该中学所有学生身高的方差为16411.已知。

福建省福州市平潭第一中学2023-2024学年高一下学期6月月考数学试题

福建省福州市平潭第一中学2023-2024学年高一下学期6月月考数学试题一、单选题 1．已知复数11iz =+，则复数z 共轭复数的虚部为（） A ．1-B ．1C ．12-D ．122．若m ，n ，l 为三条不同的直线，α，β为两个不重合的平面，则下列命题正确的是（） A ．如果m α⊂，l m ∥，则l α∥B ．如果m α⊂，n ⊂α，m β⊄，n β⊄，则αβ∥C ．如果αβ∥，l β⊂，则l α∥D ．如果αβ∥，m α⊂，n β⊂，则m n ∥3．若向量a v ，b v 满足2a b ==r r ，,120a b =or r ，则a b -=r r （）A ．4B ．12C ．2D ．4．若向量)a =r，()2,0b =-r ，则b r 在a r上的投影为（）A ．1-B ．C ．1,2⎛- ⎝⎭D ．12⎛ ⎝⎭5．在ABC V 中，cos sin a b C c B =+，则角B 是（） A ．6πB ．4π C ．3π D ．23π 6．紫砂壶是中国特有的手工制造陶土工艺品，其制作始于明朝正德年间.紫砂壶的壶型众多，经典的有西施壶､掇球壶､石瓢壶､潘壶等.其中石瓢壶的壶体可以近似看成一个圆台，如图给出了一个石瓢壶的相关数据（单位：cm ），那么该壶的最大盛水量为（）A ．368cm πB ．3152cm πC ．3cmD ．3204cm π7．在空间四边形ABCD 中，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 的中点．若2==AC BD ，且AC 与BD 所成的角为60︒，则EG 的长为（）A ．1BC ．1D81111ABCD A B C D -中，直线BD 到平面11AB D 的距离为（）A B C D二、多选题9．如图，已知正方体1111ABCD A B C D -，点E 、F 、G 分别为棱BC 、1CC 、CD 的中点，下列结论正确的有（）A ．AE 与1D F 共面B ．平面11//AB D 平面GFEC ．AE EF ⊥D ．//BF 平面11AB D10．已知ABC V ，则下列命题中，真命题的是（）A ．若sin 2sin 2AB =，则ABC V 是等腰三角形 B ．若sin cos A B =，则ABC V 是直角三角形 C ．若cos cos cos 0A B C <，则ABC V 是钝角三角形D ．若()()()cos cos cos 1A B B C C A ---=，则ABC V 是等边三角形11．如图所示，已知正方体1111ABCD A B C D -的棱长为2，线段11B D 上有两个动点E ，F ，且EF ）A ．平面AEF ∥平面1DBCB ．存在点E （E 与1D 不重合），使得BE 与1AD 共面C ．当E 点运动时，总有1AC AE ⊥D ．三棱锥B AEF -的体积为定值三、填空题12．棱长为1的正方体的外接球的表面积为．132倍，则该圆锥的体积是.14．如图，在三棱锥木块V ABC -中，VA ，VB ，VC 两两垂直，1VA VB VC ===，点P 为VAC V的重心，沿过点P 的平面将木块锯开，且使截面平行于直线VC 和AB ，则该截面的面积为．四、解答题15．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且()(s i ns i n )s i n 3s i n b c B C a A bC++=+.(1)求角A 的大小；(2)若a =ABC V ABC V 的周长.16．如图，在边长为2的正方形ABCD 中，点E 是AB 的中点，点F 是BC 的中点，将,,AED BEF DCF V V V 分别沿,,DE EF DF 折起，使A ，B ，C 三点重合于点A '(1)求证A D EF '⊥(2)求三棱锥A EFD '-的体积17．如图，在三棱锥P ABC -中，90ACB ∠=︒，PA ⊥底面ABC(1)证明：平面PBC ⊥平面P AC(2)若AC BC PA ==，M 是PB 中点，求AM 与平面PBC 所成角的正切值18．如图，在四棱锥P ABCD -中，底面ABCD 为正方形，侧面PAD 是正三角形，2AB =，侧面PAD ⊥底面ABCD ，M 是PD 的中点.(1)求证:AM ⊥平面PCD ； (2)求C 点到平面PAB 的距离；(3)求侧面PBC 与底面ABCD 所成二面面角的余弦值.19．如图，在直三棱柱111ABC A B C -中，M 为棱AC 的中点，AB BC =，2AC =，1AA =(1)求证：1//B C 平面1A BM ； (2)求证：1AC ⊥平面1A BM ；(3)在棱1BB 上是否存在点N ，使得平面1AC N ⊥平面11AAC C ？如果存在，求此时1BNBB 的值；如果不存在，请说明理由.。

2024北京理工大附中高一6月月考语文

2024北京理工大附中高一6月月考语文（2024.6)本试卷满分100分，时间90分钟。

一、诗文背诵（40分）1.在横线处填写作品原句。

(1)有善始者实繁，。

(魏征《谏太宗十思疏》）(2)吴楚东南坼，。

(杜甫《登岳阳楼》）(3)盖失强援，不能独完。

故曰：。

(苏洵《六国论》）(4)至于怨诽之多，。

(王安石《答司马谏议书》）(5)千古凭高对此，。

(王安石《桂枝香·金陵怀古》）(6)素月分辉，明河共影，。

(张孝祥《念奴娇·过洞庭》）(7)《子路、曾皙、冉有、公西华侍坐》中，生动地描绘出曾皙从容、洒脱的情态及恭敬的态度的句子是：，铿尔，。

(8)《谏太宗十思疏》中，用对比手法说明竭诚待人和放纵性情、轻视他人所带来的不同结果的句子是：，。

(9)夸张的修辞手法，可增强表达效果。

比如苏洵用“思厥先祖父，暴霜露，斩荆棘，”来表现创业者的艰难。

（苏洵《六国论》）(10)古人登高望远，多有感怀。

杜甫的“，凭轩涕泗流”表达了对国事的担忧。

（杜甫《登岳阳楼》）(11)当我们徜徉于美景时，往往会因内心与景物相合，产生只可意会不可言传的美妙体验。

这种体验，用张孝祥《念奴娇·过洞庭》中的词句来说，可谓“，。

”(12)《谏太宗十思疏》中指出所谓取天下易守天下难的缘由是：，，，。

(13)在《答司马谏议书》中，表明王安石对当时士大夫苟且偷安、墨守成规、随和世俗的不满的句子是：“，。

”(14)在《答司马谏议书》中，王安石在文章最后正面表明态度：“，，”委婉的口吻中蕴含着锐利的锋芒，一语点破以司马光为代表的保守派的思想实质，直刺对方要害。

(15)在《答司马谏议书》中，王安石举例说明先王做事也会招致百姓反对，不只是朝廷士大夫反对的句子是：“，。

”(16)中国古人为文善用形象化的表达，如《谏太宗十思疏》开篇以“求木之长者，必固其根本；欲流之远者，必浚其泉源”为喻，说明“，”的道理；《六国论》中用“子孙视之不甚，，”来批判随意赂地的愚蠢之举；《子路、曾皙、冉有、公西华侍坐》中用“浴乎沂，，咏而归”描绘出一幅美好的生活图景。

江苏省南通市海安市实验中学2023-2024学年高一下学期6月月考数学试题

江苏省南通市海安市实验中学2023-2024学年高一下学期6
月月考数学试题
学校:___________姓名：___________班级：___________考号：___________
A．23πB．
二、多选题
9．某市2022年经过招商引资后，经济收入较前一年增加了一倍，实现翻番，为更好地了解该市的经济收入的变化情况，统计了该市招商引资前后的年经济收入构成比例，得到如下扇形图：
四、解答题
15．数字人民币在数字经济时代中体现的价值、交易媒介和支付手段职能，为各地数字经济建设提供了安全、便捷的支付方式，同时也为金融监管、金融产品设计提供更多选择性和可能性．苏州作为全国首批数字人民币试点城市之一，提出了2023年交易金额达2万亿元的目标．现从使用数字人民币的市民中随机选出200人，并将他们按年龄（单位：岁）
进行分组：第1组[)
15,25，第2组[)
45,55，第5组
35,45，第4组[)
25,35，第3组[)
[]
55,65，得到如图所示的频率分布直方图．
(3)设()1i,2i a =+-r ，()i,z b =r ，z ÎC ，且复向量a r 与b r 平行，求复数z .
所以
DAB
Ð
即为圆台母线与底面所成角，
分别过点C、D在平面ABCD。

辽宁省沈阳市第一三四中学2023-2024学年七年级下学期6月月考数学试题

辽宁省沈阳市第一三四中学2023-2024学年七年级下学期6月月考数学试题一、单选题1．我国古代数学家祖冲之推算出π的近似值为355113，它与π的误差小于0.0000003．将0.0000003用科学记数法可以表示为（）A ．7310-⨯B ．80.310-⨯C ．6310-⨯D ．7310⨯ 2．下列四个图形中，对称轴最多的图形是（）A ．B ．C ．D ． 3．下列运算中，正确的是（）A ．3232a a a -=B ．()222a b a b +=+ C ．3222a b a ab ÷= D ．()224a b a b = 4．以下长度的三根小木棒能摆成三角形的是（）A ．1， 2， 3B ．3， 3， 5C ．2， 3， 5D ．3， 5， 9 5．如图，直线a ，b 被直线c 所截，若//a b ，170=︒∠，则2∠的度数是（）A ．70°B ．100°C ．110°D ．120°6．下列事件中，是必然事件的是（）A ．车辆随机到达一个路口，遇到红灯B ．将油滴在水中，油会浮在水面上C ．如果22a b =，那么a=bD ．掷一枚质地均匀的硬币，一定正面向上7．如图，已知D 、E 分别为ABC V 的边BC ，AC 的中点，连接AD ，DE ，AF 为ADE V 的中线．若四边形ABDE 的面积为24，则ABC V 的面积为（）A ．36B ．34C ．32D ．308．如图，在ABC V 中，90C ∠=︒，D E ，是AC 上两点，BD 平分EBC ∠，BE 平分ABD ∠，那么下列说法中不正确的是（）A ．CD 的长度等于D 到BE 的距离B ．BC 是ABE V 的高 C ．123∠=∠=∠D ．BD 是ABC V 的角平分线9．如图，亮亮想测量某湖A ，B 两点之间的距离，他选取了可以直接到达点A ，B 的一点C ，连接CA ，CB ，并作BD AC ∥，截取BD AC =，连接CD ，他说，根据三角形全等的判定定理，可得ABC DCB △≌△，所以AB CD =，他用到三角形全等的判定定理是（）A ．SASB ．AASC ． SSSD ．ASA10．研究表明，当每公顷氮肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系：根据表格中的数据，氮肥的施用量是（）kg 时最适宜．A ．202B ．259C ．336D ．404二、填空题11．计算2(2)x -＝．12．一个角的补角是102︒，则这个角是︒．13．某工程队承建一条长为60km 的乡村公路，预计工期为120天，若每天修建公路的长度保持不变，则还未完成的公路长度()km y 与施工时间x （天）之间的关系式为y =． 14．用七巧板摆成如图所示图形，一只蚂蚁在此图形上任意爬行，已知它停在这副七巧板上的任何一点的可能性都相同，那么它停在阴影部分的概率是．15．已知，在ABC 中，AB AC =，AB 的垂直平分线交直线BC 于点D ．当(0180)BAC αα∠=︒<<︒时，则CAD ∠的度数为．（用含α的式子表示)三、解答题16．计算：(1)()20202211π202163-⎛⎫-+-+--- ⎪⎝⎭； (2)()()()2122x x x +--+．17．先化简，再求值：()()()22222a b a b a b b b ⎡⎤+-+-+÷⎣⎦，其中 2a =，1b =． 18．如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A 、B 、C 在小正方形的顶点上．(1)在图中画出与ABC V 关于直线l 成轴对称的111A B C △；(2)1AB C V 的面积为；(3)在直线l 上找点P 使得PB PC +最小；(4)直线l 上找一点Q 使得QB QC -最小．19．如图，ABC V 中，AB AC =．(1)尺规作图（保留作图痕迹，不写作法）：①作A ∠的角平分线，交BC 于点H ；②作AB 边的垂直平分线，垂足为点D ，交AH 于点O ；(2)连接BO ，OC ，求证：OA OC =．20．如图，点B 、C 、D 在同一条直线上，AB BD ⊥，DE BD ⊥，AC CE ⊥，AB CD =．(1)求证：ABC CDE △≌△．(2)若40ACB ∠=︒，求AED ∠的度数．21．小明和小颖用一副扑克牌做摸牌游戏（去掉大小王，共52张牌），分为黑桃，梅花，红桃，方块四种花色，游戏规则如下：小明先从中任意抽取一张牌，记下牌面内容，然后放回，小颖再任意抽取一张，谁摸到的牌面大谁就获胜（规定牌面从小到大的顺序为：2，3，4，5，6，7，8，9，10，J ，Q ，K ，A ，且牌面的大小与花色无关）．(1)小明抽到红桃A 的概率为小颖抽到3的概率为；(2)若小明先摸一张牌，牌面为4；然后小颖摸牌，那么小明获胜的概率为小颖获胜的概率为；(3)若小明已经摸到的牌面为2，然后小颖摸牌，那么小明获胜的概率为小颖获胜的概率为；若小明已经摸到的牌面为A ，然后小颖摸牌，那么小明获胜的概率为，小颖获胜的概率为．(4)若小明先摸到的牌面是，那么两人获胜的概率相同．22．素材1：沈阳故宫是沈阳市中心古老的宫殿，不仅仅是一座宏伟的建筑，更是沈阳乃至整个东北地区的文化瑰宝，端午节期间，小文和小明去故宫参观游览，图1线是两人游览的路线图，且所给数据为相应两个地点之间的路程（米）．小文步行的路程s （米）与游览时间t （分钟）之间的关系部分图象如图2所示．素材2：小文以一定的速度从大清门步行出发，依次参观崇政殿→凤凰楼→清宁宫这三个宫殿，且在每个宫殿逗留的时间相同，当参观完清宁宫后直接走到文溯阁时，共用去30分钟．素材3：小文与小明同时从大清门出发，小明参观了同小文一样的三个宫殿外，还参观了大政殿，且在各宫殿逗留的时长相同，已知小明的步行速度为70米/分钟，图1 图2(1)任务一：小文步行的速度为米/分钟；图2中，点M 表示的意义；崇政殿到清宁宫的距离为米；(2)任务二：请求出小文在每个宫殿逗留的时间以及从清宁宫到文溯阁之间需步行的距离．(3)任务三：若小明与小文相约同时到达文溯阁，请帮小明设计一个参观路线(参观过的宫殿，重新路过后不再逗留)，并求出他在每个宫殿逗留的时长．23．综合与实践问题情境：如图，在ABC V 中，90ACB ∠=︒，AC BC =，点D 在ABC V 所在的平面内运动．探究图形间存在的关系．特例探究：（1）如图1，当点D 在边AB 上运动，连接CD ，以CD 为边在其右侧作等腰直角三角形CDE ，连接BE ，发现BE AB ⊥，请说明理由；求异探究：（2）如图2，点E 为AC 的中点，点F 为AB 的中点，AEF △为等腰直角三角形，点D 在ABCV 外部时，连接ED ，以ED 为边在其右侧作等腰直角三角形EDH ，连接DF 和CH ，判断DF 与CH 的关系，并证明；拓展应用：（3）如图3，当点D 在直线AC 上时，连接BD ，在线段BD 绕点B 逆时针旋转90︒得到线段BE ，连接AE ．若6CD =，10AE =，求ABD △的面积．。

云南省曲靖市2023-2024学年七年级下学期6月月考数学试题

云南省曲靖市2023-2024学年七年级下学期6月月考数学试题一、单选题1．在实数 3.14-，0，π0.1010010001中，无理数的个数有（）A ．1个B ．2个C ．3个D ．4个2．在平面直角坐标系中，属于第二象限的点是（）A ．(2,3)B ．(2,3)-C ．(2,3)-D ．(2,3)-- 3．下列运算中，正确的是（）A 6±B 3-C 1=-D 2 4．下列选项中是方程26x y +=的解的是（）A ．12x y =⎧⎨=⎩B ．41x y =⎧⎨=⎩C ．22x y =-⎧⎨=⎩D ．13x y =-⎧⎨=⎩5．下列命题中是真命题的是（）A ．两直线平行，内错角互补B ．0.1是0.1的一个平方根C ．同角的补角互补D ．平行于同一直线的两条直线平行 6．如图，数轴上所表示的不等式的解集是（）A ．1x >-B ．1x ≥-C ．1x <-D ．1x ≤- 7．如图，直线a ，b 被直线c 所截，下列条件中能判定a b P 的是（）A ．14∠=∠B ．23180∠+∠=︒C ．25∠=∠D ．45∠=∠8．已知a b >，下列不等式一定成立的是（）A ．11+<+a bB ．33a b >C ．33a b ->-D ．a c b c -<-9．如图，直线AB 与CD 相交于点O ，OE 平分AOC ∠，若28BOC ∠=︒，则AOE ∠的度数是（）A ．86︒B ．76︒C ．66︒D ．56︒10 ）A ．1B ．2C ．3D ．411．已知有理数x ，y 满足方程组3324x y y x -=⎧⎨-=-⎩，则2x y +的值为（） A ．1- B ．0 C ．1 D ．212．某校举行知识竞赛，共有30道抢答题，答对一题得5分，答错或不答扣3分，要使总得分不少于80分，则至少应该答对几道题？若设答对x 道题，可得式子为（）A ．()533080x x -->B ．()533080x x --≤C ．5380x x -≥D ．()533080x x --≥13．若一个正数的两个不同的平方根分别是34a -和2a -，则a 的值为（）A ．4B ．8C ．4-D ．4±14．已知关于x 的不等式组5311x x x a +<+⎧⎨>+⎩的解集是2x >，则a 的取值范围是（） A ．1a ≤ B ．1a < C ．1a ≥ D ．1a >15．如图，在平面直角坐标系中，11OA =，将边长为1的正方形一边与x 轴重合按图中规律摆放，其中相邻两个正方形的间距都是1，则点2024A 的坐标为（）A ．()1012,0B ．()1012,1C ．()1013,0D ．()1013,1-二、填空题16．4的算术平方根是．17．如果52x y =⎧⎨=⎩关于x 和y 的二元一次方程9x my -=解，那么m 的值为． 18．在平面直角坐标系中，已知()3,1A m +-，()1,3B m -，且直线AB y ∥轴，则m 的值为．19．关于x 的不等式组630x x a -<⎧⎨≤⎩恰好有3个整数解，则a 的取值范围是．三、解答题20．（1）计算：1（2）解方程：()219x -=．21．完成下面的证明：如图，已知A F C D ∠=∠∠=∠，，求证：BD CE ∥．22．解不等式组()22315133x x x x ⎧+>-⎪⎨+≥+⎪⎩，并把解集在数轴上表示出来 23．甲乙两人从相距36千米的两地相向而行．如果甲比乙先走2小时，那么在乙出发后3小时相遇；如果乙比甲先走2小时，那么在甲出发后2.5小时相遇．甲、乙两人每小时各走多少千米？24．解下列方程组：(1)2316210x y x y +=⎧⎨+=⎩； (2)2512432x y x y -=⎧⎨+=-⎩．25．已知ABC V 的三个顶点坐标分别为()3,3A -，()0,4B ，()1,0C -．(1)在坐标系中描出各点，画出ABC V ；(2)画出将ABC V 先向右平移3个单位长度，再向下平移5个单位长度后得到的图形111A B C △，并写出1A 、1B 、1C 的坐标；(3)求ABC V 的面积26．如图，直线CD 、EF 交于点O ，AO BO ⊥，且1290∠+∠=︒．(1)求证：AB CD ∥；(2)若OB 平分DOE ∠，2:32:5∠∠=，求AOF ∠的度数．27．为倡导读书风尚，打造书香校园．某校计划购买A 、B 两种图书共60本．已知同时购进A 种图书20本和B 种图书50本，则共需1700元，且购进A 种图书16本和购进B 种图书28本的价格相同．(1)求A ，B 两种图书的单价各是多少元；(2)根据学校预算，购买两种图书的总金额不能超过1690元，求该校最多能购买A 种图书多少本？(3)在（2）条件下，若要求两种图书都要购买，且B 种图书的数量不超过A 种图书的数量，请问学校共有哪几种购买方案？哪种方案购买的话费最少？最少花费是多少元？。

云南省玉溪市峨山彝族自治县双江中学0223-2024学年七年级下学期6月月考数学试题

云南省玉溪市峨山彝族自治县双江中学0223-2024学年七年级下学期6月月考数学试题一、单选题1．在下面四个图形中，1∠是对顶角的是（）∠与2A．B．C．D．2．下列所示的图案分别是奔驰、奥迪、长安、三菱汽车的车标，其中看作由“基本图案”经过平移得到的是（）A．B．C．D．-0，π0.101001⋯⋯中无理数的个数有（）3．在 3.14A．3个B．2个C．1个D．4个4．下列计算正确的是（）A6B2±C6=-D．8=-5．如图，描述同位角、内错角、同旁内角的关系不正确的是（）A ．1∠与4∠是同位角B ．2∠与3∠是内错角C ．3∠与4∠是同旁内角D ．2∠与4∠是同旁内角6．若一个数的平方根与它的立方根完全相同，则这个数是（）A ．1B ．1-C ．0D ．10±，7．如图，点E 在BC 的延长线上，下列条件中不能判定AB CD P 的是（）A ．12∠=∠B ．3=4∠∠C ．B DCE ∠=∠D ．180D DAB ∠+∠=︒ 8．下列说法不正确的是（）A ．125的平方根是15±B ．9-是81的一个平方根C ．0.2的算术平方根是0.04D ．27-的立方根是3- 9．如图，a b ∥，点B 在直线b 上，且AB BC ⊥，136∠=︒，那么2∠=（）A ．54︒B ．56︒C ．44︒D ．46︒10．如图，将周长为18cm 的三角形ABC 沿边BC 向右平移5cm ，得到三角形111A B C ，连接1AA ，则四边形11AAC B 的周长是（）A ．30cmB ．35cmC ．23cmD ．28cm11．如图，,4AC BC AC ⊥=，点D 是线段BC 上的动点，则,A D 两点之间的距离不可能是（）A ．3.5B ．4.5C ．5D ．5.512．已知一个数的两个平方根分别是A+3与2A-15,这个数的值为（）A ．4B ．±7C ．-7D ．4913．如图，AB CD ∥，CE 平分BCD ∠，18DCE ∠=︒，则B ∠等于A ．18︒B ．36︒C ．45︒D ．54︒14．下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离；②内错角相等；③两点之间线段最短；④过一点有且只有一条直线与已知直线平行；⑤在同一平面内，若两条直线都与第三条直线垂直，则这两条直线互相平行．A ．5个B ．4个C ．3个D ．2个15．规定用符号[m]表示一个实数m 的整数部分，例如：[23]＝0，[3.14]＝3.按此规定1]的值为（）A ．3B ．4C ．5D ．6二、填空题16．5的平方根是．17．如图，请写出能判定CE //AB 的一个条件18,a =b ．19．如图，折叠宽度相等的长方形纸条，若∠1=60°，则∠2=度.三、解答题20．计算：202412-．21．求下列各式中的x ．(1)228x =；(2)3(2)270x ++=．22．已知：如图,,12AD BC EF BC ⊥⊥=∠∠试说明DG AB ∥．解：,AD BC EF BC ⊥⊥（已知）90EFB ADB ∴∠=∠=︒（__________________）∴∥EF AD （__________________）1BAD ∴∠=∠（__________________）又12∠=∠Q （已知）∴________＝________（__________________）∴DG AB ∥（__________________）23．如图，在边长为1个单位长度的小正方形组成的网格中．把ABC V 进行平移，得到A B C '''V ，使点A 与A '对应，(1)请在网格中画出A B C '''V ；且线段AA '与线段CC '的关系是_________．(2)求出A B C '''V 的面积．24．如图，已知直线直线a b P ，1110∠=︒，270??．(1)求3∠的度数；(2)判断直线c 与d 的位置关系，并说明理由．25．已知52a +的立方根是3，31a b +-的算术平方根是4，c(1)求a ，b ，c 的值；(2)求3a b c -+的平方根．26．如图，已知四边形ABCD 中，∠D ＝100°，AC 平分∠BCD ，且∠ACB ＝40°，∠BAC ＝70°．(1)AD 与BC 平行吗？试写出推理过程；(2)求∠DAC 和∠EAD 的度数．27．如图1，AB //CD ，∠P AB =115°，∠PCD =130°，求∠APC 的度数．小红的思路是：过P 作PE ∥AB ，通过平行线性质来求∠APC ．(1)按小红的思路，易求得∠APC的度数为_____度．(2)问题迁移；如图2．AB∥CD，点P在射线OM上运动，记∠P AB=α．∠PCD=β，当点P 在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由．(3)在（2）的条件下，①如果点P运动到D点右侧（不包括D点），则∠APC与α、β之间的数量关系为___．②如果点P运动到B点左侧（不包括B点），则∠APC与α、β之间的数量关系为__．（直接写出结果）。

广西壮族自治区南宁市天桃实验学校2023-2024学年八年级下学期6月月考数学试题

广西壮族自治区南宁市天桃实验学校2023-2024学年八年级下学期6月月考数学试题一、单选题1．下列各式中，属于最简二次根式的是（）A B C D 2．下列四组线段中，可以构成直角三角形的是（）A ．456，，B ．345，，C ．234，，D ．123，， 3．为筹备班级联欢会，班长对全班学生爱吃的水果进行了民意调查，那么最终买什么水果，下面的数据最值得关注的是（） A ．众数B ．中位数C ．平均数D ．方差4．下列运算正确的是（）A =B ．2-=C ．=D 5．如图，已知函数y ＝ax +b 和y ＝kx 的图象交于点P ，则根据图象可得关于x ，y 的二元一次方程组y ax by kx =+⎧⎨=⎩的解是（）A ．24x y =-⎧⎨=-⎩B ．42x y =-⎧⎨=-⎩C ．24x y =⎧⎨=-⎩D ．42x y =-⎧⎨=⎩6．二次函数()224y x =+-的顶点坐标是（） A ．()2,4--B ．()2,4-C ．()2,4-D ．()2,47．如图所示的是由两个直角三角形和三个正方形组成的图形，其中阴影部分的面积是（）A ．50B ．16C ．25D ．418．若抛物线24y x x c =++与x 轴没有交点，则c 的值可以是（） A ．4-B ．0C ．4D ．89．我们都知道，四边形具有不稳定性．老师制作了一个正方形教具用于课堂教学，数学课代表小亮在取道具时不小心使教具发生了形变（如图），若正方形道具边长为10cm ，30D '∠=︒，则四边形的面积减少了（）A ．250cmB ．2C ．2100cmD ．210．某农户，用26m 长的篱笆围成一个一边靠住房墙（墙长12m ），且面积为280m 的长方形花园，垂直于住房墙的一条边留有一个1m 宽的门，设垂直于住房墙的另一条边的边长为m x ，如图所示，若可列方程为80x ⨯=★，则★表示的是（）A ．(262)x -B ．(272)x -C ．262x- D ．272x- 11．小王于上午8时从甲地出发去相距50千米的乙地．图中，折线OABC 是表示小王离开甲地的时间t （时）与路程S （千米）之间的函数关系的图象．根据图象给出的信息，下列判断中，错误．．的是（）A ．小王用时3小时到达乙地B ．小王在途中停了半小时C ．与8:009:30-相比，小王在10:0011:00-行进的速度较快D ．出发后1小时，小王走的路程多于25千米12．如图，在菱形ABCD 中，对角线AC BD ，相交于点O ，点M ，N 分别是边AD CD ，的中点，连接MN OM ，，若3MN =，24ABCD S =菱形，则OM 的长为（）A ．3B ．3.5C ．2D ．2.5二、填空题13x 的取值范围是． 14．如图，Y ABCD 的一个外角为38°，则∠A =度．15．将一次函数31y x =-的图象沿y 轴向上平移3个单位，所得函数表达式．16．数据 12310x x x x ⋯，，，，的方差计算公式为 ()()()2222121044410S x x x ⎡⎤=-+-++-÷⎣⎦L ，则这组数据12310x x x x ⋯，，，，的和是. 17．海伦一秦九韶公式告诉我们：三角形的三边长分别为a ，b ，c ，记()12p a b c =++，那么三角形面积可以表示为S =现已知一个三角形的三边长分别为5、6、7，那么这个三角形的面积为．18．已知点A （2，4），B （0，1），点M 在抛物线y ＝14x 2上运动，则AM ＋BM 的最小值为．三、解答题 19．计算：(2)(20．解下列方程： (1)2410x x --=； (2)()3122x x x -=-．21．某校要从王同学和李同学中挑选一人参加全县数学知识竞赛，在五次选拔测试中他们的成绩（单位：分）如下表．根据上表解答下列问题： (1)完成下表(2)若将80分以上（含80分）的成绩视为优秀，则王同学、李同学在这五次测试中的优秀率各是多少？(3)历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？请说明理由． 22．已知：如图，在平行四边形ABCD 中，AB AD <．(1)用尺规完成以下基本作图：作BAD=，∠的角平分线AE，交BC于点E，在AD上截取DF DC连接CF；（保留作图痕迹，不写作法和结论）(2)在（1）所作的图形中，求证：AE CF=．23．千百年来，手杆秤也可算作华夏“国粹”，是我国传统的计重工具，方便了人们的生活．如图1，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤），则y是x的一次函数．下表中为若干次称重时所记录的一些数据．(1)在图2中，通过描点的方法画出一次函数的图象，并求y（斤）与x（厘米）之间的函数表达式；(2)当秤钩上所挂物重是5.5斤时，秤杆上秤砣到秤纽的水平距离是多少？24．某水果商店经销一种名为“阳光玫瑰”水果，现进行春日促销，原价每千克50元，连续两次降价后每千克32元，若每次下降的百分率相同．(1)求每次下降的百分率；(2)若每千克盈利10元，每天可售出250千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少10千克，现该商场要保证每天盈利3000元，且要尽快减少库存，那么每千克应涨价多少元？25．勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因为证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．(1)应用场景1——在数轴上画出表示无理数的点．如图1，在数轴上分别找出表示数0的点O ，表示数3的点A ，过点A 作直线l OA ⊥，在l 上取点B ，使2AB =，以点O 为圆心，OB 的长为半径作弧，则弧与数轴的交点C 表示的数是______．(2)应用场景2——解决实际问题．如图2，秋千静止时，踏板离地的垂直高度0.3m BE =，将它往前推3m 至C 处时，水平距离3m CD =，踏板离地的垂直高度 1.3m CF =，秋千的绳索始终拉直，求秋千绳索AC 的长． 26．“昔日荔枝进长安，今朝草莓遍三秦．”行走在秦岭脚下的长安区，随处可见成片的草莓种植大棚．其中一种植户雷莹借助现有地势，将大棚的一端固定在离地面2米高的墙体OA 的端点A 外，另一端固定在离地面1米高的墙体BC 的端点B 处，墙体OA 、BC 均垂直于水平面OC ．测得OA 、BC 两墙体之间的水平距离为4米，且大棚横截面顶部为抛物线型，建立如图所示的平面直角坐标系，已知大棚上某处离地面的高度y （米）与其离墙体OA 的水平距离x （米）之间的关系满足：218y x bx c =-++．请根据以上信息解决下列问题：(1)求雷莹家大棚的最高处到地面的距离； (2)现要对入口处进行加固，如图所示：方式一：雷莹在距离墙体BC 左侧1米处垂直地面放置一根管材DE ，管材一端D 固定在地面OC 上，另一端点E 刚好能支撑在大棚主体钢架（抛物线AB 段）上，用角铁固定另一根管材EF ，使90DEF ∠=︒，且管材EF 的另一端F 固定在墙体OA 上；方式二：在距离墙体OA 、BC 等距（即OC 中点G ）处以相同的方式放置管材GH 、HK ．已知两种方式都等起到加固的作用，请通过计算说明，哪种方式所使用的管材更少？。

2023—2024学年江苏省江阴高级中学高一下学期6月月考数学试卷

2023—2024学年江苏省江阴高级中学高一下学期6月月考数学试卷一、单选题(★★) 1. 已知i是虚数单位，复数，则的虚部为（）A．1B．2C．i D．(★) 2. 从小到大排列的数据1，2，3，5，6，7，8，9，10，14，15，18的下四分位数为（）A．3B．4C．10D．12(★★) 3. 在中，、、分别是内角、、所对的边，若，，，则边（）A．B．或C．或D．(★★) 4. 某地区中小学生人数比例和近视情况分别如图甲和图乙所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法随机抽取2%的学生进行调查，其中被抽取的小学生有80人，则样本容量和该地区的初中生近视人数分别为（）A．100，50B．100，1050C．200，50D．200，1050 (★★) 5. 对于直线和不重合的平面，，下列命题中正确的是（）A．若，，则B．若，，则C．若，，则D．若，，，则(★★★) 6. 已知锐角满足，，则与的大小关系为（）A．B．C．D．(★★★) 7. 一个质地均匀的正四面体的四个面上分别标有数字1，2，3，4.连续抛掷这个正四面体两次，并记录每次正四面体朝下的面上的数字.记事件为“两次记录的数字和为奇数”，事件为“两次记录的数字和大于4”，事件为“第一次记录的数字为奇数”，事件为“第二次记录的数字为偶数”，则（）A．与互斥B．与对立C．与相互独立D．与相互独立(★★★★) 8. 已知三棱锥的所有顶点都在球O的球面上，AD⊥平面ABC，，，若球O的表面积为，则三棱锥（以A 为顶点）的侧面积的最大值为（）A．6B．C．D．二、多选题(★★★) 9. 已知复数，其共轭复数为，下列结论正确的是（）A．B．C．D．(★★★★) 10. 在中，D为BC的中点，点E满足.若，则（）A．B．C．D．(★★★★) 11. 如图；正方体的棱长为2，是侧面上的一个动点（含边界）；点在棱上；则下列结论正确的有（）A．若；沿正方体的表面从点到点的最短距离为B．若，三棱锥的外接球表面积为C．若；，则点的运动轨迹长度为D．若；平面被正方体截得截面面积为三、填空题(★★) 12. 甲、乙两名考生填报志愿，要求甲、乙只能在A，B，C这3所院校中选择一所填报志愿．假设每位同学选择各个院校是等可能的，则院校A，B 至少有一所被选择的概率为 _________ ．(★★) 13. 一组数据由6个数组成，将其中一个数由4改为1，另一个数由6改为9，其余数不变，得到新的一组数据，则新的一组数的方差相比原一组数的方差的增加值为 _________ ．(★★★) 14. 在中，若，则的最小值为________ .四、解答题(★★) 15. 已知平面向量，，满足，.(1)若，求向量与的夹角；(2)若，函数，求的值.(★★★) 16. 已知△ABC的内角所对的边是且(1)求；(2)若，求△ABC的面积.(★★★) 17. 在三棱柱中，侧面平面，且，，分别为棱，的中点.(1)证明：平面；(2)若，，求点到平面之间的距离.(★★★)18. 进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会、经济、生态等多方面的效益，是关乎生态文明建设全局的大事．为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为p，乙同学答对每题的概率都为q（），且在考试中每人各题答题结果互不影响已知每题甲，乙同时答对的概率为，恰有一人答对的概率为．(1)求p和q的值；(2)试求两人共答对至少3道题的概率．(★★★★) 19. 如图；在三棱柱中；侧面为矩形．(1)若面；，，求证：；(2)若二面角的大小为；，且；设直线和平面所成角为；问当变化过程中能否取到；若能；请证明；若不能请说明理由．。