带电粒子在电磁场中运动的MATLAB仿真
电磁场中matlab仿真实现工具箱
实验六:使用偏微分方程工具箱对电磁场的仿真一、实验目的与要求1.掌握微分方程工具箱的使用方法;2.掌握使用偏微分方程工具箱分析电磁场。
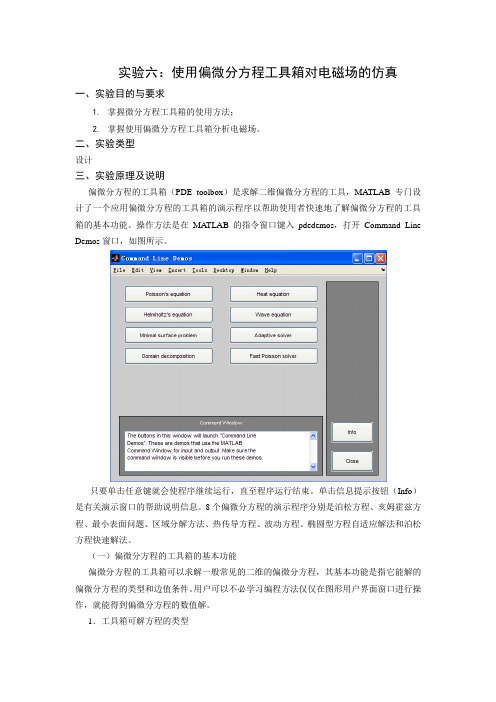
二、实验类型设计三、实验原理及说明偏微分方程的工具箱(PDE toolbox)是求解二维偏微分方程的工具,MA TLAB专门设计了一个应用偏微分方程的工具箱的演示程序以帮助使用者快速地了解偏微分方程的工具箱的基本功能。
操作方法是在MA TLAB的指令窗口键入pdedemos,打开Command Line Demos窗口,如图所示。
只要单击任意键就会使程序继续运行,直至程序运行结束。
单击信息提示按钮(Info)是有关演示窗口的帮助说明信息。
8个偏微分方程的演示程序分别是泊松方程、亥姆霍兹方程、最小表面问题、区域分解方法、热传导方程、波动方程、椭圆型方程自适应解法和泊松方程快速解法。
(一)偏微分方程的工具箱的基本功能偏微分方程的工具箱可以求解一般常见的二维的偏微分方程,其基本功能是指它能解的偏微分方程的类型和边值条件。
用户可以不必学习编程方法仅仅在图形用户界面窗口进行操作,就能得到偏微分方程的数值解。
1.工具箱可解方程的类型定义在二维有界区域Ω上的下列形式的偏微分方程,可以用偏微分方程工具箱求解:椭圆型()f au u c =+∇∙∇- 抛物型()f au u c tu d =+∇∙∇-∂∂ 双曲型()f au u c tu d =+∇∙∇-∂∂22 本征值方程()du au u c λ=+∇∙∇-式中,u 是偏微分方程的解;c 、a 、d 、f 是标量复函数形式的系数,在抛物型和双曲型方程中,它们也可以是t 的函数,λ是待求的本征值。
当c 、a 、f 是u 的函数时,称之为非线性方程,形式为()()()()u f u u a u u c =+∇∙∇-也可以用偏微分方程工具箱求解。
2.工具箱可解方程的边值条件解偏微分方程需要的边值条件一般为下面两种之一:狄里赫利(Diriclet)边值条件 hu=r广义诺曼(Generalized Neumann)边值条件 ()g qu u c n =+∇∙式中,n为边界外法向单位向量;h 、q 、r 、g 是在边界上定义的复函数。
基于matlab的电偶极子和磁偶极子的近场仿真分析

基于matlab的电偶极子和磁偶极子的近场仿真分析
对于电偶极子和磁偶极子的近场仿真分析,可以使用MATLAB中的电磁场仿真工具箱进行模拟。
首先,我们需要构建电偶极子和磁偶极子的模型。
电偶极子和磁偶极子都可以近似为一个“小电荷”和一个“小磁荷”的组合体,其中电偶极子的电荷量为q,分布在距离为d的点P1和P2上,而磁偶极子的磁荷量为m,分布在距离为d的线段上。
其次,我们需要对模型进行参数化处理。
具体来说,我们需要定义电偶极子和磁偶极子的位置、方向和大小等参数,以便进行后续的仿真计算。
然后,我们可以使用MATLAB中的电磁场仿真工具箱中的函数和工具完成具体的仿真计算。
其中,可以使用场源距离远小于波长的近场近似方法进行模拟,计算电磁场分布的幅度和相位等,并将结果可视化输出。
最后,我们可以对仿真结果进行分析,比较不同参数下电偶极子和磁偶极子产生的电磁场分布差异,并进一步优化模型参数和仿真计算方法,以提高模拟精度和可靠性。
利用MATLAB软件仿真电荷在变化磁场中的运动 (2)

利用MATLAB软件仿真电荷在变化磁场中的运动摘要:MATLAB是美国Mathworks公司于80年代推出的大型数学软件,通过多年的升级换代,现在已发展成为集数值计算、符号计算、可视化功能以及诸多的工具箱为一体的大型科学计算软件,它已广泛应用于科研院所、工程技术等各个部门,并成为大学生、研究生必备的工具软件。
本文通过MATLAB软件工具,对仿真电荷在变化磁场中的运动问题给出了直观形象的的仿真图,实现了可视化学习,丰富了学习内容,提高了对电磁场理论知识的兴趣。
关键词:MATLAB 电磁学仿真计算机模拟一、可视化的意义MATLAB是大型的数据软件,它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案。
MATLAB拥有强大的数值计算功能,但抽象的数据对于普通的用户来说往往是比较难懂的,针对这一问题,MATLAB为用户提供了更加强大的数据可视化功能,用户可以通过MATLAB的绘图函数和图形编辑窗口方便的绘制二维、三维甚至多维的图形。
MATLAB还为用户提供了各种不同的曲线元素,使图形更具表现力,更加清晰易懂。
电磁学是物理学的一个分支,是研究电场和电磁的相互作用现象。
电磁学从原来互相独立的两门科学(电学、磁学)发展成为物理学中一个完整的分支学科,主要是基于电流的磁效应和变化的磁场的电效应的发现。
这两个实验现象,加上麦克斯韦关于变化电场产生磁场的假设,奠定了电磁学的整个理论体系,发展了对现代文明起重大影响的电工和电子技术。
针对电磁场学习理论性强、概念抽象等特点,利用MATLAB强大的数值计算和图形技术,通过具体实例进行仿真,绘制相应的图形,使其形象化,便于对其的理解和掌握。
将MATLAB引入电磁学中,利用其可视化功能对电磁学实验现象进行计算机模拟,可以提高学习效率于学习积极性,使学习效果明显。
Matlab在电磁场仿真中的应用指南

Matlab在电磁场仿真中的应用指南引言:随着科技的不断进步,电磁场仿真逐渐成为理解和设计电磁系统的重要工具。
然而,对于初学者来说,电磁场仿真可能会显得有些困难。
幸运的是,Matlab提供了强大的仿真工具箱,可以简化这一过程并提供准确的结果。
本文将深入探讨Matlab在电磁场仿真中的应用,并提供一些实用的指南。
1. 电磁场建模在进行电磁场仿真前,需要对电磁场进行建模。
建模的目的是确定物理模型和相关参数,以便计算和分析电磁现象。
Matlab提供了各种建模工具,如有限元法、边界元法和有限差分法等。
根据不同的情况,选择适合的建模方法非常重要。
2. 材料属性的处理在电磁场仿真中,物体的材料属性对电磁现象起着重要作用。
Matlab提供了各种处理材料属性的函数和工具箱。
例如,可以使用Matlab的材料库来获取不同材料的电磁参数。
此外,Matlab还提供了处理非均匀材料和各向异性材料的功能。
正确理解和使用这些函数和工具箱可以提高仿真的准确性和效率。
3. 边界条件的设定在电磁场仿真中,边界条件的设定对结果的准确性至关重要。
Matlab提供了多种处理边界条件的方法。
例如,可以使用无限远场边界条件来模拟开放区域,或者使用周期性边界条件来模拟周期性结构。
Matlab还支持自定义边界条件,使用户能够根据实际需求进行设置。
4. 电磁场分析在电磁场仿真中,对电磁场进行分析是重要的一步。
Matlab提供了多种电磁场分析的函数和工具箱。
例如,可以使用电场和磁场分布函数来可视化电磁场的分布情况。
此外,还可以使用功率流密度函数来分析电磁场中的能量传输情况。
通过深入理解这些函数和工具箱,可以获得更详细的电磁场分析结果。
5. 结果验证与优化在进行电磁场仿真后,需要对结果进行验证和优化。
Matlab提供了多种验证结果的方法。
例如,可以与已知的解析解进行比较,或者与实验数据进行对比。
通过检验仿真结果的准确性,可以确保模型的可信度。
此外,Matlab还提供了多个优化函数和工具箱,可以用于对电磁系统进行优化,以达到更好的设计效果。
MATLAB在电磁学中的应用

电磁学一、1、点电荷的电场研究真空中.两个带正电的点电荷.在电量相同和电量不同情况下的电场分布。
V =V 1+V 2=101r 4q πε+2024q r πε.E=-▽V2、程序实现主程序文件名为point.mclear allep0=8.85*le-12; %真空中的电容率c0=1/<4*pi*ep0>;e=1.6e-10;h=0.018;x=-0.5:h:0.5;y=-0.5:h:0.5;str{1}=’两同号等量点电荷’;str{2}=’两同号不等量点电荷’;[X,Y]=meshgrid<x,y>;q=[e;1.9*e];for i=1:2V=c0*e./sqrt<<X+0.2>.^2+Y.^2>+c0.*q<i>./sqrt<<X-0.2>.^2+Y.^2>; %求电势[Ex,Ey]=gradient<-V,h>; %求电场figure<i>counter<X<:,:,1>,Y<:,:,1>,V,… %等势面[20,-20,19,-19,18,-18,17,-17,16,-16,15,-15,14,-14,13,-13,12,-12,11,-11,10,-10],’r ’>;Axis<[-0.38,0.38,-0.28,0.28]>hold onphi=0:pi/17:2*pi; %以下画电场线sx1=0.2+0.01*cos<phi>;sy1=0.01*sin<phi>;streamline<X<:,:,1>,Y<:,:,1>,Ex,Ey,sx1,sy1>;hold onsx2=-0.2+0.01*cos<phi>;sy2=0.01*sin<phi>;streamline<X<:,:,1>,Y<:,:,1>,Ex,Ey,sx2,sy2>;title<str<i>>text<-0.215,0,’+’,’fontsize ’,20>; %标示点电荷text<0.185,0,’+’,’fontsize ’,20>;end二、带电细棒的电场1、若电荷Q 均匀分布在长为L 的细棒上.求真空中.带电细棒的电场在xy 平面内的分布情况。
应用MATLAB及SIMION模拟磁场和电子运动轨迹

应用MATLAB及SIMION模拟磁场和电子运动轨迹2.1、MATLAB对磁场进行模拟MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,在设计研究单位和工业部门被广泛地用于研究和解决各种具体的工程问题。
MATLAB具有功能强、效率高、简单易学等特点,本文中主要使用其数值计算,程序结构控制,函数调用,输入输出,绘图等功能对磁场进行模拟。
[4]要模拟电子在磁场中的运动,需要先了解螺线管产生的磁场在整个空间中的分布,空间中每一点磁场的大小,方向。
我们选取与实验中相同的条件进行模拟,以便于与实验结果做对比。
实验中所采用的仪器分布如图2.1.1所示,五级透镜(即通电螺线管)长度为157mm,内径为67mm,用直径为1mm的铜导线缠绕1100圈,电子束初始位置距螺线管边缘127mm,接受屏距螺线管另一端的距离为163mm。
由于通电螺线管所产生的磁场大小关于轴线对称,在进行模拟时以螺线管中心为圆心,可以只选择x>0,R>0的部分进行计算,再关于x轴和中心平面做对称,即可得到整个空间中的磁场分布。
由于电子只能在管道中运动,所以不需要考虑管道以外,即半径R大于33.5mm的区域不需要进行计算。
图2.1.1 实验中所采用仪器参数利用meshgrid函数在[0,240]*[0,33.5]范围内生成网格坐标。
并将(2)式与(3)式写入,在范围内作图并计算每一点的磁场强度,即可分别得到通电螺线管在空间中每一点所产生的径向及轴向磁场。
如图2.1.2a所示为螺线管在通有5A的电流时所产生的轴向磁场在空间中的分布,图2.1.2b所示为轴向磁场沿轴线方向x方向的变化,图2.1.2c所示为轴向磁场沿径向方向R方向的变化。
图2.1.2a 通电螺线管所产生的轴向磁场在空间中的分布。
图中原点o为螺线管中心,x轴方向为螺线管轴线方向,R轴方向为螺线管径向方向,B轴方向为磁场强度。
图2.1.2b 通电螺线管所产生的轴向磁场沿轴向的变化。
基于matlab的带电粒子在环形电流磁场中的运动模拟与分析

第40卷第10期 2019年10月
湖南科技学院学报 Journal of Hunan University of Science and Engineering
Vol.40 No. 10 Oct.2019
基于MATLAB的带电粒子 在环形电流磁场中的运动模拟与分析
刘旭辉 董 辉 蒋祝平 刘志朋 许炳柠 金方亮
f, ~ flk+\ +
A @ - /I )十
心*+2 - + i + 仕 工 )2
2h,2
I _ u+>l
用泰勒展开式代替原来的积分函数,在这个区间内积 分得:
f'Mf(x)dx « ^-(4 + 44+1 + 4+2)
(17)
对k求和得到近似计算定积分的辛普森公式:
s" = 士 n —I 才 J-t (4:+紅屮+ 心+2、)
但在很多实际问题中,磁场在空间中的分布情况和带电 粒子的初值情况并不满足上述条件,本文通过研究坏形电流 在空间中的磁场分布,用毕奥-萨伐尔定律求出环形电流中 长为dl的电流元在空间中任意一点磁场,对加积分得到环 形电流在空间中任意点的磁场,MATLAB中的积分常用函 数有trapz函数、quad函数和quadl函数。trapz函数是用梯 形公式计算定积分,quad函数用自适应辛普森法计算定积 分,quadl函数用精度更高的自适应洛巴托法计算定积分, 在数值计算中也称之为高斯积分法小現一些研究者利用 MATLAB模拟带电粒子在电磁场中的运动®%
电磁场与电磁波 【matlab】实验一 带电粒子在电磁场中的受力与运动特性研究实验

电磁场与电磁波实验实验一带电粒子在电磁场中的受力与运动特性研究实验成绩:请务必填写清楚姓名、学号、班级及理论课任课老师。
一带电粒子在电磁场中的受力与运动特性研究实验一、实验目的:1.通过虚拟仿真,观察带电粒子在电磁场中的运动行为。
2.学习运用Matlab 对电磁场进行数值模拟的方法。
二、实验原理带电粒子在磁场中运动会受到磁场力的作用,且随着初始运动方向和磁场分布的不同,其运动轨迹会发生不同的变化。
设带电粒子电量为q,以速度v 运动,则受到外磁场的作用力为:F qv B=⨯ 该公式表明:(1)磁场作用力同时垂直于磁感应强度和粒子运动速度;(2)磁场作用力只作用于运动的带电粒子,且永远不对带电粒子做功,只改变其运动方向。
若带电量为q 的运动电荷所在空间同时存在电场和磁场,则它所受的电场力和磁场力的综合即为洛伦兹力:()F q E v B =+⨯ 若不考虑粒子所受重力的作用,上式综合牛顿运动定律就可以精确确定带电粒子在电磁场中的运动轨迹。
设带电粒子质量为m,电量为q,进入电场E 与磁场B 方向正交的叠加电磁场中。
以电磁场中某点为原点,以电场E 为OY 方向,以磁感应强度B 为OZ 方向建立直角坐标系O-XYZ,则电场E 只有Y 分量,磁感应强度B 只有Z 分量,带电粒子在该电磁场中的运动微分方程为:22()d r m q E v B dt=+⨯ 上式可以在直角坐标系中展开为如下形式:2222220d x qB dy dtm dt d y qE qB dx dtm m dt d z dt⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩令1w x =,2dx w dt =,3w y =,4dy w dt =,5w z =,6dz w dt =,则上式可以化简为如下一阶微分线性方程组:12243442566dw w dt dw qB w dt m dw w dt dw qE qB w dt m m dw w dt dw dt ⎧=⎪⎪⎪=⎪⎪⎪=⎪⎨⎪=-⎪⎪⎪=⎪⎪=⎪⎩通过Matlab 编写程序,即可求解上述微分方程组。
应用MATLAB及SIMION模拟磁场和电子运动轨迹

应用MATLAB及SIMION模拟磁场和电子运动轨迹2.1、MATLAB对磁场进行模拟MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,在设计研究单位和工业部门被广泛地用于研究和解决各种具体的工程问题。
MATLAB具有功能强、效率高、简单易学等特点,本文中主要使用其数值计算,程序结构控制,函数调用,输入输出,绘图等功能对磁场进行模拟。
[4]要模拟电子在磁场中的运动,需要先了解螺线管产生的磁场在整个空间中的分布,空间中每一点磁场的大小,方向。
我们选取与实验中相同的条件进行模拟,以便于与实验结果做对比。
实验中所采用的仪器分布如图2.1.1所示,五级透镜(即通电螺线管)长度为157mm,内径为67mm,用直径为1mm的铜导线缠绕1100圈,电子束初始位置距螺线管边缘127mm,接受屏距螺线管另一端的距离为163mm。
由于通电螺线管所产生的磁场大小关于轴线对称,在进行模拟时以螺线管中心为圆心,可以只选择x>0,R>0的部分进行计算,再关于x轴和中心平面做对称,即可得到整个空间中的磁场分布。
由于电子只能在管道中运动,所以不需要考虑管道以外,即半径R大于33.5mm的区域不需要进行计算。
图2.1.1 实验中所采用仪器参数利用meshgrid函数在[0,240]*[0,33.5]范围内生成网格坐标。
并将(2)式与(3)式写入,在范围内作图并计算每一点的磁场强度,即可分别得到通电螺线管在空间中每一点所产生的径向及轴向磁场。
如图2.1.2a所示为螺线管在通有5A的电流时所产生的轴向磁场在空间中的分布,图2.1.2b所示为轴向磁场沿轴线方向x方向的变化,图2.1.2c所示为轴向磁场沿径向方向R方向的变化。
图2.1.2a 通电螺线管所产生的轴向磁场在空间中的分布。
图中原点o为螺线管中心,x轴方向为螺线管轴线方向,R轴方向为螺线管径向方向,B轴方向为磁场强度。
图2.1.2b 通电螺线管所产生的轴向磁场沿轴向的变化。
Matlab仿真带电粒子在匀强正交电磁场中运动.

引言在文[1]中对匀强正交电磁场中带电粒子的运动状态进行了分析,得到了运动方程,但人们却不能对带电粒子在此电磁场中的运动有比较直观形象的想象。
Matlab 是一款通用数学工具软件,有许多常用数学组件,文[3]作了许多相关介绍。
为了能直观形象地演示带电粒子的运动过程,文[2]采用了一阶差分线性方程组进行模拟。
本文也采用了一阶差分线性方程组的方法进行数值计算,并得到了图形结果,将常见粒子的运动进行了比较,可以方便人们得到直观印象,为进一步工作提供方便。
1问题分析本文主要研究带电粒子在均匀稳定的电磁场中的运动。
带电粒子质量为m ,电量为q (q>0,此带电粒子的运动微分方程为:m d 2!"r dt2=q "E +q "v ×"B (1以电磁场中某点为原点,以E 为Oy 方向,B 为Oz 方向建立坐标系O-xyz 。
由于ω=qB/m ,则(1式的投影方程为:d 2x dt 2=ωdy dtd 2y dt 2=qE m -ωdx dt d 2z dt 2=#%%%%%%%%$%%%%%%%%&0(2将其转换为一阶微分线性方程组,以便用差分替代微分作数值计算,令w 1=x ,w 2=dy/dx,w 3=y ,w 4=dy/dt ,w 5=z ,w 6=dz/dt ,则(2式成为:dw 1dt=w2dw 2dt=ωw 4dw 3dt=w4dw 4dt =qE m -ωw 2dw 5dt =w6dw 6dt=#%%%%%%%%%%%%%%%%%’%%%%%%%%%%%%%%%%%&0(32Matlab 数值求解与仿真演示Matlab 是一款通用性很强的优秀数学软件,借助于Matlab 对(3式进行差分迭代,数值求解,并将结果逐点描绘,用图像显示其运动轨迹。
下面分三种情况考虑:(1电场强度和磁场强度都不为零;(2电场强度为零,磁场强度不为零;(3电场强度不为零,磁场强度为零。
基于MATLAB的地磁场中带电粒子运动模拟分析

大学物理实验PHYSICAL EXPERIMENT OF COLLEGE第34卷第1期2021年2月Vol.34 No.1Feb.2021文章编号:1007-2934(2021)01-0083-04基于MATLAB 的地磁场中 带电粒子运动模拟分析钟海坚,陈宗华,赵炳炎*收稿日期:2020-12-08基金项目:国家自然科学基金(No.11847144);玉林师范学院博士科研启动基金(NO.G2017012);广西高等教育本科教学改革项目(2020JGA281)。
* 通讯联系人(玉林师范学院物理与电信工程学院,广西玉林537000)摘 要:依据单粒子轨道理论和偶极磁场模型定性分析中高能带电粒子在近地区域的运动过程,并利用MATLAB 对地磁场捕获带电粒子的基本原理进行数值模拟。
结果表明,地球的磁镜结构可以将一定角度射入的带电粒子束缚在其中,粒子的漂移运动速度大小取决于粒子的能量,能量越大的粒子其 漂移速度越大;磁镜点的磁感应强度大小由粒子的抛射角决定,随着抛射角增大磁镜点的磁感应强度先快速减小然后趋于不变,当抛射角小于1.11°时,带电粒子在反射前将损失在大气层中。
关键词:地磁场;粒子运动;数值计算中图分类号:P 318;P 354;O411 文献标志码:ADOl : 10.14139/22-1228.2021.01.022宇宙中的高能粒子对航天器的具有强大的破 坏作用,如果宇宙高速粒子直接射向地球空间环 境将对航天航空[1,2],广播通信以及电力等领域 产生重大影响。
自1958年探索者1号上的盖格计数器发现范艾伦辐射带以来研究人员就对它进 行持续不断的研究,目前关于范艾伦辐射带中粒子的来源、分布、传输以及损耗等方面的已经取得了一定的成果。
研究带电粒子在地磁场中的运动有助于了解范艾伦辐射带对地球电磁环境的保护作用,预测太阳异常活动或太空天气变化引发地磁场粒子异常活动对相关领域可能产生的影响[3]o 本文主要基于磁偶极场模型,从带电粒子在电磁场中的运动方程出发,利用数值计算的方法对带电粒子在地球磁场中的部分运动情况进行分析并讨论粒子的弹跳运动、漂移运动和抛射角范围。
模拟 粒子 运动 matlab

模拟粒子运动 matlab
模拟粒子运动是一项重要的科学研究领域,它在物理学、化学、生物学等多个学科中都有广泛的应用。
在本文中,我们将介绍如何使用Matlab来模拟粒子的运动。
我们需要定义粒子的初始状态,包括位置、速度和加速度等参数。
通过设定这些参数,我们可以模拟出粒子在给定条件下的运动轨迹。
在Matlab中,可以使用向量来表示粒子的位置、速度和加速度。
通过更新粒子的位置和速度,我们可以模拟出粒子在不同时间点的运动状态。
为了模拟粒子的运动,我们需要考虑粒子所受到的力。
根据牛顿第二定律,粒子所受到的合力等于质量乘以加速度。
通过计算粒子所受到的合力,我们可以确定粒子的加速度,并进一步更新粒子的位置和速度。
在模拟粒子运动时,我们还需要考虑其他因素,如空气阻力、重力等。
这些因素会对粒子的运动轨迹产生影响。
通过在模拟中引入这些因素,我们可以更加真实地模拟粒子的运动。
除了模拟单个粒子的运动,我们还可以模拟多个粒子之间的相互作用。
例如,当粒子之间存在引力或斥力时,它们的运动轨迹将会发生变化。
通过在模拟中考虑粒子之间的相互作用,我们可以研究粒
子系统的整体行为。
在Matlab中,有许多工具和函数可以帮助我们进行粒子运动的模拟。
例如,可以使用plot函数来绘制粒子的运动轨迹,使用animate函数来生成动画效果,使用ODE求解器来求解粒子的运动方程等。
通过使用Matlab进行粒子运动的模拟,我们可以更好地理解粒子的运动规律,研究粒子系统的行为,并在实际应用中提供参考。
希望本文对读者理解和应用粒子运动模拟有所帮助。
用matlab模拟电子在磁场中的运动

本科毕业设计(论文)( 2014届 )题目:用matlab 模拟二维带电粒子在非均匀磁场下的运动学院:专业:学生姓名学号:指导教师:职称:副教授合作导师:职称:完成时间:成绩:浙江师范大学本科毕业设计(论文)正文目录摘要 (1)关键词 (1)英文摘要 (1)英文关键词 (1)1 引言 (2)2 电子在磁场中运动引起的现象及应用 (3)2.1 全天空图像和紫光图像的极光事件 (4)2.2 粒子加速器 (4)2.3 军事中的电磁炮 (4)2.4 计算机模拟电子在磁场中的运动 (5)3 计算机模拟电子在磁场运动 (5)3.1 matlab解微分方程 (5)3.2 带电拉子在磁场中的运动规律 (6)3.3 二维带电粒子的蛇形轨道 (7)4.总结和展望 (11)参考文献 (12)摘要: 带电粒子在非均匀磁场中的运动能产生很多有趣的现象和应用。
本文用matlab 模拟了二维带电粒子在非均匀磁场中的运动轨迹。
将粒子的运动方程转化为一阶常微分方程组,用matlab的ode45命令可求解粒子的运动轨迹。
我们模拟的目标是研究蛇形轨道。
考虑的垂直磁场有一个零磁场区域。
在此区域两侧的磁场都是均匀的,方向相反。
在合适的入射态下,我们得到了蛇形轨道。
关键词:matlab;带电粒子;非均匀磁场;蛇形轨道Matlab simulation on thetwo-dimensional movement of charged particles in inhomogeneous magneticfieldsYU Xiong-ting Director: ZHAI-Feng (Professor)Abstract:The motion of charged particles in inhomogeneous magnetic field gives rise to many interesting phenomena and applications. In this thesis we simulate the motion of two-dimensional charged particles in inhomogeneous magnetic fields by the matlab software. After the equation of motion is transformed into ordinary differential equations with first order, the orbit of particles can be solved by the ode45 function in matlab. The aim of our simulation is to study the snake orbit.The considered perpendicular magnetic field has a zero-field region. The magnetic fields on the left and right of this region are homogeneous but have opposite directions. Under proper incident conditions, the snake states are obtained.Key Words: matlab;charged particles; inhomogeneous magnetic fields; snake orbits1 引言带电粒子在磁场中的运动时要受到磁场对它的作用力。
基于matlab带电粒子在非匀强磁场中运动模拟

基于matlab带电粒子在非匀强磁场中运动模拟摘要:带电粒子在磁场中的运动是我们在中学的时候就学过的,但是那些都是在均匀的磁场中运动的,在一般的教材中,包括大学的电磁学中,也省略了带电粒子在非均匀的磁场中运动的讨论。
我们都知道带电粒子以一定的速度进入均匀的磁场中时,粒子的运动轨迹是一条螺旋线。
那么在非均匀的磁场中运动又会是什么样的轨迹呢?本文简单的介绍matlab的概念及在处理物理模型中作用,带电粒子在磁场中运动方程的建立,定性分析它的轨迹,用数值模拟的方法将运动轨迹模拟出来。
关键词:带电粒子,运动轨迹,模拟,非均匀磁场,matlab1.引言随着计算机迅速的发展,我们的社会已经进入了信息化的时代,计算机技术已经进入了人类社会的每一个领域,也是我们人类发展必不可少的技术手段,特别是数值模拟中,数值模拟已经成为当今社会发展的热题。
以MATLAB为工具的数值模拟为例。
MATLAB是Matrix Laboratory的缩写,它是一种数值计算和图形图像处理工具软件,它的特点是语法结构简明、数值计算高效、图形功能完备、易学易用。
它在矩阵代数、数值计算、数字信号处理、振动理论、神经网络控制、动态仿真等领域都有广泛的应用。
MATLAB的功能很强大,能使一些问题能够巧妙的解决,使一些难题变得容易解决。
所以,MATLAB为一些可视化的物理模拟提供了强有力的手段。
我觉得,作为新一代的大学生除了会运用一些简单的高等数学知识解决大学物理中的问题之外,还应该学会用计算机铺助我们解决高等数学解决不了的问题,特别是用MATLAB模拟一些很难得轨迹。
例如,我们在以前的课本上都没有见过带电粒子在非均匀磁场中的运动轨迹,甚至有些课本上直接就是一句话带过,为了搞清楚带电粒子在非均匀磁场中的运动,本文通过建立带电粒子在非均匀磁场中运动的运动学微分方程,再编写程序,然后在借助MATLAB 这个工具,把带电粒子在非均匀磁场中的运动轨迹模拟出来。
电磁场matlab仿真实验

电磁场matlab 仿真实验一实验一:[例7-5]试分析一对等量异号的电荷周围空间上的电位和电场分布情况。
分析:将等量异号的电荷的几何中心放置于坐标原点位置,则它们在空间某点p 处产生的点位为:()G q g g q r r q r q r q02102102010*******πξπξπξπξπξϕ=-=⎪⎪⎭⎫ ⎝⎛-=-=其中G 为格林函数()()22222cos 2/cos 2/1r dr d r r dr d r +-=+-=θθ将G 用片面积坐标表示为⎪⎪⎭⎫⎝⎛=12ln g g G 在编程时,将G 当作点位函数处理,并利用梯度求出唱腔E=-▽φ。
用matlab 的m 语言编写的程序如下:[x,y]=meshgrid(-10:0.1:10);[Q,R]=cart2pol(x,y);R(R<=1)=NaN;q=input('请输入电偶极子的电量q =')%原程序有误,以此为准d=input('请输入电偶极子的间距d =')%原程序有误,以此为准E0=8.85*1e-12;K0=q/4/pi/E0;g1=sqrt((d./2).^2-d.*R.*cos(Q)+R.^2);%原程序有误,以此为准g2=sqrt((d./2).^2+d.*R.*cos(Q)+R.^2);%原程序有误,以此为准G=log(K0*g2./g1);contour(x,y,G,17,'g');hold on[ex,ey]=gradient(-G);tt=0:pi/10:2*pi;%原程序未定义tt ,以此为准sx=5*sin(tt);sy=5*cos(tt);streamline(x,y,ex,ey,sx,sy);xlabel('x');ylabel('y');hold off;当运行此程序后,按提示输入电偶极子电量和嗲耨集子间距如下:请输入电偶极子的电量q =0.5*1e-10请输入电偶极子的间距d =0.01即可汇出入图说使得嗲耨集资周围的长的分布图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录第1章概述 (1)第2章MATLAB的基础知识 (2)2.1 MATLAB使用介绍 (2)2.2 MATLAB的基本知识 (2)2.3利用MATLAB作图 (5)第3章实验原理及仿真结果分析 (7)3.1 带电粒子在电磁场中运动的原理 (7)3.2 质量较大的带电微粒在复合场中的运动 (7)3.3 带电粒子垂直射入E和B正交的叠加场的运动分析 (8)3.4 实验内容 (8)第4章 MATLAB仿真的应用 (11)4.1 用MATLAB仿真带电粒子在磁场中运动的优点 (11)4.2 用MATLAB仿真在物理实验中的应用 (11)第5章总结 (12)参考文献 (13)附录 (14)第1章概述计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第三种研究手段,在基础物理学习中适当引入计算机数值方法,有助于将一些高深的物理知识深入浅出、生动形象地学习。
随着计算机的普及,MATLAB在基础物理中的应用日益广泛。
MATLAB是当今最优秀的科技应用软件之一,它以强大的科学计算与可视化功能、简单易用、开放式可扩展环境,特别是所附带的30 多种面向不同领域的工具箱支持,使得它在许多科学领域中成为计算机辅助设计和分析、算法研究和应用开发的基本工具和首选平台。
MATLAB具有其他高级语言难以比拟的一些优点,如编写简单、编程效率高、易学易懂等,因此MATLAB 语言也被通俗地称为演算纸式科学算法语言。
在控制、通信、信号处理及科学计算等领域中,MATLAB 都被广泛地应用,已经被认为能够有效提高工作效率、改善设计手段的工具软件,掌握了MATLAB 好比掌握了开启这些专业领域大门的钥匙[1]。
带电体在复合场中运动的基本分析:这里所讲的复合场指电场、磁场和重力场并存, 或其中某两场并存, 或分区域存在, 带电体连续运动时, 一般须同时考虑电场力、洛仑兹力和重力的作用。
在不计粒子所受的重力的情况下,带电粒子只受电场和洛仑兹力的作用,粒子所受的合外力就是这两种力的合力,其运动加速度遵从牛顿第二定律。
在相互垂直的匀强电场与匀强磁场构成的复合场中,如果粒子所受的电场力与洛仑兹力平衡,粒子将做匀速直线运动;如果所受的电场力与洛仑兹力不平衡,粒子将做一般曲线运动,而不可能做匀速圆周运动,也不可能做与抛体运动类似的运动。
在相互垂直的点电荷产生的平面电场与匀强磁场垂直的复合场中,带电粒子有可能绕场电荷做匀速圆周运动。
第2章MATLAB 的基础知识2.1 MATLAB 使用介绍在Windows 窗口中用鼠标双击Matlab 图标即可进入Matlab 的工作窗口(Command Window ),如图2-11所示。
没有图标可利用Matlab\bin 目录下的Matlab.exe 文件在桌面上建立一个快捷方式。
退出Matlab 的方法有三种:单击工作窗口右上角的关闭按钮;用菜单File →Exit Matlab 命令;或者直接在工作窗口中输入quit 后回车。
工作窗口是标准的Windows 窗口形式,用户在命令窗口中输入各种指令,进行运算;在左侧的变量窗口中监控当前所创立的所有变量[2]。
2.2 MATLAB 的基本知识2.2.1 MATLAB 基本命令MATLAB 基本命令如下表所示图2-1 Matlab 工作窗口表2-1 MATLAB 基本命令2.2.2 数据和变量1.表达式在命令窗口作一些简单的计算,就如同使用一个功能强大的计算器,使用变量无须预先定义类型。
几个表达式可以写在一行,用分号(;)或逗号(,)分割,用分号(;)使该表达式运算结果不显示,而逗号(,)则显示结果。
也可以将一个长表达式分在几行上写,用三点(…)续行。
若需要修改已执行过的命令行,可以在命令历史中找到该命令行复制,再粘贴至命令窗口修改。
也可以直接使用键盘↑↓调出已执行过的命令行修改。
2.数据显示格式MATLAB 默认的数据显示格式为短格式(short ):当结果为整数,就作为整数显示;当结果是实数,以小数点后四位的长度显示。
若结果的有效数字超出一定范围,以科学计数法显示(如3.2000e-006表示6102.3-⨯)。
数据显示格式可使用命令Format 改变。
3.预定义变量MATLAB 有一些预定义变量(表2-2),启动时就已赋值,可以直接使用,如前我们使用的圆周率pi 和虚数单位i 。
表2-2 常用预定义变量4.用户变量MATLAB变量名总以字母开头,以字母、数字或下划线组成,区分大小写,有效字符长度为63个。
如A,a,a1,a_b都是合法的,且a与A表示不同变量。
在Command Window中使用的变量一旦被赋值,就会携带这个值存在于工作空间,直到被清除或被赋予新的值。
2.2.3数组和矩阵运算MATLAB基本数据单元是无需指定维数的数组。
数组运算是MATLAB最鲜明的特点,一方面可以使得计算程序简明易读,另一方面可以提高计算速度。
1.数组的输入最常用的数组是双精度数值数组(double array)。
一维数组相当于向量,二维数组相当于矩阵,一维数组可以视为二维数组的特例。
二维数组的第一维称为“行”,第二维称为“列”。
MATLAB数组无需预先定义维数。
直接输入数组的元素,用中括号([])表示一个数组,同行元素间用空格或逗号分隔,不同行间用分号或回车分隔。
2.数组运算数组运算是指数组对应元素之间的运算,也称点运算。
矩阵的乘法、乘方和除法有特殊的数学含义,并不是数组对应元素的运算,所数组乘法、乘方和除法的运算符前特别加了一个点。
特别要区分数组运算在乘法、乘方和除法上的意义和表示上与矩阵运算的不同[3]。
表2-3 数组运算符3.数学函数数组的数学函数也是按每个元素的运算,使用通常的函数符号,常用数学函数见表2-4。
表2-4 数学函数2.3利用MATLAB作图1.常用作图命令和函数(表2-5)。
表2-5 常用作图命令和函数2.曲线图plot(x,y) 作出以数据(x(i),y(i))为节点的折线图,其中x,y为同长度的向量fplot('fun',[a,b]) 作出函数fun在区间[a,b]上的函数图,fun可以是M函数主名,也可是字符串ezplot(fun,lims) 绘制字符串fun(可是显函数、隐函数或参数方程)指定的函数plot3(x,y,z) 空间曲线图,其中x,y,z为同长度向量图形显示在图形窗口。
在图形窗口可以使用File菜单保存(Save)为M文件,导出(Export)为图形文件。
也可利用图形窗口Edit菜单Copy figure作为图片复制到剪贴板,从而进一步粘贴到Word或其他应用程序中。
图形的线型、标记、颜色均可根据要求设定。
常用的见表2-6。
表2-6 图形元素设定3.曲面图[x,y]=meshgrid(xa,ya) 当xa,ya分别为m维和n维行向量,得到x和y均为n行m列矩阵。
meshgrid常用于生成X-Y平面上的网格数据mesh(x,y,z) 绘制网面图,是最基本的曲面图形命令,其中x,y,z是同阶矩阵,表示曲面三维数据surf(x,y,z) 绘制曲面图,与mesh用法类似contour(x,y,z) 绘制等高线图,与mesh用法类似contour3(x,y,z) 绘制三维等高线图,与mesh用法类似4.图形说明和定制title('字符串') 图形标题说明xlabel,ylabel,zlabel 用法类似于title,分别说明坐标轴x,y,zgrid on/off 显示/不显示格栅box on/off 使用/不使用坐标框axis([a,b,c,d]) 定制二维坐标轴范围a<x<b,c<y<daxis([a,b,c,d,e,f]) 定制三维坐标轴范围a<x<b,c<y<d,e<z<ffigure 开一个新图形窗口close 关闭现有图形窗口legend(str1,str2,……) 图例,字符串str1,str2,……依次为各图形对象说明第3章 实验原理及仿真结果分析3.1 带电粒子在电磁场中运动的原理带电粒子在磁场中运动时会受到洛伦兹力的作用,且随着初始运动方向和磁场分布的不同,其运动轨迹会发生不同的变化。
由洛伦兹力的推导公式可知,它垂直于粒子的运动速度,不对运动粒子作功,只改变其运动方向,其大小为:θνsin F B q = (3—1)因此,综合牛顿运动定律就可以精确确定带电粒子在磁场中的运动轨迹。
3.2 质量较大的带电微粒在复合场中的运动这里我们只研究垂直射入磁场的带电微粒在垂直磁场的平面内的运动,并分几种情况进行讨论。
(1)只受重力和洛仑兹力:此种情况下,要使微粒在垂直磁场的平面内运动,磁场方向必须是水平的。
微粒所受的合外力就是重力与洛仑兹力的合力。
在此合力作用下,微粒不可能再做匀速圆周运动,也不可能做与抛体运动类似的运动。
在合外力不等于零的情况下微粒将做一般曲线运动,其运动加速度遵从牛顿第二定律;在合外力等于零的情况下,微粒将做匀速直线运动。
无论微粒在垂直匀强磁场的平面内如何运动,由于洛仑兹力不做功,只有重力做功,因此微粒的机械能守恒,即:mgh mv mgh mv a a b b+=+121222(3—2) (2)微粒受有重力、电场力和洛仑兹力:此种情况下。
要使微粒在垂直磁场的平面内运动,匀强磁场若沿水平方向,则所加的匀强电场必须与磁场方向垂直。
在上述复合场中,带电微粒受重力、电场力和洛仑兹力。
这三种力的矢量和即是微粒所受的合外力,其运动加速度遵从牛顿第二定律。
如果微粒所受的重力与电场力相抵消,微粒相当于只受洛仑兹力,微粒将以洛仑兹力为向心力,以射入时的速率做匀速圆周运动。
若重力与电场力不相抵,微粒不可能再做匀速圆周运动,也不可能做与抛体运动类似的运动,而只能做一般曲线运动。
如果微粒所受的合外力为零,即所受的三种力平衡,微粒将做匀速直线运动。
无论微粒在复合场中如何运动,洛仑兹力对微粒不做功。
若只有重力对微粒做功,则微粒的机械能守恒;若只有电场力对微粒做功,则微粒的电势能和动能的总和守恒;若重力和电场力都对微粒做功,则微粒的电势能与机械能的总和守恒,用公式表示为:qU mgh mv qU mgh mv a a a b b b++=++121222(3—3) 3.3 带电粒子垂直射入E 和B 正交的叠加场的运动分析带电粒子垂直射入E 和B 正交的叠加场常见的模型就是速度旋转器。
如图3-1(a )所示,粒子受力特点——电场力F 与洛仑兹力f 方向相反。
粒子匀速通过速度选择器的条件——带电粒子从小孔S 1水平射入,匀速通过叠加场,并从小孔S 2水平射出,从不同角度看有三种等效条件:从力的角度—电场力与洛仑兹力平衡,即:0νBq qE =;从速度角度——v 0的大小等于E 与B 的比值,即:v EB0=;从功的角度——电场力对粒子不做功,即:W qEd F ==0; 两个重要的功能关系——当粒子进入速度选择器时速度v E B0≠,粒子将因侧移而不能通过选择器。
