Clustering with Lattices in the Analysis of Graph Patterns
聚类分析文献英文翻译

电气信息工程学院外文翻译英文名称:Data mining-clustering译文名称:数据挖掘—聚类分析专业:自动化姓名:****班级学号:****指导教师:******译文出处:Data mining:Ian H.Witten, EibeFrank 著Clustering5.1 INTRODUCTIONClustering is similar to classification in that data are grouped. However, unlike classification, the groups are not predefined. Instead, the grouping is accomplished by finding similarities between data according to characteristics found in the actual data. The groups are called clusters. Some authors view clustering as a special type of classification. In this text, however, we follow a more conventional view in that the two are different. Many definitions for clusters have been proposed:●Set of like elements. Elements from different clusters are not alike.●The distance between points in a cluster is less than the distance betweena point in the cluster and any point outside it.A term similar to clustering is database segmentation, where like tuple (record) in a database are grouped together. This is done to partition or segment the database into components that then give the user a more general view of the data. In this case text, we do not differentiate between segmentation and clustering. A simple example of clustering is found in Example 5.1. This example illustrates the fact that that determining how to do the clustering is not straightforward.As illustrated in Figure 5.1, a given set of data may be clustered on different attributes. Here a group of homes in a geographic area is shown. The first floor type of clustering is based on the location of the home. Homes that are geographically close to each other are clustered together. In the second clustering, homes are grouped based on the size of the house.Clustering has been used in many application domains, including biology, medicine, anthropology, marketing, and economics. Clustering applications include plant and animal classification, disease classification, image processing, pattern recognition, and document retrieval. One of the first domains in which clustering was used was biological taxonomy. Recent uses include examining Web log data to detect usage patterns.When clustering is applied to a real-world database, many interesting problems occur:●Outlier handling is difficult. Here the elements do not naturally fallinto any cluster. They can be viewed as solitary clusters. However, if aclustering algorithm attempts to find larger clusters, these outliers will beforced to be placed in some cluster. This process may result in the creationof poor clusters by combining two existing clusters and leaving the outlier in its own cluster.● Dynamic data in the database implies that cluster membership may change over time.● Interpreting the semantic meaning of each cluster may be difficult. With classification, the labeling of the classes is known ahead of time. However, with clustering, this may not be the case. Thus, when the clustering process finishes creating a set of clusters, the exact meaning of each cluster may not be obvious. Here is where a domain expert is needed to assign a label or interpretation for each cluster.● There is no one correct answer to a clustering problem. In fact, many answers may be found. The exact number of clusters required is not easy to determine. Again, a domain expert may be required. For example, suppose we have a set of data about plants that have been collected during a field trip. Without any prior knowledge of plant classification, if we attempt to divide this set of data into similar groupings, it would not be clear how many groups should be created.● Another related issue is what data should be used of clustering. Unlike learning during a classification process, where there is some a priori knowledge concerning what the attributes of each classification should be, in clustering we have no supervised learning to aid the process. Indeed, clustering can be viewed as similar to unsupervised learning.We can then summarize some basic features of clustering (as opposed to classification):● The (best) number of clusters is not known.● There may not be any a priori knowledge concerning the clusters.● Cluster results are dynamic.The clustering problem is stated as shown in Definition 5.1. Here we assume that the number of clusters to be created is an input value, k. The actual content (and interpretation) of each cluster,j k ,1j k ≤≤, is determined as a result of the function definition. Without loss of generality, we will view that the result of solving a clustering problem is that a set of clusters is created: K={12,,...,k k k k }.D EFINITION 5.1.Given a database D ={12,,...,n t t t } of tuples and an integer value k , the clustering problem is to define a mapping f : {1,...,}D k → where each i t is assigned to one cluster j K ,1j k ≤≤. A cluster j K , contains precisely those tuples mapped to it; that is, j K ={|(),1,i i j t f t K i n =≤≤and i t D ∈}.A classification of the different types of clustering algorithms is shown in Figure 5.2. Clustering algorithms themselves may be viewed as hierarchical or partitional. With hierarchical clustering, a nested set of clusters is created. Each level in the hierarchy has a separate set of clusters. At the lowest level, each item is in its own unique cluster. At the highest level, all items belong to the same cluster. With hierarchical clustering, the desired number of clusters is not input. With partitional clustering, the algorithm creates only one set of clusters. These approaches use the desired number of clusters to drive how the final set is created. Traditional clustering algorithms tend to be targeted to small numeric database that fit into memory .There are, however, more recent clustering algorithms that look at categorical data and are targeted to larger, perhaps dynamic, databases. Algorithms targeted to larger databases may adapt to memory constraints by either sampling the database or using data structures, which can be compressed or pruned to fit into memory regardless of the size of the database. Clustering algorithms may also differ based on whether they produce overlapping or nonoverlapping clusters. Even though we consider only nonoverlapping clusters, it is possible to place an item in multiple clusters. In turn, nonoverlapping clusters can be viewed as extrinsic or intrinsic. Extrinsic techniques use labeling of the items to assist in the classification process. These algorithms are the traditional classification supervised learning algorithms in which a special input training set is used. Intrinsic algorithms do not use any a priori category labels, but depend only on the adjacency matrix containing the distance between objects. All algorithms we examine in this chapter fall into the intrinsic class.The types of clustering algorithms can be furthered classified based on the implementation technique used. Hierarchical algorithms can becategorized as agglomerative or divisive. ”Agglomerative ” implies that the clusters are created in a bottom-up fashion, while divisive algorithms work in a top-down fashion. Although both hierarchical and partitional algorithms could be described using the agglomerative vs. divisive label, it typically is more associated with hierarchical algorithms. Another descriptive tag indicates whether each individual element is handled one by one, serial (sometimes called incremental), or whether all items are examined together, simultaneous. If a specific tuple is viewed as having attribute values for all attributes in the schema, then clustering algorithms could differ as to how the attribute values are examined. As is usually done with decision tree classification techniques, some algorithms examine attribute values one at a time, monothetic. Polythetic algorithms consider all attribute values at one time. Finally, clustering algorithms can be labeled base on the mathematical formulation given to the algorithm: graph theoretic or matrix algebra. In this chapter we generally use the graph approach and describe the input to the clustering algorithm as an adjacency matrix labeled with distance measure.We discuss many clustering algorithms in the following sections. This is only a representative subset of the many algorithms that have been proposed in the literature. Before looking at these algorithms, we first examine possible similarity measures and examine the impact of outliers.5.2 SIMILARITY AND DISTANCE MEASURESThere are many desirable properties for the clusters created by a solution to a specific clustering problem. The most important one is that a tuple within one cluster is more like tuples within that cluster than it is similar to tuples outside it. As with classification, then, we assume the definition of a similarity measure, sim(,i l t t ), defined between any two tuples, ,i l t t D . This provides a more strict and alternative clustering definition, as found in Definition 5.2. Unless otherwise stated, we use the first definition rather than the second. Keep in mind that the similarity relationship stated within the second definition is a desirable, although not always obtainable, property.A distance measure, dis(,i j t t ), as opposed to similarity, is often used inclustering. The clustering problem then has the desirable property that given a cluster,j K ,,jl jm j t t K ∀∈ and ,(,)(,)i j jl jm jl i t K sim t t dis t t ∉≤.Some clustering algorithms look only at numeric data, usually assuming metric data points. Metric attributes satisfy the triangular inequality. The cluster can then be described by using several characteristic values. Given a cluster, m K of N points { 12,,...,m m mN t t t }, we make the following definitions [ZRL96]:Here the centroid is the “middle ” of the cluster; it need not be an actual point in the cluster. Some clustering algorithms alternatively assume that the cluster is represented by one centrally located object in the cluster called a medoid . The radius is the square root of the average mean squared distance from any point in the cluster to the centroid, and of points in the cluster. We use the notation m M to indicate the medoid for cluster m K .Many clustering algorithms require that the distance between clusters (rather than elements) be determined. This is not an easy task given that there are many interpretations for distance between clusters. Given clusters i K and j K , there are several standard alternatives to calculate the distance between clusters. A representative list is:● Single link : Smallest distance between an element in onecluster and an element in the other. We thus havedis(,i j K K )=min((,))il jm il i j dis t t t K K ∀∈∉and jm j i t K K ∀∈∉.● Complete link : Largest distance between an element in onecluster and an element in the other. We thus havedis(,i j K K )=max((,))il jm il i j dis t t t K K ∀∈∉and jm j i t K K ∀∈∉.● Average : Average distance between an element in onecluster and an element in the other. We thus havedis(,i j K K )=((,))il jm il i j mean dis t t t K K ∀∈∉and jm j i t K K ∀∈∉.● Centroid : If cluster have a representative centroid, then thecentroid distance is defined as the distance between the centroids.We thus have dis(,i j K K )=dis(,i j C C ), where i C is the centroidfor i K and similarly for j C .Medoid : Using a medoid to represent each cluster, thedistance between the clusters can be defined by the distancebetween the medoids: dis(,i j K K )=(,)i j dis M M5.3 OUTLIERSAs mentioned earlier, outliers are sample points with values much different from those of the remaining set of data. Outliers may represent errors in the data (perhaps a malfunctioning sensor recorded an incorrect data value) or could be correct data values that are simply much different from the remaining data. A person who is 2.5 meters tall is much taller than most people. In analyzing the height of individuals, this value probably would be viewed as an outlier.Some clustering techniques do not perform well with the presence of outliers. This problem is illustrated in Figure 5.3. Here if three clusters are found (solid line), the outlier will occur in a cluster by itself. However, if two clusters are found (dashed line), the two (obviously) different sets of data will be placed in one cluster because they are closer together than the outlier. This problem is complicated by the fact that many clustering algorithms actually have as input the number of desired clusters to be found.Clustering algorithms may actually find and remove outliers to ensure that they perform better. However, care must be taken in actually removing outliers. For example, suppose that the data mining problem is to predict flooding. Extremely high water level values occur very infrequently, and when compared with the normal water level values may seem to be outliers. However, removing these values may not allow the data mining algorithms to work effectively because there would be no data that showed that floods ever actually occurred.Outlier detection, or outlier mining, is the process of identifying outliers in a set of data. Clustering, or other data mining, algorithms may then choose to remove or treat these values differently. Some outlier detection techniques are based on statistical techniques. These usually assume that the set of data follows a known distribution and that outliers can be detected by well-known tests such as discordancy tests. However, thesetests are not very realistic for real-world data because real-world data values may not follow well-defined data distributions. Also, most of these tests assume single attribute value, and many attributes are involved in real-world datasets. Alternative detection techniques may be based on distance measures.聚类分析5.1简介聚类分析与分类数据分组类似。
基于属性增强的神经传感融合网络的人脸识别算法论文
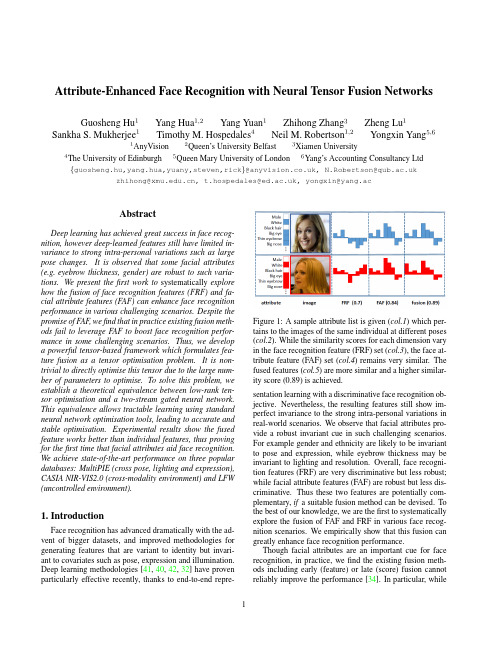
Attribute-Enhanced Face Recognition with Neural Tensor Fusion Networks Guosheng Hu1Yang Hua1,2Yang Yuan1Zhihong Zhang3Zheng Lu1 Sankha S.Mukherjee1Timothy M.Hospedales4Neil M.Robertson1,2Yongxin Yang5,61AnyVision2Queen’s University Belfast3Xiamen University 4The University of Edinburgh5Queen Mary University of London6Yang’s Accounting Consultancy Ltd {guosheng.hu,yang.hua,yuany,steven,rick}@,N.Robertson@ zhihong@,t.hospedales@,yongxin@yang.acAbstractDeep learning has achieved great success in face recog-nition,however deep-learned features still have limited in-variance to strong intra-personal variations such as large pose changes.It is observed that some facial attributes (e.g.eyebrow thickness,gender)are robust to such varia-tions.We present thefirst work to systematically explore how the fusion of face recognition features(FRF)and fa-cial attribute features(FAF)can enhance face recognition performance in various challenging scenarios.Despite the promise of FAF,wefind that in practice existing fusion meth-ods fail to leverage FAF to boost face recognition perfor-mance in some challenging scenarios.Thus,we develop a powerful tensor-based framework which formulates fea-ture fusion as a tensor optimisation problem.It is non-trivial to directly optimise this tensor due to the large num-ber of parameters to optimise.To solve this problem,we establish a theoretical equivalence between low-rank ten-sor optimisation and a two-stream gated neural network. This equivalence allows tractable learning using standard neural network optimisation tools,leading to accurate and stable optimisation.Experimental results show the fused feature works better than individual features,thus proving for thefirst time that facial attributes aid face recognition. We achieve state-of-the-art performance on three popular databases:MultiPIE(cross pose,lighting and expression), CASIA NIR-VIS2.0(cross-modality environment)and LFW (uncontrolled environment).1.IntroductionFace recognition has advanced dramatically with the ad-vent of bigger datasets,and improved methodologies for generating features that are variant to identity but invari-ant to covariates such as pose,expression and illumination. Deep learning methodologies[41,40,42,32]have proven particularly effective recently,thanks to end-to-endrepre-Figure1:A sample attribute list is given(col.1)which per-tains to the images of the same individual at different poses (col.2).While the similarity scores for each dimension vary in the face recognition feature(FRF)set(col.3),the face at-tribute feature(FAF)set(col.4)remains very similar.The fused features(col.5)are more similar and a higher similar-ity score(0.89)is achieved.sentation learning with a discriminative face recognition ob-jective.Nevertheless,the resulting features still show im-perfect invariance to the strong intra-personal variations in real-world scenarios.We observe that facial attributes pro-vide a robust invariant cue in such challenging scenarios.For example gender and ethnicity are likely to be invariant to pose and expression,while eyebrow thickness may be invariant to lighting and resolution.Overall,face recogni-tion features(FRF)are very discriminative but less robust;while facial attribute features(FAF)are robust but less dis-criminative.Thus these two features are potentially com-plementary,if a suitable fusion method can be devised.To the best of our knowledge,we are thefirst to systematically explore the fusion of FAF and FRF in various face recog-nition scenarios.We empirically show that this fusion can greatly enhance face recognition performance.Though facial attributes are an important cue for face recognition,in practice,wefind the existing fusion meth-ods including early(feature)or late(score)fusion cannot reliably improve the performance[34].In particular,while 1offering some robustness,FAF is generally less discrimina-tive than FRF.Existing methods cannot synergistically fuse such asymmetric features,and usually lead to worse perfor-mance than achieved by the stronger feature(FRF)only.In this work,we propose a novel tensor-based fusion frame-work that is uniquely capable of fusing the very asymmet-ric FAF and FRF.Our framework provides a more powerful and robust fusion approach than existing strategies by learn-ing from all interactions between the two feature views.To train the tensor in a tractable way given the large number of required parameters,we formulate the optimisation with an identity-supervised objective by constraining the tensor to have a low-rank form.We establish an equivalence be-tween this low-rank tensor and a two-stream gated neural network.Given this equivalence,the proposed tensor is eas-ily optimised with standard deep neural network toolboxes. Our technical contributions are:•It is thefirst work to systematically investigate and ver-ify that facial attributes are an important cue in various face recognition scenarios.In particular,we investi-gate face recognition with extreme pose variations,i.e.±90◦from frontal,showing that attributes are impor-tant for performance enhancement.•A rich tensor-based fusion framework is proposed.We show the low-rank Tucker-decomposition of this tensor-based fusion has an equivalent Gated Two-stream Neural Network(GTNN),allowing easy yet effective optimisation by neural network learning.In addition,we bring insights from neural networks into thefield of tensor optimisation.The code is available:https:///yanghuadr/ Neural-Tensor-Fusion-Network•We achieve state-of-the-art face recognition perfor-mance using the fusion of face(newly designed‘Lean-Face’deep learning feature)and attribute-based fea-tures on three popular databases:MultiPIE(controlled environment),CASIA NIR-VIS2.0(cross-modality environment)and LFW(uncontrolled environment).2.Related WorkFace Recognition.The face representation(feature)is the most important component in contemporary face recog-nition system.There are two types:hand-crafted and deep learning features.Widely used hand-crafted face descriptors include Local Binary Pattern(LBP)[26],Gaborfilters[23],-pared to pixel values,these features are variant to identity and relatively invariant to intra-personal variations,and thus they achieve promising performance in controlled environ-ments.However,they perform less well on face recognition in uncontrolled environments(FRUE).There are two main routes to improve FRUE performance with hand-crafted features,one is to use very high dimensional features(dense sampling features)[5]and the other is to enhance the fea-tures with downstream metric learning.Unlike hand-crafted features where(in)variances are en-gineered,deep learning features learn the(in)variances from data.Recently,convolutional neural networks(CNNs) achieved impressive results on FRUE.DeepFace[44],a carefully designed8-layer CNN,is an early landmark method.Another well-known line of work is DeepID[41] and its variants DeepID2[40],DeepID2+[42].The DeepID family uses an ensemble of many small CNNs trained in-dependently using different facial patches to improve the performance.In addition,some CNNs originally designed for object recognition,such as VGGNet[38]and Incep-tion[43],were also used for face recognition[29,32].Most recently,a center loss[47]is introduced to learn more dis-criminative features.Facial Attribute Recognition.Facial attribute recog-nition(FAR)is also well studied.A notable early study[21] extracted carefully designed hand-crafted features includ-ing aggregations of colour spaces and image gradients,be-fore training an independent SVM to detect each attribute. As for face recognition,deep learning features now outper-form hand-crafted features for FAR.In[24],face detection and attribute recognition CNNs are carefully designed,and the output of the face detection network is fed into the at-tribute network.An alternative to purpose designing CNNs for FAR is tofine-tune networks intended for object recog-nition[56,57].From a representation learning perspective, the features supporting different attribute detections may be shared,leading some studies to investigate multi-task learn-ing facial attributes[55,30].Since different facial attributes have different prevalence,the multi-label/multi-task learn-ing suffers from label-imbalance,which[30]addresses us-ing a mixed objective optimization network(MOON). Face Recognition using Facial Attributes.Detected facial attributes can be applied directly to authentication. Facial attributes have been applied to enhance face verifica-tion,primarily in the case of cross-modal matching,byfil-tering[19,54](requiring potential FRF matches to have the correct gender,for example),model switching[18],or ag-gregation with conventional features[27,17].[21]defines 65facial attributes and proposes binary attribute classifiers to predict their presence or absence.The vector of attribute classifier scores can be used for face recognition.There has been little work on attribute-enhanced face recognition in the context of deep learning.One of the few exploits CNN-based attribute features for authentication on mobile devices [31].Local facial patches are fed into carefully designed CNNs to predict different attributes.After CNN training, SVMs are trained for attribute recognition,and the vector of SVM scores provide the new feature for face verification.Fusion Methods.Existing fusion approaches can be classified into feature-level(early fusion)and score-level (late fusion).Score-level fusion is to fuse the similarity scores after computation based on each view either by sim-ple averaging[37]or stacking another classifier[48,37]. Feature-level fusion can be achieved by either simple fea-ture aggregation or subspace learning.For aggregation ap-proaches,fusion is usually performed by simply element wise averaging or product(the dimension of features have to be the same)or concatenation[28].For subspace learn-ing approaches,the features arefirst concatenated,then the concatenated feature is projected to a subspace,in which the features should better complement each other.These sub-space approaches can be unsupervised or supervised.Un-supervised fusion does not use the identity(label)informa-tion to learn the subspace,such as Canonical Correlational Analysis(CCA)[35]and Bilinear Models(BLM)[45].In comparison,supervised fusion uses the identity information such as Linear Discriminant Analysis(LDA)[3]and Local-ity Preserving Projections(LPP)[9].Neural Tensor Methods.Learning tensor-based compu-tations within neural networks has been studied for full[39] and decomposed[16,52,51]tensors.However,aside from differing applications and objectives,the key difference is that we establish a novel equivalence between a rich Tucker [46]decomposed low-rank fusion tensor,and a gated two-stream neural network.This allows us achieve expressive fusion,while maintaining tractable computation and a small number of parameters;and crucially permits easy optimisa-tion of the fusion tensor through standard toolboxes. Motivation.Facial attribute features(FAF)and face recognition features(FRF)are complementary.However in practice,wefind that existing fusion methods often can-not effectively combine these asymmetric features so as to improve performance.This motivates us to design a more powerful fusion method,as detailed in Section3.Based on our neural tensor fusion method,in Section5we system-atically explore the fusion of FAF and FRF in various face recognition environments,showing that FAF can greatly en-hance recognition performance.3.Fusing attribute and recognition featuresIn this section we present our strategy for fusing FAF and FRF.Our goal is to input FAF and FRF and output the fused discriminative feature.The proposed fusion method we present here performs significantly better than the exist-ing ones introduced in Section2.In this section,we detail our tensor-based fusion strategy.3.1.ModellingSingle Feature.We start from a standard multi-class clas-sification problem setting:assume we have M instances, and for each we extract a D-dimensional feature vector(the FRF)as{x(i)}M i=1.The label space contains C unique classes(person identities),so each instance is associated with a corresponding C-dimensional one-hot encoding la-bel vector{y(i)}M i=1.Assuming a linear model W the pre-dictionˆy(i)is produced by the dot-product of input x(i)and the model W,ˆy(i)=x(i)T W.(1) Multiple Feature.Suppose that apart from the D-dimensional FRF vector,we can also obtain an instance-wise B-dimensional facial attribute feature z(i).Then the input for the i th instance is a pair:{x(i),z(i)}.A simple ap-proach is to redefine x(i):=[x(i),z(i)],and directly apply Eq.(1),thus modelling weights for both FRF and FAF fea-tures.Here we propose instead a non-linear fusion method via the following formulationˆy(i)=W×1x(i)×3z(i)(2) where W is the fusion model parameters in the form of a third-order tensor of size D×C×B.Notation×is the tensor dot product(also known as tensor contraction)and the left-subscript of x and z indicates at which axis the ten-sor dot product operates.With Eq.(2),the optimisation problem is formulated as:minW1MMi=1W×1x(i)×3z(i),y(i)(3)where (·,·)is a loss function.This trains tensor W to fuse FRF and FAF features so that identity is correctly predicted.3.2.OptimisationThe proposed tensor W provides a rich fusion model. However,compared with W,W is B times larger(D×C vs D×C×B)because of the introduction of B-dimensional attribute vector.It is also almost B times larger than train-ing a matrix W on the concatenation[x(i),z(i)].It is there-fore problematic to directly optimise Eq.(3)because the large number of parameters of W makes training slow and leads to overfitting.To address this we propose a tensor de-composition technique and a neural network architecture to solve an equivalent optimisation problem in the following two subsections.3.2.1Tucker Decomposition for Feature FusionTo reduce the number of parameters of W,we place a struc-tural constraint on W.Motivated by the famous Tucker de-composition[46]for tensors,we assume that W is synthe-sised fromW=S×1U(D)×2U(C)×3U(B).(4) Here S is a third order tensor of size K D×K C×K B, U(D)is a matrix of size K D×D,U(C)is a matrix of sizeK C×C,and U(B)is a matrix of size K B×B.By restricting K D D,K C C,and K B B,we can effectively reduce the number of parameters from(D×C×B)to (K D×K C×K B+K D×D+K C×C+K B×B)if we learn{S,U(D),U(C),U(B)}instead of W.When W is needed for making the predictions,we can always synthesise it from those four small factors.In the context of tensor decomposition,(K D,K C,K B)is usually called the tensor’s rank,as an analogous concept to the rank of a matrix in matrix decomposition.Note that,despite of the existence of other tensor de-composition choices,Tucker decomposition offers a greater flexibility in terms of modelling because we have three hyper-parameters K D,K C,K B corresponding to the axes of the tensor.In contrast,the other famous decomposition, CP[10]has one hyper-parameter K for all axes of tensor.By substituting Eq.(4)into Eq.(2),we haveˆy(i)=W×1x(i)×3z(i)=S×1U(D)×2U(C)×3U(B)×1x(i)×3z(i)(5) Through some re-arrangement,Eq.(5)can be simplified as ˆy(i)=S×1(U(D)x(i))×2U(C)×3(U(B)z(i))(6) Furthermore,we can rewrite Eq.(6)as,ˆy(i)=((U(D)x(i))⊗(U(B)z(i)))S T(2)fused featureU(C)(7)where⊗is Kronecker product.Since U(D)x(i)and U(B)B(i)result in K D and K B dimensional vectors re-spectively,(U(D)x(i))⊗(U(B)z(i))produces a K D K B vector.S(2)is the mode-2unfolding of S which is aK C×K D K B matrix,and its transpose S T(2)is a matrix ofsize K D K B×K C.The Fused Feature.From Eq.(7),the explicit fused representation of face recognition(x(i))and facial at-tribute(z(i))features can be achieved.The fused feature ((U(D)x(i))⊗(U(B)z(i)))S T(2),is a vector of the dimen-sionality K C.And matrix U(C)has the role of“clas-sifier”given this fused feature.Given{x(i),z(i),y(i)}, the matrices{U(D),U(B),U(C)}and tensor S are com-puted(learned)during model optimisation(training).Dur-ing testing,the predictionˆy(i)is achieved with the learned {U(D),U(B),U(C),S}and two test features{x(i),z(i)} following Eq.(7).3.2.2Gated Two-stream Neural Network(GTNN)A key advantage of reformulating Eq.(5)into Eq.(7)is that we can nowfind a neural network architecture that does ex-actly the computation of Eq.(7),which would not be obvi-ous if we stopped at Eq.(5).Before presenting thisneural Figure2:Gated two-stream neural network to implement low-rank tensor-based fusion.The architecture computes Eq.(7),with the Tucker decomposition in Eq.(4).The network is identity-supervised at train time,and feature in the fusion layer used as representation for verification. network,we need to introduce a new deterministic layer(i.e. without any learnable parameters).Kronecker Product Layer takes two arbitrary-length in-put vectors{u,v}where u=[u1,u2,···,u P]and v=[v1,v2,···,v Q],then outputs a vector of length P Q as[u1v1,u1v2,···,u1v Q,u2v1,···,u P v Q].Using the introduced Kronecker layer,Fig.2shows the neural network that computes Eq.(7).That is,the neural network that performs recognition using tensor-based fu-sion of two features(such as FAF and FRF),based on the low-rank assumption in Eq.(4).We denote this architecture as a Gated Two-stream Neural Network(GTNN),because it takes two streams of inputs,and it performs gating[36] (multiplicative)operations on them.The GTNN is trained in a supervised fashion to predict identity.In this work,we use a multitask loss:softmax loss and center loss[47]for joint training.The fused feature in the viewpoint of GTNN is the output of penultimate layer, which is of dimensionality K c.So far,the advantage of using GTNN is obvious.Direct use of Eq.(5)or Eq.(7)requires manual derivation and im-plementation of an optimiser which is non-trivial even for decomposed matrices(2d-tensors)[20].In contrast,GTNN is easily implemented with modern deep learning packages where auto-differentiation and gradient-based optimisation is handled robustly and automatically.3.3.DiscussionCompared with the fusion methods introduced in Sec-tion2,we summarise the advantages of our tensor-based fusion method as follows:Figure3:LeanFace.‘C’is a group of convolutional layers.Stage1:64@5×5(64feature maps are sliced to two groups of32ones, which are fed into maxout function.);Stage2:64@3×3,64@3×3,128@3×3,128@3×3;Stage3:196@3×3,196@3×3, 256@3×3,256@3×3,320@3×3,320@3×3;Stage4:512@3×3,512@3×3,512@3×3,512@3×3;Stage5:640@ 5×5,640@5×5.‘P’stands for2×2max pooling.The strides for the convolutional and pooling layers are1and2,respectively.‘FC’is a fully-connected layer of256D.High Order Non-Linearity.Unlike linear methods based on averaging,concatenation,linear subspace learning [8,27],or LDA[3],our fusion method is non-linear,which is more powerful to model complex problems.Further-more,comparing with otherfirst-order non-linear methods based on element-wise combinations only[28],our method is higher order:it accounts for all interactions between each pair of feature channels in both views.Thanks to the low-rank modelling,our method achieves such powerful non-linear fusion with few parameters and thus it is robust to overfitting.Scalability.Big datasets are required for state-of-the-art face representation learning.Because we establish the equivalence between tensor factorisation and gated neural network architecture,our method is scalable to big-data through efficient mini-batch SGD-based learning.In con-trast,kernel-based non-linear methods,such as Kernel LDA [34]and multi-kernel SVM[17],are restricted to small data due to their O(N2)computation cost.At runtime,our method only requires a simple feed-forward pass and hence it is also favourable compared to kernel methods. Supervised method.GTNN isflexibly supervised by any desired neural network loss function.For example,the fusion method can be trained with losses known to be ef-fective for face representation learning:identity-supervised softmax,and centre-loss[47].Alternative methods are ei-ther unsupervised[8,27],constrained in the types of super-vision they can exploit[3,17],or only stack scores rather than improving a learned representation[48,37].There-fore,they are relatively ineffective at learning how to com-bine the two-source information in a task-specific way. Extensibility.Our GTNN naturally can be extended to deeper architectures.For example,the pre-extracted fea-tures,i.e.,x and z in Fig.2,can be replaced by two full-sized CNNs without any modification.Therefore,poten-tially,our methods can be integrated into an end-to-end framework.4.Integration with CNNs:architectureIn this section,we introduce the CNN architectures used for face recognition(LeanFace)designed by ourselves and facial attribute recognition(AttNet)introduced by[50,30]. LeanFace.Unlike general object recognition,face recognition has to capture very subtle difference between people.Motivated by thefine-grain object recognition in [4],we also use a large number of convolutional layers at early stage to capture the subtle low level and mid-level in-formation.Our activation function is maxout,which shows better performance than its competitors[50].Joint supervi-sion of softmax loss and center loss[47]is used for training. The architecture is summarised in Fig.3.AttNet.To detect facial attributes,our AttNet uses the ar-chitecture of Lighten CNN[50]to represent a face.Specifi-cally,AttNet consists of5conv-activation-pooling units fol-lowed by a256D fully connected layer.The number of con-volutional kernels is explained in[50].The activation func-tion is Max-Feature-Map[50]which is a variant of maxout. We use the loss function MOON[30],which is a multi-task loss for(1)attribute classification and(2)domain adaptive data balance.In[24],an ontology of40facial attributes are defined.We remove attributes which do not characterise a specific person,e.g.,‘wear glasses’and‘smiling’,leaving 17attributes in total.Once each network is trained,the features extracted from the penultimate fully-connected layers of LeanFace(256D) and AttNet(256D)are extracted as x and z,and input to GTNN for fusion and then face recognition.5.ExperimentsWefirst introduce the implementation details of our GTNN method.In Section5.1,we conduct experiments on MultiPIE[7]to show that facial attributes by means of our GTNN method can play an important role on improv-Table1:Network training detailsImage size BatchsizeLR1DF2EpochTraintimeLeanFace128x1282560.0010.15491hAttNet0.050.8993h1Learning rate(LR)2Learning rate drop factor(DF).ing face recognition performance in the presence of pose, illumination and expression,respectively.Then,we com-pare our GTNN method with other fusion methods on CA-SIA NIR-VIS2.0database[22]in Section5.2and LFW database[12]in Section5.3,respectively. Implementation Details.In this study,three networks (LeanFace,AttNet and GTNN)are discussed.LeanFace and AttNet are implemented using MXNet[6]and GTNN uses TensorFlow[1].We use around6M training face thumbnails covering62K different identities to train Lean-Face,which has no overlapping with all the test databases. AttNet is trained using CelebA[24]database.The input of GTNN is two256D features from bottleneck layers(i.e., fully connected layers before prediction layers)of LeanFace and AttNet.The setting of main parameters are shown in Table1.Note that the learning rates drop when the loss stops decreasing.Specifically,the learning rates change4 and2times for LeanFace and AttNet respectively.Dur-ing test,LeanFace and AttNet take around2.9ms and3.2ms to extract feature from one input image and GTNN takes around2.1ms to fuse one pair of LeanFace and AttNet fea-ture using a GTX1080Graphics Card.5.1.Multi-PIE DatabaseMulti-PIE database[7]contains more than750,000im-ages of337people recorded in4sessions under diverse pose,illumination and expression variations.It is an ideal testbed to investigate if facial attribute features(FAF) complement face recognition features(FRF)including tra-ditional hand-crafted(LBP)and deeply learned features (LeanFace)to improve the face recognition performance–particularly across extreme pose variation.Settings.We conduct three experiments to investigate pose-,illumination-and expression-invariant face recogni-tion.Pose:Uses images across4sessions with pose vari-ations only(i.e.,neutral lighting and expression).It covers pose with yaw ranging from left90◦to right90◦.In com-parison,most of the existing works only evaluate perfor-mance on poses with yaw range(-45◦,+45◦).Illumination: Uses images with20different illumination conditions(i.e., frontal pose and neutral expression).Expression:Uses im-ages with7different expression variations(i.e.,frontal pose and neutral illumination).The training sets of all settings consist of the images from thefirst200subjects and the re-maining137subjects for testing.Following[59,14],in the test set,frontal images with neural illumination and expres-sion from the earliest session work as gallery,and the others are probes.Pose.Table2shows the pose-robust face recognition (PRFR)performance.Clearly,the fusion of FRF and FAF, namely GTNN(LBP,AttNet)and GTNN(LeanFace,At-tNet),works much better than using FRF only,showing the complementary power of facial features to face recognition features.Not surprisingly,the performance of both LBP and LeanFace features drop greatly under extreme poses,as pose variation is a major factor challenging face recognition performance.In contrast,with GTNN-based fusion,FAF can be used to improve both classic(LBP)and deep(Lean-Face)FRF features effectively under this circumstance,for example,LBP(1.3%)vs GTNN(LBP,AttNet)(16.3%), LeanFace(72.0%)vs GTNN(LeanFace,AttNet)(78.3%) under yaw angel−90◦.It is noteworthy that despite their highly asymmetric strength,GTNN is able to effectively fuse FAF and FRF.This is elaborately studied in more detail in Sections5.2-5.3.Compared with state-of-the-art methods[14,59,11,58, 15]in terms of(-45◦,+45◦),LeanFace achieves better per-formance due to its big training data and the strong gener-alisation capacity of deep learning.In Table2,2D meth-ods[14,59,15]trained models using the MultiPIE images, therefore,they are difficult to generalise to images under poses which do not appear in MultiPIE database.3D meth-ods[11,58]highly depend on accurate2D landmarks for 3D-2D modellingfitting.However,it is hard to accurately detect such landmarks under larger poses,limiting the ap-plications of3D methods.Illumination and expression.Illumination-and expression-robust face recognition(IRFR and ERFR)are also challenging research topics.LBP is the most widely used handcrafted features for IRFR[2]and ERFR[33].To investigate the helpfulness of facial attributes,experiments of IRFR and ERFR are conducted using LBP and Lean-Face features.In Table3,GTNN(LBP,AttNet)signifi-cantly outperforms LBP,80.3%vs57.5%(IRFR),77.5% vs71.7%(ERFR),showing the great value of combining fa-cial attributes with hand-crafted features.Attributes such as the shape of eyebrows are illumination invariant and others, e.g.,gender,are expression invariant.In contrast,LeanFace feature is already very discriminative,saturating the perfor-mance on the test set.So there is little room for fusion of AttrNet to provide benefit.5.2.CASIA NIR-VIS2.0DatabaseThe CASIA NIR-VIS2.0face database[22]is the largest public face database across near-infrared(NIR)images and visible RGB(VIS)images.It is a typical cross-modality or heterogeneous face recognition problem because the gallery and probe images are from two different spectra.The。
A Fast and Accurate Plane Detection Algorithm for Large Noisy Point Clouds Using Filtered Normals

A Fast and Accurate Plane Detection Algorithm for Large Noisy Point CloudsUsing Filtered Normals and Voxel GrowingJean-Emmanuel DeschaudFranc¸ois GouletteMines ParisTech,CAOR-Centre de Robotique,Math´e matiques et Syst`e mes60Boulevard Saint-Michel75272Paris Cedex06jean-emmanuel.deschaud@mines-paristech.fr francois.goulette@mines-paristech.frAbstractWith the improvement of3D scanners,we produce point clouds with more and more points often exceeding millions of points.Then we need a fast and accurate plane detection algorithm to reduce data size.In this article,we present a fast and accurate algorithm to detect planes in unorganized point clouds usingfiltered normals and voxel growing.Our work is based on afirst step in estimating better normals at the data points,even in the presence of noise.In a second step,we compute a score of local plane in each point.Then, we select the best local seed plane and in a third step start a fast and robust region growing by voxels we call voxel growing.We have evaluated and tested our algorithm on different kinds of point cloud and compared its performance to other algorithms.1.IntroductionWith the growing availability of3D scanners,we are now able to produce large datasets with millions of points.It is necessary to reduce data size,to decrease the noise and at same time to increase the quality of the model.It is in-teresting to model planar regions of these point clouds by planes.In fact,plane detection is generally afirst step of segmentation but it can be used for many applications.It is useful in computer graphics to model the environnement with basic geometry.It is used for example in modeling to detect building facades before classification.Robots do Si-multaneous Localization and Mapping(SLAM)by detect-ing planes of the environment.In our laboratory,we wanted to detect small and large building planes in point clouds of urban environments with millions of points for modeling. As mentioned in[6],the accuracy of the plane detection is important for after-steps of the modeling pipeline.We also want to be fast to be able to process point clouds with mil-lions of points.We present a novel algorithm based on re-gion growing with improvements in normal estimation and growing process.For our method,we are generic to work on different kinds of data like point clouds fromfixed scan-ner or from Mobile Mapping Systems(MMS).We also aim at detecting building facades in urban point clouds or little planes like doors,even in very large data sets.Our input is an unorganized noisy point cloud and with only three”in-tuitive”parameters,we generate a set of connected compo-nents of planar regions.We evaluate our method as well as explain and analyse the significance of each parameter. 2.Previous WorksAlthough there are many methods of segmentation in range images like in[10]or in[3],three have been thor-oughly studied for3D point clouds:region-growing, hough-transform from[14]and Random Sample Consen-sus(RANSAC)from[9].The application of recognising structures in urban laser point clouds is frequent in literature.Bauer in[4]and Boulaassal in[5]detect facades in dense3D point cloud by a RANSAC algorithm.V osselman in[23]reviews sur-face growing and3D hough transform techniques to de-tect geometric shapes.Tarsh-Kurdi in[22]detect roof planes in3D building point cloud by comparing results on hough-transform and RANSAC algorithm.They found that RANSAC is more efficient than thefirst one.Chao Chen in[6]and Yu in[25]present algorithms of segmentation in range images for the same application of detecting planar regions in an urban scene.The method in[6]is based on a region growing algorithm in range images and merges re-sults in one labelled3D point cloud.[25]uses a method different from the three we have cited:they extract a hi-erarchical subdivision of the input image built like a graph where leaf nodes represent planar regions.There are also other methods like bayesian techniques. In[16]and[8],they obtain smoothed surface from noisy point clouds with objects modeled by probability distribu-tions and it seems possible to extend this idea to point cloud segmentation.But techniques based on bayesian statistics need to optimize global statistical model and then it is diffi-cult to process points cloud larger than one million points.We present below an analysis of the two main methods used in literature:RANSAC and region-growing.Hough-transform algorithm is too time consuming for our applica-tion.To compare the complexity of the algorithm,we take a point cloud of size N with only one plane P of size n.We suppose that we want to detect this plane P and we define n min the minimum size of the plane we want to detect.The size of a plane is the area of the plane.If the data density is uniform in the point cloud then the size of a plane can be specified by its number of points.2.1.RANSACRANSAC is an algorithm initially developped by Fis-chler and Bolles in[9]that allows thefitting of models with-out trying all possibilities.RANSAC is based on the prob-ability to detect a model using the minimal set required to estimate the model.To detect a plane with RANSAC,we choose3random points(enough to estimate a plane).We compute the plane parameters with these3points.Then a score function is used to determine how the model is good for the remaining ually,the score is the number of points belonging to the plane.With noise,a point belongs to a plane if the distance from the point to the plane is less than a parameter γ.In the end,we keep the plane with the best score.Theprobability of getting the plane in thefirst trial is p=(nN )3.Therefore the probability to get it in T trials is p=1−(1−(nN )3)ing equation1and supposing n minN1,we know the number T min of minimal trials to have a probability p t to get planes of size at least n min:T min=log(1−p t)log(1−(n minN))≈log(11−p t)(Nn min)3.(1)For each trial,we test all data points to compute the score of a plane.The RANSAC algorithm complexity lies inO(N(Nn min )3)when n minN1and T min→0whenn min→N.Then RANSAC is very efficient in detecting large planes in noisy point clouds i.e.when the ratio n minN is 1but very slow to detect small planes in large pointclouds i.e.when n minN 1.After selecting the best model,another step is to extract the largest connected component of each plane.Connnected components mean that the min-imum distance between each point of the plane and others points is smaller(for distance)than afixed parameter.Schnabel et al.[20]bring two optimizations to RANSAC:the points selection is done locally and the score function has been improved.An octree isfirst created from point cloud.Points used to estimate plane parameters are chosen locally at a random depth of the octree.The score function is also different from RANSAC:instead of testing all points for one model,they test only a random subset and find the score by interpolation.The algorithm complexity lies in O(Nr4Ndn min)where r is the number of random subsets for the score function and d is the maximum octree depth. Their algorithm improves the planes detection speed but its complexity lies in O(N2)and it becomes slow on large data sets.And again we have to extract the largest connected component of each plane.2.2.Region GrowingRegion Growing algorithms work well in range images like in[18].The principle of region growing is to start with a seed region and to grow it by neighborhood when the neighbors satisfy some conditions.In range images,we have the neighbors of each point with pixel coordinates.In case of unorganized3D data,there is no information about the neighborhood in the data structure.The most common method to compute neighbors in3D is to compute a Kd-tree to search k nearest neighbors.The creation of a Kd-tree lies in O(NlogN)and the search of k nearest neighbors of one point lies in O(logN).The advantage of these region growing methods is that they are fast when there are many planes to extract,robust to noise and extract the largest con-nected component immediately.But they only use the dis-tance from point to plane to extract planes and like we will see later,it is not accurate enough to detect correct planar regions.Rabbani et al.[19]developped a method of smooth area detection that can be used for plane detection.Theyfirst estimate the normal of each point like in[13].The point with the minimum residual starts the region growing.They test k nearest neighbors of the last point added:if the an-gle between the normal of the point and the current normal of the plane is smaller than a parameterαthen they add this point to the smooth region.With Kd-tree for k nearest neighbors,the algorithm complexity is in O(N+nlogN). The complexity seems to be low but in worst case,when nN1,example for facade detection in point clouds,the complexity becomes O(NlogN).3.Voxel Growing3.1.OverviewIn this article,we present a new algorithm adapted to large data sets of unorganized3D points and optimized to be accurate and fast.Our plane detection method works in three steps.In thefirst part,we compute a better esti-mation of the normal in each point by afiltered weighted planefitting.In a second step,we compute the score of lo-cal planarity in each point.We select the best seed point that represents a good seed plane and in the third part,we grow this seed plane by adding all points close to the plane.Thegrowing step is based on a voxel growing algorithm.The filtered normals,the score function and the voxel growing are innovative contributions of our method.As an input,we need dense point clouds related to the level of detail we want to detect.As an output,we produce connected components of planes in the point cloud.This notion of connected components is linked to the data den-sity.With our method,the connected components of planes detected are linked to the parameter d of the voxel grid.Our method has 3”intuitive”parameters :d ,area min and γ.”intuitive”because there are linked to physical mea-surements.d is the voxel size used in voxel growing and also represents the connectivity of points in detected planes.γis the maximum distance between the point of a plane and the plane model,represents the plane thickness and is linked to the point cloud noise.area min represents the minimum area of planes we want to keep.3.2.Details3.2.1Local Density of Point CloudsIn a first step,we compute the local density of point clouds like in [17].For that,we find the radius r i of the sphere containing the k nearest neighbors of point i .Then we cal-culate ρi =kπr 2i.In our experiments,we find that k =50is a good number of neighbors.It is important to know the lo-cal density because many laser point clouds are made with a fixed resolution angle scanner and are therefore not evenly distributed.We use the local density in section 3.2.3for the score calculation.3.2.2Filtered Normal EstimationNormal estimation is an important part of our algorithm.The paper [7]presents and compares three normal estima-tion methods.They conclude that the weighted plane fit-ting or WPF is the fastest and the most accurate for large point clouds.WPF is an idea of Pauly and al.in [17]that the fitting plane of a point p must take into consider-ation the nearby points more than other distant ones.The normal least square is explained in [21]and is the mini-mum of ki =1(n p ·p i +d )2.The WPF is the minimum of ki =1ωi (n p ·p i +d )2where ωi =θ( p i −p )and θ(r )=e −2r 2r2i .For solving n p ,we compute the eigenvec-tor corresponding to the smallest eigenvalue of the weightedcovariance matrix C w = ki =1ωi t (p i −b w )(p i −b w )where b w is the weighted barycenter.For the three methods ex-plained in [7],we get a good approximation of normals in smooth area but we have errors in sharp corners.In fig-ure 1,we have tested the weighted normal estimation on two planes with uniform noise and forming an angle of 90˚.We can see that the normal is not correct on the corners of the planes and in the red circle.To improve the normal calculation,that improves the plane detection especially on borders of planes,we propose a filtering process in two phases.In a first step,we com-pute the weighted normals (WPF)of each point like we de-scribed it above by minimizing ki =1ωi (n p ·p i +d )2.In a second step,we compute the filtered normal by us-ing an adaptive local neighborhood.We compute the new weighted normal with the same sum minimization but keep-ing only points of the neighborhood whose normals from the first step satisfy |n p ·n i |>cos (α).With this filtering step,we have the same results in smooth areas and better results in sharp corners.We called our normal estimation filtered weighted plane fitting(FWPF).Figure 1.Weighted normal estimation of two planes with uniform noise and with 90˚angle between them.We have tested our normal estimation by computing nor-mals on synthetic data with two planes and different angles between them and with different values of the parameter α.We can see in figure 2the mean error on normal estimation for WPF and FWPF with α=20˚,30˚,40˚and 90˚.Us-ing α=90˚is the same as not doing the filtering step.We see on Figure 2that α=20˚gives smaller error in normal estimation when angles between planes is smaller than 60˚and α=30˚gives best results when angle between planes is greater than 60˚.We have considered the value α=30˚as the best results because it gives the smaller mean error in normal estimation when angle between planes vary from 20˚to 90˚.Figure 3shows the normals of the planes with 90˚angle and better results in the red circle (normals are 90˚with the plane).3.2.3The score of local planarityIn many region growing algorithms,the criteria used for the score of the local fitting plane is the residual,like in [18]or [19],i.e.the sum of the square of distance from points to the plane.We have a different score function to estimate local planarity.For that,we first compute the neighbors N i of a point p with points i whose normals n i are close toFigure parison of mean error in normal estimation of two planes with α=20˚,30˚,40˚and 90˚(=Nofiltering).Figure 3.Filtered Weighted normal estimation of two planes with uniform noise and with 90˚angle between them (α=30˚).the normal n p .More precisely,we compute N i ={p in k neighbors of i/|n i ·n p |>cos (α)}.It is a way to keep only the points which are probably on the local plane before the least square fitting.Then,we compute the local plane fitting of point p with N i neighbors by least squares like in [21].The set N i is a subset of N i of points belonging to the plane,i.e.the points for which the distance to the local plane is smaller than the parameter γ(to consider the noise).The score s of the local plane is the area of the local plane,i.e.the number of points ”in”the plane divided by the localdensity ρi (seen in section 3.2.1):the score s =card (N i)ρi.We take into consideration the area of the local plane as the score function and not the number of points or the residual in order to be more robust to the sampling distribution.3.2.4Voxel decompositionWe use a data structure that is the core of our region growing method.It is a voxel grid that speeds up the plane detection process.V oxels are small cubes of length d that partition the point cloud space.Every point of data belongs to a voxel and a voxel contains a list of points.We use the Octree Class Template in [2]to compute an Octree of the point cloud.The leaf nodes of the graph built are voxels of size d .Once the voxel grid has been computed,we start the plane detection algorithm.3.2.5Voxel GrowingWith the estimator of local planarity,we take the point p with the best score,i.e.the point with the maximum area of local plane.We have the model parameters of this best seed plane and we start with an empty set E of points belonging to the plane.The initial point p is in a voxel v 0.All the points in the initial voxel v 0for which the distance from the seed plane is less than γare added to the set E .Then,we compute new plane parameters by least square refitting with set E .Instead of growing with k nearest neighbors,we grow with voxels.Hence we test points in 26voxel neigh-bors.This is a way to search the neighborhood in con-stant time instead of O (logN )for each neighbor like with Kd-tree.In a neighbor voxel,we add to E the points for which the distance to the current plane is smaller than γand the angle between the normal computed in each point and the normal of the plane is smaller than a parameter α:|cos (n p ,n P )|>cos (α)where n p is the normal of the point p and n P is the normal of the plane P .We have tested different values of αand we empirically found that 30˚is a good value for all point clouds.If we added at least one point in E for this voxel,we compute new plane parameters from E by least square fitting and we test its 26voxel neigh-bors.It is important to perform plane least square fitting in each voxel adding because the seed plane model is not good enough with noise to be used in all voxel growing,but only in surrounding voxels.This growing process is faster than classical region growing because we do not compute least square for each point added but only for each voxel added.The least square fitting step must be computed very fast.We use the same method as explained in [18]with incre-mental update of the barycenter b and covariance matrix C like equation 2.We know with [21]that the barycen-ter b belongs to the least square plane and that the normal of the least square plane n P is the eigenvector of the smallest eigenvalue of C .b0=03x1C0=03x3.b n+1=1n+1(nb n+p n+1).C n+1=C n+nn+1t(pn+1−b n)(p n+1−b n).(2)where C n is the covariance matrix of a set of n points,b n is the barycenter vector of a set of n points and p n+1is the (n+1)point vector added to the set.This voxel growing method leads to a connected com-ponent set E because the points have been added by con-nected voxels.In our case,the minimum distance between one point and E is less than parameter d of our voxel grid. That is why the parameter d also represents the connectivity of points in detected planes.3.2.6Plane DetectionTo get all planes with an area of at least area min in the point cloud,we repeat these steps(best local seed plane choice and voxel growing)with all points by descending order of their score.Once we have a set E,whose area is bigger than area min,we keep it and classify all points in E.4.Results and Discussion4.1.Benchmark analysisTo test the improvements of our method,we have em-ployed the comparative framework of[12]based on range images.For that,we have converted all images into3D point clouds.All Point Clouds created have260k points. After our segmentation,we project labelled points on a seg-mented image and compare with the ground truth image. We have chosen our three parameters d,area min andγby optimizing the result of the10perceptron training image segmentation(the perceptron is portable scanner that pro-duces a range image of its environment).Bests results have been obtained with area min=200,γ=5and d=8 (units are not provided in the benchmark).We show the re-sults of the30perceptron images segmentation in table1. GT Regions are the mean number of ground truth planes over the30ground truth range images.Correct detection, over-segmentation,under-segmentation,missed and noise are the mean number of correct,over,under,missed and noised planes detected by methods.The tolerance80%is the minimum percentage of points we must have detected comparing to the ground truth to have a correct detection. More details are in[12].UE is a method from[12],UFPR is a method from[10]. It is important to notice that UE and UFPR are range image methods and our method is not well suited for range images but3D Point Cloud.Nevertheless,it is a good benchmark for comparison and we see in table1that the accuracy of our method is very close to the state of the art in range image segmentation.To evaluate the different improvements of our algorithm, we have tested different variants of our method.We have tested our method without normals(only with distance from points to plane),without voxel growing(with a classical region growing by k neighbors),without our FWPF nor-mal estimation(with WPF normal estimation),without our score function(with residual score function).The compari-son is visible on table2.We can see the difference of time computing between region growing and voxel growing.We have tested our algorithm with and without normals and we found that the accuracy cannot be achieved whithout normal computation.There is also a big difference in the correct de-tection between WPF and our FWPF normal estimation as we can see in thefigure4.Our FWPF normal brings a real improvement in border estimation of planes.Black points in thefigure are non classifiedpoints.Figure5.Correct Detection of our segmentation algorithm when the voxel size d changes.We would like to discuss the influence of parameters on our algorithm.We have three parameters:area min,which represents the minimum area of the plane we want to keep,γ,which represents the thickness of the plane(it is gener-aly closely tied to the noise in the point cloud and espe-cially the standard deviationσof the noise)and d,which is the minimum distance from a point to the rest of the plane. These three parameters depend on the point cloud features and the desired segmentation.For example,if we have a lot of noise,we must choose a highγvalue.If we want to detect only large planes,we set a large area min value.We also focus our analysis on the robustess of the voxel size d in our algorithm,i.e.the ratio of points vs voxels.We can see infigure5the variation of the correct detection when we change the value of d.The method seems to be robust when d is between4and10but the quality decreases when d is over10.It is due to the fact that for a large voxel size d,some planes from different objects are merged into one plane.GT Regions Correct Over-Under-Missed Noise Duration(in s)detection segmentation segmentationUE14.610.00.20.3 3.8 2.1-UFPR14.611.00.30.1 3.0 2.5-Our method14.610.90.20.1 3.30.7308Table1.Average results of different segmenters at80%compare tolerance.GT Regions Correct Over-Under-Missed Noise Duration(in s) Our method detection segmentation segmentationwithout normals14.6 5.670.10.19.4 6.570 without voxel growing14.610.70.20.1 3.40.8605 without FWPF14.69.30.20.1 5.0 1.9195 without our score function14.610.30.20.1 3.9 1.2308 with all improvements14.610.90.20.1 3.30.7308 Table2.Average results of variants of our segmenter at80%compare tolerance.4.1.1Large scale dataWe have tested our method on different kinds of data.We have segmented urban data infigure6from our Mobile Mapping System(MMS)described in[11].The mobile sys-tem generates10k pts/s with a density of50pts/m2and very noisy data(σ=0.3m).For this point cloud,we want to de-tect building facades.We have chosen area min=10m2, d=1m to have large connected components andγ=0.3m to cope with the noise.We have tested our method on point cloud from the Trim-ble VX scanner infigure7.It is a point cloud of size40k points with only20pts/m2with less noise because it is a fixed scanner(σ=0.2m).In that case,we also wanted to detect building facades and keep the same parameters ex-ceptγ=0.2m because we had less noise.We see infig-ure7that we have detected two facades.By setting a larger voxel size d value like d=10m,we detect only one plane. We choose d like area min andγaccording to the desired segmentation and to the level of detail we want to extract from the point cloud.We also tested our algorithm on the point cloud from the LEICA Cyrax scanner infigure8.This point cloud has been taken from AIM@SHAPE repository[1].It is a very dense point cloud from multiplefixed position of scanner with about400pts/m2and very little noise(σ=0.02m). In this case,we wanted to detect all the little planes to model the church in planar regions.That is why we have chosen d=0.2m,area min=1m2andγ=0.02m.Infigures6,7and8,we have,on the left,input point cloud and on the right,we only keep points detected in a plane(planes are in random colors).The red points in thesefigures are seed plane points.We can see in thesefig-ures that planes are very well detected even with high noise. Table3show the information on point clouds,results with number of planes detected and duration of the algorithm.The time includes the computation of the FWPF normalsof the point cloud.We can see in table3that our algo-rithm performs linearly in time with respect to the numberof points.The choice of parameters will have little influence on time computing.The computation time is about one mil-lisecond per point whatever the size of the point cloud(we used a PC with QuadCore Q9300and2Go of RAM).The algorithm has been implented using only one thread andin-core processing.Our goal is to compare the improve-ment of plane detection between classical region growing and our region growing with better normals for more ac-curate planes and voxel growing for faster detection.Our method seems to be compatible with out-of-core implemen-tation like described in[24]or in[15].MMS Street VX Street Church Size(points)398k42k7.6MMean Density50pts/m220pts/m2400pts/m2 Number of Planes202142Total Duration452s33s6900sTime/point 1ms 1ms 1msTable3.Results on different data.5.ConclusionIn this article,we have proposed a new method of plane detection that is fast and accurate even in presence of noise. We demonstrate its efficiency with different kinds of data and its speed in large data sets with millions of points.Our voxel growing method has a complexity of O(N)and it is able to detect large and small planes in very large data sets and can extract them directly in connected components.Figure 4.Ground truth,Our Segmentation without and with filterednormals.Figure 6.Planes detection in street point cloud generated by MMS (d =1m,area min =10m 2,γ=0.3m ).References[1]Aim@shape repository /.6[2]Octree class template /code/octree.html.4[3] A.Bab-Hadiashar and N.Gheissari.Range image segmen-tation using surface selection criterion.2006.IEEE Trans-actions on Image Processing.1[4]J.Bauer,K.Karner,K.Schindler,A.Klaus,and C.Zach.Segmentation of building models from dense 3d point-clouds.2003.Workshop of the Austrian Association for Pattern Recognition.1[5]H.Boulaassal,ndes,P.Grussenmeyer,and F.Tarsha-Kurdi.Automatic segmentation of building facades using terrestrial laser data.2007.ISPRS Workshop on Laser Scan-ning.1[6] C.C.Chen and I.Stamos.Range image segmentationfor modeling and object detection in urban scenes.2007.3DIM2007.1[7]T.K.Dey,G.Li,and J.Sun.Normal estimation for pointclouds:A comparison study for a voronoi based method.2005.Eurographics on Symposium on Point-Based Graph-ics.3[8]J.R.Diebel,S.Thrun,and M.Brunig.A bayesian methodfor probable surface reconstruction and decimation.2006.ACM Transactions on Graphics (TOG).1[9]M.A.Fischler and R.C.Bolles.Random sample consen-sus:A paradigm for model fitting with applications to image analysis and automated munications of the ACM.1,2[10]P.F.U.Gotardo,O.R.P.Bellon,and L.Silva.Range imagesegmentation by surface extraction using an improved robust estimator.2003.Proceedings of Computer Vision and Pat-tern Recognition.1,5[11] F.Goulette,F.Nashashibi,I.Abuhadrous,S.Ammoun,andurgeau.An integrated on-board laser range sensing sys-tem for on-the-way city and road modelling.2007.Interna-tional Archives of the Photogrammetry,Remote Sensing and Spacial Information Sciences.6[12] A.Hoover,G.Jean-Baptiste,and al.An experimental com-parison of range image segmentation algorithms.1996.IEEE Transactions on Pattern Analysis and Machine Intelligence.5[13]H.Hoppe,T.DeRose,T.Duchamp,J.McDonald,andW.Stuetzle.Surface reconstruction from unorganized points.1992.International Conference on Computer Graphics and Interactive Techniques.2[14]P.Hough.Method and means for recognizing complex pat-terns.1962.In US Patent.1[15]M.Isenburg,P.Lindstrom,S.Gumhold,and J.Snoeyink.Large mesh simplification using processing sequences.2003.。
Using the Fractal Dimension to Cluster Datasets Paper 145

George Mason University Information and Software Engineering Department Fairfax, VA 22303
dbarbara,pchen @
Daniel Barbar a
Ping Chen
October 19, 1999
Paper 145
Clustering is a widely used knowledge discovery technique. It helps uncovering structures in data that were not previously known. Clustering of large datasets has received a lot of attention in recent years. However, clustering is a still a challenging task since many published algorithms fail to do well in scaling with the size of the dataset and the number of dimensions that describe the points, or in nding arbitrary shapes of clusters, or dealing e ectively with the presence of noise. In this paper, we present a new clustering algorithm, based in the fractal properties of the datasets. The new algorithm, which we call Fractal Clustering FC places points incrementally in the cluster for which the change in the fractal dimension after adding the point is the least. This is a very natural way of clustering points, since points in the same cluster have a great degree of self-similarity among them and much less self-similarity with respect to points in other clusters. FC requires one scan of the data, is suspendable at will, providing the best answer possible at that point, and is incremental. We show via experiments that FC e ectively deals with large datasets, high-dimensionality and noise and is capable of recognizing clusters of arbitrary shape.
Analyzing the Properties of Pigments and Dyes

Analyzing the Properties of Pigmentsand DyesPigments and dyes are two types of colorants used in various industries such as art, fashion, cosmetics, and printing. Both pigments and dyes have unique properties that make them suitable for different applications. In this article, we will analyze the properties of pigments and dyes.What are Pigments?Pigments are colorants that do not dissolve in the medium in which they are dispersed. Pigments are insoluble but dispersible in water, oil, or another medium. Pigments are used in a wide range of applications such as paints, inks, plastics, ceramics, and textiles. Pigments come in a variety of forms such as powders, pastes, or granules.The Properties of PigmentsPigments have several unique properties that make them ideal for various applications. Here are some of the properties of pigments:1. LightfastnessOne of the essential properties of pigments is lightfastness. The lightfastness of a pigment refers to its ability to retain its color when exposed to light. Pigments with a high level of lightfastness are resistant to fading, whereas pigments with low lightfastness will fade quickly.2. OpacityOpacity is the ability of pigments to block light. Pigments with high opacity can cover a surface entirely, whereas pigments with low opacity will allow some of the underlying surface color to show through.3. Chemical StabilityPigments must be chemically stable when exposed to various chemicals, whether they come into contact with solvents, acids, or bases. Any chemical reaction with the medium can cause a change in color or degrade the quality of the pigment.4. Particle SizeThe particle size of a pigment determines its dispersibility and the resulting color intensity. Smaller particles make pigments more translucent, whereas larger particles make pigments more opaque.5. Color StrengthThe color strength of a pigment is the intensity of its color when used at maximum concentration. Pigments with high color strength require less material to produce vivid, vibrant colors.What are Dyes?Dyes are colorants that dissolve in the medium in which they are used. Dyes are soluble in water, oil, or another medium. Dyes are used in a wide range of applications such as textiles, paper, leather, and food. Dyes come in various forms such as liquids or powders.The Properties of DyesDyes have several unique properties that make them ideal for various applications. Here are some of the properties of dyes:1. SolubilitySolubility is the ability of dyes to dissolve in liquid or other mediums. It is the essential property of dyes, which allows it to penetrate deep into the fiber and produce a vibrant color.2. WashfastnessWashfastness is the ability of dyes to resist fading when exposed to water. Dyes with high washfastness will retain their color even after repeated exposure to water and detergents.3. LightfastnessLightfastness is the ability of dyes to resist fading when exposed to light. Dyes with high lightfastness will retain their color even when exposed to sunlight or artificial light sources.4. AffinityThe affinity of dyes is the ability to attach themselves to the surface of the material they are applied to. Dyes with high affinity are more likely to produce uniform and vibrant colors.5. Color RangeOne of the essential properties of dyes is the ability to produce a wide range of colors. Dyes can create bright and vivid colors in various shades, hues, and tones.In ConclusionPigments and dyes are two unique types of colorants used for various applications. Pigments are insoluble but dispersible in water, oil, or another medium, while dyes are soluble. Pigments have properties such as lightfastness, opacity, and chemical stability, while dyes have properties such as solubility, washfastness, and affinity. Understanding the properties and differences between pigments and dyes can help you choose the best one for your specific needs.。
Hierarchical cluster analysis

Chapter 7Hierarchical cluster analysisIn Part 2 (Chapters 4 to 6) we defined several different ways of measuring distance (or dissimilarity as the case may be) between the rows or between the columns of the data matrix, depending on the measurement scale of the observations. As we remarked before, this process often generates tables of distances with even more numbers than the original data, but we will show now how this in fact simplifies our understanding of the data. Distances between objects can be visualized in many simple and evocative ways. In this chapter we shall consider a graphical representation of a matrix of distances which is perhaps the easiest to understand – a dendrogram, or tree – where the objects are joined together in a hierarchical fashion from the closest, that is most similar, to the furthest apart, that is the most different. The method of hierarchical cluster analysis is best explained by describing the algorithm, or set of instructions, which creates the dendrogram results. In this chapter we demonstrate hierarchical clustering on a small example and then list the different variants of the method that are possible.ContentsThe algorithm for hierarchical clusteringCutting the treeMaximum, minimum and average clusteringValidity of the clustersClustering correlationsClustering a larger data setThe algorithm for hierarchical clusteringAs an example we shall consider again the small data set in Exhibit 5.6: seven samples on which 10 species are indicated as being present or absent. In Chapter 5 we discussed two of the many dissimilarity coefficients that are possible to define between the samples: the first based on the matching coefficient and the second based on the Jaccard index. The latter index counts the number of ‘mismatches’ between two samples after eliminating the species that do not occur in either of the pair. Exhibit 7.1 shows the complete table of inter-sample dissimilarities based on the Jaccard index.Exhibit 7.1 Dissimilarities, based on the Jaccard index, between all pairs ofseven samples in Exhibit 5.6. For example, between the first two samples, A andB, there are 8 species that occur in on or the other, of which 4 are matched and 4are mismatched – the proportion of mismatches is 4/8 = 0.5. Both the lower andupper triangles of this symmetric dissimilarity matrix are shown here (the lowertriangle is outlined as in previous tables of this type.samples A B C D E F GA00.50000.4286 1.00000.25000.62500.3750B0.500000.71430.83330.66670.20000.7778C0.42860.71430 1.00000.42860.66670.3333D 1.00000.8333 1.00000 1.00000.80000.8571E0.25000.66670.4286 1.000000.77780.3750F0.62500.20000.66670.80000.777800.7500G0.37500.77780.33330.85710.37500.75000The first step in the hierarchical clustering process is to look for the pair of samples that are the most similar, that is are the closest in the sense of having the lowest dissimilarity – this is the pair B and F, with dissimilarity equal to 0.2000. These two samples are then joined at a level of 0.2000 in the first step of the dendrogram, or clustering tree (see the first diagram of Exhibit 7.3, and the vertical scale of 0 to 1 which calibrates the level of clustering). The point at which they are joined is called a node.We are basically going to keep repeating this step, but the only problem is how to calculated the dissimilarity between the merged pair (B,F) and the other samples. This decision determines what type of hierarchical clustering we intend to perform, and there are several choices. For the moment, we choose one of the most popular ones, called the maximum, or complete linkage, method: the dissimilarity between the merged pair and the others will be the maximum of the pair of dissimilarities in each case. For example, the dissimilarity between B and A is 0.5000, while the dissimilarity between F and A is 0.6250. hence we choose the maximum of the two, 0.6250, to quantify the dissimilarity between (B,F) and A. Continuing in this way we obtain a new dissimilarity matrix Exhibit 7.2.Exhibit 7.2 Dissimilarities calculated after B and F are merged, using the‘maximum’ method to recomputed the values in the row and column labelled(B,F).samples A(B,F)C D E GA00.62500.4286 1.00000.25000.3750(B,F)0.625000.71430.83330.77780.7778C0.42860.71430 1.00000.42860.3333D 1.00000.8333 1.00000 1.00000.8571E0.25000.77780.4286 1.000000.3750G0.37500.77780.33330.85710.37500Exhibit 7.3 First two steps of hierarchical clustering of Exhibit 7.1, using the ‘maximum’ (or ‘complete linkage’) method.The process is now repeated: find the smallest dissimilarity in Exhibit 7.2, which is 0.2500 for samplesA and E , and then cluster these at a level of 0.25, as shown in the second figure of Exhibit 7.3. Then recomputed the dissimilarities between the merged pair (A ,E ) and the rest to obtain Exhibit 7.4. For example, the dissimilarity between (A ,E ) and (B ,F ) is the maximum of 0.6250 (A to (B ,F )) and 0.7778 (E to (B ,F )).Exhibit 7.4 Dissimilarities calculated after A and E are merged, using the ‘maximum’ method to recomputed the values in the row and column labelled (A ,E ).samples(A,E)(B,F)CDG(A,E)00.77780.4286 1.00000.3750(B,F)0.777800.71430.83330.7778C 0.42860.71430 1.00000.3333D1.00000.8333 1.000000.8571G 0.37500.77780.33330.85710In the next step the lowest dissimilarity in Exhibit 7.4 is 0.3333, for C and G – these are merged, as shown in the first diagram of Exhibit 7.6, to obtain Exhibit 7.5. Now the smallest dissimilarity is 0.4286, between the pair (A ,E ) and (B ,G ), and they are shown merged in the second diagram of Exhibit 7.6. Exhibit 7.7 shows the last two dissimilarity matrices in this process, and Exhibit 7.8 the final two steps of the construction of the dendrogram, also called a binary tree because at each step two objects (or clusters of objects) are merged. Because there are 7 objects to be clustered, there are 6 steps in the sequential process (i.e., one less) to arrive at the final tree where all objects are in a single cluster. For botanists that may be reading this: this is an upside-down tree, of course!1.00.50.0B F B F A E1.00.50.0Exhibit 7.5 Dissimilarities calculated after C and G are merged, using the‘maximum’ method to recomputed the values in the row and column labelled (C,G).samples(A,E)(B,F)(C,G)D(A,E)00.77780.4286 1.0000(B,F)0.777800.77780.8333(C,G)0.42860.77780 1.0000D 1.00000.8333 1.00000Exhibit 7.6 The third and fourth steps of hierarchical clustering of Exhibit 7.1, using the ‘maximum’ (or ‘complete linkage’) method. The point at which objects (or clusters of objects) are joined is called a node.Exhibit 7.7 Dissimilarities calculated after C and G are merged, using the‘maximum’ method to recomputed the values in the row and column labelled (C,G).samples(A,E,C,G)(B,F)D samples(A,E,C,G,B,F)D (A,E,C,G)00.7778 1.0000(A,E,C,G,B,F)0 1.0000 (B,F)0.777800.8333D 1.00000D 1.00000.83330B F A EC G1.00.50.0B F A EC G1.00.50.0Exhibit 7.8 The fifth and sixth steps of hierarchical clustering of Exhibit 7.1, using the ‘maximum’ (or ‘complete linkage’) method. The dendrogram on the right is the final result of the cluster analysis. In the clustering of n objects, there are n–1 nodes (i.e. 6 nodes in this case).Cutting the treeThe final dendrogram on the right of Exhibit 7.8 is a compact visualization of the dissimilarity matrix in Exhibit 7.1, based on the presence-absence data of Exhibit 5.6. Interpretation of the structure of data is made much easier now – we can see that there are three pairs of samples that are fairly close, two of these pairs ((A,E) and (C,G)) are in turn close to each other, while the single sample D separates itself entirely from all the others. Because we used the ‘maximum’ method, all samples clustered below a particular level of dissimilarity will have inter-sample dissimilarities less than that level. For example, 0.5 is the point at which samples are exactly as similar to one another as they are dissimilar, so if we look at the clusters of samples below 0.5 – i.e., (B,F), (A,E,C,G) and (D) – then within each cluster the samples have more than 50% similarity, in other words more than 50% co-presences of species. The level of 0.5 also happens to coincide in the final dendrogram with a large jump in the clustering levels: the node where (A,E) and (C,G) are clustered is at level of 0.4286, while the next node where (B,F) is merged is at a level of 0.7778. This is thus a very convenient level to cut the tree. If the branches are cut at 0.5, we are left with the three clusters of samples (B,F), (A,E,C,G) and (D), which can be labelled types 1, 2 and 3 respectively. In other words, we have created a categorical variable, with three categories, and the samples are categorized as follows:A B C D E F G2 1 23 2 1 2Checking back to Chapter 2, this is exactly the objective which we described in the lower right hand corner of the multivariate analysis scheme (Exhibit 2.2) – to reveal a categorical variable which underlies the structure of a data set.B F A EC G1.00.50.0B F A EC G D1.00.50.0Maximum, minimum and average clusteringThe crucial choice when deciding on a cluster analysis algorithm is to decide how to quantify dissimilarities between two clusters. The algorithm described above was characterized by the fact that at each step, when updating the matrix of dissimilarities, the maximum of the between-cluster dissimilarities was chosen. This is also known as complete linkage cluster analysis, because a cluster is formed when all the dissimilarities (‘links’) between pairs of objects in the cluster are less then a particular level. There are several alternatives to complete linkage as a clustering criterion, and we only discuss two of these: minimum and average clustering.The ‘minimum’ method goes to the other extreme and forms a cluster when only one pair of dissimilarities (not all) is less than a particular level – this is known as single linkage cluster analysis. So at every updating step we choose the minimum of the two distances and two clusters of objects can be merged when there is a single close link between them, irrespective of the other inter-object distances. In general, this is not a suitable choice for most applications, because it can lead to clusters that are quite heterogeneous internally, and the usual object of clustering is to obtain homogeneous clusters.The ‘average’ method is an attractive compromise where dissimilarities are averaged at each step, hence the name average linkage cluster analysis. For example, in Exhibit 7.1 the first step of all types of cluster analysis would merge B and F. But then calculating the dissimilarity between A, for example, and (B,F) is where the methods distinguish themselves. The dissimilarity between A and B is 0.5000, and between A and F it is 0.6250. Complete linkage chooses the maximum: 0.6250; single linkage chooses the minimum: 0.5000; while average linkage chooses the average: (0.5000+0.6250)/2 = 0.5625.Validity of the clustersIf a cluster analysis is performed on a data matrix, a set of clusters can always be obtained, even if there is no actual grouping of the objects, in this case the samples. So how can we evaluate whether the three clusters in this example are not just any old three groups which we would have obtained on random data with no structure? There is a vast literature on validity of clusters (we give some references in the Bibliography, Appendix E) and here we shall explain one approach based on permutation testing. In our example, the three clusters were formed so that internally in each cluster formed by more than one sample the between-sample dissimilarities were all less than 0.5000. In fact, if we look.at the result in the right hand picture of Exhibit 7.8, the cutpoint for three clusters can be brought down to the level of 0.4286, where (A,E) and (C,G) joined together. As in all statistical considerations of significance, we ask whether this is an unusual result or whether it could have arisen merely by chance. To answer this question we need an idea of what might have happened in chance results, so that we can judge our actual finding. This so-called “null distribution” can be generated through permuting the data in some reasonable way, evaluating the statistic of interest, and doing this many times (or for all permutations if this is feasible computationally) to obtain a distribution of the statistic. The statistic of interest could be that value at which the three clusters are formed, but we need to choose carefullyhow we perform the permutations, and this depends on how the data were collected. We consider two possible assumptions, and show how different the results can be.The first assumption is that the column totals of Table Exhibit 5.6 are fixed; that is, that the 10 species are present, respectively, 3 times in the 7 samples, 6 times, 4 times, 3 times and so on. Then the permutation involved would be to simply randomly shuffle the zeros and ones in each column to obtain a new presence-absence matrix with exactly the same column totals as before. Performing the compete linkage hierarchical clustering on this matrix leads to that value where the three cluster solution is achieved, and becomes one observation of the null permutation distribution. We did this 9999 times, and along with our actual observed value of 0.4286, the 10000 values are graphed in Exhibit 7.9 (we show it as a horizontal bar chart because there are only 15 different values observed of this value, shown here with their frequencies). The value we actually observed is one of the smallest – the number of permuted matrices that generates this value or a lower value is 26 out of 10000, so that in this sense our data are very unusual and the ‘significance’ of the three-cluster solution can be quantified with a p -value of 0.0026. The other 9974 randompermutations all lead to generally higher inter-sample dissimilarities such that the level at which three-cluster solutions are obtained is 0.4444 or higher (0.4444 corresponds to 4 mistmatches out of 9.Exhibit 7.9 Bar chart of the 10000 values of the three-cluster solutions obtained by permuting the columns of the presence-absence data, including the value we observed in the original unpermuted data matrix.The second and alternative possible assumption for the computation of the null distribution could be that the column margins are not fixed, but random; in other words, we relax the fact that there were exactly 3 samples that had species sp1, for example, and assume a binomial distribution for each column, using the observed proportion (3 out of 7 forspecies sp1) and the number of samples (7) as the binomial parameters. Thus there can be 0 up to 7 presences in each column, according to the binomial probabilities for eachspecies. This gives a much wider range of possibilities for the null distribution, and leads us to a different conclusion about our three observed clusters. The permutation distributionlevel frequency0.800020.7778350.75003630.714313600.70001890.666729670.625021990.60008220.571413810.55552070.50004410.444480.4286230.400020.37501is now shown in Exhibit 7.10, and now our observed value of 0.4286 does not look sounusual, since 917 out of 10000 values in the distribution are less than or equal to it, giving an estimated P -value of 0.0917.Exhibit 7.10 Bar chart of the 10000 values of the three-cluster solutionsobtained by generating binomial data in each column of the presence-absence matrix, according to the probability of presence of each species.So, as in many situations in statistics, the result and decision depends on the initialassumptions. Could we have observed the presence of species s1 less or more than 3 times in the 7 samples (and so on for the other species)? In other words, according to thebinomial distribution with n = 7, and p = 3/7, the probabilities of observing k presences of species sp1 (k = 0, 1, …, 7) are:0 1 2 3 4 5 6 7 0.020 0.104 0.235 0.294 0.220 0.099 0.025 0.003If this assumption (and similar ones for the other nine species) is realistic, then the cluster significance is 0.0917. However, if the first assumption is adopted (that is, the probability of observing 3 presences for species s1 is 1 and 0 for other possibilities), then the significance is 0.0028. Our feeling is that perhaps the binomial assumption is more realistic, in which case our cluster solution could be observed in just over 9% of random cases – this gives us an idea of the validity of our results and whether we are dealing with real clusters or not. The value of 9% is a measure of ‘clusteredness’ of our samples in terms of the Jaccard index: the lower this measure, the more they are clustered, and the hoihger the measure, the more the samples lie in a continuum. Lack of evidence oflevel frequency0.875020.857150.8333230.8000500.7778280.75002010.71434850.7000210.666712980.625011710.60008950.571419600.55554680.500022990.44441770.42865670.40001620.37501070.3333640.300010.2857120.250030.20001‘clusteredness’ does not mean that the clustering is not useful: we might want to divide up the space of the data into separate regions, even though the borderlines between them are ‘fuzzy’. And speaking of ‘fuzzy’, there is an alternative form of cluster analysis (fuzzy cluster analysis, not treated specifically in this book) where samples are classified fuzzily into clusters, rather than strictly into one group or another – this idea is similar to the fuzzy coding we described in Chapter 3.Clustering correlations on variablesJust like we clustered samples, so we can cluster variables in terms of their correlations, or distances based on their correlations as described in Chapter 6. The dissimilarity based on the Jaccard index can also be used to measure similarity between species – the index counts the number of samples that have both species of the pair, relative to the number of samples that have at least one of the pair, and the dissimilarity is 1 minus this index.Exhibit 7.11 shows the cluster analyses based on these two alternatives, for the columns of Exhibit 5.6, using the graphical output this time of the R function hclust for hierarchical clustering. The fact that these two trees are so different is no surprise: the first one is based on the correlation coefficient takes into account the co-absences, which strengthens the correlation, while the second does not. Both have the pairs (sp2,sp5) and (sp3,sp8) at zero dissimilarity because these are identically present and absent across the samples. Species sp1 and sp7 are close in terms of correlation, due to co-absences – sp7 only occurs in one sample, sample E , which also has sp1, a species which is absent in four other samples. Notice in Exhibit 7.11(b) how species sp10 and sp1 both join the cluster (sp2,sp5) at the same level (0.5).Exhibit 7.11 Complete linkage cluster analyses of (a) 1–r (1 minus the correlation coefficient between species); (b) Jaccard dissimilarity between species (1 minus the Jaccard similarity index). The R function hclust which calculates the dendrograms places the object (species) labels at a constant distance below its clustering level.(a) (b)s p 1s p 7s p 2s p 5s p 9s p 3s p 8s p 6s p 4s p 100.00.51.01.52.0H e i g h ts p 4s p 6s p 10s p 1s p 2s p 5s p 7s p 9s p 3s p 80.00.20.40.60.81.0H e i g h tClustering a larger data setThe more objects there are to cluster, the more complex becomes the result. In Exhibit 4.5 we showed part of the matrix of standardized Euclidean distances between the 30 sites of Exhibit 1.1, and Exhibit 7.12 shows the hierarchical clustering of this distance matrix, using compete linkage. There are two obvious places where we can cut the tree, at about level 3.4, which gives four clusters, or about 2.7, which gives six clusters. To get an ideaExhibit 7.12 Complete linkage cluster analyses of the standardized Euclidean distances of Exhibit 4.5.of the ‘clusteredness’ of these data, we performed a permutation test similar to the one described above, where the data are randomly permuted within their columns and the cluster analysis repeated each time to obtain 6 clusters. The permutation distribution of levels at which 6 clusters are formed is shown in Exhibit 7.13 – the observed value in Exhibit 7.12 (i.e., where (s2,s14) joins (s25,s23,s30,s12,s16,s27)) is 2.357, which is clearly not an unusual value. The estimated p -value according to the proportion of the distribution to the left of 2.357 in Exhibit 7.13 is p = 0.3388, so we conclude that these samples do not have a non-random cluster structure – they form more of a continuum, which will be the subject of Chapter 9.s s 2s 23s 3016s 27s s s 2 4 classes6 classes7-11Exhibit 7.13 Estimated permutation distribution for the level at which 6clusters are formed in the cluster analysis of Exhibit 7.12, showing the valueactually observed. Of the 10000 permutations, including the observed value,3388 are less than or equal to the observed value, giving an estimated p -valuefor clusteredness of 0.3388.SUMMARY: Hierarchical cluster analysis1. Hierarchical cluster analysis of n objects is defined by a stepwise algorithm whichmerges two objects at each step, the two which have the least dissimilarity.2. Dissimilarities between clusters of objects can be defined in several ways; forexample, the maximum dissimilarity (complete linkage), minimum dissimilarity (single linkage) or average dissimilarity (average linkage).3. Either rows or columns of a matrix can be clustered – in each case we choose theappropriate dissimilarity measure that we prefer.4. The results of a cluster analysis is a binary tree, or dendrogram, with n – 1 nodes. Thebranches of this tree are cut at a level where there is a lot of ‘space’ to cut them, that is where the jump in levels of two consecutive nodes is large.5. A permutation test is possible to validate the chosen number of clusters, that is to seeif there really is a non-random tendency for the objects to group together. 6-clu ster level f r e q u e n c y 2.0 2.5 3.002004006008001000(observed value)。
斯普林格数学研究生教材丛书

《斯普林格数学研究生教材丛书》(Graduate Texts in Mathematics)GTM001《Introduction to Axiomatic Set Theory》Gaisi Takeuti, Wilson M.Zaring GTM002《Measure and Category》John C.Oxtoby(测度和范畴)(2ed.)GTM003《Topological Vector Spaces》H.H.Schaefer, M.P.Wolff(2ed.)GTM004《A Course in Homological Algebra》P.J.Hilton, U.Stammbach(2ed.)(同调代数教程)GTM005《Categories for the Working Mathematician》Saunders Mac Lane(2ed.)GTM006《Projective Planes》Daniel R.Hughes, Fred C.Piper(投射平面)GTM007《A Course in Arithmetic》Jean-Pierre Serre(数论教程)GTM008《Axiomatic set theory》Gaisi Takeuti, Wilson M.Zaring(2ed.)GTM009《Introduction to Lie Algebras and Representation Theory》James E.Humphreys(李代数和表示论导论)GTM010《A Course in Simple-Homotopy Theory》M.M CohenGTM011《Functions of One Complex VariableⅠ》John B.ConwayGTM012《Advanced Mathematical Analysis》Richard BealsGTM013《Rings and Categories of Modules》Frank W.Anderson, Kent R.Fuller(环和模的范畴)(2ed.)GTM014《Stable Mappings and Their Singularities》Martin Golubitsky, Victor Guillemin (稳定映射及其奇点)GTM015《Lectures in Functional Analysis and Operator Theory》Sterling K.Berberian GTM016《The Structure of Fields》David J.Winter(域结构)GTM017《Random Processes》Murray RosenblattGTM018《Measure Theory》Paul R.Halmos(测度论)GTM019《A Hilbert Space Problem Book》Paul R.Halmos(希尔伯特问题集)GTM020《Fibre Bundles》Dale Husemoller(纤维丛)GTM021《Linear Algebraic Groups》James E.Humphreys(线性代数群)GTM022《An Algebraic Introduction to Mathematical Logic》Donald W.Barnes, John M.MackGTM023《Linear Algebra》Werner H.Greub(线性代数)GTM024《Geometric Functional Analysis and Its Applications》Paul R.HolmesGTM025《Real and Abstract Analysis》Edwin Hewitt, Karl StrombergGTM026《Algebraic Theories》Ernest G.ManesGTM027《General Topology》John L.Kelley(一般拓扑学)GTM028《Commutative Algebra》VolumeⅠOscar Zariski, Pierre Samuel(交换代数)GTM029《Commutative Algebra》VolumeⅡOscar Zariski, Pierre Samuel(交换代数)GTM030《Lectures in Abstract AlgebraⅠ.Basic Concepts》Nathan Jacobson(抽象代数讲义Ⅰ基本概念分册)GTM031《Lectures in Abstract AlgebraⅡ.Linear Algabra》Nathan.Jacobson(抽象代数讲义Ⅱ线性代数分册)GTM032《Lectures in Abstract AlgebraⅢ.Theory of Fields and Galois Theory》Nathan.Jacobson(抽象代数讲义Ⅲ域和伽罗瓦理论)GTM033《Differential Topology》Morris W.Hirsch(微分拓扑)GTM034《Principles of Random Walk》Frank Spitzer(2ed.)(随机游动原理)GTM035《Several Complex Variables and Banach Algebras》Herbert Alexander, John Wermer(多复变和Banach代数)GTM036《Linear Topological Spaces》John L.Kelley, Isaac Namioka(线性拓扑空间)GTM037《Mathematical Logic》J.Donald Monk(数理逻辑)GTM038《Several Complex Variables》H.Grauert, K.FritzsheGTM039《An Invitation to C*-Algebras》William Arveson(C*-代数引论)GTM040《Denumerable Markov Chains》John G.Kemeny, urie Snell, Anthony W.KnappGTM041《Modular Functions and Dirichlet Series in Number Theory》Tom M.Apostol (数论中的模函数和Dirichlet序列)GTM042《Linear Representations of Finite Groups》Jean-Pierre Serre(有限群的线性表示)GTM043《Rings of Continuous Functions》Leonard Gillman, Meyer JerisonGTM044《Elementary Algebraic Geometry》Keith KendigGTM045《Probability TheoryⅠ》M.Loève(概率论Ⅰ)(4ed.)GTM046《Probability TheoryⅡ》M.Loève(概率论Ⅱ)(4ed.)GTM047《Geometric Topology in Dimensions 2 and 3》Edwin E.MoiseGTM048《General Relativity for Mathematicians》Rainer.K.Sachs, H.Wu伍鸿熙(为数学家写的广义相对论)GTM049《Linear Geometry》K.W.Gruenberg, A.J.Weir(2ed.)GTM050《Fermat's Last Theorem》Harold M.EdwardsGTM051《A Course in Differential Geometry》Wilhelm Klingenberg(微分几何教程)GTM052《Algebraic Geometry》Robin Hartshorne(代数几何)GTM053《A Course in Mathematical Logic for Mathematicians》Yu.I.Manin(2ed.)GTM054《Combinatorics with Emphasis on the Theory of Graphs》Jack E.Graver, Mark E.WatkinsGTM055《Introduction to Operator TheoryⅠ》Arlen Brown, Carl PearcyGTM056《Algebraic Topology:An Introduction》W.S.MasseyGTM057《Introduction to Knot Theory》Richard.H.Crowell, Ralph.H.FoxGTM058《p-adic Numbers, p-adic Analysis, and Zeta-Functions》Neal Koblitz(p-adic 数、p-adic分析和Z函数)GTM059《Cyclotomic Fields》Serge LangGTM060《Mathematical Methods of Classical Mechanics》V.I.Arnold(经典力学的数学方法)(2ed.)GTM061《Elements of Homotopy Theory》George W.Whitehead(同论论基础)GTM062《Fundamentals of the Theory of Groups》M.I.Kargapolov, Ju.I.Merzljakov GTM063《Modern Graph Theory》Béla BollobásGTM064《Fourier Series:A Modern Introduction》VolumeⅠ(2ed.)R.E.Edwards(傅里叶级数)GTM065《Differential Analysis on Complex Manifolds》Raymond O.Wells, Jr.(3ed.)GTM066《Introduction to Affine Group Schemes》William C.Waterhouse(仿射群概型引论)GTM067《Local Fields》Jean-Pierre Serre(局部域)GTM069《Cyclotomic FieldsⅠandⅡ》Serge LangGTM070《Singular Homology Theory》William S.MasseyGTM071《Riemann Surfaces》Herschel M.Farkas, Irwin Kra(黎曼曲面)GTM072《Classical Topology and Combinatorial Group Theory》John Stillwell(经典拓扑和组合群论)GTM073《Algebra》Thomas W.Hungerford(代数)GTM074《Multiplicative Number Theory》Harold Davenport(乘法数论)(3ed.)GTM075《Basic Theory of Algebraic Groups and Lie Algebras》G.P.HochschildGTM076《Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties》Shigeru IitakaGTM077《Lectures on the Theory of Algebraic Numbers》Erich HeckeGTM078《A Course in Universal Algebra》Stanley Burris, H.P.Sankappanavar(泛代数教程)GTM079《An Introduction to Ergodic Theory》Peter Walters(遍历性理论引论)GTM080《A Course in_the Theory of Groups》Derek J.S.RobinsonGTM081《Lectures on Riemann Surfaces》Otto ForsterGTM082《Differential Forms in Algebraic Topology》Raoul Bott, Loring W.Tu(代数拓扑中的微分形式)GTM083《Introduction to Cyclotomic Fields》Lawrence C.Washington(割圆域引论)GTM084《A Classical Introduction to Modern Number Theory》Kenneth Ireland, Michael Rosen(现代数论经典引论)GTM085《Fourier Series A Modern Introduction》Volume 1(2ed.)R.E.Edwards GTM086《Introduction to Coding Theory》J.H.van Lint(3ed .)GTM087《Cohomology of Groups》Kenneth S.Brown(上同调群)GTM088《Associative Algebras》Richard S.PierceGTM089《Introduction to Algebraic and Abelian Functions》Serge Lang(代数和交换函数引论)GTM090《An Introduction to Convex Polytopes》Ame BrondstedGTM091《The Geometry of Discrete Groups》Alan F.BeardonGTM092《Sequences and Series in BanachSpaces》Joseph DiestelGTM093《Modern Geometry-Methods and Applications》(PartⅠ.The of geometry Surfaces Transformation Groups and Fields)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov (现代几何学方法和应用)GTM094《Foundations of Differentiable Manifolds and Lie Groups》Frank W.Warner(可微流形和李群基础)GTM095《Probability》A.N.Shiryaev(2ed.)GTM096《A Course in Functional Analysis》John B.Conway(泛函分析教程)GTM097《Introduction to Elliptic Curves and Modular Forms》Neal Koblitz(椭圆曲线和模形式引论)GTM098《Representations of Compact Lie Groups》Theodor Breöcker, Tammo tom DieckGTM099《Finite Reflection Groups》L.C.Grove, C.T.Benson(2ed.)GTM100《Harmonic Analysis on Semigroups》Christensen Berg, Jens Peter Reus Christensen, Paul ResselGTM101《Galois Theory》Harold M.Edwards(伽罗瓦理论)GTM102《Lie Groups, Lie Algebras, and Their Representation》V.S.Varadarajan(李群、李代数及其表示)GTM103《Complex Analysis》Serge LangGTM104《Modern Geometry-Methods and Applications》(PartⅡ.Geometry and Topology of Manifolds)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM105《SL₂ (R)》Serge Lang(SL₂ (R)群)GTM106《The Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术理论)GTM107《Applications of Lie Groups to Differential Equations》Peter J.Olver(李群在微分方程中的应用)GTM108《Holomorphic Functions and Integral Representations in Several Complex Variables》R.Michael RangeGTM109《Univalent Functions and Teichmueller Spaces》Lehto OlliGTM110《Algebraic Number Theory》Serge Lang(代数数论)GTM111《Elliptic Curves》Dale Husemoeller(椭圆曲线)GTM112《Elliptic Functions》Serge Lang(椭圆函数)GTM113《Brownian Motion and Stochastic Calculus》Ioannis Karatzas, Steven E.Shreve (布朗运动和随机计算)GTM114《A Course in Number Theory and Cryptography》Neal Koblitz(数论和密码学教程)GTM115《Differential Geometry:Manifolds, Curves, and Surfaces》M.Berger, B.Gostiaux GTM116《Measure and Integral》Volume1 John L.Kelley, T.P.SrinivasanGTM117《Algebraic Groups and Class Fields》Jean-Pierre Serre(代数群和类域)GTM118《Analysis Now》Gert K.Pedersen(现代分析)GTM119《An introduction to Algebraic Topology》Jossph J.Rotman(代数拓扑导论)GTM120《Weakly Differentiable Functions》William P.Ziemer(弱可微函数)GTM121《Cyclotomic Fields》Serge LangGTM122《Theory of Complex Functions》Reinhold RemmertGTM123《Numbers》H.-D.Ebbinghaus, H.Hermes, F.Hirzebruch, M.Koecher, K.Mainzer, J.Neukirch, A.Prestel, R.Remmert(2ed.)GTM124《Modern Geometry-Methods and Applications》(PartⅢ.Introduction to Homology Theory)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM125《Complex Variables:An introduction》Garlos A.Berenstein, Roger Gay GTM126《Linear Algebraic Groups》Armand Borel(线性代数群)GTM127《A Basic Course in Algebraic Topology》William S.Massey(代数拓扑基础教程)GTM128《Partial Differential Equations》Jeffrey RauchGTM129《Representation Theory:A First Course》William Fulton, Joe HarrisGTM130《Tensor Geometry》C.T.J.Dodson, T.Poston(张量几何)GTM131《A First Course in Noncommutative Rings》m(非交换环初级教程)GTM132《Iteration of Rational Functions:Complex Analytic Dynamical Systems》AlanF.Beardon(有理函数的迭代:复解析动力系统)GTM133《Algebraic Geometry:A First Course》Joe Harris(代数几何)GTM134《Coding and Information Theory》Steven RomanGTM135《Advanced Linear Algebra》Steven RomanGTM136《Algebra:An Approach via Module Theory》William A.Adkins, Steven H.WeintraubGTM137《Harmonic Function Theory》Sheldon Axler, Paul Bourdon, Wade Ramey(调和函数理论)GTM138《A Course in Computational Algebraic Number Theory》Henri Cohen(计算代数数论教程)GTM139《Topology and Geometry》Glen E.BredonGTM140《Optima and Equilibria:An Introduction to Nonlinear Analysis》Jean-Pierre AubinGTM141《A Computational Approach to Commutative Algebra》Gröbner Bases, Thomas Becker, Volker Weispfenning, Heinz KredelGTM142《Real and Functional Analysis》Serge Lang(3ed.)GTM143《Measure Theory》J.L.DoobGTM144《Noncommutative Algebra》Benson Farb, R.Keith DennisGTM145《Homology Theory:An Introduction to Algebraic Topology》James W.Vick(同调论:代数拓扑简介)GTM146《Computability:A Mathematical Sketchbook》Douglas S.BridgesGTM147《Algebraic K-Theory and Its Applications》Jonathan Rosenberg(代数K理论及其应用)GTM148《An Introduction to the Theory of Groups》Joseph J.Rotman(群论入门)GTM149《Foundations of Hyperbolic Manifolds》John G.Ratcliffe(双曲流形基础)GTM150《Commutative Algebra with a view toward Algebraic Geometry》David EisenbudGTM151《Advanced Topics in the Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术高级选题)GTM152《Lectures on Polytopes》Günter M.ZieglerGTM153《Algebraic Topology:A First Course》William Fulton(代数拓扑)GTM154《An introduction to Analysis》Arlen Brown, Carl PearcyGTM155《Quantum Groups》Christian Kassel(量子群)GTM156《Classical Descriptive Set Theory》Alexander S.KechrisGTM157《Integration and Probability》Paul MalliavinGTM158《Field theory》Steven Roman(2ed.)GTM159《Functions of One Complex Variable VolⅡ》John B.ConwayGTM160《Differential and Riemannian Manifolds》Serge Lang(微分流形和黎曼流形)GTM161《Polynomials and Polynomial Inequalities》Peter Borwein, Tamás Erdélyi(多项式和多项式不等式)GTM162《Groups and Representations》J.L.Alperin, Rowen B.Bell(群及其表示)GTM163《Permutation Groups》John D.Dixon, Brian Mortime rGTM164《Additive Number Theory:The Classical Bases》Melvyn B.NathansonGTM165《Additive Number Theory:Inverse Problems and the Geometry of Sumsets》Melvyn B.NathansonGTM166《Differential Geometry:Cartan's Generalization of Klein's Erlangen Program》R.W.SharpeGTM167《Field and Galois Theory》Patrick MorandiGTM168《Combinatorial Convexity and Algebraic Geometry》Günter Ewald(组合凸面体和代数几何)GTM169《Matrix Analysis》Rajendra BhatiaGTM170《Sheaf Theory》Glen E.Bredon(2ed.)GTM171《Riemannian Geometry》Peter Petersen(黎曼几何)GTM172《Classical Topics in Complex Function Theory》Reinhold RemmertGTM173《Graph Theory》Reinhard Diestel(图论)(3ed.)GTM174《Foundations of Real and Abstract Analysis》Douglas S.Bridges(实分析和抽象分析基础)GTM175《An Introduction to Knot Theory》W.B.Raymond LickorishGTM176《Riemannian Manifolds:An Introduction to Curvature》John M.LeeGTM177《Analytic Number Theory》Donald J.Newman(解析数论)GTM178《Nonsmooth Analysis and Control Theory》F.H.clarke, Yu.S.Ledyaev, R.J.Stern, P.R.Wolenski(非光滑分析和控制论)GTM179《Banach Algebra Techniques in Operator Theory》Ronald G.Douglas(2ed.)GTM180《A Course on Borel Sets》S.M.Srivastava(Borel 集教程)GTM181《Numerical Analysis》Rainer KressGTM182《Ordinary Differential Equations》Wolfgang WalterGTM183《An introduction to Banach Spaces》Robert E.MegginsonGTM184《Modern Graph Theory》Béla Bollobás(现代图论)GTM185《Using Algebraic Geomety》David A.Cox, John Little, Donal O’Shea(应用代数几何)GTM186《Fourier Analysis on Number Fields》Dinakar Ramakrishnan, Robert J.Valenza GTM187《Moduli of Curves》Joe Harris, Ian Morrison(曲线模)GTM188《Lectures on the Hyperreals:An Introduction to Nonstandard Analysis》Robert GoldblattGTM189《Lectures on Modules and Rings》m(模和环讲义)GTM190《Problems in Algebraic Number Theory》M.Ram Murty, Jody Esmonde(代数数论中的问题)GTM191《Fundamentals of Differential Geometry》Serge Lang(微分几何基础)GTM192《Elements of Functional Analysis》Francis Hirsch, Gilles LacombeGTM193《Advanced Topics in Computational Number Theory》Henri CohenGTM194《One-Parameter Semigroups for Linear Evolution Equations》Klaus-Jochen Engel, Rainer Nagel(线性发展方程的单参数半群)GTM195《Elementary Methods in Number Theory》Melvyn B.Nathanson(数论中的基本方法)GTM196《Basic Homological Algebra》M.Scott OsborneGTM197《The Geometry of Schemes》David Eisenbud, Joe HarrisGTM198《A Course in p-adic Analysis》Alain M.RobertGTM199《Theory of Bergman Spaces》Hakan Hedenmalm, Boris Korenblum, Kehe Zhu(Bergman空间理论)GTM200《An Introduction to Riemann-Finsler Geometry》D.Bao, S.-S.Chern, Z.Shen GTM201《Diophantine Geometry An Introduction》Marc Hindry, Joseph H.Silverman GTM202《Introduction to Topological Manifolds》John M.LeeGTM203《The Symmetric Group》Bruce E.SaganGTM204《Galois Theory》Jean-Pierre EscofierGTM205《Rational Homotopy Theory》Yves Félix, Stephen Halperin, Jean-Claude Thomas(有理同伦论)GTM206《Problems in Analytic Number Theory》M.Ram MurtyGTM207《Algebraic Graph Theory》Chris Godsil, Gordon Royle(代数图论)GTM208《Analysis for Applied Mathematics》Ward CheneyGTM209《A Short Course on Spectral Theory》William Arveson(谱理论简明教程)GTM210《Number Theory in Function Fields》Michael RosenGTM211《Algebra》Serge Lang(代数)GTM212《Lectures on Discrete Geometry》Jiri Matousek(离散几何讲义)GTM213《From Holomorphic Functions to Complex Manifolds》Klaus Fritzsche, Hans Grauert(从正则函数到复流形)GTM214《Partial Differential Equations》Jüergen Jost(偏微分方程)GTM215《Algebraic Functions and Projective Curves》David M.Goldschmidt(代数函数和投影曲线)GTM216《Matrices:Theory and Applications》Denis Serre(矩阵:理论及应用)GTM217《Model Theory An Introduction》David Marker(模型论引论)GTM218《Introduction to Smooth Manifolds》John M.Lee(光滑流形引论)GTM219《The Arithmetic of Hyperbolic 3-Manifolds》Colin Maclachlan, Alan W.Reid GTM220《Smooth Manifolds and Observables》Jet Nestruev(光滑流形和直观)GTM221《Convex Polytopes》Branko GrüenbaumGTM222《Lie Groups, Lie Algebras, and Representations》Brian C.Hall(李群、李代数和表示)GTM223《Fourier Analysis and its Applications》Anders Vretblad(傅立叶分析及其应用)GTM224《Metric Structures in Differential Geometry》Gerard Walschap(微分几何中的度量结构)GTM225《Lie Groups》Daniel Bump(李群)GTM226《Spaces of Holomorphic Functions in the Unit Ball》Kehe Zhu(单位球内的全纯函数空间)GTM227《Combinatorial Commutative Algebra》Ezra Miller, Bernd Sturmfels(组合交换代数)GTM228《A First Course in Modular Forms》Fred Diamond, Jerry Shurman(模形式初级教程)GTM229《The Geometry of Syzygies》David Eisenbud(合冲几何)GTM230《An Introduction to Markov Processes》Daniel W.Stroock(马尔可夫过程引论)GTM231《Combinatorics of Coxeter Groups》Anders Bjröner, Francesco Brenti(Coxeter 群的组合学)GTM232《An Introduction to Number Theory》Graham Everest, Thomas Ward(数论入门)GTM233《Topics in Banach Space Theory》Fenando Albiac, Nigel J.Kalton(Banach空间理论选题)GTM234《Analysis and Probability:Wavelets, Signals, Fractals》Palle E.T.Jorgensen(分析与概率)GTM235《Compact Lie Groups》Mark R.Sepanski(紧致李群)GTM236《Bounded Analytic Functions》John B.Garnett(有界解析函数)GTM237《An Introduction to Operators on the Hardy-Hilbert Space》Rubén A.Martínez-Avendano, Peter Rosenthal(哈代-希尔伯特空间算子引论)GTM238《A Course in Enumeration》Martin Aigner(枚举教程)GTM239《Number Theory:VolumeⅠTools and Diophantine Equations》Henri Cohen GTM240《Number Theory:VolumeⅡAnalytic and Modern Tools》Henri Cohen GTM241《The Arithmetic of Dynamical Systems》Joseph H.SilvermanGTM242《Abstract Algebra》Pierre Antoine Grillet(抽象代数)GTM243《Topological Methods in Group Theory》Ross GeogheganGTM244《Graph Theory》J.A.Bondy, U.S.R.MurtyGTM245《Complex Analysis:In the Spirit of Lipman Bers》Jane P.Gilman, Irwin Kra, Rubi E.RodriguezGTM246《A Course in Commutative Banach Algebras》Eberhard KaniuthGTM247《Braid Groups》Christian Kassel, Vladimir TuraevGTM248《Buildings Theory and Applications》Peter Abramenko, Kenneth S.Brown GTM249《Classical Fourier Analysis》Loukas Grafakos(经典傅里叶分析)GTM250《Modern Fourier Analysis》Loukas Grafakos(现代傅里叶分析)GTM251《The Finite Simple Groups》Robert A.WilsonGTM252《Distributions and Operators》Gerd GrubbGTM253《Elementary Functional Analysis》Barbara D.MacCluerGTM254《Algebraic Function Fields and Codes》Henning StichtenothGTM255《Symmetry Representations and Invariants》Roe Goodman, Nolan R.Wallach GTM256《A Course in Commutative Algebra》Kemper GregorGTM257《Deformation Theory》Robin HartshorneGTM258《Foundation of Optimization》Osman GülerGTM259《Ergodic Theory:with a view towards Number Theory》Manfred Einsiedler, Thomas WardGTM260《Monomial Ideals》Jurgen Herzog, Takayuki HibiGTM261《Probability and Stochastics》Erhan CinlarGTM262《Essentials of Integration Theory for Analysis》Daniel W.StroockGTM263《Analysis on Fock Spaces》Kehe ZhuGTM264《Functional Analysis, Calculus of Variations and Optimal Control》Francis ClarkeGTM265《Unbounded Self-adjoint Operatorson Hilbert Space》Konrad Schmüdgen GTM266《Calculus Without Derivatives》Jean-Paul PenotGTM267《Quantum Theory for Mathematicians》Brian C.HallGTM268《Geometric Analysis of the Bergman Kernel and Metric》Steven G.Krantz GTM269《Locally Convex Spaces》M.Scott Osborne。
Cluster analysis

8 Cluster Analysis:Basic Concepts andAlgorithmsCluster analysis divides data into groups(clusters)that are meaningful,useful, or both.If meaningful groups are the goal,then the clusters should capture the natural structure of the data.In some cases,however,cluster analysis is only a useful starting point for other purposes,such as data summarization.Whether for understanding or utility,cluster analysis has long played an important role in a wide variety offields:psychology and other social sciences,biology, statistics,pattern recognition,information retrieval,machine learning,and data mining.There have been many applications of cluster analysis to practical prob-lems.We provide some specific examples,organized by whether the purpose of the clustering is understanding or utility.Clustering for Understanding Classes,or conceptually meaningful groups of objects that share common characteristics,play an important role in how people analyze and describe the world.Indeed,human beings are skilled at dividing objects into groups(clustering)and assigning particular objects to these groups(classification).For example,even relatively young children can quickly label the objects in a photograph as buildings,vehicles,people,ani-mals,plants,etc.In the context of understanding data,clusters are potential classes and cluster analysis is the study of techniques for automaticallyfinding classes.The following are some examples:488Chapter8Cluster Analysis:Basic Concepts and Algorithms •Biology.Biologists have spent many years creating a taxonomy(hi-erarchical classification)of all living things:kingdom,phylum,class, order,family,genus,and species.Thus,it is perhaps not surprising that much of the early work in cluster analysis sought to create a discipline of mathematical taxonomy that could automaticallyfind such classifi-cation structures.More recently,biologists have applied clustering to analyze the large amounts of genetic information that are now available.For example,clustering has been used tofind groups of genes that have similar functions.•Information Retrieval.The World Wide Web consists of billions of Web pages,and the results of a query to a search engine can return thousands of pages.Clustering can be used to group these search re-sults into a small number of clusters,each of which captures a particular aspect of the query.For instance,a query of“movie”might return Web pages grouped into categories such as reviews,trailers,stars,and theaters.Each category(cluster)can be broken into subcategories(sub-clusters),producing a hierarchical structure that further assists a user’s exploration of the query results.•Climate.Understanding the Earth’s climate requiresfinding patterns in the atmosphere and ocean.To that end,cluster analysis has been applied tofind patterns in the atmospheric pressure of polar regions and areas of the ocean that have a significant impact on land climate.•Psychology and Medicine.An illness or condition frequently has a number of variations,and cluster analysis can be used to identify these different subcategories.For example,clustering has been used to identify different types of depression.Cluster analysis can also be used to detect patterns in the spatial or temporal distribution of a disease.•Business.Businesses collect large amounts of information on current and potential customers.Clustering can be used to segment customers into a small number of groups for additional analysis and marketing activities.Clustering for Utility Cluster analysis provides an abstraction from in-dividual data objects to the clusters in which those data objects reside.Ad-ditionally,some clustering techniques characterize each cluster in terms of a cluster prototype;i.e.,a data object that is representative of the other ob-jects in the cluster.These cluster prototypes can be used as the basis for a489 number of data analysis or data processing techniques.Therefore,in the con-text of utility,cluster analysis is the study of techniques forfinding the most representative cluster prototypes.•Summarization.Many data analysis techniques,such as regression or PCA,have a time or space complexity of O(m2)or higher(where m is the number of objects),and thus,are not practical for large data sets.However,instead of applying the algorithm to the entire data set,it can be applied to a reduced data set consisting only of cluster prototypes.Depending on the type of analysis,the number of prototypes,and the accuracy with which the prototypes represent the data,the results can be comparable to those that would have been obtained if all the data could have been used.•Compression.Cluster prototypes can also be used for data compres-sion.In particular,a table is created that consists of the prototypes for each cluster;i.e.,each prototype is assigned an integer value that is its position(index)in the table.Each object is represented by the index of the prototype associated with its cluster.This type of compression is known as vector quantization and is often applied to image,sound, and video data,where(1)many of the data objects are highly similar to one another,(2)some loss of information is acceptable,and(3)a substantial reduction in the data size is desired.•Efficiently Finding Nearest Neighbors.Finding nearest neighbors can require computing the pairwise distance between all points.Often clusters and their cluster prototypes can be found much more efficiently.If objects are relatively close to the prototype of their cluster,then we can use the prototypes to reduce the number of distance computations that are necessary tofind the nearest neighbors of an object.Intuitively,if two cluster prototypes are far apart,then the objects in the corresponding clusters cannot be nearest neighbors of each other.Consequently,to find an object’s nearest neighbors it is only necessary to compute the distance to objects in nearby clusters,where the nearness of two clusters is measured by the distance between their prototypes.This idea is made more precise in Exercise25on page94.This chapter provides an introduction to cluster analysis.We begin with a high-level overview of clustering,including a discussion of the various ap-proaches to dividing objects into sets of clusters and the different types of clusters.We then describe three specific clustering techniques that represent490Chapter8Cluster Analysis:Basic Concepts and Algorithms broad categories of algorithms and illustrate a variety of concepts:K-means, agglomerative hierarchical clustering,and DBSCAN.Thefinal section of this chapter is devoted to cluster validity—methods for evaluating the goodness of the clusters produced by a clustering algorithm.More advanced clustering concepts and algorithms will be discussed in Chapter9.Whenever possible, we discuss the strengths and weaknesses of different schemes.In addition, the bibliographic notes provide references to relevant books and papers that explore cluster analysis in greater depth.8.1OverviewBefore discussing specific clustering techniques,we provide some necessary background.First,we further define cluster analysis,illustrating why it is difficult and explaining its relationship to other techniques that group data. Then we explore two important topics:(1)different ways to group a set of objects into a set of clusters,and(2)types of clusters.8.1.1What Is Cluster Analysis?Cluster analysis groups data objects based only on information found in the data that describes the objects and their relationships.The goal is that the objects within a group be similar(or related)to one another and different from (or unrelated to)the objects in other groups.The greater the similarity(or homogeneity)within a group and the greater the difference between groups, the better or more distinct the clustering.In many applications,the notion of a cluster is not well defined.To better understand the difficulty of deciding what constitutes a cluster,consider Figure 8.1,which shows twenty points and three different ways of dividing them into clusters.The shapes of the markers indicate cluster membership.Figures 8.1(b)and8.1(d)divide the data into two and six parts,respectively.However, the apparent division of each of the two larger clusters into three subclusters may simply be an artifact of the human visual system.Also,it may not be unreasonable to say that the points form four clusters,as shown in Figure 8.1(c).Thisfigure illustrates that the definition of a cluster is imprecise and that the best definition depends on the nature of data and the desired results.Cluster analysis is related to other techniques that are used to divide data objects into groups.For instance,clustering can be regarded as a form of classification in that it creates a labeling of objects with class(cluster)labels. However,it derives these labels only from the data.In contrast,classification8.1Overview491(a)Original points.(b)Two clusters.(c)Four clusters.(d)Six clusters.Figure8.1.Different ways of clustering the same set of points.in the sense of Chapter4is supervised classification;i.e.,new,unlabeled objects are assigned a class label using a model developed from objects with known class labels.For this reason,cluster analysis is sometimes referred to as unsupervised classification.When the term classification is used without any qualification within data mining,it typically refers to supervised classification.Also,while the terms segmentation and partitioning are sometimes used as synonyms for clustering,these terms are frequently used for approaches outside the traditional bounds of cluster analysis.For example,the term partitioning is often used in connection with techniques that divide graphs into subgraphs and that are not strongly connected to clustering.Segmentation often refers to the division of data into groups using simple techniques;e.g., an image can be split into segments based only on pixel intensity and color,or people can be divided into groups based on their income.Nonetheless,some work in graph partitioning and in image and market segmentation is related to cluster analysis.8.1.2Different Types of ClusteringsAn entire collection of clusters is commonly referred to as a clustering,and in this section,we distinguish various types of clusterings:hierarchical(nested) versus partitional(unnested),exclusive versus overlapping versus fuzzy,and complete versus partial.Hierarchical versus Partitional The most commonly discussed distinc-tion among different types of clusterings is whether the set of clusters is nested492Chapter8Cluster Analysis:Basic Concepts and Algorithmsor unnested,or in more traditional terminology,hierarchical or partitional.A partitional clustering is simply a division of the set of data objects into non-overlapping subsets(clusters)such that each data object is in exactly one subset.Taken individually,each collection of clusters in Figures8.1(b–d)is a partitional clustering.If we permit clusters to have subclusters,then we obtain a hierarchical clustering,which is a set of nested clusters that are organized as a tree.Each node(cluster)in the tree(except for the leaf nodes)is the union of its children (subclusters),and the root of the tree is the cluster containing all the objects. Often,but not always,the leaves of the tree are singleton clusters of individual data objects.If we allow clusters to be nested,then one interpretation of Figure8.1(a)is that it has two subclusters(Figure8.1(b)),each of which,in turn,has three subclusters(Figure8.1(d)).The clusters shown in Figures8.1 (a–d),when taken in that order,also form a hierarchical(nested)clustering with,respectively,1,2,4,and6clusters on each level.Finally,note that a hierarchical clustering can be viewed as a sequence of partitional clusterings and a partitional clustering can be obtained by taking any member of that sequence;i.e.,by cutting the hierarchical tree at a particular level. Exclusive versus Overlapping versus Fuzzy The clusterings shown in Figure8.1are all exclusive,as they assign each object to a single cluster. There are many situations in which a point could reasonably be placed in more than one cluster,and these situations are better addressed by non-exclusive clustering.In the most general sense,an overlapping or non-exclusive clustering is used to reflect the fact that an object can simultaneously belong to more than one group(class).For instance,a person at a university can be both an enrolled student and an employee of the university.A non-exclusive clustering is also often used when,for example,an object is“between”two or more clusters and could reasonably be assigned to any of these clusters. Imagine a point halfway between two of the clusters of Figure8.1.Rather than make a somewhat arbitrary assignment of the object to a single cluster, it is placed in all of the“equally good”clusters.In a fuzzy clustering,every object belongs to every cluster with a mem-bership weight that is between0(absolutely doesn’t belong)and1(absolutely belongs).In other words,clusters are treated as fuzzy sets.(Mathematically, a fuzzy set is one in which an object belongs to any set with a weight that is between0and1.In fuzzy clustering,we often impose the additional con-straint that the sum of the weights for each object must equal1.)Similarly, probabilistic clustering techniques compute the probability with which each8.1Overview493 point belongs to each cluster,and these probabilities must also sum to1.Be-cause the membership weights or probabilities for any object sum to1,a fuzzy or probabilistic clustering does not address true multiclass situations,such as the case of a student employee,where an object belongs to multiple classes. Instead,these approaches are most appropriate for avoiding the arbitrariness of assigning an object to only one cluster when it may be close to several.In practice,a fuzzy or probabilistic clustering is often converted to an exclusive clustering by assigning each object to the cluster in which its membership weight or probability is highest.Complete versus Partial A complete clustering assigns every object to a cluster,whereas a partial clustering does not.The motivation for a partial clustering is that some objects in a data set may not belong to well-defined groups.Many times objects in the data set may represent noise,outliers,or “uninteresting background.”For example,some newspaper stories may share a common theme,such as global warming,while other stories are more generic or one-of-a-kind.Thus,tofind the important topics in last month’s stories,we may want to search only for clusters of documents that are tightly related by a common theme.In other cases,a complete clustering of the objects is desired. For example,an application that uses clustering to organize documents for browsing needs to guarantee that all documents can be browsed.8.1.3Different Types of ClustersClustering aims tofind useful groups of objects(clusters),where usefulness is defined by the goals of the data analysis.Not surprisingly,there are several different notions of a cluster that prove useful in practice.In order to visually illustrate the differences among these types of clusters,we use two-dimensional points,as shown in Figure8.2,as our data objects.We stress,however,that the types of clusters described here are equally valid for other kinds of data. Well-Separated A cluster is a set of objects in which each object is closer (or more similar)to every other object in the cluster than to any object not in the cluster.Sometimes a threshold is used to specify that all the objects in a cluster must be sufficiently close(or similar)to one another.This idealistic definition of a cluster is satisfied only when the data contains natural clusters that are quite far from each other.Figure8.2(a)gives an example of well-separated clusters that consists of two groups of points in a two-dimensional space.The distance between any two points in different groups is larger than494Chapter8Cluster Analysis:Basic Concepts and Algorithmsthe distance between any two points within a group.Well-separated clusters do not need to be globular,but can have any shape.Prototype-Based A cluster is a set of objects in which each object is closer (more similar)to the prototype that defines the cluster than to the prototype of any other cluster.For data with continuous attributes,the prototype of a cluster is often a centroid,i.e.,the average(mean)of all the points in the clus-ter.When a centroid is not meaningful,such as when the data has categorical attributes,the prototype is often a medoid,i.e.,the most representative point of a cluster.For many types of data,the prototype can be regarded as the most central point,and in such instances,we commonly refer to prototype-based clusters as center-based clusters.Not surprisingly,such clusters tend to be globular.Figure8.2(b)shows an example of center-based clusters. Graph-Based If the data is represented as a graph,where the nodes are objects and the links represent connections among objects(see Section2.1.2), then a cluster can be defined as a connected component;i.e.,a group of objects that are connected to one another,but that have no connection to objects outside the group.An important example of graph-based clusters are contiguity-based clusters,where two objects are connected only if they are within a specified distance of each other.This implies that each object in a contiguity-based cluster is closer to some other object in the cluster than to any point in a different cluster.Figure8.2(c)shows an example of such clusters for two-dimensional points.This definition of a cluster is useful when clusters are irregular or intertwined,but can have trouble when noise is present since, as illustrated by the two spherical clusters of Figure8.2(c),a small bridge of points can merge two distinct clusters.Other types of graph-based clusters are also possible.One such approach (Section8.3.2)defines a cluster as a clique;i.e.,a set of nodes in a graph that are completely connected to each other.Specifically,if we add connections between objects in the order of their distance from one another,a cluster is formed when a set of objects forms a clique.Like prototype-based clusters, such clusters tend to be globular.Density-Based A cluster is a dense region of objects that is surrounded by a region of low density.Figure8.2(d)shows some density-based clusters for data created by adding noise to the data of Figure8.2(c).The two circular clusters are not merged,as in Figure8.2(c),because the bridge between them fades into the noise.Likewise,the curve that is present in Figure8.2(c)also8.1Overview495 fades into the noise and does not form a cluster in Figure8.2(d).A density-based definition of a cluster is often employed when the clusters are irregular or intertwined,and when noise and outliers are present.By contrast,a contiguity-based definition of a cluster would not work well for the data of Figure8.2(d) since the noise would tend to form bridges between clusters.Shared-Property(Conceptual Clusters)More generally,we can define a cluster as a set of objects that share some property.This definition encom-passes all the previous definitions of a cluster;e.g.,objects in a center-based cluster share the property that they are all closest to the same centroid or medoid.However,the shared-property approach also includes new types of clusters.Consider the clusters shown in Figure8.2(e).A triangular area (cluster)is adjacent to a rectangular one,and there are two intertwined circles (clusters).In both cases,a clustering algorithm would need a very specific concept of a cluster to successfully detect these clusters.The process offind-ing such clusters is called conceptual clustering.However,too sophisticated a notion of a cluster would take us into the area of pattern recognition,and thus,we only consider simpler types of clusters in this book.Road MapIn this chapter,we use the following three simple,but important techniques to introduce many of the concepts involved in cluster analysis.•K-means.This is a prototype-based,partitional clustering technique that attempts tofind a user-specified number of clusters(K),which are represented by their centroids.•Agglomerative Hierarchical Clustering.This clustering approach refers to a collection of closely related clustering techniques that producea hierarchical clustering by starting with each point as a singleton clusterand then repeatedly merging the two closest clusters until a single,all-encompassing cluster remains.Some of these techniques have a natural interpretation in terms of graph-based clustering,while others have an interpretation in terms of a prototype-based approach.•DBSCAN.This is a density-based clustering algorithm that producesa partitional clustering,in which the number of clusters is automaticallydetermined by the algorithm.Points in low-density regions are classi-fied as noise and omitted;thus,DBSCAN does not produce a complete clustering.Chapter 8Cluster Analysis:Basic Concepts and Algorithms (a)Well-separated clusters.Eachpoint is closer to all of the points in itscluster than to any point in anothercluster.(b)Center-based clusters.Each point is closer to the center of its cluster than to the center of any other cluster.(c)Contiguity-based clusters.Eachpoint is closer to at least one pointin its cluster than to any point inanother cluster.(d)Density-based clusters.Clus-ters are regions of high density sep-arated by regions of low density.(e)Conceptual clusters.Points in a cluster share some generalproperty that derives from the entire set of points.(Points in theintersection of the circles belong to both.)Figure 8.2.Different types of clusters as illustrated by sets of two-dimensional points.8.2K-meansPrototype-based clustering techniques create a one-level partitioning of the data objects.There are a number of such techniques,but two of the most prominent are K-means and K-medoid.K-means defines a prototype in terms of a centroid,which is usually the mean of a group of points,and is typically8.2K-means497 applied to objects in a continuous n-dimensional space.K-medoid defines a prototype in terms of a medoid,which is the most representative point for a group of points,and can be applied to a wide range of data since it requires only a proximity measure for a pair of objects.While a centroid almost never corresponds to an actual data point,a medoid,by its definition,must be an actual data point.In this section,we will focus solely on K-means,which is one of the oldest and most widely used clustering algorithms.8.2.1The Basic K-means AlgorithmThe K-means clustering technique is simple,and we begin with a description of the basic algorithm.Wefirst choose K initial centroids,where K is a user-specified parameter,namely,the number of clusters desired.Each point is then assigned to the closest centroid,and each collection of points assigned to a centroid is a cluster.The centroid of each cluster is then updated based on the points assigned to the cluster.We repeat the assignment and update steps until no point changes clusters,or equivalently,until the centroids remain the same.K-means is formally described by Algorithm8.1.The operation of K-means is illustrated in Figure8.3,which shows how,starting from three centroids,the final clusters are found in four assignment-update steps.In these and other figures displaying K-means clustering,each subfigure shows(1)the centroids at the start of the iteration and(2)the assignment of the points to those centroids.The centroids are indicated by the“+”symbol;all points belonging to the same cluster have the same marker shape.1:Select K points as initial centroids.2:repeat3:Form K clusters by assigning each point to its closest centroid.4:Recompute the centroid of each cluster.5:until Centroids do not change.In thefirst step,shown in Figure8.3(a),points are assigned to the initial centroids,which are all in the larger group of points.For this example,we use the mean as the centroid.After points are assigned to a centroid,the centroid is then updated.Again,thefigure for each step shows the centroid at the beginning of the step and the assignment of points to those centroids.In the second step,points are assigned to the updated centroids,and the centroids498Chapter8Cluster Analysis:Basic Concepts and Algorithms(a)Iteration1.(b)Iteration2.(c)Iteration3.(d)Iteration4.ing the K-means algorithm tofind three clusters in sample data.are updated again.In steps2,3,and4,which are shown in Figures8.3(b), (c),and(d),respectively,two of the centroids move to the two small groups of points at the bottom of thefigures.When the K-means algorithm terminates in Figure8.3(d),because no more changes occur,the centroids have identified the natural groupings of points.For some combinations of proximity functions and types of centroids,K-means always converges to a solution;i.e.,K-means reaches a state in which no points are shifting from one cluster to another,and hence,the centroids don’t change.Because most of the convergence occurs in the early steps,however, the condition on line5of Algorithm8.1is often replaced by a weaker condition, e.g.,repeat until only1%of the points change clusters.We consider each of the steps in the basic K-means algorithm in more detail and then provide an analysis of the algorithm’s space and time complexity. Assigning Points to the Closest CentroidTo assign a point to the closest centroid,we need a proximity measure that quantifies the notion of“closest”for the specific data under consideration. Euclidean(L2)distance is often used for data points in Euclidean space,while cosine similarity is more appropriate for documents.However,there may be several types of proximity measures that are appropriate for a given type of data.For example,Manhattan(L1)distance can be used for Euclidean data, while the Jaccard measure is often employed for documents.Usually,the similarity measures used for K-means are relatively simple since the algorithm repeatedly calculates the similarity of each point to each centroid.In some cases,however,such as when the data is in low-dimensional8.2K-means499Table8.1.Table of notation.Symbol Descriptionx An object.C i The i th cluster.c i The centroid of cluster C i.c The centroid of all points.m i The number of objects in the i th cluster.m The number of objects in the data set.K The number of clusters.Euclidean space,it is possible to avoid computing many of the similarities, thus significantly speeding up the K-means algorithm.Bisecting K-means (described in Section8.2.3)is another approach that speeds up K-means by reducing the number of similarities computed.Centroids and Objective FunctionsStep4of the K-means algorithm was stated rather generally as“recompute the centroid of each cluster,”since the centroid can vary,depending on the proximity measure for the data and the goal of the clustering.The goal of the clustering is typically expressed by an objective function that depends on the proximities of the points to one another or to the cluster centroids;e.g., minimize the squared distance of each point to its closest centroid.We illus-trate this with two examples.However,the key point is this:once we have specified a proximity measure and an objective function,the centroid that we should choose can often be determined mathematically.We provide mathe-matical details in Section8.2.6,and provide a non-mathematical discussion of this observation here.Data in Euclidean Space Consider data whose proximity measure is Eu-clidean distance.For our objective function,which measures the quality of a clustering,we use the sum of the squared error(SSE),which is also known as scatter.In other words,we calculate the error of each data point,i.e.,its Euclidean distance to the closest centroid,and then compute the total sum of the squared errors.Given two different sets of clusters that are produced by two different runs of K-means,we prefer the one with the smallest squared error since this means that the prototypes(centroids)of this clustering are a better representation of the points in their ing the notation in Table8.1,the SSE is formally defined as follows:。
聚类算法英文专业术语

聚类算法英文专业术语1. 聚类 (Clustering)2. 距离度量 (Distance Metric)3. 相似度度量 (Similarity Metric)4. 皮尔逊相关系数 (Pearson Correlation Coefficient)5. 欧几里得距离 (Euclidean Distance)6. 曼哈顿距离 (Manhattan Distance)7. 切比雪夫距离 (Chebyshev Distance)8. 余弦相似度 (Cosine Similarity)9. 层次聚类 (Hierarchical Clustering)10. 分层聚类 (Divisive Clustering)11. 凝聚聚类 (Agglomerative Clustering)12. K均值聚类 (K-Means Clustering)13. 高斯混合模型聚类 (Gaussian Mixture Model Clustering)14. 密度聚类 (Density-Based Clustering)15. DBSCAN (Density-Based Spatial Clustering of Applications with Noise)16. OPTICS (Ordering Points To Identify the Clustering Structure)17. Mean Shift18. 聚类评估指标 (Clustering Evaluation Metrics)19. 轮廓系数 (Silhouette Coefficient)20. Calinski-Harabasz指数 (Calinski-Harabasz Index)21. Davies-Bouldin指数 (Davies-Bouldin Index)22. 聚类中心 (Cluster Center)23. 聚类半径 (Cluster Radius)24. 噪声点 (Noise Point)25. 簇内差异 (Within-Cluster Variation)26. 簇间差异 (Between-Cluster Variation)。
Survey of clustering data mining techniques

A Survey of Clustering Data Mining TechniquesPavel BerkhinYahoo!,Inc.pberkhin@Summary.Clustering is the division of data into groups of similar objects.It dis-regards some details in exchange for data simplifirmally,clustering can be viewed as data modeling concisely summarizing the data,and,therefore,it re-lates to many disciplines from statistics to numerical analysis.Clustering plays an important role in a broad range of applications,from information retrieval to CRM. Such applications usually deal with large datasets and many attributes.Exploration of such data is a subject of data mining.This survey concentrates on clustering algorithms from a data mining perspective.1IntroductionThe goal of this survey is to provide a comprehensive review of different clus-tering techniques in data mining.Clustering is a division of data into groups of similar objects.Each group,called a cluster,consists of objects that are similar to one another and dissimilar to objects of other groups.When repre-senting data with fewer clusters necessarily loses certainfine details(akin to lossy data compression),but achieves simplification.It represents many data objects by few clusters,and hence,it models data by its clusters.Data mod-eling puts clustering in a historical perspective rooted in mathematics,sta-tistics,and numerical analysis.From a machine learning perspective clusters correspond to hidden patterns,the search for clusters is unsupervised learn-ing,and the resulting system represents a data concept.Therefore,clustering is unsupervised learning of a hidden data concept.Data mining applications add to a general picture three complications:(a)large databases,(b)many attributes,(c)attributes of different types.This imposes on a data analysis se-vere computational requirements.Data mining applications include scientific data exploration,information retrieval,text mining,spatial databases,Web analysis,CRM,marketing,medical diagnostics,computational biology,and many others.They present real challenges to classic clustering algorithms. These challenges led to the emergence of powerful broadly applicable data2Pavel Berkhinmining clustering methods developed on the foundation of classic techniques.They are subject of this survey.1.1NotationsTo fix the context and clarify terminology,consider a dataset X consisting of data points (i.e.,objects ,instances ,cases ,patterns ,tuples ,transactions )x i =(x i 1,···,x id ),i =1:N ,in attribute space A ,where each component x il ∈A l ,l =1:d ,is a numerical or nominal categorical attribute (i.e.,feature ,variable ,dimension ,component ,field ).For a discussion of attribute data types see [106].Such point-by-attribute data format conceptually corresponds to a N ×d matrix and is used by a majority of algorithms reviewed below.However,data of other formats,such as variable length sequences and heterogeneous data,are not uncommon.The simplest subset in an attribute space is a direct Cartesian product of sub-ranges C = C l ⊂A ,C l ⊂A l ,called a segment (i.e.,cube ,cell ,region ).A unit is an elementary segment whose sub-ranges consist of a single category value,or of a small numerical bin.Describing the numbers of data points per every unit represents an extreme case of clustering,a histogram .This is a very expensive representation,and not a very revealing er driven segmentation is another commonly used practice in data exploration that utilizes expert knowledge regarding the importance of certain sub-domains.Unlike segmentation,clustering is assumed to be automatic,and so it is a machine learning technique.The ultimate goal of clustering is to assign points to a finite system of k subsets (clusters).Usually (but not always)subsets do not intersect,and their union is equal to a full dataset with the possible exception of outliersX =C 1 ··· C k C outliers ,C i C j =0,i =j.1.2Clustering Bibliography at GlanceGeneral references regarding clustering include [110],[205],[116],[131],[63],[72],[165],[119],[75],[141],[107],[91].A very good introduction to contem-porary data mining clustering techniques can be found in the textbook [106].There is a close relationship between clustering and many other fields.Clustering has always been used in statistics [10]and science [158].The clas-sic introduction into pattern recognition framework is given in [64].Typical applications include speech and character recognition.Machine learning clus-tering algorithms were applied to image segmentation and computer vision[117].For statistical approaches to pattern recognition see [56]and [85].Clus-tering can be viewed as a density estimation problem.This is the subject of traditional multivariate statistical estimation [197].Clustering is also widelyA Survey of Clustering Data Mining Techniques3 used for data compression in image processing,which is also known as vec-tor quantization[89].Datafitting in numerical analysis provides still another venue in data modeling[53].This survey’s emphasis is on clustering in data mining.Such clustering is characterized by large datasets with many attributes of different types. Though we do not even try to review particular applications,many important ideas are related to the specificfields.Clustering in data mining was brought to life by intense developments in information retrieval and text mining[52], [206],[58],spatial database applications,for example,GIS or astronomical data,[223],[189],[68],sequence and heterogeneous data analysis[43],Web applications[48],[111],[81],DNA analysis in computational biology[23],and many others.They resulted in a large amount of application-specific devel-opments,but also in some general techniques.These techniques and classic clustering algorithms that relate to them are surveyed below.1.3Plan of Further PresentationClassification of clustering algorithms is neither straightforward,nor canoni-cal.In reality,different classes of algorithms overlap.Traditionally clustering techniques are broadly divided in hierarchical and partitioning.Hierarchical clustering is further subdivided into agglomerative and divisive.The basics of hierarchical clustering include Lance-Williams formula,idea of conceptual clustering,now classic algorithms SLINK,COBWEB,as well as newer algo-rithms CURE and CHAMELEON.We survey these algorithms in the section Hierarchical Clustering.While hierarchical algorithms gradually(dis)assemble points into clusters (as crystals grow),partitioning algorithms learn clusters directly.In doing so they try to discover clusters either by iteratively relocating points between subsets,or by identifying areas heavily populated with data.Algorithms of thefirst kind are called Partitioning Relocation Clustering. They are further classified into probabilistic clustering(EM framework,al-gorithms SNOB,AUTOCLASS,MCLUST),k-medoids methods(algorithms PAM,CLARA,CLARANS,and its extension),and k-means methods(differ-ent schemes,initialization,optimization,harmonic means,extensions).Such methods concentrate on how well pointsfit into their clusters and tend to build clusters of proper convex shapes.Partitioning algorithms of the second type are surveyed in the section Density-Based Partitioning.They attempt to discover dense connected com-ponents of data,which areflexible in terms of their shape.Density-based connectivity is used in the algorithms DBSCAN,OPTICS,DBCLASD,while the algorithm DENCLUE exploits space density functions.These algorithms are less sensitive to outliers and can discover clusters of irregular shape.They usually work with low-dimensional numerical data,known as spatial data. Spatial objects could include not only points,but also geometrically extended objects(algorithm GDBSCAN).4Pavel BerkhinSome algorithms work with data indirectly by constructing summaries of data over the attribute space subsets.They perform space segmentation and then aggregate appropriate segments.We discuss them in the section Grid-Based Methods.They frequently use hierarchical agglomeration as one phase of processing.Algorithms BANG,STING,WaveCluster,and FC are discussed in this section.Grid-based methods are fast and handle outliers well.Grid-based methodology is also used as an intermediate step in many other algorithms (for example,CLIQUE,MAFIA).Categorical data is intimately connected with transactional databases.The concept of a similarity alone is not sufficient for clustering such data.The idea of categorical data co-occurrence comes to the rescue.The algorithms ROCK,SNN,and CACTUS are surveyed in the section Co-Occurrence of Categorical Data.The situation gets even more aggravated with the growth of the number of items involved.To help with this problem the effort is shifted from data clustering to pre-clustering of items or categorical attribute values. Development based on hyper-graph partitioning and the algorithm STIRR exemplify this approach.Many other clustering techniques are developed,primarily in machine learning,that either have theoretical significance,are used traditionally out-side the data mining community,or do notfit in previously outlined categories. The boundary is blurred.In the section Other Developments we discuss the emerging direction of constraint-based clustering,the important researchfield of graph partitioning,and the relationship of clustering to supervised learning, gradient descent,artificial neural networks,and evolutionary methods.Data Mining primarily works with large databases.Clustering large datasets presents scalability problems reviewed in the section Scalability and VLDB Extensions.Here we talk about algorithms like DIGNET,about BIRCH and other data squashing techniques,and about Hoffding or Chernoffbounds.Another trait of real-life data is high dimensionality.Corresponding de-velopments are surveyed in the section Clustering High Dimensional Data. The trouble comes from a decrease in metric separation when the dimension grows.One approach to dimensionality reduction uses attributes transforma-tions(DFT,PCA,wavelets).Another way to address the problem is through subspace clustering(algorithms CLIQUE,MAFIA,ENCLUS,OPTIGRID, PROCLUS,ORCLUS).Still another approach clusters attributes in groups and uses their derived proxies to cluster objects.This double clustering is known as co-clustering.Issues common to different clustering methods are overviewed in the sec-tion General Algorithmic Issues.We talk about assessment of results,de-termination of appropriate number of clusters to build,data preprocessing, proximity measures,and handling of outliers.For reader’s convenience we provide a classification of clustering algorithms closely followed by this survey:•Hierarchical MethodsA Survey of Clustering Data Mining Techniques5Agglomerative AlgorithmsDivisive Algorithms•Partitioning Relocation MethodsProbabilistic ClusteringK-medoids MethodsK-means Methods•Density-Based Partitioning MethodsDensity-Based Connectivity ClusteringDensity Functions Clustering•Grid-Based Methods•Methods Based on Co-Occurrence of Categorical Data•Other Clustering TechniquesConstraint-Based ClusteringGraph PartitioningClustering Algorithms and Supervised LearningClustering Algorithms in Machine Learning•Scalable Clustering Algorithms•Algorithms For High Dimensional DataSubspace ClusteringCo-Clustering Techniques1.4Important IssuesThe properties of clustering algorithms we are primarily concerned with in data mining include:•Type of attributes algorithm can handle•Scalability to large datasets•Ability to work with high dimensional data•Ability tofind clusters of irregular shape•Handling outliers•Time complexity(we frequently simply use the term complexity)•Data order dependency•Labeling or assignment(hard or strict vs.soft or fuzzy)•Reliance on a priori knowledge and user defined parameters •Interpretability of resultsRealistically,with every algorithm we discuss only some of these properties. The list is in no way exhaustive.For example,as appropriate,we also discuss algorithms ability to work in pre-defined memory buffer,to restart,and to provide an intermediate solution.6Pavel Berkhin2Hierarchical ClusteringHierarchical clustering builds a cluster hierarchy or a tree of clusters,also known as a dendrogram.Every cluster node contains child clusters;sibling clusters partition the points covered by their common parent.Such an ap-proach allows exploring data on different levels of granularity.Hierarchical clustering methods are categorized into agglomerative(bottom-up)and divi-sive(top-down)[116],[131].An agglomerative clustering starts with one-point (singleton)clusters and recursively merges two or more of the most similar clusters.A divisive clustering starts with a single cluster containing all data points and recursively splits the most appropriate cluster.The process contin-ues until a stopping criterion(frequently,the requested number k of clusters) is achieved.Advantages of hierarchical clustering include:•Flexibility regarding the level of granularity•Ease of handling any form of similarity or distance•Applicability to any attribute typesDisadvantages of hierarchical clustering are related to:•Vagueness of termination criteria•Most hierarchical algorithms do not revisit(intermediate)clusters once constructed.The classic approaches to hierarchical clustering are presented in the sub-section Linkage Metrics.Hierarchical clustering based on linkage metrics re-sults in clusters of proper(convex)shapes.Active contemporary efforts to build cluster systems that incorporate our intuitive concept of clusters as con-nected components of arbitrary shape,including the algorithms CURE and CHAMELEON,are surveyed in the subsection Hierarchical Clusters of Arbi-trary Shapes.Divisive techniques based on binary taxonomies are presented in the subsection Binary Divisive Partitioning.The subsection Other Devel-opments contains information related to incremental learning,model-based clustering,and cluster refinement.In hierarchical clustering our regular point-by-attribute data representa-tion frequently is of secondary importance.Instead,hierarchical clustering frequently deals with the N×N matrix of distances(dissimilarities)or sim-ilarities between training points sometimes called a connectivity matrix.So-called linkage metrics are constructed from elements of this matrix.The re-quirement of keeping a connectivity matrix in memory is unrealistic.To relax this limitation different techniques are used to sparsify(introduce zeros into) the connectivity matrix.This can be done by omitting entries smaller than a certain threshold,by using only a certain subset of data representatives,or by keeping with each point only a certain number of its nearest neighbors(for nearest neighbor chains see[177]).Notice that the way we process the original (dis)similarity matrix and construct a linkage metric reflects our a priori ideas about the data model.A Survey of Clustering Data Mining Techniques7With the(sparsified)connectivity matrix we can associate the weighted connectivity graph G(X,E)whose vertices X are data points,and edges E and their weights are defined by the connectivity matrix.This establishes a connection between hierarchical clustering and graph partitioning.One of the most striking developments in hierarchical clustering is the algorithm BIRCH.It is discussed in the section Scalable VLDB Extensions.Hierarchical clustering initializes a cluster system as a set of singleton clusters(agglomerative case)or a single cluster of all points(divisive case) and proceeds iteratively merging or splitting the most appropriate cluster(s) until the stopping criterion is achieved.The appropriateness of a cluster(s) for merging or splitting depends on the(dis)similarity of cluster(s)elements. This reflects a general presumption that clusters consist of similar points.An important example of dissimilarity between two points is the distance between them.To merge or split subsets of points rather than individual points,the dis-tance between individual points has to be generalized to the distance between subsets.Such a derived proximity measure is called a linkage metric.The type of a linkage metric significantly affects hierarchical algorithms,because it re-flects a particular concept of closeness and connectivity.Major inter-cluster linkage metrics[171],[177]include single link,average link,and complete link. The underlying dissimilarity measure(usually,distance)is computed for every pair of nodes with one node in thefirst set and another node in the second set.A specific operation such as minimum(single link),average(average link),or maximum(complete link)is applied to pair-wise dissimilarity measures:d(C1,C2)=Op{d(x,y),x∈C1,y∈C2}Early examples include the algorithm SLINK[199],which implements single link(Op=min),Voorhees’method[215],which implements average link (Op=Avr),and the algorithm CLINK[55],which implements complete link (Op=max).It is related to the problem offinding the Euclidean minimal spanning tree[224]and has O(N2)complexity.The methods using inter-cluster distances defined in terms of pairs of nodes(one in each respective cluster)are called graph methods.They do not use any cluster representation other than a set of points.This name naturally relates to the connectivity graph G(X,E)introduced above,because every data partition corresponds to a graph partition.Such methods can be augmented by so-called geometric methods in which a cluster is represented by its central point.Under the assumption of numerical attributes,the center point is defined as a centroid or an average of two cluster centroids subject to agglomeration.It results in centroid,median,and minimum variance linkage metrics.All of the above linkage metrics can be derived from the Lance-Williams updating formula[145],d(C iC j,C k)=a(i)d(C i,C k)+a(j)d(C j,C k)+b·d(C i,C j)+c|d(C i,C k)−d(C j,C k)|.8Pavel BerkhinHere a,b,c are coefficients corresponding to a particular linkage.This formula expresses a linkage metric between a union of the two clusters and the third cluster in terms of underlying nodes.The Lance-Williams formula is crucial to making the dis(similarity)computations feasible.Surveys of linkage metrics can be found in [170][54].When distance is used as a base measure,linkage metrics capture inter-cluster proximity.However,a similarity-based view that results in intra-cluster connectivity considerations is also used,for example,in the original average link agglomeration (Group-Average Method)[116].Under reasonable assumptions,such as reducibility condition (graph meth-ods satisfy this condition),linkage metrics methods suffer from O N 2 time complexity [177].Despite the unfavorable time complexity,these algorithms are widely used.As an example,the algorithm AGNES (AGlomerative NESt-ing)[131]is used in S-Plus.When the connectivity N ×N matrix is sparsified,graph methods directly dealing with the connectivity graph G can be used.In particular,hierarchical divisive MST (Minimum Spanning Tree)algorithm is based on graph parti-tioning [116].2.1Hierarchical Clusters of Arbitrary ShapesFor spatial data,linkage metrics based on Euclidean distance naturally gener-ate clusters of convex shapes.Meanwhile,visual inspection of spatial images frequently discovers clusters with curvy appearance.Guha et al.[99]introduced the hierarchical agglomerative clustering algo-rithm CURE (Clustering Using REpresentatives).This algorithm has a num-ber of novel features of general importance.It takes special steps to handle outliers and to provide labeling in assignment stage.It also uses two techniques to achieve scalability:data sampling (section 8),and data partitioning.CURE creates p partitions,so that fine granularity clusters are constructed in parti-tions first.A major feature of CURE is that it represents a cluster by a fixed number,c ,of points scattered around it.The distance between two clusters used in the agglomerative process is the minimum of distances between two scattered representatives.Therefore,CURE takes a middle approach between the graph (all-points)methods and the geometric (one centroid)methods.Single and average link closeness are replaced by representatives’aggregate closeness.Selecting representatives scattered around a cluster makes it pos-sible to cover non-spherical shapes.As before,agglomeration continues until the requested number k of clusters is achieved.CURE employs one additional trick:originally selected scattered points are shrunk to the geometric centroid of the cluster by a user-specified factor α.Shrinkage suppresses the affect of outliers;outliers happen to be located further from the cluster centroid than the other scattered representatives.CURE is capable of finding clusters of different shapes and sizes,and it is insensitive to outliers.Because CURE uses sampling,estimation of its complexity is not straightforward.For low-dimensional data authors provide a complexity estimate of O (N 2sample )definedA Survey of Clustering Data Mining Techniques9 in terms of a sample size.More exact bounds depend on input parameters: shrink factorα,number of representative points c,number of partitions p,and a sample size.Figure1(a)illustrates agglomeration in CURE.Three clusters, each with three representatives,are shown before and after the merge and shrinkage.Two closest representatives are connected.While the algorithm CURE works with numerical attributes(particularly low dimensional spatial data),the algorithm ROCK developed by the same researchers[100]targets hierarchical agglomerative clustering for categorical attributes.It is reviewed in the section Co-Occurrence of Categorical Data.The hierarchical agglomerative algorithm CHAMELEON[127]uses the connectivity graph G corresponding to the K-nearest neighbor model spar-sification of the connectivity matrix:the edges of K most similar points to any given point are preserved,the rest are pruned.CHAMELEON has two stages.In thefirst stage small tight clusters are built to ignite the second stage.This involves a graph partitioning[129].In the second stage agglomer-ative process is performed.It utilizes measures of relative inter-connectivity RI(C i,C j)and relative closeness RC(C i,C j);both are locally normalized by internal interconnectivity and closeness of clusters C i and C j.In this sense the modeling is dynamic:it depends on data locally.Normalization involves certain non-obvious graph operations[129].CHAMELEON relies heavily on graph partitioning implemented in the library HMETIS(see the section6). Agglomerative process depends on user provided thresholds.A decision to merge is made based on the combinationRI(C i,C j)·RC(C i,C j)αof local measures.The algorithm does not depend on assumptions about the data model.It has been proven tofind clusters of different shapes,densities, and sizes in2D(two-dimensional)space.It has a complexity of O(Nm+ Nlog(N)+m2log(m),where m is the number of sub-clusters built during the first initialization phase.Figure1(b)(analogous to the one in[127])clarifies the difference with CURE.It presents a choice of four clusters(a)-(d)for a merge.While CURE would merge clusters(a)and(b),CHAMELEON makes intuitively better choice of merging(c)and(d).2.2Binary Divisive PartitioningIn linguistics,information retrieval,and document clustering applications bi-nary taxonomies are very useful.Linear algebra methods,based on singular value decomposition(SVD)are used for this purpose in collaborativefilter-ing and information retrieval[26].Application of SVD to hierarchical divisive clustering of document collections resulted in the PDDP(Principal Direction Divisive Partitioning)algorithm[31].In our notations,object x is a docu-ment,l th attribute corresponds to a word(index term),and a matrix X entry x il is a measure(e.g.TF-IDF)of l-term frequency in a document x.PDDP constructs SVD decomposition of the matrix10Pavel Berkhin(a)Algorithm CURE (b)Algorithm CHAMELEONFig.1.Agglomeration in Clusters of Arbitrary Shapes(X −e ¯x ),¯x =1Ni =1:N x i ,e =(1,...,1)T .This algorithm bisects data in Euclidean space by a hyperplane that passes through data centroid orthogonal to the eigenvector with the largest singular value.A k -way split is also possible if the k largest singular values are consid-ered.Bisecting is a good way to categorize documents and it yields a binary tree.When k -means (2-means)is used for bisecting,the dividing hyperplane is orthogonal to the line connecting the two centroids.The comparative study of SVD vs.k -means approaches [191]can be used for further references.Hier-archical divisive bisecting k -means was proven [206]to be preferable to PDDP for document clustering.While PDDP or 2-means are concerned with how to split a cluster,the problem of which cluster to split is also important.Simple strategies are:(1)split each node at a given level,(2)split the cluster with highest cardinality,and,(3)split the cluster with the largest intra-cluster variance.All three strategies have problems.For a more detailed analysis of this subject and better strategies,see [192].2.3Other DevelopmentsOne of early agglomerative clustering algorithms,Ward’s method [222],is based not on linkage metric,but on an objective function used in k -means.The merger decision is viewed in terms of its effect on the objective function.The popular hierarchical clustering algorithm for categorical data COB-WEB [77]has two very important qualities.First,it utilizes incremental learn-ing.Instead of following divisive or agglomerative approaches,it dynamically builds a dendrogram by processing one data point at a time.Second,COB-WEB is an example of conceptual or model-based learning.This means that each cluster is considered as a model that can be described intrinsically,rather than as a collection of points assigned to it.COBWEB’s dendrogram is calleda classification tree.Each tree node(cluster)C is associated with the condi-tional probabilities for categorical attribute-values pairs,P r(x l=νlp|C),l=1:d,p=1:|A l|.This easily can be recognized as a C-specific Na¨ıve Bayes classifier.During the classification tree construction,every new point is descended along the tree and the tree is potentially updated(by an insert/split/merge/create op-eration).Decisions are based on the category utility[49]CU{C1,...,C k}=1j=1:kCU(C j)CU(C j)=l,p(P r(x l=νlp|C j)2−(P r(x l=νlp)2.Category utility is similar to the GINI index.It rewards clusters C j for in-creases in predictability of the categorical attribute valuesνlp.Being incre-mental,COBWEB is fast with a complexity of O(tN),though it depends non-linearly on tree characteristics packed into a constant t.There is a similar incremental hierarchical algorithm for all numerical attributes called CLAS-SIT[88].CLASSIT associates normal distributions with cluster nodes.Both algorithms can result in highly unbalanced trees.Chiu et al.[47]proposed another conceptual or model-based approach to hierarchical clustering.This development contains several different use-ful features,such as the extension of scalability preprocessing to categori-cal attributes,outliers handling,and a two-step strategy for monitoring the number of clusters including BIC(defined below).A model associated with a cluster covers both numerical and categorical attributes and constitutes a blend of Gaussian and multinomial models.Denote corresponding multivari-ate parameters byθ.With every cluster C we associate a logarithm of its (classification)likelihoodl C=x i∈Clog(p(x i|θ))The algorithm uses maximum likelihood estimates for parameterθ.The dis-tance between two clusters is defined(instead of linkage metric)as a decrease in log-likelihoodd(C1,C2)=l C1+l C2−l C1∪C2caused by merging of the two clusters under consideration.The agglomerative process continues until the stopping criterion is satisfied.As such,determina-tion of the best k is automatic.This algorithm has the commercial implemen-tation(in SPSS Clementine).The complexity of the algorithm is linear in N for the summarization phase.Traditional hierarchical clustering does not change points membership in once assigned clusters due to its greedy approach:after a merge or a split is selected it is not refined.Though COBWEB does reconsider its decisions,its。
一项科学实验英语作文

A scientific experiment is an investigative procedure that aims to test a hypothesis and explore the principles governing the natural world.Heres a detailed account of a typical scientific experiment,written in English:1.Introduction:The experiment begins with a clear statement of the problem or question that needs to be addressed.This is often followed by a brief literature review to establish the context and significance of the research.2.Hypothesis:Based on existing knowledge and observations,a hypothesis is formulated. This is a testable statement that predicts the outcome of the experiment.3.Materials and Methods:This section outlines the specific materials needed for the experiment and the stepbystep procedure that will be followed.It is crucial for the success of the experiment that the methods are detailed and replicable.4.Safety Precautions:Before starting the experiment,it is important to consider and communicate any safety precautions necessary to protect the experimenter and the environment.5.Experimental Procedure:The actual steps of the experiment are carried out as described in the materials and methods section.This may involve setting up equipment, preparing samples,and conducting trials.6.Data Collection:Throughout the experiment,data is collected.This could be in the form of measurements,observations,or recordings.It is essential to record data accurately and systematically.7.Analysis:Once the data is collected,it is analyzed to determine if it supports or refutes the hypothesis.This may involve statistical analysis,graphical representation,or qualitative interpretation.8.Results:The findings of the experiment are presented in this section.The results should be objective and based solely on the data collected.9.Discussion:This section interprets the results in the context of the original hypothesis and the broader field of study.It discusses the implications of the findings,any anomalies, and potential sources of error.10.Conclusion:The experiment concludes with a summary of the findings and their significance.It may also suggest areas for further research or improvements to theexperimental design.11.References:Any sources of information,such as scientific articles or textbooks,that were referenced during the experiment are cited in this section.12.Appendices:Additional materials,such as raw data,detailed methodological descriptions,or supplementary figures,can be included in the appendices.An example of a scientific experiment could be investigating the effects of different light conditions on plant growth.The hypothesis might be that plants grow faster under higher light intensity.The experiment would involve growing plants under varying light conditions and measuring their growth over a set period.The results would then be analyzed to see if they support the hypothesis.Remember,the key to a successful scientific experiment is careful planning,precise execution,and thorough analysis of the results.。
clustering-techniques

• Minimal requirements for domain knowledge to determine input parameters
• Able to deal with noise and outliers • Insensitive to order of input records • High dimensionality • Incorporation of user-specified constraints • Interpretability and usability
2014-5-5 Intelligent Technology 10
Interval-scaled variables--2
Another example is asking a patient to describe their pain on a 1-10 scale where 1 means minimal pain and 10 means the worst pain the person has ever suffered. Even though the distances between numbers on the scale are constant and equal, a pain score of 8 does not mean that the pain is twice as bad as a score of 4. Remark: continuous measurement of a roughly linear scale
where i = (xi1, xi2, …, xip) and j = (xj1, xj2, …, xjp) are two pdimensional data objects, and q is a positive integer • If q = 1, d is Manhattan distance
数据挖掘导论第5课数据聚类技术

where m f 1 (x1 f x2 f ... xnf ) n
Calculate the
.
xif m f zif sf
standardized measurement (z-score)
Using mean absolute deviation is more robust than using
Clustering: Rich Applications and Multidisciplinary Efforts
Pattern Recognition
Spatial Data Analysis
Create thematic maps
in GIS by clustering feature spaces
Dissimilarity Between Binary Object j 1 0 Variables
Object i
sum a b cd p
A contingency table for binary data
1 0
a c
b d
sum a c b d
Distance measure for symmetric
The quality of a clustering result depends on both the
similarity measure used by the method and its implementation
The quality of a clustering method is also measured by its ability to discover some or all of the hidden patterns
高三英语学术研究方法创新思路单选题30题

高三英语学术研究方法创新思路单选题30题1. In academic research, a hypothesis is a(n) ______ that needs to be tested.A. ideaB. factC. resultD. example答案:A。
本题考查学术研究中“hypothesis(假设)”的概念。
选项A“idea(想法、主意)”符合“hypothesis”需要被测试的特点;选项B“fact( 事实)”是已经确定的,无需测试;选项C“result( 结果)”是研究得出的,不是先提出的;选项D“example( 例子)”与“hypothesis”的概念不符。
2. When conducting research, collecting data is an important step. Which of the following is NOT a common way of collecting data?A. InterviewsB. GuessingC. ObservationsD. Surveys答案:B。
本题考查学术研究中收集数据的常见方法。
选项A“Interviews( 访谈)”、选项C“Observations( 观察)”和选项D“Surveys 调查)”都是常见的数据收集方式;选项B“Guessing( 猜测)”不是科学的收集数据的方法。
3. The purpose of a literature review in academic research is to ______.A. show off one's reading skillsB. summarize existing knowledge on a topicC. copy other people's researchD. make the research longer答案:B。
BClustLonG 软件包说明书

Package‘BClustLonG’October12,2022Type PackageTitle A Dirichlet Process Mixture Model for Clustering LongitudinalGene Expression DataVersion0.1.3Author Jiehuan Sun[aut,cre],Jose D.Herazo-Maya[aut],Naftali Kaminski[aut],Hongyu Zhao[aut],and Joshua L.Warren[aut], Maintainer Jiehuan Sun<*********************>Description Many clustering methods have been proposed,butmost of them cannot work for longitudinal gene expression data.'BClustLonG'is a package that allows us to perform clustering analysis forlongitudinal gene expression data.It adopts a linear-mixed effects frameworkto model the trajectory of genes over time,while clustering is jointlyconducted based on the regression coefficients obtained from all genes.To account for the correlations among genes and alleviate thehigh dimensionality challenges,factor analysis models are adoptedfor the regression coefficients.The Dirichlet process prior distributionis utilized for the means of the regression coefficients to induce clustering.This package allows users to specify which variables to use for clustering(intercepts or slopes or both)and whether a factor analysis model is desired.More de-tails about this method can be found in Jiehuan Sun,et al.(2017)<doi:10.1002/sim.7374>. License GPL-2Encoding UTF-8LazyData trueDepends R(>=3.4.0),MASS(>=7.3-47),lme4(>=1.1-13),mcclust(>=1.0)Imports Rcpp(>=0.12.7)Suggests knitr,latticeVignetteBuilder knitrLinkingTo Rcpp,RcppArmadilloRoxygenNote7.1.0NeedsCompilation yes12BClustLonGRepository CRANDate/Publication2020-05-0704:10:02UTCR topics documented:BClustLonG (2)calSim (3)data (4)Index5 BClustLonG A Dirichlet process mixture model for clustering longitudinal gene ex-pression data.DescriptionA Dirichlet process mixture model for clustering longitudinal gene expression data.UsageBClustLonG(data=NULL,iter=20000,thin=2,savePara=FALSE,infoVar=c("both","int")[1],factor=TRUE,hyperPara=list(v1=0.1,v2=0.1,v=1.5,c=1,a=0,b=10,cd=1,aa1=2, aa2=1,alpha0=-1,alpha1=-1e-04,cutoff=1e-04,h=100) )Argumentsdata Data list with three elements:Y(gene expression data with each column being one gene),ID,and years.(The names of the elements have to be matachedexactly.See the data in the example section more info)iter Number of iterations(excluding the thinning).thin Number of thinnings.savePara Logical variable indicating if all the parameters needed to be saved.Default value is FALSE,in which case only the membership indicators are saved.infoVar Either"both"(using both intercepts and slopes for clustering)or"int"(using only intercepts for clustering)factor Logical variable indicating whether factor analysis model is wanted.hyperPara A list of hyperparameters with default values.calSim3 Valuereturns a list with following objects.e.mat Membership indicators from all iterations.All other parametersonly returned when savePara=TRUE.ReferencesJiehuan Sun,Jose D.Herazo-Maya,Naftali Kaminski,Hongyu Zhao,and Joshua L.Warren."A Dirichlet process mixture model for clustering longitudinal gene expression data."Statistics in Medicine36,No.22(2017):3495-3506.Examplesdata(data)##increase the number of iterations##to ensure convergence of the algorithmres=BClustLonG(data,iter=20,thin=2,savePara=FALSE,infoVar="both",factor=TRUE)##discard the first10burn-ins in the e.mat##and calculate similarity matrix##the number of burn-ins has be chosen s.t.the algorithm is converged.mat=calSim(t(res$e.mat[,11:20]))clust=maxpear(mat)$cl##the clustering results.##Not run:##if only want to include intercepts for clustering##set infoVar="int"res=BClustLonG(data,iter=10,thin=2,savePara=FALSE,infoVar="int",factor=TRUE)##if no factor analysis model is wanted##set factor=FALSEres=BClustLonG(data,iter=10,thin=2,savePara=FALSE,infoVar="int",factor=TRUE)##End(Not run)calSim Function to calculate the similarity matrix based on the cluster mem-bership indicator of each iteration.DescriptionFunction to calculate the similarity matrix based on the cluster membership indicator of each itera-tion.4dataUsagecalSim(mat)Argumentsmat Matrix of cluster membership indicator from all iterationsExamplesn=90##number of subjectsiters=200##number of iterations##matrix of cluster membership indicators##perfect clustering with three clustersmat=matrix(rep(1:3,each=n/3),nrow=n,ncol=iters)sim=calSim(t(mat))data Simulated dataset for testing the algorithmDescriptionSimulated dataset for testing the algorithmUsagedata(data)FormatAn object of class list of length3.Examplesdata(data)##this is the required data input formathead(data.frame(ID=data$ID,years=data$years,data$Y))Index∗datasetsdata,4BClustLonG,2calSim,3data,45。
专八英语阅读

英语专业八级考试TEM-8阅读理解练习册(1)(英语专业2012级)UNIT 1Text AEvery minute of every day, what ecologist生态学家James Carlton calls a global ―conveyor belt‖, redistributes ocean organisms生物.It’s planetwide biological disruption生物的破坏that scientists have barely begun to understand.Dr. Carlton —an oceanographer at Williams College in Williamstown,Mass.—explains that, at any given moment, ―There are several thousand marine species traveling… in the ballast water of ships.‖ These creatures move from coastal waters where they fit into the local web of life to places where some of them could tear that web apart. This is the larger dimension of the infamous无耻的,邪恶的invasion of fish-destroying, pipe-clogging zebra mussels有斑马纹的贻贝.Such voracious贪婪的invaders at least make their presence known. What concerns Carlton and his fellow marine ecologists is the lack of knowledge about the hundreds of alien invaders that quietly enter coastal waters around the world every day. Many of them probably just die out. Some benignly亲切地,仁慈地—or even beneficially — join the local scene. But some will make trouble.In one sense, this is an old story. Organisms have ridden ships for centuries. They have clung to hulls and come along with cargo. What’s new is the scale and speed of the migrations made possible by the massive volume of ship-ballast water压载水— taken in to provide ship stability—continuously moving around the world…Ships load up with ballast water and its inhabitants in coastal waters of one port and dump the ballast in another port that may be thousands of kilometers away. A single load can run to hundreds of gallons. Some larger ships take on as much as 40 million gallons. The creatures that come along tend to be in their larva free-floating stage. When discharged排出in alien waters they can mature into crabs, jellyfish水母, slugs鼻涕虫,蛞蝓, and many other forms.Since the problem involves coastal species, simply banning ballast dumps in coastal waters would, in theory, solve it. Coastal organisms in ballast water that is flushed into midocean would not survive. Such a ban has worked for North American Inland Waterway. But it would be hard to enforce it worldwide. Heating ballast water or straining it should also halt the species spread. But before any such worldwide regulations were imposed, scientists would need a clearer view of what is going on.The continuous shuffling洗牌of marine organisms has changed the biology of the sea on a global scale. It can have devastating effects as in the case of the American comb jellyfish that recently invaded the Black Sea. It has destroyed that sea’s anchovy鳀鱼fishery by eating anchovy eggs. It may soon spread to western and northern European waters.The maritime nations that created the biological ―conveyor belt‖ should support a coordinated international effort to find out what is going on and what should be done about it. (456 words)1.According to Dr. Carlton, ocean organism‟s are_______.A.being moved to new environmentsB.destroying the planetC.succumbing to the zebra musselD.developing alien characteristics2.Oceanographers海洋学家are concerned because_________.A.their knowledge of this phenomenon is limitedB.they believe the oceans are dyingC.they fear an invasion from outer-spaceD.they have identified thousands of alien webs3.According to marine ecologists, transplanted marinespecies____________.A.may upset the ecosystems of coastal watersB.are all compatible with one anotherC.can only survive in their home watersD.sometimes disrupt shipping lanes4.The identified cause of the problem is_______.A.the rapidity with which larvae matureB. a common practice of the shipping industryC. a centuries old speciesD.the world wide movement of ocean currents5.The article suggests that a solution to the problem__________.A.is unlikely to be identifiedB.must precede further researchC.is hypothetically假设地,假想地easyD.will limit global shippingText BNew …Endangered‟ List Targets Many US RiversIt is hard to think of a major natural resource or pollution issue in North America today that does not affect rivers.Farm chemical runoff残渣, industrial waste, urban storm sewers, sewage treatment, mining, logging, grazing放牧,military bases, residential and business development, hydropower水力发电,loss of wetlands. The list goes on.Legislation like the Clean Water Act and Wild and Scenic Rivers Act have provided some protection, but threats continue.The Environmental Protection Agency (EPA) reported yesterday that an assessment of 642,000 miles of rivers and streams showed 34 percent in less than good condition. In a major study of the Clean Water Act, the Natural Resources Defense Council last fall reported that poison runoff impairs损害more than 125,000 miles of rivers.More recently, the NRDC and Izaak Walton League warned that pollution and loss of wetlands—made worse by last year’s flooding—is degrading恶化the Mississippi River ecosystem.On Tuesday, the conservation group保护组织American Rivers issued its annual list of 10 ―endangered‖ and 20 ―threatened‖ rivers in 32 states, the District of Colombia, and Canada.At the top of the list is the Clarks Fork of the Yellowstone River, whereCanadian mining firms plan to build a 74-acre英亩reservoir水库,蓄水池as part of a gold mine less than three miles from Yellowstone National Park. The reservoir would hold the runoff from the sulfuric acid 硫酸used to extract gold from crushed rock.―In the event this tailings pond failed, the impact to th e greater Yellowstone ecosystem would be cataclysmic大变动的,灾难性的and the damage irreversible不可逆转的.‖ Sen. Max Baucus of Montana, chairman of the Environment and Public Works Committee, wrote to Noranda Minerals Inc., an owner of the ― New World Mine‖.Last fall, an EPA official expressed concern about the mine and its potential impact, especially the plastic-lined storage reservoir. ― I am unaware of any studies evaluating how a tailings pond尾矿池,残渣池could be maintained to ensure its structural integrity forev er,‖ said Stephen Hoffman, chief of the EPA’s Mining Waste Section. ―It is my opinion that underwater disposal of tailings at New World may present a potentially significant threat to human health and the environment.‖The results of an environmental-impact statement, now being drafted by the Forest Service and Montana Department of State Lands, could determine the mine’s future…In its recent proposal to reauthorize the Clean Water Act, the Clinton administration noted ―dramatically improved water quality since 1972,‖ when the act was passed. But it also reported that 30 percent of riverscontinue to be degraded, mainly by silt泥沙and nutrients from farm and urban runoff, combined sewer overflows, and municipal sewage城市污水. Bottom sediments沉积物are contaminated污染in more than 1,000 waterways, the administration reported in releasing its proposal in January. Between 60 and 80 percent of riparian corridors (riverbank lands) have been degraded.As with endangered species and their habitats in forests and deserts, the complexity of ecosystems is seen in rivers and the effects of development----beyond the obvious threats of industrial pollution, municipal waste, and in-stream diversions改道to slake消除the thirst of new communities in dry regions like the Southwes t…While there are many political hurdles障碍ahead, reauthorization of the Clean Water Act this year holds promise for US rivers. Rep. Norm Mineta of California, who chairs the House Committee overseeing the bill, calls it ―probably the most important env ironmental legislation this Congress will enact.‖ (553 words)6.According to the passage, the Clean Water Act______.A.has been ineffectiveB.will definitely be renewedC.has never been evaluatedD.was enacted some 30 years ago7.“Endangered” rivers are _________.A.catalogued annuallyB.less polluted than ―threatened rivers‖C.caused by floodingD.adjacent to large cities8.The “cataclysmic” event referred to in paragraph eight would be__________.A. fortuitous偶然的,意外的B. adventitious外加的,偶然的C. catastrophicD. precarious不稳定的,危险的9. The owners of the New World Mine appear to be______.A. ecologically aware of the impact of miningB. determined to construct a safe tailings pondC. indifferent to the concerns voiced by the EPAD. willing to relocate operations10. The passage conveys the impression that_______.A. Canadians are disinterested in natural resourcesB. private and public environmental groups aboundC. river banks are erodingD. the majority of US rivers are in poor conditionText CA classic series of experiments to determine the effects ofoverpopulation on communities of rats was reported in February of 1962 in an article in Scientific American. The experiments were conducted by a psychologist, John B. Calhoun and his associates. In each of these experiments, an equal number of male and female adult rats were placed in an enclosure and given an adequate supply of food, water, and other necessities. The rat populations were allowed to increase. Calhoun knew from experience approximately how many rats could live in the enclosures without experiencing stress due to overcrowding. He allowed the population to increase to approximately twice this number. Then he stabilized the population by removing offspring that were not dependent on their mothers. He and his associates then carefully observed and recorded behavior in these overpopulated communities. At the end of their experiments, Calhoun and his associates were able to conclude that overcrowding causes a breakdown in the normal social relationships among rats, a kind of social disease. The rats in the experiments did not follow the same patterns of behavior as rats would in a community without overcrowding.The females in the rat population were the most seriously affected by the high population density: They showed deviant异常的maternal behavior; they did not behave as mother rats normally do. In fact, many of the pups幼兽,幼崽, as rat babies are called, died as a result of poor maternal care. For example, mothers sometimes abandoned their pups,and, without their mothers' care, the pups died. Under normal conditions, a mother rat would not leave her pups alone to die. However, the experiments verified that in overpopulated communities, mother rats do not behave normally. Their behavior may be considered pathologically 病理上,病理学地diseased.The dominant males in the rat population were the least affected by overpopulation. Each of these strong males claimed an area of the enclosure as his own. Therefore, these individuals did not experience the overcrowding in the same way as the other rats did. The fact that the dominant males had adequate space in which to live may explain why they were not as seriously affected by overpopulation as the other rats. However, dominant males did behave pathologically at times. Their antisocial behavior consisted of attacks on weaker male,female, and immature rats. This deviant behavior showed that even though the dominant males had enough living space, they too were affected by the general overcrowding in the enclosure.Non-dominant males in the experimental rat communities also exhibited deviant social behavior. Some withdrew completely; they moved very little and ate and drank at times when the other rats were sleeping in order to avoid contact with them. Other non-dominant males were hyperactive; they were much more active than is normal, chasing other rats and fighting each other. This segment of the rat population, likeall the other parts, was affected by the overpopulation.The behavior of the non-dominant males and of the other components of the rat population has parallels in human behavior. People in densely populated areas exhibit deviant behavior similar to that of the rats in Calhoun's experiments. In large urban areas such as New York City, London, Mexican City, and Cairo, there are abandoned children. There are cruel, powerful individuals, both men and women. There are also people who withdraw and people who become hyperactive. The quantity of other forms of social pathology such as murder, rape, and robbery also frequently occur in densely populated human communities. Is the principal cause of these disorders overpopulation? Calhoun’s experiments suggest that it might be. In any case, social scientists and city planners have been influenced by the results of this series of experiments.11. Paragraph l is organized according to__________.A. reasonsB. descriptionC. examplesD. definition12.Calhoun stabilized the rat population_________.A. when it was double the number that could live in the enclosure without stressB. by removing young ratsC. at a constant number of adult rats in the enclosureD. all of the above are correct13.W hich of the following inferences CANNOT be made from theinformation inPara. 1?A. Calhoun's experiment is still considered important today.B. Overpopulation causes pathological behavior in rat populations.C. Stress does not occur in rat communities unless there is overcrowding.D. Calhoun had experimented with rats before.14. Which of the following behavior didn‟t happen in this experiment?A. All the male rats exhibited pathological behavior.B. Mother rats abandoned their pups.C. Female rats showed deviant maternal behavior.D. Mother rats left their rat babies alone.15. The main idea of the paragraph three is that __________.A. dominant males had adequate living spaceB. dominant males were not as seriously affected by overcrowding as the otherratsC. dominant males attacked weaker ratsD. the strongest males are always able to adapt to bad conditionsText DThe first mention of slavery in the statutes法令,法规of the English colonies of North America does not occur until after 1660—some forty years after the importation of the first Black people. Lest we think that existed in fact before it did in law, Oscar and Mary Handlin assure us, that the status of B lack people down to the 1660’s was that of servants. A critique批判of the Handlins’ interpretation of why legal slavery did not appear until the 1660’s suggests that assumptions about the relation between slavery and racial prejudice should be reexamined, and that explanation for the different treatment of Black slaves in North and South America should be expanded.The Handlins explain the appearance of legal slavery by arguing that, during the 1660’s, the position of white servants was improving relative to that of black servants. Thus, the Handlins contend, Black and White servants, heretofore treated alike, each attained a different status. There are, however, important objections to this argument. First, the Handlins cannot adequately demonstrate that t he White servant’s position was improving, during and after the 1660’s; several acts of the Maryland and Virginia legislatures indicate otherwise. Another flaw in the Handlins’ interpretation is their assumption that prior to the establishment of legal slavery there was no discrimination against Black people. It is true that before the 1660’s Black people were rarely called slaves. But this shouldnot overshadow evidence from the 1630’s on that points to racial discrimination without using the term slavery. Such discrimination sometimes stopped short of lifetime servitude or inherited status—the two attributes of true slavery—yet in other cases it included both. The Handlins’ argument excludes the real possibility that Black people in the English colonies were never treated as the equals of White people.The possibility has important ramifications后果,影响.If from the outset Black people were discriminated against, then legal slavery should be viewed as a reflection and an extension of racial prejudice rather than, as many historians including the Handlins have argued, the cause of prejudice. In addition, the existence of discrimination before the advent of legal slavery offers a further explanation for the harsher treatment of Black slaves in North than in South America. Freyre and Tannenbaum have rightly argued that the lack of certain traditions in North America—such as a Roman conception of slavery and a Roman Catholic emphasis on equality— explains why the treatment of Black slaves was more severe there than in the Spanish and Portuguese colonies of South America. But this cannot be the whole explanation since it is merely negative, based only on a lack of something. A more compelling令人信服的explanation is that the early and sometimes extreme racial discrimination in the English colonies helped determine the particular nature of the slavery that followed. (462 words)16. Which of the following is the most logical inference to be drawn from the passage about the effects of “several acts of the Maryland and Virginia legislatures” (Para.2) passed during and after the 1660‟s?A. The acts negatively affected the pre-1660’s position of Black as wellas of White servants.B. The acts had the effect of impairing rather than improving theposition of White servants relative to what it had been before the 1660’s.C. The acts had a different effect on the position of white servants thandid many of the acts passed during this time by the legislatures of other colonies.D. The acts, at the very least, caused the position of White servants toremain no better than it had been before the 1660’s.17. With which of the following statements regarding the status ofBlack people in the English colonies of North America before the 1660‟s would the author be LEAST likely to agree?A. Although black people were not legally considered to be slaves,they were often called slaves.B. Although subject to some discrimination, black people had a higherlegal status than they did after the 1660’s.C. Although sometimes subject to lifetime servitude, black peoplewere not legally considered to be slaves.D. Although often not treated the same as White people, black people,like many white people, possessed the legal status of servants.18. According to the passage, the Handlins have argued which of thefollowing about the relationship between racial prejudice and the institution of legal slavery in the English colonies of North America?A. Racial prejudice and the institution of slavery arose simultaneously.B. Racial prejudice most often the form of the imposition of inheritedstatus, one of the attributes of slavery.C. The source of racial prejudice was the institution of slavery.D. Because of the influence of the Roman Catholic Church, racialprejudice sometimes did not result in slavery.19. The passage suggests that the existence of a Roman conception ofslavery in Spanish and Portuguese colonies had the effect of _________.A. extending rather than causing racial prejudice in these coloniesB. hastening the legalization of slavery in these colonies.C. mitigating some of the conditions of slavery for black people in these coloniesD. delaying the introduction of slavery into the English colonies20. The author considers the explanation put forward by Freyre andTannenbaum for the treatment accorded B lack slaves in the English colonies of North America to be _____________.A. ambitious but misguidedB. valid有根据的but limitedC. popular but suspectD. anachronistic过时的,时代错误的and controversialUNIT 2Text AThe sea lay like an unbroken mirror all around the pine-girt, lonely shores of Orr’s Island. Tall, kingly spruce s wore their regal王室的crowns of cones high in air, sparkling with diamonds of clear exuded gum流出的树胶; vast old hemlocks铁杉of primeval原始的growth stood darkling in their forest shadows, their branches hung with long hoary moss久远的青苔;while feathery larches羽毛般的落叶松,turned to brilliant gold by autumn frosts, lighted up the darker shadows of the evergreens. It was one of those hazy朦胧的, calm, dissolving days of Indian summer, when everything is so quiet that the fainest kiss of the wave on the beach can be heard, and white clouds seem to faint into the blue of the sky, and soft swathing一长条bands of violet vapor make all earth look dreamy, and give to the sharp, clear-cut outlines of the northern landscape all those mysteries of light and shade which impart such tenderness to Italian scenery.The funeral was over,--- the tread鞋底的花纹/ 踏of many feet, bearing the heavy burden of two broken lives, had been to the lonely graveyard, and had come back again,--- each footstep lighter and more unconstrained不受拘束的as each one went his way from the great old tragedy of Death to the common cheerful of Life.The solemn black clock stood swaying with its eternal ―tick-tock, tick-tock,‖ in the kitchen of the brown house on Orr’s Island. There was there that sense of a stillness that can be felt,---such as settles down on a dwelling住处when any of its inmates have passed through its doors for the last time, to go whence they shall not return. The best room was shut up and darkened, with only so much light as could fall through a little heart-shaped hole in the window-shutter,---for except on solemn visits, or prayer-meetings or weddings, or funerals, that room formed no part of the daily family scenery.The kitchen was clean and ample, hearth灶台, and oven on one side, and rows of old-fashioned splint-bottomed chairs against the wall. A table scoured to snowy whiteness, and a little work-stand whereon lay the Bible, the Missionary Herald, and the Weekly Christian Mirror, before named, formed the principal furniture. One feature, however, must not be forgotten, ---a great sea-chest水手用的储物箱,which had been the companion of Zephaniah through all the countries of the earth. Old, and battered破旧的,磨损的, and unsightly难看的it looked, yet report said that there was good store within which men for the most part respect more than anything else; and, indeed it proved often when a deed of grace was to be done--- when a woman was suddenly made a widow in a coast gale大风,狂风, or a fishing-smack小渔船was run down in the fogs off the banks, leaving in some neighboring cottage a family of orphans,---in all such cases, the opening of this sea-chest was an event of good omen 预兆to the bereaved丧亲者;for Zephaniah had a large heart and a large hand, and was apt有…的倾向to take it out full of silver dollars when once it went in. So the ark of the covenant约柜could not have been looked on with more reverence崇敬than the neighbours usually showed to Captain Pennel’s sea-chest.1. The author describes Orr‟s Island in a(n)______way.A.emotionally appealing, imaginativeB.rational, logically preciseC.factually detailed, objectiveD.vague, uncertain2.According to the passage, the “best room”_____.A.has its many windows boarded upB.has had the furniture removedC.is used only on formal and ceremonious occasionsD.is the busiest room in the house3.From the description of the kitchen we can infer that thehouse belongs to people who_____.A.never have guestsB.like modern appliancesC.are probably religiousD.dislike housework4.The passage implies that_______.A.few people attended the funeralB.fishing is a secure vocationC.the island is densely populatedD.the house belonged to the deceased5.From the description of Zephaniah we can see thathe_________.A.was physically a very big manB.preferred the lonely life of a sailorC.always stayed at homeD.was frugal and saved a lotText BBasic to any understanding of Canada in the 20 years after the Second World War is the country' s impressive population growth. For every three Canadians in 1945, there were over five in 1966. In September 1966 Canada's population passed the 20 million mark. Most of this surging growth came from natural increase. The depression of the 1930s and the war had held back marriages, and the catching-up process began after 1945. The baby boom continued through the decade of the 1950s, producing a population increase of nearly fifteen percent in the five years from 1951 to 1956. This rate of increase had been exceeded only once before in Canada's history, in the decade before 1911 when the prairies were being settled. Undoubtedly, the good economic conditions of the 1950s supported a growth in the population, but the expansion also derived from a trend toward earlier marriages and an increase in the average size of families; In 1957 the Canadian birth rate stood at 28 per thousand, one of the highest in the world. After the peak year of 1957, thebirth rate in Canada began to decline. It continued falling until in 1966 it stood at the lowest level in 25 years. Partly this decline reflected the low level of births during the depression and the war, but it was also caused by changes in Canadian society. Young people were staying at school longer, more women were working; young married couples were buying automobiles or houses before starting families; rising living standards were cutting down the size of families. It appeared that Canada was once more falling in step with the trend toward smaller families that had occurred all through theWestern world since the time of the Industrial Revolution. Although the growth in Canada’s population had slowed down by 1966 (the cent), another increase in the first half of the 1960s was only nine percent), another large population wave was coming over the horizon. It would be composed of the children of the children who were born during the period of the high birth rate prior to 1957.6. What does the passage mainly discuss?A. Educational changes in Canadian society.B. Canada during the Second World War.C. Population trends in postwar Canada.D. Standards of living in Canada.7. According to the passage, when did Canada's baby boom begin?A. In the decade after 1911.B. After 1945.C. During the depression of the 1930s.D. In 1966.8. The author suggests that in Canada during the 1950s____________.A. the urban population decreased rapidlyB. fewer people marriedC. economic conditions were poorD. the birth rate was very high9. When was the birth rate in Canada at its lowest postwar level?A. 1966.B. 1957.C. 1956.D. 1951.10. The author mentions all of the following as causes of declines inpopulation growth after 1957 EXCEPT_________________.A. people being better educatedB. people getting married earlierC. better standards of livingD. couples buying houses11.I t can be inferred from the passage that before the IndustrialRevolution_______________.A. families were largerB. population statistics were unreliableC. the population grew steadilyD. economic conditions were badText CI was just a boy when my father brought me to Harlem for the first time, almost 50 years ago. We stayed at the hotel Theresa, a grand brick structure at 125th Street and Seventh avenue. Once, in the hotel restaurant, my father pointed out Joe Louis. He even got Mr. Brown, the hotel manager, to introduce me to him, a bit punchy强力的but still champ焦急as fast as I was concerned.Much has changed since then. Business and real estate are booming. Some say a new renaissance is under way. Others decry责难what they see as outside forces running roughshod肆意践踏over the old Harlem. New York meant Harlem to me, and as a young man I visited it whenever I could. But many of my old haunts are gone. The Theresa shut down in 1966. National chains that once ignored Harlem now anticipate yuppie money and want pieces of this prime Manhattan real estate. So here I am on a hot August afternoon, sitting in a Starbucks that two years ago opened a block away from the Theresa, snatching抓取,攫取at memories between sips of high-priced coffee. I am about to open up a piece of the old Harlem---the New York Amsterdam News---when a tourist。
Analyzing the Efficiency of Clustering Algorithms

Analyzing the Efficiency of ClusteringAlgorithmsClustering algorithms are widely used in data mining and machine learning to group similar data points together based on certain criteria. The efficiency of these algorithms plays a crucial role in the performance of various applications such as image segmentation, document classification, and customer segmentation. In this article, we will analyze the efficiency of clustering algorithms by examining their scalability, accuracy, and computational complexity.Firstly, scalability is an important factor to consider when evaluating the efficiencyof clustering algorithms. Scalability refers to the ability of an algorithm to handle large datasets efficiently. Some clustering algorithms, such as k-means and hierarchical clustering, are known to be scalable and can easily handle millions of data points. On the other hand, algorithms like DBSCAN may struggle with large datasets due to their high computational complexity. Therefore, it is essential to choose an algorithm that can efficiently handle the size of the dataset at hand.Secondly, accuracy is another key aspect to consider when analyzing the efficiency of clustering algorithms. The accuracy of a clustering algorithm refers to its ability to correctly group similar data points together while keeping different data points apart. Evaluating the accuracy of clustering algorithms can be challenging as it often depends on the specific dataset and the chosen evaluation metric. Common metrics used to measure the accuracy of clustering algorithms include silhouette score, Davies-Bouldin index, and Rand index. It is important to select an evaluation metric that is suitable for the specific clustering task at hand and to compare the performance of different algorithms based on this metric.Lastly, the computational complexity of clustering algorithms is a crucial factor that impacts their efficiency. The computational complexity of an algorithm refers to the amount of time and resources required to run the algorithm on a given dataset. Severalfactors can affect the computational complexity of clustering algorithms, including the number of data points, the dimensionality of the data, and the chosen algorithm parameters. Some algorithms, such as k-means, have a relatively low computational complexity and can run quickly even on large datasets. In contrast, algorithms like spectral clustering and Gaussian mixture models may require more computational resources due to their higher complexity. Therefore, it is important to consider the computational complexity of clustering algorithms when selecting an algorithm for a specific task.In conclusion, the efficiency of clustering algorithms can be analyzed based on their scalability, accuracy, and computational complexity. By carefully evaluating these factors, researchers and practitioners can choose the most suitable algorithm for their specific clustering task. Additionally, it is essential to consider the trade-offs between these factors, as improving one aspect of efficiency may come at the expense of another. Overall, a thorough analysis of the efficiency of clustering algorithms is essential for achieving optimal performance in various data mining and machine learning applications.。
y and Klaus-Robert M uller

Koji Tsuda,Motoaki Kawanabe and Klaus-Robert M¨ullerAIST CBRC,2-41-6,Aomi,Koto-ku,Tokyo,135-0064,JapanFraunhofer FIRST,Kekul´e str.7,12489Berlin,Germany Dept.of CS,University of Potsdam,A.-Bebel-Str.89,14482Potsdam,Germany koji.tsuda@aist.go.jp,nabe,klaus@first.fhg.deAbstractRecently the Fisher score(or the Fisher kernel)is increasingly used as afeature extractor for classification problems.The Fisher score is a vectorof parameter derivatives of loglikelihood of a probabilistic model.Thispaper gives a theoretical analysis about how class information is pre-served in the space of the Fisher score,which turns out that the Fisherscore consists of a few important dimensions with class information andmany nuisance dimensions.When we perform clustering with the Fisherscore,K-Means type methods are obviously inappropriate because theymake use of all dimensions.So we will develop a novel but simple clus-tering algorithm specialized for the Fisher score,which can exploit im-portant dimensions.This algorithm is successfully tested in experimentswith artificial data and real data(amino acid sequences).1IntroductionClustering is widely used in exploratory analysis for various kinds of data[6].Among them,discrete data such as biological sequences[2]are especially challenging,because efficient clustering algorithms e.g.K-Means[6]cannot be used directly.In such cases,one naturally considers to map data to a vector space and perform clustering there.We call the mapping a“feature extractor”.Recently,the Fisher score has been successfully applied as a feature extractor in supervised classification[5,15,14,13,16].The Fisher score is derived as follows:Let us assume that a probabilistic model is available.Given a parameter estimate from training samples,the Fisher score vector is obtained asThe Fisher kernel refers to the inner product in this space[5].When combined with high performance classifiers such as SVMs,the Fisher kernel often shows superb results[5,14]. For successful clustering with the Fisher score,one has to investigate how original classes are mapped into the feature space,and select a proper clustering algorithm.In this paper, it will be claimed that the Fisher score has only a few dimensions which contains the class information and a lot of unnecessary nuisance dimensions.So K-Means type clustering[6] is obviously inappropriate because it takes all dimensions into account.We will propose a clustering method specialized for the Fisher score,which exploits important dimensions with class information.This method has an efficient EM-like alternating procedure to learn, and has the favorable property that the resultant clusters are invariant to any invertible lineartransformation.Two experiments with an artificial data and an biological sequence data will be shown to illustrate the effectiveness of our approach.2Preservation of Cluster StructureBefore starting,let us determine several notations.Denote by the domain of objects(dis-crete or continuous)and by the set of class labels.The feature extraction is denoted as.Let be the underlying joint distribution and assume that the class distributions are well separated,i.e.is close to0or1. First of all,let us assume that the marginal distribution is known.Then the problem is how tofind a good feature extractor,which can preserve class information,based on the prior knowledge of.In the Fisher score,it amounts tofinding a good parametric model .This problem is by no means trivial,since it is in general hard to infer anything about the possible from the marginal without additional assumptions[12].A loss function for feature extraction In order to investigate how the cluster structure is preserved,wefirst have to define what the class information is.We regard that the class information is completely preserved,if a set of predictors in the feature space can recover the true posterior probability.This view makes sense,because it is impossible to recover the posteriors when classes are totally mixed up.As a predictor of posterior probability in the feature space,we adopt the simplest one,i.e.a linear estimator:The prediction accuracy of for is difficult to formulate,because param-eters and are learned from samples.To make the theoretical analysis possible,we consider the best possible linear predictors.Thus the loss of feature extractor for-th class is defined as(2.1)where denote the expectation with the true marginal distribution.The overall loss is just the sum over all classes.Even when the full class information is preserved,i.e.,clustering in the fea-ture space may not be easy,because of nuisance dimensions which do not contribute to clustering at all.The posterior predictors make use of an at most dimensional subspace out of the-dimensional Fisher score,and the complementary subspace may not have any information about classes.K-means type methods[6]assume a cluster to be hyperspher-ical,which means that every dimension should contribute to cluster discrimination.For such methods,we have to try to minimize the dimensionality while keeping small. When nuisance dimensions cannot be excluded,we will need a different clustering method that is robust to nuisance dimensions.This issue will be discussed in Sec.3.Optimal Feature Extraction In the following,we will discuss how to determine. First,a simple but unrealistic example is shown to achieve,without producing nuisance dimensions at all.Let us assume that is determined as a mixture model of true class distributions:(2.2)where.Obviously this model realizes the true marginal distribution,whenWhen the Fisher score is derived at the true parameter,it achieves.Lemma1.The Fisher score achieves.(proof)To prove the lemma,it is sufficient to show the existence of matrix and dimensional vector such that(2.3) The Fisher score for isand denotes matrixfilled with ones.ThenWhen we set and,(2.3)holds.Loose Models and Nuisance Dimensions We assumed that is known but still we do not know the true class distributions.Thus the model in Lemma1is never available.In the following,the result of Lemma1is relaxed to a more general class of probability models by means of the chain rule of derivatives.However,in this case,we have to pay the price:nuisance dimensions.Denote by a set of probability distributions.According to the information geometry[1],is regarded as a manifold in a Riemannian space.Let denote the manifold of:Now the question is how to determine a manifold such that,which is answered by the following theorem. Theorem1.Assume that the true distribution is contained in:where is the true parameter.If the tangent space of at contains the tangent space of at the same point(Fig.1),then the Fisher score derived from satisfies(proof)To prove the theorem,it is sufficient to show the existence of matrix and dimensional vector such that(2.4) When the tangent space of is contained in that of around,we have the following by the chain rule:With this notation,(2.5)is rewritten asThe equation(2.4)holds by setting and.xQMpFigure1:Information geometric picture of a proba-bilistic model whose Fisher score can fully extract theclass information.When the tangent space of iscontained in,the Fisher score can fully extract theclass information,i.e..Details explained inthe text.Figure2:Feature space constructed by the Fisher scorefrom the samples with two distinct clusters.The and-axis corresponds to an nuisance and an important di-mension,respectively.When the Euclidean metric isused as in K-Means,it is difficult to recover the two“lines”as clusters.In determination of,we face the following dilemma:For capturing important di-mensions(i.e.the tangent space of),the number of parameters should be sufficiently larger than.But a large leads to a lot of nuisance dimensions,which are harmful for clustering in the feature space.In typical supervised classification experiments with hidden markov models[5,15,14],the number of parameters is much larger than the number of classes.However,in supervised scenarios,the existence of nuisance dimensions is not a se-rious problem,because advanced supervised classifiers such as the support vector machine have a built-in feature selector[7].However in unsupervised scenarios without class la-bels,it is much more difficult to ignore nuisance dimensions.Fig.2shows how the feature space looks like,when the number of clusters is two and only one nuisance dimension is involved.Projected on the important dimension,clusters will be concentrated into two dis-tinct points.However,when the Euclidean distance is adopted as in K-Means,it is difficult to recover true clusters because two“lines”are close to each other.3Clustering Algorithm for the Fisher scoreIn this section,we will develop a new clustering algorithm for the Fisher score.Let be a set of class labels assigned to,respectively.The pur-pose of clustering is to obtain only from samples.As mensioned before, in clustering with the Fisher score,it is necessary to capture important dimensions.So far, it has been implemented as projection pursuit methods[3],which use general measures for interestingness,e.g.nongaussianity.However,from the last section’s analysis,we know more than nongaussianity about important dimensions of the Fisher score.Thus we will construct a method specially tuned for the Fisher score.Let us assume that the underlying classes are well separated,i.e.is close to0 or1for each sample.When the class information is fully preserved,i.e., there are bases in the space of the Fisher score,such that the samples in the-th cluster are projected close to1on the-th basis and the others are projected close to0.The objective function of our clustering algorithm is designed to detect such bases:(3.1)where is the indicator function which is1if the condition holds and0otherwise. Notice that the optimal result of(3.1)is invariant to any invertible linear transformation .In contrast,K-means type methods are quite sensitive to linear transformation or data normalization[6].When linear transformation is notoriously set,K-means can end up with a false result which may not reflect the underlying structure.1 The objective function(3.1)can be minimized by the following EM-like alternating proce-dure:1.Initialization:Set to initial putefor later use.2.Repeat3.and4.until the convergence of.3.Fix and minimize with respect to and.Each isobtained as the solution of the following problem:This problem is analytically solved aswhere1When the covariance matrix of each cluster is allowed to be different in K-Means,it becomes invariant to normalization.However this method in turn causes singularities,where a cluster shrinks to the delta distribution,and difficult to learn in high dimensional spaces.Figure3:(Upperleft)Toydataset used for cluster-ing.Contours show theestimated density with themixture of8Gaussians.(Upperright)Clustering re-sult of the proposed algo-rithm.(Lowerleft)Resultof K-Means with the Fisherscore.(Lowerright)Re-sult of K-Means with thewhitened Fisher score.typically do not scale to large dimensional or discrete problems.Standard mixture modeling methods have difficulties inmodeling such complicated cluster shapes[9,10].One straightforward way is to model each cluster as a Gaussian Mixture:However, special care needs to be taken for such a“mixture of mixtures”problem.When the pa-rameters and are jointly optimized in a maximum likelihood process,the solution is not unique.In order to have meaningful results e.g.in our dataset,one has to constrain the parameters such that8Gaussians form2groups.In the Bayesian framework, this can be done by specifying an appropriate prior distributions on parameters,which can become rather involved.Roberts et.al.[10]tackled this problem by means of the minimum entropy principle using MCMC which is somewhat more complicated than our approach. 5Clustering Amino Acid SequencesIn this section,we will apply our method to cluster bacterial gyrB amino acid sequences, where the hidden markov model(HMM)is used to derive the Fisher score.gyrB-gyrase subunit B-is a DNA topoisomerase(type II)which plays essential roles in fundamental mechanisms of living organisms such as DNA replication,transcription,recombination and repair etc.One more important feature of gyrB is its capability of being an evolutionary and taxonomic marker alternating popular16S rRNA[17].Our data set consists of55amino acid sequences containing three clusters(9,32,14).The three clusters correspond to three genera of high GC-content gram-positive bacteria,that is,Corynebacteria,Mycobacteria, Rhodococcus,respectively.Each sequence is represented as a sequence of20characters, each of which represents an amino acid.The length of each sequence is different from408 to442,which makes it difficult to convert a sequence into a vector offixed dimensionality. In order to evaluate the partitions we use the Adjusted Rand Index(ARI)[4,18].Let be the obtained clusters and be the ground truth clusters.Let be the number of samples which belongs to both and.Also let and be the number of samples in and,respectively.ARI is defined asThe attractive point of ARI is that it can measure the difference of two partitions even when23450.20.40.60.8Number of HMM States A R I ProposedK-MeansFigure 4:Adjusted Rand indices of K-Means and the proposed method in a sequence clas-sification experiment.the number of clusters is different.When the two partitions are exactly the same,ARI is 1,and the expected value of ARI over random partitions is 0(see [4]for details).In order to derive the Fisher score,we trained complete-connection HMMs via the Baum-Welch algorithm,where the number of states is changed from 2to 5,and each state emits one of characters.This HMM has initial state probabilities,terminalstate probabilities,transition probabilities and emission probabilities.Thus when for example,a HMM has 75parameters in total,which is much larger than the number of potential classes (i.e.3).The derivative is taken with respect to all paramaters asdescribed in detail in [15].Notice that we did not perform any normalization to the Fisher score vectors.In order to avoid local minima,we tried 1000different initial values and chose the one which achieved the minimum loss both in K-means and our method.In K-Means,initial centers are sampled from the uniform distribution in the smallest hypercube which contains all samples.In the proposed method,every is sampled from the normal distribution with mean 0and standard deviation 0.001.Every is initially set to zero.Fig.4shows the ARIs of two methods against the number of HMM states.Our method shows the highest ARI (0.754)when the number of HMM states is 3,which shows that important dimensions are successfully discovered from the “sea”of nuisance dimensions.In contrast,the ARI of K-Means decreases monotonically as the number of HMM states increases,which shows the K-Means is not robust against nuisance dimensions.But when the number of nuisance dimensions are too many (i.e.),our method was caught in false clusters which happened to appear in nuisance dimensions.This result suggests that prior dimensionality reduction may be effective (cf.[11]),but it is beyond the scope of this paper.6Concluding RemarksIn this paper,we illustrated how the class information is encoded in the Fisher score:most information is packed in a few dimensions and there are a lot of nuisance dimensions.Ad-vanced supervised classifiers such as the support vector machine have a built-in feature selector [7],so they can detect important dimensions automatically.However in unsuper-vised learning,it is not easy to detect important dimensions because of the lack of class labels.We proposed a novel very simple clustering algorithm that can ignore nuisance dimensions and tested it in artificial and real data experiments.An interesting aspect of our gyrB experiment is that the ideal scenario assumed in the theory section is not fulfilled anymore as clusters might overlap.Nevertheless our algorithm is robust in this respect and achieves highly promising results.The Fisher score derives features using the prior knowledge of the marginal distribution. In general,it is impossible to infer anything about the conditional distribution from the marginal[12]without any further assumptions.However,when one knows the directions that the marginal distribution can move(i.e.the model of marginal distribution), it is possible to extract information about,even though it may be corrupted by many nuisance dimensions.Our method is straightforwardly applicable to the objects to which the Fisher kernel has been applied(e.g.speech signals[13]and documents[16]). Acknowledgement The authors gratefully acknowledge that the bacterial gyrB amino acid sequences are offered by courtesy of Identification and Classification of Bacteria(ICB)database team[17].KRM thanks for partial support by DFG grant#MU987/1-1. References[1]S.Amari and H.Nagaoka.Methods of Information Geometry,volume191of Translations ofMathematical Monographs.American Mathematical Society,2001.[2]R.Durbin,S.Eddy,A.Krogh,and G.Mitchison.Biological Sequence Analysis:ProbabilisticModels of Proteins and Nucleic Acids.Cambridge University Press,1998.[3]P.J.Huber.Projection pursuit.Annals of Statistics,13:435–475,1985.[4]L.Hubert and paring partitions.J.Classif.,pages193–218,1985.[5]T.S.Jaakkola and D.Haussler.Exploiting generative models in discriminative classifiers.InM.S.Kearns,S.A.Solla,and D.A.Cohn,editors,Advances in Neural Information Processing Systems11,pages487–493.MIT Press,1999.[6] A.K.Jain and R.C.Dubes.Algorithms for Clustering Data.Prentice Hall,1988.[7]K.-R.M¨u ller,S.Mika,G.R¨a tsch,K.Tsuda,and B.Sch¨o lkopf.An introduction to kernel-basedlearning algorithms.IEEE Trans.Neural Networks,12(2):181–201,2001.[8] A.Y.Ng,M.I.Jordan,and Y.Weiss.On spectral clustering:Analysis and an algorithm.In T.G.Dietterich,S.Becker,and Z.Ghahramani,editors,Advances in Neural Information Processing Systems14.MIT Press,2002.[9]M.Rattray.A model-based distance for clustering.In Proc.IJCNN’00,2000.[10]S.J.Roberts,C.Holmes,and D.Denison.Minimum entropy data partitioning using reversiblejump markov chain monte carlo.IEEE Trans.Patt.Anal.Mach.Intell.,23(8):909–915,2001.[11]V.Roth,ub,J.M.Buhmann,and K.-R.M¨u ller.Going metric:Denoising pairwise data.InNIPS02,2002.submitted.[12]M.Seeger.Learning with labeled and unlabeled data.Technical report,In-stitute for Adaptive and Neural Computation,University of Edinburgh,2001./homes/seeger/papers/review.ps.gz.[13]N.Smith and M.Gales.Speech recognition using SVMs.In T.G.Dietterich,S.Becker,andZ.Ghahramani,editors,Advances in Neural Information Processing Systems14.MIT Press, 2002.[14]S.Sonnenburg,G.R¨a tsch,A.Jagota,and K.-R.M¨u ller.New methods for splice site recognition.In ICANN’02,2002.to appear.[15]K.Tsuda,M.Kawanabe,G.R¨a tsch,S.Sonnenburg,and K.-R.M¨u ller.A new discriminativekernel from probabilistic models.Neural Computation,2002.in press.[16] A.Vinokourov and M.Girolami.A probabilistic framework for the hierarchic organization andclassification of document collections.Journal of Intelligent Information Systems,18(2/3):153–172,2002.[17]K.Watanabe,J.S.Nelson,S.Harayama,and H.Kasai.ICB database:the gyrB database foridentification and classification of bacteria.Nucleic Acids Res.,29:344–345,2001.[18]K.Y.Yeung and W.L.Ruzzo.Principal component analysis for clustering gene expression data.Bioinformatics,17(9):763–774,2001.。
2021年下半年英语六级作文押题

【导语】就要考试了,希望我的问候短信会为你送去⼀份轻松清爽的⼼情,不要太紧张哦!不然可会把答案忘掉的!我在这⾥⽀持着你,⿎励着你,为你祝福!以下是为⼤家整理的内容,欢迎阅读参考。
1.2021年下半年英语六级作⽂押题 题⽬: Directions: For this part, you are allowed 30minutes to write a short essay entitled The Damageof E-waste. You should write at least 150 wordsfollowing the outline given below. 1. 随着电⼦设备的增多,电⼦垃圾也越来越多 2. 电⼦垃圾的危害很多 3. 为此,我们应该…… 范⽂: The Damage of E-waste Electronic waste, or e-waste, has become anissue of serious concern to the public as a growingnumber of electronic items are discarded in landfillsevery year. Many consumers are not aware that electronics like computers and cell phonesactually contain toxins that can leach out into the soil and damage the environment. E-waste compounds pose hazards to the environment as well as the human beings. Tostart with, when exposed to heat, the components of e-waste release toxic fumes and gas,polluting the air andcausing global environmental problems. When circuit breakersdeteriorate, they release toxins, such as mercury, that pollute groundwater. In addition toits damaging effect on the environment,researchers have now linked e-waste to adverseeffects on human health. In my view, it’s high time that the damage of e-wasted should be realized by the public andmeasures should be taken to cope with this issue. One idea is to put greater responsibility onthecompanies that produce the goods. It should be mandatory for them to taking theabandoned items back and dispose them in an environmentally-friendly manner.2.2021年下半年英语六级作⽂押题 “⼈⼯智能”“AI”等词都是最近⼤⽕的词,很明显,现在⼈⼯科技的发展已经触及到我们的⽣活,餐厅⾥⼈⼯上菜,⽣产间⼈⼯加⼯,电脑⼈⼯计算,家中⼈⼯做家务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Edgar H. de Graaf, Joost N. Kok, and Walter A. Kosters
Leiden Institute of Advanced Computer Science Leiden University, The Netherlands edegraaf@liacs.nl
would draw all these relations, the drawing would be shaped like a lattice, hence we call this data lattice information. We further analyse frequent subgraphs and their corresponding lattice information with different techniques in our framework Lattice2SAR for mining and analysing frequent subgraph data. One of the techniques in this framework is the analysis of graphs in which frequent subgraphs occur, via clustering. Another important functionality is the browsing of lattice information from parent to child and from child to parent. In this paper we will present the clustering.
Our working example is the analysis of patterns (fragments) in molecule data, since Lattice2SAR was originally made to handle molecule data. Obviously molecules are stored in the form of graphs, the molecules are the transactions (see Figure 1 for an example). However, the techniques presented here are not particular to molecule data (we will also not discuss any chemical or biological issues). For example one can extract user behaviour from access logs of a website. This behaviour can be stored in the form of graphs and can as such be mined with the techniques presented here. The distance between patterns can be measured by calculating in how many graphs (or molecules) only one of the two patterns occurs. If this never happens then these patterns are very close to each other. If this always happens then their distance is very large. In both cases the user is interested to know the reason. In our working example the chemist might want to know which different patterns seem to occur in the same subgroup of effective medicines or which patterns occur in different subgroups of effective medicines. In this paper we will present an approach to solve this problem that uses clustering. Furthermore all occurrences for the frequent subgraphs will be discovered by a graph mining algorithm and this occurrence information will be highly compressed before storage. Because of this, requesting these occurrences will be costly. Through our method of clustering time will be saved if the user uses the clusters to select interesting patterns, see Figure 2 for an overview. We will define our method of clustering and show its usefulness. To this end, this paper makes the following contributions: — Our first contribution will be that we will introduce an algorithm for clustering frequent subgraphs allowing the user to quickly see interesting relations, e.g., subgraphs occur in the same transactions, and quicker select the right occurrence details from the compressed storage (all sections and specifically Section 4).
C 2 C 1 C 1 C 1 N 1 C 2 O 1 O C 2 O C 2 C 1 C 1 C
C
1
d1 d
C 2
d2 d
C
1
C
Fig. 1. An example of a possible graph (the amino acid Phenylalanine) in the molecule dataset and two of its many (connected) subgraphs, also called patterns or fragments.
1
Introduction
Mining frequent patterns is an important area of data mining where we discover substructures that occur often in (semi-)structured data. The research in this work will be in the area of frequent subgraph mining. These frequent subgraphs are connected vertex- and edge-labeled graphs that are subgraphs of a given set of graphs, traditionally also referred to as transactions, at least minsupp times. The example of Figure 1 shows a graph and two of its subgraphs. In this paper we will use results from frequent subgraph mining and visualize the frequent subgraphs by means of clustering, where their co-occurrences in the same transactions are used in the distance measure. Clustering makes it possible to obtain a quicker selection of the right frequent subgraphs for a more detailed look at their occurrence. Before explaining what is meant by lattice information we first need to discuss child-parent relations in frequent subgraphs, also known as patterns. Patterns are generated by extending smaller patterns with one extra edge. The smaller pattern can be called a parent of the bigger pattern that it is exte3v1 [cs.AI] 4 May 2007
Abstract. Mining frequent subgraphs is an area of research where we have a given set of graphs (each graph can be seen as a transaction), and we search for (connected) subgraphs contained in many of these graphs. In this work we will discuss techniques used in our framework Lattice2SAR for mining and analysing frequent subgraph data and their corresponding lattice information. Lattice information is provided by the graph mining algorithm gSpan; it contains all supergraph-subgraph relations of the frequent subgraph patterns — and their supports. Lattice2SAR is in particular used in the analysis of frequent graph patterns where the graphs are molecules and the frequent subgraphs are fragments. In the analysis of fragments one is interested in the molecules where patterns occur. This data can be very extensive and in this paper we focus on a technique of making it better available by using the lattice information in our clustering. Now we can reduce the number of times the highly compressed occurrence data needs to be accessed by the user. The user does not have to browse all the occurrence data in search of patterns occurring in the same molecules. Instead one can directly see which frequent subgraphs are of interest.
