人教版初中数学第二十四章圆知识点
【初中数学精品资料】第二十四章第1节圆(二)

A
D
分析:由同弧或等弧所对的圆周角相等知,∠ADC=∠ABC=∠CAB=∠CDB,故与 ∠ADC 相等的角共有 3 个. 解:B 评析:同弧或等弧所对的圆周角相等常用来证明两角相等;或进行角的转换,将一个圆 周角转换为同弧所对的其他圆周角,从而达到题目中的要求. ︵ 例 3. 如图所示,BC 为半圆 O 的直径,G 是半圆上异于 B、C 的点,A 是BG的中点,AD ⊥BC 于点 D,BG 交 AD 于点 E,请说明 AE=BE. 分析:在圆中,有关直径的问题常常需要添加辅助线,以便利用直径所对的圆周角是直 角的性质,因此,欲说明 AE 与 BE 相等,可转化为说明∠BAD=∠ABE,圆周角∠ABE 所 ︵ 对的弧为AG,连结 AB、AC 即可解决问题.
O
(1)
解法二:如图(2)所示,连结 OB、OD. ∵OA=OB=OC=OD,∴∠A=∠B,∠C=∠D. ∵∠A=∠C,∴∠B=∠D. ∴△OAB≌△OCD,∴AB=CD. B D D
A O C A
1 2 4 3
B C
O
(2)
(3)
解法三:如图(3)所示,连结 AC. ∵OA=OC,∴∠1=∠3. 又∵∠BAO=∠DCO,∴∠2=∠4. ︵ ︵ ∴BC=AD. ︵ ︵ ︵ ︵ ︵ ︵ ∴BC+BD=AD+BD,即AB=CD, ∴AB=CD. 1 例 6. AB、BC、CA 是⊙O 的三条弦,O 到 AB 的距离 OE 等于 AB,求∠C 的度数. 2 分析:∠C 可能为一个钝角,也可能为一个锐角,要分类画图、分析和解答.
年
级
初三 安廷玲
学
科
数学
版
本
人教新课标版
内容标题 编稿老师
第二十四章 第 1 节 弧、弦、圆心角、圆周角之间的关系
人教版初中九年级上册数学课件 《点和圆的位置关系》圆

18
A.在⊙O内 B.在⊙O外 C.在⊙O上 D.不能确定
9
8.如图,在网格(每个小正方形的边长均为 1)中选取 9 个格点(格线的交点称为 格点),如果以点 A 为圆心,r 为半径画圆,选取的格点中除点 A 外恰好有 3 个在圆 内,则 r 的取值范围为( B )
A.2 2<r< 17 B. 17<r≤3 2 C. 17<r<5 D.5<r< 29
A. 10 C.34
B.189 D.10
12
11.【易错题】已知⊙O是△ABC的外接圆, 边BC=4cm,且30°⊙或15O0°半径也为4cm,则∠A的度 数是____________________.
1102或.8 【易错题】在Rt△ABC中,AB=6, BC=8,则这个三角形的外接圆直径是 ____________.
A.△ABE C.△ABD
B.△ACF D.△ADE
5
4.如图,点 A、B、C 在同一条直线上,点 D 在直线 AB 外,过这四个点中的 任意 3 个,能画的圆有( C )
A.1 个 C.3 个
B.2 个 D.4 个
6
Hale Waihona Puke 5.【四川雅安中考】如图,△ABC 内接于⊙O,BD 是⊙O 的直径,∠CBD=21°, 则∠A 的度数为_____6_9_°___.
7
6.如图,已知矩形ABCD的边 AB=3cm,BC=4cm,以点A为圆 心,4cm为半径作⊙A,则点B、C、 D与⊙A有怎样的位置关系.
解:连接AC.∵AB=3cm,BC =AD=4cm,∴AC=5cm,∴点B 在⊙A内,点D在⊙A上,点C在 ⊙A外.
人教版初中九年级上册数学课件 《正多边形和圆》圆

解:要使△PCD 的周长最小,即 PC+PD 的值最小.根
据正多边形的性质,得点 C 关于 BE 的对称点为点 A,连接 AD
交 BE 于点 P,那么有 PC+PD=AD 最小.易知四边形 ABCD
为等腰梯形,∠BAD=∠CDA=60°.作 BM⊥AD 于点 M,CN
⊥AD 于点 N.∵AB=2,∴AM=12AB=1,∴DN=AM=1,∴
能超过( A )
A.12 mm
B.12 3 mm
C.6 mm
D.6 3 mm
3.已知圆内接正三角形的面积为 3,则该圆的内接正六边形的边心距是( B )
A.2
B.1
C. 3
D.
3 2
7
4.【贵州贵阳中考】如图,正六边形 ABCDEF 内接于⊙O,连接 BD.则∠CBD 的度数是( A )
A.30° C.60°
10
8.【教材P106练习T3变式】如图,正八边 形ABCDEFGH的半径为2,求它的面积.
11
解:连接 AO、BO、CO、AC. ∵正八边形 ABCDEFGH 的半径为 2,∴AO= BO=CO=2,∠AOB=∠BOC=360°×18=45°,∴∠AOC=90°,∴AC=2 2,此时 AC⊥BO,∴S 四边形 ABCO=12BO·AC=12×2×2 2=2 2,∴正八边形 ABCDEFGH 的面 积为 2 2×4=8 2.
B.45° D.90°
8
5.如图,正六边形 ABCDEF 内接于半径为 4 的圆,则 B、E 两点间的距离为___8___.
9
6.将一个边长为 1 的正六边形补成如图所示的矩形,则矩形的周长等于 ___4_+__2__3____.(结果保留根号)
43 7.【山东滨州中考】若正六边形的内切圆半径为 2,则其外接圆半径为___3___.
【初中数学精品资料】第二十四章第1节圆(一)

级
初三 安廷玲
学
科
数学
版
本
人教新课标版
内容标题 编稿老师
第二十四章 第 1 节 圆的对称性
【本讲教育信息】
一、教学内容: 圆的对称性 1. 理解圆的定义及弧、弦、半圆、直径等有关概念. 2. 圆的对称性. 3. 垂径定理及其推论. 二、知识要点: 1. 圆的定义 (1)在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成 的图形叫做圆. 固定的端点 O 叫做圆心,线段 OA 叫做半径,以点 O 为圆心的圆,记作“⊙ O” ,读作“圆 O”. 圆可以看作是平面内到定点的距离等于定长的所有点组成的图形 . 其中,定点称为圆 心,定长称为圆的半径. 圆心确定圆的位置,半径决定圆的大小.
第 3 页 版权所有
不得复制
∴CF=FD. ︵ ︵ ︵ ︵ (2)由 MN⊥AB,MN⊥CD 得AN=BN,CN=DN, ︵ ︵ ︵ ︵ ∴AN-CN=BN-DN. ︵ ︵ 即AC=BD. 评析:本题运用了垂径定理及其逆定理. 在解第(2)问时,涉及说明两条弧相等,这 类题以前没有接触过,这里用了图形的加减,由直观的方法说明. 例 5. 已知,如图所示,在⊙O 中,AB、CD 为直径,AD 与 BC 平行吗?为什么?
【典型例题】
例 1. 判断题. (1)直径是弦,弦是直径. (2)弦是圆上两点间的部分. (3)半圆是弧,但弧不一定是半圆. (4)直径相等的两个圆是等圆. (5)等于半径两倍的线段是直径. 分析:结合图形分析概念,容易进行区分记忆. 解: (1)错(2)错(3)对(4)对(5)错 评析:正确理解圆的有关概念,是研究圆的基本性质和解决有关问题的基础,对于概念 的理解要知道它具有特征和识别两重作用. 例 2. 如图所示,菱形 ABCD 的对角线 AC、BD 相交于点 O,E、F、G、H 分别是四边的 中点. 试说明 E、F、G、H 四个点在以点 O 为圆心,OE 长为半径的圆上.
初中数学人教九年级上册第二十四章圆-切线长定理

(1)写出图中所有的垂直关系;
B
OA⊥PA,OB ⊥PB,AB ⊥OP.
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC. (3)写出图中所有的全等三角形;
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.
(4)写出图中所有的等腰三角形.△ABP △AOB
条切线,它们的切线长相
O
P
等,圆心和这一点的连线
平分两条切线的夹角. 几何语言:
PA、PB分别切⊙O于A、B
B PA = PB ∠OPA=∠OPB
注意 切线长定理为证明线段相等、角相等提供了新的方法.
拓展结论 A
PA、PB是⊙O的两条切线,A、
B为切点,直线OP交⊙O于点D
E OCD
P
、E,交AB于C.
A
P O
B
课堂小结
切线长
切线长 定理
原理 作用
辅助线
图形的轴对称性
提供了证线段和 角相等的新方法
① 分别连接圆心和切点; ② 连接两切点; ③ 连接圆心和圆外一点.
课后作业
1、《课后作业》 2、练习册
思考:PA为⊙O的一条切线,沿着直线PO对折,设圆上与点
A重合的点为B.
➢ OB是⊙O的一条半径吗?
A
➢ PB是⊙O的切线吗?
O.
P
➢ PA、PB有何关系? B
➢ ∠APO和∠BPO有何关系?
(利用图形轴对称性解释)
二 切线长定理
你能写出上述结论的证
明过程吗?
A
O.
P
B
切线长定理:
A
从圆外一点引圆的两
学习目标
1.掌握切线长定理,初步学会运用切线长定理进行计算 与证明.(重点)
人教版初中数学九年级上册 第二十四章 点和圆的位置关系

∴∠DAO=30°;
探究新知
24.2 点和圆、直线和圆的位置关系/
(2)求点A的坐标和△AOB外接圆的面积.
∵点D的坐标是(0,3),∴OD=3.
在Rt△AOD中,∵∠DOA=90° ,
∴AD为直径. 又∵∠DAO=30°,∴AD=2OD=6, OA= 3 3. 因此圆的半径为3.点A的坐标( 3 3,0), ∴△AOB外接圆的面积是9π. 解题妙招:图形中求三角形外接圆的面积时,关键是确定外 接圆的直径(或半径)长度.
P
d
d
Pd
r
r
P
r
点P在⊙O内 点P在⊙O上 点P在⊙O外
d <r d= r d>r
探究新知
24.2 点和圆、直线和圆的位置关系/
点和圆的位置关系
P
d
d
Pd
r
r
P
r
点P在⊙O内
d<r 点P在⊙O上 d=r 点P在⊙O外
d>r
数形结合: 位置关系
数量关系
探究新知
24.2 点和圆、直线和圆的位置关系/
课堂检测
24.2 点和圆、直线和圆的位置关系/
基础巩固题
1. 如图,请找出图中圆的圆心,并写出你找圆心的方法? A
O C
B
课堂检测
24.2 点和圆、直线和圆的位置关系/
2. 正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A, 则点B在⊙A 上 ;点C在⊙A 外 ;点D在⊙A 上 .
3.⊙O的半径r为5cm,O为原点,点P的坐标为(3,4),则 点P与⊙O的位置关系为 ( B )
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点 在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围? (直接写出答案)
人教版初中九年级数学上册第二十四章《圆》知识点(含答案解析)
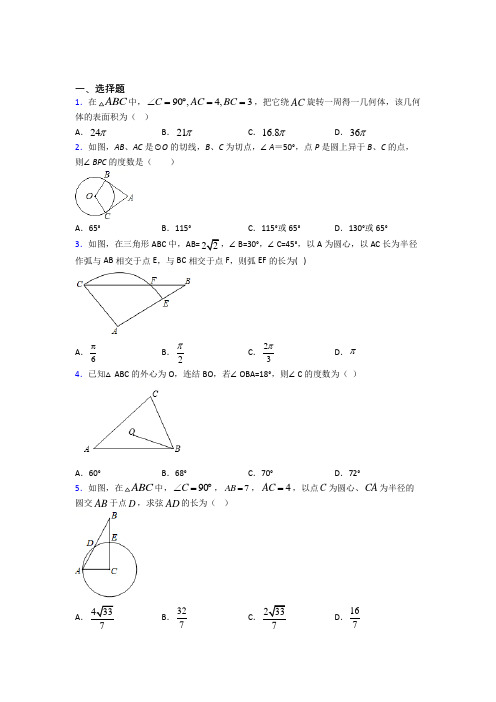
一、选择题1.在ABC 中,90,4,3C AC BC ∠=︒==,把它绕AC 旋转一周得一几何体,该几何体的表面积为( )A .24πB .21πC .16.8πD .36π 2.如图,AB 、AC 是⊙O 的切线,B 、C 为切点,∠A =50°,点P 是圆上异于B 、C 的点,则∠BPC 的度数是( )A .65°B .115°C .115°或65°D .130°或65° 3.如图,在三角形ABC 中,AB=22,∠B=30°,∠C=45°,以A 为圆心,以AC 长为半径作弧与AB 相交于点E ,与BC 相交于点F ,则弧EF 的长为( )A .6πB .2πC .23πD .π4.已知△ABC 的外心为O ,连结BO ,若∠OBA=18°,则∠C 的度数为( )A .60°B .68°C .70°D .72°5.如图,在ABC 中,90C ∠=︒,7AB =,4AC =,以点C 为圆心、CA 为半径的圆交AB 于点D ,求弦AD 的长为( )A 433B .327C .337D .1676.如图,正方形ABCD 内接于O ,直径//MN AD ,则阴影部分的面积占圆面积的( )A .12B .16C .13D .147.若圆锥的底面半径为5cm ,侧面积为265cm π,则该圆锥的高是( ) A .13cm B .12cm C .11cm D .10cm 8.如图,ABC 的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将ABC 绕点B 顺时针旋转到A B C '''的位置,且点A '、C '仍落在格点上,则线段AB 扫过的图形的面积是( )平方单位(结果保留)A .254πB .134πC .132πD .136π 9.如图,在⊙O 中,AB 是直径,弦AC=5,∠BAC=∠D .则AB 的长为( )A .5B .10C .52D .10210.如图,AB 是⊙O 的直径,C ,D 是⊙O 上的点,28CDB ∠=︒,过点C 作⊙O 的切线交AB 的延长线于点E ,则E ∠等于( )A .28︒B .34︒C .44︒D .56︒ 11.如图,⊙O 的半径为1,点 O 到直线 a 的距离为2,点 P 是直线a 上的一个动点,PA 切⊙O 于点 A ,则 PA 的最小值是( )A .1B .3C .2D .5 12.如图,ABC 的顶点A 是O 上的一个动点,90ACB ∠=︒,30BAC ∠=︒,边AC ,AB 分别交O 于点E ,D ,分别过点E ,D 作O 的切线交于点F ,且点F 恰好在边BC 上,连接OC ,若O 的半径为6,则OC 的最大值为( )A .393+B .2103+C .353+D .53 13.如图,点M 是矩形ABCD 的边BC 、CD 上的点,过点B 作BN ⊥AM 于点P ,交矩形ABCD 的边于点N ,连接DP ,若AB=6,AD=4,则DP 的长的最小值为( )A .2B .121313C .4D .514.如图,在平行四边形ABCO 中,45C ∠=︒,点A ,B 在O 上,点D 在ADB 上,DA DB =,则AOD ∠的度数为( )A.112.5°B.120°C.135°D.150°15.在△ABC中,∠ACB为锐角,分别以AB,AC为直径作半圆,过点B,A,C作弧BAC,如图所示.若AB=4,AC=2,图中两个新月形面积分别为S1,S2,两个弓形面积分别为S3,S4,S1-S2=14π,则S3-S4的值是( )A.294πB.234πC.114πD.54π二、填空题16.如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=________°.17.如图,四边形ABCD是O的内接四边形,对角线AC,BD交于点E,且AC BD AB==,若70AEB∠=︒,则AOB∠等于______︒.18.已知半径为5的圆O中,弦AB=8,则以AB为底边的等腰三角形腰长为___________.19.如图,PA,PB分别与O相切于A、B两点,点C为劣弧AB上任意一点,过点C的切线分别交AP,BP于D,E两点.若8AP=,则PDE△的周长为______.20.如图,O 的半径为6,AB 、CD 是互相垂直的两条直径,点P 是O 上任意一点,过点P 作PM AB ⊥于M ,PN CD ⊥于N ,点Q 是MN 的中点,当点P 沿着圆周从点D 逆时针方向运动到点C 的过程中,当∠QCN 度数取最大值时,线段CQ 的长为______.21.如图,已知正方形ABCD 的边长为2,点M 和N 分别从B 、C 同时出发,以相同的速度沿BC 、CD 方向向终点C 和D 运动.连接AM ,BN 交于点P ,则PC 长的最小值为____________.22.如图,直线AB 、CD 相交于点,30O AOC ∠=︒,半径为1cm 的⊙P 的圆心在直线AB 上,且与点O 的距离为8cm ,如果⊙P 以2cm/s 的速度,由A 向B 的方向运动,那么_________秒后⊙P 与直线CD 相切.23.在矩形ABCD 中,43AB =6BC =,若点P 是矩形ABCD 上一动点,要使得60APB ∠=︒,则AP 的长为__________.24.小明用一张扇形纸片做一个圆锥的侧面,已知该扇形的半径是10cm ,弧长是12πcm 2,那么这个圆锥的高是________cm .参考答案25.如图,在⊙O 中,弦AC 、BD 相交于点E ,且AB BC CD ==,若∠BEC=130°,则∠ACD 的度数为_____26.如图,已知空间站A 与星球B 距离为a ,信号飞船C 在星球B 附近沿圆形轨道行驶,B ,C 之间的距离为b .数据S 表示飞船C 与空间站A 的实时距离,那么S 的最小值________.三、解答题27.如图,AB 是O 的弦,CD 是O 的直径,CD AB ⊥,垂足为E .1CE =,3ED =.(1)求O 的半径.(2)求AB 的长.28.如图,在Rt △ABC 中,∠C =90°,以BC 为直径的圆O 交AB 于点D ,切线DE 交AC 于点E .(1)求证:∠A =∠ADE ;(2)若AD =8,DE =5,求BC 的长.29.如图,一条公路的转弯处是一段圆弧CD ,点O 是CD 的圆心,E 为 CD 上一点,OE ⊥CD ,垂足为F .已知CD=300m ,EF=50m ,求这段弯路的半径.30.如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧MN 的长度.。
第24章 圆 初中数学人教版九年级上册小结与复习课件

(3) 圆锥的侧面积为 πlr ; (4) 圆锥的全面积为 πlr πr2 .
5. 圆内接正多边形的计算
(1)
正
n
边形的中心角为
360° n
.
(2) 正 n 边形的边长 a,半径 R,边心距 r 之间的关系为
R2 r2 (a)2. 2
(3) 边长为 a,边心距 r 的正 n 边形的面积为
半径决定大小;(2) 不在同一条直线上的
三个点确定一个圆.
·
9. 圆内接正多边形、外接圆:将一个圆 n (n≥3) 等分, 依次连接各等分点所得到的多边形叫做这个圆的内接 正多边形,这个圆是这个正多边形的外接圆.
10. 三角形的外接圆 外心:三角形的外接圆的圆心叫做这个三角形的外心. [注意] (1) 三角形的外心是三角形三条边的垂直平分 线的交点;(2) 一个三角形的外接圆是唯一的.
针对训练
2.如图 ,四边形 ABCD 为 ☉O 的内接正方形,点 P 为
劣弧 BC 上的任意一点 (不与 B,C 重合),则∠BPC 的
度数是 135° .
A
D
O
B
C
P
例2 如图,已知 A、B、C、D四点都在⊙O上,OB⊥AC,
BC = CD,在下列四个说法中:① AC 2CD ;② AC =
平分弦所对的 两条弧 .
[注意] ①条件中的“弦”可以是直径;②结论中的 “平分弧”指平分弦所对的劣弧、优弧.
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于 这条弦,并且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
2. 圆周角定理及其推论 (1) 圆周角定理:圆周角的度数等于它所对弧上的 圆心角度数的一半. (2) 推论1:在同圆或等圆中,同弧或等弧所对的 圆周角相等;相等的圆周角所对弧相等. [注意] “同弧”指“在一个圆中的同一段弧”; “等弧”指“在同圆或等圆中相等的弧”;“同弧 或等弧”不能改为“同弦或等弦”. (3) 推论2:90° 的圆周角所对的弦是直径. (4) 推论3:圆的内接四边形的对角互补.
初中数学人教九年级上册第二十四章圆-直线和圆的位置关系

1、掌握直线与圆的位置关系。 2、掌握直线和圆的位置关系 的性质与判定的应用。
温故知新
1、点和圆的位置关系有几种?
点到圆心的距离为d,圆
.A.A .C.A.A . B.A.A.A 的半径为r,则:
点在圆外 d>r; 点在圆上 d=r; 点在圆内 d<r.
2、直线和圆的位置关系会有哪几种情况呢?
创设情境 温故探新
太阳要从天边升起来了,便不转眼地望着那里. 果然过了一会儿 ,在那个地方出现了太阳的小半边脸,红是真红,却没有亮光.这个太 阳好像负着重荷似地一步一步,慢慢地努力上升,到了最后,终于冲 破了云霞,完全跳出了海面,颜色红得非常可爱.
---摘自巴金《海上日出》
合作交流探究新知
一 直线与圆的位置关系的定义
2.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条
件
填写d的范围:
d > 5cm
(1)若AB和⊙O相离, 则 d = 5cm;
((32))若若AABB和和⊙⊙OO相相交切,,则则 0cm≤d <; .5cm
范例研讨运用新知
典例精析
例 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆 心,r为半径的圆与AB有怎样的位置关系?为什么? (1) r=2cm;(2) r=2.4cm; (3) r=3cm.
④若C为⊙O外一点,则过点C的直线与⊙O相交
或相离. × ⑤直线a 和⊙O有公共点,则直线a与⊙O相交.×
合作交流探究新知
二
问题1 刚才同学们用直尺在圆上移动的过程中,除
了发现公共点的个数发生了变化外,还发现有什么
量也在改变?它与圆的半径有什么样的数量关系呢
初中数学人教九年级上册第二十四章圆-圆

参考答案:
55 mm OO 4 m
课堂小结
同心圆 定义
圆 同圆
有关 概念
等圆
旋转定义
要画一个确定的 圆,关键是 确定圆心和半径
集合定义
弦(直径) 劣弧
弧 半圆 优弧
同圆半径相等 直径是圆中 最长的弦
半圆是特殊的弧
等弧
能够互相重合的两段弧
A
(3)请任选一条弦,写出这条弦所对的弧
. 答案不唯一,如:弦AF,它所对的弧是 . AF
B E
C
要点归纳
1.根据圆的定义,“圆”指的是“圆周”,而不是“圆面”. 2.直径是圆中最长的弦.
附图解释:
A
连接OC, 在△AOC中,根据三角形三边关系
·O
C
有AO+OC>AC,
B
而AB=2OA,AO=OC,所以AB>AC.
等圆 半径相同,圆心不同
想一想:1.以1cm为半径能画几个圆,以点O为圆心能画几个圆?
无数个圆
无数个圆
2.如何画一个确定的圆?
问题 从画圆的过程可以看出什么呢?
(1)圆上各点到定点(圆心O)的距离都等于 定长r . (2)到定点的距离等于定长的点都在 同一个圆上 .
圆的集合定义 圆心为O、半径为r的圆可以看成是所有 到定点O的距离等于定长r的点的集合.
D
r
A
C
r O· r
r r
E
要点归纳
圆的基本性质 同圆半径相等.
•o
典例精析
例1 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
初中数学人教九年级上册第二十四章 圆 圆周角定理PPT

(2)∵BA=BC,∴∠A=∠C. 由圆周角定理得∠A=∠E, ∴∠C=∠E,∴DC=DE.
27
28
知识点三:圆周角定理的推论
合作探究
先独立完成导学案互动探究1、3, 再同桌相互交流,最后小组交流;
1.如图,在⊙O中,弦AB=3cm,点C在 ⊙O上,∠ACB=30°.求⊙O直径. 2.如图,AB是⊙O的直径,BD是⊙O的弦 ,延长BD到点C,使AC=AB,BD与CD的 大小有什么关系?为什么?
B A
O A
O B
知识点三:圆周角定理的推论
学以致用
1、如图,AB是半圆的直径,点D是AC的中
点,∠ABC=50°,则∠DAB等于( ) C
A.55°B.60°C.65°D.70°
B
A
O
2.如图,⊙O的半径为1,AB是⊙O的一条
弦,且AB= 3,则弦AB所对的圆周角的度 A
数为( )D A.30º B.60º C.30º或150 º D.60º或120º
如果AB=CD,那么∠E和∠F是什么关系? O1 D
反过来呢?
C
A
F
结合⑴、⑵你能得到什么结论?
O2
B
21
知识点三:圆周角定理的推论
归纳总结
圆周角定理推理1
同弧或等弧所对的圆周角相等; 在同圆或等圆中,相等的圆周角所对的弧相等.
∵ AB=CD ∴∠E=∠F
在⊙O中∵∠E=∠F ∴AB=CD
E
A
F
O D
对的弧也相等;②两条弦相等,弦所对的弧也相等;③弦
心距弦心距所对的弦相等;④两个圆周角相等,圆周角所
对的弧相等;⑤弧相等弧所对的弦相等;
C
⑥弧相等弧所对的圆周角也相等。
24.1.1 圆
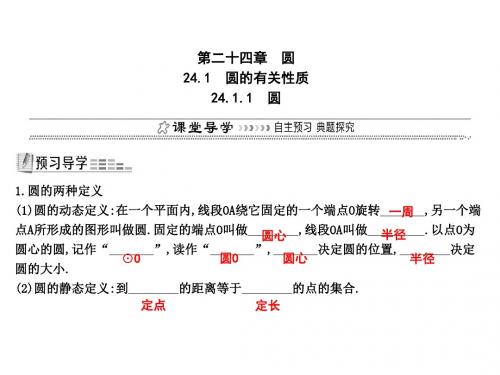
4.顺次连接圆内两条相交直径的4个端点,围成的四边形一定是( )
(A)梯形 (B)菱形 (C)矩形 (D)正方形 C
5.如图,AB是☉O的直径,点C,D在☉O上,∠BOC=110°,AD∥OC,则∠AOD等于( D )
(A)70°(B)60°
(C)50°(D)40°
6.下列语句中,正确的有( ) ①相等的圆心角所对的弧相等A ;
类型二:圆的定义应用 例2 如图,四边形ABCD是正方形,对角线AC,BD交于点O. 求证:点A,B,C,D在以O为圆心的圆上.
证明:∵四边形ABCD是正方形, ∴OA=OB=OC=OD, ∴点A,B,C,D在以O为圆心的圆上.
【方法技巧】 圆可以看作是到定点的距离等于定长的点的集合.
1.下列命题中,其中正确的有( A )
(2)圆的静态定义:到
的距离等于
的点的集合.
定点
定长
2.与圆的有关概念
(1)弦:连接圆上任意两点的 线段 叫做弦,
直径:经过圆心的 弦 叫做直径.
直径:经过圆心的 弦 叫做直径.
(2)弧:
任意两点间的部分叫做圆弧,简称弧.半圆:圆的任意一条
半圆.
弧
的两 直径
优弧: 大于 半圆的弧叫做优弧.用 三 个点表示,如图中 是优弧.
⑦等弧的长度相等
【规律总结】 直径是圆中经过圆心的特殊的弦,是最长的弦,并且等于半径的2倍, 是在研究圆的问题中出现次数最多的重要线段,但弦不一定是直径,过圆上一点和圆 心的直径有且只有一条;半圆是弧,而弧不一定是半圆;“同圆”是指圆心相同,半径 相等的圆,“同心圆”“等圆”指的是两个圆的位置、大小关系;判定两个圆是否是 等圆,常用的方法是看其半径是否相等,半径相等的两个圆是等圆;“等弧”是能够 互相重合的两条弧,而长度相等的两条弧不一定是等弧.
人教版初中数学九上第二十四章 圆 24.2.2 第2课时 切线的判定与性质

A.35°
B.45°
C.55°
D.65°
返回首页
上一页
下一页
先 锋 图 书
基础题组
中档题组
综合运用
6.如图,直线 l 为☉O 的切线,A 为切点,B 为直线 l 上一点,连接 OB,交
☉O 于点 C.若 AB=12,OA=5,则 BC 的长为
( D )
A.5
B.6
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,∴OC∥BD.
∵BD⊥CD,∴OC⊥CD.
∵点C在☉O上,∴CD为☉O的切线.
返回首页
上一页
下一页
先 锋 图 书
基础题组
中档题组
综合运用
知识点二 切线的性质
5.(2021·长春)如图,AB 是☉O 的直径,BC 是☉O 的切线.若∠BAC=
∵BC∥DE,∴∠E=∠ACB=45°.
由(1)知OD⊥DE,∴∠ODE=90°,
∴△ODE为等腰直角三角形,∴DE=OD=5.
在Rt△ODE中,OD2+DE2=OE2,
返回首页
上一页下一页Fra bibliotek先 锋 图 书
基础题组
中档题组
综合运用
14.如图,以 Rt△ ABC 的边 AC 为直径作☉O 交斜边 AB 于点 E,连接 EO 并
点”,其他条件不变,则∠ACB 的度数为
55°或125°
.
返回首页
上一页
下一页
先 锋 图 书
基础题组
中档题组
综合运用
13.(2021·郴州)如图,△ ABC 是☉O 的内接三角形,AC 是☉O 的直径,D
人教版初中九年级全一册数学素养课件 第二十四章 圆 正多边形和圆

人教版·数学 九年级全
第二十四章 圆
24.3 正多边形和圆
知识点 正多边形及其外接圆
蜂窝构造非常精巧,蜂房由许多大小、形 状都相同的房孔组成,房孔都是正六边形,正六 边形的六个顶点在同一圆上,该圆的圆心就是 这个正六边形的中心.
ห้องสมุดไป่ตู้
知识点 正多边形及其外接圆
不是任何多边形(边数大于3)都有外接圆和内切圆, 但任何正多边形都有一个外接圆和一个内切圆,这两个 圆是同心圆.
知识点 正多边形的画法
设计美丽的图案:
(1)以圆的三等分点为圆心,圆的半径为半径作三 条弧; (2)以正六边形各边的中点为圆心,正六边形的边 长为直径向圆外画半圆; (3)作圆的内接正五边形,再以正五边形的各个顶 点为圆心,边长为半径画十条弧.
知识点 正多边形及其外接圆
(1)正多边形的对称性:所有的正多边形都是轴对称图形,一个正 n边形共有n条对称轴,每条对称轴都通过正n边形的中心.n为偶 数时,它还是中心对称图形,它的中心就是对称中心. (2)圆的外切正n边形:把圆分成n(n≥3)等份,经过各分点作圆的 切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边 形.一定要注意正多边形的半径是指外接圆的半径而不是内切圆 的半径. (3)边心距与弦心距的关系:边心距是正多边形的中心到正多边 形一边的距离,此时的边心距也可以看作正多边形的外接圆中, 圆心到多边形的边(即外接圆的弦)的距离,即边心距也是弦心距; 但弦心距不一定是边心距.
人教版九年级初中数学上册第二十四章圆切线的性质定理

判定定理的表述
圆切线的判定定理:过圆外一点有且只有一条直线与圆切于一点。
证明方法:利用反证法,假设过圆外一点有两条直线与圆切于一点,则这两条直线重合,这 与已知条件矛盾,因此假设不成立,故原命题成立。
应用:在解题过程中,可以利用圆切线的判定定理来判断某一直线是否为圆的切线。
注意事项:在应用圆切线的判定定理时,需要注意前提条件是“过圆外一点”,否则结论可 能不成立。
性质定理的证明
定义:圆切线的定义是过半径的外端且垂直于这条半径的直线 性质定理:从圆外一点引圆的两条切线,它们的切线长相等 证明方法:利用相似三角形的性质进行证明 定理的应用:在解题中,可以利用这个定理来证明一些与圆有关的题目
求解与圆切线相关的问题
圆切线的定义和性质 圆切线的判定方法 圆切线的应用举例 圆切线与其他几何图形的联系
判定定理的应用
判定圆内接四边形的对角是否互补 判定一个四边形是否为圆外切四边形 判定一个四边形是否为圆内接四边形 判定一个四边形是否为圆外切四边形
性质定理的表述
圆切线的定义:过半径的外端,并且垂直于这条半径的直线是圆的切线。 性质定理:从圆外一点引圆的两条切线,它们的切线长相等。 性质定理的证明:利用勾股定理和切线的定义进行证明。 性质定理的应用:在解题中利用此定理进行证明和计算。
注意事项:注意题 目中的隐含条件, 避免出现错误
拓展:通过练习和 巩固,提高解题能 力和思维水平
与圆切线相关的其他知识点
圆切线的定义和性质
圆切线的判定定理
圆切线的应用
圆切线与其他几何图形的联系
拓展知识的应用领域
几何学:圆切线在几 何学中有着广泛的应 用,如圆内接四边形、 圆与圆的位置关系等
物理学:圆切线在 物理学中也有着重 要的应用,如圆周 运动、弹性力学等
初中数学圆知识点总结

初中圆知识点总结第二十四章圆1.圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心,定长称为半径。
2.圆心角和圆周角:顶点在圆心上的角叫做圆心角。
顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
3.内心:过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心,三角形的外心是三角形三边的垂直平分线的交点,外心到三角形三个顶点的距离相等(等于半径)。
3、外心:和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心,三角形的内心是三个内角平分线的交点,内心到三角形三边的距离相等(等于半径)。
5.扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。
6.圆锥侧面展开图是一个扇形。
这个扇形的半径称为圆锥的母线。
7.点和圆的位置关系:设⊙O的半径为r,点P到圆心O的距离是PO,(1)P 在⊙O外⇔PO>r;(2)P在⊙O上⇔PO=r;(3)P在⊙O内⇔PO<r。
8.直线与圆有3种位置关系:设⊙O的半径为r,圆心到直线 的距离为d,(1)直线 与⊙O相离⇔d>r;(2)直线 与⊙O相切⇔d=r;(3)直线 与⊙O相交⇔d<r.9.两圆之间有5种位置关系:两圆圆心之间的距离d叫做圆心距,两圆的半径分别为R和r,且R≥r:(1)外离⇔d>R+r;(2)外切⇔d=R+r;(3)相交⇔R-r <d<R+r;(4)内切⇔d=R-r(R>r);(5)内含⇔d<R-r(R>r)。
10.切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线。
11.切线的性质:(1)经过切点垂直于这条半径的直线是圆的切线。
(2)经过切点垂直于切线的直线必经过圆心。
(3)圆的切线垂直于经过切点的半径。
12、切线长定理:从园外一点引圆的两条切线,它们的切线长相等,这一点与圆心的连线平分两条切线的夹角。
13.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
14.有关定理:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(2)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(3)在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.(5)园内接四边形对角互补14、(1)正n 边形的中心角=n 3600;(2)正n 边形的中心角=它的一个外角=n360015、圆的计算公式: (1)圆的周长d 2ππ==R C ;(2)圆的面积2R S π=;(3)扇形弧长180R n π= ;(4)扇形面积R R S 21360n 2==π;(5)圆锥侧面积母侧 R S π=;(6)圆锥表面积母圆锥全 r r S ππ+=2;(7)rh S π2=圆柱侧;(8)22r 2r h S ππ+=圆柱全。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四章圆
24.1 圆的有关性质
24.1.1 圆
1.平面内到定点的距离等于定长的所有点组成的图形叫做圆.其中,定点称为圆心,定长称为半径,以点O为圆心的圆记作“☉O”,读作“圆O”.
2.确定圆的基本条件:(1)、圆心:定位置,具有唯一性,(2)、半径:定大小.
3.半径相等的两个圆叫做等圆,两个等圆能够完全重合.
4.连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.
5.圆上任意两点间的部分叫做圆弧,简称弧,弧用符号“⋂”表示,圆的任意一条直径的两个端点分圆成为两条等弧,每一条弧都叫做半圆,大于半圆的弧称为优弧,小于半圆的弧称为劣弧.
6.在同圆或等圆中,能过重合的两条弧叫做等弧.
24.1.2 垂直于弦的直径
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧.
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB是直径②AB CD
⊥③CE DE
=④弧BC=弧BD⑤弧AC=弧AD
中任意2个条件推出其他3个结论.
推论2:圆的两条平行弦所夹的弧相等. 即:在⊙O中,∵AB∥CD
AC=弧BD
B
D
24.1.3 弧、弦、圆心角
1.顶点在圆心的角叫做圆心角.圆心角的度数与他所对的弧的度数相等.
2.圆心角定理:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等.此定理也称1推3定理,即上述四个结论中,
只要知道其中的1个相等,则可以推出其它的3个结论, 即:①AOB DOE ∠=∠;②AB DE =;
③OC OF =;④弧BA =弧BD
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等,所对的弦相等. 在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角相等,那他们所对的优弧劣弧分别相等. 24.1.4 圆周角
1.顶点在圆上,并且两边都和圆相交的角叫做圆周角.
2.圆周角定理:同弧所对的圆周角等于它所对的圆心角(或弧的度数)的一半.
即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠ 3.圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;
即:在⊙O 中,∵C ∠、D ∠都是所对的圆周角
∴C D ∠=∠
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径.
即:在⊙O 中,∵AB 是直径或∵90C ∠=︒ ∴90C ∠=︒∴AB 是直径
推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
即:在△ABC 中,∵OC OA OB == ∴△ABC 是直角三角形或90C ∠=︒
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理.
注:忽略一条弦所对的弧有两条,所对的圆周角边有两种不同的角.
4.一般的,如果一个多边形的所有顶点都在同一个圆上,那么这个多边形叫做圆的内接多边形,这个圆叫做多边形的外接圆.
圆的内接四边形定理:圆的内接四边形的对角互补. 推论:圆内接四边形任何一个外角都等于他的内对角. 即:在⊙O 中,∵四边形ABCD 是内接四边形 ∴180C BAD ∠+∠=︒180B D ∠+∠=︒
DAE C ∠=∠
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
1.点与圆的位置关系是由这个点到圆心的距离d 与半径r 的大小关系决定的.
B
A
B
A
O
(1)点在圆内⇒d r <⇒点C 在圆内;
(2)点在圆上⇒d r =⇒点B 在圆上;
(3)点在圆外⇒d r >⇒点A 在圆外;
2.不在同一直线上的三个点确定一个圆且唯一一个.
3.三角形的三个顶点确定一个圆,经过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.
4.与三角形三边都相切的圆叫做这个三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.三角形的内切圆是三角形内面积最大的圆,圆心是三个角的角平分线的交点,他到三条边的距离相等:内心到三顶点的连线平分这三个角.
24.2.2 直线与圆的位置关系
1.如果圆O 的半径为r ,圆心O 到直线l 的距离为d ,那么: (1)直线与圆相离⇒d r >⇒无交点; (2)直线与圆相切⇒d r =⇒有一个交点; (3)直线与圆相交⇒d r <⇒有两个交点;
2.直线和圆有唯一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
A
的直线是圆
(1)切线的判定定理:过半径外端且垂直于半径的切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵MN OA ⊥且MN 过半径OA 外端 ∴MN 是⊙O 的切线
(2)性质定理:圆的切线垂直于过切点的半径(如上图) 推论1:过圆心垂直于切线的直线必过切点. 推论2:过切点垂直于切线的直线必过圆心. 以上三个定理及推论也称二推一定理:
即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个.
连接圆心与切点间的线段是解圆的切线问题时常用的辅助线,通常叙述为:“见切点连半径得垂直”.解决与圆的切线有关的问题时,常需要补充的线是作过切点的半径. 3.切线长定理
在经过圆外一点的圆的切线上,这点到切点之间的线段的长叫做这点到圆的切线长. 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,
圆心和圆外这一点的连线平分两条切线的夹角.
即:∵PA 、PB 是的两条切线 ∴PA PB =
PO 平分BPA ∠
4.圆的公切线
两圆公切线长的计算公式:
(1)公切线长:
12Rt O O C
∆
中,
221AB CO ==
(2)外公切线长:2CO 是半径之差;内公切线长:2CO 是半径
之和.
24.3 正多边形和圆
各边相等,各角也相等的多边形叫做正多边形.
把一个圆分成相等的弧,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做正多边形的外接圆.经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切多边形,这个圆叫做多边形的内切圆.
正多边形的外接圆(或内切圆)的圆心叫做正多边形的中心.正多边形外接圆的半径叫做正多边形的半径.正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角,正多边形内切圆半径叫做正多边形的边心距.
正n 边形的半径R 与边心距r 把正n 边形分成2n 个全等的直角三角形.
00n 0222n n n 360180=a =2sin ;
n 1801
cos ;(a );C a ;
2
11
=a n=C .
22n n n n n n n R n r R R r n n S r r α==+=••关系式:中心角;边长边心距周长面积
(1)正三角形
在⊙O 中△ABC 是正三角形,有关计算在Rt BOD ∆中进行
:
::2OD BD OB =;
(2)正四边形
同理,四边形的有关计算在Rt OAE ∆
中进行,::OE AE OA = (3)正六边形
同理,六边形的有关计算在Rt OAB ∆
中进行,::2AB OB OA =.
24.4 弧长和扇形面积
1、扇形:(1)弧长公式:
180n R l π=;
(2)扇形面积公式:
2
1
3602n R S lR π=
=
n :圆心角R :扇形多对应的圆的半径l :扇形弧长S :扇形面积
l
O。
