江淮名校联考2020届高三最新模拟卷(二)文科数学试题(含解析)
安徽省江南十校2020届高三数学冲刺联考二模试题文

2020年“江南十校”高三学生冲刺联考(二模)文科数学第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{|4}xA y y e ==-+,{|lg[(2)(3)]}B x y x x ==+-,则下列关系正确的是( ) A .A B ⊆ B .AB =∅C .R R C A C B ⊆D .R C B A ⊆2.若复数(23)z i i =--(i 是虚数单位),则z 的共轭复数是( )A .32i -B .32i +C .32i --D .32i -+3.已知向量a 与b b -也是单位向量,则向量a 与b 的夹角为( ) A .45 B .60 C .90 D .1354.已知0.44a =,0.612b -⎛⎫= ⎪⎝⎭,12log c =-,则a ,b ,c 的大小关系是( )A .a b c <<B .c a b <<C .c b a <<D .b c a << 5.下列命题中,真命题的个数是( )①已知直线1l :(1)20mx m y +++=,2l :(1)(4)30m x m y ++++=,则“2m =-”是“12l l ⊥”的充要条件;②“若22am bm <,则a b <”的逆否命题为真命题;③命题“若220a b +=,则0a b ==”的否命题是“若220a b +≠,则a ,b 至少有一个不等于0”;④命题p :[1,)x ∀∈+∞,ln 0x >,则p ⌝:0[1,)x ∃∈+∞,0ln 0x <. A .0 B .1 C .2 D .36.已知等差数列{}n a 的公差为d ,前n 项和为n S ,22017OA a OB a OC =+且AB d BC =,则2018S ( )A .0B .1009C .2017D .20187.已知实数x ,y 满足24010ln 0x y y y x --≤⎧⎪+≥⎨⎪-≤⎩,则1x y z x ++=的最大值是( )A .1B .2C .3D .48.已知实数[0,4]m ∈,则函数21()ln 2f x m x x x=-+在定义域内单调递减的概率为( ) A .14 B .12 C .34 D .589.已知某几何体的三视图如图所示,则该几何体的体积为( )A .20B .30C .40D .60 10.已知1F ,2F 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且123F PF π∠=,记椭圆和双曲线的离心率分别为1e ,2e ,则1213e e +的最大值为( ) A .223B .233C .23D .2211.执行如图所示的程序框图,则输出的结果为( )A .18-B .18 C .116- D .11612.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且A 是B 和C 的等差中项,0AB BC ⋅>,a =ABC ∆周长的取值范围是( )A .2322⎛⎫+⎪ ⎪⎝⎭ B .32⎫+⎪⎪⎭C .⎝⎭D .⎝⎭第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置) 13.下表提供了某学生做题数量x (道)与做题时间y (分钟)的几组对应数据:根据上表提供的数据,求出y 关于x 的线性回归方程为0.70.7y x =+,则表中t 的值等于 .14.已知双曲线C :221916x y -=的左右焦点为1F 、2F ,过焦点且与渐近线平行的直线与双曲线相交于点M ,则12MF F ∆的面积为 .15.已知O 为坐标原点,动点P 满足3OP =,M 、N ,则OM ON OP ++的最小值为 .16.已知函数()f x 的定义域是R ,21,(0)()9ln(2),(0)x mx x f x x x π⎧-++≤=⎨++>⎩(m 为小于0的常数),设12x x <且12'()'()f x f x =,若21x x -的最小值大于6,则m 的取值范围是 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内)17.已知等差数列{}n a 前n 项和为n S ,且满足2*3()n n a S n n n N +=+∈.(1)求数列{}n a 的通项公式;(2)设2111n n n c a S =+-,数列{}n c 的前n 项和为n T ,求证:5362n T ≤<. 18.距离2018年全国普通高等学校统一招生考试已不足一个月,相信考生们都已经做了充分的准备,进行最后的冲刺.高考的成绩不仅需要平时的积累,还与考试时的状态有关系.为了了解考试时学生的紧张程度,对某校500名学生进行了考前焦虑的调查,结果如下:男女总计正常 30 40 70 焦虑 270 160 430 总计300200500(1)根据该校调查数据,能否在犯错误的概率不超过0.01的前提下,认为“该学校学生的考前焦虑情况”与“性别”有关?(2)若从考前正常的学生中按性别用分层抽样的方法抽取7人,再从被抽取的7人中随机抽取2人,求这两人中有女生的概率.附:22()()()()()n ad bc K a b c d a c b d -=++++,n a b c d =+++.20()P K k ≥0.258 0.15 0.10 0.05 0.025 0.010 0k1.3232.0722.7063.8415.0246.63519.如图,三棱锥D ABC -中,2AB =,2AC BC ==,ADB ∆是等边三角形且以AB 为轴转动.(1)求证:AB CD ⊥;(2)当三棱锥D ABC -体积最大时,求它的表面积.20.如图所示,已知抛物线22(0)y px p =>的焦点为F ,M 是抛物线上第一象限的点,直线l 与抛物线相切于点M .(1)过M 作HM 垂直于抛物线的准线于点H ,连接MF ,求证:直线l 平分HMF ∠; (2)若1p =,过点M 且与l 垂直的直线交抛物线于另一点Q ,分别交x 轴、y 轴于A 、B两点,求AB ABAM AQ+的取值范围. 21.已知函数ln ()a xf x x+=,()g x mx =. (1)求函数()f x 的单调区间;(2)当0a =时,()()f x g x ≤恒成立,求实数m 的取值范围;(3)当1a =时,求证:当1x >时,11(1)()21x x x f x e e ⎛⎫⎛⎫++>+ ⎪ ⎪⎝⎭⎝⎭. 请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分,作答时请写清题号. 22.选修4-4:坐标系与参数方程在极坐标系中,已知直线l 的极坐标方程为1sin 32πρθ⎛⎫+= ⎪⎝⎭.以极点为坐标原点,极轴为x 轴正半轴建立直角坐标系xOy ,曲线C 的参数方程为244x my m =⎧⎨=⎩(m 为参数). (1)求直线l 的直角坐标方程和曲线C 的普通方程;(2)已知点3,2)P -,直线l 和曲线C 相交于A ,B 两点,求PA PB ⋅. 23.选修4-5:不等式选讲设对于任意实数x ,不等式53x x m ++-≥恒成立. (1)求m 的取值范围;(2)当m 取最大值时,解关于x 的不等式324x x m --≤-.2020年“江南十校”高三学生冲刺联考(二模)文科数学参考答案一、选择题1-5: CDACC 6-10: BBCAD 11、12:BB 二、填空题13. 6 14. 32315. 3 16. (16)-∞ 三、解答题17.解:(1)23n n a S n n +=+,当1n =时,11142a S a +=⇒=, 当2n =时,2122104a a a a ++=⇒=, 又∵{}n a 是等差数列,∴212d a a =-=,∴2(1)22n a n n =+-⨯=; (2)2211111(21)(21)n n n c a S n n n n =+=+-+-+11111221211n n n n ⎛⎫⎛⎫=-+- ⎪ ⎪-++⎝⎭⎝⎭. ∴n T =111111123352121n n ⎛⎫-+-+⋅⋅⋅+- ⎪-+⎝⎭1111112231n n ⎛⎫+-+-+⋅⋅⋅+- ⎪+⎝⎭111112211n n ⎛⎫⎛⎫=-+- ⎪ ⎪++⎝⎭⎝⎭31122(21)1n n ⎛⎫=-+ ⎪++⎝⎭. 当*n N ∈且n 逐渐增大时,n T 增大. ∴5362n T ≤<. 18.解:(1)假设该学校学生的考前焦虑与性别无关22500(3016027040)43070300200K ⨯-⨯=⨯⨯⨯30009.967 6.635301=≈>,∴在犯错误的概率不超过0.01的前提下,该学校学生的考前焦虑情况与性别有关; (2)男生、女生分别抽取3人,4人.记为1A ,2A ,3A ,1B ,2B ,3B ,4B .基本事件为:12A A ,13A A ,11A B ,12A B ,13A B ,14A B ,23A A ,21A B ,22A B ,23A B ,24A B ,31A B ,32A B ,33A B ,34A B ,12B B ,13B B ,14B B ,23B B ,24B B ,34B B .满足条件的有:11A B ,12A B ,13A B ,14A B ,21A B ,22A B ,23A B ,24A B ,31A B ,32A B ,33A B ,34A B ,12B B ,13B B ,14B B ,23B B ,24B B ,34B B .∴186217m P n ===. 19.(1)证明:取AB 的中点H ,连接DH ,CH ,AC BC AB CHADB AB DH CH DH H⎫==⊥⎪∆⇒⊥⎬⎪=⎭是等边三角形AB CDH AB CD CD CDH ⊥⎫⇒⇒⊥⎬⊂⎭平面平面;(2)解:111333ABC hV S h h ∆=⨯⨯=⨯⨯=,∴若V 最大,则h 最大. ∴平面ADB ⊥平面ABC .此时ABC ADB ACD BCD S S S S S ∆∆∆∆=+++表1=+20.(1)证明:设2(2,2)(0)M pt pt t >则,22p H pt ⎛⎫- ⎪⎝⎭,直线HF 的斜率122pt k t p ==--,由22(0)y px p =>得y =, ∴直线l的斜率212k t==, ∴121(2)12k k t t⋅=-⋅=-,∴l HF ⊥. 又由抛物线定义MF MH =,∴l 平分HMF ∠; (2)解:当1p =时,2(2,2)M t t ,AB 的方程:222(2)y t t x t -=--,∴2(12,0)A t +,3(0,24)B t t +.∴3224212B M AB y t t t AM y t+===+,由2222(2)2y t t x t y x⎧-=--⎪⎨=⎪⎩23420ty y t t ⇒+--=, ∴1122Q Q t y y t t t+=-⇒=--,∴342242421212B Q ABy t t t t AQ y t t t++===-++, ∴4222422121AB AB t t t AM AQ t ++=+++22222141(1,)t t t =++=+∈+∞. 21.(1)解:ln ()a xf x x+=的定义域为(0,)+∞, 且221(ln )1ln '()a x x af x x x -+--==. 由'()01ln 0f x x a >⇒-->1ln 10ax a x e -⇒<-⇒<<,∴()f x 在1(0,)ae-单调递增,在1(,)a e -+∞单调递减;(2)解:0a =,ln ()xf x x=, ∴ln ()()x f x g x x ≤⇔2ln xmx m x≤⇔≥, 令2ln ()x u x x =,∴312ln '()xu x x-=,由'()00u x x >⇒<<∴()u x在单调递增,在)+∞单调递减,∴max ln 1()2u x u e e ===,∴12m e ≥; (3)证明:11(1)()21x x x f x e e ⎛⎫⎛⎫++>+ ⎪ ⎪⎝⎭⎝⎭等价于11(1)(ln 1)211x x x x e e x xe -++⋅>++. 令(1)(ln 1)()x x p x x ++=,则2ln '()x xp x x -=,令()ln x x x ϕ=-则11'()1x x x xϕ-=-=,∵1x >,∴'()0x ϕ>,∴()x ϕ在(1,)+∞单调递增,()(1)10x ϕϕ>=>,'()0p x >,∴()p x 在(1,)+∞单调递增,∴()(1)2p x p >=,∴()211p x e e >++, 令12()1x x e h x xe -=+,则122(1)'()(1)x x x e e h x xe --=+,∵1x >,∴10xe -<,∴'()0h x <,()h x 在(1,)+∞单调递减, ∴当1x >时,2()(1)1h x h e <=+, ∴()2()11p x h x e e >>++,即11(1)()21x x x f x e e ⎛⎫⎛⎫++>+ ⎪ ⎪⎝⎭⎝⎭.22.解:(1)l10y +-=,C 的普通方程:24x y =;(2)2)P -在l 上,l的参数方程为1222x t y t ⎧=⎪⎪⎨⎪=-+⎪⎩(t 为参数),将l 的参数方程代入C得:21422t ⎛⎫⎫=⨯-+ ⎪⎪ ⎪⎭⎝⎭,即2440t -+=, ∴1244t t =,∴1244PA PB t t ==.23.解:(1)设()53f x x x =++-,则有22,5()8,5322,3x x f x x x x --<-⎧⎪=-<<⎨⎪+>⎩,根据函数的单调性有8m ≤.即m 的取值范围(,8]-∞;(2)当8m =时,324x x --≤,∴324x x -≤+, 当3x ≥时,原不等式324x x -≤+,7x ≥-,∴3x ≥; 当3x <时,原不等式324x x -≤+,13x ≥-,∴133x -≤<, ∴原不等式解集为1,3⎡⎫-+∞⎪⎢⎣⎭.。
2020届安徽省合肥市高三第二次模拟考试数学(文)试卷及解析

2020届安徽省合肥市高三第二次模拟考试数学(文)试卷★祝考试顺利★(解析版)第Ⅰ卷 (满分60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}{1,3,5,7},|28==>x A B x ,则A B =( )A. {1}B. {1,3}C. {5,7}D. {3,5,7}【答案】C【解析】 求出集合A ,B ,由此能求出A ∩B .【详解】∵集合A ={1,3,5,7},B ={x |2x >8}={x |x >3},∴A ∩B ={5,7}.故选:C .2.欧拉公式i e cos isin θθθ=+把自然对数的底数e ,虚数单位i ,三角函数cos θ和sin θ联系在一起,充分体现了数学的和谐美,被誉为“数学的天桥”,若复数z 满足()i i i e z π+⋅=,则z =( )A. 1B. 2C. 2【答案】B【解析】由新定义化为复数的代数形式,然后由复数的除法运算求出z 后再求模. 【详解】由题意(1)cos sin 1(1)(1)i ii i i i z e i i i i i i πππ--====+++-+-+--111222i i -+==-,∴2z ==. 故选:B .【点睛】本题考查复数的新定义,考查复数的除法运算和求复数的模,解题关键是由新定义化i e π为代数形式,然后求解.3.若实数x ,y 满足约束条件240403230x y x y x y +-≥⎧⎪-+≥⎨⎪+-≥⎩,则2z x y =-的最小值是( )A. 5-B. 4-C. 7D. 16 【答案】B【解析】作出可行域,作出目标函数对应的直线,平移该直线可得最优解.【详解】作出可行域,如图射线BA ,线段BC ,射线CD 围成的阴影部分(含边界),作直线:20l x y -=,向上平移直线l 时2z x y =-减小,∴当l 过点(0,4)B 时,2z x y =-取得最小值-4. 故选:B .。
【附28套精选模拟试卷】安徽省淮北市2020届高三第二次模拟考试文科数学试卷(含答案)
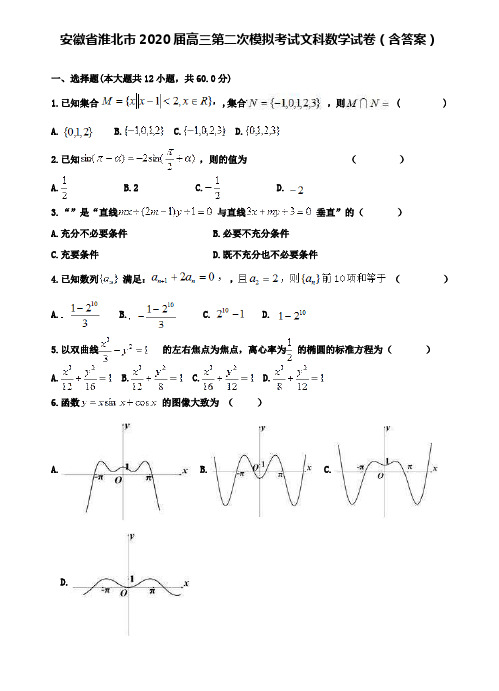
安徽省淮北市2020届高三第二次模拟考试文科数学试卷(含答案)一、选择题(本大题共12小题,共60.0分)1.已知集合 ,集合,则 ( )A. B. C. D.2.已知,则的值为()A. B.2 C. D.3.“”是“直线与直线垂直”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知数列满足:,()A. B. C. D.5.以双曲线的左右焦点为焦点,离心率为的椭圆的标准方程为()A. B. C. D.6.函数的图像大致为()A. B. C.D.7.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿. 可见“行行出状元”,卖油翁的技艺让人叹为观止. 若铜钱是直径为 3cm的圆,中间有边长为 1cm的正方形孔,若随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴正好落入孔中的概率是()A. B. C. D.8.若执行如图所示的框图,则输出的数S等于()A. B.1 C. D.9.若变量满足约束条件,则的最小值是()A.3B.1C.D.不存在10.在中,点在线段的延长线上,且,点在线段上(与点不重合),若,则的取值范围是()A. B. C. D.11.一个三棱锥的三视图如图所示:则该棱锥的外接球的体积为()A. B.C. D.12.已知为定义在上的单调递增函数,是其导函数,若对任意的总有,则下列大小关系一定正确的是()A. B. C. D.二、填空题(本大题共1小题,共5.0分)13.已知复数,则14.函数的单调递减区间是15.过点引直线与圆相交于两点,为坐标原点,当面积取最大值时,直线的斜率为16.为“精致数列”.已知等差数列的首项为1,公差不为0,若数列为“精致数列”,则数列的通项公式为三、解答题(本大题共8小题,共96.0分)17.(本题满分12分)在中,边、、分别是角、、的对边,且满足,设的最大值为.(Ⅰ)求的值;(Ⅱ)18.(本题满分12分)(I )若初中年级成绩在之间的学生中恰有4名女同学,现从成绩在该组的初中年级的学生任选2名同学,求其中至少有1名男同学的概率;(II )完成下列列联表,并回答是否有的把握认为“两个学段的学生对”四大名著”的了解有差异”?成绩小于60分人数成绩不小于60分人数合计初中年级合计附:临界值表:0.10 0.05 0.0102.7063.841 6.63520.(本题满分12分)已知椭圆 ,的两个焦点为其短轴长是,原点到过点和两点的直线的距离为。
安徽省淮北市2020届高三第二次模拟考试文科数学试卷参考答案(淮北二模)

必考题,每个试题考生都必须作答;第 22、23 题为选考题,考生根据要求作答)
17. (本小题满分 12 分)
解:(Ⅰ) 1 2 3 n n , (n N *) ①
2a1 3 2a2 3 2a3 3
2an 3 2
当
n
1
时,
a1
1 2
,
当 n 2 时, 1 2 3 n 1 n 1 ,② ………………………2 分
19.(本小题满分 12 分)
解:(Ⅰ)由题意设椭圆
C
的方程为
x2 a2
+
y2 b2
1( a
b
0
,c
将双曲线的方程化为标准形式
x2 1
y2 1
1,
22
a2 b2 ),
因为椭圆 C 焦点与双曲线的焦点重合,所以 c 1 + 1 =1,…………………………2 分 22
又点 P(0, 3 )在椭圆 C 上,所以 b 3 , b2 3 , a2 b2 c2 4 .
1)
2(2n1 3
2n11)
,……………………………………8
分
T2020
1 a1a2
1 a2a3
1 a3a4
1 a a 2020 2021
=2[( 1 1)
(1 1 ) 3
(1 1 ) 35
(1 4037
1 )] 4039
=2(1 1 ) 8080 . ………………………………………………………………………12 分 4039 4039
所以 ab 4 2(2 2) ,当且仅当 a b 2(2 2) 时等号成立, 2 2
所以 SABC
1 2
ab sin C
2 ab 4
安徽省江淮十校2020届高三第二次联考数学(文)试题Word版含答案

9.“江淮十校” 2018届高三第二次联考数 学(文科)一、选择题:本大题共 12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有 一个选项是符合题目要求的。
1.已知全集 U = R ,集合 A = {x|y = ln(1 — x)} , B = {x| x 1 2 — 2x v 0)},则 A A B = A. (0, 1) B. (0 , 2) C. (1 , 2) D. 1, 2)呻 呻呻呻呻 呻呻 呻2. 若向量a 、b 满足| a| = 5 , b = (1 , — 3), a • b = 5,则a 与b 的夹角为 A. 90° B. 60° C. 45° D. 30°3.已知p : | m + 1| v 1, q :幕函数y = ( m 2 — m — 1) x m 在(0 ,+^ )上单调递减,则p 是q 的 A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不 必要条件4. 已知等差数列{ a n }的前 n 项和 S n ,若 3( a ? + a 4) + 2( a 6 + a g +) = 12,则 S 11 = A. 6B. 11C. 33D. 485. 下列命题中正确的是A. 命题“ x € 0, 1],使 x 2 — 1 >0” 的否定为“-x € 0, 1],都有x 2 — K 0”B. 若命题p 为假命题,命题q 为真命题,则(—p) V ( -q )为假命题C. 命题“若:• b > 0,则a 与b 的夹角为锐角”及它的逆命题均为真命题D. 命题“若x 2 + x = 0,则x = 0或x =— 1”的逆否命题为“若 X M 0且X M — 1,则x 2 + X M 0” 6.已知函数f(x) = sin ®x+ ..3COS 3X ( W >0)的图像与x 轴交点的横坐标依次构成一个公差 x 轴向右平移[个单位,得到函数g(x)的图像,61 sin2 C已知△ ABC ,角A 、B 、C 的对边分别为 a 、b 、c , b = 2, B = , -S - C = 1,则厶6 1+ COS 2C ABC 的面积为为二的等差数列,把函数2则下列叙述不正确的是 f(x)的图像沿 8.A. g(x)的图像关于点(一 兀,0)对称B. g(x)的图像关于直线 D. g(x)是奇函数x =对称4G 为AB 边上一点,OG 是/ AOB 25OA + mOB ,m€ R ,则EAJ 的值为|OB| A. -2B. 1C.D. 27.在厶AOB 中, C g(x)在4,/上是增函数 的平分线,且OG =奇函数f(x)定义域为(一n 0) U (0 , n ,其导函数是f'(x),当0v x vn 时,有f '(x) sinx—f(x)x > 0,则关于x 的不等式f(x) v 2f 「)sinx 的解集为6A. ( — ■O )U (二,nB.(—O) U (0,二) 6666C. ( — n , —-)U (二,n6 6D. ( — n,-)U (0 ,) 6 6已知数列{ a n }的前n 项和S n , 1 n 定义 n i =1S 为数列{ a n }前 n 项的叠加和,若 2016项数列a 1 , a 2, a s ,…,a 2°16的叠加和为 2 2A. 2017B. 2018C. 2017D. 2018填空题:本大题共4小题,每小题5分,共20分。
安徽省江南十校2020届高三第二次联考数学文试题

(2)设 ,数列 的前n项和为 ,证明: .
20.(12分)
已知函数 ( 为常数, ).
(1)当 时,判断函数 的单调性;
(2)若函数 有两个极值点 , ,且 求实数 的取值范围.
21.(12分)
如图1,在等腰梯形ABCD中, , ,O是CD中点,将 沿AO折起,使平面 平面ABCO.如图2所示,E,F点分别是AB,CD上的点,且 .
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本大题共12小题,每小题5分,共60分、在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知i是虚数单位,则 ()
A. B. C. D.
2.已知集合 , ,则有()
A. B.
C. D.
3.已知向量 , , ,若 ,则实数 ()
A. B. C. D.
则 ,即 ,
∵ ,∴ .
14.32【解析】由 知等比数列 的公比 ,
则由题知 且 ,
则 ,求得 , ,
则 .
15. 【解析】如图,取 ,中点P,连接MP,NP,
由题知MN与BC所成的角即为MN与PN所成的角,
又正方体 的棱长为1,
则 , ,
又 平面 , 平面 ,
所以 ,则 ,
且 ,
故MN与BC所成角的正弦值为 .
17.(10分)
在 中,内角A,B,C所对的边分别为a,b,c,且
(1)求角A的大小;
(2)若 , ,求 的面积.
18.(12分)已知点 , , ,点P为曲线C上任意一点,且满足 .
(1)求曲线C的方程;
(2)若直线l过点M,求直线l被曲线C截得的最短弦长及此时直线l的方程.
2020年安徽省江南十校高考数学模拟试卷(文科)(4月份)(有答案解析)

2020年安徽省江南十校高考数学模拟试卷(文科)(4月份)一、选择题(本大题共12小题,共60.0分)1.已知集合,,则A. B. C. D.2.已知复数为虚数单位,则A. B. C. D.3.某装饰公司制作一种扇形板状装饰品,其圆心角为,并在扇形弧上正面等距安装7个发彩色光的小灯泡且在背面用导线相连弧的两端各一个,导线接头忽略不计已知扇形的半径为30厘米,则连接导线最小大致需要的长度为A. 58厘米B. 63厘米C. 69厘米D. 76厘米4.函数在上的图象大致为A. B.C. D.5.在2020年春节前夕,为了春节食品市场安全,确保人们过一个健康安全的春节,某市质检部门对辖区内的某大型超市中的一品牌袋装食品进行抽检,将超市中该袋装食品编号为1,2,3,,500,从中用系统抽样等距抽样的方法抽取20袋进行检测,如果编号为69的食品被抽到,则下列4个编号的食品中被抽到的是A. 9号B. 159号C. 354号D. 469号6.已知,则A. B. C. D.7.已知,,,则a,b,c的大小关系为A. B. C. D.8.执行如图的程序框图,则输出S的值为A. B. C. D.9.“哥德巴赫猜想”是近代三大数学难题之一,其内容是:一个大于2的偶数都可以写成两个质数素数之和,也就是我们所谓的“”问题,它是1742年由数学家哥德巴赫提出的,我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中做出相当好的成绩,若将6拆成两个正整数的和,则拆成的和式中,加数全部为质数的概率为A. B. C. D.10.在中,角A,B,C的对边分别为a,b,若,,,则的面积为A. B. C. D.11.已知椭圆C:的焦距为2c,F为右焦点,直线与椭圆C相交于A,B 两点,是等腰直角三角形.点P的坐标为,若记椭圆C上任一点Q到点P的距离的最大值为d,则的值为A. B. C. D.12.已知给出下列判断:若,,且,则;存在,使得的图象右移个单位长度后得到的图象关于y轴对称;若在上恰有7个零点,则的取值范围为若在上单调递增,则的取值范围为其中,判断正确的个数为A. 1B. 2C. 3D. 4二、填空题(本大题共4小题,共20.0分)13.已知函数,则曲线在点处的切线方程为______.14.已知双曲线C:的离心率为,则双曲线C的右顶点到双曲线的渐近线的距离为______.15.在直角坐标系xOy中,已知点和点,若点C在的平分线上,且,则向量的坐标为______.16.已知在三棱锥中,A,B,C,D四点均在以O为球心的球面上,若,,,则球O的表面积为______.三、解答题(本大题共7小题,共82.0分)17.已知数列是递增的等比数列,是其前n项和,,.求数列的通项公式;记,求数列的前n项和.18.移动支付是指移动客户端利用手机等电子产品来进行电子货币支付,移动支付将互联网、终端设备、金融机构有效地联合起来,形成了一个新型的支付体系,使电子货币开始普及.某机构为了研究不同年龄人群使用移动支付的情况,随机抽取了100名市民,得到如表格:年龄岁使用移动支付402010442不使用移动支1122410付画出样本中使用移动支付的频率分布直方图,并估计使用移动支付的平均年龄;完成下面的列联表,能否在犯错误的概率不超过的前提下认为使用移动支付与年龄有关系?年龄小于50岁年龄不小于50岁合计使用移动支付不使用移动支付合计附:,19.如图,在四棱锥中,底面ABCD为等腰梯形,,,,为等腰直角三角形,,平面底面ABCD,E为PD的中点.求证:平面PBC;求三棱锥的体积.20.已知函数.当时,讨论的单调区间;若对,成立,求实数a的取值范围.21.已知抛物线C:,若圆M:与抛物线C相交于A,B两点,且.求抛物线C的方程;过点的直线与抛物线C相切,斜率为的直线与抛物线C相交于D,E两点,直线,交于点Q,求证:.22.在直角坐标系xOy中,直线的参数方程为为参数,直线的参数方程为为参数若直,的交点为P,当k变化时,点P的轨迹是曲线C.求曲线C的普通方程;以坐标原点为极点,x轴非负半轴为极轴且取相同的单位长度建立极坐标系,设射线的极坐标方程为,,点Q为射线与曲线C的交点,求点Q的极径.23.已知函数.求不等式的解集;若不等式在R上恒成立,求实数m的取值范围.-------- 答案与解析 --------1.答案:D解析:解:集合,,.故选:D.求出集合A,B,由此能求出.本题考查交集的求法,考查交集定义等基础知识,考查运算求解能力,是基础题.2.答案:A解析:解:,.故选:A.利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.答案:B解析:解:因为弧长比较短的情况下分成6等份,每部分的弦长和弧长相差很小,可以用弧长近似代替弦长,所以导线长度为厘米.故选:B.弧长比较短的情况下分成6等份,每部分的弦长和弧长相差很小,用弧长近似代替弦长,计算导线的长度即可.本题考查了扇形的弧长计算问题,也考查了分析问题解决问题的能力,是基础题.4.答案:C解析:解:根据题意,,有,所以在上为奇函数,其图象关于原点对称,排除A,B,在上,,,,则,排除D;故选:C.根据题意,利用排除法分析:先分析函数的奇偶性,再分析在上,,可得答案.本题考查函数图象的识别,函数的奇偶性,属于基础题.5.答案:D解析:解:由题意得抽样间隔为,因为69号是第三组被抽到,即,可得,则,所以被抽中的初始编号为19号,之后被抽到的编号均是25的整数倍与19的和,四个选项中,只有D选项满足.故选:D.根据系统抽样的抽样方法,抽样间隔为,所以若第一组被抽到的编号为b,则第n组被抽到的编号为,根据69被抽到,故,再计算4个编号的食品中被抽到的即可.本题考查了系统抽样,考查了数列的通项公式得的应用,属于基础题6.答案:C解析:解:由,得,.故选:C.由已知求得,再由,结合诱导公式及倍角公式求解.本题考查三角函数的化简求值,考查诱导公式及倍角公式的应用,是基础题.7.答案:A解析:解:因为,,,故.故选:A.结合指数与对数函数的单调性分别确定a,b,c的范围即可比较.本题主要考查了利用指数函数与对数函数的单调性比较函数值大小,属于基础试题.8.答案:D解析:解:由题意得.故选:D.根据循环体的算法功能可以看出,这是一个对数列求前五项和的程序框图,计算可求解.这是一道程序框图中的循环结构问题,考查了数列求和,需要弄清楚首项与项数,计算要准确.难度不大.9.答案:A解析:解:由古典概型的基本事件的等可能性得6拆成两个正整数的和含有5个基本事件,分别为:,,,,,而加数全为质数的有,拆成的和式中,加数全部为质数的概率为.故选:A.利用列举法求出由古典概型的基本事件的等可能性得6拆成两个正整数的和含有5个基本事件,而加数全为质数的有1个,由此能求出拆成的和式中,加数全部为质数的概率.本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.10.答案:B解析:解:,,,即,,解得,,解得.,解得.则的面积.故选:B.由,利用正弦定理可得:,利用和差公式、诱导公式即可得出利用余弦定理及其,,即可得出三角形面积.本题考查了正弦定理余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.11.答案:C解析:解:由题意可知,,点A的坐标为,将其代入椭圆方程有,又,,解得或舍,,椭圆C的方程可化为.设点Q的坐标为,则,,,即,故选:C.先通过是等腰直角三角形,得出点,代入椭圆方程,并与结合,可得到b与c的关系,从而椭圆C的方程可化为,设点,利用两点间距离公式表示出,再结合配方法即可求得其最大值.本题考查椭圆的几何性质,两点间距离公式和配方法求最值,考查学生的分析能力和运算能力,属于基础题.12.答案:B解析:解:,周期.由条件知,周期为,,故错误;函数图象右移个单位长度后得到的函数为,其图象关于y轴对称,则,,故对任意整数k,,故错误;由条件,得,,故正确;由条件,得,,又,,故正确.故选:B.先将化简,对于由条件知,周期为,然后求出;对于由条件可得,然后求出;对于由条件,得,然后求出的范围;对于由条件,得,然后求出的范围,再判断命题是否成立即可.本题考查了三角函数的图象与性质和三角函数的图象变换,考查了转化思想和推理能力,属中档题.13.答案:解析:解:函数,可知,故切点为,,故,所以曲线在点处的切线方程为,即,故答案为:.根据题意,求出和,即可得解.本题考查了导数的几何意义,是基础题.14.答案:解析:解:设双曲线的焦距为2c,,,,则.故双曲线的右顶点坐标为,一条渐近线方程为.双曲线C的右顶点到双曲线的渐近线的距离为:.故答案为:.由已知结合离心率公式求得b,可得双曲线的一条渐近线方程,再由点到直线的距离公式求解.本题考查双曲线的简单性质,训练了点到直线距离公式的应用,是基础题.15.答案:解析:解:由点C在的平分线上,所以存在,使;又,所以,解得,所以向量.故答案为:.由点C在的平分线上得存在,使,再由求出的值即可.本题考查了平面向量的线性表示与坐标运算问题,是基础题.16.答案:解析:解:设球的半径为R,过A作平面BDC,垂足为,连接,,;由可得;即为的外心,所以球心在射线AO上,在中,,,的外接圆半径满足:;;连接OB,则.故球O的表面积为:.故答案为:.先求出的外接圆半径并确定球心所在位置,再建立等量关系进一步求出球的半径.本题考查球的表面积的求法,考查空间想象能力以及计算能力,是中档题.17.答案:解:数列是递增的等比数列,设公比为q,由题意可得,由,,可得,解得或舍去,则数列的通项公式为;,,,两式相减可得,化简可得.解析:设等比数列的公比为q,,运用等比数列的通项公式,解方程可得公比q,即可得到所求通项公式;求得,由数列的错位相减法求和,结合等比数列的求和公式,计算可得所求和.本题考查等比数列的通项公式和求和公式的运用,考查数列的错位相减法求和,化简运算能力,属于中档题.18.答案:解:样本中使用移动支付的人数为80人,所以每段的频率分别为,,,,,;画出样本中使用移动支付的频率分布直方图,如图所示;所以使用移动支付的平均年龄为;估计使用移动支付的平均年龄为岁;根据题意填写列联表如下,年龄小于50岁年龄不小于50岁合计使用移动支付701080不使用移动支付41620合计7426100计算,所以能在犯错误的概率不超过的前提下认为使用移动支付与年龄有关系.解析:根据题意画出样本中使用移动支付的频率分布直方图,再计算使用移动支付的平均年龄;根据题意填写列联表,计算,对照临界值得出结论.本题考查了频率分布直方图与独立性检验的应用问题,是基础题.19.答案:证明:如图,取PC的中点F,,,,.,,且,四边形ABEF为平行四边形,得,而平面PBC,平面PBC,平面PBC;解:由知,平面PBC,点E到平面PBC的距离等于A到平面PBC的距离,.如图取AB的中点O,连接PO,,,平面平面ABCD,平面平面,平面PAB,平面ABCD,为等腰直角三角形,,,.四边形ABCD为等腰梯形,且,,,梯形ABCD的高为1,则.三棱锥的体积为.解析:取PC的中点F,可得,,再由,,得到四边形ABEF为平行四边形,得,利用线面平行的判定可得平面PBC;由知,平面PBC,则点E到平面PBC的距离等于A到平面PBC的距离,可得,再求出三棱锥的体积得答案.本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.20.答案:解:函数的定义域,,当即时,当,时,,函数单调递增,当时,,函数单调递减,当即时,恒成立,故在上单调递增,当即时,时,,函数单调递减,当时,,函数单调递增;综上可得,当时,函数的单调递增区间,,单调递减区间;当时,函数的单调递增区间,没有递减区间;当时,函数的单调递增区间,,单调递减区间;因为,成立,所以,成立,即恒成立,所以,令,,则,令,,则,所以在上单调递增,且,所以当时,,即,函数单调递减,当时,,即,函数单调递增,故当时,取得最小值,所以.解析:先对函数求导,然后结合导数与单调性的关系对a进行分类讨论,确定导数的符号,即可求解函数的单调性;由已知不等式恒成立,分离参数后转化为求解相应函数的范围,构造函数,结合导数可求.本题主要考查了利用导数研究函数的单调性及不等式的恒成立求解参数范围问题,体现了分类讨论思想及转化思想的应用.21.答案:解:因为抛物线C与圆M关于x轴对称,所以交点A,B关系x轴对称,设,,因为,所以,所以,交点或舍,所以,代入抛物线的方程可得,所以,所以抛物线的方程为:;证明:设直线的方程为,,即,联立方程,整理可得,,可得,所以直线的方程为:,设直线的方程为,点D,E的坐标分别为,,联立可得,即所以,所以.联立方程,整理可得,可得,,,所以,同理可得,所以,所以.解析:由于抛物线和圆的对称性可得A,B关于x轴对称,由弦长可得A的纵坐标,代入圆的方程求出A的横坐标,再将A点代入抛物线的方程,求出p的值,求出抛物线的方程;证明设的直线方程,与抛物线联立,由判别式等于0求出k的值,可得直线的方程,设直线的方程,设D,E的坐标,联立直线,的方程求出交点Q的坐标,求出的值,联立直线的方程,与抛物线联立,求出两根之和,两根之积,,的值及之积可证得.本题考查抛物线的性质及直线与抛物线的综合应用,及求弦长的方法,属于中难题.22.答案:解:直线的参数方程为为参数,转换为直角坐标方程为.直线的参数方程为为参数,转换为直角坐标方程为.联立两直线的方程消去参数k得:.设点由,可得:.代入曲线C,得,解得或舍去,故点Q的极径为.解析:直接利用转换关系的应用,把参数方程极坐标方程和直角坐标方程之间进行转换.利用一元二次方程根和系数关系式的应用求出结果.本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.答案:解:当时,可化为,解得,无解;当时,可化为,解得,故;当时,可化为,解得,故.综上可得,的解集为;不等式在R上恒成立,可得,即,由的最小值为,此时;由,当且仅当时,取得等号,则,所以,即m的取值范围是.解析:由绝对值的定义,去绝对值符号,解不等式,再求并集可得所求解集;由题意可得,结合二次函数的最值求法,以及绝对值不等式的性质可得所求最小值,进而得到m的范围.本题考查绝对值不等式的解法和不等式恒成立问题解法,注意运用分类讨论思想和转化思想,考查化简运算能力,属于中档题.。
2020届高三第二次模拟考试卷 文科数学(一) 含答案解析

2020届高三第二次模拟考试卷文 科 数 学(一)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 满足(12i)1i z +=-,则z =( )A .2B .105C .103 D .3252.已知集合{}3A x x =∈<Z ,{}12B x x x =<->或,则()A B =R I ð( ) A .{0,1,2}B .{1,0,1}-C .{0,3}D .{1,0,1,2}-3.已知8log 7a =,3log 2b =,0.1πc =,则( ) A .a b c <<B .a c b <<C .b a c <<D .c a b <<4.长久以来,人们一直认为黄金分割比例是最美的,人们都不约而同的使用黄金分割,如果一个矩形的宽与长的比例是黄金比例512-(510.6182-≈称为黄金分割比例),这样的矩形称为黄金矩形,黄金矩形有一个特点:如果在黄金矩形中不停分割出正方形,那么余下的部分也依然是黄金矩形,已知下图中最小正方形的边长为1,则矩形ABCD 的长为( )(结果保留两位小数)A .10.09B .11.85C .9.85D .11.095.函数4()()cos (ππf x x x x x=--≤≤且0)x ≠的图象可能为( )A .B .C .D .6.某单位有840名职工,现采用系统抽样方法从中抽取56人做问卷调查,将840人按1,2,3,L ,840随机编号,若442号职工被抽到,则下列4名职工中未被抽到的是( )A .487号职工B .307号职工C .607号职工D .520号职工7.tan 645︒=( )A .23-+B .23--C .23-D .23+8.若向量a ,b 满足||3=a ,||26=b ,且满足(2)+⊥a b a ,则a 与b 的夹角为( )A .π3B .2π3C .π4D .3π49.如图给出的是计算1111352019++++L 的值的一个程序框图,则图中空白框中应填入( )A .123S S i =++ B .121S S i =++ C .11S S i =++ D .121S S i =+- 10.已知双曲线22221(0,0)x y a b a b-=>>的渐近线与圆222(1)sin 130x y -+=︒相切,则该双曲线此卷只装订不密封班级 姓名 准考证号 考场号 座位号的离心率等于( ) A .1sin 50︒B .1cos50︒C .2sin50︒D .2cos50︒11.设ABC △的内角A ,B ,C 的对边分别是a ,b ,c .已知2cos 0b a C -=,sin 3sin()A A C =+,则2bca =( ) A .74B .149C .23D .6912.已知双曲线2222:1(0,0)x y C a b a b-=>>的焦点为1(3,0)F -,2(3,0)F ,过2F 作直线l 与双曲线C 的右支交于点A ,B 两点.若22||4||BF AF =,1||||AF AB =,则C 的方程是( )A .22136x y-= B .22154x y -= C .22163x y -= D .22145x y -=二、填空题:本大题共4小题,每小题5分,共20分. 13.曲线2(3)xy x x e =-在点(0,0)处的切线方程为 . 14.已知数列{}n a 是等比数列,其前n 项和为n S ,113a =,2366a a =,则5S = . 15.函数π()sin()8cos 22xf x x =--的最小值为 .16.如下图,在五面体ABCDEF 中,AB DC ∥,π2BAD ∠=,3CD AD ==,四边形ABFE 为平行四边形,FA ⊥平面ABCD ,5FC =,则直线AB 到平面EFCD 距离为 .三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(12分)为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级100名学生进行不记名问卷调查,得到如下数据:(1)用样本估计总体思想估计该中学一年级学生的近视率;(2)能否认为在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?附:22()()()()()n ad bc K a b c d a c b d -=++++.18.(12分)已知等差数列{}n a 的前n 项和为n S ,且23a =-,60S =. (1)求数列{}n a 的通项公式;(2)求使不等式n n S a >成立的n 的最小值.19.(12分)在直四棱柱1111ABCD A B C D-中,已知1333DC DD AD AB====,AD DC⊥,AB DC∥,E为DC上一点,且1DE=.(1)求证:1D E∥平面1A BD;(2)求点D到平面1BED的距离.20.(12分)已知函数31()sin cos6f x x x x x=--,()f x'为()f x的导数.(1)证明:()f x'在区间π(0,)2上不存在零点;(2)若31()cos16f x kx x x x>---对π(0,)2x∈恒成立,求实数k的取值范围.21.(12分)已知O为坐标原点,椭圆2212yx+=的下焦点为F,过点F且斜率为k的直线与椭圆相交于A,B两点.(1)以AB为直径的圆与2x=(2)在y轴上是否存在定点P,使得PA PB⋅u u u r u u u r为定值,若存在,求出点P的坐标;若不存在,请说明理由.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】在直角坐标系xOy 中,曲线C的参数方程为241m x m y ⎧=⎪+⎪⎨⎪=⎪⎩m 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程是π2sin()16ρθ+=.(1)写出曲线C 的普通方程和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.23.(10分)【选修4-5:不等式选讲】 已知a ,b ,c 为正数,且满足8abc =,证明: (1)(4)(4)(4)216a b c +++≥; (2)222()()()48a b b c c a +++++≥.2020届高三第二次模拟考试卷文科数学(一)答 案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】B【解析】∵(12i)1i z +=-,∴1i (1i)(12i)13i12i (12i)(12i)5z -----===++-, ∴191025255z =+=,故选B . 2.【答案】D【解析】∵{}12B x x x =<->或,∴{12}B x x =-≤≤R ð,又∵{3}{2,1,0,1,2}A x x =∈<=--Z ,∴{1,0,1,2}A B =-R I ð,故选D . 3.【答案】C【解析】∵80log 71a <=<,30log 21b <=<,0.1π1c =>,223log 7log 42a =>=,333log 8log 92b =<=,∴b a <,∴b a c <<. 4.【答案】D 【解析】如下图所示,由题意可知1MK =,设KN x =,则1MF MN x ==+,112GF GM MF x x =+=++=+, 则1232FC MN OC MN HC MN GF x x x =+=+=+=+++=+, ∴32253BF EF EG GF FC GF x x x ==+=+=+++=+, ∴533285BC BF FC x x x =+=+++=+,∵1GM =,KN x =,根据黄金矩形特点可知矩形GMNQ 为黄金矩形,则有15112x -=+,解得512x =,∴518585850.61811.092BC x =+=+⨯+⨯=≈. 5.【答案】A【解析】函数4()()cos (ππf x x x x x=--≤≤且0)x ≠为奇函数,排除B ,D 选项,当πx =时,44()(π)cos ππ0ππf x =-=->,排除C . 6.【答案】D 【解析】由于组距为8401556=,因此选出的号码所成的数列是以15为公差的等差数列, 根据四个选项可知,487442153-=⨯,442307159-=⨯,6074421511-=⨯, 故选A ,B ,C 选项的职工都被抽到. 7.【答案】B【解析】tan 645tan(540105)tan105tan(6045)︒=︒+︒=︒=︒+︒tan60tan 4531231tan60tan 4513︒+︒+===---︒⋅︒-8.【答案】D【解析】∵(2)+⊥a b a ,∴(2)0+⋅=a b a ,即22||0+⋅=a a b ,22||⋅=-a b a ,设a 与b 夹角为θ,则有22||2cos ||||2326θ-===-⋅⨯a a b ,则夹角为3π4. 9.【答案】D【解析】根据选项D 运行程序得,第一次循环,011S =+=,2i =, 第二次循环,113S =+,3i =, 第三次循环,11135S =++,4i =, …,依次类推,第1010次循环,1111352019S =++++L ,1011i =, 退出循环,此时输出的S 是1111352019++++L 的值.10.【答案】B【解析】依题意,可知双曲线的一条渐近线为0bx ay -=,sin130sin 50=︒=︒,故222sin 50b c =︒,可得2222sin 50c a c -=︒,即2211sin 50e -=︒,化简得1cos50e =︒. 11.【答案】D 【解析】由题意得1cos 2b a C =, 又∵sin 3sin A B =,即3a b =,∴2cos 3C =, 由余弦定理得22243c a b ab =+-, 又∵3a b =,∴c =,∴22299bc a b ==. 12.【答案】B【解析】设2||AF m =,则2||4BF m =,根据双曲线定义可得1||2AF a m =+,1||24BF a m =+, ∵122||||||||AF AB AF BF ==+,又∵24a m m m +=+,得12m a =. ∴2||2a AF =,15||2AF a =,2||2BF a =,1||4BF a =.∴2222212125363641644cos cos 0262262a aa a AF F BF F a a +-+-∠+∠=+=⨯⨯⨯⨯,解得25a =.∵3c =,∴222954b c a =-=-=,故双曲线C 的方程为22154x y -=. 二、填空题:本大题共4小题,每小题5分,共20分. 13.【答案】0x y +=【解析】∵22(61)(3)(351)x x xy x e x x e x x e '=-+-=+-,∴结合导数的几何意义可知曲线在点(0,0)处的切线的斜率为1k =-, ∴切线方程为y x =-,即0x y +=. 14.【答案】313【解析】设数列{}n a 的公比为q ,∵2366a a =,则245116a q a q =,得162q a ==,∴551(12)313123S ⨯-==-.15.【答案】7-【解析】∵22()cos 8cos2cos 8cos 12(cos 2)92222x x x xf x x =-=--=--, 由三角函数有界性可知[]cos1,12x∈-, 故当cos12x=时,min ()297f x =-=-. 16.【解析】∵AB CD ∥,且DC ⊂平面EFCD ,AB ⊄面EFCD ,∴AB ∥面EFCD ,∴AB 到面EFCD 的距离等于点A 到面EFCD 的距离, 过点A 作AG FD ⊥于G , ∵π2BAD ∠=,AB DC ∥,∴CD AD ⊥, 又∵FA ⊥平面ABCD ,FA CD ⊥, 又FA AD A =I ,∴CD ⊥面FAD ,而AG ⊂面FAD ,∴CD AG ⊥,CD FD D =I , ∴AG ⊥面CFD ,∴AG 为直线AB 到平面EFCD 的距离, 在FCD Rt △中,4FD ==,∵FA ⊥面ABCD ,∴FA AD ⊥, 在AFD Rt △中,FA ==∴733744FA ADAGFD⋅⨯===,∴AB到平面EFCD距离为374.三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤.17.【答案】(1)12;(2)能认为.【解析】(1)该中学一年学生的近视率为5011002P==.(2)22100(20153035)9.091 6.63555455050K⨯⨯-⨯=>⨯⨯⨯≈,所以能认为在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系.18.【答案】(1)27na n=-;(2)8.【解析】(1)设数列{}na公差为d,∵616150S a d=+=,∴152a d=-,又23a=-,即13a d=--,所以2d=,15a=-,故数列{}na的通项公式为52(1)27na n n=-+-=-.(2)由(1)可知26nS n n=-,则n nS a>,可得2627n n n->-,解得1n<或7n>,所以不等式n nS a>成立的n的最小值为8.19.【答案】(1)证明见解析;(2)310.【解析】(1)由题意可知,∵AB DC∥,且33AB DC==,∴AB DE∥,AB DE=,故四边形ABED为平行四边形,∴11BE AD A D∥∥,11BE AD A D==,∴四边形11A D EB为平行四边形,∴11D E A B∥,∵1D E⊄平面1A BD,1A B⊂平面1A BD,∴1D E∥平面1A BD.(2)过D作1DM D E⊥交1D E于M,∵1111ABCD A B C D-为直四棱柱,∴1DD⊥底面ABCD,∴1DD BE⊥,由(1)得BE AD∥,∵AD DC⊥,∴BE DC⊥,而1DC DD D=I,∴BE⊥平面11DCC D,DM⊂平面11DCC D,∴BE DM⊥,又∵1DM D E⊥,1BE D E E=I,∴DM⊥平面1BED,∴点D到平面1BED的距离即为DM长,∵1DE=,13DD=,∴110D E=31010DM==,∴点D到平面1BED的距离为31010.20.【答案】(1)证明见解析;(2)4(,]π-∞.【解析】(1)由题意得211()sin(sin)22f x x x x x x x'=-=-,令1()sin2g x x x=-,则1()cos2g x x'=-,当π(0,)3x∈时,()0g x'>,()g x单增;当ππ(,)32x∈时,()0g x'<,()g x单减,∵(0)0g=,π3π()0326g=->,ππ()1024g=->,故()g x在π(0,)2上恒大于0,故()0f x'>在π(0,)2上恒成立,故()f x'在区间π(0,)2上不存在零点.(2)由31()cos 16f x kx x x x >---,得sin 1x kx >-, ∵π(0,)2x ∈,故sin 1x k x+<, 令sin 1()x t x x +=,则2cos sin 1()x x x t x x --'=, 令()cos sin 1m x x x x =--,则()sin 0m x x x '=-<恒成立,()m x 在π(0,)2上单调递减,∴()(0)10m x m <=-<,∴()0t x '<在π(0,)2上恒成立,即()t x 在π(0,)2上单减,∴π4()()2πt x t >=,∴4πk ≤, ∴k 的取值范围是4(,]π-∞.21.【答案】(1)4;(2)存在定点P ,5(0,)4P -. 【解析】由题意可设直线l 的方程为1y kx =-,11(,)A x y ,22(,)B x y ,由22121y x y kx ⎧+=⎪⎨⎪=-⎩消去y 得22(2)210k x kx +--=, 则224480Δk k =++>恒成立,12222k x x k +=+,12212x x k -=+, 121224()22y y k x x k -+=+-=+,21212222(1)(1)2k y y kx kx k -=--=+. (1)221||2k AB k +==+, 线段AB 的中点的横坐标为22kk +, ∵以AB为直径的圆与x =22kk =+,解得k =此时12||22AB +==+,∴圆的半径为4. (2)设0(0,)P y ,212102012120120()()()PA PB x x y y y y x x y y y y y y ⋅=+--=+-++u u u r u u u r222220000022224(2)2411222222y y k y y k y k k k k -+++--=+++=++++, 由22000224112y y y -++=,得054y =-,716PA PB ⋅=-u u u r u u u r , ∴y 轴上存在定点5(0,)4P -,使得PA PB ⋅u u u r u u u r 为定值.22.【答案】(1)221(43x y y +=≠10x +-=;(2)12. 【解析】(1)∵<≤且22()12x +=, ∴C的普通方程为221(43x y y +=≠,1:2cos )12l ρθθ+=sin cos 1θρθ+=, ∴l10x +-=.(2)由(1)可设C的参数方程为2cos x y θθ=⎧⎪⎨=⎪⎩(θ为参数),则可设C上任意一点坐标为(2cos )θθ, 则C 上点到l距离为d ==当sin()1θϕ+=时,min 12d =, ∴曲线C 上的点到l距离的最小值为12. 23.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)∵0a >,0b >,0c >,∴422a a +=++≥=,422b b +=++≥=422c c +=++≥=故(4)(4)(4)216a b c +++≥=,当且仅当2a b c ===时取等号,∴(4)(4)(4)216a b c +++≥.(2)22223()()()3[()()()]a b b c c a a b b c c a +++++≥=+++2223333)3(8)36431648abc ≥⨯=⨯=⨯=⨯=,当且仅当a b c ==时取等号,∴222()()()48a b b c c a +++++≥.。
安徽省江南十校2020届高三冲刺联考(二模)试题数学(文)(含解析)

姓名座位号(在此卷上答题无效}绝密★启用前2019年“江南十校”高三学生冲刺联考(二模)文科数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷第1至第2页,第II 卷第3至第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中座位号与本人座位号是否一致,务必在答題卡规定的地方填写考场/座位号、姓名、班级。
2.答第I 卷时,每小题选出答案后,用2B 铅笔把答題卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答第Ⅱ卷时,必须使用0.5亳米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰,作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚,必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
.第1卷(选择题共60分)―、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.集合 A= {1<|x x },B = {2|x x },则C R (A ∩B)= A. {2<|x x } B. {1|xx }C. {1x 2<|或x x }D. {x >>2|或xx }2.设ii z2332,复数2z 位于复平面A.第一象限B.第二象限C.第三象限D.第四象限3. 执行如图所示的程序框图,输出的S 的值为A.2B.25 C.290941 D.10294. 已知抛物线方程为2ax y,它的准线方程为81y,则a 的值为A.21 B.21 C.-2D.25. 已知圆台上、下两底面与侧囿都与球相切,它的侧面积为16,则该圆台上、下两个底面圆的周长之和为A.4B.6 C.8 D.106. 已知:31log ,)31(,411ln 11eec b a,则 a ,b ,c 的大小关系为A. c > a > bB. c > b > aC.b > a > cD.a > b > c 7. 在平行四边形ABCD 中,E 为BC 的中点,点F 在CD 上, 且DF=2FCC ,连接AE 、BF 交于G 点,则DGA.AD AB 7154 B.AD AB 7476C.ADAB7275 D.ADAB71738. 已知函数)(3cos 33sin )(R xx x x f ,曲线)(x f 与直线3y的交点中,相邻交点的距离最小值与最大值分别为A.54,3B.65,6C.95,9D.125,129.△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足BB AA Cbc ac bcos sin 3cos sin 3sin 2)2(,33)(3)1(222,则角C 为A.6B.65 C.3D.3210. 如图所示,正方形ABCD 的边长为1,等腰直角△SAD 绕其直角边AD 转动,另一直角边SD 与正方形一边DC 成角(018<90),则异面直钱SA与DB 所成角的取值范围为A.]2,0( B.]6,0( C.]3,0( D.]2,6[11.已知双曲线方程12222by ax(a>0,b>0,a≠b), A ,B 是它的两条渐近线上的点,△OAB 为直角三角形,则A ,B 两点横坐标的绝对值之比为A.ab ba 或B.||2222b aba C.2222||bab a D.||2222b aba 或2222||bab a 12. 已知函数xxee xf 4)(,则A.)(x f 在(-∞,2)单调递增,在(2, +∞)单调递减B.)(x f 在(-∞,2)单调递减,在(2, +∞)单调递增C.函数)(x f 的图象不关于直线2x 对称D.函数)(x f 的图象关于点(2,0)对称(在此卷上答题无效)绝密★启用前2019年“江南十校”高三学生冲剌联考(二模)文科数学第Ⅱ卷(非选择题共90分)考生注意事项:请用0.3毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
2020年安徽省高考文科科数学仿真模拟试题二(附答案)

2020年安徽省高考文科数学仿真模拟试题二(附答案)(满分150分,考试时间120分钟)注意事项:1.答题前,考生务必将自己的姓名、准考证号码填写在答题卡和试卷指定位置上,并将条形码准确粘贴在条形码区域内。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合}1|{≥=x x A ,{|230}B x x =->,则AB =( )A. [0,)+∞B. [1,)+∞C. 3,2⎛⎫+∞ ⎪⎝⎭D. 30,2⎡⎫⎪⎢⎣⎭2. 在复平面内,复数22ii+-对应的点位于( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限3.“x>5”是“>1”的( )A. 充分不必要条件B. 必要不充分条件C. 既不充分也不必要条件D. 充要条件4. 以A (-2,1),B (1,5)为半径两端点的圆的方程是( ) A. (x +2)2+(y -1)2=25 B. (x -1)2+(y -5)2=25C. (x +2)2+(y -1)2=25或(x -1)2+(y -5)2=25D. (x +2)2+(y -1)2=5或(x -1)2+(y -5)2=5 5. 已知函数2()21x f x a =-+(a R ∈)为奇函数,则(1)f =( ) A. 53-B. 13C. 23D. 326. 设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,510a =-,则1a =( ) A. -3B. -2C. 2D. 37. 在区间[0,1]上随机取两个数,x y ,记1p 为事件“12x y +≤”的概率,2p 为事件“12xy ≤” 的概率,则( ) A. 1212p p << B. 1212p p << C. 2112p p << D.2112p p << 8. 已知ABC ∆是边长为1的等边三角形,点D ,E 分别是边AB ,BC 的中点,连接DE 并延长到点F ,使得2DE EF =,则AF BC ⋅的值为( ) A. 58-B.118C.14D.189. 已知4616117421⨯⨯⨯⨯⨯⨯⨯= T ,若右边的框图是计算T 的程序框图,则框图中①和②处可以分别填入( ) A.i m m i +=≤,?10 B.1?10++=≤i m m i , C.i m m i +=≤,?11 D.1?11++=≤i m m i ,10.已知点()12,0F -,圆()222:236F x y -+=,点M 是圆上一动点,线段1MF 的垂直平分线与2MF 交于点N .则点N 的轨迹方程为A.22192x y -=B.320x y --=C.2236x y += D.22195x y += 11.函数()2sin sin2f x x x =-在[]0,2π的零点个数为( )A .2B .3C .4D .512.设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是( )A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦ C .5,2⎛⎤-∞ ⎥⎝⎦ D .8,3⎛⎤-∞ ⎥⎝⎦ 二、填空题:本题共4小题,每小题5分,共20分。
2020年安徽省江南十校高考数学模拟试卷(文科)(4月份) (含答案解析)

2020年安徽省江南十校高考数学模拟试卷(文科)(4月份)一、单项选择题(本大题共12小题,共60.0分)1.已知集合A={−3,−1,0,1,3},B={x|x2+3x=0},则A∩B=()A. {−3,0,3}B. {−3,0}C. {0,3}D. {−3,−1,0,1,3}2.复数2i1+i=().A. −iB. 1+iC. iD. 1−i3.半径为2的圆中,π3的圆心角所对的弧的长度为()A. π3B. 2π3C. 3π2D. 23π4.函数f(x)=sinx2+cosx(−π≤x≤π)的图象大致为()A. B.C. D.5.某校为了解高一新生数学科学习情况,用系统抽样方法从编号为001,002,003,…,700的学生中抽取14人,若抽到的学生中编号最大的为654,则被抽到的学生中编号最小的为()A. 002B. 003C. 004D. 0056.已知sin(α2+π6)=14,则cos(π3+α)cos(α2−π3)=()A. 72B. −72C. 732D. −7327.已知a=215,,,则()A. b<a<cB. c<a<bC. c<b<aD. b<c<a8.执行如图所示的程序框图,输出的s值为()A. 712B. 56C. 12D. 76 9. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想的内容是:每个大于2的偶数都可以表示为两个素数的和,例如8=3+5,在不超过14的素数中随机选取两个不同的数,其和等于14的概率为( )A. 16B. 112C. 114D. 115 10. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(2c −b)cosA =acosB .则角A 的大小为 ——;A. π2B. π4C. π3D. π5E. π6F. 2π311. 过椭圆C :x 225+y 216=1的右焦点F 2且与x 轴垂直的直线与椭圆C 相交于A 、B 两点,则弦长|AB|=( ) A. 1625 B. 165 C. 325D. 254 12. 已知函数f(x)=sin(2x +φ),其中φ为实数,若f(x)≤|f(π6)|对x ∈R 恒成立,且f(π2)<f(π).则下列结论正确的是( )A. f(1112π)=−1B. f(7π10)>f(π5)C. f(x)是奇函数D. f(x)的单调递增区间是[kπ−π3,kπ+π6](k ∈Z)二、填空题(本大题共4小题,共20.0分)13. 已知函数f (x )=x 22+x −2lnx ,求函数f (x )在点(2,f (2))处的切线方程________.14. 在平面直角坐标系xOy 中,双曲线x 24−y 2=1的顶点到它的渐近线的距离为______.15. 在平面直角坐标系xOy 中,点A(1,3),B(−2,k),若向量OA ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ,则实数k = ______ .16. 已知AB 为球面上的两点,O 为球心,且AB =3,∠AOB =120°,则球的体积为______ .三、解答题(本大题共7小题,共82.0分)17. 已知等比数列{a n }的公比大于1,且满足a 3+a 5=90,a 4=27.(1)求{a n}的通项公式;(2)记b n=log3a n,求数列{a n(b n+1)}的前n项和T n.18.某移动支付公司随机抽取了100名移动支付用户进行调查,得到如下数据:(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样随机抽取5名用户.①求抽取的5名用户中男、女用户各多少人;②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过0.05的前提下,认为“喜欢使用移动支付”与性别有关?附表及公式:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)19.如图,在正四棱锥P−ABCD中,F为AD的中点,E为BC的中点,M是棱PC的中点,AB=4.(Ⅰ)求证:直线PA//平面MFE;(Ⅱ)若PC=2√5,求三棱锥P−MFE的体积.20.已知函数f(x)=ax2−1−lnx,其中a∈R.(1)讨论f(x)的单调性;(2)若f(x)≥x对x∈(1,+∞)成立,求实数a的取值范围.21.斜率为1的直线l经过抛物线x2=4y的焦点,且与抛物线相交于A,B两点,求线段AB的长.222.在平面直角坐标系xOy中,曲线C的参数方程为{x=−1+2cosφy=2sinφ(其中φ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l1的极坐标方程为ρ=√2sin (θ+π4),设l1与C相交于A,B两点,AB的中点为M,过点M作l1的垂线l2交C于P,Q两点.(1)写出曲线C的普通方程与直线l1的直角坐标方程;(2)求|PQ||MP|⋅|MQ|的值.23.已知函数f(x)=|x−1|+|x−2|.(1)解不等式:f(x)≤x+3;(2)若不等式|m|·f(x)≥|m+2|−|3m−2|对任意m∈R恒成立,求x的取值范围.【答案与解析】1.答案:B解析:本题考查交集的求法,考查交集定义等基础知识,考查运算求解能力,是基础题.先分别求出集合A,B,由此能求出A∩B.解答】解:∵集合A={−3,−1,0,1,3},B={x|x2+3x=0}={0,−3},∴A∩B={0,−3}.故选B.2.答案:B解析:本题考查复数的代数形式的乘除运算,属基础题.根据复数的四则运算计算即可.解:化简可得复数z=2i1+i =2i(1−i)(1+i)(1−i)=1+i,故选B.3.答案:B解析:解:根据题意得出:l扇形=2×π3=2π3.故选B.根据题意可以利用扇形弧长公式l扇形直接计算.此题主要考查了扇形弧长的计算,注意掌握扇形的弧长公式是解题关键.4.答案:A解析:解:f(−x)=−sinx 2+cosx =−f(x)则函数f(x)是奇函数,排除C , 分母2+cosx >0,则当0<x <π时,sinx >0,则f(x)>0,排除D ,f(π4)=√222+√22=√24+√2<f(π2)=12,则B 不满足条件. 故选:A .利用函数的奇偶性得到图象关于原点对称,利用f(π4)<f(π2),进行排除即可.本题主要考查函数图象的识别和判断,利用函数奇偶性和函数值的对应性,利用排除法是解决本题的关键. 5.答案:C解析:本题考查了系统抽样方法的应用问题,是基础题.根据系统抽样方法求出抽样间隔,再结合题意,求出对应的样本编号即可.解:根据系统抽样方法知,抽样间隔为70014=50,抽到的学生中编号最大的为654,则654−13×50=4,则被抽到的学生中编号最小的为004故选:C . 6.答案:A解析:本题考查倍角公式以及诱导公式的的应用,属于基础题.直接根据倍角公式以及诱导公式化简,再代入条件计算,即可得到答案.解:cos(π3+α)cos(α2−π3)=cos2(π6+α2)cos(α2+π6−π2)=1−2sin 2(α2+π6)sin(α2+π6)=1−2×(14)214=72. 故选A .7.答案:C解析:解:a =215>1,0<b =log 352<log 33=1,,∴a >b >c .故选:C.利用指数函数性质和对数函数性质,判断三个数的范围,即可判断三个数的大小.本题主要考查利用指数函数性质和对数函数性质比较大小,是基础题.8.答案:A解析:本题主要考查循环结构的程序框图.当循环次数不多时,采用模拟方法解答.执行循环框图,依次写出每次循环输出的结果,当k=4时,循环终止,即可的结果.解:当k=1时,s=1−12=12;当k=2时,s=12+13=56;当k=3时,s=56−14=712;当k=4时,循环终止,输出712.故选A .9.答案:D解析:本题考查了古典概型的计算与应用,求出总基本事件数和满足条件的事件数是解题的关键,是容易题.总基本事件有15个,满足要求的只有1个,即可得到答案.解:不超过14的素数有2,3,5,7,11,13其6个,从这6个素数中任取2个,有2与3,2与5,2与7,2与11,2与13,3与5,3与7,3与11,3与13,5与7,5与11,5与13,7与11,7与13,11与13共15种结果,其中和等于的14有一组3与11,所以在不超过14的素数中随机述取两个不同的数其和等于14的概率为115.故选D.10.答案:C解析:解:∵(2c−b)cosA=acosB,∴由正弦定理可得(2sinA−sinB)cosA=sinAcosB,变形可得2sinCcosA =sinBcosA +sinAcosB =sin(A +B)=sinC ,∵C 为三角形的内角,sinC ≠0,∴cosA =12,A =π3;由正弦定理和三角函数公式可得cosA =12,可得A =π3;11.答案:C解析:本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题,考查了推理能力与计算能力,属于基础题.椭圆x 225+y 216=1,可得c =3,取焦点F(3,0).把x =3代入椭圆方程,解得y ,即可得出弦长|AB|.解:由题意可知:a 2=25,b 2=16,c 2=a 2−b 2=9,则c =3,由x =3时,y =±165,∴弦长|AB|=325,故选C . 12.答案:D解析:根据题意首先判断φ的取值,然后逐条验证.对A ,代入求值即可;对B ,代入比较大小即可;对C ,根据奇函数定义,验证是否适合;对D ,通过解不等式求单调区间的方法求解.本题借助考查命题的真假判断,考查三角函数的性质.解:∵f(x)≤|f(π6)|对x ∈R 恒成立,∴2×π6+φ=kπ+π2⇒φ=kπ+π6,k ∈Z .∵f(π2)<f(π)⇒sin(π+φ)=−sinφ<sin(2π+φ)=sinφ⇒sinφ>0.∴φ=2kπ+π6,k ∈Z.不妨取φ=π6f(11π12)=sin2π=0,∴A×;∵f(7π10)=sin(7π5+π6)=sin47π30=−sin17π30<0,f(π5)=sin(2π5+π6)=sin17π30>0,∴B×;∵f(−x)≠−f(x),∴C×;∵2kπ−π2≤2x+π6≤2kπ+π2⇒kπ−π3≤x≤kπ+π6,k∈Z.∴D√;故选D.13.答案:2x−y−2ln2=0解析:本题考查导数的几何意义,基础题型.利用导数的几何意义求解即可.解:∵函数f(x)=x22+x−2lnx,∴f′(x)=x+1−2x,∴f′(2)=2+1−1=2,f(2)=2+2−2ln2=4−2ln2,∴函数f(x)在点(2,4−2ln2)处的切线方程为y−4+2ln2=2(x−2),即2x−y−2ln2=0.故答案为2x−y−2ln2=0.14.答案:2√55解析:本题主要考查双曲线性质的应用,根据点到直线的距离公式是解决本题的关键,比较基础.根据点到直线的距离公式进行求解即可.解:双曲线x24−y2=1的一个顶点为A(2,0),双曲线的一条渐近线为y=12x,即x−2y=0,则点A到渐近线的距离d=√1+4=2√55,故答案为:2√55.15.答案:4解析:解:∵OA ⃗⃗⃗⃗⃗ =(1,3),AB ⃗⃗⃗⃗⃗ =(−2,k)−(1,3)=(−3,k −3),向量OA ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ , ∴OA ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =(1,3)⋅(−3,k −3)=−3+3(k −3)=0,解得k =4. 故答案为:4.利用向量的坐标运算和向量垂直与数量积的关系即可得出.本题考查了向量的坐标运算和向量垂直与数量积的关系,属于基础题.16.答案:4√3π解析:解:△AOB 为等腰三角形,∠AOB =120°,AB =3,通过解三角形解出OA 和OB ,即OA =OB =R =√3,从而求出球的体积4√3π, 故答案为:4√3π.通过解△AOB ,求出三角形的边长,就是球的半径,然后求出球的体积即可. 本题考查球的体积的求法,考查计算能力,是基础题.17.答案:解:(1)设{a n }的公比为q(q >1),依题意,得{a 1q 2+a 1q 4=90,a 1q 3=27, 两式相除,得1+q 2q =103,整理得3q 2−10q +3=0,结合q >1,解得q =3, 所以a 1=27q 3=2733=1,所以a n =3n−1;(2)由(1)知a n =3n−1,所以b n =log 3a n =n −1,从而a n (b n +1)=n ·3n−1, 所以T n =1×30+2×31+3×32+⋯+n ·3n−1,①两边同乘以3,得3T n =1×31+2×32+3×33+⋯+n ·3n ,② 由①−②,得−2T n =30+31+32+⋯+3n−1−n ⋅3n =1−3n 1−3−n ⋅3n =(12−n)⋅3n −12,所以T n =14(2n −1)⋅3n +14.解析:本题考查等比数列的通项公式和求和公式,考查数列的错位相减法求和,化简运算能力,属于中档题.(1)由a 3+a 5=90,a 4=27求出等比数列的公比q ,进而求得等比数列的通项公式;(2)求得b n=log3a n=n,a n b n=n⋅3n−1,再由数列的错位相减法求和,结合等比数列的求和公式,可得所求和.18.答案:解:(1)①由表格可知,样本中每周使用移动支付次数超过3次的男用户有45人,女用户30人,…(1分)在这75人中,按性别用分层抽样的方法随机抽取5名用户,其中男用户有3人,女用户有2人.…(3分)②记抽取的3名男用户分别A,B,C;女用户分别记为d,e.再从这5名用户随机抽取2名用户,共包含(A,B),(A,C),(A,d),(A,e),(B,C),(B,d),(B,e),(C,d),(C,e),(d,e),10种等可能的结果抽取的2名均为男用户这一事件包含(A,B),(A,C),(B,C)共计3种等可能的结果,由古典概型的计算公式可得P=310.(2)由图中表格可得列联表:将列联表中的数据代入公式计算得:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=100×(45×15−30×10)225×75×55×45=10033≈3.030<3.841,在犯错误概率不超过0.05的前提下,不能认为是否喜欢使用移动支付与性别有关.解析:(1)样本中每周使用移动支付次数超过3次的男用户有45人,女用户30人,按性别用分层抽样的方法随机抽取5名用户,其中男用户有3人,女用户有2人,抽取的3名男用户分别A,B,C;女用户分别记为d,e.求出这5名用户随机抽取2名用户,共包含事件总数,抽取的2名均为男用户这一事件数目,即可由古典概型的计算公式求解概率即可.(2)计算K的观测值K2,对照题目中的表格,得出统计结论.本题考查了独立性检验的应用问题,也考查了古典概型概率的求法,考查计算能力,是基础题目.19.答案:(Ⅰ)证明:∵四边形ABCD为正方形,且F为AD的中点,E为BC的中点,∴EF//AB,∵EF⊄面PAB,AB⊂面PAB,得EF//平面PAB,∵E为BC的中点,M是棱PC的中点,∴EM//PB,∵EM⊄面PAB,PB⊂面PAB,则EM//平面PAB,又EF⊂面MEF,EM⊂面MEF,且EF∩EM=E,∴平面PAB//平面MEF,则直线PA//平面MFE;(Ⅱ)解:在正三棱锥P−ABCD中,由AB=4,PC=2√5,得正四棱锥的高ℎ=√(2√5)2−(2√2)2=2√3.∵M为棱PC的中点,∴P到平面MEF与C到平面MEF的距离相等,则V P−MEF=V C−MEF.又V C−MEF=V M−CEF=12V M−FECD=14V P−FECD=18V P−ABCD=18×13×16×2√3=4√33.∴三棱锥P−MFE的体积是4√33.解析:本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.(Ⅰ)由已知可得EF//AB,EM//PB,则EF//平面PAB,EM//平面PAB,由面面平行的判定可得平面PAB//平面MEF,从而得到直线PA//平面MFE;(Ⅱ)直接利用等积法求三棱锥P−MFE的体积.20.答案:解:(1)函数f(x)=ax2−1−lnx的导数为f′(x)=2ax−1x =2ax2−1x,当a≤0时,f′(x)<0,f(x)在(0,+∞)为减函数;当a>0时,f′(x)=0可得x=√12a,当0<x<√12a 时,f′(x)<0;当x>√12a时,f′(x)>0.可得f(x)在(0,√12a )为减函数,在(√12a,+∞)为增函数,综上可得,当a≤0时,f(x)在(0,+∞)为减函数;当a>0时,f(x)在(0,√12a )为减函数,在(√12a,+∞)为增函数;(2)f(x)≥x 对x ∈(1,+∞)成立, 可得ax 2≥1+x +lnx , 当x >1时,a ≥1x 2+1x +lnx x 2,令g(x)=1x 2+1x +lnx x 2,g′(x)=−2x 3−1x 2+1−2lnx x 3=−1−x−2lnxx 3,当x ≥1时,−1−x −2lnx <0,即g′(x)<0, g(x)在[1,+∞)递减, 可得a ≥g(1)=2, 则a 的取值范围是[2,+∞).解析:(1)求出f(x)的导数,讨论当a ≤0时,当a >0时,由导数大于0,可得增区间;导数小于0,可得减区间;(2)由题意可得ax 2≥1+x +lnx ,当x >1时,a ≥1x 2+1x +lnx x 2,令g(x)=1x 2+1x +lnx x 2,求出导数,判断单调性,可得g(x)的最大值,可得a 的范围.本题考查导数的运用:求单调性,注意运用分类讨论的思想方法,考查不等式恒成立问题的解法,注意运用参数分离和构造函数法,考查转化思想和运算能力,属于中档题.21.答案:解:由已知可知,抛物线x 2=4y 的焦点为F(0,1),所以直线l 的方程为y =12x +1,由{y =12x +1x 2=4y ,得(2y −2)2=4y ,即y 2−3y +1=0, 设A(x 1,y 1),B(x 2,y 2),则y 1+y 2=3, 所以|AB|=y 1+y 2+p =3+2=5.解析:本题考查了抛物线的性质及几何意义,直线与抛物线的位置关系,属于基础题. 求出焦点坐标,求出直线方程,然后联立直线与抛物线方程,利用弦长公式求解即可.22.答案:解:(1)由曲线C 的参数方程{x =−1+2cosφy =2sinφ,消去参数φ,得曲线C 的普通方程为(x +1)2+y 2=4.由曲线l1的极坐标方程ρ=√2sin (θ+π4),得ρsinθ+ρcosθ=1,将x=ρcosθ,y=ρsinθ代入,得l1的直角坐标方程为x+y−1=0;(2)由l1⊥l2,得直线l2的斜率k l2=−1k l1=1,所以l2的倾斜角为π4,又l2过圆心(−1,0),所以l2的方程为y=x+1,与x+y−1=0联立,得AB的中点M(0,1),故l2的参数方程为{x=tcosπ4y=1+tsinπ4,(t为参数),即{x=√22ty=1+√22t,(t为参数),代入(x+1)2+y2=4中,化简、整理得t2+2√2t−2=0,设P,Q对应的参数分别为t1,t2,则由韦达定理得t1·t2=−2,又线段PQ为圆的直径,所以|PQ|=4,所以|PQ||MP|⋅|MQ|=4|−2|=2.解析:本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.(2)利用一元二次方程根和系数关系式的应用求出结果.23.答案:解:(1)∵f(x)≤x+3,∴|x−1|+|x−2|≤x+3,①当x≥2时,,②当1<x<2时,,③当x≤1时,,由①②③可得x∈[0,6];(2)①当m=0时,0≥0,∴x∈R;②当m≠0时,即f(x)≥|2m +1|−|2m−3|对m恒成立,|2 m +1|−|2m−3|≤|(2m+1)−(2m−3)|=4,当且仅当2m ≥3,即0<m≤23时取等号,∴f(x)=|x−1|+|x−2|≥4,由x ≥2,2x −3≥4,解得x ≥72; 1<x <2,x −1+2−x ≥4,解得x ∈⌀; x ≤1时,3−2x ≥4,解得x ≤−12; 综上可得x ∈(−∞,−12]∪[72,+∞).解析:(1)分别讨论x ≥2,1<x <2,x ≤1时,去掉绝对值,解不等式求并集可得;(2)讨论m =0,m ≠0,由绝对值不等式的性质可得f(x)≥4,再讨论x ≥2,1<x <2,x ≤1时,解不等式求并集可得范围.本题考查绝对值不等式的解法和绝对值不等式的性质,考查分类讨论思想方法和转化思想、运算能力,属于中档题.。
2020届安徽省江南十校高三第二次联考数学(文)试题(解析版)

2020届安徽省江南十校高三第二次联考数学(文)试题一、单选题1.已知i 是虚数单位,则20192020i i +=( ) A .1i + B .1i -+C .–1iD .–1i -【答案】B【解析】利用i 的次幂运算,将指数分别除以4,得到余数,即可得答案. 【详解】∵20192020450434505301i i i i i i i ⨯+⨯+=+=+=-+. 故选:B . 【点睛】本题考查i 的次幂运算,考查运算求解能力,属于基础题.2.已知集合{}220|A x x x =-<,{}|1B x x =≤,则有( ) A .{}|01A B x x ⋂=<<B .{|11}A B x x ⋃=-<≤C .()0{|R C A B x x ⋂=≤或1}x >D .{}()2|R C A B x x ⋃=>【答案】C【解析】解不等式对集合,A B 进行化简,再求它们的交集,最后求补集,即可得答案. 【详解】∵{}2|20{|02}A x x x x x =-<=<<,{|11}B x x =-≤≤, ∴{|01}A B x x =<I ≤,{|12}A B x x =-<<U ∴(){|0R C A B x x ⋂=≤或1}x >. 故选:C . 【点睛】本题考查集合的交、补运算,考查运算求解能力,属于基础题.3.已知向量(2,3)a =r ,(1,2)b =-r , 3,1()c =-r ,若()a b c λ+⊥r r r,则实数λ=( )A .53-B .53C .56-D .56【答案】A【解析】求出a b λ+r r ,再根据()a b c λ+⊥r r r 得到关于λ的方程,解方程即可得答案.【详解】由题意得()21,32a b λλλ+=+-rr ,又()a b c λ+⊥r r r ,∴()()321320λλ+--=,解得53λ=-. 故选:A . 【点睛】本题考查向量垂直的坐标运算,考查函数与方程思想,考查运算求解能力,属于基础题. 4.中国古代数学名著《算法统宗》中,许多数学问题都以诗歌的形式呈现,其中有一首“五兄欠钱”的诗为:“甲乙丙丁戊,酒钱欠千五,甲兄告乙弟,四百我还与,转差是几文,各人出怎取?”意为:五兄弟,共欠1500文酒钱,甲还400文,甲乙丙丁戊的还钱数依次成等差数列.在这个问题中戊该还的酒钱数是( ) A .350文 B .300文C .250文D .200文【答案】D【解析】设此等差数列为{}n a ,公差为d ,1400a =,进而求出d ,再求5a 即可得答案. 【详解】设此等差数列为{}n a ,公差为d ,由题知1400a =, 且154515002a d ⨯+=,则得50d =, 戊该还的酒钱数是()5400450200a =+⨯-=(文). 故选:D . 【点睛】本题考查等差数列模型的运用,考查函数与方程思想、转化与化归思想,考查建模能力,求解时注意读懂文字语言.5.已知两个平面α,β,直线,a b α⊂,直线,m n β⊂,则下列命题中正确的是( ) A .若//a m ,//b n 则//αβ B .若m a ⊥,n b ⊥,则αβ⊥C .若a ,b 相交,m a ⊥,n b ⊥,则αβ⊥D .若a ,b 相交,//a m ,//b n ,则//αβ【答案】D【解析】对A ,两平面可能相交;对B ,C ,两平面可能平行;对D ,利用线面平行和面面平行判定定理知正确. 【详解】对A ,两平面可能相交,故A 错误; 对B ,C ,两平面可能平行;对D ,利用线面平行和面面平行判定定理知D 正确. 故选:D. 【点睛】本题考查空间中线面、面面的位置关系,考查空间想象能力,属于基础题. 6.函数sin ()cos ||x xf x x x =+在[,]-ππ的图象大致为( )A .B .C .D .【答案】C【解析】利用函数为偶函数及()12f π=,即可得答案.【详解】∵函数()f x 的定义域为[,]-ππ关于原点对称,且()sin()()()cos()||x x f x f x x x ---==-+-∴函数()f x 为偶函数,且()12f π=所以函数()f x 能取到函数值1.故选:C . 【点睛】本题考查函数的奇偶性、特殊点函数值,考查函数与方程思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意从解析式得到函数的性质及从图象中找信息. 7.已知a R ∈,则“1104a +<”是“210ax ax +-<对x R ∀∈恒成立”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件【答案】B【解析】对两个条件分别进行化简,再转化成判断两个集合之间的关系,即可得答案. 【详解】 一方面,110404a a +<⇔-<<, 另一方面,210ax ax +-<对x R ∀∈恒成立40a ⇔-<≤, 所以“1104a +<”是“210ax ax +-<对x R ∀∈恒成立”的充分不必要条件. 故选:B . 【点睛】本题考查不等式的求解、一元二次不等式恒成立问题、简易逻辑知识,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力. 8.若正实数a ,b 满足lg lg 1a b +=,则25a b+的最小值为( ) A. B.C.2D .2【答案】D【解析】由正实数a ,b 满足其lg lg 1a b +=,得10ab =,再利用基本不等式进行求最小值. 【详解】由正实数a ,b 满足其lg lg 1a b +=,得10ab =,则由基本不等式有252a b +≥=, 当且当2510a b ab ⎧=⎪⎨⎪=⎩,即2a =,5b =时等号成立.故选:D . 【点睛】本题考查对数的运算、基本不等式求最值,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意验证等号成立的条件.9.已知不等式组222x yx yy+≤⎧⎪-≥-⎨⎪≥⎩所表示的平面区域为D,若直线1y kx=-与平面区域D有公共点,则实数k的取值范围为()A.1 ,12⎡⎤-⎢⎥⎣⎦B.1,[1,)2⎛⎤-∞-⋃+∞⎥⎝⎦C.(,2][1,)-∞-+∞U D.[2,1]-【答案】B【解析】画出不等式组222x yx yy+≤⎧⎪-≥-⎨⎪≥⎩所表示的平面区域D(图中阴影部分所示),再利用斜率公式求出,AC AB的斜率,即可得答案.【详解】画出不等式组222x yx yy+≤⎧⎪-≥-⎨⎪≥⎩所表示的平面区域D(图中阴影部分所示),直线1y kx=-过定点(0,1)A,则直线1y kx=-与平面区域D有公共点,当且仅当ACk k≤或ABk k≥,即12k≤-或1k³.故选:B.【点睛】本题考查线性约束条件下的范围问题,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意作图观察求解. 10.已知ln 33a =,ln b ππ=,0.32c =,则a ,b ,c 的大小关系为( )A .a b c <<B .c a b <<C .b a c <<D .b c a <<【答案】C【解析】构造函数ln ()xf x x=,利用导函数研究函数的图象特征,利用单调性及引入中间变量1,即可得答案. 【详解】 构造函数ln ()xf x x=,则21ln ()x f x x -'=, 当0x e <<时,()0f x '>.()f x 在()0,e 上单调递增, 当x e >时,()0f x '<,()f x 在(,)e +∞上单调递减, 则ln 3(3)3a f ==,ln ()b f πππ==, 0.31()(3)()12f f f e eπ<<=<<.∴b a c <<. 故选:C. 【点睛】本题考查数的大小比较、函数的单调性,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意引入中间变量1. 11.若4sin()125πα-=,且(0,)2πα∈,则cos(2)3πα+=( ) A .2425-B .1225C .1225-D .2425【答案】A【解析】利用诱导公式得cos(2)sin 236ππαα⎛⎫+=-- ⎪⎝⎭,再利用倍角公式,即可得答案. 【详解】由4sin()125πα-=且(0,)2πα∈,得3cos()125πα-=, cos(2)cos 2sin 23626ππππααα⎛⎫⎛⎫+=-+=-- ⎪ ⎪⎝⎭⎝⎭242sin cos 121225ππαα⎛⎫⎛⎫=---=- ⎪ ⎪⎝⎭⎝⎭.故选:A . 【点睛】本题考查诱导公式、倍角公式进行求值,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意角度之间的关系配凑.12.已知函数21ln(1),14()11,44x x f x x x ⎧+-<≤⎪⎪=⎨⎪+>⎪⎩,且关于x 的方程()0f x kx -=恰有2个实数解,则实数k 的取值范围是( ) A .51,4⎡⎤⎢⎥⎣⎦B .5[,)4+∞C .54ln,14⎡⎤⎢⎥⎣⎦D .554ln,1,44 ⎡⎤⋃⎡+∞⎢⎥⎣⎦⎫⎪⎢⎣⎭【答案】C【解析】画出函数()f x 图象,可求得1()ln(1)14f x x x ⎛⎫=+-<≤ ⎪⎝⎭图象在点()0,0O 处的切线方程为y x =,过点()0,0O 且与函数()211()44f x x x =+>图象相切的直线方程也为y x =, 观察图象即可得答案. 【详解】画出函数()f x 图象,可求得1()ln(1)14f x x x ⎛⎫=+-<≤⎪⎝⎭图象在点()0,0O 处的切线方程为y x =, 过点()0,0O 且与函数()211()44f x x x =+>图象相切的直线方程也为y x =, 即得直线y x =为函数()f x 图象的切线,且有两个切点,切点为()0,0O 和11(,)22A ,关于x 的方程()0f x kx -=恰有2个实数解, 当且仅当直线y kx =与函数()f x 图象有两个公共点, 由图可知当且仅当OB OA k k k ≤≤或OC k k ≥时符合题意,又1OA k =,1In 1544ln 144OBk ⎛⎫+ ⎪⎝⎭==,54OC k =,则可求得54ln 14k ≤≤或54k ≥. 故选:C . 【点睛】本题考查函数的零点与方程根的关系,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力和运算求解能力,求解时注意斜率公式的应用.二、填空题13.将函数()cos(2)(0)2f x x πϕϕ=+<<的图象向右平移6π个单位长度后得到函数()g x 的图象,若函数()g x 图象关于y 轴对称,则ϕ=_________.【答案】3π. 【解析】根据“左加右减”的平移原则得()cos(2)3g x x πϕ=-+,再根据函数()g x 图象关于y 轴对称得()3k k Z πϕπ=+∈,由02πϕ<<即可得答案.【详解】由题意知:()cos(2)3g x x πϕ=-+,∵函数()g x 图象关于y 轴对称,∴()g x 为偶函数,∴3k πϕπ-=,即()3k k Z πϕπ=+∈,∵02πϕ<<,∴3πϕ=.故答案为:3π. 【点睛】本题考查函数图象变换求解析式、偶函数的性质,考查函数与方程思想、转化与化归思想、,考查逻辑推理能力和运算求解能力. 14.已知等比数列{}n a 的前n 项和为n S ,且372S =,6632S =,则7a =__________.【答案】32.【解析】由632S S ≠知等比数列{}n a 的公比1q ≠,再由等比数列的前n 项和公式可得q ,1a 的值,再代入通项公式,即可得答案.【详解】由632S S ≠知等比数列{}n a 的公比1q ≠, 则由题知()3131712a q S q-==-且616(1)6312a q S q -==-,则63191q q -=-,求得2q =,112a =, 则6712322a =⨯=. 故答案为:32 【点睛】本题考查等比数列的前n 项和公式、通项公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力.15.设正方体1111ABCD A B C D -,棱长为1,M ,N 是棱1AA ,11C D 的中点,则MN 与BC 所成角的正弦值为__________.【答案】3. 【解析】如图,取11A B 中点P ,连接MP ,NP ,由题知MN 与BC 所成的角即为MN 与PN 所成的角,根据MN =MN 的值,再利用正弦函数的定义,即可得答案.【详解】如图,取11A B ,中点P ,连接MP ,NP ,由题知MN 与BC 所成的角即为MN 与PN 所成的角, 又正方体111ABCD A B C D -的棱长为1,则1PN =,22MP =, 又NP ⊥平面11ABB A ,MP ⊂平面11ABB A , 所以NP MP ⊥,则226MN PN MP =+=, 且3sin MP MNP MN ∠==, 故MN 与BC 所成角的正弦值为3. 故答案为:33. 【点睛】本题考查异面直线所成的角的正弦值,考查函数与方程思想、转化与化归思想,考查空间想象能力和运算求解能力.16.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,O 为ABC V 的外心,320OA OB OC ++=u u r u u u r u u u r r ,32OB OC ⋅=-u u u r u u u r ,则ABC V 周长的取值范围是__________.【答案】(]6,9.【解析】320OA OB OC ++=u u r u u u r u u u r r 两边平方结合32OB OC ⋅=-u u u r u u u r 可得3A π=,再利用正弦定理将a b c ++转化成角B 的三角函数,利用三角函数的性质,即可得答案. 【详解】设ABC V 的外接圆半径为R ,320OA OB OC ++=u u r u u u r u u u r r3(2)OA OB OC =-+u u r u u u r u u u r ,22223(2)4||||cos 4OA OB OC OB OB OC BOC OC =+=+∠+u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,∴224cos 2R BOC R ∠=-,得1cos 2BOC ∠=-, 则223A BOC π=∠=,3A π=,又23cos 2OB OC R BOC ⋅=∠=-u u u r u u u r ,则R =,又由正弦定理得sin sin )a b c A B C ++=++2sin sin()33B B π⎤=+-+⎥⎦6sin()36B π=++,又2(0,)3B π∈,5(,)666B πππ+∈, 则(]6,9a b c ++∈,ABC V 周长的取值范围是(]6,9.故答案为:(]6,9. 【点睛】本题考查正弦定理、向量数量积、三角函数的性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意三角函数有界性的应用.三、解答题17.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且()–sin sin sin 0b c B a A c C -+=(1)求角A 的大小;(2)若a =4B π=,求ABC V 的面积.【答案】(1) 3A π=;(2) 3+【解析】(1)利用正弦定理将角化成边得222b c a bc +-=,再由余弦定理得3A π=;(2)由(1)得3A π=,从而可求得C ,再利用正弦定理得c ,代入三角形面积公式,即可得答案. 【详解】(1)∵()sin sin sin 0B a A c c C b -+=-,∴22()0b c b a c --+=,即222b c a bc +-=,又由余弦定理得2221cos 222b c a bc A bc bc +-===,又0A π<<,所以3A π=.(2)由3A π=及4B π=得()34C πππ=-+,又a =4sin sin 3c C ==, 4sin ()4sin()3434c πππππ⎡⎤=-+=+⎢⎥⎣⎦14(2222=⨯+⨯=,则ABC V的面积为:11sin 3222ac B =⨯⨯=+ 故ABC V的面积为3+ 【点睛】本题考查正、余弦定理的应用、面积公式、内角和公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力.18.已知点()3,2A ,1(0,)2B ,()2,1M -,点P 为曲线C 上任意一点,且满足2PA PB =.(1)求曲线C 的方程;(2)若直线l 过点M ,求直线l 被曲线C 截得的最短弦长及此时直线l 的方程. 【答案】(1)()2215x y ++=;(2)30x y -+=. 【解析】(1)设点(),P x y ,由2||PA PB =得曲线C 的方程;(2)由(1)知曲线C 是以点()–1,0CCM l ⊥时,直线l 被圆C 截得的弦长最短,利用点斜式方程,即可得答案. 【详解】(1)设点(),P x y ,由2||PA PB =得=化简整理得22(1)5x y ++=,所以曲线C 的方程为()2215x y ++=.(2)由(1)知曲线C 是以点()–1,0C显然当CM l ⊥时,直线l 被圆C 截得的弦长最短,最短弦长= 此时1111021i CMk k =-==--+,直线l 方程为12y x -=+, 即30x y -+=. 【点睛】本题考查圆的轨迹方程、直线与圆相交弦最短问题,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意直线垂直关系的应用.19.已知数列{}n a 的前n 项和为n S ,满足21n n a S =+,数列{}n b 满足212n n n b b b ++=-,其中n *∈N ,且112b a =,3232b a =-. (1)求数列{}n a ,{}n b 的通项公式; (2)设2nn nb c a =,数列{}n c 的前n 项和为n T ,证明:3n T <. 【答案】(1)12n n a -=,1n b n =+;(2)证明见解析.【解析】(1)利用递推关系21n n a S =+,多递推一项再相减,可得数列{}n a 是以11a =为首项,公比为2的等比数列;又由212a n a b b b ++=-,知数列{}n b 是等差数列;分别代入等差与等比数列的通项公式,即可得答案. (2)由(1)知122n n n n b n c a +==,得用错位相减法求得332n n n T +=-,即可证得结论. 【详解】(1)由21n n a S =+①知11a =,又当2n ≥时,1121n n a S --=+②, 则由①-②得122n n n a a a --=,则12n n a a -=,12(2)nn a n a -=≥, 故数列{}n a 是以11a =为首项,公比为2的等比数列,则12n n a -=.又由212a n a b b b ++=-,知数列{}n b 是等差数列, 又1122b a ==,32324b a =-=, 则数列{}n b 的公差3112b b d -==,故1n b n =+. (2)证明:由(1)知122n n n n b n c a +==, 则有12323412222nn T +=++++L ③ 231123122222n n n n n T ++=++++L ④ 由③–④得1323112111222222n n n k n T ++⎛⎫=+++⋯+- ⎪⎝⎭ 则11111142113311222212n nn n n n T -++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭++⎢⎥⎣⎦=+-=--,故3332n n n T +=-<,得证. 【点睛】本题考查等差数列、等比数列的通项公式、错位相减法求和、不等式证明,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力.20.已知函数2(2)3()xx a x a f x e++++=(a为常数,a R ∈). (1)当[]2,2a ∈-时,判断函数()f x 的单调性;(2)若函数()f x 有两个极值点1x ,2x ,且111(,)32x ∈求实数a 的取值范围.【答案】(1)函数()f x 在R 上单调递增;(2)105(,)32--.【解析】(1)对函数求导,再由[]2,2a ∈-得()0f x '≥恒成立,即可得答案; (2)由题意得1x ,2x 为方程()0f x '=的两根,从而得到1x ,2x ,a 之间的关系,再将a 表示成关于1x 的函数,利用构造函数法研究函的值域,即可得答案. 【详解】(1)由2(2)3()xx a x a f x e++++=, 得21()xx ax f x e++'=, 当[]2,2a ∈-时,240a V =-≤,210x ax ++≥恒成立,()0f x '≥,所以函数()f x 在R 上单调递增.(2)若函数()f x 有两个极值点1x ,2x ,则1x ,2x 是关于x 的方程210x ax ++=的两个不等实根, 则由240a =->V ,得–2a <或2a >①, 又由韦达定理知12x x a +=-且12,1x x =, 则有12111()()a x x x x =-+=-+又由题知111(,)32x ∈,令函数1()()g x x x =-+,11(,)32x ∈. 则2211()(1)10g x x x '=--=->对任意11(,)32x ∈成立, 函数1()()g x x x=-+在11(,)32上单调递增,所以105()(,)32g x ∈--,即得10532a -<<-② ∴a 的取值范围是105(,)32--. 【点睛】本题考查利用导数研究函数的单调性、极值、参数的取值范围,考查函数与方程思想、转化与化归思想、分类讨论思想,考查逻辑推理能力和运算求解能力,求解时注意消元法的应用.21.如图1,在等腰梯形ABCD 中,2AB AD ==,120DAB ∠=︒,O 是CD 中点,将AOD △沿AO 折起,使平面AOD ⊥平面ABCO .如图2所示,E ,F 点分别是AB ,CD 上的点,且12AE CF BE DF ==.(1)求证://BF 平面DOE ; (2)求三棱锥B-DOF 的体积. 【答案】(1)证明见解析;(2)23. 【解析】(1)过点F 作//FG OC 交OD 于点G ,证明四边形BFGE 是平行四边形,再利用线面平行的判定定理,即可得答案;(2)过点D 作DH AO ⊥于点H ,利用等积法即23B DOF B DOC V V --=,即可得答案. 【详解】(1)证明:过点F 作//FG OC 交OD 于点G , 由题知//AB OC .连接CE ,由12AE CF BE DF ==, 得23GF OC =,23BE OC =, 所以GF BE =,且//GF BE ,所以四边形BFGE 是平行四边形,所以//BF EG , 又EG ⊂平面DOE ,BF ⊄平面DOE , 所以//BF 平面DOE .(2)过点D 作DH AO ⊥于点H ,由题知AOD △是边长为2的等边三角形,则3DH =因为12CF DF =,所以23DOF DOC S S =V V , 则23B DOF B DOC V V --=,又111(2)2sin60)1332B DOC D BOC BOC V V S DH --==⋅⋅=⨯⨯⨯⨯︒=V ,所以23B DOF V -=,即求得三棱锥B-DOF 的体积为23.【点睛】本题考查空间中线面平行判定定理的应用、三棱锥体积的求解,考查函数与方程思想、转化与化归思想,考查空间想象和运算求解能力,求解时注意三棱锥等积法的应用. 22.已知函数sin ()ln xf x x x=-. (1)证明:函数()f x 在()0,π上有唯一零点; (2)若()0,2x π∈时,不等式sin 2()ln 2x af x x x x++≤恒成立,求实数a 的取值范围.【答案】(1)证明见解析;(2)4⎡⎫+∞⎪⎢⎣⎭. 【解析】(1)对函数求导得2(cos 1)sin ()x x xf x x--'=,由(0,)x π∈可得()0f x '<,从而得到函数的单调性,再根据区间端点的函数值,即可得答案; (2)等式sin 2()ln 2x af x x x x++≤,可化为不等式1sin sin 22x x a +≤,令1()sin sin 2,(0,2)2g x x x x π=+∈利用导数求得()g x 的最大值,即可得答案.【详解】(1)证明:由sin ()ln xf x x x=-得 22cos sin 1(cos 1)sin ()x x x x x xf x x x x---'=-= 当(0,)x π∈时,cos 10x -<,sin 0x -<, 则()0f x '<,函数()f x 在()0,π上单调递减, 又3()ln066f πππ=->,()ln 0f ππ=-<所以函数()f x 在()0,π上有唯一零点,得证. (2)由题知不等式sin 2()ln 2x a f x x x x ++≤,可化为不等式1sin sin 22x x a +≤,则由题有1sin sin 22x x a +≤对()0,2x π∀∈恒成立, 令1()sin sin 2,(0,2)2g x x x x π=+∈则有()2cos cos22cos cos 1g x x x x x '=+=+-()()cos 12cos 1x x =+-,其中cos 10x +≥, 由2cos 10x -=得3x π=或53x π=则当03x π<<或523x ππ<<时,()0g x '>, 当533x ππ<<时,()'0g x ≤, 当且仅当x π=时,()0g x '=,所以函数()g x 在(0,)3π5,23ππ⎛⎫ ⎪⎝⎭上单调递增,在5,33ππ⎛⎫ ⎪⎝⎭上单调递减,又34g π⎛⎫=⎪⎝⎭,(2)0g π=,04>,所以max ()4g x =,则4a ≥,即得实数a 的取值范围是⎫+∞⎪⎣⎭. 【点睛】本题考查利用导数研究函数的零点、不等式恒成立求参数范围,考查函数与方程思想、转化与化归思想、分类讨论思想,考查逻辑推理能力和运算求解能力,求解时注意函数构造法的应用.。
安徽省江淮名校高三第二次联考数学(文)试题(扫描版,含

文科数学参考答案二、填空题(每题5分,共25分)11. 21,20140x x x ∀>-+-≤ 12. 13. 14. 15. ①⑤16.解:(1)由及,有 ……………………1分 有 解得 ………………………4分7(1)(3)310n a n n =+--=-+27(310)317222n n S n n n +-+==-+ …………………………6分(2)由题意有,又由(1)有 ………8分112(12)(32)(32)n n a a a -=++++++1121332()n n a a a -=+++++++ …12分17.(1)()2cos (sin cos cos sin )sin f x x x A x A A =-+ ……………………1分sin 2cos cos 2sin x A x A =- 在处取得最大值。
522,12A k k Z ππ∴⨯-=∈,即 , …………………………4分sin(2)12x A ∴-<-≤,即的值域为⎛⎤ ⎥ ⎝⎦。
…………………………6分 (2)由正弦定理得sin sin sin b cB C A a++=…………………………9分2222cos a b c bc A =+-得 …………………………11分1sin 2ABC S bc A ∆== …………………………12分 18.(1)a b x a x g -++-=1)1()(2,因为,所以在区间上是增函数, 故,解得. …………………………4分 (2)由已知可得,所以可化为,化为k x x ≥⋅-⎪⎭⎫⎝⎛+2122112,令,则,因,故,记,因为,故,所以的取值范围是 …………………………12分19.解:⑴在Rt△BOE中, ,在Rt△AOF中,在Rt△OEF 中, ,当点F 在点D 时,角最小, ……2分 当点E 在点C 时,角最大, ,所以50(sin cos 1),sin cos l αααα++=………4分定义域为 ……………………………6分⑵设]3,6[,cos sin ππααα∈+=t ,所以 ……………………8分250(1)1001)]112t l t t +==∈-- ……………………………10分所以当时, ,总费用最低为元 ……12分20.解:(1)由题意0,()xa f x e a '>=-, ……………………………1分 由()0xf x e a '=-=得l n x a =. 当(,l n)x a ∈-∞时, ()0f x '<;当(l n,)x a ∈+∞时,()0f x '>.∴()f x 在(,l n )a -∞单调递减,在(l n ,)a +∞单调递增 …………………………4分 即()f x 在l n x a =处取得极小值,且为最小值,其最小值为l n (l n )l n 1l n 1.af a e a a a a a =--=-- ……………………………6分 (2)()0f x ≥对任意的x ∈R 恒成立,即在x ∈R 上,m i n ()0f x ≥. 由(1),设()l n 1.g a a aa =--,所以()0g a ≥.由()1l n 1l n 0g a a a '=--=-=得1a =. ……………………………9分 易知()g a 在区间(0,1)上单调递增,在区间(1,)+∞上单调递减, ∴ ()g a 在1a =处取得最大值,而(1)0g =.因此()0g a ≥的解为1a =,∴1a = ……………………………13分 21.(Ⅰ) 当时,;当时, , ,相减得……………………………2分又, 所以是首项为,公比为的等比数列,所以 ……………………4分(Ⅱ) 由(Ⅰ) 知,所以112244+-=⋅==n n n n n n a n b所以23411232222n n n T +=++++ 34121212222n n n n ++-++++两式相减得2341211111222222n n n n T ++=++++-=2221111222122212n n n n n ++⎛⎫- ⎪+⎝⎭-=--,所以 (或写成,均可给至8分) ………8分 (Ⅲ)=()()()11221211211121122k kk k k k k k k S T k k ++++==+⋅++⎛⎫⎛⎫-⋅-++-⋅- ⎪ ⎪⎝⎭⎝⎭()()111211221212121k k k k k +++⎛⎫==- ⎪---⋅-⎝⎭…………11分 所以()1111211122121212121nnk k n k k k k k S T k ++==+⎛⎫⎛⎫=-=-< ⎪ ⎪⋅++---⎝⎭⎝⎭∑∑若不等式()121nk k k k m S T k =+<⋅++∑对任意正整数恒成立,则, 所以存在最小正整数,使不等式()121nk k kk m S T k =+<⋅++∑对任意正整数恒成立 ……14分。
2020届安徽省江淮十校高三第二次联考数学(文)试题(学生版)

江淮十校2020届高三第二次联考数学(文科)一、选择题1.若全集U =R ,集合2{|16}A x Z x =∈<,{|10}B x x =-≤,则()U A B ⋂=ð( )A. {|14}x x <„B. {|14}x x <<C. {1,2,3}D. {2,3}2.下列说法错误的是( )A. 命题“若2430x x -+=,则3x =”的逆否命题为“若3x ≠,则2430x x -+≠”B. 命题“(0,)x ∀∈+∞,23x x <”是假命题C. 若命题p 、q ⌝均假命题,则命题p q ⌝∧为真命题D. 若()f x 是定义在R 上的函数,则“(0)0f =”是“()f x 是奇函数”的必要不允分条件3.已知函数()x x f x e e -=-(e 为自然对数的底数),若0.50.7a -=,0.5log 0.7b =,0.7log 5c =,则( )A. ()()()f b f a f c <<B. ()()()f c f b f a <<C. ()()()f c f a f b <<D. ()()()f a f b f c << 4.等差数列{}n a ,若2586104()6()132a a a a a ++++=,则94a a +=( )A. 9B. 10C. 11D. 12 5.函数2sin 2x y x =-的图象大致是 A. B.C. D.6.已知向量a r ,b r 满足||3a =r ,1b r ||=,且||||a b a b -=+r r r r ,则|2|a b -r r 等于( )357 D. 3 7.平面直角坐标系xOy 中,若角α顶点为坐标原点,始边与x 轴的非负半轴重合,终边为单位圆O 交于点03,5P y ⎛⎫ ⎪⎝⎭,且,02πα⎛⎫∈- ⎪⎝⎭,则cos()6πα+=( )A. 33410-B. 43310-C. 33410+D. 43310+ 8.已知函数222,0()2,0x x x f x x x x ⎧--≥=⎨-<⎩,则满足(2)(1)0f x f -+->的x 的取值范围是( )A. (,3)-∞B. (1,3)-C. (,1)(3,)-∞-+∞UD. (3,)+∞9.长方、堑堵、阳马、鳖臑这些名词出自中国古代数学名著《九章算术·商功》,其中阳马和鳖臑是我国古代对一些特殊椎体的称呼.取一长方,如图长方体1111ABCD A B C D -,按平面11ABC D 斜切一分为二,得到两个一模一样的三棱柱,称该三棱柱为堑堵,再沿堑堵的一顶点与相对的棱剖开,得四棱锥和三棱锥各一个,其中与矩形为底另有一棱与底面垂直的三棱锥1D ABCD -称为阳马,余下的三棱锥11D BCC -是由四个直角三角形组成的四面体称为鳖臑,已知长方体1111ABCD A B C D -中2AB =,3BC =,14AA =,按以上操作得到阳马,则阳马的最长棱长为( )A. 25B. 5 29 D. 4210.已知在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin 2sin A B =,cos cos 2a B b A +=,22a =则ABC ∆面积为( )5 B. 62 C. 72 211.关于函数()2sin()16f x x ππ=-+有下述四个结论:正确的有( )个①()f x 在区间10,2⎛⎫ ⎪⎝⎭单调递增 ②()y f x =的图象关于点7,16⎛⎫⎪⎝⎭对称 ③()f x 的最小正周期为2 ④()f x 的值域为[1,3]-A. 1B. 2C. 3D. 412.已知函数2ln ,0()12,02e x x x f x x x x ⎧>⎪⎪=⎨⎪+-≤⎪⎩(e 为自然对数的底数),则满足f (x )=f [f (1)]的x 个数是( ) A. 1 B. 2 C. 3 D. 4二、填空题13.曲线2()cos f x x x =-在点(0,(0))f 处的切线方程为_______________.14.n S 是等比数列{}n a 的前n 项和,32a =,2106a a =,则6S =____________.15.函数()cos f x x x =,且对任意实数x 都有()()f x f x θθ-=+()R θ∈,则cos2θ=_______.16.当[0,1]x ∈时,不等式32320ax x x -++>恒成立,则实数a 的取值范围是________.三、解答题17.已知函数2()sin(2)sin(2)2cos 166f x x x x a ππ=++-++- (1)若()f x 的最小值是2,求a ;(2)求函数()y f x =,[0,]x π∈的单调递减区间.18.记n S 为数列{}n a 的前n 项和,已知22n n S a =-.(1)判断数列{}n a 是否为等比数列,并说明理由;(2)设21log n n b n a =-+,求数列{}n b前n 项和n T .19.已知定义在R 上的偶函数()f x 和奇函数()g x 满足1()()2x f x g x ++=.(1)求()f x ,()g x ,并证明:2(2)[()]2f x g x =+;(2)求函数()(2)2()F x f x g x =-,[1,1]x ∈-的最小值.20.已知钝角ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,其中A 为钝角,若tan b a B =,且32sin 2sin cos 2C B A =+. (1)求角B ;(2)若点D 满足2BD DC =u u u r u u u r ,且BC =AD .21.已知函数32()21f x x ax =-+()a R ∈.(1)若3a =-,求()f x 的极值;(2)若()f x 在(0,)+∞内有且仅有一个零点,求()f x 在区间[]22-,上的最大值、最小值. 22.已知函数2()(1)x f x xe a x =++()a R ∈.(1)若1a =-,求()f x '的单调区间;(2)若0a >,证明()f x 有且仅有两个零点.。
安徽省江淮十校2020届高三数学8月联考试题 文 替

安徽省江淮十校2020届高三8月联考数学文试题一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知复数21(1)()z a a i a R =-++∈为纯虚数,则z 为 ( ) A .0 B .2i C .2i - D .12i -- 2.下列函数中周期为π且图象关于直线6x π=对称的函数是 ( )A .2sin(2)6y x π=-B . 2sin()23x y π=+ C .2sin(2)6y x π=+ D .2sin()23x y π=-3.若直线2x y -=被圆22(1)()4x y a -++=所截得的弦长为22,则实数a 的值为 ( ) A .2-或6 B .0或4 C .1-或3 D . 1-或34.已知变量x ,y 满足约束条件102200x y x y x y +-≥⎧⎪-+≥⎨⎪-≤⎩,则2z x y =-的最大值为 ( )A .2B .52C .1-D .125.下列命题说法正确的是 ( ) A .命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠” B .“03x <<”是“11x -<”的必要不充分条件C .命题“x R ∃∈,使得210x x +-<”的否定是:“x R ∀∈,均有210x x +->” D .命题“若x y =,则sin sin x y =”的逆命题为真命题6.按如下程序框图,若输出结果为42S =,则判断框内应补充的条件为 ( )A .3i >B .5i >C .7i >D .9i >7.椭圆22216x y a +=与双曲线2214x y a -=有相同的焦点,则实数a 的值是 ( ) A .12B .1或2-C .1或 12D .18. 一几何体的三视图如图所示,则该几何体的表面积为 ( )A. 22015π+B. 20815π+C. 2009π+D. 20018π+9.已知函数()f x 是定义在R 上的奇函数, 且满足(2)()f x f x +=.若当[)0,1x ∈时,()22x f x =-,则12(log 42)f 的值为 ( )A .0B .1C .2D . 2- 10. 如图,已知点()2,0P,正方形ABCD 内接于圆O :221x y +=,M 、N 分别为边AB 、BC 的中点. 当正方形ABCD 绕圆心O 旋转时,PM ON ⋅u u u u r u u u r的取值范围为 ( )A .[]2,2-B .2,2⎡⎤-⎣⎦C .[]1,1-D .22,22⎡⎤-⎢⎥⎣⎦二、填空题:(本大题共5小题,每小题5分,共25分.请把答案填在答题卡上.) 11. 设n S 为等差数列{}n a 的前n 项和,若231012a a a ++=,则9S = . 12.函数()sin cos f x x x x =+在,6ππ⎡⎤⎢⎥⎣⎦上的最大值为 . 13.某市即将申报“全国卫生文明城市”,相关部门要对该市200家饭店进行卫生检查,先在这200家饭店中抽取5家大致了解情况,然后对全市饭店逐一检查.为了进行第一步抽查工作,相关部门先将这200家饭店按001号至200号编号,并打算用随机数表法抽出5家饭店,根据下面的随机数表,要求从本数表的第5列开始顺次向后读数,则这5个号码中的第二个号码是 . 随机数表:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 14.已知(,)A A A x y 是单位圆上(圆心在坐标原点O )任一点,将射线OA 绕点O 逆时针旋转3π到OB 交单位圆于点(,)B B B x y ,则2A B y y -的最大值为 .15.设函数()f x 的定义域为D ,若,x D y D ∀∈∃∈,使得()()f y f x =-成立,则称函数()f x 为“美丽函数”.下列所给出的五个函数:①2y x =;②11y x =-;③()ln(23)f x x =+;④22x xy -=-;⑤2sin 1y x =-. 其中是“美丽函数”的序号有 .三、解答题:(本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.) 16.(本小题满分12分)第10题图在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且a b c <<,sin A = (Ⅰ)求角B 的大小; (Ⅱ)若2a =,b =c 及ABC ∆的面积.17. (本小题满分12分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温x (°C)与该小卖部的这种饮料销量y (杯),得到如下数据:(Ⅰ)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;(Ⅱ)请根据所给五组数据,求出y 关于x 的线性回归方程ˆˆˆybx a =+; (Ⅲ)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.(参考公式:121()()ˆˆˆ()niii nii x x y y ba y bx x x ==--==--∑∑,.)18.(本小题满分12分)已知首项为32,公比不等于1的等比数列{}n a 的前n 项和为n S (n N *∈),且22S -,3S ,44S 成等差数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令n n b n a =,数列{}n b 的前n 项和为n T ,求n T 并比较n n T b +与6大小.19.(本小题满分13分)在如图所示的多面体ABCDEF 中,DE ⊥平面ABCD ,AD BC P ,平面BCEF I 平面FDEADEF EF =,60BAD ∠=o ,2AB =,1DE EF ==.(Ⅰ)求证:BC EF P ;(Ⅱ)求三棱锥B DEF -的体积. 20.(本小题满分13分)已知函数()ln 3()f x k x kx k R =--∈. (Ⅰ)当1k =-时,求函数()f x 的单调区间;(Ⅱ)若函数()y f x =的图象在()2,(2)f 处的切线与直线30x y --=平行,且函数322()()2tg x x x x f x '=++在区间(1,2)上有极值,求t 的取值范围.21.(本小题满分13分)已知椭圆C :()222210x y a b a b+=>>的离心率2e =,且由椭圆上顶点、右焦点及坐标原点构成的三角形面积为2. (Ⅰ)求椭圆C 的方程;(Ⅱ)已知(0,2)P ,过点(1,2)Q --作直线l 交椭圆C 于A 、B 两点(异于P ),直线PA 、PB 的斜率分别为1k 、2k .试问1k +2k 是否为定值?若是,请求出此定值,若不是,请说明理由.安徽省“江淮十校协作体”2020届高三第一次联考数学(文科)试卷及解析一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知复数21(1)()z a a i a R =-++∈为纯虚数,则z 为 ( ▲ ) A .0 B .2i C .2i - D .12i -- 答案: C【解析】:由21010a a ⎧-=⎨+≠⎩,得1a =,故2z i =,所以2z i =-.2.下列函数中周期为π且图象关于直线6x π=对称的函数是 ( ▲ )A .2sin(2)6y x π=-B . 2sin()23x y π=+ C .2sin(2)6y x π=+ D .2sin()23x y π=-答案: C【解析】:由周期为π可排除选项B 和D ,对于选项C ,当6x π=时,函数取得最大值,显然符合题意.3.若直线2x y -=被圆22(1)()4x y a -++=所截得的弦长为,则实数a 的值为( ▲ ) A .2-或6 B .0或4 C .1-D . 1-或3答案: D【解析】:由圆的性质可得圆心到直线的距离为d ==1a =-或3.4.已知变量x ,y 满足约束条件102200x y x y x y +-≥⎧⎪-+≥⎨⎪-≤⎩,则2z x y =-的最大值为 ( ▲ )A .2B .52C .1-D .12答案: A 【解析】:由线性规划知识易得.5.下列命题说法正确的是 ( ▲ ) A .命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠” B .“03x <<”是“11x -<”的必要不充分条件C .命题“x R ∃∈,使得210x x +-<”的否定是:“x R ∀∈,均有210x x +->” D .命题“若x y =,则sin sin x y =”的逆命题为真命题 答案: B【解析】:对于选项A ,命题“若21x =,则1x =”的否命题应为:“若21x ≠,则1x ≠”;对于选项B,1111102x x x -<⇔-<-<⇔<<,所以命题正确;对于选项C ,命题“x R ∃∈,使得210x x +-<”的否定应为:“x R ∀∈,均有210x x +-≥”; 对于选项D ,命题“若x y =,则sin sin x y =”的逆命题为“若sin sin x y =,则x y =”显然为假命题.6.按如下程序框图,若输出结果为42S =,则判断框内应补充的条件为 ( ▲ )A .3i >B .5i >C .7i >D .9i > 答案: B 【解析】:S=0+2=2,i=1+2=3,不满足条件,执行循环体; S=2+8=10,i=2+3=5,不满足条件,执行循环体; S=10+32=42,i=5+2=7,满足条件,退出循环体,故判断框内应补充的条件为5i >. 故选:B .7.椭圆22216x y a +=与双曲线2214x y a -=有相同的焦点,则实数a 的值是 ( ▲ ) A .12B .1或2-C .1或 12D .1答案: D【解析】:由椭圆与双曲线有关知识易得264(0)a a a -=+>,解得1a =.8. 一几何体的三视图如图所示,则该几何体的表面积为 ( ▲ )A. 22015π+B. 20815π+C. 2009π+D. 20018π+答案: B 【解析】:由三视图易得此几何体为一个长方体与半圆柱的组合体,其表面积为2(10410545)26233220815πππ⨯+⨯+⨯⨯-⨯+⨯+⨯⨯=+.9.已知函数()f x 是定义在R 上的奇函数,且满足(2)()f x f x +=.若当[)0,1x ∈时,第8题图()22x f x =-,则12(log 42)f 的值为 ( ▲ )A .0B .1C .2D . 2- 答案: A【解析】:由题意知函数()f x 是周期为2的周期函数,而125log 422=-,所以 1212511(log 42)(2)()()(22)0222f f f f =-+=--=-=--=.10. 如图,已知点()2,0P,正方形ABCD 内接于圆O :221x y +=,M 、N 分别为边AB 、BC 的中点. 当正方形ABCD 绕圆心O 旋转时,PM ON ⋅u u u u r u u u r的取值范围为 ( ▲ )A .[]2,2-B .2,2⎡⎤-⎣⎦C .[]1,1-D .22,22⎡⎤-⎢⎥⎣⎦答案: C【解析】:=()PM ON OM OP ON OM ON OP ON ⋅-⋅=⋅-⋅u u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r u u u r u u u r 202cos 2PON =-⨯∠ cos PON =-∠[]1,1∈-,所以PM ON ⋅u u u u r u u u r的取值范围为[]1,1-.二、填空题:(本大题共5小题,每小题5分,共25分.请把答案填在答题卡上.) 11. 设n S 为等差数列{}n a 的前n 项和,若231012a a a ++=,则9S = ▲ . 答案: 36【解析】:因为231012a a a ++=,由等差数列的性质知5312a =,故54a =,所以199599362a a S a +=⨯==. 12.函数()sin cos f x x x x =+在,6ππ⎡⎤⎢⎥⎣⎦上的最大值为_____▲____. 答案:2π 【解析】:()sin cos sin cos f x x x x x x x '=+-=,易得当62x ππ<<时,()0f x '>,当2x ππ<<时,()0f x '<,所以()f x 在(,)62ππ上单调递增,在(,)2ππ上单调递减,故2x π=时,()f x 取第10题图得最大值()22f ππ=.13.某市即将申报“全国卫生文明城市”,相关部门要对该市200家饭店进行卫生检查,先在这200家饭店中抽取5家大致了解情况,然后对全市饭店逐一检查.为了进行第一步抽查工作,相关部门先将这200家饭店按001号至200号编号,并打算用随机数表法抽出5家饭店,根据下面的随机数表,要求从本数表的第5列开始顺次向后读数,则这5个号码中的第二个号码是 ▲ . 随机数表:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 答案: 068 【解析】:由随机数表进行简单随机抽样的方法易得,抽取的第一个号码为175,第二个号码为068. 14.已知(,)A A A x y 是单位圆上(圆心在坐标原点O )任一点,将射线OA 绕点O 逆时针旋转3π到OB 交单位圆于点(,)B B B x y ,则2A B y y -的最大值为 ▲ .答案【解析】:设(cos ,sin )A αα,则(cos(),sin())33B ππαα++,于是22sin sin()3A B y y παα-=-+3sin )226πααα=-=-,.15.设函数()f x 的定义域为D ,若,x D y D ∀∈∃∈,使得()()f y f x =-成立,则称函数()f x 为“美丽函数”.下列所给出的五个函数:①2y x =;②11y x =-;③()ln(23)f x x =+;④22x xy -=-;⑤2sin 1y x =-. 其中是“美丽函数”的序号有 ▲ . 答案: ②③④ 【解析】:由题意知“美丽函数”即为值域关于原点对称的函数,容易判断仅有②③④符合题意. 三、解答题:(本大题共6小题,共75分.解答应写出必要的文字说明、证明过程及演算步骤.) 16.(本小题满分12分)在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且a b c <<,sin A = (Ⅰ)求角B 的大小;(Ⅱ)若2a =,b =c 及ABC ∆的面积.【解析】:(Ⅰ)sin A =Q ,2sin b A =,2sin sin A B A =, ………………………………………………2分又0A π<<Q ,sin 0A ∴>,sin B ∴=, …………………………………………4分a b c <<Q ,B C ∴<, 所以02B π<<,故3B π=. …………………………………6分(Ⅱ)2a =Q,b =22212222c c =+-⨯⨯⨯,即2230c c --=解得3c =或1c =-(舍去),故3c =. ………………………………………………10分所以11sin 232222ABC S ac B ∆==⨯⨯⨯=. ………………………………………12分 17. (本小题满分12分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温x (°C)与该小卖部的这种饮料销量y (杯),得到如下数据:(Ⅱ)请根据所给五组数据,求出y 关于x 的线性回归方程ˆˆˆybx a =+; (Ⅲ)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.(参考公式:121()()ˆˆˆ()niii nii x x y y ba y bx x x ==--==--∑∑,.)【解析】:(Ⅰ)设“选取的2组数据恰好是相邻2天数据”为事件A ,所有基本事件(m ,n )(其中m ,n 为1月份的日期数)有:(11,12),(11,13),(11,14), (11,15),(12,13),(12,14),(12,15),(13,14),(13,15),(14,15),共有10种. 事件A 包括的基本事件有(11,12),(12,13),(13,14),(14,15)共4种.所以42()105P A ==为所求. ………………………………………………………6分 (Ⅱ)由数据,求得91012118105x ++++==,2325302621255y ++++==.由公式,求得ˆ 2.1b=,ˆˆ4a y bx =-=, 所以y 关于x 的线性回归方程为ˆ 2.14yx =+. ……………………………………10分 (Ⅲ)当x =7时,ˆ 2.17418.7y=⨯+=. 所以该奶茶店这种饮料的销量大约为19杯. ………………………………………12分18.(本小题满分12分)已知首项为32,公比不等于1的等比数列{}n a 的前n 项和为n S (n N *∈),且22S -,3S ,44S 成等差数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令n n b n a =,数列{}n b 的前n 项和为n T ,求n T 并比较n n T b +与6大小. 【解析】:(Ⅰ)由题意得324224S S S =-+,即()()42430S S S S -+-=,亦即 ()4340a a a ++=,4312a a ∴=-,所以公比12q =-, ……………………………4分 于是数列{}n a 通项公式为()13122n n a n N -*⎛⎫=-∈ ⎪⎝⎭. ……………………………5分另解:由题意得324224S S S =-+,1q ≠,()()()3241111112111a q a q a q qqq---∴=-+---,化简得2210q q --=,12q ∴=-, ………………………………………………4分 ()13122n n a n N -*⎛⎫∴=-∈ ⎪⎝⎭. ………………………………………………………5分(Ⅱ)1313222n n n nn b n a n -⎛⎫==⋅⋅=⎪⎝⎭, 所以12312336932222n n n nT b b b b =++++=++++L L , ①()23131136322222n nn n n T +-=++++L L , ② ………………………………………8分 ①-②得,1231133333222222n n n nT +=++++-L111132231212n n n+⎛⎫⨯- ⎪⎝⎭=--13632n n ++=-, 所以 3662n nn T +=-, ……………………………………………………………11分 从而 6662n n n T b +=-<. (12)分19.(本小题满分13分)在如图所示的多面体ABCDEF 中,DE ⊥平面ABCD ,AD BC P ,平面BCEF I 平面ADEF EF =,60BAD ∠=o ,2AB =,1DE EF ==.(Ⅰ)求证:BC EF P ; (Ⅱ)求三棱锥B DEF -的体积.【解析】:(Ⅰ)因为AD BC P ,AD ⊂平面ADEF ,BC ⊄平面ADEF ,所以BC P 平面ADEF , ………………………………………………………………………3分 又BC ⊂平面BCEF ,平面BCEF I 平面ADEF EF =,所以BC EF P . ……………………………………………………………………………6分 (Ⅱ)在平面ABCD 内作BH AD ⊥于点H ,因为DE ⊥平面ABCD ,BH ⊂平面ABCD ,所以DE BH ⊥,又AD 、DE ⊂平面ADEF ,AD DE D =I ,所以BH ⊥平面ADEF ,所以BH 是三棱锥B DEF -的高. ………………………………………………………10分 在直角三角形ABH 中,o 60BAD ∠=,2AB =,所以BH =因为DE ⊥平面ABCD ,AD ⊂平面ABCD ,所以DE AD ⊥,又由(Ⅰ)知,BC EF P ,且AD BC P ,所以AD EF P ,所以DE EF ⊥,所以三棱锥B DEF -的体积11111332DEF V S BH ∆=⨯⨯=⨯⨯⨯. ………………13分 20.(本小题满分13分)已知函数()ln 3()f x k x kx k R =--∈.(Ⅰ)当1k =-时,求函数()f x 的单调区间;(Ⅱ)若函数()y f x =的图象在()2,(2)f 处的切线与直线30x y --=平行,且函数322()()2t g x x x x f x '=++在区间(1,2)上有极值,求t 的取值范围. 【解析】:()(0)k f x k x x'=->, …………………………………………………………………1分 (Ⅰ)当1k =-时,11()1x f x x x-'=-+=, 令()0f x '>时,解得1x >,令()0f x '<时,解得01x <<, …………………………3分 所以()f x 的单调递增区间是(1,)+∞,单调递减区间是(0,1). …………………………5分 (Ⅱ)因为函数()y f x =的图象在()2,(2)f 处的切线与直线30x y --=平行,所以(2)1f '=,即12k k -=,∴2k =-,2()2f x x-'=+, …………………………7分 ()32222t g x x x x ⎛⎫=++- ⎪⎝⎭,∴()2()342g x x t x '=++-, ………………………9分 第19题图 FA C D EB因为函数()g x 在区间(1,2)上存在极值,注意到()y g x '=的图像为开口向上的抛物线,且(0)20g '=-<,所以只需(1)0(2)0g g '<⎧⎨'>⎩, 解得95m -<<-,∴m 的取值范围为()9,5--. …………………………………………………………………13分21.(本小题满分13分)已知椭圆C :()222210x y a b a b+=>>的离心率2e =,且由椭圆上顶点、右焦点及坐标原点构成的三角形面积为2.(Ⅰ)求椭圆C 的方程;(Ⅱ)已知(0,2)P ,过点(1,2)Q --作直线l 交椭圆C 于A 、B 两点(异于P ),直线PA 、PB 的斜率分别为1k 、2k .试问1k +2k 是否为定值?若是,请求出此定值,若不是,请说明理由.【解析】:(Ⅰ)由题意得2222122a b cc abc ⎧=+⎪⎪⎪=⎨⎪⎪=⎪⎩,解得28a =,24b =, 所以椭圆C 的方程为22184x y +=. ………………………………………………………5分(Ⅱ)1k +2k 为定值4,证明如下:……………………………………………………………6分 (ⅰ)当直线l 斜率不存在时,l 方程为1x =-,由方程组221184x x y =-⎧⎪⎨+=⎪⎩易得1,2A ⎛⎫- ⎪ ⎪⎝⎭,1,2B ⎛⎫-- ⎪ ⎪⎝⎭,于是12420(1)2k -==--,22240(1)2k ⎛⎫-- ⎪+⎝⎭==--, 所以124k k +=为定值. ………………………………………………………………8分 (ⅱ)当直线l 斜率存在时,设l 方程为[](2)(1)y k x --=--,即2y kx k =+-,设()11,A x y ,()22,B x y ,由方程组222184y kx k x y =+-⎧⎪⎨+=⎪⎩消去y ,得 222(12)4(2)280k x k k x k k ++-+-=, 由韦达定理得12221224(2)122812k k x x k k kx x k --⎧+=⎪⎪+⎨-⎪=⎪+⎩(*) …………………………………………10分 ∴12122112121222(2)(2)y y y x y x k k x x x x ---+-+=+= 122112(4)(4)kx k x kx k x x x +-++-= 1212122(4)()kx x k x x x x +-+= 12122(4)x x k k x x +=+-⋅, 将(*)式代入上式得124k k +=为定值. ……………………………………………13分。
