微观部分习题答案B
西方经济学微观部分(高鸿业第六版)课后习题答案

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P 和供给函数Q s=-10+5P 代入均衡条件Q d=Q s,有50-5P =-10+5P 得 P e =6将均衡价格P e =6代入需求函数Q d=50-5P ,得Q e =50-5×6=20或者,将均衡价格P e =6代入供给函数Q s=-10+5P ,得Q e =-10+5×6=20 所以,均衡价格和均衡数量分别为P e =6,Q e =20。
如图2—1所示。
图2—1 (2)将由于消费者收入水平提高而产生的需求函数Q d =60-5P 和原供给函数Q s =-10+5P 代入均衡条件Q d=Q s,有60-5P =-10+5P 得 P e =7将均衡价格P e =7代入Q d=60-5P ,得Q e =60-5×7=25或者,将均衡价格P e =7代入Q s=-10+5P ,得Q e =-10+5×7=25 所以,均衡价格和均衡数量分别为P e =7,Q e =25。
如图2—2所示。
图2—2(3)将原需求函数Q d =50-5P 和由于技术水平提高而产生的供给函数Q s =-5+5P 代入均衡条件Q d =Q s,有50-5P =-5+5P 得 P e =5.5将均衡价格P e =5.5代入Q d=50-5P ,得Q e =50-5×5.5=22.5或者,将均衡价格P e =5.5代入Q s=-5+5P ,得Q e =-5+5×5.5=22.5 所以,均衡价格和均衡数量分别为P e =5.5,Q e =22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点。
微观经济学B附答案备课讲稿

一、名词解释(共15分,每小题3分)1. 需求和需求量的变动2. 替代效应3. 经济利润4.生产者剩余5.多余的生产能力二、单项选择题(共15分,每小题1分)1.以下问题中哪一个不属微观经济学所考察的问题?( )A.一个厂商的产出水平B.失业率的上升或下降C.联邦货物税的高税率对货物销售的影响D.某一行业中雇佣工人的数量2. 经济学家提出模型的主要理由是( )A.一个模型为验证一种假设所必需B一个模型可帮助理解对论点的思考过程C.一个模型为决定一个指数所必需D.只有模型中才可使用实际变量3.若X和Y二产品的交叉弹性是-2.3,则( )。
A.X和Y是替代品B.X和Y是正常商品C.X和Y是劣质品D.X和Y是互补品4.如果某商品富有需求的价格弹性,则该商品价格上升( )。
A.会使销售收益增加B.该商品销售收益不变C.会使该商品销售收益下降D.销售收益可能增加也可能下降5. 在消费者均衡点以上的无差异曲线的斜率( )。
A.大于预算线的斜率B.小于预算线的斜率C.等于预算线的斜率D.可能大于、小于或等于预算线斜率6. 假定X、Y的价格Px、Py已定,当MRy>Px/Py时,消费者为达到最大满足,他将( )。
A. 增购X,减少YB. 减少X,增购YC. 同时增购X、YD. 同时减少X、Y7. 若厂商增加使用一个单位劳动,减少两个单位资本,仍能生产相同产量,则MRTS Lk是( )。
A.1/2B.2C.1D.48.在生产有效区域里,等产量线( )。
A.凸向原点B.不能相交C.负向倾斜D.以上都对9. 假如增加一单位产量所带来的边际成本大于产量增加前的平均可变成本,那么在产量增加后,平均可变成本一定( )。
A.减少B.增加C.不变D.处于最低点10.当AC达到最低点时,下列哪一条是正确的( )。
A.AVC=FCB.MC=ACC.P=AVCD.P=MC11. .完全竞争市场的厂商总收益曲线的斜率为()。
A.固定不变;B.经常变动;C.1;D.012.在完全竞争市场中行业的长期供给曲线取决于()。
微观第1-2章习题(含答案)讲课讲稿

微观第1-2章习题(含答案)第一章复习题一、名词解释1、微观经济学2、生产可能性曲线3、机会成本二、选择题1.经济问题本质上是决定如何去最好的使用()。
A.几乎无限的资源来满足无限的欲望B.有限的资源来满足无限的欲望C.无限的资源来满足有限的欲望D.有限的资源来满足有限的欲望2.经济学可定义为()。
A.政府对市场制度的干预 B.企业赚取利润的活动C.研究稀缺资源如何有效配置的问题D.个人的生财之道3.学习经济学()A.帮助一个人变成一个见多识广的市民B.对一个人成为好市民是有害的,因为经济学强调利己主义C.是浪费时间,因为无论我们是否懂经济,我们都参与其中D.很重要,因为经济学是“赚钱的科学”。
4.学习经济学()A.对一个人成为好市民是有害的,因为经济学强调利己主义B.对雇主是有帮助的,但对工人和消费者是无用的C.很重要,因为经济学是“赚钱的科学”d.帮助学生提高分析技巧,这在工作中是很需要的5. 对经济学的研究()A.与管理、营销以及金融相似,因为它强调如何赚钱B.对企业有帮助,但对做出个人购买决策没有明显帮助C.主要是学术的,而不是职业科目D.从一个人自己的经济来源角度着眼经济,而不是从社会利益角度6.对经济学的研究主要关注A.防止私有公司亏损B.证明社会主义经济优于资本主义经济C.在有效使用稀缺资源时所做的选择D.决定对社会产品的最公平的分配7.“资源是稀缺的”是指()A.资源是不可再生的 B.资源必须留给下一代C.资源终将被耗费殆尽D.相对于需求而言,资源总是不足的8.失业问题如果反映在生产可能性曲线图上,可记为()。
A.生产可能性曲线内的一点 B.生产可能性曲线上的一点C.生产可能性曲线以外的一点D.不在该平面直角坐标系上9.下列哪一项会导致一国生产可能性曲线的外移?()A.股市持续走强 B.通货膨胀C.有用资源被发掘或技术进步D.消费品生产增加,资本品生产下降10.一个经济体系必须作出的基本选择是()。
西方经济学-微观部分习题和答案

第二章需求、供给和均衡价格一、解释概念需求需求弹性需求价格弹性供给供给价格弹性均衡价格支持价格限制价格二、判断1、价格分析是微观经济学分析的核心。
2、微观经济学的研究对象是包括单个消费者、单个生产者、单个市场在内的个体经济单位。
3、若某商品的需求价格弹性Ed=0.6,在其他条件不变的情况下,卖者提高价格肯定增加销售收入。
4、在其他条件不变的情况下,需求缺乏弹性的商品的价格与销售收入呈同方向变动关系。
5、需求量的变动是指商品本身价格变动所引起的该商品的需求数量的变动。
6、在其他条件不变的情况下,当消费者的收入发生变化时,会引起需求曲线的移动。
7、Ed>1的商品,在其他条件不变的情况下,降低价格会增加厂商的销售收入。
8、若某商品的Ed<1,表明当该商品价格下降20%时,该商品需求量减少小于20%。
9、卖者提高价格肯定会增加销售收入。
10、在几何图形上,供给量的变动表现为商品的价格-供给量组合点沿着同一条既定的供给曲线运动。
11、在几何图形上,需求水平的变动表现为商品的价格-需求量组合点沿着同一条既定的需求曲线运动。
12、当两种商品中一种商品的价格发生变动时,这两种商品的需求量都同时增加或减少,则这两种商品的需求交叉价格弹性系数为正。
13、某商品的可替代品越多,相近程度越高,则该商品需求弹性越大。
14、商品用途越广,需求价格弹性越大。
15、任何情况下商品的需求量与价格都是反方向变化的。
16、当对农产品的需求缺乏弹性时,粮食丰收,粮价下跌,农民收入反而会减少。
17、如果两种商品具有替代关系,则相应的需求交叉价格弹性系数为负。
18、正常物品的需求量与消费者的收入水平呈同方向变动。
三、选择题1、下列几组商品的交叉价格弹性为负向的有()。
A、面粉和大米B、汽油和汽车C、羊肉和牛肉D、录音机和磁带2、当出租车租金下调后,对公共汽车服务的()。
A、需求减少B、需求量增加C、需求曲线左移D、需求无法确定3、粮食市场的需求是缺乏弹性的,当粮食产量因灾害而减少时()。
“微观经济学”习题答案
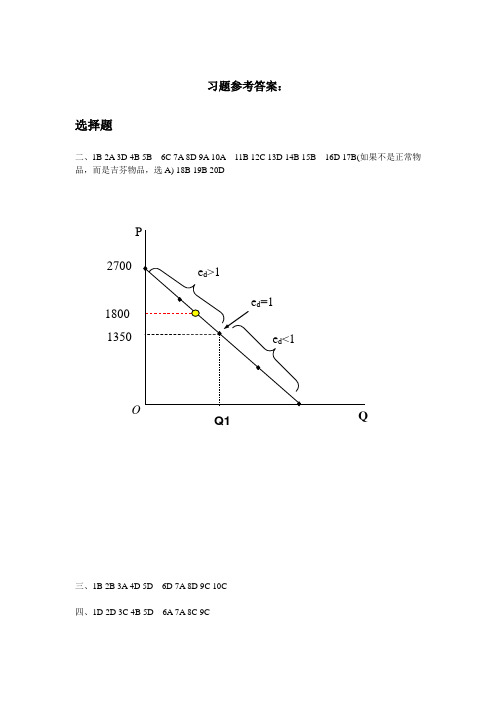
习题参考答案:选择题二、1B 2A 3D 4B 5B 6C 7A 8D 9A 10A 11B 12C 13D 14B 15B 16D 17B(如果不是正常物品,而是吉芬物品,选A) 18B 19B 20D三、1B 2B 3A 4D 5D 6D 7A 8D 9C 10C四、1D 2D 3C 4B 5D 6A 7A 8C 9C五、1C 2B 3D 4A 5B 6B 7C六、1D 2B 3B 4D 5C 6B 7A 8B 9D七、1B 2A 3B 4B 5B 6D 7A 8C 9B八、1D 2C 3C 4A 5B九、1D 2A 3D 4B 5D 6D 7C 8C 9D十一、1A 2B 3B 4B 5D 6B 7D 8B 9C计算题第二章二、计算题1.解:(1)令Q S= Q D,解得PE=2500,QE=Q S= Q D=2000(2)当P=3000时,Q S=-3000+6000= 3000,Q D=7000-6000=1000(3)当Q S=-5000+2P时,限价P=3000解得Qs=-5000+2P= 1000,Q D=7000-6000=1000此时的限价刚好等于均衡价格,均衡数量为1000。
2.解:(1)市场需求函数为Q= Q1+Q2=125-5P(2)P=20时,Q=125-5×20=253.解:(1)征收销售税使每一销售者供给曲线向上移动(销售者会把税收加到价格上),移动的垂直距离等于4美元。
或者说,在价格不变的情况下,供给量会减少,即供给曲线左移。
市场供给函数变为S1=40+6(P-4)因为市场需求函数为D=80-2P,令D=S1解得均衡价格PE=8,均衡数量QE=64政府向销售者征税,但消费者承担了部分税额。
征税后,消费者购买每单位商品支付8元,而不是征税前的5元(D=80-2P=S=40+6P,得P=5)。
销售者以单价8元出售产品,但要交税4元,纯收入仅剩下4元。
(2)政府补贴导致生产者供给曲线向下移动,移动的垂直距离为4元。
微观课后习题及答案

微观课后习题及答案可以帮助人们理解哪些主要的经济问题?答:生产可能性曲线是指在一定的技术条件下,利用现有资源所能生产的最大产量组合的点的轨迹。
生产可能性曲线有助于理解:如何分配资源,如何制定经济政策目标,如何提高生产能力等主要经济问题。
4、什么是经济理性主义?日常生活中有哪些行为是符合这个原则的,有没有“非理性”或“反理性”行为?自私自利和损人利己是理性的还是反理性的,为什么?答:经济理性主义是指这样一种观点,这种观点认为人在经济生活中总是受个人利益或利己心的动机所驱使,总能认真地对各种可能的抉择权进行比较,以便找出一个能使他耗费给定的代价取得最大限度的利益的所谓最优方案。
在日常生活中,人们花费一定金钱买进消费品时总力求消费品提供最大效用,厂商经营总力求利润最大;要素出售者提供生产要素则力求收益极大。
总之,人们无论从事何种经济活动,都力求能带来最大利益,带来最大限度满足。
一切头脑正常的人,即所谓有理性的人都会这样行动,不可能有所谓“非理性”或“反理性”的行为。
然而,理性行为不一定是自私自利的,更不一定是损人利己的。
因为如果人们不把自私自利和损人利己作为自己行为所追求的目标,而把助人为乐看作是自己行为的准则的话,则自私自利和损人利己就不会成为他们的理性行为。
当然,在自私自利或损人利己主义者看来,自私自利和损人利己行为就是理性行为。
可谓“宁可我负天下人,不愿天下人负我”,就是这样的人。
可见,如果我们说,理性行为不应当是自私自利及损人利己的行为,这种说法实际已经是规范性的而不是实证性的了。
因为这种说法实际上己包含着认为自私自利和损人利已是“不好的”、“不应当的”、“非理性的”这样一种价值判断了。
5、既然理性行为无需要完全是自私自利的,为什么经济分析又要假定个人行为的基本动力是追逐个人利益?答:理性行为无需完全是自私自利的。
众所周知,有理性的人的行为可有多种动机,获取个人经济利益只是其中一个方面。
人有理想、感情、信仰、荣誉感、正义感等,这些都会驱使人们从事各种活动,包括经济活动。
高鸿业《西方经济学(微观部分)》(第6版)课后习题答案详解(完整版)

解得:q A =4
即在竞争性市场中,A的产出为4。
(2)由题意可知,实际上厂商A生产的边际收益是私人边际收益和社会边际收益之和,即7+16=4q A+3。根据帕累托奻优状态的条件,社会最优的产出应满足:
20=4q A
解得:q A =5
即社会最优的产出应是5。
15. 一农场主的作物缺水。他需决定是否进行灌溉。如他进行灌溉,或者天下雨的话,作物带来的利润是1000元,但若是缺水,利涧只有500元。灌溉的成本是200元。农场主的目标是预期利润达到最大。
(2)他不买天气预报信息时,如上所述,他会进行灌溉,得到利润800。如果买天气预报信息并假定支付x 元费用,他若确知天下雨,就不泄溉,于是可获利涧:
冗I=1()()()—X
若确知天不下雨,就灌溉,于是可获利润:
冗2=800-x
由于他得到的信息无非是下雨和不下雨,因此,在购买信息情况下的预期利涧为:
E(冗)=0.5(
解得:社会最优产出水平矿=90
这就是该公共物品的社会奻优产出水平。
(2)如该公共物品甘I私人生产,其产出水平为80。公共物品的最优数星通常没有考虑搭便车的问题。如果考虑搭便车,可以看出,一旦B提供了80单位的公共物品,则A可搭便车(不付钱即可享受)。需要注意的是,经济学中一般的结论是公共物品由私人提供的数量<公共物品的呆优提供数量<公共物品若为私人物品时的提供数嚣。如果这个结论严格成立,那么答案可能就是0,即B可能不提供公共物品。
14.假定某个社会有A、B、C三个厂商。A的边际成本为MC=4q A (q A为A的产出),其产品的市场价格为16元。此外,A每生产一单位产品使B增加7元收益,应是多少?
(2)社会最优的产出应是多少?
经济学原理(微观部分)习题与参考答案

经济学原理(微观部分)习题与参考答案对于很多人来说,可能会觉得经济学离我们很远。
可事实上,通过认真观察就会发现,经济学的现象是普遍存在的。
在生活、工作中,激励无处不在。
从经济学角度出发,激励指的是引起一个人做出某种行为的某种东西,人们会对激励做出相应的反应。
这里的激励既可以是正向的奖励,也可以是负向的惩罚。
不同的激励机制会产生不同的激励效果。
如果某种行为能够给你带来奖励,那么人们就会做得更多、更拼尽全力;如果惩罚某种行为,人们就会在最大程度上去避免这种行为。
一般而言,当商品价格下降时,都会引起人们需求量的增加。
以每年的“双十一”购物狂欢节为例,“双十一”最普遍的营销手段是低价、折扣,这些活动会让消费者觉得购买更加划算,他们会因为大幅的降价而囤积许多的生活用品,导致需求量迅速增加。
服装店“以旧换新”的手段同样是运用了激励理论。
“以旧换新”是在消费者购买新的商品时,如果能把同类型的旧商品交给店铺,就能享受一定的折扣,其实旧商品对商家来说没有多大的经济价值,只是发挥着抵值券的作用,从而激励消费者发生购买行为。
那什么是惩罚的激励呢?关税就是惩罚的激励,所谓关税指的是引进出口商品经过一国关境时,由政府所设置的海关向其引进出口商所征收的税收。
随着国与国之间的发展,贸易战是不可避免的,而贸易战采取的主要手段就是关税,通过提高关税极大地可以减少某国的出口额,影响这个国家的国内生产和就业。
最具有代表性的案例是2009年的“轮胎事件”。
2009年4月20日,美国钢铁工人联合会以中国对美轮胎出口扰乱美国市场为由,向美国国际贸易委员会提出申请,对中国产乘用车轮胎发起特保调查。
6月29日,美国贸易委员会建议在现行进口关税(3.4%—4.0%)的基础上,对中国输美乘用车与轻型卡车轮胎连续3年分别加征55%、45%和35%的特别从价关税。
另外一个与大家息息相关的例子是交通违规的罚款,通过这种负向激励可以提高车主开车的谨慎程度,更加遵守行驶的规章制度。
微观经济学复习题及答案.doc

《微观经济学》习题答案第一章习题一、单项选择题1.“资源是稀缺的”是指(B )。
A.世界上大多数人生活在贫困中B.相对于资源的需求而言,资源总是不足的C.资源必须保留给下一代D.世界上资源最终将由于生产更多的物品和劳务而消耗光2.现有资源不能充分满足人的欲望这一事实被称为(B )。
A.机会成本B.稀缺性C.规范经济学D.生产什么的问题3.下列属于实证表述的是(C )。
A.通货膨胀对经济发展有利B.通货膨胀对经济发展不利C.只有控制货币量才能抑制通货膨胀D.治理通货膨胀比减少失业更重要4.研究单个家庭和企业决策的经济学称为(B )。
A.宏观经济学B.微观经济学C.实证经济学D.规范经济学5.下列命题中不是实证经济学命题的是(C )。
A.1982年8月美联储把贴现率降到10%B.2003年某国失业率超过4%C.联邦所得税对中等收入家庭是不公平的D.社会保险税的课税依据现已超过3万美元6.当经济学家说人们是理性的时,这是指(B )。
A.人们不会作出错误的判断B.人们总会从自己的角度作出最好的决策C.人们根据完全的信息而行事D.人们不会为自己所作出的任何决策而后悔二、判断题1.稀缺性仅仅是市场经济中存在的问题。
(×)2.在一个由行政命令来协调经济活动的社会经济中,生产什么、如何生产和为谁生产的决策是价格调节的结果。
(×)3.“所得税税率提高会引起总税收减少”,这是一个实证表述的例子。
(√)4.微观经济学是研究整体经济的。
(×)5.人们的收入差距大一点好还是小一点好”的命题属于实证经济学问题。
(×)6.如果社会不存在资源的稀缺性,也就不会产生经济学。
(√)7.资源的稀缺性决定了资源可以得到充分利用,不会出现资源浪费现象。
(×)8.微观经济学的基本假设是市场失灵。
(×)9.是否以一定的价值判断为依据是实证经济学与规范经济学的重要区别之一。
(√)三、简答题1.稀缺性的含义是什么?答:稀缺性就是资源的相对有限性。
西方经济学高鸿业版微观部分课后习题详解

第五章答案C B B C CABC BD BD CD ACD√×√×√1.答:老王种蔬菜的显性成本就是他为种植蔬菜而支付的货币,即种子、肥料和雇佣者的工资之和为200元。
隐性成本就是为将资源用于某种用途而放弃的在其他可能的最好用途中所得到的收入,即租金250元。
老王在他家门前的那块空地上种植蔬菜的总成本等于显性成本和隐性成本之和即200+250=450元,而卖蔬菜的收入为500元,所以种蔬菜对他来说是有利可图的。
土地出租是不合算的,因为虽然老王出租土地的显性成本等于零,但出租土地的隐性成本就是他种蔬菜的净收入500-200=300元,显然,出租土地的隐性成本要大于他出租的收入,故老王不会选择出租。
2.答:任何一种边际成本都是成本的增量与产量的增量之比。
故边际固定成本MFC=FC/Q=0/Q=0;边际总成本MTC=TC/Q=(FC+VC)/Q=(0+VC)/Q=MVC。
从上面的分析可见,因为固定成本的变化量为零,故边际固定成本是零,而边际总成本和边际可变成本实际上是一回事,可统称为边际成本(MC),因此,在短期内,虽然平均成本有三种,边际成本却只有一种。
图5-1 成本曲线和厂商短期供给曲线1.答:生产函数反映的是一定时期内各种生产函数投入量与产出量之间的物质技术关系;而成本函数则反映着成本与产量之间的变化关系,它是由生产函数以及投入的生产要素价格决定的。
由于在短期中,给定的生产规模实际上是为求得最低成本而设置的,在长期中,每一种生产规模都是最低成本的规模,于是,成本函数的确定,实际上可以转化为在给定产量情况下确定最低成本问题。
如果给定企业的生产函数,那么总可以求出相应的成本函数。
例如设生产函数为Q=F(L,K),TC=LPL+KPK,则我们可以利用使既定产量下成本最小的厂商均衡条件MPPL/PL=MPPK/PK求出K与L的关系式,或者将以上问题转化成求minTC=LPL+KPK,Q=F(L,K),利用拉格朗日函数分别对L、K及所设的λ求偏导得出K与L的关系式,然后分别代入生产函数中求出L(或K)与产量Q的关系,最后代入所设成本函数中即可求得成本函数。
微观经济学习题及答案 16页PPT文档

放弃一单位X商品能获得( )单位Y商品。
A、2
B、1/2
C、1/4
D、4
17.关于实现消费者均衡的条件,不正确的是( ) A、在基数效用论下,商品的边际效用之比等于其价格之比 B、在序数效用论下,两种商品的边际替代率等于其价格之比 C、基数效用论与序数效用论的均衡条件实质上是相同的 D、均衡状态下,消费者增加一种商品的数量所带来的效用增
12.如果消费者的收入增加而商品的价格不变,则无差异 曲线向右上方平行移动。
思考题
1、已知某人月收入为180元,用于购买两种商品X、Y,他的效用函数 为U=XY,且PX=2元,PY=3元,求: (1)效用极大时,他购买X、Y的数量各为多少? (2)若PX下降25%,他购买的X、Y的数量为多少?此时总效用变 化多少?
量必定大于减少的另一种商品所带来的效用减少量
18.需求曲线从( )导出。 A、价格—消费曲线 B、收入—消费曲线 C、无差异曲线 D、预算线
19.消费品价格变化时,连结消费者诸均衡点的曲线称为( )。
A、价格—消费曲线 B、收入—消费曲线 C、恩格尔曲线 D、需求曲线 20*.消费者预算线发生平移时,连结消费者诸均衡点的曲
解: (1)已知U=XY,则:
MU X ddU(X X)Y MU Y ddU(Y Y)X
根据消费者效用最大化的均衡条件:
增加其需求量
22.当消费者的爱好保持不变时,消费者( )也将保持不变 。
A、均衡点 B、满足 C、所喜爱的两种商品的无差异曲线 D、购买的商品数量
23.需求量同价格反向变化的原因是( )。 A、收入效应 B、替代效应 C、收入效应与替代效应同时发挥作用 D、以上均不正确
24.某个消费者的无差异曲线图包含无数条无差异曲线,因 为( )。
《西方经济学》-微观部分练习(有答案)

※<练习一>第二章需求曲线和供给曲线概述以及有关的基本概念一、单项选择题1.张某对面包的需求表示(C )。
A.张某买了面包B.张某没有买面包,而买了煎饼C.面包卖每个1元时,张某准备用现有的收入买4个,而每个为2元时,准备买1个D.张某准备买10个,但钱没带够E.以上都不表示需求2.需求规律说明(B )。
A.药品的价格上涨会使药品质量提高B.计算机价格下降导致销售量增加C.丝绸价格提高,游览公园的人数增加D.汽车的价格提高,小汽车的销售量减少E.羽毛球的价格下降,球拍的销售量增加3.当羽毛球拍的价格下降时,对羽毛球的需求量将(C )。
A.减少B.不变 C. 增加D.视具体情况而定E.以上都有可能4.其他条件不变,牛奶价格下降将导致牛奶的(D )。
A.需求下降B.需求增加C.需求量下降D.需求量增加E.无法确定5.当出租车租金上涨后,对公共汽车服务的(A )。
A.需求增加B.需求量增加C.需求减少D.需求量减少E.无法确定6.以下几种情况中,(B )项是需求规律的例外。
A.某商品价格上升,另一商品需求量也上升B.某商品价格上升,需求量也上升C.消费者收入增加,对某商品的需求增加7.消费者偏好改变,对某商品的消费量随着消费者收入的增加而减少,则该商品是(D )。
A.替代品B.互补品C.正常品D.低档品E.无法确定8.供求规律说明(D )。
A.生产技术提高会使商品的供给量增加B.政策鼓励某商品的生产,因而该商品的供给量增加C.消费者更喜欢某商品,使该商品的价格上升D.某商品价格上升将导致对该商品的供给量增加E.以上都对9.对大白菜供给的减少,不可能是由于(C )。
A.气候异常严寒B.政策限制大白菜的种植C.大白菜的价格下降D.化肥价格上涨E.无法确定10. 供给规律说明(D )。
A.生产技术提高会使商品的供给量增加B.政策鼓励某商品的生产,因而该商品供给量增加C.消费者更喜欢消费某商品,使该商品的价格上升D.某商品价格上升将导致对该商品的供给量增加11.需求量和价格所以反方向变化,是因为( C )。
微观第八章习题及答案3

微观第八章习题及答案3微观第八章习题一、名词解释引致需求联合需求边际产品价值边际收益产品边际要素成本完全竞争要素市场买方垄断卖方垄断二、选择题1、下列各项中不属于生产要素的是(D )A.企业管理者的管理才能 B. 农民拥有的土地C.用于生产的机器厂房 D. 在柜台上销售的服装2、完全竞争厂商对生产要素的需求曲线向右下方倾斜的原因在于()A.要素的边际成本递减B.要素的边际产量递减C.要素生产的产品的边际效用递减D.要素参加生产的规模报酬递减3、在产品X市场和要素K、L的市场都是完全竞争市场的厂商,利润最大化的条件是( D )A .X X X P MC MC =,且上升B .L K L KMPMP P P = C .1L K L K X MPMP P P MC == D .11L K L K X X MP MP P P MC P ===4、对于一个垄断企业(其所处要素市场是完全竞争的),投入品M 的价格为20元,边际产量为5,产品价格是4元,则这个企业的产量( )A.未达到利润最大化,应减少产量B.未达到利润最大化,应扩大产量C.生产出利润最大化,但是成本未达到最小化D.在成本最小条件下实现利润最大化产量5、市场中单个厂商对某种生产要素的需求曲线同全体厂商对该种生产要素的需求曲线之间的关系表现为( )A.两者是重合在一起的B.前者较后者平坦C.前者较后者陡峭D.无法确定6、在一个完全竞争的市场中,追求利润最大化的厂商的产品价格上升时,将引起劳动的边际产品价值(),从而导致劳动的需求曲线()A.降低,右移B.增加,左移C.增加,右移D.降低,左移7、完全竞争产品市场与不完全竞争产品市场两种情况下的生产要素的需求曲线相比( )A.前者比后者陡峭B.前者与后者重合C.后者比前者平坦D.均有可能8、假定生产要素A、B、C的边际产量分别是20、16、8,它们的价格分别是10、8、4,那么这一生产要素的组合( C )A.不是最小成本的组合B.是最小成本的组合C.是否为最小成本组合,视不同的要素市场而定D.是否为最小成本组合,视不同的产品市场和要素市场而定9、假定两种生产要素X和Y的价格为30元,18元,产品的边际收益是3元,那么当这两种要素的边际产量为( B )时,该生产商才能获得最大利润。
西方经济学本微观部分网考练习题含答案

西方经济学(本)微观部分网考练习题(含答案)(2—4章)第二章供求规律一、单项选择题1.需求曲线是一条倾斜的曲线,其倾斜的方向为(A)A.右下方B.右上方C.左下方D.左上方2.下列体现了需求规律的是(D)A.药品的价格上涨,使药品质量得到了提高B.汽油的价格提高,小汽车的销售量减少C.丝绸价格提高,游览公园的人数增加D.照相机价格下降,导致销售量增加3.其他因素保持不变,只是某种商品的价格下降,将产生什么样的结果(C)A.需求增加B.需求减少C.需求量增加D.需求量减少4.下列变化中,哪种变化不会导致需求曲线的位移(B)A人们的偏好和爱好B产品的价格C.消费者的收入D.相关产品的价格5.当汽油的价格上升时,在其他条件不变的情况下,对小汽车的需求量将(A)A.减少B.不变C.增加D.难以确定6.当咖啡价格急剧升高时,在其他条件不变的情况下,对茶叶的需求量将(C)A.减少B.不变C.增加D.难以确定7.消费者预期某种物品将来价格要上升,则对该物品当前的需求会(C)A.减少B.不变C.增加D.难以确定8.需求的变动与需求量的变动(B)A.都是由于一种原因引起的B.需求的变动由价格以外的其他因素的变动所引起的,而需求量的变动由价格的变动引起的C.需求量的变动是由一种因素引起的,需求变动是两种及两种以上的因素引起的D.是一回事9.整个需求曲线向右上方移动,表明(A)A.需求增加B.需求减少C.价格提高D.价格下降10.对化妆品的需求减少是指(A)A.收入减少引起的减少B.价格上升而引起的减少C.需求量的减少D.价格下降11.在同一条曲线上,价格与需求量的组合从A点移动到B点是(D)A.需求的变动B.收入的变动C.偏好的改变D.需求量的变动12.导致需求曲线发生位移的原因是(C)A.因价格变动,引起了需求量的变动B.因供给曲线发生了位移,引起了需求量的变动C.因影响需求量的非价格因素发生变动,而引起需求关系发生了变动D.因社会经济因素发生变动引起产品价格的变动13.下列因素中哪一种因素不会使需求曲线移动(B)A.消费者收入变化B.商品价格下降C.其他商品价格下降D.消费者偏好变化14.供给曲线是一条倾斜的曲线,其倾斜的方向为(B)A.右下方B.右上方C.左下方D.左上方15.鸡蛋的供给量增加是指供给量由于(C)A.鸡蛋的需求量增加而引起的增加B.人们对鸡蛋偏好的增加C.鸡蛋的价格提高而引起的增加D.由于收入的增加而引起的增加16.如果某种商品供给曲线的斜率为正,保持其他条件不变的情况下,该商品价格上升,导致(C)A.供给增加B.供给减少C.供给量增加D.供给量减少17.建筑工人工资提高将使(A)A.新房子供给曲线左移并使房子价格上升B.新房子供给曲线左移并使房子价格下降C.新房子供给曲线右移并使房子价格上升D.新房子供给曲线左移并使房子价格下降18.假如生产某种商品所需原材料的价格上升,则这种商品(B)A.需求曲线向左方移动B.供给曲线向左方移动C.需求曲线向右方移动D.供给曲线向右方移动19.供给规律中可以反映在(D)A.消费者不再喜欢消费某商品,使该商品的价格下降B.政策鼓励某商品的生产,因而该商品的供给量增加C.生产技术提高会使商品的供给量增加D.某商品价格上升将导致对该商品的供给量增加20.当供求原理发生作用时,粮食减产在市场上的作用是(B)A.政府规定个人购买粮食的数量B.粮食价格上升C.粮食价格下降D.粮食交易量增加21.关于均衡价格的正确说法是(C)A.均衡价格是需求等于供给时的价格B.供给量等于需求量时的价格C.供给曲线与需求曲线交点上的价格D.供给价格等于需求价格时的价格22.均衡价格随着(D)A.供给和需求的增加而上升B.供给和需求的减少而上升C.需求的减少和供给的增加而上升D.需求的增加和供给的减少而上升23.当某种商品的需求和供给出现同时减少的情况时,那么(C)A.均衡价格下降,均衡产量减少B.均衡价格下降,均衡产量无法确定C.均衡价格无法确定,均衡产量减少D.均衡价格上升,均衡产量减少24.已知某商品的需求函数和供给函数分别为:QD=14-3P,QS=2+6P,该商品的均衡价格是(A)A.4/3B.4/5C.2/5D.5/225.假设某商品的需求曲线为Q=3-2P,市场上该商品的均衡价格为4,那么,当需求曲线变为Q=5-2P后,均衡价格将(A)A.大于4B.小于4C.等于4D.小于或等于426.需求的变动引起(A)A.均衡价格和均衡数量同方向变动B.均衡价格反方向变动,均衡数量同方向变动C.均衡价格与均衡数量反方向变动D.均衡价格同方向变动,均衡数量反方向变动27.供给的变动引起(B)A.均衡价格和均衡数量同方向变动B.均衡价格反方向变动,均衡数量同方向变动C.均衡价格与均衡数量反方向变动D.均衡价格同方向变动,均衡数量反方向变动28.政府为了扶植农产品,规定了高于均衡价格的支持价格。
10.微观第十章思考题答案详解

第十章 思考题答案一、思考题A :1、选择题:1.1 B 解析:局部均衡指在其他市场条件不变的情况下,孤立的考察单个产品市场和单个要素市场的均衡。
1.2 A 解析:帕累托最优指的是社会资源的最优配置,实现最高效率。
1.3 C 解析:实现交换的帕累托最优的条件是两者的边际替代率相等,即B XY A XY MRS MRS =,故选C 。
1.4 D 解析:实现生产的帕累托最优的条件是两者的边际技术替代率相等,即Y LK X LK MRTS MRTS =,故选D 。
1.5 D 解析:实现交换和生产的帕累托最优的条件是两者的边际替代率等于边际转换率,即XY B XY A XY MRT MRS MRS ==,故选D 。
1.6 D 解析:要实现一个社会的帕累托最优状态必须同时满足三个条件:交换的帕累托最优、生产的帕累托最优以及交换和生产的帕累托最优。
故选D 。
1.7 C 解析:生产的契约曲线上的所有的点都是生产的最优均衡点,也是生产有效率的点。
当然也是通过生产要素的重新配置提高了总产量的点的集合。
故选C 。
1.8 D 解析:生产可能性曲线是指在其他条件(如技术、要素供给等)不变情况下,生产产品X 与Y 所能达到的最大产量的组合。
曲线上的每一点必会满足Y LKX LK MRTS MRTS =,故选D 。
1.9 D 解析:选项中A是帕累托最优的理论解释;B是交换的帕累托最优的几何解释,交换的契约曲线就是交换的帕累托最优点的集合;C是帕累托最优的效用论解释,即契约曲线转换到以效用为坐标量的平面直角图上便可得到效用可能性曲线。
实现了交换的帕累托最优当然也就实现了个人效用的最优组合。
故A、B、C都对,选D。
1.10 B 解析:转换曲线,即生产可能性曲线。
通过前面的研究推导可知,它是由生产的契约曲线导出的。
故选B。
2、简答题:(1)如果商品X的市场供给(S X)增加,按局部均衡分析,则其价格P X下降,需求量Q X增加。
微观练习题与答案

微观经济学练习题一、单项选择题1. 在得出某彩电的需求曲线时,下列因素中不会使其需求曲线移动的是()A. 购买者(消费者)收入变化B. 商品价格下降C. 相关商品价格下降D. 消费者偏好变化2. 保持所有其他因素不变,当消费者预期某种物品在未来会出现价格上涨时,则对该物品的当前需求会()A. 减少B. 增加C. 不变D. 以上三项均有可能3. 彩电行业工人工资的提高,将会导致()A. 彩电供给曲线左移,彩电价格上升B. 彩电供给曲线右移,彩电价格下降C. 彩电供给曲线左移,彩电价格下降D. 彩电供给曲线右移,彩电价格上升4. 假如生产某种物品所需要的原材料价格上升,则这种物品的()A. 供给曲线左移B. 供给曲线右移C. 需求曲线左移D. 需求曲线右移5. 若某一产品的价格上升了8%,需求量下降了15%,则()A. 商品需求缺乏弹性B. 商品需求富有弹性C. 商品需求具有单位弹性D. 生产者应该提高价格以增加总收入6. 人们常说的“多多益善”,从经济学角度来说,是指随着所消费的商品数量增多,()A. 总效用递增B. 边际效用递增C. 总效用递减D. 边际效用递减7. 若某种商品为吉芬商品,则表明()A. 该商品为低档商品B. 其替代效应超过收入效应C. 其收入效应超过替代效应D. 其为低档商品且收入效应超过替代效应8. 设某消费者的效用函数为U=XY,预算方程为Y=50-X,则消费组合(X=20,Y=30)()A. 可能是均衡点B. 不可能是均衡点C. 一定是均衡点D. 以上均有可能9. 在短期中存在,而在长期中不存在的成本是()A. 不变成本B. 平均成本C. 机会成本D.隐含成本10. 假若一条等产量线凸向原点,则意味着()A. 劳动的边际产出递减B. 资本的边际产出递减C. 边际技术替代率递减D. A和B11. 如果追求利润最大化且属于竞争性的企业在短期内亏损,则()A. P<AVCB. P<MCC. P=AVC+AFCD. P<ATC,但是P>AVC12. TP、AP、MP三者之间的关系说法正确的是()A. 当TP增大时,AP也增大B. 当AP达到最大时,AP<MPC. 当AP曲线在与MP曲线相交时达到最大D. MP递增时,AP>MP13. 以下比较接近完全竞争市场的情况是()A. 大米市场B. 街头便利店C. 汽车市场D. 自来水14. 完全竞争企业面临的需求曲线的特点是()A. 位置高低不会改变B. 水平形状不会改变C. 位置高低和水平形状都不会改变D. 位置高低和水平形状都会改变15. 如果一个企业在所有的产量水平上,其边际收益都等于平均收益,那么()A. 边际收益曲线是水平线B. 边际收益曲线向右下方倾斜C. 边际收益曲线向右上方倾斜D. 以上均有可能16. 若一个完全竞争企业在其短期利润最大化的产量点上,如果此时其平均收益小于平均成本,那么该企业会选择()A. 停产B. 继续原有的生产C. 减少产量,但是不停产D. A和B都有可能17. 一个垄断企业所要面临的一条需求曲线中,AR曲线与MR曲线之间的关系是()A. 两者的斜率是相同的B. 两者的斜率不存在内在的联系C. 前者的斜率是后者的两倍D. 后者的斜率是前者的两倍18. 下列情景不属于价格歧视的是()A. 航空公司根据订票的早晚制定不同的票价B. 邮寄一个大包裹的要价高于一个小包裹C. 餐厅对有成年人陪同的儿童免收就餐费D. 杂志社对学生收取比一般公众更少的订阅费19. 下列()体现了需求规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数 LTC=Q3-12Q2+40Q。试求: (1)当市场商品价格为P=100时,厂商实现MR=LMC时的产量、 平均成本和利润; (2)该行业长期均衡时的价格和单个厂商的产量; (3)当市场的需求函数为Q=660-15P时,行业长期均衡时的厂商 数量。 解答:(1)根据题意,有: LMC=3Q2-24Q+40 P=MR=100 MR=MC 3Q2-24Q+40=100 解得Q=10(负值舍去了) 平均成本函数:LAC(Q)=Q2-12Q+40=20 利润=TR-STC=PQ-STC=800 (2)长期均衡时的价格等于长期平均成本曲线的最低点:一阶条件 dLAC/dQ=2Q-12=0 Q=6 LAC=4 (3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线, 长期均衡价格等于单个厂商的最低的长期平均成本,即P=4。以P=4 代入市场需求函数Q=660-15P,便可以得到市场的长期均衡数量为 Q=660-15×4=600。 现已求得在市场实现长期均衡时,市场均衡数量Q=600,单个厂商 的均衡产量Q=6,于是,行业长期均衡时的厂商数量=600÷6=100 (家)。
(3)比较(1)和(2)的结果.
(3)将该垄断厂商实现最大化的结果与实现收益最大化 的结果相比较,该厂商实现利润最大化时的产量较低, 价格较高,收益较少,利润较大。显然,理性的垄断 厂商总是以利润最大化作为生产目标,而不是将收益 最大化作为生产目标.追求利润最大化的垄断厂商总 是以较高的垄断价格和较低的产量,来获得最大的利 润
4、已知某完全竞争市场的需求函数为D=6300-400P,短期市场供给函数为 SS=3000+150P;单个企业在LAC曲线最低点的价格为6,产量为50;单个 企业的成本规模不变。
(1)求市场的短期均衡价格和均衡产量;
解::(1)短期均衡的条件D=SS,有:6300-400P=3000+150P 解得Pe=6 Qe=6300-400×6=3900 (2)判断(1)中的市场是否同时处于长期均衡,求企业内的厂商数量;
4、已知某垄断厂商的成本函数为TC=0.6Q2+3Q+2,反需求函数为 P=8-0.4Q. 求: (1)该厂商实现利润最大化时的产量、价格、收益和利润. (2)该厂商实现收益最大化的产量、价格、收益和利润. (3)比较(1)和(2)的结果.
解答:(1)由题意可得:MC=dTC/dQ=1.2Q+3 且TR=PQ=8Q-0.4Q2 MR=dTR/dQ=8-0.8Q 于是,根据利润最大化原则MR=MC有:8-0.8Q=1.2Q+3 解得 Q=2.5 以Q=2.5代入反需求函数P=8-0.4Q,得:P=8-0.4×2.5=7 TR=PQ=17.5 =TR-TC=PQ-TC =(7×0.25)-(0.6×2.52+2)=4.25 (2)TR=P(Q)Q=(8-0.4Q)Q=8Q-0.4Q2 一阶条件:dTR/dQ=8-0.8Q=0 解得Q=10 二阶条件:d2TR/dQ2=-0.8<0 所以,当Q=10时,TR值达最大值. P=8-0.4×10=4 TR=40 =-52
微观经济学习题解答B
陈安国
第六章 完全竞争的市场
1、已知某完全竞争行业中的单个厂商的短期成本函数为 STC=0.1Q3-2Q2+15Q+10。试求: (1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;
解答:(1)因为STC=0.1Q3-2Q2+15Q+10 所以SMC=dSTC/dQ=0.3Q3-4Q+15
解:该市场短期均衡时的价格P=6,与单个企业在LAC曲线最低点的价格一 致,所以,该市场同时处于长期均衡。
市场长期均衡时的数量是Q=3900,在市场长期均衡时单个企业的产量为50, 所以,由此长期均衡时行业内厂商的数量为:3900÷50=78(家) (3)如果市场的需求函数变为D′=8000−400P,短期供给函数为 SS′=4700+150P,求市场的短期均衡价格和均衡产量;
(2)当市场价格下降为多少时,厂商必须停产? 解:当市场价格下降为P小于平均可变成本AVC即 P<AVC时,厂商必须停产。而此时的价格P必定小 于最小的可变平均成本AVC。 根据题意,有: AVC=TVC/Q=0.1Q2-2Q+15 令dAVC/dQ=0,即有, 0.2Q-2=0 解得 Q=10 故Q=10时,AVC(Q)达最小值。 最小的可变平均成本AVC=0.1×102-2×10+15=5 于是,当市场价格P<5时,厂商必须停产。 (3)厂商的短期供给函数。 解:SMC=0.3Q3-4Q+15 供给函数为P= 0.3Q34Q+15 Q=[4+(1.2P-2)1/2]/0.6,P ≥5 Q=0 P<5
3、已知某垄断厂商的短期成本函数为STC=0.1Q36Q2+140Q+3000,反需求函数为P=150-3.25Q 求:该垄断厂商的短期均衡产量与均衡价格. 解答:因为SMC=dSTC/dQ=0.3Q2-12Q+140 且由TR=P(Q)Q=(150-3.25Q)Q=150Q-3.25Q2 得出MR=150-6.5Q 根据利润最大化的原则MR=SMC 0.3Q2-12Q+140=150-6.5Q 解得Q=20(负值舍去) 以Q=20代入反需求函数,得: P=150-3.25Q=85 所以均衡产量为20,均衡价格为85
根据厂商实现利润最大化原则MR=SMC,且完全竞争条件下
MR=P=55,于是有: 0.3Q2-4Q+15=55 解得利润最大化的产量Q*=20(负值舍去了)
以Q*=20代入利润等式有: =TR-STC=PQ-STC
=(55×20)-(0.1×203-2×202+15×20+10)=1100-310=790 即厂商短期均衡的产量Q*=20,利润=790
6、已知完全竞争市场上单个厂商的长期成本函数为LTC=Q3-20Q2+200Q, 市场的产品价格为P=600。求: (1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡?为什么? (3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各为多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段? 解:(1)LMC=dLTC/dQ=3Q2-40Q+200 P=MR=LMC 3Q2-40Q+200=600 可得:Q=20 LAC=LTC/Q=Q2-20Q+200=200 =PQ-LTC=8000 (2) dLAC/dQ=2Q-20=0 解得Q=10 d2LAC/dQ2=2>0 LAC曲线达最小值:100。
8、用图说明完全竞争厂商短期均衡的形成 及其条件。
9、为什么完全竞争厂商的短期供给曲线是SMC曲 线上等于和高于AVC曲线最低点的部分?
10、用图 说明完全 竞争厂商 长期均衡 的形成及 其条件。
第七章 不完全竞争的市场
1、根据图中线性需求曲线d和相应的边际收益曲线 MR,试求: (1)A点所对应的MR值; (2)B点所对应的MR值
长期均衡时P等于LAC最低值、利润为零、单个厂商的产量为10
所以未处于长期均衡 (3)Q=10 P=100 =0 (4)单个厂商利润最大化的产量和价格组合发生在LAC曲线最低点的右边, 即LAC曲线处于上升段,所以,单个厂商处于规模不经济阶段。
7.某完全竞争厂商的短期边际成本函数SMC=0.6Q-10, 总收益函数TR=38Q,且已知当产量Q=20时的总成本 STC=260. 求该厂商利润最大化时的产量和利润 解:TR=PQ=38Q 因此P=38 MR=38 利润最大化时:MR=MC 38=0.6Q-10 Q=80 STC=0.3Q2-10Q+TFC Q=20时STC=260 TFC=340 STC=0.3Q2-10Q+340 Q=80 =PQ-STC=1580
3、已知某完全竞争的成本递增行业的长期供给函数LS=5500+300P。试求:
(1)当市场需求函数D=8000-200P时,市场的长期均衡价格和均衡产量; (2)当市场需求增加,市场需求函数为D=10000-200P时,市场长期均衡 价格加工和均衡产量;
(3)比较(1)、(2),说明市场需求变动对成本递增行业的长期均衡价 格和均衡产量的影响。
P
解: 需求曲线:P=3-3/15Q TR=PQ=-3/15Q2+3Q MR=dTR/dQ=-6/15Q+3 (1)当Q=5时,MR=1 (2)当Q=10时, MR=-1
3 2 1 5 A B
10
15
Q
2、图是某垄断厂商的长期成本曲线、需求曲线和收益曲线.试 在图中标出: (1)长期均衡点及相应的均衡价格和均衡产量; (2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线; (3)长期均衡时的利润量.
6.已知某垄断厂商利用一个工厂生产一种产品,其产品 在两个分割的市场上出售,他的成本函数为 TC=Q2+40Q,两个市场的需求函数分别为Q1=12-0.1P1 ,Q2=20-0.4P2.求: (1)当该厂商实行三级价格歧视时,他追求利润最大化前 提下的两市场各自的销售量、价格以及厂商的总利润.. 解:(1) 第一个市场:P1=120-10Q1,MR1=120-20Q1. 第二个市场:P2=50-2.5Q2,MR2=50-5Q2. MC=2Q+40 实行三级价格歧视时:MR1=MR2=MC. 于是:关于第一个市场:120-20Q1=2Q+40 Q=Q1+Q2 关于第二个市场:50-5Q2=2Q+40 Q1=3.6 Q2=0.4 P1=84,P2=49. л=(TR1+TR2)-TC=146
