【斯巴达高考】斯巴达教育集团总裁武继周中国数学奥林-精品文档
2024-2025学年河北省衡水市河北武强中学高三上学期期中考试物理试题
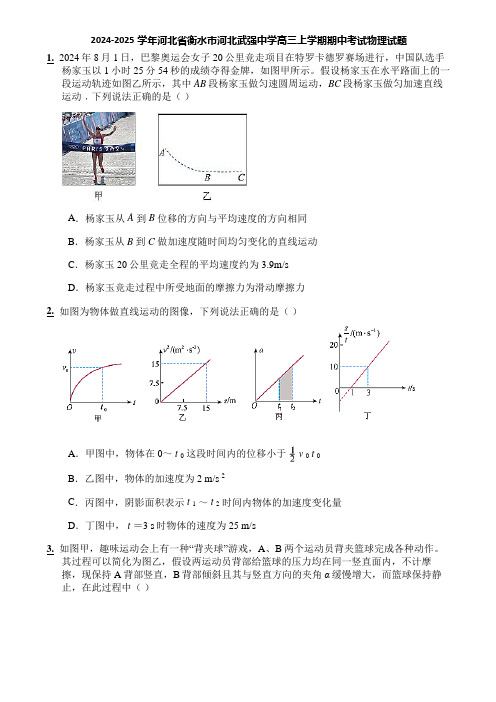
2024-2025学年河北省衡水市河北武强中学高三上学期期中考试物理试题1. 2024年8月1日,巴黎奥运会女子20公里竞走项目在特罗卡德罗赛场进行,中国队选手杨家玉以1小时25分54秒的成绩夺得金牌,如图甲所示。
假设杨家玉在水平路面上的一段运动轨迹如图乙所示,其中AB段杨家玉做匀速圆周运动,BC段杨家玉做匀加速直线运动﹐下列说法正确的是()A.杨家玉从A到B位移的方向与平均速度的方向相同B.杨家玉从B到C做加速度随时间均匀变化的直线运动C.杨家玉20公里竞走全程的平均速度约为3.9m/sD.杨家玉竞走过程中所受地面的摩擦力为滑动摩擦力2.如图为物体做直线运动的图像,下列说法正确的是()A.甲图中,物体在0~t0这段时间内的位移小于v0t0B.乙图中,物体的加速度为2 m/s 2C.丙图中,阴影面积表示t1~t2时间内物体的加速度变化量D.丁图中,t=3 s时物体的速度为25 m/s3.如图甲,趣味运动会上有一种“背夹球”游戏,A、B两个运动员背夹篮球完成各种动作。
其过程可以简化为图乙,假设两运动员背部给篮球的压力均在同一竖直面内,不计摩擦,现保持A背部竖直,B背部倾斜且其与竖直方向的夹角α缓慢增大,而篮球保持静止,在此过程中()A.A对篮球的压力大于篮球对A的压力B.A、B对篮球的合力增大C.A对篮球的压力减小D.B对篮球的压力增大4.如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右以速度v匀速移动,运动中悬线始终竖直,则橡皮的速度大小为()A.B.C.D.5.如图所示,质量分别为m和的A、B两物块,在水平恒力F作用下沿光滑的水平面一起向右运动。
A对B的作用力大小为,B对A的作用力大小为。
则()A.B.C.D.6. 2024年4月25日,神舟十八号飞船与天宫空间站顺利对接,如图所示,飞船与空间站对接前在各自预定的圆轨道Ⅰ、Ⅲ上运动,Ⅱ为对接转移轨道,下列说法正确的是()A.飞船在Ⅰ轨道运行速度小于在Ⅲ轨道上的运行速度B.飞船在三个轨道上的运行周期C.飞船在Ⅱ轨道上的机械能大于在Ⅰ轨道上的机械能D.飞船在三个轨道上运行时与地球连线在单位时间内扫过的面积相等7.如图甲所示,轻杆的一端固定一小球(可视为质点),另一端套在光滑的水平轴O上,水平轴的正上方有一速度传感器(图中未画出),可以测量小球通过最高点时的速度大小v,水平轴O处有一力传感器(图中未画出),可以测量小球通过最高点时水平轴受到的杆的作用力F,若取竖直向下为F的正方向,在最低点时给小球不同的初速度,得到的(v为小球在最高点时的速度)图像如图乙所示,取重力加速度大小。
武继周:中国数学奥林匹克竞赛“国家级”教练

二、导数
• 1.导数的几何意义和物理意义 (1)几何意义:
曲线f(x ) 在某一点(x 0 ,y 0 ) 处的导数是过点(x 0 ,y 0 ) 的切线的斜率
(2)物理意义:
若物体运动方程是s=s(t),在点P(t0 ,s(t0 )) 处导数的意义是t t0处的瞬时速度.
若物体速度方程是v=v(t),在点Q (t0 ,v( t0 )) 处导数的意义是t t0处的瞬时加速度.
y' u '(x ) v '(x )ln u(x ) v(x ) y u(x )
因此
u '(x ) y ' u(x ) [v '(x )ln u(x ) v(x ) ]. u(x )
v(x )
求y x sin x , (x 0) 的导数. 解:两边同时取对数得 ln y ln x sin x sin x ln x
三、微分运算
• 2.隐函数求导法
如果F(x,y)是变量x和y的一个解析式,在一定的条 件下,由方程 F(x,y)=0 决定了一个y关于x的函数y=y(x),称这类函数为隐函数。 在方程F(x,y)=0两边同时对x求导,并注意y是x的 函数,运用求导的四则运算法则和链式求导法则得到关 于y’的关系式,从而解得y’.这个方法称为隐函数求导 法。
于是反函数x x(y ) 的导数为
dx 1 1 x ln 2 . x dy 2 dy xe ln 2 2 ex dx x ln 2
d 2x d dx d dx dx 二阶导数为 2 ( ) ( )* dy dy dx dy dy dy
d x ln 2 dx ( x )* dx xe ln 2 2 dy
高中数学奥林匹克基础教程1.21

高中数学奥林匹克基础教程江苏沛县孙统权前言2007年7月15日至24日,江苏省高中数学奥林匹克夏令营在靖江举办,由省数学学会组织专家学者亲自授课。
编者作为夏令营中的受训教练,亲身体会到与会专家博大精深的知识厚度和深入浅出的教学风格,并做了课堂笔记,对相关教学资料进行了整理。
夏令营结束后,从自身实践出发,编成本教程。
教程共8讲,每讲4学时,共32学时。
指导思想为“领略奥赛风采,拓展数学视野,训练数学思维,启迪数学方法”,内容选取原则为“参照竞赛数学知识体系,根据学生接受能力,与当前中学数学教学内容协调互补”。
对本教程建议采用“探索-讨论-启发-再探索-直至完成”的教学模式,使学生思维密度大,所受局限少,能充分的体会数学智慧和创造的乐趣,较直接的感受竞赛数学。
在各知识点章节讲授时,宜通过具体解题展示数学体系,淡化数学术语而突出数学思想,选择、补充题目时注意结合实际情况,减少复杂度,使学生负担轻,进步感强,在领略数学美的同时达到训练目的。
本教程参考了2007年省夏令营专家的授课内容,使用了部分原题。
同时,参考了华师大版《数学奥林匹克小丛书》,安徽少儿版《初中应用数学知识竞赛辅导训练》和其他若干书籍。
在此予以感谢,并在补注中注明各题的直接来源。
本教程可以作为高中奥林匹克训练的起始教材,或供学生选修的一个模块。
将它整理出来,意在抛砖引玉,为我们江苏乃至全国的数学奥林匹克的发展作一点贡献。
虽力求严谨,由于个人能力经验所限,其中错误和不完善之处仍在所不少,恳请广大专家、教练、数学奥林匹克爱好者不吝指教。
本版版本号1.2。
编者电子信箱:suntrain@。
第一讲赛题选例一、课堂讨论:1证明:任何四面体上都存在一个顶点,可以用由它发出的三条棱组成三角形。
2用不在形内相交的对角线将正奇数边形划分为一系列三角形。
证明:其中有且只有一个锐角三角形。
3证明:可以找到4个绝对值大于10000的整数a,b,c,d,使11111+++=。
2025版高考数学一轮复习课后限时集训57古典概型文含解析北师大版

课后限时集训(五十七)(建议用时:60分钟)A 组 基础达标一、选择题1.在集合A ={2,3}中随机取一个元素m ,在集合B ={1,2,3}中随机取一个元素n ,得到点P (m ,n ),则点P 在圆x 2+y 2=9内部的概率为( )A .12 B.13 C .34 D.25B [点P (m ,n )共有(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),6种状况,只有(2,1),(2,2)这2个点在圆x 2+y 2=9的内部,所求概率为26=13.] 2.(2024·厦门月考)甲、乙两名同学分别从“象棋”“文学”“摄影”三个社团中随机选取一个社团加入,则这两名同学加入同一个社团的概率是( )A .14B .13C .12D .23 B [由题意,甲、乙两名同学各自等可能地从“象棋”“文学”“摄影”三个社团中选取一个社团加入,共有3×3=9(种)不同的结果,这两名同学加入同一个社团有3种状况,则这两名同学加入同一个社团的概率是39=13.] 3.(2024·红河州检测)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.从以上五张卡片中任取两张,这两张卡片颜色不同且标号之和小于4的概率为( )A .13B .110C .310D .23C [从五张卡片中任取两张的全部可能状况有如下10种:红1红2,红1红3,红1蓝1,红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.其中两张卡片的颜色不同且标号之和小于4的有3种状况:红1蓝1,红1蓝2,红2蓝1,故所求的概率为P =310,故选C .] 4.(2024·抚州一模)小亮、小明和小红约好周六骑共享单车去森林公园郊游,他们各自等可能地从小黄车、小蓝车、小绿车这3种颜色的单车中选择1种,则他们选择相同颜色单车的概率为( )A .13B .19C .23D .49B [由题意,小亮、小明和小红各自等可能地从小黄车、小蓝车、小绿车这3种颜色的单车中选择1种,有27种不同的结果,他们选择相同颜色的单车,有3种不同的结果,故他们选择相同颜色单车的概率为327=19,故选B.] 5.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( )A .110B .18C .16D .15D [从正六边形的6个顶点中随机选择4个顶点,方法有15种,它们作为顶点的四边形是矩形的方法种数为3,所以所求概率等于315=15.] 二、填空题6.从2,3,8,9中任取两个不同的数字,分别记为a ,b ,则log a b 为整数的概率是________. 16[从2,3,8,9中任取两个不同的数字,分别记为a ,b ,则有2,3;2,8;2,9;3,8;3,9;8,9;3,2;8,2;9,2;8,3;9,3;9,8,共12种取法,其中log a b 为整数的有(2,8),(3,9)两种,故P =212=16.] 7.将号码分别为1,2,3,4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个小球,其号码为a ,放回后,乙从今口袋中再摸出一个小球,其号码为b ,则使不等式a -2b +4<0成立的事务发生的概率为________.14[由题意知(a ,b )的全部可能结果有4×4=16个.其中满意a -2b +4<0的有(1,3),(1,4),(2,4),(3,4)共4种结果.故所求事务的概率P =416=14.] 8.(2024·成都月考)如图的茎叶图是甲、乙两人在4次模拟测试中的成果,其中一个数字被污损,则甲的平均成果不超过乙的平均成果的概率为________.0.3 [依题意,记题中的被污损数字为x ,若甲的平均成果不超过乙的平均成果,则有(8+9+12+11)-(5+3+10+x +15)≤0,x ≥7,即此时x 的可能取值是7,8,9,因此甲的平均成果不超过乙的平均成果的概率P =310=0.3.] 三、解答题9.移动公司在国庆期间推出4G 套餐,对国庆节当日办理套餐的客户进行实惠,实惠方案如下:选择套餐1的客户可获得实惠200元,选择套餐2的客户可获得实惠500元,选择套餐3的客户可获得实惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.(1)求从中任选1人获得实惠金额不低于300元的概率;(2)若采纳分层抽样的方式从参与活动的客户中选出6人,再从该6人中随机选出2人,求这2人获得相等实惠金额的概率. [解] (1)设事务A 为“从中任选1人获得实惠金额不低于300元”,则P (A )=150+10050+150+100=56. (2)设事务B 为“从这6人中选出2人,他们获得相等实惠金额”,由题意按分层抽样方式选出的6人中,获得实惠200元的有1人,获得实惠500元的有3人,获得实惠300元的有2人,分别记为:a 1,b 1,b 2,b 3,c 1,c 2,从中选出2人的全部基本领件如下:a 1b 1,a 1b 2,a 1b 3,a 1c 1,a 1c 2,b 1b 2,b 1b 3,b 1c 1,b 1c 2,b 2b 3,b 2c 1,b 2c 2,b 3c 1,b 3c 2,c 1c 2共15个.其中使得事务B 成立的有b 1b 2,b 1b 3,b 2b 3,c 1c 2,共4个.则P (B )=415. 故这2人获得相等实惠金额的概率为415. 10.(2024·西安质检)某校高一年级学生全部参与了体育科目的达标测试,现从中随机抽取40名学生的测试成果,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成果的折线图如图所示.(1)体育成果大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1 000名学生,试估计该校高一年级中“体育良好”的学生人数;(2)为分析学生平常的体育活动状况,现从体育成果在[60,70)和[80,90)的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成果在[60,70)的概率.[解] (1)由折线图,知样本中体育成果大于或等于70分的学生有14+3+13=30(人).所以该校高一年级中,“体育良好”的学生人数大约有1 000×3040=750(人). (2)设“至少有1人体育成果在[60,70)”为事务M ,记体育成果在[60,70)的数据为A 1,A 2,体育成果在[80,90)的数据为B 1,B 2,B 3,则从这两组数据中随机抽取2个,全部可能的结果有10种,即(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),(B 1,B 2),(B 1,B 3),(B 2,B 3).而事务M 的结果有7种,即(A 1,A 2),(A 1,B 1),(A 1,B 2),(A 1,B 3),(A 2,B 1),(A 2,B 2),(A 2,B 3),因此事务M 的概率P (M )=710. B 组 实力提升1.甲邀请乙、丙、丁三人加入了微信群聊“兄弟”,为庆祝兄弟相聚甲发了一个9元的红包,被乙、丙、丁三人抢完,已知三人均抢到整数元,且每人至少抢到2元,则丙获得“手气王”(即丙领到的钱数不少于其他任何人)的概率是( )A .13B .310C .25D .34C [全部基本领件有(2,2,5),(2,5,2),(5,2,2),(2,3,4),(2,4,3),(3,2,4),(3,4,2),(4,2,3),(4,3,2),(3,3,3),共10个,其中丙获得“手气王”的基本领件有(2,2,5),(2,3,4),(3,2,4),(3,3,3),共4个,故所求概率为P =410=25.] 2.(2024·威海月考)从集合{2,3,4,5}中随机抽取一个数a ,从集合{1,3,5}中随机抽取一个数b ,则向量m =(a ,b )与向量n =(1,-1)垂直的概率为( )A .16B .13C .14D .12A [由题意可知m =(a ,b )有:(2,1),(2,3),(2,5),(3,1),(3,3),(3,5),(4,1),(4,3),(4,5),(5,1),(5,3),(5,5),共12种状况.因为m ⊥n ,即m·n =0,所以a ×1+b ×(-1)=0,即a =b ,满意条件的有(3,3),(5,5)共2个.故所求的概率为16.] 3.已知集合M ={1,2,3},N ={1,2,3,4},定义映射f :M →N ,则从中任取一个映射满意由点A (1,f (1)),B (2,f (2)),C (3,f (3))构成△ABC 且AB =BC 的概率为________.316[∵集合M ={1,2,3},N ={1,2,3,4},∴映射f :M →N 有43=64种,∵由点A (1,f (1)),B (2,f (2)),C (3,f (3))构成△ABC 且AB =BC ,∴f (1)=f (3)≠f (2),∵f (1)=f (3)有4种选择,f (2)有3种选择,∴从中任取一个映射满意由点A (1,f (1)),B (2,f (2)),C (3,f (3))构成△ABC 且AB =BC 的事务有4×3=12种,∴所求概率为1264=316.]4.(2024·天津高考)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采纳分层抽样的方法从中抽取7名同学去某敬老院参与爱心活动.(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(2)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学担当敬老院的卫生工作.①试用所学字母列举出全部可能的抽取结果;②设M 为事务“抽取的2名同学来自同一年级”,求事务M 发生的概率.[解] (1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采纳分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.(2)①从抽取的7名同学中随机抽取2名同学的全部可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G }共21种.②由①,不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的全部可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种.所以,事务M 发生的概率P (M )=521。
《数学奥林匹克》大纲

数学教育专业《中学数学奥林匹克》课程教学大纲一、课程说明《中学数学奥林匹克》是数学教育专业的一门必修课。
任务是让学生了解数学奥林匹克历史、内容、特征、思想和方法;掌握数学奥林匹克解题方法与技巧。
考虑学生的实际水平和培养目标,本课程先介绍数学奥林匹克基本知识,然后分专题讲授数学奥林匹克基本解题方法与技巧。
二、课程教学目标思想教育目标:通过对中学数学奥林匹克的学习和研究,激发学生学习数学的兴趣,开阔视野,培养学生的创新精神,提高学生的数学素养、思维能力等。
同时我国中学生在IMO历史上辉煌成绩也会在学生的人格培养上发挥十分重要的作用。
知识教育目标:通过本课程学习,让学生了解数学奥林匹克的历史、内容、特征、思想和方法;掌握数学奥林匹克解题方法与技巧,开拓发展学生的思维能力与探究问题的能力,使他们走上工作岗位后,能胜任中小学数学课外辅导工作。
三、课时分配章节课内讲授课时第1章数学奥林匹克的原理一、数学奥林匹克的历史与现状二、数学奥林匹克的基本特征三、数学奥林匹克在数学教育中的地位和作用四、数学奥林匹克的命题研究3 3第2章奥林匹克的内容和方法 3 第3章华罗庚数学教育思想及治学原则 3第4章数学解题思想与原则(上)数学解题思想与原则(下)3 3第5章数学解题方法(上)数学解题方法(下)3 3第6章几何证明方法与几何变换一、对称变换二、平移变换三、旋转变换3 3 3第7章梅耐劳斯与塞瓦定理 3 第8章面积问题与面积方法 3课时可以根据每学期的具体周数作适当调整。
四、教学内容第一章数学奥林匹克的原理(一)教学目标及要求:知识要求:[了解]:数学奥林匹克的原理与方法[掌握]:数学奥林匹克的基本特征及命题原则。
(二)教学内容:一、数学奥林匹克的历史与现状。
二、数学奥林匹克的基本特征。
三、数学奥林匹克在数学教育中的地位和作用。
四、数学奥林匹克的命题研究。
(三)教学方法:讲授法、讨论法。
第二章奥林匹克的内容和方法(一)教学目标及要求:知识要求:[了解]:数学奥林匹克的内容[掌握]:奥林匹克的方法(二)教学内容:1、多项式问题:基本内容、方法评析。
【斯巴达高考】斯巴达教育集团总裁武继周:中国数学奥林匹克竞赛“高级教练” 共16页

5 A33 30
答案:C
AE
B
D
C
习题3
(华约)设A={x|x≥10,x∈N},B⊆A,且B中元素满 足:任一元素的各位数字互不相同,任一元素的任 意两个数位之和不等于9. (1)求B中的两位数和三位数的个数 (2)B中是否存在五位数,六位数; (3)若从小到大排列B中元素,求第1081个元素;
N = C 5 4 A 4 4 + 2 C 5 3 A 2 1 A 3 2 + C 5 2 A 2 2 A 2 2
四、排列组合题型
• 2.排除法 例:某小组共有10名学生,其中女生3名, 现选举2名代表,至少有1名女生当选的不 同选法共有多少种?
C120-C72 =24
四、排列组合题型
• 3.捆绑法 所谓捆绑法,指在解决对于某几个元素要 求相邻的问题时,先整体考虑,将相邻元 素视作一个整体参与排序,然后再单独考 虑这个整体内部各元素间顺序。 一般都应用在不同物体的排序问题中。
2.加法原理:做一件事情,完成它有N类方式,第 一类方式有M1种方法,第二类方式有M2种方 法,……,第N类方式有M(N)种方法,那么完成 这件事情共有M1+M2+……+M(N)种方法。
二、排列数公式
An m nn 1 * . . . * n m 1 n n! m! ( m n; m, n N)
设B1={0,9},B2={1,8},B3={2,7},B4={3,6},B5={4,5}, 则B中元素的每个数位上的数字只能从上述五个不同的集合中分别抽取, 每一个集合中至多抽取一个,所以 (1)两位数个数:C 5 222A 2 2C 4 1272
三位数个数:C 5 32 3A 3 3 C 4 22 2A 2 2 4 3 2 (2)存在五位数,从五个集合Bi(i=1,2,3,4,5)中各取一个构成;
2024_2025学年高中数学每日一题周末培优9含解析新人教版必修3

周末培优【突破1】新中国教化事业的发展及阅历教训1.缘由(1)社会主义制度的确立为其快速发展供应了牢靠的保障。
(2)经济的发展为文化教化事业的发展供应了牢靠的保障。
(3)第三次科技革命推动社会生产力的发展,也促进了中国现代教化的发展。
(4)党和政府高度重视教化事业,广阔教化工作者以极大的热忱投入到现代化建设中。
2.图示法理解新中国的教化事业3.阅历教训(1)坚持以邓小平理论为指导。
(2)教化必需为国民经济发展和社会进步服务。
(3)坚持教化的社会主义方向。
(4)从基本国情动身。
(5)切实落实教化优先发展的战略地位和实施“科教兴国”战略。
【突破2】正确理解“国运兴衰,系于教化”1.从中国历史的角度看(1)中国古代史上的汉代、唐代能成为当时的封建大帝国,与其对教化的重视、人才的培育有很大的关系。
汉代自汉武帝设立太学,创立地方学校,尊儒重教,通过察举、皇帝征召的方式来选拔人才。
唐代实行科举制使大批的庶族地主通过科举而成为对社会有用的人才。
(2)中国近代,由于遭遇列强的入侵,造成了教化的落后,国家处于危难之中。
(3)“文化大革命”时期,教化秩序被破坏,造成中国人才的断层,使中国远远落后于西方发达国家。
2.从世界历史的角度看其次次世界大战后的德国和日本的崛起是典型的例子。
作为其次次世界大战的战败国,须要重视的工作许多,但德国与日本政府投入大量的财力首先发展教化培育人才,为两国的崛起振兴奠定了基础。
20世纪60年头,两国的经济跃居世界前列。
3.从现在的国际国内形势来看(1)在当今世界上,综合国力的竞争,越来越表现为经济实力、国防实力和民族凝合力的竞争。
无论就其中哪一个方面实力的增加来说,教化都具有基础性的地位。
(2)在国内,我国的经济增长方式还没有根本转变,沉重的人口负担还没有转化为人力资源的优势。
我们的劳动力素养、学问创新和技术创新的实力不高,已经成为制约我国经济发展和国际竞争实力增加的一个主要因素。
【突破3】19世纪以来音乐作品的特点2.多样性在全球化的时代,随着民族文化的沟通与融合,艺术发展呈现多样化的特点,如20世纪现代主义音乐不仅流派众多,而且具有独特的风格,如摇滚乐就是美国黑人音乐家的“节奏和布鲁斯”与美国白人的“乡村和西部音乐”的融合。
2020国际奥林匹克数学竞赛压轴题

2020国际奥林匹克数学竞赛压轴题
摘要:
1.2020 国际奥林匹克数学竞赛概述
2.压轴题的背景和意义
3.压轴题的解答思路
4.对中国选手在比赛中的表现分析
5.总结
正文:
【2020 国际奥林匹克数学竞赛概述】
2020 国际奥林匹克数学竞赛(IMO)是全球范围内最高水平的青少年数学竞赛,吸引了来自世界各地的优秀选手参加。
该比赛每年举办一次,旨在发现和培养青少年数学人才,推动数学教育的发展。
【压轴题的背景和意义】
在2020 年的IMO 竞赛中,最后一道题目,也就是压轴题,是一道涉及复数分析和解析几何的综合性问题。
这道题目难度较大,对选手的数学基础和解题能力有很高的要求。
压轴题的背景和意义在于,它不仅考查选手的基本运算能力,还需要选手具备良好的逻辑思维和创新能力。
【压轴题的解答思路】
这道压轴题的解答思路主要包括以下几个步骤:
第一步,根据题目给出的条件,建立数学模型。
第二步,利用复数分析的相关知识,对模型进行化简和分析。
第三步,运用解析几何的方法,求解模型中的未知量。
第四步,将求得的结果进行验证,得出最终的结论。
【对中国选手在比赛中的表现分析】
在这次比赛中,中国选手表现出色,共有6 名选手获得金牌。
其中,压轴题的解答环节,中国选手们也展现出了很高的水平。
这说明我国在数学教育方面,尤其是对优秀学生的培养上,取得了显著的成果。
【总结】
2020 年国际奥林匹克数学竞赛的压轴题,既展示了数学的美妙与挑战,也展现了各国选手的才华与潜力。
对于中国选手而言,这次比赛的优异成绩是对我国数学教育成果的肯定,更是一种激励。
结缘奥林匹克数学

结缘奥林匹克数学陕西省丹凤中学李德葆一、数学奥林匹克的历史国际奥林匹克数学竞赛(International Mathematics Olympiad)是国际中学生数学大赛,是目前世界上影响最广、级别最高的中学生数学竞赛。
国际奥林匹克竞赛的目的是:发现鼓励世界上具有数学天份的青少年,为各国进行科学教育交流创造条件,增进各国师生间的友好关系。
这一竞赛1959年由东欧国家发起,得到联合国教科文组织的资助。
第一届竞赛由罗马尼亚主办,1959年7月22日至30日在布加勒斯特举行,保加利亚、捷克斯洛伐克、匈牙利、波兰、罗马尼亚和苏联共7个国家参加竞赛。
以后国际奥林匹克数学竞赛都是每年7月举行(中间只在1980年断过一次),参赛国从1967年开始逐渐从东欧扩展到西欧、亚洲、美洲,最后扩大到全世界。
目前参加这项赛事的代表队有80余支。
美国1974年参加竞赛,中国1985年参加竞赛。
经过40多年的发展,国际数学奥林匹克的运转逐步制度化、规范化,有了一整套约定俗成的常规,并为历届东道主所遵循。
国际奥林匹克数学竞赛由参赛国轮流主办,经费由东道国提供,但旅费由参赛国自理。
参赛选手必须是不超过20岁的中学生,每支代表队有学生6人,另派2名数学家为领队。
试题由各参赛国提供,然后由东道国精选后提交给主试委员会表决,产生6道试题。
东道国不提供试题。
试题确定之后,写成英、法、德、俄文等工作语言,由领队译成本国文字。
主试委员会由各国的领队及主办国指定的主席组成。
这个主席通常是该国的数学权威。
主试委员会的职责有7条:1)、选定试题;2)、确定评分标准;3)、用工作语言准确表达试题,并翻译、核准译成各参加国文字的试题;4)、比赛期间,确定如何回答学生用书面提出的关于试题的疑问;5)、解决个别领队与协调员之间在评分上的不同意见;6)、决定奖牌的个数与分数线。
考试分两天进行,每天连续进行4.5小时,考3道题目。
同一代表队的6名选手被分配到6个不同的考场,独立答题。
数学好玩《比赛场次》(教学课件)六年级 数学上册 北师大版

达标练习
一列火车往返于上海和北京之间,共要停 靠在4个车站(上海站、南京站、天津站和 北京站),要为这列火车准备多少种不同 的车票?要制定多少种不同的票价?
课后作业
作业:
想一想,画一画。 学校体操表演队为联络方便,设计了一种 联络方式。一旦有事,先由教练同时通知两位 队长,这两位队长再分别同时通知两名同学, 依此类推,每人再同时通知两个人。 如果每同时通知两人共需1分,6分可以通 知到多少名同学?
六⑴班10名同学进行乒乓球比赛, 每两名同学之间要进行一场比赛。
2.从简单的情形开始,找找有什么规律。
比赛 人数
示意图
各点之间 连线数
比赛 场次
2
1
1
3
1+2=3
3
4
1+2+3=6 6
5
1+2+3+4=10 1
0
探索新知
六⑴班10名同学进行乒乓球比赛, 每两名同学之间要进行一场比赛。
2.从简单的情形开始,找找有什么规律。
1+2+3+…+11=66(次)
小试牛刀
淘气和同组的其他9名同学进行五子棋比赛,每两人之 间进行一次比赛,这个小组共要进行几场比赛?
1+2+3+…+9=45(次)
知识总结
“比赛场次”和“联络方式”这两个问题有什么共同之处?
遇到复杂问题时可以从简单的情 形开始寻找规律。
知识总结
华罗庚
化难为易, 找出规律, 以简驭繁, 解决难题。
北师大版·第六单元
比赛场次
小学数学·六年级(上)
学习目标
会用列表、画图的方式,寻找实际问题
01
中蕴涵的简单的规律,体会图、表的简 洁性和有效性。
湖北省浠水县实验高级中学2025届高考临考冲刺数学试卷含解析

湖北省浠水县实验高级中学2025届高考临考冲刺数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知A 类产品共两件12,A A ,B 类产品共三件123,,B B B ,混放在一起,现需要通过检测将其区分开来,每次随机检测一件产品,检测后不放回,直到检测出2件A 类产品或者检测出3件B 类产品时,检测结束,则第一次检测出B 类产品,第二次检测出A 类产品的概率为( )A .12B .35C .25D .3102.已知斜率为2-的直线与双曲线()2222:10,0x y C a b a b-=>>交于,A B 两点,若()00,M x y 为线段AB 中点且4OM k =-(O 为坐标原点),则双曲线C 的离心率为( )A .5B .3C .3D .3243.复数z 满足()11i z i +=-,则z =( )A .1i -B .1i +C .2222i -D .2222i + 4.金庸先生的武侠小说《射雕英雄传》第12回中有这样一段情节,“……洪七公道:肉只五种,但猪羊混咬是一般滋味,獐牛同嚼又是一般滋味,一共有几般变化,我可算不出了”.现有五种不同的肉,任何两种(含两种)以上的肉混合后的滋味都不一样,则混合后可以组成的所有不同的滋味种数为( )A .20B .24C .25D .265.已知等比数列{}n a 满足13a =,13521a a a ++=,则357a a a ++=( )A .21B .42C .63D .846.已知集合M ={y |y =,x >0},N ={x |y =lg (2x -)},则M∩N 为( )A .(1,+∞)B .(1,2)C .[2,+∞)D .[1,+∞)7.已知双曲线221x y a+=的一条渐近线倾斜角为56π,则a =( )A .3B .3-C .33-D .3-8.已知集合A={y|y=|x|﹣1,x ∈R},B={x|x≥2},则下列结论正确的是( )A .﹣3∈AB .3∉BC .A∩B=BD .A ∪B=B9.已知向量,a b 满足||1,||3a b ==,且a 与b 的夹角为6π,则()(2)a b a b +⋅-=( ) A .12 B .32- C .12- D .3210.如图,平面四边形ACBD 中,AB BC ⊥,AB DA ⊥,1AB AD ==,2BC =,现将ABD △沿AB 翻折,使点D 移动至点P ,且PA AC ⊥,则三棱锥P ABC -的外接球的表面积为( )A .8πB .6πC .4πD .82311.若复数221a i i++(a R ∈)是纯虚数,则复数22a i +在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 12.已知复数z 满足:34zi i =+(i 为虚数单位),则z =( )A .43i +B .43i -C .43i -+D .43i --二、填空题:本题共4小题,每小题5分,共20分。
2022《试吧》高中全程训练计划·数学(文)周周测 函数综合 Word版含解析

函数综合测试第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数y =1x 2-4的定义域为( ) A .(-∞,-2) B .(2,+∞)C .(-∞,-2]∪[2,+∞)D .(-∞,-2)∪(2,+∞) 2.(2021·南昌摸底)下列函数中,在(0,+∞)上单调递减,并且是偶函数的是( )A .y =x 2B .y =-x 3C .y =-lg |x|D .y =2x3.设函数f(x)=⎩⎪⎨⎪⎧1+lg (2-x ),x <1,10x -1,x ≥1,则f(-8)+f(lg 40)=( )A .5B .6C .9D .22 4.(2021·湖北八校二联)已知定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x +1)=f (1-x ),且当x ∈[0,1]时,f (x )=log 2(x +1),则f (31)=( ) A .0 B .1 C .-1 D .25.(2021·江西八校联考)已知函数y =f (x )对任意自变量x 都有f (x )=f (2-x ),且函数f (x )在[1,+∞)上单调.若数列{a n }是公差不为0的等差数列,且f (a 6)=f (a 2011),则{a n }的前2022项之和为( )A .0B .1 008C .2 016D .4 0326.函数f (x )=log 2|2x -1|的图象大致是( )7.(2022·新课标全国卷Ⅲ)已知a =243,b =323,c =2513,则( ) A .b <a <c B .a <b <c C .b <c <a D .c <a <b 8.若方程f (x )-2=0在区间(-∞,0)内有解,则函数y =f (x )的图像可能是( ) 9.(2021·天津卷)已知定义在R 上的函数f (x )=2|x -m |-1(m 为实数)为偶函数.记a =f (log 0.53),b =f (log 25),c =f (2m ),则a ,b ,c 的大小关系为( ) A .a <b <c B .a <c <b C .c <a <b D .c <b <a10.(2021·华南师大附中测试)函数y =cos4x 2x 的图象大致是( )11.(2021·昆明检测)已知定义在R 上的函数f (x )是奇函数,且f (x )在(-∞,0)上是减函数,f (2)=0,g (x )=f (x +2),则不等式xg (x )≤0的解集是( ) A .(-∞,-2]∪[2,+∞) B .[-4,-2]∪[0,+∞) C .(-∞,-4]∪[-2,+∞) D .(-∞,-4]∪[0,+∞) 12.已知f (x )是定义域为(-1,1)的奇函数,而且f (x )是减函数,假如f (m -2)+f (2m -3)>0,那么实数m 的取值范围是( ) A .(1,53) B .(-∞,53) C .(1,3) D .(53,+∞) 第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.(2021·银川一中月考)设函数f (x )=log 3(9x )·log 3(3x ),19≤x ≤9,则f (x )的最小值为__________. 14.若一次函数f (x )的定义域为[-3,2],值域为[2,7],则f (x )=________. 15.(2021·山西监测)有四个函数:①y =x 12;②y =21-x ;③y =ln(x +1);④y =|1-x |,其中在(0,1)内单调递减的函数的序号是__________.16.(2021·福建质检)已知函数f (x )=⎩⎪⎨⎪⎧x -a ,x ≥1ln (1-x ),x <1有两个零点,则实数a的取值范围是__________.三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)假如幂函数f (x )=x -12p 2+p +32(p ∈Z )是偶函数,且在(0,+∞)上是增函数,求p 的值,并写出相应的函数f (x )的解析式.18.(本小题满分12分)设g(x)=mx2+x+1.(1)若g(x)的定义域为R,求m的范围;(2)若g(x)的值域为[0,+∞),求m的范围.19.(本小题满分12分)函数y=lg(3-4x+x2)的定义域为M,当x∈M时,求f(x)=2x+2-3×4x的最值.20.(本小题满分12分)设f(x)为定义在R上的偶函数,当0≤x≤2时,y=x;当x>2时,y=f(x)的图象是顶点为P(3,4)且过点A(2,2)的抛物线的一部分.(1)求函数f(x)在(-∞,-2)上的解析式;(2)写出函数f(x)的值域和单调区间.21.(本小题满分12分)行驶中的汽车在刹车时由于惯性作用,要连续往前滑行一段距离才能停下,这段距离叫做刹车距离.在某种路面上,某种型号汽车的刹车距离y(米)与汽车的车速x(千米/时)满足下列关系:y=x2200+mx+n(m,n是常数). 如图是依据多次试验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图.(1)求出y关于x的函数表达式;(2)假如要求刹车距离不超过25.2米,求行驶的最大速度.22.(本小题满分12分)已知函数f(x)=e x-e-x(x∈R且e为自然对数的底数).(1)推断函数f(x)的奇偶性与单调性.(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切实数x都成立?若存在,求出t;若不存在,请说明理由.1.D x 2-4>0得x >2或x <-2.2.C 函数y =x 2在(0,+∞)上单调递增,排解A ;函数y =-x 3为奇函数,排解B ;函数y =-lg|x |为偶函数且在(0,+∞)上单调递减,C 正确;函数y =2x 既不是奇函数也不是偶函数,排解D.综上所述,选C.3.B f (-8)+f (lg40)=1+lg10+10lg40-1=2+4010=6,故选B.4.C 由f (x +1)=f (1-x )得f (-x )=f (x +2),又f (-x )=-f (x ),所以f (x )=-f (x +2)=f (x +4),所以函数f (x )的周期为4,所以f (31)=f (4×8-1)=f (-1)=-f (1)=-log 22=-1,故选C.5.C ∵f (x )=f (2-x ),∴f (x )的图象关于直线x =1对称. 又∵函数f (x )在[1,+∞)上单调,且数列{a n }的公差不为0,f (a 6)=f (a 2011),∴a 6+a 2011=2,∴a 1+a 2022=a 6+a 2011=2,∴S 2022=2022(a 1+a 2022)2=2022,故选C. 6.C f (-x )=log 2|2-x -1|≠log 2|2x -1|=f (x ),即f (-x )≠f (x ),所以f (x )不是偶函数,图象不关于y 轴对称,故D 不正确;x <0时0<2x <1,所以-1<2x -1<0,所以0<|2x -1|<1,所以f (x )=log 2|2x -1|<0,故B 不正确.当0<x <1时,1<2x <2,所以0<|2x -1|<1,所以f (x )=log 2|2x -1|<0,故A 不正确,故选C.7.A 由于a =243=423>323=b ,c =2513=523>423=a ,所以b <a <c ,故选A.梳理总结:比较大小经常需要依据三个数的结构,联系相关的指数函数、对数函数、幂函数的单调性来推断,假如两个数的指数相同,底数不同,则考虑幂函数的单调性;假如指数不同,底数相同,则考虑指数函数的单调性;假如涉及对数,则考虑对数函数的单调性.8.D 对题中所给的四个图像,要使方程f (x )-2=0在区间(-∞,0)内有解,只须将函数y =f (x )的图像向下平移2个单位,平移后看哪个图像与x 轴的负半轴有交点,相当于原函数y =f (x )在y 轴左侧的图像与直线y =2有交点,由此可知正确选项为D.9.C 由f (x )=2|x -m |-1是偶函数得m =0,则f (x )=2|x |-1其图象过原点,且关于y 轴对称,x ∈(-∞,0)时单调递减.当x ∈[0,+∞)时,f (x )=2x -1单调递增,又a =f (-log 23)=f (log 23),b =f (log 25),c =f (0),且0<log 23<log 25,则f (0)<f (log 0.53)<f (log 25),即c <a <b .10.A 明显函数y =cos4x2x 不是偶函数,排解C ,D ,当x →+∞时,y →0,排解B ,故选A.11.C 依题意,如图所示,实线部分为g (x )的草图,则xg (x )≤0⇔⎩⎪⎨⎪⎧x ≥0g (x )≤0或⎩⎪⎨⎪⎧x ≤0g (x )≥0, 由图可得xg (x )≤0的解集为(-∞,-4]∪[-2,+∞).12.A 由于f (x )是奇函数,且为减函数,∴f (m -2)+f (2m -3)>0⇒f (m -2)>-f (2m -3)=f (3-2m ),∴⎩⎪⎨⎪⎧m -2<3-2m -1<m -2<1-1<3-2m <1⇒⎩⎨⎧m <531<m <31<m <2⇒1<m <53.13.-14解析:由于19≤x ≤9,所以-2≤log 3x ≤2,则f (x )=(log 3x +2)(log 3x +1)=log 23x+3log 3x +2=(log 2x +32)2-14,则当log 3x =-32,即x =39时,f (x )min =-14.梳理总结:将函数转化为关于log 3x 的二次函数为解答本题的突破口. 14.x +5或-x +4解析:设y =kx +b ,则当k >0时⎩⎨⎧-3k +b =2,2k +b =7,解得⎩⎨⎧k =1,b =5;当k <0时⎩⎨⎧-3k +b =7,2k +b =2,解得⎩⎨⎧k =-1,b =4.15.②④解析:幂函数y =x 12在(0,1)内单调递增,排解①;函数y =21-x=12x -1在(0,1)内单调递减,②正确;函数y =ln(x +1)在(0,1)内单调递增,排解③;函数y =|1-x |=1-x ,x ∈(0,1)单调递减,④正确.16.[1,+∞)解析:当x <1时,明显函数f (x )存在唯一零点x =0,所以当x ≥1时,函数f (x )存在唯一零点,又由于y =x 在[1,+∞)上单调递增且值域为[1,+∞),所以a 的取值范围为[1,+∞).解后反思:分段函数的零点要分别在每一段的定义域内求解. 17.解析:∵f (x )在(0,+∞)上是增函数,∴-12p 2+p +32>0,即p 2-2p -3<0,∴-1<p <3.5分 又∵f (x )是偶函数且p ∈Z , ∴p =1,故f (x )=x 2.10分18.解析:(1)由题知f (x )=mx 2+x +1≥0恒成立, ①当m =0时,f (x )=x +1≥0不恒成立;②当m ≠0时,要满足题意必有⎩⎨⎧ m >0,Δ=1-4m ≤0,∴m ≥14.综上可知,m 的范围为[14,+∞).6分(2)由题知,f (x )=mx 2+x +1能取到一切大于或等于0的实数. ①当m =0时,f (x )=x +1可以取到一切大于或等于0的实数;②当m ≠0时,要满足题意必有⎩⎨⎧m >0,Δ=1-4m ≥0,∴0<m ≤14.综上可知,m 的范围为[0,14].12分19.解析:由3-4x +x 2>0,得x >3或x <1,∴M ={x |x >3或x <1},f (x )=-3×(2x )2+2x +2=-3(2x -16)2+2512.6分∵x >3或x <1,∴2x >8或0<2x <2,∴当2x=16,即x =log 216时,f (x )最大,最大值为2512,f (x )没有最小值.12分 20.解析:(1)当x >2时,设f (x )=a (x -3)2+4.∵f (x )的图象过点A (2,2),∴f (2)=a (2-3)2+4=2,∴a =-2,∴f (x )=-2(x -3)2+4. 设x ∈(-∞,-2),则-x >2,∴f (-x )=-2(-x -3)2+4.又由于f (x )在R 上为偶函数,∴f (-x )=f (x ),∴f (x )=-2(-x -3)2+4,即f (x )=-2(x +3)2+4,x ∈(-∞,-2).6分(2)函数f (x )图象如图所示.由图象观看知f (x )的值域为{y |y ≤4}.单调增区间为(-∞,-3],[0,3].单调减区间为[-3,0],[3,+∞).12分21.解析:(1)由题意及函数图象,得⎩⎪⎨⎪⎧402200+40m +n =8.4,602200+60m +n =18.6,解得m =1100,n =0, 所以y =x 2200+x100(x ≥0).(2)令x 2200+x100≤25.2, 得-72≤x ≤70. ∵x ≥0,∴0≤x ≤70.故行驶的最大速度是70千米/时.22.解析:(1)由于f (x )=e x-(1e )x ,且y =e x 是增函数,y =-(1e )x 是增函数,所以f (x )是增函数.由于f (x )的定义域为R ,且f (-x )=e -x -e x =-f (x ),所以f (x )是奇函数.6分 (2)由(1)知f (x )是增函数和奇函数,所以f (x -t )+f (x 2-t 2)≥0对一切x ∈R 恒成立⇔f (x 2-t 2)≥f (t -x )对一切x ∈R 恒成立⇔x 2-t 2≥t -x 对一切x ∈R 恒成立⇔t 2+t ≤x 2+x 对一切x ∈R 恒成立⇔(t+1 2)2≤(x+12)2min⇔(t+12)2≤0⇔t=-12.即存在实数t=-12,使不等式f(x-t)+f(x2-t2)≥0对一切实数x都成立.12分。
湖北省十堰市2024高三冲刺(高考数学)苏教版考试(押题卷)完整试卷

湖北省十堰市2024高三冲刺(高考数学)苏教版考试(押题卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题集合,则()A.B.C.D.第(2)题传说国际象棋发明于古印度,为了奖赏发明者,古印度国王让发明者自己提出要求,发明者希望国王让人在他发明的国际象棋棋盘上放些麦粒,规则为:第一个格子放一粒,第二个格子放两粒,第三个格子放四粒,第四个格子放八粒……依此规律,放满棋盘的64个格子所需小麦的总重量大约为()吨.(1kg麦子大约20000粒,lg2=0.3)A.105B.107C.1012D.1015第(3)题设集合,则()A.B.C.D.第(4)题已知等差数列的前n项和为,其中,记的前n项和为,若,其中表示不超过x的最大整数值,则的值域为()A.B.C.D.第(5)题设,其中为实数,则()A.B.C.D.第(6)题在三角形中,,则的大小为A.B.C.D.第(7)题已知全集,集合,则()A.B.C.D.第(8)题设则中奇数的个数为A.2B.3C.4D.5二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题过双曲线的左焦点的直线交的左、右支分别于两点,交直线于点,若,则()A.B.C.D.第(2)题已知函数的定义域为,且,,则()A.B.为偶函数C.为周期函数,且4为的周期D.第(3)题一个袋子中有编号分别为的4个球,除编号外没有其它差异.每次摸球后放回,从中任意摸球两次,每次摸出一个球.设“第一次摸到的球的编号为2”为事件,“第二次摸到的球的编号为奇数”为事件,“两次摸到的球的编号之和能被3整除”为事件,则下列说法正确的是()A.B.事件与事件相互独立C.D.事件与事件互为对立事件三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知向量,,则的值为______.第(2)题已知,且,则________.第(3)题甲、乙、丙3所学校每所学校各派出两名同学,现从这六名同学中任取两名,安排到甲、乙、丙3所学校交流.每所学校至多安排一名同学,每名同学只能去一所学校且不能去自己原先的学校,则不同的安排方法有________种.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列满足.(1)求数列的通项公式;(2)设数列的前n项和为,若不等式对任意的恒成立,求实数t的取值范围;(3)记,求证:.第(2)题某地区的篮球协会组织民间篮球队开展比赛,一来促进全民健身,二来带动地方经济发展,比赛最后由甲、乙两队进行决赛,为增加看点及提升篮球比赛的热度,主办方在征得甲、乙两队同意后,决定决赛采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).已知甲队的主客场安排依次为“主主客客主”,甲队主场取胜的概率为0.6,客场取胜的概率为0.5,每场比赛均没有平局,且各场比赛结果相互独立.(1)在比赛进行三场结束的条件下,求甲队获胜的概率;(2)假设该地区篮球协会在前三场比赛中每场收入10万元,之后的比赛每场收入15万元.因开支的需要,该地区篮球协会需预支付球队费用万元,该地区篮球协会在至多可以预支24万元预算的条件下,同时希望比赛结束后获利(获利=总收入-预支付球队费用)的期望高于万元.请你通过数据分析,判断该地区篮球协会的预算是否可以满足预支付球队费用且达到预想结果?第(3)题如图,已知正三棱锥的侧面是直角三角形,过点作平面,垂足为,过点作平面,垂足为,连接并延长交于点.(1)证明:是线段的中点;(2)求平面与平面夹角的正弦值.第(4)题随着改革开放的不断深入,祖国不断富强,人民生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,新政策的主要内容包括:①个税起征点为5000元;②每月应纳税所得额(含税)=(收入)-(个税起征点)-(专项附加扣除);③专项附加扣除包括赡养老人、子女教育、继续教育、大病医疗等.新个税政策下赡养老人的扣除标准为:独生子女每月扣除2000元,非独生子女与其兄弟姐妹按照每月2000元的标准分摊扣除,但每个人的分摊额度不能超过1000元;子女教育的扣除标准为:每个子女每月扣除1000元(可由父母中的一方扣除,或者父母双方各扣除500元)税率表如下:级数全月应纳税所得额税率1不超过3000元的部分3%2超过3000元至12000元的部分10%3超过12000元至25000元的部分20%4超过25000元至35000元的部分25%………(1)税务部门在小李所在公司用分层抽样方法抽取某月100位不同层次员工的税前收入,并制成如图的频率分布直方图.(i)请根据频率分布直方图估计该公司员工税前收入的中位数;(ii)同一组中的数据以这组数据所在区间中点的值作代表,在不考虑他们的专项附加扣除的情况下,甲、乙两位同学用如下两种方法估计小李所在的公司员工该月平均纳税,请判断哪位同学的方法是正确的,不需说明理由.甲同学:(元);乙同学:先计算收入的均值(元),再利用均值计算平均纳税为:(元)(2)为研究某城市月薪为20000元群体的纳税情况,现收集了该城市500名公司白领(每人至多1个孩子)的相关资料,通过整理数据知道:这500人中有一个孩子符合子女教育专项附加扣除(假定由他们各自全部扣除)的有400人,不符合子女教育专项附加扣除的人有100人,符合子女专项附加扣除的人中有300人也符合赡养老人专项附加扣除,不符合子女专项附加扣除的人中有50人符合赡养老人专项附加扣除,并且他们均不符合其他专项附加扣除(统计的500人中,任何两人均不在一个家庭且为独生子女).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群每月应缴纳个税金额(单位:元)的分布列与期望.第(5)题数列前项和为,满足:,.(1)求证:数列是等比数列;(2)求和:.。
河南省漯河市2024高三冲刺(高考数学)苏教版考试(预测卷)完整试卷

河南省漯河市2024高三冲刺(高考数学)苏教版考试(预测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题古希腊数学家毕达哥拉斯通过研究正五边形和正十边形的作图,发现了黄金分割率,黄金分割率的值也可以用表示,即,设,则()A.B.C.D.第(2)题若,则()A.B.C.D.第(3)题已知定义在上的函数满足当时当时则()A.809B.811C.1011D.1013第(4)题对于任意的两个实数对和,规定当且仅当,;运算“”为:,运算“”为:,设,若则A.B.C.D.第(5)题复数在复平面内,所对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限第(6)题我国南宋时期杰出的数学家秦九韶在《数书九章》中提出了“三斜求积术”,其内容为:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积.”把以上文字写成公式,即(其中S为面积,a,b,c为的三个内角A,B,C所对的边).若,且,则利用“三斜求积”公式可得的面积()A.B.C.D.第(7)题若复数满足为纯虚数,且,则的虚部为()A.1B.C.D.1第(8)题设α、β是互不重合的平面,l、m、n是互不重合的直线,下列命题正确的是()A.若mÌα,nÌα,l⊥m,l⊥n,则l⊥αB.若l⊥n,m⊥n,则l∥mC.若m∥α,n∥β,α⊥β,则m⊥n D.若l⊥α,l∥β,则α⊥β二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题设随机变量服从正态分布,且,则实数的值可为()A.B.C.D.第(2)题对于,满足,且对于,恒有.则()A.B.C.D.第(3)题已知正方形的对角线长为,是它的内切圆一条弦,点为正方形四条边上的一个动点,当弦的长度最大时,不可能为()A.B.C.D.三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若为虚数单位,复数满足,则的最大值为_______.第(2)题在的展开式中,求含项的系数为___________.第(3)题在△ABC中,若a=2,b+c=7,,则b=_________________四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题在等差数列中,.(1)求的通项公式;(2)设,求数列的前n项和.第(2)题已知函数且.(1)讨论的单调性;(2)若,求证:,.第(3)题已知离心率为的椭圆:的上下顶点分别为,,直线:与椭圆相交于,两点,与相交于点 .(Ⅰ)求椭圆的标准方程;(Ⅱ)若,求面积的最大值;(Ⅲ)设直线,相交于点,求的值.第(4)题已知函数,(1)若,求在区间上的单调区间;(2)若,证明:时恒有第(5)题在平面直角坐标系中,曲线C的参数方程为(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.(1)求曲线C极坐标方程;(2)若A,B为曲线C上的动点,且,求的值.。
湖南省张家界市2024高三冲刺(高考数学)苏教版考试(培优卷)完整试卷

湖南省张家界市2024高三冲刺(高考数学)苏教版考试(培优卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题中国女排精神代代相传.某网站对出战2024年巴黎奥运会的中国女排12人大名单进行了预测:主攻队员4人,副攻队员3人,二传和接应各2人,自由人1人.在中国女排每场比赛7人的首发阵容中,主攻和副攻各2人,二传和接应各1人,自由人1人.如果按照该网站预测的12人大名单出战,首发阵容方案数为()A.144B.140C.72D.36第(2)题已知数列的前项和为,,若,则()A.5B.7C.9D.17第(3)题若双曲线C:的右支上存在,到点的距离相等,则双曲线C的离心率的取值范围是()A.B.C.D.第(4)题向量在向量上的投影向量为()A.B.C.D.第(5)题记“的不同正因数的个数”,“的展开式中项的系数”,则()A.B.C.D.第(6)题教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气.按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于等于.经测定,刚下课时,空气中含有的二氧化碳,若开窗通风后教室内二氧化碳的浓度为,且随时间(单位:分钟)的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准至少需要的时间为(参考数据:)()A.11分钟B.14分钟C.16分钟D.20分钟第(7)题设直线l与抛物线相交于A,B两点,与圆相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是A.B.C.D.第(8)题某批农产品的质量(单位:千克)服从正态分布,且其中质量大于0.7的数量等于质量小于0.4的数量,则下列四部分中()A.质量小于0.4的农产品数量最多B.质量大于1.09的农产品数量最多C.质量大于0.7的农产品数量最多D.质量小于0.55的农产品数量最多二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题移动互联网时代,智能终端市场商机无限,全球商家强势抢攻市场.通过同比数据发现,中国智能手机市场呈现出积极的增长趋势.据报载,年月,中国市场智能手机新机激活量为万台,同比增长(同比增长率),具体分为个品牌排名,统计数据如下表所示,则下列说法正确的有()排名品牌当月新机激活量/万台同比新机激活量/万台苹果小米荣耀华为其他A.该月个品牌新机激活量同比数据的极差为B.该月个品牌新机激活量数据的平均数大于中位数C.该月“华为”品牌新机激活量同比增长率大于D.去年同期中国市场智能手机新机激活量总量小于万台第(2)题正方体的展开图如图所示.已知为线段的中点,动点在正方体的表面上运动.则关于该正方体,下列说法正确的有()A.与是异面直线B.与所成角为C.平面平面D.若,则点的运动轨迹是正六边形第(3)题在长方体中,,,则()A.直线与所成的角为60°B.直线与所成的角为90°C.直线与平面所成的角为30°D.直线与平面所成的角的余弦值为三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题一条光线从点射出,被轴反射后经过圆的圆心C,则入射光线所在的直线方程为___________.第(2)题1955年10月29日新疆克拉玛依1号油井出油,标致着新中国第一个大油田的诞生,克拉玛依大油泡是一号油井广场上的标志性建筑,成为市民与游客的打卡网红地,形状为椭球型,中心截面为椭圆,已知动点在椭圆上,若点A的坐标为,点满足,,则的最小值是___________.第(3)题对于任一实数序列,定义为序列,它的第项是,假定序列的所有项都是,且,则_________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列,为其前项的和,满足.(1)求数列的通项公式;(2)设数列的前项和为,数列的前项和为,求证:当,时;(3)已知当,且时有,其中,求满足的所有的值.第(2)题在中,角所对的边分别是,满足.(1)求角的大小;(2)若,的面积,求的周长.第(3)题已知等差数列满足,.(1)求的通项公式;(2)若,数列满足关系式,求证:数列的通项公式为;(3)设(2)中的数列的前n项和为,对任意的正整数n,恒成立,求实数p的取值范围.第(4)题【江苏省南京师大附中2018届高三高考考前模拟考试数学试题】已知等差数列{a n}和等比数列{b n}均不是常数列,若a1=b1=1,且a1,2a2,4a4成等比数列, 4b2,2b3,b4成等差数列.(1)求{a n}和{b n}的通项公式;(2)设m,n是正整数,若存在正整数i,j,k(i<j<k),使得a m b j,a m a n b i,a n b k成等差数列,求m+n的最小值;(3)令c n=,记{c n}的前n项和为Tn,{ }的前n项和为An.若数列{pn}满足p1=c1,且对"n≥2, n∈N*,都有pn=+A n c n,设{p n}的前n项和为S n,求证:Sn<4+4lnn.第(5)题一青蛙从点开始依次水平向右和竖直向上跳动,其落点坐标依次是,(如图,的坐标以已知条件为准),表示青蛙从点到点所经过的路程.(1)点为抛物线准线上一点,点,均在该抛物线上,并且直线经过该抛物线的焦点,证明;(2)若点要么落在所表示的曲线上,要么落在所表示的曲线上,并且,试写出(不需证明);(3)若点要么落在所表示的曲线上,要么落在所表示的曲线上,并且,求的值.。
新疆博尔塔拉蒙古自治州2024高三冲刺(高考数学)苏教版能力评测(拓展卷)完整试卷

新疆博尔塔拉蒙古自治州2024高三冲刺(高考数学)苏教版能力评测(拓展卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题双纽线是1694年被瑞士数学家雅各布·伯努利用来描述他所发现的.在平面直角坐标系中,把到定点和距离之积等于的点的轨迹称为双纽线.已知点是双纽线上一点,下列说法正确的是()①双纽线关于原点对称;②;③双纽线上满足的点只有两个;④的最大值是.A.①②③B.①②④C.①②D.①②③④第(2)题若集合,,则()A.B.C.D.第(3)题等比数列的首项为正数,,,若对满足的任意,都成立,则实数的取值范围是A.B.C.D.第(4)题已知函数,若方程有3个不同的实根,则实数的取值范围为A.B.C.D.第(5)题已知,,,则,,的大小关系为()A.B.C.D.第(6)题设定义在上的函数若关于的方程有3个不同的实数解,,,则等于( )A.3B.6C.D.第(7)题设是函数的导函数,若,且,,则下列选项中不一定正确的一项是A.B.C.D.第(8)题某统计数据共有13个样本,它们依次成公差的等差数列,若第60百分位数为30,则它们的平均数为()A.19B.25C.21D.23二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题关于复数、,下列说法正确的是()A.B.若,C.若,则D.第(2)题的展开式中,下列说法正确的是()A.所有项系数和为64B.常数项为第4项C.整式共有3项D.项的系数第(3)题已知正四棱台(上下底面都是正方形的四棱台).下底面ABCD边长为2,上底面边长为1,侧棱长为,则A.它的表面积为B.它的外接球的表面积为C.侧棱与下底面所成的角为60°D.它的体积比棱长为的正方体的体积大三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题的最小正周期是______.第(2)题已知分别为双曲线的左、右焦点,点在双曲线上且不与顶点重合,满足,则该双曲线的离心率为______.第(3)题已知双曲线的左、右焦点分别为,,过点的直线与双曲线的左、右两支分别交于A,B两点,若,,则C的离心率为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知函数.(1)若,求实数的值;(2)已知且,求证:.第(2)题根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布.(1)随机购买10只该商家的海产品,求至少买到一只质量小于克该海产品的概率.(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入(千元)与年收益增量(千元)()的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线的附近,且,,,,,,,其中,=.根据所给的统计量,求关于的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.附:若随机变量,则,;对于一组数据,,,,其回归线的斜率和截距的最小二乘估计分别为,.第(3)题2024年3月28日,小米SU7汽车上市,24小时预定88898台.小米集团为了了解小米手机用户订购小米SU7的意愿与用户是小米粉丝是否有关,随机抽取了200名小米手机用户进行调查,得到下表.已订购小米SU7未订购小米SU7总计是小米粉丝80非小米粉丝4080总计(1)补全表中数据,依据小概率值的独立性检验,是否能够认为小米手机用户订购小米SU7的意愿与用户是小米粉丝有关?(2)小米集团打算从已订购小米SU7的用户中采用按比例分配的分层随机抽样的方式抽取6人,再从这6人中抽取3人听取建议,求这3人中恰有2人是小米粉丝的概率.附:,其中.0.0100.0050.0016.6357.87910.828已知数列的首项,设,且的前项和满足:.(1)求数列的通项公式;(2)令,求证:.第(5)题函数()的最大值为3,其图象相邻两条对称轴之间的距离为,(1)求函数的解析式;(2)设,则,求的值。
