北理珠数据库系统概论习题第五章

合集下载

《数据库系统概论》练习题(答案)

一、选择题 (3)二、判断题 (11)三、填空题 (11)四、名词解释 (13)五、简答题 (16)第二章关系数据模型 (31)一、选择题 (31)二、判断题 (41)三、填空题 (41)四、名词解释 (43)五、简答题 (45)第四章关系数据库设计理论 (52)一、选择题 (52)二、判断题 (65)三、填空题 (68)四、名词解释 (72)五、简答题 (74)第三章数据库的标准语言 SQL (90)一、选择题 (90)二、填空题 (101)三、简答题 (102)一、选择题 (145)二、判断题 (150)三、填空题 (150)四、简答题 (154)第一章数据库系统导论一、选择题1.在数据库中存储的是A）数据 B）数据模型C）数据以及数据之间的联系 D）信息答案：C2. 存储在计算机内有结构的数据的集合是A）数据库系统 B）数据库C）数据库管理系统 D）数据结构答案：B3.信息的数据表示形式是A）只能是文字 B）只能是声音C）只能是图形 D）上述皆可答案：D4.数据管理与数据处理之间的关系是A）两者是一回事 B）两者之间无关C）数据管理是数据处理的基本环节 D）数据处理是数据管理的基本环节答案：C5.在数据管理技术的发展过程中，经历了人工管理阶段、文件系统阶段和数据库系统阶段。

在这几个阶段中，数据独立性最高的阶段是A）数据库系统 B）文件系统C）人工管理 D）数据项管理答案：A6.下面列出的数据库管理技术发展的三个阶段中，没有专门的软件对数据进行管理的是I．人工管理阶段 II．文件系统阶段 III．数据库阶段和 II B.只有 II和 III D.只有 I答案：D是A.数据库B.数据库系统C.数据库应用软件D.数据库管理软件答案：D8.以下所列数据库系统组成中，正确的是A）计算机、文件、文件管理系统、程序B）计算机、文件、程序设计语言、程序C）计算机、文件、报表处理程序、网络通信程序D）支持数据库系统的计算机软硬件环境、数据库文件、数据库管理系统、数据库应用程序和数据库管理员答案：D9.数据库系统的核心是A）数据库 B）数据库管理系统C）数据模型 D）软件工具答案：B10．数据库 DB、数据库系统 DBS、数据库管理系统 DBMS 三者之间的关系是A）DBS 包括 DB、DBMS B）DB 包括 DBS、DBMSC）DBMS 包括 DB、DBS D）DB 就是 DBS，也就是 DBMS 答案：A11.数据库系统是采用了数据库技术的计算机系统，数据库系统由数据库、数据库管理系统、应用系统和构成。

数据库系统概论第五版课后习题答案王珊

第1章绪论1 ．试述数据、数据库、数据库系统、数据库管理系统的概念。

答：( l ）数据（ Data ) ：描述事物的符号记录称为数据。

数据的种类有数字、文字、图形、图像、声音、正文等。

数据与其语义是不可分的。

解析在现代计算机系统中数据的概念是广义的。

早期的计算机系统主要用于科学计算，处理的数据是整数、实数、浮点数等传统数学中的数据。

现代计算机能存储和处理的对象十分广泛，表示这些对象的数据也越来越复杂。

数据与其语义是不可分的。

500 这个数字可以表示一件物品的价格是 500 元，也可以表示一个学术会议参加的人数有 500 人，还可以表示一袋奶粉重 500 克。

( 2 ）数据库（ DataBase ，简称 DB ) ：数据库是长期储存在计算机内的、有组织的、可共享的数据集合。

数据库中的数据按一定的数据模型组织、描述和储存，具有较小的冗余度、较高的数据独立性和易扩展性，并可为各种用户共享。

( 3 ）数据库系统（ DataBas 。

Sytem ，简称 DBS ) ：数据库系统是指在计算机系统中引入数据库后的系统构成，一般由数据库、数据库管理系统（及其开发工具）、应用系统、数据库管理员构成。

解析数据库系统和数据库是两个概念。

数据库系统是一个人一机系统，数据库是数据库系统的一个组成部分。

但是在日常工作中人们常常把数据库系统简称为数据库。

希望读者能够从人们讲话或文章的上下文中区分“数据库系统”和“数据库”，不要引起混淆。

( 4 ）数据库管理系统（ DataBase Management sytem ，简称 DBMs ) ：数据库管理系统是位于用户与操作系统之间的一层数据管理软件，用于科学地组织和存储数据、高效地获取和维护数据。

DBMS 的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。

解析 DBMS 是一个大型的复杂的软件系统，是计算机中的基础软件。

目前，专门研制 DBMS 的厂商及其研制的 DBMS 产品很多。

数据库系统原理04735课后习题参考答案

数据库系统原理课后习题第一章. 数据库系统基本概念1.1.名词解释DB——DB是长期存储在计算机内、有组织的、统一管理的相关数据的集合。

DB能为各种用户共享，具有较小冗余度、数据间联系紧密而又有较高的数据独立性等特点。

DBMS——是位于用户与操作系统之间的一层数据管理软件，它为用户或应用程序提供访问DB的方法，包括DB的建立、查询、更新及各种数据控制。

DBS——是实现有组织地、动态地存储大量关联数据、方便多用户访问的计算机硬件、软件和数据资源组成的系统，即它是采用数据库技术的计算机系统。

联系——是实体间的相互关系。

联系的元数——与一个联系有关的实体集个数。

１：１联系——如果实体集E1中每个实体至多和实体集E2中一个实体有联系，反之亦然，那么实体集E1和E2的联系称为“一对一联系”，记为“１：１”。

１：N联系——如果实体集E1中的每个实体可以与实体集E2中的任意个（０个或多个）实体有联系，而E2中的每个实体至多和E1中的一个实体有联系，那么称E1对E2的联系是一对多联系，记作：“１：N ”。

M：N联系——如果实体集E１中的每个实体可以与实体集E2中的任意个（０个或多个）实体有联系，反之亦然，那么称E1和E2的联系是“多对多联系”，记作“M：N”。

数据模型——在数据库技术中，我们用数据模型的概念描述数据库的结构和语义，对现实世界的数据进行抽象。

根据数据抽象级别定义了四种模型：概念数据模型、逻辑数据模型、外部数据模型和内部数据模型。

概念模型——表达用户需求观点的数据全局逻辑结构的模型。

逻辑模型——表达计算机实现观点的DB全局逻辑结构的模型。

主要有层次、网状、关系模型等三种。

外部模型——表达用户使用观点的DB局部逻辑结构的模型。

内部模型——表达DB物理结构的模型。

层次模型——用树型（层次）结构表示实体类型及实体间联系的数据模型。

网状模型——用有向图结构表示实体类型及实体间联系的数据模型。

关系模型——是由若干个关系模式组成的集合。

数据库系统概论第五版课后习题答案王珊

第 1 章绪论1．试述数据、数据库、数据库系统、数据库管理系统的概念。

答：( l ）数据（Data ) ：描述事物的符号记录称为数据。

数据的种类有数字、文字、图形、图像、声音、正文等。

数据与其语义是不可分的。

解析在现代计算机系统中数据的概念是广义的。

早期的计算机系统主要用于科学计算，处理的数据是整数、实数、浮点数等传统数学中的数据。

现代计算机能存储和处理的对象十分广泛，表示这些对象的数据也越来越复杂。

数据与其语义是不可分的。

500 这个数字可以表示一件物品的价格是500元，也可以表示一个学术会议参加的人数有500 人，还可以表示一袋奶粉重500 克。

( 2 ）数据库（ DataBase ，简称 DB ) ：数据库是长期储存在计算机内的、有组织的、可共享的数据集合。

数据库中的数据按一定的数据模型组织、描述和储存，具有较小的冗余度、较高的数据独立性和易扩展性，并可为各种用户共享。

( 3 ）数据库系统（DataBas 。

Sytem，简称DBS )：数据库系统是指在计算机系统中引入数据库后的系统构成，一般由数据库、数据库管理系统（及其开发工具）、应用系统、数据库管理员构成。

解析数据库系统和数据库是两个概念。

数据库系统是一个人一机系统，数据库是数据库系统的一个组成部分。

但是在日常工作中人们常常把数据库系统简称为数据库。

希望读者能够从人们讲话或文章的上下文中区分“数据库系统”和“数据库”，不要引起混淆。

( 4 ）数据库管理系统（DataBaseManagement sytem，简称DBMs )：数据库管理系统是位于用户与操作系统之间的一层数据管理软件，用于科学地组织和存储数据、高效地获取和维护数据。

DBMS 的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。

解析DBMS 是一个大型的复杂的软件系统，是计算机中的基础软件。

目前，专门研制 DBMS 的厂商及其研制的 DBMS 产品很多。

数据库系统概论第五版课后习题答案王珊版之欧阳歌谷创编

第二章关系数据库欧阳歌谷（2021.02.01）1 ．试述关系模型的三个组成部分。

答：关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。

2 ．试述关系数据语言的特点和分类。

答：关系数据语言可以分为三类：关系代数语言。

关系演算语言：元组关系演算语言和域关系演算语言。

SQL：具有关系代数和关系演算双重特点的语言。

这些关系数据语言的共同特点是，语言具有完备的表达能力，是非过程化的集合操作语言，功能强，能够嵌入高级语言中使用。

3 （略）4 ．5 . 述关系模型的完整性规则。

在参照完整性中，为什么外部码属性的值也可以为空？什么情况下才可以为空？答：实体完整性规则是指若属性A是基本关系R的主属性，则属性A不能取空值。

若属性(或属性组)F是基本关系R的外码，它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系)，则对于R中每个元组在F上的值必须为：或者取空值(F的每个属性值均为空值)；或者等于S中某个元组的主码值。

即属性F本身不是主属性，则可以取空值，否则不能取空值。

6．设有一个SPJ数据库，包括S，P，J，SPJ四个关系模式：1）求供应工程J1零件的供应商号码SNO：πSno(σJno=‘J1’（SPJ）)2）求供应工程J1零件P1的供应商号码SNO：πSno(σJno=‘J1’∧Pno=‘P1‘(SPJ))3）求供应工程J1零件为红色的供应商号码SNO：πSno(πSno,,Pno（σJno=‘J1‘(SPJ))∞πPno（σCOLOR=’红‘（P）))4）求没有使用天津供应商生产的红色零件的工程号JNO：πJno(SPJ)- πJNO（σcity=‘天津’∧Color=‘红‘（S∞SPJ∞P）5）求至少用了供应商S1所供应的全部零件的工程号JNO：πJno，Pno(SPJ)÷πPno（σSno=‘S1‘（SPJ））7. 试述等值连接与自然连接的区别和联系。

答：连接运算符是“=”的连接运算称为等值连接。

数据库系统概论第五版课后的习题答案王珊版.doc

第二章关系数据库1 ．试述关系模型的三个组成部分。

答：关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。

2 ．试述关系数据语言的特点和分类。

答：关系数据语言可以分为三类：关系代数语言。

关系演算语言：元组关系演算语言和域关系演算语言。

SQL：具有关系代数和关系演算双重特点的语言。

这些关系数据语言的共同特点是，语言具有完备的表达能力，是非过程化的集合操作语言，功能强，能够嵌入高级语言中使用。

3 （略）4 ．5 . 述关系模型的完整性规则。

即属性F本身不是主属性，则可以取空值，否则不能取空值。

答：连接运算符是“=”的连接运算称为等值连接。

数据库系统基础教程课后答案第五章

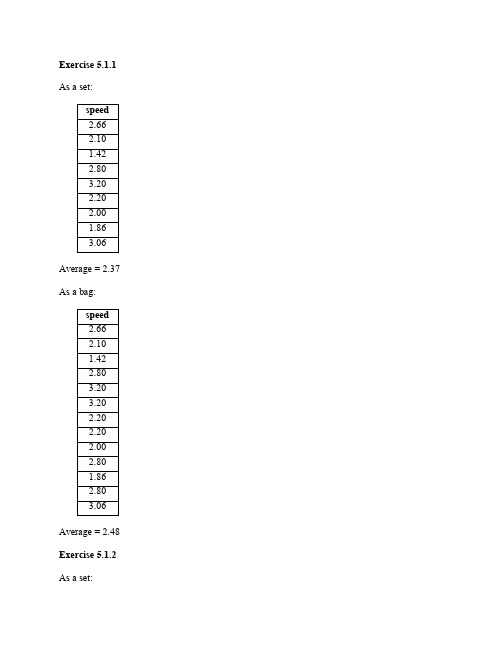
Exercise 5.1.1 As a set:Average = 2.37 As a bag:Average = 2.48 Exercise 5.1.2 As a set:Average = 218 As a bag:Average = 215 Exercise 5.1.3a As a set:As a bag:Exercise 5.1.3bπbore(Ships Classes)Exercise 5.1.4aFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the union of bags R and S will have tuple t appear n + m times. The further union of bag T with the tuple t appearing o times will have tuple t appear n + m + o times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the union of bags R and S will have tuple t appear m + o times. The further union of bag R with the tuple t appearing n times will have tuple t appear m + o + n times in the final result.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result. Since we cannot have duplicates, the result only has at most one copy of the tuple t.Exercise 5.1.4bFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the intersectionof bags R and S will have tuple t appear min( n, m ) times. The further intersection of bag T with the tuple t appearing o times will produce tuple t min( o, min( n, m ) ) times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the intersection of bags R and S will have tuple t appear min( m, o ) times. The further intersection of bag R with the tuple t appearing n times will produce tuple t min( n, min( m, o ) ) times in thefinal result.The intersection of bags R,S and T will yield a result where tuple t appears min( n,m,o ) times. For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result.Exercise 5.1.4cFor bags:On the left-hand side:Given that tuple r in R, which appears m times, can successfully join with tuple s in S,which appears n times, we expect the result to contain mn copies. Also given that tuple tin T, which appears o times, can successfully join with the joined tuples of r and s, weexpect the final result to have mno copies.On the right-hand side:Given that tuple s in S, which appears n times, can successfully join with tuple t in T,which appears o times, we expect the result to contain no copies. Also given that tuple rin R, which appears m times, can successfully join with the joined tuples of s and t, weexpect the final result to have nom copies.The order in which we perform the natural join does not matter for bags.For sets:This is a similar case when dealing with bags except the joined tuples can only appear at most once in each result. If there are tuples r,s,t in relations R,S,T that can successfully join, then the result will contain a tuple with the schema of their joined attributes.Exercise 5.1.4dFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the union of these two bags R ⋃ S, tuple t would appear n + m times. Likewise, in the union of these two bags S ⋃ R, tuple t would appear m + n times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in both sets R and S will the union R ⋃ S have the tuple t. The same reasoning holds when we take the union S ⋃ R.Therefore the commutative law for union holds.Exercise 5.1.4eFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the intersection of these two bags R ∩ S, tuple t would appear min( n,m ) times. Likewise in the intersection of these two bags S ∩ R, tuple t would appear min( m,n ) times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in at least one of the sets R and S will the intersection R ∩ S have the tuple t. The same reasoning holds when we take the intersection S ∩ R.Therefore the commutative law for intersection holds.Exercise 5.1.4fFor bags:Suppose a tuple t occurs n times in bag R and tuple u occurs m times in bag S. Suppose also that the two tuples t,u can successfully join. Then in the natural join of these two bags R S, the joined tuple would appear nm times. Likewise in the natural join of these two bags S R, the joined tuple would appear mn times. Both sides of the relation yield the same result.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuples u,v might appear respectively in sets R and S one or zero times. The combinations of number of occurrences for tuples u,v in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple u exists in Rand tuple v exists in S will the natural join R S have the joined tuple. The same reasoning holds when we take the natural join S R.Therefore the commutative law for natural join holds.Exercise 5.1.4gFor bags:Suppose tuple t appears m times in R and n times in S. If we take the union of R and S first, we will get a relation where tuple t appears m + n times. Taking the projection of a list of attributes L will yield a resulting relation where the projected attributes from tuple t appear m + n times. If we take the projection of the attributes in list L first, then the projected attributes from tuple t would appear m times from R and n times from S. The union of these resulting relations would have the projected attributes of tuple t appear m + n times.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t exists in R or S (or both R and S) will the projected attributes of tuple t appear in the result.Therefore the law holds.Exercise 5.1.4hFor bags:Suppose tuple t appears u times in R, v times in S and w times in T. On the left hand side, the intersection of S and T would produce a result where tuple t would appear min(v , w) times. With the addition of the union of R, the overall result would have u + min(v , w) copies of tuple t. On the right hand side, we would get a result of min(u + v, u + w) copies of tuple t. The expressions on both the left and right sides are equivalent.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R,S and T one or zero times. The combinations of number of occurrences for tuple t in R, S and T respectively are (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0) and (1,1,1). Only when tuple t appears in R or in both S and T will the result have tuple t.Therefore the distributive law of union over intersection holds.Exercise 5.1.4iSuppose that in relation R, u tuples satisfy condition C and v tuples satisfy condition D. Suppose also that w tuples satisfy both conditions C and D where w≤ min(v , w). Then the left hand side will return those w tuples. On the right hand side, σC(R) produces u tuples and σD(R) produces v tuples. However, we know the intersection will produce the same w tuples in the result.When considering bags and sets, the only difference is bags allow duplicate tuples while sets only allow one copy of the tuple. The example above applies to both cases.Therefore the law holds.Exercise 5.1.5aFor sets, an arbitrary tuple t appears on the left hand side if it appears in both R,S and not in T. The same is true for the right hand side.As an example for bags, suppose that tuple t appears one time each in both R,T and two times in S. The result of the left hand side would have zero copies of tuple t while the right hand side would have one copy of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5bFor sets, an arbitrary tuple t appears on the left hand side if it appears in R and either S or T. This is equivalent to saying tuple t only appears when it is in at least R and S or in R and T. The equivalence is exactly the right side’s expression.As an example for bags, suppose that tuple t appears one time in R and two times each in S and T. Then the left hand side would have one copy of tuple t in the result while the right hand side would have two copies of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5cFor sets, an arbitrary tuple t appears on the left hand side if it satisfies condition C, condition Dor both condition C and D. On the right hand side, σC(R) selects those tuples that satisfy condition C while σD(R) selects those tuples that satisfy condition D. However, the union operator will eliminate duplicate tuples, namely those tuples that satisfy both condition C and D. Thus we are ensured that both sides are equivalent.As an example for bags, we only need to look at the union operator. If there are indeed tuples that satisfy both conditions C and D, then the right hand side will contain duplicate copies of those tuples. The left hand side, however, will only have one copy for each tuple of the original set of tuples.Exercise 5.2.1bExercise 5.2.1cExercise 5.2.1dExercise 5.2.1fExercise 5.2.1gExercise 5.2.1hExercise 5.2.1iExercise 5.2.1jExercise 5.2.1kExercise 5.2.1lExercise 5.2.1mExercise 5.2.1nExercise 5.2.2aApplying the δ operator on a relation with no duplicates will yield the same relation. Thus δ is idempotent.Exercise 5.2.2bThe result of πL is a relation over the list of attributes L. Performing the projection again will return the same relation because the relation only contains the list of attributes L. Thus πL is idempotent.Exercise 5.2.2cThe result of σC is a relation where condition C is satisfied by every tuple. Performing the selection again will return the same relation because the relation only contains tuples that satisfy the condition C. Thus σC is idempotent.Exercise 5.2.2dThe result of γL is a relation whose schema consists of the grouping attributes and the aggregated attributes. If we perform the same grouping operation, there is no guarantee that the expression would make sense. The grouping attributes will still appear in the new result. However, the aggregated attributes may or may not appear correctly. If the aggregated attribute is given a different name than the original attribute, then performing γL would not make sense because it contains an aggregation for an attribute name that does not exist. In this case, the resultingrelation would, according to the definition, only contain the grouping attributes. Thus, γL is not idempotent.Exercise 5.2.2eThe result of τ is a sorted list of tuples based on some attributes L. If L is not the entire schema of relation R, then there are attributes that are not sorted on. If in relation R there are two tuples that agree in all attributes L and disagree in some of the remaining attributes not in L, then it is arbitrary as to which order these two tuples appear in the result. Thus, performing the operation τ multiple times can yield a different relation where these two tuples are swapped. Thus, τ is not idempotent.Exercise 5.2.3If we only consider sets, then it is possible. We can take πA(R) and do a product with itself. From this product, we take the tuples where the two columns are equal to each other.If we consider bags as well, then it is not possible. Take the case where we have the two tuples (1,0) and (1,0). We wish to produce a relation that contains tuples (1,1) and (1,1). If we use the classical operations of relational algebra, we can either get a result where there are no tuples or four copies of the tuple (1,1). It is not possible to get the desired relation because no operation can distinguish between the original tuples and the duplicated tuples. Thus it is not possible to get the relation with the two tuples (1,1) and (1,1).Exercise 5.3.1a)Answer(model) ← PC(model,speed,_,_,_) AND speed ≥ 3.00b)Answer(maker) ← Laptop(model,_,_,hd,_,_) AND Product(maker,model,_) AND hd ≥100c)Answer(model,price) ← PC(model,_,_,_,price) AND Product(maker,model,_) ANDmaker=’B’Answer(model,price) ← Laptop(mode l,_,_,_,_,price) AND Product(maker,model,_)AND maker=’B’Answer(model,price) ← Printer(model,_,_,price) AND Product(maker,model,_) ANDmaker=’B’d)Answer(model) ← Printer(model,color,type,_) AND color=’true’ AND type=’laser’e)PCMaker(maker) ← Product(maker,_,type) AND type=’pc’LaptopMaker(maker) ← Product(maker,_,type) AND type=’laptop’Answer(maker) ← LaptopMaker(maker) AND NOT PCMaker(maker)f)Answer(hd) ← PC(model1,_,_,hd,_) AND PC(model2,_,_,hd,_) AND model1 <>model2g)Answer(model1,model2) ← PC(model1,speed, ram,_,_) ANDPC(model2,_speed,ram,_,_) AND model1 < model2h)FastComputer(model) ← PC(model,speed,_,_,_) AND speed ≥ 2.80FastComputer(model) ← Laptop(model,speed,_,_,_,_) AND speed ≥ 2.80Answer(maker) ← Product(maker,model1,_) AND Product(maker,mod el2,_) ANDFastComputer(model1) AND FastComputer(model2) AND model1 <> model2i)Computers(model,speed) ← PC(model,speed,_,_,_)Computers(model,speed) ← Laptop(model,speed,_,_,_,_)SlowComputers(model) ← Computers(model,speed) AND Computers(model1,speed1)AND speed < speed1FastestComputers(model) ← Computers(model,_) AND NOT SlowComputers(model)Answer(maker) ← Fast estComputers(model) AND Product(maker,model,_)j)PCs(maker,speed) ← PC(model,speed,_,_,_) AND Product(maker,model,_) Answer(maker) ← PCs(maker,spe ed) AND PCs(maker,speed1) AND PCs(maker,speed2) AND speed <> speed1 AND speed <> speed2 AND speed1 <> speed2k)PCs(maker,model) ← Product(maker,model,type) AND type=’pc’Answer(maker) ← PCs(maker,model) AND PCs(maker,model1) ANDPCs(maker,model2) AND PCs(maker,model3) AND model <> model1 AND model <>model2 AND model1 <> model2 AND (model3 = model OR model3 = model1 ORmodel3 = model2)Exercise 5.3.2a)Answer(class,country) ← Classes(class,_,country,_,bore,_) AND bore ≥ 16b)Answer(name) ← Ships(name,_,launch ed) AND launched < 1921c)Answer(ship) ← Outcomes(ship,battle,result) AND battle=’Denmark Strait’ AND result= ‘sunk’d)Answer(name) ← Classes(class,_,_,_,_,displacement) AND Ships(name,class,launched)AND displacement > 35000 AND launched > 1921e)Answer(nam e,displacement,numGuns) ← Classes(class,_,_,numGuns,_,displacement)AND Ships(name,class,_) AND Outcomes (ship,battle,_) AND battle=’Guadalcanal’AND ship=namef)Answer(name) ← Ships(name,_,_)Answer(name) ← Outcomes(name,_,_) AND NOT Answer(name)g)MoreThan One(class) ← Ships(name,class,_) AND Ships(name1,class,_) AND name <>name1Answer(class) ← Classes(class,_,_,_,_,_) AND NOT MoreThanOne(class)h)Battleship(country) ← Classes(_,type,country,_,_,_) AND type=’bb’Battlecruiser(country) ← Classes(_,type,country,_,_,_) AND type=’bc’Answer(country) ← Battleship(country) AND Battlecruiser(country)i)Results(ship,result,date) ← Battles(name,date) AND Outcomes(ship,battle,result) ANDbattle=nameAnswer(ship) ← Results(ship,result,date) AND Results(ship,_,date1) ANDresult=’damaged’ AND date < date1Exercise 5.3.3A nswer(x,y) ← R(x,y) AND z = zExercise 5.4.1aAnswer(a,b,c) ← R(a,b,c)Answer(a,b,c) ← S(a,b,c)Exercise 5.4.1bAnswer(a,b,c) ← R(a,b,c) AND S(a,b,c)Exercise 5.4.1cAnswer(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)Exercise 5.4.1dUnion(a,b,c) ← R(a,b,c)Union(a,b,c) ← S(a,b,c)Answer(a,b,c) ← Union(a,b,c) AND NOT T(a,b,c)Exercise 5.4.1eJ(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)K(a,b,c) ← R(,a,b,c) AND NOT T(a,b,c)Answer(a,b,c) ← J(a,b,c) AND K(a,b,c)Exercise 5.4.1fAnswer(a,b) ← R(a,b,_)Exercise 5.4.1gJ(a,b) ← R(a,b,_)K(a,b) ← S(_,a,b)Answer(a,b) ← J(a,b) AND K(a,b)Exercise 5.4.2aAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2bAnswer(x,y,z) ← R(x,y,z) AND x < y AND y < z Exercise 5.4.2cAnswer(x,y,z) ← R(x,y,z) AND x < yAnswer(x,y,z) ← R(x,y,z) AND y < zExercise 5.4.2dChange: NOT(x < y OR x > y)To: x ≥ y AND x ≤ yThe above simplifies to x = yAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2eChange: NOT((x < y OR x > y) AND y < z)NOT(x < y OR x > y) OR y ≥ z(x ≥ y AND x ≤ y) OR y ≥ zTo: x = y OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x = yAnswer(x,y,z) ← R(x,y,z) AND y ≥ zExercise 5.4.2fChange: NOT((x < y OR x < z) AND y < z)NOT(x < y OR x < z) OR y ≥ z To: (x ≥ y AND x ≥ z) OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x ≥ y AND x ≥ zAnswer(x,y,z) ← R(x,y,z) AND y ≥zExercise 5.4.3aAnswer(a,b,c,d) ← R(a,b,c) AND S(b,c,d)Exercise 5.4.3bAnswer(b,c,d,e) ← S(b,c,d) AND T(d,e)Exercise 5.4.3cAnswer(a,b,c,d,e) ← R(a,b,c) AND S(b,c,d) AND T(d,e)Exercise 5.4.4a)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syb)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < sy AND ry < szc)Answer(rx,ry,rz,sx,sy,s z) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < syAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry < szd)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = sye)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syAnswe r(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szf)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx ≥ sy AND rx ≥ szAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szExercise 5.4.5aR1 := πx,y(Q R)Exercise 5.4.5bR1 := ρR1(x,z)(Q)R2 := ρR2(z,y)(Q)R3 := πx,y(R1 (R1.z = R2.z) R2)Exercise 5.4.5cR1 := πx,y(Q R)R2 := σx < y(R1)。

数据库系统概论第五版课后的习题答案.doc

第1章绪论1 ．试述数据、数据库、数据库系统、数据库管理系统的概念。

答：( l ）数据（ Data ) ：描述事物的符号记录称为数据。

数据的种类有数字、文字、图形、图像、声音、正文等。

数据与其语义是不可分的。

解析在现代计算机系统中数据的概念是广义的。

早期的计算机系统主要用于科学计算，处理的数据是整数、实数、浮点数等传统数学中的数据。

现代计算机能存储和处理的对象十分广泛，表示这些对象的数据也越来越复杂。

数据与其语义是不可分的。

500 这个数字可以表示一件物品的价格是 500 元，也可以表示一个学术会议参加的人数有 500 人，还可以表示一袋奶粉重 500 克。

( 2 ）数据库（ DataBase ，简称 DB ) ：数据库是长期储存在计算机内的、有组织的、可共享的数据集合。

数据库中的数据按一定的数据模型组织、描述和储存，具有较小的冗余度、较高的数据独立性和易扩展性，并可为各种用户共享。

( 3 ）数据库系统（ DataBas 。

解析数据库系统和数据库是两个概念。

数据库系统是一个人一机系统，数据库是数据库系统的一个组成部分。

但是在日常工作中人们常常把数据库系统简称为数据库。

希望读者能够从人们讲话或文章的上下文中区分“数据库系统”和“数据库”，不要引起混淆。

DBMS 的主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。

解析 DBMS 是一个大型的复杂的软件系统，是计算机中的基础软件。

目前，专门研制 DBMS 的厂商及其研制的 DBMS 产品很多。

04735数据库系统原理(2018年版)课后习题参考答案与解析

答案仅供参考第一章数据库系统概述选择题B、B、A简答题1.请简述数据,数据库,数据库管理系统,数据库系统的概念。

P27数据是描述事物的记录符号，是指用物理符号记录下来的，可以鉴别的信息。

数据库即存储数据的仓库，严格意义上是指长期存储在计算机中的有组织的、可共享的数据集合。

数据库管理系统是专门用于建立和管理数据库的一套软件，介于应用程序和操作系统之间。

数据库系统是指在计算机中引入数据库技术之后的系统，包括数据库、数据库管理系统及相关实用工具、应用程序、数据库管理员和用户。

2.请简述早数据库管理技术中，与人工管理、文件系统相比，数据库系统的优点。

数据共享性高数据冗余小易于保证数据一致性数据独立性高可以实施统一管理与控制减少了应用程序开发与维护的工作量3.请简述数据库系统的三级模式和两层映像的含义。

P31答：数据库的三级模式是指数据库系统是由模式、外模式和内模式三级工程的，对应了数据的三级抽象。

两层映像是指三级模式之间的映像关系，即外模式/模式映像和模式/内模式映像。

4.请简述关系模型与网状模型、层次模型的区别。

P35使用二维表结构表示实体及实体间的联系建立在严格的数学概念的基础上概念单一，统一用关系表示实体和实体之间的联系，数据结构简单清晰，用户易懂易用存取路径对用户透明，具有更高的数据独立性、更好的安全保密性。

第二章关系数据库选择题C、C、D简答题1.请简述关系数据库的基本特征。

P48答：关系数据库的基本特征是使用关系数据模型组织数据。

2.请简述什么是参照完整性约束。

P55答：参照完整性约束是指：若属性或属性组F是基本关系R的外码，与基本关系S的主码K 相对应，则对于R中每个元组在F上的取值只允许有两种可能，要么是空值，要么与S中某个元组的主码值对应。

3.请简述关系规范化过程。

答：对于存在数据冗余、插入异常、删除异常问题的关系模式，应采取将一个关系模式分解为多个关系模式的方法进行处理。

一个低一级范式的关系模式，通过模式分解可以转换为若干个高一级范式的关系模式，这就是所谓的规范化过程。

数据库系统概论第五版试题及答案

数据库系统概论复习资料：第一章：一选择题：1．在数据管理技术的发展过程中，经历了人工管理阶段、文件系统阶段和数据库系统阶段。

在这几个阶段中，数据独立性最高的是阶段。

A．数据库系统 B．文件系统 C．人工管理 D．数据项管理答案：A2．数据库的概念模型独立于。

A．具体的机器和DBMS B．E-R图 C．信息世界 D．现实世界答案：A3．数据库的基本特点是。

A．(1)数据可以共享(或数据结构化) (2)数据独立性 (3)数据冗余大，易移植 (4)统一管理和控制B．(1)数据可以共享(或数据结构化) (2)数据独立性 (3)数据冗余小，易扩充 (4)统一管理和控制C．(1)数据可以共享(或数据结构化) (2)数据互换性 (3)数据冗余小，易扩充 (4)统一管理和控制D．(1)数据非结构化 (2)数据独立性 (3)数据冗余小，易扩充 (4)统一管理和控制答案：B4. 是存储在计算机内有结构的数据的集合。

A．数据库系统 B．数据库 C．数据库管理系统 D．数据结构答案：B5．数据库中存储的是。

A．数据 B．数据模型 C．数据以及数据之间的联系 D．信息答案：C6. 数据库中，数据的物理独立性是指。

A．数据库与数据库管理系统的相互独立 B．用户程序与DBMS的相互独立C．用户的应用程序与存储在磁盘上数据库中的数据是相互独立的 D．应用程序与数据库中数据的逻辑结构相互独立答案：C7. ．数据库的特点之一是数据的共享，严格地讲，这里的数据共享是指。

A．同一个应用中的多个程序共享一个数据集合 B．多个用户、同一种语言共享数据C．多个用户共享一个数据文件D．多种应用、多种语言、多个用户相互覆盖地使用数据集合答案：D8.据库系统的核心是。

A．数据库B．数据库管理系统C．数据模型D．软件工具答案：B9. 下述关于数据库系统的正确叙述是。

A．数据库系统减少了数据冗余 B．数据库系统避免了一切冗余 C．数据库系统中数据的一致性是指数据类型一致D．数据库系统比文件系统能管理更多的数据答案：A10. 数将数据库的结构划分成多个层次，是为了提高数据库的①和②。

2022年北京理工大学珠海学院计算机科学与技术专业《数据库原理》科目期末试卷B(有答案)

2022年北京理工大学珠海学院计算机科学与技术专业《数据库原理》科目期末试卷B（有答案）一、填空题1、SQL Server中数据完整性包括______、______和______。

2、数据库系统在运行过程中，可能会发生各种故障，其故障对数据库的影响总结起来有两类：______和______。

3、数据库内的数据是______的，只要有业务发生，数据就会更新，而数据仓库则是______的历史数据，只能定期添加和刷新。

4、设某数据库中有商品表（商品号，商品名，商品类别，价格）。

现要创建一个视图，该视图包含全部商品类别及每类商品的平均价格。

请补全如下语句： CREATE VIEW V1（商品类别，平均价格）AS SELECT商品类别，_____FROM商品表GROUP BY商品类别；5、数据仓库主要是供决策分析用的______，所涉及的数据操作主要是______，一般情况下不进行。

6、设有关系模式R（A，B，C）和S（E，A，F），若R.A是R的主码，S.A是S的外码，则S.A的值或者等于R中某个元组的主码值，或者______取空值，这是规则，它是通过______和______约束来实现的。

7、事务故障、系统故障的恢复是由______完成的，介质故障是由______完成的。

8、关系系统的查询优化既是关系数据库管理系统实现的关键技术，又是关系系统的优点。

因为，用户只要提出______，不必指出 ______。

9、若事务T对数据对象A加了S锁，则其他事务只能对数据A再加______，不能加______，直到事务T释放A上的锁。

10、在RDBMS中，通过某种代价模型计算各种查询的执行代价。

在集中式数据库中，查询的执行开销主要包括______和______代价。

在多用户数据库中，还应考虑查询的内存代价开销。

二、判断题11、一个数据表只能有一个唯一索引。

（）12、等值连接与自然连接是同一个概念。

（）13、在一个关系中，不同的列可以对应同一个域，但必须具有不同的列名。

《数据库系统概论》第四版课后习题答案

第1章绪论1 ．试述数据、数据库、数据库系统、数据库管理系统的概念。

答：( l ）数据（Data ) ：描述事物的符号记录称为数据。

数据是数据库中存储的基本对象。

( 2 ）数据库（DataBase ，简称DB ) ：数据库是长期储存在计算机内的、有组织的、可共享的数据集合。

数据库中的数据按一定的数据模型组织、描述和储存，具有较小的冗余度、较高的数据独立性和易扩展性，并可为各种用户共享。

( 3 ）数据库系统（DataBas 。

Sytem ，简称DBS ) ：数据库系统是指在计算机系统中引入数据库后的系统构成，一般由数据库、数据库管理系统（及其开发工具）、应用系统、数据库管理员构成。

( 4 ）数据库管理系统（DataBase Management sytem ，简称DBMs ) ：数据库管理系统是位于用户与操作系统之间的一层数据管理软件，用于科学地组织和存储数据、高效地获取和维护数据。

5 ．试述数据库系统的特点。

答：数据库系统的主要特点有：( l）数据结构化数据库系统实现整体数据的结构化，这是数据库的主要特征之一，也是数据库系统与文件系统的本质区别。

( 2）数据的共享性高，冗余度低，易扩充( 3 ）数据独立性高数据独立性包括数据的物理独立性和数据的逻辑独立性。

数据库管理系统的模式结构和二级映像功能保证了数据库中的数据具有很高的物理独立性和逻辑独立性。

( 4 ）数据由DBMS 统一管理和控制DBMS 必须提供统一的数据控制功能，包括数据的安全性保护、数据的完整性检查、并发控制和数据库恢复。

6 ．数据库管理系统的主要功能有哪些？答：DBMS 的主要功能包括数据定义功能、数据组织、存储和管理、数据操纵功能、数据库的事务管理和运行管理、数据库的建立和维护功能。

9 ．定义并解释概念模型中以下术语：实体，实体型，实体集，属性，码，实体联系图（E 一R 图）答：实体：客观存在并可以相互区分的事物。

实体型：具有相同属性的实体具有相同的特征和性质，用实体名及其属性名集合来抽象和刻画同类实体实体集：同型实体的集合称为实体集。

数据库系统基础教程第五章答案

Exercise 5.1.1 As a set:Average = 2.37 As a bag:Average = 2.48 Exercise 5.1.2Average = 218 As a bag:Average = 215 Exercise 5.1.3a As a set:161418As a bag:bore1516141615151418Exercise 5.1.3b(Ships Classes)πboreExercise 5.1.4aFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively,the union of bags R and S will have tuple t appear n + m times. Thefurther union of bag T with the tuple t appearing o times will havetuple t appear n + m + o times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively,the union of bags R and S will have tuple t appear m + o times. Thefurther union of bag R with the tuple t appearing n times will havetuple t appear m + o + n times in the final result.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if allthe sets have the tuple t. Otherwise, the tuple t will not appear in the result. Since we cannot have duplicates, the result only has at most one copy of the tuple t.Exercise 5.1.4bFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively,the intersection of bags R and S will have tuple t appear min( n, m )times. The further intersection of bag T with the tuple t appearing otimes will produce tuple t min( o, min( n, m ) ) times in the finalresult.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively,the intersection of bags R and S will have tuple t appear min( m, o )times. The further intersection of bag R with the tuple t appearing ntimes will produce tuple t min( n, min( m, o ) ) times in the finalresult.The intersection of bags R,S and T will yield a result where tuple t appears min( n,m,o ) times.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result.Exercise 5.1.4cFor bags:On the left-hand side:Given that tuple r in R, which appears m times, can successfully joinwith tuple s in S, which appears n times, we expect the result tocontain mn copies. Also given that tuple t in T, which appears o times,can successfully join with the joined tuples of r and s, we expect the final result to have mno copies.On the right-hand side:Given that tuple s in S, which appears n times, can successfully joinwith tuple t in T, which appears o times, we expect the result tocontain no copies. Also given that tuple r in R, which appears m times, can successfully join with the joined tuples of s and t, we expect the final result to have nom copies.The order in which we perform the natural join does not matter for bags.For sets:This is a similar case when dealing with bags except the joined tuples can only appear at most once in each result. If there are tuples r,s,t in relations R,S,T that can successfully join, then the result will contain a tuple with the schema of their joined attributes.Exercise 5.1.4dFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the union of these two bags R ⋃ S, tuple t would appear n + m times. Likewise, in the union of these two bags S ⋃ R, tuple t would appear m + n times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in both sets R and S will the union R ⋃ S have the tuple t. The same reasoning holds when we take the union S ⋃ R.Therefore the commutative law for union holds.Exercise 5.1.4eFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the intersection of these two bags R ∩ S, tuple t would appear min( n,m ) times. Likewise in the intersection of these two bags S ∩ R, tuple t would appear min( m,n ) times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuplet in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in at least one of the sets R and S will the intersection R ∩ S have the tuple t. The same reasoning holds when we take the intersection S ∩ R.Therefore the commutative law for intersection holds.Exercise 5.1.4fFor bags:Suppose a tuple t occurs n times in bag R and tuple u occurs m times in bag S. Suppose also that the two tuples t,u can successfully join. Then in thenatural join of these two bags R S, the joined tuple would appear nm times. Likewise in the natural join of these two bags S R, the joined tuple would appear mn times. Both sides of the relation yield the same result.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuples u,v might appear respectively in sets R and S one or zero times. The combinations of number of occurrences for tuples u,v in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple u exists in R and tuple v exists in S will the natural join R S have the joined tuple. The same reasoning holds when we take the natural join S R.Therefore the commutative law for natural join holds.Exercise 5.1.4gFor bags:Suppose tuple t appears m times in R and n times in S. If we take the union of R and S first, we will get a relation where tuple t appears m + n times. Taking the projection of a list of attributes L will yield a resultingrelation where the projected attributes from tuple t appear m + n times. If we take the projection of the attributes in list L first, then the projected attributes from tuple t would appear m times from R and n times from S. The union of these resulting relations would have the projected attributes of tuple t appear m + n times.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple tmight appear in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t exists in R or S (or both R and S) will the projected attributes of tuple t appear in the result.Therefore the law holds.Exercise 5.1.4hFor bags:Suppose tuple t appears u times in R, v times in S and w times in T. On the left hand side, the intersection of S and T would produce a result where tuple t would appear min(v , w) times. With the addition of the union of R, the overall result would have u + min(v , w) copies of tuple t. On the right hand side, we would get a result of min(u + v, u + w) copies of tuple t. The expressions on both the left and right sides are equivalent.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple tmight appear in sets R,S and T one or zero times. The combinations of number of occurrences for tuple t in R, S and T respectively are (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0) and (1,1,1). Only when tuple t appears in R or in both S and T will the result have tuple t.Therefore the distributive law of union over intersection holds.Exercise 5.1.4iSuppose that in relation R, u tuples satisfy condition C and v tuples satisfy condition D. Suppose also that w tuples satisfy both conditions C and D where w≤ min(v , w). Then the left hand side will return those w tuples. On the right hand side, σ(R) produces u tuples and σD(R) produces v tuples. However,Cwe know the intersection will produce the same w tuples in the result.When considering bags and sets, the only difference is bags allow duplicate tuples while sets only allow one copy of the tuple. The example above applies to both cases.Therefore the law holds.Exercise 5.1.5aFor sets, an arbitrary tuple t appears on the left hand side if it appears in both R,S and not in T. The same is true for the right hand side.As an example for bags, suppose that tuple t appears one time each in both R,T and two times in S. The result of the left hand side would have zero copies of tuple t while the right hand side would have one copy of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5bFor sets, an arbitrary tuple t appears on the left hand side if it appears in R and either S or T. This is equivalent to saying tuple t only appears when it is in at least R and S or in R and T. The equivalence is exactly the right side’s expression.As an example for bags, suppose that tuple t appears one time in R and two times each in S and T. Then the left hand side would have one copy of tuple tin the result while the right hand side would have two copies of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5cFor sets, an arbitrary tuple t appears on the left hand side if it satisfies condition C, condition D or both condition C and D. On the right hand side,σC (R) selects those tuples that satisfy condition C while σD(R) selects thosetuples that satisfy condition D. However, the union operator will eliminate duplicate tuples, namely those tuples that satisfy both condition C and D. Thus we are ensured that both sides are equivalent.As an example for bags, we only need to look at the union operator. If there are indeed tuples that satisfy both conditions C and D, then the right hand side will contain duplicate copies of those tuples. The left hand side, however, will only have one copy for each tuple of the original set of tuples.Exercise 5.2.1aExercise 5.2.1bExercise 5.2.1cExercise 5.2.1dExercise 5.2.1eExercise 5.2.1fExercise 5.2.1gExercise 5.2.1hExercise 5.2.1iExercise 5.2.1jExercise 5.2.1kExercise 5.2.1lExercise 5.2.1mExercise 5.2.1nExercise 5.2.2aApplying the δ operator on a relation with no duplicates will yield the same relation. Thus δ is idempotent.Exercise 5.2.2bThe result of πis a relation over the list of attributes L. Performing theLprojection again will return the same relation because the relation only contains the list of attributes L. Thus πis idempotent.LExercise 5.2.2cis a relation where condition C is satisfied by every tuple. The result of σCPerforming the selection again will return the same relation because the relation only contains tuples that satisfy the condition C. Thus σisC idempotent.Exercise 5.2.2dThe result of γis a relation whose schema consists of the groupingLattributes and the aggregated attributes. If we perform the same grouping operation, there is no guarantee that the expression would make sense. The grouping attributes will still appear in the new result. However, the aggregated attributes may or may not appear correctly. If the aggregated attribute is given a different name than the original attribute, thenwould not make sense because it contains an aggregation for an performing γLattribute name that does not exist. In this case, the resulting relation would,according to the definition, only contain the grouping attributes. Thus, γLis not idempotent.Exercise 5.2.2eThe result of τ is a sorted list of tuples based on some attributes L. If Lis not the entire schema of relation R, then there are attributes that are not sorted on. If in relation R there are two tuples that agree in all attributes L and disagree in some of the remaining attributes not in L, then it is arbitrary as to which order these two tuples appear in the result. Thus, performing the operation τ multiple times can yield a different relation where these two tuples are swapped. Thus, τ is not idempot ent.Exercise 5.2.3If we only consider sets, then it is possible. We can take π(R) and do aAproduct with itself. From this product, we take the tuples where the two columns are equal to each other.If we consider bags as well, then it is not possible. Take the case where we have the two tuples (1,0) and (1,0). We wish to produce a relation that contains tuples (1,1) and (1,1). If we use the classical operations of relational algebra, we can either get a result where there are no tuples or four copies of the tuple (1,1). It is not possible to get the desired relation because no operation can distinguish between the original tuples and the duplicated tuples. Thus it is not possible to get the relation with the two tuples (1,1) and (1,1).Exercise 5.3.1a)Answer(model) ← PC(model,speed,_,_,_) AND speed ≥ 3.00b)Answer(maker) ← Laptop(model,_,_,hd,_,_) AND Product(maker,model,_) ANDhd ≥ 100c)Answer(model,price) ← PC(model,_,_,_,price) AND Product(maker,model,_)AND maker=’B’Answer(model,price) ← Laptop(mode l,_,_,_,_,price) ANDProduct(maker,model,_) AND maker=’B’Answer(model,price) ← Printer(model,_,_,price) ANDProduct(maker,model,_) AND maker=’B’d)Answer(model) ← Printer(model,color,type,_) AND color=’true’ ANDtype=’laser’e)PCMaker(maker) ← Product(maker,_,type) AND type=’pc’LaptopMaker(maker) ← Product(maker,_,type) AND type=’laptop’Answer(maker) ← LaptopMaker(maker) AND NOT PCMaker(maker)f)Answer(hd) ← PC(model1,_,_,hd,_) AND PC(model2,_,_,hd,_) AND model1 <>model2g)Answer(model1,model2) ← PC(model1,speed, ram,_,_) ANDPC(model2,_speed,ram,_,_) AND model1 < model2h)FastComputer(model) ← PC(model,speed,_,_,_) AND speed ≥ 2.80FastComputer(model) ← Laptop(model,speed,_,_,_,_) AND speed ≥ 2.80Answer(maker) ← Product(maker,model1,_) AND Product(maker,mod el2,_) AND FastComputer(model1) AND FastComputer(model2) AND model1 <> model2i)Computers(model,speed) ← PC(model,speed,_,_,_)Computers(model,speed) ← Laptop(model,speed,_,_,_,_)SlowComputers(model) ← Computers(model,speed) ANDComputers(model1,speed1) AND speed < speed1FastestComputers(model) ← Computers(model,_) AND NOTSlowComputers(model)Answer(maker) ← Fast estComputers(model) AND Product(maker,model,_)j)PCs(maker,speed) ← PC(model,speed,_,_,_) AND Product(maker,model,_) Answer(maker) ← PCs(maker,spe ed) AND PCs(maker,speed1) ANDPCs(maker,speed2) AND speed <> speed1 AND speed <> speed2 AND speed1 <> speed2k)PCs(maker,model) ← Product(maker,model,type) AND type=’pc’Answer(maker) ← PCs(maker,model) AND PCs(maker,model1) ANDPCs(maker,model2) AND PCs(maker,model3) AND model <> model1 AND model <> model2 AND model1 <> model2 AND (model3 = model OR model3 = model1 ORmodel3 = model2)Exercise 5.3.2a)Answer(class,country) ← Classes(class,_,country,_,bore,_) AND bore ≥16b)Answer(name) ← Ships(name,_,launch ed) AND launched < 1921c)Answer(ship) ← Outcomes(ship,battle,result) AND battle=’DenmarkStrait’ AND result = ‘sunk’d)Answer(name) ← Classes(class,_,_,_,_,displacement) ANDShips(name,class,launched) AND displacement > 35000 AND launched > 1921e)Answer(nam e,displacement,numGuns) ←Classes(class,_,_,numGuns,_,displacement) AND Ships(name,class,_) ANDOutcomes (ship,battle,_) AND battle=’Guadalcanal’ AND ship=namef)Answer(name) ← Ships(name,_,_)Answer(name) ← Outcomes(name,_,_) AND NOT Answer(name)g)MoreThan One(class) ← Ships(name,class,_) AND Ships(name1,class,_) ANDname <> name1Answer(class) ← Classes(class,_,_,_,_,_) AND NOT MoreThanOne(class)h)Battleship(country) ← Classes(_,type,country,_,_,_) AND type=’bb’Battlecruiser(country) ← Classes(_,type,country,_,_,_) AND type=’bc’Answer(country) ← Battleship(country) AND Battlecruiser(country)i)Results(ship,result,date) ← Battles(name,date) ANDOutcomes(ship,battle,result) AND battle=nameAnswer(ship) ← Results(ship,result,date) AND Results(ship,_,date1) AND result=’damaged’ AND date < date1Exercise 5.3.3A nswer(x,y) ← R(x,y) AND z = zExercise 5.4.1aAnswer(a,b,c) ← R(a,b,c)Answer(a,b,c) ← S(a,b,c)Exercise 5.4.1bAnswer(a,b,c) ← R(a,b,c) AND S(a,b,c)Exercise 5.4.1cAnswer(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)Exercise 5.4.1dUnion(a,b,c) ← R(a,b,c)Union(a,b,c) ← S(a,b,c)Answer(a,b,c) ← Union(a,b,c) AND NOT T(a,b,c)Exercise 5.4.1eJ(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)K(a,b,c) ← R(,a,b,c) AND NOT T(a,b,c)Answer(a,b,c) ← J(a,b,c) AND K(a,b,c)Exercise 5.4.1fAnswer(a,b) ← R(a,b,_)Exercise 5.4.1gJ(a,b) ← R(a,b,_)K(a,b) ← S(_,a,b)Answer(a,b) ← J(a,b) AND K(a,b)Exercise 5.4.2aAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2bAnswer(x,y,z) ← R(x,y,z) AND x < y AND y < z Exercise 5.4.2cAnswer(x,y,z) ← R(x,y,z) AND x < yAnswer(x,y,z) ← R(x,y,z) AND y < zExercise 5.4.2dChange: NOT(x < y OR x > y)To: x ≥ y AND x ≤ yThe above simplifies to x = yAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2eChange: NOT((x < y OR x > y) AND y < z)NOT(x < y OR x > y) OR y ≥ z(x ≥ y AND x ≤ y) OR y ≥ zTo: x = y OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x = yAnswer(x,y,z) ← R(x,y,z) AND y ≥ zExercise 5.4.2fChange: NOT((x < y OR x < z) AND y < z)NOT(x < y OR x < z) OR y ≥ zTo: (x ≥ y AND x ≥ z) OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x ≥ y AND x ≥ zAnswer(x,y,z) ← R(x,y,z) AND y ≥zExercise 5.4.3aAnswer(a,b,c,d) ← R(a,b,c) AND S(b,c,d)Exercise 5.4.3bAnswer(b,c,d,e) ← S(b,c,d) AND T(d,e)Exercise 5.4.3cAnswer(a,b,c,d,e) ← R(a,b,c) AND S(b,c,d) AND T(d,e)Exercise 5.4.4a)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syb)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < sy ANDry < szc)Answer(rx,ry,rz,sx,sy,s z) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < syAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry < szd)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = sye)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syAnswe r(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szf)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx ≥ syAND rx ≥ szAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ sz Exercise 5.4.5aR1 := πx,y(Q R) Exercise 5.4.5bR1 := ρR1(x,z)(Q)R2 := ρR2(z,y)(Q)R3 := πx,y (R1(R1.z = R2.z)R2)Exercise 5.4.5cR1 := πx,y(Q R)R2 := σx < y(R1)。

数据库系统概论课后习题及参考答案

课后作业习题数据库系统概论课程部分习题及参考答案第一章绪论教材 41页１．试述数据、数据库、数据库系统、数据库管理系统的概念;数据：描述事物的符号记录称为数据;数据的种类有文字、图形、图象、声音、正文等等;数据与其语义是不可分的;数据库：数据库是长期储存在计算机内、有组织的、可共享的数据集合;数据库中的数据按一定的数据模型组织、描述和储存,具有较小的冗余度、较高的数据独立性和易扩展性,并可为各种用户共享;数据库系统：数据库系统 DBS是指在计算机系统中引入数据库后的系统构成;数据库系统由数据库、数据库管理系统及其开发工具、应用系统、数据库管理员构成;数据库管理系统：数据库管理系统 DBMS是位于用户与操作系统之间的一层数据管理软件;用于科学地组织和存储数据、高效地获取和维护数据;DBMS主要功能包括数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能;２．使用数据库系统有什么好处使用数据库系统的好处是由数据库管理系统的特点或优点决定的;使用数据库系统的好处很多,例如可以大大提高应用开发的效率,方便用户的使用,减轻数据库系统管理人员维护的负担等;为什么有这些好处,可以结合第 5题来回答;使用数据库系统可以大大提高应用开发的效率;因为在数据库系统中应用程序不必考虑数据的定义、存储和数据存取的具体路径,这些工作都由 DBMS来完成;此外,当应用逻辑改变,数据的逻辑结构需要改变时,由于数据库系统提供了数据与程序之间的独立性;数据逻辑结构的改变是 DBA的责任,开发人员不必修改应用程序,或者只需要修改很少的应用程序;从而既简化了应用程序的编制,又大大减少了应用程序的维护和修改;使用数据库系统可以减轻数据库系统管理人员维护系统的负担;因为 DBMS在数据库建立、运用和维护时对数据库进行统一的管理和控制,包括数据的完整性、安全性,多用户并发控制,故障恢复等等都由DBMS执行;总之,使用数据库系统的优点是很多的,既便于数据的集中管理,控制数据冗余,可以提高数据的利用率和一致性,又有利于应用程序的开发和维护;３．试述文件系统与数据库系统的区别和联系;文件系统与数据库系统的区别：文件系统面向某一应用程序,共享性差、冗余度大,独立性差,纪录内有结构、整体无结构,应用程序自己控制;数据库系统面向现实世界,共享性高、冗余度小,具有高度的物理独立性和一定的逻辑独立性,整体结构化,用数据模型描述,由数据库管理系统提供数据安全性、完整性、并发控制和恢复能力;文件系统与数据库系统的联系是：文件系统与数据库系统都是计算机系统中管理数据的软件;５．试述数据库系统的特点;数据库系统的主要特点有：一、数据结构化数据库系统实现整体数据的结构化,这是数据库的主要特征之一,也是数据库系统与文件系统的本质区别;二、数据的共享性高,冗余度低,易扩充数据库的数据不再面向某个应用而是面向整个系统,因此可以被多个用户、多个应用、用多种不同的语言共享使用;由于数据面向整个系统,是有结构的数据,不仅可以被多个应用共享使用,而且容易增加新的应用,这就使得数据库系统弹性大,易于扩充;三、数据独立性高数据独立性包括数据的物理独立性和数据的逻辑独立性;数据库管理系统的模式结构和二级映象功能保证了数据库中的数据具有很高的物理独立性和逻辑独立性;四、数据由 DBMS统一管理和控制数据库的共享是并发的共享,即多个用户可以同时存取数据库中的数据甚至可以同时存取数据库中同一个数据;为此, DBMS 必须提供统一的数据控制功能,包括数据的安全性保护,数据的完整性检查,并发控制和数据库恢复;６．数据库管理系统的主要功能有哪些①数据库定义功能；②数据存取功能；③数据库运行管理；④数据库的建立和维护功能;７．试述数据模型的概念、数据模型的作用和数据模型的三个要素;数据模型是数据库中用来对现实世界进行抽象的工具,是数据库中用于提供信息表示和操作手段的形式构架;一般地讲,数据模型是严格定义的概念的集合;这些概念精确地描述系统的静态特性、动态特性和完整性约束条件;因此数据模型通常由数据结构、数据操作和完整性约束三部分组成;①数据结构：是所研究的对象类型的集合,是对系统的静态特性的描述;②数据操作：是指对数据库中各种对象型的实例值允许进行的操作的集合,包括操作及有关的操作规则,是对系统动态特性的描述;③数据的约束条件：是完整性规则的集合,完整性规则是给定的数据模型中数据及其联系所具有的制约和依存规则,用以限定符合数据模型的数据库状态以及状态的变化,以保证数据的正确、有效、相容;８．试述概念模型的作用;概念模型实际上是现实世界到机器世界的一个中间层次;概念模型用于信息世界的建模,是现实世界到信息世界的第一层抽象,是数据库设计人员进行数据库设计的有力工具,也是数据库设计人员和用户之间进行交流的语言;９．定义并解释概念模型中以下术语：实体,实体型,实体集,属性,码,实体联系图 E-R图实体：客观存在并可以相互区分的事物叫实体;实体型：具有相同属性的实体具有相同的特征和性质,用实体名及其属性名集合来抽象和刻画同类实体称为实体型;实体集：同型实体的集合称为实体集;属性：实体所具有的某一特性,一个实体可由若干个属性来刻画;码：唯一标识实体的属性集称为码;实体联系图： E-R图提供了表示实体型、属性和联系的方法：·实体型：用矩形表示,矩形框内写明实体名;·属性：用椭圆形表示,并用无向边将其与相应的实体连接起来;·联系：用菱形表示,菱形框内写明联系名,并用无向边分别与有关实体连接起来,同时在无向边旁标上联系的类型 1 : 1,1 : n或m : n;第二章关系数据库教材81页1.试述关系模型的三个组成部分;答：关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成;2.试述关系数据语言的特点和分类;答：关系数据语言可以分为三类：关系代数语言例如 ISBL关系演算语言元组关系演算语言例如 APLHA,QUEL 和域关系演算语言例如QBE具有关系代数和关系演算双重特点的语言例如 SQL这些关系数据语言的共同特点是,具有完备的表达能力,是非过程化的集合操作语言,功能强,能够嵌入高级语言中使用;3. 定义并理解下列术语,说明它们之间的联系与区别:1域,关系,元组,属性答：域：域是一组具有相同数据类型的值的集合;关系：在域 D1,D2,…,Dn上笛卡尔积D1×D2×…×Dn的子集称为关系,表示为RD1,D2,…,Dn元组：关系中的每个元素是关系中的元组;属性：关系也是一个二维表,表的每行对应一个元组,表的每列对应一个域;由于域可以相同,为了加以区分,必须对每列起一个名字,称为属性 Attribute;2主码,候选码,外部码答：候选码：若关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码 Candidate key;主码：若一个关系有多个候选码,则选定其中一个为主码 Primary key;外部码：设 F是基本关系R的一个或一组属性,但不是关系R的码,如果F与基本关系S的主码Ks相对应,则称F是基本关系R的外部码Foreign key,简称外码;基本关系 R称为参照关系Referencing relation,基本关系S称为被参照关系Referenced relation或目标关系Target relation;关系R和S可以是相同的关系;3关系模式,关系,关系数据库关系模式：关系的描述称为关系模式 Relation Schema;它可以形式化地表示为：RU,D,dom,F其中 R为关系名,U为组成该关系的属性名集合,D为属性组U中属性所来自的域,dom为属性向域的映象集合,F为属性间数据的依赖关系集合;关系：在域 D1,D2,…,Dn上笛卡尔积D1×D2×…×Dn的子集称为关系,表示为RD1,D2,…,Dn关系是关系模式在某一时刻的状态或内容;关系模式是静态的、稳定的,而关系是动态的、随时间不断变化的,因为关系操作在不断地更新着数据库中的数据;关系数据库：关系数据库也有型和值之分;关系数据库的型也称为关系数据库模式,是对关系数据库的描述,它包括若干域的定义以及在这些域上定义的若干关系模式;关系数据库的值是这些关系模式在某一时刻对应的关系的集合,通常就称为关系数据库;4.试述关系模型的完整性规则;在参照完整性中,为什么外部码属性的值也可以为空什么情况下才可以为空答：关系模型的完整性规则是对关系的某种约束条件;关系模型中可以有三类完整性约束：实体完整性、参照完整性和用户定义的完整性;参见教材在参照完整性中,外部码属性的值可以为空,它表示该属性的值尚未确定;但前提条件是该外部码属性不是其所在关系的主属性;例如,在下面的“学生”表中,“专业号”是一个外部码,不是学生表的主属性,可以为空;其语义是,该学生的专业尚未确定;学生学号,姓名,性别,专业号,年龄专业专业号,专业名而在下面的“选修”表中的“课程号”虽然也是一个外部码属性,但它又是“选修”表的主属性,所以不能为空;因为关系模型必须满足实体完整性;课程课程号,课程名,学分选修学号,课程号,成绩5．等值连接与自然连接的区别是什么答：自然连接 Natural join是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且要在结果中把重复的属性去掉;第三章关系数据库标准语言 SQL 教材148页1. 试述SQL语言的特点;答：1综合统一; SQL语言集数据定义语言DDL、数据操纵语言DML、数据控制语言DCL的功能于一体;2高度非过程化;用SQL语言进行数据操作,只要提出“做什么”,而无须指明“怎么做”,因此无需了解存取路径,存取路径的选择以及SQL语句的操作过程由系统自动完成;3面向集合的操作方式;SQL语言采用集合操作方式,不仅操作对象、查找结果可以是元组的集合,而且一次插入、删除、更新操作的对象也可以是元组的集合;4以同一种语法结构提供两种使用方式;SQL语言既是自含式语言,又是嵌入式语言;作为自含式语言,它能够独立地用于联机交互的使用方式,也能够嵌入到高级语言程序中,供程序员设计程序时使用;5语言简捷,易学易用;2. 试述SQL的定义功能;答：SQL的数据定义功能包括定义表、定义视图和定义索引;SQL语言使用CREATE TABLE语句定义建立基本表,；ALTER TABLE语句修改基本表定义,DROP TABLE语句删除基本表；建立索引使用CREATE INDEX语句建立索引, DROP INDEX语句删除索引表；SQL语言使用CREATE VIEW命令建立视图,DROP VIEW语句删除视图;3. 用SQL语句建立第3章习题3中的四个表;答：对于 S表：S SNO,SNAME,STATUS,CITY；建 S表CREATE TABLE SSNO CHAR3,SNAME CHAR10,STATUS CHAR2,CITY CHAR10；PPNO,PNAME,COLOR,WEIGHT；建 P表、建J表、建SPJ表略;4. 针对上题中建立的四个表试用SQL语言完成第3章习题3中的查询;答：1 求供应工程J1零件的供应商号码SNO；SELECT SNOFROM SPJWHERE JNO=‘J1'；2 求供应工程J1零件P1的供应商号码SNO；SELECT SNOFROM SPJWHERE JNO=‘J1'AND PNO=‘P1'；3 求供应工程J1零件为红色的供应商号码SNO；SELECT SNOFROM SPJWHERE JNO=‘J1'AND PNO INSELECT PNOFROM PWHERE COLOR=‘红'；4 求没有使用天津供应商生产的红色零件的工程号JNO；略, 注意：从 J 表入手,以包含那些尚未使用任何零件的工程号;5. 针对习题3中的四个表试用SQL语言完成以下各项操作：1找出所有供应商的姓名和所在城市;2找出所有零件的名称、颜色、重量;3找出使用供应商S1所供应零件的工程号码;4找出工程项目J2使用的各种零件的名称及其数量;5找出上海厂商供应的所有零件号码;6找出使用上海产的零件的工程名称;7找出没有使用天津产的零件的工程号码;8把全部红色零件的颜色改成蓝色;9由S5供给J4的零件P6改为由S3供应,请作必要的修改;10从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录;11请将 S2,J6,P4,200 插入供应情况关系;答：1 找出所有供应商的姓名和所在城市;SELECT SNAME, CITYFROM S;2 找出所有零件的名称、颜色、重量;SELECT PNAME, COLOR, WEIGHTFROM P;3 找出使用供应商S1所供应零件的工程号码; SELECT JNOFROM SPJWHERE SNO=‘S1';4 找出工程项目J2使用的各种零件的名称及其数量; SELECT ,FROM P, SPJWHERE =AND ='J2';5 找出上海厂商供应的所有零件号码;SELECT DISTINCT PNOFROM SPJWHERE SNO INSELECT SNOFROM SWHERE CITY='上海';6 找出使用上海产的零件的工程名称;SELECT JNAMEFROM J, SPJ, SWHERE J. JNO=SPJ. JNOAND SPJ. SNO=AND ='上海';7 找出没有使用天津产的零件的工程号码;略8 把全部红色零件的颜色改成蓝色;UPDATE PSET COLOR='蓝'WHERE COLOR='红' ;9 由S5供给J4的零件P6改为由S3供应,请作必要的修改;UPDATE SPJSET SNO='S3'WHERE SNO='S5' AND JNO='J4' AND PNO='P6';10 从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录;解析：注意删除顺序,应该先从 SPJ表中删除供应商S2所供应零件的记录,然后从从S表中删除S2;11 请将 S2,J6,P4,200 插入供应情况关系;INSERT INTO SPJSNO, JNO, PNO, QTYVALUES S2,J6,P4,200;6. 什么是基本表什么是视图两者的区别和联系是什么答：基本表是本身独立存在的表,在 SQL中一个关系就对应一个表;视图是从一个或几个基本表导出的表;视图本身不独立存储在数据库中,是一个虚表;即数据库中只存放视图的定义而不存放视图对应的数据,这些数据仍存放在导出视图的基本表中;视图在概念上与基本表等同,用户可以如同基本表那样使用视图,可以在视图上再定义视图;7. 试述视图的优点;答： 1视图能够简化用户的操作;2视图使用户能以多种角度看待同一数据;3视图对重构数据库提供了一定程度的逻辑独立性;4视图能够对机密数据提供安全保护;8. 所有的视图是否都可以更新为什么答：不是;视图是不实际存储数据的虚表,因此对视图的更新,最终要转换为对基本表的更新;因为有些视图的更新不能唯一地有意义地转换成对相应基本表的更新,所以,并不是所有的视图都是可更新的;9. 哪类视图是可以更新的,哪类视图是不可更新的各举一例说明;答：基本表的行列子集视图一般是可更新的;如教材中的例1;若视图的属性来自集函数、表达式,则该视图肯定是不可以更新的;如教材中的S_G视图;11. 请为三建工程项目建立一个供应情况的视图,包括供应商代码SNO、零件代码 PNO、供应数量QTY;针对该视图完成下列查询：1找出三建工程项目使用的各种零件代码及其数量;2找出供应商S1的供应情况;答：建视图：CREATE VIEW V_SPJ ASSELECT SNO, PNO, QTYFROM SPJWHERE JNO=SELECT JNOFROM JWHERE JNAME='三建';对该视图查询：1 找出三建工程项目使用的各种零件代码及其数量; SELECT PNO, QTYFROM V_SPJ;2 找出供应商S1的供应情况;SELECT PNO, QTY / S1供应三建工程的零件号和对应的数量/ FROM V_SPJWHERE SNO='S1';第五章关系数据理论教材 196页1．理解并给出下列术语的定义：函数依赖、部分函数依赖、完全函数依赖、候选码、主码、外码、全码;答：函数依赖：设 R U是一个关系模式,U是R的属性集合,X和Y是U的子集;对于R U的任意一个可能的关系r,如果r中不存在两个元组,它们在X上的属性值相同, 而在Y上的属性值不同, 则称"X函数确定Y"或"Y函数依赖于X",记作X→Y;完全函数依赖、部分函数依赖：在 RU中,如果X→Y,并且对于X的任何一个真子集X,都有X′→Y,则称Y对X完全函数依赖;若X→Y,但Y不完全函数依赖于X,则称Y对X部分函数依赖;候选码、主码：设 K为RU,F中的属性或属性组合,若K → U则K为R的候选码;若候选码多于一个,则选定其中的一个为主码;外码：关系模式 R中属性或属性组X并非R的码,但X是另一个关系模式的码,则称X是R的外部码也称外码;全码：整个属性组是码,称为全码 All-key;2．建立一个关于系、学生、班级、学会等诸信息的关系数据库;描述学生的属性有：学号、姓名、出生年月、系名、班号、宿舍区;描述班级的属性有：班号、专业名、系名、人数、入校年份;描述系的属性有：系名、系号、系办公室地点、人数;描述学会的属性有：学会名、成立年份、地点、人数;有关语义如下：一个系有若干专业,每个专业每年只招一个班,每个班有若干学生;一个系的学生住在同一宿舍区;每个学生可参加若干学会,每个学会有若干学生;学生参加某学会有一个入会年份;请给出关系模式,写出每个关系模式的极小函数依赖集,指出是否存在传递函数依赖,对于函数依赖左部是多属性的情况讨论函数依赖是完全函数依赖,还是部分函数依赖;指出各关系的候选码、外部码,有没有全码存在答：关系模式：学生 SS,SN,SB,DN,C,SA班级 CC,CS,DN,CNUM,CDATE系 DD,DN,DA,DNUM学会 PPN,DATE1,PA,PNUM学生 --学会SPS,PN,DATE2其中, S—学号,SN—姓名,SB—出生年月,SA—宿舍区C—班号,CS—专业名,CNUM—班级人数,CDATE—入校年份D—系号,DN—系名,DA—系办公室地点,DNUM—系人数PN—学会名,DATE1—成立年月,PA—地点,PNUM—学会人数,DATE2—入会年份每个关系模式的极小函数依赖集：S：S→SN,S→SB,S→C,C→DN,DN→SAC：C→CS,C→CNUM,C→CDATE,CS→DN,CS,CDATE→CD：D→DN,DN→D,D→DA,D→DNUMP：PN→DATE1,PN→PA,PN→PNUMSP：S,PN→DATE2S中存在传递函数依赖： S→DN, S→SA, C→SAC中存在传递函数依赖：C→DNS,PN→DATE2 和CS,CDATE→C 均为SP中的函数依赖,是完全函数依赖关系候选码外部码全码S S C,DN 无C C,CS,CDATE DN 无D D和DN 无无P PN 无无SP S,PN S,PN 无4. 试举出三个多值依赖的实例;答：1关系模式MSCM,S,C中,M表示专业,S表示学生,C表示该专业的必修课;假设每个专业有多个学生,有一组必修课;设同专业内所有学生的选修的必修课相同,实例关系如下;按照语义对于M的每一个值M i,S有一个完整的集合与之对应而不问C取何值,所以M→→S;由于C与S的完全对称性,必然有M→→C成立;M S CM 1 S1 C1M 1 S1 C2M 1 S2 C1M 1 S2 C2………………2关系模式ISAI,S,A中,I表示学生兴趣小组,S表示学生,A表示某兴趣小组的活动项目;假设每个兴趣小组有多个学生,有若干活动项目;每个学生必须参加所在兴趣小组的所有活动项目,每个活动项目要求该兴趣小组的所有学生参加;按照语义有 I→→S,I→→A成立;3关系模式RDPR,D,P中,R表示医院的病房,D表示责任医务人员,P表示病人;假设每个病房住有多个病人,有多个责任医务人员负责医治和护理该病房的所有病人;按照语义有R→→D,R→→P成立;第六章数据库设计教材241页1. 试述数据库设计过程;1 需求分析2 概念结构设计3 逻辑结构设计4 数据库物理设计5 数据库实施6 数据库运行和维护这是一个完整的实际数据库及其应用系统的设计过程;不仅包括设计数据库本身,还包括数据库的实施、数据库运行和维护;设计一个完善的数据库应用系统往往是上述六个阶段的不断反复;2. 试述数据库设计过程的各个阶段上的设计描述;答：各阶段的设计要点如下：1 需求分析：准确了解与分析用户需求包括数据与处理;2 概念结构设计：通过对用户需求进行综合、归纳与抽象,形成一个独立于具体DBMS的概念模型;3 逻辑结构设计：将概念结构转换为某个DBMS所支持的数据模型,并对其进行优化;4 数据库物理设计：为逻辑数据模型选取一个最适合应用环境的物理结构包括存储结构和存取方法;5 数据库实施：设计人员运用DBMS提供的数据语言、工具及宿主语言,根据逻辑设计和物理设计的结果建立数据库,编制与调试应用程序,组织数据入库,并进行试运行;6 数据库运行和维护：在数据库系统运行过程中对其进行评价、调整与修改;3. 试述数据库设计过程中结构设计部分形成的数据库模式;答：数据库结构设计的不同阶段形成数据库的各级模式,即：在概念设计阶段形成独立于机器特点,独立于各个 DBMS产品的概念模式,在本篇中就是E-R图；在逻辑设计阶段将 E-R图转换成具体的数据库产品支持的数据模型,如关系模型,形成数据库逻辑模式；然后在基本表的基础上再建立必要的视图View,形成数据的外模式；在物理设计阶段,根据 DBMS特点和处理的需要,进行物理存储安排,建立索引,形成数据库内模式;概念模式是面向用户和设计人员的,属于概念模型的层次；逻辑模式、外模式、内模式是 DBMS支持的模式,属于数据模型的层次;可以在DBMS中加以描述和存储;4. 试述数据库设计的特点;答：数据库设计既是一项涉及多学科的综合性技术又是一项庞大的工程项目;其主要特点有：1 数据库建设是硬件、软件和干件技术与管理的界面的结合;2 从软件设计的技术角度看,数据库设计应该和应用系统设计相结合,也就是说,整个设计过程中要把结构数据设计和行为处理设计密切结合起来;5. 需求分析阶段的设计目标是什么调查的内容是什么答：需求分析阶段的设计目标是通过详细调查现实世界要处理的对象组织、部门、企业等,充分了解原系统手工系统或计算机系统工作概况,明确用户的各种需求,然后在此基础上确定新系统的功能;调查的内容是“数据”和“处理”,即获得用户对数据库的如下要求：1信息要求;指用户需要从数据库中获得信息的内容与性质;由信息要求可以导出数据要求,即在数据库中需要存储哪些数据;2处理要求;指用户要完成什么处理功能,对处理的响应时间有什么要求,处理方式是批处理还是联机处理;3安全性与完整性要求;6. 数据字典的内容和作用是什么答：数据字典是系统中各类数据描述的集合;数据字典的内容通常包括：数据项、数据结构、数据流、数据存储、处理过程五个部分其中数据项是数据的最小组成单位,若干个数据项可以组成一个数据结构;数据字典通过对数据项和数据结构的定义来描述数据流、数据存储的逻辑内容;数据字典的作用：数据字典是关于数据库中数据的描述,在需求分析阶段建立,是下一步进行概念设计的基础,并在数据库设计过程中不断修改、充实、完善;注意,数据库设计阶段形成的数据字典与后面讲到的数据字典不同,后者是 DBMS关于数据库中数据的描述,当然两者是有联系的;7. 什么是数据库的概念结构试述其特点和设计策略;答：概念结构是信息世界的结构,即概念模型,其主要特点是：1能真实、充分地反映现实世界,包括事物和事物之间的联系,能满足用户对数据的处理要求;是对现实世界的一个真实模型;2易于理解,从而可以用它和不熟悉计算机的用户交换意见,用户的积极参与是数据库的设计成功的关键;。

北京理工大学智慧树知到“计算机科学与技术”《数据库系统应用》网课测试题答案卷5

北京理工大学智慧树知到“计算机科学与技术”《数据库系统应用》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共10题)1.关系数据模型是用关系表示()。

A.实体B.联系C.属性D.实体和联系2.SQL语言是()。

A.高级语言B.宿主语言C.汇编语言D.非过程化语言3.数据库体系结构按照()三级结构进行组织。

A.模式B.外模式C.内模式D.实际模式4.关系模式R若属于BCNF，则R不存在()。

A.主属性对非主属性的部分依赖B.任何属性间的传递依赖C.非主属性对主属性的传递依赖D.主属性对主属性的完全依赖5.嵌入式SQL中，游标的主要作用是()。

A.建立主语言与DBMS间的联系B.与主语言进行通信C.协调SQL与主语言间的不同处理方式D.SQL与主语言间交换数据6.1NF规范化为2NF，消除了()。

A.非主属性对码的部分函数依赖B.非主属性对码的传递函数依赖C.主属性对码的部分函数依赖D.主属性对码的传递函数依赖7.在E-R图中为了表示多对多的联系需要增加一个实体型。

()A.错误B.正确8.关于各种数据库系统，说法正确的是()。

A.关系数据库系统支持复合数据类型B.面向对象数据库系统与程序设计语言集成一体化C.对象-关系数据库系统查询语言功能强大D.对象-关系数据库系统高保护性9.数据库系统包括数据库和()。

A.软件B.相应硬件C.数据库管理系统D.相关的各类人员10.一个数据库应用系统的好坏，很大程度上取决于数据库设计的好坏。

()A.错误B.正确第1卷参考答案一.综合考核1.参考答案：D2.参考答案：D3.参考答案：ABC4.参考答案：B5.参考答案：C6.参考答案：A7.参考答案：A8.参考答案：BCD9.参考答案：ABCD10.参考答案：B。

数据库系统概论第五版课后习题答案 (3)之欧阳学文创编之欧阳索引创编

第二章关系数据库欧阳家百（2021.03.07）1 ．试述关系模型的三个组成部分。

答：关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。

2 ．试述关系数据语言的特点和分类。

答：关系数据语言可以分为三类：关系代数语言。

关系演算语言：元组关系演算语言和域关系演算语言。

SQL：具有关系代数和关系演算双重特点的语言。

这些关系数据语言的共同特点是，语言具有完备的表达能力，是非过程化的集合操作语言，功能强，能够嵌入高级语言中使用。

3 （略）4 ．5 . 述关系模型的完整性规则。

即属性F本身不是主属性，则可以取空值，否则不能取空值。

6．设有一个SPJ数据库，包括S，P，J，SPJ四个关系模式：1）求供应工程J1零件的供应商号码SNO：πSno(σJno=‘J1’（SPJ）)2）求供应工程J1零件P1的供应商号码SNO：πSno(σJno=‘J1’∧Pno=‘P1‘(SPJ))3）求供应工程J1零件为红色的供应商号码SNO：πSno(πSno,,Pno（σJno=‘J1‘(SPJ))∞πPno（σCOLOR=’红‘ （P）)) 4）求没有使用天津供应商生产的红色零件的工程号JNO：πJno(SPJ)- πJNO（σcity=‘天津’∧Color=‘红‘（S∞SPJ∞P）5）求至少用了供应商S1所供应的全部零件的工程号JNO：πJno，Pno(SPJ)÷πPno（σSno=‘S1‘（SPJ））7. 试述等值连接与自然连接的区别和联系。

答：连接运算符是“=”的连接运算称为等值连接。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章一单项选择题试题1 满分值：2.0分状态：已答实际得分：分试题:下述SQL语言中的权限，哪一个允许用户定义新关系时，引用其他关系的主码作为外码（）。

INSERTDELETEREFERENCESSELECT[参考答案] REFERENCES[我的答案] REFERENCES试题2 满分值：2.0分状态：已答实际得分：分试题:在表或视图上执行除了（）以外的语句都可以激活触发器。

InsertDeleteUpdateSelect[参考答案] Select[我的答案] Update试题3 满分值：2.0分状态：已答实际得分：分试题:数据库的（）是指数据的正确性和相容性。

安全性完整性并发控制恢复[参考答案] 完整性[我的答案] 完整性试题4 满分值：2.0分状态：已答实际得分：分试题:在数据库的表定义中，限制成绩属性列的取值在0到100的范围内，属于数据的（）约束。

实体完整性参照完整性用户自定义用户操作[参考答案] 用户自定义[我的答案] 用户自定义试题5 满分值：2.0分状态：已答实际得分：分试题:在关系数据库中，正确描述主键的是：（）为标识表中唯一的实体创建唯一的索引，允许空值只能是表中的第一列允许有多个主键[参考答案] 为标识表中唯一的实体[我的答案] 允许有多个主键试题6 满分值：2.0分状态：已答实际得分：分试题:在SQL Server 2005中，建立一个Student表，表中包含一个SSex列，为了保证SSex列中输入值只能是 'M' 或'F'，使用下列哪一种方法最简单：（）对Student表添加一个DEFAULT约束对SSex 列添加一个CHECK约束创建一个存储过程验证SSex列中的数据对SSex列添加一个触发器在提交后验证数据[参考答案] 对SSex 列添加一个CHECK约束[我的答案] 对SSex 列添加一个CHECK约束试题7 满分值：2.0分状态：已答实际得分：分试题:在SQL语言中PRIMARY KEY 的作用是（）定义外部码定义处部码的参照表定义主码确定主码类型[参考答案] 定义主码[我的答案] 定义主码试题8 满分值：2.0分状态：已答实际得分：分试题:在Microsoft SQL Server 2000中使用SQL语言来定义基本表时，下列那个关键词是用来定义唯一键的（）UNIQUEForeign KeyDefaultCheck[参考答案] UNIQUE[我的答案] UNIQUE试题9 满分值：2.0分状态：已答实际得分：分试题:关于主键约束以下说法错误的是（）一个表中只能设置一个主键约束允许空值的字段上不能定义主键约束允许空值的字段上可以定义主键约束可以将包含多个字段的字段组合设置为主键[参考答案] 允许空值的字段上可以定义主键约束[我的答案] 允许空值的字段上可以定义主键约束试题10 满分值：2.0分状态：已答实际得分：分试题:在数据库系统中，保证数据及语义正确和有效的功能是（）并发控制存取控制安全控制完整性控制[参考答案] 完整性控制[我的答案] 完整性控制二填空题试题1 满分值：2.0分状态：已答实际得分：分试题:数据库的数据完整性是指（①）和（②）[参考答案] 正确性相容性[我的答案] 正确性相容性试题2 满分值：3.0分状态：已答实际得分：分试题:关系数据库的完整性可以分为：① . ② 和③ 。

[参考答案] 实体完整性参照完整性用户定义完整性[我的答案] 实体完整性参照完整性用户自定义完整性试题3 满分值：1.0分状态：已答实际得分：分试题:实体完整性是指在基本表中，（）。

[参考答案] 主属性不能取空值，主键值不能重复[我的答案] 对主码方面的操作。

试题4 满分值：1.0分状态：已答实际得分：分试题:参照完整性是指在基本表中，（）。

[参考答案] 外码可以是空值或者另一个关系主码的有效值[我的答案] 参照表和被参照表之间的操作。

试题5 满分值：1.0分状态：已答实际得分：分试题:为了保护数据库的实体完整性，当用户程序对主码进行更新使主码值不惟一时，DBMS就（）。

[参考答案] 拒绝此操作[我的答案] 拒决更新试题6 满分值：2.0分状态：已答实际得分：分试题:在SQL Server 2005中，定义列的默认值使用的关键字是（① ），删除约束使用的关键字是（②）[参考答案] default Drop Constraint[我的答案] create drop三问答题试题1 满分值：10.0分状态：已答实际得分：分试题:数据库的完整性概念与数据库的安全性概念有什么区别和联系。

[参考答案] 数据的完整性和安全性是两个不同的概念,但是有一定的联系. 前者是为了防止数据库中存在不符合语义的数据,防止错误信息的输入和输出,即所谓垃圾进垃圾出(Garbage In Garbage Out)所造成的无效操作和错误结果. 后者是保护数据库防止恶意的破坏和非法的存取. 也就是说,安全性措施的防范对象是非法用户和非法操作,完整性措施的防范对象是不合语义的数据。

[我的答案] 数据的完整性事为了防止数据库中存在不符合语义的数据，也就是防止数据库中存在不正确的数据。

数据的安全性是保护数据库防止恶意的破坏和非法的存取。

因此，完整性检查和控制的防范对象是不符合语义的，不正确的数据，防止它们进入数据库。

安全性控制的防范对象是非法用户和非法操作，防止他们对数据库数据的非法存取。

试题2 满分值：15.0分状态：已答实际得分：分试题:在关系模型中，数据完整性约束有哪几种？简述在RDBMS中这些完整性约束是怎样实现的。

[参考答案] (1).实体完整性实体完整性要求表中的每一行必须是惟一的，它可以通过主键约束、惟一键约束、索引或标识属性来实现。

(2).参照完整性参照完整性要求有关联的两个或两个以上表之间数据的一致。

参照完整性可以通过建立主键和外键来实现。

参照完整性定义了一个关系数据库中，不同的表中列之间的关系（父键与外键）。

要求一个表中（子表）的一列或一组列的值必须与另一个表（父表）中的相关一列或一组列的值相匹配。

被引用的列或一组列称为父键，父键必须是主键或惟一键，通常父键为主键，主键表是主表。

(3).用户定义的完整性用户可以根据自己的业务规则定义不属于任何完整性分类的完整性。

由于每个用户的数据库都有自己独特的业务规则，所以系统必须有一种方式来实现定制的业务规则，即定制的数据完整性约束。

用户定义的完整性可以通过自定义数据类型、规则、Check约束、存储过程和触发器来实现。

[我的答案] 参照完整性实体完整性用户自定义完整性试题3 满分值：10.0分状态：已答实际得分：分试题:DBMS的完整性控制机制应具有哪些功能？[参考答案] DBMS的完整性控制机制应具有三个方面的功能: 1). 定义功能,即提供定义完整性约束条件的机制. 2. 检查功能,即检查用户发出的操作请求是否违背了完整性约束条件. 3). 违约反应:如果发现用户的操作请求使数据违背了完整性约束条件,则采取一定的动作来保证数据的完整性。

试题:RDBMS在实现参照完整性时需要考虑哪些方面？[参考答案] RDBMS在实现参照完整性时需要考虑以下几个方面: 1) 外码是否可以接受空值 2) 删除被参照关系的元组时的考虑,这时系统可能采取的作法有三种: (a)级联删除(CASCADES); (b)受限删除(RESTRICTED); (c)置空值删除(NULLIFIES) 3) 在参照关系中插入元组时的问题,这时系统可能采取的作法有: (a)受限插入 (b)递归插入 4) 修改关系中主码的问题一般是不能用UPDATE语句修改关系主码的.如果需要修改主码值,只能先删除该元组,然后再把具有新主码值的元组插入到关系中. 如果允许修改主码,首先要保证主码的唯一性和非空,否则拒绝修改.然后要区分是参照关系还是被参照关系。

试题:职工(职工号,姓名,年龄,职务,工资,部门号),其中职工号为主码; 部门(部门号,名称,经理名,电话),其中部门号为主码; 用SQL语言定义这两个关系模式,要求在模式中完成以下完整性约束条件的定义: 定义每个模式的主码;定义参照完整性;定义职工年龄不得超过60岁。

[参考答案] CREATE TABLE DEPT (Deptno NUMBER(2), Deptname VARCHAR(10), Manager VARCHAR(10), PhoneNumber Char(12) CONSTRAINT PK_SC PRIMARY KEY (Deptno)); CREATE TABLE EMP (Empno NUMBER(4), Ename VARCHAR(10), Age NUMBER(2), CONSTRAINT C1 CHECK (Age《=60), Job VARCHAR(9), Sal NUMBER(7,2), Deptno NUMBER(2), CONSTRAINT FK_DEPTNO FOREIGN KEY (Deptno) REFERENCES DEPT(Deptno));[我的答案] create table 职工( 职工号 varchar(20), 姓名 varchar(20), 年龄 int check(年龄 between 1 and 60), 职务 varchar(15), 工资 int, 部门号 varchar(15), primary key(职工号), foreign key(部门号) references 部门(部门号) ) create table 部门( 部门号 varchar(15), 名称 varchar(20), 经理名 varchar(20), 电话 varchar(20), primary key(部门号) )试题:关系系统中,当操作违反实体完整性,参照完整性和用户定义的完整性约束条件时,一般是如何分别进行处理的？[参考答案] 对于违反实体完整性和用户定义的完整性的操作一般都采用拒绝执行的方式进行处理.而对于违反参照完整性的操作,并不都是简单地拒绝执行,有时要根据应用语义执行一些附加的操作,以保证数据库的正确性。

北理珠数据库系统概论习题 第五章

《数据库系统概论》练习题(答案)

数据库系统概论第五版课后习题答案王珊

数据库系统原理04735课后习题参考答案

数据库系统概论第五版课后习题答案王珊

数据库系统概论第五版课后习题答案王珊版之欧阳歌谷创编

数据库系统概论第五版课后的习题答案王珊版.doc

数据库系统基础教程课后答案第五章

最新数据库系统概论第5版(王珊、萨师煊)课后答案第5章-数据库完整性

数据库系统概论第五版课后的习题答案.doc

04735数据库系统原理(2018年版)课后习题参考答案与解析

数据库系统概论第五版试题及答案

2022年北京理工大学珠海学院计算机科学与技术专业《数据库原理》科目期末试卷B(有答案)

《数据库系统概论》第四版课后习题答案

数据库系统基础教程第五章答案

数据库系统概论课后习题及参考答案

北京理工大学智慧树知到“计算机科学与技术”《数据库系统应用》网课测试题答案卷5

数据库系统概论第五版课后习题答案 (3)之欧阳学文创编之欧阳索引创编

北理珠数据库系统概论习题第五章