MATLAB在LTI连续系统响应分析中的应用
MATLAB与信号实验 —— 连续LTI系统的频域分析

上机实验3 连续LTI 系统的频域分析一.实验目的(1).掌握连续时间信号傅立叶变换和傅立叶逆变换的实现方法,以及傅立叶变换的时移特性,傅立叶变换的频移特性的实现方法;(2).了解傅立叶变换的频移特性及其应用;(3).掌握函数fourier 和函数ifourier 的调用格式及作用;(4).掌握傅立叶变换的数值计算方法,以及绘制信号频谱图的方法。
二.实验原理1.系统的频率特性连续LTI 系统的频率特性又称频率响应特性,是指系统在正弦信号激励下的稳态响应随频率变化的情况,又称系统函数()ωH 。
对于一个零状态的线性系统,如图2.3-1所示。
其系统函数()ωH 定义为)()()(ωωωj X j Y j H =式中,()ωX 为系统激励信号的傅里叶变换,()ωY 为系统在零状态条件下输出响应的傅里叶变换。
系统函数()ωH 反映了系统内在的固有特性,它取决于系统自身的结构及组成系统元器件的参数,与外部激励无关,是描述系统特性的一个重要参数。
()ωH 是ω的复函数,可以表示为()ωH =()ωH ()e j ωϕ。
其中,()ωH 随ω变化的规律称为系统的幅频特性:()ωϕ随ω变化的规律称为系统的相频特性。
频率特性不仅可用函数表达式表示,还可以随频率f 变化的曲线来表示。
当频率特性曲线采用对数坐标时,又称为波特图。
)(ωj X )(ωj2.连续时间信号傅里叶变换的数值计算方法算法理论依据:()ττωτωω∑⎰∞∞---∞+∞-==e e n j t j n f dt t f j F )(lim )((2.2-1)当)(t f 为时限信号时,或和近似的看做时限信号时,式(2-1)中的n 取值可认作是有限的,设为N ,则可得()()e n j N n kn f k F τωττ--=∑=10,0<=k<=N (2.2-2) 式(2.2-2)中k N k τπω2=。
编程中需要注意的是:要正确生成信号)(t f 的N 个样本)(τn f 的向量及向量e n j kτω-。
LTI线性系统 MATLAB 应用

实验二 LTI 系统的响应一、实验目的1. 熟悉连续时间系统的单位冲激响应、阶跃响应的意义及求解方法2. 熟悉连续(离散)时间系统在任意信号激励下响应的求解方法3. 熟悉应用MATLAB 实现求解系统响应的方法 二、实验原理 1.连续时间系统对于连续的LTI 系统,当系统输入为f(t),输出为y(t),则输入与输出之间满足如下的线性常系数微分方程:()()00()()nmi j ij i j a yt b f t ===∑∑,当系统输入为单位冲激信号δ(t)时产生的零状态响应称为系统的单位冲激响应,用h(t)表示。
若输入为单位阶跃信号ε(t)时,系统产生的零状态响应则称为系统的单位阶跃响应,记为g(t),如下图所示。
系统的单位冲激响应h(t)包含了系统的固有特性,它是由系统本身的结构及参数所决定的,与系统的输入无关。
我们只要知道了系统的冲激响应,即可求得系统在不同激励下产生的响应。
因此,求解系统的冲激响应h(t)对我们进行连续系统的分析具有非常重要的意义。
在MATLAB 中有专门用于求解连续系统冲激响应和阶跃响应, 并绘制其时域波形的函数impulse( ) 和step( )。
如果系统输入为f(t),冲激响应为h(t),系统的零状态响应为y(t),则有:()()()y t h t f t =*。
若已知系统的输入信号及初始状态,我们便可以用微分方程的经典时域求解方法,求出系统的响应。
但是对于高阶系统,手工计算这一问题的过程非常困难和繁琐。
在MATLAB 中,应用lsim( )函数很容易就能对上述微分方程所描述的系统的响应进行仿真,求出系统在任意激励信号作用下的响应。
lsim( )函数不仅能够求出连续系统在指定的任意时间范围内系统响应的数值解,而且还能同时绘制出系统响应的时域波形图。
以上各函数的调用格式如下: ⑴ impulse( ) 函数 函数impulse( )将绘制出由向量a 和b 所表示的连续系统在指定时间范围内的单位冲激响应h(t)的时域波形图,并能求出指定时间范围内冲激响应的数值解impulse(b,a) 以默认方式绘出由向量a 和b 所定义的连 统的冲激响应的时域波形。
MATLAB与信号实验——连续LTI系统的时域分析

MATLAB与信号实验——连续LTI系统的时域分析连续LTI系统的时域分析是信号与系统学中的重要课题。
MATLAB作为一种强大的科学计算软件,提供了丰富的工具和函数来进行信号与系统的分析。
下面将介绍MATLAB在连续LTI系统时域分析中的应用。
首先,我们需要了解连续LTI系统的基本概念。
一个连续域线性时不变系统(LTI系统)可以由它的冲激响应完全描述。
冲激响应是系统对单位冲激信号的响应。
在MATLAB中,可以使用impulse函数来生成单位冲激信号。
假设我们有一个连续LTI系统的冲激响应h(t),我们可以使用conv 函数来计算系统对任意输入信号x(t)的响应y(t)。
conv函数实现了卷积运算,可以将输入信号与冲激响应进行卷积运算得到输出信号。
例如,我们假设一个连续LTI系统的冲激响应为h(t) = exp(-t)u(t),其中u(t)是单位阶跃函数。
我们可以使用以下代码生成输入信号x(t)和计算输出信号y(t):```matlabt=-10:0.1:10;%时间范围x = sin(t); % 输入信号h = exp(-t).*heaviside(t); % 冲激响应y = conv(x, h, 'same'); % 计算输出信号```这段代码首先定义了时间范围t,然后定义了输入信号x(t)和冲激响应h(t)。
接下来,使用conv函数计算输入信号和冲激响应的卷积,设置参数’same’表示输出信号与输入信号长度相同。
最后,得到了输出信号y(t)。
在得到输出信号后,我们可以使用MATLAB的绘图功能来可视化结果。
例如,使用以下代码可以绘制输入信号和输出信号的图像:```matlabfigure;plot(t, x, 'b', 'LineWidth', 2); % 绘制输入信号hold on;plot(t, y, 'r', 'LineWidth', 2); % 绘制输出信号xlabel('时间');ylabel('幅度');legend('输入信号', '输出信号');```除了卷积运算外,MATLAB还提供了许多其他函数来进行连续LTI系统的时域分析。
在MATLAB软件下进行LTI连续系统的分析仿真

前言人们之间的交流是通过消息的传播来实现的,信号则是消息的表现形式,消息是信号的具体内容。
《信号与系统》课程是一门实用性较强、涉及面较广的专业基础课,该课程是将学生从电路分析的知识领域引入信号处理与传输领域的关键性课程,对后续专业课起着承上启下的作用. 该课的基本方法和理论大量应用于计算机信息处理的各个领域,特别是通信、数字语音处理、数字图像处理、数字信号分析等领域,应用更为广泛。
近年来,计算机多媒体教序手段的运用逐步普及,大量优秀的科学计算和系统仿真软件不断涌现,为我们实现计算机辅助教学和学生上机实验提供了很好的平台。
通过对这些软件的分析和对比,我们选择MATLAB语言作为辅助教学工具,借助MATLAB强大的计算能力和图形表现能力,将《信号与系统》中的概念、方法和相应的结果,以图形的形式直观地展现给我们,大大的方便我们迅速掌握和理解老师上课教的有关信号与系统的知识。
MATLAB 是MathWork 公司于1984 年推出的一套面向工程和科学运算的高性能软件。
它具有强大的矩阵计算能力和良好的图形可视化功能,为用户提供了非常直观和简洁的程序开发环境,因此被称为第四代计算机语言。
MATLAB 强大的图形处理功能及符号运算功能,为我们实现信号的可视化及系统分析提供了强有力的工具。
MATLAB 强大的工具箱函数可以分析连续信号、连续系统,同样也可以分析离散信号、离散系统,并可以对信号进行各种分析域计算,如相加、相乘、移位、反折、傅里叶变换、拉氏变换、Z 变换等等多种计算。
此次课程设计是在MATLAB软件下进行LTI连续系统的分析仿真,有助于我对该连续信号的分析和理解。
MATLAB 强大的功能为此次求连续信号冲激阶跃响应、系统零输入、零状态响应,及幅频相频等各种信号求解提供很好的视觉效果,对我们有很大的学习帮助。
工程概况此次的信号与系统课程设计的任务是在MATLAB软件下进行LTI连续系统的分析仿真。
技术内容是:根据时域分析原理,利用MATLAB软件求解系统零状态响应,冲激响应。
连续时间LTI系统的频率特性及频域分析

实验报告实验项目名称:运用Matlab进行连续时间信号卷积运算(所属课程:信号与系统)学院:电子信息与电气工程学院专业: 10电气工程及其自动化姓名: xx学号: ************指导老师: xxx一、实验目的1、学会运用MATLAB 分析连续系统的频率特性。
2、掌握相关函数的调用。
二、实验原理1、一个连续LTI 系统的数学模型通常用常系数线性微分方程描述,即)()()()()()(01)(01)(t e b t e b t e b t r a t r a t r a m m n n +'++=+'++ (1) 对上式两边取傅里叶变换,并根据FT 的时域微分性质可得:)(])([)(])([0101ωωωωωωE b j b j b R a j a j a m m n n +++=+++101)()()()()(a j a j a b j b j b j E j R j H n n m m ++++++==ωωωωωωω H ( jω )称为系统的频率响应特性,简称系统频率响应或频率特性。
一般H ( jω )是复函数,可表示为:)()()(ωϕωωj e j H j H =其中, )(ωj H 称为系统的幅频响应特性,简称为幅频响应或幅频特性;)(ωϕ称为系统的相频响应特性,简称相频响应或相频特性。
H ( jω )描述了系统响应的傅里叶变换与激励的傅里叶变换间的关系。
H ( jω )只与系统本身的特性有关,与激励无关,因此它是表征系统特性的一个重要参数。
MATLAB 信号处理工具箱提供的freqs 函数可直接计算系统的频率响应的数值解,其语句格式为:H=freqs(b,a,w)其中,b 和a 表示H ( jω )的分子和分母多项式的系数向量;w 为系统频率响应的频率范围,其一般形式为w1:p:w2,w1 为频率起始值,w2 为频率终止值,p 为频率取值间隔。
H 返回w 所定义的频率点上系统频率响应的样值。
MATLAB与信号实验——连续LTI系统的时域分析

MATLAB与信号实验-——-连续LTI系统的时域分析在信号处理中,MATLAB是一个强大的工具,它提供了许多功能,使我们能够模拟和分析各种信号系统。
对于连续LTI系统,时域分析是一个重要的方法,它允许我们直接观察系统的输入和输出信号之间的关系。
下面是一个关于连续LTI系统的时域分析的实验。
一、实验目的本实验的目的是验证连续LTI系统的时域响应,通过使用MATLAB模拟系统,我们可以观察到不同的输入信号产生的输出信号,从而了解系统的特性。
二、实验步骤1.定义系统:首先,我们需要定义我们的连续LTI系统。
这可以通过使用MATLAB中的lti函数来完成。
我们需要提供系统的传递函数,它描述了系统的输入和输出之间的关系。
2.设置输入信号:为了观察系统的行为,我们需要设置一个合适的输入信号。
在MATLAB中,我们可以使用square函数来生成一个方波信号,该信号具有固定的频率和幅度。
3.模拟系统:使用MATLAB的lsim函数,我们可以模拟我们的连续LTI系统。
这个函数将输入信号和系统的传递函数作为参数,然后计算出系统的输出信号。
4.分析结果:我们可以使用MATLAB的图形功能来观察输入和输出信号。
这可以帮助我们理解系统的行为,并验证我们的模型是否正确。
三、实验结果与分析在实验中,我们使用了不同的输入信号(如方波、正弦波等)来测试我们的连续LTI系统。
对于每种输入信号,我们都观察了系统的输出信号,并记录了结果。
通过对比不同的输入和输出信号,我们可以得出以下结论:1.对于方波输入,系统的输出信号是带有延迟的方波,这表明系统对突变信号的响应是瞬时的。
2.对于正弦波输入,系统的输出信号是与输入信号同频同相位的正弦波,这表明系统对正弦波的响应是具有稳定性的。
这些结果验证了连续LTI系统的基本特性:即对于单位阶跃函数(突变信号)的输入,系统的响应是瞬时的;而对于周期性输入(如正弦波),系统的响应具有稳定性。
这些结果与我们在理论上学到的知识相符,从而验证了我们的模型是正确的。
实验三连续时间LTI系统的时域分析报告

实验三 连续时间LTI 系统的时域分析一、实验目的1.学会用MATLAB 求解连续系统的零状态响应; 2. 学会用MATLAB 求解冲激响应及阶跃响应; 3.学会用MATLAB 实现连续信号卷积的方法;二、实验原理1.连续时间系统零状态响应的数值计算我们知道,LTI 连续系统可用如下所示的线性常系数微分方程来描述,()()0()()NMi j i j i j a yt b f t ===∑∑在MATLAB 中,控制系统工具箱提供了一个用于求解零初始条件微分方程数值解的函数lsim 。
其调用格式y=lsim(sys,f,t)式中,t 表示计算系统响应的抽样点向量,f 是系统输入信号向量,sys 是LTI 系统模型,用来表示微分方程,差分方程或状态方程。
其调用格式sys=tf(b,a)式中,b 和a 分别是微分方程的右端和左端系数向量。
例如,对于以下方程:''''''''''''32103210()()()()()()()()a y t a y t a y t a y t b f t b f t b f t b f t +++=+++可用32103210[,,,];[,,,];a a a a a b b b b b == (,)sys tf b a = 获得其LTI 模型。
注意,如果微分方程的左端或右端表达式中有缺项,则其向量a 或b 中的对应元素应为零,不能省略不写,否则出错。
例3-1 已知某LTI 系统的微分方程为 y’’(t)+ 2y’(t)+100y(t)=f(t)其中,'(0)(0)0,()10sin(2)y y f t t π===,求系统的输出y(t). 解:显然,这是一个求系统零状态响应的问题。
其MATLAB 计算程序如下: ts=0;te=5;dt=0.01; sys=tf([1],[1,2,100]); t=ts:dt:te; f=10*sin(2*pi*t); y=lsim(sys,f,t); plot(t,y);xlabel('Time(sec)'); ylabel('y(t)');2.连续时间系统冲激响应和阶跃响应的求解在MATLAB 中,对于连续LTI 系统的冲激响应和阶跃响应,可分别用控制系统工具箱提供的函数impluse 和step 来求解。
信号与系统matlab实验3连续时间LTI分析报告

实验三连续时间LTI系统分析姓名学号班级通信一班一、实验目的(一)掌握使用Matlab进行连续系统时域分析的方法1、学会使用符号法求解连续系统的零输入响应和零状态响应2、学会使用数值法求解连续系统的零状态响应3、学会求解连续系统的冲激响应和阶跃响应(二)掌握使用Matlab进行连续时间LTI系统的频率特性及频域分析方法1、学会运用MATLAB分析连续系统地频率特性2、学会运用MATLAB进行连续系统的频域分析(三)掌握使用Matlab进行连续时间LTI系统s域分析的方法1、学会运用MATLAB求拉普拉斯变换(LT)2、学会运用MATLAB求拉普拉斯反变换(ILT)3、学会在MATLAB环境下进行连续时间LTI系统s域分析二、实验原理及实例分析(一)连续系统时域分析(详细请参见实验指导第二部分的第5章相关部分)(二)连续时间LTI系统的频率特性及频域分析(详细请参见实验指导第二部分的第8章相关部分)(三)拉普拉斯变换及连续时间系统的s域分析(详细请参见实验指导第二部分的第10、11章相关部分)三、实验过程(一)熟悉三部分相关内容原理(二)完成作业已知某系统的微分方程如下:)(3)()(2)(3)(t e t e t r t r t r +'=+'+''其中,)(t e 为激励,)(t r 为响应。
1、用MATLAB 命令求出并画出2)0(,1)0(),()(3='==---r r t u e t e t 时系统的零状态响应和零输入响应(零状态响应分别使用符号法和数值法求解,零输入响应只使用符号法求解);>> eq='D2y+3*Dy+2*y=0';>> cond='y(0)=1,Dy(0)=2';>> yzi = dsolve(eq,cond);yzi = simplify(yzi);>> eq1 = 'D2y+3*Dy+2*y=Dx+3*x';eq2 = 'x= exp(-3*t)*Heaviside(t)';cond = 'y(-0.01)=0,Dy(-0.001)=0';yzs = dsolve(eq1,eq2,cond);yzs = simplify(yzs.y)yzs =heaviside(t)*(-exp(-2*t)+exp(-t))>> yt = simplify(yzi+yzs)yt =-3*exp(-2*t)+4*exp(-t)-exp(-2*t)*heaviside(t)+exp(-t)*heaviside(t)>> subplot(3,1,1);>> ezplot(yzi,[0,8]);grid on;>> title ('rzi');>> subplot(3,1,2);>> ezplot(yzs,[0,8]);>> grid on;>> title('rzs');>> subplot(3,1,3);>> ezplot(yt,[0,8]);grid on;>> title('完全响应')sys = tf([1,3],[1,3,2]);t = ts:dt:te;f = exp(-3*t).*uCT(t);y = lsim(sys,f,t);plot(t,y),grid on;axis([0,8,-0.02,0.27]);xlable('Time(sec)'),ylable('y(t)'); title('零状态响应')2、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''2)0(,1)0(),()(3='==---r r t u e t e t使用MATLAB 命令求出并画出系统的冲激响应和阶跃响应(数值法);用卷积积分法求系统的零状态响应并与(1)中结果进行比较;t = 0:0.001:4;sys = tf([1,3],[1,3,2]);h = impulse(sys,t);g = step(sys,t);subplot(2,1,1);plot(t,h),grid on;xlable('Time(sec)'),ylable('h(t)');title('冲激响应');subplot(2,1,2);plot(t,g),grid on;xlable('Time(sec)'),ylable('g(t)');title ('阶跃响应')_dt = 0.01;t1 = 0:dt:8;f1=exp(-3*t1);t2 = t1;sys = tf([1,3],[1,3,2]);f2 = impulse(sys,t2);[t,f]= ctsconv(f1,f2,t1,t2,dt)function[f,t] = ctsconv(f1,f2,t1,t2,dt)f = conv(f1,f2);f = f*dt;ts = min(t1)+min(t2);te = max(t1)+max(t2);t = ts:dt:te;subplot(1,1,1)plot(t,f);grid on;axis([min(t),max(t),min(f)-abs(min(f)*0.2),max(f)+abs(max(f)*0.2)]); title('卷积结果')3、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''使用MATLAB 命令求出并画出此系统的幅频特性和相频特性;使用频域分析法求解系统的零状态响应并与(1)中结果进行比较;>> w = -3*pi:0.01:3*pi;b = [1,3];a = [1,3,2];H = freqs(b,a,w);subplot(2,1,1);plot(w,abs(H)),grid on;xlabel('\omega(rad/s)'),ylabel('|H(\omega)|');title ('H(w)的幅频特性');subplot(2,1,2);plot(w,angle(H)),grid on;xlabel('\omega(rad/s)'),ylabel('\phi(\omega)');title('H(w)的相频特性')H = sym('1/(i^2*w^2+3*i*w+2)'); H= simplify(ifourier(H)); subplot(3,1,1);ezplot(H,[0,8]),grid on;title('零状态响应')4、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''使用MATLAB 命令求出并画出t t e 2cos )(=时系统的稳态响应;t = 0:0.1:20;w = 2;H = (j*w+3)/(j^2*w^2+3*j*w+2);f = cos(2*t);y = abs(H)*cos(w*t+angle(H));subplot(2,1,1);plot(t,f);grid on;ylabel('f(t)'),xlabel('Time(s)');title('输入信号的波形');subplot(2,1,2);plot(t,y);grid on;ylabel('y(t)'),xlabel('Time(sec)');title('稳态响应的波形')5、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''若已知条件同(1),借助MATLAB 符号数学工具箱实现拉普拉斯正反变换的方法求出并画出2)0(,1)0(),()(3='==---r r t u e t e t 时系统的零状态响应和零输入响应,并与(1)的结果进行比较。
MATLAB在LTI连续系统响应分析中的应用

PC +P C +…+P C =Di ( 0 11 2 2 o Di表示 f 的导数的初始值 f’ )) u( 0
p1-C1 n 1 +p2 -C2+… + p n1 n1 -C =D 。 _i
0
l
l P2
-
l p
-
C1 C2
:
-
z 0
e( :2 ,e =4 tf ) V 2 V
解 :此题有多种解法 ,现用时域经典解法求解。根据 电路形式 ,列写出系统的微分方程如下 :
嘉 ) 1 d) + ) 嘉 ) 志 将数 (+) + f 丢) ) 代 + R ( 面 2 ( + + 参
入得 :
收稿 日期 :20 —22 0 51—0 作 者简 介 :龙 飞 ( 9 8 ) 17 一,女 ,贵 州贵 阳人 ,20 级 硕 士研 究 生 ,主要研 究方 向为 E A。 04 D
维普资讯
第 l卷 第3 9 期
20 0 6年 6月
四川理工学院学报 (自 然科学版 )
J OURNAL OF S CHUAN I UNI VERS TY I OF
、 1 1 .3 , . 9NO 0
S I NC C E E&E GI E D G( T ALS I NC DI I N) N NE R NA UR C E EE T O
难。以某一实际连续系统为例 ,展 示了MA L B语言分析计算响应的全过程 ,大大提 高了计算效率 , TA 获得 了可视 化 的计 算结 果。
关键词:MA L B;连续 系统 ;分析 ;计算 TA 中 图分类 号 :T 2 1 l P7. 6
文 献标 识码 :A
引 言
MA L B是 8 TA 0年代由 Ma Wok 公司开发 ,它是一套功能强大的工程计算软件 ,被广泛应用于 t rs h 自动控制、 机械设计 、 流体力学和数理统计等工程领域 。 T A MA L B系统包括 5 个部分 : T A MA L B语言 、 MA L B工作环境 、MA L B图形处理系统 、 T A TA TA MA L B数学函数库 、 T A MA L B应用程序接 口。 MA L B具有如下优势与特点 : 1 友好的工作平台和编程环境 ; 2 简单易用的程序语言 ; TA () ()
MATLAB 3.连续时间LTI系统的时域分析

1
3.连续时间 LTI 系统的时域分析
作业题
2、某连续系统的输入为 e(t),输出为 y(t),系统的微分方程为:y ’’(t)+5y ’(6)+6y(t)=3f ’(t)+2f(t) 绘出该系统的单位冲激响应和单位阶跃响应时域图形 若f t = ������ −2������ ������(������),绘出系统的零状态响应时域图形
将激励信号和单位冲击响应进行卷积,由下图发现结果一致。
6
3.连续时间 LTI 系统的时域分析
作业题
4、如下图所示的电路中,已知 电压 y(t ) 作为系统输出:
R1 R2 R3 4() , L1 L2 1( H ) ,如果以电阻 R3 上
请画出系统的冲击响应 h(t) 请画出系统在激励e(������) = 12������(������)(v)作用下的零状态响应,要求写出系统微分方程的求 解步骤。 对所求结果进行验证。
零输入响应: eq1='D2y+4*Dy+4*y=0'; cond='Dy(-0.01)=1,y(-0.01)=1'; answer=dsolve(eq1,cond) answer = 103/(100*exp(1/50)*exp(2*t))+ (3*t)/(exp(1/50)*exp(2*t)) >> 全响应: eq1='D2y+4*Dy+4*y=Df+3*f'; eq2='f=exp(-t)*heaviside(t)'; cond='Dy(-0.01)=1,y(-0.01)=1'; answer=dsolve(eq1,eq2,cond); simplify(answer.y) ans = (3*t+2*exp(t+1/50)*heaviside(t)-2*exp(1/50)*heaviside(t)-t*exp(1/50)* heaviside(t) + 103/100)/exp(2*t + 1/50)
MATLAB仿真之连续时间LTI系统仿真和时域分析
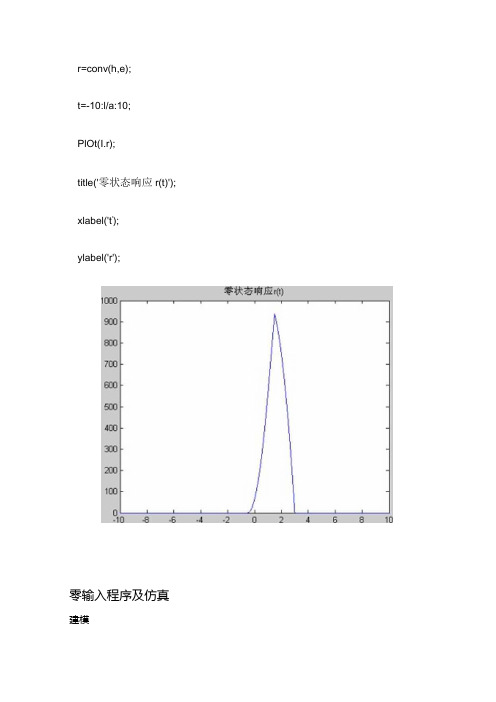
r=conv(h,e);t=-10:l/a:10;PlOt(I.r);title('零状态响应r(t)'); xlabel('t');ylabel('r');零输入程序及仿真建模当UT系统的输入为零时,其零输入响应为微分方程的其次解(即令微分方程的等号右端为零),其形式为(设特征根均为单根)Mf)=GeR÷Ge网+••••+”'其中PbP2,,∙∙,Pn是特征方程alλn+a2λn-l+∙∙∙+anλ+an=O的根,它们可以用rool(八)语句求得。
各系数IIIy及其各阶导数的初始值来确定。
对此有G+G+•…+G=NOp l C l+p2C2+--+P ll C n=Dy0PFG+〃2”工+•…3Y写成矩阵形式为:PJC+IY1C J+∙∙∙+PJC=D"*PlPi - P nC*-∣C∣t-∣JU-IP∣Pi…P…V为范德蒙矩阵,在matlab的特殊矩阵库中有Vandero以下面式子为例:√(r)+5y(0+4y(r)=2∕(∕)-4∕(r)y(OJ=l,y(OJ=5:MAT1.AB程序:a=input(,输入分母系数a=[al,a2,...]=');n=length(八)-l;YO=inputC输入初始条件向量YO=[yO,DyO,D2yO,.p=roots(八);V=rot90(vander(p));c=V∖Y0';dt=inρut('dt=');te=inpιιt('te-);t=O:dt:te;y=zeros(1,length(t));fork=kny=y÷c(k)*exp(p(k)*t);endplot(t,y);gridon:xlabel(,t');ylabel('y');litle('零输入响应');程序运行结果:用这个通用程序来解一个三阶系统,运行此程序并输入a=[l,5,4]Y0=[l,5]dt=O.Olte=6结果如下列图:依据图可以分析零输入响应,它的起始值与输入函数无关,只与它的初始状态值有关,其起始值等于y(0_)的值。
信号与系统MATLAB仿真——LTI连续系统的时域分析

信号与系统MATLAB仿真——LTI连续系统的时域分析1. 知识回顾(1)经典时域分析⽅法线性时不变(LTI)系统是最常见最有⽤的⼀类系统,描述这类系统的输⼊-输出特性的是常系数线性微分⽅程。
\begin{array}{l} {y^{(n)}}(t) + {a_{n - 1}}{y^{(n - 1)}}(t) + \cdot \cdot \cdot + {a_1}{y^{(1)}}(t) + {a_0}y(t) = \\ {b_m}{f^{(m)}}(t) + {b_{m - 1}}{f^{(m - 1)}}(t) + \cdot \cdot \cdot + {b_1}{f^{(1)}}(t) + {b_0}f(t) \end{array}齐次解:{y^{(n)}}(t) + {a_{n - 1}}{y^{(n - 1)}}(t) + \cdot \cdot \cdot + {a_1}{y^{(1)}}(t) + {a_0}y(t) = 0特征⽅程:{\lambda ^n} + {a_{n - 1}}{\lambda ^{n - 1}} + \cdot \cdot \cdot + {a_1}\lambda + {a_0} = 0均为单根:{y_h}(t) = \sum\limits_{i = 1}^n {{C_i}{e^{{\lambda _i}t}}}有重根(r重根):{y_h}(t) = \sum\limits_{i = 1}^r {{C_i}{t^{i - 1}}{e^{{\lambda _1}t}}}共轭复根({\lambda _{1,2}} = \alpha \pm j\beta ):{e^{\alpha t}}({C_1}\cos \beta t + {C_2}\sin \beta t)r重复根:{e^{\alpha t}}(\sum\limits_{i = 1}^r {{C_{1i}}{t^{i - 1}}} \cos \beta t + \sum\limits_{i = 1}^r {{C_{2i}}{t^{i - 1}}} \sin \beta t)特解:f(t) = {t^m}所有的特征根均不等于0:{y_p}(t) = {P_m}{t^m} + {P_{m - 1}}{t^{m - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}有r重等于0的特征根:{y_p}(t) = {t^r}[{P_m}{t^m} + {P_{m - 1}}{t^{m - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}] f(t) = {e^{\alpha t}}:\alpha 不是特征根:{y_p}(t) = P{e^{\alpha t}}\alpha 是特征单根:{y_p}(t) = {P_1}t{e^{\alpha t}} + {P_0}{e^{\alpha t}}\alpha 是r重特征根:{y_p}(t) = ({P_r}{t^r} + {P_{r - 1}}{t^{r - 1}} + \cdot \cdot \cdot + {P_1}t + {P_0}){e^{\alpha t}} f(t) = \cos \beta t或\sin \beta t:所有特征根均不等于 \pm j\beta :{y_p}(t) = {P_1}\cos \beta t + {P_2}\sin \beta t\pm j\beta 是特征单根:{y_p}(t) = t[{P_1}\cos \beta t + {P_2}\sin \beta t]全解:y(t) = {y_h}(t) + {y_p}(t)(2)零输⼊响应与零状态响应y(t) = {y_{zi}}(t) + {y_{zs}}(t)(3)冲激响应和阶跃响应\left\{ \begin{array}{l} \delta (t) = \frac{{{\rm{d}}\varepsilon (t)}}{{{\rm{d}}t}}\\ \varepsilon (t) = \int_{ - \infty }^t {\delta (\tau ){\rm{d}}\tau } \end{array} \right. \left\{ \begin{array}{l} h(t) = \frac{{{\rm{d}}g(t)}}{{{\rm{d}}t}}\\ g(t) = \int_{ - \infty }^t {h(\tau ){\rm{d}}\tau } \end{array} \right.(4)卷积积分y(t) = {f_1}(t) * {f_2}(t) = \int_{ - \infty }^{ + \infty } {{f_1}(\tau ){f_2}(t - } \tau ){\rm{d}}\tau系统的零状态响应:{y_{zs}}(t) = f(t) * h(t)卷积积分的性质:交换律分配率结合律任意函数与单位冲激函数卷积的结果仍是函数本⾝:f(t) * \delta (t) = f(t)2. 利⽤MATLAB求LTI连续系统的响应LTI连续系统以常微分⽅程描述,如果系统的输⼊信号及初始状态已知,便可以求出系统的响应。
lsim在matlab中的用法

lsim在matlab中的用法Lsim函数是MATLAB中用于对动态系统进行时间域仿真和响应分析的函数。
本文将详细介绍Lsim函数的使用方法和步骤。
MATLAB是一种非常强大的数值计算和仿真工具,可以用于各种工程和科学应用。
在系统动力学中,我们经常需要对线性时不变(LTI)系统进行分析,以评估其时间域响应。
Lsim函数就是一个非常有用的工具,可以简化这一过程。
Lsim函数的基本语法如下:matlablsim(sys, u, t)其中,sys是系统的传递函数或状态空间模型,u是系统的输入信号,t是所需模拟的时间点。
下面将一步一步介绍如何使用Lsim函数进行系统响应分析。
第一步是定义系统模型。
在MATLAB中,我们可以使用tf函数定义传递函数模型,也可以使用ss函数定义状态空间模型。
传递函数模型由分子和分母多项式系数组成,而状态空间模型由矩阵A、B、C和D定义。
以下是一个例子,演示如何定义传递函数模型和状态空间模型:matlab定义传递函数模型num = [1]; 分子多项式系数den = [1, 2, 1]; 分母多项式系数sys_tf = tf(num, den);定义状态空间模型A = [-1, -2; 0, -3]; 矩阵AB = [1; 0]; 矩阵BC = [1, 0]; 矩阵CD = 0; 矩阵Dsys_ss = ss(A, B, C, D);第二步是定义输入信号。
Lsim函数可以通过输入信号来模拟系统的响应。
输入信号可以是函数句柄、向量或矩阵。
以下是一些示例输入信号的定义方法:matlab步输入u_step = ones(size(t));脉冲输入u_impulse = zeros(size(t));u_impulse(1) = 1;正弦输入u_sine = sin(t);方波输入u_square = square(t);随机输入u_random = randn(size(t));第三步是定义仿真的时间点。
MATLAB仿真之连续时间LTI系统仿真和时域分析

郑州航空工业管理学院《电子信息系统仿真》课程设计级电子信息工程专业班级题目连续时间LTI系统仿真和时域分析姓名学号指导教师二О一年月日MATLAB软件简介MATLAB是MathWork 公司于1984 年推出的一套面向工程和科学运算的高性能软件,它具有强大的图形处理功能及符号运算功能,为我们实现信号的可视化及系统分析提供了强有力的工具。
MATLAB 强大的工具箱函数可以分析连续信号、连续系统,同样也可以分析离散信号、离散系统,并可以对信号进行各种分析域计算,如相加、相乘、移位、反折、傅里叶变换、拉氏变换、Z 变换等等多种计算MATLAB用于算法开发、数据可视化、数据分析以数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连Matlab开发工作界面接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
Simulink是MATLA B最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
Simulink是MATLAB最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。
在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点,并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。
设计目的掌握信号经过LTI 系统的时域分析方法。
根据连续时不变信号处理的基本概念、理论和方法对信号进行分析和处理,实现卷积积分或卷积和,零输入响应和零状态响应,学会应用MATLAB 对实际问题进行仿真,并对仿真结果进行分析。
在本次课程设计中,利用MATLAB 软件对LTI 连续系统时域进行仿真与分析。
MATLAB与信号实验 —— 连续LTI系统的时域分析

上机实验2 连续LTI 系统的时域分析一、实验目的(1)熟悉LTI 系统在典型激励信号的响应及其特性;(2)熟悉连续LTI 系统单位冲激响应的求解方法;(3)重点掌握用卷积计算连续时间系统的零状态响应;(4)熟悉MATLAB 相关函数的调用格式及作用;(5)会用MATLAB 对系统进行时域分析。
二、实验原理连续时间系统可用如下的线性常系数微分方程来描述:1()100()()...()()...()n n m n n m a y t a y t a y t b f t b f t --+++=++其中,n m ≥,系统的初始条件为(0)y -,...,(1)(0)n y --系统的响应一般包括两部分,即由当前输入所产生的响应(零状态响应)和由历史输入(初始状态)所生产的响应(零输入响应)。
对于低阶系统,一般可以通过解析的方法得到响应,但是对与高阶的系统,手工计算比较困难,这时MATLAB 强大的计算功能就比较容易确定系统的各种响应,如冲击响应,阶跃,零状态响应,全响应等。
1、直接求解法涉及到的MATLAB 函数有:impulse(冲击响应)、step(阶跃)、roots(零状态下响应)、lsim (零状态响应)等。
在MATLAB 中,要以系统向量的形式输入系统的微分方程,因此在使用前必须对系统的微分方程进行变换,得到其传递函数。
其分别用向量a,b 表示分母多项式和分子多项式的系数(按照s 的降幂排列)。
2、卷积计算法跟据系统的单位冲激响应,里用卷积计算的方法,也可以计算任意输入状态下系统的零状态响应。
设一个线性零状态系统,已知系统的单位冲激响应为h(t),当系统的激励信号为f(t)时,系统的零状态响应为:()()()()()ττττττd h t f d t h f t y zs -=-=⎰⎰∞∞-∞∞-也可简记为()()t h t f y zs*= 由于计算机采用的数值计算,因此系统的零状态响应也可以用离散序列卷积和近似为∑∞-∞=*=-=n zs k h k f T n k h n f k y )()()()()(式中)(k y zs、)(k f 和)(k h 分别对应以T 为时间间隔对连续时间信号)(k y zs 、)(k f 和)(k h 进行采样得到的离散序列。
通过MATLAB软件对LTI连续系统时域进行分析仿真

前言“信号与线性系统分析”是通信类学生一门主干课程,该课程所涉及到的许多基本概念和五种基本分析方法,是每个学生所必须熟练掌握的内容。
近年来,我了解到国内一些著名大学中有关本课程的教学实践和发展动向,做出相应的分析得出一些结论:学生的系统概念比较薄弱,而原有的教材存在着重信号而轻系统的偏向;在运用在纯工程运算方面的时间比较多,对一些重要的基本概念掌握得不够好。
虽然我们可以通过作大量信号与系统的试验来帮助学生理解《信号与系统》中的众多抽象概念。
但是,由于信号与系统实验所需的设备价格较高,试验难度较大,许多教学单位都因不具备试验条件而放弃了试验课程的开设,这极大的影响了教育质量的提高。
近年以来,随着计算机硬件性能的不断提升和计算机软件技术的飞速发展,利用计算机进行虚拟试验成为一种国际潮流,国内也逐步开始了这一方面的工作,并在取得积极的成果.而MATLAB经过多年的不断发展与完善已发展成为由MATLAB语言、MATLAB工作环境、MATLAB图象处理系统、MATLAB数据函数库和MATLAB应用程序接口五大部分组成的集数值计算、图象处理、程序开发为遗体的功能强大的系统。
它具有以下的功能和特点:高效的数值计算及符号计算功能,能使我们从繁杂的数学运算分析中解脱出来:完备的图形处理功能,实现了计算机结果和编程的可视化:友好的界面及接近数学表达式的自然化语言,便于学习和掌握。
实践证明,学生可以在几十分钟的时间内学会MATLAB的基本知识,经过几个小时的使用就能初步掌握。
所以,在此次的课程设计中我选择连续系统时域系统分析这个理论性比较强的项目。
在信号与系统分析中应用 Matlab 软件的内容,编制了多个程序与习题,使学生对信号与系统中的许多重要的概念增加了直观认识,以便加深对概念的理解,并学会应用 Matlab 软件来快速而有效地分析解决问题。
用 Matlab 软件来进行上机作业显然是本课程未来发展的一个必然趋势.学生通过上机训练,不仅能很快地理解所增加的新内容,而且也激发了学生们的学习兴趣, 对许多概念的理解加深了, 而且学会了利用 Matlab 软件来分析问题的技巧与方法.工程概况描述连续系统的输入-输出特性的是常系数微分方程。
实验3 利用matlab求LTI连续系统的响应

实验3 利用matlab 求LTI 连续系统的响应一. 实验目的:1. 了解LTI 系统的冲激响应h(t)及matlab 实现; 2. 了解LTI 系统的阶跃响应g(t)及matlab 实现; 3. 了解LTI 系统的零状态响应; 二. 实验原理:设描述连续系统的微分方程为:()()()()∑∑===Mj j jN i i i t f bt y a 0则可以用向量a 和b 来表示该系统,即: ],,,,[011a a a a a N N Λ-= ],,,,[011b b b b b M M Λ-=注意:在用向量来表示微分方程描述的连续系统时,向量a 和b 的元素一定要以微分方程时间求导的降幂次序来排列,且缺项要用零来补齐。
1. impulse()函数函数impulse()将绘出由向量a 和b 表示的连续系统在指定时间范围内的冲激响应h(t)的时域波形,并能求出指定时间范围内冲激响应的数值解。
impulse()函数有如下几种调用格式:● impulse(b,a) ● impulse(b,a,t)● impulse(b,a,t1:p:t2) ● y= impulse(b,a,t1:p:t2) 详细用法可查阅帮助文件。
2. Step()函数 函数step()将绘出由向量a 和b 表示的连续系统在指定时间范围内的阶跃响应g(t)的时域波形,并能求出指定时间范围内阶跃响应的数值解。
step()函数有如下几种调用格式:● step(b,a) ● step(b,a,t)● step(b,a,t1:p:t2) ● y= step(b,a,t1:p:t2) 3.lsim()函数 函数lsim()将绘出由向量a 和b 表示的连续系统在指定时间范围内对函数x(t)响应的时域波形,并能求出指定时间范围内响应的数值解。
lsim()函数有如下几种调用格式:● lsim(b,a,x,t) ● y=lsim(b,a,x,t) 三. 范例程序已知描述某电路的微分方程是欢迎下载 2()()()()()()t e t e t e t r t i t i 46107'"'''++=++由理论方法可推导出系统的冲激响应)(t h 和阶跃响应)(t g 为()()t u e e t t h t t )3134()(52--+-+=δ()t u e e t g t t )5215132()(52+-=--下面演示MATLAB 求解冲激响应和阶跃响应的两种方法,以及lsim 函数的多种调用方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第19卷 第3期 四川理工学院学报(自然科学版) V ol .19 No .3JOURNAL OF SICHUAN UNIVERSITY OF2006年6月 SCIENCE & ENGINEERING (NATURAL SCIENCE EDITION ) Jun .2006文章编号:1673-1549(2006)03-0101-04MATLAB 在LTI 连续系统响应分析中的应用龙 飞,刘 桥(贵州大学计算机科学与工程学院,贵阳 550025)摘 要:对信号系统的分析是由高阶微分方程或一阶线性微分方程组描述,用手工方程求解比较困难。
以某一实际连续系统为例,展示了MATLAB 语言分析计算响应的全过程,大大提高了计算效率,获得了可视化的计算结果。
关键词:MATLAB ;连续系统;分析;计算中图分类号:TP271.61 文献标识码:A引 言MATLAB 是80年代由MathWorks 公司开发,它是一套功能强大的工程计算软件,被广泛应用于自动控制、机械设计、流体力学和数理统计等工程领域。
MATLAB 系统包括5个部分:MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库、MATLAB 应用程序接口。
MATLAB 具有如下优势与特点:(1)友好的工作平台和编程环境;(2)简单易用的程序语言; (3)强大的科学计算及数据处理能力;(4)出色的图形处理功能;(5)应用广泛的模块集和工具箱;(6)实用的程序接口和发布平台;(7)模块化的设计和系统级的仿真。
MATLAB 还提供了Simulink 软件包,它是一个用来对动态系统进行建模、仿真和分析的软包,它支持线性和非线性系统,能够在连续时间域、离散时间域或者两者的混合时间域里进行建模,它同样支持具有多种采样速率的系统。
本文列举一个简单连续时间系统的例子,探索MATLAB 在信号系统LTI 连续时间系统计算分析中的应用。
1 时域分析的初值常微分方程求解法一个LTI 系统如图1所示t<0时,开关K 原来是处于1的位置而且已经达到稳定;t=0时,将开关闭合,求t ≥0时,系统零输入响应)(t i zi 和零状态响应)(t i zs 的变化规律。
其中,假设H L 41=, F C 1=,Ω=11R ,Ω=232R ,V t e 2)(1=,V e 42=解:此题有多种解法,现用时域经典解法求解。
根据电路形式,列写出系统的微分方程如下:)(11)(12)(11)()121()()211()(2222t e LC R t e dt d L R R t e dt d R t i LC R R LC t i dt d L R C R t i dt d ++=++++将参数代入得:收稿日期:2005-12-20作者简介:龙 飞(1978-),女,贵州贵阳人,2004级硕士研究生,主要研究方向为EDA 。
102 四川理工学院学报(自然科学版) 2006年6月)(4)(6)()(10)(7)(2222t e t e dt dt e dtd t i t i dt d t i dt d ++=++零输入响应:此时令外加激励源0)(=t e ,由系统在+≥0t 时刻的等效电路可知电路在V v C 56)0(=−和A i L 54)0(=−的作用下工作。
当LTI 系统的输入为零时,其零输入响应为微分方程的齐次解(即令微分方程等号右端为0),其形式为t p n t p t p zi n e C e C e C t i +++="2121)(其中n p p p ,,,21"是特征方程01121=+++++−n n n n a a a a λλλ"的根,它们可用MATLAB 中roots(a)语句求得。
各系数n C C C ,,,21"由)(t i 及其各阶导数的初始值来确定。
对此有:021i C C C n =+++" )0(0i i =02211Di C p C p C p n n =+++" (0Di 表示i 的导数的初始值)0()1(i )................................011212111i D C p C p C p n n n n n n −−−−=+++"写成矩阵形式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−−−0100211121121111i D Di i C C C p p p p p p n n n n n n n ##"#%##""即0I C V =• 其解为 0\I V C = 式中 ],,[;],,,[010,0021′=′=−i D Di i I C C C C n n ""⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=−−−1121121111n n n n n p p p p p p V "#%##""V 为范德蒙矩阵,在MATLAB 的特殊矩阵库中有vander 。
0)(10)(7)(22=++t i t i dt d t i dt d zi zi zi 和+0状态的)0(+zi i 及)0(+zi i dt d 的解。
由其等效电路可得:A i zi 56)0(−=+,s A i dtd zi /2)0(=+为求系统的零输入响应)(t i zi ,编制程序如下:a=input('输入分母系数向量a=[a1,a2,a3]=');n=length(a)-1;Y0=input('输入初始条件向量Y0=[y0,Dy0]='); p=roots(a);V=rot90(vander(p));c=V\Y0';t=0:dt:tf; tf=t(end);dt=tf/(length(t)-1;y=zeros(1,length(t)); for k=1:n y=y+c(k)*exp(p(k)*t);endplot(t,y),grid 这是一个通用解二阶系统的程序。
程序运行结果:运行此程序并输入a=[1,7,10],dt=0.2,tf=8,y0=[-6/5,2] 运行生成的)(t i zi 的变化曲线,如图2所示。
零状态响应:此时令外加激励源t t e 2sin 4)(=,这里用卷积函数求解零状态响应。
以下程序求解)(t h 和)(t i zs 并绘出了其变化曲线。
a=input('多项式分母系数向量a=');b=input('多项式分子系数向量b='); t=input('输入时间序列t=[0:dt:tf]');u=input('输入序列u=');tf=t(end);dt=tf/(length(t)-1);[r,p,k]=residue(b,a); %用极点留数法求冲激响应第19卷 第3期 龙 飞等:MATLAB 在LTI 连续系统响应分析中的应用 103 h=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t);subplot(2,1,1),plot(t,h);grid %画出冲击响应)(t hy=conv(u,h)*dt; %求u 和h 的卷积,得输出)(t y subplot(2,1,2), %画出输出)(t y plot(t,y(1:length(t)));grid程序运行结果:执行这个程序,取a=[1,7,10], b=[1,6,4],t=[0:0.1:5], u=4*sin(2*t)所得的结果如图3所示,其中图3中上图显示冲击响应)(t h图2 )(t i zi 的变化规律 图 3 )()(t i t h zs 和的变化规律不难看出,Matlab 的函数运算及函数绘图功能的强大,使得计算效率大为提高。
2 复频域分析的留数法求解在复频域分析中,设象函数为:1110111)()()(b s b s b s b a s a s a s a s b s a s F n n n n m m m m ++++++++==−−−−"" 其中)(s a 和)(s b 都是复频域s 的多项式,所有的系数都是实数。
在信号系统分析中常遇到此类问题。
为求的原函数,传统的方法一般是用部分分式法,即将分解为多个一次分式之和。
)()()()(2211s k p s r p s r p s r s b s a s F nn +−++−+−==" 众所周知,求n p p p ",2,1及n r r r ",,21的计算量是非常大的。
MATLAB 提供了一个非常好用的留数函数residue ,可以直接求出n p 、n r ,用法如下:),(],,[b a residue k p r =,其中b a ,分别为分子多项式)(s a 及分母多项式)(s b 按降幂排列的各项系数向量,而p 、r 分别为)(s F 的极点向量和留数向量,若m n >时,式为真分式,k 为空阵。
仍以图1所示系统为例,解出传递函数(系统输入与输出的关系)的形式:10746)(22++++=s s s s s G假设输入信号)2sin(4)(t t e =变换式为 :48)(2+=s s E则输出信号的变换式为 :402814732488)()()(2342++++++==s s s s s s s E s G s I zs 键入如下程序:a=[8,48,32], b=[1,7,14,28,40],[r,p,k]=residue(a,b),104 四川理工学院学报(自然科学版) 2006年6月程序运行结果如下:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+−−=i i r 4483.16207.04483.16207.03333.10920.0 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−−=i i p 0000.20000.20000.20000.5 这里 []=k 为空矩阵 显然零状态响应的原函数)(t i zs 为:t p t p t p t p zs e r e r e r e r t i 43214321)(+++=t j t j t t e j e j e e 2225)4483.16207.0()4483.16207.0(3333.10920.0−−−++−+−=可见residue 函数可直接对)(s F 进行部分分式分解并给出n n p r ,。
其函数图形和图3(b)中零状态响应)(t i zs 曲线完全相同。
3 系统构造Simulink 模型求解先打开MATLAB 命令窗口中新建模型命令,然后进一步打开Simulink 模块库,新建一个模型。
