matlab fft分析实例
用MAtlaB进行DFT及FFT频谱分析和运算结果的比较的实验

DSP MATLAB上机实验一班级:学号:姓名:函数代码:function xn()format longq=0.9+0.3*i;wn=exp(-2*pi*i/32);xn=q.^[0:31]xk1=(1-q^32)./(1-q*wn.^[0:31]) %利用公式计算XK的理论值xk2=fft(xn,32) %运用基二基2时间抽选的FFT算法计算Xkdiff=xk1-xk2 %两者的差运行xn()即得结果结果为:xn =Columns 1 through 21.000000000000000 0.900000000000000 + 0.300000000000000i Columns 3 through 40.720000000000000 + 0.540000000000000i 0.486000000000000 + 0.702000000000000i Columns 5 through 60.226800000000000 + 0.777600000000000i -0.029160000000000 + 0.767880000000000i Columns 7 through 8-0.256608000000000 + 0.682344000000000i -0.435650400000000 + 0.537127200000000i Columns 9 through 10-0.553223520000000 + 0.352719360000000i -0.603716976000000 + 0.151480368000000i Columns 11 through 12-0.588789388800000 - 0.044782761600000i -0.516475621440000 - 0.216941302080000i Columns 13 through 14-0.399745668672000 - 0.350189858304000i -0.254714144313600 - 0.435094573075200i Columns 15 through 16-0.098714357959680 - 0.467999359061760i 0.051556885554816 - 0.450813730543488i Columns 17 through 180.181645316162381 - 0.390265291822695i 0.280560372092951 - 0.296745167791711i Columns 19 through 200.341527885221169 - 0.182902539384655i 0.362245858514449 - 0.062153919879838i Columns 21 through 220.344667448626955 + 0.052735229662480i 0.294380134865516 + 0.150861941284319i Columns 23 through 240.219683538993669 + 0.224089787615542i 0.130488248809639 + 0.267585870552088i Columns 25 through 260.037163662763049 + 0.279973758139771i -0.050544830955187 + 0.263125481154709i Columns 27 through 28-0.124427992206081 + 0.221649483752682i -0.178480038111278 + 0.162156137715589i Columns 29 through 30-0.209278875614827 + 0.092396512510647i -0.216069941806538 + 0.020373198575134i Columns 31 through 32-0.200574907198425 - 0.046485103824341i -0.166571885331280 - 0.102009065601434i xk1 =Columns 1 through 20.693972803195698 + 3.499715655993840i 2.792267857648369 + 8.050455721438597i Columns 3 through 49.402964607913189 - 9.135013555028673i 1.866445467462052 - 3.833832762635439i Columns 5 through 61.131822689478846 -2.234157347130941i 0.904793922868299 - 1.534629307882413i Columns 7 through 80.799557206779214 - 1.139609357830753i 0.739605630813150 - 0.882314367550644i Columns 9 through 100.700861643199240 - 0.698565363198060i 0.673575789604202 - 0.558478478082158i Columns 11 through 120.653109437428513 - 0.446244996656357i 0.636991253015040 - 0.352689135211701i Columns 13 through 140.623788380776217 - 0.272085968296931i 0.612612873742441 - 0.200641851238978i Columns 15 through 160.602883340189454 - 0.135703205872800i 0.594200434347139 - 0.075313670713158i Columns 17 through 180.586277479436723 - 0.017949220626496i 0.578899608820263 + 0.037651723475093i Columns 19 through 200.571898466305671 + 0.092606953506914i 0.565135772013173 + 0.147983310049841i Columns 21 through 220.558492135768929 + 0.204880771267792i 0.551859131244066 + 0.264522208758452i Columns 23 through 240.545133643745847 + 0.328364940349017i 0.538214362209129 + 0.398257131749283i Columns 25 through 260.531001527230573 + 0.476677768575531i 0.523403723684219 + 0.567132338629562i Columns 27 through 280.515362483773298 + 0.674849986673143i 0.506925762334513 + 0.808101482252638i Columns 29 through 300.498467012317214 + 0.980906313951879i 0.491389377970933 + 1.219207441587793i Columns 31 through 320.490732201059483 + 1.577081955159802i 0.517353973624932 + 2.188832884536347i xk2 =Columns 1 through 20.693972803195698 + 3.499715655993839i 2.792267857648366 + 8.050455721438597i Columns 3 through 49.402964607913182 - 9.135013555028694i 1.866445467462051 - 3.833832762635439iColumns 5 through 61.131822689478844 -2.234157347130942i 0.904793922868298 - 1.534629307882413i Columns 7 through 80.799557206779213 - 1.139609357830754i 0.739605630813149 - 0.882314367550644i Columns 9 through 100.700861643199240 - 0.698565363198060i 0.673575789604202 - 0.558478478082158i Columns 11 through 120.653109437428513 - 0.446244996656356i 0.636991253015040 - 0.352689135211701i Columns 13 through 140.623788380776217 - 0.272085968296931i 0.612612873742441 - 0.200641851238978i Columns 15 through 160.602883340189454 - 0.135703205872799i 0.594200434347139 - 0.075313670713158i Columns 17 through 180.586277479436723 - 0.017949220626496i 0.578899608820263 + 0.037651723475093i Columns 19 through 200.571898466305671 + 0.092606953506913i 0.565135772013173 + 0.147983310049840i Columns 21 through 220.558492135768929 + 0.204880771267792i 0.551859131244066 + 0.264522208758452i Columns 23 through 240.545133643745847 + 0.328364940349016i 0.538214362209129 + 0.398257131749282i Columns 25 through 260.531001527230572 + 0.476677768575531i 0.523403723684219 + 0.567132338629563iColumns 27 through 280.515362483773297 + 0.674849986673143i 0.506925762334512 + 0.808101482252638i Columns 29 through 300.498467012317213 + 0.980906313951878i 0.491389377970932 + 1.219207441587794i Columns 31 through 320.490732201059480 + 1.577081955159802i 0.517353973624928 + 2.188832884536347i diff =1.0e-013 *Columns 1 through 20.001110223024625 + 0.004440892098501i 0.031086244689504Columns 3 through 40.071054273576010 + 0.213162*********i 0.013322676295502 + 0.008881784197001i Columns 5 through 60.015543122344752 + 0.004440892098501i 0.004440892098501 + 0.006661338147751i Columns 7 through 80.008881784197001 + 0.002220446049250i 0.003330669073875 - 0.001110223024625i Columns 9 through 100.006661338147751 - 0.001110223024625i 0.006661338147751 - 0.003330669073875i Columns 11 through 120.001110223024625 - 0.009992007221626i 0.002220446049250 + 0.003330669073875i Columns 13 through 14-0.002220446049250 + 0.000555111512313i 0.003330669073875 + 0.000832667268469i Columns 15 through 160.006661338147751 - 0.006938893903907i 0.002220446049250 + 0.000693889390391i Columns 17 through 180.002220446049250 - 0.000173472347598i -0.001110223024625 - 0.004302114220422i Columns 19 through 200.001110223024625 + 0.010963452368173i -0.001110223024625 + 0.006383782391595i Columns 21 through 220.001110223024625 + 0.002775557561563i 0 + 0.000555111512313i Columns 23 through 240.001110223024625 + 0.006106226635438i 0.004440892098501 + 0.003330669073875i Columns 25 through 260.004440892098501 0.001110223024625 - 0.003330669073875i Columns 27 through 280.012212453270877 - 0.002220446049250i 0.006661338147751 - 0.004440892098501i Columns 29 through 300.009992007221626 + 0.002220446049250i 0.011102230246252 - 0.006661338147751i Columns 31 through 320.028310687127941 0.035527136788005 - 0.008881784197001i 由上面结果可知,由基2时间抽选的FFT算法所得到的DFT结果与利用公式法所得的理论值稍有偏差,但误差较小,从结果可以看出大概在小数点第15位才开始出现误差,故而用计算机FFT处理数据在精度上是可以接受的。
用matlab仿真fft的频谱分析

实验二用FFT 进行信号的频谱分析1、高斯序列(1)n=0:15; %定义序列的长度是16p=8; q=2; xa1=exp(-1*(n-p).^2/q); %利用fft 函数实傅氏变换p=8; q=4; xa2=exp(-1*(n-p).^2/q); %改变信号参数,重新计算p=8; q=8; xa3=exp(-1*(n-p).^2/q);close all;figure(1);subplot(3,1,1); stem(n,xa1);subplot(3,1,2); stem(n,xa2) ;subplot(3,1,3); stem(n,xa3) ;figure(2);subplot(3,1,1);stem(n,abs(fft(xa1))) ;subplot(3,1,2); stem(n,abs(fft(xa2))) ;subplot(3,1,3); stem(n,abs(fft(xa3))) ;p=8; q=2; p=8; q=4; p=8; q=8;(2)p=8; q=8; p=13; q=8; p=14; q=8;2、衰减正弦序列n=0:15; %定义序列的长度是15a=0.1; f=0.0625; xb=exp(-a*n).*sin(2*pi*f*n);close all;subplot(2,1,1); stem(n,xb);subplot(2,1,2); stem(n,abs(fft(xb)))a=0.1; f=0.4357 a=0.1; f=0.56253、三角波序列n=0:7;for i=1:4 %设置信号前4 个点的数值xc(i)=i; %注意:MATLAB 中数组下标从1 开始endfor i=5:8 %设置信号后4 个点的数值xc(i)=9-i;endclose all; subplot(2,1,1); stem(n,xc); %绘制信号图形subplot(2,1,2); stem(n,abs(fft(xc,8))) %绘制信号的频谱4、反三角序列for i=1:4 %设置信号前4 个点的数值x(i)=5-i; %注意:MATLAB 中数组下标从1 开始endfor i=5:8 %设置信号后4 个点的数值x(i)=i-4;endclose all; subplot(2,1,1); stem(x); %绘制信号图形subplot(2,1,2); stem(abs(fft(x,8))) %绘制信号的频谱三、2、n=0:62; %定义序列的长度是15a=0.1; f=0.0625; xb=exp(-a*n).*sin(2*pi*f*n);wn=rand(1,63);yn=xb+wn;close all;figure(1);subplot(3,1,1); stem(n,xb,'.');subplot(3,1,2); stem(n,wn,'.') ;subplot(3,1,3); stem(n,yn,'.') ;figure(2);k=0:63subplot(3,1,1);stem(k,abs(fft(xb,64)),'.') ;subplot(3,1,2); stem(k,abs(fft(wn,64)),'.') ;subplot(3,1,3); stem(k,abs(fft(yn,64)),'.') ;a=0.1; f=0.4375;a=0.1; f=0.5625;。
用MATLAB进行FFT谐波分析

FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs 为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
matlab fft计算空间频谱例子

一、概述在信号处理和图像处理领域,计算空间频谱是一项非常重要的任务。
通过计算空间频谱,我们可以了解信号或图像在不同频率下的分布情况,从而对其进行分析和处理。
而在Matlab中,fft(快速傅里叶变换)则是计算空间频谱的常用工具之一。
本文将以一个实际例子来介绍如何使用Matlab进行fft计算空间频谱。
二、实例背景假设我们有一个一维的音频信号,我们希望了解该信号在频域上的分布情况。
通过计算其空间频谱,我们可以观察到该信号在不同频率下的能量分布情况,并且进一步分析和处理该信号。
三、Matlab fft计算空间频谱步骤1.准备数据我们需要准备待分析的音频信号数据。
在Matlab中,我们可以使用以下命令生成一个包含随机信号的向量:```Matlabx = randn(1,1024);```这里生成了一个包含1024个随机数的向量x,代表了我们所要分析的音频信号。
2.进行fft计算接下来,我们可以使用Matlab中的fft函数对信号进行fft计算,得到其频谱。
具体的计算步骤如下:```MatlabN = length(x); 获取信号长度Y = fft(x); 对信号进行fft计算P2 = abs(Y/N); 计算双边频谱P1 = P2(1:N/2+1); 获取单边频谱P1(2:end-1) = 2*P1(2:end-1); 根据频谱长度修正幅值f = xxx*(0:(N/2))/N; 生成频率向量```在这段代码中,我们首先获取了信号长度N,然后对信号进行fft计算得到频谱Y。
我们计算了双边频谱P2,并根据频谱长度修正了其幅值。
我们生成了频率向量f,用于后续频谱可视化。
3.频谱可视化我们可以使用Matlab中的plot函数对频谱进行可视化展示,从而更直观地了解信号在频域上的分布情况。
```Matlabplot(f,P1)title('单边幅频特性')xlabel('频率(Hz)')ylabel('|P1(f)|')```通过以上步骤,我们就可以得到该音频信号在频域上的分布情况,并且可以通过频谱图来进一步分析和处理该信号。
MATLAB中FFT的使用方法(频谱分析)

说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
用FFT对信号作频谱分析Matlab程序

对以下序列进行FFT 分析x 1(n)=R 4(n)x 2(n)=x 3(n)=x1n=[ones(1,4)]; %产生R4(n)序列向量X1k8=fft(x1n,8); %计算x1n 的8点DFTX1k16=fft(x1n,16); %计算x1n 的16点DFT%以下绘制幅频特性曲线N=8;f=2/N*(0:N-1); (不懂)figure(1);subplot(1,2,1);stem(f,abs(X1k8),'r','、'); %绘制8点DFT 的幅频特性图,abs 求得Fourier 变换后的振幅title('(1a) 8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');N=16;f=2/N*(0:N-1);subplot(1,2,2);stem(f,abs(X1k16),'、'); %绘制8点DFT 的幅频特性图title('(1b) 16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');%x2n 与 x3nM=8;xa=1:(M/2); xb=(M/2):-1:1; %从M/2到1每次递减1x2n=[xa,xb]; %产生长度为8的三角波序列x2(n)x3n=[xb,xa];X2k8=fft(x2n,8);X2k16=fft(x2n,16);X3k8=fft(x3n,8);X3k16=fft(x3n,16);figure(2);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X2k8),'r','、'); %绘制8点DFT 的幅频特性图n+1 0≤n ≤3 8-n 4≤n ≤7 0 其它n 4-n 0≤n ≤3 n-3 4≤n ≤70 其它ntitle('(2a) 8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,3);stem(f,abs(X3k8),'r','、'); %绘制8点DFT的幅频特性图title('(3a) 8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X2k16),'、'); %绘制8点DFT的幅频特性图title('(2b) 16点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,4);stem(f,abs(X3k16),'、'); %绘制8点DFT的幅频特性图title('(3b) 16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');%x4n 与 x5nN=8;n=0:N-1;x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n,8);X4k16=fft(x4n,16);X5k8=fft(x5n,8);X5k16=fft(x5n,16);figure(3);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X4k8),'r','、'); %绘制8点DFT的幅频特性图title('(4a) 8点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,3);stem(f,abs(X5k8),'r','、'); %绘制8点DFT的幅频特性图title('(5a) 8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X4k16),'、'); %绘制8点DFT的幅频特性图title('(4b) 16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度'); subplot(2,2,4);stem(f,abs(X5k16),'、'); %绘制8点DFT的幅频特性图title('(5b) 16点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');%x8nFs=64; T=1/Fs;N=16;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k16=fft(x8n,16);N=16;f=2/N*(0:N-1);figure(4);subplot(2,2,1);stem(f,abs(X8k16),'、'); %绘制8点DFT的幅频特性图title('(6a) 16点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度');N=32;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k32=fft(x8n,32);N=32;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X8k32),'、'); %绘制8点DFT的幅频特性图title('(6b) 32点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度'); N=64;n=0:N-1; %对于N=16的情况nT = n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT)X8k64=fft(x8n,64);N=64;f=2/N*(0:N-1);subplot(2,2,3);stem(f,abs(X8k64),'、'); %绘制8点DFT的幅频特性图title('(6c) 64点DFT[x_8(n)]');xlabel('ω/π');ylabel('幅度');。
MATLAB中FFT的运用方法

MATLAB中FFT的使用方法说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
MATLAB中FFT的运用

说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.00004.7782 + 7.7071i 0 +5.0000i -10.7782 -6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
matlab的FFT函数介绍(学练结合)

matlab的FFT函数2010-04-26 22:16相关语法:Y = fft(X)Y = fft(X,n)Y = fft(X,[],dim)Y = fft(X,n,dim)定义如下:相关的一个例子:Fs = 1000; % 采样频率T = 1/Fs; % 采样时间L = 1000; % 总的采样点数t = (0:L-1)*T; % 时间序列(时间轴)%产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);y = x + 2*randn(size(t)); % 混入噪声信号plot(Fs*t(1:50),y(1:50)) %画出前50个点title('Signal Corrupted with Zero-Mean Random Noise')xlabel('time (milliseconds)')NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)% 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1.plot(f,2*abs(Y(1:NFFT/2+1)))title('Single-Sided Amplitude Spectrum of y(t)')xlabel('Frequency (Hz)')ylabel('|Y(f)|')PS:前段时间,只是为了自己看明白,没有管太多,刚才上空间发现几位的留言,感觉惭愧。
matlab fft 傅里叶变换 找出定频50的数据 -回复

matlab fft 傅里叶变换找出定频50的数据-回复在MATLAB中,如何使用傅里叶变换找出定频50的数据?回答引言傅里叶变换(Fourier Transform)是一种重要的数学工具,可以将一个信号从时间域转换到频域。
在频域中,我们可以分析信号中不同频率成分的强度、相位和幅度。
这对于许多应用领域,尤其是信号处理和通信领域非常重要。
MATLAB是一种强大的数值计算和数据可视化软件,提供了丰富的工具和函数来进行傅里叶变换分析。
本文将介绍如何使用MATLAB找出定频50的数据,并详细解释其中的步骤。
步骤一:生成信号首先,我们需要生成一个信号以进行傅里叶变换分析。
在本例中,我们生成一个包含定频50的正弦波信号。
假设信号的采样频率为1000 Hz,持续时间为1秒。
matlabfs = 1000; 采样频率t = 0:1/fs:1-1/fs; 时间向量f = 50; 信号频率x = sin(2*pi*f*t); 生成正弦波信号上述代码中,首先定义了采样频率`fs`为1000 Hz。
然后,创建了时间向量`t`,其范围是从0到1秒,步长为1/fs。
接着,定义了信号的频率`f`为50 Hz。
最后,通过`sin`函数生成了正弦波信号`x`。
步骤二:进行傅里叶变换在MATLAB中,可以使用`fft`函数对信号进行傅里叶变换。
该函数将信号从时间域转换到频域,并返回一个复数数组,表示信号在不同频率下的幅度和相位。
matlabX = fft(x);在上述代码中,我们对信号`x`进行了傅里叶变换,并将结果保存在变量`X`中。
实际上,`fft`函数返回的是信号的双边频谱,包括正频率和负频率。
为了方便分析和可视化,我们通常只关注正频率的部分。
步骤三:计算频率向量为了获得与傅里叶变换结果对应的频率信息,我们可以使用`fftshift`函数将双边频谱转换为单边频谱,并创建一个频率向量。
matlabN = length(x); 信号长度fshift = (-N/2:N/2-1)*(fs/N); 频率向量Xshift = fftshift(X); 转换为单边频谱在上述代码中,首先计算了信号长度`N`。
用MATLAB进行FFT频谱分析

用MATLAB进行FFT频谱分析假设一信号:()()292.7/2cos1.0996.2/2sin1.06.0+++=ttRππ画出其频谱图。
分析:首先,连续周期信号截断对频谱的影响。
DFT变换频谱泄漏的根本原因是信号的截断。
即时域加窗,对应为频域卷积,因此,窗函数的主瓣宽度等就会影响到频谱。
实验表明,连续周期信号截断时持续时间与信号周期呈整数倍关系时,利用DFT变换可以得到精确的模拟信号频谱。
举一个简单的例子:()ππ2.0100cos+=tY其周期为。
截断时不同的持续时间影响如图一.1:(对应程序)140.0160.0180.02截断时,时间间期为周期整数倍,频谱图0.0250.0320406080100截断时,时间间期不为周期整数倍,频谱图图错误!文档中没有指定样式的文字。
.1其次,采样频率的确定。
根据Shannon 采样定理,采样带限信号采样频率为截止频率的两倍以上,给定信号的采样频率应>1/,取16。
再次,DFT 算法包括时域采样和频域采样两步,频域采样长度M 和时域采样长度N 的关系要符合M ≧N 时,从频谱X(k)才可完全重建原信号。
实验中信号R 经采样后的离散信号不是周期信号,但是它又是一个无限长的信号,因此处理时时域窗函数尽量取得宽一些已接近实际信号。
实验结果如图一.2:其中,0点位置的冲激项为直流分量造成(对应程序为)0204060801001201401601802000.40.50.60.70.800.050.10.150.20.250.30.350.40.450.550100150图 错误!文档中没有指定样式的文字。
.2♣ARMA (Auto Recursive Moving Average )模型:将平稳随机信号x(n)看作是零均值,方差为σu 2的白噪声u(n)经过线性非移变系统H(z)后的输出,模型的传递函数为()()()∑∑=-=-+==Pk kk Qr r rza zb z A z B z H 111用差分方程表示为()()()∑∑==-+--=Qr r P k k r n u b k n x a n x 01AR (Auto Recursive )自回归模型,即ARMA 模型中系数b 只有在r=0的情况下为1,其余都是零,获得一个全极点模型:()()()∑=-+==Pk kk za z A z B z H 111差分方程表示为:()()()n u k n x a n x Pk k +--=∑=1AR 模型的功率谱估计为:()()()Ω-ΩΩ=j j uj x e A e A eS 12σ程序:%%------------------------------------------------------------------------%%功能:利用MATLAB 的FFT 函数做双正弦信号频谱分析 %%------------------------------------------------------------------------ fs=16; t=0:1/fs:200;x6=+sin(2*pi*t/*+cos(2*pi*t/+2)*;subplot(2,1,1);plot(t,x6);N=length(t);subplot(212);plot((-N/2:N/2-1)*fs/N,abs(fftshift(fft(x6,N)))) %绘制信号的频谱,横轴对应实际频率axis([0 0 160]);例子:%%------------------------------------------------------------------------%%功能:连续周期信号截断对频谱的影响%%------------------------------------------------------------------------fs=8000;n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,1);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,2);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期为周期整数倍,频谱图');n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,3);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,4);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期不为周期整数倍,频谱图');。
使用Matlab的FFT分析六脉动整流的谐波
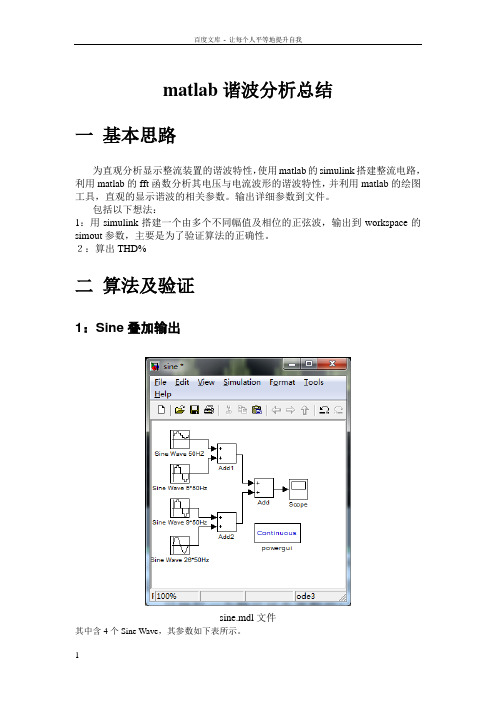
matlab谐波分析总结一基本思路为直观分析显示整流装置的谐波特性,使用matlab的simulink搭建整流电路,利用matlab的fft函数分析其电压与电流波形的谐波特性,并利用matlab的绘图工具,直观的显示谐波的相关参数。
输出详细参数到文件。
包括以下想法:1:用simulink搭建一个由多个不同幅值及相位的正弦波,输出到workspace的simout参数,主要是为了验证算法的正确性。
2:算出THD%二算法及验证1:Sine叠加输出sine.mdl文件其中含4个Sine Wave,其参数如下表所示。
Sinewave Amplitude bias Frequency(rad/sec)Phase(rad) SampleTime1 2 0.7 2*pi*50 0 -12 0.5 0 2*pi*50*5 Pi/180*90 -13 1 0 2*pi*50*9 pi/180*45 -14 0.3 0 2*pi*50*26 Pi/180/(-135) -1表达的波形为f(t)=2*sin(2*pi*50*t) +0.5*sin(2*pi*50*5*t+pi/2)+1*sin(2*pi*50*9*t+pi/4) +0.3*sin(2*pi*50*26*t-pi*3/4)为不同幅值与相位的50Hz的基波,5次、9次、26谐波的叠加。
含基波、奇次、偶次、高次谐波。
在基波上加了0.7的偏置,模拟直流分量。
示波器输出到workspace的参数名仿真参数10个周波,每周波采样点2048个使用1/50/2048的采样频率,是为了每个周波采2048个点,便于准确的FFT分析。
理论上可以分析1024次以内的谐波。
simulink的scope的输出simulink的workspace的输出ScopeData.signals.values共10*2048个点。
之所以采10个周波,是为了保证可以避开初始的过渡状态,虽然当前的仿真没有过渡状态,但六脉动整流如果负载有电容的话会有。
用Matlab对信号进行傅里叶变换实例

目录用Matlab对信号进行傅里叶变换 (2)Matlab的傅里叶变换实例 (5)Matlab方波傅立叶变换画出频谱图 (7)用Matlab对信号进行傅里叶变换1.离散序列的傅里叶变换DTFT(Discrete Time Fourier Transform)代码:1 N=8; %原离散信号有8点2 n=[0:1:N-1] %原信号是1行8列的矩阵3 xn=0.5.^n; %构建原始信号,为指数信号45 w=[-800:1:800]*4*pi/800; %频域共-800----+800 的长度(本应是无穷,高频分量很少,故省去)6 X=xn*exp(-j*(n'*w)); %求dtft变换,采用原始定义的方法,对复指数分量求和而得7 subplot(311)8 stem(n,xn);9 title('原始信号(指数信号)');10 subplot(312);11 plot(w/pi,abs(X));12 title('DTFT变换')结果:分析:可见,离散序列的dtft变换是周期的,这也符合Nyquist 采样定理的描述,连续时间信号经周期采样之后,所得的离散信号的频谱是原连续信号频谱的周期延拓。
2.离散傅里叶变换DFT(Discrete Fourier Transform)与1中DTFT不一样的是,DTFT的求和区间是整个频域,这对结果图:分析:DFT只是DTFT的现实版本,因为DTFT要求求和区间无穷,而DFT只在有限点内求和。
3.快速傅里叶变换FFT(Fast Fourier Transform)虽然DFT相比DTFT缩减了很大的复杂度,但是任然有相当大的计算量,不利于信息的实时有效处理,1965年发现的DFT解决了这一问题。
实现代码:1 N=64; %原离散信号有8点2 n=[0:1:N-1] %原信号是1行8列的矩阵3 xn=0.5.^n; %构建原始信号,为指数信号4 Xk=fft(xn,N);5 subplot(221);6 stem(n,xn);7 title('原信号');8 subplot(212);9 stem(n,abs(Xk));10 title('FFT变换')效果图:分析:由图可见,fft变换的频率中心不在0点,这是fft算法造成的,把fft改为fftshift可以将频率中心移到0点。
matlab采用fft傅里叶变换方法将信号分解得到一系列三角函数

matlab采用fft傅里叶变换方法将信号分解得到一系列三角函数在数字信号处理中,快速傅里叶变换(FFT)是一个重要的工具,它能够将信号分解为不同频率的三角函数的组合。
本文将详细介绍如何使用MATLAB 中的FFT对信号进行分解,并得到一系列三角函数。
### MATLAB中的FFT傅里叶变换#### 1.基本理论傅里叶变换表明,任何周期信号都可以看作是不同频率的正弦波和余弦波的叠加。
快速傅里叶变换(FFT)是离散傅里叶变换(DFT)的一种算法实现,可以高效地计算信号的频谱。
#### 2.MATLAB中的FFT函数MATLAB提供了`fft`函数来进行快速傅里叶变换。
以下是一个简单的示例:```matlab% 生成一个信号fs = 1000; % 采样频率t = 0:1/fs:1; % 时间向量f1 = 5; % 频率为5Hzf2 = 50; % 频率为50Hzsignal = sin(2*pi*f1*t) + 0.5*cos(2*pi*f2*t); % 信号% 进行FFT变换Y = fft(signal);% 计算幅度和频率= length(signal);P2 = abs(Y/N);P1 = P2(1:N/2);f = fs*(0:(N/2))/N;```#### 3.解析FFT结果在上面的代码中,`P1`包含了信号的幅度,而`f`是相应的频率。
由于FFT 是对称的,通常只取前半部分进行分析。
#### 4.三角函数的分解FFT将信号分解为不同频率的正弦波和余弦波的组合。
在上述例子中,原始信号由频率为5Hz和50Hz的正弦波和余弦波组成。
FFT可以帮助我们识别这些频率成分。
#### 5.实际应用在实际应用中,FFT可以用于:- 非平稳信号分析- 频谱分析- 噪声消除- 信号压缩### 结论通过MATLAB中的FFT,我们可以将复杂的信号分解为一系列三角函数(正弦波和余弦波),从而帮助我们更好地理解信号的频率成分。
matlab的FFT函数介绍

matlab的FFT函数2010-04-26 22:16相关语法:Y = fft(X)Y = fft(X,n)Y = fft(X,[],dim)Y = fft(X,n,dim)定义如下:相关的一个例子:Fs = 1000; % 采样频率T = 1/Fs; % 采样时间L = 1000; % 总的采样点数t = (0:L-1)*T; % 时间序列(时间轴)%产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);y = x + 2*randn(size(t)); % 混入噪声信号plot(Fs*t(1:50),y(1:50)) %画出前50个点title('Signal Corrupted with Zero-Mean Random Noise')xlabel('time (milliseconds)')NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)% 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1.plot(f,2*abs(Y(1:NFFT/2+1)))title('Single-Sided Amplitude Spectrum of y(t)')xlabel('Frequency (Hz)')ylabel('|Y(f)|')PS:前段时间,只是为了自己看明白,没有管太多,刚才上空间发现几位的留言,感觉惭愧。
MATLAB中FFT的使用方法频谱分析

MATLAB实现》万永革主编说明:以下资源来源于《数字信号处理的.调用方法一X=FFT(x);X=FFT(,xN);=IFFT(X); x=IFFT(X,N) x用MATLAB进行谱分析时注意:)函数返回值的数据结构具有对称性。
FFT(1例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 +7.7071i 0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;采样频率和数据点数fs=100;N=128; %.n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
用FFT作谱分析(附matlab程序)

一、实验目的学习用FFT对连续信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便正确应用FFT。
二、实验原理1.对连续时间信号进行谱分析,首先应该进行时域采样,采样频率Fs要满足乃奎斯特采样定理,及Fs大于等于信号最高频率的两倍。
2.对信号进行谱分析的重要问题是频谱分辨率D和分析误差,频谱分辨率直接和FFT的变换区间N有关,因为FFT能够实现的频谱分辨率是2π/N,因此要求2π/N≤D,可以据此是选择FFT的变换区间N。
3. 用FFT对连续信号进行谱分析的流程框图如下:三、实验内容1.对信号x=cos(8πt)+cos(16πt)+cos(20πt)进行谱分析,将cos(8πt)、cos(16πt)、cos(20πt)分别记作x1、x2、x3,那么x=x1+x2+x3。
2.观察信号在采样点数一定,分析不同采样频率对信号频谱的影响。
3.观察信号在矩形窗下,不同的截取长度对信号频谱的影响。
4.观察信号补零前后频谱的变化,以及补零后信号与截取相同长度数据下信号频谱有何不同。
四、实验步骤1.选取采样频率Fs=15、20、32、64Hz ,采样点数N 一定时,对信号x 进行采样,观察采样信号频谱有何不同,并分析原因。
2.分别取矩形窗函数的长度N=16、32、64,截取信号后观察信号的频谱有何不同,并分析原因。
3.分别取窗函数长度N=15、96截取信号。
将N=15点的信号补零至96点,观察其与N=96点的截取信号频谱有何不同,并分析原因。
五、实验结果及分析1.不同采样频率下信号的频谱比较⑴取采样频率Fs=15、20、32、64Hz ,采样点数N=64固定,信号频谱如下图5.1所示(实现程序见附录1)。
02040幅频特性Fs=15频率f/Hz幅度-10-8-6-4-20246810050100幅频特性Fs=20频率f/Hz幅度02040幅频特性Fs=32频率f/Hz幅度02040幅频特性Fs=64频率f/Hz幅度图5.1⑵结果分析从图5.1可知,不同采样频率下信号的频谱是不同的。
MATLAB中FFT的使用方法(频谱分析)

MATLAB中FFT的使用方法(频谱分析)说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 -5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 -6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
