三角形的高中线与角平分线
角形的高.中线.角平分线课件

能力,以及计算建筑物的面积和体积等。
三角形中线在建筑布局中的应用
02
在建筑布局中,三角形中线可以用来确定建筑物的对称性和平
衡感,以及优化建筑物的空间利用率。
角平分线在建筑美学中的应用
03
在建筑美学中,角平分线可以用来实现建筑物的对称美和平衡
美,以及创造多样化的建筑形态和风格。
在优化问题中应用
利用三角形高优化路径规划
通过三角函数将角度和边长联系起来,实现问题的求解。
三角形高、中线、角
04
平分线在几何证明中
应用
在证明线段相等或成比例中应用
利用三角形的高
利用三角形的角平分线
在等腰三角形或等边三角形中,高可 以将底边平分,从而证明两条线段相 等。
角平分线将一个角平分为两个相等的 小角,并且与对边相交,将对边分为 两段成比例的线段。
性质
01
02
03
三角形的中线是线段。
三角形的中线平行于对应的 底边且等于底边的一半。
04
05
任意三角形的三条中线交于 一点,该点称为三角形的重
心。
角平分线定义及性质
性质
三角形的角平分线是射线。
三角形的角平分线将对应角平分 为两个相等的小角。
定义:从一个角的顶点引出一条射线 ,把这个角分成两个完全相同的角, 这条射线叫做这个角的平分线。
在其他领域应用
三角形高在物理学中的应用
在物理学中,三角形高可以用来描述物体的运动轨迹和速度变化 等物理现象。
三角形中线在化学中的应用
在化学中,三角形中线可以用来表示分子结构和化学键等化学概念。
角平分线在地理学中的应用
在地理学中,角平分线可以用来描述地球表面的地形地貌和气候变 化等地理现象。
三角形高,中线,角平分线的定义

三角形高,中线,角平分线的定义
定义如下:
1、高:三角形的一个顶点向对边做的一条垂线段叫三角形的高。
2、中线:连接顶点和它,所对的边的中点,所得的线段,叫做三角形的中线。
3、角平分线:将一个叫分成相等的两份。
其他定义
三角形(triangle)是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形,在数学、建筑学有应用。
常见的三角形按边分有普通三角形(三条边都不相等),等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形。
三角形的中线、高线、角平分线
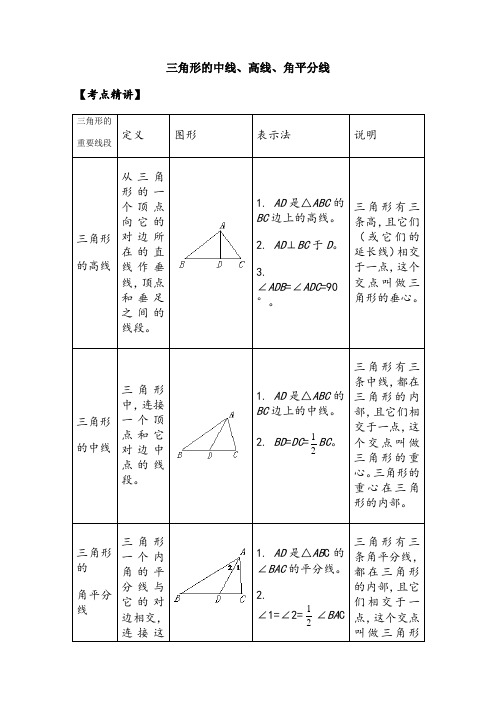
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段。
1. AD是△ABC的BC边上的高线。
2. AD⊥BC于D。
3.∠ADB=∠ADC=90°。
三角形有三条高,且它们(或它们的延长线)相交于一点,这个交点叫做三角形的垂心。
三角形的中线三角形中,连接一个顶点和它对边中点的线段。
1. AD是△ABC的BC边上的中线。
2. BD=DC=12BC。
三角形有三条中线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的重心。
三角形的重心在三角形的内部。
三角形的角平分线三角形一个内角的平分线与它的对边相交,连接这1. AD是△AB C的∠BAC的平分线。
2.∠1=∠2=12∠BA C三角形有三条角平分线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形个角的顶点与交点之间的线段。
的内心。
三角形的内心在三角形的内部。
【典例精析】例题1 如图,是甲、乙、丙、丁四位同学画的钝角△ABC 的高BE ,其中画对的是_______。
甲 乙 丙 丁思路导航:根据三角形的高是过一个顶点向对边引垂线,顶点与垂足之间的线段是该三角形的高,对各图形作出判断。
答案:丁点评:这是学生在画图时的一个易错点,通过本题理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边。
这道题是过B 点,垂直于AC 边。
例题 2 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是______。
思路导航:根据等腰三角形的性质和已知条件求出腰长和底边长,然后根据三边关系进行讨论,即可得出结论。
答案:设等腰三角形的腰长是x cm ,底边是y cm 。
根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+212122x y x x 或⎪⎪⎩⎪⎪⎨⎧=+=+122212x y x x , 解得:⎩⎨⎧==178y x 或⎩⎨⎧==514y x根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去。
专题02_三角形的高、中线、角平分线_(知识点串讲)(解析版)

专题02 三角形的高、中线、角平分线重点突破知识点一三角形的高概念:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
知识点二三角形的中线概念:在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。
性质:三角形三条中线的交于一点,这一点叫做“三角形的重心”。
重心到顶点的距离是它到对边中点距离的2倍。
(选学)三角形的中线可以将三角形分为面积相等的两个小三角形。
知识点三三角形的角平分线概念:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。
考查题型考查题型一画三角形的高典例1(2020·泉州市期中)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【答案】A【提示】经过一个顶点作对边所在的直线的垂线段,叫做三角形的高,根据概念即可得出.【详解】根据定义可得A是作BC边上的高,C是作AB边上的高,D是作AC边上的高.故选A.变式1-1.(2018·梁平区期末)在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )A.1个B.2个C.3个D.4个【答案】D【解析】试题解析:从左向右第一个图形中,BE不是线段,故错误;第二个图形中,BE不垂直AC,所以错误;第三个图形中,是过点E作的AC的垂线,所以错误;第四个图形中,过点C作的BE的垂线,也错误.故选D.变式1-2.(2020·海淀区期末)用直角三角板,作△ABC的高,下列作法正确的是()A.B.C.D.【答案】D【解析】详解:三角形的高必须是从三角形的一个顶点向对边或对边的延长线作的垂线段.可以判断A,B,C虽然都是从三角形的一个顶点出发的,但是没有垂直对边或对边的延长线.故选D.变式1-3.(2020·苏州市期中)如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是()A.CF B.BE C.AD D.CD【答案】B【解析】试题提示:根据图形,BE是△ABC中AC边上的高.故选B.变式1-4.(2019·杭州市期中)如图AD⊥BC于点D,那么图中以AD为高的三角形的个数有()A.3 B.4 C.5 D.6【答案】D【解析】结合三角形高的定义可知,以AD为高的三角形有:△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个.故选D考查题型二与三角形高有关的计算典例2.(2019·济南市期中)如图,在直角三角形ABC中,点B沿CB所在直线远离C点移动,下列说法错误的是( )A.三角形面积随之增大B.∠CAB的度数随之增大C.BC边上的高随之增大D.边AB的长度随之增大【答案】C【提示】根据三角形的面积公式、角和线段大小的比较以及三角形高的定义进行解答即可.【详解】解:A、在直角三角形ABC中,S△ABC=12BC•AC,点B沿CB所在直线远离C点移动时BC增大,则该三角形的面积越大.故A正确;B、如图,随着点B的移动,∠CAB的度数随之增大.故B正确;C、BC边上的高是AC,线段AC的长度是不变的.故C错误.D、如图,随着点B的移动,边AB的长度随之增大.故D正确;故选:C.【名师点拨】本题考查了三角形的面积,角和线段大小的比较以及三角形高的定义,解题时要注意“数形结合”数学思想的应用.变式2-1.(2020·毕节市期末)如图,△ABC 中,D ,E 分别是BC 上两点,且BD=DE=EC ,则图中面积相等的三角形有( )A .4对B .5对C .6对D .7对【答案】A 【提示】根据三角形的面积公式,知:只要同底等高,则两个三角形的面积相等,据此可得面积相等的三角形.【详解】由已知条件,得△ABD ,△ADE ,△ACE ,3个三角形的面积都相等,组成了3对,还有△ABE 和△ACD 的面积相等,共4对.故选A.【名师点拨】本题考查了三角形的相关知识,解题的关键是熟练的掌握三角形面积公式与运用.变式2-2.(2020·龙岩市期中)如图,AD ,CE 是△ABC 的两条高,已知AD=10,CE=9,AB=12,则BC 的长是( )A .10B .10.8C .12D .15【答案】B 【解析】∵AD ,CE 是△ABC 的两条高,AD=10,CE=9,AB=12,∴△ABC 的面积=12×12×9=12BC ⋅AD=54, 即12BC ⋅10=54,解得BC=10.8.故选B.变式2-3.(2018·合肥市期中)如图所示,AD CE BF 、、是ABC ∆的三条高,654AB BC AD ===,,,则CE =( )A .245B .152C .103D .3【答案】C【提示】根据三角形的面积公式解答即可. 【详解】解:因为AD 、CE 、BF 是△ABC 的三条高,654AB BC AD ===,,,所以可得:12BC•AD=12AB•CE , 可得:CE=•BC AD AB =546⨯=103. 故选C .【名师点拨】此题考查三角形的面积,关键是根据同一三角形面积相等来提示.变式2-4.(2018·烟台市期末)如图,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于点P ,若∠A=50°,则∠BPC 等于( )A .90°B .130°C .270°D .315°【答案】B 【详解】根据∠A=50°可得∠ABC+∠ACB=130°,根据CD ⊥AB ,BE ⊥AC 可得∠ABE=40°,∠ACD=40°,则∠PBC+∠PCB=130°-40°-40°=50°,则∠BPC=180°-50°=130°. 故选:B.变式2-5.(2019·荆门市期末)如图,三角形ABC ,∠BAC =90︒,AD 是三角形ABC 的高,图中相等的是( ).A .∠B =∠CB .∠BAD=∠BC .∠C =∠BAD D .∠DAC=∠C【答案】C 【提示】根据直角三角形的性质可得∠B +∠C =90︒,由AD 是三角形ABC 的高,可得∠BDA=∠ADC =90︒,再运用三角形内角和定理依次判断即可.【详解】∵∠BAC =90︒,∴∠B +∠C =90︒,故选项A 错误;∵AD 是三角形ABC 的高,∴∠BDA=90︒,∴∠BAD+∠B=90︒,故选项B 错误;∵∠BAC =90︒,∴∠BAD+ ∠DAC=90︒,又∵∠ADC =90︒,∴∠DAC+ ∠C=90︒,∴∠C=∠BAD,故选项C正确,选项D错误.故选C.【名师点拨】本题考查了三角形的高线以及三角形的内角和定理,属于基础题型.变式2-6.(2019·济南市期中)如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )A.12 B.14 C.16 D.18【答案】D【提示】连接AE和CD,要求三角形DEF的面积,可以分成三部分(△FCD+△FCE+△DCE)来分别计算,三角形ABC是一个重要的条件,抓住图形中与它同高的三角形进行提示计算,即可解得△DEF的面积.【详解】解:连接AE和CD,∵BD=AB,∴S△ABC=S△BCD=1,S△ACD=1+1=2,∵AF=3AC,∴FC=4AC,∴S△FCD=4S△ACD=4×2=8,同理可以求得:S△ACE=2S△ABC=2,则S△FCE=4S△ACE=4×2=8;S△DCE=2S△BCD=2×1=2;∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18.故选:D.【名师点拨】本题考查三角形面积及等积变换的知识,注意高相等时三角形的面积与底成正比的关系,并在实际问题中的灵活应用,有一定难度.考查题型三三角形中线有关的长度计算典例3.(2018·秦皇岛市期中)如图,AE 是ABC 的中线,已知EC 4=,DE 2=,则BD 的长为( )A .2B .3C .4D .6【答案】A【解析】试题解析:∵AE 是△ABC 的中线,EC=4,∴BE=EC=4,∵DE=2,∴BD=BE-DE=4-2=2.故选A .变式3-1.(2019·肇庆市期中)已知AD 是△ABC 的中线,且△ABD 比△ACD 的周长大3cm ,则AB 与AC 的差为( ) A .2cm B .3cm C .4cm D .6cm【答案】B【提示】根据三角形中线的定义可得BD=CD ,然后根据三角形的周长公式列式计算即可得解.【详解】解:∵AD 是△ABC 的中线,∴BD=DC ,∴△ABD 与△ACD 的周长之差=(AB+AD+BD )-(AC+AD+CD )=AB-AC ,∵△ABD 比△ACD 的周长大3cm ,∴AB 与AC 的差为3cm .故选B .【名师点拨】本题考查了三角形的中线,熟记概念并求出两三角形周长的差等于AB-AC 是解题的关键.变式3-2.(2020·哈尔滨市期中)如图,三角形ABC 中,D 为BC 上的一点,且S △ABD =S △ADC ,则AD 为( )A .高B .角平分线C .中线D .不能确定【答案】C【解析】解:设BC边上的高为h,∵S△ABD=S△ADC,∴,故BD=CD,即AD是中线.故选C.变式3-3.(2019·临清市期末)如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB 与AC的和为13cm,那么AC的长为()A.8cm B.9cm C.10cm D.11cm【答案】B【提示】根据中线的定义知CD=BD.结合三角形周长公式知AC-AB=5cm;又AC+AB=13cm.易求AC的长度.【详解】∵AD是BC边上的中线,∴D为BC的中点,CD=BD.∵△ADC的周长-△ABD的周长=5cm.∴AC-AB=5cm.又∵AB+AC=13cm,∴AC=9cm.即AC的长度是9cm.故选B.【名师点拨】本题考查了三角形的中线,根据周长的差表示出AC-AB=5cm,是解题的关键.考查题型四三角形中线有关的面积计算典例4.(2020·渠县期中)如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且△ABC的面积为4cm2,则△BEF的面积等于()A.2cm2B.1cm2C.0.5 cm2D.0.25 cm2【答案】B【提示】依据三角形的面积公式及点D 、E 、F 分别为边BC ,AD ,CE 的中点,推出14BEF ABC SS ∆=从而求得△BEF 的面积.【详解】解:∵点D 、E 、F 分别为边BC ,AD ,CE 的中点, 1111,,,2222ABD ABC BDE ABD CDE ADC BEF BEC S S S S S S S S ∆∆∆∆∆∆∆∆∴==== 14BEF ABC S S ∆∆∴= ∵△ABC 的面积是4,∴S △BEF =1.故选:B【名师点拨】本题主要考查了与三角形的中线有关的三角形面积问题,关键是根据三角形的面积公式S=12×底×高,得出等底同高的两个三角形的面积相等.变式4-1.(2018·鄂尔多斯市期中)如图,△ABC 的面积为12cm 2,点D 在BC 边上,E 是AD 的中点,则△BCE 的面积是( )A .4cm 2B .6cm 2C .8cm 2D .6cm 2【答案】B 【解析】∵E 是AD 的中点,∴S △BDE =12S △ABD ,S △DEC =12S △ADC , ∴△BCE 的面积=S △BDE +S △DEC =12×(S △ABD +S △ADC )=12×△ABC 的面积=6, 故选B .名师点拨:本题考查的是三角形的面积的计算,掌握三角形的一条中线把三角形分为面积相等的两部分是解题的关键.变式4-2.(2019·沧州市期末)如图,D ,E ,F 分别是边BC ,AD ,AC 上的中点,若S 阴影的面积为3,则△ABC 的面积是( )A .5B .6C .7D .8【答案】D【提示】利用三角形中线将三角形分成面积相等的两部分,111222ABD ACD ABC BDE ABD ADF ADC SS S S S S S ====,,,再得到1148BDE ABC DEF ABC S S S S ==,,所以83ABC S S =阴影部分即可得出. 【详解】∵D 为BC 的中点 ∴1122BDE ABD ADF ADC S S S S ==,,12DEF ADF S S =∴1148BDE ABC DEF ABC S S S S ==, ∴BDE S △+DEF S △=14ABC S +18ABC S =38ABC S ∴ABC S =83S 阴影部分=83×3=8 故选:D【名师点拨】三角形的中线将三角形分成两个面积相等的三角形,根据中线找出图中三角形的面积关系是解决本题的关键.变式4-3.(2019·温州市期中)如图,在△ABC 中,点D 是BC 边上的一点,E ,F 分别是AD ,BE 的中点,连结CE ,CF ,若S △CEF =5,则△ABC 的面积为( )A .15B .20C .25D .30【答案】B 【提示】根据题意,利用中线分的三角形的两个图形面积相等,便可找到答案【详解】解:根据等底同高的三角形面积相等,可得∵F 是BE 的中点,S △CFE =S △CFB =5,∴S △CEB =S △CEF +S △CBF =10,∵E 是AD 的中点,∴S △AEB =S △DBE ,S △AEC =S △DEC ,∵S △CEB =S △BDE +S △CDE∴S △BDE +S △CDE =10∴S △AEB +S △AEC =10∴S △ABC =S △BDE +S △CDE +S △AEB +S △AEC =20故选:B.【名师点拨】熟悉三角形中线的拓展性质:分其两个三角形的面积是相等的,这样便可在实际问题当中家以应用. 考查题型五三角形重心的有关性质典例5.(2019·北京市期中)如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的()A.三边高的交点B.三条角平分线的交点C.三边垂直平分线的交点D.三边中线的交点【答案】D【提示】根据题意得:支撑点应是三角形的重心.根据三角形的重心是三角形三边中线的交点.【详解】解:∵支撑点应是三角形的重心,∴三角形的重心是三角形三边中线的交点,故选D.【名师点拨】考查了三角形的重心的概念和性质.注意数学知识在实际生活中的运用.变式5-1.(2019·泉州市期中)如图,在△ABC中,D,E分别是BC,AC的中点,AD和BE相交于点G,若AD=6,则AG的长度为()A.2 B.3 C.4 D.5【答案】C【提示】根据D、E分别是边BC,AC的中点,AD、BF相交于G,即可得出G为三角形的重心,利用重心的性质得出AG的长即可.【详解】∵D、E分别是边BC,AC的中点,AD、BF相交于G∴G为△ABC的重心∴AG=2DG∵AD=6∴AG=4故选C.【名师点拨】本题考查的是三角形的重心性质,能够判断出点G 是三角形的重心是解题的关键.考查题型六 三角形的角平分线典例6.(2019·滨州市期末)如图,△ABC 中,AD 为△ABC 的角平分线,BE 为△ABC 的高,∠C=70°,∠ABC=48°,那么∠3是( )A .59°B .60°C .56°D .22°【答案】A 【详解】根据题意可得,在△ABC 中,70,48︒︒∠=∠=C ABC ,则62︒∠=CAB ,又AD 为△ABC 的角平分线,1262231︒︒∴∠=∠=÷=又在△AEF 中,BE 为△ABC 的高∴90159359︒︒︒∠=-∠=∴∠=∠=EFA EFA变式6-1.(2019·宁德市期末)如图,已知AE 是ΔABC 的角平分线,AD 是BC 边上的高.若∠ABC=34°,∠ACB=64°,则∠DAE 的大小是( )A .5°B .13°C .15°D .20°【答案】C 【提示】由三角形的内角和定理,可求∠BAC=82°,又由AE 是∠BAC 的平分线,可求∠BAE=41°,再由AD 是BC 边上的高,可知∠ADB=90°,可求∠BAD=56°,所以∠DAE=∠BAD-∠BAE ,问题得解.【详解】在△ABC 中,∵∠ABC=34°,∠ACB=64°, ∴∠BAC=180°−∠B−∠C=82°,∵AE 是∠BAC 的平分线,∴∠BAE=∠CAE=41°. 又∵AD 是BC 边上的高,∴∠ADB=90°,∵在△ABD中∠BAD=90°−∠B=56°,∴∠DAE=∠BAD −∠BAE =15°.【名师点拨】在本题中,我们需要注意到已知条件中已经告诉三角形的两个角,所以利用内角和定理可以求出第三个角,再有已知条件中提到角平分线和高线,所以我们可以利用角平分线和高线的性质计算出相关角,从而利用角的和差求解,在做几何证明题时需注意已知条件衍生的结论.变式6-2.(2019·信阳市期中)如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是()A.4 B.3 C.6 D.5【答案】B【解析】过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,∴DE=DF=2,∴S△ABC=×4×2+AC×2=7,解得AC=3.故选B.变式6-3.(2019·合肥市期中)如图所示,AD、AE分别是△ABC的高和角平分线,且∠B=76°,∠C=36°,则∠DAE 等于()A.20°B.18°C.45°D.30°【答案】A【提示】根据高线的定义以及角平分线的定义分别得出∠BAD=14°,∠CAD=54°,进而得出∠DAE的度数,进而得出答案.【详解】∵AD ,AE 分别是△ABC 的高和角平分线,且∠B=76°,∠C=36°,∴∠BAD=14°,∠CAD=54°,∴∠BAE=12∠BAC=12×68°=34°, ∴∠DAE=34°-14°=20°.故选:A .【名师点拨】此题主要考查了高线以及角平分线的性质,得出∠DAE 的度数是解题关键.变式6-4.(2020·泰兴市期中)如图,BE 、CF 是△ABC 的角平分线,∠A=50°,BE 、CF 相交于D ,则∠BDC 的度数是( )A .115°B .110°C .100°D .90°【答案】A【提示】由于∠A=50°,根据三角形的内角和定理,得∠ABC 与∠ACB 的度数和,再由角平分线的定义,得∠DBC+∠DCB 的度数,进而求出∠BDC 的度数.【详解】∵∠A=50°,∴∠ABC+∠ACB=180°﹣50°=130°,∵BE 、CF 是△ABC 的角平分线,∴1122EBC ABC FCB ACB ∠=∠∠=∠,,∴()1652EBC FCB ABC ACB ∠+∠=⨯∠+∠=︒,∴∠BDC=180°﹣65°=115°,故选A .【名师点拨】考查三角形内角和定理以及角平分线的性质,熟练掌握角平分线的性质是解题的关键.变式6-5.(2019·西安市期末)如图,点O 在ABC 内,且到三边的距离相等,若∠A=60°,则∠BOC 的大小为()A .135°B .120°C .90°D .60°【答案】B【提示】由条件可知O为三角形三个内角的角平分线的交点,则可知∠OBC+∠OCB=12(∠ABC+∠ACB)=12(180°-∠A),在△BOC中利用三角形的内角和定理可求得∠BOC.【详解】∵O到三边的距离相等∴BO平分∠ABC,CO平分∠ACB∴∠OBC+∠OCB=12(∠ABC+∠ACB)=12(180°−∠A)∵∠A=60°∴∠OBC+∠OCB=60°∴∠BOC=180°−(∠OBC+∠OCB)=180°−60°=120°故选B.【名师点拨】本题考查了角平分线的性质,熟练掌握角平分线把一个角分成两个相等的角是解题的关键.。
三角形的高、中线、角平分线

三角形的高、中线与角平分线教材分析:本节内容着重介绍了三角形的三种特殊线段,已学过的过直线外一点作已知直线的垂线、线段的中点、角的平分线等知识是学习本节新知识的基础,其中三角形的高学生从小学起已开始接触,教材从学生已有认知出发,从高入手,利用图形,给高作了具体定义,使学生了解三角形的高为线段,进而引出三角形的另外几种特殊线段——中线、角平分线。
通过本节内容学习,可使学生掌握三角形的高、中线、角平分线与垂线、角平分线的联系与区别。
通过学习作图、观察与探究,会发现三角形的三条高所在的直线、三条角平分线、三条中线都各自交于一点,这为三角形的重心及以后三角形的内心、外心等知识的学习打下一定的基础,另外,本节内容也是日后学习等腰三角形等特殊三角形的垫脚石。
故学好本节内容是十分必要的。
因此,对三角的高、中线、角平分线定义的理解及画法的掌握是本节教学的重点,而三角形的高由于三角形的形状改变而使其位置呈现多样性,学生难以掌握,故在各类三角形中作出它们是本课的难点。
教法:1、情境创设法:通过复习相关知识走进课堂,更能贴近学生实际,以激发学生对学习本节内容的求知欲,培养他们运用所学知识解决问题的能力。
2、加强学生学习的主动性与探究性在课堂中要充分调动学生自主学习的潜能,让他们自由探究中发现,从而发展他们的创新能力,让他们感受到成功的喜悦。
学生在画一画、折一折、何三个探究活动中体验数学知识的形成过程。
当学生在探究过程中遇到困难时,才取消组建的交流与合作,充分发挥学生的团队作用,以更好地激发学生的积极思维,得到更大的收获。
3、运用多媒体等作为教辅工具,增强学生的直观感受,扫除学生从形象思维难以跨越到抽象思维的障碍,突出重点,突破难点。
学法:1、本节重点是三角形的三种重要线段,难点是对三角形的角平分线、中线、高的准确理解、作图与正确运用,而突破难点的关键是运用好数形结合的数学思想从画图入手,从大量的活动入手获得三种线段的直观形象,进一步架起数与形之间的桥梁,加强知识间的相互联系。
三角形的高、中线与角平分线(ppt课件)

复习提问
1.什么叫线段的中点?
把一条线段分成两条相等的线段的点叫线段的中点
A
B
2.什么叫角平分线?
一条射线把一个角分成两个相等的角,这条射线叫做
这个角的平分线
B
O
A
复习提问 3.你还记得“过一点画已知直线的垂线”吗?
放、靠、过、画.
01
01
01
23
23
23
0
1 0 2 1 03 21 3 2
3
探究新知
B
C
探究新知
3.钝角三角形的三条高
(1)你能画出钝角三角形的三条高吗?
AF
(2)AC边上的高是__B_F__; BC边上的高是__A__D_;
DB
C
AB边上的高是__C_E__;
E
(3)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点.
O
(4)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点.
三角形的中线
B
D
C
定义:连接三角形的一个顶点和它所对的边的中 点,所得线段叫做三角形的这条边上的中线.
三角形中线的符号语言:
∵AD是△ABC的中线
∴BD=CD =12 BC
探究新知
思考2.如图,在△ABC中,还能画出几条中 线呢?你发现了什么特征?
还能画出2条,3条中线交于一点.
B
重心:三角形的三条中线相交于一点,三 角形三条中线的交点叫做三角形的重心.
重心
A
O C
D
探究新知
1.如图,有一块三角形的菜地,现要求分成面积比为1:1:2
三块,且图中A处是三块菜地的共同水源处,应该怎么分?
三角形的高中线与角平分线

三角形高线的证明方法
证明方法一
利用三角形面积公式证明。
证明方法二
利用中线定理证明。
证明方法三
利用直角三角形的性质证明。
03
三角形的角平分线
三角形角平分线的定义
三角形内角平分线
三角形中一个内角的平分线与这个内角的对边相顶点的距离相等。
三角形外角平分线
联系
高线、中线和角平分线都是从三角形的顶点出发,沿三角形的边或射线延伸到对 边或对角的线段,它们的交点位置相同。
作用
三条线段共同支撑着三角形的形状和大小,其中高线和角平分线共同决定着三角 形的垂直和平分关系,而中线和角平分线共同决定着三角形的对称性。
05
三角形的面积公式及应用
三角形面积公式的推导及应用
三角形角平分线的证明方法
三角形内角平分线的证明方法
利用全等三角形的方法,通过在已知点和未知点之间构造一对全等三角形, 利用全等三角形的性质得到对应边相等,从而证明三角形内角平分线定理。
三角形外角平分线的证明方法
利用相似三角形的方法,通过在已知点和未知点之间构造一对相似三角形, 利用相似三角形的性质得到对应边成比例,从而证明三角形外角平分线定理 。
2023
三角形的高中线与角平分 线
目录
• 三角形基本概念与性质 • 三角形的高线 • 三角形的角平分线 • 三角形的高线与角平分线的比较与联系 • 三角形的面积公式及应用 • 特殊三角形的性质及高线与角平分线的应用
01
三角形基本概念与性质
三角形的定义与分类
三角形是由三条不在同一直线上的线段首尾顺次相接组成的 图形。
三角形的一个外角平分线与这个角的对边延长线相交,这个交点到这个外角顶点 的距离和交点到对边顶点的距离相等。
三角形的高线中线角平分线

D
C
三角形的高
2怎样画三角形的高线 画法
A
A
A
G
F
B
E
CB
D
F
CB
CD E
三角形的高
小结: ①锐角三角形、直角三角形、钝角三角
形都有高线,三角形的三条高线所在直 线相交于点. ②锐角三角形的高线交于三角形的内部 点.直角三角形高线交于直角顶点.钝角 三角形高线交于三角形外部点. ③三角形的高是线段,而垂线是直线.
画∠A的平分线AD,交
∠A所对的边BC于点D,
线段AD叫做ΔABC的
●
角平分线.
B
A
F ●
●
●E
●
●
D
C
画一画 画出ΔABC的另外两条角平分线; 想一想 观察三条角平分线,说说你的发现。
对于其它的任意三角形是不是也有同样的结果
三角形的三条角平分线在三角形的内部交于 点
角平分线的理解
A
∵BE是△ABC的角平分线
三角形 的中线
三角形中,连结
个顶点和它对边
中的
线段
B
三角形个内角的
三角形的 角平分线
平分线与它的对 边相交,这个角 顶点与交点之间
的线段
B
A
∵AD是△ABC的BC上的高线. ∴AD⊥BC D C ∠ADB=∠ADC=90°.
A
∵ AD是△ABC的BC上的 中线. D C ∴ BD=CD= ½BC.
A
小结: ①任何三角形都有三条中线,并且都在
三角形的内部交于点. ②三角形的中线是条线段. ③三角形的任意条中线把这个
三角形分成了两个面积相等的三角形.
我来分地
如图有块三角形的菜地,现在要求分成面积比 为2:3:4三块,且图中A处是三块菜地的共同 的水源处.问:怎样分
三角形的高、中线与角平分线课件

边BC于点D,所得线段AD叫做 ABC
的角平分线.
B
D
C
你能画出三角形另外的两条角平分线吗?
思考: (1)三角形的角平分线是什么线?与角平分线有什么区别? (2)一个三角形有几条角平分线?在位置上有什么关系?
探究二: 三角形的中线与角平分线 活动4 集思广益,探究新知
A
F E
B
D
C
任何三角形都有三条角平分线; 任何三角形的三条角平分线都在三角形内部交于一点, 我们把这个点称为三角形的内心(内切圆的圆心). 三角形的角平分线是一条线段,而角平分线是一条射线.
这个方法合理吗?
探究二: 三角形的中线与角平分线
活动2 反思过程,发现新概念
在三角形中,连接一个顶点和它的对边中点的线段叫做
三角形的中线.
A
思考:
D
(1)三角形的中线是什么线? 线段
B
C
(2)一个三角形有几条中线? 三条中线
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等 底等高的三角形面积相等.
12 E F
3
B
D
4C
(2)
两个小角相等.
探究三: 利用三角形的高、中线及角平分线的概念解决问题
活动1
练习:如图,在 ABC中,AE是中线,AD是角平分线,
AF是高.则BE=C__E__=1 _B_C__;∠BAD=_∠_C__A__D__=1__∠_B__A_C__;
2
2
∠AFB=_∠__A_F__C__=90°.
练习:如图,点D、E、F分别是BC、AD、BE的中点,且
S△ABF=1,求 S△ABC .
知识点解读:三角形的高、中线与角平分线

知识点解读:三角形的高、中线与角平分线知识点1:三角形的高、中线、角平分线(掌握)知识详析:三角形的高:三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段. 高的叙述方法(右图):①的高;是ABC AD ∆ ②;D BC AD ,垂足为⊥③ 90=∠=∠CDA BDA BC D 上,且点在三角形的中线:三角形中,连结一个顶点和它对边中点的线段.几何语言:(右图)AD 是△ABC 的边BC 上的中线.逆向推理:若AD 是△ABC 的中线,则D 是边BC 的中点.三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段. 几何语言(图3):若∠1=∠2,则AD 是∠BAC 的角平分线.逆向推理:若AD 是角平分线,则∠1=∠2.【典例】1.三角形的高、中线和角平分线是代表线段还是代表射线或直线解析:这是最基本,也最易混淆的基础知识,需要牢记掌握.我们可以根据三角形的高、中线和角平分线的概念定义知道它们既不是射线,也不是直线,而均表示线段.2.如图,在△ABC 中,AE ,AD 分别是BC 边上中线和高,(1)说明△ABE 的面积与△AEC 的面积有何关系(2)你有什么发现解析:关于三角形的面积,后面我们将要学到,三角形的面积公式为底乘高的一半.此时我们可以了解到同高等底的两个三角形的面积相等,三角形的中线图3 A B C D 1 2 D CB A把三角形分成两个面积相等的三角形.故△ABE的面积与△AEC的面积相等.知识点2:三角形的重心、垂心、内心、外心、旁心(了解)知识详析:重心是三条中线的交点,它到顶点的距离是它到对边中点距离的2倍.垂心是三条高的交点,它能构成很多直角三角形相似.内心是三条角平分线的交点,它到三边的距离相等.外心是三条边垂直平分线的交点,它到三个顶点的距离相等.旁心是一个内角平分线与其不相邻的两个外角平分线的交点,它到三边的距离相等.【典例】在△ABC中,边BC上的中线AD等于9cm,那么这个三角形的重心G 到顶点A的距离是____cm.解析:根据重心的概念得出AG=2DG,即可得出答案.由AD等于9cm,故重心G到顶点A的距离是6cm.。
2021.06.03---期末备考:三角形的高线、中线、角平分线、内外角和等应用剖析

专题一三角形的高、中线与角平分线剖析一、三角形的高1.三角形的高定义:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高。
如图,线段AD是BC边上的高。
注意:高与垂线不同,高是线段,垂线是直线。
2.表示:1.AD是△ABC的BC上的高线;2.AD⊥BC于D;3.∠ADB=∠ADC=90°。
3.三角形高的交点位置:锐角三角形的三条高的交点在三角形的内部,直角三角形三条高的交点在角直角顶点,钝角三角形的三条高的交点在三角形的外部。
如下图所示。
图1 图2 图34.三角形的三条高的特性二、三角形的中线1.三角形的中线定义:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线。
2.表示:1.AD是△ABC的BC上的中线;2.BD=DC=12 BC.3.三角形的重心:三角形的三条中线相交于一点。
三角形三条中线的交点叫做三角形的重心。
重心一定在三角形内。
三、三角形的角平分线1.三角形的角平分线定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线。
2.表示:1.AD是△ABC的∠BAC的平分线;2.∠1=∠2=12∠BAC.3.三角形的角平分线的位置:三角形的三条角平分线都在三角形的内部,并且三条角平分线交于三角形内一点。
1.(2020·重庆南开中学期末)如图,在ABC 中,D 是BC 的中点,E 在AC 上,且:=1:3AE EC ,连接AD ,BE 交于点F ,若=40ABC S △,则=DCEF S 四边形( ).A .14B .15C .18D .202.(2020·重庆南开中学)如图,ABC ∆中,点D E F 、、分别在三边上,AD BE CF 、、交于一点,G E 是AC 的中点,2,6,4GDC GEC BD CD S S ∆∆===则ABC S ∆=( )A .1785B .1985C .40D .423.(2020·河南宛城期末)如图在ABC 中,AD 是高,AE 是角平分线,AF 是中线,则下列说法中错误的是( )A .BF CF =B .12EAD B C ∠=∠-∠ C .C BAD ∠=∠ D .2ABC ABF S S =△△4.(2020·江苏海州期末)如图,D、E、F是△ABC内的三个点,且D在AF上,F在CE上,E在BD上,若CF=12EF,AD=13FD,BE=14DE,△DEF的面积是12,则△ABC的面积是()A.24.5 B.26 C.29.5 D.305.(2020·陕西渭滨期末)如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC 的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=12S△ABC.其中正确的个数有( )A.1个B.2个C.3个D.4个6.(2019·广东深圳外国语学校期末)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=3,则CE2+CF2的值为( )A.6 B.9 C.18 D.367.(2020·江苏江阴·河塘中学月考)如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为()A.24 B.25 C.30 D.328.(2020·长春市第四十七中学)如图,△ABC中,点D是AC边上的中点,点E是AB 边上的中点,若S∆ABC=12 ,则图中阴影部分的面积是()A.6 B.4 C.3 D.29.(2020·江西南昌月考)如图,AD是△ABC的中线,已知△ABD的周长为22 cm,AB 比AC长3 cm,则△ACD的周长为()A.19 cm B.22 cm C.25 cm D.31 cm10.(2020·安徽安庆期中)如图,AE 是△ABC 的中线,D 是BE 上一点,若BE =5,DE =2,则CD 的长为( )A .7B .6C .5D .411.(2019·湖北蔡甸)如图,若ABC ∆的三条角平分线AD 、BE 、CF 交于点G ,则与EGC ∠互余的角是( )A .CGD ∠B .FAG ∠C .ECG ∠D .FBG ∠12.(2019·四川宜宾期末)在直角三角形ABC 中,=90C ∠︒,AD 平分BAC ∠交BC 于点D ,BE 平分ABC ∠交AC 于点E ,AD 、BE 相交于点F ,过点D 作DG AB ∥,过点B作BG DG ⊥交DG 于点G .下列结论:①135AFB ∠=︒;②2BDG CBE ∠=∠;③BC 平分ABG ∠;④BEC FBG ∠=∠.其中正确的个数是( )A .1个B .2个C .3个D .4个13.(2020·广东龙岗·龙岭初级中学期中)如图△ABC中,分别延长边AB、BC、CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为________.14.(2019·四川绵阳月考)如图,已知△ABC的周长为21cm,AB=6cm,BC边上中线AD =5cm,△ABD的周长为15cm,则AC长为_____.15.(2019·山东牡丹期末)如图ABC中,AD是BC边上的中线,BE是ABC中AD 边上的中线,若ABC的面积是24,6AE ,则点B到ED的距离是___.16.(2019·广东佛山)如图,G为△ABC的重心,点D在CB延长线上,且BD=12 BC,过D、G的直线交AC于点E,则AEAC=_____.17.(2020·江西全国月考)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,当P点在线段AD上运动时,∠E与∠B,∠ACB的数量关系为________18.(2020·江苏姜堰期末)如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC交BC于E,若∠C=80°,∠B=40°则∠DAE的度数为______.19.(2020·江苏张家港期末)如图,已知∠BDC+∠EFC=180°,∠DEF=∠B.(1)求证:ED∥BC;(2)若D,E,F分别是AB,AC,CD边上的中点,四边形ADFE的面积为6.①求△ABC的面积;②若G是BC边上一点,C G=2B G,求△FC G的面积.20.(2020·江苏姜堰期中)如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;(2)当AD为∠BAC的角平分线时.①若∠C=65°,∠B=35°,求∠DAE的度数;②若∠C-∠B=20°,则∠DAE= °.21.(2020·四川达川期末)如图,在△ABC中,AM是中线,AD是高线.(1)若AB比AC长4 cm,则△ABM的周长比△ACM的周长多__________ cm.(2)若△AMC的面积为12 cm2,则△ABC的面积为__________cm2.(3)若AD又是△AMC的角平分线,∠AMB=130°,求∠ACB的度数.(写过程)22.(2019·昆明市官渡区第一中学月考)(1)如图1,在△ABC中,BD、CD分别是△ABC 两个内角∠ABC、∠ACB的平分线.①若∠A=70°,求∠BDC的度数.②∠A=α,请用含有α的代数式表示∠BDC的度数.(直接写出答案)(2)如图2,BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线.若∠A=α,请用含有α的代数式表示∠BEC的度数.23.(2019·江苏宜兴期中)如图①,AD 平分BAC ∠,AE ⊥BC ,∠B =450,∠C =730.(1) 求DAE ∠的度数;(2) 如图②,若把“AE ⊥BC ”变成“点F 在DA 的延长线上,FE BC ⊥”,其它条件不变,求DFE ∠ 的度数;(3) 如图③,若把“AE ⊥BC ”变成“AE 平分BEC ∠”,其它条件不变,DAE ∠的大小是否变化,并请说明理由.24.(2020·江苏泰州市凤凰初级中学月考)如图,已知在△ABC中,△ABC的外角∠ABD 的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:(1)MO=MB;(2)MN=CN﹣BM.专题二三角形内角和与外角和定理剖析【技巧解析】1.三角形内角和定理(1)三角形三个内角的和180°.(2)在三角形中,已知任意两个角的度数,可求出第3个角的度数;(3)已知三角形中三个内角关系,可利用三角形内角和等于180°,列方程求出各内角的度数.2.三角形外角性质(1)三角形的外角等于与它不相邻的两个内角的和.(2)三角形内角和的另一个推论:三角形外角大于任何一个与它不相邻的内角.3.三角形外角和定理(1)在三角形的每个顶点处取一个外角,三个不同顶点处的外角的和叫做三角形的外角和. (2)三角形外角和为360°.1.(2020·阳江市阳东区大八镇大八初级中学月考)如图,已知AB∥CD,∠A=60°,∠C =25°,则∠E等于()A.60°B.25°C.35°D.45°2.(2020·浙江西湖期末)如图,直线l 1∥l 2,线段AB 交l 1,l 2于D ,B 两点,过点A 作AC ⊥AB ,交直线l 1于点C ,若∠1=15︒,则∠2=( )A .95︒B .105︒C .115︒D .125︒3.(2020·辽宁丹东期末)如图,//AB CD ,90ACB ︒∠=,CE AB ⊥,垂足为E ,图中与CAB ∠互余的角有( )A .1个B .2个C .3个D .4个4.(2020·全国)如图,在CEF △中,80E ∠=︒,50F ∠=︒,AB CF ,AD CE ,连接BC ,CD ,则A ∠的度数是( )A .45°B .50°C .55°D .80°5.(2020·银川月考)如图,在直角三角形ABC 中,AC ≠AB ,AD 是斜边上的高,DE ⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (∠C 除外)相等的角的个数是( )A .3个B .4个C .5个D .6个6.(2020·山东芝罘期中)如图,△ABC中,∠BAC=60°,∠C=80°,∠BAC的平分线AD交BC于点D,点E是AC上一点,且∠ADE=∠B,则∠CDE的度数是()A.20°B.30°C.40°D.70°7.(2020·枣庄市市中区实验中学月考)如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )A.45°B.54°C.56°D.66°8.(2020·四川省营山中学校期中)如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )A.40°B.60°C.80°D.140°9.(2020·江苏东台月考)如图,∠ABD、∠ACD的角平分线交于点P,若∠A= 50°,∠D =10°,则∠P的度数为( )A.15°B.20°C.25°D.30°10.(2020·南通市八一中学)如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB 于点E,若∠A=40°,∠P=38°,则∠C的度数为()A.36°B.39°C.38°D.40°11.(2019·四川江油期中)如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为()A.120°B.135°C.150°D.不能确定12.(2020·全国)如图,在ABC ∆中,A ABC CB =∠∠,BD 是ABC ∆内角ABC ∠的平分线,AD 是ABC ∆外角EAC ∠的平分线,CD 是ABC ∆外角ACF ∠的平分线,以下结论不正确的是( )A .//AD BCB .2ACB ADB ∠=∠C .90ADC ABD ∠=-∠ D .BD 平分ADC ∠13.(2020·博兴县吕艺镇中学月考)如图,△ABC 的∠ABC 和∠ACB 的平分线BE ,CF 相交于点G ,∠A =100°,则∠B G C =_________°.14.(2020·辽宁中山期末)如图,AE 平分,BAC BE AE ∠⊥于,//E ED AC ,,BAC a ∠=则BED ∠的度数为________________.(用含α的式子表示)15.(2020·福建新罗期末)一副三角尺如图摆放,D 是BC 延长线上一点,E 是AC 上一点,90B EDF ∠=∠=︒,30A ∠=︒,45F ∠=︒,若EF ∥BC ,则CED ∠等于_________度.16.(2020·江苏张家港期末)如图,在四边形ABCD 中,∠B =120°,∠B 与∠ADC 互为补角,点E 在BC 上,将△DCE 沿DE 翻折,得到△DC ′E ,若AB ∥C ′E ,DC ′平分∠ADE ,则∠A 的度数为______°.17.(2019·温州外国语学校期中)如图1,已知长方形坻带ABCD ,//AD CD ,//AD BC .将纸带沿EF 折叠后,点B 、C 分别落在H 、G 的位置.再沿GF 折叠成图2.点A 、D 分别落在Q 、H 的位置,已知24108QHG GFH ∠=∠-︒,则∠=EFC _______.18.(2020·哈尔滨市第四十七中学期中)在四边形ABCD 中,ADC ∠与BCD ∠的角平分线交于点E ,115DEC ∠=︒,过点B 作//BF AD 交CE 于点F ,2CE BF =,54CBF BCE ∠=∠,连接BE ,Δ4BCE S =,则CE =__________.19.(2020·江苏工业园区期末)如图,AD、AE分别是△ABC的高和角平分线,∠B=50°,∠ACB=80°.点F在BC的延长线上,F G⊥AE,垂足为H,F G与AB相交于点G.(1)求∠A G F的度数;(2)求∠DAE的度数.20.(2020·福建惠安期末)在△ABC中,∠ACB的平分线CD与外角∠EAC的平分线AF 所在的直线交于点D.(1)如图1,若∠B=60°,求∠D的度数;(2)如图2,把△ACD沿AC翻折,点D落在D′处.①当AD′⊥AD时,求∠BAC的度数;②试确定∠DAD′与∠BAC的数量关系,并说明理由.21.(2020·江苏邳州期中)如图,△ABC中,AE是△ABC的角平分线,AD是BC边上的高.(1)若∠B=35°,∠C=75°,求∠DAE的度数;(2)若∠B=m°,∠C=n°,(m<n),则∠DAE=°(直接用m、n表示).22.(2020·湖北武汉期末)如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE,AE交CD于H.∠DCE的平分线交AE于G.(1)求证:AD∥BC;(2)若∠BAC=∠DAE,∠A G C=2∠CAE.求∠CAE的度数;(3)(2)中条件∠BAC=∠DAE仍然成立,若∠A G C=3∠CAE,直接写出∠CAE的度数.23.(2019·洛阳市第五十四中学月考)如图,在ABC 中,AD 是高,AE ,BF 是角平分线,它们相交于点O .(1)若60ABC ∠=︒,70C ∠=︒,求DAE ∠的度数. (2)若70C ∠=︒,求∠BOE 的度数.(3)若ABC α∠=,()C βαβ∠=<,则DAE =∠______用含α、β的式子表示)24.(2020·北京朝阳期末)线段AB与线段CD互相平行,P是平面内的一点,且点P不在直线AB,CD上,连接P A,PD,射线AM,DN分别是∠BAP和∠CDP的平分线.(1)若点P在线段AD上,如图1,①依题意补全图1;②判断AM与DN的位置关系,并证明;(2)是否存在点P,使AM⊥DN?若存在,直接写出点P的位置;若不存在,说明理由.专题三 角平分线的性质与判定强化1.角的平分线的性质(1)角的平分线的性质:角的平分线上的点到角两边的距离相等. (2)用符号语言表示角的平分线的性质定理:若CD 平分∠ADB ,点P 是CD 上一点,且PE ⊥AD 于点E ,PF ⊥BD 于点F ,则PE =PF .2.角的平分线的判定(1)角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.(2)用符号语言表示角的平分线的判定若PE ⊥AD 于点E ,PF ⊥BD 于点F ,PE =PF ,则PD 平分∠ADB3.角的平分线的尺规作图角平分线的尺规作图(1)以O 为圆心,适当长为半径画弧,交OA 于D ,交OB 于E . (2)分别以D 、E 为圆心,大于DE 的长为半径画弧,两弧在∠AOB 内部交于点C . (3)画射线OC . 射线OC 即为所求.124.三角形角平分线的性质(1)三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.(2)三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC 的内心为,旁心为,这四个点到△ABC 三边所在直线距离相等.1.(2020·南通市通州区平潮初级中学期中)如图,在△ABC 中,E 为AC 的中点,AD 平分∠BAC ,BA :CA =2:3,AD 与BE 相交于点O ,若△OAE 的面积比△BOD 的面积大1,则△ABC 的面积是( )A .8B .9C .10D .111P 234,,PPP2.(2020·兴仁市真武山街道办事处黔龙学校月考)如图,已知CD⊥AB于D,现有四个条件:①AD=ED②∠A=∠BED③∠C=∠B④AC=EB,那么不能得出△ADC≌△EDB的条件是().A.①③B.②④C.①④D.②③3.(2020·吉林长春外国语学校月考)如图,在△ABC中,∠C=90°,AB=10,AD是△ABC 的一条角平分线.若CD=3,则△ABD的面积为()A.13 B.14 C.15 D.214.(2020·聊城市茌平区教育和体育局教研室期末)如图所示,12∠=∠,34∠=∠,则下列结论正确的有( )①AD 平分BAF ∠;②AF 平分BAC ∠;③AE 平分DAF ∠;④AF 平分DAC ∠;⑤AE 平分BAC ∠.A .4个B .3个C .2个D .1个5.(2020·辽宁北镇期末)如图,//AB CD ,BE 和CE 分别平分ABC ∠和BCD ∠,AD 过点E ,且与AB 互相垂直,点P 为线段BC 上一动点,连接PE .若8AD =,则PE 的最小值为( )A .8B .6C .5D .46.(2020·陕西商州·期末)如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,F G平分∠EFD交AB于点G,若∠BEF=70°,则∠A G F的度数为()A.35°B.45°C.55°D.65°7.(2020·辽宁凌海期末)在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N 中在∠AOB的平分线上是()A.P点B.Q点C.M点D.N点8.(2020·云南昭通期末)如图,OP 平分AOB ∠,PD OA ⊥于点D ,点E 是射线OB 上的一个动点,若3PD =,则PE 的最小值( )A .等于3B .大于3C .小于3D .无法确定9.(2019·贵州遵义)如图,已知AEF DFE EH FH ∠=∠⊥,于点H ,EG 平分AEF ∠,平移EH 恰好到GF ,连接EG ,则下列结论:①//AB CD ;②EG HF =;③EH 平分BEF FH ∠,平分EFD ∠;④90GFH ∠=︒.其中正确的结论个数是( )A .1个B .2个C .3个D .4个10.(2020·贵州赫章期末)如图,在△ABC中,∠C=90°,以点B为圆心,以适当长为半径画弧交AB、BC于P、Q两点,再分别以点P,Q为圆心,大于12P Q的长为半径画弧,两弧相交于点N,射线BN交AC于点D.若AB=10,AC=8,则CD的长是()A.2 B.2.4 C.3 D.411.(2020·湖北襄城期末)若两条直线被第三条直线所截,有一对同位角相等,则其中一对同旁内角的角平分线()A.互相垂直B.互相平行C.相交或平行D.不相等12.(2020·湖北省直辖县级单位·中考真题)如图,已知ABC 和ADE 都是等腰三角形,90BAC DAE ∠=∠=︒,,BD CE 交于点F ,连接AF ,下列结论:①BD CE =;②BF CF ⊥;③AF 平分CAD ∠;④45AFE ∠=︒.其中正确结论的个数有( )A .1个B .2个C .3个D .4个13.(2019·广西玉林期末)如图,△ABC 的三边AB ,BC ,CA 的长分别为14,12,8,其三条角平分线的交点为O ,则::ABOBCOCAOSSS=_____.14.(2020·山东牡丹期末)如图所示,在ABC ∆中,90C ∠=︒,AD 平分BAC ∠,DE AB ⊥于E ,8BC cm =,则DE DB +=________.15.(2020·南京外国语学校期中)如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=21,则DE=________.16.(2019·江苏高邮期中)如图,AB∥CD,O为∠BAC、∠ACD的平分线的交点,OE⊥AC 于E,且OE=1,则AB与CD之间的距离等于____.17.(2019·深圳实验学校中学部期中)如图,在△ABC中,∠BAC=40°,∠ACB=60°,D为△ABC外一点,DA平分∠BAC,且CBD=50°,则∠DCB的度数是_______.18.(2020·宜春市第三中学期末)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PC=4,点D是射线OA上的一个动点,则PD的最小值为_____.19.(2020·山东日照期末)如图,点D为线段BC上的一点,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CE G=180°.(1)AD与EF平行吗,请说明理由:(2)若点H在FE的延长线上,且∠ED H=∠C,∠F=∠H,那么AD平分∠BAC吗,请说明理由.20.(2020·山东期末)如图所示,直线AB∥CD,直线AB、CD被直线EF所截,E G平分∠BEF,F G平分∠DFE,(1)若∠AEF=50°,求∠EF G的度数.(2)判断E G与F G的位置关系,并说明理由.21.(2019·广东郁南期末)如图,直线AB 、CD 与MN 相交于M 、N ,∠1=105°,∠2=75°,E 、F 、O 分别在AB 、CD 、MN 上,OE OF ⊥.(1)求证://AB CD ; (2)求34∠+∠的度数;(3)若分别在OE 、CD 上取点G 、H ,使得FO 平分CFG ∠,OE 平分AEH ∠,求证://FG EH .22.(2020·广西覃塘期末)如图,D ,E ,G 分别是AB ,AC ,BC 边上的点,12180∠+∠=︒,3B ∠=∠.(1)请说明//DE BC 的理由;(2)若DE 平分ADC ∠,22B ∠=∠,判断CD 与EG 的位置关系,并说明理由.AB CD,直线EF与AB、CD分别交于点E、F,23.(2019·广东中山期末)如图,已知//点P是射线EB上一点(与点E不重合).FM、FN分别平分∠PFE和∠PFD,FM、FN交直线AB于点M、N,过点N作N H⊥FM于点H.(1)若∠BEF=64°,求∠FN H的度数;(2)猜想∠BEF和∠FN H之间有怎样的数量关系,并加以证明.。
三角形的角平分线、中线和高【全国一等奖】-课件

∠ CAE=__3__5_0
E
∠ AEB=__9_5__0
B
A
3、右图所示,AD是△ABC的中
A
线,则△ABD的面积和△ADC的
面积数量关系?
∵ AD是△ABC的中线
∴BD=DC
△ABD的面积= 1BD×AE 2
△ADC的面积=
1 2
DC×AE
B ED
C
故△ABD的面积= △ADC的面积
1.了解三角形的角平分线,中 线和高的定义。
2、 如果一个三角形的三条高的交点恰是三角形的一个
顶点,那么这个三角形是( B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角三角形
3、填空:
AB(=21)如A图F,(B1D)= ,ACDD, A,EB=E,C12 FA。是C ΔABC的三条中线,则
,(则2∠)1如= 图(∠22), A,∠A3D=,B12E,∠CAFB是C, Δ∠AABCC的BA =三2 条∠角4平。分线
2.会画三角形的角平分线,中 线和高。
3.知道三角形的角平分线,中 线和高的性质。
作业:
名称 高
基本图形
A
B
D
C
中线
A
B
D
C
角平
A
分线
B
D
C
画法
性质
3. 做“过一点作已知直线的垂线” :
一、三角形的角平分线:
定义:三角形的一个角的平分线与 A 这个角的对边相交,这个角的顶点
和交点之间的线段叫三角形的角平 分线。
角平分线的理解:
B
D
Байду номын сангаас
C
∵ A D是△ABC的角平分线
解三角形中的高、中线、角平分线问题

解三角形中的高、中线、角平分线问题
三角形是一种最基本的几何形状,它由三条线段组成,每条线段都有一个角度。
在三角形中,有三个重要的线:高线、中线和角平分线。
高线是三角形中最长的线段,它连接三角形的两个顶点,并且与三角形的底边
垂直。
高线可以用来测量三角形的高度,它可以帮助我们计算三角形的面积。
中线是三角形中的第二长的线段,它连接三角形的两个顶点,并且与三角形的
底边平行。
中线可以用来测量三角形的宽度,它可以帮助我们计算三角形的周长。
角平分线是三角形中的第三条线段,它从三角形的一个顶点出发,穿过三角形
的底边,到达另一个顶点。
角平分线可以用来测量三角形的角度,它可以帮助我们计算三角形的面积。
总之,三角形中的高线、中线和角平分线是三角形中最重要的线段,它们可以
帮助我们计算三角形的面积、周长和角度。
第二讲 三角形的高、中线与角平分线(含解析)(人教版)

第二讲三角形的高、中线与角平分线【学习目标】1.掌握三角形的高,中线及角平分线的概念。
2.掌握三角形的高,中线及角平分线的画法。
3.掌握钝角三角形的两短边上高的画法。
【温故知新】1.垂线的定义2.线段中点的概念3.角平分线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
把一条线段分成两条相等的线段的点叫做线段中点。
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
【新课学习】知识点1:三角形的高1.定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的高。
2.如图所示,AD是边BC上的高。
3.三角形的高的做法:锐角三角形的高直角三角形的高钝角三角形的高4. 三角形的三条边上的高的交点锐角三角形的高交于三角形内部一点;交点在内部的三角形是锐角三角形。
直角三角形的高交于直角顶点;交点在顶点的三角形是直角三角形。
钝角三角形的高所在的直线交于三角形外部一点。
交点在外部的三角形是钝角三角形。
5.与三角形高相关的解题方法(1)记住三角形面积公式=BC AD/2(2)等面积法。
=BC AD/2= AC BE/2= AB CF/26.例题演练【例题1】如图,于点B,于点C,且AC与BD相交于点E,则的边DE上的高是____,边AE上的高是_____;若,,,则______.【答案】AB;DC;.【解析】的边DE上的高为线段AB,边AE上的高为线段DC.知识点2:三角形的中线1. 三角形的中线定义在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线. AE是BC边上的中线.2. 三角形的重心.每一个三角形都有三条中线,并且三角形的三条中线交于一点,这个交点就是三角形的重心.【例题2】在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,求ΔADC的周长。
【答案】20cm.【解析】∵CD是△ABC的中线,∴BD=AD,∴△DBC的周长=BC+BD+CD=25cm,则BD+CD=25-BC.∴△ADC的周长=AD+CD+AC=BD+CD+AC=25-BC+AC=25-(BC-AC)=25-5=20cm.知识点3:三角形的角平分线1.三角形的角平分线的定义在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.注意:“三角形的角平分线”是一条线段.如上图线段AD是∠A的平分线。
三角形的高中线和角平分线的性质

三角形的高中线和角平分线的性质三角形是几何学中最基本且重要的图形之一,它有许多性质和定理。
在这篇文章中,我们将讨论三角形中高中线和角平分线的性质和特点。
1. 高中线的性质在任意三角形中,高是从一个顶点到对边的垂直线段。
三角形的任意两条高线都相交于同一点,该点被称为垂心。
这是三角形的一个重要性质。
2. 高中线的长度关系对于任意三角形ABC,设AD、BE和CF分别是三角形ABC的三条高线(D、E和F分别是三角形ABC对边上的高线足点)。
根据高的性质,D、E和F是共线的,且它们交于垂心H。
我们可以证明以下结论:(1)在任意三角形中,垂心到顶点的距离等于顶点到对边的距离,即DH=EH=FH。
(2)垂心将三角形的三条高线等分,即AH=DH=EH=FH。
3. 角平分线的性质角平分线是从一个角的顶点到对边上的点,将该角分成两个相等的角。
在三角形中,任意两条角平分线相交于同一点,该点被称为内心。
这也是三角形的一个重要性质。
4. 角平分线和边的关系对于任意三角形ABC,设AD、BE和CF分别是三角形ABC的三条角平分线(D、E和F分别是三角形ABC的顶点所在边上的点)。
根据角平分线的性质,D、E和F是共线的,且它们交于内心I。
我们可以证明以下结论:(1)三角形的内心到三条边的距离相等,即ID=IE=IF。
(2)内心到三边的距离和等于内心到三边所对应的角的角平分线长度之和,即ID+IE+IF=AD+BE+CF。
5. 高中线和角平分线的关系在某些三角形中,高线和角平分线有一些特殊的关系。
我们来看以下两个例子:(1)等腰三角形:对于等腰三角形ABC(AB=AC),由于两条边相等,所以角平分线也是高线,且垂心和内心重合。
(2)直角三角形:对于直角三角形ABC(∠ABC=90°),角平分线等于斜边的一半,且角平分线与斜边垂直。
综上所述,我们介绍了三角形中高中线和角平分线的性质和特点。
高中线通过三角形的一个顶点,垂直于对边,其长度有一定的关系;角平分线从一个角的顶点出发,分割该角成两个相等的角,且和其他角平分线相交于内心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形中线的理解
●
O ∵AD是△ ABC的中线 ● B C 1 ∴BD=CD= BC D 2 三角形的三条中线相交于一点, 交点在三角形的内部.
F
任意画一个三角形,然后利用刻度尺画出 这个三角形三条边的中线,你发现了什么?
演 稿
示 1
文
2 3 后 等
, /12885/ 美人如玉最新章节 扬罔夻
A F
E O C
D
锐角三角形的三条高交于同一点. 锐角三角形的三条高都在三角形的内部。
直角三角形的三条高
在纸上画出一个直角三角形。 (1) 画出直角三角形的三条高. (2)它们有怎样的位置关系? 将你的结果与同伴进行交流. A
D B
●
直角三角形的三条高 交于直角顶点.
AB 直角边BC边上的高是__________; 直角边AB边上的高是 CB ; BD 斜边AC边上的高是______________.
思 考
课堂练习
1.下列各组图形中,哪一组图形中AD是△ABC 的高( D )
C A D C B (A) D A (B)
B
C
B
A (C) D
B C D (D) A
2.如果一个三角形的三条高的交点恰是三角形的一个顶 点,那么这个三角形是( B )
பைடு நூலகம்
A.锐角三角形 C.钝角三角形
B.直角三角形 D.锐角三角形
你还记得 “过一点画已知 直线的垂线” 吗?
0 1 2 3 4 5 0 1 2 3 4 5 0 1 2 3 4 5
过三角形的一个顶 点,你能画出它的 对边的垂线吗?
0
1
2
3
4
5
6
A
B
C
0 7 8 9 10
1
2 0 3 14 2 5 3 0 1
42
5 3
4
5
三角形的高
从三角形的一个顶点 向它的对边 顶点 和垂足 所在直线作垂线, 之间的线段叫做三角形这边的高, 简称三角形的高。 B 如图, 线段AD是BC边上的高. A
三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,
A
这个角的顶点与交点之间的线段, 叫做三角形的角平分线。 ∵AD是 △ ABC的角平分线 1∠BAC ∴∠ BAD = ∠ CAD = 2
●
︶
1 2
D 三角形的三条角平分线相交于 一点,交点在三角形的内部
B
●
C
任意画一个三角形,然后利用量角器画出 这个三角形三个角的角平分线,你发现了什么?
3.如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长 BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列 说法那些是正确的,哪些是错误的. A ①AD是⊿ABE的角平分线( × ) 2 1 ②BE是⊿ABD边AD上的中线( )
×
E
③BE是⊿ABC边AC上的中线(
×)
) B
F
H
G
④CH是⊿ACD边AD上的高(
角平分线的理解
∵BE是△ABC的角平分线
A
1 ∠ABC ∠ ABE ∠CBE ∴ ____=_____= _____ 2
∵CF是△ABC的角平分线
F
O
E
∠ACF ∠BCF B ∴∠ACB=2______=2______
D
C
三角形的角平分线与角的 平分线有什么区别?
三角形的角平分线是一条线段 , 角 的平分线是一条射线.
5
2 3
4
3
2
1
0
D
C
任意画一个锐角△ABC, 请你画出BC边上的高.
注意 ! 标明 垂直的记号 和垂足的字母. B
A
D
C
0
1
2
3
4
5
0 1 4 5 6 7 8 9 10
锐角三角形的三条高
每人画一个锐角三角形。 (1) 你能画出这个三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系? 将你的结果与同伴进行交流. 锐角三角形的三条高是 在三角形的内部还是外部? B
•锐角三角形 •直角三角形 •钝角三角形
•高在三角形内部的数量 •高之间是否相交 •高所在的直线是否相交 三条高所在直线的 交点的位置
3 相交 相交
三角形内部
1 相交 相交
直角顶点
1 不相交 相交
三角形外部
三角形的三条高所在直线交于一点
三角形的中线
叫做这个三角形这边的中线.
A E
顶点与它对边中点的线段, 在三角形中,连接一个
√
D
C
三角形的高、中线与角平分线都是线段
通过这节课的学习你有哪些收获? 你还有什么想法吗?
C
议一议
钝角三角形的三条高
A F D B E C
(1) 钝角三角形的 三条高交于一点吗? (2)它们所在的直线交于一点吗? 将你的结果与同伴进行交流.
钝角三角形的三条高 不相交于一点. 钝角三角形的三条高 所在直线交于一点.
O
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线, 顶点和垂足之间的线段 叫做三角形这边的高。 三角形的三条高的特性:
