第32讲 振动(2)
振动知识点总结

振动知识点总结一、振动的基本概念振动是指物体或系统在围绕某一平衡位置或状态发生往复移动的现象。
振动是一种常见的物理现象,几乎存在于自然界的各个领域,比如机械系统、电气系统、声学系统、光学系统等。
振动的基本特征包括振幅、周期、频率、相位等。
1. 振幅(Amplitude)是指在振动过程中物体偏离平衡位置的最大距离,通常用A表示。
振幅越大,振动的幅度越大。
2. 周期(Period)是指振动完成一个完整的往复运动所需的时间,通常用T表示。
周期与频率有倒数关系,即T=1/f。
3. 频率(Frequency)是指单位时间内振动完成的往复运动次数,通常用f表示。
频率与周期有倒数关系,即f=1/T。
4. 相位(Phase)是指在振动过程中某一时刻相对于参考位置的偏移角度。
相位可以用角度或弧度表示。
振动的种类有很多,基本可以分为自由振动、受迫振动和阻尼振动。
二、自由振动自由振动是指物体在不受外力作用的情况下,由于初位移或初速度引起的振动。
自由振动的特点是振幅大小不受外界影响,周期和频率由系统固有的物理参数决定。
自由振动的系统通常可以用简谐振动模型描述。
1. 简谐振动简谐振动是指物体沿着直线或围绕平衡位置作简谐往复运动的现象。
简谐振动的特点包括振动物体的加速度与位移成正比,加速度与位移的方向相反,振动物体的速度与位移成正弦关系。
简谐振动的运动方程可以用以下公式表示:x(t) = A*cos(ωt+φ)其中,x(t)表示位移与时间的函数关系,A表示振幅,ω表示角频率,φ表示初始相位。
2. 振幅与能量在简谐振动中,振幅和能量之间存在一定的关系。
振动系统的总能量等于势能和动能之和,在振动过程中,势能和动能不断转化,但总能量保持不变。
振动系统的总能量与振幅的平方成正比,即E=1/2*k*A^2,其中E表示总能量,k表示振动系统的刚度,A表示振幅。
3. 振动的衰减在现实中,自由振动的系统往往受到阻尼和摩擦的影响,导致振动幅度逐渐减小。
经济法讲义 第32讲_第四章(2)考情分析、交不交消费税
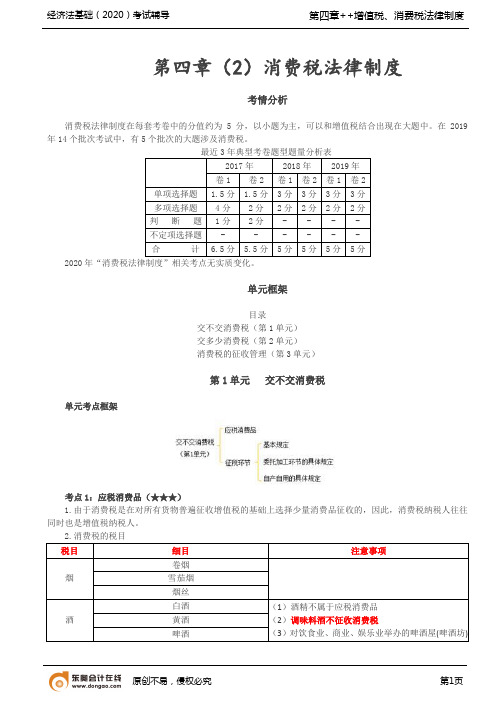
第四章(2)消费税法律制度考情分析消费税法律制度在每套考卷中的分值约为5分,以小题为主,可以和增值税结合出现在大题中。
在2019年14个批次考试中,有5个批次的大题涉及消费税。
最近3年典型考卷题型题量分析表2017年2018年2019年卷1卷2卷1卷2卷1卷2单项选择题 1.5分 1.5分3分3分3分3分多项选择题4分2分2分2分2分2分判断题1分2分----不定项选择题------合计 6.5分 5.5分5分5分5分5分2020年“消费税法律制度”相关考点无实质变化。
单元框架目录交不交消费税(第1单元)交多少消费税(第2单元)消费税的征收管理(第3单元)第1单元交不交消费税单元考点框架考点1:应税消费品(★★★)1.由于消费税是在对所有货物普遍征收增值税的基础上选择少量消费品征收的,因此,消费税纳税人往往同时也是增值税纳税人。
2.消费税的税目税目细目注意事项烟卷烟雪茄烟烟丝酒白酒(1)酒精不属于应税消费品(2)调味料酒不征收消费税(3)对饮食业、商业、娱乐业举办的啤酒屋(啤酒坊)黄酒啤酒其他酒(例如,红酒、药酒、果木酒、汽酒等利用啤酒生产设备生产的啤酒,应当征收消费税高档化妆品高档美容、修饰类化妆品舞台、戏剧、影视演员化妆用的上妆油、卸妆油、油彩,不属于本税目的征收范围高档护肤类化妆品成套化妆品贵重首饰及珠宝玉石金银首饰、铂金首饰、钻石及钻石饰品宝石坯是经采掘、打磨、初级加工的珠宝玉石半成品,对宝石坯应按规定征收消费税其他贵重首饰和珠宝玉石(如珍珠、碧玺、琥珀、珊瑚等)鞭炮、焰火包括但不限于炮竹类、组合烟花类、礼花弹类体育上用的发令纸、鞭炮药引线,不征收消费税成品油包括汽油、柴油、石脑油、溶剂油、航空煤油、润滑油、燃料油不包括原油摩托车气缸容量为250毫升的摩托车气缸容量250毫升(不含)以上的摩托车对最大设计车速不超过50公里/小时,发动机气缸总工作容量不超过50毫升的三轮摩托车不征收消费税小汽车乘用车(1)不包括大型商用客车(2)电动汽车不征收消费税(3)沙滩车、雪地车、卡丁车、高尔夫车不征收消费税(4)对于购进乘用车和中轻型商用客车整车改装生产的汽车,征收消费税中轻型商用客车超豪华小汽车(每辆不含增值税零售价格130万元及以上的乘用车和中轻型商用客车)高尔夫球及球具包括高尔夫球、高尔夫球杆及高尔夫球包(袋)、高尔夫球杆的杆头、杆身和握把高档手表销售价格(不含增值税)每只在10000元(含)以上的各类手表游艇无动力艇、帆艇不征消费税木制一次性筷子(1)竹制一次性筷子不征消费税(2)木制筷子(非一次性)不征收消费税实木地板(1)按生产工艺不同,分为独板(块)实木地板、实木指接地板和实木复合地板(2)按表面处理状态不同,分为未涂饰地板(白坯板、素板)和漆饰地板电池包括原电池、蓄电池、燃料电池、太阳能电池和其他电池涂料【经典考题1•多选题】根据消费税法律制度的规定,下列各项中,属于消费税征税范围的有()。
振动的基本知识课件

振动的基本知识
9
多频率成分的产生
• 每个振源都要产生自己独特的振动频率成分 或振动形态。
• 对已知的设备,找到了它所产生的各振动频 率成分,也就知道了振源所在。
• 对一台机器所进行的振动分析1/3 是由其振 动频率成分查找振源。
• 其余2/3 的振动分析是从已知机器的历史中 找到问题所在。
• 参考脉冲也用于测量转子的转速。
振动的基本知识
43
振动相位
• The relationship of the movement of part of a machine to a reference – for example the position of the shaft as it rotates
• 传感器质量小, 可测很高振级。
• 现场测量要注意 电磁场、声场和 接地回路的干扰。
振动的基本知识
50
非接触式位移传感器
振动的基本知识
51
加速度传感器的频响特性
振动的基本知识
52
波德图和极坐标图
波德图(Bode Plot)和极坐标图(Polar Plot)两者所含信息相同,都表示基频振动 的幅值和相位随机器转速的变化规律。
风机转速 = 5 Hz or 300 RPM
振动的基本知识
17
一个简单振动试验--提高频率
➢风机转速提高一倍 ➢波形图中的波形靠得很近 ➢风机转速 = 10 Hz or 600 RPM
振动的基本知识
18
一个简单振动试验--提高幅值
➢由于加在风机叶片上的不平衡重量,当 风机转速提高后,其振动幅值增加 ➢波形的高度是幅值.
• Phase indicates how a machine is moving
振动的基本知识

高频
总振动
低ind频ividual vibration signals
combine to form a complex time waveform showing overall vibration
简单时域波形转换到频谱
例子
一般时域波形转换到频谱
频谱与采样
公式
1. 谱线- Line 100 200 400 800 1600 3200 6400线 2. 频宽- Fmax 0-20kHz,可编程
振动周期/频率
频率(Hz)=转速(转每分钟,RPM)/60 频率f(Hz)=1/ 周期T(秒)
振动相位(1)
振动相位-(相位差)
振动相位(2)
振动相位-(相位差)
振动相位应用(1)
振动相位- 例子
振动相位应用(2)
振动相位- 例子
振动时域波型
齿轮啮合
轴承故障
振动幅值
不平衡
总振动
时间
complex time waveform 合成后的时域波形
因传感器输出的是模拟信号,而用计算机处理的 信号必须是数字信号,因此必须对采集的信号进 行模/数转换:包括采样、量化、采样保持等
信号分析系统-数字信号处理器
这是信号分析系统的核心环节,通常是由仪器中 的CPU来执行的,它包括对信号的时域、幅值域 及频域分析,同时它还有运算功能,如时域或频 域的微分、积分等
10
振幅 (mils, in/sec, g’s) 1.0
100 Displacement (mils)
Acceleration (g's)
Velocity (in/sec)
0.1 1
0.01
Common Machinery Operating Range
课程资料:第32讲_资产组的减值(2)

第四节资产组的认定及减值处理二、资产组减值测试(二)资产组减值的会计处理资产组的可收回金额如低于其账面价值的,应当确认相应的减值损失。
减值损失金额应当按照以下顺序进行分摊:首先,抵减分摊至资产组中商誉的账面价值;然后,根据资产组中除商誉之外的其他各项资产的账面价值所占比重,按比例抵减其他各项资产的账面价值。
以上资产账面价值的抵减,应当作为各单项资产(包括商誉)的减值损失处理,计入当期损益。
抵减后的各资产的账面价值不得低于以下三者之中最高者:①该资产的公允价值减去处置费用后的净额(如可确定的)②该资产预计未来现金流量的现值(如可确定的)③零【补充例题】甲公司通过吸收合并方式取得乙分公司,将乙分公司确定为一个资产组。
2017年12月31日,乙分公司出现减值迹象,需要进行减值测试。
乙分公司资产组的账面价值220万元(含合并商誉20万元),已知乙分公司资产组可收回金额为170万元。
乙分公司资产组中包括一项设备和一项专利权,2017年12月31日其账面价值分别为150万元和50万元,各资产的剩余使用寿命相同。
两项资产的可收回金额均无法确定。
资产组的减值损失应按资产组中各项资产账面价值所占比重进行分配。
不考虑其他因素的影响。
要求:计算资产组的相关减值并编制相关的会计分录。
【答案】乙分公司资产组的账面价值220万元,可收回金额为170万元,发生减值损失50万元,先冲减商誉20万元,剩余的30万元分配给设备和专利权。
设备应承担的减值损失金额=30×150÷(150+50)=22.50(万元)专利权应承担的减值损失金额=30×50÷(150+50)=7.50(万元)借:资产减值损失50贷:商誉减值准备20固定资产减值准备 22.50无形资产减值准备7.50【手写板】商誉的账面价值=20-20=0设备的账面价值=150-22.5=127.5专利权的账面价值=50-7.5=42.5【手写板】如果减值15万元借:资产减值准备15贷:商誉减值准备15商誉的账面价值=20-15=5【补充例题•多选题】(2017年)2×16年末,甲公司某项资产组(均为非金融长期资产)存在减值迹象,经减值测试,预计资产组的未来现金流量现值为4 000万元、公允价值减去处置费用后的净额为3 900万元;该资产组资产的账面价值为5 500万元,其中商誉的账面价值为300万元。
《振动基础》PPT课件

s2 n2 0
xs2est x est
通解
s1,2 in
xce 精选PPs1 Tt 1
c2es2t
44
xc1 eintc2e in t
c1co sntisinntc2co sn tisinn t
引入: b 1 c 1 c 2 ,b 2 i( c 1 c 2 )
x (t 0 ) x 0 ,x (t 0 ) x 0 x b 1 c o sn t b 2 s inn t
模型。由了机器人结构的复杂性,机器人的动力学模型也常
常很复杂,因此很难实现基于机器人动力学模型的实时控制。
精选PPT
3
3、Application
Mars e精xp选lPoPrTation
4
3、Application
Special Purpose Dex精t选eProPTus Manipulator
xAsint
T
2
1)振幅A的物理含义? 与哪些因素有关?
A
x02
x0
n
2)初始相位的物理含义 与哪些因素有关?
tg1 nx0
x0
精选PPT
47
六、单自由度扭转振动
I k
K
d精4G选PPT 32l
48
七、固有频率的计算
1)静变形法 (Static Deformation Method)
对于单自由度振动系统,当系统处于平衡时,其重力应
定系统由此发生的无阻尼自由振动。
精选PPT
54
精选PPT
22
①第i关节的有效惯量: D i i
D 11m 1m 2 l1 2m 2l2 22m 2l1l2cos2
D 22m 2l2 2
大学物理上册振动课件

振动
同方向同频率的两个简谐振动的合成
振动
A2
AA 1A2
20
A1
0
10
x1
x2
x
x
O
xAcots(0)
A A 1 2A 2 22A 1A 2co2s 0(1)0 tg0A A11csoin11s00 A A22scion220s0
A A3
3
x
A2
2
1 A1
多个同方向同频率简谐运动合成仍为简谐运动
振动
*二. 同方向不同频率简谐振动的合成
分振动 x1Aco1 st (0)
x2A co2 st (0)
合振动 xx1x2
x 2 A co22 s1 ()tco22 s1 (t0 )
AA1A2 两分振动相互减弱
如 A1=A2 , 则 A=0
振动
多个同方向同频率简谐运动的合成
x 1 A 1 co t s1 ) ( x 2 A 2 co t s2 ) (
x n A ncot sn ( )
x x 1 x 2 x n
xA co ts () o
合振动不是简谐振动
振动
x 2 A co 22 s 1 ()tco 22 s 1 (t 0)
当21时,21 21 则: xA(t)cost
式中 A(t)2Aco s2(1)t
2
c ostc o s2(1)t
2
随t 缓变 随t 快变
某一时刻
E =Ek+Ep
vA si n t (0)
xAcost(0)
Ek
振动的描述优秀课件

3.周期T与频率f • (1)周期T:完成一次全振动所需要的时间。 • (2)频率f:单位时间内完成全振动的次数。
1.T=t/N • f=1/T 【思考】实验:如何测弹簧振子的周期?简谐运动的周 期与振幅2有.何一关系次? 全振动有四个振幅 组成 3.所以S路=N•4•A ❖周期T和频率f:描述振动快慢的物理量,其大小 由振动系统本身的性质决定,所以也叫固有周期 和固有频率,与振幅无关.
(不是物体的实际运动轨迹)
思考:由振动图像可得到的那些信息?
4.由振动图像可得到的物理量
(1)、直接描述量: ①任意时刻的位移x ; ②周期T;
/cm 10
③振幅A.
(2)、间接描述量
-10
①频率f=1/T
② x-t图线上任一点的切线的斜率等于v.
③任一时刻t的振动方向
④ .任一时刻t的加速度a(F)
2、 叫做圆频率,表示简谐运动的快慢。它与频率
之间的关系为: =2f
简3、谐运“动的t表+达”式 这个量就是简谐
运动的相位,它是随时t不断变 化的物理量,表示振动所处的状
叫初相位,简态称初. 相,即t=0时的相位.
4、相位差:常指两个具有相同频率的简谐 运动的初相之差(2- 1).对频率相同的两 个简谐运动有确定的相位差为零, 一般地为=2n (n=0,1,2,……)
2、反相:相位差为 , 一般地为=(2n+1) (n=0,1,2,……)
例1:
s
s
写出振动方程.
例2
一个质点作简谐运动的振动图像如图5-15所示.从 图中可以看出,该质点的振幅A= ______m,频率 f=______Hz,从t=0开始在△t=1.8s内质点的位 移=______,路程=______.
振动知识点总结简洁易懂

振动知识点总结简洁易懂一、振动的基本概念振动是指物体在某一平衡位置附近以一定频率来回摆动的运动形式。
物体在振动过程中会不断地改变位置,即从平衡位置到最大位移再到平衡位置,然后又达到最大位移再到平衡位置再往复循环。
振动可以是机械振动,也可以是电磁振动,是一种常见的自然现象。
二、振动的分类1.按照振动形式的特点,可以分为简谐振动和非简谐振动。
简谐振动是指物体在振动过程中,其位移与时间的关系呈正弦函数规律变化,振动的周期性较强;而非简谐振动则是指物体在振动过程中,其位移与时间的关系不一定呈正弦函数规律变化,振动的周期性较弱。
2.按照振动形式的不同,可以分为机械振动和电磁振动。
机械振动是指物体在外力作用下产生的振动,比如弹簧振子、摆锤振动等;而电磁振动则是指电磁场中电荷的振动,比如天线的振动、电磁波的传播等。
3.按照振动的自由度,可以分为一维振动、二维振动和三维振动。
一维振动是指物体在振动过程中只能向一个方向运动,比如弹簧振子;二维振动是指物体在振动过程中能够向平面内的两个方向运动,比如摆锤振动;三维振动则是指物体在振动过程中能够在空间内的三个方向上同时运动,比如球形振子。
三、振动的基本规律1.振动的标准形式是正弦函数。
物体在振动过程中,其位移与时间的关系一般可以用正弦函数来表示:y=A*sin(ωt+ϕ),其中y表示位移,A表示振幅,ω表示角频率,t表示时间,ϕ表示初相位。
2.振动的频率与周期的关系。
振动的频率是指单位时间内振动的次数,用f来表示,单位是赫兹(Hz);而振动的周期是指完成一个完整振动所需的时间,用T来表示,与频率的关系可以用公式f=1/T来表示。
3.振动的能量转换。
在振动过程中,物体的动能和势能不断地相互转化。
当物体位移最大时,动能最大、势能最小;当物体经过平衡位置时,动能为零、势能最大。
因此,振动系统的能量守恒。
四、振动的参数与特性1.振幅是振动的一个重要参数,是指物体在振动过程中离开平衡位置的最大位移。
振动的描述-课件

10 5 0 -5 -10
x/cm
1 2 3 4 5 6 t/s
1 下图一质点做简谐运动的图象,从图中 可以知道( D )
A 在t=0时,质点的位移为零,速度和加速度也 为零
C O B
完成一次全振动的路径为B→O→C →O →B 由于对称性, O→C需时0.1s, C→O 需时0.1s, O→B需时0.1s
课堂例题3
• 一弹簧振子的周期是0.5s,振幅为2cm。当振 子通过平衡位置向右运动时开始计时,那么 4 次全振动,振子通过的 在2s内振子完成_____ 路程为______ 0.32m ,振子经过的位移为_____ 0 。在 右 侧,向 2.125s末,振子位于平衡位置_____ 左 运动。 _____
f=1/T
弹簧振子的周期由哪些因素决定? 猜想:弹簧振子的振动周期可能由哪些 因素决定?
设计实验: 控制变量法
结论:弹簧振子的周期T由振动系统本身的质量m和弹簧 的劲度系数k决定,而与振幅A无关。
• 简谐运动的周期由振动系统本身性质 决定,与振幅大小无关,称为振动的 固有周期,相应的频率称为固有频率。
B 在t=4s时,质点速度最大,方向沿X轴负方向 C 在t=2s时, 质点的振幅为-2cm,周期为4s D 无论何时,质点的振幅为2cm,周期为4s
• 在水平方向上做简谐运动的质点,其振动 图象如图11-1所示,假设向右为正方向, 则物体加速度向右且速度向右的时间是( ) A.0—1 s内 B.1 s—2 s C.2 s—3 s D.3 s—4 s
振动-公开课

【名师示范课】振动-公开课课件(推 荐)
小结
1.阻尼振动:振幅越来越小的振动
2.受迫振动:物体在外界驱动力作用下的振动
3.物体做受迫振动时,振动稳定后的频率等于驱
动力的频率,跟物体的固有频率无关。
Байду номын сангаас
4.共振:驱动力的频率等于振动系统的固有频率
时,受迫振动的振幅增大,这种现象叫做共振。
5.利用共振时,应使驱动力的频率接近或等于振
【名师示范课】振动-公开课课件(推 荐)
【名师示范课】振动-公开课课件(推 荐)
4.核磁共振
核磁共振(MRI)又叫核磁共振成像技术。是 继CT后医学影像学的又一重大进步。自80 年代应用以来,它以极快的速度得到发展。 其基本原理:是将人体置于特殊的磁场中, 用无线电射频脉冲激发人体内氢原子核, 引起氢原子核共振,并吸收能量。在停止 射频脉冲后,氢原子核按特定频率发出射 电信号,并将吸收的能量释放出来,被体 外的接受器收录,经电子计算机处理获得 图像,这就叫做核磁共振成像
动物体的固有频率;防止共振时,应使驱动力的
频率与振动物体的固有频率不同,而且相差越大
越好。
【名师示范课】振动-公开课课件(推 荐)
【名师示范课】振动-公开课课件(推 荐)
Eg1:实验室可以做“声波碎杯”的实验。用手指轻弹一只酒 杯,可以听到清脆的声音,测得这声音的频率为500Hz。将这 只酒杯放在两只大功率的声波发生器之间,操作人员通过调 整其发出的声波,就能使酒杯碎掉。下列说法中正确的是( ) A.操作人员一定是把声波发生器的功率调到很大 B.操作人员可能是使声波发生器发出了频率很高的超声波 C.操作人员一定是同时增大了声波发生器发出声波的频率 和功率 D.操作人员一定要将声波发生器发出的声波频率调到500Hz
物理全振动知识点总结

物理全振动知识点总结振动是物体在某一参考点周围来回运动的现象。
振动是物体的固有性质,是物体内部原子和分子间相对位置的振动。
在自然界中,振动现象无处不在,从地震和海啸到家用电器和交通工具的发动机都涉及到振动。
因此,振动是物理学中一个重要的研究领域。
本文将系统地总结物理全振动的知识点,涵盖了振动的基本概念、振动的特征、简谐振动、阻尼振动、受迫振动、共振现象等内容。
第一部分:振动的基本概念振动是物体围绕某一平衡位置来回运动的现象。
在实际中,我们可以通过观察物体的周期性运动来判断它是否在振动。
振动的周期性指的是物体以相同的周期(或频率)来回运动。
振动的周期T是一个完整的振动所需的时间,频率f是单位时间内振动的次数。
振动的幅度是指物体在振动过程中偏离平衡位置的最大距离。
振动的频率和振幅决定了振动的特征,不同物体的振动特征各有差异,这也是振动研究的重点之一。
第二部分:振动的特征振动的特征受到许多因素的影响,例如物体的质量、弹性系数、阻尼因子、外部作用力等。
振动的特征有时候可以通过一些基本的参数来描述,比如振动的频率和振幅。
在实际中,我们通常使用振动的周期T或频率f来描述振动的特征。
振动的强弱一般取决于振动的振幅,振幅越大,振动的强度越大。
振动的频率越高,振动的速度越快。
第三部分:简谐振动简谐振动是指物体在受到一定的恢复力作用下以简谐方式振动的现象。
当物体受到外力的作用时,会产生恢复力,使其回到平衡位置,从而产生振动。
简谐振动具有周期性,即在振动过程中,物体以相同的周期T来回振动。
简谐振动的频率与物体的质量和弹簧的弹性系数有关。
简谐振动常常在弹簧和振子系统中出现,这种振动具有周期性和稳定性,因此在实际中有许多应用。
第四部分:阻尼振动阻尼振动是指物体在振动过程中受到外部阻力的作用而逐渐减小振幅,最终停止振动的现象。
在阻尼振动中,振动的幅度不再保持稳定,而是逐渐减小,直到最终停止振动。
阻尼振动的频率和振幅取决于阻尼因子,不同的阻尼因子对振动的影响也有所不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2单元:简谐运动(二)一、教法建议【抛砖引玉】本单元的研究目的是使学生掌握简谐运动的图象,并使学生了解振动的能量,阻尼振动、受迫振动和共振等现象和规律。
在研究振动的图象时,一定要做好实验,为了使硬纸板做匀速直线运动,可以用一个电动机通过减速齿轮带动一个轮轴拉动硬纸板;砂漏可以用饮料筒制做,漏斗下口不要太小,直径3~5毫米即可,有利于砂子流速合适,使演示顺利进行。
通过实验引导学生,使学生认识到振动的位移随时间变化的规律。
在演示阻尼振动时,也可以用上述实验、不过硬纸板要拉慢点,摆的振幅要小点。
受迫振动的演示也是很重要的,通过演示实验,使学生Array直观地了解做受迫振动的物体,它的周期等于驱动力的周期。
为了演示好这一实验可以组装一个如图的装置,电动机通电后,能够通过皮带轮带动曲轴转动,对弹簧施以驱动力,可使弹簧振子振动起来,在演示开始时首先演示弹簧振子自由振动,测出该振子的周期,而后演示受迫振动,给电动机通电,用滑动变阻器改变电动机转速,可以使学生能直观地看到弹簧振子的周期与其固有周期不同,而只与驱动力周期一致。
在上述实验基础上再通过改变电动机转速而改变驱动力的周期,会发现驱动力周期越接近弹簧振子的固有周期时,弹簧振子的振幅越大,在二者周期相同时,弹簧振子振同幅最大,当驱动力周期小于固有周期时,振幅又将减小,再减小驱动力周期,振幅会变得更小。
由此可定性地画出共振曲线。
【指点迷津】1.同学们在观察振动图象的演示实验时要弄通:单摆摆动是围绕平衡位置做往复运动,硬纸板垂直摆动方向匀速拉动,砂子漏在硬纸板上得到图象实质上是振动位移在时间轴上的展开。
所以用它可以表示质点振动在各个时刻的位移,即该图象描述了振动质点在不同时刻对平衡位置的位移随时间的变化规律。
2.同学们可观察出图象的特征:是个正弦(或余弦)的曲线。
3.这个图象的作用:(a)你可以从图上找出振幅(b)你可以从图上找出振动周期和频率(c)你可以描述不同时刻质点对平衡位置的位移(d)你可以描述某时刻的速度、加速度4.简谐运动的能量:振子运动时能量的转化是和位移有密切关系的,请同学你在研究了弹簧振子的振动过程后,完成下表:如果没有摩擦和空气阻力,在振动过程中只有动能和势能的相互转化,振动的机械能就是守恒的。
5.机械振动的分类:(a )依据振动的特点分: (1)一般振动。
(2)简谐振动。
(b )依据振动形成的原因分:(1)自由振动:使物体振动起来后,不再补充能量。
其振动周期叫固有周期(频率)。
(2)受迫振动:物体在驱动力作用下(周期性变化的外力)的振动。
其振动的周期等于驱动力的周期(频率)。
而与本身的固有周期(频率)无关。
驱动力的作用过程就是在不断地向振动物体提供机械能,补充能量,使振动继续下去。
当驱动力的周期(频率)与物体的固有周期(频率)相等时,受迫振动的振幅最大,此时发生共振现象,所以产生共振的条件是f 驱=f 周(c )依据振幅的变化情况分:(1)等幅振动(又叫无阻尼振动)(2)减幅振动(又叫阻尼振动)二、学海导航【思维基础】在掌握了以上知识后,请看以下必须掌握的基础知识:1.能从振动图象上看出振动的周期、频率和振幅。
例:如图所示,四个质点做简谐运动的图象,若它们是从同一时刻开始记时的。
则:(1)哪个质点的振幅最大?振幅为多少?(2)哪个质点的周期最长?周期为多少?(3)哪个质点的频率最大?频率为多少?分析:这个题要求我们能利用数学知识,判断有关的物理量。
这里要求我们首先要看清横坐标、纵坐标分别表示了什么?振幅是一个什么样的物理量?在图上如何表示?周期是一个什么样的物理量?在图上如何表示?频率是一个什么样的物理量?从图上怎么看出来?以上这些问题都讨论清楚了,此题也就迎刃而解了。
(1)a 图振幅为1米,b 图和c 图振幅都是2米,d 图振幅为3米。
(2)c 图是半个周期的图象,所以它的周期为8秒,其余三个a 、d 图周期为4秒,b 图为2秒。
(3)∵f =1T;∴b 图频率最大,f = 0.5赫兹 2.能从图象上比较质点的速度、加速度、回复力等物理量。
例:上题四个图中,在第1秒末,哪个质点的加速度最小?分析:首先要弄清,何时加速度最小?加速度与什么有关?第2秒末在图象上如何找? 横坐标是时间轴,从坐标轴上可找到1秒的位置,然后再想,什么时候加速度最小?加速度最小时,必定是回复力最小时,而回复力:F = -kx ,只有x = 0时回复力最小,因此看图象,哪个图象在1秒时x = 0。
3.要求知道物体做简谐振动时机械能的转化情况,以及机械能守恒,并能定性地分析机械能随便振动位移的变化关系。
例:弹簧振子和单摆,在振动过程中动能和势能是不断变化的,在平衡位置动能 ,势能 ;在位移最大时势能 ,动能 ;在任意位置时其动能与势能的和就是振动物体的 能。
振动的 越大,表示振动的机械能越大。
分析:要知道做简谐运动的物体在平衡位置时,动能最大,势能为零,而在最大位移时势能最大,动能为零。
并且能知道振动物体从平衡位置向最大位移运动时,是由动能转化为势能的过程,而从最大位移向平衡位置运动的过程是由势能转化为动能的过程,在转化过程中机械能总量不变。
其机械能的总量决定于振幅的大小。
4.知道什么是受迫振动,并且清楚决定受迫振动频率的因素。
例:物体做受迫振动的频率等于 的频率,而跟物体的 频率无关。
分析:物体做受迫振动的频率等于驱动力的频率,而与物体的固有频率无关。
5.能利用机械能的知识计算单摆的机械能。
例:一个单摆的摆长为l ,摆球质量为m ,当摆角为θ时,单摆的总机械能为多大?分析:首先要弄清单摆的总机械能决定于什么因素?机械能的变化规律是什么?当单摆摆角为θ时,摆球的重力势能如何求?此题关键能找出摆球离开平衡位置后升高的高度,即可求出单摆的势能,∆h l =-(cos )1θ则总机械能E = E 势= mgl (1-cos θ)6.能简单解释共振现象例:洗衣机甩干时,每当它逐渐停下来的时候,机身总是在某一段很短的时间内发生强烈振动,这是什么原因?分析:当甩干机转动的频率与洗衣机的固有频率一致时,就要发生共振现象,此时就要发生强烈的振动。
7.能理解共振曲线的意义,并根据共振曲线分析有关具体问题。
例:如图示,是某物体作受迫振动的共振曲线,从图中可知这个物体振动的固有频率为 赫兹,当驱动力频率由150赫增大到250赫的过程中,物体振动的振幅变化趋势是 。
【学法指要】例1.如图所示为一弹簧振子的振动图象,在A 、B 、C 、D 、E 、F 各时刻中:(1)哪些时刻振子有最大动能?(2)哪些时刻振子有相同速度?(3)哪些时刻振子有最大的势能?(4)哪些时刻振子有最大相同的加速度?分析:解决这个问题所需基础知识有:(1)会分析振动图象,知道各时刻振动方向。
(2)知道图象上哪些点有最大位移?哪些点有最大速度?并且知道它们的方向。
(3)知道动能与速率平方成正比。
(4)知道最大势能在大小与振幅大小有关。
(5)知道最大回复力与最大位移的关系。
∵振动图象是振动在时间轴上的展开。
∴O 、B 、D 、F 点是在平衡位置上。
而A 、C 、E 点是在最大位移处。
再根据振动方向看:B 、F 两点是向下振动,D 点是向上振动,可知它们虽速率相同但方向却相反。
最后再根据位移看:A 、E 两点位移相同,C 点位移虽大小与上述两点相同,但方向相反。
可知它们虽受力相同,但方向相反,这样加速度也是大小相等,方向相反。
例2.如图所示为一单摆的振动图象,若取g = 9.8米/秒,求(1)单摆的摆长。
(2)从计时开始经过多少时间第一次达到势能最大?(3)在第2秒到第3秒这段时间内单摆的速度、动有和势能各是如何变化的?分析:要想解决这个问题,必须掌握如下知识:单摆的周期公式,单摆的摆动时动能与势能变化的规律,单摆的机械能决定于什么?最后还要懂得振动图象如何表示振幅、周期、平衡位置,如何描述单摆做简谐运动。
要想求单摆的摆长,只有利用周期公式来求:T = 2422ππl g l g 。
=T 。
周期T 可从图象上确定:T = 4秒。
这样可算出l = 3.972米。
从图示的振动图象可知,在计时开始,摆球恰好以沿x 轴正方向的速度通过平衡位置O 点,此时单摆有最大动能,随时间的延续,摆球越摆越高,速度不断变小,经过T 4其速度为0,此时势能最大,t = 1秒。
由图象可看出t = 2秒时,摆球恰好通过平衡位置,此时速度最大,动能最大,势能为零;从t = 2秒到t = 3秒过程中,从图象上可看出是平衡位置摆向最高点,这过程中速度不断减小,动能不断减小,势能不断增大,当t = 3秒时,速度变为零,动能等于零,势能最大。
例3.汽车在一条起伏不平的公路上行驶,路面上凸起处相隔的距离大约都是16米,汽车的车身是装在弹簧上的,当汽车以8米/秒的速度行驶时,车身起伏振动得最激烈,求弹簧的固有周期为多少?分析:这个题要弄清题目叙述的是个什么现象?驱动力是如何产生的?驱动力的周期如何求?汽车每行走16米经过一凸起处,汽车振动一次,形成一驱动力,当这驱动力的周期与弹簧的固有周期相同时,汽车发生共振,此时汽车振动最大,驱动力周期等于汽车经过两个凸起部分所用的时间,即T = S υ=168= 2 (秒)三、智能显示【心中有数】本单元要掌握下述知识:1.简谐振动的图象:表示了做简谐运动的质点的位移随时间变化的规律。
简谐运动的图象是一条正弦(或余弦)曲线,从该图象上可看出,质点在振动过程中各个时刻的离平衡位置的位移。
在图象中还可看出振幅和周期。
2.简谐运动的能量:某时刻做简谐运动的系统总能量等于该时刻的动能与势能的和。
简谐运动的总能量是一个恒量,不随时间而改变,它等于最大位移处的势能,或在平衡位置时的动能。
单摆的总能量可用E = mgl (cos )1-α来计算。
【动脑动手】1.如图所示为某一作简谐振动物体的振动图象,在t = 3秒时,物体(1)位移为零、速度为零;(2)位移为零、加速度为零;(3)速度最大、速度方向为正方向; (4)动能最大、势能为零。
2.如图,某单摆若分别从通过甲、乙、丙、丁四个位置开始计时,并规定向右为正方向,则它们跟A 、B 、C 、D 四个振动图象的对应关系是:(1)甲对应B ;(2)乙对应D ;(3)丙对应C ;(4)丁对应A 。
3.如图所示为一单摆和它的振动图象,O 为平衡位置B 、C 为最大位移处,规定向右为正方向,试回答:(1)振幅和周期各为多大?(2)单摆在振动过程中通过哪个位置时,作为起始时刻(即t =0)?(3)当t = 0.75秒时,单摆通过哪个位置?运动的方向向哪里?(4)在t= 0.5─0.75秒的时间内,单摆的位移、速度、加速度、动能、势能、机械能的大小分别怎样变化?4.当行驶着的火车的车轮接触到两条钢轨相接处的缝隙时,受撞击,使车厢在支持它的弹簧上振动起来。
