3第三章复变函数的积分54997

合集下载

复变函数与积分变换第3章

y
Z
C z n −1
zk
z0
把曲线C分割为n个小段. (如图)
o
z1 z2
zk −1
x
在每个小弧段 zk −1 zk ( k = 1,2,⋯ , n ) 上任取一点 ζ n ( k = 1, 2,⋯ , n ), 做和数
n
S n = ∑ f (ζ k )∆zk ,
k =1
其中， ∆zk = zk − zk −1
∫
C
f ( z )dz 存在，并且
n k =1
n k =1
∑ f (ζ k )∆zk = ∑ [u(ξ k ,ηk )∆xk − v(ξ k ,ηk )∆yk ]
n
+ i ∑ [v (ξ k ,η k )∆xk + u(ξ k ,η k )∆yk ]
k =1
∫C f ( z )dz = ∫C udx − vdy + i ∫
其中C是圆周: z − z0 = r ( r > 0) 的正向. 解积分路径的参数方程为
y
z
θ ⋅ z r
0
θ
z = z0 + re iθ
(0 ≤ θ ≤ 2π ),
o
x
∫C
2π 1 ire iθ dz = ∫ n+1 i ( n+1)θ dθ n+1 0 r ( z − z0 ) e i 2π − inθ = n ∫ e dθ , r 0
C
∫
C
zdz 积分值相同. 是否可以讨论积分与积分
路径的关系? 注意2 一般不能将函数f (z)在以α为起点, 以β 为终点的曲线C上的积分记成
∫
β
α
f ( z )dz , 因为

【复变函数】第三章复变函数的积分(工科2版)

C1 z0
D
C
f ( z)dz f ( z )dz
C C1
推广2 :设D内有n个奇点z1 , z2… zn , 作n个闭曲线C1,
C2 z2
C2 … , Cn , 且 zk Ck , Ck C j ,(k j), 则：
zn
C
目录上页下页返回结束
z1
f ( z)dz f ( z)dz
C
Proof : ∵f (z) 是解析函数
B M N A
BNA
∴积分与路径无关

AMB

ANB

AMB
f ( z )dz
c
f ( z )dz
BNA
f ( z)dz 0
例如：设 C: |z|=1, 则由于cos z在|z|=1内没有奇点, 有
1 C cos z dz 0
0
2
e
目录
上页
下页
返回
结束
1 1 1 (4) 2 r 1 z z dz |z|1 ( z 1 z )dz r | z| 1 1 r 1 z 1 dz |z|1 z dz r | z|
2i 2i 0
0 1
c2
c1
1 1 2z 1 (5) 2 r r 1 z z dz |z|1 ( z 1 z )dz | z| 1 1 r 1 z 1 dz |z|1 z dz r | z|

c
f ( z )dz

c
f ( z )dz lim f ( k )zk
0
k 1
n
若C为封闭曲线，则记为
f ( z )dz .

[工学]第3章复变函数的积分

n n k 1 k k
k
k 1 k
3.1.2积分存在的条件及其计算方法

1) 当 f ( z )是连续函数且C 是光滑(或按段光滑) 曲线时，则积分C f ( z )dz一定存在。 2)可以通过两个二元实变函数的积分来计算。

C
f ( z )dz (u iv)(dx idy) udx vdy i vdx udy
1 0
2tdt 1;
例4计算 z dz 的值，其中 C 为沿从（0， c 0）到（1，0）的线段与从（1，0）到（1， 1）的线段所连结成的折线。

解 :

c
zdz zdz zdz
c1 c2
tdt 1 it idt
0 0
1
1
1 1 i 1 i 2 2
第三章复变函数的积分

本章中,我们将给出复变函数积分的概念,然后讨论解析函数积分的性质,其中最重要的就是解析函数积分的基本定理与基本公式。这些性质是解析函数积分的基础,借助于这些性质,我们将得出解析函数的导数仍然是解析函数这个重要的结论。
本章学习目标
1了解复变函数积分的概念; 2了解复变函数积分的性质; 3掌握积分与路经无关的相关知识; 4熟练掌握柯西—古萨基本定理; 5会用复合闭路定理解决一些问题; 6会用柯西积分公式; 7会求解析函数的高阶导数.
f z dz 1
c

c
f z dz;

2
k f z dz k f z dz
c c

3 c f z g z dz c f z dz c g z dz;

第3章1复变函数的积分

1
2.复变函数积分的定义 2.复变函数积分的定义定义在区域D 内起点为A 设函数 w = f ( z ) 定义在区域D内, C是D内起点为A 终点为B 一条光滑有向曲线，终点为B的一条光滑有向曲线， n—1个分点，个分点，用将C分成n个小弧段， ∆ z k = z k − z k −1 分成n个小弧段，沿曲线C 沿曲线C的积如果极限存在, 则称该极限值为函数如果极限存在, 则称该极限值为函数 f ( z ) 分 n f ( z ) d z = lim f (ζ k ) ∆zk 记为 n→∞ →∞ C D k =1
1 + i 2) 解终点A
C2 起点 C1
1
∫
C
z d z = ∫ (1 − i ) x (1 + i )d x = 2∫ x d x= 1 0
0
1
1
z C1参数方程： = x , x : 0 → 1 参数方程：
∫
C1
z dz = ∫
1
1
0
C2参数方程： z = 1 + i y , 参数方程：
1 xd x = 2
半径为r 正向圆周半径为r的正向圆周
dz = r e idt
∫
∫
∫
∫
z d z 其中C为正向圆周: 其中C为正向圆周: 例3 计算 ∫ C |z| 1) | z |= 2, 2) | z |= 4. 解 1) | z |= 2, z = 2e it d z = 2 e it i d t z = 2e − it t : 0 → 2π − it 2π z 2π 2e 2ie it d t = ∫ 2i d t = 4π i ∫ C | z | d z = ∫0 2 0 4 解法2 解法2 由 | z |= 2 得到 z = z 4 d z = 2 1 d z = 2 ⋅2π i = 4π i 原式= 原式= ∫ ∫C z C 2z 16 2) 解由 | z |= 4 得到 z = 16 d z = 4 1 d zz= 4 ⋅2π i = 8π i 原式= 原式= ∫ ∫C z C 4z

复变函数第三章复变函数的积分

u iv d x id y
c

F x t , y t r t d t

c
u d x vd y i vd x u d y
c
一个复积分的实质是
两个实二型线积分

f x t , y t z t dt
c
dx
A x , y
d r dz
dy
x x t t y y t

复积分
f
z u x , y iv x , y
f
z x iy , d z d x id Nhomakorabeay
c
z dz
复积分存在的一个充分条件：
设函数 f ( z ) u ( x , y ) iv ( x , y ) 在逐段光滑的曲线上 C 连续，则 f z d z 必存在 .
c
f ( z ) 连续 u ( x , y )， v ( x , y ) 连续

C
udx vdy 与 vdx udy 存在
|zz0|=R全部在C的内部, 且R <.
f ( z)
0
z z
C
d z
K
f ( z) z z0
z z0
dz

zz
K
f ( z0 )
0
dz

K
f ( z ) f ( z0 )
dz
C
z
K
R z0
D
2 π if ( z 0 )

3第三章复变函数的积分

第三章复变函数的积分复变函数积分是研究解析函数的一个重要工具。

解析函数的许多重要性质，诸如“解析函数的导函数连续”及“解析函数的任意阶导数都存在”这些表面上看来只与微分学有关的命题，却是通过解析函数的复积分表示证明的，这是复变函数论在方法上的一个特点。

同时，复变函数积分理论既是解析函数的应用推广，也是后面留数计算的理论基础。

§3.1 复变函数积分的概念1 积分的定义复变函数积分主要考察沿复平面上曲线的积分。

今后除特别声明，当谈到曲线时一律是指光滑或逐段光滑的曲线，其中逐段光滑的简单闭曲线简称为围线或周线或闭路。

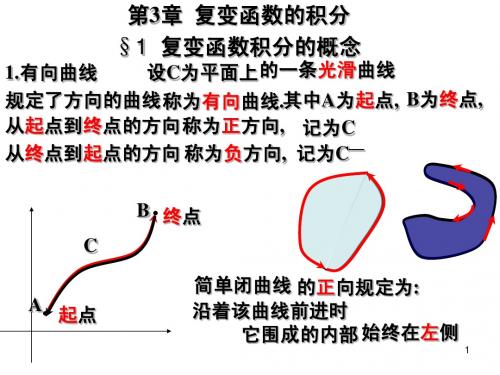
在第一章中曾定义了曲线的方向，这里回顾并作更仔细些的说明：对于光滑或逐段光滑的开曲线，只要指明了其起点和终点，从起点到终点，也就算规定了该曲线的正方向C ；对于光滑或逐段光滑的闭曲线C ，沿着曲线的某方向前进，如果C 的内部区域在左方，则规定该方向为C 的正方向（就记为C ），反之，称为C 的负方向（记为-C ）（或等价地说，对于光滑或逐段光滑的闭曲线，规定逆时针方向为闭曲线的正方向，顺时针为方向为闭曲线的负方向）；若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==，)(βα≤≤tt 为实参数，则规定t 增加的方向为正方向，即由)(αz a =到)(βz b =的方向为正方向。

定义3.1.1 复变函数的积分设有向曲线C ：)(t z z =，βα≤≤t ，以)(αz a =为起点，)(βz b =为终点，)(z f 沿C 有定义。

在C 上沿着C 从a 到b 的方向（此为实参数t 增大的方向，作为C 的正方向）任取1-n 个分点：b z z z z a n n ==-,,,,110 ，把曲线C 分成n 个小弧段。

在每个小弧段上任取一点k ζ，作和∑=∆=nk k k n z f S 1)(ζ，其中1--=∆k k k z z z ，记{}n z z ∆∆=,,max 1 λ，若0→λ时（分点无限增多，且这些弧段长度的最大值趋于零时），上述和式的极限存在，极限值为J （即不论怎样沿C 正向分割C ，也不论在每个小弧段的什么位置上取k ζ，当0→λ时n S 都趋于同一个数J ），则称)(z f 沿C 可积，称J 为)(z f 沿C （从a 到b ）的积分，并记为⎰=Cdz z f J )(，即为（3.1.1）C 称为积分路径，⎰Cdz z f )(表示沿C 的正方向的积分，⎰-C dz z f )(表示沿C 的负方向的积分。

复变函数积分

复变函数积分复变函数是数学分析中一个重要的概念，它是指从复数域到复数域的映射。

复变函数可以用于描述电磁场、流体力学等现象，也是解析几何、函数论等数学领域的基础。

在复变函数中，积分是一个重要的概念。

复变函数的积分包括曲线积分、路径无关积分、面积积分等，下面对这些内容进行详细介绍。

1. 曲线积分：曲线积分是复变函数论中的基础概念之一。

对于一个可微曲线C，我们可以定义复变函数f(z)在C上的积分。

曲线积分的计算可以使用参数方程，将积分转化为对参数的积分，并通过换元法或者分部积分等方法进行计算。

2. 路径无关积分：路径无关积分是复变函数最重要的性质之一。

当复变函数f(z)在开集D上解析时，f(z)在D上的曲线积分与路径无关，即积分结果与路径选择无关。

这个性质保证了复变函数的积分是唯一的，不受路径的影响。

3. 格林公式：格林公式是复变函数论中的基本公式之一，它与曲线积分和面积积分有密切的关系。

格林公式可以用于计算曲线积分和面积积分，并给出了二者之间的关系。

格林公式是复变函数的积分理论的重要基础。

4. 应用举例：复变函数的积分在物理学和工程学中有广泛的应用。

比如，电磁场的描述中经常使用电磁场复变函数，通过对复变函数进行积分可以得到电场、磁场等物理量。

在流体力学中，也可以使用复变函数进行描述，并通过积分得到流体速度、流量等参数。

综上所述，复变函数的积分是复变函数论中的重要内容之一，它包括曲线积分、路径无关积分、格林公式等内容。

复变函数的积分在物理学和工程学中有广泛的应用，并为这些领域提供了一种描述和计算复杂问题的方法。

复变函数的积分是复变函数论基础知识，对于进一步研究复变函数的性质和应用具有重要意义。

03_复变函数的积分

1 1
例二计算积分 n为正整数.
1 dz，其中l为 | z z0 | r正向一周， l ( z z )n 0
解： l的参数方程为z z0 rei， [0, 2 )，则
2 1 1 dz d ( z0 rei ) l ( z z0 )n 0 r n ei n
蜒f ( z )dz
l i 1
n
li
f ( z )dz 0
（4）
其中l为区域的外边界，诸li为区域的内边界，积分均沿边界的正方向进行
l
A A
B B
l1 l2
D D
C C
图3.2.2
证明：如图所示，考虑以l , l1 , l2 , , ln为边界的复通区域 D。做适当的割线连接内外边界，则原来的闭复通区域 D变成了闭单通区域 D，由于f ( z )在D上解析，按照单通区域Cauchy定理，有
2 i , n 1 1 dz l ( z z0 )n 0 , n 1
复积分的性质
性质1 若积分 f1 ( z )dz， f 2 ( z )dz都存在，则
l l
[ f ( z) f ( z)]dz
l 1 2
l
f1 ( z )dz f 2 ( z )dz；
（3）
定理2
若函数f ( z )在单通区域D内解析，则f ( z)沿D内任一分段光滑闭合曲线l的积分值为零。
另外，定理1的条件还可以减弱，即有定理3
若函数f ( z )在单通区域D内解析，在闭单通区域 D上连续，则f ( z )沿 D内任一分段光滑闭合曲线l （也可以是D的边界）的积分为零。

单通区域Cauchy定理

第三章复变函数的积分

第三章复变函数的积分复变函数的积分(简称复积分)是研究解析函数的有力工具,解析函数许多重要的性质都需要利用复积分来证明.本章主要介绍复变函数积分的定义、性质与基本计算方法，解析函数积分的基本定理——柯西-古萨定理及其推广，柯西积分公式及其推论以及解析函数与调和函数的关系.柯西-古萨定理和柯西积分公式是复变函数的理论基础，以后各章都直接地或间接地用到它们.§3.1 复变函数积分的概念1.复变函数积分的定义在介绍复变函数积分的定义之前，首先介绍有向曲线的概念.设平面上光滑或分段光滑曲线C 的两个端点为A 和B .对曲线C 而言，有两个可能方向：从点A 到点B 和从点B 到点A .若规定其中一个方向(例如从点A 到点B 的方向)为正方向，则称C 为有向曲线.此时称点A 为曲线C 的起点，点B 为曲线C 的终点.若正方向指从起点到终点的方向，那么从终点B 到起点A 的方向则称为曲线C 的负方向，记作C -.定义3.1 设C 为一条光滑或分段光滑的有向曲线，其中A 为起点，B 为终点.函数f (z )在曲线C 上有定义.现沿着C 按从点A 到点B 的方向在C 上依次任取分点：A =z 0,z 1,…,z n -1,z n =B ,图3.1将曲线C 划分成 n 个小弧段.在每个小弧段1k k z z -(k =1,2,…,n )上任取一点,k ξ,并作和式1().nn k k k S f z ξ==∆∑其中1k k k z z z -∆=-.记λ为n 个小弧段长度中的最大值.当λ趋向于零时，若不论对曲线C 的分法及点k ξ的取法如何，n S 极限存在，则称函数f (z )沿曲线C 可积，并称这个极限值为函数f (z )沿曲线C 的积分.记作1()d lim (),nkkk Cf z z f z λξ→==∆∑⎰f (z )称为被积函数，f (z )d z 称为被积表达式.若C 为闭曲线，则函数f (z )沿曲线C 的积分记作()d Cf z z ⎰.2.复变函数积分的性质性质3.1（方向性）若函数f (z )沿曲线C 可积，则()d ()d .CC f z z f z z -=-⎰⎰ (3.1)性质3.2（线性性）若函数f (z )和g (z )沿曲线C 可积，则(()())d ()d ()d ,CCCf zg z z f z z g z z αβαβ+=+⎰⎰⎰ (3.2)其中αβ,为任意常数.性质3.3（对积分路径的可加性）若函数f (z )沿曲线C 可积，曲线C 由曲线段12,,,n C C C ,依次首尾相接而成，则12()d ()d ()d ()d .nCC C C f z z f z z f z z f z z =+++⎰⎰⎰⎰(3.3)性质3.4（积分不等式）若函数f (z )沿曲线C 可积，且对z C ∀∈,满足()f z M ≤, 曲线C 的长度为L ,则()d ()d ,CCf z z f z s ML ≤≤⎰⎰(3.4)其中d d s z ==, 为曲线C 的弧微分.事实上，记k s ∆为z k -1与z k 之间的弧长，有111()()().nn nkkk k k k k k k f zf z f s ξξξ===∆≤∆≤∆∑∑∑令0λ→,两端取极限，得到()d ()d .CCf z z f z s ≤⎰⎰又由于11(),nnk k k k k f s M s ML ξ==∆≤∆=∑∑所以有()d ()d .CCf z z f z s ML ≤≤⎰⎰3.复变函数积分的基本计算方法定理3.1 若函数f (z )=u (x,y )+iv (x,y )沿曲线C 连续，则f (z )沿C 可积，且()d d d d d .CCCf z z u x v y i v x v y =-++⎰⎰⎰ (3.5)证明：设11,,,,k k k k k k k k k k k k z x iy i x x x y y y ξζη--=+=+∆=-∆=-则11111()()()().k k k k k k k k k k k k k z z z x iy x iy x x i y y x i y -----∆=-=+-+=-+-=∆∆从而1111()((,)(,))()((,)(,))((,)(,)).nnkk k k k k k k k k nk k k k k k k nk k k k k k k f z u iv x i y u x v y i v x u y ξζηζηζηζηζηζη====∆=+∆+∆=∆-∆+∆+∆∑∑∑∑上式右端的两个和数是两个实函数的第二类曲线积分的积分和.已知f (z ) 沿C 连续，所以必有u 、v 都沿C 连续，于是这两个第二类曲线积分都存在.因此积分存在()d Cf z z ⎰，且()d d d d d .CCCf z z u x v y i v x u y =-++⎰⎰⎰注(3.5)式可以看作是f (z )=u +iv 与d z =d x +i d y 相乘后得到：()d ()(d d )d d d d d d d d d .CCCCCf z z u iv x i y u x iv x iu y v yu x v y i v x u x u y =++=++-=-+++⎰⎰⎰⎰⎰定理3.1给出的条件仅仅是积分()d Cf z z ⎰存在的充分条件.该定理告诉我们，复变函数积分的计算问题可以化为其实部和虚部两个二元实函数第二类曲线积分的计算问题.下面介绍另一种计算方法--- 参数方程法.设C 为一光滑或为分段光滑曲线，其参数方程为()()()(),z z t x t iy t a t b ==+≤≤参数t =a 时对应曲线C 的起点，t =b 时对应曲线C 的终点.设f (z )沿曲线C 连续，则(())((),())((),())()().f z t u x t y t iv x t y t u t iv t =+=+由定理3.1有()d d d d d (()()()())d (()()()())d ,CCCb baaf z z u x v y i v x u yu t x t v t y t t i u t y t v t x t t =-++''''=-++⎰⎰⎰⎰⎰容易验证Re((())())()()()(),Im((())())()()()().f z t z t u t x t v t y t f z t z t u t y t v t x t '''=-'''=+所以()d (())()d .baCf z z f z t z t t '=⎰⎰(3.6)例3.1 分别沿下列路径计算积分2d Cz z ⎰和Im()d Cz z ⎰.(1) C 为从原点(0,0)到(1,1)的直线段；(2) C 为从原点(0,0)到(1,0)再到(1,1)的直线段. 解： (1) C 的参数方程为：z =(1+i )t, t 从0到1 .11222033310d ((1))d((1))(1)((1))d (1)(1).33Cz z i t i t i i t t t i i =++=++⎛⎫+=+⋅= ⎪⎝⎭⎰⎰⎰(2) 这两直线段分别记为C 1和C 2,C 1的参数方程为：y =0, x 从0到1; C 2的参数方程为：x =1, y 从0到1.1122203312103d d (1)d(1)33122(1)1.3333Cz z x x iy iy x y i y iy i i i i =+++⎛⎫=+-+ ⎪⎝⎭-+=+--==⎰⎰⎰ ()111000Im()d 0d d 1i d .2Ciz z x y y i y y =++==⎰⎰⎰⎰ 例3.2 计算积分d Czz z⎰,其中C 为图3.2所示半圆环区域的正向边界.图3.2解：积分路径可分为四段，方程分别是：C 1:z =t (-2≤ t ≤ -1); C 2:z =,i e θθ从π到0; C 3:z =t (1≤ t ≤ 2);C 4:z =2,i e θθe 从0到π.于是有123412π2π10d d d d d e 2e d e d d 2d e 2e24411.333CC C C C i i i i i i z z z z z z z z z z z z z z zt t t i t ie t t θθθθθθθθ----=+++=+++=++-=⎰⎰⎰⎰⎰⎰⎰⎰⎰例3.3 计算积分101d ()n Cz z z +-⎰,其中C 为以z 0为中心，r 为半径的正向圆周，n 为整数.解：曲线C 的方程为：0(02π)i z z re θθ=+≤≤.从而有2π11(1)002π2πd e ()e d ed .e i n n i n Cin n in nzir I z z r i i r r θθθθθθ+++-==-==⎰⎰⎰⎰图3.3当n =0时，2πd 2πI i i θ==⎰当n ≠0时，2π(cos sin )d 0niI n i n rθθθ=-=⎰.所以有0102π,0;d 0,0.()n z z ri n zn z z +-==⎧=⎨≠-⎩⎰ (3.7) 由此可见，该积分与积分路线圆周的中心和半径无关，在后面还要多次用到这个结果，需记住.§3.2 柯西-古萨定理(C auchy-Gour s at)及其推广1.柯西-古萨定理首先我们来看看上一节所举的例题，例3.1中被积函数f (z )=z 2在z 平面上处处解析，它沿连接起点与终点的任何路径的积分值相同，也就是说，该积分与路径无关.即沿z 平面上任何闭曲线的积分为零.而例3.1中另一被积函数()Im()f z z =在z 平面上处处不解析，其积分值依赖于连接起点与终点的路径.由例3.3得积分1d 2π0Cz i z z =≠-⎰,曲线C 表示圆周：|z -z 0|=r >0.其中被积函数01()f z z z =-在z 平面上除去点z 0外处处解析，但这个区域是复连通区域.由此可见，积分值与路径是否无关，可能与被积函数的解析性及区域的单连通性有关.其实，在实函数的第二类曲线积分中就有积分值与路径无关的问题.由于复变函数的积分可以用相应的两个实函数的第二类曲线积分表示，因此对于复积分与路径无关的问题，我们很自然地会想到将其转化为实函数积分与路径无关的问题来讨论.假设函数f (z )=u +iv 在单连通域D 内处处解析，f '(z )在D 内连续,由第二章2.3节中的(2.9)式知u,v 对x,y 的偏导数在D 内连续.设z =x +iy ，C 为D 内任一条简单闭曲线.则由(3.5)式，有()d d d d d .CCCf z z u x v y i v x u y =-++⎰⎰⎰记G 为C 所围区域，由格林(Green)公式有d d d d ,G Cv u u x v y x y x y ⎛⎫∂∂-=-- ⎪∂∂⎝⎭⎰⎰⎰ 由于f (z )=u +iv 在D 内解析，所以u 、v 在D 内处处都满足柯西-黎曼方程,即,.u v v ux y x y∂∂∂∂==-∂∂∂∂ 因此d d d d 0.CCu x v y v x u y -=-=⎰⎰从而()d 0.Cf z z =⎰下面的定理告诉我们去掉条件“f '(z )在D 内连续”条件，这个结论也成立.这是复变函数中最基本的定理之一.定理3.2（柯西-古萨定理）若函数f (z )是单连通域D 内的解析函数，则f (z )沿D 内任一条闭曲线C 的积分为零，即()d 0.Cf z z =⎰注：其中曲线C 不一定要求是简单曲线.事实上，对于任意一条闭曲线，它都可以看成是由有限多条简单闭曲线衔接而成的，如图3.4.图3.4这个定理是由柯西提出来的，后来由古萨给出证明.由于证明过程较复杂，我们略去其证明.由柯西-古萨定理可以得到如下两个推论：推论3.1 设C 为z 平面上的一条闭曲线，它围成单连通域D ,若函数f (z )在D D C=上解析，则()d 0.Cf z z =⎰推论3.2 设函数f (z )在单连通域D 解析,则f (z )在D 内积分与路径无关.即积分()d Cf z z⎰不依赖于连接起点z 0与终点z 1的曲线C ,而只与z 0、z 1的位置有关.证明：图3.5设C 1和C 2为D 内连接z 0 与z 1的任意两条曲线.显然C 1和2C -连接成D 内一条闭曲线C .于是由柯西-古萨定理，有12()d ()d ()d 0.CC C f z z f z z f z z -=+=⎰⎰⎰即12()d ()d .C C f z z f z z =⎰⎰2.原函数由推论\re f {cor2可知，解析函数在单连通域D 内的积分只与起点z 0 和终点z 1有关，而与积分路径无关.因此，函数f (z )沿曲线C 1和C 2的积分又可以表示为1212()d ()d ()d .z z C C f z z f z z f z z ==⎰⎰⎰固定下限z 0，让上限z 1在区域D 内变动，并令z 1=z ,则确定了一个关于上限z 的单值函数()()d .zz F z f ξξ=⎰ (3.8)并称F (z )为定义在区域D 内的积分上限函数或变上限函数.定理3.3 若函数f (z )在单连通域D 内解析，则函数F (z )必在D 内解析，且有F '(z )=f (z ). 证明：若D 内任取一点z ,以z 为中心作一个含于D 内的小圆B ，在B 内取点(0)z z z +∆∆≠,则由(3.8)式有()()()d ()d .z zzz z F z z F z f f ξξξξ+∆+∆-=-⎰⎰因为积分与路径无关，所以()d z zz f ξξ+∆⎰的积分路径可取从z 0到z 再从z 到z z +∆，其中从z 0到z 取与()d zz f ξξ⎰的积分路径相同.于是有()()()d .z zzF z z F z f ξξ+∆+∆-=⎰由于f (z )是与积分变量ξ无关的值，故()d ()d ().z zz zzzf z f z f z z ξξ+∆+∆==∆⎰⎰从而()()1()()d()1(()())d .z zz z zzF z z F z f z f f z z zf f z zξξξξ+∆+∆+∆--=-∆∆=-∆⎰⎰又f (z )在D 内解析，显然f (z )在D 内连续.所以对于任给的0ε>,必存在0δ>,使得当z ξδ-<(且ξ落在圆B 内)，即当z δ∆<时，总有()()<f f z ξε-.图3.6由复积分的性质\re f {ji f e n xi n g z hi4，有()()1()(()())d 1()()d 1.z zzz zzF z z F z f z f f z z zf f z z z zξξξξεε+∆+∆+∆--=-∆∆≤-∆≤∆=∆⎰⎰即0()()lim()z F z z F z f z z ∆→+∆-=∆,也就是()()F z f z '=.与实函数相似，复变函数也有原函数的概念及类似于牛顿-莱布尼兹(Newton-Leibniz)公式的积分计算公式.定义3.2 若在区域D 内，()z ϕ的导数等于f (z )，则称()z ϕ为f (z )在D 内的原函数. 由定理定理3.3可知，变上限函数0()()d zz F z f ξξ=⎰为f (z )的一个原函数.那么函数f (z )的全体原函数可以表示为()()z F z C ϕ=+,其中C 为任意常数.事实上，因为(()())()()()()0z F z z F z f z f z ϕϕ'''-=-=-=，所以()()z F z C ϕ-=，即()()z F z C ϕ=+.这说明了f (z )的任何两个原函数仅相差一个常数.利用这一性质我们可以得到解析函数的积分计算公式.定理3.4 若函数f (z )在单连通域D 内处处解析，()z ϕ为f (z )的一个原函数，则11010()d ()()()z zz z f z z z z z ϕϕϕ=-=⎰, (3.9)其中z 0、z 1为D 内的点.证明：由于0()()d zz F z f ξξ=⎰为f (z )的一个原函数.所以()()d ().zz F z f z C ξξϕ==+⎰当z =z 0时，根据柯西-古萨定理可知0()C z ϕ=-,于是()d ()()zz f z z ξξϕϕ=-⎰.需要特别注意的是这个公式仅适用于定义在单连通域内的解析函数.例3.4 求积分π2sin 2d i z z ⎰的值.解：因为sin2z 在复平面上解析，所以积分与路径无关.可利用（3.9）式来计算.容易验证1cos 22z -是sin2z 的一个原函数, ππ2200ππππ11sin 2d (cos πcos 0)cos 22211e e .12242i iz z i z e e --=-=--+⎛⎫+=-=-- ⎪⎝⎭⎰例3.5 求积分0(1)e d iz z z --⎰的值.解：因为(z -1)e -z 在复平面上解析，所以积分与路径无关.可利用(3.9)式来计算.(1)e d e d e d iiizzzz z z z z ----=-⎰⎰⎰, 上式右边第一个积分的计算可采用分部积分法，第二个积分可用凑微分法，得(1)e d e d e d esin1cos1.iiiizzz z i z z z zz ie i ------=+--=-=--⎰⎰⎰例3.6 设D 为直线3,2z t t ⎛=+-∞<<∞+ ⎝ 和直线4,55z t t i ⎛=+-∞<<∞-+ ⎝⎭所围成的区域. 求积分23d 2izz z +-⎰的值. 解：尽管212z z +-在复平面上存在两个奇点1和-2，但是单连通域D 包含点3和i ，又不含奇点1和-2，因此212z z+-在区域D内解析，这样就可以用(3.9)式来计算.233311d dd2312i i iz zzz z z z⎛⎫=-⎪+--+⎝⎭⎰⎰⎰函数ln(z-1)和ln(z+2)在单连通域D内可以分解为单值的解析分支，ln(z-1)的各分支导数都为11z-,ln(z+2)的各个分支的导数都为12z+.我们可以应用任何一个分支来计算积分值，在这里我们都取主支. 所以()23311d ln(1)ln(2)231153π1ln arctan3224215π1ln arctan.62432iiz z zz zii i=--++-⎛⎫⎛⎫=++⎪⎪⎝⎭⎝⎭=++⎰3.复合闭路定理柯西-古萨定理定理可推广到多连通域.设有n+1条简单闭曲线C0、C1、C2、…、C n,其中C1、C2、…、C n互不相交也互不包含，并且都含于C0的内部.这n+1条曲线围成了一个多连通区域D, D的边界C称作复闭路，它的正向为C0取逆时针方向，其它曲线都取顺时针方向.因此复闭路记作012nC C C C C---=++++.沿复闭路的积分通常取的是沿它的正向.定理 3.5若f(z)在复闭路012nC C C C C---=++++及其所围成的多连通区域内解析，则012()d()d()d()dnC C C Cf z z f z z f z z f z z=+++⎰⎰⎰⎰, (3.10) 也就是()d0Cf z z=⎰.为了叙述的简便，我们仅对n=2的情形进行说明.图3.7在图3.7中，做辅助线l1、l2和l3将C0、C1及C2连接起来，从而把多连通区域D划分为两个单连通区域D1及D2，并分别用1Γ及2Γ表示这两个区域的边界，由柯西-古萨定理有12()d 0, ()d 0.f z z f z z ΓΓ==⎰⎰于是12()d ()d 0.f z z f z z ΓΓ+=⎰⎰上式左端，沿辅助线l 1、l 2和l 3的积分，恰好沿相反方向各取了一次，从而相互抵消.因此上式左端为沿曲线C 0、1C -及2C -上的积分，即有：12()d ()d ()d 0.C C C f z z f z z f z z --=⎰⎰⎰也就是12()d ()d ()d .C C C f z z f z z f z z =+⎰⎰⎰例3.7 计算2d2Czz +⎰的值,C 为包含圆周|z |=1在内的任何正向简单闭曲线. 解：显然z =0和z =-1是函数21z z+的两个奇点，由于C 为包含圆周|z |=1在内的任何正向简单闭曲线，因此也包含了这两个奇点.在C 的内部作两个互不包含互不相交的正向圆周C 1和C 2，其中C 1的内部只包含奇点z =-1，C 2的内部只包含奇点z =0.图3.8因为21z z+在由C 、C 2、C 2所围成的复连通域内解析，所以由定理3.5、定理3.2及(3.7)式，得1211222222d d d d d d d 1102π2π00.CCC C C C C z z zz z z z z z z z z zz z z z i i =++++=-+-++=-+-=⎰⎰⎰⎰⎰⎰⎰ §3.3 柯西(C auchy)积分公式及其推论1.柯西积分公式利用复合闭路定理我们可以导出解析函数的积分表达式，即柯西积分公式.定理3.6 若f (z )是区域D 内的解析函数，C 为D 内的简单闭曲线，C 所围内部全含于D 内，z 为C 内部任一点，则1()()d 2πCf f z iz ξξξ=-⎰, (3.11) 其中积分沿曲线C 的正向.证明：取定C 内部一点z .因为f (z )在D 内解析，所以f (z )在点z 连续.即对任给的0ε∀>,必存在0δ>,当|z δξ<-时，有()()f f z εξ<-.令()()f F zξξξ=-,则()F ξ在D 内除去点z 外处处解析.现以z 为中心，r 为半径作圆周:B r z ξ=-(见图3.9),使圆B 的内部及边界全含于C 的内部.图3.9根据复合闭路定理有()()d d .C Bf f z z ξξξξξξ=--⎰⎰ 上式右端积分与圆B 的半径r 无关.令0r →，只需证明()d 2π()Bf if z z ξξξ→-⎰ 即可.由例3.3可知，1d 2πBi z ξξ=-⎰,而f (z )与ξ无关.于是 ()()()()()d 2π()d d d ()()d 2πd BB BBBBf f f z f f z if z z z z zf f z si rzξξξξξξξξξξξξξξ---==-----≤≤=-⎰⎰⎰⎰⎰⎰从而定理得证.公式(3.11)称为柯西积分公式.在柯西积分公式中,等式左端表示函数f (z )在C 内部任一点处的函数值，而等式右端积分号内的()f ξ表示f (z )在C 上的函数值.所以，柯西积分公式反映了解析函数在其解析区域边界上的值与区域内部各点处值之间的关系：函数f (z )在曲线C 内部任一点的值可用它在边界上的值来表示，或者说f (z )在边界曲线C 上的值一旦确定，则它在C 内部任一点处的值也随之确定.这是解析函数的重要特征.例如，若函数f (z )在曲线C 上恒为常数K ,z 0为C 内部任一点，则根据柯西积分公式有0001()1()d d 2π.2π2π2πC Cf KKf z i K iz i z i ξξξξξ===⋅=--⎰⎰ 即f (z )在曲线C 的内部也恒为常数K .又如，若C 为圆周:0z R ξ-=,即0Re i z θξ=+(02π)θ≤≤,则d Re d i i θξθ=,从而2π00002π00(Re )Re 1()1()d d 2π2πRe 1(Re )d .2πi i i Ci f z i f f z iz i f z θθθθξξθξθ+⋅==-=+⎰⎰⎰即解析函数在圆心z 0处的值等于它在圆周上的平均值，这就是解析函数的平均值定理.若f (z )在简单闭曲线C 所围成的区域内解析，且在C 上连续，则柯西积分公式仍然成立. 柯西积分公式可以改写成()d 2π()Cf if z z ξξξ=-⎰. (3.12) 此公式可以用来计算某些复变函数沿闭路积分.例3.8 计算积分221d z z z z =+⎰的值. 解：因为{z ^2+1在|z |=2内解析，由柯西积分公式(3.12)有22021d 2π2π.(1)z zz z i i z z ==+=⋅=+⎰ 例3.9 计算积分2πsin6d 1Czz z -⎰的值，其中C 为: 33(1)1;(2)1;(3) 3.22z z z ===-+ 解： (1) 被积函数πsin61zz +在312z =-的内部解析，由(3.12)式有， 21ππsinsinπ11πsin 66d d 2π2π.6111421CCz zzz i z z i i z z z z =⎛⎫ ⎪=⋅==⋅=-+- ⎪⎝+⎭⎰⎰(2) 被积函数πsin61zz -在312z =+的内部解析，由(3.12)式有 21ππsinsinπ11πsin 66d d 2π2π.6111421CCz zzz i z z i i z z z z =-⎛⎫ ⎪=⋅==⋅=--+ ⎪⎝-⎭⎰⎰(3) 被积函数2πsin61zz -在|z |=3的内部有两个奇点1z =±.在C 的内部作两个互不包含互不相交的正向圆周C 1和C 2，其中C 1的内部只包含奇点z =1，C 2的内部只包含奇点z =-1.由定理3.5的（3.10）式及(3.12)式，有12222πππsinsin sinππ666d d d π.11122CC C z z zi i z z z i z z z =+=+=---⎰⎰⎰例3.10 求积分42d 1z zz =-⎰的值, 其中C 为:|z |=2为正向. 解：因为z 4-1=0之解为z 1=1, z 2=i, z 3=-1, z 4=-i,分别作简单正向闭路C j 包围z j ,使C j (j =1, 2, 3, 4)互不包含，互不相交，均位于｜z ｜=2内，则由复合闭路定理有4441d d 11jj CCz zz z ==--∑⎰⎰ 又由Cauchy 积分公式得()()()()()()()()()1141213121121312d 1d 112121i 111i πi πiπi2C Cz zz z z z z z z z z z z z z z z =⋅-----=---==-++⎰⎰同理可得234444d d d ,,1212π2π1πi C CC z z z z z z =-=-=---⎰⎰⎰. 所以 44412d d 011j j z C z zz z ====--∑⎰⎰.2.高阶导数公式我们知道，一个实函数在某一区间上可导，并不能保证该函数在这个区间上二阶导数存在.但在复变函数中，如果一个函数在某一区域内解析，那么根据3.3节中的柯西积分公式推知，该解析函数是无穷次可微的.定理3.7 定义在区域D 的解析函数f (z )有各阶导数，且有()1!()()d (1,2,),2π()n n Cn f f z n iz ξξξ+==-⎰(3.13)其中C 为区域D 内围绕z 的任何一条简单闭曲线，积分沿曲线C 的正向.证明：用数学归纳法证明. 当n =1时，即证明21()()d .2π()Cf f z iz ξξξ'=-⎰也就是要证明2()1()limd .2π()z Cf z z f z iz ξξξ∆→+∆=∆-⎰由柯西积分公式(3.11)有1()()d ,2π1()()d .2πCCf f z i z f f z z iz z ξξξξξξ=-+∆=--∆⎰⎰于是22222()()1()d 2π()()()11()d d d 2π2π()1()1()d d 2π()()2π()()()()1d d ()()()()2πCC C CCCCC f z z f z f z iz f f f z z z i z i z f f i z z z z iz zf f f z z z z z ξξξξξξξξξξξξξξξξξξξξξξξξξξξξ+∆--∆-⎛⎫--= ⎪--∆-∆-⎝⎭-=∆--∆--∆+-=--∆---⎰⎰⎰⎰⎰⎰⎰⎰2d .Cξ⎰令上式为Q,显然2()1d .()()2πCzf Q z z z ξξξξ∆=--∆-⎰根据积分不等式(3. 4)有2()1d .2πCf z Q z z zξξξξ∆≤--∆-⎰因为f (z )在区域D 内解析，所以在闭曲线C 上解析并连续，从而在C 上是有界的. 即对于z C ∀∈,一定存在一个正数M ,使得|f (z )|≤M .设d 为从z 到C 上各点的最短距离，取z ∆充分小，满足2dz <∆.那么 ,.2d d z z z z z ξξξ≥≥->---∆-∆因此33212d ,d 2π2πd πd d 2CM M ML z z Q s L z ∆∆<=⋅=∆⋅⎰这里L 为C 的长度. 令0z ∆→,则0Q →,于是有()()1()()lim.2π()z Cf z z f z f f z d z iz ξξξ∆→+∆-'==∆-⎰假设n =k 时的情形成立，证明n =k +1时的情形成立.证明方法与n =1时的情形相似，但证明过程稍微复杂，这里就不证明了.这个定理实际上说明了解析函数具有无穷可微性.即定理3.8 若f (z )为定义在区域D 内的解析函数，则在D 内其各阶导数都存在并且解析.换句话说，解析函数的导数也是解析函数.由解析函数的无穷可微性，我们可以得到判断函数在区域内解析的又一个充要条件.定理3.9 函数f (z )=u (x ,y )+iv (x ,y )在区域D 内解析的充要条件是(1),,,x y x y u u v v 在D 内连续；(2)(,),(,)u x y v x y 在D 内满足柯西-黎曼方程.证明：充分性即是定理2.8.下面证明必要性. 条件(2)的必要性由定理2.7给出.再来看条件(1)，由于解析函数的导数仍然是解析函数，所以f '(z )在D 内解析，从而在D 内连续.而()x x y y f z u iv v iu '=+=-,所以,,,x y x y u u v v 在D 内连续.下面我们来看高阶导数公式的应用.高阶导数公式(3.13)可改写为()1()2πd ().()!n n Cf i f z z n ξξξ+=-⎰(3.14)可通过此式计算某些复变函数的积分.例3.11 求积分的1e d ()zn Cz ξξ+-⎰值, 其中C 为: 226x y y +=. 解：226x y y +=可化为22(3)9x y +-=，即|z -3i|=3. 被积函数2e π2z i z ⎛⎫- ⎪⎝⎭在C 的内部有一个奇点π2iz =,由(3.14)式有 π/22π/2e 2πe 2π2π.2π(e )π2zi z z i Ci i i i i z ====⋅=-'⎛⎫- ⎪⎝⎭⎰例3.12 求积分32cos πd (1)Czz z z -⎰的值，其中C 为: |z |=2.解被积函数32cos π(1)zz z -在C 的内部有两个奇点z =0和z =1,作两条闭曲线C 1和C 2互不相交且互不包含，分别包围奇点z =0和z =1，且两曲线所围区域全含于C 的内部，则根据复合闭路定理3.5和高阶导数公式(3.14)，有1212323232233223022cos πcos πcos πd d d (1)(1)(1)cos π1cos π1d d (1)(1)2πcos πcos π2π2π32!(1)(6π)π6π(12π)π.CC C C C z z z z zz z z z z z z z z z z z z z z z z i z z i i z z i i i ===+---=⋅+⋅--'''⎛⎫⎛⎫=++⋅ ⎪⎪-⎝⎭⎝⎭=-+=-⎰⎰⎰⎰⎰§3.4 解析函数与调和函数的关系根据解析函数的导数仍是解析函数这个结论，我们来讨论解析函数与调和函数的关系. 定义3.3 在区域D 内具有二阶连续偏导数并且满足拉普拉斯方程22220x yϕϕ∂∂+=∂∂ 的二元实函数(,)x y ϕ称为在D 内的调和函数.调和函数是流体力学、电磁学和传热学中经常遇到的一类重要函数.定理3.10 任何在区域D 内解析的函数f (z )=u (x ,y )+iv (x ,y )，它的实部u (x ,y )和虚部v (x ,y )都是D 内的调和函数.证明由柯西-黎曼方程有,.v u v x y y xϕ∂∂∂∂==-∂∂∂∂ 于是222222,.u v u v x y x y x y∂∂∂∂==-∂∂∂∂∂∂ 由定理3.8可知，u (x ,y )与v (x ,y )具有任意阶连续偏导，所以22.v vy x x y∂∂=∂∂∂∂ 从而22220.u vx y ∂∂+=∂∂ 同理可证22220.v vx y∂∂+=∂∂ 即u (x ,y )与v (x ,y )都是调和函数.使u (x ,y )+iv (x ,y )在区域D 内构成解析函数的调和函数v (x ,y )称为u (x ,y )的共轭调和函数.或者说，在区域D 内满足柯西-黎曼方程u x =v y ,v x =-u y 的两个调和函数u 和v 中，v 称为u 的共轭调和函数.注意：u 与v 的关系不能颠倒，任意两个调和函数u 与v 所构成的函数u +iv 不一定就是解析函数.例如，f (z )=z 2=x 2-y 2+2xyi ,其中实部u =x 2-y 2,虚部v =2xy .由于f (z )=z 2解析，显然v =2xy 是u =x 2-y 2的共轭调和函数.但是v x =2y ,u y =-2y .因此以v 作为实部、u 作为虚部的函数g (z )=v +iu 不解析.下面介绍已知单连通域D 内的解析函数f (z )=u +iv 的实部或虚部，求f (z )的方法. 这里仅对已知实部的情形进行说明,关于已知虚部求f (z )的方法可以类似得到. (1) 偏积分法利用柯西-黎曼方程(2.5)先求得v 对y 的偏导v y =u x ,此式关于y 积分得d ()uv y g x x ∂=+∂⎰,然后两边对x 求偏导,由v x =-u y ,于是有d ().y uu y g x x x∂∂'-=+∂∂⎰ 从而()d .-d u u g x x C y x x x ∂∂∂⎛⎫=+- ⎪∂∂∂⎝⎭⎰⎰故d d .-d u u u v y x C y x x x x ∂∂∂∂⎛⎫=++- ⎪∂∂∂∂⎝⎭⎰⎰⎰ 例3.13 已知u (x ,y )=2(x -1)y , f (2)=-i ,求其共轭调和函数，并写出f (z )的形式.解由柯西－黎曼方程(2.5)，有v y =u x =2y ,此式两边关于y 积分：2d ()().uv y g x y g x x∂=+=+∂⎰而(),x v g x '=又2(1),x y v u x =-=-所以2()2(1)d 2,g x x x x x C =-=-+⎰其中C 为实常数. 于是222.v y x x C =-++从而22()2(1)(2).f z x y i y x x C =-+-++由条件 f (2)=-i ,得C =-1,故22222()2(1)(21)(22()1)(1).f z x y i y x x i x y ixy x iy i z =-+-+-=--+-++=-- (2) 线积分法利用柯西-黎曼方程(2.5)有d d d d d x y y x v v x v y u x u y =+=-+,故00(,)(,)d d .x y y x x y v u x u y C =-++⎰由于该积分与积分路径无关，因此可选取简单路径(如折线)进行计算.其中(x 0,y 0)为区域D 中的点.以例3.13进行说明，u x =2y , u y =2x -2 .取(x 0,y 0)=(0,0),路径为从(0,0)到(x ,0)的直线段再从(x ,0)到(x ,y )的直线段.于是(,)(0,0)22(22)d 2d (22)d 2d 2.x y yxv x x y y Cx x y x C x x y C =-++=-++=-++⎰⎰⎰以下同前.(3) 不定积分法根据柯西-黎曼方程(2.5)及解析函数的导数公式(2.9)有().x x x y f z u iv u iu '=+=-.将x y u iu -表示成z 的函数h (z ),于是()()d .f z h z z C =+⎰还是以例3.13进行说明，2,2 2.x y u y u x ==-()2(22)2(1)2(1).f z y i x i x iy i z '=--=-+-=--从而2()2(1)d 2.f z i z z C iz iz C =--+=-++⎰由条件 f (2)=-i ,得C =-i ,故2()(1).f z i z =--小结复变函数的积分定义与微积分中定积分的定义在形式上十分相似，只是被积函数由后者的一元实函数换成了前者的复变函数，积分区间[a ,b ]换成了平面区域内的一条光滑有向曲线.复变函数的积分值不仅与积分曲线的起点和终点有关，而且一般也与积分路径有关.这些特点与微积分中第二类曲线积分相似，因而具有与第二类曲线积分类似的性质.计算复变函数的积分有两个基本方法：(1) 若被积函数为f (z )=u (x ,y )+iv (x ,y ),积分曲线为C ,则()d d d d d .C C Cf z z u x v y i v x v y =-++⎰⎰⎰ (2) 参数方程法. 设积分曲线C 的参数方程为()()z z t a t b =≤≤,则()d (())()d .bC af z z f z t z t t '=⎰⎰ 解析函数积分的基本定理主要包括柯西－古萨定理、柯西积分公式、高阶导数公式及它们的一些推论.柯西－古萨定理指在单连通域D 内解析的函数f (z )沿该区域内任一条闭曲线C 的积分为零，即()d 0C f z z =⎰.由此定理可以得到一个重要推论：在单连通域D 内解析的函数f (z )沿该区域内任一条曲线积分与路径无关.复变函数与实函数一样也有原函数的概念，并且任何两个原函数之间仅相差一个常数.基于此，对于单连通域内的解析函数有类似于实函数的牛顿－莱布尼兹公式.即1010()d ()()z z f z z z z ϕϕ=-⎰,其中f (z )为单连通域D 内的解析函数，()z ϕ为f (z )的一个原函数，01,z z D ∈分别为积分曲线的起点和终点.复合闭路定理是柯西－古萨定理的推广，即若函数f (z )在复闭路C =C 0+C 1-+C 2-+…+C n-及其所围成的多连通区域内解析，则 01()d ()d ,k nk C C f z z f z z ==∑⎰⎰ 也就是0()d 0C f z z =⎰.柯西积分公式1()()d 2πf f z i z ξξξ=-⎰ 与高阶导数公式1!()()d , 1,2,2π()n n n f z f z n i z ξξ+==-⎰是复变函数两个十分重要的公式，它们都是计算积分的重要工具.柯西积分公式反映了解析函数在其解析区域边界上的值与区域内部各点处之间的密切关系，而高阶导数公式表明解析函数的导数仍是解析函数，即解析函数具有无穷可微性.这是解析函数与实函数的本质区别.下面归纳复变函数积分的计算方法.(1)如果被积函数不是解析函数，那么不论积分路径是否封闭，只能运用上面提到的两种基本计算方法，即化为二元实函数的线积分和参数方程法.(2)如果被积函数是解析函数(包括含有有限个奇点的情形)，并且积分路径封闭，那么可以考虑柯西积分公式、高阶导数公式,并常常需要联合运用柯西－古萨定理、复合闭路定理，有时还需将被积函数作变形化为公式中的相应形式.若积分路径不封闭，那么只要被积函数在单连通域内解析，就可用定理3.4进行计算.(3)若被积函数是解析函数(含有有限个或无限个奇点)，积分路径封闭，而被积函数不能表示为柯西积分公式和高阶导数公式中所要求的形式，那么就只能用到第五章中的留数方法.解析函数f (z )=u +iv 的虚部v 为实部u 的共轭调和函数，u 与v 的关系不能颠倒，任意两个调和函数u 与v 所构成的函数u+iv 不一定是解析函数.已知单连通域D 内的解析函数f (z )的实部或虚部求f (z )的方法要求掌握，前面已经详细介绍了三种方法，这里不再赘述.重要术语及主题复积分柯西－古萨定理复合闭路定理原函数柯西积分公式高阶导数公式调和函数习题三1. 计算积分2()d C x y ix z -+⎰,其中C 为从原点到点1+i 的直线段.2. 计算积分(1)d C z z -⎰，其中积分路径C 为(1) 从点0到点1+i 的直线段;(2) 沿抛物线y =x 2，从点0到点1+i 的弧段.3. 计算积分d C z z ⎰，其中积分路径C 为(1) 从点-i 到点i 的直线段;(2) 沿单位圆周|z |=1的左半圆周，从点-i 到点i ;(3) 沿单位圆周|z |=1的右半圆周，从点-i 到点i .4. 计算积分23d Cz z z -⎰，其中积分路径C 为 (1) 从z =-2到z =2沿圆周|z |=2的上半圆周;(2) 从z =-2到z =2沿圆周|z |=2的下半圆周;(3) 沿圆周|z |=2的正向.5. 计算积分1d (31)C z z z +⎰，其中C 为16z =. 6. 计算积分(e sin )d z C z z z -⎰，其中C 为0a z =>. 7. 计算积分，其中积分路径C 为：12341(1):;23(2):;21(3):;23(4):.2C z C z C z i C z i ===+=-8.利用1d 0,:12C z C z z ==+⎰,证明： π12cos d 0.54cos θθθ+=+⎰ 9. 计算积分1d (1)2C z i z z ⎛⎫+- ⎪⎝⎭⎰，其中C 为|z |=2. 10. 利用牛顿-莱布尼兹公式计算下列积分. π200π211(1)cos d ;(2)e d ;2ln(1)(3)(2)d ;(4)d ;1iz i ii z z z z iz z z z +--+++⎰⎰⎰⎰ 12011tan (5)sin d ;(6)d cos i z z z z z z +⎰⎰ (沿1到i 的直线段) . 11. 求积分2e d 1z C z z +⎰，其中C 为： 12. 计算积分221d 1C z z z z -+-⎰，其中C 为|z |=2. 13. 计算积分41d 1Cz z +⎰，其中C 为222x y x +=.14. 求积分2sin d 9r zz z z =+⎰，其中C 为|z -2i |=2. 15. 求积分()33d d (1)1C z z z z +-⎰，其中r ≠1. 16. 求下列积分的值,其中积分路径C 均为|z |=1. 53020e cos (1)d ;(2)d ;tan /21(3)d ,.()2z C CC z z z z z z z z z z <-⎰⎰⎰17. 计算积分33d d (1)(1)C z z z z -+⎰，其中C 为: (1) 中心位于点z =1，半径为R <2的正向圆周;(2) 中心位于点z =-1，半径为R <2的正向圆周;(3) 中心位于点z =1，半径为R >2的正向圆周;(4) 中心位于点z =-1，半径为R >2的正向圆周.18. 设函数3223()d f z ax bx y cxy y =+++是调和函数，其中a,b,c 为常数.问a,b,c 之间应满足什么关系？19. 验证下列函数为调和函数.3223(1)632;(2)e cos 1(e sin 1).x x x x y xy y y i y ωω=--+=+++ 20. 证明：函数2222,x u x y v x y =-=+都是调和函数，但f (z )=u +iv 不是解析函数. 21. 设u 是调和函数，且不恒为常数，问：(1) u 2是否是调和函数?(2) 对怎样的f ，函数f (u )为调和函数?22. 由下列各已知调和函数，求解析函数f (z )=u +iv ：2222(1);(2),(1)0;(3)e (cos sin ),(0)2;(4)arctan ,0.x u x y xy y u f x y v y y x y x y f y v x x=-+==+=+++==> 23.设12()()()()n p z z a z a z a =---,其中(1,2,,)i a i n =各不相同，闭路C 不通过12,,,n a a a ,证明积分1()d 2π()C p z z i p z '⎰ 等于位于C 内的p(z )的零点的个数.24.试证明下述定理(无界区域的柯西积分公式):设f (z )在闭路C 及其外部区域D 内解析，且lim ()z f z A →∞=≠∞，则 (),,1()d ,.2πC f z A z D f A z G i zξξξ-+∈⎧=⎨∈-⎩⎰ 其中G 为C 所围内部区域.。

复变积分知识点总结

复变积分知识点总结一、复变函数的积分1. 复变函数的积分复变函数的积分是指对复平面上的函数进行积分，其中积分路径可以是一条曲线或者一条闭合曲线。

复变函数的积分包括对于实部和虚部的积分两部分，也可以看作是对于复变函数的实部和虚部的积分的和。

复变函数的积分可以用复积分的方式来表示，即对于积分路径上的每一个点，都可以对应一个复数，这样对于整个路径上的所有点的积分就可以用复数来表示。

2. 复变函数的积分性质复变函数的积分具有一些独特的性质，比如线性性、可微性、路径无关性等。

其中线性性是指对于复变函数的积分满足线性组合的性质，即对于两个复变函数的积分和它们的线性组合的积分是相同的。

而可微性是指对于复变函数的积分可以通过对积分路径上的点进行微分来得到，这与实部和虚部的积分分别成立。

路径无关性是指对于一个复变函数在不同的积分路径上积分得到的结果是相同的。

3. 古代积分定理古代积分定理是复变积分的重要定理之一，它是复平面上函数积分的一个基本定理，也是复变函数在复平面上的积分与在实数轴上的积分之间的联系的一个重要桥梁。

古代积分定理表明，对于一个复变函数在一个简单闭合曲线内的积分等于该函数在这个闭合曲线上的积分。

古代积分定理同时也说明了对于一个复变函数在整个复平面上的积分等于该函数在所有简单闭合曲线上的积分之和。

4. 柯西-黎曼积分定理柯西-黎曼积分定理是复变积分的另一个重要定理，它是复变函数积分在实数轴上的积分的推广和深化，也是复变积分的一个基本定理。

柯西-黎曼积分定理表明了对于一个复变函数来说，如果它在一个闭合曲线内保持解析，那么对于这个曲线内的复变函数的积分一定等于零。

柯西-黎曼积分定理是复变积分中一个非常重要且基础的定理，它为复变函数积分的计算和应用提供了一个非常重要的方法和途径。

5. 积分的应用复变积分在工程、物理、数学等领域都有广泛的应用，比如它可以用来求解一些特殊的积分问题，解决一些特殊的微分方程问题，描述一些特殊的物理现象等。

复变函数与积分变换第三章

第三章复变函数的积分
§3.1 复变函数积分的概念
1. 有向曲线 2. 积分的定义 3. 积分性质 4. 积分存在的条件及其计算法
1. 有向曲线
约定: C 光滑或分段光滑曲线(因而可求长).
C的表示 : z(t) x(t) iy(t) ( t ) (1)
z'(t)连续且z'(t) 0
1
(3
4i)2 tdt
(3
4i )2
1
tdt
o
C
0
0
x
(3 4i)2 . 2
另解：因为Czdz C ( x iy)(dx idy)
y
C zdz C xdx ydy iC ydx xdy
A
这两个积分都与路线C 无关
所以不论C 是怎样从原点连接到点3 4i 的 o
x
曲线,
zdz (3 4i)2 .
定理3.1 若f (z) u( x, y) iv( x, y)在光滑曲线C
上连续,则f (z)沿C可积,即C f (z)dz存在.
且 C f (z)dz C udx vdy iC vdx udy (4)
记忆
C (u iv)(dx idy)
证明令zk xk iyk xk xk xk1 yk yk yk1
k k ik u(k ,k ) uk v(k ,k ) vk
n
n
Sn f ( k )zk (uk ivk )(xk iyk )
k 1 n
k 1 n
u(k ,k )xk v(k ,k )yk
k 1
k 1
当 0时，均是
n
n
实函数的曲线积分.
i[ v(k ,k )xk u(k ,k )yk ]

复变函数-第三章-复变函数的积分

19
例10 求 z cos zdz 的值.
0
i
另解
0 z cos zdz 0 zd(sin z )
[ z sin z ] sin zdz
i 0 0 i
i
i
i [ z sin z cos z ]0 e 1 1.
20
4.3 柯西积分公式
定理设f ( z )在简单(或复合)闭曲线C上及所围区域D内解析, 则对任意z0 D,皆有
2

C
vdx udy
u( x(t ), y(t )) y(t ) v( x( t ), y( t )) x( t ) dt u( t ) y( t ) v( t ) x( t ) dt

这样 : f ( z )dz 可以通过两个二元实变函数的线
第三章复变函数的积分
本章主要内容：
1、 2、 3、 4、 5、复积分的概念柯西积分定理柯西积分公式高阶导数公式解析函数与调和函数的关系
1
§1 复变函数积分的概念 3、复积分计算的参数方程法

C
f ( z )dz udx vdy i vdx udy
C C
若能写出C的参数方程为: C: z(t)=x(t)+iy(t) t 则因为C是光滑曲线x(t),y(t)C[,] :
C

积分来计算.

C
f ( z )dz
u(t ) x(t ) v (t ) y(t ) dt

i

v(t ) x(t ) u(t ) y(t ) dt
{u(t ) iv(t )}{ x(t ) iy(t )}dt

第三章复变函数的积分

估值定理
(6) 积分的模不大于被积表达式模的积分
∫
C
f ( z )dz ≤ ∫ f ( z ) dz = ∫ f ( z ) dS
C C
其中，dS =
( dx ) + ( dy )
2
2
9
复积分的计算
设C : z = z (t ) = x(t ) + iy (t ) (α ≤ t ≤ β )是一条光滑曲线，z (α )是C的起点, z ( β )是C的终点，则
O x
I1 = ∫ z dz = ∫ (2t + it ) 2 (2 + i )dt
2 C1 0
1
t = (2 + i ) 3
3
3 1
0
2 11 = + i 3 3
12
例计算 ∫C z dz , 其中 C 为 : 圆周 z = 2.
解积分路径的参数方程为
z = 2e
iθ
(0 ≤ θ ≤ 2 π),
z = z0 + re
iθ
(0 ≤ θ ≤ 2 π),
dz
o
⋅ z0
θ
r
∫C
=∫
1 ( z − z0 )
n +1
x
ireiθ 2π n +1 i ( n +1)θ 0 r e
dθ
=
i r
2 π −inθ e dθ , n 0
∫
14
当 n = 0 时,
∫C
1 ( z − z0 )
dz n +1
= i∫
β
∫C
f ( z )dz = ∫α {u[ x(t ), y (t )]x′(t ) − v[ x(t ), y (t )] y′(t )}dt + i ∫α {v[ x(t ), y (t )]x′(t ) + u[ x(t ), y (t )] y′(t )}dt

复变函数与积分变换__第3章

二、复积分的性质
(1) (2) (3)
C [ f ( z ) g( z )]dz C f ( z ) dz C g( z ) dz .
C f ( z ) dz C
C f ( z ) dz C
1

f ( z ) dz .
f ( z ) dz ,
f ( z ) dz
C
f (z k )zk [u( k ,k )xk v( k ,k )yk ]
k 1 k 1
n
n
i [v ( k ,k )xk u( k ,k )yk ]
k 1
n
C f ( z )dz C udx vdy i
C
vdx udy .
I z dz
C3
i C3 C1 1
C2
( t i t ) d( t i t )
0
1
x
(1 i ) (1 i ) t d t
0
1
1 21 2 t 1. 0 2
注意1 从例题看到, 积分

C
zd z
和 C zdz ,
都是从相同的起点到相同的终点, 沿着两条不相同的路径进行时,
D C
则有
C f ( z ) d z 0 .
二、闭路变形原理
将柯西积分定理推广到二连域定理设二连域 D 的边界为 C C1 C2 (如图)，
C1
D
则函数 f ( z ) 在 D 内解析，在 D+C 上连续，
C2
b a
C f ( z ) d z 0
C

或
C
1
f (z) dz

第3章复变函数的积分

k k ik u(k ,k ) uk v(k ,k ) vk
n
n
Sn f ( k )zk (uk ivk )(xk iyk )
k 1
k 1
n
n
u(k ,k )xk v(k ,k )yk
k 1
k 1
当 0时，均是
n
n
实函数的曲线积分.
i[ v(k ,k )xk u(k ,k )yk ] (5)
C的方向规定: 开曲线: 指定起点a,终点b, 若a b为正,
则b a为负,记作 C ; 闭曲线 : 正方向观察者顺此方向沿C前进
一周, C的内部一直在观察者的左边。
B(终点)
C
A(起点)
C
C
2. 积分的定义
y
定义设(1)w f (z) z D (2)C为区域D内点A 点B
的一条光滑有向曲线.
上连续时, f (z)必沿C可积,即C f (z)dz存在.
且 C f (z)dz C udx vdy i C vdx udy (4)
记忆
C (u iv)(dx idy)
注这个定理表明 C f (z)dz可通过二个二元
实变函数的第二型曲线积分来计算.
证明令zk xk iyk xk xk xk1 yk yk yk1
A z2dz 1(1 i)t2 d((1 i)t)
C
0
1
(1
i
)(1
i
)t
2
dt
0
o
x
(1
i)3
t3 3
1 0
(1 i)3 3
.
(2)这两直线段分别记为 C1和C2 :
C1的参数方程为： y 0, x从0到1.

第三章复变函数的积分.

1
0
1
( t it 2 )(1 2it )dt
[( t 2t 3 ) i 3t 2 ]dt i;
0
(3) 积分路径由两段直线段构成 x轴上直线段的参数方程为 z( t ) t (0 t 1),
于是 Re z t , dz dt ,
1到1+i直线段的参数方程为 z( t ) 1 it (0 t 1),
例 5 计算 Re zdz ,
C
C zdz 其中 C 为 :
(1)从原点到点 1 i 的直线段; (2) 抛物线 y x 2 上从原点到点 1 i 的弧段; (3) 从原点沿 x 轴到点 1 再到 1 i 的折线.
解 (1) 积分路径的参数方程为
y
z( t ) t it (0 t 1),
y A 0
B x
那么 B 到 A 就是曲线 C 的负向,
记为 C .

关于曲线方向的说明: 以后把两个端点中的一个作为起点, 另一个作为终点, 除特殊声明外, 正方向总是指从起点到终点的方向.
简单闭曲线 C 的正向
是指当曲线上的点 P 沿此
y P 0
C
方向前进时, 邻近 P 点的曲
线的内部始终位于 P 点的左方.
(3) 如果 C 是开曲线, 那么沿曲线正向的积分记为 f ( z )dz . 沿曲线反向的积分记为 f ( z )dz .
C C
2. 积分的计算及积分性质
如果 f ( z ) 是连续函数而 C 是光滑曲线时, 积分 f ( z )dz 一定存在.
C
f ( k )zk [u( k ,k )xk v( k ,k )yk ]

3第三章 复变函数的积分54997

复变函数与积分变换第3章

【复变函数】第三章 复变函数的积分(工科2版)

[工学]第3章复变函数的积分

第3章1复变函数的积分

复变函数 第三章 复变函数的积分

3第三章 复变函数的积分

复变函数 积分

03_复变函数的积分

第三章 复变函数的积分

复变积分知识点总结

复变函数与积分变换第三章

复变函数-第三章-复变函数的积分

第三章 复变函数的积分

复变函数与积分变换__第3章

第3章 复变函数的积分

第三章 复变函数的积分.

3第三章复变函数的积分54997

【复变函数】第三章复变函数的积分(工科2版)

复变函数第三章复变函数的积分

3第三章复变函数的积分

复变函数积分

第三章复变函数的积分

第三章复变函数的积分

第3章复变函数的积分

第三章复变函数的积分.