高一数学人教A版必修2课后导练:1.3.1柱体、锥体、台体的表面积与体积
高中数学人教A版必修2课件-1.3.1柱体、椎体、台体的表面积与体积

二、棱柱、棱台、棱锥的表面积
用空间几何体的展开图来求它的面积
几何体的展开图
侧面展开图的构成
一组平行四边 形
一组三角形
一组梯形
表面积=侧面积+底面积
问题:圆柱、圆锥、圆台的侧面积分别和矩形、三角形、 梯形的面积有什么类似的地方?
空间体侧面展开图
空间体的侧面积 平面图形面积
矩 形
三 角 形
梯 形
三、圆柱、圆锥、圆台表面积
侧面展开图
侧面积
表面积
练习
1、已知棱长为a,各面均为等边三角形的四面
体S-ABC(即三棱锥),求它的表面积。
练习
2、已知棱长为a,底面为正方形,各侧面 均为等边三角形的四棱锥S-ABCD,求 它的表面积。
知识探究:柱体、锥体、台体的体积 思考1:正方体、长方体和圆柱的体积公 式吗?它们可以统一为一个什么公式? 思考2:推广到一般的棱柱和圆柱,猜想 柱体的体积公式是什么?
上底面 积S′
高h
下底面 积S
练习
已知棱长为a,底面为正方形,各侧面均 为等边三角形的四棱锥S-ABCD,求它 的体积。
作业:
P28习题1.3 A组: 2,3,4 题
小结
1.多面体表面积:各面面 积之和
2.旋转体表面积:侧面展 开图面积+底面积
思考题:
已知棱长为a,各面均为等边三角形 的四面体S-ABC(即三棱锥),求 它的体积。
高h
底面积S
将一个三棱柱按如图所示分解成三 个三棱锥,那么这三个三棱锥的体积有 什么关系?它们与三棱柱的体积有什么 关系?
3 2
1 1
3 2
思考3:推广到一般的棱锥和圆锥,你猜 想锥体的体积公式是什么?
2020版人教A数学必修2:1.3.1 柱体、锥体、台体的表面积与体积

的底面积 S= 1 ×4×2=4,棱锥的高 h=4,所以棱锥的体积 V= 1 ×4×4= 16 .
2
3
3
故选 B.
[备用例2] 1.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和 最长母线长分别为2和3,求该几何体的体积.
解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱 的体积为π×22×5=20π,故所求几何体的体积为10π.
2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图, 则此几何体的体积为( B )
(A)6 (B)9 (C)12 (D)18 解析:由三视图可知该几何体为底面是斜边为 6 的等腰直角三角形,高为 3 的 三棱锥,其体积为 1 × 1 ×6×3×3=9.
32
3.(2018·天津河西区高一期中)一个几何体的三视图如图所示,则该几何
体的体积为
.
解析:几何体上部是圆锥,下部是圆柱,所以几何体的体积为π·12×4+ 1 × 3
22π×2= 20π . 3
答案: 20π 3
4.(2018·杭州高一期中)某几何体的三视图如图所示,则该几何体的体积
是
;表面积是
.
解析:由题意几何体是棱长为 2 的正方体,挖去一底面半径为 1,高为 1 的圆锥,
π rl+π
r2
. .
圆台
上底面面积:S上底= 下底面面积:S下底=
π r′2 . π r2 .
侧面积:S侧= π l(r+r′) .
表面积:S= π (r′2+r2+r′l+rl) .
2.柱体、锥体、台体的体积公式 柱体的体积公式 V=Sh(S 为底面面积,h 为高);
高一数学人教A版必修2课后导练:1.3.1柱体、锥体、台体的表面积与体积含解析

课后导练基础达标1 圆锥的轴截面是正三角形,那么,它的侧面积是底面积的( )A.4倍B.3倍C. 2倍D.2倍解:设底面半径为 R ,由条件知母线长为2R ,2S 侧 =π R · 2R=2πR =2S 底. 答案: D6 2 正三棱锥的底面边长为a,高为a ,则三棱锥的侧面积等于( )63232A.aB. a423 3 23 32C.aD.2 a4解: VO=6 a , OA= a ? 3 3 a ,6 2 36∴ V A= 1a ,21 1 3∴S 侧=·3a · a=a 2,224应选 A.答案: A3 圆锥母线长为 1,侧面睁开图的圆心角为 240 °,该圆锥体积为() A.2 2 B. 8C.4 5D.10818181 81解:设圆锥底面半径为 R ,高为 h ,240 则 2πR=180∴R= 2,h= 14 15 , 3931 ∴V=32πR h=45,应选C.81答案: C4 长方体的高等于 h,底面积等于 a ,过相对侧棱的截面面积等于 b ,则此长方体的侧面积等于( )A. 2 b 2 ah 2B. 2 2b 2 ah 2C. 2b 22ah 2D. b 22ah 2解:如图,由条件知AB ·BC=a ,且 AC ·h=b ,∴ A C= b,hb 2 即 AB 2+BC 2= 2 =( AB+BC )2-2a ,h∴AB+BC=b 22ah 2 .h∴S 侧 =2( AB+BC ) ·h= 2 b 2 2ah 2 ,应选 C.答案: C5 直棱柱的侧面睁开图是 ________,正棱锥的侧面睁开图是一些全等的________.答案: 矩形 等腰三角形6 轴截面是正方形的圆柱,轴截面面积为 S ,则它的全面积是 ________.分析: 设底面半径为 R ,则高为2R ,∴ 4R 2=S ,2+2 2S 3Sπ R · 2R=6πR =6π·π S.全42答案:3πS27 已知长方体中,有一个公共极点的三个面面积分别为 2,3,6,求长方体的体积 .解:设长方体的棱长分别为a ,b ,c ,则由条件知 ab=2, ac=3, bc=6.∴( abc ) 2=36 ,∴ V=abc=6.8 用一块矩形铁皮作圆台形铁桶的侧面,要求铁桶的上底半径是 24 cm ,下底半径为 16 cm ,母线长为 48 cm ,则矩形铁皮的长边长最少是多少?解:如图,设圆台的侧面睁开图的圆心角为∠ A ′OB=α,OA=x ,由相像三角形知识得x16 , x48 24∴x=96 ,则 α=60°,∴△ BOB ′为等边三角形 . BB ′ =OB=144 cm ,即矩形铁皮的长边长最少为144 cm.综合运用9 已知棱台的两个底面面积分别是 245 cm 2 和 80 cm 2,截得这棱台的棱锥的高为35 cm ,则这个棱台的高为( )A.20 cmB.15 cmC.10 cmD.25 cm分析:设棱台高为 h ,则截去的小棱锥的高为35-h ,由截面性质知80(35h)2 解得 h=1524535cm. 答案: B10 已知正四周体ABCD 的表面积为 S ,其四个面的中心分别为 E 、F 、G 、H ,设四周体 EFGH的表面积为 T ,则 T等于()1 S4 C.11 A.B.D.9943分析: 设正四周体 ABCD 的棱长为 a ,如下图, 则 EF= 2 MN= 1 BD= 1a ,333因此T=1,选 A.S 9答案: A11 圆柱的侧面睁开图是边长为 6π和 4π的矩形,则圆柱的全面积为()A.6 π( 4π +3)B.8 π( 3π +1)C.6 π( 4π +3)或 8π( 3π +1)D.6 π( 4π +1)或 8π( 3π +2)分析: 圆柱的侧面积 S 侧=4π× 6π=24.π(1)以边长为 6π的边为底时, 2πR=6π, R=3,222∴S 全 =2πR +24 π=18 π +24 π.(2)以边长为 4π的边为底时, 2πR=4π, R=2,∴S 2 2 2全 =2πR +24 π=8π +24 π.选 C.答案: C拓展研究12 如图,已知正三棱柱 ABC — A 1B 1C 1 的全部棱长都相等, D 是 A 1C 1 的中点,则直线 AD 与平面 B 1DC 所成角的正弦值为 _____________.分析: 不如设 A 在面 B 1DC 的射影为 H ,连接 DH ,(令棱长为 a )则∠ ADH 为 AO 与面 B 1DC 所成角 . 即 sinADH=AH,AD下边求 AH.由等体积公式易知VA B 1DCVB 1ADC,1B 1D ? AC ? A 1A2 5AH=21a.5?B 1D?DC22 5 a4 ∴sinADH=5.5 a 52答案:45。
人教A高中数学必修二导练课件:1.3.1柱体、锥体、台体的表面积与体积

1.3空间几何体的表面积与体积1.3. 1柱体、锥体、台体的表面积与体积目标导舟几新知导学•素养养成1•柱体、锥体、台体的表面积公式表面积公式~ 各个即多面体的表面积就楹—的面积的和,也就崑的面积旋转体til2irr 底面积:S底前「严侧面积:S踊「|十2卄表面积:S二nr21 1 1底面积:s底下+皿z -F- E c W ri+TTF侧面积:s侧二表面积:S二图形多面体溺面积:S 二 锥体的体积公式V 二-Sh (S 为底面面积,h 为高); 台体的体积公式v=| (S z +腐+S )h.J旋转体圆台2.体、锥体、台体的体积公式上底面面积:S 上隘J 下底面面积:珥缢◎TT (r 2+r 2Wrl )侧面积:s 侧二名师点津c c 1 Q J f、\ 1 *= 0 c rS2兀rXS 圆台侧一 Ji (r +r)l »S 圆锥侧一 Ji rl・ (2)柱体、锥体、台体的体积公式之间的关系:g=S ]S= 0 IV 柱二Sh -- V 台二-0 + 阿 +S) h ------- >V 锥二-Sh ・3 3系:课堂探究•素养提升题型一空间几何体的表面积[例1] (1煤几何体的三视图如图所示,则该几何体的侧面积是()IT1 0(A)4n (B)6TTIT(2)棱长为a的正四面体的表面积是()解析:(2)因为边长为a的正四面体的表面为4个边长为a的正三角形, 所以表面积为4乂护乂总皿•故选D・方法技巧结合三视图考查几何体的表面积是高考的热点,解决此类问题的关键是正确地观察二视图,把它址原为直观图,特别要汪意从二视图中得到儿何体的相关量,再结合表面积公式求解. -----------------------------------------------------即时训练1T :(2018 •雅安高一期末)如图是一个几何体的三视图,图中每个小正方形边长均为訥该几何体的表面积是()⑷ 3+V2 + V5 (B) 6+2 72 +2 ^5(08+石 + 厲(D)10+A/2解析:由几何体的三视图可知几何体的直观图如图:P0丄底面ABCD,P0 二2, AB 二BC 二2, ABCD 是正方形,AB1AD, 则PB二PA二运,APCD的高为2逅.则该几何体的表面积是1 X2X2+2X2+2X- XT? X2+- X2X2匝二6+2 2 2p2迈+2厉•故选B. A[备用例1] (201&四川乐山期末)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积是()(D)8解析:因为四棱锥的侧棱长都相等,底面是正方形,所以该四棱锥为正四棱锥其主视图为原图形中的三角形PEF,如图.题型二空间几何体的体积[例2] (12分)圆锥的轴截面是等腰直角三角形,侧面积是16厲工,求圆锥的体积.变式探究:例2中将条件“侧面积是16迈",改为“若其体积为①n ” ,求此圆锥的侧面积是多少?方法技巧(1)常见的求几何体体积的方法①公式法:直接代入公式求解.②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积.(2)求几何体体积时需注意的问题柱锥、台的休积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.即时训练2T:(201 &合肥高一期末)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()3分别为2和3,求该几何体的体积.解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱的体积为TIX 22 X 5二20兀故所求几何体的体积为10n.题型三组合体的表面积与体积[例3]已知ZXABC的三边长分别是AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.解:如图,在△ ABC中,过C作CD丄AB,垂足为D.SAC = 3/BC=4/AB=5, 知AC2+BC2 二AB2 则AC丄BC.因为BC・AC二AB・CD,所以CD二詩,记为厂£,那么AABC以AB所在直线为轴旋转所得旋转体是1?两个同底的圆锥,且底面半径I-#,母线长分别是AO3, BO4,12所以s 表面积二兀r • (AC+BC)二JI X-X (3+4) = - n,J JV中現AD+BD)中宀AB斗X(¥)*j.所以,所求旋转体的表面积是罗□,体积是:31.J J方法技巧求组合体的表面积与体积的关键是弄清组合体中各简单几何体的结构特征及组合形式,对十与旋转体有关的组合体冋题,要根据条件分清各个简单儿何体的底面半径及母线长,再分别代入公式求解. -----------------------------------------即时训练3T:某几何体的三视图如图所示,若图中小正方形的边长均为1,则该几何体的体积是()28兀(B) 3271(0 5271(A)3333解析:由题意可知:几何体是如图所示上面是半圆锥,下部是半个圆柱,底面半径是2,圆柱的高为4,圆锥的高为2,几何体的体积对X.X4.1 X III •22X2=?•故选A.即时训练3-2:如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是()俯视图(A) (5+ &) cm2 (C) (6+ ^2) cm2(B) - cm24 (D)6 cm2解析:由已知中的三视图,可知该几何体是下部是一个四棱柱(正方体)与上部是四棱锥的组合体,四棱柱(正方体)的棱长为1 cm,故每个面的面积为IXlg四棱锥的底面边长为1沁高为£ cm,故斜高为亍血故每个侧面的面积为丄XIX纟二鸣cm2;2 2 4故组合体的表面积S=5X1+4X — = (5+^2)(cm2).故选A.4课堂达标1.若圆锥的底面半径为1,高为靠,则圆锥的表面积为(c)(A) n (B) 2 Ji (C) 3 Ji (D) 4 Ji2如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()B(A)6 侣)9 (C)12 (D)18解析:由三视图可知该几何体为底面是斜边为6的等腰直角三角形,高为33.(2018 •天津河西区咼一期中)一个几何体的三视图如图所示,则该几何体的体积 为 ________ ・—I —pI丨4.(2018 •杭州高一期中)某几何体的三视图如图所示,则该几何体的体积是_______ ;表面积是____________正视俯视图解析:由题意几何体是棱长为2的正方体,挖去一底面半径为1,高为1的圆锥, 则V=23--X1- JI3 3S二2X2X6-兀•12+JI• IX 7?=24+(匝-1)答案:8丄24+(匝-1"3。
人教新课标版数学 高一人教A版必修二练习 1.3.1柱体、锥体、台体的表面积与体积

第一章 空间几何体 1.3 空间几何体的表面积与体积 1.3.1 柱体、锥体、台体的表面积与体积A 级 基础巩固一、选择题1.轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( ) A .4倍 B .3倍 C.2倍D .2倍解析:设轴截面正三角形的边长为2a ,所以S 底=πa 2,S 侧=πa ·2a =2πa 2,因此S 侧=2S 底. 答案:D2.如图所示,ABC A ′B ′C ′是体积为1的棱柱,则四棱锥C -AA ′B ′B 的体积是( )A.13B.12C.23D.34解析:因为V C A ′B ′C ′=13V 柱=13,所以V C AA ′B ′B =1-13=23.答案:C3.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( ) A .π B .2π C .4π D .8π解析:设圆柱的底面半径为r ,则圆柱的母线长为2r ,由题意得S 圆柱侧=2πr ·2r =4πr2=4π,所以r =1,所以V 圆柱=πr 2·2r =2πr 3=2π.答案:B4.(2015·课标全国Ⅰ卷 )《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依恒内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图所示,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放米约有( )A .14斛B .22斛C .36斛D .66斛解析:由l =14×2πr =8得圆锥底面的半径r =16π≈163,所以米堆的体积V =14×13πr 2h =14×2569×5=3209(立方尺),所以堆放的米有3209÷1.62≈22(斛). 答案:B5.已知正方体的8个顶点中,有4个为侧面是等边三角形的一三棱锥的顶点,则这个三棱锥与正方体的表面积之比为( )A .1∶ 2B .1∶ 3C .2∶ 2D .3∶ 6解析:棱锥B ′ ACD ′为适合条件的棱锥,四个面为全等的等边三角形,设正方体的边长为1,则B ′C =2,S △B ′AC =32. 三棱锥的表面积S 锥=4×32=23, 又正方体的表面积S 正=6. 因此S 锥∶S 正=23∶6=1∶ 3. 答案:B 二、填空题6.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm ,4 cm ,则该棱柱的侧面积为________cm 2.解析:棱柱的侧面积S 侧=3×6×4=72(cm 2). 答案:727.下图是一个空间几何体的三视图,这个几何体的体积是________.解析:由图可知几何体是一个圆柱内挖去一个圆锥所得的几何体,V =V 圆柱-V 圆锥=π×22×3-13π×22×3=8π.答案:8π8.(2015·福建卷)某几何体的三视图如图所示,则该几何体的表面积等于________.解析:由三视图知,该几何体是直四棱柱,底面是直角梯形,且底面梯形的周长为4+2.则S 侧=8+22,S 底=2×(1+2)2×1=3.故S 表=S 侧+S 底=11+2 2. 答案:11+22 三、解答题9.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积. 解:设圆锥的底面半径为r ,母线l , 则2πr =13πl ,得l =6r .又S 锥=πr 2+πr ·6r =7πr 2=15π,得r =157, 圆锥的高h =l 2-r 2=36r 2-r 2=35·r =35×157=53, 体积V =13πr 2h =13π×157×53=2537π.10.一个正三棱柱的三视图如图所示(单位:cm),求这个正三棱柱的表面积与体积.解:由三视图知直观图如图所示,则高AA ′=2 cm ,底面高B ′D ′=23cm ,所以底面边长A ′B ′=23×23=4(cm). 一个底面的面积为12×23×4=43(cm 2).所以表面积S =2×43+4×2×3=24+83(cm 2), V =43×2=83(cm 3).所以表面积为(24+83)cm 2,体积为83(cm 3).B 级 能力提升1.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D .3解析:设圆台较小底面半径为r ,较大底面半径为r 2,圆台的母线为l . 依题意r 2=3r 1,且l =3,又S 侧=π(r 1+r 2)l =12πr 1. 所以12πr 1=84π,则r 1=7. 答案:A2.(2015·江苏卷)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为__________.解析:底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱的总体积为13π×52×4+π×22×8=196π3. 设新的圆锥和圆柱的底面半径为r ,则13π·r 2×4+π·r 2×8=28π3r 2=196π3,解得r =7.答案:73.某几何体的三视图如图所示(单位:cm),求该几何体的体积.解:由三视图知,该几何体是一个四棱柱与一个四棱锥的组合体. V 四棱柱=23=8,V 四棱锥=13×22×2=83.故几何体的体积V =V 四棱柱+V 四棱锥=8+83 =323(cm 3).。
人教版数学高一-必修二(人教A)练习 1.3柱体、锥体、台体的表面积与体积

1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积1.3.2 球的体积和表面积一、选择题(本大题共7小题,每小题5分,共35分)1.如图L131所示,圆锥的底面半径为1,高为3,则圆锥的表面积为( )图L131A .πB .2πC .3πD .4π2.球的表面积与它的内接正方体的表面积之比是( ) A.π3 B.π4 C.π2D .π 3.一个几何体的三视图如图L132所示,其正视图和侧视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )图L132A .6πB .12πC .18πD .24π4.图L133是一个几何体的三视图,则该几何体的体积为( ' ) A .1 B .3 C.12 D.32图L133图L1345.图L134是一个几何体的三视图,若该几何体的表面积为9π,则该几何体的正视图中实数a 的值为( )A .1B .2C .3D .46.已知长方体的长、宽、高分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对7.一个空间几何体的三视图如图L135所示,其中正视图为等腰直角三角形,侧视图与俯视图均为正方形,则该几何体的体积和表面积分别为( )图L135A .64,48+16 2B .32,48+16 2 C.643,32+16 2 D.323,48+16 2 二、填空题(本大题共4小题,每小题5分,共20分)8.一个几何体的三视图及其尺寸如图L136所示,则该几何体的体积为 ________.图L136图L1379.已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为________.10.如图L137所示,半径为2的半球内有一内接正六棱锥P-ABCDEF,则该正六棱锥的体积为________.11.已知正四棱锥V-ABCD的底面的面积为16 m2,侧棱长为 2 11 m,则它的侧面积为________.三、解答题(本大题共2小题,共25分)12.(12分)某个几何体的三视图如图L138所示(单位:m).求:(1)该几何体的表面积(结果保留π);(2)该几何体的体积(结果保留π).图L13813.(13分)图L139是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm).(1)该几何体是什么图形?(2)画出该几何体的直观图(坐标轴如图L1310所示),并求它的表面积.(只需作出图形,不要求写作法)图L139图L131014.(5分)一个几何体的三视图如图L1311所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )图L1311A .36πB .9π C.92π D.278π 15.(15分)如图L1312所示,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =2 2,AD =2,求四边形ABCD 绕AD 所在直线旋转一周所成的几何体的表面积及体积.图L13121.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积1.3.2 球的体积和表面积1.C [解析] 设圆锥的母线长为l ,则l =3+1=2,所以圆锥的表面积为S =π×1×(1+2)=3π.2.C [解析] 设内接正方体的棱长为a ,则球的直径为3a ,所以球的表面积与它的内接正方体的表面积之比是4π⎝⎛⎭⎫3a 22∶6a 2=π2. 3.B [解析] 结合三视图可知该几何体是一个圆台,其上,下底面的半径分别为2,1,则该几何的侧面积S =π(2×4+1×4)=12π.4.B [解析] 该几何体是直三棱柱,其底面三角形的面积为12×1×2=1,高为3,所以该几何体的体积为3.5.C [解析] 该几何体是一个圆柱上面叠加一个圆锥,其表面积S =2π×1×a +π×1×(3)2+12+π×12=2πa +3π=9π,所以a =3.6.B [解析] 由题意知球为长方体的外接球.设球的半径为R ,则(2R )2=32+42+52,∴R 2=252,∴S 球=4πR 2=4π×252=50π.7.B [解析] 由三视图可知,该几何体是一个三棱柱,其直观图如图所示.体积V =12×4×4×4=32,表面积S =2×12×42+4×(4+4+4 2)=48+16 2.8.54π [解析] 由几何体的三视图知该几何体是一个底面半径为3,高为6的圆柱,则该几何体的体积V =π×32×6=54π.9.50π [解析] 因为圆锥的侧面展开图半圆的面积即为该圆锥的侧面积,且该半圆的半径即为圆锥的母线长10,所以圆锥的侧面积为12π×102=50π.10.4 3 [解析] 由题意得正六棱锥的底面边长和高都为2,故该六棱锥的体积为13×34×22×6×2=4 3.11.16 10 m 2 [解析] 如图所示,取AD 的中点E ,连接VE .∵正四棱锥V -ABCD 的底面的面积为16 m 2,∴AE =12AD =2 m .在Rt △VAE 中,VE =VA 2-AE 2=(2 11)2-22=2 10(m),∴正四棱锥V -ABCD 的侧面积为12×4×2 10×4=16 10(m 2).12.解:由三视图可知,该几何体的下半部分是棱长为2 m 的正方体,上半部分是半径为1 m 的半球.(1)几何体的表面积S =12×4π×12+6×22-π×12=(24+π)m 2.(2)几何体的体积V =23+12×43π×13=⎝⎛⎭⎫8+23πm 3. 13.解:(1)由三视图可知该几何体是三棱柱.(2)直观图如图所示.因为该几何体的底面是边长为4 cm 的等边三角形,高为2 cm ,所以它的表面积S 三棱柱=2S 底+S侧=2×34×42+3×4×2=(24+8 3)cm 2. 14.C [解析] ∵俯视图是一个腰长为2的等腰直角三角形,∴底面外接圆半径r = 2.由正视图中棱锥的高h =1,得棱锥的外接球半径R =⎝⎛⎭⎫122+(2)2=32, 故该几何体外接球的体积V =43πR 3=92π.15.解:易知所得的几何体是由一个圆台截去一个圆锥所得的组合体,且CE =DE =AD =2,BC =5,则S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面=π×52+π×(2+5)×5+π×2×2 2=60π+4 2π,V =V 圆台-V 圆锥=13π(22+2×5+52)×4-13π×22×2=1483π.。
人教A版高一数学必修二1.3.1柱体、锥体、台体的表面积与体积课件

A
V = VP-ABCD - VP-ABCD
1 (S SS S)h 3
P
A
D
S
C
B
h
D
S C
B
棱台(圆台)的体积公式
其中 S , S分别为上、下底面面积,h为棱台
(圆台)的高.
【提升总结】
公式有 它的统 一性.
柱体、锥体、台体的体积公式之间有什么关系?
上底扩大
上底缩小
S为底面面积, S,S 分别为上、下底 S为底面面积,
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积
赫尔佐格
“鸟巢(nest)”
德梅隆
我们的身边存在着各种各样的几何体、建筑进行装饰时, 都需要知道它们的表面积或体积,以便计算用料和工时, 如何计算呢?
1.了解柱体、锥体、台体的表面积和体积公式的推 导过程. (重点) 2.能运用公式求解柱体、锥体和台体的表面积与体 积.(难点) 3.熟悉台体与柱体和锥体之间的转换关系,培养转 化与化归的思想与空间想象能力.
【解析】先求△SBC的面积,过点S作 SD BC, S
交BC于点D.
因为BC=aS,D = SB sin60o =
3 a, 2
A
所以
SΔSBC
=
1 BC 2
SD
=
1 a× 2
3 2
a=
3 a2. 4
B
D
C
因此,四面体S-ABC 的表面积为4× 3 a2 = 3a2.
4
【变式练习】
在直三棱柱ABC-A1B1C1中,AB⊥BC,且AB=BC=1, AA1=2.求三棱柱的全面积S. 【解析】因为AB⊥BC,AB=BC=1, 所以S△ABC=12 AB·BC=12 ,AC=AB2 BC2 2 因为三棱柱ABC-A1B1C1是直三棱柱, 所以四边形AA1B1B、AA1C1C和BB1C1C都是矩形, 因为AA1=2,所以矩形AA1B1B的面积S为AA1B1B =同A理A可1×得AB=2S,AA1C1C 2 2,SBB1C1C 2.
数学人教a版必修2:1.3 第1课时 柱体、锥体、台体的表面积与体积

课下能力提升(五) [学业水平达标练]题组1 柱体、锥体、台体的侧面积与表面积 1.棱长为3的正方体的表面积为( ) A .27 B .64 C .54 D .362.若圆锥的高等于底面直径,则它的底面积与侧面积之比为( ) A .1∶2 B .1∶ 3 C .1∶ 5 D.3∶23.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( )A .7B .6C .5D .34.一个高为2的圆柱,底面周长为2π,该圆柱的表面积为________. 题组2 柱体、锥体、台体的体积5.若长方体的长、宽、高分别为3 cm 、4 cm 、5 cm ,则长方体的体积为( ) A .27 cm 3 B .60 cm 3 C .64 cm 3 D .125 cm 36.(2016·朔州高一检测)如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为1,则三棱锥D 1-ADC 的体积是( )A.16B.13C.12D .1 7.若圆锥的侧面展开图为一个半径为2的半圆,则圆锥的体积是________. 题组3 与三视图有关的表面积、体积问题8.(2016·广州高一检测)一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的表面积为( )A .12πB .18πC .24πD .36π9.(2016·贵港高一检测)已知某几何体的三视图如图所示,则该几何体的体积为( )A.8π3 B .3π C.10π3D .6π10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________cm 3.[能力提升综合练]1.如图,ABC -A ′B ′C ′是体积为1的棱柱,则四棱锥C -AA ′B ′B 的体积是( )A.13B.12C.23D.342.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( ) A .π B .2π C .4π D .8π3.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 24.(2015·邯郸高一检测)在正方体ABCD -A 1B 1C 1D 1中,三棱锥D 1-AB 1C 的表面积与正方体的表面积的比为( )A .1∶1B .1∶ 2C .1∶ 3D .1∶25.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 6.(2016·贵阳高一检测)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸) 7.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积. 8.已知一个几何体的三视图如下,试求它的表面积和体积.(单位: cm)答案 [学业水平达标练]题组1 柱体、锥体、台体的侧面积与表面积1.解析:选C 根据表面积的定义,组成正方体的面共6个,且每个都是边长为3的正方形.从而,其表面积为6×32=54.2.解析:选C 设圆锥底面半径为r ,则高h =2r ,∴其母线长l =5r .∴S 侧=πrl =5πr 2,S 底=πr 2.则S 底∶S 侧=1∶ 5.3.解析:选A 设圆台较小底面半径为r ,则另一底面半径为3r .由S =π(r +3r )·3=84π,解得r =7.4.解析:由底面周长为2π可得底面半径为1.S 底=2πr 2=2π,S 侧=2πr ·h =4π,所以S表=S 底+S 侧=6π.答案:6π题组2 柱体、锥体、台体的体积5.解析:选B 长方体即为四棱柱,其体积为底面积×高,即为3×4×5=60 cm 3. 6.解析:选A 三棱锥D 1-ADC 的体积V =13S △ADC ×D 1D =13×12×AD ×DC ×D 1D =13×12=16. 7.解析:易知圆锥的母线长为2,设圆锥的底面半径为r ,则2πr =12×2π×2,∴r =1,则高h =l 2-r 2= 3.∴V 圆锥=13πr 2· h =13π×3=3π3.答案:3π3题组3 与三视图有关的表面积、体积问题8.解析:选C 由三视图知该几何体为圆锥,底面半径r =3,母线l =5,∴S 表=πrl+πr 2=24π.9.解析:选B 由三视图可知,此几何体(如图所示)是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的14,所以V =34×π×12×4=3π.10.解析:由三视图可知原几何体如图所示.所以V =V ABC -A 1B 1C 1-V M -ABC =S △ABC ·5-13S △ABC ·3 =12×3×4×5-13×12×3×4×3=30-6=24. 答案:24[能力提升综合练]1.解析:选C ∵V C -A ′B ′C ′=13V 棱柱=13,∴V C -AA ′B ′B =1-13=23. 2.A .π B .2π C .4π D .8π解析:选B 设圆柱的底面半径为r ,则圆柱的母线长为2r ,由题意得S 圆柱侧=2πr ×2r =4πr 2=4π,所以r =1,所以V 圆柱=πr 2×2r =2πr 3=2π.3.解析:选B 根据三视图还原几何体如图所示,其中侧面ABD ⊥底面BCD ,另两个侧面ABC ,ACD 为等边三角形,则有S 表面积=2×12×2×1+2×34×(2)2=2+ 3.故选B.4.解析:选C 如图,三棱锥D 1-AB 1C 的各面均是正三角形, 其边长为正方体的面对角线.设正方体的棱长为a ,则面对角线长为2a ,S 锥=4×12(2a )2×32=23a 2,S 正方体=6a 2,故S 锥∶S 正方体=1∶ 3.5.解析:设圆锥的母线为l ,圆锥底面半径为r ,由题意可知,πrl +πr 2=3π,且πl =2πr .解得r =1,即直径为2.答案:26.解析:圆台的轴截面是下底长为12寸,上底长为28寸,高为18寸的等腰梯形,雨水线恰为中位线,故雨水线直径是20寸,所以降水量为π3(102+10×6+62)×9π×142=3(寸).答案:37.解:设圆锥的底面半径为r ,母线为l , 则2πr =13πl ,得l =6r .又S 圆锥=πr 2+πr ·6r =7πr 2=15π,得r =157, 圆锥的高h =⎝⎛⎭⎫61572-⎝⎛⎭⎫1572=35·157,V =13πr 2h =13π×157×35×157=2537π. 8.解:图中的几何体可看成是一个底面为直角梯形的直棱柱,且直棱柱的某个侧面在水平面上.直角梯形的上底为1,下底为2,高为1;棱柱的高为1. 可求得直角梯形的四条边的长度为1,1,2, 2.所以此几何体的体积V =S 梯形·h =12×(1+2)×1×1=32(cm 3).表面积S 表 =2S 底+S 侧=12×(1+2)×1×2+(1+1+2+2)×1=(7+2)(cm 2).。
数学必修Ⅱ人教新课标A版1-3-1柱体-锥体-台体的表面积与体积练习-1

7.(山东高考)如图,正方体ABCDA1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1EDF的体积为________.
答案:
8.一个正四Βιβλιοθήκη 台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13cm,则其表面积为________ cm2.
答案:1 012
三、解答题
9.如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.(单位:cm)
解:由三视图知该几何体是一个组合体,下半部是长方体,上半部是半圆柱,其轴截面的大小与长方体的上底面大小一致.长方体的长、宽、高分别是8,4,6,圆柱的高是8,底面半径是2,
∴表面积为S=8×4+2×8×6+2×4×6+2× ×π×22+ ×2π×2×8=176+20π(cm2),
体积为V=8×4×6+ ×π×22×8=192+16π(cm3),
故该几何体的表面积为(176+20π)cm2,体积为(192+16π)cm3.
10.已知正三棱锥VABC的正视图、俯视图如图所示,其中VA=4,AC=2 ,求该三棱锥的表面积.
解:由正视图与俯视图可得正三棱锥的直观图如图所示,
且VA=VB=VC=4,
课时达标检测(五) 柱体、锥体、台体的表面积与体积
一、选择题
1.如图,ABCA′B′C′是体积为1的棱柱,则四棱锥CAA′B′B的体积是()
A. B.
C. D.
答案:C
2.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于()
A.πB.2π
C.4πD.8π
答案:B
3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()
2019年高中数学必修二人教A版练习:1.3.1柱体、锥体、台体的表面积与体积含解析

1.3 空间几何体的表面积与体积1.3.1 柱体、锥体、台体的表面积与体积【选题明细表】1.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( B ) (A) (B) (C)2π (D)4π解析:由题意,该几何体可以看作是两个底面半径为,高为的圆锥的组合体,其体积为2××π×()2×=π.2.(2018·河南焦作期末)一个圆锥的侧面展开图是一个半径为2的半圆,则该圆锥的体积为( D )(A)2π (B)π (C) (D)解析:由题圆锥的底面周长为2π,底面半径为1,圆锥的高为,圆锥的体积为π·12·=π,故选D.3.(2018·河北沧州高一检测)圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为( A )(A)7 (B)6 (C)5 (D)3解析:设上、下底面半径为r,R.则2πR=3×2πr,所以R=3r.又π(r1+r2)l=S侧,所以S侧=π(3r+r)×3=84π,所以r=7.4.(2018·安徽马鞍山期中)若圆锥的高等于底面直径,则它的底面积与侧面积之比为( C )(A)1∶2 (B)1∶ (C)1∶ (D)∶2解析:若圆锥的高等于底面直径,则h=2r,则母线l==r,而圆锥的底面面积为πr2,圆锥的侧面积为πrl=πr2,故圆锥的底面积与侧面积之比为1∶,故选C.5.(2018·桂林调研)正六棱柱的一条最长的对角线长是13,侧面积为180,棱柱的全面积为.解析:如图,设正六棱柱的底面边长为a,侧棱长为h,易知CF′是正六棱柱的一条最长的对角线,即CF′=13.因为CF=2a,FF′=h,所以CF′===13. ①因为正六棱柱的侧面积为180,所以S侧=6a·h=180, ②联立①②解得或当a=6,h=5时,S底=6×a2×2=108.所以S全=180+108.当a=,h=12时,S底=6×a2×2=,所以S全=180+.答案:180+或180+1086.如图,直三棱柱ABC A1B1C1的高为6 cm,底面直角三角形的边长分别为3 cm,4 cm,5 cm,以上、下底的内切圆为底面,挖去一个圆柱,求剩余部分形成的几何体的体积为.(π取3.14)解析:由题意知,Rt△ABC的内切圆O的半径为r=1(cm),所以所求几何体的体积为V=×3×4×6-π×12×6≈17.16(cm3).即剩余部分形成的几何体的体积为17.16 cm3.答案:17.16 cm37.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为.解析:由题底面半径是1,圆锥的母线为2,则圆锥的高为,所以圆锥的体积为××π=.答案:8.(2018·湖南郴州二模)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( B )(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V=(S上++S下)·h)(A)2寸(B)3寸(C)4寸(D)5寸解析:如图,由题意可知,天池盆上底面半径为14寸,下底面半径为6寸,高为18寸.因为积水深9寸,所以水面半径为(14+6)=10寸,则盆中水的体积为π×9(62+102+6×10)=588π(立方寸),所以平地降雨量等于=3(寸).故选B.9.(2018·辽宁抚顺一中月考)如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,则多面体ABCDEF的体积为.解析:多面体ABCDEF的体积等于四棱锥D ABEF和三棱锥A BCD的体积之和.因为=×S四边形ABEF×BC=×(1+2)×2×1=1,=×S△BCD×AB=××1×1×2=.所以多面体ABCDEF的体积V多面体ABCDEF=+1=.答案:10.已知正四棱锥底面正方形的边长为4 cm,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积.解:如图,正四棱锥的高PO,斜高PE,底面边心距OE组成Rt△POE.因为OE=2 cm,∠OPE=30°,所以PE=2OE=4 cm.因此S侧=4×PE·BC=4××4×4=32(cm2),S表面积=S侧+S底=32+16=48(cm2).11.(2018·江苏省连云港市高一期末)如图,正方体ABCD A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.(1)点Q在何位置时,直线D1Q,DC,AP交于一点,并说明理由;(2)求三棱锥B1-DBQ的体积;(3)若点Q是棱CC1的中点时,记过点A,P,Q三点的平面截正方体所得截面面积为S,求S.解:(1)当Q是棱CC1的中点时,直线D1Q,DC,AP交于一点,理由:延长D1Q、DC交于点O,则QC为△DD1O的中位线,所以C为DO的中点,延长AP、DC交于点O′,则PC为△ADO′的中位线,所以C为DO′的中点,所以点O与点O′重合,所以直线D1Q、DC、AP交于一点.(2)==×(×2×2)×2=.(3)连接AD1、PQ,由(1)知,AD1∥PQ,所以梯形APQD1为所求截面,梯形APQD1的高为=,S=(+2)×=.。
人教新课标版数学高一A版必修2导学案 1.3.1柱体、锥体、台体的表面积与体积(第1课时)

第1课时柱体、锥体、台体的表面积1.了解柱体、锥体、台体侧面展开图,掌握柱体、锥体、台体的表面积的求法.2.能运用公式求解柱体、锥体和台体的表面积,并了解柱体、锥体和台体表面积之间的关系.3.初步掌握面积在实际生活中的应用.1.柱体的表面积(1)侧面展开图:棱柱的侧面展开图是__________,一边是棱柱的侧棱,另一边等于棱柱的________,如图a所示;圆柱的侧面展开图是____,其中一边是圆柱的母线,另一边等于圆柱的底面周长,如图b所示.(2)面积:柱体的表面积S表=S侧+2S底.特别地,圆柱的底面半径为r,母线长为l,则圆柱的侧面积S侧=____,表面积S表=________.表面积是几何体表面的面积,它表示几何体表面的大小.常把多面体展开成平面图形,利用平面图形求多面体的表面积.侧面积是指侧面的面积,与表面积不同.一般地,表面积=侧面积+底面积.【做一做1】圆柱OO′的底面半径r=2 cm,母线l=3 cm,则圆柱OO′的表面积等于______cm2.2.锥体的表面积(1)侧面展开图:棱锥的侧面展开图是由若干个______拼成的,则侧面积为各个三角形面积的__,如图a所示;圆锥的侧面展开图是____,扇形的半径是圆锥的____,扇形的弧长等于圆锥的________,如图b所示.(2)面积:锥体的表面积S表=S侧+S底.特别地,圆锥的底面半径为r,母线长为l,则圆锥的侧面积S侧=____,表面积S表=________.【做一做2】圆锥的母线长为5,底面半径为3,则其侧面积等于()A.15 B.15π C.24π D.30π3.台体的表面积(1)侧面展开图:棱台的侧面展开图是由若干个____拼接而成的,则侧面积为各个梯形面积的__,如图a所示;圆台的侧面展开图是扇环,其侧面积可由大扇形的面积减去小扇形的面积而得到,如图b所示.(2)面积:台体的表面积S表=S侧+S上底+S下底.特别地,圆台的上、下底面半径分别为r′,r,母线长为l,则侧面积S侧=________,表面积S表=____________.圆柱、圆锥、圆台的侧面积有如下关系:【做一做3】圆台的上、下底面半径分别是3和4,母线长为6,则其表面积等于() A.72 B.42π C.67π D.72π答案:1.(1)平行四边形底面周长矩形(2)2πrl2πr(r+l)【做一做1】20π2.(1)三角形和扇形母线底面周长(2)πrlπr(l+r)【做一做2】B3.(1)梯形和(2)π(r+r′)lπ(r2+r′2+rl+r′l)【做一做3】C面积公式对比 剖析:如下表所示.题型一:求几何体的表面积 【例1】 如图所示的几何体是一棱长为4 cm 的正方体,若在其中一个面的中心位置上,挖一个直径为2 cm 、深为1 cm 的圆柱形的洞,求挖洞后几何体的表面积是多少?(π取3.14)反思:求几何体的表面积时,通常将所给几何体分成基本的柱、锥、台体,再通过这些基本的柱、锥、台体的表面积,进行求和或作差,从而获得几何体的表面积.本题中将几何体的表面积表达为正方体的表面积与圆柱侧面积的和是非常有创意的想法,如果忽略正方体没有被打透这一点,思考就会变得复杂,当然结果也会是错误的.题型二:与三视图有关的面积计算【例2】一个几何体的三视图如图所示,则这个几何体的表面积为()A.72 B.66 C.60 D.30反思:已知三视图求面积的步骤:(1)根据三视图明确几何体的结构特征;(2)明确三视图中各数据所反映的几何体的特征;(3)代入相应的面积公式.题型三:实际应用问题【例3】粉碎机的下料斗是正四棱台形(两个底面均是正方形,侧棱相等,侧面是全等的等腰梯形),如图所示,它的两个底面边长分别是80 mm和440 mm,侧棱是300 mm.计算制造这个下料斗所需铁板的面积是多少?反思:解决此类问题首先要分清是求几何体的表面积还是侧面积,其次将实物转化为空间图形,最后转化到平面图形上进行处理,这是常用的方法.答案:【例1】解:正方体的表面积为4×4×6=96(cm2),圆柱的侧面积为2π×1×1≈6.28(cm2),则挖洞后几何体的表面积约为96+6.28=102.28(cm2).【例2】 A【例3】 解:如图所示,设四边形ABCD 是该下料斗的一个侧面,过点A 作AE ⊥CD 于点E ,则AE =AD 2-DE 2.由题意,CD =440 mm ,AB =80 mm ,AD =BC =300 mm , 故DE =440-802=180(mm).∴AE =AD 2-DE 2=3002-1802=240(mm).∴S 梯形ABCD =12×(440+80)×240=62 400(mm 2).故四棱台的侧面积为62 400×4=249 600(mm 2). ∴制造这个下料斗所需铁板面积为249 600 mm 2.1.如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )A .6πB .12πC .18πD .24π2.已知圆柱OO ′的母线l =4 cm ,表面积为42π cm 2,则圆柱OO ′的底面半径r =____cm.3.一个几何体的三视图如图所示,若图中圆半径为1,等腰三角形腰长为3,则该几何体的表面积为__________.4.已知各棱长为5,底面为正方形,各侧面均为正三角形的四棱锥S-ABCD ,如图所示,求它的表面积.5.牧民居住的蒙古包的形状是一个圆柱与一个圆锥的组合体,尺寸如图所示,请你算出要搭建这样的一个蒙古包至少需要多少篷布?(精确到0.01 m 2)答案:1.B 2.3 3.5π4.解:∵四棱锥S -ABCD 的各棱长均为5, 各侧面都是全等的正三角形, 设E 为AB 的中点, 则SE ⊥AB ,∴S 侧=4S △SAB =4×12×5×2=,S 底=52=25,∴S 表面积=S 侧+S 底=25=1).5.解:m ,则其侧面积为S 1=π×52(m 2). 下部分圆柱体的侧面积为S 2=π×5×1.8=9π (m 2). 所以搭建这样的一个蒙古包至少需要的篷布为S =S 1+S 2=π×529π≈50.03(m 2), 即至少需要约50.03 m 2的篷布.。
高一数学人教A版必修2试题:1.3.1柱体、锥体、台体的表面积与体积 含解析

第一章 1.3 1.3.1A 级 基础巩固一、选择题1.若圆锥的正视图是正三角形,则它的侧面积是底面积的导学号 09024157( C ) A .2倍B .3倍C .2倍D .5倍[解析] 设圆锥的底面半径为r ,母线长为l ,则由题意知,l =2r ,于是S 侧=πr ·2r =2πr 2,S 底=πr 2.故选C .2.长方体的高为1,底面积为2,垂直于底的对角面的面积是5,则长方体的侧面积等于导学号 09024158( C )A .27B .43C .6D .3[解析] 设长方体的长、宽、高分别为a 、b 、c , 则c =1,ab =2,a 2+b 2·c =5, ∴a =2,b =1,故S 侧=2(ac +bc )=6.3.圆柱的侧面展开图是长12 cm ,宽8 cm 的矩形,则这个圆柱的体积为导学号 09024159( C )A .288πcm 3B .192π cm 3C .288π cm 3或192πcm 3D .192π cm 3[解析] 圆柱的高为8 cm 时,V =π×(12)2×8=288cm 3,当圆柱的高为12 cm 时,V =π×(82π)2×12=192πcm 3.4.圆台的体积为7π,上、下底面的半径分别为1和2,则圆台的高为导学号 09024160( A )A .3B .4C .5D .6[解析] 由题意,V =13(π+2π+4π)h =7π,∴h =3.5.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为导学号 09024161( D )A .1B .12C .32D .34[解析] 设圆柱底面半径为R ,圆锥底面半径r ,高都为h ,由已知得2Rh =rh ,∴r =2R ,V 柱︰V 锥=πR 2h ︰13πr 2h =3︰4,故选D .6.(2015·山东文)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为导学号 09024162( B )A .22π3B .42π3C .22πD .42π[解析] 绕等腰直角三角形的斜边所在的直线旋转一周形成的曲面围成的几何体为两个底面重合,等体积的圆锥,如图所示.每一个圆锥的底面半径和高都为2,故所求几何体的体积V =2×13×2π×2=42π3.二、填空题7.一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的表面积为__24导学号 09024163[解析] 该几何体是三棱柱,且两个底面是边长为2的正三角形,侧面是全等的矩形,且矩形的长是4,宽是2,所以该几何体的表面积为2×(12×2×3)+3×(4×2)=24+2 3.8.设甲、乙两个圆柱的底面积分别为S 1、S 2,体积分别为V 1、V 2,若它们的的侧面积相等且S 1︰S 2=9︰4,则V 1︰V 2=__3︰2__.导学号 09024164[解析] 设甲圆柱底面半径r 1,高h 1,乙圆柱底面半径r 2,高h 2,S 1S 2=πr 21πr 22=94,∴r 1r 2=32,又侧面积相等得2πr 1h 1=2πr 2h 2,∴h 1h 2=23.因此V 1V 2=πr 21h 1πr 22h 2=32.三、解答题9.如图所示的几何体是一棱长为4 cm 的正方体,若在其中一个面的中心位置上,挖一个直径为2 cm 、深为1 cm 的圆柱形的洞,求挖洞后几何体的表面积是多少?(π取3.14)导学号 09024165[解析] 正方体的表面积为4×4×6=96(cm 2), 圆柱的侧面积为2π×1×1≈6.28(cm 2),则挖洞后几何体的表面积约为96+6.28=102.28(cm 2).B 级 素养提升一、选择题1.(2017·浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是导学号 09024166( A )A .π2+1B .π2+3C .3π2+1D .3π2+3[解析] 由几何体的三视图可知,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长是2的等腰直角三角形,高为3的三棱锥的组合体,∴该几何体的体积V =13×12π×12×3+13×12×2×2×3=π2+1.故选A .2.某几何体的三视图如图所示,则该几何体的表面积为导学号 09024167( D )A .180B .200C .220D .240[解析] 几何体为直四棱柱,其高为10,底面是上底为2,下底为8,高为4,腰为5的等腰梯形,故两个底面面积的和为12×(2+8)×4×2=40,四个侧面面积的和为(2+8+5×2)×10=200,所以直四棱柱的表面积为S =40+200=240.3.(2015·全国卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为导学号 09024168( D )A .18B .17C .16D .15[解析] 由三视图得,在正方体ABCD -A 1B 1C 1D 1中,截去四面体A -A 1B 1D 1,如图所示,设正方体棱长为a ,则VA -A 1B 1D 1=13×12a 3=16a 3,故剩余几何体体积为a 3-16a 3=56a 3,所以截去部分体积与剩余部分体积的比值为15.4.(2017·全国卷Ⅰ理,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为导学号 09024169( B )A .10B .12C .14D .16[解析] 观察三视图可知该多面体是由直三棱柱和三棱锥组合而成的,且直三棱柱的底面是直角边长为2的等腰直角三角形,侧棱长为2.三棱锥的底面是直角边长为2的等腰直角三角形,高为2,如图所示.因此该多面体各个面中有2个梯形,且这两个梯形全等,梯形的上底长为2,下底长为4,高为2,故这些梯形的面积之和为2×12×(2+4)×2=12.故选B .二、填空题5.已知圆柱OO ′的母线l =4 cm ,全面积为42π cm 2,则圆柱OO ′的底面半径r = __3__cm.导学号 09024170[解析] 圆柱OO ′的侧面积为2πrl =8πr (cm 2),两底面积为2×πr 2=2πr 2(cm 2), ∴2πr 2+8πr =42π, 解得r =3或r =-7(舍去), ∴圆柱的底面半径为3 cm.6.已知斜三棱柱的三视图如图所示,该斜三棱柱的体积为__2__.导学号 09024171[解析] 由三视图可知,斜三棱柱的底面三角形的底边长为2,高为1,斜三棱柱的高为2,故斜三棱柱的体积为V =12×2×1×2=2.C 级 能力拔高1.如图在底面半径为2,母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.导学号 09024172[解析] 设圆锥的底面半径为R ,圆柱的底面半径为r ,表面积为S .则R =OC =2,AC =4, AO =42-22=2 3.如图所示易知△AEB ∽△AOC , ∴AE AO =EB OC ,即323=r 2,∴r =1, S 底=2πr 2=2π,S 侧=2πr ·h =23π. ∴S =S 底+S 侧=2π+23π=(2+23)π.2.在长方体ABCD -A 1B 1C 1D 1中,截下一个棱锥C -A 1DD 1,求棱锥C -A 1DD 1的体积与剩余部分的体积之比.导学号 09024173[解析] 设矩形ADD 1A 1的面积为S ,AB =h , ∴VABCD -A 1B 1C 1D 1=VADD 1A 1-BCC 1B 1=Sh .而棱锥C -A 1DD 1的底面积为12S ,高为h ,故三棱锥C -A 1DD 1的体积为:VC -A 1DD 1=13×12S ×h =16Sh ,余下部分体积为:Sh -16Sh =56Sh .所以棱锥C -A 1DD 1的体积与剩余部分的体积之比为1∶5.。
高中数学必修二人教A版情境导学:1.3.1柱体、锥体、台体的表面积与体积

最新中小学教案、试题、试卷
【情境导学】
在1889年巴黎埃菲尔铁塔落成前的四千多年的漫长岁月中,被誉为世界七大奇迹之首的胡夫大金字塔一直是世界上最高的建筑物.在四千多年前生产工具很落后的中古时代,埃及人是怎样采集、搬运数量如此之多,每块又如此之重的巨石垒成如此宏伟的大金字塔的?这真是一个十分难解的谜.胡夫大金字塔是一个正四棱锥外形的建筑,塔底边长230 m,塔高146.5 m,你能计算出建此金字塔用了多少石块吗?
棱柱、棱锥、棱台、圆柱、圆锥、圆台的表面积如何求呢? (把这些几何体的侧面、底面展开,转化为已学过的平面图形的面积计算问题,进而求和解决)。
人教新课标版数学高一人教A版必修②作业 1.3.1柱体、锥体、台体的表面积与体积

课时作业5 柱体、锥体、台体的表面积与体积 |基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.若圆柱的底面面积为S ,侧面展开图是一个正方形,则这个圆柱的侧面积是( )A .4πSB .2πSC .πS D.233πS解析:设圆柱的底面半径为r ,则πr 2=S ,r =S π.又侧面展开图是正方形,所以圆柱的侧面积S 侧=⎝⎛⎭⎪⎫2πS π2=4πS . 答案:A2.正方体ABCD -A 1B 1C 1D 1中,以顶点A 、C 、B 1、D 1为顶点的正三棱锥的全面积为43,则该正方体的棱长为( )A. 2 B .2 C .4 D .2 2解析:设正方体棱长为a ,侧面的对角线长为2a ,所以正三棱锥A -CB 1D 1的棱长为2a ,其表面积为4×34×(2a )2=43,可得a 2=2,即a = 2.答案:A 3.如图是一个几何体的三视图,其中主视图是边长为2的等边三角形,俯视图是半径为1的半圆,则该几何体的体积是( )A.433πB.36πC.12πD.33π解析:由三视图,可知该几何体是一个圆锥的一半,其中高为22-12=3,故所求的体积为V =12×13×π×12×3=36π. 答案:B4.若棱台的上、下底面面积分别为4,16,高为3,则该棱台的体积为( )A .26B .28C .30D .32解析:所求棱台的体积V =13×(4+16+4×16)×3=28. 答案:B5.已知某几何体的三视图如图所示,则它的体积为( )A .12πB .45πC .57πD .81π解析:该几何体的上部是一个圆锥,下部是一个圆柱,由三视图可得该几何体的体积V =V 圆锥+V 圆柱=13×π×32×52-32+π×32×5=57π.故选C.答案:C二、填空题(每小题5分,共15分)6.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm,4 cm ,则该棱柱的侧面积为________ cm 2.解析:棱柱的侧面积S 侧=3×6×4=72(cm 2). 答案:727.已知正三棱锥的高为1,底面边长为26,则该三棱锥的表面积为________.解析:易知底面正三角形的中心到一边的距离为13×32×26=2,则正三棱锥侧面的斜高为12+(2)2=3,所以S 侧=3×12×26×3=92,所以S 表=S 侧+S 底=92+34×(26)2=92+6 3.答案:92+6 38.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是________.解析:由题意知r :R =1:3,r 、R 分别为上、下底面的半径,故(V -52):V =1:27,解出V =54.答案:54三、解答题(每小题10分,共20分) 9.已知棱长为a ,各面均为等边三角形的四面体S -ABC 如图所示,求它的表面积.解析:因为四面体S -ABC 的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面面积的4倍.不妨求△SBC 的面积,过点S 作SD ⊥BC ,交BC 于点D ,如图所示.因为BC =SB =a ,SD =SB 2-BD 2=a 2-⎝ ⎛⎭⎪⎫a 22=32a , 所以S △SBC =12BC ·SD =12a ×32a =34a 2.故四面体S -ABC 的表面积S =4×34a 2=3a 2. 10.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的体积.解析:如图,过C 作CE 垂直于AD ,交AD 延长线于E ,则所求几何体的体积可看成是由梯形ABCE 绕AE 旋转一周所得的圆台的体积,减去△EDC 绕DE 旋转一周所得的圆锥的体积.所以所求几何体的体积V =V 圆台-V 圆锥=13π×(52+5×2+22)×4-13π×22×2=1483π. |能力提升|(20分钟,40分)11.(2016·烟台检测)如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( )A .πB .2πC .4πD .8π解析:设轴截面正方形的边长为a , 由题意知S 侧=πa ·a =πa 2. 又因为S 侧=4π,所以a =2.所以V 圆柱=π×2=2π. 答案:B12.已知圆锥的母线长为5 cm ,侧面积为15π cm 2,则此圆锥的体积为________ cm 3.解析:设圆锥的底面半径为r ,高为h ,则有πrl =15π,知r =3, ∴h =52-32=4.∴其体积V =13Sh =13πr 2h =13×π×32×4=12π. 答案:12π13.如图是一建筑物的三视图(单位:m),现需将其外壁用油漆粉刷一遍,已知每平方米用漆0.2 kg ,问需要油漆多少千克?(无需求近似值)解析:由三视图知建筑物为一组合体,自上而下分别是圆锥和正四棱柱,并且圆锥的底面半径为3 m ,母线长为5 m ,正四棱柱的高为4 m ,底面是边长为3 m 的正方形,圆锥的表面积为πr 2+πrl =9π+15π=24π (m 2);四棱柱的一个底面积为9 m 2,正四棱柱的侧面积为4×4×3=48 (m 2),所以外壁面积为24π-9+48=(24π+39) (m 2).所以需要油漆(24π+39)×0.2=(4.8π+7.8) (kg).14.如图,已知某几何体的三视图如图(单位:cm).(1)画出这个几何体的直观图(不要求写画法); (2)求这个几何体的表面积及体积.12×(2)2×2=10(cm3).V=23+。
人教A版高中数学必修2:1.3.1 柱体、锥体、台体的表面积与体积(3)

9.有一个面是多边形,其余各面是三角形的几
何体是棱锥。错误 10.棱锥的各侧棱长都相等。 错误
1.下列四种说法: ①在圆柱的上、下两底面的圆周上各取一点, 则这两点的连线是圆柱的母线; ②圆锥的顶点与底面圆周上任意一点的连线是 圆锥的母线; ③在圆台上、下两底面的圆周上各取一点,则 这两点的连线是圆台的母线; ④圆柱的任意两条母线相互平行. 其中正确的是( ② ④ )
2.下图是由选项中的哪个图形旋转得到的( A)
3.如下图,圆锥的母线长是3,底面半径是1,A是 底面圆周上一点,从点A出发绕侧面一周,再回到 点A的最短的路线长是( 3 3 )
空间几何体
看图回答问题
判断正误:
1.底面是正多边形的棱锥是正棱锥。 错误 2.棱柱的侧面是都是平行四边形。 正 错误 4.四面体的任何一个面都可以是底面。正确
5.用一个平面去截棱锥,平面与截面之间的部分
是棱台。 错误
6.棱锥的侧面都是三角形,且所有的侧面交于
高一数学人教A版必修2课后训练:1.3.1 柱体、锥体、台体的表面积与体积 Word版含解析
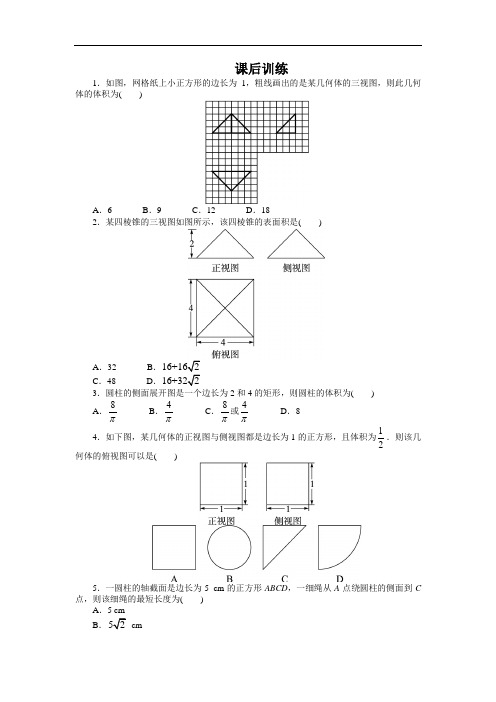
课后训练1.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .182.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32B .C .48D .3.圆柱的侧面展开图是一个边长为2和4的矩形,则圆柱的体积为( ) A .8π B .4π C .8π或4πD .8 4.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12.则该几何体的俯视图可以是( )5.一圆柱的轴截面是边长为5 cm 的正方形ABCD ,一细绳从A 点绕圆柱的侧面到C 点,则该细绳的最短长度为( )A .5 cmB .cmC.5π cmD6.棱台的体积为76 cm3,高为6 cm,一个底面面积为18 cm2,则另一个底面面积为__________.7.如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A -DED1的体积为__________.8.在△ABC中,AB=2,BC=1.5,∠ABC=120°(如下图所示),若将△ABC绕直线BC 旋转一周,则所形成的旋转体的体积是__________.9.已知一个几何体的三视图如下,试求它的表面积和体积.(单位:cm)10.一底面半径为r,母线长为3r的圆锥内有一内接正方体,求该正方体的表面积.参考答案1答案:B 2答案:B 3答案:C 4答案:C 5答案:D 6答案:8.cm 27答案:16 8答案:329答案:几何体的表面积为()cm 2,体积为32cm 3 10答案:正方体的表面积为2163r。
高一数学人教A版必修2课后训练:1.3.1柱体、锥体、台体的表面积与体积(第1课时) Word版含解析
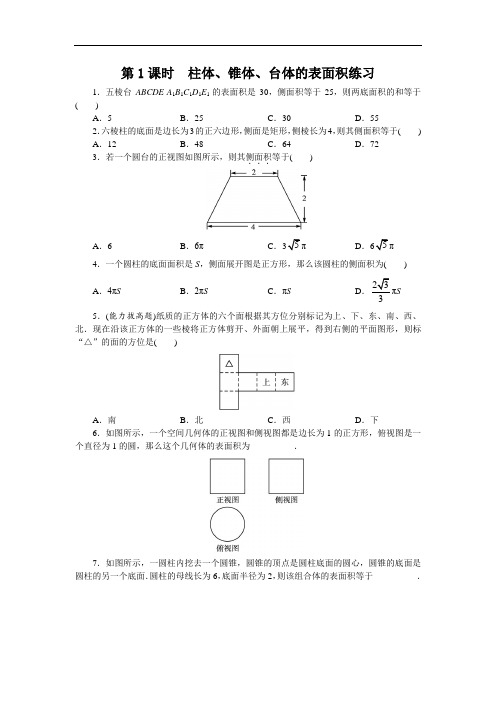
第1课时柱体、锥体、台体的表面积练习1.五棱台ABCDE-A1B1C1D1E1的表面积是30,侧面积等于25,则两底面积的和等于()A.5 B.25 C.30 D.552.六棱柱的底面是边长为3的正六边形,侧面是矩形,侧棱长为4,则其侧面积等于() A.12 B.48 C.64 D.723.若一个圆台的正视图如图所示,则其侧面积...等于()A.6 B.6πC.D.π4.一个圆柱的底面面积是S,侧面展开图是正方形,那么该圆柱的侧面积为()πS A.4πS B.2πS C.πS D.3 5.(能力拔高题)纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面的方位是()A.南B.北C.西D.下6.如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为__________.7.如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2,则该组合体的表面积等于__________.8.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面积是__________.9.已知圆台的上、下底面半径分别是2,5,且侧面积等于两底面面积之和,求该圆台的母线长.10.有位油漆工用一把长度为50 cm,横截面半径为10 cm的圆柱形刷子给一块面积为10 m2的木板涂油漆,且圆柱形刷子以每秒5周的速度在木板上匀速滚动前进,则油漆工完成任务所需的时间是多少?(精确到0.01秒)参考答案1.答案:A2.答案:D3.答案:C4.答案:A5.答案:B6.答案:3 2π7.答案:28)π8.答案:2S9.解:设圆台的母线长为l,则圆台的上底面面积为S上=π×22=4π,圆台的下底面面积为S下=π×52=25π,所以圆台的底面面积为S=S上+S下=29π.又圆台的侧面积S侧=π(2+5)l=7πl,则7πl=29π,解得l=297,即该圆台的母线长为297.10. 解:圆柱形刷子滚动一周涂过的面积就等于圆柱的侧面积,∵圆柱的侧面积为S侧=2πrl=2π×0.1×0.5=0.1π (m2),且圆柱形刷子以每秒5周的速度匀速滚动,∴圆柱形刷子每秒滚过的面积为0.5π m2.因此油漆工完成任务所需的时间t=100.5π=20π≈6.37(秒).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课后导练
基础达标
1圆锥的轴截面是正三角形,那么,它的侧面积是底面积的( )
A.4倍
B.3倍
C.2倍
D.2倍
解:设底面半径为R ,由条件知母线长为2R ,
S 侧=πR·2R=2πR 2=2S 底.
答案:D
2正三棱锥的底面边长为a,高为
66a ,则三棱锥的侧面积等于( ) A.43a 2 B.2
3a 2 C.433a 2 D.2
33a 2 解:VO=
66a ,OA=63332=∙a a , ∴VA=2
1a ,
∴S 侧=21·3a·21a=4
3a 2, 故选A.
答案:A
3圆锥母线长为1,侧面展开图的圆心角为240°,该圆锥体积为( ) A.8122π B.818π C.81
54π D.8110π 解:设圆锥底面半径为R ,高为h ,
则2πR=180
240π ∴R=32,h=53
1941=-, ∴V=31πR 2h=π581
4,故选C. 答案:C
4长方体的高等于h,底面积等于a ,过相对侧棱的截面面积等于b ,则此长方体的侧面积等
于( ) A.222ah b + B.2222ah b + C.2222ah b + D.222ah b +
解:如图,由条件知AB·BC=a ,且AC·h=b ,
∴AC=h
b , 即AB 2
+BC 2=22
h b =(AB+BC )2-2a , ∴AB+BC=h
ah b 2
22+. ∴S 侧=2(AB+BC )·h=2222ah b +,故选C.
答案:C
5直棱柱的侧面展开图是________,正棱锥的侧面展开图是一些全等的________.
答案:矩形 等腰三角形
6轴截面是正方形的圆柱,轴截面面积为S ,则它的全面积是________.
解析:设底面半径为R ,则高为2R ,∴4R 2=S ,
S 全=2πR 2+2πR·2R=6πR 2=6π·
234=S πS. 答案:2
3πS 7已知长方体中,有一个公共顶点的三个面面积分别为2,3,6,求长方体的体积.
解:设长方体的棱长分别为a ,b ,c ,
则由条件知ab=2,ac=3,bc=6.
∴(abc )2=36,∴V=abc=6.
8用一块矩形铁皮作圆台形铁桶的侧面,要求铁桶的上底半径是24 cm ,下底半径为16 cm ,母线长为48 cm ,则矩形铁皮的长边长最少是多少?
解:如图,设圆台的侧面展开图的圆心角为∠A′OB=α,OA=x , 由相似三角形知识得
24
1648=+x x , ∴x=96,则α=60°,
∴△BOB′为等边三角形.
BB′=OB=144 cm ,即矩形铁皮的长边长最少为144 cm.
综合运用
9已知棱台的两个底面面积分别是245 cm 2和80 cm 2,截得这棱台的棱锥的高为35 cm ,则这个棱台的高为( )
A.20 cm
B.15 cm
C.10 cm
D.25 cm
解析:设棱台高为h ,则截去的小棱锥的高为35-h ,由截面性质知2)35
35(24580h -=解得h=15 cm.
答案:B
10已知正四面体ABCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H ,设四面体EFGH
的表面积为T ,则
S
T 等于( ) A.91 B.94 C.41 D.31
解析:设正四面体ABCD 的棱长为a ,如图所示,
则EF=
32MN=31BD=3
1a , 所以S T =91,选A. 答案:A
11圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的全面积为( )
A.6π(4π+3)
B.8π(3π+1)
C.6π(4π+3)或8π(3π+1)
D.6π(4π+1)或8π(3π+2)
解析:圆柱的侧面积S 侧=4π×6π=24π2.
(1)以边长为6π的边为底时,2πR=6π,R=3,
∴S 全=2πR 2+24π2=18π+24π2.
(2)以边长为4π的边为底时,2πR=4π,R=2,
∴S 全=2πR 2+24π2=8π+24π2.
选C.
答案:C
拓展探究
12如图,已知正三棱柱ABC —A 1B 1C 1的所有棱长都相等,D 是A 1C 1的中点,则直线AD 与平面B 1DC 所成角的正弦值为_____________.
解析:不妨设A 在面B 1DC 的射影为H ,
连结DH ,(令棱长为a ) 则∠ADH 为AO 与面B 1DC 所成角. 即sinADH=AD AH
,
下面求AH.
由等体积公式易知 AD C B D C B A V V --=11, AH=55
22121
111=∙∙∙∙DC
D B A
A AC D
B a.
∴sinADH=54
255
52=a
a
. 答案:54。
