吉林省长市双阳区八年级数学上册 第13章 全等三角形 13.2 全等三角形的判定 13.2.3 边角
【配套K12】[学习]吉林省长春市双阳区八年级数学上册 第13章 全等三角形 13.2 全等三角形的
![【配套K12】[学习]吉林省长春市双阳区八年级数学上册 第13章 全等三角形 13.2 全等三角形的](https://img.taocdn.com/s3/m/67801686d1f34693daef3e9f.png)
留给学生一定的思考和回顾知识的时间。
为学生创设表现才华的平台。
一知识:
1.全等形:
能够完全重合的两个图形叫做全等形.
2.全等三角形:
能够完全重合的两个三角形叫做全等三角形.
3.全等三角形的性质:
全等三角形的对应边相等.全等三角形的对应角相等.
4.全等三角形的对应部分及表示方法.
二应用:
1.探究 全等三角形的性质
△ABC与△DEF重合
这时,点A与点D重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互 相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等 于△DEF”.
全等三角形
教学目标
知识与技能
理解全等三角形及相关概念,能够从图形中寻找全等三角形,探索并掌握全等三角形的性质,能够利用性质解决简单的问题.
过程与方法
在探索全等三角形性质的过程中,体会研究问题的方法,感受图形变化途径.
情感态度与价值观
培养学生的识图能力、归纳总结能力和应用意识.培养学生仔细认真的学习态度。
2.拿一张纸对折后,剪成两个全等的三角形,△ABC和△ECD,把这两个三角形一起放在下列图中△ABC的位置上,试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到下列图中的各图形,从中你能得到什么启发?
课后小结:全等三角形的相关知识.
课后练习:请见教材61页的练习.
课后作业:预习下一节课的内容.
教师引导学生观察,再合作交流,抓住图形能 够重合这一特性
吉林省长春市双阳区八年级数学上册第13章全等三角形直
你作对没有?有什么问题吗?
巩固训练题:
1.如图,
Rt△ACE≌Rt△DFB(
(1) ∵ CE=BF,(
)C)E Nhomakorabea B(3) ∵ AB=DE,( ) Rt△ACE≌Rt△DFB(HL) D
F
练习题1
问题1如图,在△ABC中,D是BC的中点, DE⊥AB,DF⊥AC,点E﹑F为垂足,DE=DF. 求证:△BED≌△CFD.
利用知识解决问题:
例7 如图,已知AC=BD, ∠C= ∠D=90°. 求证:BC=AD.
看一看你证的对不对:
证明:∵ ∠C= ∠D=90°(已知) ∴△ABC与△BAD都是直角三角形(直角三 角形的定义) 在Rt △ABC和Rt △BAD中, ∵AB=BA(公共边), AC=BD(已知), ∴ Rt △ABC≌Rt △BAD(H.L) ∴BC=AD(全等三角形的对应边相等)
练习题2
问题2.如图,AC=AD, ∠C= ∠D=90°. 求证:BC=BD.
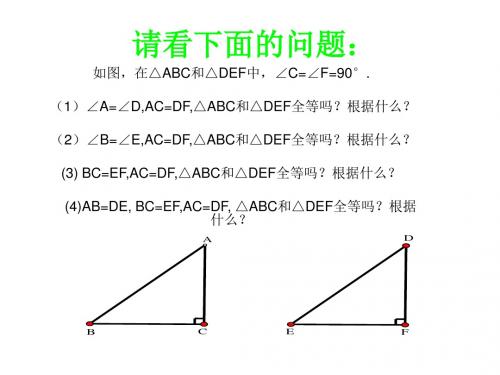
请看下面的问题:
如图,在△ABC和△DEF中,∠C=∠F=90°. (1)∠A=∠D,AC=DF,△ABC和△DEF全等吗?根据什么?
(2)∠B=∠E,AC=DF,△ABC和△DEF全等吗?根据什么?
(3) BC=EF,AC=DF,△ABC和△DEF全等吗?根据什么?
(4)AB=DE, BC=EF,AC=DF, △ABC和△DEF全等吗?根据 什么?
A D
B
C
E
F
直角三角形全等的判定:
根据所给的条件做一做:
㎝,b=3㎝. 画一直角三角形,使一直角边长为2㎝,斜边长为3㎝.
已知,线段a和b.a=2
a b
吉林省长春市双阳区八年级数学上册 第13章 全等三角形 直角三角形全等判定课件 (新版)华东师大版
练习题2
问题2.如图,AC=AD, ∠C= ∠D=90°. 求证:BC=BD.
编后语
折叠课件作用 ①向学习者提示的各种教学信息; ②用于对学习过程进行诊断、评价、处方和学习引导的各种信息和信息处理; ③为了提高学习积极性,制造学习动机,用于强化学习刺激的学习评价信息; ④用于更新学习数据、实现学习过程控制的教学策略和学习过程的控制方法。 对于课件理论、技术上都刚起步的老师来说,POWERPOINT是个最佳的选择。因为操作上非常简单,大部分人半天就可以基本掌握。所以,就可以花
2019/10/18
11
谢谢欣赏!
2019/10/18
12
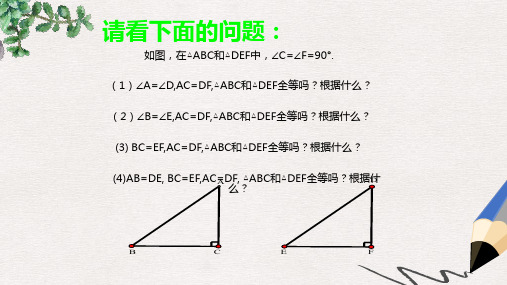
请看下面的问题:
如图,在△ABC和△DEF中,∠C=∠F=90°. (1)∠A=∠D,AC=DF,△ABC和△DEF全等吗?根据什么? (2)∠B=∠E,AC=DF,△ABC和△DEF全等吗?根据什么?
(3) BC=EF,AC=DF,△ABC和△DEF全等吗?根据什么? (4)AB=DE, BC=EF,AC=ADF, △ABC和△DEF全等吗?根据D 什
利用知识解决问题:
例7 如图,已知AC=BD, ∠C= ∠D=90°. 求证:BC=AD.
看一看你证的对不对:
证明:∵ ∠C= ∠D=90°(已知) ∴△ABC与△BAD都是直角三角形(直角三角形的定义) 在Rt △ABC和Rt △BAD中, ∵AB=BA(公共边), AC=BD(已知), ∴ Rt △ABC≌Rt △BAD(H.L) ∴BC=AD(全等三角形的对应边相等)
么?
B
C
E
F
直角三角形全等的判定:
根据所给的条件做一做:
已知,线段a和b.a=2㎝,b=3㎝.
吉林省长春市双阳区八年级数学上册第13章全等三角形13.2全等三角形的判定13.2.3边角边教案华

吉林省长春市双阳区八年级数学上册第13章全等三角形13.2 全等三角形的判定13.2.3 边角边教案(新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(吉林省长春市双阳区八年级数学上册第13章全等三角形13.2 全等三角形的判定13.2.3 边角边教案(新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为吉林省长春市双阳区八年级数学上册第13章全等三角形13.2 全等三角形的判定13.2.3 边角边教案(新版)华东师大版的全部内容。
边角边教学目标知识与技能1。
使学生掌握SAS 的内容,会运用SAS 来判定两个三角形全等;2.通过判定全等三角形的判定的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;3.经历如何总结出全等三角形判定方法,体会如何探讨、实践、总结,培养学生的合作能力过程与方法通过学生自主、合作交流、动手画图对比等方法探究全等的方法———-边角边。
情感态度与价值观通过创设情境,激发学生的求知欲.通过知识的探索过程,让学生体会成功的喜悦。
教学重点 三角形全等的判定:SAS ;教学难点 对全等三角形的判定的理解和运用。
教学内容与过程教法学法设计 复习回顾知识:1.什么叫全等图形?2.什么叫做全等三角形?3。
.已知:如图,在ABC ∆中,︒=∠30B ,︒=∠100A .的度数求C ∠.面向全体学生提出相关的问题。
明确要研究,探索的问题是什么,怎样去研究和讨论。
.本节课我们继续研究三角形全等的判定方法。
一.知识:全等三角形的判定方法:如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简写成“边角边”或简记为(S.A.S。
吉林省长春市双阳区八年级数学上册 第13章 全等三角形 13.2 全等三角形的判定 13.2.2 全等三角形的判定条件
把几个学生所做的三角形放在一起进行比较研究知识.
教学反思
2.如图,△ABC是等腰三角形,AD是底边上的高,△ABD和△ACD全等吗?试根据等腰三角形的有关知识说明理由
课后小结:全等三角形的判定.
课后作业:预习下一课 的内容.
面向全体学生 提出相关的问题。明确要研究,探索的问题是什 么,怎样去研究和讨论。.
留给学生一定的思考和回顾知识的时间。
为学生创设表现才华的平台。
全等三角形的判定条件
教学目标
知识与技能
经历探索三角形全等条件的过程,体会如何探索研究问题.培养学生合作的精神,让学生体验分类的 思想;使学生懂得如何提出问题,分类讨论,并为以后研究提出问题.
过程与方法
结合实例让学生意识到证明的必要性,培养学生说理有据,有条 理地表达自己想法的良好意识.
情感态度与价值观
巩固练习
1.如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180º,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__ ________,OB与____ ______,BA与_________ _;对应角是∠AOB与_______ _,∠OB A与_________,∠B AO与___________.
通过创设情境,激发学生的求知欲。通过知识的探索过程,让学生体会成功的喜悦。
教学重点
培养学生探索问题能力
教学难点
掌握探索问题的方法.
教学内容与过程
教法学法设计
请看下面的问题;
1.请一位同学叙述上一节所学的知识.
2.如图,△A BC≌△AEC , ,
吉林省长春市双阳区八年级数学上册第13章全等三角形教案2华东师大版(2021年整理)

二。导入课题,研究知识:
为了理解同学们对这一段时间所学知识掌握的情况,本解课我们对这部分知识进行验收
了解学生的出席情况
明确本节课的任务
三。明确要求
四.试题印发给学生。
五。学生笔答卷。
六.预习下节课的内
.
明确要求
要求学生认真的进行答卷
教学反思
必须手写,是检查备课的重要依据。
全等三角形
教学目标
知识与技能
了解学生对所学知识的掌握和理解情况,学生应用知识的分析解题情况,为期末复习打好基础。
过程与方法
出问感态度与价值观
培养学生良好的学习习惯和实事求是的科学态度。
教学重点
全等三角形的知识
教学难点
灵活运用知识解决问题。
教学内容与过程
教法学法设计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC= .
请你制作符合条件的△ABC和△ .
请把你们制作的三角形放在一起你会有什么发现?
教学反思
情感态度与价值观
通过创设情境,激发学生的求知欲。通过知识的探索过程,让学生体会成功的喜悦。
教学重点
三角形全等 的判定:SAS;
教学难点
对 全等三角形 的判定的理解和运用.
教学内容与过程
教法学法设计
复习 回顾知识:
1.什么叫全等图形?
2.什么叫做全等三角形?
3..已知:如图,在 中, , .
本节课我们继续研究三角形全等的判定方法。
边角边
教学目标
知识与技能
1.使学生掌握 SAS的内容,会运用SAS来判定两个三角形全等;2.通过判定全等三角形的判定的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;
3.经历如何总结出全等三角形判定方法,体会如何探讨、实践、总结,培养 学生的合作能力
过程与方法
通过学生自主、合作交流、动手画图对比等方法探究全等的方法----边角边。
请把你们制作的三角形放在一起你会有什么发现?
见教材65页的练习.
课后小结:全等三角形课后作业:复印给学生.
面向全体学生提出相关的问题。明确要研究,探索的 问题是什么, 怎样去研究和讨论。.
留给学生一定的思考和回顾知识的时间。
为学生创设表现才华的平台。
给出条件:
一.知识:
全等三角形的判定方法:
如果两个三角形有两边及 其 夹角分别对应相等,那么这两个三角 形全等.简写成“边角边”或简记为(S.A.S.)
二应用:
例1.如图已知线段AC,BD相交于点E,AE=DE, BE=CE,
求证: ≌△DCE.
巩固练习:给出条件:
AB= ; A= ;
AC= .
请你制作符合条件的△ABC和 △ .
