06-2贝叶斯分类
合集下载
基于贝叶斯的文本分类方法

Ab t a t woi otn co sntx ls i ct naedsu sd-ag r h a dfauea s a t n h r cia y sa lo tm sr c :T mp r t a tr t a sf ai r ic se - l oi m n tr b t ci .T ep at l a f i e c i o - t e r o c Ba ei ag r h n i
1 朴 素 贝 叶 斯 方 法 . 1
设 训练样 本集分 为七 , 为C- c ,2 } 则每 个类 类 记 - 。 , { C …, , G的先验 概 率为p G)i 1 , 七 ( ,= , …,,其 值 为G类 的样本 数 除 以 2
文本特征 的提取有 词频法 、 互信 息、 H 统计 、 息增量 CI 信
LUO i e, W U n , Y Ha- i f Ga g ANG i-h n Jn s e g
(c o l f o w r n ier g hn h ii tn i r t h n h i 0 2 0 C ia S h o o f ae g ei ,S ag a J oo g v s y ag a 2 0 4 , h ) St E n n a Un e i ,S n
表示等 方法 。本 文分析 了上述方法 的优缺 点。 而提 出了 进
一
训 练集 总样 本数 n 对于 新 样本d 其属 于 G类 的条件 概 率是 ,
p C) f 。
种该 进型的 C I H以表述为在给 定的数 据样 本和相关参数 信 息的条件下 , 寻求 具有最大 后验概率 的模型 。在 给定 的样 本 D下 ,某 一模型 M 的后 验概率 与 M 的先验概 率和似然 函
验 证 明 了通过 以上 方面 的改进 , 文本 分类 的正确 率得到 了提 高。
1 朴 素 贝 叶 斯 方 法 . 1
设 训练样 本集分 为七 , 为C- c ,2 } 则每 个类 类 记 - 。 , { C …, , G的先验 概 率为p G)i 1 , 七 ( ,= , …,,其 值 为G类 的样本 数 除 以 2
文本特征 的提取有 词频法 、 互信 息、 H 统计 、 息增量 CI 信
LUO i e, W U n , Y Ha- i f Ga g ANG i-h n Jn s e g
(c o l f o w r n ier g hn h ii tn i r t h n h i 0 2 0 C ia S h o o f ae g ei ,S ag a J oo g v s y ag a 2 0 4 , h ) St E n n a Un e i ,S n
表示等 方法 。本 文分析 了上述方法 的优缺 点。 而提 出了 进
一
训 练集 总样 本数 n 对于 新 样本d 其属 于 G类 的条件 概 率是 ,
p C) f 。
种该 进型的 C I H以表述为在给 定的数 据样 本和相关参数 信 息的条件下 , 寻求 具有最大 后验概率 的模型 。在 给定 的样 本 D下 ,某 一模型 M 的后 验概率 与 M 的先验概 率和似然 函
验 证 明 了通过 以上 方面 的改进 , 文本 分类 的正确 率得到 了提 高。
统计决策论

➢求解步骤
Step1 Step2
H1
计算似然函数、似然比,并写出判决表达式 (y) fY|H1(y| H1)
化简
fY|H0(y| H0)
H0
Step3 根据统计量计算 fY|H1(y| H1)和 fY|H0(y| H0)
Step4 在P D 1H 0fY|H 0yH 0d y约束下,计算判决门限
Chapter 5 Statistical Decision
Theroy
01 介绍
02 贝叶斯准则
03 极小化极大准则(Minimax)
04 Neyman-Pearson准则
05 复合假设检验
06 序列检测
2
Review
• 贝叶斯判决准则
最小平均 错误概率 判决准则
H1
fY|H1(y| H1) P0(C10C00)
•R对P1取导数
( C 1 C 1 0 ) 0 ( C 0 C 1 1 ) P M 1 ( C 1 C 0 0 ) P F 0 0
•当C00=C11=0
C01PMC10PF
•进一步C01=C10=1
PF PM
此时,平均代价最小即转化为平均错误概率最小。
C00=C11=0
C01=C10=1
(a)Find the dicision regions for which the probability of error is minimum.
P(ε)=P0PF+P1PM=PM(P0+P1)=Q(m/2δ)
例1:在闭启键控通信系统中,两个假设下的观察信号模型为:
H0: xn H1: xAn
若两个假设的先验概率未知,且 c00c110 c01c101
贝叶斯判别分析课件

02
03
与决策树比较
贝叶斯判别分析提供了更稳定的预测 ,而决策树可能会因为数据的微小变 化而产生大的预测变化。
05
贝叶斯判别分析的案例分 析
案例一:信用卡欺诈检测
总结词
信用卡欺诈检测是一个经典的判别分析应用场景,通过贝叶斯判别分析可以有效地识别 出欺诈交易,减少经济损失。
详细描述
信用卡欺诈检测是金融领域中一个非常重要的问题。随着信用卡交易量的增长,欺诈行 为也日益猖獗,给银行和消费者带来了巨大的经济损失。贝叶斯判别分析可以通过对历 史交易数据的学习,建立分类模型,对新的交易进行分类,判断是否为欺诈行为。通过
市场细分
在市场营销中,贝叶斯判别分析 可以用于市场细分,通过消费者 行为和偏好等数据,将消费者划 分为不同的群体。
02
贝叶斯判别分析的基本概 念
先验概率与后验概率
先验概率
在贝叶斯理论中,先验概率是指在考 虑任何证据之前对某个事件或假设发 生的可能性所做的评估。它是基于过 去的经验和数据对未来事件的预测。
的类别。
它基于贝叶斯定理,通过将先验 概率、似然函数和决策函数相结 合,实现了对未知样本的分类。
贝叶斯判别分析在许多领域都有 广泛的应用,如金融、医疗、市
场营销等。
贝叶斯判别分析的原理
01
02
03
先验概率
在贝叶斯判别分析中,先 验概率是指在进行观测之 前,各类别的概率分布情 况。
似然函数
似然函数描述了观测数据 在给定某个类别下的概率 分布情况。
后验概率
后验概率是指在考虑了某些证据之后 ,对某个事件或假设发生的可能性所 做的评估。它是基于新的信息和证据 对先验概率的修正。
似然函数与贝叶斯定理
机器学习基础教程课件:分类与聚类学习算法

如图5.6展示了二维数据的决策边界
图5.6 决策边界为直线
这样,特征空间被决策边界划分成不同的区域,每个区域对应一个类别,称为决策区域。 当我们判定待识别的样本位于某个决策区域时,就判决它可以划归到对应的类别中。需要注意的是,决策区域包含类别中样本的分布区域,但不等于类别的真实分布范围。
数据实际属于类别π1
数据实际属于类别π2
分类操作结果属于类别π1
分类操作结果属于类别π2
表5.1 分类情况表
图5.4 错误分类概率情况图
分类情况的好坏可以使用错误分类代价(简称错分代价) 来进行衡量。由于正确分类没有出现错误,因此正确分类的错分代价为0。而将本来属于类别 的数据错分为类别 的错分代价为 ;同样的,将本来属于类别 的数据错分为类别 的错分代价为 。在两分类的情况下,综合所有的因素,可以使用期望错分代价(ECM)来进行评价: 优良的分类结果应该式(5.5)的错分代价最小。对于图5.4所示的两个分类区域,应该有:对于R2有: 对于 有: 对于 有:
式中, 为两类数据的均值(期望),S为两类数据相同的协方差阵。对式(5.14)有: (5.15) 可得线性分类函数为: (5.16) 对于两类方差不同的总体,其分类域变为: (5.17) (5.18)
式中, (5.19) 可见,当两个总体的方差相同时 ,将其代入式(5.19)。式(5.17)、(5.18)就退化为式(5.12)、(5.13)。 对于多个正态总体的数据集进行分类,可以将两类数据的分类方法进行推广。对于期望错分代价函数来讲,如果有n类数据,且将第一类数据错分为各个n-1类的数据,则借鉴两个总体期望错分代价函数的情况,有:
图5.5 SigmoidБайду номын сангаас数曲线
图5.6 决策边界为直线
这样,特征空间被决策边界划分成不同的区域,每个区域对应一个类别,称为决策区域。 当我们判定待识别的样本位于某个决策区域时,就判决它可以划归到对应的类别中。需要注意的是,决策区域包含类别中样本的分布区域,但不等于类别的真实分布范围。
数据实际属于类别π1
数据实际属于类别π2
分类操作结果属于类别π1
分类操作结果属于类别π2
表5.1 分类情况表
图5.4 错误分类概率情况图
分类情况的好坏可以使用错误分类代价(简称错分代价) 来进行衡量。由于正确分类没有出现错误,因此正确分类的错分代价为0。而将本来属于类别 的数据错分为类别 的错分代价为 ;同样的,将本来属于类别 的数据错分为类别 的错分代价为 。在两分类的情况下,综合所有的因素,可以使用期望错分代价(ECM)来进行评价: 优良的分类结果应该式(5.5)的错分代价最小。对于图5.4所示的两个分类区域,应该有:对于R2有: 对于 有: 对于 有:
式中, 为两类数据的均值(期望),S为两类数据相同的协方差阵。对式(5.14)有: (5.15) 可得线性分类函数为: (5.16) 对于两类方差不同的总体,其分类域变为: (5.17) (5.18)
式中, (5.19) 可见,当两个总体的方差相同时 ,将其代入式(5.19)。式(5.17)、(5.18)就退化为式(5.12)、(5.13)。 对于多个正态总体的数据集进行分类,可以将两类数据的分类方法进行推广。对于期望错分代价函数来讲,如果有n类数据,且将第一类数据错分为各个n-1类的数据,则借鉴两个总体期望错分代价函数的情况,有:
图5.5 SigmoidБайду номын сангаас数曲线
06-2贝叶斯分类

A graphical model of causal relationships,Represents dependency(依 赖关系) among the variables A probability table : Gives a specification of joint probability distribution
9
Naive Bayesian Classifier
P(Ci):
P(buys_computer = “yes”) = 9/14 P(buys_computer = “no”) = 5/14 P(age = “<=30” | buys_computer = “yes”) = 2/9 = 0.222 P(age = “<= 30” | buys_computer = “no”) = 3/5 = 0.6 P(income = “medium” | buys_computer = “yes”) = 4/9 = 0.444 P(income = “medium” | buys_computer = “no”) = 2/5 = 0.4 P(student = “yes” | buys_computer = “yes) = 6/9 = 0.667 P(student = “yes” | buys_computer = “no”) = 1/5 = 0.2 P(credit_rating = “fair” | buys_computer = “yes”) = 6/9 = 0.667 P(credit_rating = “fair” | buys_computer = “no”) = 2/5 = 0.4
Native Bayes Classifier 单纯贝氏分类
基础算法

1.访问顶点v;
2.依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
3.若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶 点均被访问过为止。
深度优先搜索属于盲目搜索,是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序 表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现 DFS算法。
快速排序算法
快速排序算法快速排序是由东尼·霍尔所发展的一种排序算法,算法步骤如下:
1.从数列中挑出一个元素,称为“基准”。
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的 数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作。
1.初始时令S={V0},T={其余顶点},T中顶点对应的距离值。若存在,d(V0,Vi)为弧上的权值;若不存在, d(V0,Vi)为。
2.从T中选取一个其距离值为最小的顶点W且不在S中,加入S。
3.对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值。
4.重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止。
归并排序
归并排序归并排序(Mergesort),又称合并排序,是建立在归并作上的一种有效的排序算法。该算法是 采用分治法(DivideandConquer)的一个非常典型的应用。算法步骤如下:
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列; 2.设定两个指针,最初位置分别为两个已经排序序列的起始位置; 3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置; 4.重复步骤3直到某一指针达到序列尾; 5.将另一序列剩下的所有元素直接复制到合并序列尾。 归并排序的平均时间复杂度为Ο(nlogn)。
2.依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
3.若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶 点均被访问过为止。
深度优先搜索属于盲目搜索,是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序 表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。一般用堆数据结构来辅助实现 DFS算法。
快速排序算法
快速排序算法快速排序是由东尼·霍尔所发展的一种排序算法,算法步骤如下:
1.从数列中挑出一个元素,称为“基准”。
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的 数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作。
1.初始时令S={V0},T={其余顶点},T中顶点对应的距离值。若存在,d(V0,Vi)为弧上的权值;若不存在, d(V0,Vi)为。
2.从T中选取一个其距离值为最小的顶点W且不在S中,加入S。
3.对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值。
4.重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止。
归并排序
归并排序归并排序(Mergesort),又称合并排序,是建立在归并作上的一种有效的排序算法。该算法是 采用分治法(DivideandConquer)的一个非常典型的应用。算法步骤如下:
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列; 2.设定两个指针,最初位置分别为两个已经排序序列的起始位置; 3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置; 4.重复步骤3直到某一指针达到序列尾; 5.将另一序列剩下的所有元素直接复制到合并序列尾。 归并排序的平均时间复杂度为Ο(nlogn)。
朴素贝叶斯模型

朴素贝叶斯分类器的公式
假设某个体有n项特征(Feature),分别为F1、F2、...、Fn。
现有m个类别(Category),分别为C1、C2、...、Cm。贝叶 斯分类器就是计算出概率最大的那个分类,也就是求下面这 个算式的最大值: P(C|F1F2...Fn) = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)
决策树的决策程序
决策树法的决策程序如下:
(1)绘制树状图,根据已知条件排列出各个方案和 每一方案的各种自然状态。 (2)将各状态概率及损益值标于概率枝上。 (3)计算各个方案期望值并将其标于该方案对应的 状态结点上。 (4)进行剪枝,比较各个方案的期望值,并标于方 案枝上,将期望值小的(即劣等方案剪掉)所剩的最后 方案为最佳方案。
性别分类的例子
下面是一组人类身体特征的统计资料
性别 身高(英尺) 男 6 男 5.92 男 5.58 男 5.92 女 5 女 5.5 女 5.42 女 5.75 体重(磅) 180 190 170 165 100 150 130 150 脚掌(英寸) 12 11 12 10 6 8 7 9
已知某人身高6英尺、体重130磅,脚掌8英寸,请问该人是男是女? 根据朴素贝叶斯分类器,计算下面这个式子的值。 P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别) 这里的困难在于,由于身高、体重、脚掌都是连续变量,不能采用离散变
P(F1|C)P(F2|C)P(F3|C)P(C)
账号分类的例子
上面这些值可以从统计资料得到,但是:F1和F2是连续变量,不适宜按照
某个特定值计算概率。 一个技巧是将连续值变为离散值,计算区间的概率。比如将F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三个区间,然后计算每个区间的概率。 在我们这个例子中,F1等于0.1,落在第二个区间,所以计算的时候,就 使用第二个区间的发生概率。 根据统计资料,可得: F1: 日志数量/注册天数(0.1) P(F1|C0) = 0.5, P(F1|C1) = 0.1 P(F2|C0) = 0.7, P(F2|C1) = 0.2 F2: 好友数量/注册天数 (0.2) P(F3|C0) = 0.2, P(F3|C1) = 0.9 F3: 是否使用真实头像 (0) 因此, P(F1|C0) P(F2|C0) P(F3|C0) P(C0) = 0.5 x 0.7 x 0.2 x 0.89 = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1) = 0.1 x 0.2 x 0.9 x 0.11 = 0.00198 可以看到,虽然这个用户没有使用真实头像,但是他是真实账号的概率, 比虚假账号高出30多倍,因此判断这个账号为真。
贝叶斯分类

《贝叶斯分类》
贝叶斯分类(BayesianDectoral)是一种机器学习算法,它能够从训练数据中提取出有用的信息来进行分类预测,其目标就是找到一个函数来表示数据集合的分布情况。
贝叶斯分类(BayesianDectoral)是一种机器学习算法,它能够从训练数据中提取出有用的信息来进行分类预测,其目标就是找到一个函数来表示数据集合的分布情况。
贝叶斯分类算法的主要思想如下:
1.首先确定分类规则,然后利用该规则对输入样本进行分类;
2.如果某些样本符合规则,那么它们被认为属于同一类别;
3.如果某些样本不满足规则,那么它们被认为属于另外一类;
4.如果所有样本都符合分类规则,那么最终结果将是一个分类。
贝叶斯分类算法的基本原理如下:
1.对每一个新的输入,都要计算其相应的概率值;
2.对每一个输入,都采用贝叶斯公式进行计算,得到新的概率值;
3.根据这两组概率值,判断两者之间是否存在关系;
4.若二者之间没有关系,则将这两个概率值合并成一个概率值;
5.如果二者之间有关系,则按照贝叶斯公式进行修正,重复步骤4~6,直至达到满意的结果。
【精品PPT】数据挖掘--分类课件ppt

16:06
9
分类模型的评估
对于非平衡(unblanced)的数据集,以上指标并不能很好的 评估预测结果。
非平衡的数据集是指阳性数据在整个数据集中的比例很 小。比如,数据集包含10只爬行动物,990只爬行动物, 此时,是否预测正确爬行动物对准确率影响不大。
更平衡的评估标准包括马修斯相关性系数(Matthews correlation coefficient)和ROC曲线。
数据集有10只非爬行动物,其中8只被预测为非爬行动物,特 异度为8/10
精度(Precision):
TP/(TP+FP)
分类器预测了12只动物为爬行动物,其中10只确实是爬行动 物,精度为10/12
准确率(Accuracy): (TP+TN)/(TP+TN+FN+FP)
数据集包含23只动物,其中18只预测为正确的分类,准确率 为18/23
训练集应用于建立分类模型 测试集应用于评估分类模型
K折叠交叉验证(K-fold cross validation):将初 始采样分割成K个子样本(S1,S2,...,Sk),取K-1个 做训练集,另外一个做测试集。交叉验证重复K 次,每个子样本都作为测试集一次,平均K次的 结果,最终得到一个单一估测。
16:06
16
K-近邻分类算法
K-近邻分类算法(K Nearest Neighbors,简称KNN)通过 计算每个训练数据到待分类元组的距离,取和待分类元组 距离最近的K个训练数据,K个数据中哪个类别的训练数据 占多数,则待分类元组就属于哪个类别。
算法 4-2 K-近邻分类算法
输入: 训练数据T;近邻数目K;待分类的元组t。
贝叶斯网络简介

DBN: Dynamic Bayesian networks
? Dealing with time ? In many systems, data arrives sequentially ? Dynamic Bayes nets (DBNs) can be used to
分类语义理解军事目标识别多目标跟踪战争身份识别生态学生物信息学贝叶斯网络在基因连锁分析中应编码学分类聚类时序数据和动态模型图分割有向分割dseparated分割变量x和y通过第三个变量z间接相连的三种情况
贝叶斯网络简介
Introduction to Bayesian Networks
基本框架
? 贝叶斯网络: ? 概率论 ? 图论
hidden structure learning)
一个简单贝叶斯网络例子
一个简单贝叶斯网络例子
? 计算过程:
? (1)
? P(y1|x1)=0.9
? P(z1|x1)=P(z1|y1,x1)P(y1|x1)+P(z1|y2,x1)P(y2|x1)
?
=P(z1|y1)P(y1|x1)+P(z1|y2)P(y2|x1)
? 使得运算局部化。消元过程实质上就是一个边缘化的过程。 ? 最优消元顺序:最大势搜索,最小缺边搜索
贝叶斯网络推理(Inference)
2. 团树传播算法
?利用步骤共享来加快推理的算法。
?团树(clique tree)是一种无向树,其中每 一个节点代表一个变量集合,称为团(clique) 。团树必须满足变量连通性,即包含同一变 量的所有团所导出的子图必须是连通的。
Conditional Independence
基本概念
例子
P(C, S,R,W) = P(C)P(S|C)P(R|S,C)P(W|S,R,C) chain rule = P(C)P(S|C)P(R|C)P(W|S,R,C) since = P(C)P(S|C)P(R|C)P(W|S,R) since
? Dealing with time ? In many systems, data arrives sequentially ? Dynamic Bayes nets (DBNs) can be used to
分类语义理解军事目标识别多目标跟踪战争身份识别生态学生物信息学贝叶斯网络在基因连锁分析中应编码学分类聚类时序数据和动态模型图分割有向分割dseparated分割变量x和y通过第三个变量z间接相连的三种情况
贝叶斯网络简介
Introduction to Bayesian Networks
基本框架
? 贝叶斯网络: ? 概率论 ? 图论
hidden structure learning)
一个简单贝叶斯网络例子
一个简单贝叶斯网络例子
? 计算过程:
? (1)
? P(y1|x1)=0.9
? P(z1|x1)=P(z1|y1,x1)P(y1|x1)+P(z1|y2,x1)P(y2|x1)
?
=P(z1|y1)P(y1|x1)+P(z1|y2)P(y2|x1)
? 使得运算局部化。消元过程实质上就是一个边缘化的过程。 ? 最优消元顺序:最大势搜索,最小缺边搜索
贝叶斯网络推理(Inference)
2. 团树传播算法
?利用步骤共享来加快推理的算法。
?团树(clique tree)是一种无向树,其中每 一个节点代表一个变量集合,称为团(clique) 。团树必须满足变量连通性,即包含同一变 量的所有团所导出的子图必须是连通的。
Conditional Independence
基本概念
例子
P(C, S,R,W) = P(C)P(S|C)P(R|S,C)P(W|S,R,C) chain rule = P(C)P(S|C)P(R|C)P(W|S,R,C) since = P(C)P(S|C)P(R|C)P(W|S,R) since
贝叶斯决策理论

第二章 贝叶斯决策理论
➢ 如果将一个“-“样品错分为”+“类所造成的损失要比将” +“分成”-“类严重。
➢ 偏向使对”-“类样品的错分类进一步减少,可以使总的损 失最小,那么B直线就可能比A直线更适合作为分界线。
12
2.1 Bayes决策的基本概念
第二章 贝叶斯决策理论
➢ 分类器参数的选择或者学习过程得到的结果取决于 设计者选择什么样的准则函数。
概率密度函数 P(X | 1) 是正常药品的属性分布,概率密度函数
P(X | 2 ) 是异常药品的属性分布。
24
2.1 Bayes决策的基本概念
第二章 贝叶斯决策理论
在工程上的许多问题中,统计数据往往满足正态分 布规律。
正态分布简单,分析简单,参量少,是一种适宜 的数学模型。
如果采用正态密度函数作为类条件概率密度的函数 形式,则函数内的参数(如期望和方差)是未知的, 那么问题就变成了如何利用大量样品对这些参数进行 估计。
➢ 不同准则函数的最优解对应不同的学习结果,得到 性能不同的分类器。
13
2.1 Bayes决策的基本概念
第二章 贝叶斯决策理论
➢ 错分类往往难以避免,这种可能性可用 P(i | X ) 表 示。
➢ 如何做出合理的判决就是Bayes决策所要讨论的问题。
➢ 其中最有代表性的是:
基于错误率的Bayes决策 基于最小风险的Bayes决策
05
2.1 Bayes决策的基本概念
第二章 贝叶斯决策理论
例:某制药厂生产的药品检验识别 目的:说明Bayes决策所要解决的问题!!
06
2.1 Bayes决策的基本概念
第二章 贝叶斯决策理论
如图4-1所示,正常药品“+“,异常药品”-”。 识别的目的是要依据X向量将药品划分为两类。
贝叶斯算法

标题文基于本属预性设独立性假设,贝叶斯公式可重写为:
此部分内容作为文字排版占位显示 (建议使用主题字体)
朴素贝叶斯分类
朴素贝叶斯分类的正式定义如下:
01
设
为一个待分类项,而每个a为x的一个特征属性。
02
有类别集合
03
计算
04
如果
01 找到一个已知分类的待分类项集合,这个集合叫做训练样本集 02 统计得到在各类别下各个特征属性的条件概率估计。即
1%的概率是假阴性,99%是真阳性。而在未得病的人中做实验,有1%的概率是 假阳性,99%是真阴性。
于是张某根据这种解释,估计他自己得了X疾病的概率为99%。张某的理 理是,既然只有1%的假阳性率,那么99%都是真阳性,那我已被感染X病的概率 便应该是99%。
张某咨询了医生,医生说:“99%?哪有那么大的感染几率啊。99%是测
P(C1)=P(买电脑) = P(C2)=P(不买电脑)
2:计算P(X|Ci):
(1)P (年龄<=30,收入=中,是学生,信用一般|买电脑)
(2)P (年龄<=30,收入=中,是学生,信用一般|不买电脑)
朴素贝叶斯分类的应用
1: P (年龄<=30,收入=中,是学生,信用一般|买电脑) =
P (年龄<=30| 买电脑)* P (收入=中| 买电脑)*P(是 学生| 买电脑)*P (信用一般| 买电脑)
全概率公式 由上可以推断出: 在上一节的推导当中,我们已知:
所以全概率公式为: 条件概率的另一种写法:
贝叶斯推断 对条件概率公式进行变形,可以得到如下形式:
所以,条件概率可以理解为下面的式子:
1:如果”可能性函数“P(B|A)/P(B)>1,意味着”先验概率“增强,事件A的发生的可能性变大; 2:如果”可能性函数“P(B|A)/P(B)=1,意味着B事件无助于事件A的可能性; 3:如果”可能性函数“P(B|A)/P(B)<1,意味着”先验概率“被消弱,事件A发生的可能性变小。
此部分内容作为文字排版占位显示 (建议使用主题字体)
朴素贝叶斯分类
朴素贝叶斯分类的正式定义如下:
01
设
为一个待分类项,而每个a为x的一个特征属性。
02
有类别集合
03
计算
04
如果
01 找到一个已知分类的待分类项集合,这个集合叫做训练样本集 02 统计得到在各类别下各个特征属性的条件概率估计。即
1%的概率是假阴性,99%是真阳性。而在未得病的人中做实验,有1%的概率是 假阳性,99%是真阴性。
于是张某根据这种解释,估计他自己得了X疾病的概率为99%。张某的理 理是,既然只有1%的假阳性率,那么99%都是真阳性,那我已被感染X病的概率 便应该是99%。
张某咨询了医生,医生说:“99%?哪有那么大的感染几率啊。99%是测
P(C1)=P(买电脑) = P(C2)=P(不买电脑)
2:计算P(X|Ci):
(1)P (年龄<=30,收入=中,是学生,信用一般|买电脑)
(2)P (年龄<=30,收入=中,是学生,信用一般|不买电脑)
朴素贝叶斯分类的应用
1: P (年龄<=30,收入=中,是学生,信用一般|买电脑) =
P (年龄<=30| 买电脑)* P (收入=中| 买电脑)*P(是 学生| 买电脑)*P (信用一般| 买电脑)
全概率公式 由上可以推断出: 在上一节的推导当中,我们已知:
所以全概率公式为: 条件概率的另一种写法:
贝叶斯推断 对条件概率公式进行变形,可以得到如下形式:
所以,条件概率可以理解为下面的式子:
1:如果”可能性函数“P(B|A)/P(B)>1,意味着”先验概率“增强,事件A的发生的可能性变大; 2:如果”可能性函数“P(B|A)/P(B)=1,意味着B事件无助于事件A的可能性; 3:如果”可能性函数“P(B|A)/P(B)<1,意味着”先验概率“被消弱,事件A发生的可能性变小。
基于类约束的贝叶斯网络分类器学习_王双成

之前进行, 需要进行大量的 高维条件概率计算, 这样降低了学 习效率和准确性, 同时碰撞 识别方法也有局限性. 本文给出了 基于弧的 因果语义的 定向方法, 并与碰 撞识别定 向方法相结 合, 有效地 避免 了上 述问题, 能 够显著 提高 学习 效率和 准确 性.
让 X 1, …, X n, C 分别 表示离 散随机 属性变 量和类 变量, 简称为属性变量和类变量, x 1, …, x n, c 为其值, 在概率模式中 的变量和表示概率模式的图形模式中的结点有时不加区分.
…, x i- 1, c) , , 根据定理* 的证明, 可知在 X1, …, X i- 1, C 中存在
最小的变 量集∏Xi 使 X i 和∏Xi ∪ { C} 外 的变 量集 条件 独立,
那么, 以∏Xi为 X i 的父结点集所构 成的有向无环图便 是 P 的
属 性贝叶斯网络, 用 PXi表示∏Xi 的配置, 可得 P ( x 1, …, x n ûc)
2( D ep artme nt of Comp ut er Sc ience N ort heast U ni v ersity , Chang chun 130024, Chi na)
Abstract: T he classificat ion is an impor tant and basic ability for huma n o bt ained by lear ning . I t has been consider ed a s
a key r esear ch ar ea in machine lear ning , patter n r eco gnit ion and dat a mining . It is pr ov ed that a Bayesian net wo rk clas-
06-3.5 贝叶斯判别——最小期望误判代价法

若d 2 x, 1 d 2
x, 2
2ln
Σ 2 1/2 Σ1 1/2
其中 d 2 x, i x-μi Σi1 x-μi , i 1, 2 。
Σ1≠ Σ2时的距离判别:
x x
,1 ,2
若d 2 x,1 d 2 x, 2 若d2 x,1 d 2 x,2
0 0
13
❖ 例3(书中的例5.2.2和前面的例2) 设p=1,组π1和π2的分布分别为
的。
可见书中
❖
例5.2.1。
x1, 若x
x
,2
若x
❖ 实践中,因未知参数需用样本值替代,故实际所使用的上述判别规则 只是渐近最优的。
12
❖
x ,1
x
,2
若
f1 f2
x x
c 1| 2 p2 c 2 |1 p1
若
f1 f2
x x
c 1| 2 p2 c 2 |1 p1
Σ1Σ2
x,1
j1
式:
x ,l
若pl
fl
x
max 1 i k
pi
fi
x
❖ 它等价于最大后验概率法的判别规则。
❖ 当p1=p2=⋯ =pk=1/k时,上式又进一步简化为
x l, 若P l | x max P i | x 1i k
P i| x
pi fi x
k
, i 1,2,, k
pj f j x
x
,
2
若W x <0
其中 W x ax
μ , a Σ 1 μ1
μ2 , μ
1 2
μ1
μ2 。
这也是Σ1=Σ2=Σ时 的距离判别。
贝叶斯估计

已上升到0.883 , 可投资了 .
贝塔分布(beta distribution)
若 0, 0 为两个实数,则由下列密度函数
1 1 1 x (1 x ) f ( x) B( , ) 0 0 x 1 x 0, x 1
其中 B( , )
设自然状态有k种, 1,2,…, k, P(i)表示自然状态i发生的先验概率分布, P(x︱i)表示在状态i条件,事件为x的概 率。 P(i ︱x )为i发生的后验概率。 全概率公式:P(x)为x在各种状态下可能出现 的概率综合值。
全概率公式: P ( x) P ( x | i ) P ( i )
p ( x; ) , 它表示在参数空间 { } 中不同的 对应不
同的分布。可在贝叶斯统计中记为 p( x | ) ,它表示 在随机变量 给定某个值时,总体指标 X 的条件分 布。 2、 根据参数 的先验信息确定先验分布 ( ) (prior distribution)。这是贝叶斯学派在最近几十年里重点 研究的问题。已获得一大批富有成效的方法。
( | x)
h( x, ) p( x | ) ( ) m( x) p( x | ) ( )d
这就是贝叶斯公式的密度函数形式。 这个在样本 x 给定 下, 的条件分布被称为 的后验分布。它是集中了总 体、 样本和先验等三种信息中有关 的一切信息, 而又 排除一切与 无关的信息之后所得到的结果。
( )( ) , 确定的随机变量 X 的分布称为贝塔分 ( )
布,记为 beta( , ) 贝塔分布 beta( , ) 的均值 E ( X ) ,
方差 Var ( X ) ( )2 ( 1)
贝塔分布(beta distribution)
若 0, 0 为两个实数,则由下列密度函数
1 1 1 x (1 x ) f ( x) B( , ) 0 0 x 1 x 0, x 1
其中 B( , )
设自然状态有k种, 1,2,…, k, P(i)表示自然状态i发生的先验概率分布, P(x︱i)表示在状态i条件,事件为x的概 率。 P(i ︱x )为i发生的后验概率。 全概率公式:P(x)为x在各种状态下可能出现 的概率综合值。
全概率公式: P ( x) P ( x | i ) P ( i )
p ( x; ) , 它表示在参数空间 { } 中不同的 对应不
同的分布。可在贝叶斯统计中记为 p( x | ) ,它表示 在随机变量 给定某个值时,总体指标 X 的条件分 布。 2、 根据参数 的先验信息确定先验分布 ( ) (prior distribution)。这是贝叶斯学派在最近几十年里重点 研究的问题。已获得一大批富有成效的方法。
( | x)
h( x, ) p( x | ) ( ) m( x) p( x | ) ( )d
这就是贝叶斯公式的密度函数形式。 这个在样本 x 给定 下, 的条件分布被称为 的后验分布。它是集中了总 体、 样本和先验等三种信息中有关 的一切信息, 而又 排除一切与 无关的信息之后所得到的结果。
( )( ) , 确定的随机变量 X 的分布称为贝塔分 ( )
布,记为 beta( , ) 贝塔分布 beta( , ) 的均值 E ( X ) ,
方差 Var ( X ) ( )2 ( 1)
贝叶斯决策理论
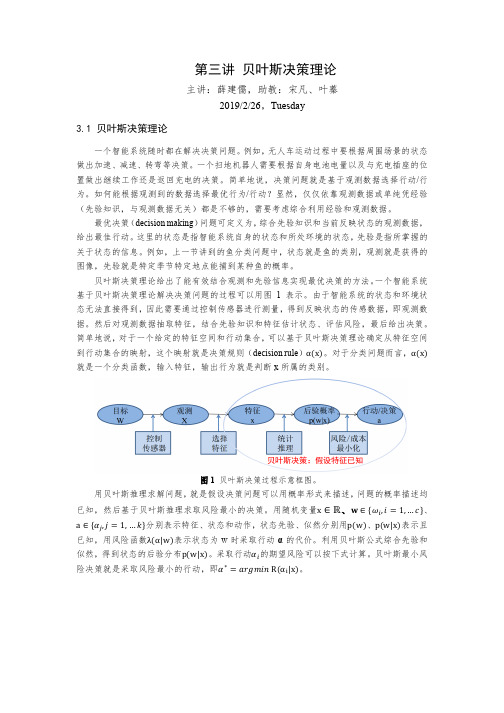
图 1 贝叶斯决策过程示意框图。 用贝叶斯推理求解问题,就是假设决策问题可以用概率形式来描述,问题的概率描述均
已知,然后基于贝叶斯推理求取风险最小的决策。用随机变量x ∈ ℝ、������ ∈ {������*, ������ = 1, … ������}、
a ∈ {������4, ������ = 1, … ������}分别表示特征、状态和动作,状态先验、似然分别用p(w)、p(w|x)表示且 已知,用风险函数λ(α|w)表示状态为 w 时采取行动 α 的代价。利用贝叶斯公式综合先验和 似然,得到状态的后验分布p(w|x)。采取行动������*的期望风险可以按下式计算。贝叶斯最小风 险决策就是采取风险最小的行动,即������∗ = ������������������������������������ R(αC|x)。
(3.2)
这里,状态 w 的取值为ωC,������ = 1, … , … , ������. ������4为行为,j = 1, … , … , k,p(������*)是先验概率, p(x|������*)是似然概率(likelihood),在分类问题中称为类条件概率,p(x)被称为证据(evidence), p(������*|x)是后验概率。类条件概率是指该类所有特征的概率分布。类条件概率和先验一般可
在二分类问题中,用������*4 表示当实际类别为������4 而误判为������* 时所引起的代价。用贝叶斯最 小风险决策可以得到三种等价的决策规则。
决策规则-1: 若R ������L x < R ������M x 则采取决策������L:“decide ������L”
R ������L x = ������LL������ ������L ������ + ������LM������ ������M ������ R ������M x = ������ML������ ������L ������ + ������MM������ ������M ������ 对于决策规则-1,因为不等号两边都有 p(x)证据(evidence)这一项,可以约去,就得到 决策规则-2: 若有(������ML − ������LL)������(������|������L)������ ������L > (������LM − ������MM)������(������|������M)�
已知,然后基于贝叶斯推理求取风险最小的决策。用随机变量x ∈ ℝ、������ ∈ {������*, ������ = 1, … ������}、
a ∈ {������4, ������ = 1, … ������}分别表示特征、状态和动作,状态先验、似然分别用p(w)、p(w|x)表示且 已知,用风险函数λ(α|w)表示状态为 w 时采取行动 α 的代价。利用贝叶斯公式综合先验和 似然,得到状态的后验分布p(w|x)。采取行动������*的期望风险可以按下式计算。贝叶斯最小风 险决策就是采取风险最小的行动,即������∗ = ������������������������������������ R(αC|x)。
(3.2)
这里,状态 w 的取值为ωC,������ = 1, … , … , ������. ������4为行为,j = 1, … , … , k,p(������*)是先验概率, p(x|������*)是似然概率(likelihood),在分类问题中称为类条件概率,p(x)被称为证据(evidence), p(������*|x)是后验概率。类条件概率是指该类所有特征的概率分布。类条件概率和先验一般可
在二分类问题中,用������*4 表示当实际类别为������4 而误判为������* 时所引起的代价。用贝叶斯最 小风险决策可以得到三种等价的决策规则。
决策规则-1: 若R ������L x < R ������M x 则采取决策������L:“decide ������L”
R ������L x = ������LL������ ������L ������ + ������LM������ ������M ������ R ������M x = ������ML������ ������L ������ + ������MM������ ������M ������ 对于决策规则-1,因为不等号两边都有 p(x)证据(evidence)这一项,可以约去,就得到 决策规则-2: 若有(������ML − ������LL)������(������|������L)������ ������L > (������LM − ������MM)������(������|������M)�
动态朴素贝叶斯网络分类器的特征子集选择

5 8
计 算机应 用 与软件
21 02皋
D T N 1 , [ ] …, 是对应数据集 中的例子数量 。 [ ], [ ]N 2 , Ⅳ[
是 Dl 一1 中 C1 t J J= [ 一1 ( ≤ ≤t ) Ct 0 J 一1 的情 况 数 量 。
( )属性条件 密度估计 2
Ab t a t sr c C a sf ain a c r c St e mo t mp ra t ef r n ei d c t r fca sf r.F au e s b e s lci n i a f cie me h d l s i c t c u a y i h s ot n roma c n iao l si e s e tr u s t ee t S n ef t t o i o i p o i o e v
酬
g
蓑
[ ) z l
( ,v ]I, ]
图 1 D B N N分 类 器 结 构
12 D N 分类 器表 示形 式 . I
基 于贝叶斯 网络理论 和贝 叶斯公式 , 据图 1中所 体 现 的 依 条件独立性关系可得 : P( []I [ ] … ,[ 一1 ,。0 , , [ ] C t O , C t ] [ ] … 0 , c DB N N分类 器分类准确性估计是衡量分 类器分类 准确性 的 个标准 , 静态分类器 的分 类准确 性评价标 准是 基于例 子之 间 独立 同分 布的假 设 , 时序例子数据之 间强 调时序依 赖 , 因此需要
中图分类号
动态朴 素贝叶斯网络
T 11 P 8
分 类器
特征子集选择 高斯核 函数
A
文献标识码
F EATL E S BS T E CⅡ oN 瓜 U E S LE
几类反问题的贝叶斯反演理论及算法

预测结果
利用更新后的后验分布,对未 知数据进行预测。
算法优化策略与方法
调整参数
根据训练数据和未知数据的特 性,调整贝叶斯反演算法的参
数,以优化预测效果。
选择合适的先验分布
根据样本数据的特性,选择合 适的先验分布,以更好地反映 未知数据的特征。
采用并行计算
利用并行计算技术,加快贝叶 斯反演算法的计算速度。
随机反问题的贝叶斯反演算法
随机反问题
贝叶斯反演算法
算法流程
这类问题主要涉及到的是随机 过程参数的估计,如天气预报 、气候变化预测等领域中的模 型参数估计问题。
该算法同样基于贝叶斯定理, 但在处理随机问题时需要考虑 随机因素的影响。
首先利用随机模拟方法对模型 参数进行模拟,得到参数的一 组样本;然后利用贝叶斯定理 计算后验分布,得到参数的分 布情况;最后通过抽样得到参 数的估计值。
03
几类反问题的贝叶斯反演算法
线性反问题的贝叶斯反演算法
01
线性反问题
02
贝叶斯反演算法
这类问题主要涉及到的是线性方程组 的求解,如声呐、雷达等探测性问题 的反向求解。
该算法基于贝叶斯定理,通过已知的 先验信息和观测数据,对未知的参数 进行估计。
03
算法流程
先对未知参数进行合理的先验分布假 设,然后结合观测数据和先验信息, 利用贝叶斯定理得到后验分布,最后 通过抽样得到参数的估计值。
贝叶斯反演
贝叶斯反演是将贝叶斯定理应用于反演理论的一种方法,它通过已 知的部分信息来推断未知系统的状态或参数。
贝叶斯反演的数学模型
概率模型
01
贝叶斯反演涉及建立概率模型,该模型描述了可观测数据与系
统状态或参数之间的关系。
聚类及贝叶斯分类

分类问题1
去年 税号 退税 1 是 2 否 3 否 4 是 5 否 6 否 7 是 8 否 9 否 10 否 可征税 婚姻状况 收入 125k 单身 100k 婚姻中 70k 单身 120k 婚姻中 95k 离婚 60k 婚姻中 220k 离婚 85k 单身 75k 婚姻中 90k 单身 逃税 否 否 否 否 是 否 否 是 否 是
分类问题1
税号 1 2 3 4 5 6 7 8 9 10 去年退税 是 否 否 是 否 否 是 否 否 否 婚姻状况 单身 婚姻中 单身 婚姻中 离婚 婚姻中 离婚 单身 婚姻中 单身 可征税收入 125k 100k 70k 120k 95k 60k 220k 85k 75k 90k 逃税 否 否 否 否 是 否 否 是 否 是
P (收入 120 | 否)
0.0072
分类问题1
去年 税号 退税 1 是 2 否 3 否 4 是 5 否 6 否 7 是 8 否 9 否 10 否 可征税 婚姻状况 收入 125k 单身 100k 婚姻中 70k 单身 120k 婚姻中 95k 离婚 60k 婚姻中 220k 离婚 85k 单身 75k 婚姻中 90k 单身 逃税 否 否 否 否 是 否 否 是 否 是
10 9 8 7 6
reassign
Update the cluster means
5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
2013-7-31
6
• K均值的流程
Y
输入
读 入
标 准 化
归 一 化
初 始 化 簇
计 算 簇 平 均 值
更 改 簇 中 心
重新 决定 点归 何簇
簇中心 是否变 化
Assign each objects to most similar center
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天气=多云 温度=66 湿度=90 有风,是否打网球?
15
Naive Bayesian
Naive Bayesian prediction requires each conditional prob. be non-zero. Otherwise, the predicted prob. will be zero
n k 1
P( X | Ci ) p( xk | Ci ) p( x1 | ci ) p( x2 | ci ) ... p( xn | ci )
9
Bayesian Classification
Bayes Theorem: P(H|X)=P(X|H)P(H)/P(X)
68 64
80
65 72
96
80 65
90
70 95
有
3
3
69
75 75 72 81 晴 2/9 3/5 0/5 均值 73 标准差 6.2
71
70
80 70 90 75
91
74.6 7.9
均值 79
86.2
无 有
6/9 3/9
2/5 3/5
9/14
5/14
多云 4/9
标准差 10.2 9.7
雨
3/9
Therefore, X belongs to class (“buys_computer = yes”)
13
连续属性值
天气 yes 晴 2 no 3 yes 83 温度 no 85 湿度 yes 86 no 85 无 有风 yes 6 no 2 yes 9 打网球 no 5
多云 4
雨 3
0
2
70
P(student = “yes” | buys_computer = “yes) = 6/9 = 0.667 P(student = “yes” | buys_computer = “no”) = 1/5 = 0.2
P(credit_rating = “fair” | buys_computer = “yes”) = 6/9 = 0.667
2/5
14
连续属性值
假设温度和湿度符合正态分布,概率密度函数为:
1 f ( x) e 2 ( x )2 2 2
天气=晴 温度=66 湿度=90 有风,是否打网球? f(温度=66|yes)=公式=0.034 f(温度=66|no)=公式=0.022 yes似然= No似然=
P( B | A) P( A) P( B | A) P( A) PAB c c P( B) P( B | A) P( A) P B A P( A )
0.3 0.97 0.8962 0.3 0.97 0.7 0.05
8
Native Bayes Classifer
1.D是训练元组集合,每个元组X={x1,x2,„,xn}有 n个属性 2.假设有m个类C1,C2,„,Cm, 给定 X,分类法将预 测X属于具有最高后验概率的类.
P( X | Ci ) P(Ci ) max P(Ci | X ) P( X )
需要分子最大(分母一样), ( X | Ci ) P(Ci ) 最大 P 即可。假设属性值相互独立,则:
主要用于大型数据库,分类结果准确且高效率。
2
概率论
随机实验(Random Experiment)是一种实验过程, 实验前已知所有可能结果,但不能预测实验结果, 相同状况下实验可重复试行。
1. 新生婴儿性别实验 2. 产品检验
样本空间:随机试验所有可能结果集合。样本空 间内的元素称为样本点。
P( X | H ) P( H ) P(H|X)= P( X )
7
案例
旅客搭乘飞机必须经电子仪器检查是否身上携带金属 物品,携带金属仪器会发出声音的机会是97%,但身 上无金属物品仪器会发出声音的机会是5%。若已知 一般乘客身上带有金属物品的机会是30%,若某旅客 经过仪器检查时发出声音,请问他身上有金属物品的 概率是多少? 解:设A=[有金属物],B= [仪器会发声]则
Prob(income = low) = 1/1003
Prob(income = medium) = 991/1003 Prob(income = high) = 11/1003
The “corrected” prob. estimates are close to their “uncorrected” counterparts
16
单纯贝氏分类器实例
办信用卡意愿:
项目
1 2 3 4 5 6 7 8 9 10
性别
男 女 女 男 女 女 女 男 男 女
年龄
>45 31~45 20~30 <20 20~30 20~30 31~45 31~45 31~45 <20
学生身分
否 否 是 是 是 否 否 是 否 是
收入
高 高 低 低 中 中 高 中 中 低
P(学生=否|办卡=会)=5/7
P(学生=否|办卡=不会)=0/3 P(收入=中|办卡=会)=2/7 P(收入=中|办卡=不会)=2/3
Example
X: a red and round object C: being an apple or an orange H: being an apple (H ? C)
10
Naive Bayesian Classifier: Training Data
age <=30 C1: buys_computer = <=30 ‘yes’ 31…40 C2: buys_computer = ‘no’ >40 >40 >40 Data sample 31…40 X = (age <=30, <=30 <=30 Income = medium, >40 Student = yes <=30 31…40 Credit_rating = Fair) 31…40 >40
1.新生婴儿性别实验 S={男性、女性} 2.产品检验 S={良品、不良品}
3
概率理论
概率:衡量某一事件可能发生的程度,并量化。
考试会录取的概率、明天会下雨的概率
probability)
一、古典概率:又称先验概率(prior 事前概率,满足下列条件:
或
1.样本空间的样本点数是有限的 2.样本空间内所有样本点发生概率为相同的 P(E)=事件E样本点个数/样本空间样本点个数
=40/160 = 0.25
6
贝叶斯定理
假设D由age \ income\ buy computer属性构成;H是 顾客购买计算机; P(H): 任意顾客购买计算机的概率,叫做先验概率。 P(H|X):当我们知道顾客收入和年龄后(一位年龄 为35岁,收入40000美元的顾客),顾客购买计算 机的概率,叫做后验概率。基于更多信息的概率。
n P( X | C i) P( x k | C i) k 1
Ex. Suppose a dataset with 1000 tuples, income=low (0), income= medium (990), and income = high (10), Use Laplacian correction (or Laplacian estimator) Adding 1 to each case
P(credit_rating = “fair” | buys_computer = “no”) = 2/5 = 0.4
12
Naive Bayesian Classifier
X = (age <= 30 , income = medium, student = yes, credit_rating = fair)
Let X is a data sample whose class label is unknown
Let H be a class label P(H) is the prior probability of H P(H|X) is the posterior probability of H conditioned on X
P(age = “<= 30” | buys_computer = “no”) = 3/5 = 0.6 P(income = “medium” | buys_computer = “yes”) = 4/9 = 0.444
P(income = “medium” | buys_computer = “no”) = 2/5 = 0.4
Class:
income student redit_rating c buys_compu high no fair no high no excellent no high no fair yes medium no fair yes low yes fair yes low yes excellent no low yes excellent yes medium no fair no low yes fair yes medium yes fair yes medium yes excellent yes medium no excellent yes high yes fair yes medium no excellent no
办卡
会 会 会 不会 不会 会 会 不会 会 会
