一次函数与全等三角形综合题
(完整版)《一次函数与几何图形综合》专题

《一次函数与几何图形综合》专题总论:函数与几何是初中数学中的重点内容,是中考命题重点考查的内容之一;函数中的几何问题,能使代数知识图形化,而几何中的函数问题,能使图形性质代数化;由于函数与几何结合的综合题的形式灵活、立意新颖,能更好地考查学生的思维水平和数学思想方法,因而成为近几年各地中考的一类热门试题;函数知识与几何知识有机结合的综合题,根据构成命题的主要要素可分为以下两类:一类是几何元素间的函数关系问题(这类问题不妨称简称为“几函”问题),这类问题的特点是:根据已知几何图形间的位置和数量关系(如平行、全等、相似,特别是成比例)建立自变量与函数所表示的几何元素间的等量关系,求出函数关系式,运用函数的性质解决几何图形中的问题;另一类是函数图像中的几何图形的问题(如三角形、四边形,特别是圆)(这类问题不妨简称为“函几”问题),这类问题的特点是:根据已知函数图像中的几何图形的位置特征,运用数形结合方法解决有关函数、几何问题。
一次函数与几何综合题是八年级学生初次接触一种用代几综合解决问题的方法,这种方法和能力是九年级解决中考压轴题所必须具备的。
1.代数(1)表达什么函数(包括其系数的代数意义、几何意义、物理意义)(2)显现怎样的图形(自身、与坐轴、与其他图形)(3)既是一个方程,也是一个坐标4)藏有那些数据,含有什么些关系(5)要建立某种代数关系缺少那些数据2.几何(1)基本图象有几个(2)图象之间有怎样关系(3)图象与所要证明(求解)的结论怎样的关联(4)要建立图象与图象之间的关系缺少那些数据3.代数与几何(1)代数(几何)在那些地方为几何(代数)提供了怎样的数据(2)几何(代数)通过什么方式为几何(代数)提供关系式(3)怎样设数据(坐标或线段长)函数与几何综合题的解题思想方法:“函几问题”与“几函问题”涉及的知识面广、知识跨度大、综合性强,应用数学方法多、纵横联系较复杂、结构新颖灵活、注重基础能力、探索创新和数学思想方法,它要求学生有良好的心理素质和过硬的数学基本功,能从已知所提供的信息中提炼出数学问题,从而灵活地运用所学知识和掌握的基本技能创造性的解决问题,正因如此,解决这类问题时,要注意解决问题的策略,常用的解题策略一般有以下几种:1.综合使用分析法和综合法。
八年级上数学一次函数与三角形全等专练(含答案)(2套)

八年级上数学一次函数与三角形全等专练及答案(2套)【模拟试题1】 (答题时间:80分钟)一、填空题1、把2x +y =1写成y 是x 的函数关系式是 .2、已知直线y =kx +b 过(0,1)和(-1,0)两点,则函数关系式为 .3、直线y =kx +b 的图像过第一、二、四象限,且过点(1,-3),则k +b = .4、如图,BAD ABC ∆≅∆,A 和B 是对应点,C 和D 是对应点,若AB =8cm ,BC =13cm ,AC =7cm ,BD = .5、如图,AB 、CD 相交于O ,AO =BO ,要判定图中的两个三角形全等,只需再补充一个条件,这个条件是 ,或 ,或 ,或 .6、等腰三角形的周长为10cm ,一边长为3cm ,则其他两边长分别为 .7、等腰三角形的一个角为70,则其它两个角分别是 .8、如图,已知∆ABC 中,AB =AC ,120=∠BAC ,DE 垂直平分AC 交BC 于D ,垂足为E ,DE =2cm ,则BC = .9、一次函数y =kx +b )0(≠k 的图像与直线2x +y =5平行,且经过点(1,-1),则此一次函数的解析式是 .10、P (-1,2)关于x 轴的对称点坐标是 ;关于y 轴对称点的坐标是 ;关于直线x =1为对称轴的对称点坐标是 ;关于直线y =-2为对称轴的对称点坐标是 .二、选择题1、点(1,m ),(2,n )在函数y =-x +1的图像上, 则( ) A . m >n B . m <n C . m =n D . m 与n 大小关系不确定2、等腰三角形的周长是24cm ,其两边的差是6cm ,则三角形的腰长是( ) A . 5cm B .6cm C . 10cm D .6cm 或10cm3、下列各条件中,不能判定两个直角三角形全等的是( ) A . 一条直角边和一个锐角分别相等; B . 两条直角边对应相等;C . 斜边和一条直角边对应相等;D . 直角和一个锐角对应相等;4、到三角形三个顶点距离相等的点是( )A . 三边高线的交点B . 三个内角平分线的交点C . 三条中线的交点D . 三边中垂线的交点5、一次函数y =3x +m -1的图像不经过第二象限,则m 的取值范围( )A . 1≤mB . 1-≤mC .m >1D .m <16、某移动通讯公司推出“心灵通”通话收费标准为:前3分钟(不足3分钟按3分钟计)为0.2元;3分钟后每分钟收0.1元,则一次通话时间为x 分(x >3)与这次通话的费用y (元)之间的关系式是( )A . y =0.2+0.1xB . y =0.1xC . y =-0.1+0.1xD . y =0.5+0.1x 7、如图,在ABC ∆中,已知∠B 和∠C 的平分线相交于点F ,过点F 作DF //BC ,交AB 于点D , 交AC 于点E ,若BD +CE =9,则线段DE 的长为( )A . 6B . 7C . 8D .98、如图,有一块直角三角形纸片,将AC 边沿直线AD 折叠,使它落在斜边AB 上,已知BC =6cm ,且CD :DB =1:2,则D 到AB 的距离为( )A . 1cmB . 2cmC . 3cmD . 不确定9、下列图形中,不是轴对称图形的是( ) A . 钝角 B . 正多边形 C . 平行四边形D . 等腰梯形三、解答题1、一根弹簧原长13厘米,它最多能挂的重物质量为16千克,并且每挂重1千克,就伸长0.5厘米.求:(1)挂重后弹簧的长度y (厘米)与挂重x (千克)之间的函数关系; (2)自变量的取值范围;2、已知一次函数的图像经过A (1,2),B (-1,1)两点. (1)求函数解析式并画出图像. (2)x 为何值时,y >0,y =0,y <0? (3)当-3<x <1时,求y 的取值范围. (4)当-3≤y ≤1时,求x 的取值范围.3、已知如图AB =DE ,AC =DF ,BF =EC ,求证:AC //DF ,AB //ED .4、(作图题)(1)根据下列语句画图:画锐角ABC ∆,延长AB 至E ,延长AC 至D .画∠CBE 、∠BCD 的平分线并交于点F .(2)问度量点F 到∠A 的两边的距离,它们是否相等?(3)根据画图过程和度量的结果,结合图形写出“已知”和“求证”,并加以证明.5、已知,如图AB =AC ,DE //BC ,求证:BD =CE .6、已知如图AD 是∠BAC 的平分线,∠B =∠EAC ,EF ⊥AD 于F .求证:EF 平分∠AED .7、在ABC ∆中,AD 是∠A 的平分线,且AB +BD =AC .求证:∠B =2∠C .【试题1答案】一、填空题1、x y 21-=2、1+=x y3、-34、7cm5、CO =DO ∠A =∠B ∠C =∠DAC //DB6、3cm ,4cm 或3.5cm ,3.5cm .7、55554070,或,. 8、12cm9、y =-2x +1 10、(-1,-2) (1,2) (3,2) (-1,-6)二、选择题 1、A 2、C 3、D 4、D 5、A 6、C 7、D 8、B 9、C三、解答题1、(1)y =13+0.5x (2)160≤≤x2、(1)y =0.5x +1.5 图像略(2)x >-3时,y >0;当x =-3时,y =0; 当x <-3时,y <0;(3)当-3<x <1时,0<y <2 (4)当-3≤y ≤1时,-9≤x ≤-1 3、证明:,EC BF = .EF BC =∴.//,//.,,DF AC DE AB DFE ACB E B DEFABC DF AC DE AB ∴∠=∠∠=∠∴∆≅∆∴==4、略5、,AC AB = .C B ∠=∠∴CEBD AE AC AD AB AE AD AED ADE C AED B ADE BC DE =∴-=-∴=∴∠=∠∴∠=∠∠=∠∴,..,//6、,BAC AD ∠平分 ,CAD BAD ∠=∠∴ AED EF AD EF DEAE DAE ADE EAC B EAC CAD DAE BAD B ADC ∠∴⊥=∴∠=∠∴∠=∠∠+∠=∠∠+∠=∠平分又 7、证明:AB AE AC =上截取在【模拟试题2】一. 选择题:(共30分)1. 下列函数中,是正比例函数的是( ) A . y x =2B .y x =12C . y x =2D . y x =-21 2. 下列式子中正确的是( )A . 22m m m -=B . --=440x xC . ab a b 220-=D . --=-325a a a3.()()-+---+232222x x x 的值是( ) A . -+x x 23 B . -+-x x 334C . ---3342x xD . -+332x x4. 若kb <0,且b k ->0,则函数y kx b =+的大致图像是( )5.如图,AB//DE,CD=BF,若△ABC≅△EDF,还需补充的条件可以是( )A.AC=EF B.AB=DEC.∠B=∠D D.不用补充DC AFEB6.下列命题正确的是( )A.有两条边分别相等的两个直角三角形全等B.有一条边相等的两个等腰直角三角形全等C.有两条直角边分别相等的两个直角三角形全等D.有两边和其中一边上的高对应相等的两个三角形全等7.AD是△ABC的角平分线,自D向AB、AC两边作垂线,垂足为E、F,那么下列结论中错误的是( )A.DE=DF B.AE=AFC.BD=CD D.∠ADE=∠ADF8.如下几个图形是国际通用的交通标志,其中不是轴对称图形的是( )A B C D!9.已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为( ) A.12 B.17 C.17或19 D.1910.已知△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.EF=1,则BF=( )A.4 B.6 C.12 D.8AEB F C二.填空题:(共30分)1.若函数yxx=+1,则x的自变量取值范围是_____________.2.直线y=kx经过点A(-5,3),则k=_____________,如果这条直线上点A的横坐标x A=4,那么它的纵坐标y A=___________.E3. 如下左图,AB =CD ,AE =BF =4cm ,CE =6cm ,要使△ACE ≅△BDF ,则需DF =___cm .ABC ED F4. 如上右图,已知AB ⊥BD 于B ,ED ⊥BD 于D ,AB =CD ,BC =DE ,则∠ACE =____.5. 如图:∠B =∠E =90°,EF =AB ,AD =CF ,则CB 和ED 的位置关系是___________,数量关系是___________.FB6. 在△ABC 中,∠C =90°,AD 平分∠BAC ,交BC 于D ,DE ⊥AB 于E ,若DE =3cm ,则CD =___________,若∠B =50°,则∠EAD =_____________. 7. 若△ABC 是轴对称图形,∠A =80°,则∠C =______________. 8. 写出六个成轴对称图形的汉字或英文字母______________. 9. 点P (1,2)关于直线x =-1的对称点的坐标是______________.10. 等腰三角形一腰上的高等于这腰的一半,则顶角的度数为______________.三. 解答题:(共40分) 1. 先作图,再证明.(1)在给出的图形中,完成以下作图(保留作图痕迹): ①作∠ACB 的平分线CD ,交AB 于点D ; ②延长BC 到E ,使CE =CA ,连接AE .AB C(2)求证:CD //AE . 2. 如图:在等腰三角形ABC 中,AB =AC ,点D 在BC 上,AD =BD ,AC =DC ,求∠BAC 的度数.AB D C3. 如图:在△ABC 中,AC ⊥BC ,AC =BC ,D 为AB 上一点,AF ⊥CD 交CD 的延长线于F ,BE ⊥CD 于E ,求证:EF =CF -AF .BFDEA C4.如图,△ACB、△ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD 交于F.请你在图中找出一对全等三角形,并写出证明它们全等的过程.AEC BFD5.在三角形ABC中,AD平分∠BAC,交BC于D,且∠B=2∠C.求证:AB+BD=AC.AC D B6.如图:在△ABC中,AB=AC,AD是中线,BE=CF.(1)求证:△BDE≅△CDF;(2)当∠B=60°时,过AB中点G,作GH//BD交AD于H,求证:GH AB=14.AG HE FB D C7.某高速公路收费站预计“十·一”这天将通过大小汽车1200辆次,该收费站的收费标准为:大车每辆次10元,小车每辆次5元,解答下面的问题:(1)写出“十·一”这天该收费站的收费金额y(元)与小车通过辆次x(辆)之间的函数关系,并指出自变量x的取值范围;(2)如果小车通过辆次占过车总辆次的65%,请你估计“十·一”这天此收费站的总收费金额.【试题2答案】一.1. A 2. D 3. B 4. B 5. B6. D 7. C8. C 9. C10. A二. 1. x x ≥-≠10且 2. k y A =-=-0624.., 3. 6cm 4. 90° 5. 平行,相等 6. 3cm 7. 50°或20°,20°或80° 8. 略 9. (-3,2) 10. 30°,150° 三.1. 作图略 2. ∠BAC =108° 3. 可证:△BEC ≅△CF A (AAS ) ∴CE =AF 又∵EF =CF -CE ∴EF =CF -AF 4. △ACE ≅△BCD (SAS )5. 在AC 上截取AE =AB ,连接DE ,△ABD ≅△AED (SAS ) ∴AE =AB ,ED =BD ,∠B =∠AED ∵∠AED =∠C +∠CDE ∠B =2∠C ∴2∠C =∠C +∠CDE ∴∠C =∠CDE ∴CE =DE ∴CE =BD ∵AE +CE =AC ∴AB +BD =AC6. (1)△BDE ≅△CDF (SAS ) (2)∵∠B =60°,AB =AC ∴△ABC 是等边三角形 又∵AD 是中线,∴∠ADB =90°,∠BAD =30° 又∵GH //BC ,∴∠GHA =90° ∴GH =0.5AG =0.25AB7. Y x =-+512000(0<x <1200),8100。
一次函数和几何综合题含答案

一次函数和几何综合题含答案1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共10小题)1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,证明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.(3)本题分三种情况进行讨论,设点P的坐标为(t,0):①当P在x轴正半轴上时,即t>0时,关键是求出D点的纵坐标,方法同(2),在直角三角形DBG中,可根据BD即OP的长和∠DBG的正弦函数求出DG的表达式,即可求出DH的长,根据已知的△OPD的面积可列出一个关于t的方程,即可求出t的值.②当P在x轴负半轴,但D在x轴上方时.即<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出DG,进而求出GF的长,然后同①.③当P在x轴负半轴,D在x轴下方时,即t≤时,方法同②.综合上面三种情况即可求出符合条件的t的值.解答:解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F.由已知得:BF=OE=2,OF==,∴点B的坐标是(,2)设直线AB的解析式是y=kx+b(k≠0),则有.解得.∴直线AB的解析式是y=x+4;(2)如图2,∵△ABD由△AOP旋转得到,∴△ABD≌△AOP,∴AP=AD,∠DAB=∠PAO,∴∠DAP=∠BAO=60°,∴△ADP是等边三角形,∴DP=AP=.如图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.方法(一)在Rt△BDG中,∠BGD=90°,∠DBG=60°.∴BG=BD•cos60°=×=.DG=BD•sin60°=×=.∴OH=EG=,DH=∴点D的坐标为(,)方法(二)易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,∴;而AE=2,BD=OP=,BE=2,AB=4,则有,解得BG=,DG=;∴OH=,DH=;∴点D的坐标为(,).(3)假设存在点P,在它的运动过程中,使△OPD的面积等于.设点P为(t,0),下面分三种情况讨论:①当t>0时,如图,BD=OP=t,DG=t,∴DH=2+t.∵△OPD的面积等于,∴,解得,(舍去)∴点P1的坐标为(,0).②∵当D在y轴上时,根据勾股定理求出BD==OP,∴当<t≤0时,如图,BD=OP=﹣t,DG=﹣t,∴GH=BF=2﹣(﹣t)=2+t.∵△OPD的面积等于,∴,解得,,∴点P2的坐标为(,0),点P3的坐标为(,0).③当t≤时,如图3,BD=OP=﹣t,DG=﹣t,∴DH=﹣t﹣2.∵△OPD的面积等于,∴(﹣t)[﹣(2+t)]=,解得(舍去),∴点P4的坐标为(,0),综上所述,点P的坐标分别为P1(,0)、P2(,0)、P3(,0)、P4(,0).点评:本题综合考查的是一次函数的应用,包括待定系数法求解析式、旋转的性质、相似三角形的判定和性质、三角形面积公式的应用等,难度较大.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.专题:压轴题.分析:(1)根据直线y=﹣x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=﹣x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则∵OQ=FQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴8﹣3t=t,解得:t=2;如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8﹣2t,∴QP=t﹣(8﹣2t)=3t﹣8,∴t=3t﹣8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,当t=﹣=时,S矩形PEFQ的最大值为:=,如图2,当Q在P点的右边时,∵OQ=t,PA=2t,∴2t>8﹣t,∴t,∴QP=t﹣(8﹣2t)=3t﹣8,∴S矩形PEFQ=QP•QF=(3t﹣8)•t=3t2﹣8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴<t≤4,当t=﹣=时,S矩形PEFQ的最大,∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.考点:一次函数综合题.专题:压轴题.分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.解答:解:(1)解方程x2﹣14x+48=0得x1=6,x2=8.∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,∴OC=6,OA=8.∴C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).由(1)知,OA=8,则A(8,0).∵点A、C都在直线MN上,∴,解得,,∴直线MN的解析式为y=﹣x+6;(3)∵A(8,0),C(0,6),∴根据题意知B(8,6).∵点P在直线MNy=﹣x+6上,∴设P(a,﹣a+6)当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);②当PC=BC时,a2+(﹣a+6﹣6)2=64,解得,a=,则P2(﹣,),P3(,);③当PB=BC时,(a﹣8)2+(a﹣6+6)2=64,解得,a=,则﹣a+6=﹣,∴P4(,﹣).综上所述,符合条件的点P有:P1(4,3),P2(﹣,)P3(,),P4(,﹣).点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)通过解一元二次方程x2﹣(+1)x+=0,求得方程的两个根,从而得到A、B两点的坐标,再根据两点之间的距离公式可求AB的长,根据AB:AC=1:2,可求AC的长,从而得到C点的坐标;(2)分①当点M在CB边上时;②当点M在CB边的延长线上时;两种情况讨论可求S关于t的函数关系式;(3)分AQ=AB,BQ=BA,BQ=QA三种情况讨论可求Q点的坐标.解答:解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,﹣2),Q3(1,2),Q4(1,).点评:考查了一次函数综合题,涉及的知识点有:解一元二次方程,两点之间的距离公式,三角形面积的计算,函数思想,分类思想的运用,菱形的性质,综合性较强,有一定的难度.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.考点:一次函数综合题;解二元一次方程组;待定系数法求一次函数解析式;三角形的面积;角平分线的性质;勾股定理;菱形的性质.专题:计算题.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得到方程组,求出即可;(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P 在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.解答:(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BAC=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.考点:一次函数综合题.专题:压轴题.分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.解答:(1)证明:∵∠AOG=∠ADG=90°,∴在Rt△AOG和Rt△ADG中,∵,∴△AOG≌△ADG(HL);(2)解:PG=OG+BP.由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,故∠PAG=∠DAG+∠DAP=45°,∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP;(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,∴∠1=∠2=30°,在Rt△AOG中,AO=3,AG=2OG,AG2=AO2+OG2,∴OG=,则G点坐标为:(,0),CG=3﹣,在Rt△PCG中,PG=2CG=2(3﹣),PC==3﹣3,则P点坐标为:(3,3﹣3),设直线PE的解析式为y=kx+b,则,解得,所以,直线PE的解析式为y=x﹣3.点评:本题考查了一次函数的综合运用.关键是根据正方形的性质证明三角形全等,根据三角形全等的性质求角、边的关系,利用特殊角解直角三角形,求P、G两点坐标,确定直线解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.考点:一次函数综合题.专题:压轴题;探究型.分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=,t=AB﹣BC=﹣1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;(3)根据题意可直接得出b=1﹣t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1﹣),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,又AB=,所以t=AB﹣BC=﹣1;(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.∵PC⊥OC,∴∠OCP=90°,∵OA=OB=1,∴∠OBA=45°,∵TH∥OB,∴∠BCH=45°,又∠CHB=90°,∴△CHB为等腰直角三角形,∴CH=BH,∵∠AOB=∠OBH=∠BHT=90°,∴四边形OBHT为矩形,∴OT=BH,∴OT=CH,∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,∴∠TCO=∠CPH,∵HB⊥x轴,TH∥OB,∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,∴△OTC≌△CHP,∴OC=CP;(3)①∵△OTC≌△CHP,∴CT=PH,∴PH=CT=AT=AC•cos45°=t,∴BH=OT=OA﹣AT=1﹣t,∴BP=BH﹣PH=1﹣t,∴;(0<t<)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,PB=BC,则﹣t=|1﹣t|,解得t=1或t=﹣1(舍去),∴当t=1时,△PBC为等腰三角形,即P点坐标为:P(1,1﹣).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.考点:一次函数综合题.专题:综合题;数形结合.分析:(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标.②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可.(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.解答:解:(1)①由题意,(2分)解得所以C(4,4)(3分)②把y=0代入y=﹣2x+12得,x=6,所以A点坐标为(6,0),(4分)所以.(6分)(2)存在;由题意,在OC上截取OM=OP,连接MQ,∵OQ平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ,∴△POQ≌△MOQ(SAS),(7分)∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.即AQ+PQ存在最小值.∵AB⊥ON,所以∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=4,∵△OAC的面积为6,所以AM=12÷4=3,∴AQ+PQ存在最小值,最小值为3.(9分)点评:本题主要考查一次函数的综合应用,具有一定的综合性,要求学生具备一定的数学解题能力,有一定难度.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:开放型.分析:(1)已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标.推出AO=QO,可得出∠PAB=45°.(2)先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB ﹣S△AOQ积列式求解即可求出m的值,从而也可求出n的值,继而可推出点P的坐标以及直线PA与PB的函数表达式.(3)本题要依靠辅助线的帮助.求证相关图形为平行四边形,继而求出D1,D2,D3的坐标.解答:解:(1)在直线y=x+m中,令y=0,得x=﹣m.∴点A(﹣m,0).在直线y=﹣3x+n中,令y=0,得.∴点B(,0).由,得,∴点P(,).在直线y=x+m中,令x=0,得y=m,∴|﹣m|=|m|,即有AO=QO.又∵∠AOQ=90°,∴△AOQ是等腰直角三角形,∴∠PAB=45°.(2)∵CQ:AO=1:2,∴(n﹣m):m=1:2,整理得3m=2n,∴n=m,∴==m,而S四边形PQOB=S△PAB﹣S△AOQ=(+m)×(m)﹣×m×m=m2=,解得m=±4,∵m>0,∴m=4,∴n=m=6,∴P().∴PA的函数表达式为y=x+4,PB的函数表达式为y=﹣3x+6.(3)存在.过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.①∵PD1∥AB且BD1∥AP,∴PABD1是平行四边形.此时PD1=AB,易得;②∵PD2∥AB且AD2∥BP,∴PBAD2是平行四边形.此时PD2=AB,易得;③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.∵BD3∥AP且B(2,O),∴y BD3=x﹣2.同理可得y AD3=﹣3x﹣12,得,∴.点评:本题的综合性强,主要考查的知识点为一次函数的应用,平行四边形的判定以及面积的灵活计算.难度较大.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:综合题.分析:(1)先求出A、B两点的坐标,再由一个角等于30°,求出AC的长,从而计算出面积;(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.。
2024年中考数学复习重难点题型训练—一次函数与几何图形综合题一(含答案解析)

2024年中考数学复习重难点题型训练—一次函数与几何图形综合题二(含答案解析)类型一与三角形有关1.(2022·天津)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x 轴,若AB=6,OA=OB=5,则点A的坐标是()A.(5,4)B.(3,4)C.(5,3)D.(4,3)【答案】D【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.【详解】解:∵AB⊥x轴,∴∠ACO=∠BCO=90°,∵OA=OB,OC=OC,∴△ACO≌△BCO(HL),∴AC=BC=12AB=3,∵OA=5,∴=4,∴点A的坐标是(4,3),故选:D.【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.2.(2020·宁夏中考真题)如图,直线542y x =+与x 轴、y 轴分别交于A 、B 两点,把AOB 绕点B 逆时针旋转90°后得到11AO B ,则点1A的坐标是_____.【答案】(4,125)【解析】【分析】首先根据直线AB 来求出点A 和点B 的坐标,A 1的横坐标等于OB ,而纵坐标等于OB-OA ,即可得出答案.【详解】解:在542y x =+中,令x=0得,y=4,令y=0,得5042x =+,解得x=8-5,∴A (8-5,0),B (0,4),由旋转可得△AOB ≌△A 1O 1B ,∠ABA 1=90°,∴∠ABO=∠A 1BO 1,∠BO 1A 1=∠AOB=90°,OA=O 1A 1=85,OB=O 1B=4,∴∠OBO 1=90°,∴O 1B ∥x 轴,∴点A 1的纵坐标为OB-OA 的长,即为48-5=125;横坐标为O 1B=OB=4,故点A 1的坐标是(4,125),故答案为:(4,125).【点睛】本题主要考查了旋转的性质以及一次函数与坐标轴的交点问题,利用基本性质结合图形进行推理是解题的关键.3.(2021·广西贺州市·中考真题)如图,一次函数4y x =+与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且45OPC ∠=︒,PC PO =,则点P 的标为________.【答案】(--【分析】过P 作PD ⊥OC 于D ,先求出A ,B 的坐标,得∠ABO=∠OAB=45°,再证明△PCB ≌△OPA ,从而求出BD =,OD =,进而即可求解.【详解】如图所示,过P 作PD ⊥OC 于D ,∵一次函数4y x =+与坐标轴分别交于A ,B 两点,∴A(-4,0),B(0,4),即:OA=OB ,∴∠ABO=∠OAB=45°,∴△BDP 是等腰直角三角形,∵∠PBC=∠CPO=∠OAP=45°,∴∠PCB+∠BPC=135°=∠OPA+∠BPC,∴∠PCB=∠OPA,又∵PC=OP,∴△PCB≌△OPA(AAS),∴AO=BP=4,∴Rt△BDP中,BD=PD=2=2,∴OD=OB−BD=2,∴P(2,2).故答案是:P(2,2).【点睛】本题主要考查了一次函数图象上点的坐标特征以及等腰三角形的性质,结合等腰三角形的性质,判定全等三角形是解决问题的关键.4.(2022·湖北黄冈)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C 匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为________.【答案】252+##2+25【分析】根据函数图像可得AB=4=BC ,作∠BAC 的平分线AD ,∠B =36°可得∠B =∠DAC =36°,进而得到ADC BAC △△,由相似求出BD 的长即可.【详解】根据函数图像可得AB=4,AB+BC=8,∴BC=AB=4,∵∠B =36°,∴72BCA BAC ∠∠︒==,作∠BAC 的平分线AD ,∴∠BAD =∠DAC =36°=∠B ,∴AD=BD ,72BCA DAC ∠∠︒==,∴AD=BD=CD ,设AD BD CD x ===,∵∠DAC =∠B =36°,∴ADC BAC △△,∴AC DC BC AC =,∴x 4x 4x-=,解得:1225x =-+,225x =--,∴252AD BD CD ===,此时521AB BD t +==(s),故答案为:52.【点睛】此题考查了图形与函数图象间关系、相似三角形的判定与性质、解一元二次方程,关键是证明ADC BAC △△.5.(2020·四川内江?中考真题)如图,在平面直角坐标系中,点A (-2,0),直线33:33l y x =+与x 轴交于点B ,以AB 为边作等边1ABA ∆,过点1A 作11//A B x 轴,交直线l 于点1B ,以11A B 为边作等边112A B A ∆,过点2A 作22//A B x 轴,交直线l 于点2B ,以22A B 为边作等边223A B A ∆,以此类推……,则点2020A 的纵坐标是______________【答案】20203(21)2-【解析】【分析】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),且与x 轴夹角为30º,则有AB=1,然后根据平行线的性质、等边三角形的性质、含30º的直角三角形的性质,分别求的A 1、A 2、A 3、的纵坐标,进而得到A n 的纵坐标,据此可得A 2020的纵坐标,即可解答.【详解】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),与y 轴交于点D (0,33),∴OB=1,OD=33,∴∠DBO=30º由题意可得:∠A 1B 1B=∠A 2B 2B 1=30º,∠B 1A 1B=∠B 2A 2B 1=60º∴∠A 1BB 1=∠A 2B 1B 2=90º,∴AB=1,A 1B 1=2A 1B=21,A 2B 2=2A 2B 1=22,A 3B 3=2A 3B 2=23,…A n B n =2n∴A 1C=2AB=2×1,A 1纵坐标为32×1=13(21)2-;A 2C 1=32A 1B 1=1322⨯,A2的纵坐标为32×1+1322⨯=013(22)2+=332⨯=23(21)2-;A 3C 2=32A 2B 2=2322⨯,A 3的纵坐标为32×1+1322⨯+2322⨯=0123(222)2++=372⨯=33(21)2-;…由此规律可得:A n C n-1=1322n -⨯,A n 的纵坐标为01213(2222)2n -++++ =3(21)2n -,∴A 2020=20203(21)2-,故答案为:20203(21)2-【点睛】本题是一道点的坐标变化规律探究,涉及一次函数的图象、等边三角形的性质、含30º角的直角三角形的性质,数字型规律等知识,解答的关键是认真审题,观察图象,结合基本图形的有关性质,找到坐标变化规律.6.(2022·陕西)如图,ABC 的顶点坐标分别为(23)(30)(11)A B C ----,,,,,.将ABC 平移后得到A B C '''V ,且点A 的对应点是(23)A ',,点B 、C 的对应点分别是B C '',.(1)点A 、A '之间的距离是__________;(2)请在图中画出A B C '''V .【答案】(1)4(2)见解析【分析】(1)由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4;(2)根据题意找出平移规律,求出103-1B C ''(,),(,),进而画图即可.(1)解:由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4.故答案为:4.(2)解:由题意,得103-1B C ''(,),(,),如图,A B C '''V 即为所求.【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.7.(2021·贵州毕节市·中考真题)如图,在平面直角坐标系中,点()11,1N 在直线:l y x =上,过点1N 作11N M l ⊥,交x 轴于点1M ;过点1M 作12M N x ⊥轴,交直线l 于点2N ;过点2N 作22N M l ⊥,交x 轴于点2M ;过点2M 作23M N x ⊥轴,交直线l 于点3N ;…;按此作法进行下去,则点2021M 的坐标为_____________.【答案】(20212,0).【分析】根据题目所给的解析式,求出对应的1M 坐标,然后根据规律求出n M 的坐标,最后根据题目要求求出最后答案即可.【详解】解:如图,过点N 作NM ⊥x 轴于M将1x =代入直线解析式y x =中得1y =∴1OM MN ==,MON ∠=45°∵1ONM =∠90°∴1ON NM =∵1ON NM ⊥∴11OM MM ==∴1M 的坐标为(2,0)同理可以求出2M 的坐标为(4,0)同理可以求出3M 的坐标为(8,0)同理可以求出n M 的坐标为(2n ,0)∴2021M 的坐标为(20212,0)故答案为:(20212,0).【点睛】本题主要考查了直线与坐标轴之间的关系,解题的关键在于能够发现规律.8.(2020·湖南湘西?中考真题)在平面直角坐标系中,O 为原点,点(6,0)A ,点B 在y 轴的正半轴上,30ABO ∠=︒.矩形CODE 的顶点D ,E ,C 分别在,,OA AB OB 上,2OD =.将矩形CODE 沿x 轴向右平移,当矩形CODE 与ABO 重叠部分的面积为时,则矩形CODE 向右平移的距离为___________.【答案】2【解析】【分析】先求出点B 的坐标(0,3),得到直线AB 的解析式为:33y =+,根据点D 的坐标求出OC 的长度,利用矩形CODE 与ABO 重叠部分的面积为63列出关系式求出3D G '=,再利用一次函数关系式求出OD '=4,即可得到平移的距离.【详解】∵(6,0)A ,∴OA=6,在Rt △AOB 中,30ABO ∠=︒,∴63tan 30OA OB ==∴B (0,63),∴直线AB 的解析式为:33y =+,当x=2时,y=43∴E (2,3,即DE=3∵四边形CODE 是矩形,∴OC=DE=43设矩形CODE 沿x 轴向右平移后得到矩形C O D E '''',D E ''交AB 于点G ,∴D E ''∥OB ,∴△AD G '∽△AOB ,∴∠AGD '=∠AOB=30°,∴∠EGE '=∠AGD '=30°,∴GE ''=,∵平移后的矩形CODE 与ABO 重叠部分的面积为,∴五边形C O D GE '''的面积为∴12O D O C EE GE ''''''⋅-⋅=,∴122EE ''⨯-⨯=,∴2EE '=,∴矩形CODE 向右平移的距离DD '=2EE '=,故答案为:2.【点睛】此题考查了锐角三角函数,求一次函数的解析式,矩形的性质,图形平移的性质,是一道综合多个知识点的综合题型,且较为基础的题型.9.(2021·浙江金华市·中考真题)在平面直角坐标系中,点A 的坐标为(,点B 在直线8:3l y x =上,过点B 作AB 的垂线,过原点O 作直线l 的垂线,两垂线相交于点C .(1)如图,点B ,C 分别在第三、二象限内,BC 与AO 相交于点D .①若BA BO =,求证:CD CO =.②若45CBO ∠=︒,求四边形ABOC 的面积.(2)是否存在点B ,使得以,,A B C 为顶点的三角形与BCO 相似?若存在,求OB 的长;若不存在,请说明理由.【答案】(1)①见解析;②552;(2)存在,44+-4,9,1【分析】(1)①等腰三角形等角对等边,则BAD AOB ∠=∠,根据等角的余角相等和对顶角相等,得到CDO COD ∠=∠,根据等角对等边,即可证明CD CO =;②添加辅助线,过点A 作AH OB ⊥于点H ,根据直线l 的解析式和角的关系,分别求出线段AB 、BC 、OB 、OC 的长,则11+22ABC CBO ABOC S S S AB BC OB OC =+=⨯⨯ 四边形;(2)分多钟情况进行讨论:①当点C 在第二象限内,ACB CBO ∠=∠时;②当点C 在第二象限内,ACB BCO ∠=∠时;③当点C 在第四象限内,ACB CBO ∠=∠时.【详解】解:(1)①证明:如图1,∵BA BO =,∴12∠=∠.∴BA BC ⊥,∴2590∠+∠=︒.而45∠=∠,∴2490∠+∠=︒.∵OB OC ⊥,∴1390∠+∠=︒.∴34∠=∠,∴CD CO =.②如图1,过点A 作AH OB ⊥于点H .由题意可知3tan 18∠=,在Rt AHO 中,3tan 18AH OH ∠==.设3m AH =,8m OH =.∵222AH OH OA +=,∴()()22238m m +=,解得1m =.∴38AH OH ==,.∵4590CBO ABC ∠=︒∠=︒,,∴45ABH ∠=︒,∴3,tan 45sin 45AH AH BH AB ====︒︒∴5OB OH BH =-=.∵45OB OC CBO ⊥∠=︒,,∴tan 455,cos 45OB OC OB BC =⨯︒===︒,∴111522ABC S AB BC =⨯=⨯= ,112555222CBO S OB OC =⨯=⨯⨯= :∴552ABC CBO ABOC S S S =+= 四边形.(2)过点A 作AH OB ⊥于点H ,则有38AH OH ==,.①如图2,当点C 在第二象限内,ACB CBO ∠=∠时,设OB t=∵ACB CBO ∠=∠,∴//AC OB .又∵AH OB OC OB ⊥⊥,,∴3AH OC ==.∵AH OB AB BC ⊥⊥,,∴12902390∠+∠=︒∠+∠=︒,,∴13∠=∠,∴AHB BOC ∽,∴AH HB BO OC=,∴383t t -=,整理得2890t t -+=,解得4t =±∴4OB =±②如图3,当点C 在第二象限内,ACB BCO ∠=∠时,延长AB CO ,交于点G ,则ACB GCB ≌,∴AB GB =.又∵AH OB OC OB ⊥⊥,,∴90AHB GOB ∠=∠=︒,而ABH GBO ∠=∠,∴ABH GBO ≌,∴142OB HB OH ===③当点C 在第四象限内,ACB CBO ∠=∠时,AC 与OB 相交于点E ,则有BE CE =.(a)如图4,点B 在第三象限内.在Rt ABC 中,1290,90ACB CAB ∠+∠=︒∠+∠=︒,∴2CAB∠=∠∴AE BE CE ==,又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒,而AEH CEO∠=∠∴AHE COE ≌,∴142HE OE OH ===∴225AE AH HE =+=,∴5BE =,∴9OB BE OE =+=(b)如图5,点B 在第一象限内.在Rt ABC 中90,90ACB CAB CBO ABE ∠+∠=︒∠+∠=︒∴CAB ABE ∠=∠,∴AE BE CE ==.又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒而AEH CEO ∠=∠,∴AHE COE≌∴142HE OE OH ===∴5AE ==,∴5BE =,∴1OB BE OE =-=综上所述,OB 的长为44+4,9,1.【点睛】本题涉及到等腰三角形、等角的余角相等、利用切割法求四边形的面积和相似三角形等知识,综合性较强.在题中已知两个三角形相似时,要分情况考虑.10.(2020·河南中考真题)小亮在学习中遇到这样一个问题:如图,点D 是弧BC 上一动点,线段8,BC cm =点A 是线段BC 的中点,过点C 作//CF BD ,交DA 的延长线于点F .当DCF ∆为等腰三角形时,求线段BD 的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:()1根据点D 在弧BC 上的不同位置,画出相应的图形,测量线段,,BD CD FD 的长度,得到下表的几组对应值.操作中发现:①"当点D 为弧BC 的中点时, 5.0BD cm =".则上中a 的值是②"线段CF 的长度无需测量即可得到".请简要说明理由;()2将线段BD 的长度作为自变量x CD ,和FD 的长度都是x 的函数,分别记为CD y 和FD y ,并在平面直角坐标系xOy 中画出了函数FD y 的图象,如图所示.请在同一坐标系中画出函数CD y 的图象;()3继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当DCF ∆为等腰三角形时,线段BD 长度的近似值.(结果保留一位小数).【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm 或5.0cm 或6.3cm ;【解析】【分析】(1)①点D 为弧BC 的中点时,△ABD ≌△ACD ,即可得到CD=BD ;②由题意得△ACF ≌△ABD ,即可得到CF=BD ;(2)根据表格数据运用描点法即可画出函数图象;(3)画出CF y 的图象,当DCF ∆为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD 的近似值.【详解】解:(1)①点D 为弧BC 的中点时,由圆的性质可得:AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD ,∴CD=BD=5.0,∴ 5.0a =;②∵//CF BD ,∴BDA CFA ∠=∠,∵BDA CFA BAD CAF AD AF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACF ≌△ABD ,∴CF=BD ,∴线段CF 的长度无需测量即可得到;(2)函数CD y的图象如图所示:(3)由(1)知=CF BD x =,画出CF y 的图象,如上图所示,当DCF ∆为等腰三角形时,①CF CD =,BD 为CF y 与CD y 函数图象的交点横坐标,即BD=5.0cm ;②CF DF =,BD 为CF y 与DF y 函数图象的交点横坐标,即BD=6.3cm ;③CD DF =,BD 为CD y 与DF y 函数图象的交点横坐标,即BD=3.5cm ;综上:当DCF ∆为等腰三角形时,线段BD 长度的近似值为3.5cm 或5.0cm 或6.3cm .【点睛】本题考查一次函数结合几何的应用,学会用描点法画出函数图象,熟练掌握一次函数的性质以及三角形全等的判定及性质是解题的关键.11.(2020·河北中考真题)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN-匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持APQ B∠=∠.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将ABC∆的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当03x≤≤及39x≤≤时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角APQ∠扫描APQ∆区域(含边界),扫描器随点P从M到B再到N共用时36秒.若94AK=,请直接..写出点K被扫描到的总时长.【答案】(1)3;(2)43MP=;(3)当03x≤≤时,24482525d x=+;当39x≤≤时,33355d x=-+;(4)23t s=【解析】【分析】(1)根据当点P在BC上时,PA⊥BC时PA最小,即可求出答案;(2)过A点向BC边作垂线,交BC于点E,证明△APQ∽△ABC,可得2APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,根据SS上下=45可得24=9APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,可得23APAB=,求出AB=5,即可解出MP;(3)先讨论当0≤x≤3时,P在BM上运动,P到AC的距离:d=PQ·sinC,求解即可,再讨论当3≤x≤9时,P在BN上运动,BP=x-3,CP=8-(x-3)=11-x,根据d=CP·sinC即可得出答案;(4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3;(2)过A 点向BC 边作垂线,交BC 于点E,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AP AD PQ AB AC BC==,∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,∴23AP AB =,AE=2BC ·tan 3C =,根据勾股定理可得AB=5,∴2253AP MP AB +==,解得MP=43;(3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35,∴d=35PQ ,∵AP=x+2,∴25AP x PQ AB BC+==,∴PQ=285x +⨯,∴d=23855x +⨯⨯=24482525x +,当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335,综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94,移动的速度=936=14,①从Q 平移到K ,耗时:92414-=1秒,②P 在BC 上时,K 与Q 重合时CQ=CK=5-94=114,∵∠APQ+∠QPC=∠B+∠BAP ,APQ B∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-,整理得y 2-8y=554-,(y-4)2=94,解得y 1=52,y 2=112,52÷14=10秒,112÷14=22秒,∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键.12.(2020·湖南衡阳?中考真题)如图1,平面直角坐标系xOy 中,等腰ABC ∆的底边BC 在x 轴上,8BC =,顶点A 在y 的正半轴上,2OA =,一动点E 从(3,0)出发,以每秒1个单位的速度沿CB 向左运动,到达OB 的中点停止.另一动点F 从点C 出发,以相同的速度沿CB 向左运动,到达点O 停止.已知点E 、F 同时出发,以EF 为边作正方形EFGH ,使正方形EFGH 和ABC ∆在BC 的同侧.设运动的时间为t 秒(0t ≥).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与ABC ∆重叠面积为S ,请问是存在t 值,使得9136S =若存在,求出t 值;若不存在,请说明理由;(3)如图2,取AC 的中点D ,连结OD ,当点E 、F 开始运动时,点M 从点O 出发,以每秒OD DC CD DO ---运动,到达点O 停止运动.请问在点E 的整个运动过程中,点M 可能在正方形EFGH 内(含边界)吗?如果可能,求出点M 在正方形EFGH 内(含边界)的时长;若不可能,请说明理由.【答案】(1)t=1;(2)存在,143t =,理由见解析;(3)可能,3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析【解析】【分析】(1)用待定系数法求出直线AC 的解析式,根据题意用t 表示出点H 的坐标,代入求解即可;(2)根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,用待定系数法求出直线AB 的解析式,求出点H 落在BC 边上时的t 值,求出此时重叠面积为169﹤9136,进一步求出重叠面积关于t 的表达式,代入解t 的方程即可解得t 值;(3)由已知求得点D (2,1),AC=,结合图形分情况讨论即可得出符合条件的时长.【详解】(1)由题意,A(0,2),B(-4,0),C(4,0),设直线AC 的函数解析式为y=kx+b ,将点A 、C 坐标代入,得:402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =-+,当点H 落在AC 边上时,点E(3-t ,0),点H (3-t ,1),将点H 代入122y x =-+,得:11(3)22t =--+,解得:t=1;(2)存在,143t =,使得9136S =.根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,设直线AB 的函数解析式为y=mx+n ,将点A 、B 坐标代入,得:402m n n -+=⎧⎨=⎩,解得:122m n ⎧=⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =+,当t ﹥4时,点E (3-t ,0)点H (3-t ,t-3),G(0,t-3),当点H 落在AB 边上时,将点H 代入122y x =+,得:13(3)22t t -=-+,解得:133t =;此时重叠的面积为221316(3)(3)39t -=-=,∵169﹤9136,∴133﹤t ﹤5,如图1,设GH 交AB 于S ,EH 交AB 于T,将y=t-3代入122y x =+得:1322t x -=+,解得:x=2t-10,∴点S(2t-10,t-3),将x=3-t 代入122y x =+得:11(3)2(7)22y t t =-+=-,∴点T 1(3,(7))2t t --,∴AG=5-t ,SG=10-2t ,BE=7-t ,ET=1(7)2t -,211(7)24BET S BE ET t ∆==- ,21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-,由2527133424t t -+-=9136得:1143t =,29215t =﹥5(舍去),∴143t =;(3)可能,35≤t≤1或t=4.∵点D 为AC 的中点,且OA=2,OC=4,∴点D (2,1),AC=,易知M 点在水平方向以每秒是4个单位的速度运动;当0﹤t ﹤12时,M 在线段OD 上,H 未到达D 点,所以M 与正方形不相遇;当12﹤t ﹤1时,12+12÷(1+4)=35秒,∴t =35时M 与正方形相遇,经过1÷(1+4)=15秒后,M 点不在正方行内部,则3455t ≤≤;当t=1时,由(1)知,点F 运动到原E 点处,M 点到达C 处;当1≤t≤2时,当t=1+1÷(4-1)=43秒时,点M 追上G 点,经过1÷(4-1)=13秒,点M 都在正方形EFGH 内(含边界),4533t ≤≤当t=2时,点M 运动返回到点O 处停止运动,当t=3时,点E 运动返回到点O 处,当t=4时,点F 运动返回到点O 处,当35t ≤≤时,点M 都在正方形EFGH 内(含边界),综上,当3455t ≤≤或4533t ≤≤或35t ≤≤时,点M 可能在正方形EFGH 内(含边界).【点睛】本题考查了一次函数与几何图形的综合,涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识,解答的关键是认真审题,提取相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,进而推理、探究、发现和计算.13.(2020·黑龙江哈尔滨?中考真题)已知,在平面直角坐标系中,点O 为坐标原点,直线AB 与x 轴的正半轴交于点A ,与y 轴的负半轴交于点B ,OA OB =,过点A 作x 轴的垂线与过点O 的直线相交于点C ,直线OC 的解析式为34y x =,过点C 作CM y ⊥轴,垂足为,9M OM =.(1)如图1,求直线AB 的解析式;(2)如图2,点N 在线段MC 上,连接ON ,点P 在线段ON 上,过P 点作PD x ⊥轴,垂足为D ,交OC 于点E ,若NC OM =,求PE OD的值;(3)如图3,在(2)的条件下,点F 为线段AB 上一点,连接OF ,过点F 作OF 的垂线交线段AC 于点Q ,连接BQ ,过点F 作x 轴的平行线交BQ 于点G ,连接PF 交x 轴于点H ,连接EH ,若,DHE DPH GQ FG ∠=∠-=,求点P 的坐标.【答案】(1)12y x =-;(2)94;(3)1236(,)55P .【解析】【分析】(1)根据题意求出A ,B 的坐标即可求出直线AB 的解析式;(2)求出N (3,9),以及ON 的解析式为y=3x ,设P (a ,3a ),表达出PE 及OD 即可解答;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,先证明四边形OSRA 为矩形,再通过边角关系证明△OFS ≌△FQR ,得到SF=QR ,进而证明△BSG ≌△QRG ,得到SG=RG=6,设FR=m ,根据GQ FG -=,以及在Rt △GQR 中利用勾股定理求出m 的值,得到FS=8,AR=4,证明四边形OSFT 为矩形,得到OT=FS=8,根据∠DHE=∠DPH ,利用正切函数的定义得到DE DH DH PD=,从而得到DH=32a ,根据∠PHD=∠FHT ,得到HT=2,再根据OT=OD+DH+HT ,列出关于a 的方程即可求出a 的值,从而得到点P 的坐标.【详解】解:(1)∵CM ⊥y 轴,OM=9,∴当y=9时,394x =,解得:x=12,∴C (12,9),∵CA ⊥x 轴,则A (12,0),∴OB=OA=12,则B (0,-12),设直线AB 的解析式为y=kx+b ,∴12012k b b +=⎧⎨=-⎩,解得:112k b =⎧⎨=-⎩,∴12y x =-;(2)由题意可得,∠CMO=∠OAC=∠MOA=90°,∴四边形MOAC 为矩形,∴MC=OA=12,∵NC=OM ,∴NC=9,则MN=MC-NC=3,∴N (3,9)设直线ON 的解析式为1y k x =,将N (3,9)代入得:193k =,解得:13k =,∴y=3x ,设P (a ,3a )∵PD ⊥x 轴交OC 于点E ,交x 轴于点D ,∴3(,)4E a a ,(a,0)D ,∴PE=39344a a a -=,OD=a ,∴9944a PE OD a ==;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,∵GF ∥x 轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR ,∴∠OSR=∠R=∠AOS=∠BSG=90°,则四边形OSRA为矩形,∴OS=AR,SR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°-∠AFR=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵QF⊥OF,∴∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠SOF+∠OFS=90°,∴∠SOF=∠QFR,∴△OFS≌△FQR,∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB,∴BS=SF=QR,∵∠SGB=∠RGQ,∴△BSG≌△QRG,∴SG=RG=6,设FR=m,则AR=m,∴QR=SF=12-m,∴=,-=,∵GQ FG∴66m m +-=+,∵QG 2=GR 2+QR 2,即222(6)6(12)m m +=+-,解得:m=4,∴FS=8,AR=4,∵∠OAB=∠FAR ,FT ⊥OA ,FR ⊥AR ,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT 为矩形,∴OT=FS=8,∵∠DHE=∠DPH ,∴tan ∠DHE=tan ∠DPH ,∴DE DH DH PD=,由(2)可知,DE=34a ,PD=3a ,∴343a DH DH a=,解得:DH=32a ,∴tan ∠PHD=3232PD a DH a ==,∵∠PHD=∠FHT ,∴tan ∠FHT=2TF HT =,∴HT=2,∵OT=OD+DH+HT ,∴3282a a ++=,∴a=125,∴1236(,)55P 【点睛】本题考查了一次函数与几何综合问题,涉及了一次函数解析式的求法,矩形的判定与性质,全等三角形的判定与性质以及锐角三角函数的定义等知识点,第(3)问难度较大,解题的关键是正确做出辅助线,熟悉几何的基本知识,综合运用全等三角形以及锐角三角函数的概念进行解答.类型二与平行四边形有关14.(2022·山东泰安)如图,四边形ABCD 为平行四边形,则点B 的坐标为________.【答案】()2,1--【分析】根据平行四边形的性质以及点的平移即可得出结论.【详解】解: 四边形ABCD 为平行四边形,∴DA CB ∥,即将D 点平移到A 的过程与将C 点平移到B 的过程保持一致,将D 点平移到A 的过程是::134x --=-(向左平移4各单位长度);:220y -=(上下无平移);∴将C 点平移到B 的过程按照上述一致过程进行得到()24,1B --,即()2,1B --,故答案为:()2,1--.【点睛】本题考查平行四边形的性质及点的平移,掌握点的平移的代数表示是解决问题的关键.15.(2022·甘肃武威)如图1,在菱形ABCD 中,60A ∠=︒,动点P 从点A 出发,沿折线AD DC CB →→方向匀速运动,运动到点B 停止.设点P 的运动路程为x ,APB △的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为()AB .C .D .【答案】B【分析】根据图1和图2判定三角形ABD 为等边三角形,它的面积为【详解】解:在菱形ABCD 中,∠A=60°,∴△ABD 为等边三角形,设AB=a ,由图2可知,△ABD 的面积为∴△ABD 的面积24a ==解得:a=故选B【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.16.(2020·黑龙江牡丹江?中考真题)如图,已知直线AB 与x 轴交于点A ,与y 轴交于点B ,线段OA 的长是方程27180x x --=的一个根,12OB OA =.请解答下列问题:(1)求点A ,B 的坐标;(2)直线EF 交x 轴负半轴于点E ,交y 轴正半轴于点F ,交直线AB 于点C .若C 是EF 的中点,6OE =,反比例函数k y x=图象的一支经过点C ,求k 的值;(3)在(2)的条件下,过点C 作CD OE ⊥,垂足为D ,点M 在直线AB 上,点N 在直线CD 上.坐标平面内是否存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形?若存在,请写出点P 的个数,并直接写出其中两个点P 的坐标;若不存在,请说明理由.【答案】(1)A (9,0),B (0,92);(2)-18;(3)存在5个,(9,12)或(9,-12)或(1,0)或(-7,4)或(-15,0).【解析】【分析】(1)解一元二次方程,得到点A 的坐标,再根据12OB OA =可得点B 坐标;(2)利用待定系数法求出直线AB 的表达式,根据点C 是EF 的中点,得到点C 横坐标,代入可得点C 坐标,根据点C 在反比例函数图像上求出k 值;(3)画出图形,可得点P 共有5个位置,分别求解即可.【详解】解:(1)∵线段OA 的长是方程27180x x --=的一个根,解得:x=9或-2(舍),而点A 在x 轴正半轴,∴A (9,0),∵12OB OA =,∴B (0,92);(2)∵6OE =,∴E (-6,0),设直线AB 的表达式为y=kx+b ,将A 和B 代入,得:0992k b b =+⎧⎪⎨=⎪⎩,解得:1292k b ⎧=-⎪⎪⎨⎪=⎪⎩,∴AB 的表达式为:1922y x =-+,∵点C 是EF 的中点,∴点C 的横坐标为-3,代入AB 中,y=6,则C (-3,6),∵反比例函数k y x=经过点C ,则k=-3×6=-18;(3)存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形,如图,共有5种情况,在四边形DM 1P 1N 1中,M 1和点A 重合,∴M 1(9,0),此时P 1(9,12);在四边形DP 3BN 3中,点B 和M 重合,可知M 在直线y=x+3上,联立:31922y x y x =+⎧⎪⎨=-+⎪⎩,解得:14x y =⎧⎨=⎩,∴M (1,4),∴P 3(1,0),同理可得:P 2(9,-12),P 4(-7,4),P 5(-15,0).故存在点P 使以D ,M ,N ,P 为顶点的四边形是正方形,点P 的坐标为P 1(9,12),P 2(9,-12),P 3(1,0),P 4(-7,4),P 5(-15,0).【点睛】本题考查了解一元二次方程,一次函数表达式,正方形的性质,反比例函数表达式,难度较大,解题的关键是根据图像画出符合条件的正方形.类型三最值问题17.(2020·江苏宿迁?中考真题)如图,在平面直角坐标系中,Q是直线y=﹣12x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为()A.455B C.523D.655【答案】B【解析】【分析】利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即可解决问题.【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,设Q(m,122m-+),则PM=1m﹣,QM=122m-+,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N ,在△PQM 和△Q′PN 中,'90''PMQ PNQ QPM PQ N PQ Q P ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△PQM ≌△Q′PN(AAS),∴PN=QM=122m -+,Q′N=PM=1m ﹣,∴ON=1+PN=132m -,∴Q′(132m -,1m ﹣),∴OQ′2=(132m -)2+(1m ﹣)2=54m 2﹣5m+10=54(m ﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′故选:B .【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键18.(2020·湖南永州?中考真题)已知点()00,P x y 和直线y kx b =+,求点P 到直线y kx b =+的距离d可用公式d =C 的圆心C 的坐标为()1,1,半径为1,直线l 的表达式为26y x =-+,P 是直线l 上的动点,Q 是C 上的动点,则PQ 的最小值是()A .355B .3515-C .6515-D .2【答案】B 【解析】【分析】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,利用公式计算即可.【详解】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,如图,∵点C 到直线l 的距离()00222116355112kx y b d k -+-⨯-+==++-,C 半径为1,∴PQ 的最小值是3515-,故选:B.【点睛】此题考查公式的运用,垂线段最短的性质,正确理解公式中的各字母的含义,确定点P与点Q最小时的位置是解题的关键.A B-,在x19.(2020·辽宁鞍山?中考真题)如图,在平面直角坐标系中,已知(3,6),(2,2)CD=,线段CD在x轴上平移,当轴上取两点C,D(点C在点D左侧),且始终保持1+的值最小时,点C的坐标为________.AD BC【答案】(-1,0)【解析】【分析】作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,得到此时AD+BC的值最小,求出直线AB″,得到点D坐标,从而可得点C坐标.【详解】解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,可知四边形B′B″DC为平行四边形,则B′C=B″D,由对称性质可得:BC=B′C,∴AD+BC=AD+B′C=AD+B″D=AB″,则此时AB″最小,即AD+BC最小,∵A(3,6),B(-2,2),∴B′(-2,-2),∴B″(-1,-2),设直线AB″的表达式为:y=kx+b,则632k bk b=+⎧⎨-=-+⎩,解得:2kb=⎧⎨=⎩,∴直线AB″的表达式为:y=2x,令y=0,解得:x=0,即点D坐标为(0,0),∴点C坐标为(-1,0),故答案为:(-1,0).【点睛】本题考查了轴对称的性质,最短路径问题,一次函数表达式,解题的关键是找到AD+BC最小时的情形20.(2020•连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=34x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.首先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE的面积最小.【解析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x﹣3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,﹣3),∴OD =4,OE =3,∴DE =32+42=5,∵∠MDN =∠ODE ,∠MND =∠DOE ,∴△DNM ∽△DOE ,∴MN OE=DM DE,∴MN 3=35,∴MN =95,当点C 与C′重合时,△C′DE 的面积最小,最小值=12×5×(95−1)=2,故答案为2.21.(2020·江苏连云港?中考真题)如图,在平面直角坐标系xOy 中,半径为2的O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D 、E ,则CDE △面积的最小值为________.【答案】2【解析】【分析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .首先证明点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C′.求出MN ,当点C 与C′重合时,△C′DE的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴5 DE===,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MN DM OE DE=,∴3 35 MN=,∴95 MN=,当点C 与C′重合时,△C′DE 的面积最小,△C′DE 的面积最小值1951225⎛⎫=⨯⨯-= ⎪⎝⎭,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.22.(2020·北京中考真题)在平面直角坐标系xOy 中,⊙O 的半径为1,A ,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB ,得到⊙O 的弦A B ''(,A B ''分别为点A ,B 的对应点),线段AA '长度的最小值称为线段AB 到⊙O 的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为1的弦12PP 和34P P ,则这两条弦的位置关系是;在点1234,,,P P P P 中,连接点A 与点的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线y =+上,记线段AB 到⊙O 的“平移距离”为1d ,求1d 的最小值;(3)若点A 的坐标为32,2⎛⎫ ⎪⎝⎭,记线段AB 到⊙O 的“平移距离”为2d ,直接写出2d 的取值范围.【答案】(1)平行,P 3;(2)32;(3)233922d ≤≤。
一次函数和全等三角形

一次函数和全等三角形一次函数是指函数的最高次数为1的函数,即表达式为y = ax + b的函数形式,其中a和b为常数。
一次函数在代数学中有着重要的应用,也是数学中最基础的函数类型之一全等三角形是指具有相同形状和大小的三角形,它们的对应边长和对应角度都相等。
全等三角形是几何学中的重要概念之一,它可以帮助我们解决很多与三角形相关的问题。
在很多数学问题中,我们可以运用一次函数和全等三角形的概念来求解。
下面将结合具体的例子来说明一次函数和全等三角形的应用。
首先,我们来看一个关于一次函数的问题:假设一个人的学费每年增加1000元,第一年学费为5000元,问经过n年后,这个人的学费是多少?这个问题可以用一次函数来解决。
设第n年的学费为f(n),由题意可知f(1)=5000,且每年增加1000元,即f(n)=1000n+b。
我们只需要找出b的值即可。
将已知条件带入到一次函数的表达式中,可以得到5000=1000×1+b,从而得出b=4000。
所以,经过n年后的学费可以表示为f(n)=1000n+4000。
接下来,我们来看一个关于全等三角形的问题:在平面直角坐标系中,已知三角形ABC的顶点坐标分别为A(1,2),B(4,6),C(8,4),求与三角形ABC全等的三角形的顶点坐标。
要求与三角形ABC全等的三角形,意味着对应的边长和角度都相等。
所以我们可以将两个三角形的对应边长和角度进行比较来求解。
首先,我们可以计算出三角形ABC的边长和角度。
由于ABC是直角三角形,我们可以通过勾股定理求得三条边的长度。
AB=√((4-1)²+(6-2)²)=√(9+16)=√25=5BC=√((8-4)²+(4-6)²)=√(16+4)=√20=2√5AC=√((8-1)²+(4-2)²)=√(49+4)=√53接下来,我们需要找到与ABC的对应边长相等的三条边,同时保持相应的位置关系不变。
一次函数与几何图形综合题(含答案)

一次函数与几何图形综合题(含答案)近日,举行了一次关于一次函数与几何图形综合的专题讲座。
在思想方法方面,介绍了函数方法和数形结合法。
函数方法是通过观察运动和变化来分析数量关系,并将其抽象升华为函数模型,从而解决问题的方法。
数形结合法则是将数与形结合起来,分析研究并解决问题的一种思想方法,对于与函数有关的问题,使用数形结合法能够事半功倍。
在知识规律方面,讲座介绍了常数k和b对直线y=kx+b(k≠0)位置的影响。
当b大于0时,直线与y轴的正半轴相交;当b等于0时,直线经过原点;当b小于0时,直线与y轴的负半轴相交。
当k和b异号时,即b大于0时,直线与x轴正半轴相交;当k和b同号时,即k和b的乘积小于0时,直线与x轴负半轴相交。
当k大于0且b大于0时,图象经过第一、二、三象限;当k大于0且b等于0时,图象经过第一、三象限;当b大于0且b小于0时,图象经过第一、三、四象限;当k小于0且b大于0时,图象经过第一、二、四象限;当k小于0且b等于0时,图象经过第二、四象限;当b小于0且b小于0时,图象经过第二、三、四象限。
讲座还介绍了直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系。
当b大于0时,将直线y=kx向上平移b个单位,即可得到直线y=kx+b;当b小于0时,将直线y=kx向下平移|b|个单位,即可得到直线y=kx+b。
另外,当k1不等于k2时,y1与y2相交;当k1等于k2且b1不等于b2时,y1与y2平行但不重合;当k1等于k2且b1等于b2时,y1与y2重合。
最后,讲座还通过一个例题对知识规律进行了精讲。
题目是直线y=-2x+2与x轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB。
要求求出AC的解析式。
的性质,需要灵活运用几何知识和代数知识。
在解答过程中,要注意清晰的逻辑思路和准确的计算,避免出现错误。
2) 在OA的延长线上任取一点P,作PQ⊥BP,交直线AC于Q。
我们来探究一下BP与PQ的数量关系,并证明结论。
中考数学重难点专题12 一次函数与几何综合问题(学生版)

中考数学复习重难点与压轴题型专项突围训练(全国通用版)专题12一次函数与几何综合问题【典型例题】1.(2022·四川成都·九年级期末)如图,在平面直角坐标系中,点A,B分别在x轴,y轴正半轴上,AO=2BO,点C(3,0)(A点在C点的左侧),连接AB,过点A作AB的垂线,过点C作x轴的垂线,两条垂线交于点D,已知△ABO△△DAC,直线BD交x轴于点E.(1)求直线AD的解析式;(2)直线AD有一点F,设点F的横坐标为t,若△ACF与△ADE相似,求t的值;(3)如图2,在直线AD上找一点G,直线BD上找一点P,直线CD上找一点Q,使得四边形AQPG是菱形,求出G点的坐标.【专题训练】一、选择题1.(2022·山东龙口·七年级期末)对于函数y=-3x+1,下列结论正确的是()A.它的图象必经过点(1,3)B.y的值随x值的增大而增大C.当x>0时,y<0D.它的图象与x轴的交点坐标为(13,0)2.(2022·江苏溧阳·八年级期末)如图,直线122y x=-+与x轴、y轴交于A、B两点,在y轴上有一点C(0,4),动点M从A点发以每秒1个单位的速度沿x轴向左移动.当动到△COM与△AOB全等时,移的时间t是()A.2B.4C.2或4D.2或63.(2022·陕西·辋川乡初级中学八年级期末)数学课上,老师提出问题:“一次函数的图象经过点A(3,2),B(-1,-6),由此可求得哪些结论?”小明思考后求得下列4个结论:①该函数表达式为y=2x-4;②该一次函数的函数值随自变量的增大而增大:③点P(2a,4a-4)在该函数图象上;④直线AB与坐标轴围成的三角形的面积为8.其中错误的结论是()A.1个B.2个C.3个D.4个4.(2022·江苏启东·八年级期末)如图,在平面直角坐标系中,O为原点,点A,C,E的坐标分别为(0,4),(8,0),(8,2),点P,Q是OC边上的两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为()A.(2,0)B.(3,0)C.(4,0)D.(5,0)二、填空题5.(2022·江苏滨湖·八年级期末)如图,直线y=﹣43x+8与坐标轴分别交于A、B两点,P是AB的中点,则OP的长为_____.6.(2021·山东济阳·八年级期中)如图,一次函数y =x +2的图像与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且△OPC =45°,PC =PO ,则点P 的坐标为______.7.(2021·湖北阳新·模拟预测)如图,直线AB 的解析式为y =﹣x +b 分别与x ,y 轴交于A ,B 两点,点A的坐标为(3,0),过点B 的直线交x 轴负半轴于点C ,且31OB OC ::,在x 轴上方存在点D ,使以点A ,B ,D 为顶点的三角形与△ABC 全等,则点D 的坐标为_____.8.(2022·山东龙口·七年级期末)正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示放置,点A 1,A 2,A 3,和点C 1,C 2,C 3,…,分别在直线y =kx +b (k >0)和x 轴上,已知点B 1,B 2,B 3,B 4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn 的坐标为_____三、解答题9.(2022·江苏海州·八年级期末)已知直线l 1经过点A (3,2)和点B (0,5),直线l 2:y =2x ﹣4经过点A 且与y 轴相交于点C .(1)求直线l 1的函数表达式;(2)已知点M 在直线l 1上,过点M 作MN //y 轴,交直线l 2于点N .若MN =6,请求出点M 的横坐标.10.(2022·广西·桂林市雁山中学九年级期末)如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=mx在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:(1)点A、B、C的坐标;(2)这个反比例函数的表达式;(3)这个一次函数的表达式.11.(2022·江苏溧阳·八年级期末)如图,在平面直角坐标系中长方形AOBC的顶点A、B坐标分别为(0,8)、(10,0),点D是BC上一点,将△ACD沿直线AD翻折,使得点C落在OB上的点E处,点F是直线AD 与x轴的交点,连接CF.(1)点C坐标为____________;(2)求直线AD的函数表达式_______________________;(3)点P是直线AD上的一点,当△CFP是直角三角形时,请你直接写出点P的坐标.。
一次函数综合题(难度较大)带答案

一次函数综合题一.解答题(共10小题)1.如图,在直角坐标系中,△ABC满足∠BCA=90°,点A、C分别在x轴和y轴上,AC=BC=2,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.(1)当AB∥y轴时,求B点坐标.(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是16?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.2.如图,在平面直角坐标系中,直线y=2x+6与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(6,0).(1)求直线BC的解析式;(2)点G是线段BC上一动点,若直线AG把△ABC的面积分成1:2的两部分,请求点G的坐标;(3)已知D为AC的中点,点P是平面内一点,当△CDP是以CD为直角边的等腰直角三角形时,直接写出点P 的坐标.3.如图,在平面直角坐标系中,直线l1:y=kx+1交y轴于点A,交x轴于点B(4,0),过点E(2,0)的直线l2平行于y轴,交直线l1于点D,点P是直线l2上一动点(异于点D),连接P A、PB.(1)求直线l1的解析式;(2)设P(2,m),求△ABP的面积S的表达式(用含m的代数式表示);(3)当△ABP的面积为3时,则以点B为直角顶点作等腰直角△BPC,请直接写出点C的坐标.4.如图,在平面直角坐标系中,一次函数y=﹣2x﹣1的图象分别交x轴、y轴于点A和B,已知点C的坐标为(﹣3,0).若点P是x轴上的一个动点,(1)求直线BC的函数解析式;(2)过点P作y轴的平行线交AB于点M,交BC于点N,当点P恰好是MN的中点时,求出P点坐标.(3)若以点B、P、C为顶点的△BPC为等腰三角形时,请直接写出所有符合条件的P点坐标.5.如图,在平面直角坐标系中,直线m经过点(﹣1,2),交x轴于点A(﹣2,0),交y轴于点B,直线n与直线m交于点P,与x轴、y轴分别交于点C、D(0,﹣2),连接BC,已知点P的横坐标为﹣4.(1)求直线m的函数表达式和点P的坐标;(2)求证:△BOC是等腰直角三角形;(3)直线m上是否存在点E,使得S△ACE=S△BOC?若存在,求出所有符合条件的点E的坐标,若不存在,请说明理由.6.如图,在平面直角坐标系中,A(﹣1,0),B(0,3),直线y=﹣x+1与x轴相交于点C,与直线AB交于点D,交y轴于点E.(1)求直线AB的解析式及点D的坐标;(2)如图2,H是直线AB上位于第一象限内的一点,连接HC,当S△HCD=时,点M、N为y轴上两动点,点M在点N的上方,且MN=,连接HM、NC,求HM+MN+NC的最小值;(3)将△OEC绕平面内某点旋转90°,旋转后的三角形记为△O'E'C',若点E'落在直线AB上,点O'落在直线CD上,请直接写出满足条件的点E'的坐标.7.如图所示,平面直角坐标系中,直线l1:y=﹣2x+3与直线l2:y=x+1相交于点A,直线l2与x轴相交于点B.过直线l2上的一点P(a,﹣1)作y轴的垂线,交直线l1于点C,连接BC.(1)求点A的坐标;(2)求△ABC的面积;(3)将直线l1向下平移4个单位长度得到直线l3,设直线l3与y轴相交于点D,则直线l2上是否存在一点Q,使得△DPQ是以DP为腰的等腰三角形?若存在,请直接写出Q的坐标,若不存在,请说明理由.8.如图,在平面直角坐标系中,一次函数y=kx+b经过A(a,0),B(0,b)两点,且a,b满足(a+8)2+=0,∠ABO的平分线交x轴于点E.(1)求直线AB的表达式;(2)求直线BE的表达式;(3)点B关于x轴的对称点为点C,过点A作y轴的平行线交直线BE于点D,点M是线段AD上一动点,点P 是直线BE上一动点,则△CPM能否为不以点C为直角顶点的等腰直角三角形?若能,请直接写出点P的坐标;若不能,说明理由.9.如图,直线y=﹣x+8与x轴,y轴分别交于A,B两点,点C的坐标为(﹣6,0),连结BC,过点O作OD⊥AB于点D,点Q为线段BC上一个动点.(1)求BC,OD的长;(2)在线段BO上是否存在一点P,使得△BPQ与△ADO全等?若存在,请求出点Q的坐标;若不存在,请说明理由;(3)当点C关于OQ的对称点恰好落在△OBD的边上,请直接写出点Q的坐标.10.已知,如图1,直线AB分别交平面直角坐标系中x轴和y轴于A,B两点,点A坐标为(﹣3,0),点B坐标为(0,6),点C在直线AB上,且点C坐标为(﹣a,a).(1)求直线AB的表达式和点C的坐标;(2)点D是x轴上的一动点,当S△AOB=S△ACD时,求点D坐标;(3)如图2,点E坐标为(0,﹣1),连接CE,点P为直线AB上一点,且∠CEP=45°,求点P坐标.参考答案与试题解析一.解答题(共10小题)1.【分析】(1)根据勾股定理,可得AB的长,根据勾股定理,可得AO的长,可得B点坐标;(2)根据全等三角形的判定与性质,可得BE=OC =x,EC=OA=x,根据勾股定理,可得x的长,可得A点坐标;(3)分类讨论:①D在y轴的正半轴上;②D在y 轴的负半轴上,根据面积的和差,可得关于y的方程,根据解方程,可得答案.【解答】解:(1)∵∠BCA=90°,AC=BC=2,∴∠BAC=45°,AB ==2,∵AB∥y轴,∴∠BAO=90°=∠COA,∴∠CAO=45°=∠OCA,∴CO=AO,∵AO2+CO2=AC2,∴2AO2=(2)2,∴AO =,∴点B 坐标为(,2);(2)如图,过点B作BE⊥y轴,垂足为点E,∵∠BCE+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCE=∠CAO,且AC=BC,∠BEO=∠AOC,∴△AOC≌△CEB(AAS),∴BE=CO,AO=CE,∵点B落在直线y=3x上,∴设B(x,3x),∴BE=x=OC,OE=3x,∴CE=OA=2x,∵OA2+OC2=AC2,∴(2x)2+x2=20,∴x=2,∴OA=2x=4,∴点A(4,0);(3)设点D(0,y),由(2)得B(2,6),当点D在y轴正半轴上,如图,连接OB,∵S四边形ABDO=S△AOB+S△BDO=16,∴×4×6+×y×2=16,∴y=4,∴点D(0,4);若点D在y轴负半轴上,如图,连接OB,∵S四边形ABDO=S△AOB+S△ADO=16,∴×4×6+×4×(﹣y)=16,∴y=﹣2,∴点D坐标为(0,﹣2).综上,存在点D,使以O、A、B、D为顶点的四边形面积是16,点D的坐标为(0,4)或(0,﹣2).2.【分析】(1)根据题意,求得点C的坐标,结合B的坐标,利用待定系数法求解析式即可;(2)求出S△ABC=27,设G(m,﹣m+6),分两种情况:①S△ABG:S△ACG=1:2时,②S△ABG:S△ACG=2:1时,分别求得m的值,进而求得G点的坐标;(3)分类讨论,①当点D为直角顶点时,②当点C 为直角顶点时,根据等腰直角三角形以及全等三角形的性质即可求解.【解答】解:(1)由y=2x+6得:A(﹣3,0),C(0,6),∵点B(6,0).设直线BC的解析式为y=kx+b(k≠0):∴,解得:,∴直线BC的解析式为y=﹣x+6;(2)∵A(﹣3,0),C(0,6),B(6,0).∴AB=9,∴S△ABC =×9×6=27,设G(m,﹣m+6),(0<m<6),①当S△ABG:S△ACG=1:2时,即S△ABG =S△ABC=9,∴×9(﹣m+6)=9,∴m=4,∴G(4,2);当S△ABG:S△ACG=2:1时,即S△ABG =S△ABC=18,∴×9(﹣m+6)=18,∴m=2,∴G(2,4).综上,点G的坐标为(4,2)或(2,4);(3)∵A(﹣3,0),C(0,6),D为AC的中点,∴D (﹣,3),①当点D为直角顶点时,如图,过点D作DE⊥y轴于E,过点P作PF⊥DE交ED的延长线于F,交x 轴于H,∴∠F=∠CED=90°,∵△CDP是等腰直角三角形,∴DP=CD,∠CDB=90°,∴∠PDF+∠CDE=∠DCE+∠CDE=90°,∴△PDF≌△CDE(AAS),∴DF=CE,PF=DE,∵D (﹣,3),C(0,6).∴DE=PF =,OE=3,CE=DF=6﹣3=3,∴EF=3+=,PH=3+=,∴P (﹣,),同理得:P ′(,);∴P (﹣,)或(,);②当点C为直角顶点时,如图,过点D作DN⊥y轴于N,过点P作PM⊥y轴于M,同①可得△PCM≌△CDN(AAS),∴DN=CM,PM=CN,∵D (﹣,3),C(0,6).∴DN=CM =,ON=3,CN=PM=6﹣3=3,∴OM=6﹣=,∴P(3,),同理得:P′(﹣3,);∴P(3,)或(﹣3,).综上,点P的坐标为(﹣,)或(,)或(3,)或(﹣3,).3.【分析】(1)将B(4,0)代入y=kx+1得到y =﹣x+1;(2)由两直线交点的求法得到点D的坐标;易得线段PD的长度,所以根据三角形的面积公式即可得到结论;(3)根据三角形的面积公式列方程求得m=2,于是得到点P(2,2),推出∠EPB=∠EBP=45°.第1种情况,如图2,过点C作CF⊥x轴于点F根据全等三角形的性质得到BF=CF=PE=EB=2,于是得到C(6,2);第2种情况,如图3根据全等三角形的性质得到PC =CB=PE=EB=2,于是得到C(2,﹣2);第3种情况,当点P在点D下方时,得到(3,2)或(5,﹣2).【解答】解:(1)∵直线l1:y=kx+1交x轴于点B (4,0),∴0=4k+1.∴k =﹣.∴直线l1:y =﹣x+1;(2)由得:.∴D(2,).∵P(2,m),∴PD=|m ﹣|.∴S =×|4﹣0|•PD =×|m ﹣|×4=|2m﹣1|.当m时,S=2m﹣1;当m <时,S=1﹣2m;(3)当S△ABP=3时,2m﹣1=3,解得m=2,∴点P(2,2),∵E(2,0),∴PE=BE=2,∴∠EPB=∠EBP=45°,如图2,∠PBC=90°,BP=BC,过点C作CF⊥x轴于点F,∵∠PBC=90°,∠EBP=45°,∴∠CBF=∠PBE=45°,在△CBF与△PBE中,,∴△CBF≌△PBE(AAS).∴BF=CF=PE=EB=2.∴OF=OB+BF=4+2=6.∴C(6,2);如图3,△PBC是等腰直角三角形,∴PE=CE,∴C(2,﹣2),∴以点B为直角顶点作等腰直角△BPC,点C的坐标是(6,2)或(2,﹣2).当1﹣2m=3时,n=﹣1,可得P(2,﹣1),同法可得C(3,2)或(5,﹣2).综上所述,满足条件的点C坐标为(6,2)或(2,﹣2)或(3,2)或(5,﹣2).4.【分析】(1)由y=﹣2x﹣1得A (﹣,0),B(0,﹣1),设直线BC为y=kx﹣1,用待定系数法可得直线BC为y =﹣x﹣1;(2)设P(m,0),则M(m,﹣2m﹣1),N (﹣m ﹣1),根据点P恰好是MN的中点,可得﹣2m﹣1﹣0=0﹣(﹣m﹣1),即可解得P (﹣,0);(3)设P(t,0),则BC2=10,BP2=t2+1,CP2=(t+3)2,分三种情况:①当BC=BP时,BC2=BP2,10=t2+1,解得P(3,0);②当BC=CP时,10=(t+3)2,解得P (﹣3,0)或(﹣﹣3,0);③当BP=CP时,t2+1=(t+3)2,解得P (﹣,0).【解答】解:(1)在y=﹣2x﹣1中,令x=0得y=﹣1,令y=0得x =﹣,∴A (﹣,0),B(0,﹣1),设直线BC为y=kx﹣1,将C(﹣3,0)代入得:﹣3k﹣1=0,解得k =﹣,∴直线BC解析式为y =﹣x﹣1;(2)设P(m,0),则M(m,﹣2m﹣1),N (﹣m ﹣1),∵点P恰好是MN的中点,∴PM=PN,即﹣2m﹣1﹣0=0﹣(﹣m﹣1),解得m =﹣,∴P (﹣,0);(3)设P(t,0),∵B(0,﹣1),C(﹣3,0),∴BC2=10,BP2=t2+1,CP2=(t+3)2,①当BC=BP时,BC2=BP2,∴10=t2+1,解得t=3或t=﹣3(与B重合,舍去),∴P(3,0);②当BC=CP时,∴10=(t+3)2,解得t =﹣3或t =﹣﹣3,∴P (﹣3,0)或(﹣﹣3,0);③当BP=CP时,∴t2+1=(t+3)2,解得t =﹣,∴P (﹣,0);综上所述,P坐标为(3,0)或(﹣3,0)或(﹣﹣3,0)或(﹣,0).5.【分析】(1)设直线m的函数表达式为y=kx+b(k≠0),把(﹣1,2),(﹣2,0)代入,得,解方程组即可得到结论;(2)设直线n的函数表达式为y=sx+t(s≠0),根据直线n经过点(﹣4,﹣4),(0,﹣2),得到方程组,解方程组得到.求得点B的坐标为(0,4),点C的坐标为(4,0),于是得到结论;(3)根据三角形的面积公式得到,根据题意列方程即可得到结论.【解答】(1)解:设直线m的函数表达式为y=kx+b (k≠0).∵直线m经过点(﹣1,2),(﹣2,0),∴,解得,∴直线m的函数表达式为y=2x+4.将x=﹣4代入y=2x+4,得y=2×(﹣4)+4=﹣4,∴点P的坐标为(﹣4,﹣4);(2)证明:设直线n的函数表达式为y=sx+t(s≠0).∵直线n经过点(﹣4,﹣4),(0,﹣2),∴,解得,∴直线n 的函数表达式为.在y=2x+4中,令x=0,得y=4,即点B的坐标为(0,4).在中,令y=0,得,解得x=4,即点C的坐标为(4,0),∴OB=OC=4,又∵∠BOC=90°,∴△BOC是等腰直角三角形;(3)解:∵OB=OC=4,∠BOC=90°,∴,又∵S△ACE=S△BOC,∴S△ACE=8,即,∵AC=6,∴,即或.①当时,,解得,∴此时点E 的坐标为;②当时,,解得,∴此时点E 的坐标为.综上可知,直线m上存在点E,使得S△ACE=S△BOC,点E 的坐标为或.6.【分析】(1)用待定系数法求函数解析式,再将两个一次函数的解析式联立方程组即可求交点D的坐标;(2)判断△HCD是直角三角形,利用△HCD的面积求出HD的长,再由两点间距离公式求出H点的坐标,作H点关于y轴的对称点H',过点C作CG⊥x轴,且CG =,连接H'G交y轴于点M,当H'、M'、G 三点共线时,HM+MN+NC的值最小,求出H'G的长即可求解;(3)分两种情况,△AOB逆时针旋转90°和顺时针旋转90°分别讨论;根据旋转后O'E'∥x轴,OE=O'E'=1,求出DE'=,设E'(m,3m+3),即可求E'的坐标.【解答】解:(1)设直线AB的解析式为y=kx+b,将A(﹣1,0),B(0,3)代入,∴,∴,∴y=3x+3,联立方程组,∴,∴D (﹣,);(2)设H(t,3t+3),∵OA=1,OB=3,∴tan∠ABO =,直线y =﹣x+1与y轴的交点为(0,1),与x轴的交点C(3,0),∴tan∠DCA =,∴∠DCA=∠ABO,∴∠CDB=90°,∵CD =,∵S△HCD ==××DH,∴DH =,∵=,∴t=﹣3或t =,∵H是直线AB上位于第一象限内的一点,∴t =,∴H (,),如图1,作H点关于y轴的对称点H',过点C作CG ⊥x轴,且CG =,∴G(3,),H'(﹣,),连接H'G交y轴于点M,∵MN =,∴四边形MNCG是平行四边形,∴MG=CN,由对称性可知,MH=MH',∴HM+MN+NC=MH'+MN+MG≥1+H'G,∴当H'、M'、G三点共线时,HM+MN+NC的值最小,∵H'G =,∴HM+MN+NC 的最小值为+;(3)令x=0,则y=1,∴E(0,1),令y=0,则x=3,∴C(3,0),当△OCE绕点逆时针旋转90°时,∵点E'落在直线AB上,点O'落在直线CD上,∴E'O'∥CO,∴∠DO'E'=∠ECO,∵OE=O'E'=1,CO=3,∴EC =,∴sin∠ECO ==,∴DE'=,设E'(m,3m+3),∴=(﹣﹣m)2+(3m+3﹣)2,∴m =﹣或m =﹣,∵此时E'在D点下方,∴m =﹣,∴E'(﹣,);当△OCE绕点顺时针旋转90°时,∵点E'落在直线AB上,点O'落在直线CD上,∴E'O'∥CO,∴∠DO'E'=∠ECO,∵OE=O'E'=1,CO=3,∴EC =,∴sin∠ECO ==,∴DE'=,设E'(m,3m+3),∴=(﹣﹣m)2+(3m+3﹣)2,∴m =﹣或m =﹣,∵此时E'在D点上方,∴m =﹣,∴E'(﹣,);综上所述:E'点坐标为(﹣,)或(﹣,).7.【分析】(1)联立方程组可求解;(2)分别求出点B,点C坐标,由三角形的面积公式可求解;(3)先求出点D坐标,由等腰三角形的性质和两点之间的距离公式可求解.【解答】解:(1)由题意可得:,解得:,∴点A (,);(2)∵直线l2与x轴相交于点B,∴点B(﹣1,0),∵点P(a,﹣1)在直线l2上,∴﹣1=a+1,∴a=﹣2,∴点P(﹣2,﹣1),∴点C的纵坐标为﹣1,∴﹣1=﹣2x+3,∴x=2,∴点C(2,﹣1),如图,设直线l1与x轴相交于点H,∴0=﹣2x+3,∴x =,∴点H (,0),∴BH =,∴△ABC 的面积=××(+1)=;(3)存在,理由如下:∵将直线l1向下平移4个单位长度得到直线l3,∴直线l3,的解析式为:y=﹣2x﹣1,∴点D(0,﹣1),如图,∵点P(﹣2,﹣1),点D(0,﹣1),∴PD⊥y轴,PD=2,设点Q(a,a+1),∵△DPQ是以DP为腰的等腰三角形,∴PQ=PD=2或PD=QD=2,当PQ=PD=2时,则(﹣2﹣a)2+(﹣1﹣a﹣1)2=4,∴a =±﹣2,∴点Q (﹣2,﹣1)或(﹣﹣2,﹣﹣1);当PD=QD=2时,则(a﹣0)2+(﹣1﹣a﹣1)2=4,∴a=0或﹣2(不合题意舍去),∴点Q(0,1),综上所述:点Q坐标为:(﹣2,﹣1)或(﹣﹣2,﹣﹣1)或(0,1).8.【分析】(1)求出点A与点B的坐标,再由待定系数法求直线AB的解析式即可;(2)过点E作EH⊥AB于点H,求出点E的坐标,再由再由待定系数法求直线BE的解析式即可;(3)①当∠MPC=90°时,P点在C点下,过点P 作GH⊥y轴交AD于点G,交y轴于点H,证明△PMG ≌△CPH(AAS),可得8+t=2t+12,求出t即可求P (﹣4,2);②当∠MPC=90°,P点在C点上时,由①得8+t=﹣2t﹣12,求出t即可求P (﹣,);③当∠PMC=90°时,过点M作KL⊥y轴交y轴于点L,过P点作PK⊥KL交于K,证明△PKM≌△MLC (AAS),由8=﹣2t﹣6﹣(14+t),求出t =﹣,即可求P (﹣,).【解答】解:(1)∵(a+8)2+=0,∴a=﹣8,b=﹣6,∴A(﹣8,0),B(0,﹣6),∵一次函数y=+b经过A(﹣8,0),B(0,﹣6),∴,∴,∴直线AB的表达式y =﹣x﹣6;(2)∵A(﹣8,0),B(0,﹣6),∴OA=8,OB=6,∴在Rt△AOB中AB=10,过点E作EH⊥AB于点H,∵∠ABO的平分线交x轴于点E,∴EH=EO,AE=8﹣EO,AH=10﹣6=4,在Rt△AEH中,(8﹣EO)2=42+EO2,解得:EO=3,∴E(﹣3,0),设直线BE的表达式为y=k1x+b1,∴,∴,∴直线BE的表达式为y=﹣2x﹣6;(3)设P(t,﹣2t﹣6),①如图1,当∠MPC=90°时,P点在C点下,过点P作GH⊥y轴交AD于点G,交y轴于点H,∵∠MPC=90°,∴∠MPG+∠CPH=90°,∵∠MPG+∠GMP=90°,∴∠CPH=∠GMP,∵PM=PC,∴△PMG≌△CPH(AAS),∴MG=PH,CH=GP,∵PH=﹣t,CH=6﹣(﹣2t﹣6)=2t+12,∴GP=8﹣(﹣t)=8+t=2t+12,∴t=﹣4,∴P(﹣4,2);②如图2,当∠MPC=90°,P点在C点上时,由①得,HC=﹣2t﹣6﹣6=﹣2t﹣12,GP=8﹣(﹣t)=8+t,∴8+t=﹣2t﹣12,∴t =﹣,∴P (﹣,);③如图3,当∠PMC=90°时,过点M作KL⊥y轴交y轴于点L,过P点作PK⊥KL 交于K,∵∠PMC=90°,∴∠PMK+∠CML=90°,∵∠PMK+∠MPK=90°,∴∠CML=∠MPK,∵PM=CM,∴△PKM≌△MLC(AAS),∴KM=CL,PK=ML,∴ML=PK=8,CL=KM=﹣8﹣t,∴LO=6﹣(﹣8﹣t)=14+t,∴PK=8=﹣2t﹣6﹣(14+t),∴t =﹣,∴P (﹣,);综上所述:点P的坐标为:(﹣4,2)或(﹣,)或(﹣,).9.【分析】(1)先求出点A,点B坐标,由勾股定理和面积法可求解;(2)分两种情况讨论,先求出BQ解析式,由全等三角形的性质可求解;(3)分两种情况讨论,利用折叠的性质,三角形面积公式,等腰三角形的性质可求解.【解答】解:(1)∵直线y =﹣x+8与x轴,y轴分别交于A,B两点,∴点A(6,0),点B(0,8),∴OA=6,OB=8,∵点C的坐标为(﹣6,0),∴OC=6,∴BC ===10,∵OA=OC=6,BO⊥AC,∴AB=BC=10,∵S△AOB =×AB×OD =×OA×OB,∴OD ==;(2)存在,理由如下:∵AB=BC,∴∠BCA=∠BAO,∵∠CBO+∠BCA=90°=∠AOD+∠BAO,∴∠CBO=∠AOD,设直线BC的解析式为y=kx+b,,解得:,∴直线BC的解析式为y =x+8,设点Q(a ,a+8)当△BPQ≌△OAD时,BQ=OD =,∴(a﹣0)2+(a+8﹣8)2=,∴a =±,∵点Q在第二象限,∴点Q (﹣,),当△BPQ≌△ODA时,BQ=OA=6,∴(a﹣0)2+(a+8﹣8)2=36,∴a =±,∵点Q在第二象限,∴点Q (﹣,),综上所述:点Q坐标为:(﹣,)或(﹣,);(3)如图,当点C关于OQ的对称点落在OB上时,作OE⊥CO于点E,OF⊥BO于点F,∴∠COQ=∠C'OQ=45°,又∵OE⊥CO,OF⊥BO,∴OE=OF,∵S△OBC =×OB×OC =×OC×OE +×OB×OF,∴6×8=(6+8)×OE,∴OE=OF =,∴点Q 的坐标为(﹣,).点C关于OQ的对称点落在AB上时,∴OC=OC'=OA,CQ=C'Q,∠OCQ=∠OC'Q,∴∠C'AO=∠OC'A,∴∠OCQ=∠OC'Q=∠C'AO=∠OC'A,∴∠CBA=∠QC'B,∴BQ=C'Q,∴CQ=BQ=C'Q,∴点Q是BC的中点,∴点Q(﹣3,4),综上所述:点Q坐标为(﹣3,4)或(﹣,).10.【分析】(1)用待定系数法求直线AB的解析式即可;(2)由题意可得AD=9,设D(x,0),则|x+3|=9,即可求D的坐标;(3)分两种情况讨论:①当点P在射线CB上时,过点C作CF⊥CE交直线EP于点F,过C作x轴垂线l,分别过F,E作FM⊥l,EN⊥l,证明△FMC≌△CNE(AAS),即可得F点坐标为(1,4),用待定系数法求出直线EF的解析式为y=5x﹣1,联立方程组,即可求P (,);②当点P在射线CA上时,过点C作CH⊥CE交直线EP于点H,过点H作HK⊥y轴交于K,过点H作GH⊥x轴,过点C作CG⊥GH交于G,证明△CHG≌△EHK(AAS),可求得H (﹣,﹣),求出直线HE的解析式为y=﹣x﹣1,联立方程组,则可求P (﹣,﹣).【解答】解:(1)设直线AB的解析式为y=kx+b,∵A(﹣3,0),B(0,6),则有,∴,∴y=2x+6,∵C(﹣a,a),∴C(﹣2,2);(2)∴S△AOB =×3×6=9,∴S△ACD =×2×AD=9,∴AD=9,设D(x,0),∴|x+3|=9,∴x=6或x=﹣12,∴D(6.0)或(﹣12,0);(3)①如图,当点P在射线CB上时,过点C作CF ⊥CE交直线EP于点F,∵∠CEF=45°,∴CE=CF,过C作x轴垂线l,分别过F,E作FM⊥l,EN⊥l,∴∠FMC=∠CNE=90°,∠MCF+∠MFC=90°,∵CF⊥CE,∴∠MCF+∠NCE=90°,∴∠MFC=∠NCE,∴△FMC≌△CNE(AAS),∴FM=CN=3,CM=EN=2,即F点坐标为(1,4),设直线EF的解析式为y=kx+b,∴,∴,∴直线EF的解析式为y=5x﹣1,联立,解得,∴P (,);②当点P在射线CA上时,过点C作CH⊥CE交直线EP于点H,过点H作HK ⊥y轴交于K,过点H作GH⊥x轴,过点C作CG⊥GH交于G,∵∠CHK=90°,∴∠CHG+∠KHE=90°,∵∠CHG+∠HCG=90°,∴∠KHE=∠HCG,∵∠DEP=45°,∴DH=HE,∴△CHG≌△EHK(AAS),∴CG=KE,GH=HK,∵E(0,﹣1),C(﹣2,2),∴GH=3﹣CG=2+OK=2+CG,∴CG =,∴H (﹣,﹣),设直线HE的解析式为y=k'x+b',,∴,∴y =﹣x﹣1,联立方程组,解得,∴P (﹣,﹣),综合上所述,点P 坐标为(,)或(﹣,﹣).第21页(共21页)。
一次函数全等三角形轴对称的复习 典型例题

一. 本周教学内容:一次函数、全等三角形、轴对称的复习【典型例题】(一)一次函数 例1:马戏团演出场地的外围围墙是若干块长为5m ,宽为2.5m 的长方形帆布缝制而成的,两块帆布缝合的公共部分是0.1m ,围成的围墙高2.5m 。
(1)若先用6块帆布缝制成宽为2.5m 的条形,求其长度;(2)若用x 块帆布缝制成密封的圆形围墙,求圆形场地的周长y 与所用帆布的块数x 之间的函数关系式;(3)要是围成的圆形场地的半径为10m ,至少需要买几块这样的帆布缝制围墙。
解:(1)6块帆布缝制成条形后,有五块公共部分,所以6块帆布缝制后的总长度为: m 5.291.0556=⨯-⨯(2)x 块帆布缝制成密封的圆形围墙后有x 块公共部分。
设圆形围墙的周长为ymx y x x x y 9.4,9.41.05=∴=-=∴(3)要围成半径10m 的圆形场地,则x 9.4102=⨯π82.129.48.629.420≈≈=∴πx 块 答:需要买这样的帆布13块。
例2:已知等腰三角形周长为20cm ,求:(1)它的底边y 和腰长x 的函数关系式; (2)出自变量的取值范围; (3)画出函数图像。
解:(1)y =20-2x ;⎪⎩⎪⎨⎧>>>.2,0,0)2(y x y x ⎪⎩⎪⎨⎧->>->∴.2202,0220,0x x x x ⎪⎩⎪⎨⎧><>∴.5,10,0x x x ;105<<∴x(3)当x =5时,y =10;当x =10时,y =0连结A (5,10)、B (10,0)则线段AB (A 、B 两点除外)就是所求函数图像,如图。
例3:(1)在某一电路中,若电压保持不变,电流强度I 与电阻R 成反比例关系。
当电阻R =10欧姆时,电流强度I =4安培,则I 关于R 的函数关系式是( )A. I =40R (R>0)B. )0(401>=R R I C. )0(40>=R RID. )0(401>=R RI(2)生物学指出:生物系统中,每输入一个营养级的能量,大约只有10% 的能量能够流动到下一个营养级。
一次函数综合练习题(难度较大)带答案

一次函数练习一.解答题(共16小题)1.如图,在平面直角坐标系中,A(2,0),B(0,6).(1)如图1,过A,B两点作直线AB,求直线AB的解析式;(2)如图2,点C在x轴负半轴上,C(﹣6,0),点P为直线BC上一点,若S△ABC=2S△ABP,求满足条件的点P的坐标;(3)在(2)的条件下,点E在直线BC上,点F在y轴上,当△AEF为一个等腰直角三角形时,请你直接写出E点坐标.2.如图,在平面直角坐标系中,直线l:y=x+b(b<0)与x轴交于点C.点D为直线l上第一象限内一点,过D 作DE⊥y轴于点E,CA⊥DE于点A.点B在线段DA上,DB=AC.连接CB,P为线段CB上一动点,过点P 作PR⊥x轴,分别交x轴、CD、DE于点R、Q、S.(1)若点D坐标为(12,3).①求直线BC的函数关系式;②若Q为RS中点,求点P坐标.(2)在点P运动的过程中,的值是否变化?若不变,求出该值;若变化,请说明理由.3.已知:如图,一次函数y=x﹣3的图象分别与x轴、y轴相交于点A、B,且与经过x轴负半轴上的点C的一次函数y=kx+b的图象相交于点D,直线CD与y轴相交于点E,E与B关于x轴对称,OA=3OC.(1)直线CD的函数表达式为;点D的坐标;(直接写出结果)(2)点P为线段DE上的一个动点,连接BP.①若直线BP将△ACD的面积分为7:9两部分,试求点P的坐标;②点P是否存在某个位置,将△BPD沿着直线BP翻折,使得点D恰好落在直线AB上方的坐标轴上?若存在,求点P的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,直线分别与x轴,y轴交于A,B两点,把线段AB绕点B顺时针旋转90°后得到线段BC,连结AC,OC.(1)当时,求点C的坐标;(2)当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)当S△AOB=2S△BOC时,在x轴上找一点P,使得△P AB是等腰三角形,求满足条件的所有P点的坐标.5.如图,在平面直角坐标系xOy中,A(0,3)、B(﹣4,0),连接AB,点C为线段AB上的一个动点(点C不与A、B重合),过点C作CP⊥x轴,垂足为P,将线段AP绕点A逆时针旋转至AQ,且∠P AQ=∠BAO.连接OQ,设点C的横坐标为m.(1)求经过点A、B的直线的函数表达式;(2)当m为何值时,△ACP≌△AOQ;(3)点C在运动的过程中,①在y轴上是否存在一点D,使得∠ADQ的大小始终不发生变化?若存在,请求出点D的坐标;若不存在,请说明理由;②连接OQ,请直接写出OQ长度的取值范围.6.如图,在平面直角坐标系中,A(﹣1,0),B(0,3),直线y=﹣x+1与x轴交于点C,与直线AB交于点D.(1)求直线AB的解析式及点D的坐标;(2)如图2,H是直线AB上位于第一象限内的一点,连接HC,当S△HCD=时,点M、N为y轴上两动点,点M在点N的上方,且MN=1,连接HM、NC,求HM+MN+NC的最小值;(3)将△OAB绕平面内某点E旋转90°,旋转后的三角形记为△O′A′B′,若点O′落在直线AB上,点A′落在直线CD上,请直接写出满足条件的点O′的坐标以及对应的点E的坐标.7.已知直线l:y=3x+3与x轴交于点A,点B在直线l上,且位于y轴右侧某个位置.(1)求点A坐标;(2)过点B作直线BC⊥AB,交x轴于点C,当△ABC的面积为60时,求点B坐标;(3)在(2)问条件下,D,E分别为射线AO与AB上两动点,连接DE,DB,是否存在当△ADE为直角三角形同时△DEB为等腰三角形的情况,若存在,求出点E坐标;若不存在,说明理由.8.【阅读理解】定义:在同一平面内,有不在同一条直线上的三点M,N,P,连接PM,PN,设∠MPN=α,=k,则我们把(a,k)称为点M到N关于点P的“度比坐标”,把(α,)称为点N到M关于点P的“度比坐标”.【迁移运用】如图,直线l1:y=x+5分别与x轴,y轴相交于A,B两点,过点C(0,10)的直线l2与l1在第一象限内相交于点D.根据定义,我们知道点A到C关于点O的“度比坐标”为(90°,).(1)请分别直接写出A,B两点的坐标及点B到A关于点O的“度比坐标”;(2)若点A到C关于点D的“度比坐标”与点C到B关于点D的“度比坐标”相同.(ⅰ)求直线l2的函数表达式;(ⅱ)点E,F分别是直线l1,l2上的动点,连接OE,OF,若点E到F关于点O的“度比坐标”为(90°,),求此时点E的坐标.9.如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足+(p ﹣1)2=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ 是以BC为底边的等腰直角三角形,直角顶点为Q.若存在,请求出点Q坐标;若不存在,请说明理由.10.在平面直角坐标系xOy中,对于M,N两点,若在y轴上存在点T,使得∠MTN=90°,且MT=NT,则称M,N两点互相等垂,其中一个点叫做另一个点的等垂点.已知A点的坐标是(2,0).(1)如图①,在点B(2,﹣2),C(0,1),D(﹣2,0)中,点A的等垂点是(选填“B”,“C”或“D”)(2)如图②,若一次函数y=2x﹣1的图象上存在点A的等垂点A',求A'点的坐标;(3)若一次函数y=kx+b(k≠0)的图象上存在无数个点A的等垂点,试写出该一次函数的所有表达式:.11.如图1,在平面直角坐标系xOy中,直线l:y=x+4交x轴于点C,交y轴于点D,AB∥CD,A(2,3),点P 是直线l上一动点,连接AP,BP.(1)求直线AB的表达式;(2)求AP+CP的最小值;(3)如图2,将三角形ABP沿BP翻折得到△A′BP,当点A′落在坐标轴上时,请直接写出直线BP的表达式.12.如图,在平面直角坐标系xOy中,直线y=x+2+交x轴于点A,过该直线上一点B作BC⊥y轴于点C,且OC=2.(1)求点B的坐标及线段AB的长;(2)取OC的中点D,作直线BD交x轴于点E,连接AD.(ⅰ)求证:AD是∠BAE的平分线;(ⅱ)若点M,N分别是线段AO,AD上的动点,连接MN,ON,试问MN+ON是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.13.如图1,直线y=x+6与x轴交于点A,直线y=﹣x+m(m>0)与x轴、y轴分别交于B、C两点,并与直线y =x+6相交于点D,若AB=5.(1)求直线BC的解析式;(2)求出四边形AOCD的面积;(3)如图2,若P为直线AD上一动点,当△PBD的面积是四边形AOCD的面积的一半时,求点P的坐标.14.如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),点P是直线AB 上方第一象限内的动点.(1)求直线AB的表达式和点A的坐标;(2)点P是直线x=2上一动点,当△ABP的面积与△ABO的面积相等时,求点P的坐标;(3)当△ABP为等腰直角三角形时,请直接写出点P的坐标.15.如图1,在平面直角坐标系中,直线y=x﹣12分别交x轴、y轴于A、B两点,过点A作x轴的垂线交直线y=x 于点C,D点是线段AB上一点,连接OD,以OD为直角边作等腰直角三角形ODE,使∠ODE=90°,且E点在线段AC上,过D点作x轴的平行线交y轴于G,设D点的纵坐标为m.(1)点C的坐标为;(2)用含m的代数式表示E点的坐标,并求出m的取值范围;(3)如图2,连接BE交DG于点F,若EF=DF﹣2m,求m的值.16.如图,在平面直角坐标系中,点A坐标为(6,0),在B在y轴的正半轴上,且S△AOB=24.(1)求点B坐标;(2)若点P从B出发沿y轴负半轴运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共16小题)1.【分析】(1)利用待定系数法解决问题即可;(2)分两种情形,利用中点坐标公式求解即可;(3)分四种情形,分别画出图形,利用全等三角形的性质求解即可.【解答】解:(1)设直线AB的解析式为y=kx+b,把A(2,0),B(0,6)代入y=kx+b,得到,解得,∴直线AB的解析式为y=﹣3x+6.(2)如图2中,当点P在线段BC上时,∵S△ABC=2S△ABP,∴CP=PB,∵C(﹣6,0),B(0,6),∴P(﹣3,3),当点P′在CB的延长线上时,BP′=PB,此时P′(3,9),综上所述,满足条件的点P的坐标为(﹣3,3)或(3,9);(3)如图3﹣1中,当AE=AF,∠EAF=90°时,过点E作EH⊥AC于点H.∵∠AHE=∠AOF=∠EAF=90°,∴∠EAH+∠F AO=90°,∠F AO+∠AFO=90°,∴∠EAH=∠AFO,∵AE=AF,∴△AHE≌△FOA(AAS),∴EH=OA=2,∵直线BC的解析式为y=x+6,当y=2时,x=﹣4,∴E(﹣4,2);如图3﹣2中,当EF=EA,∠AEF=90°,过点E作ED⊥OB于点D,EH⊥OC于点H.同法可证,△EDF≌△EHA(AAS),∵ED=EH,∵E(﹣3,3);如图3﹣3中,当AE=AF,∠EAF=90°时,同法可证,△AHE≌△FOA(AAS),∴EH=OA=2,∴E(﹣8,﹣2);如图3﹣4中,当FE=F A,∠EF A=90°时,同法可证,△EHF≌△FOA,∴FH=OA=2,EH=OF,设E(m,m+6),∴OH=m+6=﹣m﹣2,∴m=﹣4,∴E(﹣4,2),综上所述,满足条件的点E的坐标为(﹣3,3)或(﹣4,2)或(﹣8,﹣2).2.【分析】(1)①求出,B,C两点坐标,利用待定系数法解决问题即可;②设P(m ,m ﹣),则R(m,0),Q(m ,m﹣1),S(m,3),根据QS=QR,构建方程求出m即可解决问题;(2)结论:=.如图,过点D作DT⊥x轴于点T.设D(m ,m+b),用m,b表示出直线BC的解析式y =x +b,设P(t ,t +b),则R(t,0),Q(t ,t+b),用t,b表示出PQ,CR的长,可得结论.【解答】解:(1)①∵点D(12,3)在直线y =x+b 上,∴3=×12+b,∴b=﹣1,∴直线l的解析式为y =x﹣1,∴C(3,0),∵DE⊥y轴,∴OE=3,∵CA⊥OC,∴AC=OE=3,∴DB=AC=3,∴B(9,3),设直线BC的解析式为y=kx+b ,则有,解得,,∴直线BC的解析式为y =x ﹣;②设P(m ,m ﹣),则R(m,0),Q(m ,m﹣1),S(m,3),∵QS=QR,∴3﹣(m﹣1)=m﹣1,∴m =,∴P (,);(2)结论:=.理由:如图,过点D作DT⊥x轴于点T.设D(m ,m+b),∵C(﹣3b,0),∴OC=3b,OT=m,DT =m+b,∴CT=OT﹣OC=m+3b,∴AC=DT=BD =m+b,∴B (m﹣b ,m+b),∴直线BC的解析式为y =x +b,设P(t ,t +b),则R(t,0),Q(t ,t+b),∴PQ =t +b ﹣(t+b )=t +b,CR=t﹣(﹣3b)=t+3b,∴==.3.【分析】(1)先求出点A和点B的坐标,根据题意,得出点C和点E的坐标,用待定系数法可求出直线CD的解析式,联立直线CD和直线AB的解析式可求出点D的坐标;(2)①过点D向x轴作DF⊥x轴于点F,先求出△ACD的面积,直线BP将△ACD的面积分为7:9两部分,需要分两种情况:当点P在线段CD上时,则有S△BDP =S△ACD,表达△BDP的面积,建立方程求解即可;当点P在线段CE上时,设直线BP与x 轴交于点Q,则S△ABQ =S△ACD,表达△ABQ的面积,建立方程求解即可;②将△BPD沿着直线BP翻折,使得点D恰好落在直线AB上方的坐标轴上时,需要分三种情况:当点D 落在x轴负半轴上;当点D落在y轴上;当点D落在x轴正半轴上,画出图形,求解即可.【解答】解:(1)∵一次函数y =x﹣3的图象分别与x轴、y轴相交于点A、B,∴A(4,0),B(0,﹣3),∴OA=4,∵E与B关于x轴对称,OA=3OC.∴E(0,3),OC =,∴C (﹣,0).把点C和点E的坐标代入一次函数y=kx+b,∴,解得,∴直线CD的解析式为:y =x+3;令x+3=x﹣3,解得x=﹣4,∴y =×(﹣4)﹣3=﹣6,∴点D的坐标为(﹣4,﹣6).故答案为:y =x+3;(﹣4,﹣6);(2)①如图1,过点D作DF⊥x轴于点F,连接BC,∴DF=6,∵OA=4,OC =,∴AC =,∴S△ACD =•AC•DF =××6=16.∵A(4,0),B(0,﹣3),D(﹣4,﹣6),∴点B是线段AD的中点,∴S△DBC=S△ACB.当点P在线段CD上时,则有S△BDP =S△ACD,∵S△BDP =(x P﹣x D)•BE,∴(x P+4)•6=×16,解得x P =﹣,∴P (﹣,﹣).当点P在线段CE上时,设直线BP与x轴交于点Q,如图2,此时有S△ABQ =S△ACD,∵S△ABQ =•AQ•BO,∴AQ•3=7,解得AQ =,∴OQ =﹣3=,∴Q (﹣,0).∴直线BQ的解析式为:y =﹣x﹣3,令x+3=﹣x﹣3,解得x =﹣,∴P (﹣,1).综上所述,若直线BP将△ACD的面积分为7:9两部分,点P 的坐标为(﹣,﹣);(﹣,1).②存在,理由如下:将△BPD沿着直线BP翻折,使得点D恰好落在直线AB上方的坐标轴上时,需要分三种情况:当点D落在x轴负半轴上D1处,如图3,由折叠可知,∠DBP=∠D1BP,BD=BD1,由题意可知,OB=3,OA=4,则AB=5,∴BD=AB=5,∴BD1=5,∴OD1=4,∴△ABO≌△D1BO(SSS),∴∠OAB=∠OD1B,∵∠DBD1=∠OAB+∠OD1B,∴∠OD1B=∠D1BP,∴BP∥x轴,∴点P的纵坐标为﹣3,∴P (﹣,﹣3).当点D落在y轴上D2处,如图4,过点P作PG⊥AD 于点G,作PH⊥y轴于点H,过点D作DM⊥y轴于点M,由折叠可知,BP平分∠DBD2,∴PG=PH,∵S△BDP=S△BEP+S△BDE,∴•BE•DM =•BD•PG +•BE•PH ,即×6×4=×5•PG +×6•PH,解得PG=PH =;∴P (﹣,﹣).当点D落在x轴正半轴上D3处,如图5,此时点A 和点D3重合,不符合题意,舍去.综上所述,存在点P,将△BPD沿着直线BP翻折,使得点D恰好落在直线AB上方的坐标轴上,此时点P的坐标为:(﹣,﹣3)或(﹣,﹣).4.【分析】(1)证明△AOB≌△BDC,求得CD和BD 的长,从而得出点C坐标;(2)由(1)得,CD=OB=4,可求得三角形BCO 的面积不变;(3)由条件求得OA,AB的长,△P AB是等腰三角形,分为三种情形:P A=PB,P A=AB,PB=AB,当P A=PB时,设点P坐标,根据P A2=PB2列出方程求得,当P A=AB时,可根据长度直接求得,当PB=AB时,根据等腰三角形“三线合一”求得结果.【解答】解:(1)如图1,当m =时,y =﹣,当x=0时,y=4,∴OB=4,当y =时,﹣,∴x=5,∴OA=5,作CD⊥OB于D,∴∠BDC=∠AOB=90°,∴∠ABO+∠OAB=90°,∵∠ABC=90°,∴∠ABO+∠CBD=90°,∴∠OAB=∠CBD,在△AOB和△BDC中,,∴△AOB≌△BDC(AAS),∴CD=OB=4,BD=OA=5,∴OD=BD﹣OB=5﹣4=1,∴C(﹣4,﹣1);(2)△BOC的面积不变,理由如下:由(1)知:CD=4,OB=4,∴=8;(3)∵S△BOC=8,∴S△AOB=2S△BOC=16,∴,∴OB=8,∵∠AOB=90°,∴AB ===4,当P A=AB=4时,OP=P A﹣OA=4﹣8或OP=P A+OA=4+8,∴P(8﹣4,0)或(4+8),如图2,当PB=AB时,∵OB⊥AP,∴OP=OA=8,∴点P(﹣8,0);如图3,当P A=PB时,(8﹣OP)2=OP2+42,∴OP=3,∴P(3,0),综上所述:点P(8﹣4,0)或(4+8)或(﹣8,0)或(3,0).5.【分析】(1)设AB的函数表达式是:y=kx+b,将点A、B两点坐标代入,进而求得结果;(2)可得AC=OA=3时,△ACP≌AOQ,表示出点C的坐标,根据AC=3列出方程求得结果;(3)①当AD=AB时,△BAP≌△DAQ,此时AD=AB=5,求得D(﹣2,0),从而∠ADQ=∠ABC,故∠ADQ不变;②因为点Q在①中的直线上运动,故当OQ⊥DV时,值最小,当点P运动到点O时,OQ最大=AC,进而求得AC,从而确定结果.【解答】解:(1)设直线AB的表达式是:y=kx+b,∴,∴,∴y =;(2)∵∠BAO=∠P AQ,∴∠BAO﹣∠P AO=∠P AQ﹣∠P AO,即:∠BAP=∠QAO,∵AP=AQ,∴当AC=AO=3时,△ACP≌△AOQ(SAS),∵C(m ,),∴m2+()2=32,∴m =﹣;(3)①如图,存在点D(﹣2,0)使∠ADQ=∠ABC,理由如下:∵D(﹣2,0),A(0,3),∴AD=5,∵∠AOB=90°,OA=3,OB=4,∴AB=5,∴AD=AB,由(2)得:∠BAP=∠DAQ,AP=AQ,∴△BAP≌△DAQ(SAS),∴∠ADQ=∠ABC,∴∠ADQ不变;②如图2,由①知:点Q在直线DV上运动,作OE⊥DV于E,AF⊥DV于F,当Q点运动到E点时,OQ最小,当运动到F点,OQ最大,可得AF=OA=OC=3,而C (﹣,),∴OF=OC ==,可得OE =,∴.6.【分析】(1)用待定系数法求函数解析式,再将两个一次函数的解析式联立方程组即可求交点D的坐标;(2)判断△HCD是直角三角形,利用△HCD的面积求出HD的长,再由两点间距离公式求出H点的坐标,作H点关于y轴的对称点H',过点C作CG⊥x轴,且CG=1,连接H'G交y轴于点M,当H'、M'、G 三点共线时,HM+MN+NC的值最小,求出H'G的长即可求解;(3)分两种情况,△AOB逆时针旋转90°和顺时针旋转90°分别讨论;根据旋转后O'A'∥y轴,OA=O'A'=1,可求O'的坐标,再由△OEO'是等腰直角三角形,再求E点的坐标即可.【解答】解:(1)设直线AB的解析式为y=kx+b,将A(﹣1,0),B(0,3)代入,∴,∴,∴y=3x+3,联立方程组,∴,∴D (﹣,);(2)设H(t,3t+3),∵OA=1,OB=3,∴tan∠ABO =,直线y =﹣x+1与y轴的交点为(0,1),与x轴的交点C(3,0),∴tan∠DCA =,∴∠DCA=∠ABO,∴∠CDB=90°,∵CD =,∵S△HCD ==××DH,∴DH =,∵=,∴t=2或t =﹣,∵H是直线AB上位于第一象限内的一点,∴t=2,∴H(2,9),如图1,作H点关于y轴的对称点H',过点C作CG ⊥x轴,且CG=1,∴G(3,1),H'(﹣2,9),连接H'G交y轴于点M,∵MN=1,∴四边形MNCG是平行四边形,∴MG=CN,由对称性可知,MH=MH',∴HM+MN+NC=MH'+MN+MG≥1+H'G,∴当H'、M'、G三点共线时,HM+MN+NC的值最小,∵H'G =,∴HM+MN+NC 的最小值为+1;(3)将△OAB逆时针旋转90°时,如图2,∵点O′落在直线AB上,点A′落在直线CD上,设A'(m,3m+3),∵OA⊥y轴,∴O'A'⊥x轴,则O'(m ,﹣m+1),∵OA=O'A'=1,∴﹣m+1﹣3m﹣3=1,∴m =﹣,∴O'(﹣,),∵OE=O'E,OE⊥O'E,∴△OEO'是等腰直角三角形,∵O'O =,∴OE =,过点E作GH⊥x轴,交B'O'于G,交x轴于H,∵∠HOE+∠HEO=90°,∠HEO+∠GEO'=90°,∴∠EOH=∠GEO',∵EO=EO',∴△HEO≌△GO'E(AAS)∴HO=GE,GO'=EH,设E(x,y),∴﹣x+y =,∵y =+x,∴=,∴x =﹣(舍)或x =﹣,∴E (﹣,);将△OAB顺时针旋转90°时,如图3,∵点O′落在直线AB上,点A′落在直线CD上,设A'(m,3m+3),∵OA⊥y轴,∴O'A'⊥x轴,则O'(m ,﹣m+1),∵OA=O'A'=1,∴3m+3﹣(﹣m+1)=1,∴m =﹣,∴O'(﹣,),∵OE=O'E,OE⊥O'E,∴△OEO'是等腰直角三角形,∵O'O =,∴OE =,过点E作PQ⊥x轴,交B'O'于P,交x轴于Q,∵∠QOE+∠QEO=90°,∠QEO+∠O'EP=90°,∴∠QOE=∠PEO',∵EO=EO',∴△QEO≌△PO'E(AAS),∴QO=PE,PO'=EQ,设E(x,y),∴x+y =,∵y =﹣x,∴=,∴x =或x =(舍),∴E (,);综上所述:O'(﹣,),E (﹣,)或O'(﹣,),E (,).7.【分析】(1)在y=3x+3中,令y=0得x=﹣1,即得A(﹣1,0);(2)过B作BF⊥x轴于F,设B(m,3m+3),由△ABF∽△BCF,即得=,CF =,即有AC=AF+CF =,根据△ABC的面积为60,得××|3m+3|=60,即可解得m=1或m=﹣3(因B在y轴右侧,舍去),故B(1,6);(3)当∠AED=90°,BE=DE时,设E(n,3n+3),由E在射线AB上知n≥﹣1,由A(﹣1,0),B(1,6),得AB=2,BC=6,而△AED∽△ABC,得=,且DE=BE,即有=,解得E (﹣,),当∠ADE=90°,BE=BD时,设E(t,3t+3),由BE=BD,可得BE=AB=2,根据AD2+DE2=AE2,即可解E(3,12).【解答】解:(1)在y=3x+3中,令y=0得x=﹣1,∴A(﹣1,0);(2)过B作BF⊥x轴于F,如图:设B(m,3m+3),∵∠ABF=90°﹣∠CBF=∠FCB,∠ABC=∠AFB =90°,∴△ABF∽△BCF,∴=,即=,∴CF =,∴AC=AF+CF=|m +1|+=,∵△ABC的面积为60,∴××|3m+3|=60,∴×10(m+1)2×3=60,解得m=1或m=﹣3(因B在y轴右侧,舍去),∴B(1,6);CF ==18,OC=19,∴C(19,0),B(1,6);(3)存在当△ADE为直角三角形同时△DEB为等腰三角形,当∠AED=90°,BE=DE时,如图:由(2)知C(19,0),设E(n,3n+3),由E在射线AB上知n≥﹣1,∵A(﹣1,0),B(1,6),∴AB=2,BC=6,∵∠AED=∠ABC=90°,∠EAD=∠BAC,∴△AED∽△ABC,∴=,而DE=BE,∴=,即=,解得n=﹣2(舍去)或n =﹣,∴E (﹣,),当∠ADE=90°,BE=BD时,如图:设E(t,3t+3),∴AD=t+1,DE=3t+3,∵BE=BD,∴∠BED=∠BDE,∴∠BAD=90°﹣∠BED=90°﹣∠BDE=∠BDA,∴AB=BD,∴BE=AB=2,∴AE=4,∵AD2+DE2=AE2,∴(t+1)2+(3t+3)2=(4)2,解得t=﹣5(舍去)或t=3,∴E(3,12),综上所述,点E 坐标为(﹣,)或(3,12).8.【分析】(1)在y=x+5中,令x=0时,y=5,令y =0时,x=﹣5,即得A(﹣5,0),B(0,5),故,而∠BOA=90°,即得点B到A关于点O的“度比坐标”为(90°,1);(2)(i)过D作DH⊥x轴于H,连接AC,根据点A 到C关于点D的“度比坐标”与点C到B关于点D 的“度比坐标”相同,可得,∠ADC=∠CDB,即知△ADC∽△CDB,从而AD =CD,CD =BD,可得AD=5BD,即=5,即得AH=5OH,OA=4OH,故D (,),设直线l2的函数表达式为y=mx+n,用待定系数法可得直线l2的函数表达式为y=﹣3x+10;(ⅱ)过E作EK⊥x轴于K,过F作FT⊥x轴于T,由点E到F关于点O的“度比坐标”为(90°,),得∠AOF=90°,=,根据△EKO∽△OTF,得===,设E(t,t+5),可得F (,﹣),把F (,﹣)代入y=﹣3x+10,即可解得t =﹣,E (﹣,).【解答】解:(1)在y=x+5中,令x=0时,y=5,令y=0时,x=﹣5,∴A(﹣5,0),B(0,5),∴OA=5,OB=5,∴,∵∠BOA=90°,∴点B到A关于点O的“度比坐标”为(90°,1);(2)(i)过D作DH⊥x轴于H,连接AC,如图:∵C(0,10),A(﹣5,0),B(0,5),∴BC=5,AC ==5,∵点A到C关于点D的“度比坐标”与点C到B关于点D的“度比坐标”相同,∴,∠ADC=∠CDB,∴△ADC∽△CDB,∴====,∴AD =CD,CD =BD,∴AD=5BD ,即=5,∵DH⊥x轴于H,∴OB∥DH,∴==5,∴AH=5OH,∴OA=4OH,∴OH =,在y=x+5中,令x =得y =,∴D (,),设直线l2的函数表达式为y=mx+n,将C(0,10),D (,)代入得:,解得,∴直线l2的函数表达式为y=﹣3x+10;(ⅱ)过E作EK⊥x轴于K,过F作FT⊥x轴于T,如图:∵点E到F关于点O的“度比坐标”为(90°,),∴∠AOF=90°,=,∴∠EOK=90°﹣∠FOT=∠OFT,又∠EKO=∠OTF=90°,∴△EKO∽△OTF,∴===,设E(t,t+5),则OK=﹣t,EK=t+5,∴==,∴OT =,FT =﹣,∴F (,﹣),把F (,﹣)代入y=﹣3x+10得:﹣3×+10=﹣,解得t =﹣,∴E (﹣,).9.【分析】(1)由+(p﹣1)2=0,得a=﹣3,p =1,即得P(1,0),A(0,﹣3),设直线AP的解析式为y=kx+b,用待定系数法可得直线AP的解析式为y=3x﹣3;(2)过M作MD∥AP交x轴于D,连接AD,由MD ∥AP,△MAP面积等于6,可得DP•|y A|=6,即DP ×3=6,即知D(﹣3,0),用待定系数法可得直线DM为y=3x+9,令x=﹣2即得M(﹣2,3);(3)设B(t,3t﹣3),①当Q在x轴负半轴时,过B 作BE⊥x轴于E,可证△BEQ≌△QNC(AAS),即得QN=BE=3﹣3t,QE=CN=4,故OQ=QE﹣OE=ON+QN,即4﹣t=2+3﹣3t,可得Q (﹣,0),②当Q在y轴正半轴时,过C作CF⊥y轴于F,过B 作BG⊥y轴于G,证明△CQF≌△QBG(AAS),可得CF=QG=2,QF=BG=t,故OQ=OG﹣QG=OF ﹣QF,即3t﹣3﹣2=4﹣t,可得Q(0,);③Q在y轴正半轴,过C作CF⊥y轴于F,过B作BT⊥y轴于T,证明△CFQ≌△QTB(AAS),得QF=BT=t,QT=CF=2,故OQ=OT+QT=OF+QF,即3t﹣3+2=4+t,即得Q(0,).【解答】解:(1)∵+(p﹣1)2=0,∴a+3=0,p﹣1=0,∴a=﹣3,p=1,∴P(1,0),A(0,﹣3),设直线AP的解析式为y=kx+b,∴,解得,∴直线AP的解析式为y=3x﹣3;(2)过M作MD∥AP交x轴于D,连接AD,如图:∵MD∥AP,△MAP面积等于6,∴△DAP面积等于6,∴DP•|y A|=6,即DP×3=6,∴DP=4,∴D(﹣3,0),设直线DM为y=3x+c,则0=3×(﹣3)+c,∴c=9,∴直线DM为y=3x+9,令x=﹣2得y=3,∴M(﹣2,3);(3)存在,设B(t,3t﹣3),①当Q在x轴负半轴时,过B作BE⊥x轴于E,如图:∴OE=t,BE=3﹣3t,∵△BCQ是以BC为底边的等腰直角三角形,∴BQ=CQ,∠BQC=90°,∴∠BQE=90°﹣∠NQC=∠QCN,又∠BEQ=∠QNC,∴△BEQ≌△QNC(AAS),∴QN=BE=3﹣3t,QE=CN=4,∴OQ=QE﹣OE=ON+QN,即4﹣t=2+3﹣3t,∴t =,∴OQ =,∴Q (﹣,0),②当Q在y轴正半轴时,过C作CF⊥y轴于F,过B 作BG⊥y轴于G,如图:∴BG=t,OG=3t﹣3,∵△BCQ是以BC为底边的等腰直角三角形,∴BQ=CQ,∠BCQ=90°,∴∠CQF=90°﹣∠BQG=∠GBQ,又∠CFQ=∠BGQ=90°,∴△CQF≌△QBG(AAS),∴CF=QG=2,QF=BG=t,∴OQ=OG﹣QG=OF﹣QF,即3t﹣3﹣2=4﹣t,∴t =,∴OQ=4﹣t =,∴Q(0,);③Q在y轴正半轴,过C作CF⊥y轴于F,过B作BT⊥y轴于T,如图:∴BT=t,OT=3t﹣3,同②可证△CFQ≌△QTB(AAS),∴QF=BT=t,QT=CF=2,∴OQ=OT+QT=OF+QF,即3t﹣3+2=4+t,∴t =,∴OQ=4+t =,∴Q(0,);综上所述,Q的坐标为(﹣,0)或(0,)或(0,).10.【分析】(1)取点T(0,2),连接DT,AT,可得△ADT是等腰直角三角形,即知点A的等垂点是点D;(2)①当A'在x轴上方时,过A'作A'F⊥y轴于F,证明△A'FE≌△EOA(AAS),得EF=AO=2,A'F=OE,设OE=A'F=m,则OF=OE+EF=m+2,则A'(m,m+2),将A'(m,m+2)代入y=2x﹣1可得A'(3,5);②当A'在x轴上方时,过A'作A'H⊥y轴于H,同理可得A'(﹣,﹣);(3)设直线y=x+2上任意一点A'(t,t+2),连接AA',作AA'的垂直平分线交y轴于R,交AA'于P,过P作PM⊥x轴于M,PN⊥y轴于N,可得RA=RA',P A=P A',P (,),从而可得△PRN≌△P AM (ASA),PR=P A=P A',即知∠ARA'=90°,故A'是A的等垂点,即直线y=x+2上任意一点都是A的等垂点,一次函数y=x+2的图象上存在无数个点A的等垂点,同理可证一次函数y=﹣x﹣2的图象上存在无数个点A的等垂点.【解答】解:(1)取点T(0,2),连接DT,AT,如图:∵D(﹣2,0),A(2,0),T(0,2),∴OT=OD=OA=2,∴△ADT是等腰直角三角形,∴在点B(2,﹣2),C(0,1),D(﹣2,0)中,点A的等垂点是点D,故答案为:D;(2)①当A'在x轴上方时,过A'作A'F⊥y轴于F,如图:∵A'是A的等垂点,∴∠A'EA=90°,A'E=AE,∴∠A'EF=90°﹣∠AEO=∠EAO,∵∠A'FE=∠EOA=90°,∴△A'FE≌△EOA(AAS),∴EF=AO=2,A'F=OE,设OE=A'F=m,则OF=OE+EF=m+2,∴A'(m,m+2),将A'(m,m+2)代入y=2x﹣1得:m+2=2m﹣1,解得m=3,∴A'(3,5);②当A'在x轴下方时,过A'作A'H⊥y轴于H,如图:同①可证明△AOG≌GHA'(AAS),∴A'H=OG,GH=OA=2,设A'H=OG=n,则OH=GH﹣OG=2﹣n,∴A'(﹣n,n﹣2),将A'(﹣n,n﹣2)代入y=2x﹣1得:n﹣2=﹣2n﹣1,解得n =,∴A'(﹣,﹣);综上所述,A'点的坐标为(3,5)或(﹣,﹣);(3)若一次函数y=kx+b(k≠0)的图象上存在无数个点A的等垂点,该一次函数的所有表达式为y=x+2或y=﹣x﹣2,理由如下:当一次函数为y=x+2时,设直线y=x+2上任意一点A'(t,t+2),连接AA',作AA'的垂直平分线交y轴于R,交AA'于P,过P作PM⊥x轴于M,PN⊥y轴于N,如图:∵PR是线段AA'的垂直平分线,∴RA=RA',P A=P A',∴∠RP A=∠RP A'=90°,∵A(2,0),A'(t,t+2),∴P (,),∵PM⊥x轴于M,PN⊥y轴于N,∴PM=PN=||,而∠RPN=90°﹣∠NP A=∠APM,∠PNR=∠PMA =90°,∴△PRN≌△P AM(ASA),∴PR=P A,∴PR=P A=P A',∴△PRA与△PRA'都是等腰直角三角形,∴∠ARP=∠A'RP=45°,∴∠ARA'=90°,根据等垂点定义,A'是A的等垂点,即直线y=x+2上任意一点都是A的等垂点,∴一次函数y=x+2的图象上存在无数个点A的等垂点,同理可证一次函数y=﹣x﹣2的图象上存在无数个点A的等垂点,故答案为:y=x+2或y=﹣x﹣2.11.【分析】(1)由题意设AB的关系式是:y=x+b,然后把点A的坐标代入求得b,进而求得AB的关系式(2)作CE∥y轴,作PE⊥CE于E,先求得∠OCP =∠ODC=45°,于是可得PE =CP,进而只需求AP+PE,从而当A、P、E共线时,AP+PE最小,此时作AF⊥CE,最小值就是AF的长;(3)当点A′在y轴上时,根据A′B=AB=3,进而求得A′(0,),设P(x,x+4),根据A′P2=AP2,列出关于x的方程,求得点P的坐标,进而求得BP的关系式,当A′在x轴上时,同样方法求得BP的关系式.【解答】解:(1)∵AB∥CD,∴可设AB的表达式是:y=x+b,∴2+b=3,∴b=1,∴y=x+1;(2)如图1,作CE∥y轴,作PE⊥CE于E,∴∠OCE=90°,由y=x+4得:C(﹣4,0),D(0,4),∴OC=OD,∵∠COD=90°,∴∠OCP=∠ODC=45°,∴∠PCE=90°﹣∠OCP=45°,∴PE=CP•sin∠PCE =CP,∴AP +CP=AP+PE,∴当A、P、E共线时,AP+PE最小,此时作AF⊥CE,即E和F重合,P在P′时,∵C(﹣4,0),A(2,3),∴AF=2﹣(﹣4)=6,∴AP +CP的最小值是6;(3)如图2,∵AB的关系式是:y=x+1,∴B(﹣1,0),∴OB=1,当点A′在y轴上时,∵A′B=AB ==3,∴A′O ===,∴A′(0,),设P(x,x+4),由A′P2=AP2得,x2+(x+4﹣)2=(x﹣2)2+(x+4﹣3)2,∴x =,∴P (,),设BP的关系式是:y=kx+b,∴,∴,∴y =x,如图3,当A′在x轴上时,∵A′B=AB=3,OB=1,∴A′(﹣3﹣1,0),由(x +3)2+(x+4)2=(x﹣2)2+(x+4﹣3)2,∴x =,∴P (,),设BP的关系式是y=mx+n,∴,∴,∴y =﹣()x ﹣(),如图4,当点A′再次落在y轴上时,连接A′B,由上知:A′(0,﹣),此时BP的关系式:y =,如图5,当A′再次落在x轴上时,此时BP的关系式是:y =()x+(﹣1),综上所述:BP的关系式是:y =x或y=﹣()x﹣()或y =或y =()x+(﹣1),12.【分析】(1)由OC=2,得y B=2,在y=x +2+中,令y=2得B (﹣2,2),由y=x +2+得A(﹣2﹣,0),即可得AB=4;(2)(ⅰ)由D是OC中点,得D(0,),设直线BD为y=kx +,用待定系数法得直线BD为y=(﹣1﹣)x +,即得E(2﹣,0),从而可得AB=AE,根据CD=OD,∠BDC=∠EDO,∠BCD =∠EOD=90°,可证△BCD≌△EOD(ASA),有BD=ED,故AD是∠BAE的平分线;(ⅱ)作O关于AD的对称点H,连接DH,由AD 是∠BAE的平分线,知H在线段AB上,当MN+ON 最小时,即是MN+HN最小,此时H、N、M共线,且HM⊥OA,HM的长即是MN+ON的最小值,由AH =OA=2+,根据直线y=x +2+与x轴夹角为45°,得△AHM是等腰直角三角形,故HM ==+1,即得MN+ON 的最小值是+1.【解答】解:(1)∵OC=2,∴y B=2,在y=x +2+中,令y=2得x =﹣2,∴B (﹣2,2),在y=x +2+中,令y=0得x=﹣2﹣,∴A(﹣2﹣,0),∴AB ==4,∴点B的坐标为(﹣2,2),线段AB的长为4;(2)(ⅰ)∵D是OC中点,∴D(0,),CD=OD,设直线BD为y=kx +,把B (﹣2,2)代入得:2=(﹣2)k +,解得k=﹣1﹣,∴直线BD为y=(﹣1﹣)x +,在y=(﹣1﹣)x +中,令y=0得x=2﹣,∴E(2﹣,0),∴AE=2﹣﹣(﹣2﹣)=4,由(1)知AB=4,∴AB=AE,即△ABE是等腰三角形,∵CD=OD,∠BDC=∠EDO,∠BCD=∠EOD=90°,∴△BCD≌△EOD(ASA),∴BD=ED,∴AD是∠BAE的平分线;(ⅱ)MN+ON存在最小值,作O关于AD的对称点H,连接DH,如图:由(ⅰ)知AD是∠BAE的平分线,∴H在线段AB上,∵N在AD上,∴ON=HN,∴MN+ON=MN+HN,当MN+ON最小时,MN+HN最小,此时H、N、M共线,且HM⊥OA,HM的长即是MN+ON的最小值,由对称性可得AH=OA=2+,∵直线y=x +2+与x轴夹角为45°,即∠HAM=45°,∴△AHM是等腰直角三角形,∴HM ===+1,∴MN+ON 的最小值是+1.13.【分析】(1)由y =x+6求出A(﹣4,0),根据AB =5得B(1,0),把B(1,0)代入y=﹣x+m即可解得直线BC的解析式为y=﹣x+1;(2)由y=﹣x+1得C(0,1),解得D(﹣2,3),可得S△ABD =AB•|y D|=,S△BOC =OB •OC =,故四边形AOCD的面积为7;(3)分两种情况:P在BD上方时,过P作PM∥BD 交x轴于M,连接DM,可得S△MBD =S四边形AOCD =7,即BM×3=,可得M (,0),直线PM为:y=﹣x +,解即得P (﹣,),当P在BD下方时,过P'作P'M'∥BD交x轴于M',同理可得P'(﹣,).【解答】解:(1)在y =x+6中,令y=0得x=﹣4,∴A(﹣4,0),∵AB=5,∴B(1,0),把B(1,0)代入y=﹣x+m得:0=﹣1+m,解得m=1,∴直线BC的解析式为y=﹣x+1;(2)在y=﹣x+1中,令x=0得y=1,∴C(0,1),解得,∴D(﹣2,3),∴S△ABD =AB•|y D|=×5×3=,S△BOC =OB•OC =×1×1=,∴S四边形AOCD=S△ABD﹣S△BOC=7,即四边形AOCD的面积为7;(3)P在BD上方时,过P作PM∥BD交x轴于M,连接DM,如图:∵PM∥BD,∴S△PBD=S△MBD,∵△PBD的面积是四边形AOCD的面积的一半,∴S△MBD =S四边形AOCD =7,∴BM•|y D|=,即BM×3=,∴BM =,∴OM=OB+BM =,∴M (,0),设直线PM为:y=﹣x+b,将M (,0)代入得:0=﹣+b,∴b =,∴直线PM为:y=﹣x +,解得,∴P (﹣,),当P在BD下方时,过P'作P'M'∥BD交x轴于M',如图:∵P'M'∥BD,∴S△P'BD=S△M'BD,∵△P'BD的面积是四边形AOCD的面积的一半,∴S△M'BD =S四边形AOCD =7,∴BM'•|y D|=,即BM'×3=,∴BM'=,∴OM'=BM'﹣OB =,∴M'(﹣,0),设直线P'M'为:y=﹣x+b',将M (﹣,0)代入得:0=+b',∴b'=﹣,∴直线PM为:y=﹣x ﹣,解得,∴P'(﹣,),综上所述,P的坐标为(﹣,)或(﹣,).14.【分析】(1)把B的坐标代入直线AB的解析式,即可求得k的值,然后在解析式中,令x=0,求得y的值,即可求得A的坐标;(2)过点A作AM⊥PD,垂足为M,求得AM的长,即可求得△BPD和△P AD的面积,二者的和即可表示S△P AB,在根据△ABP的面积与△ABO的面积相等列方程即可得答案;(3)分三种情况:当P为直角顶点时,过P作PN ⊥y轴于N,过B作BM⊥PN于M,由△APN≌△PBM (AAS),可得AN+1=PN①,PN+AN=3②,即得P (2,2);当A为直角顶点时,过P作PK⊥y轴于K,由△APK≌△BAO,可得P(1,4),当B为直角顶点时,过P作PR⊥x轴于R,同理可得P(4,3).【解答】解:(1)∵直线AB:y=kx+1(k≠0)交y 轴于点A,交x轴于点B(3,0),∴0=3k+1,∴k =﹣,∴直线AB的解析式是y =﹣x+1.当x=0时,y=1,∴点A(0,1);(2)如图1,过点A作AM⊥PD,垂足为M,则有AM=2,设P(2,n),∵x=2时,y =﹣x+1=,∴D(2,),∵P在点D的上方,∴PD=n ﹣,∴S△APD =AM•PD =×2×(n ﹣)=n ﹣,由点B(3,0),可知点B到直线x=2的距离为1,即△BDP的边PD上的高长为1,∴S△BPD =×1×(n ﹣)=(n ﹣),∴S△P AB=S△APD+S△BPD =n ﹣;∵△ABP的面积与△ABO的面积相等,∴n ﹣=×1×3,解得n =,∴P(2,);(3)当P为直角顶点时,过P作PN⊥y轴于N,过B作BM⊥PN于M,如图2:∵△ABP为等腰直角三角形,∴AP=BP,∠NP A=90°﹣∠BPM=∠PBM,∵∠ANP=∠BMP=90°,∴△APN≌△PBM(AAS),∴BM=PN,PM=AN,∵∠NOB=∠ONM=∠OBM=90°,∴四边形OBMN是矩形,∴MN=OB=3,BM=ON=AN+1=PN①,∴PN+PM=PN+AN=3②,由①②解得PN=2,AN=1,∴ON=OA=AN=2,∴P(2,2);当A为直角顶点时,过P作PK⊥y轴于K,如图3:∵△ABP为等腰直角三角形,∴AP=AB,∠KAP=90°﹣∠OAB=∠ABO,而∠PKA=∠AOB=90°,∴△APK≌△BAO(AAS),∴AK=OB=3,PK=OA=1,∴OK=OA+AK=4,∴P(1,4),当B为直角顶点时,过P作PR⊥x轴于R,如图4:同理可证△AOB≌△BRP(AAS),∴BR=OA=1,PR=OB=3,∴P(4,3),综上所述,P坐标为:(2,2)或(1,4)或(4,3).15.【分析】(1)求出点A坐标可得结论.(2)如图1中,延长CA交GD的延长线于H.证明△DGO≌△EHD(AAS),推出DG=EH,OG=DH,由题意D(12+m,m),推出OG=AH=﹣m,DG=EH=12+m,推出AE=12+m﹣(﹣m)=12+2m,可得E(12,12+2m).(3)求出直线BE的解析式,再求出点F的坐标,求出DF,EF,构建方程,可得结论.【解答】解:(1)∵直线y=x﹣12分别交x轴、y轴于A、B两点,∴A(12,0),B(0,﹣12),∵AC⊥x轴,∴C(12,9).故答案为:(12,9).(2)如图1中,延长CA交GD的延长线于H.∵∠DGO=∠DHE=∠ODE=90°,∴∠ODG+∠EDH=90°,∠EDH+∠DEH=90°,∴∠ODG=∠DEH,∵OD=DE,∴△DGO≌△EHD(AAS),∴DG=EH,OG=DH,由题意D(12+m,m),∴OG=AH=﹣m,DG=EH=12+m,∴AE=12+m﹣(﹣m)=12+2m,∴E(12,12+2m),∵E点在线段AC上,∴0≤12+2m≤9,∴﹣6≤m ≤﹣.(3)如图2中,∵B(0,﹣12),E(12,2m+12),∴直线BE的解析式为y=(2+m)x﹣12,∴F(6,m),∵D(12+m,m),∴DF=6+m,EF =,∵EF=DF﹣2m,∴=6+m﹣2m,解得m=﹣4.16.【分析】(1)根据三角形的面积公式求出OB的长即可;(2)分0≤t<4和t≥4两种情况,根据三角形面积公式计算即可;(3)根据题意和三角形的面积公式求出OP、BP的长,根据相似三角形的性质求出点E的坐标,根据中点的性质确定点F的坐标,运用待定系数法求出直线ef的解析式,根据等底的两个三角形面积相等,它们的高也相等分x=y和x=﹣y两种情况计算即可.【解答】解:(1)∵点A坐标为(6,0),∴OA=6,∴S△AOB =×OA×OB=24,则OB=8,∴点B坐标为(0,8);(2)当0≤t<4时,S =×(8﹣2t)×6=24﹣6t,当t≥4时,S =×(2t﹣8)×6=6t﹣24;(3)∵S△AOP+S△ABP=S△AOB,∴点P在线段OB上,∵S△AOP:S△ABP=1:3,∴OP:BP=1:3,又∵OB=8,∴OP=2,BP=6,线段AB的垂直平分线上交OB于E,交AB于F,∵OB=8,OA=6,∴AB ==10,则点F的坐标为(3,4),∵EF⊥AB,∠AOB=90°,∴△BEF∽△BAO,∴=,即=,解得,BE =,则OE=8﹣=,∴点E的坐标为(0,),设直线EF的解析式为y=kx+b,则,解得,k =,b =,∴直线EF的解析式为y =x +,∵△AOQ的面积与△BPQ的面积相等,又OA=BP,∴x=y,或x=﹣y,当x=y时,x =x +,解得,x=7,则Q点坐标为(7,7);当x=﹣y时,﹣x =x +,解得,x=﹣1,则Q点坐标为(﹣1,1),∴Q点坐标为(7,7)或(﹣1,1).。
10 专题十:一次函数与全等三角形存在性问题(方法专题)

1.如图,点E,F在线段BC上,ABF∆与DCE∆全等,点A与点D,点B与点C是对应顶点,AF与DE 交于点M,则(DCE∠=)A.ABF∠B.BAF∠C.EMF∠D.AFB∠【答案】A.2.如图,ABC∆的顶点分别为(0,3)A,(4,0)B-,(2,0)C,且BCD∆与ABC∆全等,则点D坐标可以是( )A.(2,3)--B.(2,3)-C.(2,3)D.(0,3)【答案】A.3.如图,直线1:33y x=-+与x轴、y轴分别相交于点A、B,AOB∆与ACB∆关于直线l对称,则点C的坐标为.【答案】3(2,3).专题导入一次函数与全等存在性全等三角形存在性问题的处理流程:分析不变特征: 从顶点入手,分析定点、动点,在两个三角形中逐层分析确定的角、边长,把公共边作为对应边. 分析形成因素:根据分析得到的不变特征,结合两个三角形全等的判定,同时考虑两个三角形出现的对应关系,综合在一起分析.画图求解:根据上面的分析,画出符合题意的图形,结合图形特征,设计方案.结果验证:回归点的运动范围进行验证;估算数值,结合图形进行验证.例1、如图,ABC ∆的顶点分别为(0,3)A ,(4,0)B -,(2,0)C ,且BCD ∆与ABC ∆全等,则点D 坐标可以是______________.【答案】解:如图所示,BCD ∆与ABC ∆全等,点D 坐标可以是(2,3)-或(2,3)--或(0,3)-. 故答案为:(2,3)-或(2,3)--或(0,3)-.专题精析解法点睛【举一反三】1.线段AB 的两端点的坐标为(0,3)A ,(2,0)B -,现请你在坐标系中(不能在坐标轴上)找一个格点P ,使得以P 为顶点且与AOB ∆共一边的三角形与AOB ∆全等,则满足条件的P 点的坐标是 ________ (写出所有情况)【答案】解:如图所示:1(2,3)P-,2(2,3)P ,3(2,3)P --, 故答案为:(2,3)-、(2,3)、(2,3)--.2.如图,直线24y x =-+分别与x 轴、y 轴相交于点A 和点B ,如果线段CD 两端点在坐标轴上滑动(C 点在y 轴上,D 点在x 轴上),且CD AB =.(1)当COD ∆和AOB ∆全等时,求C 、D 两点的坐标;(2)是否存在经过第一、二、三象限的直线CD ,使CD AB ⊥?如果存在,请求出直线CD 的解析式;如果不存在,请说明理由.【答案】解:(1)由题意,得(2,0)A ,(0,4)B ,即2AO =,4OB =.①当线段CD 在第一象限时,点(0,4)C ,(2,0)D 或(0,2)C ,(4,0)D .②当线段CD 在第二象限时,点(0,4)C ,(2,0)D -或(0,2)C ,(4,0)D -.③当线段CD 在第三象限时,点(0,4)C -,(2,0)D -或(0,2)C -,(4,0)D -.④当线段CD 在第四象限时,点(0,4)C -,(2,0)D 或(0,2)C -,(4,0)D(2)(0,2)C ,(4,0)D -.直线CD 的解析式为122y x =+.例2、在平面直角坐标系中,点A 的坐标(0,4),点C 的坐标(6,0),点P 是x 轴上的一个动点,从点C 出发,沿x 轴的负半轴方向运动,速度为2个单位/秒,运动时间为t 秒,点B 在x 轴的负半轴上,且3AOC AOB S S ∆∆=.(1)求点B 的坐标;(2)若点D 在y 轴上,是否存在点P ,使以P 、D 、O 为顶点的三角形与AOB ∆全等?若存在,直接写出点D 坐标;若不存在,请说明理由(3)点Q 是y 轴上的一个动点,从点A 出发,向y 轴的负半轴运动,速度为2个单位/秒.若P 、Q 分别从C 、A 两点同时出发,求:t 为何值时,以P 、Q 、O 三点构成的三角形与AOB ∆全等.【答案】解:(1)点A 的坐标(0,4),点C 的坐标(6,0),4OA ∴=,6OC =,11641222AOC S OC OA ∆∴==⨯⨯=, 3AOC AOB S S ∆∆=.4AOB S ∆=,设(,0)B x ,点B 在x 轴的负半轴上,OB x ∴=-,11()4422AOB S OB OA x ∆∴==⨯-⨯=, 2x ∴=-,(2,0)B ∴-;(2)P 在x 轴上,D 在y 轴,90POD AOB ∴∠=∠=︒,以P 、D 、O 为顶点的三角形与AOB ∆全等,∴①POD AOB ∆≅∆,2OD OB ∴==,(0,2)D ∴或(0,2)-②DOP AOB ∆≅∆,4OD OA ∴==,(0,4)D ∴或(0,4)-, 即:满足条件的D 的坐标为(0,4),(0,4)-,(0,2),(0,2)-.(3)P 在x 轴上,Q 在y 轴,90POQ AOB ∴∠=∠=︒,由运动知,2CP t =,2AQ t =,|26|OP t ∴=-,|24|OQ t =-,当02t <<时,62OP t =-,42OQ t =-,以P 、Q 、O 为顶点的三角形与AOB ∆全等,1t ∴=462OP OA t ===-,1t ∴=,∴满足条件,即:1t s =②QOP AOB ∆≅∆,442OQ OA t ∴===-,0t ∴=,262OP OB t ===-,2t ∴=,∴不满足条件,舍去;当23t <<时,62OP t =-,24OQ t =-,以P 、Q 、O 为顶点的三角形与AOB ∆全等,∴①POQ AOB ∆≅∆,224OQ OB t ∴===-,3t ∴=,462OP OA t ===-,1t ∴=,∴不满足条件,舍去;②QOP AOB ∆≅∆,424OQ OA t ∴===-,4t ∴=,262OP OB t ===-,2t ∴=,∴不满足条件,舍去;当3t >时,26OP t =-,24OQ t =-,以P 、Q 、O 为顶点的三角形与AOB ∆全等,3t ∴=426OP OA t ===-,5t ∴=,∴不满足条件,舍去;,②QOP AOB ∆≅∆,424OQ OA t ∴===-,4t ∴=,226OP OB t ===-,4t ∴=,∴满足条件,即:4t s =即:满足条件的时间1t s =或4s .13.直线1l 与x 轴的交点A 的坐标为(2,0)-,与y 轴的交点B 的坐标为(0,1).(1)求这条直线的表达式.(2)直线2l 经过第二、三、四象限,且与x 轴、y 轴分别交于点C ,点D ,如果COD ∆和AOB ∆全等,求直线2l 的表达式.【答案】解:(1)设1l 一次函数表达式为y kx b =+,直线1l 与x 轴的交点A 的坐标为(2,0)-,与y 轴的交点B 的坐标为(0,1).代入可得201k b b -+=⎧⎨=⎩,解得121k b ⎧=⎪⎨⎪=⎩,1l ∴一次函数表达式为112y x =+;(2)点A 的坐标为(2,0)-,点B 的坐标为(0,1).2OA ∴=,1OB =,专题过关COD ∆和AOB ∆全等, 2OC ∴=或1,1OD =或2,(2,0)C ∴-,(0,1)D -或(1,0)C -,(0,2)D -,设2l 一次函数表达式为y mx n =+,∴201m n n -+=⎧⎨=-⎩或02m n n -+=⎧⎨=-⎩ 解得121m n ⎧=-⎪⎨⎪=-⎩或22m n =-⎧⎨=-⎩∴直线2l 的表达式为112y x =--或22y x =--. 2.已知直线25y x =-与x 轴和y 轴分别交于点A 和点B ,点(1,)C n 在直线AB 上,点D 在y 轴的负半轴上,且CD =(1)求点C 、点D 的坐标.(2)若点M 为x 轴上一动点(点M 不与点O 重合),N 为直线25y x =-上一动点,是否存在点M 、N ,使得AMN ∆与AOB ∆全等?若存在,求出点N 的坐标;若不存在,请说明理由.【答案】解:(1)如图1中,点(1,)C n 在直线25y x =-上,3n ∴=-,(1,3)C ∴-,作CF y ⊥轴于F ,10CD =,1CF =,在Rt CDF ∆中,3DF ,(0,6)D ∴-或(0,0)(舍弃)(0,6)D ∴-.(2)如图2中,①当AMN AOB ∆≅∆时, 2.5AM OA ==,5NM OB ==5OM ∴=,(5,5)N ∴.②当△AN M AOB ''≅∆时,52AN OA '==,可得N ',. ③当△AN M AOB ''''≅∆时,52AN OA ''==,可得N '',.综上所述,满足条件的点N 坐标:(5,5)或或 3 3.直线(0)y x b b =+>与x ,y 轴分别交于A ,B 两点,点A 的坐标为(6,0)-,过点B 的另一直线交x 轴正半轴于点C ,且13OC OB =. (1)求点B 的坐标及直线BC 的解析式;(2)在线段OB 上存在点P ,使点P 到点B ,C 的距离相等,求出点P 坐标;(3)在x 轴上方存在点D ,使以点A ,B ,D 为顶点的三角形与ABC ∆全等,画出ABD ∆并请直接写出点D 的坐标.【答案】解:(1)把A 的坐标为(6,0)-代入y x b =+中,得到6b =, (0,6)B ∴,13OC OB =,2OC ∴=,(2,0)C ∴,设直线BC 的解析式为y kx b =+,则有620b k b =⎧⎨+=⎩,解得36k b =-⎧⎨=⎩,∴直线BC 的解析式为36y x =-+.(2)如图1中,由题意PB PC =,设PB PC x ==.在Rt POC ∆中,6OP x =-,PC x =,2OC =,222(6)2x x ∴=-+,103x ∴=,108633OP ∴=-=,8(0,)3P ∴.(3)如图2中,设点C 关于直线AB 的对称点为D ,则ABD ABC ∆≅∆,直线AB 的解析式为6y x =+,∴直线CD 的解析式为2y x =-+,由62y x y x =+⎧⎨=-+⎩,解得24x y =-⎧⎨=⎩,(2,4)H ∴-,DH HC =,(6,8)D ∴-,根据对称性点D 关于直线y x =-的对称点(8,6)D '-也满足条件.综上所述,满足条件的点D 的坐标为(6,8)-或(8,6)-.4.如图,直线124:5l y kx =+与x 轴、y 轴分别相交于A 、B 两点,直线2:2l y x b =-+与x 轴、y 轴、直线1l 分别相交于点C 、D 、P .已知点A 的坐标为(6,0),点D 的坐标为(0,6),点M 是x 轴上的动点.(1)求k ,b 的值及点P 的坐标;(2)当POM ∆为等腰三角形时,求点M 的坐标;(3)是否存在以点M 、O 、D 为顶点的三角形与AOB ∆全等?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】解:(1)直线124:5l y kx =+与x 轴相交于(6,0)A , 24605k ∴+=,45k ∴=-, ∴直线1424:55l y x =-+① 直线2:2l y x b =-+与y 轴相交于点(0,6)D ,6b ∴=,∴直线2:26l y x =-+②,联立①②解得,14x y =⎧⎨=⎩,(1,4)P ∴;(2)点M 是x 轴上的动点,∴设(,0)M m ,(1,4)P ,OP ∴=||OM m =,MP =POM ∆为等腰三角形,∴当OM OP =时,∴||m =,m ∴=(M ∴0)或0)当OM MP =时,||m ∴=172m ∴=,17(2M ∴,0), 当OP MP =时,∴,0m ∴=(舍)或2m =,(2,0)M ∴,即:点M 的坐标为(0)或0)或17(2,0)或(2,0);(3)点A 的坐标为(6,0),点D 的坐标为(0,6),6OA OD ∴==,点M 在x 轴上,90AOB DOM ∴∠=∠=︒,以点M 、O 、D 为顶点的三角形与AOB ∆全等,AOB DOM ∴∆≅∆, OM OB ∴=,直线1424:55l y x =-+与y 轴相交于B , 24(0,)5B ∴,245OB ∴=,245OM ∴=, 24(5M ∴,0)或24(5-,0).5.已知直线443y x =-+与x 轴和y 轴分别交与A 、B 两点,另一直线过点A 和点(7,3)C .(1)求直线AC 对应的函数关系式;(2)求证:AB AC ⊥;(3)若点P 是直线AC 上的一个动点,点Q 是x 轴上的一个动点,且以P 、Q 、A 为顶点的三角形与AOB ∆全等,求点Q 的坐标.【答案】解:(1)在443y x =-+中,令0y =,则4043x =-+,3x ∴=,(3,0)A ∴,设直线AC 对应的函数关系式为y kx b =+,∴0337k b k b =+⎧⎨=+⎩,∴3494k b ⎧=⎪⎪⎨⎪=-⎪⎩,∴直线AC 对应的函数关系式为3944y x =-,(2)在直线443ABy x =-+中,143k =-, 在直线3944ACy x =-中,234k =, 121k k ∴=-,AB AC ∴⊥;(3)在443y x =-+中,令0x =,则4y =,3OA ∴=,4OB =,由勾股定理得5AB =,①当90AQP ∠=︒时,如图1,AOB AQP ∆≅∆,4AQ OB ∴==,1(7,0)Q ∴,2(1,0)Q -,②当90APQ ∠=︒时,如图2,AOB AQP ∆≅∆,5AQ AB ∴==,3(8,0)Q ∴,4(2,0)Q -.③当90PAQ ∠=︒时,这种情况不存在,综上所述:点Q 的坐标为:(7,0)(8,0)(1-,0)(2-,0).6.如图,直线:3l y kx =+与x 轴、y 轴分别交于A 、B 两点,34OB OA =,OM AB ⊥,垂足为点M ,点P 为直线l 上的一个动点(不与A 、B 重合).(1)求直线3y kx =+的解析式;(2)当点P 运动到什么位置时BOP ∆的面积是6;(3)在y 轴上是否存在点Q ,使得以O ,P ,Q 为顶点的三角形与OMP ∆全等,若存在,请求出所有符合条件的点P 的坐标,若不存在,请说明理由.【答案】解:(1)直线:3l y kx =+与y 轴交于点B(0,3)B ∴,3OB =34OB OA =,4OA ∴=,即(4,0)A点A 在直线l 上,430k ∴+= 解得:34k =-∴直线l 的解析式为334y x =-+(2)过P 作PC y ⊥轴于C ,如图1,162BOP S OB PC ∆∴==4PC ∴=∴点P 的横坐标为4或4-点P 为直线l 上的一个动点且不与A 、B 重合∴横坐标不为4,纵坐标为:3(4)364-⨯-+=∴点P 坐标为(4,6)-时,BOP ∆的面积是6;(3)存在满足条件的P 、QOM AB ⊥,5AB ==90OMP ∴∠=︒ 125OA OB OM AB ==∴以O ,P ,Q 为顶点的三角形与OMP ∆全等时,斜边OP 为对应边,90OQP ∠=︒, ①OMP PQO ∆≅∆125PQ OM ∴==,即P 点横坐标为125-或125,如图2和图3,31224()3455-⨯-+=,31263455-⨯+= ∴点12(5P -,24)5或12(5,65)②OMP OQP ∆≅∆125OQ OM ∴==,即点P 、点Q 纵坐标为125-或125,如图4和图5,312345x -+=- 解得:365x =312345x -+= 解得:45x = ∴点36(5P ,12)5-或4(5,12)5 综上所述,符合条件的点P 的坐标为12(5-,24)5,12(5,6)5,36(5,12)5-,4(5,12)5。
专题09 一次函数中的三角形问题(解析版)

1专题09 一次函数中的三角形问题知识对接考点一、怎样解直线与坐标轴围成图形的面积问题1.求直线与坐标围成的三角形的面积时,一般将在坐标轴上的其中一边作为底,另一边作为高来求面积专项训练一、单选题1.已知直线1:1l y kx k =++与直线2:(1)2l y k x k =+++,(k 为正整数),记直线1l 和2l 与x 轴围成的三角形面积为k S ,则12310S S S S +++⋅⋅⋅+的值为( ) A .511B .1011C .920D .50101【答案】A 【分析】变形解析式得到两条直线都经过点(1,1)-,即可证出无论k 取何值,直线1l 与2l 的交点均为定点(1,1)-;先求出1y kx k =++与x 轴的交点和(1)2y k x k =+++与x 轴的交点坐标,再根据三角形面积公式求出k S ,求出11112124S =⨯=⨯,21(2S =⨯11)23-,以此类推101(2S =⨯11)1011-,相加后得到11(1)211⨯-. 【详解】解:直线1:1(1)1l y kx k k x =++=++,∴直线1:1l y kx k =++经过点(1,1)-;直线2:(1)2(1)(1)1(1)(1)1l y k x k k x x k x =+++=++++=+++,∴直线2:(1)2l y k x k =+++经过点(1,1)-.∴无论k 取何值,直线1l 与2l 的交点均为定点(1,1)-.直线1:1l y kx k =++与x 轴的交点为1(k k+-,0), 直线2:(1)2l y k x k =+++与x 轴的交点为2(1k k +-+,0), 1121||1212(1)K k k S k k k k ++∴=⨯-+⨯=++, 11112124S ∴=⨯=⨯;123101111[]212231011S S S S ∴+++⋯+=++⋯⨯⨯⨯111111[(1)()()]22231011=-+-+⋯+- 11(1)211=⨯- 110211=⨯ 511=, 故选:A . 【点睛】此题考查了一次函数的综合题;解题的关键是一次函数的图象与两坐标轴的交点坐标特点,与x 轴的交点的纵坐标为0,与y 轴的交点的横坐标为0.2.已知2,2a b b a +=≤,那么对于一次函数y ax b =+,给出下列结论:①函数y 一定随x 的增大而增大;①此函数图象与坐标轴所围成的三角形面积最大为43,下列判断正确的是( )A .①正确,①错误B .①错误,①正确C .①,①都正确D .①,①都错误【答案】A 【分析】根据一次函数的性质、配方法即可解决问题; 【详解】 解:2a b +=,2b a ∴=-,2b a ≤,22a a ∴-≤,23a ∴≥, 2y ax a ∴=+-,0a >,y ∴随x 的增大而增大,故①正确,函数图象与坐标轴所围成的三角形面积211||||22b b S b a a==,此函数没有最大值,故①错误, 故选:A . 【点睛】本题考查一次函数的性质,一次函数与坐标轴的交点问题,解题的关键是灵活运用一次函数3知识解决问题,属于中考常考题型.3.将一次函数y =2x +4的图象向右平移后所得直线与坐标轴围成的三角形面积是9,则平移距离是( ) A .4 B .5 C .6 D .7【答案】B 【分析】直接利用一次函数的图象平移规律得出平移后的解析式,进而根据三角形面积公式得出答案 【详解】设平移的距离为k (k >0),则将一次函数y =2x +4向右平移后所得直线解析式为:y =2(x -k )+4=2x -2k +4. 易求得新直线与坐标轴的交点为(k -2,0)、(0,-2k +4)所以,新直线与坐标轴所围成的三角形的面积为:2?2429k k --+÷=,变形得229k -=(),解得k =5或k =-1(舍去). 故选:B . 【点睛】此题主要考查了一次函数图象与几何变换,正确得出平移后解析式是解题关键. 4.下列关于一次函数2y x =-+的图象性质的说法中,不正确的是( ) A .直线与x 轴交点的坐标是(0,2) B .与坐标轴围成的三角形面积为2 C .直线经过第一、二、四象限 D .若点(1,)A a -,(1,)B b 在直线上,则a b >【答案】A 【分析】根据一次函数的图像与性质可直接进行排除选项. 【详解】解:由一次函数2y x =-+,可得:10,20k b =-<=>, ①一次函数经过第一、二、四象限,故C 不符合题意; 令x=0时,则y=2,令y=0时,则02x =-+,解得:2x =, ①直线与x 、y 轴的交点坐标为()2,0和()0,2,故A 错误,符合题意; ①直线与坐标轴围成的三角形面积为12222⨯⨯=,故B 正确,不符合题意;①k <0,①y 随x 的增大而减小,①若点(1,)A a -,(1,)B b 在直线上,则a b >,故D 正确,不符合题意; 故选A .【点睛】本题主要考查一次函数的图像与性质,熟练掌握一次函数的图像与性质是解题的关键.5.如图,直线y=-2x+2与x轴和y轴分别交与A、B两点,射线AP①AB于点A.若点C 是射线AP上的一个动点,点D是x轴上的一个动点,且以C、D、A为顶点的三角形与①AOB 全等,则OD的长为()A.2B.3C.2D.3【答案】D【分析】利用一次函数与坐标轴的交点求出①AOB的两条直角边,并运用勾股定理求出AB.根据已知可得①CAD=①OBA,分别从①ACD=90°或①ADC=90°时,即当①ACD①①BOA时,AD =AB,或①ACD①①BAO时,AD=OB,分别求得AD的值,即可得出结论.【详解】解:①直线y=-2x+2与x轴和y轴分别交与A、B两点,当y=0时,x=1,当x=0时,y=2,①A(1,0),B(0,2).①OA=1,OB=2.①AB=①AP①AB,点C是射线AP上,①①BAC=90°,即①OAB+①CAD=90°,①①OAB+①OBA=90°,①①CAD=①OBA,若以C、D、A为顶点的三角形与①AOB全等,则①ACD=90°或①ADC=90°,即①ACD①①BOA或①ACD①①BAO.如图1所示,当①ACD①①BOA时,①ACD=①AOB=90°,AD=AB,5①OD =AD +OA1;如图2所示,当①ACD①①BAO 时,①ADC =①AOB =90°,AD =OB =2,①OD =OA +AD =1+2=3. 综上所述,OD 的长为31. 故选:D . 【点睛】此题考查了一次函数的应用、全等三角形的判定和性质以及勾股定理等知识,掌握一次函数的图象与性质是解题的关键.6.将一次函数y =3x 向左平移后所得直线与坐标轴围成的三角形面积是24,则平移距离( ) A .4 B .6C .D .12【答案】A 【分析】根据题意直接利用一次函数的图象平移规律得出平移后的解析式,进而根据三角形面积公式得出答案. 【详解】解:设平移的距离为k (k >0),则将一次函数y =3x 向左平移后所得直线解析式为:y =3(x+k )=3x+3k .易求得新直线与坐标轴的交点为(﹣k ,0)、(0,3k ) 所以,新直线与坐标轴所围成的三角形的面积为:12k •3k =24, 解得:k =4或﹣4(舍去). 故选:A . 【点睛】本题主要考查一次函数图象与几何变换,由题意正确得出平移后解析式是解题的关键. 7.已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( ) A .y=1.5x+3 B .y=1.5x -3 C .y=-1.5x+3 D .y=-1.5x -3【答案】C 【分析】设这个一次函数的表达式为y=kx+b (k≠0),与x 轴的交点是(a ,0),根据三角形的面积公式即可求得a 的值,然后利用待定系数法即可求得函数解析式. 【详解】设这个一次函数的表达式为y=kx+b (k≠0),与x 轴的交点是(a ,0), ①一次函数y=kx+b (k≠0)图象过点(0,3), ①b=3,①这个一次函数在第一象限与两坐标轴所围成的三角形面积为3, ①12×3×|a|=3, 解得:a=2,把(2,0)代入y=kx+3,解得:k=-1.5,则函数的解析式是y=-1.5x+3; 故选:C . 【点睛】本题考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积,正确求得与x 轴的交点坐标是解题的关键.8.如图,在直角坐标系中,一次函数25y x =-+的图象1l 与正比例函数的图象2l 交于点(,3)M m ,一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 能围成三角形,则在下列四个数中,k 的值能取的是( )7A .﹣2B .1C .2D .3【答案】C 【分析】把M (m ,3)代入一次函数y=-2x+5得到M (1,3),求得l 2的解析式为y=3x ,根据l 1,l 2,l 3能围成三角形,l 1与l 3,l 3与l 2有交点且一次函数y=kx+2的图象不经过M (1,3),于是得到结论. 【详解】解:把M (m ,3)代入一次函数y=-2x+5得,可得m=1, ①M (1,3),设l 2的解析式为y=ax , 则3=a , 解得a=3,①l 2的解析式为y=3x , ①l 1,l 2,l 3能围成三角形,①l 1与l 3,l 3与l 2有交点且一次函数y=kx+2的图象不经过M (1,3), ①k≠3,k≠-2,k≠1, ①k 的值能取的是2, 故选C . 【点睛】本题考查了两直线平行或相交问题,一次函数图象及性质;熟练掌握函数解析式的求法,直线平行的条件是解题的关键.9.在平面直角坐标系中,一次函数26y x =-+与坐标轴围成的三角形面积是:( ) A .6 B .9 C .15 D .18【答案】B 【分析】根据函数关系式求出图像与坐标轴的交点坐标,即可求出图像与坐标轴围成的三角形的面积. 【详解】根据题中的关系式,可画出函数图像当0x =时,6y =,所以点A 的坐标为()06, 当0y =时,3x =,所以点B 的坐标为()30,12OABS OB OA =⨯ 1362=⨯⨯ 9=故答案为B. 【点睛】解题的关键是能够根据函数关系式求出函数与坐标轴的交点坐标.10.如图,在Rt①ABO 中,AB①OB ,且AB=OB=3,设直线x=t 截此三角形所得的阴影部分 的面积为S ,则S 与t 之间的函数关系式为( )A .S=t (0<t ≤3)B .S=12t 2 (0<t ≤3) C .S=t 2 (0<t ≤3) D .S=12t 2 -1(0<t ≤3)【答案】B 【分析】由AB 、OB 的长度求出点A 、点B 的坐标,进而求出OA 所在直线的解析式,令x =t ,求出y ,确定t 的范围,利用三角形面积公式表示出S 即可. 【详解】 ①AB =OB =3, ①A (3,3),①OA 所在直线解析式为y =x , 当0<t ≤3时,令x =t ,则y =t , ①S =12t 2(0<t ≤3).故选B.9【点睛】本题为一次函数与几何综合题,主要考查一次函数解析式的求解. 二、填空题11.直线44y x =-与坐标轴所围成的三角形面积为__________. 【答案】2 【分析】利用一次函数图象上点的坐标特征可求出直线与两坐标轴的交点坐标,再利用三角形的面积计算公式可求出直线与坐标轴所围成的三角形面积. 【详解】解:当0x =时,4044y =⨯-=-,①直线44y x =-与y 轴的交点坐标为()0,4-; 当0y =时,440x -=,解得:1x =, ①直线44y x =-与x 轴的交点坐标为()1,0.①直线44y x =-与坐标轴所围成的三角形面积14122=⨯⨯=.故答案为:2. 【点睛】本题考查的知识点是一次函数图象上点的坐标特征,解题关键是把求线段的长的问题转化为求函数的交点.12.已知点A (7,0),B (0,m ),且直线AB 与坐标轴围成的三角形面积等于28,则m 的值是__________. 【答案】8± 【分析】先分别求出点A 、点B 到坐标轴的距离即OA 、OB ,再利用三角形的面积公式求解即可. 【详解】解:①点A (7,0),B (0,m ), ①OA =7,OB =|m |,①直线AB 与坐标轴围成的三角形面积等于28, ①12×7×|m |=28, 解得:m =±8, 故答案为:±8. 【点睛】本题考查了坐标与图形性质、三角形的面积公式,熟练掌握坐标与图形的性质,会利用点的坐标求图形的面积的方法是解答的关键.13.已知直线1l :23y x =-+,和直线2l :6y x =-,若直线3l :2y kx =-与1l 、2l 不能围成三角形,则k =_________.【答案】2-或1或13-【分析】由题分析可得,平面直角坐标系中,三条直线123,,l l l 不能围成三角形,有三种情况:①l 1①l 3,①l 2①l 3,①三条直线交于同一点,由此展开讨论即可求得答案. 【详解】解:若l 1①l 3则2k =-; 若l 2①l 3,则1k =; 若三条直线交于一点,236y x y x =-+⎧⎨=-⎩,解得33x y =⎧⎨=-⎩, 即1l 与2l 交于一点(3,3)-, 则3l 过该点,代入: 332k -=-,解得13k =-,综上所述,k 为2-或1或13-,故填:2-或1或13-.【点睛】本题考查一次函数图像和性质,两直线平行k 相等,一次函数与二元一次方程组,解题关键是理解和掌握一次函数图像与性质与求两一次函数交点的方法.14.已知一次函数4y kx =-的图像与两坐标轴围成的三角形周长为12,则k 的值为________. 【答案】43±【分析】先求出直线与坐标轴的交点坐标,再根据三角形的周长列出方程求得k 即可. 【详解】解:令x =0,有y =0−4=−4, 令y =0,有kx −4=0,x =4k,①直线4y kx =-与坐标轴的交点坐标为(0,−4)和(4k,0),①一次函数4y kx =-的图象与两坐标轴所围成的三角形的周长等于12,①|−4|+|4 k①k=43±,经检验:k=43±是方程的解,故答案是:43±.【点睛】本题考查的是一次函数图象与坐标轴的交点坐标,根据三角形的周长列出方程是解答此题的关键.15.将平面直角坐标系中一次函数的图像与坐标轴围成的三角形,叫做此一次函数的坐标轴三角形.如图中的一次函数图像与,x y轴分别交于点,,A B那么ABO为此一次函数的坐标轴三角形.一次函数142y x=-+的坐标轴三角形的面积是_____.【答案】16【分析】求出点A,点B坐标,根据三角形的面积公式解答即可.【详解】解:对于142y x=-+,当x=0时,y=4,当y=0时,x=8①A(8,0)B(0,4),所以OA=8,OB=4,①S①AOB=12×8×4=16.故答案为:16.【点睛】本题考查了一次函数问题,本题中根据一次函数和坐标轴的交点坐标,求坐标三角形的三边长是解题的基础.三、解答题1116.如图,在平面直角坐标系中,ABC 的各顶点坐标分别()2,0A -,()2,0B ,(0,C ,直线l 过点B ,且与x 轴的正半轴成60︒角,将ABC 绕点B 按顺时针方向旋转,记旋转角为α.解答下列问题:(1)填空:ABC 为________三角形(选择“等腰”或“等边”一种),直线l 的函数表达式为_______;(2)若0180α<<︒,在ABC 的旋转过程中,当ABC 的一边与直线l 互相垂直时,记A 点的对应点为A ',求点A '的坐标;(3)当210α︒=时,记旋转后顶点A ,C 的对应点分别为M ,N PQ 在直线l 上移动,连结MQ ,NP ,试求四边形MQPN 周长的最小值.【答案】(1)等边,y -(2)A ´(2-2)或(2,4)或(2);(3).【分析】(1)利用点的坐标,求出OA =OB =2,OC ,利用勾股定理得出边长即可;设l :y =kx +b ,把B 、E 点的坐标代入即可;(2)分'A B l ⊥,''A C l ⊥,'BC l ⊥三种情况分别画出符合的图形,然后再分别求解即可;(3)由题意先确定出点N 坐标,在四边形MQPN 中,MN=4,则只需要MQ +PN 的值最小即可,如图,过点M 作MH //BE ,然后取MF =PQ 作出点M 、F 关于直线l 的对称点M ′,F ′,再分别过点M ′、F ′作x 轴、y 轴的垂线,两垂线交于点G ,连接NF ′,则NF ′的长就是MQ +PN 长的最小值,求出NF ′的长即可. 【详解】(1)①x 轴①y 轴,13①OC ①AB ,又①A (-2,0),B (2,0),C (0,), ①OA =OB =2,OC, ①OC 是AB 的垂直平分线, ①BC =BA ,在Rt OBC 中,BC4= , AB =OA +OB , ①AB =BC =AC =4, ①ABC 为等边三角形;设直线l 与y 轴的交点为E ,在Rt OBE 中,①OBE =60°,OB =2 ①OE. ①E (0,-, 设l :y=kx +b ,代入B (2,0),E (0,-,① 20k b b +=⎧⎪⎨=-⎪⎩,解得k b ⎧=⎪⎨=-⎪⎩,①y-(2)如图,当'A B l ⊥时,过点'A 作'A F x ⊥轴于点F ,①'90A BE ∠=︒,'90A FB ∠=︒, ① ①OBE =60°,①α=①A′BF =90°-60°=30°, ①A′F =1'22A B =,BF=, ①OF =BF -OB =A´B -OB-2,①A ´(2-2);如图,当''A C l ⊥时,垂足为F ,①1'''302A BF A BC ∠=∠=︒,'90A FB ∠=︒,① ①OBE =60°,①α=①A′BA =180°-30°-60°=90°, ①'A B AB ⊥,即'A B x ⊥轴, ①A ´(2,4);如图,当'BC l ⊥时,''A C 交x 轴于点F ,①'90EBC ∠=︒, ① ①OBE =60°,①①FBC ′=180°-90°-60°=30°,①①A′BF =①A′BC ′-①FBC ′=60°-30°=30°, ①α=①A′BA =180°-30°=150°,①A′FB =90°, ①''A C AB ⊥,即''A C x ⊥轴,①A′F =2,BF =①OF=OB+BF①A´(2);综上,A′的坐标为:(2-2)或(2,4)或(2);(3)α=210°时,①ABM=360°-210°=150°,①①ABN=①ABM-①MBN=90°,①N(2,-4)在四边形MQPN中,MN=4,MQ+PN的值最小即可,如图,过点M作MH//BE,然后取MF=PQ分别作出点M、F关于直线l的对称点M′,F′,再分别过点M′、F′作x轴、y轴的垂线,两垂线交于点G,连接NF′,则NF′的长就是MQ+PN长的最小值,①''M F=由对称性可知点①M′BA=30°,又(1)可知M′(2-2),在①M′F′G中,1'''2F G M F==3'4M G=,①3'224F⎛⎫--⎪⎪⎝⎭,即5'24F⎛⎫⎪⎪⎝⎭,①'F N①15【点睛】本题考查了旋转,一次函数的应用等知识,熟练掌握相关知识,正确进行分类讨论是解题的关键.17.如图,在平面直角坐标系中,直线1l :43y x =与直线2l :y kx b =+相交于点A ,点A 的横坐标为3,直线2l 交y 轴负半轴于点B ,且OB OA =. (1)求点B 的坐标及直线2l 的函数表达式;(2)过点B 作31//l l 交x 轴于点C ,连接AC ,求ABC 的面积.【答案】(1)35y x =-;(2)758【分析】(1)利用直线1l 的解析式求出点A 的坐标,再根据勾股定理求出OA 的长度,从而可以得到OB 的长度,根据图象求出点B 的坐标,然后利用待定系数法列式即可求出直线2l 的函数表达式;(2)根据题意易求得直线3l 为453y x =-,即可求得15(4C ,0),根据直线2l 的解析式求得与x 轴的交点D 的坐标,然后根据三角形面积公式即可求得结果.【详解】解:(1)点A 的横坐标为3, ①将x =3代入43y x =,得:4343y =⨯=,∴点A 的坐标是(3,4),5OA ∴=,OA OB =,5OB OA ∴==,17∴点B 的坐标是(0,5)-,把A 、B 的坐标代入y kx b =+得:345k b b +=⎧⎨=-⎩, 解得35k b =⎧⎨=-⎩,∴直线2l 的函数表达式是35y x =-;(2)①31//l l 且点B 的坐标是(0,5)-,∴直线3l 为453y x =-, 令0y =,则154x =, 15(4C ∴,0),设直线2l 与x 轴的交点为D , 将y =0代入35y x =-,得:53x =,5(3D ∴,0),155254312CD ∴=-=, ABC ∴的面积12575(45)2128=⨯⨯+=.【点睛】本题考查了两直线相交或平行的问题,待定系数法求直线的解析式,三角形的面积,求出交点的坐标是解题的关键.18.定义:如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为平面图形的一条面积等分线.(1)如图1,已知ABC ,请用尺规作出ABC 的一条面积等分线.(2)已知:如图2,在平面直角坐标系xOy 中,矩形OABC 的边OA 在x 轴的正半轴上、OC 在y 轴的正半轴上,6,4OA OC ==. ①请判断直线4833y x =-是否为矩形OABC 的面积等分线,并说明理由; ①若矩形OABC 的面积等分线与坐标轴所围成的三角形面积为4,请直接写出此面积等分线的函数表达式.(3)如图3,在ABC 中,点A 的坐标为()2,0-,点B 的坐标为()4,3,点C 的坐标为()2,0,点D 的坐标()0,2-,求过点D 的一条ABC 的面积等分线的解析式.(4)在ABC 中点A 的坐标为()1,0-,点B 的坐标为()1,0,点C 的坐标为()0,1,直线()0y ax b a =+>是ABC 的一条面积等分线,请直接写出b 的取值范围.【答案】(1)见解析;(2)①直线4833y x =-不是矩形OABC 的面积等分线;①y =2x −4或y =29x +43;(3)22y x =-;(4)01b << 【分析】(1)作出线段BC 的垂直平分线,找到BC 中点D ,连接AD ,AD 即所求的ABC 的一条面积等分线.(2)①连接AC ,OB 交于点M ,根据6,4OA OC ==求出点M 的坐标,然后由矩形性质可知形OABC 的面积等分线必过点M ,将M 点的坐标代入4833y x =-判断M 点不在一次函数图像上,即可判断出直线4833y x =-不是矩形OABC 的面积等分线; ①先设出矩形面积等分线的解析式,利用和坐标轴围城的三角形面积是4建立方程求解即可; (3)根据题意设出三角形面积等分线的解析式,求出直线AB 的解析式,然后两条直线联立表示出交点坐标,根据三角形面积的一半列出方程求解即可; (4)根据图像结合面积等分线的性质即可求出b 的取值范围.19【详解】解:(1)如图1所示,作出BC 的垂直平分线交BC 于点D ,连接AD , ①AD 是三角形ABC 的中线,①AC 所在直线即要求的ABC 的一条面积等分线.(2)①如图2所示,连接AC ,OB 交于点M .①OA =6,OC =4, ①()6,0A ,()0,4C , ①()3,2M ,①四边形OABC 是矩形,①矩形OABC 的面积等分线必过点M , 将x =3代入4833y x =-中,得: 48432333y =⨯-=≠,①直线4833y x =-不过点M , ①直线4833y x =-不是矩形OABC 的面积等分线; ①如图所示,由①知,矩形OABC的面积等分线必过点M(3,2),设矩形OABC的面积等分线的解析式为y=kx+b与x轴相交于点E,与y轴相交于F,①3k+b=2,①b=2−3k,①矩形OABC的面积等分线的解析式为y=kx+2−3k,令x=0,y=2−3k,①F(0,2−3k),①OF=|2−3k|,令y=0,①x=32kk-,①E(32kk-,0),①OE=32kk-,①矩形OABC的面积等分线与坐标轴所围成的三角形面积为4,①142OE OF•=,①OE①OF=8,①|2−3k|①|32kk-|=8,①k=2或k=29,①矩形OABC的面积等分线函数表达式为y=2x−4或y=29x+43.(3)如图所示,设三角形ABC面积的等分线的表达式为y kx b=+,交x轴于点F,交AB 于点E.21①三角形ABC 面积的等分线y kx b =+过点D , ①将D ()0,2-代入表达式得:b =-2, ①表达式为2y kx =-.将y =0代入2y kx =-得:x =2k ,①F 20k ⎛⎫⎪⎝⎭,. ①AF =22k+. ①点A 的坐标为()2,0-,点B 的坐标为()4,3, 利用待定系数法可得AB 的表达式为112y x =+, ①DE 和AB 交于点E , ①联立表达式得:1122y x y kx ⎧=+⎪⎨⎪=-⎩,解得:6216221x k y k ⎧=⎪⎪-⎨⎪=-⎪-⎩.①14362ACB S =⨯⨯=△,①132AEF ACB S S ==△△, ①132E AF y ⨯⨯=, 代入得:126223221k k k ⎛⎫⎛⎫⨯+⨯-= ⎪⎪-⎝⎭⎝⎭, 整理得:24720k k --=,解得:12124k k ==-,(舍去),①三角形ABC 面积的等分线的表达式为22y x =-. (4)如图所示,①直线()0y ax b a =+>是ABC 的一条面积等分线, 由图像可知,当1b ≥或0b ≤时,无论a 取何值,直线()0y ax b a =+>都不能把ABC 的面积平分, ①01b <<. 【点睛】此题考查了待定系数法求一次函数表达式,三角形中线的性质,基本作图,矩形的性质等知识,解题的关键是设出直线表达式,根据三角形面积列出方程求解.19.在如图所示的平面直角坐标系中,直线n 过点A (0,﹣2)且与直线l 交于点B (3,2),直线l 与y 轴正半轴交于点C . (1)求直线n 的函数表达式;(2)若①ABC 的面积为9,求点C 的坐标;(3)若①ABC 是等腰三角形,且AB =BC ,求直线l 的函数表达式.【答案】(1)y =423x -;(2)C (0,4);(3)y =463x -+.【分析】(1)用待定系数法求直线n 的函数解析式;23(2)根据①ABC 的面积为9可求得AC 的长,可得出结论;(3)过点B 作BD ①y 轴于点D ,则CD =AD =4,得C (0,6),设直线l 的解析式为:y =kx +b ,将B ,C 代入即可. 【详解】解:(1)设直线n 的解析式为:y =kx +b ,①直线n :y =kx +b 过点A (0,﹣2),点B (3,2),①232b k b =-⎧⎨+=⎩,解得:432k b ⎧=⎪⎨⎪=-⎩, ①直线n 的函数解析式为:y =423x -; (2)①若①ABC 的面积为9, ①9=132AC , ①AC =6, ①OA =2,①点C 在y 轴正半轴, ①C (0,4);(3)当AB =BC 时,过点B 作BD ①y 轴于点D ,①CD =AD =4, ①C (0,6),设直线l 的解析式为:y =kx +b , 将B (3,2),C (0,6)代入得:326k b b +=⎧⎨=⎩, 解得436k b ⎧=-⎪⎨⎪=⎩,①直线l 的解析式为:y =463x -+.【点睛】本题主要考查一次函数的综合问题,待定系数法求一次函数解析式,两直线交点问题,一次函数与坐标轴交点问题,解题的关键是运用数形结合的思想解题. 20.如图,直线135y x =-与反比例函数21k y x-=的图象交于点()2,A m 、(),6B n -两点,连接OA 、OB .(1)求m 、n 、k 的值; (2)求AOB 的面积;(3)直接写出12y y <时,x 的取值范围.【答案】(1)11,,33m n k ==-=;(2)356;(3)02x << 或13x <-【分析】(1)根据题意可先出m ,n ,可得()2,1A 、1,63⎛⎫⎪⎝--⎭B ,再代入反比例函数解析式求出即可;(2)先求出直线与y 轴的交点坐标,可得AOB 的面积AODBODSS=+,即可求解;(3)观察一次函数图象在反比例函数图象下方时的x 的取值范围,即可求解. 【详解】解:(1)①直线135y x =-与反比例函数21k y x-=的图象交于点()2,A m 、(),6B n -两点, ①当2x = 时,2351m =⨯-= ,当6y =- 时,635n -=- ,解得:13n =- ,①()2,1A 、1,63⎛⎫⎪⎝--⎭B ,将()2,1A 代入反比例函数21k y x -=,得:112k -=, 解得:3k = ,(2)设直线AB 与x 轴交于点C ,交y 轴于点D ,25当0x = ,15y =- , ①()0,5D - , 即OD =5, ①AOB 的面积1112223AODBODSSOD OD =+=⨯⨯+⨯⨯ 111352552236=⨯⨯+⨯⨯= ; (3)①直线135y x =-与反比例函数21k y x -=的图象交于点()2,1A 、1,63⎛⎫⎪⎝--⎭B , ①由图象可知,当12y y <时,02x << 或13x <- . 【点睛】本题主要考查了用待定系数法求反比例函数的解析式,反比例函数与一次函数的交点问题、函数图象上点的坐标特征等知识点,利用反比例函数与一次函数的交点解答是解题的关键. 21.如图直线l 1=kx +5与y 轴交于点A 直线l2=﹣x +1与直线l 1交于B ,与y 轴交于C ,已知点B 的纵坐标为2.(1)确定直线l 1的解析式;(2)直线l 1、l 2与y 轴所围成的三角形的面积为 ;(3)垂直于x 轴的直线x =a 与直线l 1、l 2分别交于M 、N ,若线段MN 的长为2,求a 的值.【答案】(1)35y x ==;(2)2;(3)12a =-或32a =-【分析】(1)根据B 点的纵坐标为2且B 是两直线的交点,先把B 纵坐标代入l 2求出B 点坐标,然后代入l 1解析式即可求解;(2)分别求出A 、C 两点的坐标,然后求解面积即可得到答案;(3)把x a =代入两直线解析式分别求出M 、N 的坐标,然后根据MN =2求解即可得到答案. 【详解】解:(1)解:把2y =代入1y x =-+中 得1x =-①B 点坐标为(-1,2)把1x =-时2y =代入5y kx =+中 得25k =-+3k =直线l 1的解析式为35y x =+(2)①直线l 1的解析式为35y x =+ 与y 轴交于A 点 ①A (0,5)①直线l 2的解析式为1y x =-+ 与y 轴交于C 点 ①C (0,1)27①两直线与y 轴围成的面积=14122⨯⨯=(3)把x a =分别代入21y x =-+,和135y x =+中 得21y a =-+ 135y a =+①M (a ,3a +5),N (a ,-a +1) ①1352a a -+--= 112a +=①12a =-或32a =-【点睛】本题主要考查了两一次函数的交点问题,与坐标轴围成的面积问题,解题的关键在于能够熟练掌握一次函数的相关知识点.22.如图,一次函数y =kx +b (k 、b 为常数,k ≠0)的图象与反比例函数12y x=-的图象交于A 、B 两点,且与x 轴交于点C ,与y 轴交于点D ,点A 的横坐标与点B 的纵坐标都是3. (1)求一次函数的表达式; (2)求①AOB 的面积.【答案】(1)y=-x-1;(2)7 2【分析】(1)根据题意得出A,B点坐标,进而利用待定系数法得出一次函数解析式;(2)求出一次函数与x轴交点,进而利用三角形面积求法得出答案.【详解】解:(1)把x=3代入12yx=-,得y=-4,故A(3,-4),把y=3代入12yx=-,得x=-4,故B(-4,3),把A,B点代入y=kx+b得:34 43k bk b+=-⎧⎨-+=⎩,解得:11kb=-⎧⎨=-⎩,故直线解析式为:y=-x-1;(2)由(1)知:当y=0时,x=-1,故C点坐标为:(-1,0),则①AOB的面积为:12×1×3+12×1×4=72.【点睛】本题主要考查了反比例函数与一次函数的交点问题以及待定系数法求一次函数解析式、三角形面积求法等知识,正确得出A,B点坐标是解题关键.23.已知直线L1为y1=x+1,直线L2为y2=ax+b(a≠0),两条直线如图所示,这两个图象的交点在y轴上,直线L2与x轴的交点B的坐标为(2,0).(1)求a、b的值.(2)求使y1、y2的值都大于0的x的取值范围.(3)求这两条直线与x轴所围成的①ABC的面积.【答案】(1)a=12-,b=1;(2)-1<x<2;(3)32【分析】(1)首先根据直线l1的解析式可求得C点的坐标,进而可由B、C的坐标,利用待定系数法确定a、b的值.(2)根据两个函数的图象以及A、B点的坐标进行解答即可.(也可通过解不等式来求得)(3)根据(1)得到的直线l1的解析式,可求得点A的坐标,以AB为底、OC为高即可求得①ABC的面积.【详解】解:(1)由直线l1的解析式为y1=x+1,可求得C(0,1);则依题意可得:201a bb+=⎧⎨=⎩,解得:a=12-,b=1;(2)由(1)知,直线l2:112y x=-+,①y1=x+1>0,①x>-1;①y2=112x-+>0,①x<2;①-1<x<2.(3)由题意知A(-1,0),则AB=3,且OC=1;①S①ABC=12AB•OC=12×3×1=32.【点睛】此题主要考查了一次函数解析式的确定、一次函数与一元一次不等式的联系以及三角形面积29的计算方法,难度适中.。
人教版_部编版八年级数学上册第十二章第一节全等三角形考试复习题(含答案) (67)

人教版_部编版八年级数学上册第十二章第一节全等三角形考试复习题(含答案)已知ABC 与DEC 是两个大小不同的等腰直角三角形.()1如图①所示,连接AE ,DB ,试判断线段AE 和DB 的数量和位置关系,并说明理由;()2如图②所示,连接DB ,将线段DB 绕D 点顺时针旋转90到DF ,连接AF ,试判断线段DE 和AF 的数量和位置关系,并说明理由.【答案】(1)AE DB =,AE DB ⊥,证明见解析;(2)DE AF =,DE AF ⊥,证明见解析.【解析】【分析】(1)根据等腰直角三角形的性质,全等三角形的判定定理证明RtBCD ≌Rt △ACE ,根据全等三角形的性质进行解答即可;(2)证明△EBD ≌△ADF ,根据全等三角形的性质证明即可.【详解】(1)AE DB =,AE DB ⊥,理由如下:如图①,延长DB 交AE 于点H ,∵ABC 与DEC 是等腰直角三角形,∴AC BC =,EC DC =,在Rt BCD 和Rt ACE 中,AC BC ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩, ∴Rt BCD Rt ACE ≅,∴AE BD =,AEC BDC ∠∠=,∵BCD 90∠=,∴DHE 90∠=,∴AE DB ⊥;(2)DE AF =,DE AF ⊥,理由如下:如图②,设DE 与AF 交于N ,由题意得,BE AD =,∵EBD C BDC 90BDC ∠∠∠∠=+=+,ADF BDF BDC 90BDC ∠∠∠∠=+=+,∴EBD ADF ∠∠=,在EBD 和ADF 中,BE AD EBD ADF DE DF =⎧⎪∠=∠⎨⎪=⎩, ∴EBD ADF ≅,∴DE AF =,E FAD ∠∠=,∵E 45∠=,EDC 45∠=,∴FAD 45∠=,∴AND 90∠=,即DE AF ⊥.【点睛】本题考查了等腰直角三角形的性质、全等三角形的判定与性质,熟练掌握全等三角形的判定与性质定理是解题的关键.62.在正方形ABCD 的边AB 上任取一点E ,作EF AB ⊥交BD 于点F ,取FD 的中点G ,连接EG 、CG ,如图()1,易证 EG CG =且EG CG ⊥.()1将BEF 绕点B 逆时针旋转90,如图()2,则线段EG 和CG 有怎样的数量关系和位置关系?请直接写出你的猜想.()2将BEF 绕点B 逆时针旋转180,如图()3,则线段EG 和CG 又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.【答案】()1EG CG =,EG CG ⊥;()2EG CG =,EG CG ⊥.【解析】【分析】从图(1)中寻找证明结论的思路:延长FE 交DC 边于M ,连MG .构造出△GFE ≌△GMC .易得结论;在图(2)、(3)中借鉴此解法证明.【详解】解:()1EG CG =,EG CG ⊥.()2EG CG =,EG CG ⊥.证明:延长FE 交DC 延长线于M ,连MG .∵90AEM ∠=,90EBC ∠=,90BCM ∠=,∴四边形BEMC 是矩形.∴BE CM =,90EMC ∠=,由图()3可知,∵BD 平分ABC ∠,90ABC ∠=,∴45EBF ∠=,又∵EF AB ⊥,∴BEF 为等腰直角三角形∴BE EF =,45F ∠=.∴EF CM =.∵90EMC ∠=,FG DG =, ∴12MG FD FG ==.∵BC EM =,BC CD =,∴EM CD =.∵EF CM =,∴FM DM =,又∵FG DG =,1452CMG EMC ∠=∠=, ∴F GMC ∠=∠.∵在GFE 与GMC 中,FG MG F GMC EF CM =⎧⎪∠=∠⎨⎪=⎩, ∴()GFE GMC SAS ≅.∴EG CG =,FGE MGC ∠=∠.∵90FMC ∠=,MF MD =,FG DG =,∴MG FD ⊥,∴90FGE EGM ∠+∠=,∴90MGC EGM ∠+∠=,即90EGC ∠=,∴EG CG ⊥.【点睛】此题综合考查了旋转的性质及全等三角形的判断和性质,如何构造全等的三角形是难点,因此难度较大.63.如图,在 Rt ABC ,ACB 90∠=,AC BC =,分别过A 、B 作直线l 的垂线,垂足分别为M 、N .()1求证:AMC ≌CNB ;()2若AM 3=,BN 5=,求AB 的长.【答案】(1)证明见解析(2)【解析】【分析】()1根据AM l ⊥,BN l ⊥,ACB 90∠=,可得MAC NCB ∠∠=,再根据AAS 即可判定AMC ≌CNB ; ()2根据AMC ≌CNB ,即可得出CM BN 5==,再根据Rt ACM 中,AC 的长,即可得出等腰直角三角形ABC 中AB 的长.【详解】()1AM l ⊥,BN l ⊥,ACB 90∠=,AMC ACB BNC 90∠∠∠∴===,MAC MCA 90∠∠∴+=,MCA NCB 1809090∠∠+=-=,MAC NCB ∠∠∴=,在AMC 和CNB 中,AMC BNC MAC NCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, AMC ∴≌()CNB AAS ;()2AMC ≌CNB ,CM BN 5∴==,Rt ACM ∴中,AC ==Rt ABC ,ACB 90∠=,AC BC ==,AB ∴===【点睛】本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质的运用,解题时注意:两角及其中一个角的对边对应相等的两个三角形全等.64.如图,若△OAD≌△OBC,且∠O=65°,∠BEA=135°,求∠C 的度数.【答案】35º【解析】【分析】根据全等三角形对应角相等可得∠C=∠D,∠OBC=∠OAD,再根据三角形的内角和等于180°表示出∠OBC,然后利用四边形的内角和等于360°列方程求解即可.【详解】∴∠C=∠D,∠OBC=∠OAD,∵∠O=65º,∴∠OBC=180º−65º−∠C=115º−∠C,在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360º,∴65º+115º−∠C+135º+115º−∠C=360º,解得∠C=35º.【点睛】此题考查了全等三角形的性质和四边形的内角和等于360°,熟练掌握这两个性质是解题的关键.65.如图,直线y=﹣√3x+1与x轴、y轴分别交于点A、B,以线段AB3为直角边在第﹣象限内作等腰直角△ABC,△BAC=90°,(1)求点A、B、C的坐标;(2)如果在第二象限内有﹣点P(a,1),且△ABP的面积与△ABC的面2积相等,求a的值;(3)请直接写出点Q的坐标,使得以Q、A、C为顶点的三角形和△ABC 全等.【答案】(1)A(√3,0),B(0,1),C(√3+1,√3);(2)a=√3−4;2(3)点Q的坐标为:(1,√3+1 );(2√3,﹣1 );(2√3+1,√3﹣1).【解析】【分析】(1)由直线解析式可求得A、B的坐标,过C作CD⊥x轴于点D,则可证得△AOB≌△CDA,则可求得CD和AD的长,可求得C点坐标;(2)过作PE⊥x 轴于点E,依据△ABP的面积与△ABC的面积相等,即可得到S△AOB+S梯形BOEP﹣S△AEP=2,得到关于a的方程,从而求得a的值;(3)依据以Q、A、C为顶点的三角形和△ABC全等,A(√3,0),B(0,1),C(√3+1,√3),即可得到点Q的坐标.【详解】(1)根据题意,直线y=﹣√33x+1与x轴、y轴分别交于A、B,令x=0,则y=1;令y=0,则x=√3,即A(√3,0),B(0,1),即OA=√3,OB=1,则AB=2;如图,过C作CD⊥AO于D,则∠ADC=∠BOA=90°,∵△ABC是等腰直角三角形,∴AB=AC=2,∠BAC=90°,∴∠BAO=∠ACD,∴△ABO≌△CAD,∴AD=BO=1,CD=AO=√3,∴C(√3+1,√3);(2)由题可得,S△ABC=12×2×2=2,如图,作PE⊥x 轴于点E,则EO=﹣a,PE=12,AE=√3﹣a,∵S△ABC=S△ABP=2,∴S△AOB+S梯形BOEP﹣S△AEP=2,即12×√3×1+12×(12+1)×(﹣a)﹣12×(√3﹣a)×12=2,解得a=√32-4;(3)以Q、A、C为顶点的三角形和△ABC全等,A(√3,0),B(0,1),C(√3+1,√3),分三种情况:如图,当点Q在AC左上方时,过Q1作Q1F⊥y轴于F,连接BQ1,依据△ABO与△BFQ1全等,可得Q1F=BO=1,BF=AO=√3,∴Q1(1,√3+1 );如图,当点Q在AC的右下方时,过Q2作Q2G⊥x轴于G,依据△AOB与△AGQ2全等,可得Q2G=BO=1,AG=AO=√3,∴Q2(2√3,﹣1 );如图,当点Q在AC的右上方时,过C作CH∥y轴,过Q3作Q3H∥x轴,依据△AOB与△CHQ3全等,可得Q3H=AO=√3,CH=BO=1,而C(√3+1,√3),∴Q3(2√3+1,√3﹣1).综上所述,点Q的坐标为:(1,√3+1 );(2√3,﹣1 );(2√3+1,√3﹣1).【点睛】本题考查了一次函数的综合应用,涉及了一次函数的图象,全等三角形的性质以及等腰直角三角形的性质的运用;解决函数图象与面积结合的问题,要把相关三角形用其他图形的面积来表示,这样面积与坐标就建立了联系,把S△ABP表示成其它图形面积的和、差关系是正确解答本题的关键.66.如图1,在△ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,点D是直线MN上一点,不与点A重合.(1)若点E是图1中线段AB上一点,且DE=DA,请判断线段DE与DA 的位置关系,并说明理由;(2)请在下面的A,B两题中任选一题解答.A:如图2,在(1)的条件下,连接BD,过点D作DP⊥DB交线段AC 于点P,请判断线段DB与DP的数量关系,并说明理由;B:如图3,在图1的基础上,改变点D的位置后,连接BD,过点D作DP⊥DB交线段CA的延长线于点P,请判断线段DB与DP的数量关系,并说明理由.我选择:.【答案】(1)DE⊥DA,详见解析;(2)A、DB=DP;B、DB=DP.详见解析.【解析】【分析】(1)根据等腰直角三角形的性质得到∠B=∠C=45°,根据平行线的性质得到∠DAE=∠B=45°,根据等腰三角形的性质即可得证;(2)A:根据同角的余角相等得到∠BDE=∠ADP,证明∠DEB∠∠DAP,根据全等三角形的性质定理证明结论;B:与题A的证明方法类似,延长AB至F,连接DF,使DF=DA,证明∠DFB∠∠DAP即可.【详解】解:(1)DE∠DA;证明:∠∠BAC=90°,AB=AC,∠∠B=∠C=45°,∠MN∠BC,∠∠DAE=∠B=45°(两直线平行,内错角相等),又∠DA=DE,∠∠DEA=∠DAE=45°,∠∠ADE=90°,即DE∠DA;(2)A:DB=DP;证明:∠DP∠DB,∠∠BDE+∠EDP=90°,又∠DE∠DA,∠∠ADP+∠EDP=90°,∠∠BDE=∠ADP,∠∠DEA=∠DAE=45°,∠∠BED=135°,∠PAD=135°,∠∠BED=∠PAD ,在∠DEB 和∠DAP 中,BED PAD BDE PDA DE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∠∠DEB ∠∠DAP (AAS ),∠DB=DP (三角形全等其对应边相等).B :DB=DP ;证明:如图3,延长AB 至F ,连接DF ,使DF=DA ,由(1)得,∠∠DFA=∠DAF=45°,∠∠ADF=90°,又∠DP ∠DB ,∠∠FDB=∠AMP ,∠∠BAC=90°,∠DAF=45°,∠∠PAM=45°,∠∠BFD=∠PAM ,在∠DFB 和∠DAP 中,FDB AMP DF DABFD PAM ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠∠DFB ∠∠DAP (ASA ),∠DB=DP (三角形全等其对应边相等).67.(1)如图1,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.(2)如图2,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AB=DE.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)如图1中,连接BD.证△BDC≌△BDA(SSS),可得∠C=∠A.(2)由B EBC EFACB EFD∠=∠⎧⎪=⎨⎪∠=∠⎩,证得△ACB≌△DFE(ASA),得AB=DE.【详解】证明:(1)如图1中,连接BD.在△BDC和△BDA中,BD BDBA BCDC DA=⎧⎪=⎨⎪=⎩∴△BDC≌△BDA(SSS),∴∠C=∠A.(2)如图2中,∵FB=CE,∴BC=EF ,∵AB ∥ED ,AC ∥FD ,∴∠B=∠E ,∠ACB=∠EFD ,在△ABC 和△DEF 中,B E BC EFACB EFD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACB ≌△DFE (ASA ),∴AB=DE .【点睛】本题考核知识点:全等三角形的判定. 解题关键点:构造三角形,熟记全等三角形的判定和性质.68.如图,△ACF ≌△DBE ,∠E=∠F ,若AD=11,BC=7.(1)试说明AB=CD .(2)求线段AB 的长.【答案】(1)见解析;(2)2.【分析】(1)由△ACF≌△DBE,得AC=DB,故AC﹣BC=DB﹣BC;(2)由(1)结论可得AB=12(AD﹣BC).【详解】解:(1)∵△ACF≌△DBE,∴AC=DB,∴AC﹣BC=DB﹣BC,即AB=CD(2)∵AD=11,BC=7,∴AB=12(AD﹣BC)=12(11﹣7)=2即AB=2【点睛】本题考核知识点:全等三角形性质. 解题关键点:熟记全等三角形性质. 69.如图,△ADF△△CBE,点E、B、D、F在同一条直线上.(1)线段AD与BC之间的数量关系是,其数学根据是.(2)判断AD与BC之间的位置关系,并说明理由.【答案】(1)见解析;(2)见解析.【解析】根据全等三角形对应角相等,对应边相等,可得答案.【详解】解:(1)∠∠ADF∠∠CBE,∠AD=BC(全等三角形的对应边相等),故答案为AD=BC,全等三角形的对应边相等;(2)结论:AD∠BC.理由:∵△ADF∠∠CBE,∠∠ADF=CBE,∠∠ADB=∠CBD,∠AD∠BC.【点睛】本题考核知识点:全等三角形性质. 解题关键点:熟记全等三角形性质. 70.如图,△ADF≌△BCE,∠B=32°,∠F=28°,BC=5cm,CD=1cm 求:(1)∠1的度数(2)AC的长【答案】(1)60°;(2)6cm.【解析】【分析】(1)由全等三角形性质得∠E=∠F=28°,故∠1=∠B+∠E=32°+28°;(2)由全等三角形性质得AD=BC=5cm,又CD=1cm,故AC=AD+CD=6cm.【详解】解:(1)∵△ADF≌△BCE,∠F=28°,∴∠E=∠F=28°,∴∠1=∠B+∠E=32°+28°=60°;(2)∵△ADF≌△BCE,BC=5cm,∴AD=BC=5cm,又CD=1cm,∴AC=AD+CD=6cm.【点睛】本题考核知识点:全等三角形性质. 解题关键点:运用全等三角形性质证角相等和边相等.。
第六章一次函数(动点、全等、三角形存在性问题压轴)(原卷版)

第六章 一次函数(压轴题专练)一、动点函数问题1.如图,在长方形ABCD 中,动点P 从A 出发,以一定的速度,沿A B C D A ®®®®方向运动到点A 处停止(提示:当点P 在AB 上运动时,点P 到DC 的距离始终等于AD 和BC ).设点P 运动的路程为x ,PCD V 的面积为y ,如果y 与x 之间的关系如图所示,那么长方形ABCD 的面积为( )A .6B .9C .15D .182.已知动点H 以每秒x 厘米的速度沿图1的边框(边框拐角处都互相垂直)按从A B C D E F -----的路径匀速运动,相应的HAF △的面积 ()2cm S 关于时间(s)t 的关系图象如图2,已知8cm AF =,则下列说法正确的有几个( )①动点H 的速度是2cm/s ;②BC 的长度为3cm ;③b 的值为14;④在运动过程中,当HAF △的面积是230cm 时,点H 的运动时间是3.75s 和1025s ..A .1个B .2个C .3个D .4个3.如图1,四边形ABCD 中,90DAB ∠=︒,AB CD ∥,点P 从点A 出发,以每秒1个单位长度的速度,沿路线A -B-C -D 运动.设P 点的运动时间为ts ,PAD V 的面积为S ,当P 运动到BC 的中点时,PAD V 的面积为A .7B .7.5C .84.如图,在长为形ABCD 中,5cm 16cm AB AD ==,,点3cm 4cm AM AE ==,,连线CE ,动点P 从点B 出发,以运动到点A 即停止运动,连接MP ,设点P 运动的时间为(1)如图1,线段CE = cm ;当10t =时,线段EP = cm ;(2)如图1,点P 在线段BC 上运动的过程中,连接EM EP ,,当EMP V 是以EM 为直角边的直角三角形时,请求出对应的时间的值;(1)求线段OC的长;(2)若点E是点C关于y轴的对称点,求(3)已知y轴上有一点P,若以点标.(1)求n和b的值;△是直角三角形,求点P的坐标;(2)若ACP∠=∠,求点P的坐标.(3)当PBE BAC(1)求点D的坐标;(2)点E是线段CD上一动点,直线BE与x轴交于点i)若BDFV的面积为8,求点F的坐标;ii)如图2,当点F在x轴正半轴上时,将直线接FM,若1OF MF=+,求线段MF的长.(1)求直线AB的解析式;(2)已知点D为直线BC上第三象限的一点,连接AD,设点D的横坐标为t 间的函数关系式(不要求写出变量t的取值范围);(3)在(2)的条件下,256S=,点D关于y轴的对称点为点E,点F在第一象限直线。
八年级一次函数及全等三角形综合试卷及详细答案

八年级一次函数及全等三角形综合试卷一.选择题(共10小题,每小题4分,共40分)1.如图,在一次函数y=﹣x+3的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足为B,且矩形OAPB的面积为2,则这样的点P个数共有()2.直线y=kx+b不经过第三象限,a>e,且A(a,m)、B(e,n)、C(﹣m,c)、D(﹣n,d)这四点都在直线上,33.(2007•牡丹江)将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为().C D.4.(2013•绥化)如图,在平面直角坐标系中,长、宽分别为2和1的矩形ABCD的边上有一动点P,沿A→B →C→D→A 运动一周,则点P的纵坐标y与P所走过的路程x之间的函数关系用图象表示大致是().C D.5.(2012•武汉)甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()6.(2011•玉溪)如图(1),在Rt△ABC中,∠ACB=90°,D是斜边AB的中点,动点P从B点出发,沿B→C→A 运动,设S△DPB=y,点P运动的路程为x,若y与x之间的函数图象如图(2)所示,则△ABC的面积为()7.(2011•黄石)已知梯形ABCD的四个顶点的坐标分別为A(﹣1,0),B(5,0),C(2,2),D(0,2),直线.C D.8.(2013•哈尔滨模拟)甲乙两人在一个400米的环形跑道上练习跑步.两人同时、同向出发,两人之间的距离s (单位:米)与两人跑步的时问t(单位:分)之间的函数关系图象如图所示.下列四种说法:①l5分时两人之间距离为50米;②跑步过程中两人休息了5分;③20~30分之间一个人的速度始终是另一个人速度的2倍;③40分时一个人比另一个人多跑了400米.其中一定正确的个数是()9.(2013•长春一模)一次函数y=﹣x+b的图象如图所示,则b的值可能是()10.(2012•义乌市模拟)A、B两地相距360km,甲车以100km/h的速度从A地驶往B地,乙车以80km/h的速度从B地驶往A地,两车同时出发.设乙车行驶的时间为x(h),两车之间的距离为y(km),则y与x之间的函数.C D.二.填空题(共6小题,每小题5分共30分)11.如图,直线y=kx+b和y=mx+n交于点P(1,1),直线y=mx+n交x轴于点(2,0),那么不等式组0<mx+n <kx+b的解集是_________.12.甲、乙两人在一段长为1200米的笔直路上匀速跑步,甲、乙的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处.若同时起跑,甲、乙两人在从起跑至其中一人先到达终点的过程中,他们之间的距离y(m)与时间t(s)的函数图象如图所示.则t1=_________s,y2=_________m.13.在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示),点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交点D,连接OD,设P在x轴的正半轴上,若△POD为等腰三角形,则点P的坐标为_________.14.已知函数y=(m﹣1)+1是一次函数,则m=_________.15.若f(x)=2x﹣1,如[f(﹣2)=2×(﹣2)﹣1],则=_________.16.(2005•包头)若一次函数y=ax+1﹣a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则|a﹣1|+= _________.三.解答题(共7小题,共80分)17.(12分)甲、乙两车分别从相距350千米的A、B两地同时出发相向而行,两车在途中S城相遇后,甲车接到返城通知,于是按原路返回A地,乙车在S城停留一会儿后,继续向A地行驶.设甲、乙两车在行驶过程中速度保持不变,两车离A地距离y(千米)与时间x(小时)之间的函数关系如图所示,根据所提供的信息,回答下列问题:(1)甲、乙两车的行驶速度各是多少?(2)乙车出发几小时后到达A地?(3)两车出发后几小时第二次相遇?18.(12分)已知△ABC中,∠A=60°.(1)如图①,∠ABC、∠ACB的角平分线交于点D,则∠BOC=_________°.(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C=_________°.(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…O n﹣1(内部有n﹣1个点),求∠BO n﹣1C(用n 的代数式表示).(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…O n﹣1,若∠BO n﹣1C=90°,求n的值.19.(10分)已知:△ABC中,记∠BAC=α,∠ACB=β.(1)如图1,若AP平分∠BAC,BP,CP分别平分△ABC的外角∠CBM和∠BCN,BD⊥AP于点D,用α的代数式表示∠BPC的度数,用β的代数式表示∠PBD的度数(2)如图2,若点P为△ABC的三条内角平分线的交点,BD⊥AP于点D,猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.20.(12分)如图,y轴的负半轴平分∠AOB,P为y轴负半轴上的一动点,过点P作x轴的平行线分别交OA、OB于点M、N.(1)如图1,MN⊥y轴吗?为什么?(2)如图2,当点P在y轴的负半轴上运动到AB与y轴的交点处,其他条件都不变时,等式∠APM=(∠OBA﹣∠A)是否成立?为什么?(3)当点P在y轴的负半轴上运动到图3处(Q为BA、NM的延长线的交点),其他条件都不变时,试问∠Q、∠OAB、∠OBA之间是否存在某种数量关系?若存在,请写出其关系式,并加以证明;若不存在,请说明理由.21.(12分)已知,直线与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;(2)请说明不论a取任何实数,三角形BOP的面积是一个常数;(3)要使得△ABC和△ABP的面积相等,求实数a的值.22、(10分)已知,如图,给出以下五个论断:①∠D=∠E;②CD=BE;③AM=AN;④∠DAB=∠EAC;⑤AB=AC.以其中三个论断作为题设,另外两个中的一个论断作为结论.(1)请你写出一个满足条件的真命题(书写形式如:如果×××,那么×××),并加以证明;(2)请你再写出至少两个满足上述条件的真命题,并加以证明。
一次函数综合练习(全等三角形,勾股定理)
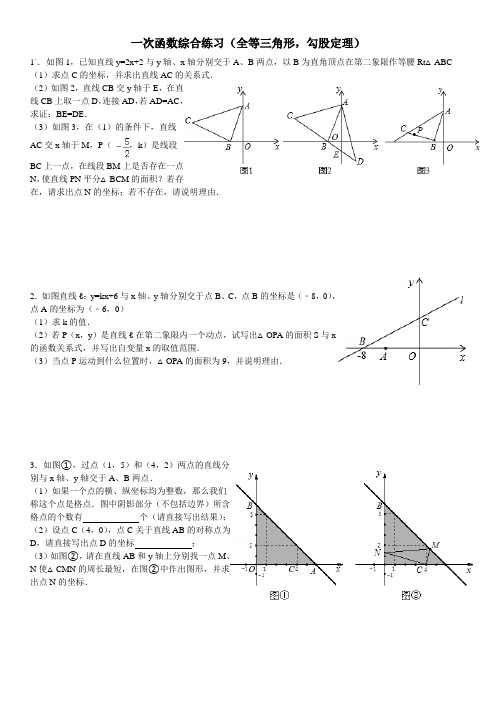
一次函数综合练习(全等三角形,勾股定理)1`.如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC (1)求点C的坐标,并求出直线AC的关系式.(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)如图3,在(1)的条件下,直线AC交x轴于M,P(,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.2.如图直线ℓ:y=kx+6与x轴、y轴分别交于点B、C,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0)(1)求k的值.(2)若P(x,y)是直线ℓ在第二象限内一个动点,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围.(3)当点P运动到什么位置时,△OPA的面积为9,并说明理由.3.如图①,过点(1,5)和(4,2)两点的直线分别与x轴、y轴交于A、B两点.(1)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.图中阴影部分(不包括边界)所含格点的个数有_________个(请直接写出结果);(2)设点C(4,0),点C关于直线AB的对称点为D,请直接写出点D的坐标_________;(3)如图②,请在直线AB和y轴上分别找一点M、N使△CMN的周长最短,在图②中作出图形,并求出点N的坐标.4.若直线y=mx+8和y=nx+3都经过x轴上一点B,与y轴分别交于A、C(1)填空:写出A、C两点的坐标,A_________,C_________;(2)若∠ABO=2∠CBO,求直线AB和CB的解析式;(3)在(2)的条件下若另一条直线过点B,且交y轴于E,若△ABE为等腰三角形,写出直线BE的解析式(只写结果).5.如图,在平面直角坐标系中,O为坐标原点,P(x,y),PA⊥x轴于点A,PB⊥y轴于点B,C(a,0),点E在y 轴上,点D,F在x轴上,AD=OB=2FC,EO是△AEF的中线,AE交PB于点M,﹣x+y=1.(1)求点D的坐标;(2)用含有a的式子表示点P的坐标;(3)图中面积相等的三角形有几对?6.如图,在平面直角坐标系中,直线l经过点A(2,﹣3),与x轴交于点B,且与直线平行.(1)求:直线l的函数解析式及点B的坐标;(2)如直线l上有一点M(a,﹣6),过点M作x轴的垂线,交直线于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.7.已知如图,直线y=﹣x+4与x轴相交于点A,与直线y=x相交于点P.(1)求点P的坐标;(2)求S△OPA的值;(3)动点E从原点O出发,沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,F的坐标为(a,0),矩形EBOF与△OPA重叠部分的面积为S.求:S与a之间的函数关系式.8.如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且A点的坐标是(1,0).(1)直线经过点C,且与x轴交于点E,求四边形AECD的面积;(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;(3)若直线l1经过点F()且与直线y=3x平行.将(2)中直线l沿着y轴向上平移1个单位,交x轴于点M,交直线l1于点N,求△NMF的面积.9.如图,直线y=x+6与x轴、y轴分别相交于点E、F,点A的坐标为(﹣6,0),P(x,y)是直线y=x+6上一个动点.(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;(2)当P运动到什么位置,△OPA的面积为,求出此时点P的坐标;(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.10.如图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.(1)若直线AB解析式为y=﹣2x+12,①求点C的坐标;②求△OAC的面积.(2)如图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.度的速度沿AB向点B运动,同时动点N从C点出发,以每秒2个单位长度的速度沿CO向O点运动.当其中一个动点运动到终点时,两个动点都停止运动.(1)求B点坐标;(2)设运动时间为t秒;①当t为何值时,四边形OAMN的面积是梯形OABC面积的一半;②当t为何值时,四边形OAMN的面积最小,并求出最小面积;③若另有一动点P,在点M、N运动的同时,也从点A出发沿AO运动.在②的条件下,PM+PN的长度也刚好最小,求动点P的速度.12.如图,在平面直角坐标系xoy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、b满足.(1)求直线AP的解析式;(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.。
专题四 一次函数中的三角形综合式问题 2020年中考数学冲刺难点突破 一次函数问题(解析版)

2020年中考数学冲刺难点突破一次函数问题专题四一次函数中的三角形综合式问题1、如图,直线y=﹣x+8与x轴、y轴分别交于点A和点B,M是OB的上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B′处.(1)求A、B两点的坐标;(2)求直线AM的表达式;(3)在x轴上是否存在点P,使得以点P、M、B′为顶点的三角形是等腰三角形,若存在,请直接写出所有点P的坐标;若不存在,请说明理由.解:(1)当x=0时,y=8,∴B(0,8),当y=0时,﹣x+8=0,x=6,∴A(6,0);(2)在Rt△AOB中,∠AOB=90°,OA=6,OB=8,∴AB=10,由折叠得:AB=AB'=10,∴OB'=10﹣6=4,设OM=a,则BM=B'M=8﹣a,由勾股定理得:a2+42=(8﹣a)2,a=3,∴M(0,3),设AM:y=kx+b,则,解得:,∴直线AM的解析式为:y=﹣x+3;(3)在x轴上存在点P,使得以点P、M、B′为顶点的三角形是等腰二角形,如图∵M(0,3),B′(﹣4,0),∴B′M=5,当PB′=B′M时,P1(﹣9,0),P2(1,0);当B′M=PM时,P3(4,0),当PB′=PM时,作BM的垂直平分线,交x轴于P4,交B′M与Q,易证得△P4B′Q∽△MB′O,则=,即=,∴P4B′=,∴OP4=4﹣=,∴P4(﹣,0),综上,P点的坐标为(﹣9,0)或(1,0)或(4,0)或(﹣,0).2、如图,在平面直角坐标系中,一次函数y=kx+3的图象与x轴、y轴分别交于点A,B,点A的坐标为(2,0).(1)求k的值;(2)已知点Q在第四象限,且到两坐标轴距离相等,若△AOB的面积是△AOQ面积的2倍,求点Q的坐标.解:(1)∵点A(2,0)在一次函数y=kx+3上,∴0=2k+3,得k=﹣1.5,即k的值是﹣1.5;(2)∵k=﹣1.5,∴一次函数解析式为y=﹣1.5x+3,∴当x=0时,y=3,即点B的坐标为(2,0),∴OB=3,∵点A(2,0),∴OA=2,∴△AOB的面积是==3,又∵△AOB的面积是△AOQ面积的2倍,∴△AOQ的面积是1.5,设点Q的坐标为(a,﹣a),∴1.5=,得a=1.5,∴点Q的坐标为(1.5,﹣1.5).3、如图,一次函数的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).(1)求m的值及l2的解析式;(2)若点D在x轴上,使得S△DOC=2S△BOC的值,请求出D点的坐标;(3)一次函数y=kx+1的图象为l3,且l1,l2,l3不能围成三角形,则k的值为.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得4=﹣m+5,解得m=2,∴C(2,4),设l2的解析式为y=ax,则4=2a,解得a=2,∴l2的解析式为y=2x;(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,在y=﹣x+5中,令x=0,则y=5;令y=0,则x=10,∴A(10,0),B(0,5),∴AO=10,BO=5,∵S△DOC=2S△BOC,∴OD×4=2×,∴OD=5,∴D点的坐标为(5,0)或(﹣5,0);(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,∴当l3经过点C(2,4)时,k=;当l2,l3平行时,k=2;当11,l3平行时,k=﹣;故k的值为或2或﹣,故答案为或2或﹣.4、如图,过点A(1,3)的一次函数y=kx+6(k≠0)的图象分别与x轴,y轴相交于B,C两点.(1)求k的值;(2)直线l与y轴相交于点D(0,2),与线段BC相交于点E.(i)若直线l把△BOC分成面积比为1:2的两部分,求直线l的函数表达式;(△)连接AD,若△ADE是以AE为腰的等腰三角形,求满足条件的点E的坐标.解:(1)将点A的坐标代入一次函数y=kx+6并解得:k=﹣3;(2)一次函数y=﹣3x+6分别与x轴,y轴相交于B,C两点,则点B、C的坐标分别为:(2,0)、(0,6);(i)S△BCO=OB×CO=2×6=6,直线l把△BOC分成面积比为1:2的两部分,则S△CDE=2或4,而S△CDE=×CD×x E=4×x E=2或4,则x E=1或2,故点E(1,3)或(2,0),将点E的坐标代入直线l表达式并解得:直线l的表达式为:y=±x+2;(△)设点E(m,﹣3m+6),而点A、D的坐标分别为:(1,3)、(0,2),则AE2=(m﹣1)2+(3﹣3m)2,AD2=2,ED2=m2+(4﹣3m)2,当AE=AD时,(m﹣1)2+(3﹣3m)2=2,解得:m=或;当AE=ED时,同理可得:m=;综上,点E的坐标为:(,)或(,)或(,).5、如图,在平面直角坐标系xOy中,直线l1:y=x+2与x轴交于点A,直线l2:y=3x﹣6与x轴交于点D,与l1相交于点C.(1)求点D的坐标;(2)在y轴上一点E,若S△ACE=S△ACD,求点E的坐标;(3)直线l1上一点P(1,3),平面内一点F,若以A、P、F为顶点的三角形与△APD全等,求点F的坐标.解:(1)△直线l2:y=3x﹣6与x轴交于点D,△令y=0,则3x﹣6=0,△x=2,△D(2,0);(2)如图1,△直线l1:y=x+2与x轴交于点A,△令y=0.△x+2=0,△x=﹣2,△A(﹣2,0),由(1)知,D(2,0),△AD=4,联立直线l1,l2的解析式得,,解得,,△C(4,6),△S△ACD=AD•|y C|=×4×6=12,△S△ACE=S△ACD,△S△ACE=12,直线l1与y轴的交点记作点B,△B(0,2),设点E(0,m),△BE=|m﹣2|,△S△ACE=BE•|x C﹣x A|=|m﹣2|×|4+2|=4|m﹣2|=12,△m=﹣2或m=6,△点E(0,﹣2)或(0,6);(3)如图2,△当点F在直线l1上方时,△以A、P、F为顶点的三角形与△APD全等,△△、当△APF'△△APD时,连接DF',BD,由(2)知,B(0,2),由(1)知,A(﹣2,0),D(2,0),△OB=OA=OD,△△ABO=△DBO=45°,△△ABD=90°,△DB△l1,△△APF'△△APD,△PF'=PD,AF'=AD,△直线l1是线段DF'的垂直平分线,△点D,F'关于直线l1对称,△DF'△l1,△DF'过点B,且点B是DF'的中点,△F'(﹣2,4),△、当△P AF△△APD时,△PF=AD,△APF=△P AD,△PF△AD,△点D(2,0),A(﹣2,6),△点D向左平移4个单位,△点P向左平移4个单位得,F(1﹣4,6),△F(﹣3,3),△当点F在直线l1下方时,△△P AF''△△APD,由△△知,△P AF△△APD,△△P AF△△P AF'',△AF=AF'',PF=PF'',△点F与点F'关于直线l1对称,△FF''△l1,△DF'△l1,△FF'△DF',而点F'(﹣2,4)先向左平移一个单位,再向下平移一个单位,△D(2,0),向左平移1个单位,再向下平移一个单位得F''(2﹣1,0﹣1),△F''(1,﹣1),即:点F的坐标为(﹣3,3)或(﹣2,4)或(1,﹣1).6、如图1,直线l:y=x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).(1)求出点A,点B的坐标.(2)P是直线AB上一动点,且△BOP和△COP的面积相等,求点P坐标.(3)如图2,平移直线l,分别交x轴,y轴于交于点A1B1,过点C作平行于y轴的直线m,在直线m 上是否存在点Q,使得△A1B1Q是等腰直角三角形?若存在,请直接写出所有符合条件的点Q的坐标.解:(1)设y=0,则x+2=0,解得:x=﹣4,设x=0,则y=2,△点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);(2)△点C(﹣2,0),点B(0,2),△OC=2,OB=2,△P是直线AB上一动点,△设P(m,m+2),△△BOP和△COP的面积相等,△×2|m|=2×(|m|+2),解得:m=±4,当m=﹣4时,点P与点A重合,△点P坐标为(4,4);(3)存在;理由:如图1,△当点B1是直角顶点时,△B1Q=B1A1,△△A1B1O+△QB1H=90°,△A1B1O+△OA1B1=90°,△△OA1B1=△QB1H,在△A1OB1和△B1HQ中,,△△A1OB1△△B1HQ(AAS),△B1H=A1O,OB1=HQ=2,△B1(0,﹣2)或(0,2),当点B1(0,﹣2)时,Q(﹣2,2),当点B1(0,2)时,△B(0,2),△点B1(0,2)(不合题意舍去),△直线AB向下平移4个单位,△点Q也向上平移4个单位,△Q(﹣2,2),△当点A1是直角顶点时,A1B1=A1Q,△直线AB的解析式为y=x+2,由平移知,直线A1B1的解析式为y=x+b,△A1(﹣2b,0),B1(0,b),△A1B12=4b2+b2=5b2,△A1B1△A1Q,△直线A1Q的解析式为y=﹣2x﹣4b△Q(﹣2,4﹣4b),△A1Q2=(﹣2b+2)2+(4﹣4b)2=20b2+40b+20,△20b2﹣40b+20=5b2,△b=2或b=,△Q(﹣2,﹣4)或(﹣2,);△当Q是直角顶点时,过Q作QH△y轴于H,△A1Q=B1Q,△△QA1C1+△A1QC=90°,△A1QC+△CQB1=90°,△△QA1C=△CQB1,△m△y轴,△△CQB1=△QB1H,△△QA1C=△QB1H在△A1QC与△B1QH中,,△△A1QC△△B1QH(AAS),△CQ=QH=2,B1H=A1C,△Q(﹣2,2)或(﹣2,﹣2),即:满足条件的点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,12)或(﹣2,).7、如图1,在平面直角坐标系xOy中,点A(2,0),点B(﹣4,3).(1)求直线AB的函数表达式;(2)点P是线段AB上的一点,当S△AOP:S△AOB=2:3时,求点P的坐标;(3)如图2,在(2)的条件下,将线段AB绕点A顺时针旋转120°,点B落在点C处,连结CP,求△APC 的面积,并直接写出点C的坐标.解:(1)设直线AB的函数表达式为y=kx+b,△点A(2,0),点B(﹣4,3),△,解得:,△直线AB的函数表达式为y=﹣x+1;(2)过B作BE△x轴于E,过P作PD△x轴于D,△PD△BE,△S△AOP:S△AOB=2:3,△=,△点B(﹣4,3),△BE=3,△PD△BE,△△APD△△ABE,△==,△PD=2,当y=2时,x=﹣2,△P(﹣2,2);(3)点A(2,0)、点B(﹣4,3),点P(﹣2,2),则AP=2,AB=CA=3,过点P作HP△AC交AC的延长线于点H,则AH=AP=,PH=AP sin60°=,△APC的面积=AC×PH=×3×=;设点C(x,y),则PC2=PH2+HC2=15+(+3)2=95=(x+2)2+(y﹣2)2…△,CA2=45=(x﹣2)2+y2…△,联立△△并解得:x=,y=,故点C(,).8、如图1,等腰直角三角形ABC中,△ACB=90°,CB=CA,直线DE经过点C,过A作AD△DE于点D,过B作BE△DE于点E,则△BEC△△CDA,我们称这种全等模型为“K型全等”.(不需要证明)【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD 的长;(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;(3)当k的取值变化时,点A随之在x轴上运动,将线段BA绕点B逆时针旋转90°得到BQ,连接OQ,求OQ长的最小值.解:(1)由题意可知:△BEO△△AOD(K型全等),△OE=AD,△k=﹣1,△y=﹣x+4,△B(0,4),△OB=4,△BE=3,△OE=,△AD=;(2)k=﹣时,y=﹣x+4,△A(3,0),△当BM△AB,且BM=AB时,过点M作MN△y轴,△△BMN△△ABO(AAS),△MN=OB,BN=OA,△MN=4,BN=3,△M(4,7);△当AB△AM,且AM=AB时,过点M作x轴垂线MK,△△ABO△△AMK(AAS),△OB=AK,OA=MK,△AK=4,MK=3,△M(7,3);△当AM△BM,且AM=BM时,过点M作MH△x轴,MG△y轴,△△BMG△△AHM(AAS),△BG=AH,GM=MH,△GM=MH,△4﹣MH=MH﹣3,△MH=,△M(,);综上所述:M(7,3)或M(4,7)或M(,);(3)当k>0时,AO=,过点Q作QS△y轴,△△ABO△△BQS(AAS),△BS=OA,SQ=OB,△Q(4,4﹣),△OQ=,△当k=1时,QO最小值为4;当k<0时,Q(4,4﹣),△OQ=,△当k=1时,QO最小值为4,与k<0矛盾,△OQ的最小值为4.9、定义:在平面直角坐标系中,对于任意P(x1,y1),Q(x2,y2),若点M(x,y)满足x=3(x1+x2),y=3(y1+y2),则称点M是点P,Q的“美妙点”.例如:点P(1,2),Q(﹣2,1),当点M(x,y)满足x=3×(1﹣2)=﹣3,y=3×(2+1)=9时,则点M(﹣3,9)是点P,Q的“美妙点”.(1)已知点A(﹣1,3),B(3,3),C(2,﹣2),请说明其中一点是另外两点的“美妙点”;(2)如图,已知点D是直线y=+2上的一点.点E(3,0),点M(x,y)是点D、E的“美妙点”.△求y与x的函数关系式;△若直线DM与x轴相交于点F,当△MEF为直角三角形时,求点D的坐标.解:(1)△3×(﹣1+2)=3,3×(3﹣2)=3,△点B是A、C的“美妙点”;(2)设点D(m,m+2),△△M是点D、E的“美妙点”.△x=3(3+m)=9+3m,y=3(0+m+2)=m+6,故m=x﹣3,△y=(x﹣3)+6=x+3;△由△得,点M(9+3m,m+6),如图1,当△MEF为直角时,则点M(3,4),△9+3m=3,解得:m=﹣2;△点D(﹣2,);当△MFE是直角时,如图2,则9+3m=m,解得:m=﹣,△点D(﹣,);当△EMF是直角时,不存在,综上,点D(﹣2,)或(﹣,).10、在平面直角坐标系xOy中,图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图1,矩形ABCD为△DEF的投影矩形,其投影比k=.(1)若点A(1,1),B(2,3),则△OAB投影比k的值为;(2)若点M(﹣2,0),点N(2,1)且△MNP投影比k=,则点P的坐标可能是(填写序号);△(﹣1,3);△(2,﹣2);△(3,3);△(0,2).(3)已知点C(4,0),在函数y=2x﹣4(其中x<2)的图象上有一点D,若△OCD的投影比k=3,求点D的坐标.解:(1)如图2,过点B作BC△x轴于点C,作BD△y轴于点D,则矩形OCBD为△OAB的投影矩形,△点B(2,3),△OC=2,BC=3,△△OAB投影比k的值=.(2)如图3,△点P的坐标为(﹣1,3)时,△MNP投影比k=;△点P的坐标为(2,﹣2)时,△MNP投影比k=;△点P的坐标为(3,3)时,△MNP投影比k=;△点P的坐标为(0,2)时,△MNP投影比k==2.则点P的坐标可能是△(﹣1,3);△(2,﹣2);(3)△点D为函数y=2x﹣4(其中x<2)的图象上的点,设点D坐标为(x,2x﹣4)(x<2).分以下两种情况:△当0≤x≤2时,如图4所示,作投影矩形OMNC.△OC≥OM,△k====3,解得x=,△D(,﹣);△当x<0时,如图5所示,作投影矩形MDNC.△点D坐标为(x,2x﹣4),点M点坐标为(x,0),△DM=|2x﹣4|=4﹣2x,MC=4﹣x,△x<0,△DM>CM,△k===3,解得x=8.△当x<0时,满足条件的点D不存在.综上所述,点D的坐标为D(,﹣).故答案为:;△△.11、阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图△:在△ABC中,△ACB=90°,AC=BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:△ADC△△CEB.(1)探究问题:如果AC≠BC,其他条件不变,如图△,可得到结论;△ADC△△CEB.请你说明理由.(2)学以致用:如图△,在平面直角坐标系中,直线y=x与直线CD交于点M(2,1),且两直线夹角为α,且tanα=,请你求出直线CD的解析式.(3)拓展应用:如图△,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接BE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC,PD.若△DPC 为直角三角形时,请你探究并直接写出BE的长.解:(1)理由:△△ACB=90°,△△ACD=△BCE=90°,又△△ADC=90°,△△ACD+△DAC=90°,△△BCE=△DAC,且△ADC=△BEC=90°,△△ADC△△CEB;(2)如图,过点O作ON△OM交直线CD于点N,分别过M、N作ME△x轴NF△x轴,由(1)可得:△NFO△△OEM,△,△点M(2,1),△OE=2,ME=1,△tanα==,△,△NF=3,OF=,△点N(﹣,3),△设直线CD表达式:y=kx+b,△△△直线CD的解析式为:y=﹣x+;(3)当△CDP=90°时,如图,过点P作PH△BC,交BC延长线于点H,△△ADC+△CDP=180°,△点A,点D,点P三点共线,△△BAP=△B=△H=90°,△四边形ABHP是矩形,△AB=PH=3,△将线段AE绕点E顺时针旋转90°,△AE=EP,△AEP=90°,△△AEB=△PEH=90°,且△BAE+△AEB=90°,△△BAE=△PEH,且△B=△H=90°,AE=EP,△△ABE△△EHP(AAS),△BE=PH=3,当△CPD=90°时,如图,过点P作PH△BC,交BC延长线于点H,延长HP交AD的延长线于N,则四边形CDNH是矩形,△CD=NH=3,DN=CH,设BE=x,则EC=5﹣x,△将线段AE绕点E顺时针旋转90°,△AE=EP,△AEP=90°,△△AEB=△PEH=90°,且△BAE+△AEB=90°,△△BAE=△PEH,且△B=△EHP=90°,AE=EP,△△ABE△△EHP(AAS),△PH=BE=x,AB=EH=3,△PN=3﹣x,CH=3﹣(5﹣x)=x﹣2=DN,△△DPC=90°,△△DPN+△CPH=90°,且△CPH+△PCH=90°,△△PCH=△DPN,且△N=△CHP=90°,△△CPH△△PDH,△,△△x=△点P在矩形ABCD外部,△x=,△BE=,综上所述:当BE的长为3或时,△DPC为直角三角形.。
人教版数学八年级上册重点题型

人教版数学八年级上册重点题型一、三角形全等证明题型。
题型1:已知:在△ABC和△DEF中,AB = DE,∠A = ∠D,AC = DF。
求证:△ABC≌△DEF。
解析:在△ABC和△DEF中,已知AB = DE,∠A = ∠D,AC = DF。
根据三角形全等判定定理中的“边角边”(SAS),即两边及其夹角对应相等的两个三角形全等。
所以可以得出△ABC≌△DEF。
题型2:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE 交AC于F。
求证:∠AEF = ∠EAF。
解析:延长AD到G,使DG = AD,连接BG。
因为AD是BC边上的中线,所以BD = CD。
在△BDG和△CDA中,BD = CD,∠BDG=∠CDA(对顶角相等),DG = DA。
所以△BDG≌△CDA(SAS)。
则BG = AC,∠G = ∠EAF。
又因为BE = AC,所以BE = BG,所以∠G = ∠AEF。
所以∠AEF = ∠EAF。
二、等腰三角形性质与判定题型。
题型3:已知等腰三角形的一个内角为70°,求这个等腰三角形的另外两个内角的度数。
解析:当70°角为顶角时,设底角为x。
根据等腰三角形两底角相等和三角形内角和为180°,可得2x+70° = 180°,解得x = 55°。
所以另外两个内角都是55°。
当70°角为底角时,另一个底角也是70°,则顶角为180° - 70°×2 = 40°。
所以另外两个内角为70°和40°。
题型4:在△ABC中,AB = AC,D是AC上一点,且AD = BD = BC。
求∠A的度数。
解析:设∠A=x。
因为AD = BD,所以∠ABD = ∠A=x。
则∠BDC = ∠A+∠ABD = 2x。
又因为BD = BC,所以∠C = ∠BDC = 2x。
一次函数与全等

一次函数与几何全等问题
学习目标:1.能利用几何条件构造全等
2.能将几何问题转化为代数问题
学习重难点:重点:1.利用已知条件,找三角形全等
2.将线段转化为点坐标,利用一次函数求解
难点:构造全等,将几何问题转化为代数问题
学习过程:
一.知识回顾
1.待定系数法求直线解析式
2.直线与x 轴、y 轴的交点坐标
3.相交直线求点坐标
二.例题讲解
如图,直线y=2x -4与x 轴交于点A ,与y 轴交于点B ,与直线y=21x 交于点C ,E 为射线CO 上一点,且y 轴平分∠EBC ,求点E 的坐标。
三.练习
如图,在正方形OBAC 中,A (-2,2),B 、C 分别在x 轴、y 轴上,D (0,1),CE ⊥BD 于E ,求E 点的坐标。
x
y A O E C B
四.拓展
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,且C(-2,0),直线y=kx-k 与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF。
(1)求直线BC的解析式及点D的坐标;
(2)求k的值Array五.小结:
几何图形→线段→点坐标→一次函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
27题精选1(2011-11-27)
1、直线y=-2x+2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC=OB (1)求AC 的解析式;
(2)在OA 的延长线上任取一点P,作PQ ⊥BP,交直线AC 于Q,试探究BP 与PQ 的数量关系,并证明你的结论。
(3)在(2)的前提下,作PM ⊥AC 于M,BP 交AC 于N,下面两个结论:①(MQ+AC)/PM 的值不变;②(MQ-AC)/PM 的值不变,期中只有一个正确结论,请选择并加以证明。
2、如图①所示,直线L :5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、B 两点。
(1)当OA=OB 时,试确定直线L 的解析式;
(2)在(1)的条件下,如图②所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM ⊥OQ 于M ,BN ⊥OQ 于N ,若AM=4,BN=3,求MN 的长。
(3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点,如图③。
问:当点B 在 y 轴正半轴上运动时,试猜想PB 的长是否为定值,若是,请求出其值,若不是,说明理由。
x
y
o B
A C
P
Q
x
y
o B
A C
P
Q
M
第2题图① 第2题图② 第2题图③
3、如图,直线1l 与x 轴、y 轴分别交于A 、B 两点,直线2l 与直线1l 关于x 轴对称,已知直线1l 的解析式为3y x =+, (1)求直线2l 的解析式;
(2)过A 点在△ABC 的外部作一条直线3l ,过点B 作BE ⊥3l 于E,过点C 作CF ⊥3l 于F 分别,请画出图形并求证:BE +CF =EF
(3)△ABC 沿y 轴向下平移,AB 边交x 轴于点P ,过P 点的直线与AC 边的延长线相交于点Q ,与y 轴相交与点M ,且BP =CQ ,在△ABC 平移的过程中,①OM 为定值;②MC 为定值。
在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值。
4、如图,在平面直角坐标系中,A (a ,0),B (0,b ),且a 、b 满足.
(1)求直线AB 的解析式;
(2)若点M 为直线y =mx 上一点,且△ABM 是以AB 为底的等腰直角三角形,求m 值;
(3)过A 点的直线
交y 轴于负半轴于P ,N 点的横坐标为-1,过N 点的直
线交AP 于点M ,试证明
的值为定值.
C
B
A
l 2
l 1
x
y
C B A 0x y M P
C
B
A 0x y
5、如图,直线AB:y=-x-b分别与x、y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴
于C,且OB:OC=3:1。
(1)求直线BC的解析式:
(2)直线EF:y=kx-k(k≠0)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,说明理由?
(3)如图,P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由。
6、如图l,y=-x+6与坐标轴交于A、B两点,点C在x轴负半轴上,S△OBC=S△AOB.
(1)求直线BC的解析式;
(2)直线EF:y=kx-k交AB于E点,与x轴交于D点,交BC的延长线于点F,且S△BED=S△FBD,求k的值;
(3)如图2,M(2,4),点P为x轴上一动点,AH⊥PM,垂足为H点.取HG=HA,连CG,当P点运动时,∠CGM大小是否变化,并给予证明.
7、在平面直角坐标系中,一次函数y=ax+b的图像过点B(-1,),与x轴交于点A(4,0),与y轴交于点C,与直线y=kx交于点P,且PO=PA
(1)求a+b的值;
(2)求k的值;
(3)D为PC上一点,DF⊥x轴于点F,交OP于点E,若DE=2EF,求D点坐标. 8、如图,在平面直角坐标系中,直线y=2x+2交y,轴交于点A,交x轴于点B,将A绕B点逆时针旋转90°到点C.
(1)求直线AC的解析式;
(2)若CD两点关于直线AB对称,求D点坐标;
(3)若AC交x轴于M点P(,m)为BC上一点,在线段BM上是否存在点N,使PN平分△BCM的面积?若存在,求N点坐标;若不存在,说明理由.
9、如图,直线AB 交x 轴正半轴于点A (a ,0),交y 轴正半轴于点
B (0, b ),且a 、b 满足4 a + |4-b |=0 (1)求A 、B 两点的坐标;
(2)D 为OA 的中点,连接BD ,过点O 作OE ⊥BD 于F ,交AB 于E ,求证∠BDO =∠EDA ;
(3)如图,P 为x 轴上A 点右侧任意一点,以BP 为边作等腰Rt △PBM ,其中PB =PM ,直线
MA 交y 轴于点Q ,当点P 在x 轴上运动时,线段OQ 的长是否发生变化?若不变,求其值;若变化,求线段OQ 的取值范围.
10、如图,平面直角坐标系中,点A 、B 分别在x 、y 轴上,点B 的坐标为(0,1),∠BAO =30°.
(1)求AB 的长度;
(2) 以AB 为一边作等边△ABE ,作OA 的垂直平分线MN 交AB 的垂线AD 于点D .求证:BD =OE .
D
E
N
M B
O
x
y
A
(3)在(2)的条件下,连结DE 交AB 于F .求证:F 为DE 的中点.
D
E
B
O
x
y
F A
A
B
O D
E
F
y x
A
B
O
M
P
Q
x
y
1. 2. 已知△ABC,分别以AB,AC为边在△ABC外侧作△ABD和△ACE,
使AB=AD,AC=AE且∠BAD=∠EAC,BE与CD交于点P.
(1)求证:CD=BE
(2)当∠DAB=60°时,求证PD=PA+PB
3. 直线m//n ,点A 、B 分别在直线m 、n 上,点P 在直线m 上,AP=
AB 3
1
, 连接BP, 以PB 为一边在PB 右侧做等边∆BPC, 连接AC, 过点P 作n PD ⊥,垂足位点D ,︒=∠60ABD .
(1)当点P 在点A 的右侧时(如图1),求证AC BD 8
5
=
(2)当点P 在点A 的左侧时,线段BD 与AC 之间的数量关系为
(图1)
m n
A B C
D P。
