采用邻接表存储结构-编写一个求无向图的连通分量个数的算法
中南大学数据结构与算法第7章图课后作业答案分解

第7章图(基础知识)习题练习答案7.1 在图7.23所示的各无向图中:(1)找出所有的简单环。
(2)哪些图是连通图?对非连通图给出其连通分量。
(3)哪些图是自由树(或森林)?答:(1)所有的简单环:(同一个环可以任一顶点作为起点)(a)1231(b)无(c)1231、2342、12341(d)无(2)连通图:(a)、(c)、(d)是连通图,(b)不是连通图,因为从1到2没有路径。
具体连通分量为:(3)自由树(森林):自由树是指没有确定根的树,无回路的连通图称为自由树:(a)不是自由树,因为有回路。
(b)是自由森林,其两个连通分量为两棵自由树。
(c)不是自由树。
(d)是自由树。
7.2 在图7.24(下图)所示的有向图中:(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
(3) 请给出每个顶点的度,入度和出度。
(4) 请给出其邻接表、邻接矩阵及逆邻接表。
答:(1)该图是强连通的,所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径。
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4、另包括所有有向环,有向环如下:v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)(3)每个顶点的度、入度和出度:D(v1)=3ID(v1)=1OD(v1)=2D(v2)=2 ID(v2)=1OD(v2)=1D(v3)=3 ID(v3)=2OD(v3)=1D(v4)=2 ID(v4)=1OD(v4)=1(4)邻接表:(注意边表中邻接点域的值是顶点的序号,这里顶点的序号是顶点的下标值-1)vertex firstedge next┌─┬─┐┌─┬─┐┌─┬─┐0│v1│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘1│v2│─→│ 2│∧│├─┼─┤├─┼─┤2│v3│─→│ 0│∧│├─┼─┤├─┼─┤3│v4│─→│ 2│∧│└─┴─┘└─┴─┘逆邻接表:┌─┬─┐┌─┬─┐0│v1│─→│ 2│∧│├─┼─┤├─┼─┤1│v2│─→│ 0│∧│├─┼─┤├─┼─┤┌─┬─┐2│v3│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘3│v4│─→│ 0│∧│└─┴─┘└─┴─┘邻接矩阵:0 1 0 10 0 1 01 0 0 00 0 1 07.3 假设图的顶点是A,B...,请根据下述的邻接矩阵画出相应的无向图或有向图。
计算机学科专业基础综合数据结构-图(二)_真题-无答案

计算机学科专业基础综合数据结构-图(二)(总分100,考试时间90分钟)一、单项选择题(下列每题给出的4个选项中,只有一个最符合试题要求)1. 具有6个顶点的无向图至少应有______条边才能确保是一个连通图。
A.5 B.6 C.7 D.82. 设G是一个非连通无向图,有15条边,则该图至少有______个顶点。
A.5 B.6 C.7 D.83. 下列关于无向连通图特性的叙述中,正确的是______。
①所有顶点的度之和为偶数②边数大于顶点个数减1③至少有一个顶点的度为1A.只有① B.只有② C.①和② D.①和③4. 对于具有n(n>1)个顶点的强连通图,其有向边的条数至少是______。
A.n+1B.nC.n-1D.n-25. 下列有关图的说法中正确的是______。
A.在图结构中,顶点不可以没有任何前驱和后继 B.具有n个顶点的无向图最多有n(n-1)条边,最少有n-1条边 C.在无向图中,边的条数是结点度数之和 D.在有向图中,各顶点的入度之和等于各顶点的出度之和6. 对于一个具有n个顶点和e条边的无向图,若采用邻接矩阵表示,则该矩阵大小是______,矩阵中非零元素的个数是2e。
A.n B.(n-1)2 C.n-1 D.n27. 无向图的邻接矩阵是一个______。
A.对称矩阵 B.零矩阵 C.上三角矩阵 D.对角矩阵8. 从邻接矩阵可知,该图共有______个顶点。
如果是有向图,该图共有4条有向边;如果是无向图,则共有2条边。
A.9 B.3 C.6 D.1 E.5 F.4 G.2 H.09. 下列说法中正确的是______。
A.一个图的邻接矩阵表示是唯一的,邻接表表示也唯一 B.一个图的邻接矩阵表示是唯一的,邻接表表示不唯一 C.一个图的邻接矩阵表示不唯一,邻接表表示唯一 D.一个图的邻接矩阵表示不唯一,邻接表表示也不唯一10. 用邻接表存储图所用的空间大小______。
A.与图的顶点数和边数都有关 B.只与图的边数有关 C.只与图的顶点数有关 D.与边数的二次方有关11. 采用邻接表存储的图的深度优先搜索算法类似于二叉树的______,广度优先搜索算法类似于二叉树的层次序遍历。
数据结构作业答案第章图作业答案

第7章 图 自测卷解答 姓名 班级一、单选题(每题1分,共16分) 前两大题全部来自于全国自考参考书!( C )1. 在一个图中,所有顶点的度数之和等于图的边数的 倍。
A .1/2 B. 1 C. 2 D. 4 (B )2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的 倍。
A .1/2 B. 1 C. 2 D. 4 ( B )3. 有8个结点的无向图最多有 条边。
A .14 B. 28 C. 56 D. 112 ( C )4. 有8个结点的无向连通图最少有 条边。
A .5 B. 6 C. 7 D. 8 ( C )5. 有8个结点的有向完全图有 条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列C. 树D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列C. 树D. 图 ( )8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是( D )9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 1 3 4 2 5 6 ( )10. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是A . 0 2 4 3 6 5 1 B. 0 1 3 6 4 2 5 C. 0 4 2 3 1 5 6 D. 0 1 3 4 2 5 6 (建议:0 1 2 3 4 5 6) ( C )11. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是A . 0 2 4 3 1 6 5 B. 0 1 3 5 6 4 2 C. 0 1 2 3 4 6 5 D. 0 1 2 3 4 5 6A .0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 4 2 3 1 6 5D. 0 3 6 1 5 4 2建议:先画出图,再深度遍历⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110( A )12. 已知图的邻接表如下所示,根据算法,则从顶点0出发不是深度优先遍历的结点序列是A.0 1 3 2 B. 0 2 3 1C. 0 3 2 1D. 0 1 2 3(A)14. 深度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(D)15. 广度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(A)16. 任何一个无向连通图的最小生成树A.只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1. 图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
第7章自测题与答案

第7章图自测卷解答姓名班级题号一二三四五总分题分1620241030100得分一、单选题(每题1分,共16分)(C)1.在一个图中,所有顶点的度数之和等于图的边数的倍。
A.1/2B.1C.2D.4(B)2.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A.1/2B.1C.2D.4(B)3.有8个结点的无向图最多有条边。
A.14B.28C.56D.112(C)4.有8个结点的无向连通图最少有条边。
A.5B.6C.7D.8(C)5.有8个结点的有向完全图有条边。
A.14B.28C.56D.112(B)6.用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A.栈B.队列C.树D.图(A)7.用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A.栈B.队列C.树D.图(C)8.已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是01111011001001A.02431561000100B.0136542C.042316511001101011010D.03615420001101建议:01342561100010(D)9.已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A.0243156B.0135642C.0423165D.0134256(B)10.已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是A.0243651B.0136425C.0423156D.0134256(建议:0123456)(C)11.已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按广度优先遍历的结点序列是A.0243165B.0135642C.0123465D.01234561(D)12.已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是A.0132B.0231C.0321D.0123(A)13.已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是A.0321B.0123C.0132D.0312(A)14.深度优先遍历类似于二叉树的A.先序遍历B.中序遍历C.后序遍历D.层次遍历(D)15.广度优先遍历类似于二叉树的A.先序遍历B.中序遍历C.后序遍历D.层次遍历(A)16.任何一个无向连通图的最小生成树A.只有一棵B.一棵或多棵C.一定有多棵D.可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1.图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
图练习与答案
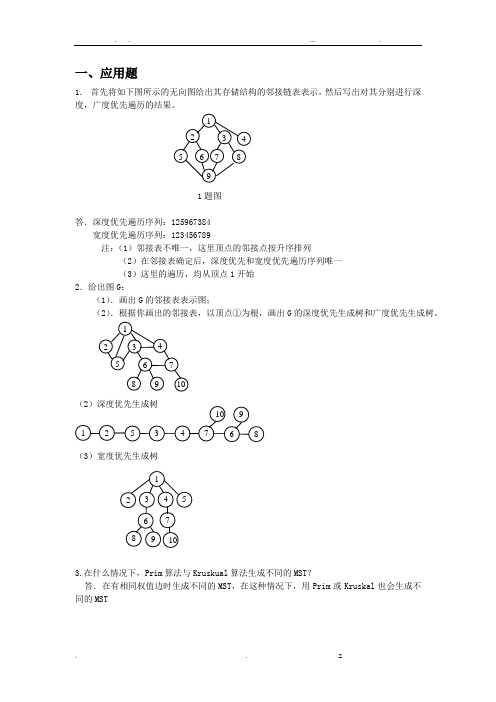
一、应用题1.首先将如下图所示的无向图给出其存储结构的邻接链表表示,然后写出对其分别进行深度,广度优先遍历的结果。
1题图答.深度优先遍历序列:125967384宽度优先遍历序列:123456789注:(1)邻接表不唯一,这里顶点的邻接点按升序排列(2)在邻接表确定后,深度优先和宽度优先遍历序列唯一(3)这里的遍历,均从顶点1开始2.给出图G:(1).画出G的邻接表表示图;(2).根据你画出的邻接表,以顶点①为根,画出G的深度优先生成树和广度优先生成树。
(3)宽度优先生成树3.在什么情况下,Prim算法与Kruskual算法生成不同的MST?答.在有相同权值边时生成不同的MST,在这种情况下,用Prim或Kruskal也会生成不同的MST4.已知一个无向图如下图所示,要求分别用Prim 和Kruskal 算法生成最小树(假设以①为起点,试画出构造过程)。
答.Prim 算法构造最小生成树的步骤如24题所示,为节省篇幅,这里仅用Kruskal 算法,构造最小生成树过程如下:(下图也可选(2,4)代替(3,4),(5,6)代替(1,5))5.G=(V,E)是一个带有权的连通图,则:(1).请回答什么是G 的最小生成树; (2).G 为下图所示,请找出G 的所有最小生成树。
28题图答.(1)最小生成树的定义见上面26题 (2)最小生成树有两棵。
(限于篇幅,下面的生成树只给出顶点集合和边集合,边以三元组(Vi,Vj,W )形式),其中W 代表权值。
V (G )={1,2,3,4,5} E1(G)={(4,5,2),(2,5,4),(2,3,5),(1,2,7)};E2(G)={(4,5,2),(2,4,4),(2,3,5),(1,2,7)}6.请看下边的无向加权图。
(1).写出它的邻接矩阵。
(2).按Prim 算法求其最小生成树,并给出构造最小生成树过程中辅助数组的各分量值。
辅助数组各分量值:7.已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa)、伦敦(L) 、东京(T) 、墨西哥(M),下表给定了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)(1).画出这六大城市的交通网络图;(2).画出该图的邻接表表示法;(3).画出该图按权值递增的顺序来构造的最小(代价)生成树.8.已知顶点1-6和输入边与权值的序列(如右图所示):每行三个数表示一条边的两个端点和其权值,共11行。
图练习与答案
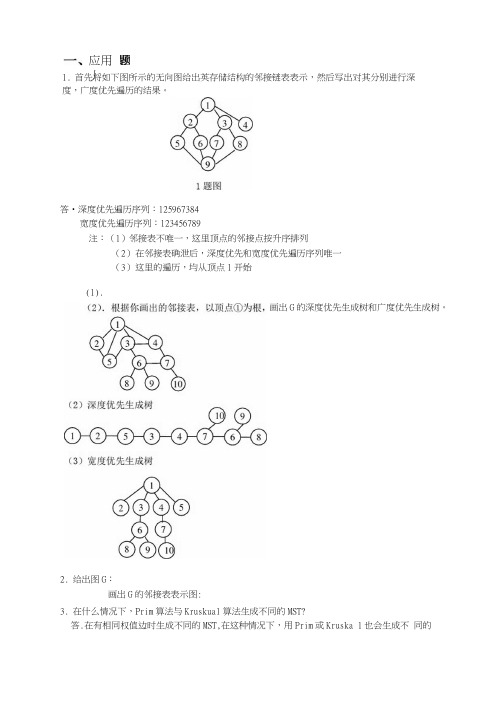
1. 首先将如下图所示的无向图给出英存储结构的邻接链表表示,然后写出对其分别进行深度,广度优先遍历的结果。
答•深度优先遍历序列:125967384宽度优先遍历序列:123456789注:(1)邻接表不唯一,这里顶点的邻接点按升序排列(2) 在邻接表确泄后,深度优先和宽度优先遍历序列唯一 (3) 这里的遍历,均从顶点1开始 2. 给出图G :画岀G 的邻接表表示图:3. 在什么情况下,Prim 算法与Kruskual 算法生成不同的MST?答.在有相同权值边时生成不同的MST,在这种情况下,用Prim 或Kruska 1也会生成不 同的应用丿 画出G 的深度优先生成树和广度优先生成树。
(1).HST4・已知一个无向图如下图所示,要求分别用Prim和Kruskal算法生成最小树(假设以①为起点,试画出构适过程)。
答.Prim算法构造最小生成树的步骤如24题所示,为节省篇幅,这里仅用Kruskal算法, 构造最小生成树过程如下:(下图也可选(2, 4)代替(3, 4), (5, 6〉代替⑴5))5.G=(V,E)是一个带有权的连通图,则:(1). ifi回答什么是G的最小生成树:(2). G为下图所示,请找出G的所有最小生成树。
答.(1)最小生成树的左义见上而26题(2)最小生成树有两棵。
邙艮于篇幅,下而的生成树只给岀顶点集合和边集合,边以三元组(Vi,Vj,W)形式),其中 W代表权值。
V (G) ={1, 2, 3, 4, 5} E1(G) = {(4, 5, 2), (2, 5, 4), (2, 3, 5), (1, 2,7) }:E2(G)={(4, 5, 2), (2, 4, 4), (2, 3, 5), (b 2、7) }6.请看下边的无向加权图。
(1).写出它的邻接矩阵。
(2).按Prim算法求其最小生成树, 并给出构造最小生成树过程中辅助数组的各分量值。
辅助数组各分量值:7.已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa).伦敦(L)、东京仃).墨西哥(M), 下表给泄了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)(1) .画岀这六大城市的交通网络图;(2) .画出该图的邻接表表示法;(3) .画岀该图按权值递增的顺序来构造的最小(代价)生成树.8.已知顶点1-6和输入边与权值的序列(如右图所示):每行三个数表示一条边的两个端点和貝权值,共11行。
算法与数据结构重考复习题(0910)

i列1的元素之和 )。对于含n个顶点和e条边的图,采用邻接矩阵表示的空间复杂度为( O(n2) )。连通图
是指图中任意两个顶点之间(都连通的无向图 )。一个有n个顶点的无向连通图,它所包含的连通分量个数最
保持青春的秘诀,是有一颗不安分的心。
算法与数据结构重考复习题(0910)
一、单选题(斜体为答案)
1.数据结构被形式地定义为(D,R),其中D 是
A. 算法 B. 操作的集合 C. 数据元素的集合 D. 数据关系的集合
2.顺序表是线性表的
A. 顺序存储结构 B. 链式存储结构 C. 索引存储结构 D. 散列存储结构
5.已知栈的输入序列为1,2,3....,n,输出序列为a1,a2,...,an,a2=n的输出序列共有(n-1)种输出序列。
队列的特性是先入先出,栈的特性是(后入先出)。如果以链栈为存储结构,则出栈操作时必须判别(栈空 )。与顺序栈相比,链栈有一个明显的优势是( 不易出现栈满 )。
6.循环队列采用数组data[1..n]来存储元素的值,并用front和rear分别作为其头尾指针。为区分队列的满和空,约定:队中能够存放的元素个数最大为(n-l),也即至少有一个元素空间不用,则在任意时刻,至少可以知道一个空的元素的下标是(front) ;入队时,可用语句(rear=rear+1%n)求出新元素在数组data中的下标。
(3)双向链表:q=p->prior; temp=q->data; q->data=p->data;p->data=temp;
2.内存中一片连续空间(不妨设地址从1到m),提供给两个栈S1和S2使用,怎样分配这部分存储空间,使得对任意一个栈,仅当这部分全满时才发生上溢。(为了尽量利用空间,减少溢出的可能,可采用栈顶相向,栈底分设两端的存储方式,这样,对任何一个栈,仅当整个空间全满时才会发生上溢。)
数据结构(第二版)习题

第一章绪论一、问答题1.什么是数据结构?2.叙述四类基本数据结构的名称与含义。
3.叙述算法的定义与特性。
4.叙述算法的时间复杂度。
5.叙述数据类型的概念。
6. 叙述线性结构与非线性结构的差别。
7.叙述面向对象程序设计语言的特点。
8.在面向对象程序设计中,类的作用是什么?9.叙述参数传递的主要方式及特点。
10.叙述抽象数据类型的概念。
二、判断题(在各题后填写“√”或“×”)1.线性结构只能用顺序结构来存放,非线性结构只能用非顺序结构来存放。
()2.算法就是程序。
()3. 在高级语言(如C或PASCAL)中,指针类型是原子类型。
()三、计算下列程序段中X=X+1的语句频度for(i=1;i<=n;i++)for(j=1;j<=i;j++)for(k=1;k<=j;k++)x=x+1;四、试编写算法,求一元多项式Pn(x)=a0+a1x+a2x2+a3x3+…anxn的值Pn(x0),并确定算法中的每一语句的执行次数和整个算法的时间复杂度,要求时间复杂度尽可能小,规定算法中不能使用求幂函数。
注意:本题中的输入ai(i=0,1,…,n),x和n,输出为Pn(x0)。
通常算法的输入和输出可采用下列两种方式之一:(1)通过参数表中的参数显式传递。
(2)通过全局变量隐式传递。
试讨论这两种方法的优缺点,并在本题算法中以你认为较好的一种方式实现输入和输出。
第二章线性表2.1描述以下三个概念的区别:头指针,头结点,首元素结点。
2.2填空:(1)在顺序表中插入或删除一个元素,需要平均移动____元素,具体移动的元素个数与__插入或删除的位置__有关。
(2)在顺序表中,逻辑上相邻的元素,其物理位置______相邻。
在单链表中,逻辑上相邻的元素,其物理位置______相邻。
(3)在带头结点的非空单链表中,头结点的存储位置由______指示,首元素结点的存储位置由______指示,除首元素结点外,其它任一元素结点的存储位置由____指示。
数据结构_图_采用邻接矩阵存储,构造无向图

1.采用邻接矩阵(邻接表)存储,构造无向图(网)输入:顶点数、边数、顶点信息、边信息输出:图的顶点,图的边邻接矩阵(数组表示法)处理方法:用一个一维数组存储图中顶点的信息,用一个二维数组(称为邻接矩阵)存储图中各顶点之间的邻接关系。
假设图G=(V,E)有n个顶点,则邻接矩阵是一个n×n 的方阵,定义为:如果(vi,vj)属于边集,则edges[i][j]=1,否则edges[i][j]=0。
邻接表存储的处理方法:对于图的每个顶点vi,将所有邻接于vi的顶点链成一个单链表,称为顶点vi的边表(对于有向图则称为出边表),所有边表的头指针和存储顶点信息的一维数组构成了顶点表。
程序代码:#include<iostream>using namespace std;#define MAX_VERTEX_NUM 20 //最大顶点个数#define OK 1typedef int Status;//图的数组(邻接矩阵)存储表示typedef struct ArcCell { // 弧的定义int adj; // VRType是顶点关系类型。
// 对无权图,用1或0表示相邻否;// 对带权图,则为权值类型。
int *info; // 该弧相关信息的指针} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct { // 图的定义char vexs[MAX_VERTEX_NUM];//顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数、弧数} MGraph;int LocateV ex(MGraph G, char v){int a;for (int i = 0; i <= G.vexnum; i++){if (G.vexs[i] == v)a= i;}return a;}Status CreateUDN(MGraph &G) { //采用邻接矩阵表示法,构造无向网Gint i, j, k, w;char v1, v2;cout <<"输入顶点数,边数:"<< endl;cin >> G.vexnum >> G.arcnum;//IncInfo为0,表示各弧无信息cout <<"各顶点分别为:"<< endl;for (i = 0; i<G.vexnum; i++)cin >> G.vexs[i]; //构造顶点向量for (i = 0; i<G.vexnum; i++) //初始化邻接矩阵for (j = 0; j<G.vexnum; j++){G.arcs[i][j].adj =NULL;}cout <<"顶点信息、边信息:"<< endl;for (k = 0; k<G.arcnum; k++) { //构造邻接矩阵cin >> v1 >> v2 >> w; //输入一条边依附的顶点及权值i = LocateV ex(G, v1); j = LocateV ex(G, v2);G.arcs[i][j].adj = w;G.arcs[j][i] = G.arcs[i][j];} return OK;} //CreateUDN (p162 算法7.2)Status printf1(MGraph G){cout <<"该图的顶点分别为:";for (int i = 0; i<G.vexnum; i++)cout << G.vexs[i] <<"";return OK;}Status printf2(MGraph G){cout <<"该图的边为:";for (int i = 1; i<G.vexnum; i++) //初始化邻接矩阵for (int j = 0; j<i; j++){if (G.arcs[i][j].adj !=NULL)cout << G.vexs[j]<< G.vexs[i] <<"," ;}return OK;}int main(){MGraph G;CreateUDN(G);printf1(G);cout << endl;printf2(G);cout << endl;system("pause");return 0;}。
计算机专业基础综合数据结构图历年真题试卷汇编7_真题无答案

计算机专业基础综合数据结构(图)历年真题试卷汇编7(总分62, 做题时间90分钟)7. 设计题1.已知连通图如下:(1)若从顶点B出发对该图进行遍历,在(1)的基础上分别给出本图的按深度优先搜索和按广度优先搜索的顶点序列;(2)写出按深度优先搜索的递归程序。
【厦门大学200l三(12%分)】SSS_TEXT_QUSTI2.设计算法以实现对无向图G的深度遍历,要求:将每一个连通分量中的顶点以一个表的形,式输出。
例如,下图的输出结果为:(1,3)(2,6,7,4,5,8)(9,10)。
注:本算法中可以调用以下几个函数:firstadj(g,1,)——返回图g中顶点v的第一个邻接点的号码,若不存在,则返回0。
nextadj(g,v,w)——返回图g中顶点v的邻接点中处于w之后的邻接点的号码,若不存在,则返回0。
nodes(g)——返回图g中的顶点数。
【合肥工业大学2000五、4(8分)】SSS_TEXT_QUSTI3.请设计一个图的抽象数据类型(只需要用类Pascal或类C/C++语言给出其主要功能函数或过程的接口说明,不需要指定存储结构,也不需要写出函数或过程的实现方法),利用抽象数据类型所提供的函数或过程编写图的广度优先周游算法。
算法不应该涉及具体的存储结构,也不允许不通过函数或过程而直接引用图结构的数据成员,抽象数据类型和算法都应该加足够的注释。
【北京大学1999二、1(10分)】SSS_TEXT_QUSTI4.设计算法以判断给定的无向图G中是否存在一条以网为起点的包含所有顶点的简单路径,若存在,返回TRUE,否则,返回FALSE(注:本算法中可以调用以下几个函数:FIRSTADJ(G,V)——返回图G中顶点V的第一个邻接点的号码,若不存在,则返回0;NEXTADJ(G,W)——返回图G中顶点V的邻接点中处于W之后的邻接点的号码,若不存在,则返回0;NODES(G)——返回图G中的顶点数)。
【合肥工业大学1999五、5(8分)】SSS_TEXT_QUSTI5.已有邻接表表示的有向图,请编程判断从第u顶点至第v顶点是否有简单路径,若有,则印出该路径上的顶点。
数据结构第7章习题答案

第7章 《图》习题参考答案一、单选题(每题1分,共16分)( C )1. 在一个图中,所有顶点的度数之和等于图的边数的倍。
A .1/2 B. 1 C. 2 D. 4 (B )2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A .1/2 B. 1 C. 2 D. 4 ( B )3. 有8个结点的无向图最多有条边。
A .14 B. 28 C. 56 D. 112 ( C )4. 有8个结点的无向连通图最少有条边。
A .5 B. 6 C. 7 D. 8 ( C )5. 有8个结点的有向完全图有条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A .栈 B. 队列 C. 树 D. 图( C )8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是( D )9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 1 23465 ( D )10. 已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是( A )11. 已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是A .0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 1 3 4 2 5 6D. 0 3 6 1 5 4 2⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110A .0 1 3 2 B. 0 2 3 1 C. 0 3 2 1 D. 0 1 2 3A.0 3 2 1 B. 0 1 2 3C. 0 1 3 2D. 0 3 1 2(A)12. 深度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(D)13. 广度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(A)14. 任何一个无向连通图的最小生成树A.只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1. 图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
无向图的连通分量统计(数组)

#include<iostream>#include<vector>using namespace std;#define INFINITY 0 //最大值为无限大#define MAX_VERTEX_NUM 20 //最大顶点个数bool visited[MAX_VERTEX_NUM]={false}; //数组的遍历标志//typedef enum{DG,DN,UDG,UDN} GraphKind; //{有向图,有向网,无向图,无向网} typedef struct ArcCell{int adj; //对无权图,用1或0表示是否相邻;对带权图,则为权值int* info; //边的信息} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct{int vexs[MAX_VERTEX_NUM]; //顶点向量AdjMatrix arcs; //邻接矩阵int vexnum,arcnum; //图的当前顶点数和弧数int kind; //图的类型}MGraph;int CreateUDN(MGraph &G){cout<<"请输入顶点个数和弧数:";cin>>G.vexnum>>G.arcnum;int i;for( i=0; i<G.vexnum; i++)G.vexs[i]=i+1;for( i=0; i<G.vexnum; i++){for(int j=0; j<G.vexnum; j++){G.arcs[i][j].adj=INFINITY;G.arcs[i][j].info=NULL;}}for( i=0; i<G.arcnum; i++){cout<<"请输入两个顶点和权值:";int v1,v2,w;cin>>v1>>v2>>w;G.arcs[v1-1][v2-1].adj=w;G.arcs[v2-1][v1-1].adj=w;}return 1;int CreateUDG(MGraph& G){cout<<"请输入顶点个数和弧数:";cin>>G.vexnum>>G.arcnum;int i;for( i=0; i<G.vexnum; i++)G.vexs[i]=i+1;for( i=0; i<G.vexnum; i++){for(int j=0; j<G.vexnum; j++){G.arcs[i][j].adj=INFINITY;G.arcs[i][j].info=NULL;}}for(i=0; i<G.arcnum; i++){cout<<"请输入两个顶点和权值:";int v1,v2,w;cin>>v1>>v2>>w;G.arcs[v1-1][v2-1].adj=w;G.arcs[v2-1][v1-1].adj=w;}return 1;}int CreateDN(MGraph& G){cout<<"请输入顶点个数和弧数:";cin>>G.vexnum>>G.arcnum;int i;for( i=0; i<G.vexnum; i++)G.vexs[i]=i+1;for( i=0; i<G.vexnum; i++){for(int j=0; j<G.vexnum; j++){G.arcs[i][j].adj=INFINITY;G.arcs[i][j].info=NULL;}}for( i=0; i<G.arcnum; i++){cout<<"请输入两个顶点和权值:";int v1,v2,w;cin>>v1>>v2>>w;G.arcs[v1-1][v2-1].adj=w;}return 1;}int CreateDG(MGraph& G){cout<<"请输入顶点个数和弧数:";cin>>G.vexnum>>G.arcnum;int i;for( i=0; i<G.vexnum; i++)G.vexs[i]=i+1;for( i=0; i<G.vexnum; i++){for(int j=0; j<G.vexnum; j++){G.arcs[i][j].adj=INFINITY;G.arcs[i][j].info=NULL;}}for( i=0; i<G.arcnum; i++){cout<<"请输入两个顶点和权值:";int v1,v2,w;cin>>v1>>v2>>w;G.arcs[v1-1][v2-1].adj=w;}return 1;}int CreateGraph(MGraph& G){cout<<"请输入你想要的图的类型:";cin>>G.kind;switch(G.kind){case 0:return CreateDG(G); //构造有向图case 1:return CreateDN(G); //构造有向网case 2:return CreateUDG(G); //构造无向图case 3:return CreateUDN(G); //构造无向网default:return 0;}}int FirstAdjVex(MGraph& G,int i){for(int j=0; j<G.vexnum; j++){if(G.arcs[i][j].adj!=0)return j;}return -1;}int NextAdjVex(MGraph& G,int i,int w){for(int j=w+1; j<G.vexnum; ++j){if(G.arcs[i][j].adj!=0)return j;}return -1;}void DFS(MGraph& G,int i){visited[i]=true;cout<<G.vexs[i]<<" "<<endl;for(int w=FirstAdjVex(G,i); w>=0; w=NextAdjVex(G,i,w)){ if(!visited[w])DFS(G,w);}}void DFSTraverse(MGraph& G){int number=0;for(int i=0; i<G.vexnum; i++){if(!visited[i]){number++;DFS(G,i);}}cout<<"图的连通分量有"<<number<<"个"<<endl;}int main(){MGraph G;CreateGraph(G);for(int i=0; i<G.vexnum;i++){for(int j=0; j<G.vexnum; j++)cout<<G.arcs[i][j].adj<<" ";cout<<endl;}cout<<endl;DFSTraverse(G);return 0;}。
实验五?无向图邻接表存储结构的创建、遍历及求连通分量

实验五?无向图邻接表存储结构的创建、遍历及求连通分量实验五无向图邻接表存储结构的创建、遍历及求连通分量#include<iostream.h>typedef char vextype;const MAXVER=21;typedef struct listnode{int adjvex;struct listnode* next;}listnode;//表结点typedef struct{vextype data;listnode *first;}headnode;//头结点typedef struct{headnode vexs[MAXVER];int vexnum,arcnum;} ALgraph;//图void createALgraph(ALgraph &G){int i, s, d;listnode *p,*q;cout<<"输入图的顶点数和边数:";cin>>G.vexnum>>G.arcnum;for(i=1;i<=G.vexnum;i++){cout<<"\n输入第"<<i<<"个顶点信息:";cin>>G.vexs[i].data;G.vexs[i].first=NULL;} //输入第i个结点值并初始化第i个单链表为空for(i=1; i<=G.arcnum; i++){cout<<"\n输入第"<<i<<"条边的始点和终点:";cin>>s>>d;//s为始点,d为终点p=new listnode; p->adjvex=d;p->next=G.vexs[s].first;G.vexs[s].first=p;//将新建的以d为信息的表结点p插入s单链表的头结点后q=new listnode;q->adjvex=s;q->next=G.vexs[d].first;G.vexs[d].first=q;//将新建的以s为信息的表结点q插入d单链表的头结点后}}int visited[MAXVER];//定义全局数组遍历visitedvoid dfs(ALgraph G, int v)//被遍历的图G采用邻接表作为存储结构,v为出发顶点编号{listnode *p;cout<<G.vexs[v].data;visited[v]=1;p=G.vexs[v].first;while(p!=NULL){if(visited[p->adjvex]==0) dfs(G,p->adjvex);//若p所指表结点对应的邻接顶点未访问则递归地从该顶点出发调用dfsp=p->next;}}void dfsTraverse(ALgraph G){int v;//遍历图之前初始化各未访问的顶点for(v=1; v<=G.vexnum; v++)visited[v]=0;//从各个未被访问过的顶点开始进行深度遍历for(v=1;v<=G.vexnum;v++)if(visited[v]==0) dfs(G,v);}void dsfComp(ALgraph G){ int v;//遍历G以前,初始化visited数组为0for(v=1;v<=G.vexnum;v++)visited[v]=0;for(v=1;v<=G.vexnum;v++)if(visited[v]==0){cout<<endl<<"\n一个深度遍历连通分量为:";dfs(G,v);}}void BFS(ALgraph G, int v)//从顶点编号v出发,广度遍历邻接表存储的图G{int queue[MAXVER], front ,rear; listnode* p;front=rear=0;cout<<G.vexs[v].data;visited[v]=1;queue[++rear]=v;while(front!=rear){v=queue[++front];p=G.vexs[v].first;while(p!=NULL){if(visited[p->adjvex]==0){v=p->adjvex;cout<<G.vexs[v].data;visited[v]=1;queue[++rear]=v;}p=p->next;}}}void BFSTraverse(ALgraph G){int v;//遍历G以前,初始化visited数组为0 for(v=1;v<=G.vexnum;v++)visited[v]=0;for(v=1;v<=G.vexnum;v++)if(visited[v]==0)BFS(G,v);}void BFSComp(ALgraph G){int v;//遍历G以前,初始化visited数组为0for(v=1;v<=G.vexnum;v++)visited[v]=0;for(v=1;v<=G.vexnum;v++)if(visited[v]==0){cout<<endl<<"\n一个广度遍历连通分量为:"; BFS(G,v);}}void main(){ALgraph g;createALgraph(g);cout<<endl<<"深度遍历结果为:"; dfsTraverse(g);dsfComp(g);cout<<endl<<"广度遍历结果为:"; BFSTraverse(g);BFSComp(g);cout<<endl;}。
以邻接多重表为存储结构-实现连通无向图的深度优先和广度优先遍历

/*【基本要求】以邻接多重表为存储结构,实现连通无向图的深度优先和广度优先遍历。
以用户指定的结点为起点,分别输出每种遍历下的结点访问序列和相应生成树的边集*///________头文件___________________________________________________________#include<iostream>usingnamespacestd;//_______无向图的邻接多重表存储表示p166____________________________________constintNUM=20;constintData_Num=2;//每个顶点所表示的数据typedefcharVertexType[Data_Num];~/*#defineMAX_VERTEX_NUM20typedefstructemnu{intunvisited;intvisited;}VisitIf;typedefstructInfoType{};typedefstructVertexType{};*/typedefstructEBox{intmark;//访问标记intivex,jvex;//该边依附的2个顶点位置·structEBox*ilink,*jlink;//分别指向依附这2个顶点的下一条边//InfoType*info;//该边信息指针}EBox;typedefstructVexBox{VertexTypedata;EBox*firstedge;//指向第一条依附该顶点的边}VexBox;typedefstruct{VexBoxadjmulist[NUM];-intvexnum,edgenum;//无向图的当前顶点和边数}AMLGraph;//_________________________队列的定义_____________________________________typedefintQElemType;typedefstructQNode{QElemTypedata;structQNode*next;}QNode,*QueuePtr;"typedefstruct{QueuePtrfront,rear;}LinkQueue;//_____________________寻找指定数据______________________________________________//寻找输入的数据在图中的位置,若不存在则返回-1intLocateVex(AMLGraphG,VertexTypeu){;inti;for(i=0;i<G.vexnum;i++)if(strcmp(u,G.adjmulist[i].data)==0)returni;return-1;}//________________________构造无向图_______________________________________________//采用邻接多重表存储表示,构造无向图GintCreateGraph(AMLGraph&G){!cout<<"请输入图的顶点数:";cin>>G.vexnum;//输入图当前的顶点数cout<<"请输入图的弧数:";cin>>G.edgenum;//输入图当前的边数cout<<"请输入每个顶点所对应的值:"<<endl;for(inti=0;i<G.vexnum;i++){cin>>G.adjmulist[i].data;//输入顶点值G.adjmulist[i].firstedge=NULL;//初始化指针]}VertexTypev1,v2;EBox*p;intj;//每条弧所关联的两个结点for(intk=0;k<G.edgenum;k++){cout<<"请输入第"<<k+1<<"弧的始点和终点:";cin>>v1;cin>>v2;i=LocateVex(G,v1);j=LocateVex(G,v2);//确定v1和v2在图G中的位置…p=(EBox*)malloc(sizeof(EBox));//对弧结点进行赋值(*p).mark=0;(*p).ivex=i;(*p).jvex=j;(*p).ilink=G.adjmulist[i].firstedge;(*p).jlink=G.adjmulist[j].firstedge;G.adjmulist[i].firstedge=G.adjmulist[j].firstedge=p;}\return1;}//返回V的值VertexType*GetVex(AMLGraphG,intv){if(v>G.vexnum||v<0)exit(0);return&G.adjmulist[v].data;}…//返回V的第一个邻接点的序号,若没有则返回-1intFirstAdjVex(AMLGraphG,VertexTypev){inti;i=LocateVex(G,v);if(i<0)return-1;if(G.adjmulist[i].firstedge)//V有邻接结点if(G.adjmulist[i].firstedge->ivex==i)#returnG.adjmulist[i].firstedge->jvex;elsereturnG.adjmulist[i].firstedge->ivex;elsereturn-1;}//返回V的(相对于W)的下一个邻接结点的序号,若W是V的最后一个邻接结点,则返回-1intNextAdjVex(AMLGraphG,VertexTypev,VertexTypew){inti,j;&EBox*p;i=LocateVex(G,v);j=LocateVex(G,w);if(i<0||j<0)return-1;p=G.adjmulist[i].firstedge;while(p)if(p->ivex==i&&p->jvex!=j)p=p->ilink;elseif(p->jvex==i&&p->ivex!=j)?p=p->jlink;elsebreak;if(p&&p->ivex==i&&p->jvex==j){p=p->ilink;if(p&&p->ivex==i)returnp->jvex;elseif(p&&p->jvex==i)returnp->jvex;|}if(p&&p->ivex==j&&p->jvex==i){p=p->jlink;if(p&&p->ivex==i)returnp->jvex;elseif(p&&p->jvex==i)returnp->jvex;}&return-1;}//__________________________队列的操作_________________________________________intvisite[NUM];//访问标志数组int(*VisitFunc)(VertexTypev);voidDFS(AMLGraphG,intv)!{intj;EBox*p;VisitFunc(G.adjmulist[v].data);visite[v]=1;//该顶点已经被访问p=G.adjmulist[v].firstedge;while(p){j=p->ivex==vp->jvex:p->ivex;if(!visite[j])(DFS(G,j);p=p->ivex==vp->ilink:p->jlink;}}//________深度优先搜索_______________________________________________________voidDFSTraverse(AMLGraphG,int(*Visit)(VertexType)){intv,start;VisitFunc=Visit;(for(v=0;v<G.vexnum;v++)visite[v]=0;cout<<"请输入你要开始进行查找的位置:";cin>>start;cout<<"按广深度优先搜索的结果是:"<<endl;for(v=start;v<G.vexnum;v++){if(v>=G.vexnum){for(v=0;v<G.vexnum;v++)、{if(!visite[v])DFS(G,v);}//内层for}//ifelse{if(!visite[v])DFS(G,v);}//else(}//外层forcout<<"\b\b\b";cout<<endl;}//队列的初始化intInitQueue(LinkQueue*Q){(*Q).front=(*Q).rear=(QueuePtr)malloc(sizeof(QNode));[if(!(*Q).front)exit(0);(*Q).front->next=NULL;return1;}//判断队列是否为空,为空则返回1,否则返回0intQueueEmpty(LinkQueueQ){if(Q.front==Q.rear)#return1;elsereturn0;}//向队列中插入元素intEnQueue(LinkQueue*Q,QElemTypee){QueuePtrp=(QueuePtr)malloc(sizeof(QNode));if(!p)exit(0);—p->data=e;p->next=NULL;(*Q).rear->next=p;(*Q).rear=p;return1;}//若队列不为空,则删除对头元素,并返回1;否则返回0intDeQueue(LinkQueue*Q,QElemType*e){QueuePtrp;;if((*Q).front==(*Q).rear)return0;p=(*Q).front->next;*e=p->data;(*Q).front->next=p->next;if((*Q).rear==p)(*Q).rear=(*Q).front;free(p);return1;}^/**Booleanvisited[MAX];//访问标志数组Status(*VisitFunc)(intv);//函数变量voidDFSTraverse(GraphG,Status(*Visit)(intv)){//对图G做深度优先遍历VisitFunc=Visit//使用全局变量VisitFunc,使DFS不必设函数指针参数for(v=0;v<G.vexnum;++v)visited[v]=FALSE;//访问标志数组初始化for(v=0;v<G.vexnum;++v)if(!visited[v])DFS(G,v);//对尚未访问的顶点调用DFS)}voidDFS(GraphG,intv){//从第V个顶点出发递归地深度优先遍历图Gvisited[v]=TRUE;VisitFunc(v);//访问第v个顶点for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w)if(!visited[w])DFS(G,w);}**///_________广度优先搜索_____________________________________________________//广度优先非递归遍历图G%voidBFSTraverse(AMLGraphG,int(*Visit)(VertexType)){intu,v,w,start=0;VertexTypew1,u1;LinkQueueQ;for(v=0;v<G.vexnum;v++)visite[v]=0;InitQueue(&Q);cout<<"请输入你要开始进行查找的位置:";cin>>start;}cout<<"按广度优先搜索的结果是:"<<endl;for(v=start;v<G.vexnum;v++){if(!visite[v]){visite[v]=1;Visit(G.adjmulist[v].data);EnQueue(&Q,v);//v入队列while(!QueueEmpty(Q)){!DeQueue(&Q,&u);strcpy(u1,*GetVex(G,u));for(w=FirstAdjVex(G,u1);w>=0;w=NextAdjVex(G,u1,strcpy(w1,*GetVex(G,w))))if(!visite[w]){visite[w]=1;Visit(G.adjmulist[w].data);EnQueue(&Q,w);}}/}}//forInitQueue(&Q);for(v=0;v<start;v++){if(!visite[v]){visite[v]=1;Visit(G.adjmulist[v].data);:EnQueue(&Q,v);//v入队列while(!QueueEmpty(Q)){DeQueue(&Q,&u);strcpy(u1,*GetVex(G,u));for(w=FirstAdjVex(G,u1);w>=0;w=NextAdjVex(G,u1,strcpy(w1,*GetVex(G,w))))if(!visite[w]){visite[w]=1;Visit(G.adjmulist[w].data);(EnQueue(&Q,w);}}}}//forcout<<"\b\b\b";cout<<endl;}\//把边的访问标记设置为0,即未被访问voidMarkUnVisited(AMLGraphG){inti;EBox*p;for(i=0;i<G.vexnum;i++){p=G.adjmulist[i].firstedge;while(p){、p->mark=0;if(p->ivex==i)p=p->ilink;elsep=p->jlink;}}}/**.voidBFSTraverse(GraphG,Status(*visit)(intv)){//按广度优先非递归遍历图G。
无向图邻接表的构造

⽆向图邻接表的构造⼀、⽬的和要求(需求分析):1、掌握邻接表的存储结构以及邻接表的建⽴和操作。
2、构造⼀个⽆向图的邻接表,要求从键盘输⼊图的顶点数和图的边数,并显⽰所构造的邻接表)实验拓展:1. 构建有向图的邻接表2. 判断边是否存在3. 求顶点的度数以下是代码:#include<stdio.h>#include<iostream>#include<stdlib.h>#define vnum 20using namespace std;typedef struct arcnode{int adjvex; //边所对应的顶点编号struct arcnode * next; //指向下⼀条边的指针}ArcNode;typedef struct vexnode{int vertex; //顶点编号ArcNode *first; //指向第⼀条依附该顶点的边的指针}AdjList[vnum];typedef struct{AdjList adjlist;int vexnum,arcnum; //顶点和边的个数}Graph;void Init(Graph *GA,int a,int b) //初始化{int i;GA->vexnum=a;GA->arcnum=b;for(i=0;i<GA->vexnum;i++){GA->adjlist[i].vertex=i; //初始化顶点信息GA->adjlist[i].first=NULL; //初始化i的第⼀个邻接点为NULL}}void InsertArcnode(Graph *GA) //⽆向图的构造{ArcNode *p;int i,j,k;for(k=0;k<GA->arcnum;k++){cout << "请输⼊第"<<k+1<<"条边【两个顶点(从0开始)之间⽤空格隔开】:"; scanf("%d %d",&i,&j);p=(ArcNode *)malloc(sizeof(ArcNode));//⽣成j的表结点p->adjvex=j;p->next=GA->adjlist[i].first; //将结点j链接到i的单链表中GA->adjlist[i].first=p;p=(ArcNode *)malloc(sizeof(ArcNode));//⽣成i的表结点p->adjvex=i;p->next=GA->adjlist[j].first; //将结点i链接到j的单链表中GA->adjlist[j].first=p;}}void PrintGraph(Graph *GA) //打印图{cout<<endl;cout << "⽣成邻接表如下:" << endl;for(int i=0;i<GA->vexnum;i++){printf("v%d:",i);ArcNode *p=GA->adjlist[i].first;while(p!=NULL){printf("-->%d",p->adjvex);p=p->next;}printf("\n");}printf("-----------------------------------\n");}void CreateLink(Graph *GA){ //有向图的建⽴ArcNode *p;int i,j,k;for(k=0;k<GA->arcnum;k++){cout << "请输⼊第"<<k+1<<"条边【两个顶点(从0开始)之间⽤空格隔开】:"; scanf("%d %d",&i,&j);p=(ArcNode *)malloc(sizeof(ArcNode));p->adjvex=j;p->next=GA->adjlist[i].first;GA->adjlist[i].first=p;}}void Judge(Graph *GA){ //判断有向图中是否存在边int i,j;cout << "请输⼊欲判断的边:";scanf("%d %d",&i,&j);ArcNode *p=GA->adjlist[i].first;while(p!=NULL){if(p->adjvex==j){cout<<"该边存在"<<endl;break;}else p=p->next;}if(p==NULL){cout<<"该边不存在"<<endl;}}void Count_degree(Graph *GA){ //计算有向图中顶点的出度⼊度int i;int out=0,in=0; //out储存出度,in储存⼊度cout << "请输⼊顶点编号(从0开始):";scanf("%d",&i);if(GA->adjlist[i].first==NULL){out=0;}else {ArcNode *p=GA->adjlist[i].first;while(p!=NULL){out++;p=p->next;}}for(int k=0;k<GA->vexnum;k++){ArcNode *p=GA->adjlist[k].first;while(p!=NULL){if(p->adjvex==i){in++;break;}p=p->next;}}cout << "该顶点的出度为:"<<out<<endl;;cout << "该顶点的⼊度为:"<<in<<endl;;}void choice(){ //选择界⾯int choice1;cout << "请选择功能:"<<"1.⽆向图 2.有向图 3.退出"<<endl; cin >> choice1;if(choice1==1){int a,b;Graph GA;printf("-----------------------------------\n");printf("请输⼊⽆向图的顶点数和边数:");scanf("%d %d",&a,&b);Init(&GA,a,b);InsertArcnode(&GA);PrintGraph(&GA);choice();}if(choice1==2){int a,b;Graph GA;printf("-----------------------------------\n");printf("请输⼊有向图的顶点数和边数:");scanf("%d %d",&a,&b);Init(&GA,a,b);CreateLink(&GA);PrintGraph(&GA);cout << "功能:1.查询边是否存在 2.查询顶点的出度⼊度 3.返回上⼀级"<<endl; int choice2;cin >> choice2;while(choice2!=3){switch(choice2){case 1:Judge(&GA);break;case 2:Count_degree(&GA);break;}cout << "功能:1.查询边是否存在 2.查询顶点的出度⼊度 3.返回上⼀级"<<endl; cin >> choice2;}choice();}if(choice1==3){return;}}int main(){choice(); //功能界⾯return 0;}。
java邻接矩阵计算连通分量

java邻接矩阵计算连通分量以java邻接矩阵计算连通分量为题,我们将从以下几个方面进行讨论。
一、连通分量的概念和应用在图论中,连通分量是指无向图中的一个最大连通子图,即这个子图中的任意两个顶点之间都存在一条路径。
计算连通分量可以帮助我们了解图的结构和性质,例如在社交网络中找出朋友圈、在通信网络中找出通信子网等等。
二、邻接矩阵的介绍和表示方法邻接矩阵是一种常见的图的表示方法,它使用一个二维数组来表示图中顶点之间的连接关系。
对于一个有n个顶点的图,邻接矩阵是一个n*n的矩阵,其中矩阵的第i行第j列的元素表示顶点i和顶点j之间是否存在一条边。
如果存在边,则元素的值为1,否则为0。
三、使用邻接矩阵计算连通分量的步骤1. 创建一个邻接矩阵表示图的数据结构,其中矩阵的大小为n*n,n为图中顶点的个数。
2. 初始化一个数组visited,用于记录每个顶点是否被访问过。
初始时,visited数组的所有元素均为false。
3. 遍历图中的每个顶点,对于每个未被访问过的顶点,进行深度优先搜索(DFS)。
4. 在DFS的过程中,设置当前顶点为已访问,并将visited数组中对应位置的元素置为true。
5. 遍历当前顶点的所有邻接顶点,如果某个邻接顶点未被访问过,则递归调用DFS函数。
6. 当DFS函数返回时,表示当前连通分量中的所有顶点已经访问完毕,记录下一个连通分量的编号,并继续寻找下一个未被访问过的顶点进行DFS。
7. 直到所有顶点都被访问过,即遍历完整个图的所有连通分量。
四、使用Java代码实现邻接矩阵计算连通分量下面是使用Java代码实现邻接矩阵计算连通分量的一个示例:```javapublic class ConnectedComponents {private int[][] graph;private boolean[] visited;private int numComponents;public ConnectedComponents(int[][] graph) {this.graph = graph;int numVertices = graph.length;visited = new boolean[numVertices];numComponents = 0;}public int calculateConnectedComponents() {for (int i = 0; i < graph.length; i++) {if (!visited[i]) {dfs(i);numComponents++;}}return numComponents;}private void dfs(int vertex) {visited[vertex] = true;for (int i = 0; i < graph[vertex].length; i++) { if (graph[vertex][i] == 1 && !visited[i]) { dfs(i);}}}public static void main(String[] args) {int[][] graph = {{0, 1, 0, 1},{1, 0, 1, 0},{0, 1, 0, 0},{1, 0, 0, 0}};ConnectedComponents cc = new ConnectedComponents(graph);int numComponents = cc.calculateConnectedComponents();System.out.println("连通分量个数:" + numComponents);}}```以上代码中,我们首先创建了一个ConnectedComponents类,其中包含了邻接矩阵graph、visited数组和numComponents变量。
java邻接矩阵计算连通分量

java邻接矩阵计算连通分量以Java邻接矩阵计算连通分量为主题,我们将介绍如何使用Java 编程语言来实现连通分量的计算,并且通过邻接矩阵来表示图的结构。
在此之前,我们先来了解一下什么是连通分量。
连通分量是图论中的一个概念,用来描述图中的若干个顶点组成的子集,其中任意两个顶点之间都存在路径。
换句话说,连通分量是指图中可以互相到达的顶点的集合。
在计算连通分量之前,我们需要先了解一下邻接矩阵的概念。
邻接矩阵是一种常用的图的表示方法,它是一个二维矩阵,其中矩阵的行和列分别表示图中的顶点,矩阵的元素表示顶点之间的边的关系。
如果两个顶点之间存在边,则对应的邻接矩阵元素为1;如果两个顶点之间不存在边,则对应的邻接矩阵元素为0。
接下来我们将介绍如何使用Java编程语言来实现邻接矩阵的计算连通分量。
我们需要定义一个Graph类来表示图的结构。
这个类需要包含一个邻接矩阵作为成员变量,并且提供一些方法来操作邻接矩阵。
```javapublic class Graph {private int[][] adjacencyMatrix;public Graph(int numVertices) {adjacencyMatrix = new int[numVertices][numVertices]; }public void addEdge(int source, int destination) {adjacencyMatrix[source][destination] = 1;adjacencyMatrix[destination][source] = 1;}public void removeEdge(int source, int destination) {adjacencyMatrix[source][destination] = 0;adjacencyMatrix[destination][source] = 0;}public boolean isConnected(int source, int destination) {return adjacencyMatrix[source][destination] == 1;}// 其他操作方法...}```在Graph类中,我们使用一个二维数组adjacencyMatrix来表示邻接矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
flag=temp;
scanf("%d",&k);
while(k!=-1){
temp=(struct VNode*)malloc(sizeof(struct VNode));
temp->position=k;
temp->next=NULL;
flag->next=temp;
flag=temp;
struct VNode* L;
w->mark=1;
L=w->first;
while(L!=NULL){
if((v+(L->position))->mark==0){
DFS(v,(v+L->position)); //递归调用
}
L=L->next;
}
}
int main(){
int i,j,k;
int num=0;
struct ArcNode* p;
struct VNode* temp;
struct VNode* flag;
printf("\n请输入顶点个数n:");
scanf("%d",&n);
while(n<1){
printf("你输入的值不合理,请重新输入:\n");
scanf("%d",&n);
}
p=(struct ArcNode*)malloc(n*sizeof(struct ArcNode));
/*说明:1.Vi表示第i个顶点,它在表中的位置为i-1,如V3在表中的位置为2;
2.如果输入以V1为弧尾的所有弧(假设存在弧<V1,V3>和<V1,V2>)
则输入:2 1 -1(只需输入弧头的位置,并用-1表示结束)*/
for(i=0;i<n;i++){ //创建无向图
printf("\n请输入以V%d为弧尾的所有弧,并以-1结束输入\n",i+1);
scanf("%d",&k);
}
}
}
i=0;
while(p[i].mark==0){ //计算连通分量的个数
DFS(p,(p+i));
num++;
i=0;
while(p[i].mark!=0&&i<n){
i++;
}
}
printf("此图的连通分量个数为:%d\n",num);
system("pause");
return 0;
}
五、实验结果与分析
习题1:这题主要还是用到深度优先搜索,先从任意一个顶点开始进行深度优先搜索,搜索完后,连通分量个数增1。然后再从没有遍历过的顶点找一个出来进行深度优先搜索,搜索完后,连通分量个数增1。一直到所有的顶点都被遍历过。
实验结果如图:
六、实验心得及体会
通过本次实验,我更好的掌握了图的相关操作,能够熟练的进行图的建立、遍历。
在编写程序时,有很多不明白的地方,在得到同学的鼎立相助后,基本解决了这些问题。
#include<malloc.h>
int n;
struct VNode{ //顶点
int position;
struct VNode* next;
};
struct ArcNode{ //弧
int mark;
struct VNode* first;
};
void DFS(struct ArcNode* v,struct ArcNode* w){ //深度优先搜索
scanf("%d",&k);
if(k==-1){
p[i].mark=0;
p[i].first=NULL;
}
else{
temp=(struct VNode*)malloc(sizeof(struct VNode));
temp->position=k;
temp->next=NULL;
p[i].first=temp;
学院名称
专业班级
实验成绩
学生姓名
学号
实验日期
课程名称
数据结构
实验题目
3 图
一、实验目的与要求
熟悉图的存储结构,掌握有关算法的实现,了解图在计算机科学及其他工程技术中的ห้องสมุดไป่ตู้用。
二、主要仪器设备
Cfree
三、实验内容和原理
[问题描述]
采用邻接表存储结构,编写一个求无向图的连通分量个数的算法。
[输入]
图顶点的个数,和以各个顶点为弧尾的所有弧,并以-1结束输入。
[输出]
连通分量的个数。
[存储结构]
图采用邻接矩阵的方式存储。
[算法的基本思想]
用到深度优先搜索,先从任意一个顶点开始进行深度优先搜索,搜索完后,连通分量个数增1。然后再从没有遍历过的顶点找一个出来进行深度优先搜索,搜索完后,连通分量个数增1。一直到所有的顶点都被遍历过。
[参考源程序]
#include<stdio.h>
