多元正态分布及检验
多元正态分布的性质

多元正态分布的性质正态分布是统计分析中最重要的概率分布之一,它能够帮助我们更好地理解数据的特性,也可以帮助我们做出更好的决策。
多元正态分布可以用来描述一组随机变量之间的关系,在许多计量方法和定量分析中,它被广泛应用。
本文尝试回答以下三个问题:一是什么是多元正态分布?二是多元正态分布的性质是什么?三是多元正态分布如何使用?首先,什么是多元正态分布?多元正态分布是指一个有两个或多个变量的正态分布,可以用来描述一组随机变量之间的关系,可以用来解释一个变量的分布特征。
与单变量正态分布不同的是,多元正态分布的特征取决于对角矩阵中的参数,即协方差矩阵或协方差矩阵。
与单变量正态分布不同,多元正态分布是以向量形式定义的,但可以使用同样的统计分析理论来描述多变量正态分布的性质,例如期望和方差。
其次,多元正态分布的性质是什么?多元正态分布存在着许多性质,根据多元数学理论可以列举出以下性质:1.元正态分布的期望向量表示为 m = (m_1,m_2,...,m_n),这里的m_i表示每个随机变量的期望值;2.元正态分布的协方差矩阵S表示为:S=[s_ij],sij表示第i 个和第j个随机变量之间的协方差;3.元正态分布的方差向量表示为:var=(var_1,var_2,...,var_n),其中var_i表示第i个随机变量的方差;4.元正态分布的对称性,即对于n个随机变量X_1,X_2,...,X_n 及其期望向量m和协方差矩阵S,当存在变换矩阵A,使得AX=y有解,则有:E(X) = mvar(X) = S5.元正态分布的共轭性,即如果X_1,X_2,...,X_n是一组多元正态分布随机变量,则任意一组X_1X_2...,X_n也是多元正态分布随机变量,且具有相同的期望向量m和协方差矩阵S。
最后,多元正态分布怎么使用?多元正态分布的使用是建立在统计分析的基础之上的。
在使用多元正态分布时,可以根据观测数据来估计期望向量m和协方差矩阵S。
多元正态分布参数的假设检验

( ) ( ) 3. 计算统计量T的具体值 T02 = n X − μ0 ′ Σ−1 X − μ0 .
4. 按规定的小概率标准α,查 χ 2分布表,得临界
值 χα2 ( p),并作出判断: 当 T02 ≤ χα2 ( p),接受H0,拒绝H1,即认为与没有显
著差异。 当 T02 > χα2 ( p),接受H1,拒绝H0,即认为与有显著
当p = 1时,因为,X
~
N1 ( μ1 ,
σ2
n
)
,Y
~
N1 ( μ2
,
σ2
m
)
,
且相
互独立,在,H0成立条件下,有
(X −Y) 1 + 1
t=
nm
~ t(n + m− 2)
∑ ∑ ⎡ n
⎢
(Xi
− X)2
+
m
(Yi
−Y
)2
⎤ ⎥
(n+m−2)
⎣ i=1
j=1
⎦
∑ ∑ 显然
t2 = nm
⎡ ⎢
n
Xj −X
Xj −X ′
9
武汉理工大学统计学系唐湘晋
( )( ) ∑ 在
H 0 :μ
=
μ0下, S=
X~
n
X
1 NP (μ0 , n Σ)
j -X Xj -X
′
,
~
X − μ0 ~
Wp (n −1,
NP (0,
Σ).
1 n
Σ)
j =1
故由T2分布定义知
( ) ( ) T 2 = (n −1) ⎡⎣ n X − μ0 ⎤⎦′ S−1 ⎡⎣ n X − μ0 ⎤⎦ ~ T 2 ( p, n −1)
《多元正态分布》课件

度概率密度函数的乘积。
高维正态分布在机器学习中的应用
降维处理
高维正态分布可以用于降维处理,通过保留数据的主要特征,降低 数据的维度,提高数据的可解释性和处理效率。
特征选择
高维正态分布可以用于特征选择,通过分析特征之间的相关性,选 择与目标变量高度相关的特征,去除冗余和无关的特征。
概率模型
高维正态分布可以用于构建概率模型,通过估计数据的概率分布, 进行分类、回归和聚类等机器学习任务。
总结词
检验多元正态分布的协方差矩阵是否与预期 协方差矩阵一致。
详细描述
通过对比样本协方差矩阵与预期协方差矩阵 ,评估样本数据是否符合多元正态分布的假 设。常用的方法包括样本协方差矩阵与预期 协方差矩阵的差异检验、样本数据的散点图 和拟合曲线分析等。
多元正态分布的其他假设检验方法
总结词
其他用于检验多元正态分布的方法。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
02
二元正态分布
二元正态分布的定义
总结词
二元正态分布是多元正态分布在两个维度上的特例,其概率密度函数呈钟形, 且服从二维高斯分布。
详细描述
二元正态分布是一种连续概率分布,描述了两个随机变量之间的关系,当这两 个随机变量相互独立时,其联合概率分布是二元正态分布。它的概率密度函数 由均值向量和协方差矩阵决定,呈现出钟形曲线。
多元正态分布的均值向量和协方差矩阵决定了其 分布形态。
多元正态分布的应用场景
多元统计分析
多元正态分布在多元统计分析中 广泛应用,如主成分分析、因子 分析、聚类分析等。
机器学习
在机器学习中,多元正态分布用 于描述特征之间的相关性,以及 在隐含层节点中实现特征的映射 。
多元正态分布参数的假设检验

2 22.74 32.56 51.49 61.39 9 22.62 32.57 51.23 61.39 16 23.02 33.05 51.48 61.44
3 22.60 32.76 51.50 61.22 10 22.67 32.67 51.64 61.50 17 23.02 32.95 51.55 61.62
5
武汉理工大学统计学系唐湘晋
一、Σ已知时单个总体均值向量的检验
设 X1, X2,…, Xn 是来自正态总体 N p ( μ , Σ ) 的样本, 考虑假设: H 0 :μ = μ 0 ,
H 1 :μ ≠ μ 0
a) p = 1 b) p > 1
U 1 )
T02 = n ( X − μ 0 )′ Σ − 1 ( X − μ 0 ) .
4
武汉理工大学统计学系唐湘晋
§3.2 多元正态分布的均值向量的检验
p维正态总体 N p (μ, Σ) 的统计推断问题,包括均 值向量的检验和均值的置信域问题。 p维正态随 机向量的每一个分量都是一元正态变量,若将p 维均值向量的检验问题化为p个一元正态的均值 检验问题,虽然可以使问题简化,但忽略了p个 分量间的互相依赖关系,常常得不出正确的结 论。
13
武汉理工大学统计学系唐湘晋
解:
⎡ X 1 ⎤ ⎡ 22.82 ⎤ ⎢ ⎥ ⎢ X 2 ⎥ ⎢ 32.79 ⎥ ⎥ = X=⎢ ⎢ X 3 ⎥ ⎢ 51.45 ⎥ ⎢ ⎥ ⎢ ⎥ X 4 ⎥ ⎣ 61.38 ⎦ ⎢ ⎦ ⎣
1 21 V= ∑ (Xi − X)(Xi − X)′ 21 − 1 i=1 ⎡ 70.3076 ⎤ ⎢ −52.1469 ⎥ 73.5511 ⎥ =⎢ ⎢ 3.4462 −19.3637 ⎥ 90.4098 ⎢ ⎥ 1.2022 −33.6989 40.0895⎦ −6.9624 ⎣
多元正态分布

混合模型
除了高斯混合模型,还有其他类 型的混合模型,如多项式混合模 型、泊松混合模型等。
扩展应用领域
多元正态分布在许多领域都有广 泛的应用,如心理学、经济学、 生物统计学等。
THANKS
感谢观看
02
联合分布的均值向量和协方差矩阵由各个分量的均 值和协方差决定。
03
当各分量之间相互独立时,其联合分布的协方差矩 阵为各分量协方差矩阵的线性组合。
04
多元正态分布的推断
参数估计
最大似然估计
01
通过最大化样本数据的似然函数来估计多元正态分布的参数,
包括均值向量和协方差矩阵。
最小二乘估计
02
将多元正态分布的均值向量作为回归系数,利用最小二乘法进
多元正态分布
• 多元正态分布概述 • 多元正态分布的参数 • 多元正态分布的性质 • 多元正态分布的推断 • 多元正态分布在统计和机器学习中的
应用 • 多元正态分布的扩展和变种
01
多元正态分布概述
定义与性质
定义
多元正态分布是多个连续随机变量的 概率分布,其概率密度函数是多元高 斯函数。
性质
多元正态分布具有旋转对称性、椭球 等高性、边缘分布的独立性和最大熵 等性质。
当其他维度固定时,该维度的边缘分 布是关于均值对称的,且方差与该维 度与其他维度的协方差成正比。
随机变量的线性变换
对于多元正态分布的随机变量,对其 进行线性变换后,新变量的分布仍然 是多元正态分布。
线性变换包括平移、旋转、缩放等, 这些变换不会改变变量的分布形态。
随机向量的联合分布
01
对于多元正态分布的随机向量,其各分量之间的联 合分布也是正态分布。
06
多元统计分析 第一章 多元正态分布

1、城镇居民消费水平通常用八项指标来描述,如人均粮食支出、人均副食 支出、人均烟酒茶支出、人均衣着商品支出、人均日用品支出、人均燃 料支出、人均非商品支出。这八项指标存在一定的线性关系。为了研究 城镇居民的消费结构,需要将相关强的指标归并到一起,这实际就是对 指标进行聚类分析。(经济学)
2、在企业经济效益的评价中,涉及到的指标往往很多,如百元固定资产原 值实现产值、百元固定资产原值实现利税、百元资金实现利税、百元工 业总产值实现利税、百元销售收入实现利税、每吨标准煤实现工业产值、 每千瓦时电力实现工业产值、全员劳动生产率、百元流动资金实现产值。 如何将这些具有错综复杂关系的指标综合成几个较少的因子,既有利于 对问题进行分析和解释,又能便于抓住主要矛盾做出科学的评价。可用 主成分分析和因子分析法。
3、某一产品是用两种不同原料生产的,试问此两种原料生产的产品寿命有 无显著差异?又比如,若考察某商业行业今年和去年的经营状况,这时 需要看这两年经营指标的平均水平是否有显著差异以及经营指标之间的 波动是否有显著差异。可用多元正态总体均值向量和协差阵的假设检验。
4、按现行统计报表制度,农村家庭纯收入是指农村常住居民家庭总收入中 扣除从事生产和非生产经营用支出、税款和上交承包集体任务金额以后 剩余的、可直接用于进行生产的、非生产性建设投资、生产性消费的那 一部分收入。如果我们收集某年各个省、自治区、直辖市农民家庭人均 纯收入的数据,可以用相应分析,揭示全国农民人均纯收入的特征以及 各省、自治区、直辖市与各收入指标的关系。
预备知识
线性代数方面的知识——向量和矩阵是研究多元数据 的重要工具;(要掌握矩阵逆、矩阵特征值、特征向量的 求解)
初等数理统计的知识——多元分析是建立在一元统计 分析基础上的,其许多理论可由一元统计直接推广过来;
【教学课件】第一章 多元正态分布

k个变量是两两不相关,另一方面,
在尽可能保持原有信息的基础上,使
得 k尽可能的小。
.
16
定理3.2.1 设 的 p 个顺序特征值为
1 p 0, 1 2 p ,
其中
j
(
j
1,2,,
p)是对应于
的标准
j
正交特征向量,则 I , X 的第 j 个
主成分 Yj 表达式的系数向量 a j j ,
X)(Xi
X)( 样 本 协 方 差 )
.
11
或检验统计量
F n p T2 p(n1)
当F
F
(
p,n
p)时 , 拒 绝 H 0
注T : 2p n (n p 1 )F (p ,np )
.
12
两个多元正态总体均值成组比较
设X1, X2,, Xn1和Y1,Y2,,Yn2分别取
自于p维正态总体Np (1, )和Np (2 , )
即Y j
j X ,且D(Yj )
。
j
.
17
贡献率
p
定义3.2.1 称j j 为主成分Yj的 j1
k
p
贡献率,称j j 为前k个主成分
j1
j1
Y1,Y2 ,,Yk的累积贡献率。
.
18
原始变量与主成分的相关系数
因子负荷量
(Xi,Yj)
coX vi,Yj
Va XirVaYjr
j ij
1
.
20
第四章 因子分析
正交因子模型
因子模型的参数估计
因子旋转
因子得分
应用实例
.
21
有关记号
3.多元正态分布-讲解(下)
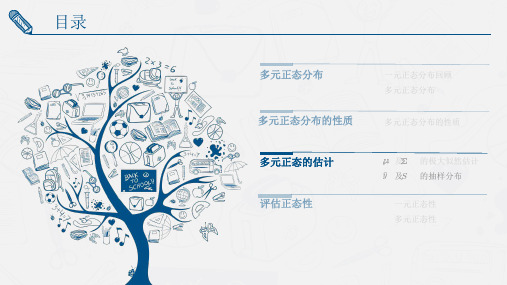
目录一元正态分布回顾多元正态分布多元正态分布及 的极大似然估计 及 的抽样分布多元正态的估计一元正态性多元正态性评估正态性多元正态分布的性质多元正态分布的性质多元正态的估计一元情形的回顾基于服从正态分布 的总体的独立同分布样本 :样本均值 服从:样本方差 服从:与 相互独立多元正态的估计多元情形类似于一元的情形,基于服从正态分布 总体的独立同分布样本 :样本均值 服从:样本方差 服从:这里的 表示 个自由度的Wishart分布 与 相互独立多元正态的估计Wishart分布Wishart 分布的定义:假设 维向量 独立同分布且服从 ,则:假设两个 的随机矩阵 和 分别服从分布 、且彼此独立,则:如果 , , 为 的常数矩阵,则有:目录一元正态分布回顾多元正态分布多元正态分布及 的极大似然估计 及 的抽样分布多元正态的估计一元正态性多元正态性评估正态性多元正态分布的性质多元正态分布的性质评估一元正态性图像方法:直方图、QQ图偏度和峰度统计检验:•Shapiro-Wilks 检验•Kolmogorov-Smirnov 检验•Cramer-von Mises 检验•Anderson-Darling 检验•……Histogram for 100 random numbers from N (0,1)y1F r e q u e n c y-4-20240102030Histogram for 100 random numbers from Exp(2)y2F r e q u e n c y0.00.5 1.0 1.52.0 2.53.0 3.50204060Histogram for 100 random numbers from t(1)y3F r e q u e n c y-4-202451020Histogram for 100 random numbers from -Exp(2)y4F r e q u e n c y-3.5-3.0-2.5-2.0-1.5-1.0-0.50.00204060-2-112-3-1012Q-Q plot for Y1 from N (0,1)Theoretical Quantiles S a m p l e Q u a n t i l e s-2-10120.01.02.03.0Q-Q plot for Y2 from Exp(2)Theoretical QuantilesS a m p l e Q u a n t i l e s-2-112-60-40-2020Q-Q plot for Y3 from t(1)Theoretical Quantiles S a m p l e Q u a n t i l e s-2-1012-3.0-2.0-1.00.0Q-Q plot for Y4 from -Exp(2)Theoretical QuantilesS a m p l e Q u a n t i l e s根据QQ图的形状来判断正态性:直线(公式箭头) 正态反“S”形 比正态厚尾“S”形比正态薄尾凸弯曲右偏凹弯曲左偏评估一元正态性偏度和峰度我们可以用偏度和峰度对正态性进行粗略的判断,它们应该在(0,3)左右评估一元正态性统计检验图像方法的缺点:•图像方法对于小样本并不适用•图像方法以及偏度峰度法只提供了一个粗糙而不正式的检验方法,没有一个明确的决定准则。
多元正态分布及检验PPT共59页

谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
多元正态分布及检验
1、纪律是管理关系的形式。——阿法 德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
厦门大学《应用多元统计分析》习题第03章 多元正态分布均值向量和协差阵的检验

1
4
4
1
2
14
2
1
2
5
2
3
2
15
4
1
1
6
4
0
2
16
2
2
1
7
3
2
1
17
3
3
1
8
4
0
1
18
3
2
2
9
2
1
1
19
3
1
1
10
3
1
2
20
4
0
2
假定三组都服从多元正态分布,检验这三组的总体均值是否有显著性差异
(α = 0.05 )。
3.7 某医生观察了 16 名正常人的 24 小时动态心电图,分析出早晨 3 个小
2 LF HF 4.29 3.03 4.69 4.77 5.28 4.41 5.05 3.28 4.94 3.56 4.54 3.28 4.26 3.11 5.56 5.36
3 LF HF 4.77 3.57 4.58 3.04 5.37 4.79 4.65 2.86 4.68 3.97 4.61 4.40 5.27 3.88 5.55 5.00
3 LF HF 4.16 2.70 3.30 3.10 4.64 3.87 5.54 4.89 5.21 3.88 5.26 3.84 5.43 4.50 4.57 2.32
3.8 根据习题 3.5 中的数据,检验男性婴幼儿与女性婴幼儿的协差阵是否
相等(α = 0.05 )。
3.9 根 据 习 题 3.6 中 的 数 据 , 检 验 三 位 候 选 人 的 协 差 阵 是 否 相 等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
协方差分析
以前介绍的方差分析可用于两组或多组均数间 的比较,其处理因素一般是可以控制的。方差 分析要求各比较组除了所施加的处理因素不同 外,其他对观察指标有影响得因素齐同或均衡, 即要求控制对观察指标有影响的其它因素。在 实际工作中,有时有些因素无法加以控制,或 由于实验设计的疏忽、实验条件的限制等原因, 造成对观察指标有影响的个别因素未加控制或 难以控制。此时用方差分析不合适,应考虑用 协方差分析。
0.252 5.550
2.773 61.049
Sc- 1 = 轾 犏 犏 臌- 09..432761
- 0.426 0.200
( ) ( ) T 2 = n1n2
n1 + n2
X1 -
X2
Sc- 1
X1 -
X2
= 42? (0.50
13
3.10)轾 犏 犏 臌- 09..432761
-
0.426 0.200
0.245 4.267
, S2
=
轾 犏 犏 臌00..029588
0.258 6.619
Sc =
1 n1 + n2 -
2 轾 臌(n1 -
1)S1 + (n2 -
1)S2
= 1 创[5
6+ 7- 2
S1 + 6? S2 ]
1? 11
轾 犏 犏 臌12..370703
= 轾 犏 犏 臌00..215128
(n - 1)m (5- 1)? 3
df1 = 3, df2 = 2
两组比较
对于单变量且服从正态分布资料的两样
本的比较 变形
t = (X1 - X2)
n1 + n2 n1n2
Sc2
( ) ( ) t2 = n1n2
n1 + n2
X1 -
X2
Sc- 2
X1 -
X2
当为多元资料时,此公式推广为HotelingT 2
轾 犏 犏 臌30..1500
= 9.50
F = n1 + n2 - m - 1T 2 = 10 ? 9.50
(n1 + n2 - 2)m
22
4.32, df1 = 2, df2 = 10
SAS计算程序:
proc glm; class gr; model y1 y2=gr; contrast 'gr1 vs gr2' gr 1 -1 0; contrast 'gr1 vs gr3' gr 1 0 -1; contrast 'gr2 vs gr3' gr 0 1 -1; anova h=gr; run;
其中 X 为样本均数向量,S 为样本协方差阵,m0 总体均
数向量。
当
H0
成立时
n-
F=
(n -
m
1)m
T
2,
df1
=
m, df2 =
n-
m
例1:
如随机抽取某单位5名有冠心病的成年男 性,测量其甘油三脂(mmol/L),总 胆固醇(mmol/L),和高密度脂蛋白 胆固醇(mmol/L)含量,已知某单位 正常成年男性的甘油三脂、总胆固醇、 和高密度脂蛋白胆固醇的均数是1.02 mmol/L、2.73 mmol/L和 2.04mmol/L。问该单位冠心病成年男 性的血脂与正常成年男性有无差别?
样 甘油 本 三脂 号
X1 - 1.02
1 1.78 2 0.67 3 0.56 4 0.66 5 0.21
总胆 固醇
X 2 - 2.73
0.83 0.96 0.83 1.12 0.16
高密度脂蛋白 胆固醇
X3 - 2.04
-1.01 -0.84 -0.39 -1.03 -0.40
计算:
X - m0 = 骣 ççççççç桫- 000...775787604÷÷÷÷÷÷÷÷
1
11
2
x2
22
2
2
212
x1
1
11
x2
2
22
图1: 两个二元正态分布
11 22 且 12 0
11 22 且 12 0.75
多元正态分布的性质
= 5? (0.776, 0.780,
0.574)鬃轾 犏 犏 犏 犏 犏 臌134787...535109
47.59 182.86 134.32
38.30 134.32 103.60
骣 ççççççç桫- 000...775877064÷÷÷÷÷÷÷÷
= 295.743
F = n - m T 2 = 5- 3 ? 295.743
A2 x2 y2
17 97 16 90 18 100 18 95 21 103 22 106 19 99 18 94
A3 x3 y3
22 89 24 91 20 83 23 95 25 100 27 102 30 105 32 110
协方差分析中称需比较的因素为因子称 影响观察指标,需排除其影响的数量因 素为协变量。
x2 2i
2
x2i n
n 1
12 21 Corr X1, X 2 S21
x1i x2i
x1i n
n 1
x2i
12 21 /
11 22 r12
x1ix2i
x1i
x2i
n
x2
多元正态均值检验
H0 : 1 2 L k
H1 : 至少存在,使 i j i j
统计量的构造
组间协方差阵:B
k
n
X X
'
X X
1
组内协方差阵:E k
n
X
j
X
'
K
X
j
X
A
1 j1
1i
x1i
2
n
x2 2i
x2i
2
n
协方差阵与逆阵
11 21
12
22
1
1
11
22
2 12
22 Fra bibliotek12 21
11
1122
2 12
11 22
1 2 12
样本协方差阵与逆阵
实例
为研究三种饲料(A1,A2,A3)对猪催肥效果, 用每种饲料喂养8头猪,实验用猪的初始 体重未控制。喂养一段时间后观察小猪 的增重,所得资料如下表,试分析三种 饲料对猪催肥效果是否相同。
三组小猪的初始体重与增重 (kg)
A1 x1 y1
15 85 13 83 11 65 12 76 12 80 16 91 14 84 17 90
反之,如果出现下列情况之一,就难以得出
结论: 1.两组指标虽有显著差别,但趋势不一。或无 显著差别,但P接近0.05。 2 .两组间有些指标有显著差别,有些却无显著 差别。
多元正态分布 定义
P维正态分布定义:对随机变量 X=(X1,X2,…,XP) 的密度函数是
f (X )
2
1 X 1 X / 2 e p / 2 1/ 2
三种检验
(1)检验饲料A与初始体重x间是否存在交 互作用。、因为若两者有交互作用,则 意味着在x的不同取值下A对观察值的作 用不同,即可能对x的某些取值,A1的效 果最好,而对x的另一些取值,A2的效果 最好,因而撇开x谈A的主效应无多大意 义。相应的检验假设是A与x的交互效应 为0。
三种检验
(2)若A与x间无交互作用,则进一步检验 初始体重x与增重y间是否存在线性关系。 若不存在线性关系,则不能用协方差分 析比较三组均数间的差别。因为协方差 分析是利用协变量x与观察指标y间的线 性回归扣除x对y的影响。相应的检验假 设为x与y间的回归系数为0。
53
9
3.00
45
4
3.64
50
10
3.35
47
5
3.60
52
11
2.60
50
6
4.00
55
12
3.15
50
13
3.55
52
计算:
X1 = 轾 犏 犏 臌531..6657 , X2 = 轾 犏 犏 臌438..1557 , X1 - X2 = 轾 犏 犏 臌30..1500
S1 = 轾 犏 犏 臌00..124425
1.有限个多元正态的线性组合为多元正 态分布。 2.一个多元正态分布的所有子集分布有 一个多元正态分布。 3.零协方差意味着相应的随机变量是独 立的。 4 .分量的条件分布是正态分布。
多元正态性的判定
通常对多元正态分布的判断采用对边缘 分布的判断,即:若对多元变量X而言它 所有的一元分布都是正态分布的话,就 认为X是多元正态分布,此时很少出现非 正态的多元数据集。
S = 轾 犏 犏 犏 犏 犏 臌- 000...302584
0.08 0.13 - 0.20
- 0.24 - 0.21
0.36
轾犏17.51 S- 1 = 犏犏47.59
犏犏臌38.30
47.59 182.86 134.32
38.30 134.32 103.60
