C4.5 分类决策树
数据挖掘中的数据分类算法综述

分析Technology AnalysisI G I T C W 技术136DIGITCW2021.021 决策树分类算法1.1 C 4.5分类算法的简介及分析C4.5分类算法在我国是应用相对较早的分类算法之一,并且应用非常广泛,所以为了确保其能够满足在对规模相对较大的数据集进行处理的过程中有更好的实用性能,对C4.5分类算法也进行了相应的改进。
C4.5分类算法是假如设一个训练集为T ,在对这个训练集建造相应的决策树的过程中,则可以根据In-formation Gain 值选择合理的分裂节点,并且根据分裂节点的具体属性和标准,可以将训练集分为多个子级,然后分别用不同的字母代替,每一个字母中所含有的元组的类别一致。
而分裂节点就成为了整个决策树的叶子节点,因而将会停止再进行分裂过程,对于不满足训练集中要求条件的其他子集来说,仍然需要按照以上方法继续进行分裂,直到子集所有的元组都属于一个类别,停止分裂流程。
决策树分类算法与统计方法和神经网络分类算法相比较具备以下优点:首先,通过决策树分类算法进行分类,出现的分类规则相对较容易理解,并且在决策树中由于每一个分支都对应不同的分类规则,所以在最终进行分类的过程中,能够说出一个更加便于了解的规则集。
其次,在使用决策树分类算法对数据挖掘中的数据进行相应的分类过程中,与其他分类方法相比,速率更快,效率更高。
最后,决策树分类算法还具有较高的准确度,从而确保在分类的过程中能够提高工作效率和工作质量。
决策树分类算法与其他分类算法相比,虽然具备很多优点,但是也存在一定的缺点,其缺点主要体现在以下几个方面:首先,在进行决策树的构造过程中,由于需要对数据集进行多次的排序和扫描,因此导致在实际工作过程中工作量相对较大,从而可能会使分类算法出现较低能效的问题。
其次,在使用C4.5进行数据集分类的过程中,由于只是用于驻留于内存的数据集进行使用,所以当出现规模相对较大或者不在内存的程序及数据即时无法进行运行和使用,因此,C4.5决策树分类算法具备一定的局限性。
2.决策树(DecisionTree)-ID3、C4.5、CART比较

2.决策树(DecisionTree)-ID3、C4.5、CART⽐较1. 前⾔上⽂介绍了决策树原理和算法,并且涉及了ID3,C4.5,CART3个决策树算法。
现在⼤部分都是⽤CART的分类树和回归树,这三个决策树算法是⼀个改进和补充的过程,⽐较它们之间的关系与区别,能够更好的理解决策时算法。
2. ID3算法2.1 ID3原理ID3算法就是⽤信息增益⼤⼩来判断当前节点应该⽤什么特征来构建决策树,⽤计算出的信息增益最⼤的特征来建⽴决策树的当前节点。
算法具体过程看2.2 ID3的不⾜ID3算法虽然提出了新思路,但是还是有很多值得改进的地⽅。
1. ID3没有考虑连续特征,⽐如长度,密度都是连续值,⽆法在ID3运⽤。
这⼤⼤限制了ID3的⽤途。
2. ID3采⽤信息增益⼤的特征优先建⽴决策树的节点。
很快就被⼈发现,在相同条件下,取值⽐较多的特征⽐取值少的特征信息增益⼤。
⽐如⼀个变量有2个值,各为1/2,另⼀个变量为3个值,各为1/3,其实他们都是完全不确定的变量,但是取3个值的⽐取2个值的信息增益⼤。
如果校正这个问题呢?3. ID3算法对于缺失值的情况没有做考虑4. 没有考虑过拟合的问题ID3 算法的作者昆兰基于上述不⾜,对ID3算法做了改进,这就是C4.5算法,也许你会问,为什么不叫ID4,ID5之类的名字呢?那是因为决策树太⽕爆,他的ID3⼀出来,别⼈⼆次创新,很快就占了ID4,ID5,所以他另辟蹊径,取名C4.0算法,后来的进化版为C4.5算法。
下⾯我们就来聊下C4.5算法3. C4.5算法3.1 C4.5对ID3的改进C4.5改进了上⾯ID3的4个问题,C4.5算法流程具体过程看1. 对于ID3不能处理连续特征,C4.5的思路是将连续的特征离散化。
⽐如m个样本的连续特征A有m个,从⼩到⼤排列为a1,a2,...,a m,则C4.5取相邻两样本值的平均数,⼀共取得m−1个划分点,其中第i个划分点Ti表⽰为:T i=a i+a i+12。
常见决策树分类算法都有哪些?

在机器学习中,有一个体系叫做决策树,决策树能够解决很多问题。
在决策树中,也有很多需要我们去学习的算法,要知道,在决策树中,每一个算法都是实用的算法,所以了解决策树中的算法对我们是有很大的帮助的。
在这篇文章中我们就给大家介绍一下关于决策树分类的算法,希望能够帮助大家更好地去理解决策树。
1.C4.5算法C4.5算法就是基于ID3算法的改进,这种算法主要包括的内容就是使用信息增益率替换了信息增益下降度作为属性选择的标准;在决策树构造的同时进行剪枝操作;避免了树的过度拟合情况;可以对不完整属性和连续型数据进行处理;使用k交叉验证降低了计算复杂度;针对数据构成形式,提升了算法的普适性等内容,这种算法是一个十分使用的算法。
2.CLS算法CLS算法就是最原始的决策树分类算法,基本流程是,从一棵空数出发,不断的从决策表选取属性加入数的生长过程中,直到决策树可以满足分类要求为止。
CLS算法存在的主要问题是在新增属性选取时有很大的随机性。
3.ID3算法ID3算法就是对CLS算法的最大改进是摒弃了属性选择的随机性,利用信息熵的下降速度作为属性选择的度量。
ID3是一种基于信息熵的决策树分类学习算法,以信息增益和信息熵,作为对象分类的衡量标准。
ID3算法结构简单、学习能力强、分类速度快适合大规模数据分类。
但同时由于信息增益的不稳定性,容易倾向于众数属性导致过度拟合,算法抗干扰能力差。
3.1.ID3算法的优缺点ID3算法的优点就是方法简单、计算量小、理论清晰、学习能力较强、比较适用于处理规模较大的学习问题。
缺点就是倾向于选择那些属性取值比较多的属性,在实际的应用中往往取值比较多的属性对分类没有太大价值、不能对连续属性进行处理、对噪声数据比较敏感、需计算每一个属性的信息增益值、计算代价较高。
3.2.ID3算法的核心思想根据样本子集属性取值的信息增益值的大小来选择决策属性,并根据该属性的不同取值生成决策树的分支,再对子集进行递归调用该方法,当所有子集的数据都只包含于同一个类别时结束。
机器学习总结(八)决策树ID3,C4.5算法,CART算法

机器学习总结(⼋)决策树ID3,C4.5算法,CART算法本⽂主要总结决策树中的ID3,C4.5和CART算法,各种算法的特点,并对⽐了各种算法的不同点。
决策树:是⼀种基本的分类和回归⽅法。
在分类问题中,是基于特征对实例进⾏分类。
既可以认为是if-then规则的集合,也可以认为是定义在特征空间和类空间上的条件概率分布。
决策树模型:决策树由结点和有向边组成。
结点⼀般有两种类型,⼀种是内部结点,⼀种是叶节点。
内部结点⼀般表⽰⼀个特征,⽽叶节点表⽰⼀个类。
当⽤决策树进⾏分类时,先从根节点开始,对实例的某⼀特征进⾏测试,根据测试结果,将实例分配到⼦结点。
⽽⼦结点这时就对应着该特征的⼀个取值。
如此递归对实例进⾏测试分配,直⾄达到叶结点,则该实例属于该叶节点的类。
决策树分类的主要算法有ID3,C4.5。
回归算法为CART算法,该算法既可以分类也可以进⾏回归。
(⼀)特征选择与信息增益准则特征选择在于选取对训练数据具有分类能⼒的特征,⽽且是分类能⼒越强越好,这样⼦就可以提⾼决策树的效率。
如果利⽤⼀个特征进⾏分类,分类的结果与随机分类的结果没有差异,那么这个特征是没有分类能⼒的。
那么⽤什么来判别⼀个特征的分类能⼒呢?那就是信息增益准则。
何为信息增益?⾸先,介绍信息论中熵的概念。
熵度量了随机变量的不确定性,越不确定的事物,它的熵就越⼤。
具体的,随机变量X的熵定义如下:条件熵H(Y|X)表⽰在已知随机变量X的条件下随机变量Y的不确定性,随机变量X给定的条件下随机变量Y的条件熵为H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:信息增益表⽰在已知特征X的情况下,⽽使得Y的信息的不确定性减少的程度。
信息增益的定义式如下:g(D,A)表⽰特征A对训练集D的信息增益,其为集合D的经验熵H(D)与在特征A给定条件下D的经验条件熵H(D|A)之差。
⼀般熵与条件熵之差,称为互信息。
在决策树中,信息增益就等价于训练数据集中的类与特征的互信息。
C45算法

• 定理表明, 对连续属性A , 使得实例集合的平均类熵达 到最小值的T , 总是处于实例序列中两个相邻异类实例 之间。
整理ppt
14
(2)能够完成对连续属性的离散化处理
信息增益(Gain) :
G a ( V ) i H n ( C ) H ( C |V ) io n ( T ) i fo n v ( T )f
属性V的信息熵:
n
H(V) p(vi)log2(p(vi)) i1
n
i1
|Ti | |T|
log2||TTi ||
spli_t info(V)
整理ppt
政治成绩的信息增益为:
G ai(政 n 治成 I(r1 绩 ,r2,r3 ) ,r4)E(政治成绩 0.559
整理ppt
5
(1)用信息增益率代替信息增益来选择属性;
设T 为训练数据集,共有k 个类别,集合表示为 { C1 ,C2 , ⋯,Ck } , | Cj |为Cj 类的例子数, | T |为数据集T 的例子数。 选择一个属性V, 设它有n个互不重合的取值va ( 1≤a≤n) ,则T 被分为n个子集{ T1,T2⋯,Tn } , 这里 Ti 中的所有实例的取值均为vi。|Ti|为V =vi 的例子 数, |Cjv|是V =vi 的例子中,具有Cj 类别的例子数。
整理ppt
15
(2)能够完成对连续属性的离散化处理
当需要离散化的属性的属性值越多, 而所属类别越少 时, 性能提高越明显;
当出现最不理想情况, 即每个属性值对应一个类别, 改进算法运算次数与未改进算法相同, 不会降低算法 性能。
C4.5决策树
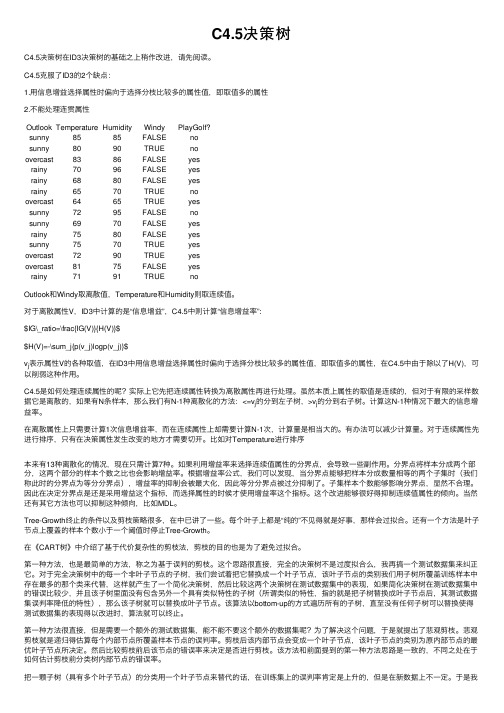
C4.5决策树C4.5决策树在ID3决策树的基础之上稍作改进,请先阅读。
C4.5克服了ID3的2个缺点:1.⽤信息增益选择属性时偏向于选择分枝⽐较多的属性值,即取值多的属性2.不能处理连贯属性Outlook Temperature Humidity Windy PlayGolf?sunny8585FALSE nosunny8090TRUE noovercast8386FALSE yesrainy7096FALSE yesrainy6880FALSE yesrainy6570TRUE noovercast6465TRUE yessunny7295FALSE nosunny6970FALSE yesrainy7580FALSE yessunny7570TRUE yesovercast7290TRUE yesovercast8175FALSE yesrainy7191TRUE noOutlook和Windy取离散值,Temperature和Humidity则取连续值。
对于离散属性V,ID3中计算的是“信息增益”,C4.5中则计算“信息增益率”:$IG\_ratio=\frac{IG(V)}{H(V)}$$H(V)=-\sum_j{p(v_j)logp(v_j)}$v j表⽰属性V的各种取值,在ID3中⽤信息增益选择属性时偏向于选择分枝⽐较多的属性值,即取值多的属性,在C4.5中由于除以了H(V),可以削弱这种作⽤。
C4.5是如何处理连续属性的呢?实际上它先把连续属性转换为离散属性再进⾏处理。
虽然本质上属性的取值是连续的,但对于有限的采样数据它是离散的,如果有N条样本,那么我们有N-1种离散化的⽅法:<=v j的分到左⼦树,>v j的分到右⼦树。
计算这N-1种情况下最⼤的信息增益率。
在离散属性上只需要计算1次信息增益率,⽽在连续属性上却需要计算N-1次,计算量是相当⼤的。
有办法可以减少计算量。
c4.5决策树原理

c4.5决策树原理C4.5(也称为C5.0)是一种经典的决策树算法,由Ross Quinlan于1993年提出。
它是一种用于机器学习和数据挖掘的强大工具,主要用于分类问题。
以下是C4.5决策树算法的原理概述:1. 信息熵和信息增益:C4.5使用信息熵和信息增益来构建决策树。
信息熵是对数据集的纯度度量,信息增益表示通过某个属性对数据集进行划分所带来的纯度提升。
C4.5的目标是选择信息增益最大的属性作为划分依据。
2. 决策树构建过程:2.1 选择最佳属性:•对每个属性计算信息增益。
•选择信息增益最大的属性作为当前节点的划分属性。
2.2 划分数据集:•使用选定的属性对数据集进行划分,生成子节点。
•对于每个子节点,递归执行上述过程,直到满足停止条件。
2.3 停止条件:•数据集已经纯净(属于同一类别)。
•到达树的最大深度。
•不再有可用属性进行划分。
3. 剪枝:C4.5在决策树构建完成后执行剪枝,以避免过度拟合。
剪枝的目标是去除一些不必要的叶子节点,提高模型的泛化性能。
4. 缺失值处理:C4.5能够处理缺失值,当在某个节点上某个属性的值缺失时,它会考虑所有可能的取值,并按照缺失值所占比例计算信息增益。
5. 数值型属性处理:对于数值型属性,C4.5采用二分法进行处理。
它通过在属性上选择一个阈值,将数据集分为两个子集,然后选择信息增益最大的阈值进行划分。
6. 实例加权:在C4.5中,每个样本都有一个权重,这个权重可以用于调整每个样本在信息增益计算中的贡献度。
7. 优缺点:7.1 优点:•生成的决策树易于理解和解释。
•能够处理混合属性类型。
•能够处理缺失值。
•具有较好的泛化性能。
7.2 缺点:•对噪声敏感。
•生成的树可能过于复杂,需要进行剪枝。
•处理大量数据时可能效率较低。
8. 应用领域:C4.5广泛应用于分类问题,例如医学诊断、金融风险评估、客户分类等领域。
9.C4.5决策树算法通过利用信息熵和信息增益来构建树结构,是一种强大的分类工具。
c4.5算法例题

c4.5算法例题C4.5(也称为J48)是一种用于决策树分类的经典算法。
它是ID3算法的改进版本,能够处理连续属性和缺失值,并使用信息增益比来选择最佳分裂属性。
下面是一个示例题目,展示了如何使用C4.5算法构建决策树。
假设我们有一个数据集,描述了一些动物的特征,并指示它们是否属于"哺乳动物"这一类别。
数据集的特征包括体温(连续值,单位为摄氏度)、鳞片覆盖(离散值,取值为"有"或"无")、生育类型(离散值,取值为"胎生"或"卵生")、是否有爪子(离散值,取值为"是"或"否")。
下面是一个简化的数据集示例:现在我们使用C4.5算法构建一个决策树来预测动物的类别。
首先,我们计算每个特征的信息增益比,并选择信息增益比最高的特征作为根节点。
在这个例子中,我们的目标是预测动物的类别,因此我们计算每个特征相对于类别的信息增益比。
1. 计算体温的信息增益比:-计算体温的信息增益。
-计算体温的分裂信息(使用离散化的方法,例如将体温分为几个范围)。
-计算体温的信息增益比。
2. 计算鳞片覆盖的信息增益比:-计算鳞片覆盖的信息增益。
-计算鳞片覆盖的分裂信息。
-计算鳞片覆盖的信息增益比。
3. 计算生育类型的信息增益比:-计算生育类型的信息增益。
-计算生育类型的分裂信息。
-计算生育类型的信息增益比。
4. 计算是否有爪子的信息增益比:-计算是否有爪子的信息增益。
-计算是否有爪子的分裂信息。
-计算是否有爪子的信息增益比。
选择信息增益比最高的特征作为根节点,并根据该特征的不同取值构建子节点。
重复这个过程,直到所有的数据都被正确分类或没有更多的特征可用为止。
这只是一个简化的例子,实际应用中可能涉及更多的特征和数据。
C4.5算法会自动选择最佳的特征和分裂点,以构建一个准确且具有解释性的决策树模型。
c4.5决策树例题

c4.5决策树例题决策树是一种常见的机器学习算法,用于分类和预测任务。
C4.5是决策树算法的一种改进版本,可以处理具有多个特征和多个类别的数据集。
下面是一个关于购买电子产品的例题,展示C4.5决策树的具体步骤:假设我们要根据以下属性来预测一个人是否会购买电子产品:1.年龄:青年、中年、老年2.收入:低、中、高3.学历:中学、大学、研究生4.信用等级:差、一般、良好、优秀我们有一个包含以下训练数据的数据集:以下是C4.5决策树的具体步骤:步骤1:计算初始熵计算每个可能的类别的初始熵。
在这个例子中,购买电子产品的可能类别是是和否,因此初始熵为:H(D) = -((6/10) * log2(6/10) + (4/10) * log2(4/10)) ≈ 0.971步骤2:计算每个属性的信息增益计算每个属性的信息增益(即使用该属性进行划分后的熵的减少量)。
对于每个属性,计算其每个可能值的条件熵,并将其与初始熵进行比较来计算信息增益。
具体步骤如下:a) 对于属性"年龄",计算其各个值的条件熵:•年龄=青年:购买(2是, 2否),条件熵=-((2/4) * log2(2/4) + (2/4) * log2(2/4)) = 1.0•年龄=中年:购买(3是, 1否),条件熵=-((3/4) * log2(3/4) + (1/4) * log2(1/4)) ≈ 0.811•年龄=老年:购买(1是, 1否),条件熵=-((1/2) * log2(1/2) + (1/2) * log2(1/2)) = 1.0然后,计算年龄属性的信息增益:Gain(年龄) = H(D) - ((4/10) *1.0 + (4/10) * 0.811 + (2/10) * 1.0) ≈ 0.124b) 对于属性"收入",计算其各个值的条件熵:•收入=低:购买(1是, 1否),条件熵=-((1/2) * log2(1/2) + (1/2) * log2(1/2)) = 1.0•收入=中:购买(3是, 1否),条件熵=-((3/4) * log2(3/4) + (1/4) * log2(1/4)) ≈ 0.811•收入=高:购买(2是, 2否),条件熵=-((2/4) * log2(2/4) + (2/4) * log2(2/4)) = 1.0然后,计算收入属性的信息增益:Gain(收入) = H(D) - ((2/10) * 1.0 + (4/10) * 0.811 + (4/10) * 1.0) ≈ 0.291c) 对于属性"学历",计算其各个值的条件熵:•学历=中学:购买(1是, 1否),条件熵=-((1/2) * log2(1/2) + (1/2) * log2(1/2)) = 1.0•学历=大学:购买(3是, 2否),条件熵=-((3/5) * log2(3/5) + (2/5) * log2(2/5)) ≈ 0.971•学历=研究生:购买(3是, 1否),条件熵=-((3/4) * log2(3/4) + (1/4) * log2(1/4)) ≈ 0.811然后,计算学历属性的信息增益:Gain(学历) = H(D) - ((2/10) *1.0 + (5/10) * 0.971 + (3/10) * 0.811) ≈ 0.128d) 对于属性"信用等级",计算其各个值的条件熵:•信用等级=差:购买(0是, 1否),条件熵=0•信用等级=一般:购买(1是, 1否),条件熵=-((1/2) * log2(1/2) + (1/2) * log2(1/2)) = 1.0•信用等级=良好:购买(2是, 1否),条件熵=-((2/3) * log2(2/3) + (1/3) * log2(1/3)) ≈ 0.918•信用等级=优秀:购买(3是, 1否),条件熵=-((3/4) * log2(3/4) + (1/4) * log2(1/4)) ≈ 0.811然后,计算信用等级属性的信息增益:Gain(信用等级) = H(D) - ((1/10) * 0 + (2/10) * 1.0 + (3/10) * 0.918 + (4/10) * 0.811) ≈ 0.115步骤3:选择信息增益最大的属性作为当前节点的划分属性根据信息增益,选择信息增益最大的属性作为当前节点的划分属性。
决策树C4.5算法总结

数据集准备
数据清洗
去除异常值、缺失值,对数据进行预处理,使其满足算法要 求。
数据分割
将数据集分为训练集和测试集,用于训练和评估决策树模型 。
特征选择与划分
特征重要性评估
计算每个特征对目标变量的影响程度,选择最重要的特征作为划分标准。
特征划分
根据特征的重要性和信息增益率,将数据集划分为不同的子集,形成决策树的 节点。
THANKS
感谢观看
案例二:医疗诊断分类
数据集
医疗诊断数据集包含了1452 条样本,每个样本有11个特 征,目标变量为是否患有某
种疾病。
算法应用
使用C4.5算法构建决策树模 型,对数据进行训练和测试 ,评估模型的准确率、召回
率和F1分数等指标。
结果分析
通过决策树模型,可以辅助 医生进行疾病诊断,提高诊 断的准确性和效率。
处理连续属性和缺失值的方法优化
• C4.5算法在处理连续属性和缺失值时采用了一些简单的策略,如将连续属性离散化或忽略缺失值。这些策略可 能导致决策树无法充分利用数据中的信息。因此,一些研究者提出了更复杂的方法来处理连续属性和缺失值, 如使用插值或回归方法来处理连续属性,以及使用特殊标记或填充值来处理缺失值。这些方法可以提高决策树 对连续属性和缺失值的处理能力,从而提高模型的分类准确率。
2
C4.5算法采用了信息增益率、增益率、多变量增 益率等更加复杂的启发式函数,提高了决策树的 构建精度和泛化能力。
3
C4.5算法还引入了剪枝策略,通过去除部分分支 来避免过拟合,提高了决策树的泛化性能。
决策树C4.5算法的应用场景
数据挖掘
C4.5算法广泛应用于数据挖掘 领域,用于分类、回归和聚类
决策树分类算法c4.5的具体应用场景

一、概述决策树分类算法是数据挖掘和机器学习领域中常用的算法之一,它可以用于对数据进行分类和预测。
其中C4.5算法是决策树分类算法中的一种经典方法,它采用了信息增益作为划分属性的标准,具有较好的泛化能力和分类精度。
在实际应用中,C4.5算法被广泛应用于各种领域,本文将介绍C4.5算法的具体应用场景。
二、金融领域1. 信用评分在金融领域,银行和信用卡机构经常需要对客户的信用进行评分,以判断其是否具有偿还借款的能力。
C4.5算法可以根据客户的个人信息、贷款记录和其他相关数据构建决策树模型,用于预测客户的信用水平,帮助金融机构做出信贷决策。
2. 欺诈检测另外,C4.5算法也可以在金融领域用于欺诈检测。
金融交易中存在大量的欺诈行为,通过分析交易数据和客户行为特征,C4.5算法可以构建欺诈检测模型,帮助金融机构及时发现和防范欺诈风险。
三、医疗领域1. 疾病诊断在医疗领域,C4.5算法可以应用于疾病的诊断预测。
通过对医疗数据进行分析,包括患者的症状、体征、生化指标等信息,利用C4.5算法可以建立疾病的分类模型,帮助医生进行疾病诊断和预测,提高诊断的准确性和效率。
2. 药物治疗预测C4.5算法也可以用于预测患者对药物治疗的反应。
通过分析患者的遗传信息、生理特征和药物治疗记录等数据,C4.5算法可以构建个性化的药物治疗模型,帮助医生选择最适合患者的治疗方案,提高治疗效果。
四、市场营销领域1. 客户分类在市场营销领域,企业需要对客户进行分类,以制定针对不同客户裙体的营销策略。
C4.5算法可以根据客户的消费行为、偏好信息、地理位置等数据构建客户分类模型,帮助企业对客户进行精细化管理和营销。
2. 产品推荐C4.5算法还可以用于产品推荐。
通过分析客户的购物历史、浏览行为和偏好信息,C4.5算法可以构建产品推荐模型,帮助企业向客户推荐符合其偏好的产品,提高销售额和客户满意度。
五、交通领域1. 交通流量预测在交通领域,C4.5算法可以应用于交通流量的预测。
c4.5算法 例题

c4.5算法例题一、算法简介C4.5算法是一种决策树生成算法,它是在C4算法的基础上进行改进得到的,具有更高的生成效率和准确性。
C4.5算法通过选择最佳特征、构建决策树、剪枝优化等步骤,生成可用于分类和预测的决策树模型。
二、算法步骤1. 特征选择:从输入数据中选择出与目标变量相关性最强、信息增益最大的特征作为最佳特征。
2. 构建决策树:根据最佳特征建立决策树的各个节点,每个节点包含一个属性值和一个分支,指向满足该属性值的样本集合。
3. 剪枝优化:通过剪枝算法对决策树进行优化,减少决策树的复杂度,提高模型的准确性和稳定性。
三、例题说明假设我们有一组葡萄酒品质的数据,数据集包括多个特征,如酒精度、酸度、甜度等,目标变量为葡萄酒的品质评分。
我们希望使用C4.5算法构建一个决策树模型,对新的葡萄酒进行品质预测。
1. 准备数据:将数据集导入到数据分析软件中,确保数据格式正确,特征和目标变量分离。
2. 特征选择:使用C4.5算法的特征选择步骤,从多个特征中选择出与品质评分相关性最强、信息增益最大的特征,如酒精度、酸度等。
3. 构建决策树:根据选定的特征,使用C4.5算法构建决策树。
首先,选择酒精度作为最佳特征,建立第一个节点。
根据酒精度的不同值,将样本分为两个子集。
然后,在每个子集中继续选择最佳特征建立分支,不断重复这个过程,直到达到决策树的终止条件(如叶节点)。
4. 剪枝优化:对决策树进行剪枝优化,减少其复杂度。
可以通过设置剪枝阈值、限制树的最大深度等方式进行优化。
5. 模型评估:使用测试数据集对优化后的决策树模型进行评估,评估指标包括准确率、召回率、AUC值等。
四、代码实现由于C4.5算法的实现较为复杂,需要一定的编程知识和技能。
这里以Python语言为例,展示使用Scikit-learn库实现C4.5算法的基本步骤。
假设已经将数据集加载到一个Pandas数据框中,命名为df。
```pythonfrom sklearn.model_selection import train_test_splitfrom sklearn.tree import C4_5, export_graphvizimport graphviz# 划分训练集和测试集X_train, X_test, y_train, y_test =train_test_split(df.drop('quality', axis=1), df['quality'],random_state=42)# 创建C4.5模型对象clf = C4_5()# 训练模型clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)# 模型评估accuracy = clf.score(X_test, y_test)print('Accuracy:', accuracy)```五、总结通过以上步骤,我们可以使用C4.5算法构建一个用于葡萄酒品质预测的决策树模型。
c4.5算法的基本原理 -回复

c4.5算法的基本原理-回复什么是C4.5算法?C4.5算法是机器学习领域中的一种决策树算法,是ID3算法的改进版本。
它由Ross Quinlan于1993年提出,是一种用于分类问题的监督学习算法。
C4.5算法的基本原理是通过对数据集进行划分来构建决策树,以实现对新样本进行分类。
下面将详细介绍C4.5算法的基本原理和步骤。
C4.5算法的基本原理是基于信息增益来选择最优特征进行划分。
在构建决策树的过程中,C4.5算法通过计算每个特征的信息增益比来选择最优特征,从而实现对数据集的划分。
信息增益是指在得知某个特征的取值后,对分类结果的不确定性减少的程度。
C4.5算法的步骤如下:1. 选择最优特征:计算每个特征的信息增益比,选择具有最大信息增益比的特征作为当前节点的划分特征。
2. 划分数据集:根据划分特征将数据集划分为多个子数据集,每个子数据集包含具有相同特征值的样本。
3. 递归构建子树:对每个子数据集递归地应用步骤1和步骤2,构建子树。
4. 停止划分:当数据集的所有属性都已经被使用或者数据集中的样本都属于同一类别时,停止划分,将当前节点标记为叶节点,并将叶节点标记为数据集中样本数最多的类别。
5. 构建决策树:将步骤3中得到的子树连接到当前节点,构成完整的决策树。
具体来说,C4.5算法的核心步骤是选择最优特征和划分数据集。
在选择最优特征时,C4.5算法通过计算每个特征的信息增益比来选择最优特征。
信息增益比是信息增益除以划分数据集的熵,熵是度量数据集的纯度的指标。
信息增益比能够避免特征取值较多而导致的信息增益偏大的问题,从而更加准确地选择最优特征。
划分数据集是将数据集根据划分特征的取值划分为多个子数据集,每个子数据集包含具有相同特征值的样本。
划分后的子数据集可以分别作为子树的训练数据,递归地构建子树。
每个子树的构建过程都是通过选择最优特征和划分数据集来实现的。
当数据集的所有属性都已经被使用或者数据集中的样本都属于同一类别时,停止划分,将当前节点标记为叶节点,并将叶节点标记为数据集中样本数最多的类别。
C4 5算法

信息增益实际上是ID3算法中用来进行属性选择度量的。它选择具有最高信息增益的属性来作为节点N的分裂 属性。该属性使结果划分中的元组分类所需信息量最小。对D中的元组分类所需的期望信息为下式:
Info(D)又称为熵。
现在假定按照属性A划分D中的元组,且属性A将D划分成v个不同的类。
其它特征
C4.5算法与ID3算法一样使用了信息熵的概念,并和ID3一用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习:给定一个数据集,其中 的每一个元组都能用一组属性值来描述,每一个元组属于一个互斥的类别中的某一类。C4.5的目标是通过学习, 找到一个从属性值到类别的映射关系,并且这个映射能用于对新的类别未知的实体进行分类。
C4.5算法
ID3算法的一个扩展
01 产品介绍
目录
02 改进表现
03 优缺点
04 算法描述
05 属性选择度量
06 其它特征
C4.5算法是由Ross Quinlan开发的用于产生决策树的算法。该算法是对Ross Quinlan之前开发的ID3算法的 一个扩展。C4.5算法产生的决策树可以被用作分类目的,因此该算法也可以用于统计分类。
对非离散数据也能处理。
能够对不完整数据进行处理 。
优缺点
C4.5算法优点:产生的分类规则易于理解,准确率较高。
缺点:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。此外,C4.5只 适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行。
算法描述
C4.5并不一个算法,而是一组算法—C4.5,非剪枝C4.5和C4.5规则。以下算法将给出C4.5的基本工作流程: Input:an attibute-valued dataset D 1:Tree={} 2:if D is "pure"OR other stopping criteria met then 3: terminate 4: end if 5:for all attribute a∈ D do 6: Compute inforation-theoretic criteria if we split on a 7:end for 8:a(best)=Best attribute according to above computed criteria 9: Tree=Create a decision node that tests a(best) in the root
数据挖掘中的十大算法

数据挖掘中的十大算法数据挖掘是当今最火热的技术之一,而算法则是数据挖掘的核心,其中有十大算法是数据挖掘领域中最常用的,这十大算法分别是:C4.5决策树算法、朴素贝叶斯算法、k-近邻算法、支持向量机算法、Apriori算法、EM算法、PageRank算法、AdaBoost算法、k-均值聚类算法以及PCA算法。
1. C4.5决策树算法决策树算法是以树形结构来模拟分析决策过程的一类算法,C4.5决策树算法是一种非常常见的决策树算法,它可以适用于多分类、连续值和缺失值情况,同时还可以通过剪枝技术降低过拟合现象。
2. 朴素贝叶斯算法朴素贝叶斯算法是一种基于贝叶斯定理的概率模型,它通常用于解决分类和回归问题。
朴素贝叶斯算法可以通过估计概率来预测结果,因此需要大量的训练数据。
3. k-近邻算法k-近邻算法是一种基于距离的分类算法,它通过比较样本之间的距离来确定它们之间的相似度。
k-近邻算法通常在训练数据已知的情况下使用,它使用最近邻居的标签来预测新的标签。
4. 支持向量机算法支持向量机算法是一种最优化算法,它通常用于解决分类和回归问题。
支持向量机算法通过找到最大间隔超平面来进行分类,同时还可以使用核函数来处理非线性问题。
5. Apriori算法Apriori算法是一种关联规则算法,它通过寻找频繁项集来确定标签之间的关联性。
Apriori算法通常用于市场分析和推荐系统中。
6. EM算法EM算法是一种用于模型参数估计的迭代算法,它被广泛应用于未观测数据的概率推断中。
EM算法通常用于高斯混合模型和隐马尔科夫模型中。
7. PageRank算法PageRank算法是一种用于网页排名的算法,它基于网页的链接结构确定网页的权重。
PageRank算法被广泛应用于搜索引擎中。
8. AdaBoost算法AdaBoost算法是一种基于多个弱分类器构建强分类器的算法,它通常用于解决分类问题。
AdaBoost算法可以通过加权算法使得数据分布发生变化,从而提高分类的精度。
常用的决策树有哪些,有什么异同【面试经验】

常用的决策树有哪些?ID3、C4.5、CART有哪些异同?常用的决策树算法包括ID3、C4.5和CART。
这些算法在构建决策树时有一些共同点和不同点。
共同点:1.目标:它们的目标都是创建一个能够预测未知数据的树状模型。
2.递归过程:都是通过递归的方式划分数据集,生成决策树的各个节点和分支。
3.特征选择:在构建决策树的过程中,都需要选择最优的特征作为划分标准。
不同点:1.特征选择准则:o ID3:使用信息增益作为特征选择的准则。
它只能处理离散型特征,并且没有考虑连续型特征或缺失值的情况。
o C4.5:是ID3的改进版,使用信息增益比作为特征选择的准则。
它既能处理离散型特征,也能处理连续型特征,并且考虑了缺失值的情况。
o CART:使用基尼不纯度作为特征选择的准则。
它既能处理分类问题,也能处理回归问题,并且既支持离散型特征也支持连续型特征。
2.树的结构:o ID3和C4.5:生成的是多叉树,即每个节点可以有多个子节点。
o CART:生成的是二叉树,即每个节点只有两个子节点。
3.剪枝策略:o ID3:通常没有剪枝过程,容易产生过拟合。
o C4.5:有剪枝过程,可以通过后剪枝来优化决策树结构。
o CART:也有剪枝过程,可以通过设置参数来控制剪枝的程度。
4.应用范围:o ID3:主要用于处理离散型特征的分类问题。
o C4.5:既可以处理分类问题,也可以处理回归问题,并且支持离散型和连续型特征。
o CART:既可以处理分类问题,也可以处理回归问题,并且支持离散型和连续型特征。
总结来说,ID3、C4.5和CART是三种常用的决策树算法,它们在特征选择准则、树的结构、剪枝策略和应用范围等方面有所不同。
选择哪种算法取决于具体的问题和数据特征。
c4.5决策树算法例题

c4.5决策树算法例题例题:预测鸢尾花分类题目描述:给定鸢尾花的三种类型:山鸢尾(setosa)、杂色鸢尾(versicolor)和维吉尼亚鸢尾(virginica),以及鸢尾花的四个特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。
使用这些特征来预测鸢尾花的类型。
数据集:以下是一个鸢尾花数据集的样例,每一行表示一个样本,每个特征用一个数字表示。
最后一列是鸢尾花的类型。
1.4 3.5 5.1 1.7 setosa5.0 3.6 5.5 2.6 versicolor4.9 3.05.1 1.8 virginica解题思路:使用C4.5决策树算法对鸢尾花数据集进行分类。
首先,我们需要将数据集分成训练集和测试集,然后使用训练集训练决策树模型。
在训练过程中,我们需要计算每个特征的信息增益率,选择信息增益率最大的特征作为划分标准。
在每个节点处,我们需要计算划分后的数据集的纯度,选择最优的划分标准。
最后,我们使用测试集对决策树模型进行评估,计算分类准确率。
C4.5决策树算法的具体步骤如下:1. 将数据集分成训练集和测试集。
2. 初始化根节点,选择一个特征作为划分标准,计算划分后的数据集的纯度。
3. 如果数据集的纯度已经达到要求,则将该节点标记为叶子节点,并将该节点的类标签作为最终分类结果。
4. 如果数据集的纯度未达到要求,则选择信息增益率最大的特征作为划分标准,将数据集划分为子数据集。
5. 对每个子数据集重复步骤2-4,直到满足停止条件。
6. 构建决策树,将每个节点的最优划分标准记录下来。
7. 使用测试集对决策树模型进行评估,计算分类准确率。
python决策树c4.5例题经典案例

一、概述Python是一种高效的编程语言,广泛应用于数据分析和机器学习领域。
决策树是一种常用的机器学习算法,C4.5是其中一种经典的决策树算法。
本文将以Python为工具,以C4.5算法为基础,通过经典案例的解析,深入探讨C4.5决策树算法的原理和实践应用。
二、C4.5算法介绍1. C4.5算法是基于信息熵的一种决策树算法,其主要目的是通过对训练数据的分析,构建出一颗能够高效分类的决策树。
2. C4.5算法的关键步骤包括:计算信息增益、选择最优特征、递归构建决策树、处理缺失值等。
3. C4.5算法对连续型特征的处理采用二分策略,对离散型特征的处理采用多分策略,能够有效地处理不同类型的数据。
三、经典案例分析1. 数据准备我们以一个经典的鸢尾花数据集为例,数据集包括花萼长度、花萼宽度、花瓣长度、花瓣宽度等特征,以及鸢尾花的种类标签。
2. 数据预处理我们首先需要对数据进行预处理,包括数据清洗、特征选择、数据划分等步骤,以确保数据的质量和准确性。
3. 模型训练接下来,我们使用Python中的决策树库来训练C4.5决策树模型,通过对训练数据的拟合,构建出一颗能够有效分类的决策树。
4. 模型评估我们使用测试数据来评估模型的性能,包括准确率、召回率等指标,以验证模型的有效性和泛化能力。
四、Python实践1. 数据分析我们可以使用Pandas库对数据集进行加载和分析,通过统计分析和可视化等手段,对数据的特征和分布进行深入了解。
2. 模型构建在Python中,我们可以使用scikit-learn等机器学习库来构建C4.5决策树模型,通过设置参数、训练模型等步骤,得到一颗高效的决策树模型。
3. 模型调优在实践中,我们可以通过交叉验证、网格搜索等技术,对模型进行进一步优化,以获得更好的分类效果。
4. 模型应用我们可以将训练好的决策树模型应用到新的数据中,进行预测和分类,以解决实际的分类问题。
五、总结与展望C4.5决策树算法作为经典的机器学习算法,在实际应用中具有广泛的价值和意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。
它的目标是监督学习:给定一个数据集,其中的每一个元组都能用一组属性值来描述,每一个元组属于一个互斥的类别中的某一类。
C4.5的目标是通过学习,找到一个从属性值到类别的映射关系,并且这个映射能用于对新的类别未知的实体进行分类。
C4.5由J.Ross Quinlan在ID3的基础上提出的。
ID3算法用来构造决策树。
决策树是一种类似流程图的树结构,其中每个内部节点(非树叶节点)表示在一个属性上的测试,每个分枝代表一个测试输出,而每个树叶节点存放一个类标号。
一旦建立好了决策树,对于一个未给定类标号的元组,跟踪一条有根节点到叶节点的路径,该叶节点就存放着该元组的预测。
决策树的优势在于不需要任何领域知识或参数设置,适合于探测性的知识发现。
从ID3算法中衍生出了C4.5和CART两种算法,这两种算法在数据挖掘中都非常重要。
下图就是一棵典型的C4.5算法对数据集产生的决策树。
数据集如图1所示,它表示的是天气情况与去不去打高尔夫球之间的关系。
图1 数据集
图2 在数据集上通过C4.5生成的决策树
算法描述
C4.5并不一个算法,而是一组算法—C4.5,非剪枝C4.5和C4.5规则。
下图中的算法将给出C4.5的基本工作流程:
图3 C4.5算法流程
我们可能有疑问,一个元组本身有很多属性,我们怎么知道首先要对哪个属性进行判断,接下来要对哪个属性进行判断?换句话说,在图2中,我们怎么知道第一个要测试的属性是Outlook,而不是Windy?其实,能回答这些问题的一个概念就是属性选择度量。
属性选择度量
属性选择度量又称分裂规则,因为它们决定给定节点上的元组如何分裂。
属性选择度量提供了每个属性描述给定训练元组的秩评定,具有最好度量得分的属性被选作给定元组的分裂属性。
目前比较流行的属性选择度量有--信息增益、增益率和Gini指标。
先做一些假设,设D是类标记元组训练集,类标号属性具有m个不同值,m个不同类Ci(i=1,2,…,m),CiD是D中Ci类的元组的集合,|D|和|CiD|分别是D和CiD中的元组个数。
(1)信息增益
信息增益实际上是ID3算法中用来进行属性选择度量的。
它选择具有最高信息增益的属性来作为节点N的分裂属性。
该属性使结果划分中的元组分类所需信息量最小。
对D中的元组分类所需的期望信息为下式:
(1)
Info(D)又称为熵。
现在假定按照属性A划分D中的元组,且属性A将D划分成v个不同的类。
在该划分之后,为了得到准确的分类还需要的信息由下面的式子度量:
(2)
信息增益定义为原来的信息需求(即仅基于类比例)与新需求(即对A划分之后得到的)之间的差,即
(3)
我想很多人看到这个地方都觉得不是很好理解,所以我自己的研究了文献中关于这一块的描述,也对比了上面的三个公式,下面说说我自己的理解。
一般说来,对于一个具有多个属性的元组,用一个属性就将它们完全分开几乎不可能,否则的话,决策树的深度就只能是2了。
从这里可以看出,一旦我们选择一个属性A,假设将元组分成了两个部分A1和A2,由于A1和A2还可以用其它属性接着再分,所以又引出一个新的问题:接下来我们要选择哪个属性来分类?对D中元组分类所需的期望信息是Info(D) ,那么同理,当我们通过A将D划分成v个子集
Dj(j=1,2,…,v)之后,我们要对Dj的元组进行分类,需要的期望信息就是Info(Dj),而一共有v个类,所以对v个集合再分类,需要的信息就是公式(2)了。
由此可知,如果公式(2)越小,是不是意味着我们接下来对A分出来的几个集合再进行分类所需要的信息就越小?而对于给定的训练集,实际上Info(D)已经固定了,所以选择信息增益最大的属性作为分裂点。
但是,使用信息增益的话其实是有一个缺点,那就是它偏向于具有大量值的属性。
什么意思呢?就是说在训练集中,某个属性所取的不同值的个数越多,那么越有可能拿它来作为分裂属性。
例如一个训练集中有10个元组,对于某一个属相A,它分别取1-10这十个数,如果对A 进行分裂将会分成10个类,那么对于每一个类Info(Dj)=0,从而式(2)为0,该属性划分所得到的信息增益(3)最大,但是很显然,这种划分没有意义。
(2)信息增益率
正是基于此,ID3后面的C4.5采用了信息增益率这样一个概念。
信息增益率使用“分裂信息”值将信息增益规范化。
分类信息类似于
Info(D),定义如下:
(4)
这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。
信息增益率定义:
(5)
选择具有最大增益率的属性作为分裂属性。
(3)Gini指标
Gini指标在CART中使用。
Gini指标度量数据划分或训练元组集D 的不纯度,定义为:
(6)
其它特征
树剪枝
在决策树的创建时,由于数据中的噪声和离群点,许多分枝反映的是训练数据中的异常。
剪枝方法是用来处理这种过分拟合数据的问题。
通常剪枝方法都是使用统计度量,剪去最不可靠的分枝。
剪枝一般分两种方法:先剪枝和后剪枝。
先剪枝方法中通过提前停止树的构造(比如决定在某个节点不再分裂或划分训练元组的子集)而对树剪枝。
一旦停止,这个节点就变成树
叶,该树叶可能取它持有的子集最频繁的类作为自己的类。
先剪枝有很多方法,比如(1)当决策树达到一定的高度就停止决策树的生长;(2)到达此节点的实例具有相同的特征向量,而不必一定属于同一类,也可以停止生长(3)到达此节点的实例个数小于某个阈值的时候也可以停
止树的生长,不足之处是不能处理那些数据量比较小的特殊情况(4)
计算每次扩展对系统性能的增益,如果小于某个阈值就可以让它停止生长。
先剪枝有个缺点就是视野效果问题,也就是说在相同的标准下,也许当前扩展不能满足要求,但更进一步扩展又能满足要求。
这样会过早停止决策树的生长。
另一种更常用的方法是后剪枝,它由完全成长的树剪去子树而形成。
通过删除节点的分枝并用树叶来替换它。
树叶一般用子树中最频繁的类别来标记。
C4.5采用悲观剪枝法,它使用训练集生成决策树又用它来进行剪枝,不需要独立的剪枝集。
悲观剪枝法的基本思路是:设训练集生成的决策树是T,用T来分类训练集中的N的元组,设K为到达某个叶子节点的元组个数,其中分类错误地个数为J。
由于树T是由训练集生成的,是适合训练集的,因此J/K不能可信地估计错误率。
所以用(J+0.5)/K来表示。
设S为T的子树,其叶节点个数为L(s),为到达此子树的叶节点的元组个数总和,为此子树中被错误分类的元组个数之和。
在分类新的元组时,则其错误分类个数为,其标准错误表示为:。
当用此树分类训练集时,设E为分类错误个数,当下面的式子成立时,则删掉子树S,用叶节点代替,且S的子树不必再计算。
