13 体积和表面积比较的练习课

合集下载

体积和表面积的比较

体积和表面积的比较教材简析本节课的整理和复习，主要是对长方体和正方体的特征、表面积与体积的意义和计算方法，以及体积、容积单位以及进率等知识的回顾。

通过整理让学生更好地掌握所学知识，学会使用所学知识解决一些简单的实际问题，培养学生解决问题的水平增加应用知识。

学情分析方体、正方体的基础上实行教学的。

通过学习长方体和正方体，学生对自己周围的空间和空间中的物体形成了初步的空间观点，是进一步学习其他几何图形的基础。

通过这部分的学习，绝大部分学生都深入理解了长方体、正方体，掌握了它们的表面积、容积和体积的计算方法，了解了体积和容积单位以及进率换算。

但因为知识点多，很多概念学生很容易混淆。

学生常常会把公式记得滚瓜烂熟，但是在解答一些实际问题时，却不会灵活使用。

所以，本节课除了要协助学生梳理知识，还应通过迁移比较，促动学生掌握混淆知识的联系与区别，加深印象，形成表象。

教学内容教科书第56页中的习题1、2、3、4以及相对应的练习。

教学目标1、通过学生的自主探究等实践活动，使学生准确区分长方体与正方体的表面积和体积的概念，知道两个知识点间的联系和区别。

2、使学生在准确区分概念的基础上，使用知识解决实际的问题。

3、培养学生独立思考和团结合作的精神。

教学重点区分长、正方体的表面积与体积的概念．教学难点进一步建立体积和表面积的空间观点．教学过程一、开门见山，导入新知教师谈话，导入新课：我们已经学会了长方体、正方体的表面积和体积的计算，在以前的练习中，有些同学容易将这两个概念实行比较。

板书：体积和表面积的比较．二、合作学习，探究新知．（一）说说长方体和正方体有什么相同点和不同点。

（书第56页第一题）长方体有个面，相对的面；有条棱，相对的棱；有个顶点。

正方体有个面，每个面；有条棱，每条棱；有个顶点。

（二）体积和表面积的对比．1、教师让学生拿出准备好的长方体牙膏盒，要求学生分小组看着牙膏盒说说：（1）什么是长方体或正方体的表面积？什么是长方体或正方体的体积？相对应的计算公式各是什么？（2）常用的表面积和体积的计量单位各是什么？相邻两个单位间的进率各是多少归纳小结：长方体或正方体的表面积指它的六个面的总面积，而体积则是指它所占空间的大小．表面积用面积单位来计量，常用的面积单位有平方米、平方分米、平方厘米．体积用体积单位来计量，常用的体积单位有立方米、立方分米、立方厘米．2、教师引导学生思考，要计算出牙膏盒的体积和表面积，一般要知道哪些条件？也就是要测量哪些长度？学生四人小组合作，先测量牙膏盒的体积和表面积的长度（取整厘米数），然后计算出该物体的体积和表面积，教师在活动中，适时指导。

空间几何体的体积和表面积复习课(定)

问题（3）：若在奖杯中间部分堆塑一条龙，缠绕奖杯一圈，且使龙的首与尾在一条竖直线上。两种设计方案中如何堆塑使得龙的身长最短？
图（1）
图（2）
小结：
1、几何体的体积
2、几何体的表面积
3、用分割与组合方法求几何体的体积
4、空间图形问题
平面图形问题
想一想：
一个棱锥的三视图如图，则该棱锥的全面积（单位：cm2）为（A）48+12 2 （B）48+24 2 （C）36+12 2 （D）36+24 2
S (r r r l rl )
'2 2 '
2r `
O`
2r
O
1、多面体的表面积 2、旋转体的表面积
各面面积之和
S球 4 r
空间图形问题平面图形问题
2
O O'
E
O O'
H F
S总 S球 S棱柱侧 S棱台全 1 4 4 8 4 20 14 20 （14 4 20 4） 5 2 64 1576 1777
8
8 20
4
14 20
图（1）图（2）
圆柱的展开图是一个矩形：
如果圆柱的底面半径为 r ，母线为 l ，那么圆柱 2 r 的底面积为，侧面积为 2rl 。因此圆柱的表面积为
S 2r 2rl 2r (r l )
2
O`
O
圆台的展开图是一个扇环，它的表面积等于上、下两个底面和加上侧面的面积，即
锥体的体积
1 V Sh 3
4 3 V r 3
S/=0
球的体积：
用分割与组合方法求几何体的体积。

体积和表面积的比较

体积和表面积的比较
小组交流提纲：小组交流提纲：
（1）长方体、正方体的表面积指的长方体、是什么？体积指的是什么？是什么？体积指的是什么？ (2） (2）表面积和体积分别用什么计量单位表示？位表示？（3）计算长方体、正方体的表面积，计算长方体、正方体的表面积，需要知道什么？计算它的体积呢？需要知道什么？计算它的体积呢？怎样计算它们的体积和表面积？样计算它们的体积和表面积？
长方体、长方体、正方体体积和表面积的比较
不
意义
同
计量单位
点
计算方法
相同点
表面积
体积
长方体、长方体、正方体体积和表面积的比较
不
意义
同
点
计算方法
相同点
计量单位

长方体：长方体：长方体=（长×高+长计算时一平方米、长方体= 6个面平方米、表面积 ×宽+宽×高）×2 般要知道平方分米、的总面平方分米、长、宽、 2 正方体= 平方厘米正方体=棱长 ×6 积高的长度。高的长度。长方体=长×宽×高长方体= 立方米、或底面积× 所占空立方米、或底面积×高体积立方分米、间的大立方分米、正方体=棱长 3 或底正方体= 立方厘米小面积× 面积×高正方体：正方体：一般要知道棱长。道棱长。

空间几何体的表面积和体积经典例题(教师讲义打印一份)

空间几何体的表面积和体积一．课标要求：了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）。

二．命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题，也有已知面积或体积求某些元素的量或元素间的位置关系问题。

即使考查空间线面的位置关系问题，也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想，会把组合体求积问题转化为基本几何体的求积问题，会等体积转化求解问题，会把立体问题转化为平面问题求解，会运用“割补法”等求解。

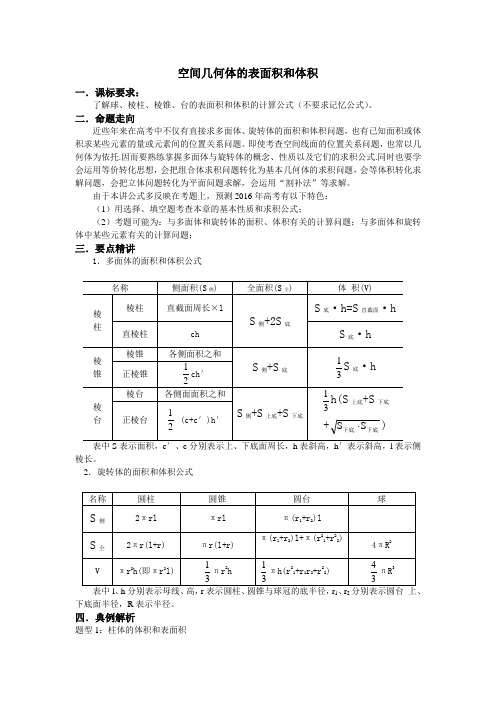
由于本讲公式多反映在考题上，预测2016年高考有以下特色：（1）用选择、填空题考查本章的基本性质和求积公式；（2）考题可能为：与多面体和旋转体的面积、体积有关的计算问题；与多面体和旋转体中某些元素有关的计算问题；三．要点精讲1．多面体的面积和体积公式表中S表示面积，c′、c分别表示上、下底面周长，h表斜高，h′表示斜高，l表示侧棱长。

2．旋转体的面积和体积公式表中l、h分别表示母线、高，r表示圆柱、圆锥与球冠的底半径，r1、r2分别表示圆台上、下底面半径，R表示半径。

四．典例解析题型1：柱体的体积和表面积例1．一个长方体全面积是20cm 2，所有棱长的和是24cm ，求长方体的对角线长. 解：设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得：⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由（2）2得：x 2+y 2+z 2+2xy+2yz+2xz=36（3）由（3）－（1）得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。

点评：涉及棱柱面积问题的题目多以直棱柱为主，而直棱柱中又以正方体、长方体的表面积多被考察。

我们平常的学习中要多建立一些重要的几何要素（对角线、内切）与面积、体积之间的关系。

例2．如图1所示，在平行六面体ABCD —A 1B 1C 1D 1中，已知AB=5，AD=4，AA 1=3，AB ⊥AD ，∠A 1AB=∠A 1AD=3π。

生活数学探究数学

生活数学探究数学-----“体积和表面积”练习课的教学案例和反思背景介绍：体积和表面积比较的教学是在学生弄懂了长方体和正方体表面积与体积的基础上进行教学的。

通过这一节课的学习要让学生进一步理解和掌握长方体和正方体表面积、体积。

在教学中让学生学会把实际问题转化为数学问题，用解决数学问题的方法解决实际问题，从而使学生感受到数学源于生活，数学用于生活。

在设计中，我注意了练习题的开放性，注重让学生自己动手探挖，从探挖中掌握方法，发现问题，分析问题，解决问题。

一、案例描述片段一：活动四：漫步数学园，灵活用一用创设情境：我为亚运出份力。

教师：为迎接2010年广州亚运会，开展全民健身活动，将在我们学校建一个游泳池，小朋友们请开动你们的小脑袋，加入这个建设行列中来吧。

（生答略）教师：在这个游泳池的四周和底面抹上水泥，抹水泥的面积有多大？生：求这个长方体五个面的面积和。

教师：怎样求这五个面的面积？生1：每个面先求出来，再相加。

生2：两个前面+两个右面+一个下面生3：先求6个面的总面积，再减去上面的面积。

生4：四周是4个面，再加一个下面。

教师：说得好，无论是哪一种方法，都必需知道哪些条件？你能独立解决这个问题吗？生：能（学生独立列式计算）（意图：选用学校游泳池的建设来激发学生学习的兴趣，让学生体会数学来源于生活，也应用到生活实际中去。

让学生更好地理解长方体的表面积的意义，同时，这又是一个开放性的练习，让学生用不同的方法解决问题，促进学生创新意识及创新能力的发展。

）片段二：教师：学校的游泳池在大家的努力下，相信很快能建起来了。

通过解决这个问题你有什么收获？生1：我知道了占地面积是下面长方形的面积。

生2：我学会区别一个面、四个面、五个面的应用。

生3：我看到了表面积与体积的区别。

生4：挖泥的高度与装水的深度都是长方体的高。

教师：非常好，你在生活中会找出这样的数学来吗？生：我想计算一下做这个书桌要用多少木板？……教师：下面大家小组合作，完成活动五。

小升初球体的表面积和体积专题练习

小升初球体的表面积和体积专题练习
介绍
本文档旨在通过专题练帮助小升初学生提高对球体表面积和体
积的理解和计算能力。

通过掌握球体相关公式并进行实际应用，学
生将能够更好地解决与球体相关的问题。

球体表面积
球体的表面积指的是球体外部的总面积。

计算球体表面积的公
式如下：
表面积= 4π * r²
其中，π为圆周率，约为3.，r为球体的半径。

练题示例
1. 已知一个球体的半径为5cm，计算其表面积。

2. 如果一个篮球的表面积为314平方厘米，求它的半径是多少？
球体体积
球体的体积指的是球体内部所占据的空间。

计算球体体积的公式如下：
体积= (4/3) * π * r³
其中，π为圆周率，约为3.，r为球体的半径。

练题示例
1. 一个球体的半径为10cm，计算其体积。

2. 若一个球体的体积为52
3.6立方厘米，求它的半径是多少？
总结
通过完成上述练习题，小升初学生可以巩固对球体表面积和体积计算方法的掌握，并能够灵活运用这些知识解决与球体相关的问题。

这些练习题既能提高学生的计算能力，又能培养他们的逻辑思维和问题解决能力。

祝愿学生们在小升初考试中取得优异的成绩！。

球的表面积与体积计算教案

球的表面积与体积计算教案教学目标：1. 理解球体的基本概念和特征。

2. 掌握计算球体表面积和体积的方法。

3. 能够应用所学知识解决实际问题。

教学内容：1. 球体的定义和性质介绍。

2. 球体的表面积计算方法。

3. 球体的体积计算方法。

4. 实际问题应用。

教学过程：一、引入（5分钟）教师可通过展示一个球体实物或者图片，向学生介绍球体的形状和特征。

引导学生思考球体的表面积与体积之间的关系。

二、理论讲解（15分钟）1. 球体的定义和性质：球体是由所有离球心距离小于或等于半径的点组成，具有圆形平面的特点。

球体的半径是由球心到球面上任意一点的距离，用字母r表示。

2. 球体的表面积计算方法：球体的表面积公式为S = 4πr²，其中π取近似值3.14。

解释公式的各个部分含义，强调半径的重要性。

3. 球体的体积计算方法：球体的体积公式为V = (4/3)πr³，其中π取近似值3.14。

解释公式的各个部分含义，与表面积的公式进行对比。

三、计算示范与练习（20分钟）1. 教师通过几个实际例题的计算示范，引导学生掌握球体表面积和体积的计算方法。

示例题1：求半径为5cm的球体的表面积和体积。

解：表面积S = 4πr² = 4π(5)² = 4π×25 = 100π ≈ 314cm²体积V = (4/3)πr³ = (4/3)π(5)³ = (4/3)π×125 ≈ 523.33cm³2. 学生进行练习，巩固计算方法。

请学生计算不同球体半径的表面积和体积，并在课后进行检查。

四、实际问题应用（15分钟）教师出示一些和球体相关的实际问题，引导学生应用所学知识解决问题，如：1. 有一个球形鱼缸，直径为60cm，求球形鱼缸的表面积和体积。

2. 一个篮球的表面积是486cm²，求篮球的半径和体积。

五、总结与拓展（5分钟）教师对本节课所学的内容进行总结，并提出一些拓展问题供学生思考，如球体表面积和体积的应用领域有哪些？附加练习题：1. 求球体的表面积和体积：a) 半径为8cm的球体；b) 直径为12cm的球体。

小学数学教学备课教案长方体的表面积和体积计算

小学数学教学备课教案长方体的表面积和体积计算小学数学教学备课教案长方体的表面积和体积计算一、引言长方体是小学数学中的重要内容，学生需要学会计算长方体的表面积和体积。

本教案旨在帮助教师有效地教授长方体的表面积和体积计算。

二、教学目标1. 理解长方体的概念和基本特征；2. 掌握长方体表面积的计算方法；3. 掌握长方体体积的计算方法；4. 能够灵活运用表面积和体积的计算方法解决问题。

三、教学准备1. 教师准备：投影仪、计算器、教学课件；2. 学生准备：铅笔、橡皮、尺子。

四、教学过程本节课的教学过程主要分为三个部分：导入新知识、知识讲解、练习与巩固。

导入新知识：教师通过投影仪呈现一个长方体的图形，引导学生观察长方体的形状和特点。

然后，教师提问学生：你们对长方体有什么了解？知识讲解：1. 表面积的计算方法：教师通过教学课件呈现长方体表面积的计算公式：2*(长×宽 + 长×高 + 宽×高)，并分步骤进行讲解。

教师通过实例演示如何应用公式计算长方体的表面积。

2. 体积的计算方法：教师通过教学课件呈现长方体体积的计算公式：长×宽×高，并分步骤进行讲解。

教师通过实例演示如何应用公式计算长方体的体积。

练习与巩固：教师提供一些练习题，学生在教师的引导下，独立进行计算长方体的表面积和体积。

然后，学生互相交换答案，教师给予评价和反馈。

五、教学延伸1. 拓展知识：教师可以引导学生进一步探索其他几何体的表面积和体积计算方法，如立方体、正方体等。

2. 应用实践：教师可以引导学生在实际生活中应用长方体的表面积和体积计算方法，如计算一个长方形房间的墙面涂料的用量、长方体水桶的容积等。

六、课堂总结本节课我们学习了长方体的表面积和体积计算方法。

通过掌握这些计算方法，我们可以在生活中灵活运用，解决各种实际问题。

七、作业布置请同学们完成课堂上未解答完的练习题，并写一篇小结，总结长方体的表面积和体积计算方法。

高中数学必修二 8 3 简单几何体的表面积与体积(精练)(含答案)

8.3 简单几何体的表面积与体积（精练）【题组一多面体表面积】1．（2020·全国高一课时练习）长方体的高为2，底面积等于12，过不相邻两侧棱的截面（对角面）的面积为10，则此长方体的侧面积为( )A ．12B ．24C ．28D ．32 【答案】C【解析】设长方体底面矩形的长与宽分别为,a b ，则12ab =.210=，解得4,3a b ==或3,4a b ==.故长方体的侧面积为()243228⨯+⨯=.故选：C.2．（2021·江苏南通市）一个正四棱锥的底面边长为2A ．8B ．12C ．16D ．20 【答案】B，所以该四棱锥的全面积为212+422=122⋅⋅⋅. 故选B3．（2020·全国高一课时练习）若正三棱台上、下底面边长分别是a 和2a ，棱台的高为6a ，则此正三棱台的侧面积为（）A ．2aB ．212aC ．292aD ．232a 【答案】C 【解析】如图，1,O O 分别为上、下底面的中心，1,D D 分别是AC ，11A C 的中点，过1D 作1D E OD ⊥于点E .在直角梯形11ODD O 中，12323OD a a =⨯⨯=，111326O D a a =⨯⨯=，116DE OD O D a ∴=-=.在1Rt DED 中，16D E a =，则1D D =a ==. 2193(2)22S a a a a ∴=⨯+=侧.故选：C4．（2020·河北沧州市一中高一月考）正四棱锥底面正方形的边长为4，高与斜高的夹角为30，则该四棱锥的侧面积（）A ．32B ．48C ．64D ．323【答案】A【解析】如图:正四棱锥的高PO ，斜高PE ，底面边心距OE 组成直角△POE ．∵OE =2cm ，∠OPE =30°，∴斜高h ′=PE =4sin 30o OE =，∴S 正棱锥侧=114443222ch =⨯⨯⨯=' 故选：A5．（2020·全国高一课时练习）已知正四棱锥的底面边长是2，则该正四棱锥的表面积为（）A B ．12 C ．8 D ．【答案】B【解析】如图所示，在正四棱锥S ABCD -中，取BC 中点E ，连接SE ，则SBE △为直角三角形，所以2SE ==，所以表面积1422422122SBC ABCD S S S =+⨯=⨯+⨯⨯⨯=正方形△.故选：B.6．（2021·内蒙古包头市·高三期末（文））已知一个正四棱锥的底面边长为4，以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则该正四棱锥的侧面积为（）A ．)41B 1C ．)41D ．)81 【答案】D【解析】正四棱锥如图，设四棱锥的高OE h =，由底面边长为4，可知2OF =，斜高EF故2142h =⨯2=2h +故侧面积为(214448812h ⨯⨯==+=+，故选：D. 7．（2020·山西吕梁市）已知,AB CD 是某一棱长为2的正方体展开图中的两条线段，则原正方体中几何体ABCD 的表面积为（）A ．2+B ．2+C ．2+D ．2+【答案】A 【解析】由所给正方体的展开图得到直观图，如图：则此三棱锥的表面积为：△△△△+++=BCD ABC ADC ABD S S S S1111222222222⨯⨯+⨯⨯⨯⨯⨯=+故选：A8．（2020·黑龙江哈师大青冈实验中学）长方体一个顶点上的三条棱长分别为3，4，a ，表面积为108，则a 等于（）A ．2B ．3C ．5D ．6 【答案】D【解析】长方体一个顶点上的三条棱长分别为3，4，a ，则长方体的表面积为342+2423108a a ⨯⨯⨯+⨯=，解得a =6，故选：D9．（2020·湖北省汉川市第一高级中学高一期末）一个正四棱柱的各个顶点都在一个半径为2cm 的球面上，如果正四棱柱的底面边长为2cm ，那么该棱柱的表面积为（）A ．2(2+B ．2(4+C ．2(8+D ．2(16+ 【答案】C【解析】∵一个正四棱柱的各个顶点都在一个半径为2cm 的球面上，正四棱柱的底面边长为2cm ， ∴球的直径为正四棱柱的体对角线∴正四棱柱的体对角线为4，正四棱柱的底面对角线长为= ∴该棱柱的表面积为2×22+4×2×＋(2cm )，故选：C【题组二多面体台体积】1．（2021·扶风县法门高中）正方体的全面积为18cm 2，则它的体积是_________ 3cm【答案】【解析】设该正方体的棱长为a cm ，由题意可得，2618a =，解得a =所以该正方体的体积为3V a ==3cm .故答案为：2．（2021·湖南长沙市）如图，在长方体1AC 中，棱锥1A ABCD -的体积与长方体的体积之比为（）A ．2∶3B ．1∶3C ．1∶4D ．3∶4【答案】B 【解析】设长方体过同一顶点的棱长分别为,,a b c则长方体的体积为1V abc =，四棱锥1A ABCD -的体轵为213V abc =，所以棱锥1A ABCD -的体积与长方体1AC 的体积的比值为13. 故选：B.3．（2020·浙江高一期末）由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥（底面是正方形，侧棱长都相等的四棱锥），四个侧面由673块玻璃拼组而成，塔高21 米，底宽34米，则该金字塔的体积为（）A ．38092mB ．34046mC ．324276mD ．312138m【答案】A 【解析】如图正四棱锥P ABCD -中，34AB BC ==，21PO =，所以正四棱锥P ABCD -的体积为311343421809233ABCD S PO m ⨯⨯=⨯⨯⨯=，故选：A4．（2020·辽宁沈阳市·沈阳二中高一期末）《九章算术》问题十：今有方亭，下方五丈，上方四丈．高五丈．问积几何（今译：已知正四棱台体建筑物（方亭）如图，下底边长5a =丈，上底边长4b =丈．高5h =丈．问它的体积是多少立方丈？（）A ．75B ．3053C ．3203D ．4003 【答案】B【解析】(()2211+=33V S S h a b h '=+⋅ ()2211305545615333=⨯=⨯⨯=. 故选:B 5．（2021·浙江高一期末）出华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥（底面是正方形，侧楼长都相等的四棱锥），四个侧面由673块玻璃拼组而成，塔高21米，底宽34米，则该金字塔的体积为（）A ．38092mB ．34046mC ．32427mD ．312138m【答案】A【解析】如图正四棱锥P ABCD -中，PO ⊥底面ABCD ，21PO =，34AB =，底面正方形的面积为234341156S m =⨯=，则正四棱锥P ABCD -的体积为311115621809233S PO m ⨯⨯=⨯⨯=，故选：A6．（2020·济南市·山东师范大学附中高一月考）如图，在棱长为2的正方体1111ABCD A B C D -中，截去三棱锥1A ABD -，求（1）截去的三棱锥1A ABD -的表面积；（2）剩余的几何体1111A B C D DBC -的体积.【答案】（1）6+；（2）203【解析】（1）由正方体的特点可知三棱锥1A ABD -中，1A BD 是边长为1A AD 、1A AB 、ABD △都是直角边为2的等腰直角三角形，所以截去的三棱锥1A ABD -的表面积(111231322642A BD A AD A AB ABD S S S S S =+++=⨯+⨯⨯⨯=+（2）正方体的体积为328=，三棱锥1A ABD -的体积为111142223323ABD SAA ⨯⨯=⨯⨯⨯⨯=，所以剩余的几何体1111A B C D DBC -的体积为420833-=. 【题组三旋转体的表面积】1．（2021·浙江丽水市）经过圆锥的轴的截面是面积为2的等腰直角三角形，则圆锥的侧面积是（）A ．B ．4πC ．D ．2π 【答案】C【解析】设圆锥的底面半径为r ，母线长为l ，则l =，由题可知)2122⨯=，∴2r l ==，侧面积为rl π=，故选：C.2．（2020·全国高一课时练习）某圆台的上、下底半径和高的比为1:4:4，母线长为10，则该圆台的表面积为（）A ．81πB ．100πC ．168πD ．169π 【答案】C【解析】该圆台的轴截面如图所示.设圆台的上底面半径为r ，则下底面半径4r r '=，高4h r =则它的母线长510l r ====∴2r，8r '=. ∴()(82)10100S r r l πππ'=+=+⨯=侧，22100464168S S r r ππππππ'=++=++=表侧.故选：C3．（2020·全国高一课时练习）用一个平行于圆锥底面的平面截这个圆锥，截得圆台上下底面半径的比是1：4，且该圆台的母线长为9，则截去的圆锥的母线长为（）A ．94B ．3C ．12D ．36【答案】B【解析】根据题意，设圆台的上、下底面的半径分别为r 、R ，设圆锥的母线长为L ，截得小圆锥的母线长为l ，∵圆台的上、下底面互相平行 ∴14l r L R ==，可得L=4l ∵圆台的母线长9，可得L ﹣l =9 ∴3L 4=9，解得L=12， ∴截去的圆锥的母线长为12-9=3故选B4．（2020·全国高一课时练习）圆台的一个底面圆周长是另一个底面圆周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面圆的半径为( )A ．3B ．5C ．6D ．7 【答案】D【解析】设圆台较小底面圆的半径为r ，由已知有另一底面圆的半径为3r ，而圆台的侧面积公式为(3)4384,7r r l r r πππ+=⨯⨯==，选D.5．（2020·江苏淮安市·淮阴中学高一期末）圆柱底面半径为1，母线长为2，则圆柱侧面积为（）A ．4πB ．3πC ．5πD ．2π 【答案】A【解析】圆柱底面半径为1，母线长为2，圆柱侧面积为224S rl =π=π⨯1⨯2=π ,故选：A6．（2021·广西河池市·高一期末）已知圆柱的底面半径为1，若圆柱的侧面展开图的面积为8π，则圆柱的高为________．【答案】4【解析】设圆柱的高为h ，有28h ππ=，得4h =．故答案为：4.7．（2021·河南焦作市·高一期末）已知圆锥的底面半径为2，高为4，在圆锥内部有一个圆柱，则圆柱的侧面积的最大值为______.【答案】4π【解析】如图是圆锥与圆柱的轴截面，设内接圆柱的高为a ，圆柱的底面半径为r ()02r <<，则由224r a-=，可得42a r =-，所以圆柱的侧面积()22242484(1)4S r r r r r πππππ=⋅-=-+=--+，所以1r =时，该圆柱的侧面职取最大值4π. 故答案为：4π．8．（2020·北京高一期末）将底面直径为8，高为最大值为______.【答案】【解析】欲使圆柱侧面积最大，需使圆柱内接于圆锥；设圆柱的高为h ，底面半径为r ，4r =，解得2h r =；所以()2224S rh r r r ππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧；当2r时，S 圆柱侧取得最大值为故答案为：. 【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.9．（2021·陕西西安市·西安中学高一期末）若圆锥的侧面展开图是圆心角为90︒的扇形，则该圆锥的侧面积与底面积之比为___________. 【答案】4:1【解析】设圆锥的底面半径为r ，母线长为l ，由题意得：22l r ππ=,即4l r ，所以其侧面积是214S rl r ππ==，底面积是22S r π=，所以该圆锥的侧面积与底面积之比为4:1 故答案为：4:1【题组四旋转体的体积】1．（2020·山东菏泽市·高一期末）若圆锥的底面半径为3cm ，侧面积为215cm π，则该圆锥的体积为（） A ．4π3cm B ．9π3cmC ．12π3cmD ．36π3cm【答案】C【解析】设圆锥母线长为l ，则侧面积为123152S l r l πππ=⋅==，故5l =.故圆锥的高4h =，圆锥体积为21123V r h ππ==3cm .故选：C.2．（2021·黑龙江双鸭山市·双鸭山一中）现用一半径为10cm ，面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器（假定衔接部分及铁皮厚度忽略不计，且无损耗），则该容器的容积为__________3cm . 【答案】128π【解析】设铁皮扇形的半径和弧长分别为R 、l ，圆锥形容器的高和底面半径分别为h 、r ，则由题意得R=10，由1802Rl π=，得16l π=，由2lr π=得8r =.由222R r h =+可得6h =.∴()231164612833V r h cm πππ==⋅⋅=∴该容器的容积为3128cm π.故答案为128π.3．（2020·湖南长沙市·高一期末）圆锥的母线与底面所成的角为60︒，侧面积为8π，则其体积为________.【答案】3【解析】如图所示，圆锥的母线与其底面所成角的大小为60︒，60SAO ∴∠=︒，由题意设圆锥的底面半径为r ，则母线长为2l r =，高为h =圆锥的侧面积为8π，2228S rl r r r ππππ∴==⋅⋅==侧面积，解得2r ，h =∴圆锥的体积为2211233V r h ππ=⋅⋅=⨯⨯=圆锥．故答案为：3．4．（2020·江苏南京市·高一期末）把一个棱长为2的正方体木块，切出一个最大体积的圆柱，则该圆柱的体积为（） A ．23πB ．πC ．2πD ．4π【答案】C【解析】正方体棱长为2，所以正方体底面正方形的内切圆半径为1，面积为21ππ⨯=，以此内切圆为底、高为2的圆柱是可切出的最大圆柱.且该圆柱的体积为22ππ⨯=. 故选：C5．（2020·山东日照市·高一期末）《五曹算经》是我国南北朝时期数学家甄驾为各级政府的行政人员编撰的一部实用算术书，其第四卷第九题如下：“今有平地聚粟，下周三丈，高四尺，问粟几何”?其意思为场院内有圆锥形稻谷堆，底面周长3丈，高4尺，那么这堆稻谷有多少斛？已知1丈等于10尺，1斛稻谷的体积约为1.62立方尺，圆周率约为3，估算堆放的稻谷约有多少斛（保留两位小数）（） A ．61.73 B ．61.71C ．61.70D ．61.69【答案】A【解析】设圆锥的底面半径为r ，高为h ，体积为V ，则230r π=，所以=5r ，故221135410033V r h π==⨯⨯⨯=（立方尺），因此10061.731.62V =≈（斛）. 故选：A.6．（2020·江苏无锡市·高一期末）某养路处有一圆锥形仓库用于储藏食盐（供融化高速公路上的积雪之用），已建的仓库的底面直径为12米，高4米，为存放更多的食盐，养路处拟重建仓库，将其高度增加4米，底面直径不变，则新建仓库比原仓库能多储藏食盐的体积为（） A ．24π米3 B ．48π米3C ．96π米3D ．192π米3【答案】B【解析】原仓库圆锥的底面半径为6米，高为4米，则容积为21614483V ππ=⨯⨯⨯=立方米；仓库的高增加4米，底面直径不变,则仓库的容积为22618963V ππ=⨯⨯⨯=立方米. 所以新建仓库比原仓库能多储藏食盐的体积为2148V V π-=立方米. 故选：B. 【题组五球】1．（2021·天津滨海新区）在正方体1111ABCD A B C D -中，三棱锥11A B CD -的表面积为外接球的体积为（）A ． BC ．D ．【答案】B【解析】设正方体的棱长为a ，则111111B D AC AB AD B C D C ======，由于三棱锥11A B CD -的表面积为所以)121442AB CS S==⨯=a ==，所以正方体的外接球的体积为34632π⎛⎫= ⎪ ⎪⎝⎭故选：B ．2．（2020·广东高二期末）在长方体1111ABCD A B C D -中，22AB BC ==，若此长方体的八个顶点都在体积为92π的球面上，则此长方体的表面积为（） A ．16 B ．18C ．20D ．22【答案】A【解析】根据长方体的结构特征可得，长方体外接球直径等于长方体体对角线的长，因为长方体外接球的体积为92π，设外接球半径为R ，则33924R ππ=，解得32R =，因此2R =22AB BC ==，所以3=12BB =，因此长方体的表面积为：1122248416S AB BC AB BB BC BB =⨯⨯+⨯⨯+⨯⨯=++=. 故选：A.3．（2020的内切球，则此棱柱的体积是（）.A ．3B ．354cmC ．327cmD ．3【答案】B的内切球，则正三棱柱的高为，，设底面正三角形的边长为a cm,13⨯=6a =cm ，∴正三棱柱的底面面积为16622⨯⨯⨯=2，故此正三棱柱的体积V ＝54=cm 3．故选：B ．4．（2021·全国高一）如图所示，球内切于正方体．如果该正方体的棱长为a ，那么球的体积为（）A ．343a π B ．3aC 3aD ．316a π【答案】D【解析】因为球内切于正方体，所以球的半径等于正方体棱长的12，所以球的半径为2a ，所以球的体积为334326a a ππ⎛⎫= ⎪⎝⎭，故选：D.5．（2021·湖南邵阳市·高一期末）一个球的体积为36π，则这个球的表面积为（） A ．12π B ．36πC ．108πD ．4π【答案】B【解析】设球的半径为R ,球的体积为3436=3R ππ,解得3R =,则球的表面积244936R πππ=⨯=，故选：B6．（2020·浙江高一期末）已知正方体外接球的体积是323π，那么该正方体的内切球的表面积为_____________．【答案】163π【解析】设正方体棱长为a ，则3432323ππ⎛⎫⨯= ⎪ ⎪⎝⎭，解得a =∴内切球半径为23a r ==，表面积为21643S ππ=⨯=⎝⎭．故答案为：163π．【题组六组合体的体积表面积】1．（2020·全国高一课时练习）如图是某机械零件的几何结构，该几何体是由两个相同的直四棱柱组合而成的，且前后、左右、上下均对称，每个四棱柱的底面都是边长为2的正方形，高为4，且两个四棱柱的侧棱互相垂直．则这个几何体有________个面，其体积为________．【答案】20 323-【解析】由图形观察可知，几何体的面共有2(242)20⨯⨯+=个，该几何体的直观图如图所示，该几何体的体积为两个四棱柱的体积和减去两个四棱柱交叉部分的体积. 两个四棱柱的体积和为222432V =⨯⨯⨯=. 交叉部分的体积为四棱锥S ABCD -的体积的2倍.在等腰ABS 中，SB SB =边上的高为2，则SA =由该几何体前后，左右上下均对称，知四边形ABCD 的菱形. 设AC 的中点为H ，连接,BH SH 易证SH 即为四棱锥S ABCD -的高，在Rt ABH 中， 2.BH ==又AC SB ==所以 1222ABCDS=⨯⨯=因为BH SH =，所以112233ABCDS ABCD V S -=⨯=⨯=四棱柱所以求体积为3223233-⨯=-故答案为：20；323-2．（2020·新疆巴音郭楞蒙古自治州·高一期末）如图，直三棱柱，高为6，底边三角形的边长分别为3、4、5，以上下底面的内切圆为底面，挖去一个圆柱，求剩余部分几何体的体积.【答案】366π-【解析】因为222345+=，所以底面是直角三角形，所以上、下底面内切圆半径34512r +-==，所以剩余部分几何体的体积21346163662V ππ=⨯⨯⨯⨯=-⨯-，所以剩余部分几何体的体积为366π-.3．（2021·江西九江市）在底面半径为2，高为面积之比为1：4，求圆柱的表面积.【答案】1)π【解析】由圆柱的底面积与圆锥的底面积之比为1:4，知：底面半径比为1:2，即圆柱底面半径1r =，若设圆柱的高为h 12=，即h = ∴由圆柱的表面积等于侧面积加上两底面的面积，即：2221)S rh r πππ=+=.。

体积和表面积的比较_教案教学设计_2

体积和表面积的比较教学目标正确区分长方体与正方体的表面积和体积的概念，熟练掌握各自的计算方法．教学重点区分长、正方体的表面积与体积的概念．教学难点进一步建立体积和表面积的空间观念．教学步骤一、铺垫孕伏．1、复习长方体体积与表面积的计算方法．2、列式：（1）一个长方体的长是3分米，宽是2分米，高是1分米．它的表面积是多少？体积是多少？（2）一个长方体的长是6分米，宽是4分米，高是2分米．它的表面积是多少？体积是多少？导入：同学们已经学会计算长方体和正方体的表面积和体积，那么，表面积和体积有什么联系和区别呢？这节课我们就来学习“”的内容．板书：．二、探究新知．（一）体积和表面积的对比．1、区分体积和表面积这两个概念．归纳小结：长方体的表面积指它的六个面的总面积，而体积则是指它所占空间的大小．2、区分表面积和体积的计量单位．归纳小结：表面积用面积单位来计量，常用的面积单位有平方米、平方分米、平方厘米．体积用体积单位来计量，常用的体积单位有立方米、立方分米、立方厘米．3、区分体积和表面积的计算方法．在计算表面积和体积时，所需的条件相同，计算方法为什么不同？归纳小结：计算长方体的体积和表面积，所需的条件相同，但因计算内容不同，所以计算方法不相同．（二）教学例7．例7、光明纸盒厂生产一种长方体纸箱，长8分米，宽5分米，高6分米．（1）做一个纸箱至少要多少平方分米硬纸板？（2）它的体积是多少？（求做纸箱要用多少纸板，需要计算纸箱的表面积）表面积：（长×宽＋长×高＋宽×高）×2 体积：长×宽×高．（1）表面积（8×5＋5×6＋8×6）×2＝118×2＝236（平方分米）（2）体积8×5×6＝240（立方分米）答：做一个纸箱至少要236平方分米的硬纸板，它的体积是240立方分米．（三）练习：一个正方体的棱长是12厘米，求它的表面积和体积区别：正方体的体积和表面积是两个不同的概念答：它的表面积是864平方厘米，体积是1728立方厘米．三、全课小结．今天这节课我们学习了哪些知识？体积和表面积的主要区别是什么？四、随堂练习．1、计算正方体的表面积和体积．2、计算长方体的表面积和体积．3、在（）里填上合适的计量单位．（1）一个粉笔盒的表面积大约是6（）．（2）一个火柴盒的体积大约是14（）．（3）一个游泳池，它最多可容水3000（）．4、判断．（1）一个棱长是6分米的正方体，它的体积和表面积相等．（）（2）表面积是6平方米的正方体，体积是1立方米．（）五、课后作业．1、人民革制品厂用合成革做长方体的箱子，长0.9米，宽0.6米，高0.4米．做一个箱子至少要用多少合成革？2、黎明纸盒厂做正方体的纸盒，棱长0.6米，做一个纸盒至少要用多少硬纸板？纸盒的体积是多少？3、永丰水泵厂计划25天制造1575台水泵，实际每天比原计划多制造12台．照这样计算，完成原定生产任务可少用多少天？六、板书设计．例7、光明纸盒厂生产一种长方体纸箱，长8分米，宽5分米，高6分米．（1）做一个纸箱至少要多少平方分米硬纸板？（2）它的体积是多少？答：做一个纸箱至少要236平方分米硬纸板，它的体积是240立方分米．感谢您的阅读，本文如对您有帮助，可下载编辑，谢谢。

表面积和体积的比较

表面积和体积的比较教学目标:1、分清体积和表面积的概念和计算方法的不同。

2、进一步培养空间观念，利用所学知识解决实际问题。

重点难点：区分体积和表面积两个概念，利用体积、表面积解决实际问题。

教、学具准备：小黑板、投影仪、大小相同的火柴盒。

教学过程：（一）学前准备1、长方体的表面积指什么？长方体的体积指什么？2、怎样求长方体的体积？怎样求长方体的表面积？3、表面积和体积分别用什么计量单位表示？4、要计算一个长方体的表面积需要知道什么？怎样计算它的体积呢？（二）探究新知1、小组合作练习，区分概念。

（1）动手操作：拿出准备好的火柴盒，让一个有棱的面对着自己放好，测量一下它的长、宽、高。

（2）说一说测量结果。

（3）计算：火柴盒上下两个面的总面积是多少？火柴盒前后两个面的总面积是多少？火柴盒左右两个面的总面积是多少？火柴盒的表面积都包括那几个面的面积和？是多少？火柴盒的体积怎样求？是多少？（4）汇报交流。

2、拓展练习，灵活掌握。

（1）把火柴盒的内盒拿出来。

观察火柴盒的外套有几个面？分别是哪几个面？火柴盒的内盒有几个面，是哪几个面？（2）求做一个火柴盒外套需用多少纸，是求什么？需要什么条件？怎样求？（3）求做一个火柴盒的内盒需用多少纸，是求什么？需要什么条件？怎样求？（4）火柴盒内盒的容积是多少？（5）汇报交流。

3、动手操作，强化训练。

（1）四人合作完成。

把火柴盒的最大面相对拼成一个长方体，这个长方体的表面积是多少？怎样计算？体积呢？（2）汇报交流。

（3）还可以怎样把两个完全一样的火柴盒拼成一个长方体？哪种拼得的长方体表面积最大? 哪种拼得的长方体表面积最小?（4）如果把10盒火柴包一包,怎样包装最省包装纸?小组合作,动手拼一拼,摆一摆,算一算。

（５）汇报交流。

如果用长45厘米，宽30厘米，高15厘米的长方体纸箱装包好的火柴，怎样求装多少盒？4、出示例7（投影出示）独立完成，反馈订正。

5、小结：在实际生活中经常需要用表面积和体积的有关知识解决一些实际问题，这就需要认真审题，联系实际分清是求体积还是求表面积，是求几个面的面积，根据实际寻求解决的方法。

题目：比较两个球体的体积和表面积。

比较两个球体的体积和表面积
本文将比较两个球体的体积和表面积。

我们知道，球体是一种具有圆形表面的三维几何体。

比较它们的体积和表面积可以帮助我们更好地理解它们的几何性质。

体积的比较
球体的体积可以通过以下公式计算：V = (4/3) * π * r^3，其中V表示体积，π表示圆周率，r表示球体的半径。

假设我们有两个球体，分别为球体A和球体B，它们的半径分别为r1和r2。

我们可以分别计算出它们的体积，并进行比较。

球体A的体积：V1 = (4/3) * π * r1^3
球体B的体积：V2 = (4/3) * π * r2^3
我们可以比较V1和V2的大小，从而得出它们的体积大小关系。

表面积的比较
球体的表面积可以通过以下公式计算：A = 4 * π * r^2，其中A 表示表面积，π表示圆周率，r表示球体的半径。

同样地，我们可以计算出球体A和球体B的表面积，并进行比较。

球体A的表面积：A1 = 4 * π * r1^2
球体B的表面积：A2 = 4 * π * r2^2
比较A1和A2的大小可以帮助我们了解它们的表面积大小关系。

结论
通过比较两个球体的体积和表面积，我们可以得出它们的大小关系。

如果V1 > V2，则球体A的体积大于球体B的体积；如果A1 > A2，则球体A的表面积大于球体B的表面积。

了解球体的体积和表面积比较可以在数学、工程和科学领域中提供有用的信息。

希望本文对您有所帮助。

参考资料：。

球的体积和表面积习题课

关键：找正方体的棱长a与球半径R之间的关系
谢谢您的关注
习题课
两个几何体相切:
一个几何体的各个面与另一个几何体的各面相切.
两个几何体相接:
一个几何体的所有顶点都在另一个几何体的面上.
D A
D1 A1
C B
O C1
B1
求球与它的外切圆柱、外切等边圆锥的体积之比。
求球与它的外切圆柱、外切等边圆锥的体积之比。
V球 :V柱 :V锥 4 : 6 : 9
QS球 4R2
S圆锥全 2
S球
1
本课小结:
解决两类问题:
两个几何体相切和相接
处理方法:
作适当的轴截面
例3.如图，正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上，问球O的表面积。
分析：正方体内接于球，则由球和正方体都是中心对称图形可知，
它们中心重合，则正方体对角线与球的直径相等。
则圆柱的底面半径为R,高为2R.
得: S球 4R2
RO
S圆柱侧 2R 2R 4R2
S球 S圆柱侧
(2) Q S圆柱全 4R 2 + 2R 2 6R 2
S球 4R2
S球
2 3
S圆柱全
例2.若一个球的外切圆锥的高是这个球的直径的两倍，
求圆锥的全面积与球的表面积之比。
P
解：过圆锥的轴做截面截圆锥和内切球分别得轴截面PAB和球的大圆圆O,且圆O
(变式)一个倒等边圆锥形容器，将一个半径为r的铁球放入其中，并向容器内注水，使水面恰与铁球相切，将球取出后,容器内的水深为多少?
3r
3 15r
例1.如图,圆柱的底面直径与高都等于球的直径,求证: (1)球的表面积等于圆柱的侧面积. (2)球的表面积等于圆柱全面积的三分之二.

小学生数学习题练习几何体的表面积和体积计算

小学生数学习题练习几何体的表面积和体积计算在小学数学教学中，几何体的表面积和体积计算是一个重要的内容。

通过练习习题，不仅可以巩固学生对几何体的认识，还可以提高他们的计算能力和问题解决能力。

本文将介绍一些常见的习题，并提供详细解答，帮助小学生更好地理解和掌握几何体的表面积和体积计算。

一、长方体的表面积和体积计算题目1：一个长方体的长为5厘米，宽为3厘米，高为4厘米，求它的表面积和体积。

解答：这个题目可以使用公式进行计算。

长方体的表面积计算公式为：2 * (长*宽 + 长*高 + 宽*高)，体积计算公式为：长*宽*高。

根据题目中给出的数据，将其代入公式进行计算：表面积 = 2 * (5*3 + 5*4 + 3*4) = 2 * (15 + 20 + 12) = 2 * 47 = 94平方厘米体积 = 5 * 3 * 4 = 60立方厘米所以，这个长方体的表面积为94平方厘米，体积为60立方厘米。

题目2：某长方体的表面积为120平方厘米，长为6厘米，宽为4厘米，求它的高和体积。

解答：我们可以使用表面积计算公式解这道题。

将已知信息代入公式：120 = 2 * (6*4 + 6*h + 4*h)。

进行运算得到：120 = 2 * (24 + 10h)。

化简得：120 = 48 + 20h。

继续计算得到：20h = 72。

解方程得：h = 72 / 20 = 3.6（约等于3.6）。

所以，这个长方体的高约为3.6厘米。

将已知的长、宽、高代入体积计算公式，进行计算得到：体积 = 6 * 4 * 3.6 = 86.4立方厘米（约等于86.4）。

所以，这个长方体的高约为3.6厘米，体积约为86.4立方厘米。

二、正方体的表面积和体积计算题目1：一个正方体的边长为3厘米，求它的表面积和体积。

解答：正方体的表面积计算公式为：6 * 边长的平方，体积计算公式为：边长的立方。

根据题目中给出的数据进行计算：表面积 = 6 * 3^2 = 6 * 9 = 54平方厘米体积 = 3^3 = 27立方厘米所以，这个正方体的表面积为54平方厘米，体积为27立方厘米。