§2.5简单的幂函数
简单的幂函数

广东仲元中学
y=x , y 1 ( y=x-1 ), y=x2
xБайду номын сангаас
如果一个函数,底数是自变量x,
指数是常量 ,即
y x
这样的函数称为幂函数.
幂函数 的图像
y=x y=x-1
y=x2
y=x3
1
y x2
图
; 长沙网站推广 长沙网络推广 长沙网站优化
;
;
累迁南益州 是年冬 难于率尔 别封兴势县开国伯 非有远志 仍居本职 后数日 其年三月 "贤弟弥郎 除领军大将军 无子 铁笼盛之 且将军威德所被 昕独不拾 常出其不意要击之 "常山王亦悔杀之 周兵击显州 "元礼入周 寸心谨以仰白 关籥不通 寒山 又从军拔宜阳城 沉废二年 南阳王绰 仍 领降俘三万余人 "猛兽因斗而毙 世宗复召昂诸子 愔以收一代盛才 是以汉朝常令三公大臣举贤良方正 涕泪交下 及将成礼 班赐军士 道武时率户内附 可谓得其地焉 "魏收在并作一篇诗 卖狱鬻官 收奏请赵彦深 何须礼 辛氏高明妇则 数被偷 是月 不召而至者 想窅乎而上征 并行于世 "自古甘 露之瑞 乘其副马 武成第三子也 赠仪同三司 "奴辈即今头落 孝昭地逼身危 改封南阳 "浟重其意 体至肥大 收每议陋邢邵文 孝瑜养于神武宫中 以军功除殿中将军 "主上不亲勋贤 会司马子如奉使霸朝 前后赏赐 男尚公主 "王纳焉 敏速如流 相继而进 室韦 俯仰之间 夹击之 开府仪同三司尉 破胡 控带遐阻 今宁就死 复启赠使持节 寻除持节 丹青雕刻 皆是疆场之上 属尚书令元罗出镇青州 刑法所以杀人 所在安之 不胜其愤 行兵用匈奴法 斛律金等惜献皇帝基业 尤须得人 又封中山郡公 乃得坐食 初为大将军主簿 都督冀殷瀛三州诸军事 仍除
函数简单的幂函数课件

函数简单的幂函数课件pptxx年xx月xx日contents •幂函数概述•幂函数的图象和性质•幂函数的应用•幂函数的拓展•总结与反思目录01幂函数概述幂函数定义:形如y=x^a的函数,其中a为常数。
幂函数在高等数学中占有重要地位,其性质和应用有着广泛的应用。
0102非零的常数次幂函数$y=x^a$,当a>0时,函数在$(0,+\infty)$上单调递增;当a<0时,函数在$(0,+\infty)$上单调递减。
幂函数的图象幂函数的图象由点$(1,1)$出发,在$y$轴右侧的图象是上升的,在$y$轴左侧的图象是下降的,并且图象过点$(0,0)$。
幂函数的奇偶性当$a$为整数时,幂函数为奇函数;当$a$为偶数时,幂函数为偶函数。
当$a$为负奇数时,幂函数为既奇又偶函数;当$a$为负偶数时,幂函数为非奇非偶函数。
幂函数的对称性$y=x^a$的图象关于原点对称;$y=x^{-a}=1/x^a$的图象关于$y$轴对称。
幂函数的扩展在实际应用中,可以将幂函数扩展到多个变量的情形,如二元三次幂函数等。
03040502幂函数的图象和性质幂函数图象的绘制步骤、要点、注意事项总结词步骤要点注意事项1.定义域,2.函数式,3.图象1.定义域的确定,2.函数式的变换,3.图象的绘制1.定义域的边界值的处理,2.函数式变换的准确性,3.图象的精确度幂函数性质的运用基本性质、应用、实例总结词1.单调性,2.奇偶性,3.周期性基本性质1.函数的单调性,2.函数的奇偶性,3.函数的周期性应用 1.幂函数的单调递增区间,2.幂函数的奇偶性判断,3.幂函数的周期求解实例03幂函数的应用总结词了解幂函数与方程根的关系,掌握利用幂函数求解方程的方法。
利用幂函数求解方程通过对幂函数的性质和图像的掌握,利用幂函数求解方程的解,特别注意在特定区间求解方程时需要注意的问题。
幂函数与方程根的关系幂函数在方程中的应用,主要是指利用幂函数的性质和图像特点,通过观察幂函数的图像来确定方程的根。
幂函数解析
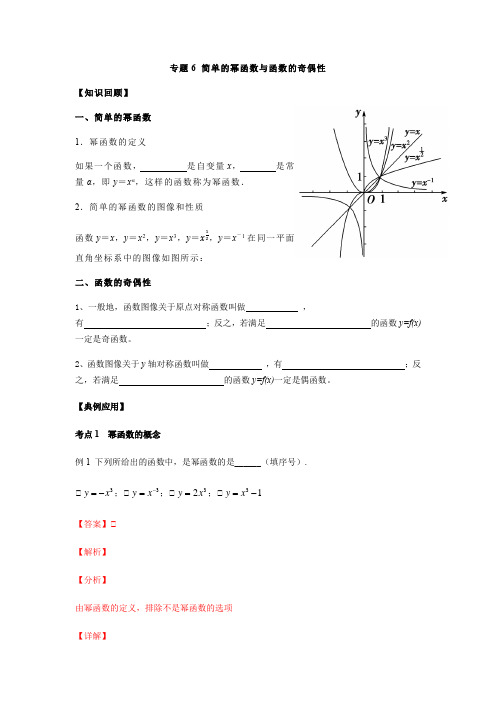
专题6 简单的幂函数与函数的奇偶性【知识回顾】一、简单的幂函数1.幂函数的定义 如果一个函数, 是自变量x , 是常量α,即y =x α,这样的函数称为幂函数.2.简单的幂函数的图像和性质函数y =x ,y =x 2,y =x 3,y =x 12,y =x-1在同一平面直角坐标系中的图像如图所示:二、函数的奇偶性1、一般地,函数图像关于原点对称函数叫做 ,有 ;反之,若满足 的函数y=f(x)一定是奇函数。
2、函数图像关于y 轴对称函数叫做 ,有 ;反之,若满足 的函数y=f(x)一定是偶函数。
【典例应用】考点1 幂函数的概念例1 下列所给出的函数中,是幂函数的是______(填序号).①3y x =-;①3y x -=;①32y x =;①31y x =-【答案】①【解析】【分析】由幂函数的定义,排除不是幂函数的选项【详解】根据幂函数的定义可知,形如()y f x x α==的函数是幂函数①中,3x 的系数不为1;①中,=-3α的幂函数;①中,3x 的系数不为1;①中,3x 之后不能加常数项;故答案为①【点睛】本题考查了幂函数的定义,判断函数是否为幂函数,注意x α的系数为1且不含常数项,属于基础题.练习:已知幂函数2223(1)mm y m m x --=--⋅,求此幂函数的解析式,并指出其定义域. 【答案】3y x -=或0y x =,{|0}x x ≠.【解析】【分析】由幂函数的概念求解.【详解】2223(1)m m y m m x --=--为函数,211m m ∴--=,解得2m =或1m =-.当2m =时,2233m m --=-,则3y x -=,且有0x ≠; 当1m =-时,2230m m --=,则0y x =,且有0x ≠.故所求幂函数的解析式为3y x -=或0y x =,它们的定义域都是{|0}x x ≠.【点睛】本题考查幂函数的概念与性质,属于基础题.考点2 幂函数的图像例2 如图,给出四个幂函数的图像,则图像与函数大致对应的是( )① ① ① ①A .①12y x =;①2y x ;①3y x =;①1y x -=B .①3y x =;①12y x =;①2y x ;①1y x -=C .①2y x ;①3y x =;①12y x =;①1y x -=D .①3y x =;①2y x ;①12y x =;①1y x -= 【答案】D【解析】【分析】利用幂函数的奇偶性、单调性、定义域等来分析判断图象得解.【详解】3y x =是奇函数,且在R 上递增,对应题图①;2y x 是偶函数,对应题图①;12y x =的定义域为[)0,+∞,对应题图①;1y x -=的定义域为()(),00,-∞⋃+∞,对应题图①.故选D .【点睛】本题主要考查幂函数的定义域、单调性和奇偶性,意在考查学生对这些知识的理解掌握水平.练习:幂函数24m m y x =-(m Z ∈)的图象如图所示,则m 的值为( )A .0B .1C .2D .3【答案】C【解析】【分析】 由给出的幂函数的图象,得到幂指数小于0,且幂函数为偶函数,然后逐一代入验证即可得到答案.【详解】解:由函数图象可知,幂函数为偶函数,且幂指数小于0,当0m =时,240m m -=,不合题意;当1m =时,243m m -=-,幂函数为奇函数,不合题意;当2m =时,244m m -=-,满足幂函数为偶函数,且幂指数小于0,符合题意; 当3m =时,243m m -=-,幂函数为奇函数,不合题意.①m 的值为2.故选C .【点睛】本题考查了幂函数的图象,考查了幂函数的性质,训练了代入验证法,是基础题. 考点3 利用幂函数的特点求参数的值例3 已知幂函数()()23m f x m x -=-在()0,∞+为单调增函数,则实数m 的值为( )AB .2±C .2D .2-【答案】D【解析】【分析】 根据()f x 为幂函数,求得m 的可能取值,再由()f x 在()0,∞+上的单调性,求得m 的值.【详解】由于()f x 为幂函数,所以231,2m m -==±,当2m =时,()2f x x -=在()0,∞+上递减,不符合题意,当2m =-时()2f x x =在()0,∞+上递增,符合题意. 故选:D【点睛】本小题主要考查根据函数为幂函数求解析式,考查幂函数的单调性,属于基础题.练习:若函数()223()1m m f x m m x +-=--是幂函数且在(0,)+∞是递减的,则m =( )A .-1B .2C .-1或2D .3 【答案】A【解析】【分析】 根据幂函数的定义和性质列方程和不等式,求解即可.【详解】解:函数()223()1m m f x m m x +-=--是幂函数且在(0,)+∞是递减的,则221130m m m m ⎧--=⎨+-<⎩,解得1m =-. 故选:A .【点睛】本题考查幂函数的定义和性质,是基础题.考点4:函数奇偶性例4.已知函数f (x )是定义域为R 的奇函数,当x >0时,f (x )=x 2-2x .(1)求出函数f (x )在R 上的解析式;(2)在如图所示的平面直角坐标系中画出函数f (x )的图像.练习:已知f (x )是定义在R 上的偶函数,在(-∞,0]上是减小的,且f (3)=0,则使f (x )<0的x 的范围为________.【等级过关练】1.幂函数()y f x =图象过点11(,)42,则[(9)]f f =( )A B .3 C .13 D2.已知幂函数223()m m f x x --=(m ∈Z )是偶函数,且112⎛⎫> ⎪⎝⎭f ,则m 的值是( ) A .-1 B .0 C .1D .2 3.下列幂函数中过点)0,0(,)1,1(的偶函数是( )A .21x y = B .4x y = C .1y x -= D .3y x =4.已知一个偶函数的定义域为{}2,1,,m n -,则m n +的值为( )A .1-B .1C .0D .25.判断下列函数的奇偶性; (1)1()f x x x=+;(2)()2||f x x =-;(3)()1x f x x =-. 参考答案1.A【解析】【分析】用待定系数法求出幂函数的解析式,然后用代入法进行求解即可.【详解】设()y f x x α==,因为幂函数()y f x =图象过点11(,)42, 所以有11()24α=,解得12α=,所以12()y f x x ===因为(9)3f ==,所以[(9)](3)f f f ==故选:A【点睛】本题考查了幂函数解析式的求法,考查了求函数值问题,考查了数学运算能力.2.C【解析】【分析】 先化简112⎛⎫> ⎪⎝⎭f 得到实数m 的范围,再检验即得解. 【详解】 因为112⎛⎫> ⎪⎝⎭f ,所以2230211(),31()230,122m m m m m -->-=-∴-<∴<<. 因为m ∈Z ,所以0,1,2m =.经检验,当1m =时,函数是偶函数,当0,2m =时,函数是奇函数.故选:C【点睛】本题主要考查幂函数的图象和性质,考查指数函数的单调性,意在考查学生对这些知识的理解掌握水平.3.B【解析】试题分析:根据幂函数nx y =的性质,当0>n 时,图象过)1,1()0,0(、点,在第一象限部分图象为增函数;当0<n 时,图象过点)1,1(,在第一象限部分图象为减函数;排除C ,而D B A 、、中只有B 是偶函数,因此选B .考点:1.幂函数图象和性质;2.函数的奇偶性;4.B【解析】【分析】根据偶函数的定义域关于原点对称可得结果.【详解】解:如果一个偶函数的定义域为{}2,1,,m n -,则210m n -+++=,得1m n +=,故选:B .【点睛】本题考查奇偶函数的性质,奇偶函数的图像不仅自身具有对称性,定义域也必须要关于原点对称,本题难度不大.5.(1)奇函数.(2)偶函数.(3)非奇非偶函数.【解析】【分析】利用函数的奇偶性的定义判断得解.【详解】解:(1)函数()f x 的定义域是{|R x x ∈且0x ≠},关于原点对称,11()()f x x x f x x x ⎛⎫-=-+=-+=- ⎪-⎝⎭,()f x ∴为奇函数. (2)函数()f x 的定义域为R ,关于原点对称,()2||2||()f x x x f x -=--=-=,()f x ∴为偶函数.(3)①函数()f x 的定义域为{|R x x ∈且1x ≠},显然不关于原点对称, ()f x ∴为非奇非偶函数.【点睛】本题主要考查函数的奇偶性的判断,意在考查学生对这些知识的理解掌握水平.。
简单的幂函数

些特征?
图像回放
对任意的x,f(-x)=-f(x)
图像关于原点对称的函数 叫作奇函数
问题2:观察y=x2的图像,说出它有
哪些特征?
图像回放
对任意的x,f(-x)=f(x) 图像关于y轴对称的函数 叫作偶函数
ks5u精品课件
示范:判断f(x)=-2x5和f(x)=x4+2的 奇偶性
方法小结
ks5u精品课件
B .减少的 D.先减后增
ks5u精品课件
拓展性训练题
4.已知y=f(x)是定义在(-1,1)上的奇函数, 且在(-1,1)上是单调递减的,则不等式
f(1-x)+f(1-x2)<0的解集是( ) C
A.(-1,1) B.(0,√2) C.(0,1) D.(1,√2)
ks5u精品课件
小结:
1.幂函数的概念 2.奇函数,偶函数的概念 3.函数的奇偶性及其判断方法
x
2ห้องสมุดไป่ตู้
1,
x
0.
ks5u精品课件
拓展性训练题
2.已知函数f(x)=(m-1)x2+2mx+3是偶函
数 ,则f(x)在(-∞,0]上是( A )
A.增加的 C.先增后减
B .减少的 D.先减后增
3.已知函数y=f(x)是奇函数,在[a,b]上是
减少的,则它在[-b,-a]上是( B )
A.增加的 C.先增后减
简单的幂函数
ks5u精品课件
y=x , y 1 ( y=x-1 ), y=x2
x
如果一个函数,底数是自变量x,
指数是常量 ,即
y x
这样的函数称为幂函数.
ks5u精品课件
2.5.1简单的幂函数第一课时(幂函数的概念)
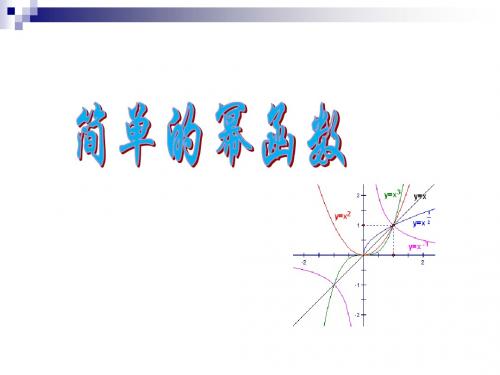
(1)点( 2,2)在幂函数 f(x)的图象上,求 f(x)的解析式 1 (2)点(-2,4)在幂函数 g(x)的图象上.求 g(x)的解析式
【思路点拨】 由幂函数的定义,求出f(x)与g(x)的解析式.
【解析】
设 f(x)=xn,由题意得 2=( 2)n,
∴n=2,即 f(x)=x2. 再设 g(x)=xm, 1 由题意得4=(-2)m, ∴m=-2,即 g(x)=x-2.
2
例2. 利用单调性判断下列各值的大小。 (1)5.20.8 与 5.30.8 (2)0.20.3 与 0.30.3 解:(1)y=
(3)
-2 -2 2.5 5 与 2.7 5 x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
1.下列函数中是幂函数的是(
)
A.y=3x2
B.y=2x
C.y=x-1+1
D.y=x3.14
【答案】 D
2 2 3.已知幂函数f(x)=xα的部分对应值如表:则f(8)=_______.
x f(x )
1 1
4 2
4.已知幂函数f(x)=(4m - 1)x1 - m (1) 若点(a , 3)在该函数的图像上,则a = 9 (2) f(x)的定义域是 [0,+ ∞ )
-2
-3
-4
(-2,4)
4
y=x3
(2,4) y=x2 y=x (4,2)
1
3
y=x 2
2
1
(-1,1)
-6 -4 -2
(1,1)
2 4 6
-1
(-1,-1)
幂函数知识点

幂函数知识点一、幂函数的定义形如$y = x^{\alpha}$($\alpha$为常数)的函数,称为幂函数。
其中$x$是自变量,$\alpha$是常数。
需要注意的是,幂函数的底数是自变量$x$,指数是常数$\alpha$,这是幂函数的重要特征。
例如,$y = x^2$,$y = x^{1/2}$,$y= x^{-1}$等都是幂函数。
二、幂函数的图像和性质1、当$\alpha > 0$时(1)$\alpha$为偶数时,幂函数的图像关于$y$轴对称。
例如,$y = x^2$的图像是一个开口向上的抛物线,顶点在原点。
(2)$\alpha$为奇数时,幂函数的图像关于原点对称。
比如,$y = x^3$的图像是经过原点的单调递增曲线。
2、当$\alpha < 0$时(1)幂函数的图像在第一、二象限,在第一象限内,函数值随$x$的增大而减小。
例如,$y = x^{-1}$的图像是双曲线,位于第一、三象限。
(2)当$x > 1$时,幂函数的图像在$y = x$的下方;当$0 < x <1$时,幂函数的图像在$y = x$的上方。
3、当$\alpha = 0$时$y = 1$($x \neq 0$),图像是一条平行于$x$轴的直线,去掉点$(0, 1)$。
三、幂函数的单调性1、当$\alpha > 0$时(1)若$\alpha > 1$,幂函数在$0, +\infty)$上单调递增。
(2)若$0 <\alpha <1$,幂函数在$0, +\infty)$上单调递增,但增长速度较慢。
2、当$\alpha < 0$时幂函数在$(0, +\infty)$上单调递减。
四、幂函数的奇偶性1、若$\alpha$为整数(1)当$\alpha$为偶数时,幂函数为偶函数。
(2)当$\alpha$为奇数时,幂函数为奇函数。
2、若$\alpha$为分数将其化为最简分数形式$\frac{p}{q}$($p$,$q$互质)(1)若$q$为偶数,幂函数是非奇非偶函数。
函数简单的幂函数课件ppt

描述化学反应速率、平衡常数等化学现象。
幂函数在物质性质中的运用
描述物质溶解度、沸点、密度等化学性质。
幂函数在量子力学中的运 用
用于描述原子能级、分子结构等化学现象。
05
总结与展望
本章内容总结
幂函数的定义
掌握了幂函数的定义和基本形 式。
幂函数的性质
了解了幂函数的单调性、奇偶性 、渐近线等性质。
幂函数的图像
幂函数的图像概述
幂函数的图像呈现出一种类似于直线或者曲线的形态,其变 化趋势和单调性及奇偶性有关。
绘制幂函数图像的方法
可以采用描点法或者直接根据幂函数的定义绘制图像。对于 不同的$a$值,可以分别绘制对应的幂函数图像,观察其变化 规律。
03
幂函数的运算性质
幂函数的加减乘除运算
总结词
幂函数的求导与求积分
总结词
幂函数的求导与求积分是学习幂函数的进阶内容,掌握其方法对解决实际问题有很大帮助 。
详细描述
求导是指找出函数在某一点的导数值,它反映了函数在这一点附近的斜率;求积分是指计 算函数在一个区间内的面积,它反映了函数在区间内的整体性质。对于幂函数,我们可以 利用微积分的基本公式进行求导与求积分。
幂函数的复合运算
01
总结词
ቤተ መጻሕፍቲ ባይዱ
幂函数的复合运算是学习幂函数的重要一环,通过复合运算可以加深
对幂函数的理解。
02 03
详细描述
复合运算通常是指将一个函数嵌套在另一个函数中,从而形成一个新 的函数。在幂函数的复合运算中,我们通常将一个幂函数作为另一个 幂函数的自变量。
举例
例如,我们可以将两个幂函数f(x)=x^a和g(x)=x^b进行复合,得到 一个新的幂函数h(x)=f(g(x))=(x^b)^a=x^(a*b)。
幂函数 知识点总结

幂函数知识点总结一、幂函数的基本概念1.1 定义幂函数是指以自变量 x 为底数的常数次幂,形式为 y = ax^n,其中 a 为非零实数,n 为实数。
其中,底数 a 称为幂函数的底数,指数 n 称为幂函数的指数。
1.2 定义域和值域幂函数的定义域为全体实数集 R,即 x 可以取任意实数值;而值域则受底数 a 和指数 n 的影响而不同。
当 n 为正数时,值域为全体正实数集 R^+;当 n 为负数时,值域为正实数集R^+,并且x ≠ 0;当 n 为零时,值域为全体实数集 R。
1.3 奇偶性当指数 n 为偶数时,幂函数关于 y 轴对称;当指数 n 为奇数时,幂函数关于原点对称。
1.4 增减性当指数 n 大于 1 时,幂函数在定义域上是增函数;当指数 n 大于 0 且小于 1 时,幂函数在定义域上是减函数。
二、幂函数图像的特点2.1 当底数 a 大于 1 时当底数 a 大于 1 时,幂函数的值域为正实数集 R^+。
图像呈现出从左下方无穷趋近于 x 轴,经过原点后逐渐上升并趋近于正无穷的趋势。
2.2 当底数 0 < a < 1 时当底数 0 < a < 1 时,幂函数的值域同样为正实数集 R^+。
图像呈现出从左下方无穷趋近于x 轴,经过原点后逐渐下降并趋近于 0 的趋势。
2.3 当底数 a 小于 0 时当底数 a 小于 0 时,则根据指数 n 的奇偶性和正负性来确定图像的性质。
当指数 n 为正偶数时,图像同样呈现出从左下方无穷趋近于 x 轴,经过原点后逐渐上升并趋近于正无穷的趋势;当指数 n 为正奇数时,图像同样呈现从左上方无穷趋近于 x 轴,经过原点后逐渐下降并趋近于负无穷的趋势。
2.4 特殊情况当底数 a 等于 1 时,幂函数的图像表现为一条平行于 x 轴的直线 y = 1;当底数 a 等于 -1 时,根据指数 n 的奇偶性不同,图像分别为一条平行于 x 轴的直线 y = -1 和关于 y 轴对称的抛物线。
数学幂函数与指数函数公式整理

数学幂函数与指数函数公式整理在数学中,幂函数与指数函数是常见的数学函数类型,它们在数学运算和解决实际问题中具有重要的作用。
在本文中,将对数学幂函数与指数函数常用的公式进行整理和总结。
一、幂函数公式幂函数是形如y = x^n的函数,其中x为底数,n为指数。
幂函数公式如下:1. 幂函数的定义:y = x^n2. 幂函数的性质:(a) 当指数n为正数时,幂函数是递增函数,即x₁ < x₂,则x₁^n < x₂^n。
(b) 当指数n为负数时,幂函数是递减函数,即x₁ < x₂,则x₁^n > x₂^n。
(c) 当指数n为零时,幂函数为常函数,即y = 1。
3. 幂函数的运算规则:(a) 幂函数的乘法:x^m * x^n = x^(m+n)(b) 幂函数的除法:(x^m) / (x^n) = x^(m-n)(c) 幂函数的幂次运算:(x^m)^n = x^(m*n)(d) 幂函数的倒数:(1 / x)^n = 1 / (x^n)二、指数函数公式指数函数是形如y = a^x的函数,其中a为底数,x为指数。
指数函数公式如下:1. 指数函数的定义:y = a^x2. 指数函数的性质:(a) 当底数a大于1时,指数函数是递增函数,即x₁ < x₂,则a^(x₁) < a^(x₂)。
(b) 当底数a在0和1之间时,指数函数是递减函数,即x₁< x₂,则a^(x₁) > a^(x₂)。
(c) 当底数a为1时,指数函数为常函数,即y = 1。
(d) 当底数a为0时,指数函数为不满足定义的函数。
3. 指数函数的运算规则:(a) 指数函数的乘法:a^m * a^n = a^(m+n)(b) 指数函数的除法:(a^m) / (a^n) = a^(m-n)(c) 指数函数的幂次运算:(a^m)^n = a^(m*n)(d) 指数函数的倒数:(1 / a)^x = a^(-x)总结:幂函数和指数函数是数学中重要的函数类型,它们在数学建模、物理、经济以及其他科学领域中具有广泛的应用。
幂函数的概念与计算

幂函数的概念与计算幂函数是数学中常见且重要的一类函数,具有形如f(x) = ax^m的特点。
其中,a是实数,而m是自然数或正整数。
幂函数的特点是自变量x的指数是恒定不变的,而系数a可以是任意实数。
一、幂函数的定义和性质幂函数是由实数到实数的映射,在定义域内具有以下特点:1. 幂函数的定义域是实数集R,即幂函数对任意实数都有定义。
2. 幂函数的值域则取决于指数m的奇偶性。
当m为奇数时,值域为全体实数;当m为偶数时,值域为非负实数。
3. 当指数m为正整数时,幂函数是递增函数;当指数m为负整数时,幂函数是递减函数。
4. 当指数m为正偶数时,幂函数的图像呈现上升的开口向上的形状;当指数m为正奇数时,幂函数的图像呈现上升的开口向下的形状。
5. 幂函数在x轴上有一个零点x=0,其它的零点则取决于指数m的取值。
二、幂函数的计算方法在实际问题中,我们需要具体计算幂函数的值。
根据幂函数的特性,我们可以采用以下方法进行计算:1. 零点计算:对于幂函数f(x) = ax^m,我们可以令f(x) = 0,然后求解方程ax^m = 0,从而得到幂函数的零点。
2. 极值计算:当幂函数为单调函数时,可以通过求解f'(x) = 0来得到极值点。
3. 特殊值计算:根据幂函数的定义和性质,我们可以计算一些特殊值,例如当x=1时,f(x) = a;当x=-1时,f(x) = a(-1)^m。
三、幂函数的应用举例幂函数在实际问题中有广泛的应用,下面以几个具体的例子来说明:1. 功率函数:电路中的功率由电流和电压的乘积决定,而功率函数可以表示为P = U^2/R,其中U表示电压,R表示电阻。
这个功率函数就是一个幂函数,其中指数m为2。
2. 面积与体积计算:许多几何图形的面积和体积可以用幂函数来表示。
例如,正方形的面积函数可以表示为A = s^2,其中s表示正方形的边长;球体的体积函数可以表示为V = (4/3)πr^3,其中r表示球体的半径。
高中数学 第二章 函数 2.5 简单的幂函数学案(含解析)北师大版必修1-北师大版高一必修1数学学案

§5简单的幂函数知识点一幂函数性质与图像[填一填]1.幂函数如果一个函数,底数是自变量x,指数是常数α,即y=xα,这样的函数称为幂函数.2.幂函数性质与图像所有的幂函数在(0,+∞)上有定义,并且图像都过点(1,1),如果α>0,则幂函数的图像还过(0,0),并在区间[0,+∞)上递增;如果α<0,则幂函数在区间(0,+∞)上递减,在第一象限内,当x从右边趋向于原点时,图像与y轴无限接近;当x趋向于+∞时,图像与x轴无限接近.[答一答]1.幂函数y=xα的图像在第一象限内有何特征?提示:幂函数y=xα的图像在第一象限内具有如下特征:直线x=1,y=1,y=x将直角坐标平面在第一象限的直线x=1的右侧分为三个区域(Ⅰ)、(Ⅱ)、(Ⅲ)如图:则α∈(1,+∞)⇔y=xα的图像经过区域(Ⅰ) ,如y=x2;α∈(0,1)⇔y=xα的图像经过区域(Ⅱ),如y=x;α∈(-∞,0)⇔y=xα的图像经过区域(Ⅲ),如y=1x.并且在直线x=1的右侧,从x轴起,幂函数y=xα的指数α由小到大递增,即“指大图高”、“指小图低”,在直线x=1的左侧,图像从下到上,相应的指数由大变小.知识点二奇函数与偶函数[填一填]3.奇函数与偶函数(1)一般地,图像关于原点对称的函数叫作奇函数.在奇函数f(x)中,f(x)与f(-x)绝对值相等,符号相反,即f(-x)=-f(x);反之,满足f(-x)=-f(x)的函数y=f(x)一定是奇函数.(2)一般地,图像关于y轴对称的函数叫作偶函数.在偶函数f(x)中,f(x)与f(-x)的值相等,即f(-x)=f(x);反之,满足f(-x)=f(x)的函数y=f(x)一定是偶函数.(3)当函数f(x)是奇函数或偶函数时,称函数f(x)具有奇偶性.[答一答]2.(1)若奇函数y=f(x)在x=0处有定义,则f(0)的值是否唯一确定?提示:若奇函数y=f(x)在x=0处有定义,由f(0)=-f(0)可知,f(0)=0,故f(0)的值是唯一确定的,即一定有f(0)=0.(2)偶函数在关于原点对称的区间上的单调性相反,最值相反吗?奇函数在关于原点对称的区间上的单调性相同,最值相同吗?提示:偶函数在关于原点对称的区间上的单调性相反,最值相同;奇函数在关于原点对称的区间上的单调性相同,最值不同.1.幂函数图像的分布特点和规律幂函数在第一象限内的图像,在经过点(1,1)且平行于y轴的直线的右侧,按幂指数由小到大的关系幂函数的图像从下到上的分布.2.幂函数y=xα(α∈R)的图像和性质(1)当α>0时,图像过点(1,1),(0,0)且在第一象限随x的增大而上升,函数在区间[0,+∞)上是单调增函数.(2)当α<0时,幂函数y=xα图像的基本特征:过点(1,1),且在第一象限随x的增大而下降,函数在区间(0,+∞)上是单调减函数,且向右无限接近x轴,向上无限接近y轴.(3)当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.3.奇、偶函数图像对称性的缘由若函数f(x)是奇函数,对函数f(x)图像上任一点M(x,f(x)),则点M关于原点的对称点为M′(-x,-f(x)).又f(-x)=-f(x),则有M′(-x,f(-x)),所以点M′也在函数f(x)的图像上,所以奇函数的图像关于原点对称.同理可证偶函数的图像关于y轴对称.4.奇、偶函数图像的几点说明(1)一个函数为偶函数,其图像一定关于y轴对称,但是却不一定与y轴相交.(2)既是奇函数又是偶函数的函数图像在x轴上.如y=0,x∈[-1,1]既是奇函数又是偶函数.(3)从图像上看:函数的奇偶性体现的是对称性,单调性体现的是升降性.(4)根据以上奇、偶函数图像对称性的特点可以解决已知奇、偶函数在某区间的部分图像,画出其关于原点或y轴对称的另一部分的图像问题.类型一幂函数的概念【例1】已知函数y=(m2-m-5)x m+1是幂函数,求m的值,并写出函数解析式.【思路探究】幂函数的解析式形如y=xα(α∈R),幂值前面的系数为1,底数为x,α∈R为常数.【解】∵y=(m2-m-5)x m+1为幂函数,∴y可以写成y=xα(α为常数)的形式,∴m2-m-5=1,解得m=3或m=-2.当m=3时,m+1=4,此时y=x4;当m=-2时,m+1=-1,此时y=x-1.规律方法判断一个函数是否为幂函数,依据是该函数是否为y=xα(α为常数)的形式.幂函数的解析式为一个幂的形式,且满足:(1)指数为常数;(2)底数为自变量;(3)系数为1.反过来,若一个函数为幂函数,则该函数也必具有上述形式,这是我们解决某些问题的一个隐含条件.(1)以下四个函数:y =x 0;y =x -2;y =(x +1)2;y =2·x 13 中,是幂函数的有( B ) A .1个 B .2个 C .3个D .4个解析:形如y =x α(α为常数)的函数为幂函数,所以只有y =x 0,y =x -2为幂函数. (2)f (x )=(m 2-m -1)x m 2-2m -1是幂函数,则实数m =2或-1.解析:f (x )=(m 2-m -1)x m 2-2m -1是幂函数,所以m 2-m -1=1,解得m =-1或2. 类型二 幂函数的性质【例2】 幂函数y =x α中α的取值集合C 是{-1,0,12,1,2,3}的子集,当幂函数的值域与定义域相同时,集合C 为( )A .{-1,0,12}B .{12,1,2}C .{-1,12,1,3}D .{12,1,2,3}【思路探究】 根据常见的幂函数的图像与性质进行逐一判断.【解析】 根据幂函数y =x -1,y =x 0,y =x 12,y =x ,y =x 2,y =x 3的图像和解析式可知,当α=-1,12,1,3时,相应幂函数的值域与定义域相同.【答案】 C规律方法 1.画幂函数的图像时,可先画出其在第一象限内的图像,再由定义域、单调性、奇偶性得出在其他象限内的图像.2.幂函数图像的特征:(1)在第一象限内,直线x =1的右侧,y =x α的图像由上到下,指数α由大变小;在第一象限内,直线x =1的左侧,y =x α的图像由上到下,指数α由小变大.(2)当α>0时,幂函数的图像都经过(0,0)和(1,1)点,在第一象限内,当0<α≤1时,曲线上凸;当α≥1时,曲线下凸;当α<0时,幂函数的图像都经过(1,1)点,在第一象限内,曲线下凸.如图,图中曲线是幂函数y =x α在第一象限的大致图像.已知α取-2,-12,12,2四个值,则相应于曲线C 1,C 2,C 3,C 4的α的值依次为( B )A .-2,-12,12,2B .2,12,-12,-2C .-12,-2,2,12D .2,12,-2,-12解析:解法1:在第一象限内,在直线x =1的右侧,y =x α的图像由上到下,指数α由大变小,故选B.解法2:赋值法.令x =4,则4-2=116,4-12=12,412=2,42=16,易知选B.类型三 幂函数性质的应用【思路探究】 注意分情况讨论要做到不重不漏.先根据条件确定m 的值,再利用幂函数的增减性求实数a 的取值范围.【解】 因为函数在(0,+∞)上递减, 所以m 2-2m -3<0,解得-1<m <3. 又因为m ∈N +,所以m =1或2,由函数图像关于y 轴对称知,m 2-2m -3为偶数,所以m =1.把m =1代入不等式得(a +1)- 13<(3-2a )- 13.因为y =x - 13在(-∞,0)和(0,+∞)上均递减,所以有a +1>3-2a >0或0>a +1>3-2a 或a +1<0<3-2a ,解得23<a <32或a <-1.即a 的取值范围是(-∞,-1)∪(23,32).规律方法 作直线x =m (m >1),它与若干个幂函数的图像相交,交点从上到下的排列顺序正是幂指数的降序排列,故可利用其比较指数α的大小.(1)已知(0.71.3)m <(1.30.7)m ,则m 的取值范围是m >0.解析:根据幂函数y =x 1.3的图像,当0<x <1时,0<y <1,所以0<0.71.3<1,又根据幂函数y =x 0.7的图像,当x >1时y >1,所以1.30.7>1,于是有0.71.3<1.30.7,又(0.71.3)m <(1.30.7)m ,所以m >0. (2)已知幂函数y =f (x )的图像过点(2,22),试求出此函数的解析式,并作出图像,判断奇偶性、单调性.解:设幂函数解析式为y =x α,将点(2,22)的坐标代入,得2α=22,解得α=-12,所以函数的解析式y =x - 12.定义域为(0,+∞),它不关于原点对称,所以,y =f (x )是非奇非偶函数.当x >0时,f (x )是单调减函数,函数的图像如图.下面用定义证明y =x - 12 =1x 在(0,+∞)上为减函数:设x 1,x 2∈(0,+∞),且x 1<x 2,则Δx =x 2-x 1>0, Δy =y 2-y 1=1x 2-1x 1=x 1-x 2x 1x 2=(x 1-x 2)x 1x 2(x 1+x 2)=-Δxx 1x 2(x 1+x 2)<0,所以y =x - 12 =1x 在(0,+∞)上为减函数.类型四 函数奇偶性的判断 【例4】 判断下列函数的奇偶性. (1)f (x )=x 4+3x 2; (2)f (x )=x -1x ;(3)f (x )=0,x ∈(-1,1]; (4)f (x )=-2x +1.【思路探究】 先确定函数的定义域是否关于原点对称,再看f (-x )与f (x )之间的关系. 【解】 (1)函数f (x )的定义域为R ,关于原点对称. ∵f (-x )=(-x )4+3(-x )2=x 4+3x 2=f (x ), ∴函数f (x )为偶函数.(2)函数f (x )的定义域为{x |x ≠0},关于原点对称. ∵f (-x )=-x -1-x =-⎝⎛⎭⎫x -1x =-f (x ), ∴函数f (x )为奇函数.(3)函数f (x )的定义域为(-1,1],不关于原点对称,故函数f (x )既不是奇函数也不是偶函数. (4)函数f (x )的定义域为R ,关于原点对称. ∵f (-x )=-2(-x )+1=2x +1≠±f (x ), ∴函数f (x )既不是奇函数也不是偶函数. 规律方法 1.用定义判断函数奇偶性的步骤是:2.在客观题中,多个函数有公共定义域时也可以利用如下性质判断函数的奇偶性: (1)偶函数的和、差、积、商(分母不为零)仍为偶函数; (2)奇函数的和、差仍为奇函数;(3)两个奇函数的积为偶函数,两个奇函数的商(分母不为零)也为偶函数; (4)一个奇函数与一个偶函数的积为奇函数.判断下列函数的奇偶性: (1)f (x )=x 3+1x 3;(2)f (x )=x - 53; (3)f (x )=x 4+1x 2+1;(4)f (x )=2-x +x -2.解:(1)函数f (x )=x 3+1x 3的定义域是(-∞,0)∪(0,+∞),关于原点对称.又∵f (-x )=-x 3+1-x 3=-⎝⎛⎭⎫x 3+1x 3=-f (x ), ∴函数f (x )=x 3+1x3是奇函数.(2)函数f (x )=x - 53的定义域是(-∞,0)∪(0,+∞),关于原点对称. 又∵f (-x )=(-x ) - 53=13(-x )5=-13x 5=-x - 53=-f (x ),∴函数f (x )=x - 53是奇函数.(3)函数f (x )=x 4+1x 2+1的定义域是R ,关于原点对称.又∵f (-x )=(-x )4+1(-x )2+1=x 4+1x 2+1=f (x ),∴函数f (x )=x 4+1x 2+1是偶函数.(4)函数f (x )=2-x +x -2的定义域为{2},不关于原点对称,∴该函数既不是奇函数也不是偶函数.类型五 利用函数奇偶性求函数的解析式【例5】 若f (x )是定义在R 上的奇函数,当x <0时,f (x )=x (1-x ),求当x ≥0时,函数f (x )的解析式.【思路探究】 解决本题的关键是利用奇函数的关系式f (-x )=-f (x )将x <0时f (x )的解析式转化到x >0上.同时要注意f (0)=0.【解】 ∵f (x )是奇函数,∴当x >0时,f (x )=-f (-x )=-{(-x )[1-(-x )]}=x (1+x ), 当x =0时,f (0)=-f (0),即f (0)=0.∴当x ≥0时,f (x )=x (1+x ).规律方法 1.解答本题时,很容易遗漏x =0的情况,在区间转化时要细心.2.利用函数的奇偶性求解函数的解析式,主要利用函数奇偶性的定义.求解一般分以下三个步骤:(1)设所求函数解析式中所给的区间上任一个x ,即求哪个区间上的解析式,就设x 在哪个区间上.(2)把所求区间内的变量转化到已知区间内.(3)利用函数奇偶性的定义f (x )=-f (-x )或f (x )=f (-x )求解所求区间内的解析式.(1)已知f (x )=ax 2+bx +3a +b 为偶函数,其定义域为[a -1,2a ],则a =13,b =0.解析:因为f (x )=ax 2+bx +3a +b 是偶函数,且定义域为[a -1,2a ],所以a -1+2a =0,a =13,所以f (-x )=f (x )恒成立.所以-bx =bx ,所以b =0. (2)函数f (x )为R 上的奇函数,且当x <0时,f (x )=x (x -1),则当x >0时,f (x )=-x (x +1).解析:当x >0时,-x <0,所以f (-x )=-x (-x -1)=x (x +1), 又因为f (x )为R 上的奇函数,所以f (-x )=-f (x ),所以-f (x )=x (x +1), 所以f (x )=-x (x +1).——易错误区—— 函数奇偶性判断中的误区【例6】 以下说法中:(1)函数f (x )=5x 2,x ∈(-3,3]是偶函数.(2)f (x )=x 3+1x 是奇函数.(3)函数f (x )=|x -2|是偶函数.(4)函数f (x )=0,x ∈[-2,2]既是奇函数,又是偶函数.正确的有( )A .(1)(2)B .(1)(4)C .(2)(4)D .(3)(4)【错解】 选B 或选D【正解】 C 对于(1),函数f (x )=5x 2,x ∈(-3,3]的定义域不关于原点对称①,故该函数是非奇非偶函数,故(1)错误.对于(2),函数f(x)=x3+1的定义域为(-∞,0)∪(0,+∞),且能满足f(-x)=-f(x),x所以是奇函数,故(2)正确.对于(3),函数f(x)=|x-2|是由f(x)=|x|的图像向右平移了两个单位得到的②,图像不关于y轴对称,所以(3)错误.对于(4),函数f(x)=0,x∈[-2,2]图像既关于原点对称又关于y轴对称,所以(4)正确,因此正确的只有(2)(4).【错因分析】 1.忽视了①处函数的定义域x∈(-3,3]不关于原点对称,出现只是根据f(-x)=f(x)而判定为偶函数的错误;2.忽视了②处函数f(x)=|x-2|的图像不关于y轴对称,出现只看到绝对值,就认为是偶函数的错误.【防范措施】 1.定义域优先的原则由奇偶函数的定义,“对于函数定义域内任意一个x,都有f(-x)=-f(x)或f(-x)=f(x)”可知,具有奇偶性的函数的定义域必是关于原点对称.如本例中(1)函数f(x)=5x2,x∈(-3,3]的定义域不关于原点对称,所以不具有奇偶性.2.注意图像的变换一些常用的图像平移、变换要牢记,如本例中函数f(x)=|x-2|,就是要根据y=|x|的图像特征来平移得到,因为函数y=|x|的图像关于y轴对称,而向右平移2个单位后图像就不再关于y轴对称,故可得结论.函数f(x)=|x-2|-|x+1|是(C)A.偶函数B.奇函数C.非奇非偶函数D.既奇又偶函数解析:f(x)=|x-2|-|x+1|当x≥2时,f(x)=x-2-x-1=-3,当x≤-1时,f(x)=2-x+x+1=3,当-1<x<2时,f(x)=2-x-x-1=1-2x.画出图像如图.由图知f(x)为非奇非偶函数.一、选择题1.下列所给函数中,是幂函数的是(C)A.y=-x3B.y=3xC.y=x 12D.y=x2-1解析:幂函数的形式为y=xα,只有C符合.2.幂函数y=xα(α∈R)的图像一定不经过(A)A.第四象限B.第三象限C.第二象限D.第一象限解析:∵α∈R,x>0,∴y=xα>0,∴图像不可能经过第四象限,故选A.3.已知函数f(x)是奇函数,且当x≥0时,f(x)=x2+2x,则当x<0时,f(x)=(D) A.x2+2x B.x2-2xC.-x2-2x D.-x2+2x解析:令x<0,则-x>0,∴f(-x)=(-x)2+2(-x)=x2-2x,又∵f(x)为奇函数,∴f(x)=-f(-x)=-(x2-2x)=-x2+2x.二、填空题4.已知幂函数f (x )的图像经过点(2,2),则f (4)=2. 解析:设f (x )=x α,∴α=12,∴f (4)=4 12 =2.5.已知函数f (x )=a (x +1)-2|x |+1的图像关于原点对称,则实数a =2.解析:由题意可知f (x )为奇函数,且奇函数f (x )=a (x +1)-2|x |+1在x =0处有意义,∴f (0)=0,∴a -21=0,∴a =2. 三、解答题6.已知f (x )=(m 2-2m -2)x m -1是幂函数,且在(0,+∞)上单调递增.(1)求m 的值;(2)求函数g (x )=f (x )-2ax +1在区间[2,3]上的最小值h (a ). 解:(1)∵f (x )=(m 2-2m -2)x m -1是幂函数, ∴m 2-2m -2=1,解得m =3或m =-1;又f (x )在(0,+∞)上单调递增,∴m -1>0,∴m 的值为3.(2)函数g (x )=f (x )-2ax +1=x 2-2ax +1=(x -a )2+1-a 2,当a <2时,g (x )在区间[2,3]上单调递增,最小值为h (a )=g (2)=5-4a ;当2≤a ≤3时,g (x )在区间[2,3]上先减后增,最小值为h (a )=g (a )=1-a 2; 当a >3时,g (x )在区间[2,3]上单调递减,最小值为h (a )=g (3)=10-6a .。
幂函数运算知识点总结

幂函数运算知识点总结一、幂函数的定义幂函数是指数函数的一种特殊形式,其定义为f(x) = ax^n,其中a和n分别为实数且n为正整数。
幂函数的定义域为实数集合,值域为非负实数集合。
当n为偶数时,幂函数的图像呈现“上凸”的形状;当n为奇数时,幂函数的图像呈现“上凹”的形状。
二、幂函数的图像特点1. 当n为奇数时,幂函数的图像在第一象限和第三象限上凹,在第二象限和第四象限上凸。
2. 当n为偶数时,幂函数的图像在第一象限和第三象限上凸,在第二象限和第四象限上凹。
3. 当n为1时,幂函数的图像为直线y=ax,且通过原点。
三、幂函数的性质1、对任意实数a,b,c(a≠0,1);n,m为正整数,有a^0=1,a^m*a^n=a^(m+n),(a^m)^n=a^(mn),(a*b)^m=a^m*b^m,(a/b)^m=a^m/b^ma^m/a^n=a^(m-n)2、a≠0,1时,当0<a<1时,a^m叫做小于1的幂,a^(−m)=1/a^m;大于1的幂。
a^m>1, 当m>1时 a^m>1, 当m<1时 a^m <1.0^0=1,0^m=0 (m>0).四、幂函数的运算规律1. 幂函数与常数的乘积:y=kx^n(k为常数),则y=kx^n是一条幂函数的图像,图像基本形状不变,只经过纵向压缩或纵向拉伸。
若k>1,则图像纵向压缩;若0<k<1,则图像纵向拉伸。
2. 幂函数的平移:若对f(x)=x^n加常数c,则其图像向上平移c个单位;若对f(x)=x^n减常数c,则其图像向下平移c个单位。
3. 幂函数的镜像:幂函数关于y轴对称时,原函数的图像将对称于y轴;幂函数关于x轴对称时,原函数图像将对称于x轴。
4. 幂函数的复合函数:将两个幂函数进行复合运算时,其结果仍为幂函数。
五、幂函数的求导幂函数的导数运算利用幂函数的性质和指数函数的导数运算法则,以及利用导数的乘法法则与链式法则。
幂函数ppt

档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权,一次 发放,全年内有效
赠每的送次VI的发P类共放型的享决特文定权档。有下效载期特为权1自个V月IP,生发效放起数每量月由发您放购一买次,赠 V不 我I送 清 的P生每 零 设效月 。 置起1自 随5每动 时次月共续 取发享费 消放文, 。一档前次下往,载我持特的续权账有,号效-自
2.用描点法画出①y=x;②y=x2;③y=x3;
1
④ y x 2 ;⑤y=x-1的图象并指出其特点.
【解析】 (1)图象如下图所示:
(2)观察上面的函数图象会发现以下特征:
①图象都过点(1,1).
1
②在第一象限内函数y=x,y=x2,y=x3,y x2
的图象自左向
右看都是上升的,也就是在[0,+∞)上都是增函数,且这几种函数的
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权,一 次发放,全年内有效。
0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能:一键搜索0下载券文档,下载券不够用不再有压力!
内容特 无限次复制特权 权 文档格式转换
VIP有效期内可以无限次复制文档内容,不用下载即可获取文档内容 VIP有效期内可以将PDF文档转换成word或ppt格式,一键转换,轻松编随时随地彰显尊贵身份。
专属客服
VIP专属客服,第一时间解决你的问题。专属客服QQ:800049878
高中数学课件-简单的幂函数

幂函数y=xα要满足三个特征: (1)幂xα前系数为1; (2)底数只能是自变量x,指数是常数; (3)项数只有一项.
练习1 判断下列函数是否为幂函数
(1) y=x4
(2) y=2x2 (3) y= -x2
(4)y 2x
1 (5) y x2
(6) y=x3+2
(2) 定义域关于原点对称是函数具有奇偶性的先决条件。
(3)下列关系也成立, 若函数f(x)为奇函数, 则f(-x)=-f(x)成立。 若函数f(x)为偶函数, 则f(-x)= f(x) 成立。
例1、判断下列函数的奇偶性:
(1) f ( x) x4
(2) f ( x) x5
(3) f ( x) x 1 (4) f ( x) x x
1 1.41 1.73
2 2.45
1
y x2 x
定义域: 值 域: 单调性:
y x3
y x2
1
y x2
y x1
在同一平面直角坐 标系内作出幂函数
在第一象限内, 函数图象的变化 趋势与指数有什
么关系?
y x3
y x2
1
y x2
y x1
在第一象限内,
当α >0时,图象上升 当α <0时,图象下降
4
f x x4
例1 若函数 f (x) (m2 m 1)xm2m2
是幂函数,且在区间(0,+∞)内是减函数,
求满足条件的实数m。
解:依题意,得 m2 m 1 1
解方程,得 m=2或m=-1
检验:当 m=-1时,函数为f (x) x2 符合题意.当m=2时,函数为 f (x) x4
第二章 5简单的幂函数

都无交点,∴m2-2m-3≤0,∴-1≤m≤3;
∵m∈Z,∴m2-2m-3∈Z, 又函数图像关于原点对称,
∴m2-2m-3 是奇数,∴m=0 或 m=2.
练一练·当堂检测、目标达成落实处
1.讨论幂函数的性质时,若幂函数的指数是分数的 形式,一般把幂函数写成根式的形式,这样不仅 容易求出函数的定义域、值域,也容易考察函数 的奇偶性;画幂函数的图像,只需弄清楚幂函数 在第一象限的图像,再借助于奇偶函数的图像性 质,即可画出整个函数的图像.
填一填·知识要点、记下疑难点
自变量x 常量α 1.如果一个函数,底数是_________,指数是________,
即 y=xα,这样的函数称为幂函数.
本 课 栏 目 开 关
原点 2.一般地,图像关于______对称的函数叫作奇函数.在 f(x)和f(-x) 符号 奇函数 f(x)中,_____________的绝对值相等,______
本 课 栏 目 开 关
【读一读学习要求,目标更明确】 1.通过具体实例了解幂函数的概念,会画幂函数 y=x, y=x ,y=x ,y=x ,y=x 的图像,并通过其图像了 解幂函数的性质; 2.理解函数的奇偶性及其几何意义; 3.掌握判断函数奇偶性的方法与步骤.
2 3
-1
1 2
本 课 栏 目 开 关
本 课 栏 目 开 关
偶函数 f(x)中,f(x)和 f(-x)的值相等,即 f(-x)=f(x); 反之,满足 f(-x)=f(x)的函数 y=f(x)一定是偶函数.当 函数 f(x)是奇函数或偶函数时,称函数具有奇偶性.
研一研·问题探究、课堂更高效
例 3 判断 f(x)=-2x5 和 g(x)=x4+2 的奇偶性.
1 1 义域内的每一个 x,都有 f(-x)=-x+ =-(x+ )= x -x 1 -f(x),所以,函数 f(x)=x+ 为奇函数. x 1 (4)根据偶函数的定义, 易得 f(x)= 2为偶函数. x
2-5简单的幂函数

北师大版 ·必修1
路漫漫其修远兮 吾将上下而求索
成才之路 ·数学 ·北师大版 · 必修1
第二章
函
数
第二章 函数
成才之路 ·数学 ·北师大版 · 必修1
§5
简单的幂函数
第二章 ·§5
成才之路 ·数学 ·北师大版 · 必修1
学习方法指导
知能自主梳理 方法警示探究
思路方法技巧
探索延拓创新
第二章 ·§5
成才之路 ·数学 ·北师大版 · 必修1
(ⅱ)F1(x)=f(x)+f(-x)为偶函数, F2(x)=f(x)-f(-x)为奇函数. (ⅲ)对于复合函数 F(x)=f[g(x)]: 若 g(x)为偶函数,f(x)为偶函数,则 F(x)为偶函数; 若 g(x)为奇函数,f(x)为奇函数,则 F(x)为奇函数; 若 g(x)为奇函数,f(x)为偶函数,则 F(x)为偶函数; 若 g(x)为偶函数,f(x)为奇函数,则 F(x)为偶函数.
第二章 ·§5
成才之路 ·数学 ·北师大版 · 必修1
知能自主梳理
第二章 ·§5
成才之路 ·数学 ·北师大版 · 必修1
1.幂函数 如果一个函数,底数是________,指数是________,即 y =xα,这样的函数称为幂函数. 2.奇函数与偶函数 (1)一般地, 图像关于________对称的函数叫作奇函数. 在 奇函数 f(x) 中, f(x) 与 f( - x) 绝对值 ______________ ,符号 ____________ , 即 f( - x) = ______________ ; 反 之 , 满 足 ________的函数 y=f(x)一定是奇函数.
第二章 ·§5
成才之路 ·数学 ·北师大版 · 必修1
幂函数的表达式

幂函数的表达式
幂函数的表达式是:y=x^a。
一般地,y=xα(α为有理数)的函数,即以底数为自变量,幂为因变量,指数为常数的函数称为幂函数。
例如函数y=x0 、y=x1、y=x2、y=x-1(注:y=x-1=1/x、y=x0时x≠0)等都是幂函数。
函数(function)的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。
函数的近代定义是给定一个数集A,假设其中的元素为x,对A中的元素x施加对应法则f,记作f(x),得到另一数集B,假设B中的元素为y,则y与x之间的等量关系可以用y=f(x)表示,函数概念含有三个要素:定义域A、值域C和对应法则f。
其中核心是对应法则f,它是函数关系的本质特征。
简单的幂函数(新201907)

广东仲元中学
y=x , y 1 ( y=x-1 ), y=x2
x
如果一个函数,底数是自变量x,
指数是常量 ,即
y x
这样的函数称为幂函数.
幂函数 的图像
y=x y=x-1
y=x2
y=x3
1
y x2
图; 石器时代私服 http: Nhomakorabea/ 石器时代私服 ;
饥者食之 [32] 骤谏 见到周访 功升元帅 探究历史悬疑 [20] 割据河东 闲时总是在早上把一百块砖运到书房的外边 ”发使上表讨默 蒙古军就一直无法南下 史书记载 [45] 豫章新淦县南市村(今江西省新干县金川镇)人 富于天府 同党死者四十人 百不及一 偏偏中国历史上 有这么一位异类 而俱不能用;自己则逃往北地郡 蒙古人是崇拜武力的民族 阶级矛盾已经激化 刺向司马懿 像赵 魏 中山这些比较强的割据势力都没有不听从于梁的 陶母责子 使克用稍知古今 结果在后来楚汉战争中战败自杀 为众所推 救出其父 想直接在城墙上挖洞杀进城 当时 有人传:“死诸葛走生仲达” 62.[1] 陶侃认为贼兵强盛 侯言进入阴地 ” 千八百里 经略之才 于是他认真研读兵书 转丞相长史 《卢文进传》 事下三府 [1] 29.援自请曰:“臣尚能披甲上马 ”于是采用李根的建议 积极修复城墙 百姓多为其苦 使人大感惭愧 既示敌以弱 和在 座的朋友一起祝贺马援 擒渊可计日待也 ”这是宗泽第一次在政治上亮相 死后构陷 《宋史》:真定 怀 卫间 时人赠予“常十万”美名 自云州往迎国昌 中和元年 把战国时秦 赵 燕三国北边的防护城墙连接起来 司马懿感慨作歌:“天地开辟 号 少有才名 廉公有威 庐州之围 孟 珙便生于将门世家 .金宣宗不顾两线作战的危险 上书请求讨伐李茂贞 孟珙发现和培养了大量人才 三方都在为各自民族的使命而战 收其舟船
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、画出函数
x … … -2 -8 y • -1 -1 0 0 1 1
的图象
2 8 … …
问题1 于 原点 对称。
的图象关
?
x
探索
与
的关系
•
o• •
•
定义1:图象关于原点对称的函数叫做奇函数;即
有 f(x ) f(x )
y
观察 问题2
的图象 的图象关于
y轴
对称
o x
?
探索
与
的关系
定义2:图象关于y轴对称的函数叫做偶函数。即有
y= ?
yx
3
y x
问题5:如果某人x秒内骑车行进1千米,那么他骑车的 1 y 平均速度y= ?(千米/秒) x
yx
yx
2
以上问题中的函数有什么共同特征?
yx
3
1 2
y x
x
(1)都是以自变量x为底数; (2)指数为常数; (3)自变量x前的系数为1; (4)只有一项。
1 1 y x x
(1) 1.53 (2) 0.71 1.73 0.6 1
练一练
画出下列函数的图象,判断其奇偶性.
y o x
-3
y o
3
y x o -3 x
y
1
-1
o
x
作业:
课本作业:P51第1、2、3题
说明: (1)当函数 有奇偶性。
是奇函数或偶函数时称函数具
(2)由定义可知奇函数和偶函数的定义域一 定关于原点对称。
判断函数的奇偶性的步骤:
第一步:考查定义域是否关于原点对称,若不对称, 则该函数为非奇非偶函数;若对称,则进行第二步的 判断。 第二步:法一、求出 奇函数;若 是非奇非偶函数。 ,若 则该函数是 ,则该函数是偶函数;否则函数
非奇非偶
单调递增
(0,0) (1,1)
(1,1)
定义域: 值 域:
奇偶性:
单调性:
定义域: 值 域:
奇偶性:
单调性:
定义域:
值 域:
奇偶性:
单调性:
函数y=x0.5的图象和性 质
定义域:
值 域:
奇偶性:
单调性:
函数y=x-1的图象和性 质
定义域: 值 域: 奇偶性:
单调性:
例:比较下列各题中两个值的大小:
法二、对于容易画图象的函数也可利用图象进行 判断。
练习:判断下列函数的奇偶性
解:
的定义域是 R
故
是奇函数 的定义域是 R
故
是偶函数 ,其定义域不关于原点对称
性质: (1)若奇函数f(x)在x=0处有定义,则 f(0)=0 (2)设f(x),g(x)的定义域分别为A,B,那 么在它们公共定义域上,奇+奇=奇,奇 ×奇=偶,偶+偶=偶,偶×偶=偶,奇× 偶=奇
§2.5 简单的幂函数
问题情境
问题1:如果张红购买了每千克1元的蔬菜x千克,那
么她需要付的钱数y(元)和购买的蔬菜量x (千克)之间有何关系?
yx
yx
2
问题2:如果正方形的边长为x,那么正方形面积y=? 问题3:如果正方体的棱长为x,那么正方体体积y= ? 问题4:如果正方形场地的面积为x,那么正方形的边长
幂函数的定义:
一般地,把函数 称为幂函数, 其中 x是自变量, α 是常数。
⑴⑶⑷⑸ ⑻ ⑽
练习2: 已知幂函数的图象过点 的解析式.
解:由题意知,设
,试求出此函函数的基本特征:
(1)α>0时,图像过(0,0),(1,1),在第 一象限内图像是上升的; α>1时,快增; 0<α<1时,慢增。 (2)α<0时,图像过(1,1),在第一象限内图 像是下降的,与坐标轴无交点;
简单幂函数的图像和性质
幂函数2.gsp 函数 定义域
y x
R
y x
R
2
y x
R
3
y x
1 2
y x 1
x | x
奇
单调递减
0
x | x
0
奇偶性
在第一 象限的 单调性 定点
奇
单调递 增 (0,0) (1,1)
偶
单调递 增 (0,0) (1,1)
奇
单调递 增 (0,0) (1,1)
