福建省莆田市2018届高三下学期教学质量检测(3月)+数学(理)+Word版含答案

合集下载

福建省莆田市2018届高三下学期教学质量检测(3月)+英语+Word版含答案

2018年莆田市高中毕业班教学质量检测试卷英语试题第I卷第一部分听力(共两节，满分30分)做题时，先将答案标在试卷上，录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节(共5小题; 每小题1. 5分，满分7. 5分)听下面5段对话，每段对话后有一个小题。

从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. £19.15.B. £9.15.C. £9.18.答案是C。

1. Why does the man call the woman?A. To tell her about his birthday.B. To introduce Sandra to her.C. To invite her to a party.2. Where does the conversation probably take place?A. In a car.B. On a bus.C. On a plane3. What does the man mean?A. He has no tickets.B. The group is well known.C. The woman should be serious.4. What will the man do first?A. Finish the report.B. Send the e-mail.C.Move the furniture.5. When are the speakers going to the theatre?A. On the 18th.B. On the 19th.C. On the 20th.第二节(共15小题; 每小题1. 5分，满分22. 5分)听下面5 段对话或独白。

福建省莆田市2018届高三下学期教学质量检测(3月)数学(理)含答案

A. 乙丑年 B.丙寅年 C.丁卯年 D.戊辰年
7.如图 ,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图 ,则此几何体的体积为
4 A. 3 B.
8
4
8
2
2
3 C.
3 D.
3
f (x)
8.
2x, x a x 1,x a 在 R 上是增函数的一个充分不必要条件是
A. a=0B. a=2C. a≥ 1Da.≤1
9.甲乙两人被安排在某月 1 日至 4 日值班 ,要求每天安排一人值班
恰好值班两天的概率为
13
3
6
,每人至少值班一天 ,则甲
A. 3 B. 7
C. 8
D. 7
10.已知函数 f (x) sin( x )(0
8) ,且
f
() 6
5
2 f( )
3
2
则下列结论正确的是
A. f(x)的图象关于直线 24 对称 B.f(x)的图象关于点 ( 12 ,0)对称
6. “干支纪年法 ”是中国历法上自古以来就一直使用的纪年方法干支是天干和地支的总称把干支顺序相配正好六十为一周 ,周而复始 ,循环记录 ,这就是俗称的 “干支表 ”甲、乙、丙、丁、戊、己、庚、辛、王、癸等十个符号叫天干 ; 子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥等十个符号叫地支如 :公元 1984 年农历为甲子年 ,公元 1985 年农历为乙丑年 ,公元 1986 年农历为丙寅年则公元 2047 年农历为
cos 的值为
36 36
63
36
A. 3 B. 3
C. 3
D.
3
4.执行右面的程序框图 ,如果输入的 a=1,b=2,n=3,则输出的 S=

福建省莆田市高三理综下学期教学质量检测(3月)试题

2018年莆田市高中毕业班教学质量检测试卷理科综合能力测试注意事项:本试题分第1卷(选择题)和第Ⅱ卷(非选择题)两部分2.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。

3,全部答案在答题卡上完成,答在本试题卷上无效。

4.考试结束后,将本试题卷和答题卡一并交回。

可能用到的相对原子质量:H1 C12 N14 O16 Cl35.5 Sn119第I卷(选择题共126分)一、选择题:本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求的。

1.关于下图所示生物或细胞的叙述,正确的是A a、b、c、d都能独立繁殖和代谢 B. a和d都属于生命系统的结构层次C. a、b、c、d的遗传物质都是DNAD. b和c不具有以核膜为界限的细胞核2.癌症是严重威胁人类健康的疾病之一,健康的生活方式有利于预防癌症,下列有关叙述正确的是A.黄曲霉素属于生物致癌因子B.艾滋病患者与正常人患癌症的几率相同C.焦油含量低的香烟不会诱发癌症D.亚硝酸盐可通过改变基因的结构而致癌3.下列有关人体内环境及其稳态的叙述,正确的是A.内环境中不可能发生化学反应B.内环境稳态受体内细胞代谢活动的影响C.内环境稳态是指内环境理化性质恒定不变D.突触小泡内的神经递质属于内环境的成分4.下列关于生态学知识的叙述,正确的是A.食物链的营养级越多,能量传递效率越高B.种群数量K/2时是鱼类捕捞、虫害防治的最佳时期C.生态系统自我调节能力大小主要取决于无机环境D.利用生态系统的信息传递作用能够调节生物的种间关系5.下列与植物激素有关的叙述,错误的是A.顶端优势现象体现了生长素作用的两重性B.植物激素的作用方式是直接参与细胞代谢C.植物激素的合成受基因组和环境因素的共同作用D.生长素在植物体内可以进行极性运输和非极性运输6.现有甲、乙两种类型的豌豆各若干,下列相关叙述正确的是A.甲×甲、甲x乙都可用于验证基因的分离定律B.若甲品种连续自交,A的基因频率将会不断升高C.乙品种自交后代中基因型为 AaBbDd个体占1/8D.乙细胞中等位基因B、b分离一定发生在减数第一次分裂29.(10分)某研究小组以洋葱为实验材料开展相关的研究,洋葱的叶分两种:绿色管状叶伸展于空中,进行光合作用;鳞片叶层层包裹形成鳞茎,富含营养物质。

福建省莆田市2018届高三下学期教学质量检测(3月)理综

2018年莆田市高中毕业班教学质量检测试卷理科综合能力测试注意事项本试题分第1卷(选择题)和第Ⅱ卷(非选择题)两部分2.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。

3,全部答案在答题卡上完成,答在本试题卷上无效。

4.考试结束后,将本试题卷和答题卡一并交回。

可能用到的相对原子质量H1 C12 N14 O16 Cl35.5 Sn119第I卷(选择题共126分)一、选择题本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求的。

1.关于下图所示生物或细胞的叙述,正确的是A a、b、c、d都能独立繁殖和代谢 B. a和d都属于生命系统的结构层次C. a、b、c、d的遗传物质都是DNAD. b和c不具有以核膜为界限的细胞核2.癌症是严重威胁人类健康的疾病之一,健康的生活方式有利于预防癌症,下列有关叙述正确的是A.黄曲霉素属于生物致癌因子B.艾滋病患者与正常人患癌症的几率相同C.焦油含量低的香烟不会诱发癌症D.亚硝酸盐可通过改变基因的结构而致癌3.下列有关人体内环境及其稳态的叙述,正确的是A.内环境中不可能发生化学反应B.内环境稳态受体内细胞代谢活动的影响C.内环境稳态是指内环境理化性质恒定不变D.突触小泡内的神经递质属于内环境的成分4.下列关于生态学知识的叙述,正确的是A.食物链的营养级越多,能量传递效率越高B.种群数量/2时是鱼类捕捞、虫害防治的最佳时期C.生态系统自我调节能力大小主要取决于无机环境D.利用生态系统的信息传递作用能够调节生物的种间关系5.下列与植物激素有关的叙述,错误的是A.顶端优势现象体现了生长素作用的两重性B.植物激素的作用方式是直接参与细胞代谢C.植物激素的合成受基因组和环境因素的共同作用D.生长素在植物体内可以进行极性运输和非极性运输6.现有甲、乙两种类型的豌豆各若干,下列相关叙述正确的是A.甲×甲、甲乙都可用于验证基因的分离定律B.若甲品种连续自交,A的基因频率将会不断升高C.乙品种自交后代中基因型为AaBbDd个体占1/8D.乙细胞中等位基因B、b分离一定发生在减数第一次分裂29.(10分)某研究小组以洋葱为实验材料开展相关的研究,洋葱的叶分两种绿色管状叶伸展于空中,进行光合作用;鳞片叶层层包裹形成鳞茎,富含营养物质。

福建省莆田市2018届高三下学期教学质量检测(3月)+数学(文)

2018年莆田市高中毕业班教学质量检测试卷数学（文科）第Ⅰ卷一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合2{|60}A x x x =--<，{|31}x B x =>，则A B = （） A ．(1,2) B ．(1,3) C ．(0,2) D ．(0,3)2.设复数z 满足z i 3i ⋅=-，则z =（）A ．13i +B ．13i --C ．13i -+D ．13i -3.等比数列{}n a 的前n 项和为n S ，已知2132S a a =+，41a =，则4S =（） A ．78 B ．158C ．14D ．15 4.执行下面的程序框图，如果输入的1,2,3a b n ===，则输出的S =（）A ．5B ．6 C.8 D ．135.为了解某校一次期中考试数学成绩情况，抽取100位学生的数学成绩，得如图所示的频率分布直方图，其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]，则估计该次数学成绩的中位数是（）A ．71.5B ．71.8 C.72 D ．756.“干支纪年法”是中国历法上自古以来就一直使用的纪年方法．干支是天干和地支的总称．把干支顺序相配正好六十为一周，周而复始，循环记录，这就是俗称的“干支表”．甲、乙、丙、丁、戊、己、庚、辛、壬、葵等十个符号叫天干；子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥等十二个符号叫地支．如：公元1984年农历为甲子年、公元1985年农历为乙丑年，公元1986年农历为丙寅年．则公元2047年农历为（） A ．乙丑年 B ．丙寅年 C.丁卯年 D ．戊辰年7.已知O 为坐标原点，F 为抛物线2:8C y x =的焦点，过F 作直线l 与C 交于,A B 两点．若||10AB =，则OAB ∆重心的横坐标为（）A ．43 B ．2 C. 83D ．3 8.已知函数2()sin f x x =，则下列说法正确的是（） A ．()f x 的最小正周期为2π B ．()f x 在区间[,]22ππ-上是增函数C. ()f x 的图像关于点(,0)4π对称 D ．()f x 的图像关于直线2x π=对称9.甲乙两人被安排在某月1日至4日值班，每人各值班两天，则甲、乙均不连续值班的概率为（） A ．16 B ．13 C. 23 D ．1210.如图，网络纸的各小格都是正方形，粗线画出的是一个几何体的三视图，则这个几何体是（）A ．三棱锥B ．四棱锥 C.三棱柱 D ．四棱柱11.已知圆22:1O x y +=．若,A B 是圆O 上不同两点，以AB 为边作等边ABC ∆，则||OC 的最大值是（） A1 12.已知直三棱柱111ABC A B C -外接球的表面积为8π，90BAC ∠=︒．若,E F 分别为棱11,BC B C 上的动点，且1BE C F =，则直线EF 被该三棱柱外接球球面截得的线段长为（）A．．2 C.4 D ．不是定值第Ⅱ卷二、填空题：本题共4小题，每题小5分，共20分．13.已知向量(2,4)a = ，(1,)b m =-．若//a b ，则a b ⋅= ．14.若,x y 满足约束条件222022x y y x y +≥⎧⎪-≤⎨⎪-≤⎩，则z x y =+的最大值为．15.已知数列{}n a 满足11a =，112n n n n a a a a ++-=，则6a = ．16.已知()f x 是R 上的偶函数，且2,01()1()1,12x x x f x x ≤≤⎧⎪=⎨+>⎪⎩．若关于x 的方程22()()0f x af x -=有三个不相等的实数根，则a 的取值范围是．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.17.ABC ∆的内角,,A B C 的对边分别为,,a b c，已知cos c B a =．（1）求C ；（2）如图，若a b =，D 为ABC ∆外一点，//AD BC ，2AD CD ==，求四边形ABCD 的面积．18.某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近13年的宣传费i x 和年销售量i y (1,2,,13)i = 数据作了初步处理，得到下面的散点图及一些统计量的值．由散点图知，按b y a x =+建立y 关于x 的回归方程是合理的．令1xω=，则y a b ω=+，经计算得如下数据：（1）根据以上信息，建立y 关于ω的回归方程；（2）已知这种产品的年利润z 与,x y 的关系为10z y x =-．根据（1）的结果，求当年宣传费20x =时，年利润的预报值是多少？附：对于一组数据(,)(1,2,,)i i u i n υ= ，其回归直线u υαβ=+的斜率和截距的最小二乘估计分别为1221ni i inii u nu unuυυβ∧==-=-∑∑，u αυβ∧∧=-．19.如图，四棱锥E ABCD -中，底面ABCD 是平行四边形，,M N 分别为,BC DE 中点．（1）证明：//CN 平面AEM ；（2）若ABE ∆是等边三角形，平面ABE ⊥平面BCE ，CE BE ⊥，2BE EC ==，求三棱锥N AEM -的体积．20.已知两定点1(2,0)A -，2(2,0)A ，动点M 使直线12,MA MA 的斜率的乘积为14-．（1）求动点M 的轨迹E 的方程；（2）过点(F 的直线与E 交于,P Q 两点，是否存在常数λ，使得||PQ FP FQ λ=⋅？并说明理由．21.已知函数()xp x e =，()ln(1)q x x =+．（1）若()()()f x p x aq x =+在定义域上是增函数，求a 的取值范围；（2）若存在b Z ∈，使得21()(1)()2q x b x p x ≤+≤，求b 的值，并说明理由．（二）选考题：共10分．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线C的参数方程为3cos x y αα=⎧⎪⎨=⎪⎩（α是参数）．以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系，直线l 的极坐标方程为cos()13πρθ+=．（1）求l 的直角坐标方程和C 的普通方程；（2）l 与C 相交于,A B 两点，设点P 为C 上异于,A B 的一点，当PAB ∆面积最大时，求点P 到l 的距离．23.选修4-5：不等式选讲已知函数()|||1|f x x a x =-+-．（1）当2a =时，求不等式()4f x <的解集；（2）若2()21f x a a ≥--，求a 的取值范围．试卷答案一、选择题1-5:DBDCC 6-10:CBDBA 11、12：CA二、填空题13. 10- 14.4 15.11116. (0,2][3,4] 三、解答题17.解：（1）在ABC ∆中，由正弦定理得sin cos sin C B B A =，又()A B C π=-+，所以sin cos sin()C B B B C =+，故sin cos C B B +sin cos cos sin B C B C =+，所以sin cos 2B C B =，又(0,)B π∈，所以sin 0B ≠，故cos 2C =，又(0,)C π∈，所以6C π=．（2）因为//AD BC ，故6CAD ACB π∠=∠=，在ACD ∆中，2AD CD ==，所以6ACD CAD π∠=∠=，故23ADC π∠=，所以222222222cos 123AC π=+-⨯⨯=，又6ACB π∠=，AC BC =，所以211sin 3264ACB S AC BC AC π∆=⋅==，又12sin23ACD S CD AD π∆=⋅=所以四边形ABCD 的面积为318.解：（1）131132211313()i ii ii y yb ωωωω∧==-=-∑∑ 2.10100.21-==-， 109.94100.16111.54a y b ω∧∧=-=+⨯=，则y 关于ω的回归方程为111.5410y ω∧=-．（2）依题意1010(111.5410)z y x x ω∧∧=-=⨯--1001115.4x x=--，当20x =时，1090.4z ∧=，所以年利润的预报值是1090.4.19.解：（1）取AE 中点F ，连结,MF FN ．因为AED ∆中，,F N 分别为EA ED 、中点，所以1//2FN AD ．又因为四边形ABCD 是平行四边形，所以//BC AD ．又M 是BC 中点，所以1//2MC AD ，所以//FN MC ．所以四边形FMCN 为平行四边形，所以//CN MF ，又CN ⊄平面AEM ，MF ⊂平面AEM ，所以//CN 平面AEM ．（2）取BE 中点H ，连结AH ，则AH BE ⊥，因为平面ABE ⊥平面BCE ，平面ABE 平面BCE BE =，AH ⊂平面ABE ，所以AH ⊥平面BCE ．又由（1）知//CN 平面AEM ，所以N AEM C AEM A MEC V V V ---==．又因为M 为BC 中点，所以1133A MEC MEC V S AH -∆=⋅=11112322BEC S AH ∆⋅⋅=⨯⨯22⨯⨯=．所以三棱锥N AEM -的体积为3．20.解：（1）设(,)M x y ，由1214A M A M k k ⋅=-，得1224y y x x ⋅=-+-，即2214x y +=．所以动点M 的轨迹方程是221(2)4x y x +=≠±．（2）因为2x ≠±，当直线PQ 的斜率为0时，与曲线C 没有交点，不合题意，故可设直线PQ的方程为x ty =，联立22440x y x ty ⎧+-=⎪⎨=⎪⎩，消去x得22(4)10t y +--=，设1122(,),(,)P x y Q x y，则12y y +=12214y y t =-+，21224(1)|||4t PQ y y t +=-=+ ．12(FP FQ x x ⋅= 22121221(1)4t y y t y y t ++=+=-+．故存在实数4λ=-，使得||4PQ FP FQ =-⋅恒成立．21.解：（1）因为()ln(1)xf x e a x =++在定义域上为增函数．所以'()01xaf x e x =+≥+在(1,)-+∞上恒成立，即(1)x a x e ≥-+在(1,)-+∞上恒成立．令()(1)xu x x e =-+，(1)x >-，则'()(2)0xu x x e =-+<，所以()u x 在(1,)-+∞上为减函数，故()(1)0u x u <-=，所以0a ≥．故a 的取值范围为[0,)+∞．（2）因为21()(1)()2q x b x p x ≤+≤，取1x =，得ln 22b e ≤≤，又b Z ∈，所以1b =．所以存在整数b ，当1b =时，21ln(1)(1)(1)2x x b x e x +≤+≤>-．令21()(1)ln(1)2g x x x =+-+，则1(2)'()111x x g x x x x +=+-=++，令'()0g x =，得0x =．()g x ，'()g x 的变化情况如下表：所以0x =时，()g x 取到最小值，且最小值为1(0)02g =>．即21()(1)2q x x ≤+．令21()(1)2x h x e x =-+，则'()(1)xh x e x =-+，令()1x k x e x =--，由'()10xk x e =-=，得0x =，所以当10x -<<时，'()0k x <，()k x 在(1,0)-上单调递减，当0x >时，'()0k x >，()k x 在(0,)+∞上单调递增，所以()(0)0k x k ≥=，即1xe x ≥+．因此'()0h x ≥，从而()h x 在(1,)-+∞上单调递增，所以1()(1)0h x h e >-=>，即21(1)()2x p x +≤．综上，1b =．22.解：（1）因为直线l 的极坐标方程为cos()13πρθ+=，- 11 -所以1(cos )122ρθθ-=，所以直线l的直角坐标方程为20x -=．曲线C的参数方程为3cos x y αα=⎧⎪⎨=⎪⎩，（α是参数），所以曲线C 的普通方程为22193x y +=．（2）直线:20l x -=与曲线22:193x y C +=相交于A B 、两点，所以||AB 为定值．要使PAB ∆的面积最大，只需点P 到直线l 的距离d 最大．设点(3cos )P αα为曲线C 上任意一点．则点P 到直线l 的距离|3cos 3sin 2|2d αα--=|)2|42πα+-=，当cos()14πα+=-时，d取最大值为||1=+．所以当PAB ∆面积最大时，点P 到l的距离为1+23.解：（1）当2a =时，不等式()4f x <，即|2||1|4x x -+-<．可得2214x x x ≥⎧⎨-+-<⎩，或12214x x x <<⎧⎨-+-<⎩，或1214x x x ≤⎧⎨-+-<⎩．解得1722x -<<．所以不等式的解集为17{|}22x x -<<．（2）因为()|||1||1|f x x a x a =-+-≥-．当且仅当()(1)0x a x --≤时，()f x 取得最小值|1|a -．又因为对任意的2,()21x f x a a ≥--恒成立，所以2|1|21a a a -≥--，即2(1)|1|20a a ----≤，故|1|2a -≤，解得13a -≤≤．所以a 的取值范围为[1,3]-．。

福建省莆田市2018届高三数学第三次月考试题理

莆田一中2018届高三年级第三次月考数学（理科）试题一、选择题：(每小题5分，共60分．)1.已知全集R U =，设集合{|lg(1)}A x y x ==-，集合{}2,1,xB y y x ==≥则()U AC B =（） A ．[]1,2B ．[)1,2 C ．()1,2D ．(]1,22.如图，将半径为1的圆分成相等的四段弧，再将四段弧围成星形放在圆内(阴影部分)．现在往圆内任投一点，此点落在星形区域内的概率为( ) A.4π－1 B.1π C ．1－1π D.2π3.若复数z 满足z(i ＋1)＝2i －1，则复数z 的虚部为( )A ．－1B ．0C ．iD ．14.已知{}n a 是公差为1的等差数列,n S 为{}n a 的前项和,若844S S =,则10a =（）. A.172 B. 192C.10D.12 5.已知函数1)1ln()(2+-+=x x x f ，则(lg 2)f ＋1(lg )2f 等于( ) A ．－1 B ．0 C ．1 D ．26.已知(1)nx +的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（） A.122 B ．112 C ．102 D ．92 7.《九章算数》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为( ) A ．2 B ．4＋2 2 C ．4＋4 2 D ．6＋4 28.如图,给出的是计算12＋14＋…＋1100的值的一个程序框图，则图中判断框内①处和执行框中的②处应填的语句是( ) A.i>100，n ＝n ＋1 B ．i>100，n ＝n ＋2 C ．i>50，n ＝n ＋2 D ．i≤50，n ＝n ＋29.已知双曲线222:14x y C b -= (0)b >的一条渐近线方程为62y x =，12,F F 分别为双曲线C 的左右焦点，P 为双曲线C 上的一点，12||:||3:1PF PF =，则21||PF PF +的值是（） A ．4 B．．．510. 已知函数)sin()(ϕω+=x A x f (ϕω,,A 均为正的常数)的最小正周期为π，当π32=x 时，函数)(x f 取得最小值，则下列结论正确的是（） A ．)0()2()2(f f f <-< B ．)2()2()0(-<<f f f C ．)2()0()2(f f f <<- D ．)2()0()2(-<<f f f11. 已知F 为抛物线2y x =的焦点，点,A B 在该抛物线上且位于x 轴的两侧，且·6OAOB=（O 为坐标原点），若ABO ∆与AFO ∆的面积分别为1S 和2S ，则124S S +最小值是( )6 C. 132D. 12. 已知函数()()ln 224(0)f x x a x a a =+--+>,若有且只有两个整数1x , 2x 使得()10f x >,且()20f x >,则a 的取值范围是（）A. ()ln3,2B. [)2ln3,2-C. (]0,2ln3- D. ()0,2ln3-二、填空题：(每小题5分，满分20分)13.已知向量)1,1(-=a ，)4,6(-=b ,若)(b a t a +⊥，则实数t 的值为________.14. 若实数,x y 满足不等式组221x y y x y +≤⎧⎪-≤⎨⎪≥⎩，则22(+2)+(3)x y -的最大值和最小值之和为__.15. 某运动队对,,,A B C D 四位运动员进行选拔,只选一人参加比赛,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下：甲说：“是C 或D 参加比赛”；乙说：“是B 参加比赛”；丙说：“,A D 都未参加比赛”；丁说：“是C 参加比赛”.若这四位教练中只有两位说的话是对的,则获得参赛的运动员是________.16．在△ABC 中，若3sin 2sin C B =，点E ，F 分别是AC ，AB 的中点，则BECF的取值范围为．三、解答题：(本大题共6小题，共70分．解答应写出文字说明，演算步骤或证明过程.)17.(12分）已知数列{}n a 的前n 项和24n S n n =-．（1）求数列{}n a 的通项公式（2）求数列72n na -⎧⎫⎨⎬⎩⎭的前n 项和.n T18.(12分）矩形ABCD 中， 1AB =， 2AD =，点E 为AD 中点，沿BE 将ABE ∆折起至PBE ∆，如下图所示，点P 在面BCDE 的射影O 落在BE 上.（1）求证： BP CE ⊥；（2）求二面角B PC D --的余弦值.19．(12分）2018年莆田市创建文明城市圆满结束，成绩优异。

福建省莆田市2018届高三下学期教学质量检测(3月)数学(理)试卷(含答案)

2018年莆田市高中毕业班教学质量检测试卷数学(理科)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟注意事项1.答题前,考生先将自己的姓名、准考证号填写在答题卡上2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答, 超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚4.保持答题卡卡面清洁,不折叠、不破损考试结束后,将本试卷和答题卡一并交回第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1已知集合{}{}23230,log 0x A x x x B x =--<=>,则A∩B=A. φB.(0,1)C.(0,3)D.(1,3)2.设复数z 满足(1)3z i i ⋅+=- ,则z=A. 12i +B. 12i -C. 2i +D. 2i -3.已知tan 2α=-,α为第二象限角,则sin cos αα-的值为A. 36+B. 36-C. 63-D. 36-- 4.执行右面的程序框图,如果输入的a=1,b=2,n=3,则输出的S=A.5B.6C.8D.135.已知F 是双曲线E: 22214x y b-=的右焦点,F 到E 的渐近线的距离为1,则E 的离心率为 A.2 B. 5 C. 32 D. 526.“干支纪年法”是中国历法上自古以来就一直使用的纪年方法干支是天干和地支的总称把干支顺序相配正好六十为一周,周而复始,循环记录,这就是俗称的“干支表”甲、乙、丙、丁、戊、己、庚、辛、王、癸等十个符号叫天干;子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥等十个符号叫地支如:公元1984年农历为甲子年,公元1985年农历为乙丑年,公元1986年农历为丙寅年则公元2047年农历为A.乙丑年B.丙寅年C.丁卯年D.戊辰年7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A. 43π+B. 83π+C. 423π+D. 823π+ 8. 2,()1,x x a f x x x a≤⎧=⎨+>⎩在R 上是增函数的一个充分不必要条件是A. a =0B. a =2C.a ≥1D. a ≤19.甲乙两人被安排在某月1日至4日值班,要求每天安排一人值班,每人至少值班一天,则甲恰好值班两天的概率为A.13 B. 37 C. 38 D. 6710.已知函数()sin()(08)f x x ωϕω=+<<,且2()()263f f ππ+=则下列结论正确的是 A. f (x )的图象关于直线24π对称 B. f (x )的图象关于点(512π,0)对称 C. f (x )在区间[12π-,0]上是减函数 D.存在m ∈[6π-.0],使得f (x +m )为偶函数 11.已知F 为抛物线E: 22y px =的焦点,过F 作斜率为2的直线l ,与E 交于A 、B 两点,过A 、B 向E 的准线作垂线,垂足分别为C 、D,设CD 的中点为M,则直线MF 的斜率为A.-2B.-1C. 1 2- D.1212.已知直三棱柱ABC-A1B1C1外接球的表面积为8π,∠BAC=90°,BC=CC1,E为BC中点,F为BB1中点,则直线EF被该三棱柱外接球球面截得的线段长为A. 2B. 2C.6D. 6第Ⅱ卷本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答二、填空题:本大题共4小题,每小题5分,共20分.13.若x、y满足约束条件222022x yyx y+≥⎧⎪-≤⎨⎪-≤⎩,则2=x-y的最大值为________。

福建省莆田市2018届高三数学下学期教学质量检测(3月)试题文

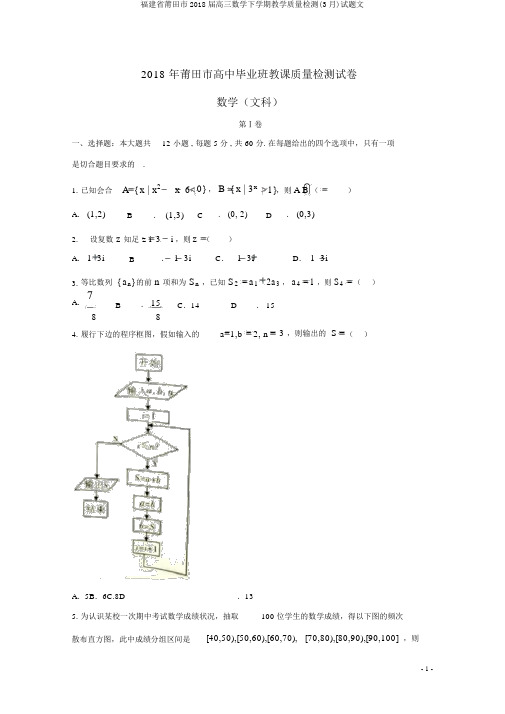
2018 年莆田市高中毕业班教课质量检测试卷数学（文科）第Ⅰ卷一、选择题：本大题共12 小题 , 每题 5 分 , 共 60 分. 在每题给出的四个选项中，只有一项是切合题目要求的 .1. 已知会合 A { x | x 2x 6 0} ， B { x | 3x 1}，则A B （）A ． (1,2) B． (1,3)C． (0, 2)D． (0,3)2.设复数 z 知足 z i 3i ，则 z （）A ． 1 3i B． 1 3i C ． 1 3iD ． 1 3i3. 等比数列 { a n } 的前 n 项和为 S n ，已知 S 2 a 1 2a 3 ， a 4 1 ，则 S 4 （）A ．7B． 15C ．14D． 15884. 履行下边的程序框图，假如输入的a 1,b 2, n 3 ，则输出的 S （）A ．5B ．6C.8D ．135. 为认识某校一次期中考试数学成绩状况，抽取 100 位学生的数学成绩，得以下图的频次散布直方图，此中成绩分组区间是[40,50),[50,60),[60,70), [70,80),[80,90),[90,100] ，则预计该次数学成绩的中位数是（）A． 71.5B．71.8 C.72D．756.“干支纪年法”是中国历法上自古以来就向来使用的纪年方法．干支是天干和地支的总称．把干支次序相当正好六十为一周，循环往复，循环记录，这就是俗称的“干支表”．甲、乙、丙、丁、戊、己、庚、辛、壬、葵等十个符号叫天干；子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥等十二个符号叫地支．如：公元1984 年阴历为甲子年、公元1985 年阴历为乙丑年，公元1986 年阴历为丙寅年．则公元2047 年阴历为（）A．乙丑年B．丙寅年 C.丁卯年D．戊辰年7. 已知O为坐标原点， F 为抛物线C : y28x 的焦点，过F作直线l与C交于A, B两点．若| AB | 10 ，则OAB 重心的横坐标为（）A．4B．2 C.8D．3 338. 已知函数 f ( x) sin2 x ，则以下说法正确的选项是（）A．f ( x)的最小正周期为2B．f ( x)在区间[,] 上是增函数22C. f ( x) 的图像对于点( ,0) 对称D．f ( x)的图像对于直线x对称429.甲乙两人被安排在某月 1 日至 4 日值班，每人各值班两天，则甲、乙均不连续值班的概率为（）A．1B．1C.2D．1 633210.如图，网络纸的各小格都是正方形，粗线画出的是一个几何体的三视图，则这个几何体是（）A．三棱锥B．四棱锥 C.三棱柱D．四棱柱11.已知圆 O : x2y21．若A, B是圆O上不一样两点，以AB为边作等边ABC ，则 |OC |的最大值是（）A．26B．3C.2D．3 1 212.已知直三棱柱ABC A1 B1C1外接球的表面积为8 ，BAC 90 ．若 E, F 分别为棱BC, B1C1上的动点，且BE C1F ，则直线EF被该三棱柱外接球球面截得的线段长为（）A．22B．2 C.4D．不是定值第Ⅱ卷二、填空题：此题共 4 小题，每题小 5 分，共 20 分．13.已知向量 a (2,4)， b( 1, m) ．若 a / /b ，则 a b．2x y214.若 x, y 知足拘束条件y20 ，则 z x y 的最大值为．2x y215. 已知数列 { a n } 知足 a 1 1， a na n 12a nan1 ，则 a 6．2x,0 x 116. 已知 f (x) 是 R 上的偶函数，且f ( x)1) x 1, x ．若对于 x 的方程( 122 f 2 ( x) af ( x) 0 有三个不相等的实数根，则a 的取值范围是．三、解答题：共70 分 . 解答应写出文字说明、证明过程或演算步骤.17.ABC 的内角 A, B, C 的对边分别为 a, b,c ，已知 c cos B3 b a ．2（1）求 C ；（ 2）如图，若 ab ， D 为 ABC 外一点， AD / /BC ， AD CD 2 ，求四边形 ABCD 的面积．18. 某企业为确立下一年度投入某种产品的宣传费，需认识年宣传费x （单位：千元）对年销售量 y （单位： t ）和年收益z （单位：千元）的影响，对近13 年的宣传费 x i 和年销售量y i (i 1,2,,13) 数据作了初步办理，获得下边的散点图及一些统计量的值．由散点图知，按 y ab 1 a b ，经成立 y 对于 x 的回归方程是合理的．令，则 yxx计算得以下数据：xy13 13 13i y i 13 y2 13( )2213( y) 2iy ii 1i 1i 110.15 109.940.16 -2.100.2121.22（ 1）依据以上信息，成立 y 对于的回归方程；（ 2）已知这类产品的年收益z 与 x, y 的关系为 z10 y x ．依据（ 1）的结果，求当年宣传费 x20 时，年收益的预告值是多少？附：对于一组数据 (u i , i )(i 1,2,,n) ，其回归直线u 的斜率和截距的最小二乘估nui inuu ．计分别为i 1 ，nu i 22nui119. 如图，四棱锥E ABCD 中，底面 ABCD 是平行四边形， M , N 分别为 BC,DE 中点．（ 1）证明： CN / / 平面 AEM ；（ 2）若 ABE 是等边三角形，平面ABE 平面 BCE ， CE BE ， BE EC 2 ，求三棱锥 N AEM 的体积．20. 已知两定点A ( 2,0) ， A (2,0) ，动点 M 使直线 MA , MA 的斜率的乘积为1 ．12124（ 1）求动点 M 的轨迹 E 的方程；2F ( 3,0)的直线与 E 交于 P,Q 两点，能否存在常数，使得| PQ|FP FQ？（）过点并说明原因．21. 已知函数( ) x ，．p xe q( x) ln( x 1)f (x)p(x)aq (x) a（ 2）若存在b Z ，使得 q(x)1b( x 1)2p( x) ，求 b 的值，并说明原因．2（二）选考题：共10 分．请考生在22、 23两题中任选一题作答，假如多做，则按所做的第一题记分 .22. 选修 4-4 ：坐标系与参数方程在直角坐标系 xOy 中，曲线 C 的参数方程为x3cosy （是参数）．以坐标原点为极点，3 sinx 轴的正半轴为极轴，成立极坐标系，直线l 的极坐标方程为cos() 1．3（ 1）求l的直角坐标方程和 C 的一般方程；（ 2）l与C订交于A, B两点，设点P为C上异于A, B的一点，当PAB 面积最大时，求点 P 到 l 的距离．23.选修 4-5 ：不等式选讲已知函数 f ( x) | x a | | x1| ．（ 1）当a 2 时，求不等式 f ( x) 4 的解集；（ 2）若f (x) a 22a1，求 a 的取值范围．试卷答案一、选择题1-5:DBDCC 6-10:CBDBA 11 、 12：CA二、填空题13.1014.415.1 (0,2] [3,4]16.11三、解答题17. 解：（ 1）在 ABC 中，由正弦定理得sin C cos B3sin B sin A ，2又 A( B C ) ，所以 sin C cos B3sin B sin( B C) ，2故 sin C cos B3sin Bsin B cosC cos Bsin C ，23所以sin B cosCsin B ，23又 B (0, ) ，所以 sin B0 ，故 cosC，2又 C(0, )，所以 C6．（ 2）由于 AD / /BC ，故CADACB ，6在 ACD 中， AD CD 2 ，所以ACDCAD，故ADC2 6，2cos23 所以 AC 222 22 2212 ，3又ACB， AC BC ，6所以 S ACB1 AC BC sin 61 AC 23 ，2 4 又S ACD1CD AD sin23 ，23所以四边形 ABCD 的面积为 33 ．13iy i 13 y2.1018. 解：（ 1） bi 110 ，130.212 2i 13( )i 1a y b109.94 10 0.16111.54 ，则 y 对于的回归方程为 y111.54 10 ．（ 2）依题意 z10 y x 10(111.54 10 ) x 1115.4100x ，x当 x 20 时， z1090.4 ，所以年收益的预告值是1090.4.19. 解：（ 1）取 AE 中点 F ，连接 MF , FN ．由于AED 中， F , N 分别为 EA 、 ED 中点，1AD ．所以FN//2又由于四边形 ABCD 是平行四边形，所以 BC/ /AD ．又M 是BC 中点，所以 MC//1AD ，所以 FN//MC ．2所以四边形 FMCN 为平行四边形，所以CN / /MF ，又 CN 平面 AEM ， MF平面 AEM ，所以CN//平面 AEM ．（ 2）取 BE 中点 H ，连接 AH ，则 AH BE ，由于平面 ABE 平面 BCE ，平面 ABE平面 BCE BE ， AH平面 ABE ，所以 AH平面 BCE ．又由（ 1）知 CN / / 平面 AEM ，所以 V N AEM VC AEMVA MEC．又由于 M 为 BC 中点，所以 V A MEC1S MEC AH1 1S BEC AH 1 1 12 233 ．33 23 2 23所以三棱锥 NAEM 的体积为3 ．320. 解：（ 1）设 M (x, y) ，由 k A MkA M12得y y1 ，即 x2 y 2 1．x 2 x 2442所以动点 M 的轨迹方程是xy 21(x 41 ，42) ．（ 2）由于 x 2 ，当直线 PQ 的斜率为 0 时，与曲线 C 没有交点，不合题意，故可设直线 PQ 的方程为 x ty3 ，x 2 4 y 2 4 04) y22 3ty 1 0 ，联立ty，消去 x 得 (t2x3设 P( x 1, y 1 ), Q( x 2 , y 2 ) ，则 y 1 y 22 3t， y 1 y 2214，t 2 4t|PQ |1 t 2| y 1 y 2 |4(1 t 2 ) ．t 2 4FP FQ ( x 13)( x 23) y 1 y 2(1 t 2 ) y 1y 21 t2 ．t 2 4故存在实数4，使得 |PQ | 4FP FQ 恒成立．21. 解：（ 1）由于 f (x) e x aln( x 1) 在定义域上为增函数．所以 f '( x)e xa0 在 ( 1, ) 上恒成立，x 1即 a (x 1)e x 在 ( 1, ) 上恒成立．( ) ( 1) x ，，则x，所以 u(x) 在 ( 1,) 上为减函数，故 u(x) u(1)0，所以 a0 ．故 a 的取值范围为[0,) ．（ 2）由于q( x)1b( x1)2p( x) ，2取 x 1 ，得 ln 22b e ，又 b Z ，所以 b1．所以存在整数 b ，当 b1时， ln( x 1)1b( x1) 2e x (x1) ．2令 g(x)1(x 1)2ln( x 1)，则 g '(x)x11x( x2) ，2x1x 1令 g '( x)0 ，得 x0 ．g( x) ， g '( x) 的变化状况以下表：1所以 x 0 时， g( x) 取到最小值，且最小值为g (0)0 ．2即 q( x)1(x1)2．2令 h(x) e x 1(x 1)2，则h '(x)e x( x 1) ，2令 k( x)e x x1，由 k '(x)e x 1 0 ，得x0 ，所以当1x0时， k '( x)0 ， k ( x) 在 ( 1,0)上单一递减，当 x 0 时， k '( x)0 ， k( x)在 (0,) 上单一递加，所以 k (x)k(0)0，即 e x x 1 ．所以 h '( x)0，进而h( x) 在 (1,) 上单一递加，所以 h(x)h(1)10 ，即1( x1)2p( x) ．e2综上， b1．22. 解：（ 1）由于直线l的极坐标方程为cos() 1，3福建省莆田市2018届高三数学下学期教学质量检测(3月)试题文1 3 ) 1 ，所以 ( cos sin2 2所以直线 l 的直角坐标方程为 x 3 y 2 0． x 3cos 曲线 C 的参数方程为 3 sin ，（是参数）， y 所以曲线 C 的一般方程为 x 2 y 2 1． 9 3 （ 2）直线 l : x 3y 2 0 与曲线 C : x 2 y 2 1 订交于 A 、 B 两点，所以 | AB |为定值．9 3 要使 PAB 的面积最大，只要点 P 到直线 l 的距离 d 最大．设点 P(3cos , 3sin ) 为曲线 C 上随意一点．| 3cos3sin 2 | | 32 cos() 2 | 则点 P4 ，到直线 l 的距离 d 2 2 当 cos( )1时， d 取最大值为 | 32 2|13 2 ．4 2 2 3所以当 PAB 面积最大时，点 P 到 l 的距离为 1 2 ．223. 解：（ 1）当 a 2 时，不等式 f ( x) 4 ，即 | x 2| | x 1| 4 ．可得 x 2 1 x 2x 1．x 2 x 1 4 ，或，或 2 x x 1 4 2 x 1 x 4 解得 1 x 72 ． 2 所以不等式的解集为 { x | 1 x 7} ． 2 2 （ 2）由于 f ( x) | x a | | x 1| | a 1| ．当且仅当 (x a)( x 1) 0 时， f (x) 获得最小值 | a 1| ．又由于对随意的 x, f ( x) a 2 2a 1 恒成立，所以 | a 1| a 2 2a 1，即 ( a 1)2 | a 1| 2 0 ，故 | a 1| 2 ，解得 1 a3 ．所以 a 的取值范围为 [ 1,3] ．-11-。

【学期】福建省莆田市2020届高三数学下学期教学质量检测3月试题理

【关键字】学期2018年莆田市高中毕业班教学质量检测试卷数学(理科)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟注意事项1.答题前,考生先将自己的姓名、准考证号填写在答题卡上2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚4.保持答题卡卡面清洁,不折叠、不破损考试结束后,将本试卷和答题卡一并交回第I卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1已知集合,则A∩B=A. B.(0,1) C.(0,3) D.(1,3)2.设复数z满足,则z=A. B. C. D.3.已知,α为第二象限角,则的值为A. B. C. D.4.执行右面的程序框图,如果输入的a=1,b=2,n=3,则输出的S=A.5B.6C.8D.135.已知F是双曲线E: 的右焦点,F到E的渐近线的距离为1,则E的离心率为A.2B.C.D.6.“干支纪年法”是中国历法上自古以来就一直使用的纪年方法干支是天干和地支的总称把干支顺序相配正好六十为一周,周而复始,循环记录,这就是俗称的“干支表”甲、乙、丙、丁、戊、己、庚、辛、王、癸等十个符号叫天干;子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥等十个符号叫地支如:公元1984年农历为甲子年,公元1985年农历为乙丑年,公元1986年农历为丙寅年则公元2047年农历为A.乙丑年B.丙寅年C.丁卯年D.戊辰年7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A. B. C. D.8. 在R 上是增函数的一个充分不必要条件是A. a=0B. a=2C.a≥1D. a≤19.甲乙两人被安排在某月1日至4日值班,要求每天安排一人值班,每人至少值班一天,则甲恰好值班两天的概率为A. B. C. D.10.已知函数,且则下列结论正确的是A. f(x)的图象关于直线对称B. f(x)的图象关于点(,0)对称C. f(x)在区间[,0]上是减函数D.存在m ∈[.0],使得f(x+m)为偶函数11.已知F 为抛物线E: 的焦点,过F 作斜率为2的直线l,与E 交于A 、B 两点,过A 、B 向E 的准线作垂线,垂足分别为C 、D,设CD 的中点为M,则直线MF 的斜率为A.-2B.-1C.D.12.已知直三棱柱ABC-A1B1C1外接球的表面积为8,∠BAC=90°,BC=CC1,E 为BC 中点,F 为BB1中点,则直线EF 被该三棱柱外接球球面截得的线段长为A. B. C. D.第Ⅱ卷本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答二、填空题:本大题共4小题,每小题5分,共20分.13.若x 、y 满足约束条件,则2=x-y 的最大值为________。