新版Matlab中神经网络训练函数Newff的使用方法
MATLAB神经网络工具箱的详细使用步奏
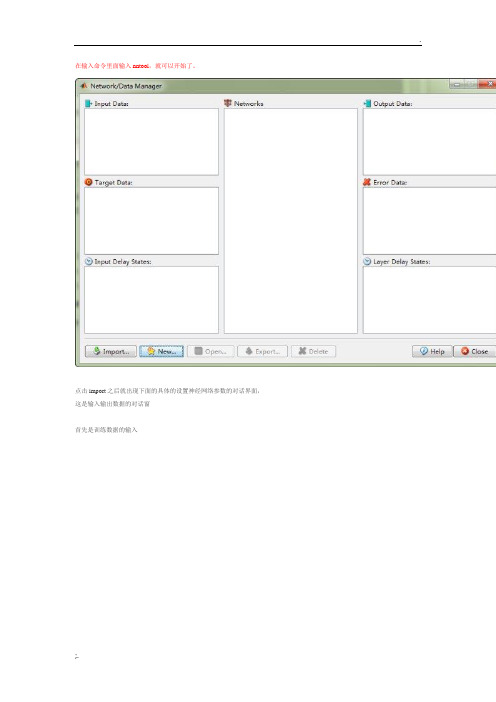
在输入命令里面输入nntool,就可以开始了。
点击import之后就出现下面的具体的设置神经网络参数的对话界面,这是输入输出数据的对话窗
首先是训练数据的输入
然后点击new,创建一个新的神经网络network1,并设置其输入输出数据,包括名称,神经网络的类型以及隐含层的层数和节点数,还有隐含层及输出层的训练函数等
点击view,可以看到这是神经网络的可视化直观表达
创建好了一个network之后,点击open,可以看到一个神经网络训练,优化等的对话框,选择了输入输出数据后,点击train,神经网络开始训练,如右下方的图,可以显示动态结果
下面三个图形则是点击performance,training state以及regression而出现的
下面就是simulate,输入的数据是用来检验这个网络的数据,output改一个名字,这样就把输出数据和误差都存放起来了
在主界面上点击export就能将得到的out结果输入到matlab中并查看
下图就是输出的两个outputs结果。
用神经网训练一个网络函数

学号:姓名:班级:用神经网络训练一个非线性函数一、MATLAB 神经网络工具箱的简单介绍MATLAB 神经网络工具箱以人工神经网络为基础,根据自己的需要调用相关函数,就可以完成网络设计、权值初始化、网络训练等。
本设计中使用了工具箱中BP 神经网络,BP 神经网络工具箱主要包括newff,sim 和train 三个神经网络函数。
newff函数的功能是构建一个BP 神经网络。
其函数形式:net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)。
sim函数的功能是用训练数据训练BP 神经网络。
其函数形式:[net,tr] =train(NET,X,T,Pi,Ai)。
train函数的功能是用训练好的BP 神经网络预测函数输出,其函数形式:y=sim(net,x)。
二、设要逼近的非线性函数为:y=2*cos(2*pi*x),-0.4<X<3.6。
(1)网络建立:使用net=newff(x,y,20,{'tansig','purelin'},'trainlm','learngdm');语句建立一个前馈BP 神经网络。
该BP神经网络只含有一个隐含层,神经元的个数为20,隐层传递函数tansig,输出层传递函数purelin,训练函数为Leven-berg_Marquardt 的BP 算法训练函数trainlm,网络学习函数是带动量项的BP 学习规则learngdm。
(2)网络训练:使用net=train(net,x,y);语句训练建立喊的BP 神经网络。
在训练网络之前设置好训练参数。
用“net.trainParam.epochs=50;net.trainParam.goal=0.01;net.train-Param.lr=0.01;net.trainParam.show=10;”语句实现。
(3)网络仿真:使用“y1=sim(net,x);y2=sim(net,x);”语句仿真训练前后的BP 神经网络。
matlab神经网络工具箱简介和函数及示例

目前,神经网络工具箱中提供的神经网络模型主 要应用于:
函数逼近和模型拟合 信息处理和预测 神经网络控制 故障诊断
神经网络实现的具体操作过程:
• 确定信息表达方式; • 网络模型的确定; • 网络参数的选择; • 训练模式的确定; • 网络测试
• 确定信息表达方式:
将领域问题抽象为适合于网络求解所能接受的 某种数据形式。
函数类型 输入函数
其它
函数名 称
netsum netprcd concur dotprod
函数用途
输入求和函数 输入求积函数 使权值向量和阈值向量的结构一致 权值求积函数
BP网络的神经网络工具箱函数
函数类型
函数名称 函数用途
前向网络创建 函数
传递函数
学习函数
函数类型 性能函数 显示函数
函数名 函数用途 称
三、BP网络学习函数
learngd 该函数为梯度下降权值/阈值学习函数,通过神经 元的输入和误差,以及权值和阈值的学习速率, 来计算权值或阈值的变化率。
调用格式; [dW,ls]=learngd(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
二、神经元上的传递函数
传递函数是BP网络的重要组成部分,必须是连续可 微的,BP网络常采用S型的对数或正切函数和线性函数。
• Logsig 传递函数为S型的对数函数。 调用格式为: • A=logsig(N)
N:Q个S维的输入列向量; A:函数返回值,位于区间(0,1) 中
② info=logsig(code)
问题形式的种类:
数据样本已知; 数据样本之间相互关系不明确; 输入/输出模式为连续的或者离散的; 输入数据按照模式进行分类,模式可能会 具有平移、旋转或者伸缩等变化形式; 数据样本的预处理; 将数据样本分为训练样本和测试样本
Matlab中的神经网络实现方法

Matlab中的神经网络实现方法近年来,神经网络技术在各个领域中得到了广泛的应用。
通过对大量的数据进行学习和训练,神经网络可以用于解决诸如图像识别、语音识别、自然语言处理等复杂的问题。
而Matlab作为一种强大的科学计算工具,提供了丰富的神经网络实现方法,帮助研究人员和工程师更好地应用神经网络技术。
在Matlab中,实现神经网络有多种方法,包括使用神经网络工具箱、编写自定义的函数和使用深度学习工具箱等。
下面将分别介绍这些方法的特点和应用。
一、神经网络工具箱Matlab的神经网络工具箱是一个功能强大的工具,可以帮助用户在短时间内搭建和训练神经网络模型。
通过在Matlab中调用神经网络工具箱中的函数,用户可以实现包括前馈神经网络、递归神经网络、自动编码器等各种类型的神经网络模型。
使用神经网络工具箱,用户只需要简单地定义网络的拓扑结构、选择合适的激活函数和学习算法,然后通过输入训练数据进行网络的训练。
训练完成后,用户可以使用训练好的神经网络模型对新的数据进行预测和分类。
神经网络工具箱提供了丰富的函数和工具,帮助用户实现各种复杂的操作,例如特征选择、模型评估和可视化等。
此外,神经网络工具箱还支持并行计算和分布式计算,提高了神经网络模型的训练效率。
二、自定义函数除了使用神经网络工具箱,用户还可以编写自定义的函数来实现神经网络。
这种方式可以更加灵活地控制网络的结构和参数。
在Matlab中,用户可以通过编写自定义的函数来定义网络的拓扑结构、激活函数、学习算法等。
同时,用户还可以使用Matlab提供的矩阵运算和优化工具,对神经网络的参数进行更新和优化。
使用自定义函数实现神经网络需要较高的编程能力和数学知识,但是可以满足对网络结构和参数精细控制的需求。
此外,用户还可以在自定义函数中加入其他自己的算法和操作,提升神经网络的性能和应用效果。
三、深度学习工具箱随着深度学习技术的兴起,Matlab还引入了深度学习工具箱,帮助用户实现包括卷积神经网络、循环神经网络等深度学习模型。
matlab newff函数新版用法

matlab newff函数新版用法Matlab是一种强大的数值计算软件,用于工程、物理、化学、金融等领域的科学计算,尤其是在神经网络相关的计算上得到了广泛应用,其newff函数也是神经网络中的一个核心函数。
在matlab神经网络工具箱中,newff 函数是一个用于构建前向传播神经网络的函数,其可以自动帮助用户建立完整的神经网络模型。
在这篇文档中,我们将研究newff函数的新版用法,包括如何使用newff函数构建前向传播神经网络模型、如何设置网络结构参数、如何训练神经网络模型以及如何进行预测。
一、使用newff函数构建前向传播神经网络模型在matlab神经网络工具箱中使用newff函数,只需执行以下命令:net = newff(inputs, targest, hiddenSizes)其中,inputs表示输入训练样本参数的矩阵,targets表示训练结果的矩阵,hiddenSizes表示隐藏层神经元的个数和层数。
执行这个命令后,我们将得到一个前向传播神经网络变量net。
二、设置网络结构参数在构建神经网络模型之前,我们需要设置一些网络结构参数。
具体而言,我们需要设置输入和输出层的神经元数、隐藏层数和神经元数、学习率、训练算法、误差函数等参数。
我们可以使用set函数轻松地设置这些参数。
例如,下面的命令可以设置前向传播神经网络的输入和输出层神经元数:net.inputs{1}.size=5;net.outputs{2}.size=1;其中“net.inputs{1}.size”表示第一层输入神经元数,本例中设置为5,“net.outputs{2}.size”表示第二层输出神经元数,本例中设置为1。
我们还可以使用下面的命令确定隐藏层神经元数和层数,learning rate(学习率)以及 transfer function(激活函数)等:yers{1}.size=10;yers{2}.size=5;net.trainFcn = 'trainscg';net.learningRate=0.1;net.divideFcn = '';net.performFcn = 'mse';其中“yers{1}.size”表示第一层隐藏神经元数,本例中设置为10,“yers{2}.size”表示第二层隐藏神经元数,本例中设置为5。
Matlab的神经网络工具箱实用指南(3)

静态网络中的批处理方式批处理方式可以用adapt或train函数来实现,虽然由于由于采用了更高效的学习算法,train通常是最好的选择。
增加方式只能用adapt来实现,train函数只能用于批处理方式。
让我们用前面用过的静态网络的例子开始,学习速率设置为0.1。
net = newlin([-1 1;-1 1],1,0,0.1);net.IW{1,1} = [0 0];net.b{1} = 0;用adapt函数实现静态网络的批处理方式,输入向量必须用同步向量矩阵的方式放置:P = [1 2 2 3; 2 1 3 1];T = [4 5 7 7];当我们调用adapt时将触发adaptwb函数,这是缺省的线性网络调整函数。
learnwh是缺省的权重和偏置学习函数。
因此,Widrow-Hoff学习法将会被使用:[net,a,e,pf] = adapt(net,P,T);a = 0 0 0 0e = 4 5 7 7注意网络的输出全部为0,因为在所有要训练的数据提交前权重没有被更新,如果我们显示权重,我们就会发现:>>net.IW{1,1}ans = 4.9000 4.1000>>net.b{1}ans =2.3000经过了用adapt函数的批处理方式调整,这就和原来不一样了。
现在用train函数来实现批处理方式。
由于Widrow-Hoff规则能够在增加方式和批处理方式中应用,它可以通过adapt和train触发。
我们有好几种算法只能用于批处理方式(特别是Levenberg-Marquardt算法),所以这些算法只能用train触发。
网络用相同的方法建立:net = newlin([-1 1;-1 1],1,0,0.1);net.IW{1,1} = [0 0];net.b{1} = 0;在这种情况下输入向量即能用同步向量矩阵表示也能用异步向量细胞数组表示。
用train函数,任何异步向量细胞数组都会转换成同步向量矩阵。
matlab神经网络newff函数的使用

matlab神经网络newff函数的使用设[P,T]是训练样本,[X,Y]是测试样本;net=newrb(P,T,err_goal,spread); %建立网络q=sim(net,p);e=q-T;plot(p,q); %画训练误差曲线q=sim(net,X);e=q-Y;plot(X,q); %画测试误差曲线训练前馈网络的第一步是建立网络对象。
函数newff建立一个可训练的前馈网络。
这需要4个输入参数。
第一个参数是一个Rx2的矩阵以定义R个输入向量的最小值和最大值。
第二个参数是一个设定每层神经元个数的数组。
第三个参数是包含每层用到的传递函数名称的细胞数组。
最后一个参数是用到的训练函数的名称。
举个例子,下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init 来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
下面就是网络如何初始化的:net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
net.initFcn用来决定整个网络的初始化函数。
前馈网络的缺省值为initlay,它允许每一层用单独的初始化函数。
newff函数的使用(含一个新的函数)

matlab神经网络newff函数的使用设[P,T]是训练样本,[X,Y]是测试样本;net=newrb(P,T,err_goal,spread); %建立网络q=sim(net,p);e=q-T;plot(p,q); %画训练误差曲线q=sim(net,X);e=q-Y;plot(X,q); %画测试误差曲线训练前馈网络的第一步是建立网络对象。
函数newff建立一个可训练的前馈网络。
这需要4个输入参数。
第一个参数是一个Rx2的矩阵以定义R个输入向量的最小值和最大值。
第二个参数是一个设定每层神经元个数的数组。
第三个参数是包含每层用到的传递函数名称的细胞数组。
最后一个参数是用到的训练函数的名称。
举个例子,下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
下面就是网络如何初始化的:net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
net.initFcn用来决定整个网络的初始化函数。
前馈网络的缺省值为initlay,它允许每一层用单独的初始化函数。
matlab神经网络工具箱简介和函数及示例参考PPT

代码运行结果: 网络训练误差
结论:隐含层节点设为8
BP网络训练步骤
步骤1: 初始化 步骤2:计算网络各层输出矢量 步骤3:计算网络各层反向传播的误差变化,并计算各 层权值的修正值及修正值 步骤4:再次计算权值修正后的误差 平方和 步骤5:检查误差 平方和是否小于 误差期望值,若是, 停止训练,否则继续.
函数类型 输入函数
其它
函数名 称
netsum netprcd concur dotprod
函数用途
输入求和函数 输入求积函数 使权值向量和阈值向量的结构一致 权值求积函数
BP网络的神经网络工具箱函数
函数类型
函数名称 函数用途
前向网络创建 函数
传递函数
学习函数
函数类型 性能函数 显示函数
函数名 函数用途 称
MATLAB的神经网络工具箱函
数
函数类型
通用函数
函数名 函数用途 称
仿真函数 训练函数
学习函数 初始化函数
SIM train trainh adapt learn int intlay
针对给定的输入,得到网络输出 调用其它训练函数,对网络进行训练 对权值和阈值进行训练 自适应函数 网络权值和阈值的学习 对网络进行初始化 对多层网络初始化
说明:
参数TFi可以采用任意的可微传递函数,比如transig, logsig和purelin等; 训练函数可以是任意的BP训练函数,如trainm,trainbfg, trainrp和traingd等。BTF默认采用trainlm是因为函数的速度 很快,但该函数的一个重要缺陷是运行过程会消耗大量的内 存资源。如果计算机内存不够大,不建议用trainlm,而建议 采用训练函数trainbfg或trainrp。虽然这两个函数的运行速度 比较慢,但它们的共同特点是内存占用量小,不至于出现训 练过程死机的情况。
Matlab_中神经网络算法指令newff的使用

Matlab 中神经网络算法指令newff的使用设[P,T]是训练样本,[X,Y]是测试样本;net=newrb(P,T,err_goal,spread); %建立网络q=sim(net,p);e=q-T;plot(p,q); %画训练误差曲线q=sim(net,X);e=q-Y;plot(X,q); %画测试误差曲线训练前馈网络的第一步是建立网络对象。
函数newff建立一个可训练的前馈网络。
这需要4个输入参数。
第一个参数是一个Rx2的矩阵以定义R个输入向量的最小值和最大值。
第二个参数是一个设定每层神经元个数的数组。
第三个参数是包含每层用到的传递函数名称的细胞数组。
最后一个参数是用到的训练函数的名称。
举个例子,下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init 来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
下面就是网络如何初始化的:net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
net.initFcn用来决定整个网络的初始化函数。
前馈网络的缺省值为initlay,它允许每一层用单独的初始化函数。
Matlab软件和其中人工神经网络函数的用法

Matlab软件和其中人工神经网络函数的用法,试着对之前正交试验的结果进行模拟。
输入层有4个神经元,分别是水胶比(W/B)、硅灰与水泥的质量比(SF/C)、砂胶比(S/B)、钢纤维的体积掺量(V%)。
输出层有】个神经元,即RPC自然养护7d的抗压强度。
隐含层有10个神经元,之所以选择10个神经元,是通过尝试得出的结果,当选用9个神经元时,结果不能收敛,而选择10个神经元时,结果收敛。
隐含层的传递函数为:tan诵5)=2∕(l+e乎(-2〃))-1,输出层的传递函数为线性函数,采用BP算法对网络进行训练,坍落度神经网络预测模型源程序如下:P=[0,160.160.160.160.180.180.180.180.20.20.20.20.220.220.220.22;0.20.30.40.50.2030.40.50.20.30.40.50.20.30.40.5;0.811.21.410.81.41.21.21.40.811.41.210.8;0123321010322301]T=[73.5109.8120.0114.880.586.275.274.463.555.491.781.756.253.454.569.7]net=newff(minmax(P),L10,1],('tansig','purelin'))net.trainparam.epochs=1000net.trainparam.goal=0.000000000000001net=train(net,P,T)y=sim(net,P)error=y-Tres=norm(error)P_test=[0.180.20.220.18;0.30.40.50.4:1.211.41.4;1230]T_test=[78.979.672.471.8]y_test=sim(net,P_test)error_test=y_test-T_testres_test=norm(error_test)fori=l:4Y(i)=error_test(i)/T_test(i)end迭代23次,网络学习均方误差MSE达到7.86e-016,即达到要求,训练结果如图1所∕J∖o图1神经网络训练结果对验证组试验结果进行预测,预测结果MSE=35.7735,误差较大,预测结果及误差见表Io表1预测结果及误差特别是其中C组的误差达40%以上,需要对神经网络模型再进行修改。
Matlab中的神经网络训练技术

Matlab中的神经网络训练技术导言神经网络是一种模拟人类神经系统的计算模型,它能够通过学习和训练,从大量的数据中提取有用的信息,并进行模式识别和预测。
在许多领域中,神经网络已经成为一种强大而广泛应用的工具。
而Matlab作为一种强大的科学计算软件,提供了丰富的神经网络训练技术和工具,使得神经网络的研究和应用更加便捷和高效。
本文将介绍Matlab中的神经网络训练技术,包括基本的神经网络模型、训练算法和应用示例。
第一节神经网络基础神经网络是由大量的神经元组成的,每个神经元通过连接权重和激活函数来进行信号的传递和处理。
在Matlab中,可以通过构建网络对象来定义神经网络结构,并通过设置神经网络的各种属性来实现不同的功能。
例如,可以选择不同的网络拓扑结构(如前馈神经网络、循环神经网络等),不同的激活函数和训练算法等。
第二节神经网络训练算法神经网络的训练是指通过调整网络连接权重和激活函数来使网络拟合输入数据,从而实现某种特定的任务。
在Matlab中,提供了丰富的神经网络训练算法,包括反向传播算法、遗传算法、粒子群算法等。
这些算法各有特点和适用范围,可以根据具体问题选择合适的算法进行网络训练。
第三节神经网络应用示例神经网络在许多领域中都有广泛的应用,如模式识别、预测分析、控制系统等。
在Matlab中,提供了许多神经网络的应用示例,通过这些示例可以更好地理解和应用神经网络技术。
例如,可以通过神经网络实现手写数字识别、语音识别、股票预测等。
这些示例不仅提供了具体的实现代码,还提供了数据集和演示程序,方便用户进行实践和调试。
第四节神经网络性能评估神经网络的性能评估是指通过指标来评价网络的训练效果和泛化能力。
在Matlab中,提供了多种常用的性能评估指标,如均方误差、准确率、召回率等。
通过这些指标,可以衡量网络在训练数据和测试数据上的表现,并对网络的参数进行调整,改进网络性能。
第五节神经网络与深度学习深度学习是近年来兴起的一种基于神经网络的机器学习方法,其具有强大的特征提取和模式识别能力。
MATLAB神经网络算法与应用

MATLAB神经网络算法与应用引言人工智能领域的快速发展,为各行各业带来了许多机会和挑战。
神经网络作为人工智能的关键技术之一,具有良好的模拟人类智能的能力,并在许多领域中发挥着重要的作用。
本文将着重介绍MATLAB中神经网络算法的原理与应用。
一、神经网络的基本原理神经网络是一种模拟人脑神经系统工作的算法模型,它由大量的神经元和连接它们的权重组成,通过调整权重来实现对输入和输出之间的映射关系推断。
神经网络的训练过程通常分为两个阶段:前向传播和反向传播。
在前向传播过程中,神经网络根据输入数据和当前的权重值,通过一系列计算将输入数据映射到输出。
每个神经元根据输入的加权和以及一个激活函数产生输出,并将输出传递给下一层神经元,最后生成最终的输出。
反向传播是神经网络的学习过程,它通过比较神经网络的输出和真实值之间的误差,来调整权重的值。
具体来说,反向传播需要计算每个权重对误差的贡献,并根据这个贡献来更新权重。
这个过程会不断迭代,直到神经网络的输出与真实值的误差足够小。
二、MATLAB中的神经网络算法MATLAB提供了丰富的神经网络算法工具箱,包括了多层感知机、自组织映射网络、径向基函数网络等多种类型的神经网络。
这些工具箱易于使用,使得神经网络模型的建立和训练变得更加简单。
在MATLAB中,我们可以使用`newff`函数来创建一个多层感知机神经网络模型。
该函数可以指定输入、隐藏和输出层的神经元数量、激活函数等。
例如,下面的代码创建了一个包含一个隐藏层的多层感知机:```net = newff(X, y, [10]);```其中,`X`是输入数据,`y`是输出数据,`[10]`表示隐藏层有10个神经元。
创建好神经网络后,我们可以使用`train`函数来训练模型。
例如,通过以下代码可以训练神经网络模型:```net = train(net, X, y);```在训练完成后,就可以使用训练好的神经网络模型对新的数据进行预测。
Matlab中各种神经网络的使用示例

Matlab中各种神经网络的使用示例Matlab中各种神经网络的使用示例%通用BP神经网络 (2)%通用径向基函数网络......... 错误!未定义书签。
%广义回归神经网络 (11)%通用感应器神经网络 (14)%通用BP神经网络P=[-1 -1 2 2;0 5 0 5];t=[-1 -1 1 1];net=newff(minmax(P),[3,1],{'tansig','purelin'},'t raingd');%输入参数依次为:'样本P范围',[各层神经元数目],{各层传递函数},'训练函数'%训练函数traingd--梯度下降法,有7个训练参数.%训练函数traingdm--有动量的梯度下降法,附加1个训练参数mc(动量因子,缺省为0.9)%训练函数traingda--有自适应lr的梯度下降法,附加3个训练参数:lr_inc(学习率增长比,缺省为1.05;% lr_dec(学习率下降比,缺省为0.7);max_perf_inc(表现函数增加最大比,缺省为1.04)%训练函数traingdx--有动量的梯度下降法中赋以自适应lr的方法,附加traingdm和traingda 的4个附加参数%训练函数trainrp--弹性梯度下降法,可以消除输入数值很大或很小时的误差,附加4个训练参数:% delt_inc(权值变化增加量,缺省为1.2);delt_dec(权值变化减小量,缺省为0.5);% delta0(初始权值变化,缺省为0.07);deltamax(权值变化最大值,缺省为50.0) % 适合大型网络%训练函数traincgf--Fletcher-Reeves共轭梯度法;训练函数traincgp--Polak-Ribiere共轭梯度法;%训练函数traincgb--Powell-Beale共轭梯度法%共轭梯度法占用存储空间小,附加1训练参数searchFcn(一维线性搜索方法,缺省为srchcha);缺少1个训练参数lr%可以通过net=newrbe(P,T,spread)生成网络,且误差为0%可以通过net=newrb(P,T,goal,spread)生成网络,神经元由1开始增加,直到达到训练精度或神经元数目最多为止%GRNN网络,迅速生成广义回归神经网络(GRNN)P=[4 5 6];T=[1.5 3.6 6.7];net=newgrnn(P,T);%仿真验证p=4.5;v=sim(net,p)%PNN网络,概率神经网络P=[0 0 ;1 1;0 3;1 4;3 1;4 1;4 3]';Tc=[1 1 2 2 3 3 3];%将期望输出通过ind2vec()转换,并设计、验证网络T=ind2vec(Tc);net=newpnn(P,T);Y=sim(net,P);Yc=vec2ind(Y)%尝试用其他的输入向量验证网络P2=[1 4;0 1;5 2]';Y=sim(net,P2);Yc=vec2ind(Y)%应用newrb()函数构建径向基网络,对一系列数据点进行函数逼近P=-1:0.1:1;T=[-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609...0.1336 -0.2013 -0.4344 -0.500 -0.3930 -0.1647 -0.0988...0.3072 0.3960 0.3449 0.1816 -0.0312 -0.2189 -0.3201];%绘制训练用样本的数据点plot(P,T,'r*');title('训练样本');xlabel('输入向量P');ylabel('目标向量T');%设计一个径向基函数网络,网络有两层,隐层为径向基神经元,输出层为线性神经元%绘制隐层神经元径向基传递函数的曲线p=-3:.1:3;a=radbas(p);plot(p,a)title('径向基传递函数')xlabel('输入向量p')%隐层神经元的权值、阈值与径向基函数的位置和宽度有关,只要隐层神经元数目、权值、阈值正确,可逼近任意函数%例如a2=radbas(p-1.5);a3=radbas(p+2);a4=a+a2*1.5+a3*0.5;plot(p,a,'b',p,a2,'g',p,a3,'r',p,a4,'m--')title('径向基传递函数权值之和')xlabel('输入p');ylabel('输出a');%应用newrb()函数构建径向基网络的时候,可以预先设定均方差精度eg以及散布常数sceg=0.02;sc=1; %其值的选取与最终网络的效果有很大关系,过小造成过适性,过大造成重叠性net=newrb(P,T,eg,sc);plot(P,T,'*')xlabel('输入');X=-1:.01:1;Y=sim(net,X);hold onplot(X,Y);hold offlegend('目标','输出')%应用grnn进行函数逼近P=[1 2 3 4 5 6 7 8];T=[0 1 2 3 2 1 2 1];plot(P,T,'.','markersize',30)axis([0 9 -1 4])title('待逼近函数')xlabel('P')ylabel('T')%网络设计%对于离散数据点,散布常数spread选取比输入向量之间的距离稍小一些spread=0.7;net=newgrnn(P,T,spread);A=sim(net,P);hold onoutputline=plot(P,A,'o','markersize',10,'color',[1 0 0]);title('检测网络')xlabel('P')ylabel('T和A')%应用pnn进行变量的分类P=[1 2;2 2;1 1]; %输入向量Tc=[1 2 3]; %P对应的三个期望输出%绘制出输入向量及其相对应的类别plot(P(1,:),P(2,:),'.','markersize',30)for i=1:3text(P(1,i)+0.1,P(2,i),sprintf('class %g',Tc(i))) endaxis([0 3 0 3]);title('三向量及其类别')xlabel('P(1,:)')ylabel('P(2,:)')%网络设计T=ind2vec(Tc);spread=1;net=newgrnn(P,T,speard);%网络测试A=sim(net,P);Ac=vec2ind(A);%绘制输入向量及其相应的网络输出plot(P(1,:),P(2,:),'.','markersize',30)for i=1:3text(P(1,i)+0.1,P(2,i),sprintf('class %g',Ac(i))) endaxis([0 3 0 3]);title('网络测试结果')xlabel('P(1,:)')ylabel('P(2,:)')%广义回归神经网络%%GRNN神经网络,主要用于函数逼近。
新版Matlab中神经网络训练函数Newff的使用方法

新版Matlab中神经网络训练函数Newff的使用方法一、介绍新版newffSyntax•net = newff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) Descriptionnewff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) takes several argumentsExamplesHere is a problem consisting of inputs P and targets T to be solved with a network.•P = [0 1 2 3 4 5 6 7 8 9 10];T = [0 1 2 3 4 3 2 1 2 3 4];Here a network is created with one hidden layer of five neurons.•net = newff(P,T,5);The network is simulated and its output plotted against the targets.•Y = sim(net,P);plot(P,T,P,Y,'o')The network is trained for 50 epochs. Again the network's output is plotted.•net.trainParam.epochs = 50;net = train(net,P,T);Y = sim(net,P);plot(P,T,P,Y,'o') 二、新版newff与旧版newff调用语法对比Example1比如输入input(6*1000),输出output为(4*1000),那么旧版定义:net=newff(minmax(input),[7,1],{'tansig','purelin'},'trainlm');新版定义:net=newff(input,output,7,{'tansig','purelin'},'trainlm'); Example2比如输入input(6*1000),输出output为(4*1000),那么旧版定义:net=newff(minmax(input),[49,10,1],{'tansig','tansig','tansig'},'traingdx');新版定义:net=newff(input,output, [49,10], {'tansig','tansig','tansig'},'traingdx');三、旧版newff使用方法在新版本中使用提示:旧版本定义的newff虽也能在新版本中使用,但会有警告,警告如下:Warning: NEWFF used in an obsolete way.> In obs_use at 18In newff>create_network at 127In newff at 102See help for NEWFF to update calls to the new argument list.四、新版newff与旧版newff使用的训练效果对比旧版本:旧用法训练次数多,但精度高新版本:新用法训练次数少,但精度可能达不到要求造成上述原因是:程序里面的权值、阈值的初始值是随机赋值的,所以每次运行的结果都会不一样,有好有坏。
MATLAB神经网络工具箱函数精品文档5页

MATLAB 神经网络工具箱函数说明:本文档中所列出的函数适用于 MATLAB5.3 以上版本,为了简明起见,只列出了函数名,若需要进一步的说明,请参阅 MATLAB 的帮助文档。
1. 网络创建函数newp 创建感知器网络newlind 设计一线性层newlin 创建一线性层newff 创建一前馈 BP 网络newcf 创建一多层前馈 BP 网络newfftd 创建一前馈输入延迟 BP 网络newrb 设计一径向基网络newrbe 设计一严格的径向基网络newgrnn 设计一广义回归神经网络newpnn 设计一概率神经网络newc 创建一竞争层newsom 创建一自组织特征映射newhop 创建一Hopfield 递归网络newelm 创建一 Elman 递归网络2. 网络应用函数sim 仿真一个神经网络init 初始化一个神经网络adapt 神经网络的自适应化train 训练一个神经网络3. 权函数dotprod 权函数的点积ddotprod 权函数点积的导数dist Euclidean 距离权函数normprod 规范点积权函数negdist Negative 距离权函数mandist Manhattan 距离权函数linkdist Link 距离权函数4. 网络输入函数netsum 网络输入函数的求和dnetsum 网络输入函数求和的导数5. 传递函数hardlim 硬限幅传递函数hardlims 对称硬限幅传递函数purelin 线性传递函数tansig 正切 S 型传递函数logsig 对数 S 型传递函数dpurelin 线性传递函数的导数dtansig 正切 S 型传递函数的导数 dlogsig 对数 S 型传递函数的导数compet 竞争传递函数radbas 径向基传递函数satlins 对称饱和线性传递函数6. 初始化函数initlay 层与层之间的网络初始化函数initwb 阈值与权值的初始化函数initzero 零权/阈值的初始化函数initnw Nguyen_Widrow 层的初始化函数initcon Conscience 阈值的初始化函数midpoint 中点权值初始化函数7. 性能分析函数mae 均值绝对误差性能分析函数mse 均方差性能分析函数msereg 均方差 w/reg 性能分析函数dmse 均方差性能分析函数的导数dmsereg 均方差 w/reg 性能分析函数的导数8. 学习函数learnp 感知器学习函数learnpn 标准感知器学习函数learnwh Widrow_Hoff 学习规则learngd BP 学习规则learngdm 带动量项的 BP 学习规则learnk Kohonen 权学习函数learncon Conscience 阈值学习函数learnsom 自组织映射权学习函数9. 自适应函数adaptwb 网络权与阈值的自适应函数10. 训练函数trainwb 网络权与阈值的训练函数traingd 梯度下降的 BP 算法训练函数traingdm 梯度下降 w/动量的 BP 算法训练函数traingda 梯度下降 w/自适应 lr 的 BP 算法训练函数traingdx 梯度下降 w/动量和自适应 lr 的 BP 算法训练函数trainlm Levenberg_Marquardt 的BP 算法训练函数trainwbl 每个训练周期用一个权值矢量或偏差矢量的训练函数11. 分析函数maxlinlr 线性学习层的最大学习率errsurf 误差曲面12. 绘图函数plotes 绘制误差曲面plotep 绘制权和阈值在误差曲面上的位置plotsom 绘制自组织映射图13. 符号变换函数 ind2vec 转换下标成为矢量vec2ind 转换矢量成为下标矢量14. 拓扑函数gridtop 网络层拓扑函数hextop 六角层拓扑函数randtop 随机层拓扑函数希望以上资料对你有所帮助,附励志名言3条:1、生气,就是拿别人的过错来惩罚自己。
神经网络的matlab函数介绍

[分享]Matlab的神经网络工具箱实用指南第一章介绍1.神经网络神经网络是单个并行处理元素的集合,我们从生物学神经系统得到启发。
在自然界,网络功能主要由神经节决定,我们可以通过改变连接点的权重来训练神经网络完成特定的功能。
一般的神经网络都是可调节的,或者说可训练的,这样一个特定的输入便可得到要求的输出。
如下图所示。
这里,网络根据输出和目标的比较而调整,直到网络输出和目标匹配。
作为典型,许多输入/目标对应的方法已被用在有监督模式中来训练神经网络。
神经网络已经在各个领域中应用,以实现各种复杂的功能。
这些领域包括:模式识别、鉴定、分类、语音、翻译和控制系统。
如今神经网络能够用来解决常规计算 腿四岩越饩龅奈侍狻N颐侵饕 ü 飧龉ぞ呦淅唇 ⑹痉兜纳窬 缦低常 ⒂τ玫焦こ獭⒔鹑诤推渌 导氏钅恐腥ァ?BR>一般普遍使用有监督训练方法,但是也能够通过无监督的训练方法或者直接设计得到其他的神经网络。
无监督网络可以被应用在数据组的辨别上。
一些线形网络和Hopfield网络是直接设计的。
总的来说,有各种各样的设计和学习方法来增强用户的选择。
神经网络领域已经有50年的历史了,但是实际的应用却是在最近15年里,如今神经网络仍快速发展着。
因此,它显然不同与控制系统和最优化系统领域,它们的术语、数学理论和设计过程都已牢固的建立和应用了好多年。
我们没有把神经网络工具箱仅看作一个能正常运行的建好的处理轮廓。
我们宁愿希望它能成为一个有用的工业、教育和研究工具,一个能够帮助用户找到什么能够做什么不能做的工具,一个能够帮助发展和拓宽神经网络领域的工具。
因为这个领域和它的材料是如此新,这个工具箱将给我们解释处理过程,讲述怎样运用它们,并且举例说明它们的成功和失败。
我们相信要成功和满意的使用这个工具箱,对范例和它们的应用的理解是很重要的,并且如果没有这些说明那么用户的埋怨和质询就会把我们淹没。
所以如果我们包括了大量的说明性材料,请保持耐心。
newff函数

newff函数编辑本词条缺少名片图,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧!newff函数,功能是训练前馈网络的第一步是建立网络对象。
中文名newff函数外文名Newff function实质newff函数的参数PR:Rx2的矩阵目录.1功能.2函数参数.3举例.4网络初始化.5函数调用功能编辑训练前馈网络的第一步是建立网络对象。
函数参数编辑newff函数的格式为:net=newff(PR,[S1 S2 ...SN],{TF1 TF2...TFN},BTF,BLF,PF),函数newff建立一个可训练的前馈网络。
输入参数说明:PR:Rx2的矩阵以定义R个输入向量的最小值和最大值;Si:第i层神经元个数;TFi:第i层的传递函数,默认函数为tansig函数;BTF:训练函数,默认函数为trainlm函数;BLF:权值/阈值学习函数,默认函数为learngdm函数;PF:性能函数,默认函数为mse函数。
举例编辑下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
网络初始化编辑net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
MATLAB神经网络及其应用讲课文档

BLF - Backprop weight/bias learning function, default = 'learngdm'.
PF - Performance function, default = 'mse'.
(2) Use TRAINBFG, which is slower but more memory efficient than TRAINLM.
(3) Use TRAINRP which is slower but more memory efficient than TRAINBFG.
第6页,共22页。
第9页,共22页。
输出参数说明
and returns,
NET - New network. TR - Training record (epoch and perf). Y - Network outputs. E - Network errors. Pf - Final input delay conditions. Af - Final layer delay conditions.
MATLAB神经网络及其应用
第1页,共22页。
2 BP网络
第2页,共22页。
3 MATLAB中的newff命令
NEWFF Create a feed-forward backpropagation network.
Syntax
net = newff net = newff(PR,[S1 S2...SNl],{TF1
第21页,共22页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新版Matlab中神经网络训练函数Newff的使用方法
一、介绍新版newff
Syntax
•net = newff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) Description
newff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) takes several arguments
Examples
Here is a problem consisting of inputs P and targets T to be solved with a network.
•P = [0 1 2 3 4 5 6 7 8 9 10];T = [0 1 2 3 4 3 2 1 2 3 4];
Here a network is created with one hidden layer of five neurons.
•net = newff(P,T,5);
The network is simulated and its output plotted against the targets.
•Y = sim(net,P);plot(P,T,P,Y,'o')
The network is trained for 50 epochs. Again the network's output is plotted.
•net.trainParam.epochs = 50;net = train(net,P,T);Y = sim(net,P);plot(P,T,P,Y,'o') 二、新版newff与旧版newff调用语法对比
Example1
比如输入input(6*1000),输出output为(4*1000),那么
旧版定义:net=newff(minmax(input),[7,1],{'tansig','purelin'},'trainlm');
新版定义:net=newff(input,output,7,{'tansig','purelin'},'trainlm'); Example2
比如输入input(6*1000),输出output为(4*1000),那么
旧版定义:net=newff(minmax(input),[49,10,1],{'tansig','tansig','tansig'},'traingdx');新版定义:net=newff(input,output, [49,10], {'tansig','tansig','tansig'},'traingdx');
三、旧版newff使用方法在新版本中使用
提示:旧版本定义的newff虽也能在新版本中使用,但会有警告,警告如下:
Warning: NEWFF used in an obsolete way.
> In obs_use at 18
In newff>create_network at 127
In newff at 102
See help for NEWFF to update calls to the new argument list.
四、新版newff与旧版newff使用的训练效果对比
旧版本:旧用法训练次数多,但精度高
新版本:新用法训练次数少,但精度可能达不到要求
造成上述原因是:
程序里面的权值、阈值的初始值是随机赋值的,所以每次运行的结果都会不一样,有好有坏。
你可以把预测效果不错的网络的权值和阈值作为初始值。
具体可以查看net.iw{1,1}、net.lw{2,1}、net.b{1}、net.b{2}的值。
现在给一个完整的例子
%% 清空环境变量
clc
clear
%% 训练数据预测数据
data=importdata('test.txt');
%从1到768间随机排序
k=rand(1,768);
[m,n]=sort(k);
%输入输出数据
input=data(:,1:8);
output =data(:,9);
%随机提取500个样本为训练样本,268个样本为预测样本input_train=input(n(1:500),:)';
output_train=output(n(1:500),:)';
input_test=input(n(501:768),:)';
output_test=output(n(501:768),:)';
%输入数据归一化
[inputn,inputps]=mapminmax(input_train);
%% BP网络训练
% %初始化网络结构
net=newff(inputn,output_train,10);
net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0000004;
%% 网络训练
net=train(net,inputn,output_train);
%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
%网络预测输出
BPoutput=sim(net,inputn_test);
%% 结果分析
%根据网络输出找出数据属于哪类
BPoutput(find(BPoutput<0.5))=0;
BPoutput(find(BPoutput>=0.5))=1;
%% 结果分析
%画出预测种类和实际种类的分类图
figure(1)
plot(BPoutput,'og')
hold on
plot(output_test,'r*');
legend('预测类别','输出类别')
title('BP网络预测分类与实际类别比对','fontsize',12) ylabel('类别标签','fontsize',12)
xlabel('样本数目','fontsize',12)
ylim([-0.5 1.5])
%预测正确率
rightnumber=0;
for i=1:size(output_test,2)
if BPoutput(i)==output_test(i)
rightnumber=rightnumber+1;
end
end
rightratio=rightnumber/size(output_test,2)*100; sprintf('测试准确率=%0.2f',rightratio)。
