南京理工大学物理光学-1996真题
物理(波动)光学试卷

南京理工大学课程考试试卷(学生考试用)第 1 页共 1 页南京理工大学课程考试答案及评分标准南京理工大学课程考试试卷(学生考试用)6. Suppose we spread white light out into a fan of wavelengths by means of a diffraction grating and then pass a small select region of that spectrum out through a slit. Because of the slit, a band of wavelengths 1.2 nm wide centeredDetermine the frequency bandwidth and the coherence length of this light. (7. What is the general expression for the separation of the fringes of a Fresnel biprism of第 1 页共 1 页08A1. Given the wavefunctions 14sin 2(0.23)x t ψπ=-, and 2[sin(7 3.5)]/2.5x t ψ=+, determine in each case the values of (a) frequency, (b)wavelength, (c) period, (d)amplitude, (e)phase velocity, and (f) direction of motion. Time is in seconds and x is in meters. (12 points)2. Write an expression for the E -and B -fields that constitute a plane harmonic wave traveling in the +z-direction. The wave is linearly polarized with its plane of vibration at 450 to the yz -plane. (8 points)3. A 3.0-V flashlight bulb draws 0.25A, converting about 1.0% of the dissipated power into light(550nm λ≈). If the beam has a cross-sectional area of 10cm 2 and is approximately cylindrical, (a) How many photons are emitted per second? (b) How many photons occupy each meter of the beam? (c) What is the flux density of the beam as it leaves the flashlight? (346.62610h J s -=⨯⋅) (9 points)4. A ray of yellow light from a sodium discharge lamp falls on the surface of a diamond in air at 450. If at that frequency 2.42d n =, compute the angular deviation suffered upon transmission. (8 points)5. A beam of light in air strikes the surface of a smooth piece of plastic having an index of refraction of 1.55 at an angle with the normal of 20.00. The incident light has component E-field amplitudes parallel and perpendicular to the plane-of-incidence of 10.0V/m and 20.0V/m, respectively. Determine the corresponding reflected field amplitudes. (10 points)6. A magnetic-field technique for stabilizing a He-Ne laser to 2 parts in 1010 has been patented. At 632.8nm, what would be the coherence length of a laser with such a frequency stability? (8 points)7. An expanded beam of red light from a He-Ne laser (0632.8nm λ=) is incident on a screen containing two very narrow horizontal slits separated by 0.200mm. A fringe pattern appears on a white screen held 1.00m away. (a) How far (in radians and millimeters) above and below the central axis are the first zeros of irradiance? (b) How far (in mm) from the axis is the fifth bright band? (c) Compare these two results. (12 points)8. One of the mirrors of a Michelson Interferometer is moved, and 1000 fringe-pairs shift past the hairline in a viewing telescope during the process. If the device is illuminated with 500-nm light, how far was the mirror moved? (8 points)9. Suppose that we have a laser emitting a diffraction-limited beam (0632.8nm λ=) with a 2-mm diameter. How big a light spot would be produced on the surface of the Moon a distance of 337610km ⨯ away from such a device? Neglect any effects of the Earth ’s atmosphere. (7 points)10. Sunlight impinges on a transmission grating that is formed with 5000 lines per centimeter. Does the third-order spectrum overlap the second-order spectrum? Take red to be 780nm and violet to be 390 nm. (10 points)11. Imagine that we have randomly polarized room light incident almost normally on the glass surface of a radar screen. A portion of it would be specularly reflected back toward the viewer and would thus tend to obscure the display. Suppose now that we cover the screen with a right-circular polarizer, as shown in the Figure. Trace the incident and reflected beams, indicating their polarization states. What happens to the reflected beam? (8 points)08A答案07a1. Consider a lightwave having a phase velocity of 8310/m s ⨯ and a frequency of14610Hz ⨯. What is the shortest distance along the wave between any two points that have aphase difference of 300? What phase shift occurs at a given point in 10-6s, and how many waves have passed by in that time? (12 points)2. The electric field of an electromagnetic wave traveling in the positive x -direction is given by 00ˆE jsin()cos()E z z kx t πω=-, (a) Describe the field verbally. (b) Determine an expression for k . (c) Find the phase speed of the wave. (7 points)3. How many photons per second are emitted from a 100-W yellow lightbulb if we assume negligible thermal losses and a quasi-monochromatic wavelength of 550nm ? In actuality only about 2.5% of the total dissipated power emerges as visible radiation in an ordinary 100-W lamp. (346.62610h J s -=⨯⋅) (8 points)4. A laserbeam impinges on an air-liquid interface at an angle of 550. The refracted ray is observed to be transmitted at 400. What is the refractive index of the liquid? (7 points)5. Light is incident in air perpendicularly on a sheet of crown glass having an index of refraction of 1.522. Determine both the reflectance and the transmittance. (12 points)6. Imagine that we chop a continuous laserbeam (assumed to be monochromatic at0632.8nm λ=) into 0.1-ns pulses, using some sort of shutter. Compute the resultantlinewidth λ∆, bandwidth, and coherence length. Find the bandwidth and linewidth that would result if we could chop at 1015Hz . (8 points)7. With regard to Young ’s Experiment, derive a general expression for the shift in the vertical position of the m th maximum as a result of placing a thin parallel sheet of glass of index n and thickness d directly over one of the slits. Identify your assumptions. (10 points)8. Suppose we place a chamber 10.0cm long with flat parallel windows in one arm of a Michelson Interferometer that is being illuminated by 600-nm light. If the refractive index of air is 1.00029 and all the air is pumped out of the cell, how many fringe-pairs will shift by in the process? (10 points)9. If you peered through a 0.75-mm hole at an eye chart, you would probably notice a decrease in visual acuity. Compute the angular limit of resolution, assuming that it ’s determined only by diffraction; take 0550nm λ=. Compare your results with the value of41.710rad -⨯, which corresponds to a 4.0-mm pupil. (10 points)10. Light having a frequency of 144.010Hz ⨯ is incident on a grating formed with 10000 lines per centimeter. What is the highestorder spectrum that can be seen with this device? Explain. (8 points)11. A Babinet compensator is positioned at 450 between crossed linear polarizers and is being illuminated with sodium light. When a thin sheet of mica (indices 1.599 and 1.594) is placed on the compensator, the black bands all shift by 1/4 of the space separating them. Compute the retardance of the sheet and its thickness. (8 points)1. Solution:814/310/5100.6c m λνμ==⨯⨯= 83/310/60510c km λν==⨯=⨯2. Solution:The number of waves is 0/AB λ. With the glass in place, there are 0()/AB L λ- waves in vacuum and an additional /L λwaves in glass for a total of 00(/)(1/1/)AB L λλλ-. The difference in number is 0(1/1/)L λλ-, giving a phase shift of φ∆ of 2π for each wave; hence , 0002(1/1/)2(/1/)2/22000L L n L πλλπλλπλπ-=-==.3. Solution:(a) The phase angle is retarded by an amount (2/)2/n y y πλπλ∆-∆ or (1)/n y c ω-∆. Thus0exp [(1)//]p E E i t n y c y c ω=--∆- or 0exp[(1)/]exp (/)p E E i n y c i t y c ωω=--∆- (b) Since 1x e x ≈+ for small x, if 1n ≈ of 1y ∆ , exp[(1)/]1(1)/i n y c i n y c ωω--∆≈--∆ and since exp(/2)i i π-=-, (1)(/)exp(/2)p u u E E n y E c i ωπ=+-∆-4. Solution:/t i t i r n n n n -+ . Air-water: 4/311/70.144/31r -===+. Air-crown glass:3/211/50.203/21r -===+.More reflectance for glass. 2/r i I I R r ==.Air-water: 2(1/7)0.02R ==. Air-crown glass: 2(1/5)0.04R ==5. Solution:/21sin sin it ti n n θθθθ==/2/1sin sin t i n n θθ=/21sin sin t i n n θθ= and /t i i θθ=__/cos AB d t =θ ___/)sin(AB a t i =-θθ t t i daθθθcos )sin(=- a d t t i =-θθθcos )sin(6. Solution:99//(1.210)/(50010)0.0024m m ννλλ--∆=∆=⨯⨯=c νλ=, so 8914/(310/)/(50010) 6.0010c m s m Hz νλ-==⨯⨯=⨯1412(0.0024)(6.0010) 1.4410Hz ν∆=⨯=⨯131/ 6.9410c t s ν-∆∆=⨯8134(310/)(6.9410) 2.0810c c l c t m s s m --∆∆=⨯⨯=⨯7. Solution:)(2//0n n d s y -=∆αλ8.Solution :λ=nd 2m nd 71084.12-⨯==λ9. Solution:θαsin 2k a =,θβsin 2k b=,mb a =,πβαm m 2==N=number of fringes=m m a 2/2/==πππ10. Solution:sin m a m θλ=sin /m m Y R θ6(/)10,000/10/m Y m a R lines cm lines m λ=== So 610a m -=761(589.5923)[1(5.89592310)/10](1.00)0.5895923Y nm m m m m--=⨯='761(588.9953)[1(5.88955310)/10](1.00)0.5889953Y nm m m m m--=⨯='411 5.9710Separation Y Y m -=-=⨯11. Solutionsin /sin i t ti n θθ=; sin sin /sin(40)/1.5t i ti n θθ== ; 25.4t θ= .2222tan ()/tan ()tan (14.6)/tan (65.4)0.014i t i t R θθθθ=-+=-=2222sin ()/sin ()sin (14.6)/sin (65.4)0.077i t i t R θθθθ⊥=-+=-=1()0.04552R R R ⊥=+= /()()/()67%p p n V I I I R R R R R ⊥⊥=+=+++=。
2020年南京理工大学819光学工程[物理光学(75分)、应用光学(75分)]考研真题汇编
![2020年南京理工大学819光学工程[物理光学(75分)、应用光学(75分)]考研真题汇编](https://img.taocdn.com/s3/m/d3700222844769eae009edd7.png)
2020年南京理工大学819光学工程[物理光学(75分)、应用光学(75分)]考研真题汇编
说明:本套考研资料由本机构多位高分研究生潜心整理编写,2020年考研初试首选资料。
一、南京理工大学819光学工程[物理光学(75分)、应用光学(75分)]考研真题汇编
1.南京理工大学819光学工程[物理光学(75分)、应用光学(75分)]2010-2015年考研真题,暂无答案。
说明:分析历年考研真题可以把握出题脉络,了解考题难度、风格,侧重点等,为考研复习指明方向。
二、资料全国统一零售价
2.本套考研资料全国统一零售价:[¥120.00]
三、2020年研究生入学考试指定/推荐参考书目(资料不包括教材)
3.南京理工大学819光学工程考研初试参考书
《物理光学》(修订本)机械工业出版社,梁铨廷(浙大)
《应用光学》机械工业出版社,张以漠
《应用光学与光学设计基础》东南大学出版社,迟泽英、陈文建。
南京理工大学课程考试试卷(大学物理)

第 1 页
a I b I 120
0
I S1 t1 n1 t2 n2 r1 p r2
L c b I I I d c b I
S2
图1
图2
6.一衍射光栅对某一定波长的垂直入射光,在屏幕上只能出现零级和一级主极大, 欲使屏幕上出现更高级次的主极大,应该 ( ) A.换一个光栅常数较小的光栅; B.换一个光栅常数较大的光栅; C.将光栅向靠近屏幕的方向移动;D.将光栅向远离屏幕的方向移动。 7.自然光以某入射角 i ( i arctg(n) )由空气入射到一玻璃表面上(玻璃的折射率 为 n) ,其反射光和折射光的偏振程度为: A.反射光为偏振光,折射光为部分偏振光; B.反射光为部分偏振光,折射光为偏振光; C.反射光和折射光都为部分偏振光; D.反射光和折射光都为偏振光。 ) 8.一宇航员要到离地球为 5 光年的星球去旅行,如果宇航员希望把这距离缩短为 3 光年,则他所乘的火箭相对于地球的速度应是: (c 表示真空中光速) ( A.υ=c/2; B.υ=3c/5; C.υ=4c/5; D.υ=9c/10。 ( ) ( )
南京 理工大学 课程考试试卷 课程名称:
试卷编号: 组卷日期: 学生班级:
大学物理(下) A 卷
学分:
3.5
大纲编号
11120804
分钟
考试方式: 闭卷笔试 满分分值: 100 2013 年 1 月 1 日 组卷教师(签字) : 学生学号:
考试时间: 120
审定人(签字) : 学生姓名:
一、选择题(每题 2 分,共 20 分) 1.一电荷量为 q 的粒子在均匀磁场中运动,下列哪种说法是正确的?( A.只要速度大小相同,粒子所受的洛仑兹力就相同; B.洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆; C.粒子进入磁场后,其动能和动量都不变;
南京理工大学历年大物试卷及答案

2011级大物试卷及答案一、选择题(每题2分,共20分)1、一质点从静止出发绕半径为R 的圆周作匀变速圆周运动,角加速度为α,当该质点走完一圈回到出发点时,所经历的时间为 ( B )(A )R 221α; (B )απ4; (C )απ2; (D )条件不够不能确定。
2、有一个小球,置于一个光滑的水平桌面上,有一绳其一端连接此小球,另一端穿过桌面中心的小孔,该小球原以角速度ω在距孔为r 的圆周上转动,今将绳从小孔缓慢往下拉的过程中,则对小球下列叙述正确的是 ( C ) (A )角动量、动能、动量都不变; (B )角动量、动能、动量都改变; (C )角动量不变,动能、动量都改变; (D )角动量和动量不变,动能改变。
3、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图1。
今使棒从水平位置由静止开始下落。
在棒摆动到竖直位置的过程中,则应 ( A ) (A )角速度从小到大,角加速度从大到小; (B )角速度从小到大,角加速度从小到大; (C )角速度从大到小,角加速度从大到小; (D )角速度从大到小,角加速度从小到大。
4、一简谐振动曲线如图2所示,则振动周期为 ( D ) (A )2.62s ; (B )0.42s ; (C )0.38s ; (D )2.40s5、传播速度为100m/s ,频率为50Hz 的平面简谐波,在波线上相距为0.5m 的两点之间的位相差为 ( C )(A )3π; (B )6π; (C )2π; (D )4π。
6、如图3所示,设某热力学系统经历一个准静态过程b →c →a ,a ,b 两点在同一条绝热线上,则该系统在b →c →a 过程中 ( D ) (A )只吸热,不放热; (B )只放热,不吸热;(C )有的阶段吸热,有的阶段放热,吸收的热量等于放出的热量; (D )有的阶段吸热,有的阶段放热,吸收的热量大于放出的热量; (E )有的阶段吸热,有的阶段放热,吸收的热量小于放出的热量。
南理工物理光学02-04

2n
与楔角成反比 与波长成正比
(4)楔板的楔角
h e 2ne
(5)
e
不同形状的楔形板对应不同形状的干涉条纹
(a)楔形平板 (b)柱形表面平板 (c)球形表面平板 (d)任意形状表面平板
【例题2-9】图示为测平板平行性的装置, 已知:光源有 白炽灯,
钠灯( 589.3nm, 0.6nm
镜焦距f=40mm。(1)若屏F上的干涉环中心是暗的,问屏上所看 到的第一个暗环半径r是多少? (2)为了在给定的系统参数下看到
干涉环, 照射在板上的谱线最大允许宽度是多少? 解: ( 1 )设干涉环中心的干涉级次为
m0( 不一定为整数 ) ,则由平板上、下表 面反射出来的两支光的光程差
2nh cos 2 N
一、干涉条纹的定域(实质上是空间相干性问题) 1.条纹定域: 点光源照明:产生非定域条纹 扩展光源照明:由于空间相干性 某些区域条纹对比度下降, 条纹消失 但在定域区仍可观察到清晰 的条纹——定域条纹
S
P
n
M1 M2
S1 S2
能够得到清晰干涉条纹的区域——定域区或定域面。
非定域条纹:在空间任何区域都能得到的干涉条纹
(3)亮条纹的角半径1N
1N
1 n N 1 q n' h
——N称为干涉序数 ——q称为中心干涉级小数
rN
从中心往外数第N个亮纹对透镜中心的倾角 , 称为第N个条纹的角半径,其条纹半径:
rN f 1N
求法:第N个亮纹相对于中心处的干涉级差
→两处程差变化→相应条纹角半径
中 2nh N 2nh cos 2 N 2 m0 (m1 q) 2 [m1 ( N 1)]
南理工物理光学03-06

80%能量转移并集中到1级光谱 对B 的一级光谱闪耀的光栅对B /2的2级光谱和 B /3的3级 光谱也闪耀。
闪耀光栅在同一级光谱中只对闪耀波长产生极大光强度, 而对其他波长不能产生极大光强度。 应用时是根据B,确定 由于中央衍射有一定的宽 度,所以闪耀波长附近的 谱线也有相当大的强度, 因而闪耀光栅可用于一定 的波长范围。
16
(三)阶梯光栅
a
平行的平面玻璃板成阶梯状排列而 成的相位光栅
nh (n cos )h a sin (n 1)h a
h atg a a cos h cos a sin
h
阶梯光栅
' A B h C atg a/cos
14
按题意,光栅常数为
1 103 d 5.0 106 m 200
由图可以看出 1 和 2 都很小,所以 sin tan , 根据光栅方程,有
m11 x sin 1 d f
m2 2 x x sin 2 d f
因此:
m11 d x 5.0 5.0 106 0.5 106 m 500nm f 50
阶梯光栅的方程为:
a
(n 1)h a=m
特点: h较大,m很大(闪耀级次很高) 分辨本领很高
a
光谱范围很小
用于超精细结构小范围光谱分析
h
d=a,又a较大,中央衍射极大中只有一个或至多二个次主极大
对于反射式,有 2h-a=m
(四)正弦(振幅型)光栅 正弦(或余弦)光栅其振幅透射系数是正弦(或余弦)型分布 (如图)可表示为:
南理工物理光学01

z z E=f1 ( t ) f 2 ( t ) v v
2、解的意义: z z z z E=f1 ( t ) f 2 ( t ) f1 和 f2 是以( t )和( t ) v v v v z z 为变量的任意函数。 B = f1 ( t ) f 2 ( t ) v v z z f1 ( -t )表示沿 z轴正向传播, f 2 ( +t )表示沿 z轴负向传播。 v v 取正向传播: z E=f1 ( t ) 这是行波的表示式,表示 v 源点的振动经过一定的时 z B=f1 ( t ) 间推迟才传播到场点。 v
光的电磁理论基础
★十九世纪六十年代,麦克斯韦(Maxwell)在前 人工作基础上,完成了题为“电磁场的动力学” 的论文,从而建立起经典的电磁理论,即电磁 场的基本方程 —麦克斯韦方程组。他在研究电磁 场理论的同时,还把光学现象和电磁现象联系起 来,进一步指出光也是一种电磁波。这种把光波当做电磁 波来处理的理论称为光的电磁理论,它是波动光学的理论 基础。 麦克斯韦电磁理论方程式是在安培 定律、高斯定律、法拉第定律和无自由 磁荷等的基础上得到的!
对于电磁场远离辐射源(无限大、均匀、各向同性、透明介质): =0,j=0
E 0 B E t E B t
B 0
结果: E B
2
2
2E t 2 2B t
2
0 0
(11-13)
(11-14)
拉普拉斯算符:
2 2 2 x 2 y 2 z 2
D B 0 B E t D H j t
(11-1) (11-2)
(11-3)
揭示了电流、电场、磁 场相互激励的性质
南京理工大学《大学物理》(上)课程试卷B及答案

南 京 理 工 大 学 考 试 卷课程名称 大学物理 姓 名 学 号适用专业考试形式闭卷考试时间 120分钟一、选择题(每题3分,共30分) 1、下列各种说法正确的是( )(A )作用力的冲量与反作用力的冲量总是等值反向的; (B )系统的内力可以改变系统的总动量; (C )冲量的方向与物体动量的方向相同;(D )以恒力作用于物体,时间越长,物体的动量越大。
2、一炮弹由于特殊原因在飞行过程中突然炸裂成两块,其中一块作自由下落,另一块的着地点( )(A )比原来更远; (B )比原来更近; (C )和原来一样; (D )无法判断。
3、两个匀质圆盘A 和B 的密度分别为A ρ和B ρ。
若B A ρρ>,但两圆盘质量和厚度相同,若两盘对通过盘心垂直于盘面的轴的转动惯量分别为A J 和B J ,则 ( ) (A )B J J >A ; (B )B J J <A ; (C )B J J =A ; (D )不能确定哪个大。
4、任何一个实际弹簧都是有质量的,若考虑其质量,则弹簧振子振动周期将:( ) (A )不变; (B )变小; (C )变大; (D )无法确定。
5、机械波在弹性媒质中传播时,若媒质中媒质元刚好经过平衡位置,则它的能量为( ) (A )动能最大,势能也最大; (B )动能最小,势能也最小; (C )动能最大,势能最小; (D )动能最小,势能最大。
6、某容器种有理想气体,若绝对温度提高为原来的2倍,用P 和k ε分别表示气体的压强和气体分子的平均动能,则: ( ) (A )k P ε,均提高为原来的2倍; (B )k P ε,均提高为原来的4倍; (C )P 提高为原来的2倍,k ε提高为原来的4倍; (D )k P ε,均不变。
7、关于热力学过程,下列说法正确的是: ( ) (A )准静态过程一定是可逆过程;(B )非准静态过程不一定是不可逆过程; (C )可逆过程一定是准静态过程; (D )不可逆过程一定是非准静态过程。
南理工物理光学04-02

最重要的特点: 衍射斑的方位角与光栅的空间频率一一对应。
余弦光栅的衍射特征: (x,y)
F
+1
+1 -1
0 -1
理论说明;平面波正入射,其入射波前为:U1 ( x, y) A1
南理工物理光学03

• 前面讨论了,光在非导电(=0)各向同性 均匀介质及其界面上的传播规律。 • 对于金属,它与各向同性介质的主要差别 是电导率()不等于0 ,金属导致光波衰 减,金属对光波几乎不透明。 11.3.1 光波在金属中的传播 11.3.2 光在金属表面的反射和折射 11.3.3 金属表面反射的频率特性
11.3.1 光波在金属中的传播
• 设金属是一种介电常数为ε、磁导率为μ,电导率为σ的 均匀各向同性介质,则物质方程中的J=σE必须予以考虑。
• 由麦克斯韦方程,可得金属中光波所满足的波动方程为 2 E • 其中 1 i 2 E 2 0 t 这两个波动方程与(11-13)式 2 的差别在于以复数值μεα H 2 H 0 2 代替了με。 t 金属中的单色平面光波, 其光场表示式为 ~ i ( t k k 0 r ) 0
• 不同金属自由电子密度越大(电导率越大),反射本领越大。 • 同一种金属,入射光频率(波长)不同, 反射率也不同。频率较低 的红外线主要对金属中的自由电子发生作用,而频率较高的可见光 和紫外光可对金属中的束缚电子发生作用。
p ~ rp
2
1 2 2 n n cos1 2 1 2 2 n n cos1
2
正入射时有
~ 1 2 n 2 1 2 1 2n n ~ 2 n 1 n (1 2 ) 1 2n
11.3.2 光在金属表面的反射和折射
• 光在金属表面上的反射和折射, 其讨论方法与电介质界面的情 况相同。 • 分别讨论s分量、p分量的反射 和折射特性。 • 具体讨论不作要求。 ~ • 结论: sin
南理工物理光学04-01

重要内容 1、 波前变换和相因子分析 2、 余弦光栅的衍射场 3、 傅立叶变换光学大意 4、 阿贝成像原理与空间滤波 5、 泽尼克的相衬法
概要:
惠更斯-菲涅耳原理 光波衍射
菲涅耳衍射
衍 射 分 析 结 构
夫琅禾费衍射
x2 y2 ik 2f
,忽略透镜表面反射, A1 A2
是一种相位型衍射屏函数
注意对于凹透镜和凸透镜的情况相同,只是焦距一个为正,一个为负。
例题:利用相因子法求薄透镜傍轴成像公式:
s
ik ~ 在傍轴条件下: U1 ( x, y ) A1e x2 y2 2f
x y 2s
2
2
s’
透镜函数: ~ tL ( x, y ) e
1 2
U1 U2U3
U
~ U2 ~ ~ ~ t1 t2 U1
衍射的再说明:
i ~ U ( x' , y ' )
ikr ikr e i e ~ ~ ~ t ( x, y ) U1 ( x, y) dxdy U1 ( x, y) dxdy (0 ) r ( 0 ) r
ik x2 y2 2 z0
1 A1t1e 2
ik
x2 y2 2 z0
~ ~ ~ U 0 U 1 U 1
0级为正出射的平面波 ~ 1级U 1代表发散球面波,发散 点为(0, 0, z0 ) ~ 1级U 1代表汇聚球面波,汇聚 点为(0, 0,z0 )
i ~ U ( x' , y ' )
~ U ~ 2 ( x, y ) 衍射屏函数的定义: t ( x, y) ~ U1 ( x, y)
1995-2016年南京理工大学819光学工程考研真题及答案解析 汇编

2017版南京理工大学《819光学工程》全套考研资料我们是布丁考研网南理工考研团队,是在读学长。
我们亲身经历过南理工考研,录取后把自己当年考研时用过的资料重新整理,从本校的研招办拿到了最新的真题,同时新添加很多高参考价值的内部复习资料,保证资料的真实性,希望能帮助大家成功考入南理工。
此外,我们还提供学长一对一个性化辅导服务,适合二战、在职、基础或本科不好的同学,可在短时间内快速把握重点和考点。
有任何考南理工相关的疑问,也可以咨询我们,学长会提供免费的解答。
更多信息,请关注布丁考研网。
以下为本科目的资料清单(有实物图及预览,货真价实):南京理工大学《光学工程》全套考研资料包含:一、南京理工大学《光学工程》历年考研真题及答案解析2016年南京理工大学《光学工程》考研真题(含答案解析)(11月份统一更新)2015年南京理工大学《光学工程》考研真题2012年南京理工大学《光学工程》考研真题2011年南京理工大学《光学工程》考研真题2010年南京理工大学《光学工程》考研真题2009年南京理工大学《光学工程》考研真题2008年南京理工大学《光学工程》考研真题2007年南京理工大学《光学工程》考研真题2006年南京理工大学《光学工程》考研真题(含答案解析)2005年南京理工大学《光学工程》考研真题(含答案解析)2004年南京理工大学《光学工程》考研真题(含答案解析)2003年南京理工大学《光学工程》考研真题2002年南京理工大学《物理光学》考研真题2001年南京理工大学《物理光学》考研真题2000年南京理工大学《物理光学》考研真题1999年南京理工大学《物理光学》考研真题1998年南京理工大学《物理光学》考研真题2002年南京理工大学《应用光学》考研真题2001年南京理工大学《应用光学》考研真题2000年南京理工大学《应用光学》考研真题1999年南京理工大学《应用光学》考研真题1998年南京理工大学《应用光学》考研真题1997年南京理工大学《应用光学》考研真题1996年南京理工大学《应用光学》考研真题1995年南京理工大学《应用光学》考研真题二、南京理工大学《光学工程》期中期末试题汇编三、南京理工大学《光学工程》考研复习笔记1、《光学工程》公式定律总结四、南京理工大学《光学工程》考研复习题1、《光学工程》重难点例题解析2、《光学工程》考研练习题3、《光学工程》核心模拟题4、《光学工程》历年模拟题与答案5、《光学工程》模拟题库6、《光学工程》考研本校各章节练习题(英语版)以下为截图及预览2015年考研真题公式定律总结模拟题库重难点例题解析。
南理工物理光学02-06

瑞利判据:两个波长的亮条纹只
有当它们合强度中央的极小值低 于两边的极大值的0.81时,两个条 纹才能被分开。
1 0.81
( )m
G点的光强分布 Ii Ii I G= 2 1 F sin ( 1 2) 1 F sin 2 ( 2 2) 当I F 0.81I G 时,两个峰值才能分辨 开。 在G点, 1 2m ,
【例题】 已 知 汞 绿 线 的 超 精 细 结 构 为 546.0753nm 、 546.0745nm 、 546.0734nm 及 546.0728nm 。 设 法 布 里 — 珀罗标准具工作面的反射比 0.9, 问用该标 准具分析这一结构时应如何选取标准具间距h?
解:根据设条件,光源的平均波长为:
令 : N 0.97s 称为标准具的有效光束 数,则:A=m N
【例题】 法布里—珀罗(F-P)干涉仪两工作板的振幅反射系数
r 0.9 ,假设不考虑光在干涉仪两板内表面反射时的相位变化, 问:
(1) 该干涉仪的最小分辨本领是多大?
m) 的双线,即 (2)要能分辨开氢红线 H (0.6563
当很小时, sin , 则有 4 4 4 21- = = ,当 1时,变得很小。 F
(7) 条纹精细度s
定义:相邻条纹相位差2 与条纹锐度 之比称为条纹的精细度。 2 F s 2 1 反射比 越趋近于1, s值越大, 条纹越精细,条纹锐度也越好。
(546.0753 546.0746 546.0734 546.0728 ) / 4 546.074nm
超精细结构的最大波长差:
( ) Max 546.0753 546.0728 0.0025 nm
南理工物理光学02
n2 cosq 2 A2 s n2 cosq 2 2 s ts n1 cosq1 A1s n1 cosq1
A1' p p A1 p
2 q1 q 2 tg 2 rp 2 q1 q 2 tg 2
在分界面(z=0)处: E1t E2t
s E2s E1s E1
r - 1 t A2s expik 2 r - 2 t A1s expik1 r - 1t A1' s expik1
由上式得
1 '1 2
单位时间内入射到分界面单位面积上的能量(入射波的能流):
W1 W0 1 1 2 1 0 I 1 cosq1 A1 cosq1 n1 A12 cosq1 S 2 1 2 0
反射光、折射光单位时间内从界面单位面积上带走的能量, 即,反射光的能流:
W1' I1' cosq1
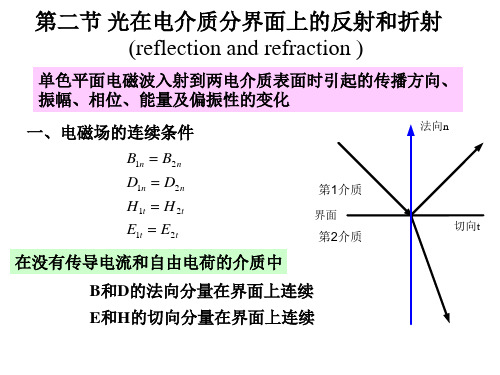
第二节 光在电介质分界面上的反射和折射 (reflection and refraction )
单色平面电磁波入射到两电介质表面时引起的传播方向、 振幅、相位、能量及偏振性的变化 一、电磁场的连续条件
B1n B2 n D1n D2 n H1t H 2t E1t E2t
第1介质
界面 切向t 法向n
第2介质
在没有传导电流和自由电荷的介质中
B和D的法向分量在界面上连续
E和H的切向分量在界面上连续
几个概念
入射面:界面法线与入射光线组成的平面 k1,n
振动面:电场矢量的方向与入射光线组成的平面, E,k1 方位角 任一方位振动的光矢量E可分解成两个互相垂直的分量 P分量:平行于入射面振动 ----Parallel S分量:垂直于入射面振动 ----Senkrecht E’1p E1p P、S分量正负号的规定: E’1s q’1 E 1s 二、反射定律和折射定律 q
南理工物理光学03-05
o P1 f P2
z
观察屏
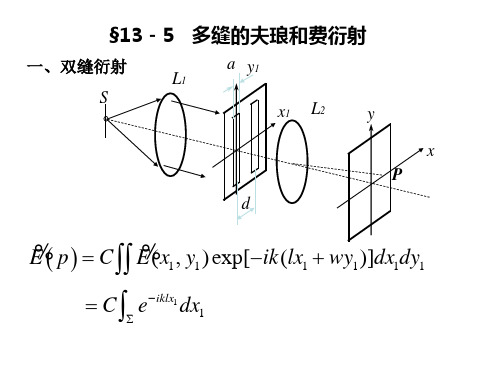
解: 这是一个偏振光单缝衍射与双缝干涉的综合问题,可将单 缝的上下两部分分别考虑。设自然光经偏振片P后的线偏振光 的复振幅为A,则: 1 经x>0区域到达观察屏的光分量为:E1 y A cos 45 cos 45 2 A 经x<0区域到达观察屏的光分量为:E2 y
其中,
a sin , 2
2 a sin 2 2
整理后,得:
i sin 1 1 i 2 i 2 i sin E ( P) A(1 e ) Ae e e 2 2 2
( sin
多光束干涉因子。 单缝衍射因子,
20 y z f 10
2 )
(1)多光束干涉因子的影响 1)主极大值条件:
当
2
0
d sin =m
d sin =2m
2
0 x 2
2
4
时, [ sin(N / 2) ]2 N 2 sin / 2
20
在方向上产生极大,极值为:
~ sin sin(N / 2) i ( N 1) / 2 E0 e sin / 2
sin 2 sin(N / 2) 2 ~ ~* ) [ ] 0 所以P点处光强度为: I EE I( sin / 2
2. 光强分布特点
光强度由两个因子决定: [ sin(N / 2) ] 2 sin / 2
根据夫琅和费衍射公式,观察屏上P点处光场复振幅为:
a ~ ~ E ( x ) C E ( x1 )e iklx1 dx1 a 0
南理工物理光学02-03

讨论:
b K sin b
1)光源的临界宽度:条纹可见度 为0时的光源宽度
K 1 0.9
临界宽度bc
2)光源的允许宽度:能够清晰地观察 到干涉条纹时,允许的光源宽度
/4
/
2 /
b
允许宽度b p 4
2、空间相干性 若通过光波场横向两点的光在空间相遇时能够发生 干涉,则称通过空间两点的光具有空间相干性。 横向相干宽度
影响干涉条纹可见度的主要因素:
振幅比、光源的大小、光源的非单色性
一、振幅比 对条纹可见度的影响
A1 2 A 2 I1I 2 2 A1 A2 2 K = 2 2 2 I1 I 2 A1 +A2 A1 1 A 2
当A1 A2时,K=1,对比度最好,条纹最清楚。 当A1 A2时,K 1,对比度变差。 当A1和A2相差越多时,K 值越小。
可见度:
K
sin k k 2
2
讨论:
K
sin k k 2
2
K 1 0
k ()
max 2 /
最大光程差
max
2 2 k
相干长度:对于光谱宽度为(或k)的光源能够产 生干涉的最大光程差。
相干长度与波列长度一致
P0
解(3)由图,从两个缝发出的光,到达P0点时的光程差为
(n 1)t
这一光程差如果大于准单色光的相干长度,则P0点附近干涉 条纹消失。准单色光的相干长度为:
max
因此,当
2
max
2 (n 1)t
t
