03 图像增强-复立叶-选修

合集下载

图像的增强图象处理及应用教学课件

i M 1 j N 1
f (x, y) 1
2
2
f (x i, y i)
MN I M 1 j N 1
2
2
图象处理及应用
如果图象中的噪声是随机不相关的加性噪声，窗口内各点的噪声是独立等分布的，则经过上面的平滑后，信噪比可提高倍。图象的平滑这种做法实现的是一种简单的低通滤波器（low pass filter）。它可以有效地减弱或去除傅里叶空间的高频分量，保留低频的有效信号。使图象中灰度值突变的边缘得以平滑，图象将变得柔和一些（也模糊一些）。使用滤波器对图象进行处理中最有意义的操作是利用模板对图象进行卷积处理，所谓的模板就是形如下式所示线性距阵：
图象处理及应用
中值滤波：
中值滤波也是一种典型的低通滤波器，它的目的是在保护图象边缘的同时去除噪声。所谓中值滤波，就是指把以某点(x,y)为中心的小窗口内的所有象素的灰度按从大到小的顺序排列，将中间值作为(x,y)处的灰度值(若窗口中有偶数个象素，则取两个中间值的平均)。这种平滑方法对脉冲干扰和椒盐噪声效果较好。中值滤波与邻域平均法就处理效果相比较而言，应用邻域平滑模板，图象平滑了，但是也使边界模糊了。而中值滤波不仅能很容易去除孤立点、线等形式的噪声和去除二值噪声并且可以很好地保持原有的图象边缘；Gauss模板对付高斯噪声非常有效，而中值滤波对于高斯噪声则无能为力。但要注意的是，当窗口内噪声点的个数大于窗口宽度的一半时，中值滤波的效果不好。这是很显然的。
LPBITMAPINFO lpbmi;
lpbmi = (LPBITMAPINFO)lpDIB;
LPBITMAPINFOHEADER pbi=(LPBITMAPINFOHEADER)lpbmi;

图像增强技术-PPT文档资料

设有一幅N×N的图像f(x,y)，若平滑图像为 g(x,y),则有
g(x,y)1 f(i,j)
M i,j s
(4.21)
式中x,y=0,1,…,N-1； s为（x,y）邻域内像素坐标的集合； M表示集合s内像素的总数。可见邻域平均法就是将当前像素邻域内各像素的灰度平均值作为其输出值的去噪方法。
通过细心调整折线拐点的位置及控制分段直线的斜率，可对任一灰度区间进行拉伸或压缩。
获取变换函数的方法之一
固定函数：指数函数、正弦函数、分段直线、
对数函数，如显示傅立叶的s =clog(1+|r|)
255
255
216
142
23
0
0
灰度切割
❖ 应用：
增强特征（卫星图象中大量的水）增强X射线图象中的缺陷
乘以系数255/max;
加法运用的例子：图象平均处理
空间滤波基础
在待处理的图象中逐点移动模板 R=w(-1,-1)f(x-1,y-1)+
w(-1,0)f(x-1,y)+ w(-1,1)f(x-1,y+1)+ w(0,-1)f(x,y-1)+ w(0,0)f(x,y)+ w(0,1)f(x,y+1)+ w(1,-1)f(x+1,y-1)+ w(1,0)f(x+1,y)+ w(1,1)f(x+1,y+1)
图象反转
适用于增强嵌入于图象暗色区域的白色或者灰色细节，特别是黑色面积占主导地位的时候
对数变换
❖ s = c log(1+r) ❖ 压缩图象灰度的动态范围 ❖ 典型运用是傅立叶谱的显示
❖ 大于1 ❖ 小于1 ❖ 等于1

数字图像处理第四章图像增强 ppt课件

图像质量退化的原因
✓ 对比度局部或全部偏低 ✓ 噪声干扰，包括热噪声、量化噪声、椒盐噪声、
背景干扰等 ✓ 清晰度下降，图像模糊
图像增强通过针对性技术，如直方图均衡、平滑去噪、边缘锐化等对图像的退化加以修正，已达到改进图像质量的目的。
6
图像增强的主要内容
空间域
✓ 点运算 ✓ 局部运算图像平滑，图像锐化
11
4.1.2灰度变换
灰度变换：将图像的灰度级映射到另一灰度级。分类：线性变换，非线性变换一、线性变换由于成像时曝光不足或过度，以及成像设备的非线性或图像记录设备动态范围太窄等因素，对图像都会产生对比度不足的弊病，使图像中的细节分辨不清，这时如将图像灰度线性扩展，常能显著改善图像的主观质量。
[b，Mf ]被压缩
17
二、非线性灰度变换
对数变换 g (i， j) = a+ ln [f(i, j) + 1 ] b ln c
低灰度拉伸，高灰度压缩指数变换
g (i， j) = b c[f(i,j)-a] 1 使图像高灰度拉伸
对数变换
指数变换
18
附：PS相关命令
通过命令“图像曲线”调整灰度
具体实现
实际处理对象
✓ 对理想系统的输入图像f(i,j)和实际获得降质图像g(i,j)的关系用公式表示为 g(i,j)=e(i,j)f(i,j)
其中e(i,j)为降质函数/系统的灰度失真系数
✓ 采用一幅灰度级为常数C的图像成像，实际输出为gc(i,j)，即gc(i,j)=e(i,j)C，代入前式可得
基本思想是提出希望的局部均值和方差对原图像每个像素分别进行处局部均值平均灰度方差平均对比度局部方差平均对比度局部统计法主要内容图像增强的作用及目的空间域点运算空间域平滑空间域锐化频率域增强彩色增强代数运算空间滤波的概念平滑滤波空间域滤波概念空间域滤波属于局部处理空间域滤波分类空域滤波按不同条件分类空间域滤波线性滤波器定义空间域滤波42空间域平滑图a原图像图b阈值化处理后的图像图c平滑处理后的图像空间域平滑平滑滤波器的用途平滑滤波器的用途一局部平滑法像素灰度像素邻域内各像素的灰度平均值s表示去心邻域常用4邻域8邻域

《图像增强技术》课件

三、新兴的图像增强技术
SRGAN
具备超分辨率图像生成能力的生成对抗网络，可提高图像细节和清晰度。
ESRGAN
在SRGAN基础上进一步改进的超分辨率图像生成算法，提供更高质量的图像增强效果。
StyleGAN
基于神经网络的图像生成算法，能够生成高质量、更具艺术风格的图像。
CycleG一种图像风格转化为另一种图像风格。
二、传统图像增强技术
直方图均衡化
通过重新分配图像的像素值来改善图像对比度和亮度，从而增强图像细节。
滤波器增强
利用滤波器进行图像平滑、边缘增强或噪声去除，以提高图像质量。
空间域增强
基于图像的空间域特征，如边缘和纹理等，对图像进行局部增强。
频率域增强
利用傅里叶变换将图像转换到频率域，在频率域进行增强处理，如降噪和图像恢复。
四、应用
人脸识别
图像增强技术可提高人脸图像质量、对比度和细节，以提升人脸识别的准确性和可靠性。
视频增强
通过图像增强技术，可以改善视频的清晰度、稳定性和色彩表现，提供更好的观看体验。
医学图像分析
图像增强技术在医学领域的应用可以帮助医生更准确地诊断和分析医学图像，提高医疗质量。
五、总结
《图像增强技术》PPT课件
欢迎来到《图像增强技术》PPT课件！在本课件中，我们将探索图像增强的概念、传统与新兴的增强技术，以及应用领域和发展趋势。准备好了吗？让我们开始吧！
一、介绍
图像增强的概念
图像增强是通过处理技术改善图像质量，使其更具视觉吸引力和可用性。
增强的目的和意义
图像增强的目的是提高图像的视觉效果、清晰度、对比度和颜色等特征，以便更好地满足人类视觉需求。

第5章傅立叶变换与频域图像增强

1 F (u , v) N

x பைடு நூலகம் y 0
N 1
N 1
2(ux vy ) 2(ux vy ) f ( x, y )[cos( ) j sin( )] N N
F(u,v)通常是复数。
7
1 F (u , v) N

x 0 y 0
N 1 N 1
f ( x, y ) cos(
频谱图像|F(u,v)|特点：
低频部分集中了大部分能量；
F (0,0) N f
高频部分对应边缘和噪声等细节内容。

频域增强是通过改变图像中不同频率分量来实现的。频域滤波器：不同的滤波器滤除的频率和保留的频率不同，因而可获得不同的增强效果。
30

频域增强方法的三个步骤：
1.将图像从图像空间转换到频域空间（如傅里叶变换）；

x 0 y 0
N 1
N 1
ux vy f ( x, y ) exp[ j2( )] N
2(ux vy ) 2(ux vy ) f ( x, y )[cos( ) j sin( )] N N

x 0 y 0
N 1
N 1
F (u, v) R(u, v) jI (u, v) F (u, v) exp j (u, v)

f (x,y)、h (x,y)均补零扩充为P×Q，
P=2N-1;
Q=2N-1.
G(u, v) H (u, v) F (u, v) g ( x, y) : N N

图像进行傅立叶变换，需将其看作周期函数的一个周期；
周期函数进行卷积，为避免周期折叠误差，需对函数进行补零扩展。

5.图像的频域增强及傅里叶变换Word版

5. 图像的频域增强及傅里叶变换傅立叶变换在图像处理中有非常非常的作用。

因为不仅傅立叶分析涉及图像处理的很多方面，傅立叶的改进算法，比如离散余弦变换，gabor与小波在图像处理中也有重要的分量。

印象中，傅立叶变换在图像处理以下几个话题都有重要作用：1.图像增强与图像去噪绝大部分噪音都是图像的高频分量，通过低通滤波器来滤除高频——噪声; 边缘也是图像的高频分量，可以通过添加高频分量来增强原始图像的边缘；2.图像分割之边缘检测提取图像高频分量3.图像特征提取：形状特征：傅里叶描述子纹理特征：直接通过傅里叶系数来计算纹理特征其他特征：将提取的特征值进行傅里叶变换来使特征具有平移、伸缩、旋转不变性4.图像压缩可以直接通过傅里叶系数来压缩数据；常用的离散余弦变换是傅立叶变换的实变换；傅立叶变换傅里叶变换是将时域信号分解为不同频率的正弦信号或余弦函数叠加之和。

连续情况下要求原始信号在一个周期内满足绝对可积条件。

离散情况下，傅里叶变换一定存在。

冈萨雷斯版<图像处理>里面的解释非常形象：一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。

棱镜是可以将光分解为不同颜色的物理仪器，每个成分的颜色由波长（或频率）来决定。

傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。

当我们考虑光时,讨论它的光谱或频率谱。

同样,傅立叶变换使我们能通过频率成分来分析一个函数。

傅立叶变换有很多优良的性质。

比如线性，对称性（可以用在计算信号的傅里叶变换里面）;时移性：函数在时域中的时移，对应于其在频率域中附加产生的相移，而幅度频谱则保持不变；频移性：函数在时域中乘以e jwt，可以使整个频谱搬移w。

这个也叫调制定理，通讯里面信号的频分复用需要用到这个特性（将不同的信号调制到不同的频段上同时传输）；卷积定理：时域卷积等于频域乘积；时域乘积等于频域卷积（附加一个系数）。

（图像处理里面这个是个重点）信号在频率域的表现在频域中，频率越大说明原始信号变化速度越快；频率越小说明原始信号越平缓。

数字图像处理的主要研究内容有哪些

数字图像处理的主要研究内容有哪些？并简要说明。

主要研究内容有：图像增强、图像编码、图像复原、图像分割、图像分类和图像重建。

图像增强用于改善图像视觉质量；图像复原是尽可能地恢复图像本来面目；图像编码是在保证图像质量的前提下压缩数据，使图像便于存储和传输；图像分割就是把图像按其灰度或集合特性分割成区域的过程；图像分类是在将图像经过某些预处理（压缩、增强和复原）后，再将图像中有用物体的特征进行分割，特征提取，进而进行分类；图像重建是指从数据到图像的处理，即输入的是某种数据，而经过处理后得到的结果是图像。

图像可以分为哪几类，常见位图有哪些？图像有许多分类方法，按照图像的动态特性，可以分为静止图像和运动图像；按照图像的色彩，可以分为灰度图像和彩色图像；按照图像的维数，可以分为二维图像、三维图像和多维图像等。

位图通过许多像素点来表示一幅图像，每个像素具有颜色属性和位置属性。

位图分为四种，即二值图像、亮度图像、索引图像和RGB图像。

请用MATLAB程序实现灰度图像camera.jpg的二值化处理，阈值取0.7，并显示原图和处理后的图像。

A=imread('camera.jpg');B=im2bw(A,0.7);subplot(1,2,1),imshow(A);subplot(1,2,2),imshow(B);一帧256灰度级图像由1280X1024个像素构成，那么该帧图像的数据量有多大？数据量为1280X1024X8=10485760bit=1310720Byte=1280KB=1.25MB已知某个像素点p的坐标为（x,y），请指出N4(p)、N D(p)和N8(p)。

N4(p)：（x+1,y），（x-1,y），（x,y+1），（x,y-1）N D(p)：（x+1,y+1）、（x+1,y-1）、（x-1,y+1）、（x-1,y-1）N8(p)：N4(p)+ N D(p)灰度级插值用在什么情况下，有哪些插值处理方法？变换后所产生的图像中的像素在原图像中没有相对应的像素点时，就需要进行灰度级的插值运算，此时可以采用不同复杂程度的线性插值法填充放大后多出来的相关像素点的灰度值。

第五章图像增强课件

数字图像的直方图
其中
5.3.1 直方图基本概念
原始图像
直方图
5.3.1 直方图基本概念
不同图像内容具有相同直方图的实例。
由灰度直方图的定义可知，数字图像的灰度直方图具有以下几个特性：
（1）直方图的位置缺失性。
灰度直方图仅仅反映了数字图像中各灰度级出现频数的分布，但对那些
具有同一灰度值的像素在图像中的空间位置一无所知，即灰度直方图具有位
（1）空间域法。
是指在空间域中，直接对图像进行各种线性或非线性运算，对图像的
像素灰度值作增强处理。
（2）频域法。
是在图像的变换域中，把图像看成一种二维信号，对其进行基于二维
傅立叶变换的信号增强。
二、图像增强分类
点运算
空域法
模板处理
点运算是作用于单个像素的空间域处理方法，包括图像灰度变换、直
方图修正、伪彩色增强等技术；
当邻域为单个像素，即1×1时，输出仅仅依赖 f在(x,y) 处的像素灰度
值，此时的处理方式通常称为点处理。
5.2.2 线性灰度变换
线性变换的表达式
5.2.2 线性灰度变换
[0-32]范围
[0-128]范围
[0-64]范围
[0-256]范围
5.2.2 线性灰度变换
灰度拉伸的范围越小，像素间的灰度值越相近，图像的表现力越差。
（1）在 0 ≤ ≤ 1
区间内， T[r] 为单值单调递增函数；
（2）对于 0 ≤ ≤ 1 ，对应有0≤s=T[r]≤1 。
变换函数的求解：
5.3.2 直方图均衡化
对于数字图像，其灰度 k 出现的概率可近似表示：
5.3.2 直方图均衡化
利用直方图均衡进行图像增强的过程可分成以下几个步骤：

遥感影像空间增强与傅立叶变换滤波处理

研究区地形地貌特征：发现平坦地区在DEM 图像呈现高亮，呈树枝状的是山脊。

二、完成如下卷积增强运算，比较变换前后影像中地形/地貌信息上的差异：高通滤波：工具：Toolbox—Filter—Convolutions and Morphology；参数：Convolutions 选择卷积类型为High Pass(高通滤波)；Kernel Size 设置卷积核大；（ENVI 默认卷积核大小以奇数来表示）；Image Add Back代表影像加回值。

(1)选择Kernel Size设置默认的3*3；Image Add Back设置默认值0：浮雕效果更佳显著，在影像中可以更加清晰地看见河流与沟谷以及山体褶皱。

(4)选择Kernel Size设置默认的3*3；Image Add Back设置默认值30%：拉普拉斯变换：工具：Toolbox—Filter—Convolutions and Morphology；Convolutions 选择卷积类型为Laplacian (拉普拉斯变换)；(1)Kernel Size设置默认的3*3, Image Add Back设置默认值0：影像立体感大大增强，浮雕效果增强，对沟谷的表现力增强。

选择Kernel Size设置默认的3*3；Image Add Back设置默认值30%：影像立体感明显增强，呈现较强的浮雕效果。

对于山体表现效果极佳，能清晰的反映出山体边缘、沟谷及褶皱。

高斯高通滤波：Toolbox —Filter—Convolutions and Morphology；Convolutions 选择卷积类型为Gaussian High Pass；(1)Kernel Size（卷积核大小）设置为3*3, Image Add Back(影像加回值)设置默认值0%：此操作后，影像整体无值呈现白色，在部分地势变化起伏较大的高频区域，影像中呈现不明显的表现。

因此，此操作对于突出体现影像中高频区域有较好的效果。

(图像增强技术)第一章图像的基础知识

能够覆盖更广泛的颜色空间，适用于印刷和打印行业。
3
CMYK色彩模型的局限性
颜色转换较为复杂，需要专业知识和技能。
色彩空间与色域
80%
色彩空间的概念
色彩空间是指颜色的表示范围或范围，不同的色彩空间对应不同的应用场景。
100%
色域的概念
色域是指一种特定的颜色集合或颜色的范围，不同的显示设备或打印设备具有不同的色域。
图像增强技术：第一章图像的基础知识
目
CONTENCT
录
• 图像的基本概念 • 图像的色彩理论 • 图像的获取与显示 • 图像的质量评价 • 图像的压缩与编码 • 图像增强技术的发展与应用
01
图像的基本概念
图像的定义与分类
总结词
了解图像的定义和分类是图像增强技术的基础。
详细描述
图像是客观景物或场景在某种介质上的再现，可以是照片、绘画、电视画面等。根据不同的分类标准，图像可以分为多种类型，如灰度图像、彩色图像、静态图像和动态图像等。
详细描述
像素是构成图像的最小单位，每个像素包含了颜色和亮度信息。分辨率是指图像中像素的数量，通常以像素数量或显示设备的物理尺寸来表示。分辨率越高，图像的细节表现越丰富，但同时也需要Hale Waihona Puke 多的存储空间和计算资源。02
图像的色彩理论
色彩的基本概念
色彩的本质
色彩是光的一种表现形式，是由物体反射或发射出来的光的特定波长所形成的。
传输效率
大尺寸图像需要更长的时间来传输，影响用户体验。
计算资源
处理大尺寸图像需要更多的计算资源，增加处理成本。
无损压缩与有损压缩
无损压缩
无损压缩算法能够完全还原原始图像，不会造成任何图像信息的损失。常见的无损压缩算法有哈夫曼编码、 LZ77等。

图像处理的基础知识

医学影像分割
利用图像分割技术，将医学图像中的感兴趣区域与背景或其他组织进行分离，为后续分析和诊断提供基础。
遥感影像处理案例分析
遥感影像预处理
对遥感影像进行辐射定标、大气校正等预处理，消除成像过程中的误差和干扰。
遥感影像分类
利用分类算法对遥感影像中的地物进行分类和识别，提取感兴趣的地物信息。
图像压缩编码标准简介（JPEG、MPEG等）
JPEG标准
采用DCT变换和哈夫曼编码等技术，适用于静态图像的压缩编码。
MPEG标准
针对动态图像压缩编码的标准，采用运动补偿、DCT变换和变长编码等技术。
其他标准
如H.264、AV1等，采用更先进的压缩编码技术，提高压缩效率和图像质量。
无损压缩与有损压缩比较
常见频率域滤波方法
低通滤波、高通滤波、带通滤波等。
应用场景
适用于图像去噪、边缘增强、特征提取等任务。
对比度拉伸与压缩技术
01
02
03
04
对比度拉伸原理
通过扩展图像中感兴趣区域的灰度级范围来增强图像对比度
。
对比度压缩原理
通过减小图像中灰度级的范围来压缩图像对比度。
实现方法
线性拉伸与压缩、分段线性拉伸与压缩、非线性拉伸与压缩
空间域滤波方法介绍
80%
空间域滤波原理
直接在图像空间进行像素操作，通过模板卷积实现图像滤波。
100%
常见空间域滤波方法
均值滤波、中值滤波、高斯滤波等。
80%
应用场景
适用于去除噪声、平滑图像等任务。
频率域滤波方法探讨
频率域滤波原理
将图像从空间域转换到频率域，在频率域进行滤波操作后再转换回空间域。

“数字图像处理算法基础”课程标准

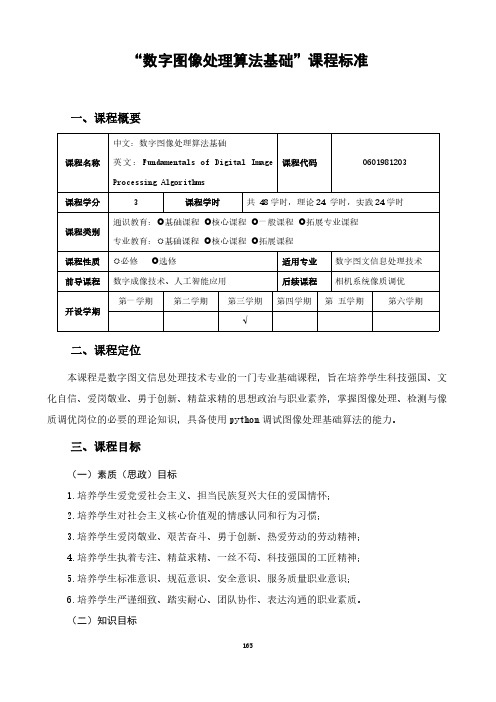
“数字图像处理算法基础”课程标准一、课程概要课程名称中文：数字图像处理算法基础英文：Fundamentals of Digital ImageProcessing Algorithms课程代码0601981203课程学分3课程学时共48学时，理论24学时，实践24学时课程类别通识教育：基础课程核心课程一般课程拓展专业课程专业教育：基础课程核心课程拓展课程课程性质必修选修适用专业数字图文信息处理技术前导课程数字成像技术、人工智能应用后续课程相机系统像质调优开设学期第一学期第二学期第三学期第四学期第五学期第六学期√二、课程定位本课程是数字图文信息处理技术专业的一门专业基础课程，旨在培养学生科技强国、文化自信、爱岗敬业、勇于创新、精益求精的思想政治与职业素养，掌握图像处理、检测与像质调优岗位的必要的理论知识，具备使用python调试图像处理基础算法的能力。

三、课程目标（一）素质（思政）目标1.培养学生爱党爱社会主义、担当民族复兴大任的爱国情怀；2.培养学生对社会主义核心价值观的情感认同和行为习惯；3.培养学生爱岗敬业、艰苦奋斗、勇于创新、热爱劳动的劳动精神；4.培养学生执着专注、精益求精、一丝不苟、科技强国的工匠精神；5.培养学生标准意识、规范意识、安全意识、服务质量职业意识；6.培养学生严谨细致、踏实耐心、团队协作、表达沟通的职业素质。

（二）知识目标1.掌握数字成像技术基本原理；2.掌握python语言的编程语法特点；3.掌握数字图像特征；4.掌握图像基本运算规则；5.掌握形态学图像处理原理；6.掌握图像滤波和应用；7.掌握图像增强原理。

（三）能力目标1.具备编程实现简单的图像处理算法能力；2.具备pycharm编程软件环境配置能力；3.具备基础图像处理算法调试能力；4.具有较强的思考、分析和解决问题的能力；5.具有跟踪新技术和科技文献搜索阅读能力；6.具有编程技术的学习和应用能力。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8
一维傅立叶变换举例
方波信号：
A f ( x) 0
X /2 x X /2 其他
振幅图形
经过傅立叶变换：
9
一维离散傅立叶变换一维离散傅立叶变换公式为：变换因子
1 F ( u) N
逆变换为：
N 1 x ห้องสมุดไป่ตู้0
f ( x )e
j
j
2ux N
u 0,1,, N 1
E(u, v) [R2 (u, v) I 2 (u, v)]
] R(u, v)
11
二维傅立叶变换举例对于二维方波信号
傅立叶变换为：
幅度：
12
二维离散傅立叶变换(DFT) 对于二维傅立叶变换，其离散形式为：
变换因子
ux vy j 2 M N

线性位移不变系统的输出等于系统的输入和系统脉冲响应（点扩散函数）的卷积

傅立叶积分的定义调谐信号：
e
jt
cos( t ) j si n( t )
其中j2=-1 变换因子
傅立叶积分：
H( f )

h( t )e j 2ft dt
其中t代表时间，f代表频率
u=0,1,2,….N/4-1
24
例如，N=8，求F(1)?
1 1 F (1) [ F偶 (1) F奇 (1)W8 ] 2 1 1 1 1 1 [ [ F偶偶 (1) F偶奇 (1)W4 ] W8 [ F奇偶 (1) F奇奇 (1)W41 ]] 2 2 2 1 [ f (0) f (2)W82 f (4)W84 f (6)W86 4 1 3 5 7 f (1)W8 f (3)W8 f (5)W8 f (7)W8 ]
f ( x) exp( j 2 xu / N )
N 1 u 0
F ( u) e xp(j 2ux / N )
j 2 ux 1 N 1 N F ( u) f ( x )e N x 0 1 N 1 ux f ( x)WN N x 0
记W e
ux N
则有：
20
N 1
j 2ux / N
j 2vy / N 1 1 F ( u , v ) e F { F u v [ F ( u, v )]}
14
4、平移性质
空间位移性： f ( x x0 , y y0 ) F (u, v ) exp[ j 2 (ux0 / M vy0 / N )] 频率位移性质：
1 F (u , v) MN
逆变换为：
M 1 N 1 x 0 y 0
f ( x, y)e
f ( x, y) F (u, v)e
u 0 v 0
M 1 N 1
ux vy j 2 M N
13
二维离散傅立叶变换的性质 1. 线性性质：
f ( x, y ) f ( x M , y ) f ( x, y N ) f ( x M , y N )
共轭对称性： F * (u,v ) F (u, v )
F (u, v ) F (u,v )
16
周期性的应用图形的频谱分析和显示
7、旋转不变性以极坐标表示x, y, u, v：
f ( x, y)e j 2 ( u0 xv0 y ) / N F (u u0 , v v0 )
图像中心化把图像进行傅立叶变换后，往往要把中心移到 u0=v0=N/2的位置上
j 2 (u0 x v0 y )/ N j ( x y ) x y
e
e
(1)
f ( x, y )(1)
x r cos u w cos
y r si n v w si n
f(x,y)和F(u,v)可由f(r,θ)和F(w,φ)来表示，代入傅立叶变换的公式，可以得到：
f ( r , 0 ) F ( , 0 )
17
旋转不变性的例子
8、平均值平均值定义：
1 f ( x, y ) 2 N
N 1 N 1 x 0 y 0
f ( x, y )
N 1 N 1 x 0 y 0
由傅立叶变换定义：
1 F (0,0) 2 N
f ( x, y )
18
因此，f(x,y)的平均值与傅立叶变换的关系为：
F (0,0) f ( x, y)
• 快速傅立叶变换(FFT)
比用定义式(DFT)计算傅立叶变换快得多.
要求：
参与傅立叶变换的图像像素数N为２的整数次幂，即 N=2n
19
快速傅立叶变换（FFT）的推导过程
离散正变换：离散反变换：
1 F (u ) N
1 f ( x) N
j 2 ux N
变换因子

x 0
N 1
W
ux 2 N 2
,
WN
N
2
1
2 ux ux WN WN
2
u N / 2 u N /2 u WN WN WN W N
21
设N=2m，f(x)的定义域分为偶数部分和奇数部分，即f (2x) 和f (2x+1) N 1
F (u ) 1 ux f ( x ) W N N x 0
N 1 2
12 2N 12 2 N

x 0
f (2 x)W
2ux N
2 N 2 N
N 1 2

x 0 x 0
f (2 x 1)W
u (2 x 1) N

N 1 2

x 0
f (2 x)W
ux N 2
N 1 2

f (2 x 1)W W
23
用这种方法继续分解，
1 u [ F偶偶 ( u) W N / 2 F偶奇 ( u)] 2 1 u F偶 ( u N / 4) [ F偶偶( u) W N / 2 F偶奇 ( u)] 2 F偶 ( u)
1 u F奇 ( u) [ F奇偶( u) W N / 2 F奇奇 ( u)] 2
逆变换： f ( x, y ) 复数形式：振幅：
F ( x, y) exp[j 2π(ux vy)]dudv
2 2 1 2
F(u,v)=R(u,v)+jI(u,v)
F (u, v) R (u, v) I (u, v)
相位：
能量：
(u, v) arct g[ I (u, v)

虚部： I (u) f ( x)sin(2 ux)dx
振幅： F (u ) R (u ) I (u )
2 2 1 2

相位： (u ) arct g[ I (u ) / R(u )]
2 2 E ( u ) [ R ( u ) I (u)] 能量：
F奇 ( u N / 4)
u=0,1,2,….N/4-1
1 u [ F奇偶( u) W N / 2 F奇奇 ( u)] 2
式中：
1 N / 4 1 F奇奇( u) f (4 x 3)W ux N / 4 N / 4 x 0
1 N / 4 1 F偶偶( u) f (4 x )W ux N / 4 N / 4 x 0 1 N / 4 1 F偶奇( u) f (4 x 2)W ux N / 4 N / 4 x 0 1 N / 4 1 F奇偶( u) f (4 x 1)W ux N / 4 N / 4 x 0
a1 f1 ( x, y) a2 f 2 ( x, y) a1F1 (u, v ) a2 F2 (u, v )
1 u v F , 2. 比例性质： f (ax, by) ab a b
3、可分离性
1 F (u , v) N
j 2 x / N e x 0
7

傅立叶变换的定义(一维) f(x)为连续可积函数，其傅立叶变换定义为：
F ( u)

f ( x )e j 2ux dx

其反变换为： f ( x)

F (u)e j 2 ux du
复数形式：F (u ) R(u ) jI (u ) 实部： R(u) f ( x) cos(2 ux)dx
25
奇偶分组和比特倒序
n2 n1 n0
x (000) n0 =0 x (100) x (010) x (110) x (001) x (011) x (101) x (111) n0 =1
单位园表示（N取不同的值）：
W43
W85 W86 W87 W80 W83 W81
W42
W40
W84
W41 N=4 时 W 的值
W82
N=8 时 W 的值
WNux的性质：
(1) 对称性： (2) 周期性：
W (3) 可分性：
ux N
u ( N x) ux ux * WN WN (WN ) ux (u N ) x u ( N x) WN WN WN
数字图像处理
本章包含的主要内容
傅立叶变换卷积和卷积定理
离散图像变换的一般表达式
其他形式的图像变换
2
问题1：傅立叶变换
•
空间域/灰度
•
频率域/幅值与频率
4
• 傅立叶变换的预备知识二维线性不变系统
满足线性和齐次性条件的系统称为二维线性系统线性
T[ f1 ( x, y) f2 ( x, y)] T[ f1 ( x, y)] T[ f2 ( x, y)]