树和二叉树2
第7章-树和二叉树第2讲-二叉树的概念

第一层
树的特 点?
第二层 第三层 第四层
复习:二、树的基本术语
1.结点A、D的度?树的度? 2;3;3; 2.根结点?分支结点?叶子结点? A;BCDE;GHIJF;
在二叉链中,空指针的个数?
b A
B∧
C
∧D
∧E∧
∧F∧
∧G∧
n个结点 2n个指针域 分支数为n-1 非空指针域有n-1个 空指针域个数 = 2n-(n-1) = n+1
n=7 空指针域个数=8
39/10
40/10
二叉树
当n=3,结果为ห้องสมุดไป่ตู้。
第n个Catalan数
41/23
有n个结点并且高度为n的不同形态的二叉树个数是多少? 该二叉树:有n层,每层一个结点,该结点可以
43/23
结点个数为n,树形可以唯一确定 叶子结点个数为n0,树形不能唯一确定 n为奇数时,n1=0; n为偶数时,n1=1。 n0=n2+1 高度h= log2(n+1),是n个结点高度最小的二叉树
44/23
含有60个叶子结点的二叉树的最小高度是多少?
在该二叉树中,n0=60,n2=n0-1=59,n=n0+n1+n2=119+n1。 当n1=0且为完全二叉树时高度最小。 此时高度h=log2(n+1)= log2120=7。
作为双亲结点的左孩子,也可以作为右孩子 这样的二叉树的个数=1×2×…×2=2n-1。
例如,当n=3时有22=4个这样的二叉树。
二叉树,树,森林遍历之间的对应关系

二叉树,树,森林遍历之间的对应关系一、引言在计算机科学中,数据结构是非常重要的知识点之一。
而树这一数据结构,作为基础的数据结构之一,在软件开发中有着广泛的应用。
本文将重点探讨二叉树、树和森林遍历之间的对应关系,帮助读者更加全面地理解这些概念。
二、二叉树1. 二叉树的定义二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以为空,也可以是一棵空树。
2. 二叉树的遍历在二叉树中,有三种常见的遍历方式,分别是前序遍历、中序遍历和后序遍历。
在前序遍历中,节点的访问顺序是根节点、左子树、右子树;在中序遍历中,节点的访问顺序是左子树、根节点、右子树;在后序遍历中,节点的访问顺序是左子树、右子树、根节点。
3. 二叉树的应用二叉树在计算机科学领域有着广泛的应用,例如用于构建文件系统、在数据库中存储有序数据、实现算法中的搜索和排序等。
掌握二叉树的遍历方式对于理解这些应用场景非常重要。
三、树1. 树的定义树是一种抽象数据类型,由n(n>0)个节点组成一个具有层次关系的集合。
树的特点是每个节点都有零个或多个子节点,而这些子节点又构成了一颗子树。
树中最顶层的节点称为根节点。
2. 树的遍历树的遍历方式有先根遍历、后根遍历和层次遍历。
在先根遍历中,节点的访问顺序是根节点、子树1、子树2...;在后根遍历中,节点的访问顺序是子树1、子树2...,根节点;在层次遍历中,节点的访问顺序是从上到下、从左到右依次访问每个节点。
3. 树的应用树广泛用于分层数据的表示和操作,例如在计算机网络中的路由算法、在操作系统中的文件系统、在程序设计中的树形结构等。
树的遍历方式对于处理这些应用来说至关重要。
四、森林1. 森林的定义森林是n(n>=0)棵互不相交的树的集合。
每棵树都是一颗独立的树,不存在交集。
2. 森林的遍历森林的遍历方式是树的遍历方式的超集,对森林进行遍历就是对每棵树进行遍历的集合。
3. 森林的应用森林在实际编程中经常用于解决多个独立树结构的问题,例如在数据库中对多个表进行操作、在图像处理中对多个图形进行处理等。
说明树与二叉树的主要区别

说明树与二叉树的主要区别摘要:一、引言二、树与二叉树的定义及基本概念1.树的定义及特点2.二叉树的定义及特点三、树与二叉树的主要区别1.节点数量的限定2.节点连接方式的差异3.遍历方式的差异四、实例分析1.满二叉树与满树的对比2.完全二叉树与完全树的对比五、总结与展望正文:一、引言在计算机科学中,树和二叉树是广泛应用于数据结构和组织的重要概念。
尽管它们在某些方面具有相似之处,但它们之间仍存在显著差异。
本文将详细介绍树与二叉树的主要区别,以帮助读者更好地理解这两种数据结构。
二、树与二叉树的定义及基本概念1.树的定义及特点树(Tree)是一种非线性的数据结构,它由若干个节点组成,这些节点通过边连接在一起。
树中最顶层的节点称为根节点,最底层的节点称为叶节点,中间层节点称为内部节点。
树具有以下特点:(1)只有一个根节点。
(2)每个节点最多有若干个子节点,最少有一个子节点(除了根节点)。
(3)节点之间的连接顺序呈层次结构。
2.二叉树的定义及特点二叉树(Binary Tree)是一种特殊的树结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。
根据这个定义,二叉树可以进一步细分为满二叉树、完全二叉树和不完全二叉树等。
二叉树具有以下特点:(1)每个节点最多有两个子节点。
(2)节点之间的连接呈二叉树结构。
三、树与二叉树的主要区别1.节点数量的限定树中每个节点可以有任意数量的子节点,而二叉树中每个节点最多有两个子节点。
这是树与二叉树最明显的区别。
2.节点连接方式的差异树中节点之间的连接顺序呈层次结构,呈放射状分布。
而二叉树中节点之间的连接呈二叉树结构,呈线性分布。
3.遍历方式的差异树的遍历方式有前序遍历、中序遍历和后序遍历等。
二叉树的遍历方式有前序遍历、中序遍历和后序遍历等。
不过,二叉树的遍历方式通常与树的遍历方式有所不同。
四、实例分析1.满二叉树与满树的对比满二叉树是一种特殊的二叉树,其每个节点都有两个子节点,且所有叶子节点都在同一层。
树和二叉树的知识点总结

树和二叉树的知识点总结一、树的基本概念1. 树的定义:树是一种非线性数据结构,由 n(n>=1)个结点组成的有限集合。
对于每个非终端节点,都有一个被称为根的结点,且除根节点外,其他结点可以分为 m(m>=0)个互不相交的子集合,而每个子集合本身又是一个树。
2. 树的基本特点:树是一种分层数据的抽象模型,具有层级关系的数据结构。
树的结点包括根结点、子节点、叶子结点、父节点等。
3. 树的术语解释:树的根节点是树的顶端结点,没有父节点;子节点是一个结点向下连接的结点;叶子结点是没有子节点的结点;父节点是有一个或多个子节点的结点。
二、树的分类1. 二叉树:一种特殊的树,每个结点最多有两个子结点,分别为左子结点和右子结点。
二叉树的子树有左子树和右子树,必须遵循左子树 < 根节点 < 右子树的顺序。
2. 平衡树:每个结点的左子树和右子树的高度之差不能超过1的二叉树。
3. 满二叉树:每个结点要么没有子节点,要么有两个子节点的二叉树。
4. 完全二叉树:除了最底层,所有层的结点数都达到最大,并且最底层的结点都依次从左到右排列。
三、二叉树的基本概念1. 二叉树的特点:每个结点最多有两个子结点,分别为左子结点和右子结点。
二叉树的子树都遵循左子树 < 根节点 < 右子树的顺序。
2. 二叉树的遍历:分为前序遍历、中序遍历和后序遍历。
前序遍历先访问根节点,再递归左右子树;中序遍历先递归左子树,再访问根节点,最后递归右子树;后序遍历先递归左右子树,最后访问根节点。
3. 二叉树的存储:二叉树的存储方式可以采用链式存储和顺序存储。
链式存储是通过结点间的指针链接,顺序存储是通过数组或列表进行存储。
四、二叉树的应用1. 二叉搜索树:是一种特殊的二叉树结构,对于任意节点,其左子树上的结点值都小于该节点的值,右子树上的结点值都大于该节点的值。
2. 堆:是一种特殊的完全二叉树,分为最大堆和最小堆。
最大堆的每个结点的值都大于或等于其子节点的值,最小堆的每个结点的值都小于或等于其子节点的值。
第7章树和二叉树(2)-数据结构教程(Java语言描述)-李春葆-清华大学出版社

二叉树也称为二分树,它是有限的结点集合,这个集合或者是空,或者由 一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。 二叉树中许多概念与树中的概念相同。 在含n个结点的二叉树中,所有结点的度小于等于2,通常用n0表示叶子结 点个数,n1表示单分支结点个数,n2表示双分支结与度为2的树是不同的。
度为2的树至少有3个结点,而二叉树的结点数可以为0。 度为2的树不区分子树的次序,而二叉树中的每个结点最多有 两个孩子结点,且必须要区分左右子树,即使在结点只有一棵 子树的情况下也要明确指出该子树是左子树还是右子树。
2/35
归纳起来,二叉树的5种形态:
Ø
4/35
3. 满二叉树和完全二叉树
在一棵二叉树中,如果所有分支结点都有左孩子结点和右孩子结点,并且 叶子结点都集中在二叉树的最下一层,这样的二叉树称为满二叉树。
可以对满二叉树的结点进行层序编号,约定编号从树根为1开始,按照层 数从小到大、同一层从左到右的次序进行。
满二叉树也可以从结点个数和树高度之间的关系来定义,即一棵高度为h 且有2h-1个结点的二叉树称为满二叉树。
R={r} r={<ai,aj> | ai,aj∈D, 1≤i,j≤n,当n=0时,称为空二叉树;否则其中
有一个根结点,其他结点构成根结点的互不相交的左、右子树,该 左、右两棵子树也是二叉树 } 基本运算: void CreateBTree(string str):根据二叉树的括号表示串建立其存储结构。 String toString():返回由二叉树树转换的括号表示串。 BTNode FindNode(x):在二叉树中查找值为x的结点。 int Height():求二叉树的高度。 … }
5
E
树和二叉树的基本知识

树和二叉树的基本知识Jsoi2006春季函授 B层次讲义(3)常州市第一中学林厚从 1/53树和二叉树的基本知识树是一种非线性的数据结构,用它能很好地描述有分支和层次特性的数据集合。
树型结构在现实世界中广泛存在,如把一个家族看作为一棵树,树中的结点为家族成员的姓名及相关信息,树中的关系为父子关系,即父亲是儿子的前驱,儿子是父亲的后继;把一个国家或一个地区的各级行政区划分看作为一棵树,树中的结点为行政区的名称及相关信息,树中的关系为上下级关系,如一个城市包含有若干个区,每个区又包含有若干个街道,每个街道又包含有若干个居委会;把一本书的结构看作是一棵树,树中的结点为书、章、节的名称及相关信息,树中的关系为包含关系。
树在计算机领域中也有广泛应用,如在编译系统中,用树表示源程序的语法结构;在数据库系统中,树型结构是数据库层次模型的基础,也是各种索引和目录的主要组织形式。
在许多算法中,常用树型结构描述问题的求解过程、所有解的状态和求解的对策等。
在树型结构中,二叉树是最常用的结构,它的分支个数确定,又可以为空,具有良好的递归特性,特别适宜于程序设计,因此我们常常将一般树型结构转换成二叉树进行处理。
第一节树一、树的定义一棵树(tree)是由n(n>0)个元素组成的有限集合,其中:1.每个元素称为结点(node);2.有一个特定的结点,称为根结点或树根(root);3.除根结点外,其余结点被分成m(m>=0)个互不相交的有限集合T0,T1,T2,……Tm-1,而每一个子集Ti又都是一棵树(称为原树的子树subtree)。
图1图1就是一棵典型的树结构。
从树的定义可以看出:1.树是递归定义的,这就决定了树的操作和应用大都是采用递归思想来解决;2.一棵树中至少有1个结点,这个结点就是根结点,如上图中的结点1;3.只有根结点没有前趋结点,其余每个结点都有唯一的一个前趋结点;4.所有结点都可以有0或多个后继结点;二、树的基本概念下面以图1为例给出树结构中的一些基本概念:1.一个结点的子树个数,称为这个结点的度(degree),如结点1的度为3,结点3的度为0。
计算机学科专业基础综合数据结构-树与二叉树(二)

计算机学科专业基础综合数据结构-树与二叉树(二)(总分:100.00,做题时间:90分钟)一、{{B}}单项选择题{{/B}}(总题数:44,分数:44.00)1.在下面关于树的相关概念的叙述中,正确的是______。
∙ A.只有一个结点的二叉树的度为1∙ B.二叉树的度一定为2∙ C.二叉树的左右子树可任意交换∙ D.深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树(分数:1.00)A.B.C.D. √解析:只有一个结点的二叉树的度为零。
二叉树的度可以为0、1、2;二叉树的左右子树不能任意交换。
2.已知一算术表达式的中缀形式为A+B+C-D/E,后缀形式为ABC*+DE/-,其前缀形式为______。
∙ A.-A+B*C/DE∙ B.-A+B*CD/E∙ C.-+*ABC/DE∙ D.-+A*BC/DE(分数:1.00)A.B.C.D. √解析:根据题目给出的中缀和后缀表达式可以得到其算术表达式为:(A+B*C)-D/E,前缀表达式:-+A*BC/DE。
3.算术表达式a+b*(c+d/e)转为后缀表达式后为______。
∙ A.ab+cde/*∙ B.abcde/+*+∙ C.abcde/*++∙ D.abcde*/++(分数:1.00)A.B. √C.D.解析:根据表达式a+b*(c+d/e)可知其后缀表达式为abcde/+*+。
4.某二叉树的先序遍历序列为IJKLMNO,中序遍历序列为JLKINMO,则后序遍历序列是______。
∙ A.JLKMNOI∙ B.LKNJOMI∙ C.LKJNOMI∙ D.LKNOJMI(分数:1.00)A.B.C. √D.解析:由先序和中序遍历序列确定一棵二叉树,再给出这棵二叉树的后序遍历序列。
[*] 由此图可以确认后序遍历的序列为LKJNOMI。
5.设森林F对应的二叉树为B,它有m个结点,B的根为P,P的右子树结点个数为n,森林F中第一棵树的结点个数是______。
计算机专业基础综合数据结构(树与二叉树)模拟试卷2(题后含答案及解析)

计算机专业基础综合数据结构(树与二叉树)模拟试卷2(题后含答案及解析)题型有:1. 单项选择题 2. 综合应用题单项选择题1-40小题,每小题2分,共80分。
下列每题给出的四个选项中,只有一个选项是最符合题目要求的。
1.设树T的度为4,其中度为1、2、3和4的结点个数分别为4、1、1、1,则T中的叶子数为( )。
A.10B.11C.9D.7正确答案:D解析:根据题中条件可知,1×4+2×1+3+4+1=4+1+1+1+n0,由此可以得出:n0=1×4+2×1+3+4+1一(4+1+1+1)=14—7=7. 知识模块:数据结构2.用下列元素序列(22,8,62,35,48)构造平衡二叉树,当插入( )时,会出现不平衡的现象。
A.22B.35C.48D.62正确答案:C解析:由题中所给的结点序列构造二叉排序树的过程如下图:当插入48后,首次出现不平衡子树,虚线框内即为最小不平衡子树。
知识模块:数据结构3.下面的算法实现了将二叉树中每一个结点的左右子树互换。
addQ(Q,bt)为进队的函数,delQ(Q)为出队的函数,empty(Q)为判别队列是否为空的函数,空白处应填的内容是( )。
typedef struct node{ int data;struct node*lchild,*rchild;}btnode;void exchange(btnode*bt){ btnode*p,*q;if(bt){ addQ(Q,bt);while(!EMPTY(Q)){ p=delQ(Q);q=p->rchild;p一>rchild=p一>lchild;( (1) )=q;if(p->lchild) ( (2) );if(p->rchild)addQ(Q,p->rchild);} }} A.p->lchild,delQ(Q,p一>lchild)B.p->rchild,delQ(Q,p->lchild)C.p->lchild,addQ(Q,p->lchild)D.p->rchild,addQ(Q,p->lchild)正确答案:C 涉及知识点:数据结构4.已知有一棵二叉树,其高度为n,并且有且只有n个结点,那么二叉树的树形有( )种。
树和二叉树的计算公式

树和二叉树的计算公式
树和二叉树是计算机科学中重要的数据结构,它们可以用于各种算法和数据处理应用。
在计算树和二叉树的性质和操作时,需要使用一些计算公式。
一、树的计算公式
1. 节点总数公式:假设一棵树有n个节点,那么它的节点总数
为n=1+r1+r2+...+rk,其中r1、r2、...、rk分别表示每个节点的
子节点数。
2. 叶子节点数公式:一棵树的叶子节点数等于每个非叶节点子
节点数之和加1,即l=r1+r2+...+rk+1。
3. 深度公式:一棵树的深度为从根节点到最深叶子节点的路径
长度,可以用递归的方式计算:d(T)=max{d(T1),d(T2),...,d(Tk)}+1,其中T1、T2、...、Tk是根节点的子树,d(Ti)表示第i个子树的深度。
二、二叉树的计算公式
1. 节点总数公式:假设一棵二叉树有n个节点,那么它的节点
总数为n=2^h-1,其中h为树的高度。
2. 叶子节点数公式:一棵二叉树的叶子节点数等于度数为2的
节点数加1,即l=n/2+1。
3. 深度公式:一棵二叉树的深度为从根节点到最深叶子节点的
路径长度,可以用递归的方式计算:d(T)=max{d(T1),d(T2)}+1,其
中T1、T2是根节点的左右子树,d(Ti)表示第i个子树的深度。
以上是树和二叉树的一些常用计算公式,可以用于分析和设计算法,帮助开发人员更好地理解和应用这些数据结构。
第6章树和二叉树(2)培训讲学

第6章树和二叉树(2)第六章树和二叉树一、选择题1.算术表达式a+b*(c+d/e)转为后缀表达式后为()A.ab+cde/* B.abcde/+*+ C.abcde/*++ D.abcde*/++2. 设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是()A.m-n B.m-n-1 C.n+1 D.条件不足,无法确定3.若度为m的哈夫曼树中,其叶结点个数为n,则非叶结点的个数为()。
A.n-1 B.⎣n/m⎦-1 C.⎡(n-1)/(m-1)⎤ D.⎡n/(m-1)⎤-1E.⎡(n+1)/(m+1)⎤-14.深度为h的满m叉树的第k层有()个结点。
(1=<k=<h)A.m k-1 B.m k-1 C.m h-1 D.m h-15. 若X是二叉中序线索树中一个有左孩子的结点,且X不为根,则x的前驱为( )A.X的双亲B.X的右子树中最左的结点C.X的左子树中最右结点D.X的左子树中最右叶结点6. 引入二叉线索树的目的是()A.加快查找结点的前驱或后继的速度 B.为了能在二叉树中方便的进行插入与删除C.为了能方便的找到双亲 D.使二叉树的遍历结果唯一7.由3 个结点可以构造出多少种不同的二叉树?()A.2 B.3 C.4 D.58.下述编码中哪一个不是前缀码()。
A.(00,01,10,11) B.(0,1,00,11) C.(0,10,110,111)D.(1,01,000,001)二、判断题1. 给定一棵树,可以找到唯一的一棵二叉树与之对应。
2.将一棵树转成二叉树,根结点没有左子树;3. 在中序线索二叉树中,每一非空的线索均指向其祖先结点。
4. 一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和。
5.当一棵具有n个叶子结点的二叉树的WPL值为最小时,称其树为Huffman树,且其二叉树的形状必是唯一的。
三、填空题1.一棵树T中,包括一个度为1的结点,两个度为2的结点,三个度为3的结点,四个度为4的结点和若干叶子结点,则T的叶结点数为___ ___。
数据结构树和二叉树知识点总结

数据结构树和二叉树知识点总结
1.树的概念:树是一种非线性的数据结构,由节点和边构成,每个节点只能有一个父节点,但可以有多个子节点。
2. 二叉树的概念:二叉树是一种特殊的树结构,每个节点最多只有两个子节点,一个是左子节点,一个是右子节点。
3. 二叉树的遍历:二叉树的遍历分为前序遍历、中序遍历和后序遍历三种方式。
前序遍历是先访问根节点,再访问左子树,最后访问右子树;中序遍历是先访问左子树,再访问根节点,最后访问右子树;后序遍历是先访问左子树,再访问右子树,最后访问根节点。
4. 二叉搜索树:二叉搜索树是一种特殊的二叉树,它满足左子树中所有节点的值均小于根节点的值,右子树中所有节点的值均大于根节点的值。
因此,二叉搜索树的中序遍历是一个有序序列。
5. 平衡二叉树:平衡二叉树是一种特殊的二叉搜索树,它的左子树和右子树的高度差不超过1。
平衡二叉树的插入和删除操作可以保证树的平衡性,从而提高树的查询效率。
6. 堆:堆是一种特殊的树结构,它分为最大堆和最小堆两种。
最大堆的每个节点的值都大于等于其子节点的值,最小堆的每个节点的值都小于等于其子节点的值。
堆常用于排序和优先队列。
7. Trie树:Trie树是一种特殊的树结构,它用于字符串的匹配和检索。
Trie树的每个节点代表一个字符串的前缀,从根节点到叶子节点的路径组成一个完整的字符串。
以上是数据结构树和二叉树的一些基本知识点总结,对于深入学
习数据结构和算法有很大的帮助。
第四章二叉树_2

9
二叉搜索树插入操作
利用插入操作可以构造一棵二叉搜索树 首先给出结点序列: 首先给出结点序列 13、8、23、5、18、37 、 、 、 、 、
Φ13
8 5 5 18
83 18 5 2 37 23 37 37 18
10
template<class T> void BST<T>::insertNodeHelper(const T& el) { BSTNode<T> *p = root, *prev = 0; while (p != 0) { prev = p; if( p->data < el ) p = p->rchild; else p = p->lchild; } if( root == 0 ) root = new BSTNode<T>(el); else if( prev->data < el ) p = prev->rchild = new BSTNode<T>(el); else p = prev->lchild = new BSTNode<T>(el); } //find a place for inserting new node; //插入节点 插入节点
20
课堂练习
4.14 对于3个关键码值A、B、C,有多 少个不同的二叉搜索树?画出相应二叉 树。
21
平衡的二叉搜索树(AVL)
BST受输入顺序影响 受输入顺序影响
最好O(log n) 最好 最坏O(n) 最坏
怎样使得BST始终保持 始终保持O(log n)级的平衡状态? 级的平衡状态 怎样使得 始终保持 级的平衡状态? Adelson-Velskii和Landis发明了AVL树 发明了AVL Adelson-Velskii和Landis发明了AVL树
第六章-树和二叉树

之
树 和 二 叉 树 13
1 2 3 A B C
4 5 6 7 0 D E F
8 0
9 10 0 G
¾ 二叉树顺序存储的算法描述
数 据 结 构
¾ 初始化二叉树
之
树 和 二 叉 树 14
#define Max_Size 100 typedef int TElemType; typedef TElemType SqBT[Max_Size+1]; void InitBT(SqBT bt){//设置空树 int i; for(i=1;i<=Max_Size;i++) bt[i]=0; }
数 据 结 构
之
树 和 二 叉 树 19
¾ 后序遍历顺序二叉树算法 void PostBT(SqBT bt,int i){ if(i>Max_Size||!bt[i]) return; PostBT(bt,2*i); PostBT(bt,2*i+1); printf("%3d ",bt[i]); }
数 据 结 构
之
树 和 二 叉 树 4
5. 孩子结点、双亲结点、兄弟结点、堂兄弟 结点、祖先结点、子孙结点…… 6. 结点的层次从根开始,根为第一层,根的 孩子为第二层;若某结点在第L层,则其 子树的根就在第L+1层。 7. 树的深度或高度:树中结点的最大层次。 8. 有序树:如果将树中结点的各子树看成是 从左至右有次序的;反之,则是无序树。 9. 森林:是m棵互不相交的树的集合。
数 据 结 构
之
树 和 二 叉 树 25
¾ 打印一维数组 void printSq(SqBT bt){ int i; printf("\nSeqArray:"); for(i=1;i<=Max_Size;i++) printf("%3d ",bt[i]); }
数据结构(树和二叉树)练习题与答案2

1、一颗二叉树的括号表示为“1(2(4,5(6,7)),3)”)。
设N代表二叉树的根,L代表根节点的左子树,R代表根节点的右子树。
若遍历后的节点序列为3,1,7,5,6,2,4,则其遍历方式是()。
A.NRLB.RLNC.LRND.RNL正确答案:D2、若二叉树(每个节点值为单个字符)的中序遍历序列是abcdef,且c为根节点,则()。
A.二叉树有两个度为0的节点B.二叉树的高度为5C.节点c有两个孩子D.以上都不对正确答案:C解析: C、从中序序列看出,节点c的左右子树均不空。
3、若知道一棵二叉树的(),便可以唯一确定该二叉树。
A.中序序列B.先序和后序序列C.中序和后序序列D.先序序列正确答案:C4、一棵二叉树的先序遍历序列为ABCDEFG,它的中序遍历序列可能是()。
A.ADCFEGB.ABCDEFGC.DACEFBGD.CABDEFG正确答案:B解析: B、当一棵二叉树所有节点的左子树为空时,先序遍历序列和中序遍历序列相同。
先序序列和中序序列可以确定一棵二叉树,这里由选项A、C和D的中序序列无法确定一棵二叉树。
5、一棵二叉树的先序遍历序列为ABCDEF,中序遍历序列为CBAEDF,则后序遍历序列为()A.FEDCBAB.CBEFDAC.CBEDFAD.不确定正确答案:B6、某棵二叉树中,X节点有左孩子Y节点,则在其先序遍历中()。
A.访问Y节点后,接着遍历Y节点的左子树,然后访问X节点B.访问X节点后,接着遍历Y节点的左子树,然后访问Y节点C.访问Y节点后立即访问X节点D.访问X节点后立即访问Y节点正确答案:D解析: D、其先序遍历序列为…XY…。
7、关于二叉树(含2个以上的节点)的先序遍历序列中,以下正确的是()。
A.先序遍历序列的最后一个节点是根节点B.先序遍历序列的最后一个节点一定是叶子节点C.以上都不对D.先序遍历序列的第一个节点一定是叶子节点正确答案:B解析: B、先序遍历过程是:NLR,最后访问的节点的L、R均为空,所以为叶子节点。
数据结构PPT(树和二叉树)

徽 理
第6章 树和二叉树
工
大 本章学习导读
学
树型结构是一类重要的非线性结构。它的特点是结点之
间有分支,并具有明显的层次关系的结构。树在计算机领
域中有着广泛的应用,例如在编译程序中,用树来表示源
程序的语法结构;在数据库系统中,可用树来组织信息;
在分析算法的行为时,可用树来描述其执行过程。
本章重点讨论二叉树的存储表示及其各种运算,并研究
假设对所有j, 1≤j﹤i,命题成立,即第j层上至多有2 j-1 个
结点。
由归纳假设第i-1 层上至多有 2i -2个结点。
由于二叉树的每个结点的度至多为2,故在第i层上的最大结
点数为第i-1层上的最大结点数的2倍,即2×2i -2= 2 i-1。
安
徽 理
6.2.2 二叉树的性质
工
大 学
性质2 深度为 k 的二叉树至多有 2 k-1个结点(k ≥1)。
一般树和森林与二叉树的转换关系,最后介绍树的应用实
例。
安
徽 理
6.1 树的定义和基本术语
工
大 学
❖ 什么是树?树是由 n (n ≥ 0) 个结点的有限集合。如果 n
= 0,称为空树;如果 n > 0,则
▪ 有且仅有一个特定的称之为根(Root)的结点,它只有直
接后继,但没有直接前驱;
▪ 当n > 1,除根以外的其它结点划分为 m (m >0) 个互不
相交的有限集 T1, T2 ,…, Tm,其中每个集合本身又是一棵 树,并且称为根的子树(SubTree)。
安
徽 理
树的示例
A
工
B
C
D
大
学
E
2023年高考信息技术专题13 树与二叉树 知识点梳理(选修)(浙教版2019)
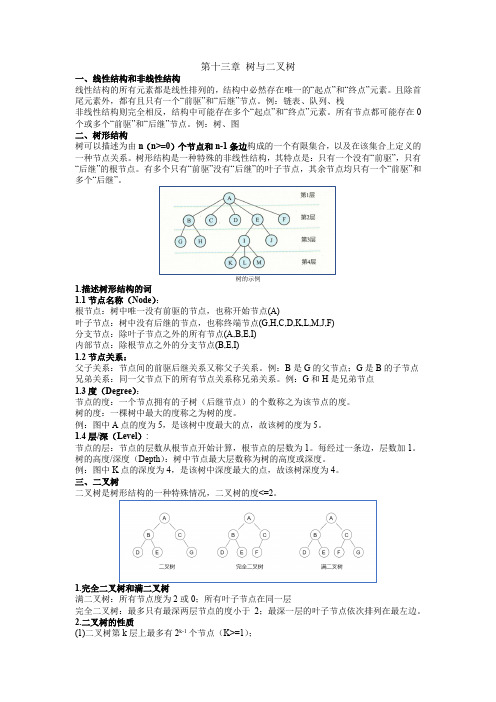
第十三章树与二叉树一、线性结构和非线性结构线性结构的所有元素都是线性排列的,结构中必然存在唯一的“起点”和“终点”元素。
且除首尾元素外,都有且只有一个“前驱”和“后继”节点。
例:链表、队列、栈非线性结构则完全相反,结构中可能存在多个“起点”和“终点”元素。
所有节点都可能存在0个或多个“前驱”和“后继”节点。
例:树、图二、树形结构树可以描述为由n(n>=0)个节点和n-1条边构成的一个有限集合,以及在该集合上定义的一种节点关系。
树形结构是一种特殊的非线性结构,其特点是:只有一个没有“前驱”,只有“后继”的根节点。
有多个只有“前驱”没有“后继”的叶子节点,其余节点均只有一个“前驱”和多个“后继”。
树的示例1.描述树形结构的词1.1节点名称(Node):根节点:树中唯一没有前驱的节点,也称开始节点(A)叶子节点:树中没有后继的节点,也称终端节点(G,H,C,D,K,L,M,J,F)分支节点:除叶子节点之外的所有节点(A,B,E,I)内部节点:除根节点之外的分支节点(B,E,I)1.2节点关系:父子关系:节点间的前驱后继关系又称父子关系。
例:B是G的父节点;G是B的子节点兄弟关系:同一父节点下的所有节点关系称兄弟关系。
例:G和H是兄弟节点1.3度(Degree):节点的度:一个节点拥有的子树(后继节点)的个数称之为该节点的度。
树的度:一棵树中最大的度称之为树的度。
例:图中A点的度为5,是该树中度最大的点,故该树的度为5。
1.4层/深(Level):节点的层:节点的层数从根节点开始计算,根节点的层数为1。
每经过一条边,层数加1。
树的高度/深度(Depth):树中节点最大层数称为树的高度或深度。
例:图中K点的深度为4,是该树中深度最大的点,故该树深度为4。
三、二叉树二叉树是树形结构的一种特殊情况,二叉树的度<=2。
1.完全二叉树和满二叉树满二叉树:所有节点度为2或0;所有叶子节点在同一层完全二叉树:最多只有最深两层节点的度小于2;最深一层的叶子节点依次排列在最左边。
软件技术--树与二叉树

(3 ) 若*p结点的左子树和右子树均不为空。
五、哈夫曼树的应用
1、什么是哈夫曼树
假设有n个权值{w1,w2,…,wn},试构造一棵有n 个叶子结点的二叉树,每个叶子结点带权wi,则其中带 权路径长度WPL最小的二叉树称作最优二叉树或哈夫 曼树。
2、 树的基本术语
结点的度:一个结点拥有的子树数称为该结点的度。 叶子结点:度为0的结点称为叶子(Leaf)或终端结点。 非终端结点:度不为0的结点称为非终端结点或分支结点。除根结 点之外,分支结点也称为内部结点。
树的度:树内各结点的度的最大值称为树的度。 树中结点之间的关系:在描述结点之间的关系时,通常用家族关 系来形象的称呼结点之间的联系。结点的子树的根称为该结点的孩 子(Child),相应的,该结点称为孩子的双亲(Parents)或父结点。 同一个双亲的孩子之间称为兄弟(Sibling)。 结点的层次(Level):一棵树从根开始定义起,根为第一层,根的 孩子为第二层,…,依此类推。若某结点在第i层,则其子树的根就 在第i+1层。其双亲在同一层的结点互为堂兄弟。
(4) 性质4: 具有n个结点的完全二叉树的深度为log2n+1。
3、几种特殊的二叉树
• 满二叉树:深度为K,且存在2K-1个结点的二叉树。 • 完全二叉树:至多只有最下面两层上的结点度数可以小于
2,并且最下层结点都集中在该层最左边的位置。 • 平衡二叉树:或是一棵空树,或是具有下列性质的二叉树:
每次插入一个结点的递归算法
struct node {anytype data; struct node *lchild; struct node *rchild; } *root; void insnode(t,d) struct node *t; anytype d;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
霍夫曼树 和 编码
//从k个结点中选取权重最小的两个根结点s1,s2 void Select( HTNode * HT, int k, int &s1, int &s2) { int i; s1=s2=0; HT[s1].weight=HT[s2].weight=Max; for(i=1;i<=k;i++) { if(HT[i].parent==0) if(HT[i].weight<HT[s1].weight) s1=i; else if(HT[i].weight<HT[s2].weight) s2=i; } }
霍夫曼树 和 编码
哈夫曼编码的存储结构 typedef struct { char bits[n]; int start; char ch; } codetype; codetype code[n];
霍夫曼树 和 编码
哈夫曼编码的存储结构 bit 1 1 1 1 1 1 1 1 1 1 0 0 0 0 ch start a b c d e 2 5 3 2 4
0 14 1 08 1 4 A 04 1 2 2 C S T: ; : A: C: S: 00 01 10 110 111
字符出现频率 w={2, 4, 2, 3, 3}
06 1 3 3 T ;
霍夫曼树 和 编码
从Huffman树根开始,从待译码电文中逐位取码。 若编码是“0”,则向左走;若编码是“1”,则向右走,一旦到 达叶子结点,则译出一个字符;再重新从根出发,直到电文结束 。
霍夫曼编码树
霍夫曼树 和 编码
在进行数据通讯时,涉及数据编码问题。所谓数据编码就 是数据与二进制字符串的转换。 例如:邮局发电报
原文 电文(二进制字符串) 原文
发送方
要传输的原文为ABACCDA 等长编码 A:00 B:01 C:10
接收方
D:11
发送方:将ABACCDA 转换成 00010010101100 接收方:将 00010010101100 还原为 ABACCDA
霍夫曼树 和 编码
for(i=n+1;i<=m;++i) //建哈夫曼树 { Select(HT,i-1,s1,s2); //选择parent为0且weight最小的两个结点, //其序号分别为:s1和s2。 HT[s1]. parent=i; HT[s2]. parent=i; HT[i]. lchild=s1; HT[i]. rchild=s2; HT[i]. weight=HT[s1].weight+HT[s2].weight; }
转换成 0110010101110
所得的译码是唯一的。
霍夫曼树 和 编码
思想:根据字符出现频率编码,使电文总长最短。 编码:根据字符出现频率构造Huffman树,然后将树中结点引 向其左孩子的分支标“0”,引向其右孩子的分支标“1”;每 个字符的编码即为从根到每个叶子的路径上得到的0、1序列。 要传输的字符集 D={C, A, S, T, ; }
霍夫曼树 和 编码
可利用二叉树设计前缀编码:
例 某通讯系统只使用8种字符a、b、c、d、e、f、g、h,其 使用频率分别为0.05,0.29,0.07,0.08, 0.14,0.23,0.03, 0.11,利用二叉树设计一种不等长编码。
霍夫曼树 和 编码
构造以 a、b、c、d、e、f、g、h为叶子结点的二叉树。
霍夫曼树 和 编码
//从叶子到根逆向求每个字符的哈夫曼编码 HC=new (char**)[n+1]; //分配n个字符编码的头指针向量 cd=new (char *)[n]; //分配求编码的工作空间 cd[n-1]=„\0‟; //编码结束符位置 for(i=1;i<=n;i++) // 逐个字符求哈夫曼编码 { start=n-1; for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent) //从叶子到根逆向求编码写入cd if(HT[f].lchild==c)cd[--start]=„0‟; else cd[--start]=„1‟; HC[i]=new(char*)[n-start];//为第i个字符编码分配空间 strcpy(HC[i],&cd[start]); //从cd复制编码(串)到HC[i] } delete cd; //释放工作空间 }
的二叉树,置新二叉树根结点权值为其左右子树上根结 点权值之和。
删除这两棵树,同时将新得到的二叉树加入集合中。 重复上述两步,直到集合中只含一棵树为止,这棵树即
是哈夫曼树
霍夫曼树 (Huffman Tree)
例
7 a 7 a 5 b 5 b 2 c 2 c 4 d 6 4 d 18
7 a
5 b
霍夫曼树 和 编码
//求哈夫曼编码的算法 void HuffmanCoding(HTNode*&HT, HuffmanCode &HC, int *w,int n) { //w存放n个字符的权值(均>0),构造哈夫曼树HT, //并求出n个字符的哈夫曼编码HC。 int c,f,i,m,s1,s2,start; char *cd; HTNode *p; if(n<=1)return; m=2*n-1; HT=new HTNode[m+1]; //动态分配数组存储哈夫曼树 0号单元不用 for(p=HT,i=1;i<=n;++i,++p,++w) p->weight=*w;
哈夫曼解码算法
Decode(codetype code[],hufmtree tree[]) { int i,j,c,p,b; int endflag=-1; i=m; scanf(“%d”,&b); while (b!=endflag) { if (b==0) i=tree[i].lchild-1; else i=tree[i].rchild-1; if (tree[i].lchild==0) { putchar(code[i].ch); i=m; } scanf(“%d”,&b); } if (tree[i].lchild!=0) printf(“\nERROR\n”); }
序号 1 2 3 4 5
哈夫曼编码算法(根据已构成的哈夫曼树,求出编码)
Huffmancode (codetype code[ ], hufmtree tree[ ]) { int i,j,c,p; codetype ed; for (i=0;i<n;i++) { cd.start=n; c=i+1; p=tree[i].parent; while (p!=0) { cd.start--; if (tree[p-1].lchild==c) cd.bits[cd.start]=„0‟; else cd.bits[cd.start]=„1‟; c=p; p=tree[p-1].parent; } code[i]=cd; }}
WPL=7*1+5*2+的理解_2
树的理解_3
霍夫曼树 (Huffman Tree)
构造Huffman树步骤 根据给定的n个权值{w1,w2,……wn},构造n棵只有根结 点(权值为wi)的二叉树的集合,其左右子树均空。
选取两棵根结点权值最小的树作左右子树,构造一棵新
HUFFMAN(hufmtree tree[]) { int i,j,p1,p2; float small1,small2,f; for (i=0;i<m;i++) { tree[i].parent=0; tree[i].lchild=0; tree[i].rchild=0; tree[i].weught=0; } for (i=0;i<n;i++) { scanf(“%f”,&f); tree[i].weight=f; } for (i=n;i<m;i++) { p1=0; p2=0; small1=maxval; small2=maxval; for (j=0;j<i-1;j++) if (tree[j].parent==0) if (tree[j].weight<small1) { small2=small1; p2=p1; p1=j; }
n
WPL
W
k 1
c
K
2
LK
4 d a 7 b 5
WPL=7*3+5*3+2*1+4*2=46
WPL=?
霍夫曼树 (Huffman Tree)
要使二叉树WPL小,就须在构造树时, 将权值大的结点 靠近根。 WPL=? 7 a
5 b
a 7 b 5 c 2 d 4 2 c d 4
WPL=7*2+5*2+2*2+4*2=36
编码
化整为 { 2, 7, 4, 5 },以 它们为各叶结点上的权值, 建立霍夫曼树。 左分支赋 0,右分支赋 1,得 霍夫曼编码(变长编码)。 A:0 T:10 C:110 S:111 它的总编码长度: 7*1+5*2+( 2+4 )*3 = 35。 比等长编码的情形要短。 总编码长度正好等于霍夫曼 树的带权路径长度WPL。
100 42 58
23
11
19
8 5 3
29
14
29
15 7 8
霍夫曼树 和 编码
哈夫曼树的存储结构 #define n 7 #define m 2*n-1 typedef int datatype; typedef struct { float weight; int lchild,rchild,parent; } hufmtree; hufmtree tree[m];
