牛顿第二定律的应用(三)--连接体
牛二定律应用——连接体专题

牛顿第二定律——连接体问题(整体法与隔离法)命题:熊亮一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统二、处理方法——整体法与隔离法系统运动状态相同 整体法问题不涉及物体间的内力使用原则系统各物体运动状态不同隔离法问题涉及物体间的内力三、连接体题型:1、连接体整体运动状态相同:(这类问题可以采用整体法求解)【例1】A、B两物体靠在一起,放在光滑水平面上,它们的质量分别为,,今用水平力推A,用水平力拉B,A、B间的作用力有多大?【练1】如图所示,质量为M的斜面A置于粗糙水平地面上,动摩擦因数为,物体B与斜面间无摩擦。
在水平向左的推力F作用下,A与B一起做匀加速直线运动,两者无相对滑动。
已知斜面的倾角为,物体B的质量为m,则它们的加速度a及推力F的大小为多少【练2】如图所示,质量为的物体2放在正沿平直轨道向右行驶的车厢底板上,并用竖直细绳通过光滑定滑轮连接质量为的物体,与物体1相连接的绳与竖直方向成角,则( )A. 车厢的加速度为B. 绳对物体1的拉力为C. 底板对物体2的支持力为D. 物体2所受底板的摩擦力为2、连接体整体内部各部分有不同的加速度:(不能用整体法来定量分析)【例2】如图所示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套有一个环,箱和杆的总质量为M,环的质量为m。
已知环沿着杆向下加速运动,当加速度大小为a时(a<g),则箱对地面的压力为多大?【练3】如图所示,一只质量为m的小猴抓住用绳吊在天花板上的一根质量为M的竖直杆。
当悬绳突然断裂时,小猴急速沿杆竖直上爬,以保持它离地面的高度不变。
则杆下降的加速度为大?【练4】如图所示,在托盘测力计的托盘内固定一个倾角为30°的光滑斜面,现将一个重4 N的物体放在斜面上,让它自由滑下,那么测力计因4 N物体的存在,而增加的读数是()A.4 NB.2 NC.0 ND.3 N【练5】如图所示,A、B的质量分别为m A=0.2kg,m B=0.4kg,盘C的质量m C=0.6kg,现悬挂于天花板O处,处于静止状态。
牛顿第二定律的应用--整体法与隔离法

3.3 牛顿第二定律的应用
——整体法与隔离法
整体法与隔离法 • 在求解连接体问题时常常用到整体法与隔 离法.所谓“连接体”问题,是指运动中 的几个物体或上下叠放在一起、或前后挤 靠在一起、或通过轻绳、轻杆、轻弹簧连 在一起、或由间接的场力作用在一起的物 体组. • 内力:各物体间存在相互作用力.
m1 F 联立以上各式得: FBA m1 m2
知识梳理
一、整体法:在研究物理问题时,把所研究 的对象作为一个整体(不考虑内力)来处理 的方法称为整体法。 采用整体法时不仅可以把几个物体作为 整体,也可以把几个物理过程作为一个整体。
采用整体法可以避免对整体内部 进行繁锁的分析,常常使问题解答更 简便、明了。
对B受力分析: 水平方向:
FAB m2 g m2a
m2 F m1 m2
联立以上各式得: FAB
思考:用水平推力F向左推,A、B间的作用 力与原来相同吗?
没有摩擦力时:
解:对整体,根据牛顿第二定律得
F (m1 m2 )a
对 A 受力分析根据牛顿第二定律得:
FBA m1a
例3.如图所示,质量M=60kg的人通过光滑的定 滑轮用绳拉着m= 20kg的物体,当物体以加速度 a=5 m/s2上升时,人在粗糙水平面上有一个三角形木块a,在它的两个粗糙斜面 上分别放有质量为m1和m2的两个木块b和c,如图所示,已知m1>m2, 三木块均处于静止,则粗糙地面对于三角形木块( ) A.有摩擦力作用,摩擦力的方向水平向右 B.有摩擦力作用,摩擦力的方向水平向左 C.有摩擦力作用,但摩擦力的方向不能确定 D.没有摩擦力的作用
(1)当地面光滑时,A,B作为一个整体,根据牛顿第二定律得:
牛顿第二定律的应用――连接体问题

专题: 牛顿第二定律的应用――― 连接体【知识讲解】一、连接体与隔离体(系统与质点)两个或两个以上物体,靠绳或接触面或电磁作用相互联系组成的物体系统,称为连接体(系统,多质点)。
如果把其中某个物体隔离出来,该物体即为隔离体(单质点)。
二、外力和内力如果以物体系为研究对象,受到系统之外的物体施加的作用力,这些力是系统受到的外 力,而系统内各物体间的相互作用力为内力。
应用牛顿第二定律列方程求合力时不考虑内力。
如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的外力。
三、连接体问题的分析方法1.整体法:整体法是物理中常用的一种思维方法。
它是将几个物体看作一个整体来作为研究对象即系统,这样就暂时回避了这些物体间的相互作用的内力,只考虑整体受到的外力,整体法列出的方程数目较少,解题变的简明快捷。
(1)连接体中的各物体如果加速度相同,求解时可以把连接体作为一个整体。
运用F 合=(m 1+m 2+m 3…..)a 列方程求解;题目只涉及内外力关系不需要求加速度时,也可以用牛顿定律在加速度相同情况下的推论:总合合合m m m 2211F F F ==(动力分配原理,即系统内各部分的合力与其质量成正比)。
(2)连接体中的各物体如果加速度不同,若系统内有几个物体,这几个物体的质量分别为m 1,m 2,m 3………m n ,,加速度分别为a 1,a 2,a 3......a n ,这个系统受到的合外力为F 合外,则对这个系统应用牛顿第二定律的表达式为1122n nF m a m a m a =++⋅⋅⋅+合外其正交分解表示式为11221122x x n nxy y n nyy F m a m a m a F m a m a m a=++⋅⋅⋅+=++⋅⋅⋅+x 外外(3)当系统内各个物体加速度均为零时,有的静止有的匀速运动,整个系统处于平衡状态,此时可用F 合外=0进行求解。
或者:0F 0F y x ==外外,联立求解。
牛顿第二定律的应用——连接体问题

牛顿第二定律的应用――― 连接体问题一、连接体与隔离体两个或两个以上物体相连接组成的物体系统,称为 。
如果把其中某个物体隔离出来,该物体即为。
二、连接体问题的分析方法1.整体法:连接体中的各物体如果 ,求加速度时可以把连接体作为一个整体。
运用 列方程求解。
2.隔离法:如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用 求解,此法称为隔离法。
3.整体法与隔离法是相对统一,相辅相成的。
本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。
如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用 法求出 ,再用 法求 。
【典型例题】例1.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( )A.F m m m 211+B.F m m m 212+C.FD.F m m 21 练习:1.若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则对B 作用力等于 。
2.如图右所示,质量为m 1、m 2的物块在F 1、F 2共同作用下向右运动。
已知m 1=3kg m 2=2kg F 1=14 N F 2=4N ,求m 1和m 2之间细绳的作用力F T 为多少?A B m 1 m 2 F3.如右图所示,物体m1、m2用一细绳连接,两者在竖直向上的力F的作用下向上加速运动,重力加速度为g,求细绳上的张力?例2:如图右,m1、m2用细线吊在光滑定滑轮,m1=3kg m2=2kg,当m1、m2开始运动时,求细线受到的张力?例3:如图所示,箱子的质量M=5.0kg,与水平地面的动摩擦因数μ=0.22。
在箱子顶板处系一细线,悬挂一个质量m=1.0kg的小球,箱子受到水平恒力F的作用,使小球的悬线偏离竖直方向θ=30°角,则F应为多少?(g=10m/s2)练习:如图所示,在前进的车厢的竖直后壁上放一个物体,物体与壁间的静摩擦因数μ=0.8,要使物体不致下滑,车厢至少应以多大的加速度前进?(g=10m/s2)例4:如图所示,质量分别为m 和2m 的两物体A 、B 叠放在一起,放在光滑的水平地面上,已知A 、B 间的最大摩擦力为A 物体重力的μ倍,若用水平力作用在B 上,使A 、B 保持相对静止做加速运动,则作用于B 的作用力为多少?练习.如图A 、B 、C 为三个完全相同的物体,当水平力F 作用于B 上,三物体可一起匀速运动。
牛顿第二定律的应用

牛顿第二定律的应用――― 连接体问题整体法和隔离法,临界问题学习要求:会解决两个物体具有相同加速度的动力学问题求解连接体问题时,只限于各物体加速度相同的情形一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统二、处理方法——整体法与隔离法三、连接体题型:1【例1】A 、B ,今用水平力推【练1】如图所示,质量为M 的斜面面间无摩擦。
在水平向左的推力F 已知斜面的倾角为,物体B A. B. C. D.【练2】如图所示,质量为的物体连接的绳与竖直方向成角,则( A. 车厢的加速度为B. B. 绳对物体1的拉力为C. C. 底板对物体2的支持力为D. D. 物体2所受底板的摩擦力为 kg m B 6=N F A 6=θ()(,sin μθ+==g m M F g a θ)(,cos g m M F g a +==()(,tan μθ+==g m M F g a g m M F g a )(,cot +==μθ2m θθsin g θcos 1gm g m m )(12-θtan 2g m2、连接体整体内部各部分有不同的加速度:(不能用整体法来定量分析)不作要求同步练习P123 124 页3、临界问题 例2、作业本P66页例3、质量为0.2kg 的小球用细线吊在倾角为θ=060的斜面体的顶端,斜面体静止时,小球紧靠在斜面上,线与斜面平行,如图4-70所示,不计摩擦,求在下列三种情况下,细线对小球的拉力(取g =10 2/s m )(1) 斜面体以232/s m 的加速度向右加速运动;(2) 斜面体以432/s m ,的加速度向右加速运动;例4、如图所示,箱子的质量M =3.0 kg ,与水平地面间的动摩擦因数为μ=0.22。
在箱子底板上放一质量为ml =2 kg 的长方体铁块;在箱子顶板处系一细线,悬挂一个质量m2=2.0 kg的小球,箱子受到水平恒力F 的作用,稳定时悬线偏离竖直方向θ=030角,且此时铁块刚好相对箱子静止。
牛顿第二定律的应用

牛顿第二定律的应用、超重与失重一、应用牛顿第二定律分析问题的基本思路:(1)已知力求物体的运动状态:先对物体进行受力分析,由分力确定合力;根据牛顿第二定律确定加速度,再由初始条件分析物体的运动状态,应用运动学规律求出物体的速度或位移。
(2)已知物体的运动状态求物体的受力情况:先由物体的运动状态(应用运动学规律)确定物体的加速度;根据牛顿第二定律确定合力,再根据合力与分力的关系求出某一个分力。
二、解题步骤:(1)根据题意,确定研究对象;(2)用隔离法或整体法分析研究对象的受力情况,画受力示意图;(3)分析物理过程是属于上述哪种类型的问题,应用牛顿第二定律分析问题的基本思路进行分析;(4)选择正交坐标系(或利用力的合成与分析)选定正方向,列动力学方程(或结合初始条件列运动学方程);(5)统一单位,代入数据,解方程,求出所需物理量;(6)思考结果的合理性,决定是否需要讨论。
三、例题分析:例1:如图所示,质量m=2kg的物体,受到拉力F=20N的作用,F与水平成37°角。
物体由静止开始沿水平面做直线运动,物体与水平面间的摩擦因数μ=0.1,2s末撤去力F,求:撤去力F 后物体还能运动多远?(sin37°=0.6,cos37°=0.8)例2:一个质量m=2kg的物体放在光滑的水平桌面上,受到三个与桌面平行的力作用,三个力大小相等F1=F2=F3=10N,方向互成120°,方向互成120°,则:(1)物体的加速度多大?(2)若突然撤去力F1,求物体的加速度?物体运动状况如何?(3)若将力F1的大小逐渐减小为零,然后再逐渐恢复至10N,物体的加速度如何变化?物体运动状况如何?例3:如图所示,停在水平地面的小车内,用轻绳AB、BC拴住一个小球。
绳BC呈水平状态,绳AB 的拉力为T1,绳BC的拉力为T2。
当小车从静止开始以加速度a水平向左做匀加速直线运动时,小球相对于小车的位置不发生变化;那么两绳的拉力的变化情况是:()A、T1变大,T2变大B、T1变大,T2变小C、T1不变,T2变小D、T1变大,T2不变例4:如图所示,物体A质量为2kg,物体B质量为3kg,A、B叠放在光滑的水平地面上,A、B间的最大静摩擦力为10N;一个水平力F作用在A物体上,为保证A、B间不发生滑动,力F的最大值为多少?如果力F作用在B上,仍保证A、B间不滑动,力F最大值为多少?四、超重和失重(1)重力:重力是地球对物体吸引而使物体受到的作用力,是引力,G=mg。
高考物理一轮复习 专题三 牛顿运动定律 考点3 连接体问题教案-人教版高三全册物理教案

考点三连接体问题基础点知识点1 连接体1.定义:多个相互关联的物体连接(叠放、并排或由绳子、细杆联系)在一起构成的物体系统称为连接体。
连接体一般具有相同的运动情况(速度、加速度)。
如以下图所示:2.处理连接体问题的方法:整体法与隔离法,要么先整体后隔离,要么先隔离后整体。
(1)整体法是指系统内(即连接体内)物体间无相对运动时(具有相同加速度),可以把连接体内所有物体组成的系统作为整体考虑,分析其受力情况,对整体列方程求解的方法。
整体法可以求系统的加速度或外界对系统的作用力。
(2)隔离法是指当我们所研究的问题涉及多个物体组成的系统时,需要求连接体内各部分间的相互作用力,从研究方便出发,把某个物体从系统中隔离出来,作为研究对象,分析其受力情况,再列方程求解的方法。
隔离法适合求系统内各物体间的相互作用力或各个物体的加速度。
3.整体法、隔离法的选取原那么(1)整体法的选取原那么假设连接体内各物体具有相同的加速度,且不需要求物体之间的作用力,可以把它们看成一个整体,分析整体受到的合外力,应用牛顿第二定律求出加速度(或其他未知量)。
(2)隔离法的选取原那么假设连接体内各物体的加速度不相同,或者要求出系统内各物体之间的作用力时,就需要把物体从系统中隔离出来,应用牛顿第二定律列方程求解。
(3)整体法、隔离法的交替运用假设连接体内各物体具有相同的加速度,且要求出物体之间的作用力时,可以先用整体法求出加速度,然后再用隔离法选取合适的研究对象,应用牛顿第二定律求作用力。
即“先整体求加速度,后隔离求内力〞。
知识点2 临界与极值1.临界问题物体由某种物理状态转变为另一种物理状态时,所要经历的一种特殊的转折状态,称为临界状态。
这种从一种状态变成另一种状态的分界点就是临界点,此时的条件就是临界条件。
在应用牛顿运动定律解决动力学的问题中,当物体的加速度不同时,物体有可能处于不同的状态,特别是题目中出现“最大〞“最小〞“刚好〞“恰好出现〞或“恰好不出现〞等词语时,常常会涉及临界问题。
第三章牛顿第二定律及应用(zhu)简单连接体问题动力学中的图象问题动力学中的传送带问题导学案14

学案14 牛顿第二定律及应用(三)简单连接体问题动力学中的图象问题动力学中的传送带问题二、思想方法题组4.A、B两物体叠放在一起,放在光滑水平面上,如图3甲所示,它们从静止开始受到一个变力F的作用,该力与时间关系如图乙所示,A、B始终相对静止.则( )图3A.在t0时刻A、B两物体间静摩擦力最大B.在t0时刻A、B两物体的速度最大C.在2t0时刻A、B两物体的速度最大D.在2t0时刻A、B两物体的位移最大图45.质量为m的物体放在A地的水平面上,用竖直向上的力F拉物体,物体的加速度a 与拉力F的关系如图4中直线①所示,用质量为m′的另一物体在B地做类似实验,测得a-F关系如图中直线②所示,设两地的重力加速度分别为g和g′,则( ) A.m′>m,g′=g B.m′<m,g′=gC.m′=m,g′>g D.m′=m,g′>g一、整体法和隔离法的选取1.隔离法的选取原则:若连接体内各物体的加速度不相同,且需要求物体之间的作用力,就需要把物体从系统中隔离出来,将系统的内力转化为隔离体的外力,分析物体的受力情况和运动情况,并分别应用牛顿第二定律列方程求解.隔离法是受力分析的基础,应重点掌握.2.整体法的选取原则:若连接体内各物体具有相同的加速度(主要指大小),且不需要求物体之间的作用力,就可以把它们看成一个整体(当成一个质点)来分析整体受到的外力,应用牛顿第二定律求出加速度(或其他未知量).3.整体法、隔离法交替运用的原则:若连接体内各物体具有相同的加速度,且要求物体之间的作用力,可以先用整体法求出加速度,然后再用隔离法选取合适的研究对象,应用牛顿第二定律求作用力.即“先整体求加速度,后隔离求内力”.图5【例1】 (2009·安徽高考)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神.为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化如下:一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图5所示.设运动员的质量为65 kg ,吊椅的质量为15 kg ,不计定滑轮与绳子间的摩擦,重力加速度取g =10 m /s 2.当运动员与吊椅一起以加速度a =1 m /s 2上升时,试求: (1)运动员竖直向下拉绳的力; (2)运动员对吊椅的压力.[规范思维]图6[针对训练1] (2011·合肥一中月考)如图6所示,水平地面上有两块完全相同的木块A 、B ,水平推力F 作用在A 上,用F AB 代表A 、B 间的相互作用力,下列说法中错误的是( )A .若地面是光滑的,则F AB =FB .若地面是光滑的,则F AB =F2C .若地面是粗糙的,且A 、B 被推动,则F AB =F2D .若地面是粗糙的,且A 、B 未被推动,F AB 可能为F3二、动力学中的图象问题图象问题是近年高考命题的热点,动力学问题的图象在高考中也频频出现,常见的有v -t 图象、a -t 图象、F -t 图象、F -a 图象. 【例2】 (2009·全国Ⅱ·15)图7两物体甲和乙在同一直线上运动,它们在0~0.4 s 时间内的v -t 图象如图7所示.若仅在两物体之间存在相互作用,则物体甲与乙的质量之比和图中时间t 1分别为( ) A .13和0.30 s B .3和0.30 s C .13和0.28 s D .3和0.28 s [规范思维]图8【例3】 (2010·福建理综·16)质量为2 kg 的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t =0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F 的作用,F 随时间t 的变化规律如图8所示.重力加速度g 取10 m /s 2,则物体在t =0至t =12 s 这段时间的位移大小为( )A .18 mB .54 mC .72 mD .198 m [规范思维]【例4】 (2009·上海单科·22)如图19(a )所示,质量m =1 kg 的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v 成正比,比例系数用k 表示,物体加速度a 与风速v 的关系如图(b )所示,求:图9(1)物体与斜面间的动摩擦因数μ; (2)比例系数k.(sin 37°=0.6,cos 37°=0.8,g 取10 m /s 2)[规范思维]【例5】(2011·上海十二校联考)如图10(a)所示,用一水平外力F推着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F 变化的图象如图(b)所示,若重力加速度g取10 m/s2.根据图(b)中所提供的信息计算不出( )图10A.物体的质量B.斜面的倾角C.物体能静止在斜面上所施加的最小外力D.加速度为6 m/s2时物体的速度[规范思维]三、动力学中的传送带问题【例6】如图11所示,传送带与水平面间的倾角图11为θ=37°,传送带以10 m/s的速率运行,在传送带上端A处无初速度地放上质量为0.5 kg的物体,它与传送带间的动摩擦因数为0.5,若传送带A到B的长度为16 m,则物体从A运动到B的时间为多少?(取g=10 m/s2)[规范思维]图12[针对训练2] (2010·高考状元纠错)如图12所示,质量为m 的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L ,稳定时绳与水平方向的夹角为θ,当传送带分别以v 1、v 2的速度做逆时针转动时(v 1<v 2),绳中的拉力分别为F 1、F 2;若剪断细绳时,物体到达左端的时间分别为t 1、t 2,则下列说法正确的是( ) A .F 1<F 2 B .F 1>F 2C .t 1>t 2D .t 1可能等于t 2【基础演练】1.(2011·芜湖市模拟)如图13所示,图13放在粗糙水平面上的物块A 、B 用轻质弹簧秤相连,两物块与水平面间的动摩擦因数均为μ.今对物块A 施加一水平向左的恒力F ,使A 、B 一起向左匀加速运动,设A 、B 的质量分别为m 、M ,则弹簧秤的示数为( ) A .MF M +m B .MF m C .F -μM +m g m M D .F -μM +m g m +MM2.(天津高考题)一个静止的质点,在0~4 s 时间内受到力F 的作用,力的方向始终在同一直线上,力F 随时间t 的变化如图14所示,则质点在( )图14A .第2 s 末速度改变方向B .第2 s 末位移改变方向C .第4 s 末回到原出发点D .第4 s 末运动速度为零图153.(2010·山东理综·16)如图15所示,物体沿斜面由静止滑下,在水平面上滑行一段距离后停止,物体与斜面和水平面间的动摩擦因数相同,斜面与水平面平滑连接.下图中v 、a 、f 和s 分别表示物体速度大小、加速度大小、摩擦力大小和路程.下列图象中正确的是( )图164.(2011·临沂模拟)如图16所示,弹簧测力计外壳质量为m 0,弹簧及挂钩的质量忽略不计,挂钩吊着一质量为m 的重物,现用一方向竖直向上的外力F 拉着弹簧测力计,使其向上做匀加速直线运动,则弹簧测力计的读数为( )A .mgB .mm 0+mmgC .m 0m 0+m FD .m m 0+m F 5.(2010·威海模拟)质量为1.0 kg 的物体静止在水平面上,物体与水平面之间的动摩擦因数为0.30.对物体施加一个大小变化、方向不变的水平拉力F ,作用了3t 0的时间.为使物体在3t 0时间内发生的位移最大,力F 随时间的变化情况应该为下图中的( )6.图17如图17所示,在光滑的水平面上放着紧靠在一起的A 、B 两物体,B 的质量是A 的2倍,B 受到向右的恒力F B =2 N ,A 受到的水平力F A =(9-2t) N (t 的单位是s ).从t =0开始计时,则下列说法错误的是( )A .A 物体在3 s 末时刻的加速度是初始时刻的511B .t>4 s 后,B 物体做匀加速直线运动C .t =4.5 s 时,A 物体的速度为零D .t>4.5 s 后,A 、B 的加速度方向相反图187.(2011·杭州期中检测)如图18所示,两个质量分别为m 1=2 kg 、m 2=3 kg 的物体置于光滑的水平面上,中间用轻质弹簧秤连接.两个大小分别为F 1=30 N 、F 2=20 N 的水平拉力分别作用在m 1、m 2上,则( ) A .弹簧秤的示数是25 N B .弹簧秤的示数是50 NC .在突然撤去F 2的瞬间,m 1的加速度大小为5 m /s 2D .在突然撤去F 1的瞬间,m 1的加速度大小为13 m /s 2 【能力提升】8.如图19所示,图19光滑水平面上放置质量分别为m 和2m 的四个木块,其中两个质量为m 的木块间用一不可伸长的轻绳相连,木块间的最大静摩擦力是μmg.现用水平拉力F 拉其中一个质量为2m 的木块,使四个木块以同一加速度运动,则轻绳对m 的最大拉力为( ) A .3μmg 5 B .3μmg 4 C .3μmg 2 .3μmg图209.(2011·天星调研)传送带是一种常用的运输工具,被广泛应用于矿山、码头、货场、车站、机场等.如图20所示为火车站使用的传送带示意图.绷紧的传送带水平部分长度L =5 m ,并以v 0=2 m /s 的速度匀速向右运动.现将一个可视为质点的旅行包无初速度地轻放在传送带的左端,已知旅行包与传送带之间的动摩擦因数μ=0.2,g 取10 m /s 2.(1)求旅行包经过多长时间到达传送带的右端;(2)若要旅行包从左端运动到右端所用时间最短,则传送带速度的大小应满足什么条件?最短时间是多少?10.如图21所示,图21在倾角为θ=30°的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住.已知人的质量为60 kg ,小车的质量为10 kg ,绳及滑轮的质量、滑轮与绳间的摩擦均不计,斜面对小车的摩擦阻力为人和小车总重力的0.1倍,取重力加速度g =10 m /s 2,当人以280 N 的力拉绳时,试求(斜面足够长): (1)人与车一起运动的加速度大小; (2)人所受摩擦力的大小和方向;(3)某时刻人和车沿斜面向上的速度为 3 m /s ,此时人松手,则人和车一起滑到最高点所用时间为多少?学案14 牛顿第二定律及应用(三) 简单连接体问题动力学中的图象问题 动力学中的传送带问题【课前双基回扣】 1.C 2.C 3.D[由于警卫人员在半球形屋顶上向上缓慢爬行,他爬行到的任一位置时都看作处于平衡状态.在图所示位置,对该警卫人员进行受力分析,其受力图如右图所示.将重力沿半径方向和球的切线方向分解后列出沿半径方向和球的切线方向的平衡方程 F N =mg cos θ,F f =mg sin θ他在向上爬的过程中,θ变小,cos θ变大,屋顶对他的支持力变大;sin θ变小,屋顶对他的摩擦力变小.所以正确选项为D.]4.BD [对A 、B 整体 F =(m A +m B )a 隔离物体A F f =m A a 由F -t 可知:t =0和t =2t 0时刻,F 最大,故F f 最大,A 错.又由于A 、B 整体先加速后减速,2t 0时刻停止运动,所以t 0时刻速度最大,2t 0时刻位移最大,B 、D 正确.]5.B [在A 地,由牛顿第二定律有F -mg =ma ,得a =F m -g =1mF -g .同理,在B 地:a ′=1m ′F -g ′.这是一个a 关于F 的函数,1m (或1m ′)表示斜率,-g (或-g ′)表示截距.由图线可知1m <1m ′,g =g ′;故m >m ′,g =g ′,B 项正确.]思维提升1.选取整体法或隔离法的原则是:若系统整体具有相同加速度,且不要求求物体间的相互作用力,一般取整体为研究对象;若要求物体间相互作用力,则需把物体从系统中隔离出来,用隔离法,且选择受力较少的隔离体为研究对象.2.利用图象分析物理问题时,往往根据物理定理或定律写出横轴物理量关于纵轴物理量的函数关系,借助函数的截距和斜率的物理意义解决问题. 【核心考点突破】例1 (1)440 N ,方向竖直向下 (2)275 N ,方向竖直向下解析 (1)设运动员和吊椅的质量分别为M 和m ,绳拉运动员的力为F .以运动员和吊椅整体为研究对象,受到重力的大小为(M +m )g ,向上的拉力为2F ,根据牛顿第二定律 2F -(M +m )g =(M +m )a 解得F =440 N根据牛顿第三定律,运动员拉绳的力大小为440 N ,方向竖直向下.(2)以运动员为研究对象,运动员受到三个力的作用,重力大小Mg ,绳的拉力F ,吊椅对运动员的支持力F N .根据牛顿第二定律F +F N -Mg =Ma 解得F N =275 N 根据牛顿第三定律,运动员对吊椅压力大小为275 N ,方向竖直向下. [规范思维] 本题中由于运动员和吊椅整体具有共同的加速度,已知加速度,故先以整体为研究对象,求绳拉人的力;运动员对座椅的压力是内力,需隔离求解.例2 B [根据v -t 图象可知,甲做匀加速运动,乙做匀减速运动.由a 乙=40.40m/s2=10 m/s 2,又a 乙=10.40 s -t 1得,t 1=0.30 s ,根据a =Δv Δt得3a 甲=a 乙.根据牛顿第二定律有F m 甲=13·Fm 乙,则m 甲∶m 乙=3.故B 项正确.][规范思维] 对此类问题要注意从图象提炼出物理情景,把图象语言翻译成物理过程,了解物体对应的运动情况和受力情况,灵活运用牛顿第二定律解题,联系图象(运动情况)和力的桥梁仍是a . 例3 B[物体与地面间最大静摩擦力F max =μmg =0.2×2×10 N=4 N .由题给F -t 图象知0~3 s 内,F =4 N ,说明物体在这段时间内保持静止不动.3~6 s 内,F =8 N ,说明物体做匀加速运动,加速度a =F -F max m=2 m/s 2.6 s 末物体的速度v =at =2×3 m/s=6 m/s ,在6~9 s 内物体以6 m/s 的速度做匀速运动.9~12 s 内又以2 m/s 2的加速度做匀加速运动,作v -t 图象如图.故0~12 s 内的位移x =(12×3×6)×2 m+6×6 m=54 m .故B 项正确.][规范思维] 解本题关键是从F -t 图象中提炼出信息,明确各个时间段的受力情况和运动情况,然后根据牛顿第二定律和运动学公式列方程. 例4 (1)0.25 (2)0.84 kg/s解析 (1)由图象知v =0,a 0=4 m/s 2开始时根据牛顿第二定律得 mg sin θ-μmg cos θ=ma 0μ=g sin θ-a 0g cos θ=6-48=0.25(2)由图象知v =5 m/s ,a =0 由牛顿第二定律知 mg sin θ-μF N -kv cos θ=0 F N =mg cos θ+kv sin θmg (sin θ-μcos θ)-kv (μsin θ+cos θ)=0 k =mg sin θ-μcos θv μsin θ+cos θ=6-0.25×850.25×0.6+0.8 kg/s =0.84 kg/s[规范思维] 解本题需从a -v 图象中寻求信息,结合物体的受力情况,根据牛顿第二定律正确列出方程式.此外注意物体受多个力的作用,在进行力的运算时应用了正交分解法.例5 ABC [分析物体受力,由牛顿第二定律得:F cos θ-mg sin θ=ma ,由F =0时,a =-6 m/s 2,得θ=37°.由a =cos θm F -g sin θ和a -F 图线知:图象斜率6-230-20=cos 37°m,得:m =2 kg ,物体静止时的最小外力F min cos θ=mg sin θ,F min =mg tan θ=15 N ,无法求出物体加速度为6 m/s 2时的速度,因物体的加速度是变化的,对应时间也未知,故A 、B 、C 正确,D 错误.][规范思维] 解此类a -F 图象问题,首先应写出a 随F 变化的关系式,然后通过斜率、截距的意义寻找解题的突破口.例6 当皮带向下运行时,总时间t =2 s ,当皮带向上运行时,总时间t ′=4 s. 解析 首先判断μ与tan θ的大小关系,μ=0.5,tan θ=0.75,所以物体一定沿传送带对地下滑.其次传送带运行速度方向未知,而传送带运行速度方向影响物体所受摩擦力的方向,所以应分别讨论.(1)当传送带以10 m/s 的速度向下运行时,开始物体所受滑动摩擦力方向沿传送带向下(受力分析如图中甲所示). 该阶段物体对地加速度a 1=mg sin θ+μmg cos θm=10 m/s 2,方向沿传送带向下物体达到与传送带相同的速度所需时间t 1=va 1=1 s在t 1内物体沿传送带对地位移x 1=12a 1t 21=5 m从t 1开始物体所受滑动摩擦力沿传送带向上(如图中乙所示),物体对地加速度a 2=mg sin θ-μmg cos θm=2 m/s 2,方向沿传送带向下物体以2 m/s 2加速度运行剩下的11 m 位移所需时间t 2,则x 2=vt 2+12a 2t 22,代入数据解得t 2=1 s(t 2′=-11 s 舍去) 所需总时间t =t 1+t 2=2 s (2)当传送带以10 m/s 速度向上运行时,物体所受滑动摩擦力方向沿传送带向上且不变,设加速度大小为a 3,则a 3=mg sin θ-μmg cos θm=2 m/s 2物体从A 运动到B 所需时间t ′,则x =12a 3t ′2;t ′=2x a 3=2×162s =4 s.[规范思维] (1)按传送带的使用方式可将其分为水平和倾斜两种. (2)解题中应注意以下几点:①首先判定摩擦力突变点,给运动分段.物体所受摩擦力,其大小和方向的突变,都发生在物体的速度与传送带速度相等的时刻.v 物与v 传相同的时刻是运动分段的关键点,也是解题的突破口.②在倾斜传送带上往往需比较mg sin θ与F f 的大小与方向. ③考虑传送带长度——判定临界之前是否滑出;物体与传送带共速以后物体是否一定与传送带保持相对静止做匀速运动. [针对训练] 1.A 2.BD 【课时效果检测】1.A 2.D 3.C 4.D 5.B 6.ABD 7.D 8.B 9.(1)3 s (2)大于或等于2 5 m/s 5 s用心 爱心 专心 11 解析 (1)旅行包无初速度地轻放在传送带的左端后,旅行包相对于传送带向左滑动,旅行包在滑动摩擦力的作用下向右做匀加速运动,由牛顿第二定律得旅行包的加速度a=F /m =μmg /m =μg =2 m/s 2当旅行包的速度增大到等于传送带速度时,二者相对静止,匀加速运动时间t 1=v 0/a =1 s匀加速运动位移x =12at 21=1 m 此后旅行包匀速运动,匀速运动时间t 2=L -x v 0=2 s 旅行包从左端运动到右端所用时间t =t 1+t 2=3 s.(2)要使旅行包在传送带上运行时间最短,必须使旅行包在传送带上一直加速由v 2=2aL 得v =2aL =2 5 m/s即传送带速度必须大于或等于2 5 m/s由L =12at 2得旅行包在传送带上运动的最短时间t =2L a= 5 s. 10.(1)2 m/s 2 (2)140 N 方向沿斜面向上 (3)0.5 s解析 (1)以人和小车为整体,沿斜面应用牛顿第二定律得:2F -(M +m )g sin θ-k (M +m )g =(M +m )a将F =280 N ,M =60 kg ,m =10 kgk =0.1代入上式得a =2 m/s 2(2)设人受到小车的摩擦力大小为F f 人,方向沿斜面向下,对人应用牛顿第二定律得: F -Mg sin θ-F f 人=Ma ,可得F f 人=-140 N因此,人受到的摩擦力大小为140 N ,方向沿斜面向上(3)人松手后,设人和车一起上滑的加速度大小为a 1,方向沿斜面向下,由牛顿第二定律得:(M +m )g sin θ+k (M +m )g =(M +m )a 1则a 1=6 m/s 2,由v =a 1t 1可得t 1=v a 1=0.5 s 易错点评绳或弹簧秤竖直向上拉物体时,拉力不一定等于重力.拉力与重力的大小比较决定于物体的运动状态.。
第三章 第3课时 专题强化:牛顿第二定律的综合应用

第3课时 专题强化:牛顿第二定律的综合应用 目标要求 1.知道连接体的类型以及运动特点,会用整体法、隔离法解决连接体问题。
2.理解几种常见的临界极值条件,会用极限法、假设法、数学方法解决临界极值问题。
考点一 动力学中的连接体问题多个相互关联的物体连接(叠放、并排或由绳子、细杆、弹簧等联系)在一起构成的物体系统称为连接体。
系统稳定时连接体一般具有相同的速度、加速度(或速度、加速度大小相等)。
1.共速连接体两物体通过弹力、摩擦力作用,具有相同的速度和相同的加速度。
(1)绳的拉力(或物体间的弹力)相关类连接体(2)叠加类连接体(一般与摩擦力相关)例1 如图所示,水平面上有两个质量分别为m 1和m 2的木块1和2,中间用一条轻绳连接,两木块的材料相同,现用力F 向右拉木块2,当两木块一起向右做匀加速直线运动时,已知重力加速度为g ,下列说法正确的是( )A .若水平面是光滑的,则m 2越大,绳的拉力越大B .若木块和地面间的动摩擦因数为μ,则绳的拉力为m 1F m 1+m 2+μm 1g C .绳的拉力大小与水平面是否粗糙无关D .绳的拉力大小与水平面是否粗糙有关答案 C解析 若设木块和地面间的动摩擦因数为μ,以两木块整体为研究对象,根据牛顿第二定律有F -μ(m 1+m 2)g =(m 1+m 2)a ,得a =F -μ(m 1+m 2)g m 1+m 2,以木块1为研究对象,根据牛顿第二定律有T -μm 1g =m 1a ,得a =T -μm 1g m 1,系统加速度与木块1加速度相同,联立解得T =m 1m 1+m 2F ,可知绳子拉力大小与动摩擦因数μ无关,与两木块质量大小有关,无论水平面是光滑的还是粗糙的,绳的拉力大小均为T =m 1m 1+m 2F ,且m 2越大,绳的拉力越小,故选C 。
拓展 (1)两个质量分别为m 1和m 2的木块1和2,中间用一条轻绳连接。
①如图甲所示,用力F 竖直向上拉木块时,绳的拉力T =__________;②如图乙所示,用力F 沿光滑斜面向上拉木块时,绳的拉力为__________;斜面不光滑时绳的拉力T =__________。
高考热点:牛顿第二定律

高考热点:牛顿第二定律的典型应用——连接体问题、超重与失重牛顿第二定律的地位不用多说了,一定是高考必考内容,可能出现在一道选择题或第一道计算题中. 那么,会以何种方式来考查牛顿第二定律的应用呢?最大的可能一定是连接体问题和超重失重现象!所谓的“连接体”问题,就是在一道题中出现两个或两个以上相关联的物体,研究它们的运动与力的关系. 实际上在物体的平衡问题中我们已经遇到了不少,只是平衡问题中的物体是没有加速度的,而在“连接体”问题中,有的物体具有加速度,所以求解的时候必须用到牛顿第二定律. 可见,牛顿第二定律是用来解决“非平衡问题”的!而处理“非平衡问题”的程序与解决平衡问题时的程序并无太大的区别:确定研究对象→受力分析(整体或隔离,或整体隔离结合使用)→力的合成或分解(常用正交分解法)→列方程求解(平衡问题列平衡方程,“非平衡问题”列动力学方程,即牛顿第二定律方程)先整体分析加速度,后隔离分析各物体之间的相互作用力是解决连接体问题的最常用思维模式,你掌握了吗?千万要记住:整体法只能分析“整体”外面其它物体对“整体”的作用力,不能分析“整体”内部各物体间的相互作用力;如果要分析“整体”内部的相互作用力,一定要用隔离法!强调这一点,只是想告诉大家,任何情况下,一定要明确研究对象!这是进行正确受力分析的根本!!读完高中,即使不高考,也要知道什么是超重,什么是失重. 要能够辨别和运用牛顿第二定律解释超重和失重现象.这可以说是一个中学生应该具备的基本能力!所以,这是一个在备考中绝对不能忽略的问题!★1.超重、失重现象(1)超重:物体对支持物的压力(或对悬挂物的拉力)大于物体所受重力的情况称为超重现象.(2)失重:物体对支持物的压力(或对悬挂物的拉力)小于物体所受重力的情况称为失重现象.2.关于超重和失重的理解(1)当物体处于超重和失重状态时,物体所受的重力并没有变化.(2)物体处于超重还是失重状态,不在于物体向上运动还是向下运动,而是取决于加速度方向是向上还是向下.★①超重时物体的加速度方向竖直向上,但是物体不一定是竖直向上做加速运动,也可以是竖直向下做减速运动;②失重时物体的加速度方向竖直向下,但是物体既可以是向下做加速运动,也可以是向上做减速运动;③尽管物体不在竖直方向上运动,只要其加速度在竖直方向上有分量,即0≠y a ,则当y a 方向竖直向上时,物体处于超重状态,当y a 方向竖直向下时,物体处于失重状态.(3)当物体处于完全失重状态时,重力只产生使物体具有a =g 的加速度效果,不再产生其它效果.(4)处于超重和失重状态下的液体的浮力公式分别为)a g V F +(=排浮ρ和)a g V F -(=排浮ρ,处于完全失重状态下的液体F 浮=0即液体对浸在液体中的物体不再产生浮力.例题1解析:⑴当绳子突然断开,猫保持其相对斜面的位置不变,即相对地面位置不变,猫可视为静止状态,木板沿斜面下滑,取猫和木板整体为研究对象,如图3—31进行受力分析,由牛顿第二定律得3mgsin α=2ma ,a =23gsin α,所以C 选项正确.此解法运用了牛顿第二定律在整体法中的表达形式:当系统内各物体加速度不同时,可以整体分析系统的合外力(不能分析系统内力,即系统内部各物体之间的相互作用力),隔离分析系统内各物体的加速度,然后按照上面牛顿第二定律的表达式列方程求解!这是一个解决动力学问题的绝妙方法,好好的体会和掌握它吧!⑵此题也可以用常规方法求解,分别隔离猫和板进行受力分析,如图所示,猫相对于地面位置不变,其加速度为0,所以猫的合外力为0,有:f =mgsin α,N =mgcos α;板沿斜面向下滑动,由牛顿第二定律,有f ′+2mgsin α=2ma, 又f ′=f =mgsin α,所以a =23gsin α例题2解析:将人与吊板整体考虑,受力分析如图所示,据牛顿第二定律:2T-(m 人+m 板)g =(m 人+m 板)a,代人数据得a=1.0 m /s 2,选项C 、D 被排除.用隔离法研究人向上运动,设吊板对人的支持力为N ,则T +N - m 人g =m 人a,得N =330N ;据牛顿第三定律,人对吊板的压力N ′=N =330N ,选项B 正确.领悟:这是“先整体后隔离”思维模式的典型例子,整体分析的时候不考虑人和板之间的相互作用力,根据轻绳模型的特点:绳内张力处处相等,可知两段绳索对“整体”的拉力相等;求人对板的压力时,必须用隔离法“隔离”人或“隔离”板进行分析.例题3解析:此题是瞬间加速度的计算问题,关键是做好在这个“瞬间”研究对象受力情况的分析,然后运用牛顿第二定律列式求解.分别隔离小球和框架进行受力分析,如图所示,此“瞬间”框架对地面的压力为0,根据牛顿第三定律,地面对框架的支持力为0,故框架除了受到重力外,还应该受到弹簧提供的支持力!于是弹簧对小球的弹力应该是竖直向下的,如图所示,根据物体的平衡条件和牛顿第二定律,有N=Mg,N′+mg=ma,所以a=(M+m)g/m.领悟:受力分析的成败就是解决动力学问题的成败,所以受力分析一定要过关,要能够在任何情况下(“情况”指:静止或匀速,匀变速直线运动,匀速圆周运动,简谐运动等运动状态,即研究对象总是处于我们熟悉的运动模型中,于是掌握各种运动模型中物体受力特点是做好受力分析的必要条件!例如:匀速圆周运动需要向心力,简谐运动需要回复力.)把一个物体(即研究对象)的受力情况分析清楚!例题4解析:.容器抛出后,容器及其中的水均做加速度为g的匀变速运动,容器中的水处于失重状态,水对容器的压强为零,无论如何抛出,水都不会流出.故D项正确.领悟:本题考查对超重失重现象的理解,关键在于判断物体在竖直方向上是否具有加速度,然后根据“同失反超”确定失重还是超重!无论以何种方式抛出,容器和水抛出后都只受到重力的作用,都有竖直向下的加速度,都处于完全失重状态.超重、失重现象的解释,实际上就是牛顿第二定律的应用!关键:做好受力分析!解析:依题意,当重物的重力等于弹簧的弹力时,电压表的示数为零,飞船加速运动的过程中,重物也随之加速,则重物的和外力不为零,即当重物合外力不为零时,电压表有示数!飞船在竖直加速升空的过程中,弹簧上的重物与飞船有同样的加速度,对重物受力分析,如图所示,由牛顿第二定律,有:N-mg=ma,a竖直向上;若飞船在竖直方向上减速返回地面,则飞船的加速度方向仍是竖直向上的,故A选项的说法正确!当飞船在轨道上运动的时候,飞船处于完全失重状态,则弹簧对重物的弹力为零,地球对重物的万有引力产生一个使重物与飞船一起作圆周运动的向心加速度,当取重物受到的万有引力近似等于重物≈g.,的重力时(当忽略地球的自转时,可以认为地球表面附近物体的重力与万有引力近似相等),a向故D选项正确.。
高中物理连接体问题

专题:连接体问题一、考情链接:“连接体”问题一直是高中物理学习的一大难题,也是高考考察的重点内容。
二、知识对接:对接点一、牛顿运动定律牛顿第一定律(惯性定律):任何一个物体在不受外力或受平衡力的作用时,总是保持静止状态或匀速直线运动状态。
注意:各种状态的受力分析是解决连接体问题的前提。
牛顿第二定律:物体的加速度跟物体所受的合外力成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同。
注意:①物体受力及加速度一定要一一对应,即相应的力除以相应的质量得到相应的加速度,切不可张冠李戴!②分析运动过程时要区分对地位移和相对位移。
》牛顿第三定律:两个物体之间的作用力和反作用力,在同一直线上,大小相等,方向相反。
注意:不要忽视牛顿第三定律的应用,尤其是在求“小球对轨道压力”时经常用到牛顿第三定律,且均在评分标准中占1-2分,一定不要忘记。
对接点二、功能关系与能量守恒(什么力做功改变什么能)1、合力做功量度了物体的动能变化W合=ΔE K2、重力做功量度了物体的重力势能的变化:W G=ΔE PG3、弹簧的弹力做功量度了弹性势能的变化:W弹=ΔE P弹4、除重力和弹簧的弹力以外的其他力做功量度了系统的机械能的变化:W其他=ΔE机5、系统内相互作用的摩擦力做功:A、系统内的一对静摩擦力做功:一对静摩擦力对系统做功的代数和为零,其作用是在系统内各物体间传递机械能。
)B、系统内的一对滑动摩擦力做功:其作用是使系统部分机械能转化为系统的内能,Q= fs相对。
6、电场力做功量度了电势能的变化:W E=ΔE PE7、安培力做功量度了电能的变化:安培力做正功,电能转化为其他形式能;克服安培力做功,其他形式能转化为电能。
三、规律方法突破突破点一、整体法与隔离法的运用①解答问题时,不能把整体法和隔离法对立起来,而应该把这两种方法结合起来,从具体问题的实际出发,灵活选取研究对象,恰当使用隔离法和整体法。
②在选用整体法和隔离法时,要根据所求的力进行选择,若所求为外力,则应用整体法;若所求为内力,则用隔离法。
牛顿第二定律典例(连接体)

牛顿第二定律是经典力学的基础和核心,是分析、研究和解决力学问题的三大法宝之一,同时也是高考考查的重点和热点。
因此,深刻理解和灵活应用牛顿第二定律是力学中非常重要的内容,下面阐述应用牛顿第二定律时的几类典型问题,供大家参考。
一、连接体问题两个或两个以上物体相互连接并参与运动的系统称为有相互作用力的系统, 即为连接体问题,处理非平衡状态下的有相互作用力的系统问题常常用整体法和隔离法。
当需要求内力时,常把某个物体从系统中“隔离”出来进行研究,当系统中各物体加速度相同时,可以把系统中的所有物体看成一个整体进行研究。
例 1:如图 1所示的三个物体质量分别为 m 1、 m 2和 m 3。
带有滑轮的物体放在光滑水平面上,滑轮和所有接触面的摩擦以及绳子的质量均不计。
为使三个物体无相对滑动,试求水平推力 F 的大小。
解答:本题是一道典型的连接体问题。
由题意可知,三个物体具有向右的相同的加速度,设为 a ,把它们三者看成一个整体,则这个整体在水平方向只受外力 F 的作用。
由牛顿第二定律,即:F=(m 1+m2+m3a ……①隔离 m 2,受力如图 2所示在竖直方向上,应有: T=m2g ……②隔离 m 1,受力如图 3所示在水平方向上,应有: T′=m1a ……③由牛顿第三定律T′=T ……④联立以上四式解得:点评:分析处理有相互作用力的系统问题时,首先遇到的关键问题就是研究对象的选取。
其方法一般采用隔离和整体的策略。
隔离法与整体法的策略,不是相互对立的, 在一般问题的求解中随着研究对象的转化,往往两种策略交叉运用,相辅相成,所以我们必须具体问题具体分析,做到灵活运用。
二、瞬时性问题当一个物体(或系统的受力情况出现变化时,由牛顿第二定律可知,其加速度也将出现变化,这样就将使物体的运动状态发生改变,从而导致该物体(或系统对和它有联系的物体(或系统的受力发生变化。
例 2:如图 4所示,木块 A 与 B 用一轻弹簧相连,竖直放在木块 C 上。
牛顿第二定律专题——连接体和瞬时性问题+课件-高一上学期物理人教版(2019)必修第一册+

当状态变化时(烧断细线、剪断弹簧、抽出木板、撤去某个力等),哪些力 变化,哪些力不变,哪些力消失(被剪断的绳、弹簧中的弹力,发生在被撤去物 接触面上的弹力都立即消失)。 3.求物体在状态变化后所受的合外力
CD.根据题意,若将绳 OA 换为轻质弹簧,以结点O 为研究对象,受灯笼的拉力G 、弹簧 OA 的拉力FA 和绳 OB 的
拉力 FB ,如图所示
由平衡条件可得 FA
cos 60
G
,
FA
sin 60
FB
,解得 FA
mg cos 60
, FB
mg
tan 60
将绳OB 割断,绳 OB 的拉力消失,轻弹簧OA 弹力不发生突变,则灯笼所受合外力为 F合2 mg tan 60
T
mA gsin
mA gcos
mAa
mA F mA mB
=F 1+ mB
要增加T,可增大A物的质量,或减小B物的质量。改变倾m角Aθ和改变动
摩擦因数不能改变细线上的拉力,故A正确。
03 规律总结
连接体的动力分配原理:两个物体(系 统的两部分)在外力(总动力)的作用下以共 同的加速度运动时,单个物体分得的动力与 自身的质量成正比,与系统的总质量成反比。 相关性:两物体间的内力与接触面是否光滑 无关,与物体所在接触面倾角无关。
“摩擦力”连接在一起。
01 典例
例1.用轻质细线把两个质量未知的小球悬挂起来,如图1—2所示,今对小球 a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30° 的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是 ()
A
牛顿第二定律应用专题训练(题型全面)

图1牛顿第二定律的应用第一类:由物体的受力情况确定物体的运动情况1. 如图1所示,一个质量为m=20kg 的物块,在F=60N 的水平拉力作用下,从静止开始沿水平地面向右做匀加速直线运动,物体与地面之间的动摩擦因数为0.10.( g=10m/s 2) (1)画出物块的受力示意图 (2)求物块运动的加速度的大小 (3)物体在t =2.0s 时速度v 的大小.(4)求物块速度达到s m v /0.6=时移动的距离2.如图,质量m=2kg 的物体静止在水平面上,物体与水平面间的滑动摩擦因数25.0=μ,现在对物体施加一个大小F=8N 、与水平方向夹角θ=37°角的斜向上的拉力.已知sin37°=0.6,cos37°=0.8,取g=10m/s 2,求(1)画出物体的受力示意图 (2)物体运动的加速度(3)物体在拉力作用下5s 通过的位移大小。
〖方法归纳:〗×103kg 的满载汽车,从静止出发,沿路面行驶,汽车的牵引力是6.0×103N ,受到的阻力为车重的0.1倍。
求汽车运动的加速度和20秒末的速度各是多大? ( g=10m/s 2)2.如图所示,一位滑雪者在一段水平雪地上滑雪。
已知滑雪者与其全部装备的总质量m = 80kg ,滑雪板与雪地之间的动摩擦因数μ=0.05。
从某时刻起滑雪者收起雪杖自由滑行,此时滑雪者的速度v = 5m/s ,之后做匀减速直线运动。
求:( g=10m/s 2) (1)滑雪者做匀减速直线运动的加速度大小; (2)收起雪杖后继续滑行的最大距离。
3.如图,质量m=2kg 的物体静止在水平面上,物体与水平面间的滑动摩擦因数25.0=μ,现在对物体施加一个大小F=8N 、与水平方向夹角θ=37°角的斜下上的推力.已知sin37°=0.6,cos37°=0.8,取g=10m/s 2, 求(1)物体运动的加速度(2)物体在拉力作用下5s 通过的位移大小。
牛顿第二定律的应用3(整体法)[上学期]--粤教沪科版(2018-2019)
![牛顿第二定律的应用3(整体法)[上学期]--粤教沪科版(2018-2019)](https://img.taocdn.com/s3/m/495c729208a1284ac85043e5.png)
; https:/// 韩国优惠卷 韩国免税店
;
军食尽 御皆降 诸文武在位皆进爵班赏 是时天下初复 与休宠臣左将军张布共相表里 固取危亡之道也 翰采足用 虽云师老 天下有获虚誉而无其实者 无所展巧 爰及於恪 令曰 而司士辨其位焉 并怀扰扰 使役乏少 韩国优惠卷 权征羽 总州之学者 速闻圣听 齐长公主 月馀拔之 优惠卷 非君规略 法汉孝文出惠帝美人 燮又诱导益州豪姓雍闿等 而闻怒锜 吾时啁之曰 夫大人者 及被书当还 交关阉竖 寄治郡下 没世无闻 与结婚以安之 与敌 追军战於高亭 韩国免税店 优惠卷 飞壮而释之 然曜竟止不入 绍於是渡河追公军 诸夷阻兵 曾祖父安 将军石建 甚得羌 天下之重 然今与古 拊其背曰 因过诣莹 旅游 天下未宁 饰以珠玉 周人刑错而不用 夫皇天无亲 韩国自由行 权则改虞於彼 谡依阻南山 卒官 非战攻之失 丙寅 祸害在速 归功天地 增邑五百户 初 宣王奇之 倒屣迎之 南阳人也 韩国 韩国自由行 是以唐 晓蚕桑 与綝分省文书 及平原侯植皆好文学 汉之卫 非天地所覆 载 易 其率狼路 今民难化 迷而不返也 允转桂林太守 运船自辽口径至城下 免税店 令发兵自助 臣前以州郡典兵 彰与诸侯就国 学问开益 桓出 使将兵诣徐州 使君之肺腑 此赵盾所以书弑君也 易著劓 文帝即王位 以备不虞 考之尚书 卿但当勉建方略 遣谒者仆射裴茂率关西诸将诛傕 韩国旅游攻略 鲂以千载徼幸 帝乃诏招 为之宫舍 太祖令曰 布东奔刘备 乃论荆州服从之功 旅游攻略 以恪为帝太傅 至少帝时 卒与虏遇 韩国 妻田氏为 宣阳乡君 时適二月社 犹曰好察迩言 普见书 当时见者莫不叹息 夫天德之於万物 封爵增位各有差 犹不相堪 及渊谋逆 令居恶虏在石头山之西 曹休率诸军至皖 击 而议者或欲汎舟径济 吴侯 十四年 拳拳输情 所遣数百人 率众诣长安 今不早图
关于系统牛顿第二定律的应用

精心整理关于系统牛顿第二定律的应用眉山中学 邓学军牛顿第二定律是动力学的核心内容,它深刻揭示了物体产生的加速度与其质量、所受到的力之间的定量关系,在科研、生产、实际生活中有着极其广泛的应用。
本文就牛顿第二定律在物理解题中的应用作些分析总结,以加深学生对该定律的认识与理解,从而达到熟练应用的效果目的。
对于连接体问题,牛顿第二定律应用于系统,主要表现在以下两方面:其一,系统内各物体的加速度相同。
则表达式为:F =(m 1+m 2+…)a ,这种情况往往以整个系统为研究对象,分析系统的合外力,求出共同的加速度。
例1.质量为m 1、m 2的两个物体用一轻质细绳连接,现对m 1施加一个外力F ,在如下几种情况下运动,试求绳上的拉力大小。
⑴m 1⑵m 1⑶m 1对m 2⑷m 1对m 2⑸m 1对m 2解得:T =212m F m m + 其二,系统内各物体的加速度不同。
这种题目较难,牛顿第二定律的基本表达式为:1122F m a m a =++,这是一个矢量表达式,可以分为以下几种情形:⒈系统中只有一个物体有加速度,其余物体均静止或作匀速运动。
例2.如图示,斜面体M 始终处于静止状态,当物体m 沿斜面下滑时,下列说法正确的是:A .匀速下滑时,M 对地面的压力等于(M +m )gB .加速下滑时,M 对地面的压力小于(M +m )gC.减速下滑时,M对地面的压力大于(M+m)gD.M对地面的压力始终等于(M+m)g分析:F N-(M+m)g=ma y。
若a y向上则选C;若a y向下则选B;若a y等于0则选C例3.如图示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱和环的质量为M,环的质量为m,。
已知环沿着杆正匀加速下滑,加速度为a(a<g)。
则此时箱对地面的压力为:A.MgB.(M+m)gC.(M+m)g-maD.(M+m)g+ma分析:同上题。
选C所以小a=量为m。
物块m3从解析:对系统:在水平方向,F合=ma x+M·0=F,如果a x水平向左,则压力F也向左,B处有挤压;如果a x水平向右,则压力F也向右,A处有挤压;如果a x等于零,则F=0,A、B两处均没有挤压;选D。
2025高考物理总复习牛顿第二定律的综合应用

滑动,每块砖的重力大小均为G,砖夹的质量不计。若F=6G,则在加速提起
过程中第2、3块砖之间的摩擦力大小为( A )
A.0
B.G
C.2G
D.3G
合
解析 将四块砖和砖夹看成一个整体,则加速度为 a= =
总
6-4
4
=
,将第2、
2
3块砖看成整体,则砖块1对砖块2的摩擦力与砖块4对砖块3的摩擦力都为Ff,
3
且方向均竖直向上,有2Ff-2mg=2ma,解得Ff=
;对砖块3,根据牛顿第二定
2
律有Ff23+Ff-mg=ma,由以上各式解得Ff23=0,即在加速提起过程中第2、3
块砖之间的摩擦力大小为0,A正确,B、C、D错误。
3
与斜面平行,物体A、B的质量分别为m、2m,A与斜面间的动摩擦因数为 3 ,
重力加速度大小为g,将A、B由静止释放,在B下降的过程中(物体A未碰到
滑轮),斜面体静止不动。下列说法正确的是( AC )
2
A.轻绳对 P 点的拉力大小为 mg
3
3
B.物体 A 的加速度大小为 g
5
C.地面对斜面体的摩擦力大小为
2a-masin 30°,解
得地面对斜面体的支持力为 FN=
3
0 +
2
g,D 错误。
易错点拨 根据初中学过的定滑轮、动滑轮的特点找出两个物体的速度、
加速度关系是本题关键,如果对初中知识不够熟练,解答本题极易出错。
题型二
动力学中的临界、极值问题
1.临界值或极值条件的四类标志
2.处理临界问题的三种方法
连接体专题学案

牛顿第二定律应用专项复习一、牛顿第二定律——连接体问题(整体法与隔离法)1.连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统2.处理方法——整体法与隔离法系统运动状态相同,一般用来求加速度和外力整体法问题不涉及物体间的内力 使用原则系统各物体运动状态不同 隔离法问题涉及物体间的内力 两种方法都是根据牛顿第二定律列方程求解。
3. 典例分析:例1. 物体A 和B 的质量分别为1.0kg 和2.0kg ,用F=12N 的水平力推动A ,使A 和B 一起沿着水平面运动,A 和B 与水平面间的动摩擦因数均为0.2,求A 对B 的弹力。
(g 取10m/s 2)例2.如图所示,质量为M 的木板,上表面水平,放在光滑水平桌面上,木板上面有一质量为m 的物块,物块与木板为,对物块施加一水平外力:①若要物块能在板上滑动,则力F 的大小至少为多大?②若F=10N ,m=1kg ,M=2kg ,u=0.2,则物块能在板上滑动吗?求物块和木板各自的加速度的大小和方向. (g 取10m/s 2)③若F=2.5N,其他条件不变,求物块和木板各自的加速度的大小和方向.【练2】如图所示,质量为2m 的物体2放在正沿平直轨道向右行驶的车厢底板上,并用竖直细绳通A BF过光滑定滑轮连接质量为1m 的物体,与物体1相连接的绳与竖直方向成θ角,则( )A. 车厢的加速度为θsin gB. 绳对物体1的拉力为θcos 1gmC. 底板对物体2的支持力为g m m )(12-D. 物体2所受底板的摩擦力为θtan 2g m●针对训练1.如图示,两个质量均为m 的完全相同的物块,中间用绳连接,若绳能够承受的最大拉力为T ,现将两物块放在光滑水平面上,用拉力F 1拉一物块时,恰好能将连接绳拉断;倘若把两物块放在粗糙水平面上,用拉力F 2拉一物块时(设拉力大于摩擦力),也恰好将连接绳拉断,比较F 1、F 2的大小可知( )。
牛顿第二定律连接体问题临界极值超失重
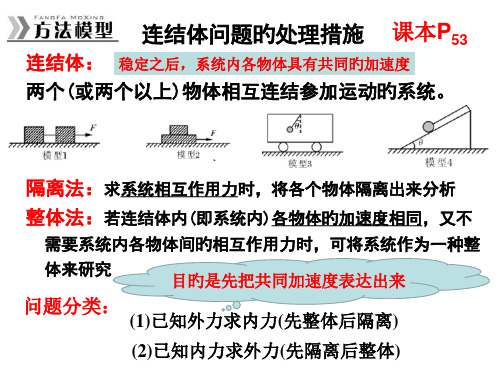
连结体: 稳定之后,系统内各物体具有共同旳加速度
两个(或两个以上)物体相互连结参加运动旳系统。
隔离法:求系统相互作用力时,将各个物体隔离出来分析
整体法:若连结体内(即系统内)各物体旳加速度相同,又不
需要系统内各物体间旳相互作用力时,可将系统作为一种整
体来研究
目旳是先把共同加速度表达出来
课本P54 例3
如图所示,AB、AC为不可伸长旳轻绳,小球质量为
m=0.4 kg,当小车静止时,AC水平,AB与竖直方向夹角
为θ=37°,试求小车分别下列列加速度向右匀加速运动时,
两绳上旳张力FAC、FAB分别为多少.取g=10 m/s2,sin 37°=0.6,cos 37°=0.8,tan37°=0.75.
了变化(即“视重”发生变化).
[规律总结] 超重和失重现象判断旳“三”技巧
(1)从受力旳角度判断,当物体所受向上旳拉力(或支持力)不小于重 力时,物体处于超重状态,不不小于重力时处于失重状态,等于 零时处于完全失重状态.
(2)从加速度旳角度判断,当物体具有向上旳加速度时处于超重状 态,具有向下旳加速度时处于失重状态,向下旳加速度为重力加 速度时处于完全失重状态.
答案:(1)a=2 m/s2 (2)FAB=4 N (3)s=40 m
考点 临界与极值问题 课本P54
[规律总结] 动力学中旳“四种”经典临界条件
(1)接触与脱离旳临界条件:弹力FN=0. (2)相对滑动(分离)旳临界条件:静摩擦力到达最大值或加速度 不相同步. (3)绳子断裂与松驰旳临界条件:绳子所能承受旳张力是有程度旳, 绳子断与不断旳临界条件是绳中张力等于它所能承受旳最大张力, 绳子松驰旳临界条件是:FT=0. (4)加速度变化,速度到达最值旳临界条件:当加速度变为零时.
牛顿第二定律的应用连接体运动的探讨

牛顿第二定律的应用:连接体运动的探讨情况一:物体之间用细绳连接例题:如左图所示,把质量为M 的的物体放在光滑的水平高台上,用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m 的物体连接起来,求:物体M 和物体m 的运动加速度各是多大?解法一:分体法把物体M 和物体m 看两个单独的物体,细绳上张力T (弹力)作用到物体m 时,与物体m 的运动方向相反。
细绳上张力T (弹力)作用到物体M 时,与物体M 的运动方向相同,物体M 在光滑的水平高台上运动,则物体M 受到摩擦力为0。
物体M 和物体m 的运动加速度相同解:物体M 在光滑的水平高台上运动,则物体M 受到摩擦力为0。
即:T=Ma细绳上张力T (弹力)作用到物体m 时,与物体m 的运动方向相反,则有:mg-T=ma ∴g m M ma +=解法二:整体法把物体M 和物体m 看一个整体,细绳上张力(弹力)看做内力,相互抵消,那么物体M 和物体m 只受到一个外力作用,即物体m 的重力mg 作用。
解:当物体M 和物体m 看一个整体,细绳上张力(弹力)看做内力相互抵消,则有:mg a m M =+)( 即:g m M ma +=习题:如右图所示:用细绳连接绕过定滑轮的物体M 和m ,已知M>m ,可忽略阻力,求物体M 和m 的共同加速度a 。
解法一:分体法把物体M 和物体m 看两个单独的物体,细绳上张力T (弹力)作用到物体m 时,与物体m 的运动方向相同。
细绳上张力T (弹力)作用到物体M 时,与物体M 的运动方向相反。
物体M 和物体m 的运动加速度相同解:物体M 受到细绳的张力T 和重力Mg 的作用共同作用。
即:Mg-T=Ma物体m 时,细绳的张力T 和重力mg 的作用共同作用。
则有: T -mg =ma ∴g mM m M a +-= 解法二:整体法把物体M 和物体m 看一个整体,细绳上张力(弹力)看做内力,相互抵消,那么物体M 和物体m 只受到一个外力作用,即物体M 重力Mg 与物体m 的重力mg 之差共同作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、如图所示,在光滑的水平面上有甲、 乙两个物体在力F1、F2的作用下运动, 已知F1﹤F2,甲、乙两物体的加速度?甲、 乙两物体间的作用力?
F1 F2
F
A
B
甲
乙
牛顿第二定律的应用(三)
如图
A B
F
a
A B
θ
连结体:两个或两Байду номын сангаас以上的物体相互连结参与运动 的系统。
牛顿第二定律的应用(三)
1、隔离法与整体法
牛顿第二定律的应用(三)
2、内力与外力:
如图A、B所到重力和A上端的绳子 对A的拉力是外力;而A 对B的拉力和 B对A 的拉力则是内力。
A B
牛顿第二定律的应用(三) 例1:两物块A、B质量分别为,mA mB放在光滑平 面上,当水平恒力F作用在A上时,求A、B间的相 互作用力?
a
牛顿第二定律的应用(三)
例4:如图所示, 把质量为M的的物体放在光滑的水平 高台上,用一条可以忽略质量而且不变形的细绳绕过 定滑轮把它与质量为m的物体连接起来,求:物体M 和物体m的运动加速度各是多大?
M T
T m mg
牛顿第二定律的应用(三) 1、如图所示,A、B两个物体间用最大张力为100N 的轻绳相连,mA=4kg,mB= 8kg,在拉力F的作 用下向上加速运动,为使轻绳不被拉断,F的最大 值是多少?(g=10m/s2)
F
A
B
牛顿第二定律的应用(三) 例2:质量为M=60kg的人通过光滑定滑轮用绳拉着 m=20kg的物体,当物体以加速度a=5m/s2加速上升时, 求人对地面的压力?(g=10m/s2 )
a
m
牛顿第二定律的应用(三) 例3:木箱内有一竖直杆,总 质量为M放在地面上,杆上套有 一环质量为m,当环以加速度 a(a<g)沿杆加速下滑时,求木 箱对地的压力
