Matlab绘图系列之高级绘图

合集下载

matlab 回旋曲线画法

回旋曲线画法是利用Matlab软件进行绘图时常用的一种技术，它能够以一定的数学公式为基础，通过一系列的运算和绘图步骤，最终在图像界面上呈现出具有艺术美感的回旋曲线。

那么，如何使用Matlab软件进行回旋曲线的绘制呢？下面将介绍详细的步骤和方法，以使读者能够清晰地掌握绘制回旋曲线的过程。

1. 准备工作在开始绘制回旋曲线之前，首先得准备好Matlab软件。

确保已经正确安装并打开软件，并且能够熟练操作Matlab的基本绘图功能。

2. 设定参数在Matlab中，绘制回旋曲线需要设定一系列的参数，如曲线的方程、图像的大小和比例等。

通常采用极坐标系来描述回旋曲线，因此需要设定极径和角度的范围。

3. 编写代码利用Matlab的编程功能，编写回旋曲线的绘制代码。

通常采用for循环结合极坐标系的数学公式来实现回旋曲线的绘制，代码的编写需要具备一定的数学基础和编程能力。

4. 运行程序在编写完回旋曲线的绘制代码后，将代码输入到Matlab的命令窗口或脚本文件中，并执行程序。

在程序执行完毕后，将在Matlab的图像界面上显示出绘制好的回旋曲线图案。

5. 调整优化绘制出的回旋曲线可能不尽如人意，可能需要进行一些调整和优化。

比如调整曲线的颜色、线型和粗细，使图案更加美观和符合要求。

6. 结果展示将绘制好的回旋曲线图案展示给其他人，或者保存为图片文件进行共享。

也可以将绘制过程和结果发布到Matlab社区或论坛上，与他人交流和学习经验。

通过以上步骤，我们可以清晰地了解到使用Matlab软件进行回旋曲线的绘制过程。

借助Matlab强大的数学计算和图像处理功能，我们能够轻松绘制出令人赏心悦目的回旋曲线，为科研和艺术创作提供了便利和可能。

希望本文能够对读者有所帮助，谢谢！绘制回旋曲线是Matlab中的一项高级绘图技术，在科学研究和工程领域具有广泛的应用。

随着计算机软件和硬件的不断发展，利用Matlab绘制回旋曲线也变得更加简便和高效。

Matlab绘图高级部分

18 for i = 1:n
19Biblioteka row = izs(i);
20
fvcd(fvd(row,:)) = i;
21 end
22 set(ch,'FaceVertexCData',fvcd)
23 %图片会以渐变的方式着色，效果非常不错
24 subplot(1,3,3);
25 h=bar(Z);
26 ch = get(h,'Children');
50 end
51 set(ch,'FaceVertexCData', fvcd); % Apply the vertex coloring
52 set(ch,'EdgeColor','k');
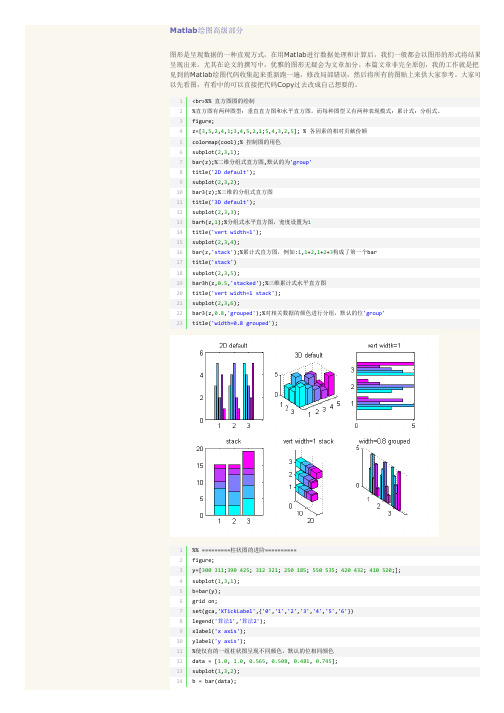
1 %% 绘制统计直方图 2 %hist(y)：如果y是向量，则把其中元素放入10个条目中，且返回每条中的元素的个数；如果y为矩阵，则分别对 3 每列进行处理，显示多组条形。 4 %[n,xout]=hist(y,x)：非递减向量x的指定bin的中心。向量xout包含频率计数与条目的位置。 5 x=‐10:.1:10; 6 y1=randn(2008,1); 7 y2=randn(2008,3); 8 figure; 9 colormap(winter); 10 subplot(2,2,1); 11 hist(y1);%把其中元素放入10个条目中 12 title('y1为向量，default,n=10'); 13 subplot(2,2,2); 14 hist(y2);%分别对每列进行处理，显示多组条形 15 title('y2为矩阵'); 16 subplot(2,2,3); 17 hist(y1,x);%用户也可以使用[n,xout]=hist(y1,x);bar(xout,n)绘制条形直方图 18 title('向量x指定条目'); 19 subplot(2,2,4); 20 hist(y2,1000);%第二个参数为标量时指定bin的数目

3Matlab高级绘图V2.0

MATLAB语言基础实习指导实习三MATLAB高级绘图目的：通过实习MA TLAB高级绘图指令，能够绘制各种标准图件以及一些特殊图件要求：掌握MATLAB二维绘图指令plot（semilogx、semilogy、loglog），掌握图形加注的各个函数，掌握三维绘图指令mesh、surf，掌握三维图形的加注与修饰，掌握MATLAB绘图颜色控制；熟悉特殊二维图形的绘图函数。

一、二维绘图1．plot（1）单窗口、单曲线绘图>>x=0:0.1:2*pi;y=sin(x);plot(x,y);确定MATLAB绘图的默认线型；把plot(x,y)改为plot(y)看有何异同，为什么？（2）单窗口、多曲线绘图>>x=0:0.1:2*pi;y1=sin(x);y2=cos(x);y3=cos(x)+1;plot(x,y1,x,y2,x,y3);确定MATLAB绘图的默认色序，把plot(x,y1,x,y2,x,y3)改为plot(x,y1);plot(x,y2);plot(x,y3)看有何区别，为什么？（3）开关格式绘图>>x=0:0.1:2*pi;y=sin(x);plot(x,y,’r-’,x,y,’b*’);掌握MATLAB的点型和线型，掌握MATLAB的颜色指定字母。

（4）单窗口分幅绘图subplot的两种调用格式：subplot(nrow,ncol,nfig);subplot(‘position’,[left bottom width height]);第一种格式的调用：t=0:0.1:2*piy=sin(t);y1=sin(t+0.25);y2=sin(t+0.5);subplot(3,1,1);plot(t,y)subplot(3,1,2);plot(t,y3)subplot(3,1,3);plot(t,y2)查看运行结果，为什么？第二种格式的调用：t=0:0.1:2*piy=sin(t);y1=sin(t+0.25);y2=sin(t+0.5);subplot('position',[0.05,0.55,0.4,0.45]);plot(t,y)subplot('position',[0.55,0.55,0.4,0.45]);plot(t,y3)subplot('position',[0.35,0.05,0.4,0.45]);plot(t,y2)查看运行结果，注意MATLAB中对窗口大小的指定可以使用归一化坐标，如果把subplot('position',[0.35,0.05,0.4,0.45]);改成subplot('position',[0.35,0.05,0.4,0.55]);查看运行结果，为什么？（5）多窗口绘图%figure(n) ——创建窗口函数，n为窗口顺序号。

第6章 MATLAB高级图形设计

%h_obj是图形对象的句柄； %funname是函数名，每个创建的图形对象函数名与对象
名相同； %'PropertyName'是属性名，属性名是字符串； %PropertyValue是属性值。
例： >> h_f=figure('Position',[200 300 500 400]) >> h_a1=axes('position',[0.1,0.05,.85,.85]) %创建条形图的坐标轴练习
gcf %查找符合指定属性值的对象句柄
例
第6章 MATLAB高级图形设计
3. 句柄图形对象属性的获取和设置 a=set(h_obj,'PropertyName',PropertyValue,...)
%设置图形对象的属性值
a=get(h_obj,'PropertyName')
Uicontrol 控件对象
Uicontextmenu 上下文菜单
Uimenu 菜单
Uipanel 面板
Uitoolbar 工具栏
第6章 MATLAB高级图形设计
6.1.2 句柄图形对象的操作
1. 创建句柄图形对象 h_obj＝
funname('PropertyName',PropertyValue,……)
%获取图形对象的属性值PropertyValue
第6章 MATLAB高级图形设计
例6-2 使用句柄图形对象绘制正弦曲线

>> x=0:0.1:10; >> y=sin(x); %创建无标题窗口 >> h_f=figure('Position',[200 300 300 300],'menubar','none'); >> h_a1=axes('position',[0.1,0.1,.8,.8]); >> h_t=title(h_a1,'正弦曲线'); %创建标题 >> h_l=line(x,y); %设置坐标轴刻度及刻度标注 >> set(gca,'xtick',[0 pi/2 pi 3*pi/2 2*pi 5*pi/2 3*pi]) >> set(gca,'xticklabel',{'0','pi/2','pi','3*pi/2','2pi','5*pi/2','3pi'}) >> set(gca,'xgrid','on','ygrid','on'); %设置坐标轴属性 >> set(h_l,'linewidth',2) %设置线属性 >> set(get(h_t,'parent'),'color','y') %设置标题的父对象属性 %创建矩形框 >> h_ann0=annotation(gcf,'rectangle',[0.1 0.5 .8 0.4],... 'FaceAlpha',.7,'FaceColor','red');

教你如何用matlab绘图(全面)

强大的绘图功能是Matlab的特点之一，Matlab提供了一系列的绘图函数，用户不需要过多的考虑绘图的细节，只需要给出一些基本参数就能得到所需图形，这类函数称为高层绘图函数。

此外，Matlab还提供了直接对图形句柄进行操作的低层绘图操作。

这类操作将图形的每个图形元素（如坐标轴、曲线、文字等）看做一个独立的对象，系统给每个对象分配一个句柄，可以通过句柄对该图形元素进行操作，而不影响其他部分。

本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法，在此基础上，再介绍可以操作和控制各种图形对象的低层绘图操作。

一．二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。

可以采用不同的坐标系，如直角坐标、对数坐标、极坐标等。

二维图形的绘制是其他绘图操作的基础。

一．绘制二维曲线的基本函数在Matlab中，最基本而且应用最为广泛的绘图函数为plot，利用它可以在二维平面上绘制出不同的曲线。

1．plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图，要提供一组x坐标和对应的y坐标，可以绘制分别以x和y为横、纵坐标的二维曲线。

plot函数的应用格式plot(x,y) 其中x,y为长度相同的向量，存储x坐标和y坐标。

例51 在[0 , 2pi]区间，绘制曲线程序如下：在命令窗口中输入以下命令>> x=0:pi/100:2*pi;>> y=2*exp(-0.5*x).*sin(2*pi*x);>> plot(x,y)程序执行后，打开一个图形窗口，在其中绘制出如下曲线注意：指数函数和正弦函数之间要用点乘运算，因为二者是向量。

例52 绘制曲线这是以参数形式给出的曲线方程，只要给定参数向量，再分别求出x,y向量即可输出曲线：>> t=-pi:pi/100:pi;>> x=t.*cos(3*t);>> y=t.*sin(t).*sin(t);>> plot(x,y)程序执行后，打开一个图形窗口，在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量，这是最常见、最基本的用法。

MATLAB高级图形处理教程()

• 句柄是存取图形对象唯一规范识别符。不同对象的句柄不可能重复和混淆。
• 每个计算机，根对象只有一个，即屏幕。它的句柄总是数字0。而图形窗（Figure Windows）的句柄总是正整数，它用来标识图形窗的序号。除以上两种对象外，其余对象的句柄则是双精度浮点数。
• 注意：对根屏幕、图形窗对象来说，数字可直接作为调用对象的句柄。但不要企图通过直接输入浮点数，作为其他对象的句柄；这些对象的句柄只能由相关指令运作而得。
axes 创建轴
line
创建线
surface 创建面
h=axes(‘position’,[left,bottom,width,height]) 定义坐标盒的位置和尺寸
h= line(x,y,z) 绘制向量x,y,z确定的直线。如果不指定z，则在x-y平面上画线
h= surface(x,y,z,c) x,y,z定义三维曲面，c是色彩矩阵。
创建对象的低层指令（2）
指令名功能
调用格式举例
rectangle 创建方 h=rectangle(’position’,[x,y,w,h],’curvature’[xc,yc])
x,y左下顶点坐标，w,h长方形的高和宽；xc,yc曲率
patch image
创建块创ห้องสมุดไป่ตู้象
h=patch(’faces’,fac,’vertices’,vert) vert为顶点矩阵，fac为定义多边形的顶点序号矩阵
• 每个图形对象可以被独立地操作。 • 在MATLAB中生成的每个具体图形都由
若干不同对象构成。每个具体图形不必包含全部对象，但每个图形必须具备根对象（根屏幕）和图形窗。
2、对象句柄
• 每个具体对象都有一个“与生俱来、终生不变”的独特“身份（Identifier）”，即句柄（Handle）。

MATLAB第五讲 MATLAB高级图形绘制技术

subplot(221), ellipsoid(0,0,0,1,2,3, 3),title('N=3') subplot(222), ellipsoid(0,0,0,1,2,3, 6),title('N=6') subplot(223), ellipsoid(0,0,0,1,2,3),title('N=20') subplot(224), ellipsoid(0,0,0,1,2,3, 50),title('N=50')
5.2 其他三维图形绘制技术
例子：
[x,y]=meshgrid(-3:0.1:3,-2:0.1:2); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); surfl(x,y,z) light('pos',[-3 2 1.5])；shading flat;
5.2 其他三维图形绘制技术
2 1.5 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2 0 2 1 0.5 0 -0.5 -1 2 0 -2 -2 2 0
5.2 其他三维图形绘制技术
瀑布式曲面 waterfall(x, y, z )
[x,y]=meshgrid(-3:0.1:3,-2:0.1:2); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); waterfall(x, y, z)
N=6
1
1
1
1
5.2 其他三维图形绘制技术
三维表面网格图： mesh(x, y, z, c) x, y 分别构成该曲面的 x 和 y 矩阵 z 为高度矩阵, c 为颜色矩阵一般来说， x, y 可以由函数 meshgrid 函数来生成。

Matlab绘图-很详细,很全面

Matlab绘图强大的绘图功能是Matlab的特点之一，Matlab提供了一系列的绘图函数，用户不需要过多的考虑绘图的细节，只需要给出一些基本参数就能得到所需图形，这类函数称为高层绘图函数。

此外，Matlab还提供了直接对图形句柄进行操作的低层绘图操作。

这类操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄，可以通过句柄对该图形元素进行操作,而不影响其他部分。

本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法,在此基础上，再介绍可以操作和控制各种图形对象的低层绘图操作。

一．二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。

可以采用不同的坐标系，如直角坐标、对数坐标、极坐标等。

二维图形的绘制是其他绘图操作的基础.一．绘制二维曲线的基本函数在Matlab中，最基本而且应用最为广泛的绘图函数为plot，利用它可以在二维平面上绘制出不同的曲线。

1．plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图，要提供一组x坐标和对应的y坐标，可以绘制分别以x和y为横、纵坐标的二维曲线。

plot函数的应用格式plot(x，y) 其中x，y为长度相同的向量，存储x坐标和y坐标。

例51 在[0 ，2pi］区间，绘制曲线程序如下:在命令窗口中输入以下命令〉〉x=0：pi/100：2＊pi；>〉y=2*exp（-0。

5*x).*sin（2*pi*x)；>> plot（x,y）程序执行后，打开一个图形窗口，在其中绘制出如下曲线注意：指数函数和正弦函数之间要用点乘运算，因为二者是向量。

例52 绘制曲线这是以参数形式给出的曲线方程，只要给定参数向量，再分别求出x,y向量即可输出曲线：〉〉t=-pi：pi/100:pi;〉> x=t.*cos(3*t）;>> y=t.*sin（t）.*sin（t)；>〉plot（x，y）程序执行后，打开一个图形窗口，在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量，这是最常见、最基本的用法。

Matlab的高级绘图

subplot(3,1,1);plot(t,y); subplot(3,1,2);plot(t,y1); subplot(3,1,3);plot(t,y2);
4. 多窗口绘图
figure(n) —— 创建窗口函数，n为窗口顺序号。
t=0:pi/100:2*pi; y=sin(t);y1=sin(t+0.25);y2=sin(t+0.5); plot(t,y) %—— 自动出现第一个窗口 figure(2) plot(t,y1) %—— 在第二窗口绘图 figure(3) plot(t,y2) %——在第三窗口绘图
t=0:pi/50:10*pi;plot3(t,sin(t),cos(t),'r:')
例：二维图形在三维空间的排列
x=linspace(0,3*pi); %x轴的数据 z1=sin(x); %在x-z的平面内画图 z2=sin(2*x); z3=sin(3*x); y1=zeros(size(x));%数据的预定义 y3=zeros(size(x)); y2=y3/2; plot3(x,y1,z1,x,y2,z2,x,y3,z3); grid on; xlabel('x-axis');ylabel('y-axis');zlabel('z-axis'); title('sin(x),sin(2x),sin(3x)');
或plot(x1,y1,’s1’,x2,y2,’s2’，…)
S的标准设定值如下：
字母 y m c r g b w 白色黑色
标点： -. --
线型线型实线点线点虚线虚线
顶点标记
类型
符号
实点

MATLAB进阶的绘图功能

MATLAB进阶的绘图功能横轴和纵轴的控制☆☆☆☆☆要控制绘图的横轴及纵轴比例，可以用axis配合下列的相关的选项：上述的各个指令的语法也可以将关键字放在括弧内的单引号之间，如axis(' ')。

以下是应用axis的范例：>> x=linspace(0,2*pi,30); y=sin(x); z=cos(x);>> plot(x,y,x,z)>> axis off>> axis on>> axis('square','equal')>> axis('xy','normal')☆☆☆☆☆子图☆☆☆☆☆要将数个相关的图画在同一页时，可以用subplot这个指令。

其语法为subplot(m,n,p)，其中m,n代表绘图成m x n个子图，m表示在y方向有m个图，n表示在x 方向有n个图，p是代表第几个子图。

下例是以subplot分别画出线性及对数尺度的四个子图：>> x=[0 2 5 7 10 12 15 17 20 21];>> y=[0.1 0.2 0.5 0.6 0.9 1 1.2 1.26 1.22 1.2];>> subplot(2,2,1), plot(x,y) % 画左上角的图>> subplot(2,2,2), semilogx(x,y) % 画右上角的图>> subplot(2,2,3), semilogy(x,y) % 画左下角的图>> subplot(2,2,4), loglog(x,y) % 画右下角的图☆☆☆☆☆图形放大及缩小☆☆☆☆☆zoom指令可以将图形放大或缩小，若要将图形放大时用zoom on，zoom out，当不再须要放大或缩小图形时用zoom off。

Matlab绘图教程大量实例

图形上添加希腊字母、数学符号及公式等内容。例如，text(0.3,0.5,‘sin({\omega}t+{\beta})’)将得到标注效果sin(ωt+β)。
例7 在0≤x≤2区间内，绘制曲线y1=2e-0.5x和 y2=cos(4πx)，并给图形添加图形标注。
程序如下：
x=0:pi/100:2*pi;
极坐标图
polar函数用来绘制极坐标图，其调用格式为： polar(theta,rho,选项) 其中theta为极坐标极角，rho为极坐标矢径，选项
旳内容与plot函数相同。例12 绘制r=sin(t)cos(t)旳极坐标图，并标识数据点。程序如下： t=0:pi/50:2*pi; r=sin(t).*cos(t); polar(t,r,'-*');
plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)
例6 在同一坐标内，分别用不同线型和颜色绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)，标识两曲线交叉点。
程序如下：
x=linspace(0,2*pi,1000);
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
(2) 当输入参数有矩阵形式时，配正确x,y按相应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵旳列数。
例3 分析下列程序绘制旳曲线。 x1=linspace(0,2*pi,100); x2=linspace(0,3*pi,100); x3=linspace(0,4*pi,100); y1=sin(x1); y2=1+sin(x2); y3=2+sin(x3); x=[x1;x2;x3]'; y=[y1;y2;y3]'; plot(x,y,x1,y1-1)

matlab figure的用法

文章标题：探索MATLAB Figure的用法1. 引言MATLAB作为一种常用的科学计算软件，其图形绘制功能十分强大。

其中，Figure作为MATLAB中的绘图窗口，提供了丰富的功能和灵活的操作方式，能够帮助用户实现各种复杂的图形展示和数据可视化。

在本文中，将深入探讨MATLAB Figure的用法，帮助读者更好地理解和应用这一功能。

2. MATLAB Figure的基本操作在MATLAB中，Figure是用来显示图形的窗口。

通过简单的命令，可以创建、操作和定制Figure窗口。

在创建Figure时，可以指定标题、大小、位置等属性，以及添加各种绘图元素，如曲线、散点图、柱状图等。

通过设定坐标轴范围、刻度、标签等属性，可以使图形更加清晰、直观。

还可以通过设置图例、注释和标题等元素，使图形更具可读性和美观性。

3. MATLAB Figure的高级功能除了基本的图形绘制功能外，MATLAB Figure还提供了丰富的高级功能，如图形交互、三维绘图、动态图形、多图合并等。

通过设置交互式图形，可以让用户与图形进行交互，实现数据筛选、放大缩小、数据标注等操作。

在三维绘图方面，MATLAB Figure可以实现3D曲面、立体图、体绘图等，展示更加复杂和丰富的数据结构。

也可以利用动态图形功能，实现对数据的实时展示和动态变化的可视化。

通过多图合并，可以将多个图形组合在一个Figure窗口中，进行比较和分析。

4. 个人观点和理解在我看来，MATLAB Figure的用法不仅仅限于简单的图形展示，更重要的是其在科学计算和数据分析中的应用。

通过合理地利用MATLAB Figure的功能，可以实现对复杂数据的可视化和分析，进而发现数据中的规律和特点。

也可以借助MATLAB Figure，与其他功能模块结合，实现对数据的处理和解读。

对MATLAB Figure的深入了解与熟练运用，可以帮助我们更好地进行科学研究和工程应用。

第五章 matlab绘图ppt课件

16.07.2020
.
17
给坐标加网格线用grid命令来控制。grid on/off命令控制是画还是不画网格线，不带参数的grid命令在两种状态之间进行切换。给坐标加边框用box命令来控制。box on/off命令控制是加还是不加边框线，不带参数的box命令在两种状态之间进行切换。
例5-8 在同一坐标中，可以绘制3个同心圆，并加坐标控制。
当输入参数是复数矩阵时，则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
16.07.2020
.
6
2. 含多个输入参数的plot函数
调用格式为：
plot(x1,y1,x2,y2,…,xn,yn)
(1) 当输入参数都为向量时，x1和y1，x2和 y2，…，xn和yn分别组成一组向量对，每一组向量对的长度可以不同。每一向量对可以绘制出一条曲线，这样可以在同一坐标内绘制出多条曲线。
16.07.2020
.
7
(2) 当输入参数有矩阵形式时，配对的x,y按对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
例5-3 分析下列程序绘制的曲线。
16.07.2020
.
8
3. 具有两个纵坐标标度的图形
在MATLAB中，如果需要绘制出具有不同纵坐标标度的两个图形，可以使用plotyy 绘图函数。调用格式为：
例5-2 绘制曲线。
16.07.2020
.
3
plot函数最简单的调用格式是只包含一个输入参数：
plot(x)
在这种情况下，当x是实向量时，以该向量元素的下标为横坐标，元素值为纵坐标画出一条连续曲线，这实际上是绘制折线图。
16.07.2020

matlab的tplot函数

MATLAB是一种被广泛应用于科学计算和工程领域的高级编程语言和数值计算环境。

其丰富的函数库和强大的绘图能力使其成为工程师和科学家们重要的工具之一。

在MATLAB中，tplot函数是用于绘制时间序列数据的重要工具，本文将对tplot函数进行详细介绍和使用方法分析。

一、tplot函数的基本介绍tplot函数是MATLAB中用于绘制时间序列数据的函数，其基本语法如下：tplot(Y)其中Y是一个包含时间序列数据的向量或矩阵。

当Y为向量时，tplot 函数将绘制出Y的时间序列图像；当Y为矩阵时，tplot函数将绘制出矩阵各列的时间序列图像。

二、tplot函数的参数设置tplot函数有许多可调参数，用于设置绘图的样式和格式。

其中最常用的参数包括：1. tplot(Y, 'LineSpec')：用于设置曲线的样式和颜色，例如'r-'表示红色实线，'g--'表示绿色虚线等；2. tplot(Y, Name, Value)：用于设置曲线的属性，例如'LineWidth'表示设置曲线的宽度，'Marker'表示设置数据点的标记样式等；3. tplot(Y, x)：用于设置时间轴的坐标，其中x为时间序列数据对应的时间坐标。

三、tplot函数的使用示例下面通过一个简单的示例来演示tplot函数的使用方法：```matlabt = 0:0.1:10;y = sin(t);tplot(y, 'r-')xlabel('Time')ylabel('Amplitude')title('Sin Wave')```在上面的示例中，我们首先生成了一个时间序列t，然后计算出对应的正弦曲线y，最后使用tplot函数绘制出了正弦曲线的时间序列图像，并设置了曲线的颜色为红色。

四、tplot函数的应用领域由于tplot函数具有绘制时间序列数据图像的功能，因此在工程领域和科学研究中具有广泛的应用。

Matlab绘图系列之高级绘图

Matlab绘图系列之高级绘图Matlab绘图系列之高级绘图一、目录1.彗星图二维彗星图三维彗星图2.帧动画3.程序动画4.色图变换5.V oronoi图和三角剖分V oronoi图三角剖分6.四面体7.彩带图彩带图三维流彩带图8.伪彩图9.切片图切片图切片轮廓线图10.轮廓图显示轮廓线显示围裙瀑布效果带光照模式的阴影图11.函数绘图轮廓线、网格图、曲面图、轮廓网格图轮廓曲面图、二维曲线、极坐标曲线图、自定义函数12.三维图形控制视点灯光效果色彩控制二、图形示例1．彗星图二维彗星图t=0:.01:2*pi;x=cos(2*t).*(cos(t).^2);y=sin(2*t).*(sin(t).^2);comet(x,y);title('二维彗星轨迹图')hold onplot(x,y)三维彗星图a=12;b=9;T0=2*pi;%T0是轨道的周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2);%地球与另一焦点的距离th=12.5*pi/180;%未经轨道与x-y平面的倾角E=exp(-t/20);%轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t));plot3(x,y,z,'g')%画全程轨线hold on,sphere(20);%画地球axis offtitle('卫星返回地球示例')x1=-18*T0;x2=6*T0;y1=-12*T0;y2=12*T0;z1=-6*T0;z2=6*T0;axis([x1 x2 y1 y2 z1 z2])% axis([-15 10 -15 10 -10 10])axis equalcomet3(x,y,z,0.02);%画运动轨线hold off2．帧动画Z=peaks;surf(Z)%绘制网格表面图axis tightset(gca,'nextplot','replacechildren');%设定axis覆盖重画模式title('帧动画播放示例')for j=1:20surf(sin(2*pi*j/20)*Z,Z)%重新绘制网格表面图，这里后面一个Z 当成了颜色矩阵F(j)=getframe;%创建帧endmovie(F,20)%播放动画20次3．程序动画t=0:pi/50:10*pii=1;h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none');%设定擦除模式grid onaxis([-2 2 -2 2 -1 10*pi])title('程序动画示例')for i=2:length(t)set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));drawnowpause(0.01)end4．色图变换load spineimage(X)colormap coolspinmap(10)5．V oronoi图和三角剖分V oronoi图rand('state',5)x=rand(1,10);y=rand(1,10);subplot(131)voronoi(x,y);%绘制voronoi图形axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(132)[vx,vy]=voronoi(x,y);plot(x,y,'r+',vx,vy,'b-');%应用返回值绘制axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(133)rand('state',5);x=rand(10,2);[v,c]=voronoin(x);%返回值v参数维voronoi顶点矩阵，返回值c参数为voronoi元胞数组for i=1:length(c)if all(c{i}~=1)patch(v(c{i},1),v(c{i},2),i);%应用色图iendendaxis equalaxis([-0.2 1.6 -0.5 2.5])box on三角剖分[x,y]=meshgrid(1:15,1:15);tri=delaunay(x,y);z=peaks(15);trimesh(tri,x,y,z)6．四面体d=[-1 1];[x,y,z]=meshgrid(d,d,d);%定义一个立方体x=[x(:);0];y=[y(:);0];z=[z(:);0];%[x,y,z]分别为加上中心的立方体顶点X=[x(:) y(:) z(:)];Tes=delaunayn(X);%返回m×n的数组值tetramesh(Tes,X);%绘制四面体图camorbit(20,0);%旋转摄像目标位置7．彩带图彩带图[x,y]=meshgrid(-3:.5:3,-3:.1:3);z=peaks(x,y);ribbon(y,z)三维流彩带图load wind%打开保存的数据lims=[100.64 116.67 17.25 28.75 -0.02 6.86];%定义坐标轴范围[x,y,z,u,v,w]=subvolume(x,y,z,u,v,w,lims);%lims来定义数据子集[sx sy sz]=meshgrid(110,20:5:30,1:5);%定义网格点verts=stream3(x,y,z,u,v,w,sx,sy,sz,.5);%计算彩带顶点cav=curl(x,y,z,u,v,w);%计算卷曲角速度wind_speed=sqrt(u.^2+v.^2+w.^2);%计算流速h=streamribbon(verts,x,y,z,cav,wind_speed,2);%绘制流彩带图view(3)8．伪彩图n=6%定义轮数r=(0:n)'/n;%定义轮的半径theta=pi*(-n:n)/n;%定义轮的扇区角X=r*cos(theta);Y=r*sin(theta);%定义网格顶点C=r*cos(2*theta);%定义色图pcolor(X,Y,C)%绘制伪彩图axis equal tight 9．切片图切片图[x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2);v = x.*exp(-x.^2-y.^2-z.^2);xslice = [-1.2,.8,2]; yslice = 2; zslice = [-2,0];slice(x,y,z,v,xslice,yslice,zslice)colormap hsv切片轮廓线图[x y z v]=flow;%打开水流数据h=contourslice(x,y,z,v,[1:9],[],[0],linspace(-8,2,10));%切片轮廓线view([-12 30])10．轮廓图显示轮廓线[x,y,z]=peaks;subplot(1,2,1)meshc(x,y,z);%同时画出网格图与轮廓线title('meshc 网格图与轮廓线')axis([-inf inf -inf inf -inf inf]);subplot(1,2,2)surfc(x,y,z);%同时画出曲面图与轮廓线title('surfc 曲面图与轮廓线')axis([-inf inf -inf inf -inf inf]);显示围裙[x y z]=peaks;meshz(x,y,z);瀑布效果[X,Y,Z]=peaks(30);waterfall(X,Y,Z)带光照模式的阴影图[x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);surfl(x,y,z);shading interp%着色处理colormap(gray);%灰度处理axis([-3 3 -3 3 -8 8])11．函数绘图轮廓线、网格图、曲面图、轮廓网格图%图1绘制轮廓线、网格图、曲面图、轮廓网格图subplot(221)f=['3*(1-x)^2*exp(-(x^2)-(y+1)^2)-10*(x/5-x^3-y^5)*exp(-x^2-y^2)-1/3*exp(-(x+1)^2-y^2)'];%定义双变量x、y的函数式ezcontour(f,[-3,3],49)%x、y为[-3 3]，网格为49×49 subplot(222) ezmesh('sqrt(x^2+y^2)');subplot(223)ezsurf('real(atan(x+i*y))')%经过滤波，如果相同数据surf绘图没有滤波subplot(224)ezmeshc('y/(1+x^2+y^2)',[-5,5,-2*pi,2*pi])%x、y的数值范围分别为[-5 5]、[-2*pi 2*pi]轮廓曲面图、二维曲线、极坐标曲线图、自定义函数%图2绘制轮廓曲面图、二维曲线、极坐标曲线图、自定义函数figure(2)subplot(221)ezsurfc('sin(u)*sin(v)')subplot(222)ezplot('x^2-y^4');subplot(223)ezpolar('1+cos(t)')subplot(224)fplot('myfun',[-20 20])function Y=myfun(x)Y(:,1)=200*sin(x(:))./x(:);Y(:,2)=x(:).^2;三维曲线图%绘制三维曲线图figure(3)ezplot3('sin(t)','cos(t)','t',[0,6*pi])12．三维图形控制视点View图形旋转subplot(121)surf(peaks);title('旋转前图形');subplot(122)h=surf(peaks);rotate(h,[1 0 1],180)title('旋转后图形');灯光效果%灯光效果(1)camlight(2)light(3)lightangle(4)lighting(5)materialsphere;camlight色彩控制%色彩控制(1)缺省设置colordef、whitebg(2)色图colormap(3)浓淡处理shadingload flujetimage(X)colormap(jet)subplot(131)sphere(16)axis squareshading flattitle('Flat Shading')subplot(132)sphere(16)axis squareshading facetedtitle('Faceted Shading')subplot(133)sphere(16)axis squareshading interptitle('Interpolated Shading')。

第5章 Matlab绘图功能

第五章 Matlab 绘图功能5.1 二维图形的绘制5.1.1 常用的二维图形绘图函数基本的二维绘图函数有 plot —— 绘制2维曲线； title —— 给图形加标题； grid —— 显示网格线； xlabel —— 给x 轴加标记； ylabel —— 给y 轴加标记；text —— 在坐标图中加入文字注释。

例：画出函数x y π2sin =，其中x 从0到π2步进100/π的曲线图。

X=0:pi/100:2*pi; Y=sin(X); plot(X,Y); % 作图grid on;% 网格线显示，若该为grid off 则不显示网格 ylabel('y=sin 2\pi x'); % Y 轴标注，可以有汉字 xlabel('x');% X 轴标注，可以有汉字 title('function plot y=sin 2\pi x');% 图标题text(0.5,sin(0.5),'\leftarrow sin 2 \pi 0.5'); % text()可以在指定坐标处写文字标注 text(2.3,sin(2.3),'\leftarrow sin 2 \pi 2.3');% 所有标注中均可使用汉字% 对于特殊符号，如希腊字母，箭头等需要采用LaTeX 格式结果如图5.1 所示。

图5.1 基本的二维绘图函数用法5.1.2 图形的线型和颜色控制在命令plot的高级用法中，可以设置作图的线型，标记类型，线和标记的颜色，粗细等特征。

用命令doc LineSpec和doc plot可以查询详细的帮助文档。

线型的定义如下：- solid line (default) 实线-- dashed line 虚线: dotted line 虚点连线-. dash-dot line 点划线常用标记的定义为：+ plus sign 十字标记o circle 小圈标记* asterisk 星号标记. point 黑点标记x cross 叉号标记s square 方框标记d diamond 菱形标记^ upward pointing triangle 上三角标记v downward pointing triangle 下三角标记> right pointing triangle 右三角标记< left pointing triangle 左三角标记p five-pointed star (pentagram) 五角星标记h six-pointed star (hexagram) 六角星标记颜色的定义是：r red 红g green 绿b blue 蓝c cyan 兰绿色m magenta 洋红y yellow 黄k black 黑w white 白另外，利用线型属性和标记属性可以随心所欲地设计作图图式。