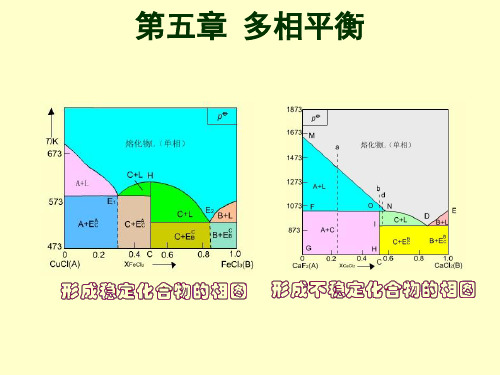
[05章_多相平衡]解析
第05章 相平衡

第五章相平衡§5.1 引言相平衡是热力学在化学领域中的重要应用之一。
化工中很多分离提纯过程,例如精馏、吸收、结晶、萃取等,都涉及到物质在不同相中的分配,它们主要利用物质的挥发性或溶解度等方面的差异,以达到分离提纯的目的,相平衡亦可为此提供理论依据。
因此研究相平衡有着重要现实意义。
一、相(phase)体系内部物理和化学性质完全均匀的部分称为相。
相与相之间在指定条件下有明显的界面。
(1)气体,不论有多少种气体混合,只有一个气相。
(2)液体,按其互溶程度可以组成一相、两相或三相共存。
(3)固体,一般有一种固体便有一个相。
两种固体粉末无论混合得多么均匀,仍是两个相(固体溶液除外,它是单相)。
体系中相的总数用Φ表示。
二、相变物质从一个相流动到另一个相的过程,称为相变化,简称相变。
相变包括气化(boil)、冷凝(condensation)、熔化(melt)、凝固(freeze)、升华(sublimation)、凝华以及晶型转化等。
三、相图(phase diagram)将多相体系的状态随组成、温度、压力等强度性质的改变而发生的过程用图形表示,称为相图。
根据组成相的物态不同分为气-液相图、液-液相图和液-固相图。
根据用途不同可将相图分为温度-蒸汽压图(T-p图,P314 图5.1)、蒸汽压-组成图(p-x图,P318 图5.3):恒定温度,研究P-x,y之间的关系。
称为压力组成图。
温度-组成图(T -x 图,P321 图5.5):在恒定压力下表示二组分系统气-液平衡时温度与组成关系的相图。
研究T-x ,y 之间的关系。
和温度-蒸汽压-组成图(T -p -x 图,P322 图5.6),T-x-y ,x-y ,p-x-y 相图等。
四、自由度(degrees of freedom )确定平衡体系的状态所必须的压力、温度和浓度等独立强度性质的数目称为自由度,用字母f 表示。
如果已指定某个强度性质,除该性质以外的其它强度性质数称为条件自由度,用*f 表示。
物理化学 第5章 (5)概论

平衡时各相的温度和压力;
• 平衡时每一组分在每一相中的化学势相等
1(1)=1(2)=1(3)=…= 1() 2(1)=2(2)=2(3)=…= 2()
…
f= (K-1)+2-K(-1)=K- +2
K(1)=K(2)=K(3)=…= K()
• 如指定了温度T或压力p f=K-+1 如指定了温度T和压力p f=K- 如考虑其它因素(磁场等) f=K-+n
首页
上一页
下一页
末页
4
§5.1 相律
1、基本概念
(1)相(phase) • 系统中物理及化学性质完全均匀的部分,称为相。 • 多相系统中,相与相间有着明显的界面; 越过界面时,物理或化
学性质发生突变。
• 相数:系统中所包含的相的总数。以符号表示。
例:(1)气体: 任何气体均能无限混和——一个气相。=1
有下列形式:
f =K– +2 如果除T,p外,还受其它力场影响,则2改用n表示,即:
首页
f =K– +n
上一页
下一页
末页
14
§5.1 相律
(3) 推导过程:
• 假设一平衡系统中有K 个组分, 个相。
K 个组分指定 (K – 1) 个组分的浓度;
个相指定 (K–1)个浓度;
f ’ = (K – 1) + 2
化学平衡条件: BB=0
• 相图(phase diagram): 表达多相体系的状态如何随温度、压力、 组成等强度性质变化而变化的图形,称为相图。
首页
上一页
下一页
末页
3
第五章 多相平衡
(一)单组分系统 (二) 二组分系统
多相平衡

= KΦ–Φ + 2 – KΦ+K
f=K–Φ+2
讨 论
① 相律只适应平衡系统(对非平衡系统不适应)。 ②只说明数目,不说明具体内容 (这些数目的具体内容,必须通过实验确定)。
如纯水(单组分)体系: ƒ =1–Φ+2=3-Φ 相律
∵ ƒ ≥ 0
∴ Φ ≤ 3
(即最多只能有三相平衡共存。g、l、s 还是 s、s、s 必须通过实验确定。)
例4 固体NaCl, KCl, NaNO3, KNO3与H2O达平衡 解: Na+ Cl-, K+ , NO3-, H2O : S=5 电中性 [Na+]+[K+]=[Cl-]+[NO3-], R′=1 K= 5– 1= 4
或 饱和水溶液,有固体存在 NaCl, KCl, NaNO3, KNO3, Na+, Cl-, K+ , NO3-, H2O : S= 9, R=4: NaCl(s) Na++ Cl-,…… R′=1:电中性 [Na+]+[K+]=[Cl-]+[NO3-], K=9– 4 –1= 4
相等。
纯物质 i α相(T、P)
纯物质 i
β相(T、P)
Gα = Gβ 在平衡条件下,dT、dP,相应 α相摩尔自由焓 dGα,
β相改变 dGβ,两相仍成平衡,即:
T, p平衡
相 ( ) dG()
G=0
相 ( ) dG()
T+dT, p+dp 平衡
Gα + dGα = dGα = 由于 于是 即
如由NaCl和H2O组成的系统
例1 NaCl-H2O系统 1)NaCl,H2O: S=2, R=0, R′=0, K=2 2)NaCl不饱和水溶液 Na+, Cl-, H2O : S=3, R=0, R′=1: [Na+]=[Cl-], K= 3– 1=2 3)NaCl饱和水溶液,有NaCl(s)存在 NaCl(s), Na+, Cl-, H2O : S=4, R=1: NaCl(s) Na++ Cl-, R′=1: [Na+]=[Cl-], K= 4 – 1– 1=2
相平衡

第五章多相平衡§5.1 引言热力学应用于化学领域,其主要任务是解决三个方面的问题,即:热平衡、化学平衡和相平衡问题。
也就是说,热平衡、相平衡、化学平衡是化学热力学的主要研究对象。
前面,大家学习了热力学基本原理以及在多组分系统的应用,下面将讨论多相平衡问题。
对多相平衡的研究有着重要的实际意义。
多相平衡现象在自然界及化工生产中经常遇到。
如:自然界的冰水共存,盐湖中盐块与湖水共存等都是多相平衡;在化工上,溶液的蒸发与蒸馏,固体的升华与融化,气体、固体、液体的相互溶解,原料、产品的分离和提纯—结晶、萃取、凝结,等等,均涉及到多相平衡问题。
多相平衡现象,虽然种类繁多,但都遵守一个共同的规律—相律。
本章主要讨论的问题是:相律和相图,它们是研究相平衡的主要工具。
相律:描述多相平衡中,相数、独立组分数、独立变量数之间的关系。
对系统可作出定性的描述。
相图:表示多相系统的状态如何随温度、压力、浓度等条件而改变的几何图形,亦称状态图。
说明外界条件变化时,状态如何变化;并可指出一定条件下,系统有哪些相,各相的组成是什么。
本章通过在相律指导下各种相图的研究,使大家认识相图,掌握相图,并能利用相图解决实际问题。
下面介绍几个基本概念。
1.相系统中物理性质和化学性质完全均匀的部分。
在多相系统中,相与相之间有明显的界面,超过界面,物理或化学性质发生突变。
系统中所包含相的总数,称为“相数”,以“Φ”表示。
说明:(1)对气体,由于任何气体均能无限混合,所以系统中不论有多少种气体,都只有一个气相。
(2)对液体,视其相互溶解的程度不同,可以是一相,两相或三相。
(3)对固体,一般一种固体物质为一相,固体溶液是一相。
(4)没有气相的系统,称为凝聚系统。
(5)相与相之间有明显的界面。
(6)同一相不一定连在一起,连在一起的不一定是一相。
2.自由度描述多相平衡系统所必需的独立变量数,称为自由度,用符号f表示。
实质:在不引起旧相消失和新相形成的前提下,可以在一定范围内独立变动的强度性质(温度、压力、浓度)。
物化第五章多相平衡

一、基本概念
2. 物种数和组分数
物种数S随着考虑问题的角度不同而不同,但是K值总是一样的.
如:NaCl,H2O构成系统,只考虑相平衡,S=K=2.
Sol(NaCl+H2O),考虑NaCl电离平衡,S=3,有H2O,Na+,Cl,因为溶解是电中性的, mol(Na+)=mol(Cl-),R`=1,K=3-1=2.
Gibbs 热力学研究
1871年吉布斯成为耶鲁学院数学物理学教授,也是全美第一个这一学科的 教授。由于吉布斯并没有发表过文章,所以在他担任这一教职的最初几年并没 有薪水。吉布斯担任这一教职一直到去世,他终身未婚,始终和妹妹与妹夫住 在离耶鲁不远的一间小屋子里,过着平静的生活。在他的坚持下,美国的工程 师教育开始注入了理论的因素。1873年34岁的吉布斯才发表他的第一篇重要论 文,采用图解法来研究流体的热力学,并在其后的论文中提出了三维相图。麦 克斯韦对吉布斯三维图的思想赞赏不已,亲手作了一个石膏模型寄给吉布斯。 1876年吉布斯在康涅狄格科学院学报上发表了奠定化学热力学基础的经典之作 《论非均相物体的平衡》的第一部分。1878年他完成了第二部分。这一长达三 百余页的论文被认为是化学史上最重要的论文之一,其中提出了吉布斯自由能, 化学势等概念,阐明了化学平衡、相平衡、表面吸附等现象的本质。但由于吉 布斯本人的纯数学推导式的写作风格和刊物发行量太小,美国对于纯理论研究 的轻视等原因,这篇文章在美国大陆没有引起回应。随着时间的推移,这篇论 文开始受到欧洲大陆同行的重视。1892年由奥斯特瓦尔德译成德文,1899年 由勒·沙特列翻译为法语。
再考虑H2O的电离平衡,S=6, NaCl,H2O, Na+,Cl-, H+,
OH-.此时,R=2,R`=2
第五章 多相平衡

-- 13 --
• 例: 求食盐水溶液的自由度?
• 解: (1)
• •
S=2
R=0 无化学反应 R’=0 无浓度限制条件
•
•
K= S-R-R’= 2-0-0= 2
f = K- + 2 = 2-1+2 = 3
• 体系在一般情况下的独立变量数为3, 如T,p和NaCl的浓度.
2019/1/7
2019/1/7
-- 11 --
相律公式的应用
指导平衡系统的研究和分析相图 ① 确定系统的自由度数目. ② 确定给定系统允许存在的最大相数目.
2019/1/7
-- 12 --
• 例: 将NH4HS放入抽空的瓶中分解,求体系的 f ? • 解: 有反应: NH4HS(s) = NH3(g) + H2S(g) 分解反应平衡
3 组分数
能够表示系统中各相组成所需要的最少独立物 种数, 用K表示.
即 K S R R'
R — 表示独立的化学平衡数目. R’— 表示化学平衡中同一相浓度限制条件的个数.
2019/1/7
-- 6 --
• 例: 由O2,C,CO,CO2组成体系,求体系的独立化学反应数R?
• 解: 对于由O2,C,CO,CO2组成体系,存在如下化学反应:
• 但因两者分别存在于固相和气相,不在同一相中,所以不能构 成浓度限制条件, 故R’=0. 体系的组分数为:
•
2019/1/7
K=S-R-R’=3-1-0=2
-- 9 --
4 自由度(degrees of freedom) 在不引起旧相消失和新相形成的前提下,可以在一 定范围内独立变动的强度性质,用f 表示。这些强 度变量通常是压力、温度和浓度等。 如果已指定某个强度变量,除该变量以外的其它强 * f 度变量数称为条件自由度,用 表示。 f * f 1 例如:指定了压力,
多相平衡

• 因此,表明系统状态所需的变量数应为
f=Φ(K-1)+2
• 但是,这些变量之间不是相互独立的,因为 在多相平衡时,还必须有“每一组分在每一 相中的化学势相等”这一热力学条件,即
f=Φ(K-1)+2-K(Φ-1)=K-Φ+2
在某一相中少了一个组分,则在该相中的 浓度变量亦减少一个;在考虑相平衡时, 亦将减少一个化学势相等的关系式。
即在Φ(K-1)中减少1时,K(Φ-1)中也必然 减少1。所以 f=K-Φ+2仍成立。
• 若指定了温度或指定了压力,则
f=K-Φ+1
• 若温度与压力均指定,则
即
K=S-R
R即为系统中的“独立化学平衡数”。
• 如系统中有C(s)、CO(g)、H2O(g)、CO2(g)和 H2(g)五种物质,在它们之间可以有三个化学 平衡式:
•
⑴C H O CO H (s)+ 2 (g)====
(g)+ 23;
2(g)====
(g)
•
⑶CO H O CO H (g)+ 2 (g)====
• 在不考虑重力场、磁场等因素,只考虑温度和压 力的影响时,平衡系统中相数、组分数和自由度 数之间的关系可以有下列形式:
•
f=K-Φ+2
• f表示系统的自由度,K表示组分数,Φ表示相数, 2即为温度和压力两变量。
相律的推导如下:
• 假设一平衡系统中有K个组分,Φ个相。如 果K个组分在每个相中均存在。
第五章多相体系—相平衡Heter...

第五章多相体系—相平衡Heterogeneous SystemPhase EquilibriumIntroduction: 多相体系的分离& 提纯第一节相律1.1 基本概念相:体系中物理性质与化学性质完全均匀的部分相数:一个体系所含相的数目,用符号P表示气体:一般只有一相;(P=1)液体:完全互溶,只有一相;部分互溶,有几层就有几相;(P=1,2,3……)固体:有几种固体就有几相。
固态溶液:“固溶体”(P=1)相变化过程(相变);相平衡状态;相界面独立组分数:形成一个热力学平衡体系所需要的最少物种数,简称组分数,用符号C 表示。
组分数=物种数-独立的化学平衡数-独立的限制条件数C =S -R -R ´S :物种数,即体系所含物质的数目R :独立的化学平衡反应数R ´:独立的限制条件数,比如浓度,比例等例如,由NH 4Cl(s)、HCl(g)和NH 3(g)构成的体系,①体系的S=3②三种物质之间又存在化学反应NH 4Cl(s)=HCl(g)+NH 3(g) R=1③若该混合物是由NH 4Cl(s)分解而得,则体系中HCl(g)与NH 3(g)的浓度比保持1:l ,即存在关系式y HCl = y NH 3,则R'=1因此:由NH 4Cl(s)分解而得到的混合物,C=3-1-1=1,该体系为单组分体系独立组分数:形成一个热力学平衡体系所需要的最少物种数,简称组分数,用符号C表示。
组分数=物种数-独立的化学平衡数-独立的限制条件数C=S -R-R´S:物种数,即体系所含物质的数目R:独立的化学平衡反应数R´:独立的限制条件数,比如浓度,比例等例如:N2+3H2= 2NH3高温、催化剂存在时S = 3, R = 1, R´= 0, 则:C=3-1-0 = 2 (双组分系统)高温、催化剂存在且N2:H2=1 : 3 时S = 3, R = 1, R´= 1, 则:C=3-1-1 = 1 (单组分系统)自由度数:确定和保持平衡状态所需的独立改变的变量的数目,称为自由度数,用F 表示。
相平衡解析PPT课件

线性关系
第24页/共94页
p-x-y 图
l,f *=2 l g, f *=1
p pB* ( pA* pB* )xA
p
pA pB pA ( pA pB ) yA
液相线
g,f *=2
第25页/共94页
气相线
yA yB
p*A x A pB* xB
如果
p* A
p* B
则 yA xA
返回
2. T-x图
三条两相平衡线
=2, f =1,压力与温度只能改变一个,
指定了压力,则温度由系统自定。
一个三相点
=3, f =0,三相点的温度和压力皆由系统自定。
第16页/共94页
2.2107
液-固两相平衡线
610.62
气-固两相平衡线
汽相区
超
E临
界 水
F 气-液两相平衡线
AO的延长线,是过冷水 和水蒸气的介稳平衡线
647.4
第17页/共94页
气相区
三条两相平衡线的斜率均可由Clapeyron方程求得。
OA线 OB线 OC线
dp dT
lg H m TlgVm
dp sg Hm dT TsgVm
dp dT
ls H m TlsVm
lg Hm 0,
sg Hm 0,
lsHm 0, lsVm 0
斜率为负。
lgVm 0
B
第5页/共94页
5.3 相律
相律相平衡系统中揭示相数 ,独立组分数C和
自由度 f 之间关系的规律。
自由度
f C 2
T、p
相数
独立组分数
第6页/共94页
相律的导出
体系的自由度指的是确定平衡系统的状态所必须的独 立强度变量的数目,用 f 表示。
第五章相律和多相平衡

∴ C = S R R´ = 2
b. 若同时考虑 H2O 的电离,溶液中有两个 化学平衡,R = 2 :
HAc H+ + Ac
及
H2O H+ + OH
S = 5 ( H2O, HAc, H+, OH, Ac )
由电中性原理,溶液相中正、负离子有
一个浓度关系, R´= 1
分的浓度也已确定。
现在共有 个相,所以需要指定:
(C1)
个浓度,才能确定体系中各个相的浓度。
热力学平衡时,各相的温度和压力均相
同,故整个体系只能再加(温度、压力) 两个变量。
因此,确定体系所处的状态所需的变量
数应为:
f = (C1) + 2 … ①
但是,这些变量彼此并非完全独立。
这两个概念的区别:
体系中有几种物质,则物种数
S 就是多
少;而组分数 C 则不一定和物种数相同。
1)如果体系中各物种之间没有发生化学
反应,一般说来此时组分数等于物种
数:C = S
例如:乙醇 溶于水,组分数 C= S =2
2)如果体系中各物质之间发生了化学反应,
建立了化学平衡,此时:
组分数 (C) = 物种数 (S) - 独立化学平衡数 (R)
(3). NaOH Na+ + OH
(4). H2O H+ + OH
• 由电中性原理,溶液中正、负离子有如 下浓度关系, R´= 1
[Na+] + [H+] = [Ac] +[OH]
(1). NaAc + H2O NaOH + HAc (2). HAc H+ + Ac
第五章多相平衡
(1)液-气平衡 Vm =Vm(g)Vm(l)≈ Vm(g),并设气体为理想气体
dp dT
vapH m TVm (g)
vapH m RT 2
p
d
ln{ p} dT
vap H m RT 2
此式称为克劳修斯—克拉佩龙方程的微分形式。
§5.2 克劳修斯—克拉佩龙方程
当温度变化范围不大时,vapHm可近似地看作常数。 将上式积分,可得
指定了压力和温度,f* = f – 2
(2) 相律的推导
相律就是在平衡系统中,联系系统内相数、组分数、自 由度数及影响物质性质的外界因素(如温度、压力、重 力场、磁场等)之间关系的规律。
(2) 相律的推导
设有 S 种物质在 Φ 个相中, 描述一个相的状态要 T,p,(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= Φ(S –1) + 2
p2
p1
fusH m V fus m
ln
T2 T1
§5.2 克劳修斯—克拉佩龙方程
令 T2 T1 x
则
T1
ln T2 ln 1x
T1
当x很小时,ln(1+x)≈x。上式可以写成
p2
p1
fusH m V fus m
(T2 T1) T1
§5.3 水的相图
373) 368
0.1782
p2=(1.00×105× 0.8367) Pa =8.37×104Pa
(2)
ln 1.10105 226018 (T2 373)
1.00105 8.314373T2
解之: T2=375K,即102℃
第五章 多相平衡

2021/7/14
-- 29 --
OA 是气-液两相平衡线,即水的蒸气压曲线。它 不能任意延长,终止于临界点。临界点 T 647K, p2.2107Pa,这时气-液界面消失。高于临界温 度,不能用加压的方法使气体液化。
OB 是固-气两相平衡线,即 冰的升华曲线,理论上可延长 至0 K附近。
• • 体系:
CaCO3(s) = CaO(s) + CO2(g) S=3, R=1, =3.
• 有关系: n(CaO)=n(CO2) • 但因两者分别存在于固相和气相,不在同一相中,所以不能构
成浓度限制条件, 故R’=0. 体系的组分数为:
•
C=S-R-R’=3-1-0=2
2021/7/14
-- 9 --
2021/7/14
-- 25 --
实验表明: 对正常液体(非极性液体且分子间 无缔合现象)在正常沸点下:
SvapH88Jm ol1K1 —特鲁顿规则 Tb
2021/7/14
-- 26 --
二. 水的相图
单组分体系的相数与自由度
C 1 f13
当 F 1
单相
f 2 双变量体系 面
F 2 两相平衡
f 1 单变量体系 线
dpvapHmvapHm dT TV(g) T(RT/p)
ddT lnpR va pH T2m
此式称为Clausius-Clapeyron方程.
2021/7/14
-- 24 --
计算讨论:
若△vapHm不随温度变化时, 积分得:
ln pvaH pm1C(常)数 RT
l
np2 p1
vR aH pmT 11T 12
相律和多相平衡

(1). NaAc + H2O NaOH + HAc (2). HAc H+ + Ac (3). NaOH Na+ + OH (4). H2O H+ + OH (5). NaAc Na+ + Ac
事实上: (5) = (1) + (2) + (3) (4) 所以 (5) 式不是独立的化学平衡,R = 4
即体系中有两个变量(T, P)可任意改 变,而体系仍为水一个相。
当然,所谓水温度和压力的任意改变, 是指在一定的范围之内的任意改变。
例如:
P = 1atm 下,稳定水相的温度只能在 0C 100C 之间任意改变;
当温度改变到 0C 时,开始有冰产生 (产生新相);
当温度改变到 100C 时,将有蒸汽相 产生(产生新相)。
•以上这些都是我们常见的多相平衡的例 子,这些类型多相平衡各有一定的方法 来研究它们的规律,例如:
拉乌尔定律、亨利定律、分配定律、 平 衡常数及某些其他经验性规则。
而下面要介绍的 “相律”,却不同于上 述这些规律。
“相律”是一种从统一的观点来处理各 种类型多相平衡的理论方法。
相律所反映的是多相平衡中最有普遍性 的规律,即独立变量数、组分数和相数 之间的关系。
而同一种固体的不同颗粒仍属同一相, 因为尽管颗粒之间有界面,但体相的 性质是相同的。
例如:糖和沙子混合,尽管混得很均 匀,仍然是两个相。
2. 组分数
足以表示平衡体系中各物种的组成所至 少需要的独立物种数,称为体系的 “组 分数”,用符号 C 来表示。
注意:体系中的物种数(S)和组分数(C) 这两个概念的区别:
第五章相律和多相平衡

而同一种固体的不同颗粒仍属同一相,
因为尽管颗粒之间有界面,但体相的
性质是相同的。
例如:糖和沙子混合,尽管混得很均
匀,仍然是两个相。
2. 组分数
足以表示平衡体系中各物种的组成所至
少需要的独立物种数,称为体系的 “组 分数”,用符号 C 来表示。
注意:体系中的物种数 (S ) 和组分数 (C )
f=C+2
f :体系的自由度数;
C:独立组分数; :相数; “ 2 ”:温度和压力两个变量。
f=C+2
由相律公式可以看出:
体系每增加 1 个组分,自由度也要增加 1; 体系每增加 1 个相,自由度则要减小 1。
这些基本现象和规律早就为人们所公认,但
直到1876年,才由吉布斯(Gibbs)推导出上 述简洁而有普遍意义的形式。
这两个概念的区别:
体系中有几种物质,则物种数
S 就是多
少;而组分数 C 则不一定和物种数相同。
1)如果体系中各物种之间没有发生化学
反应,一般说来此时组分数等于物种
数:C S =2
2)如果体系中各物质之间发生了化学反应,
建立了化学平衡,此时:
组分数 (C) = 物种数 (S) - 独立化学平衡数 (R)
② 减去的化学平衡数必须是独立的化学 平衡数,否则将会得出荒谬的结论。
3)某些特殊情况下的特殊限制条件,会使 独立组分数减少。
例如 NH4Cl 分解体系:
NH4Cl (s) NH3 (g) + HCl (g)
当起始体系中没有 NH3 (g) 和 HCl (g) 存 在,或存在的 NH3 (g) 和 HCl (g) 的物质 量相等,则达到平衡时,NH3 (g) 和 HCl (g) 之间有一定的比例关系。
物理化学第五章 多相平衡
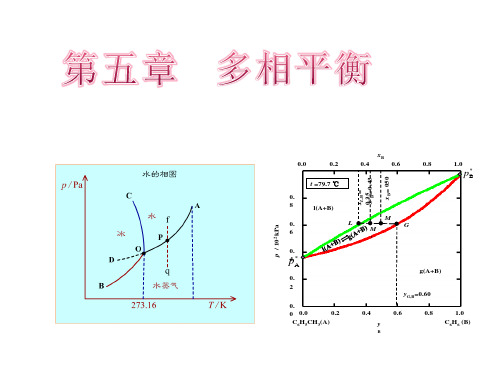
f ( K 1) 2 K ( 1) K 2
F = K – Φ + 2 吉布斯相律
f=自由度,K=独立组分数,Φ=相数
一定条件下,f=K-Φ+1(凝固相系统或指定一个变量)
如果考虑电场、磁场,则f=K-Φ+n
例1 (1) 仅由 NH4Cl(s) 部分分解,建立如下反应平衡: NH4Cl (s) =NH3(g)+HCl(g) (2) 由任意量的 NH4Cl (s) 、NH3(g)、HCl(g) 建立如下反应 平衡: NH4Cl (s) =NH3(g)+HCl(g) 试求(1) 、(2)两种情况下,系统的 组分数 K=?自由度数f =? 解: (1) K = S - R - R´= 3 - 1 - 1=1 f = K - Φ + 2= 1 - 2 + 2 = 1 (2) K = S - R - R´= 3 - 1 - 0 =2 f =K-Φ+2= 2-2+2=2
xB 0.0 0.2 t =79.7 ℃ 0. 8 p / 102 kPa 0. 6 0. 4 p* 0. 2 yG,B=0.60 0. 0.2 0 0.0 C6H5CH3(A) 0.4 y
B
0.4 xL,B= 0.35 0.43 x' = xB= 050
0.6
0.8
1.0
* pB
l(A+B) L M ' M G
K=S-R=3-1=2
要注意独立二字:
C ( s) H 2O( g ) CO( g ) H 2 ( g ) C (s) C O2 (g) 2 C O(g) C O (g) H2O (g) C O2 ( g) H2 (g) (1) (2) (3)
相平衡概念及公式总结

第五章相平衡一、多相系统平衡的一般条件1•相是指系统中宏观上看来化学组成、物理性质和化学性质完全均匀的部分。
没有气相的系统称之为“凝聚系统”2.确定平衡系统的状态所需要的独立的強度变童称为“系统的自由度”3.相的性质:》同一相不一定连在一起,连在一起的并不一定是一相>相与相之间有明显的界限>气体只有一相,液体最多有三相,因体可有无数相>没有气体的体系称为“凝聚体系”热平衡的条件:於"压力平衡条件:卩口 =pB相平衡条件:话=能二、相1.C = S(组分数)-R (独立化学反应数目)・R'(浓度的限制条件)2.厂 +。
= C + 23.性质:>必须正确判断独立组分数、独立化学反应式、相数以及限制条件数才能正确应用相律;>只表示系统中组分和相的数目,不能指明组分和相的类型和含童;>自由度只取“0”以上的正值,如釆出现负值,则说明系统可能处于非平衡态当0=1,单相,f =2; 0 =2 ,两相平衡,r=l; 0 =3,三项共存,/=0 三、单组分系统的相平衡(Clapeyfon方程)1. 在相图中表示某一个相的状态的点简称为“相点”4•楚顿规则: 悴如2 88丿七一―mo 厂丄 T b(正常沸点:l()1.325Kpa 下液体的沸点) 在液态中若分子没有蒂合现象,則能较好地体现此规則。
四、相图1•三相点:是指物质自身的物性,不能加以改变2. 冰点:冰点是在大气压力下由压力、水中溶有空气的彭响3. 蒸气压越离,沸点越低;蒸气压越低,沸点越高4. 杠杆規则:混合物中A 的总的物质的童为n (总)耳,应等于气、液两相中A 物质的童n (1) X ]的加和n (g) X2的加和,公示表示为:n(L) • CD = n{g) • cE 2.任何纯物质的两相平衡都有:刍=啓;(珂拉伯珑方程) 3.Clausius-Clapcyron 方程:皿MP _ baP Hm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上一内容 下一内容 回主目录
返回
2020/11/23
(1)相
相:系统内部物理和化学性质完全均匀的部分称 为相。相与相之间在指定条件下有明显的界面, 在界面上宏观性质的改变是飞跃式的。系统中相
的总数称为相数,用 表示。
HCl(g)+NH3(g)=NH4Cl(s) 达到平衡。
上一内容 下一内容 回主目录
返回
2020/11/23
5.2 克劳修斯-克拉贝龙方程
T,p
相
dG ()
G = 0 平衡
相
dG ()
T + dT,p + dp 相
G = 0 平衡
相
dG () = dG ()
-S () dT + V () dp =-S () dT + V () dp
5.2 克劳修斯-克拉贝龙方程
d ln p dT
vap H m RT 2
积分: ln p vapHm K K为积分常数。 RT
ln p 1 T 作图,直线的斜率为ΔvapHm。
定积分:ln p2 vapHm (T2 T1)
(1)试说明标准压力下,与碳酸钠水溶液和冰共存的含水 盐最多有几种? (1)试说明在30 oC时,可与水蒸气平衡共存的含水盐最 多有几种?
上一内容 下一内容 回主目录
返回
2020/11/23
(4)相律
例题2.试说明下列平衡系统的自由度为多少? (1) 25 oC及标准压力下,NaCl(s)与其水溶液平衡共存; (2) I2(s)与I2(g)呈平衡; (3) 开始时用任意量HCl(g)和NH3(g)组成的系统中,反应
物理化学电子教案—第五章
多相平衡
上一内容 下一内容 回主目录
返回
2020/11/23
第五章 多相平衡
1. 相律 2. 克劳修斯-克拉贝龙方程 单组分系统 3. 水的相图 二组分系统 4. 完全互溶的双液系
上一内容 下一内容 回主目录
返回
2020/11/23
5.1 相律
相平衡是热力学在化学领域中的重要应用之一。 研究多相体系的平衡在化学、化工的科研和生产中 有重要的意义,例如:溶解、蒸馏、重结晶、萃取、 提纯等方面都要用到相平衡的知识。
(1) C(s) H2O(g) CO(g) H2 (g)
+ (2) C(s) CO2 (g) 2CO(g) = (3) CO(g) H2O(g) CO2 (g) H2 (g) 三个化学平衡,但独立化学平衡数为2
∴组分数K = S-R = 5-2 = 3
PCl5 (g) PCl3(g) Cl2 (g)
即:K = S-R- R’=3-1-1=1
K S R R'
注意:浓度关系数只有在同一相中才能应用,在不同 相中不存在这种限制条件。
上一内容 下一内容 回主目录
返回
2020/11/23
(2)物种数和组分数
CaCO3(s) CaO(s) CO2 (g)
即使反应开始只有CaCO3,并且n(CaO):n(CO2)=1:1, 但由于CaO为固相,CO2为气相,所以不存在浓度限制。
以又称为Gibbs相律。
f = K– +1 指定温度或压力
f = K–
温度和压力都指定
如除T,p外,还受其它力场影响,则2改用n表示,即:
f + = K+n
上一内容 下一内容 回主目录
返回
2020/11/23
(4)相律
例题1.碳酸钠和水可以形成下列几种化合物: Na2CO3·H2O; Na2CO3·7H2O; Na2CO3·10H2O
气体,不论有多少种气体混合,只有一个气相。
液体,按其互溶程度可以组成一相、两相或三 相共存。 固体,一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀,仍是两个相(固体溶液 除外,它是单相)。
上一内容 下一内容 回主目录
返回
2020/11/23
(2)物种数和组分数
物种数S
系统中所含的化学物质数
能够表示系统中各相组成所需的最少独立物种数称为 组分数K。
若多相系统中无化学平衡存在,则:K = S。
若多相系统中有化学平衡存在,则:
K = S-R。 R指独立的化学平衡数
上一内容 下一内容 回主目录
返回
2020/11/23
(2)物种数和组分数
系统中存在C (s) , CO (g), CO2(s), H2O (g), CO2(g), H2(g)。
克拉贝龙方程指出两相平衡时平衡压力随温度的变化率。
应用到液气平衡: Vm Vm (g) Vm (s) Vm (g)
dp dT
Hm T Vm
vap Hm TVm (g)
vap Hm RT 2
p
或:d ln p vap Hm
dT
RT 2
克劳修斯-克拉贝龙方程
上一内容 下一内容 回主目录
返回
2020/11/23
若反应开始只有PCl5,则平衡时PCl3:Cl2=1:1,存 在一浓度关系限制条件R’。
上一内容 下一内容 回主目录
返回
2020/11/23
(2)物种数和组分数
在 PCl5、PCl3(g)和Cl2 (g) 构成的系统中, 组分数K = S-R = 3-1 = 2
但若反应开始只有PCl5 组分数=物种数-独立化学平衡数-独立浓度关系数
不饱和食盐水 f=3 (T、p、c)
饱和食盐水 f=2 (T和p, T,p确定则c也确定)
上一内容 下一内容 回主目录
返回
2020/11/23
(4)相律
相律:是相平衡系统中揭示相数 ,独立组分数K和自
由度 f 之间关系的规律,可用公式表示为:
f = K– +2
式中2通常指T,p两个变量。相律最早由Gibbs提出,所
[V ()-V ()] dp = [S ()-S ()] dT
即: dp S( ) S( ) Sm dT V ( ) V ( ) Vm
上一内容 下一内容 回主目录
返回
2020/11/23
5.2 克劳修斯-克拉贝龙方程
对于可逆相变: Sm
Hm T
H
为相变热。
m
dp Hm
克拉贝龙方程
dT T Vm
组分数K = S-R- R’=3-1-0=2
上一内容 下一内容 回主目录
返回
2020/11/23
(3)自由度
自由度:
在不引起旧相消失和新相形成的前提下,可以在一 定范围内独立变动的强度性质称为平衡系统的自由度f 。 这些强度变量通常是压力、温度和浓度等。
液体水
f=2(T和p)
水及水汽共存 f=1 (T或p, T确定则p也确定)
