第十一章 章末小结
农安县第八中学八年级物理全册 第十一章 小粒子与大宇宙章末小结与提升分层精炼 沪科版

章末小结与提升小粒子与大宇宙1.劣质的油性油漆、板材、涂料、胶粘剂等材料含有较多的甲醛、苯、二甲苯等有毒有机物,用来装修房屋,会造成室内环境污染,这是因为有毒有机物分子都在做永不停息的无规则运动,这种现象在夏天时特别严重,因为温度越高, 分子热运动越剧烈。
2.热熔胶是一种在常温下为固态的黏合剂,使用时先用热熔胶枪加热使其熔化,再凝固来黏合物体。
用如图所示的一款热熔胶枪给热熔胶加热时,会闻到熔胶的气味,这是扩散现象。
热熔胶被胶枪挤出,并“粘”在物体上,说明分子间存在引力。
3.随着科技的进步,霍金提出的黑洞理论和宇宙无边界的设想,正逐步得到证实。
如图a、b、c、d四点分别表示处女座、大熊座、牧夫座和长蛇座四大星系离银河系的距离与它们的运动速度之间的关系。
由图可知,星系离我们越远,运动的速度越快;可推知宇宙处在膨胀之中。
4.1911年,卢瑟福建立了原子的核式结构模型。
下列关于这个模型的说法中正确的是( B )A.原子核带负电B.原子核位于原子的中心C.电子静止在原子核周围D.原子核占据了原子内大部分空间5.下列现象中,不能说明分子在做永不停息的无规则运动的是( C )6.静置的密封容器内只有氢气,若以“○”表示氢气分子,如图中最能代表容器内氢气分子分布的是( A )7.2019年四月以来,甘肃省大部分地区遭遇强沙尘天气,空气质量指数AQI爆表,AQI空气质量评价的主要污染物为PM2.5、NO22分子、电子、原子核按照空间尺度由大到小排序正确的是( A )2分子→原子核→电子B.NO2分子→PM2.5→原子核→电子C.NO2分子→原子核→PM2.5→电子D.NO2分子→原子核→电子→PM2.58.如图所示,在玻璃注射器内吸入一定量的某种液体,然后排出内部的空气,并用橡皮塞封住注射孔。
这时人无论怎样用力推动活塞,也难以使其体积发生微小的变化。
关于这一现象下列说法正确的是( B )A.说明该液体压缩成固体了,所以体积不变B.说明液体分子间存在斥力,所以很难被压缩C.说明该液体分子的体积大,很难被压缩D.说明液体分子间有引力,所以很难被压缩9.如图所示是氦原子的核式结构模型,其核外有两个电子绕核旋转,请你在图中用“ ”表示质子,根据电子数在相应位置画出数量对应的质子。
第十一章 三角形小结(构建知识体系)作业练习

作业练习一、填空题1.下列长度的各组线段能围成一个三角形的有______.①4 cm,5 cm,6 cm;②4 cm,5 cm,10 cm;③3 cm,8 cm,5 cm;④15 cm,10 cm,7 cm.2.等腰三角形的两边长分别为4,9,则该等腰三角形的周长为____.3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AB=15,BC=9,AC=12,则CD=____.4.如图,在△ABC中,点D,E分别是AC,AB的中点,且S△ABC=12,则S△BDE=________5.如图,D是△ABC边BC延长线上的一点,∠A=75°,∠ACD=105°,则∠B=______6.如图,l1∥l2,∠1=80°,∠2=45°,则∠3= ____.7.如图,已知在△ABC 中,∠B =90°,角平分线AD ,CF 相交于点E ,则∠AEC =______.8.若△ABC 足∠A =12∠B = 13∠C ,则△ABC 是______三角形. 9.(1)六边形的内角和为___°,外角和为_____°;(2)一个正多边形的每个内角都为135°,则它是__边形.10.如图,在五边形ABCDE 中,AE ∥BC ,则∠C +∠D +∠E 的度数为_______.二、解答题1.在△ABC 中,AB =AC ,DB 为△ABC 的中线,且BD 将△ABC 周长分为12cm 与15cm 两部分,求三角形各边长.2.∠A ,∠B ,∠C 是△ABC 的三个内角,且分别满足下列条件,求∠A ,∠B ,∠C 中未知角的度数.(1)∠A -∠B =16°,∠C =54°;(2)∠A:∠B:∠C =2:3:4.3.如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4. 求∠CAD的度数.4.如图,在△ABC中,BD是∠ABC的平分线,CD是△ABC的外角∠ACE的平分线.(1)若∠A=80°,求∠D的度数;(2)请写出∠D和∠A的数量关系并证明.5.如图,已知BD,CD分别是△ABC的外角∠EBC和∠FCB的平分线.(1)若∠ABC=50°,∠ACB=70°,则∠D的度数为_______;(2)若∠A=80°,求∠D的度数;(3)请直接写出∠D和∠A的数量关系.。
人教版八年级数学上册第11章知识总结与复习题11解析答案
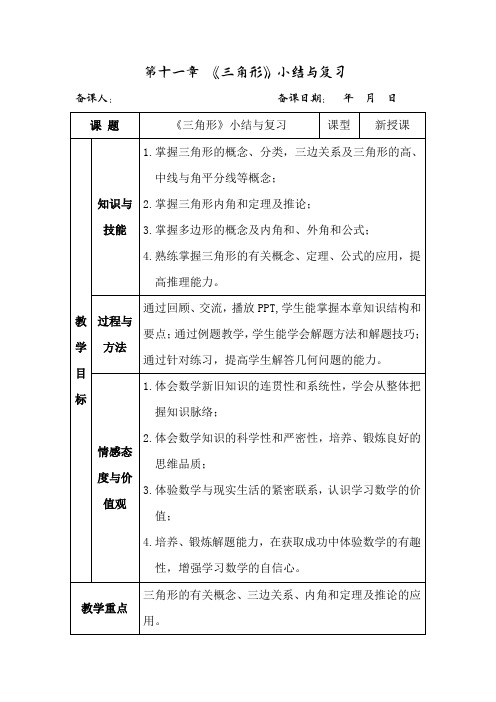
例3如图,AB∥DE,∠ABC=120°,∠CDE=130°.求∠C的度数.
分析:本题有多种解法:①过点C作CF∥AB,利用平行线的性质解答;②过点D作DF∥BC,利用平行线的性质解答;③延长ED交CB于点F,构建△CDF利用三角形内角和定理的推论进行解答;④分别延长AB,CD,两延长线交于点F,构建△CDF利用三角形内角和定理的推论进行解答。
个三角形,九边形的内角和等于个三角形的内角和。
2.如果四边形的两个对角互补,那么另两个对角。
4.求出下列各图中的x值。
5.如图,D是△ABC的边AC上一点,AD=BD。
(1)判断AC与BC的大小;
(2)若∠ADB=72°,∠C∶∠DBC=2∶1,求∠C的度数。
6.如图所示,△ABC的内角平分线与外角平分线交于点P。请你分析∠P与∠A的关系.
第十一章 《三角形》小结与复习
备课人: 备课日期: 年 月 日
课题
《三角形》小结与复习
课型
新授课
教学目标
知识与技能
1.掌握三角形的概念、分类,三边关系及三角形的高、中线与角平分线等概念;
2.掌握三角形内角和定理及推论;
3.掌握多边形的概念及内角和、外角和公式;
4.熟练掌握三角形的有关概念、定理、公式的应用,提高推理能力。
②这个多边形的每个外角都等于180°-108°=72°,根据多边形的外角和公式,得 72n=360,解得n=5。
【指点迷津】运用多边形的内角和、外角和公式有两种方法:直接运用与根据公式列方程求解。一般地,求多边形的边数,可根据多边形的内角和公式或外角和公式列方程求解。
四、巩固提升
1.从九边形的一个顶点出发,可以作条对角线,把九边形分成
人教版初中八年级上册数学第十一章《三角形(小结复习课)》精品教案

A
D
1
2
B
C
本题源自《教材帮》
深化练习 4
∠ABD和∠ACE是△ABC的两个外角,若∠A=55°,则∠ABD+∠ACE=( 235° ).
解:∵∠ABD和∠ACE是△ABC的外角, ∴∠ABD=∠A+∠ACB, ∠ACE=∠A+∠ABC. ∴∠ABD+∠ACE =∠A+∠ACB+∠A+∠ABC =∠A+∠ACB+∠ABC+∠A =180°+55° =235°.
深化练习 3
如图,已知BD平分∠ABC交AC于点D,且∠ABC=∠C=2∠A,求△ABC各角的度数.
解:∵BD平分∠ABC,∠ABC=∠C=2∠A, ∴∠1=∠2=∠A. 设∠1=∠2 =∠A=x°,则∠ABC=∠C=2x°. ∵在△ABC中,∠A+∠ABC+∠C=180°. ∴x+2x+2x=180,解得x=36. ∴∠A=36°,∠ABC=∠C=2∠A=72°.
从三角形的一个顶点向它所对的边所在直线画垂线,顶点与垂足之间的线段叫做三 角形的这条边上的高. 连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形这条边上的中线. 三角形一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线 段叫做三角形的角平分线.
知识梳理
与三角形有关的线段
3、三角形的重心 三角形的三条中线的交点叫做三角形的重心.
知识梳理
与三角形有关的角
1、三角形的内角和定理 三角形三个内角的和等于180°.
2、直角三角形的性质 直角三角形的两个锐角互余. 有两个角互余的三角形是直角三角形.
知识梳理
与三角形有关的角 3、三角形内角和定理的推论 三角形的外角等于与它不相邻的两个内角的和. 4、三角形外角和的性质 三角形的外角和等于360°.
27第十一章期末处理

注 意(续)
如果没有启用库存管理和核算管理两 个子系统,并且不需要查看采购余额一 览表,那么采购管理系统可以不进行月 末结账。
第四节 年度结转
在一个会计年度结束,新的会计年度 开始这个新老会计年度交接之际,需要 把上年度各项会计数据的最后余额结转 到新的会计年度账上来。这项工作叫作 “年度结转”。
年度结转分“建立年度账”和“结转 上年数据”两大步骤。这两大步骤都要 由账套主管在〖系统管理〗模块中完成。
年度结转操作流程
(二)月末结账
完成了月末处理以后,就可以 进行月末结账了。
请注意观摩操作演示
休 息
五、总账系统的月末处理
(一) 其它子系统生成凭证的处理
在总账系统进入月末处理程序之前,首 先要把所有其它子系统传递过来的凭证审核 完,并且进行记账。实际上这项工作属於日 常处理的工作范围。平时,除了总账系统自 身产生的凭证,其它子系统每天总会有凭证 传送到总账系统里来。要注意对这些凭证及 时进行处理,不要积压。
(二)月末结转
企业期末账务处理中的某些业务,每个 月往往是重复的,程序化的,处理方法相对 固定不变,如各种费用的计提、期间损益的 结转等等。我们可以为这些处理方法相对固 定的期末账务处理业务,预先定义好自动转 账凭证模板。每个月的月底,只要调用凭证 模板,就可以让计算机自动生成转账凭证。
自动转账的种类
请注意观摩操作演示
恢复期末处理。
如果在期末处理以后发现哪 个仓库的数据处理有错误,可 以恢复到期末处理以前的状态。
医学生理学期末重点笔记--第十一章-内分泌

第十一章内分泌【目的】掌握内分泌系统的概念,内分泌系统在调节主要生理过程中的作用及机理。
内分泌系统与神经系统的紧密联系,相互作用,相互配合的关系。
下丘脑、垂体、甲状腺、肾上腺等的内分泌功能及其调节。
熟悉信号转导机制及其新进展,了解糖皮质激素作用机制的有关进展。
【重点】1.下丘脑-垂体的功能单位,下丘脑调节肽。
2.腺垂体激素的生物学作用及调节。
3.甲状腺的功能、作用机理及调节。
4.肾上腺皮质激素的作用及调节。
第一节概述内分泌系统和神经系统是人体的两个主要的功能调节系统,它们紧密联系、相互协调,共同完成机体的各种功能调节,从而维持内环境的相对稳定。
一、激素的概念内分泌系统是由内分泌腺和散在的内分泌细胞组成的,由内分泌腺或散在的内分泌细胞分泌的高效能生物活性物质,称为激素〔hormone〕,是细胞与细胞之间信息传递的化学媒介;它不经导管直接释放入内环境,因此称为内分泌。
二、激素的作用方式1.远距分泌多数激素经血液循环,运送至远距离的靶细胞发挥作用,称为远距分泌〔telecrine〕。
2.旁分泌某些激素可不经血液运输,仅通过组织液扩散至邻近细胞发挥作用,称为旁分泌〔paracrine〕。
3.神经分泌神经细胞分泌的激素可沿神经细胞轴突借轴浆流动运送至所连接的组织或经垂体门脉流向腺垂体发挥作用,称为神经分泌〔neurocrine〕。
4.自分泌由内分泌细胞所分泌的激素在局部扩散又返回作用于该内分泌细胞而发挥反馈作用,称为自分泌〔autocrine〕。
三、激素的分类按其化学结构可分为:1.含氮类激素:〔1〕蛋白质激素,如生长素、催乳素、胰岛素等;〔2〕肽类激素,如下丘脑调节肽等;〔3〕胺类激素,如肾上腺素、去甲肾上腺素、甲状腺激素等。
2.类固醇激素:〔1〕肾上腺皮质激素,如皮质醇、醛固酮等;〔2〕性激素,如雌二醇、睾酮等。
3.固醇类激素:包括维生素D3、25-羟维生素D3、1,25-二羟维生素D3。
4.脂肪酸衍生物:前列腺素。
八年级数学上册教学课件《第十一章 章末复习》

三
角
三角形的内角和
形
三角形的外角和
边 高 中线 角平分线 多边形的内角和
多边形的外角和
① 三角形的定义
a.边:组成三角形的线段 b.顶点:相邻两边的交点 c.角:相邻两边组成的角 d.表示法:△ABC
② 三角形的分类:
a.按边分:等腰三角形和不等边三角形 b.按角分:锐角三角形、直角三角形、钝角三 角形
解:(1)S△ABC
1 2
AC·BC
1 512 2
30(cm2 ).
S△ABC
1 2
AB·CD,
CD AC·BC 60 (cm).
AB 13
(2)S△ABE
S△BCE
1 2
S△ABC
15(cm2 ).
拓展延伸 3.一轮船由B 处向C处航行,在B 处测得C
处在B 的北偏东75°方向上,在海岛上的观察 所A 测得B 在A 的南偏西30°方向,C 在A的南 偏东25°方向;若轮船行使到C 处,那么从C 处 看A、B 两处的视角∠ACB是多少度?
解:根据题意,画出示意图如图所示: 另求出∠ABC =75°- 30°= 45°, ∠BAC = 30°+25°= 55°, 所以∠ACB =180°- 45°- 55°= 80°.
课堂小结 边
与三角形有关的线段
高 中线
三
角
三角形的内角和
形
角平分线 多边形的内角和
三角形的外角和
多边形的外角和
课后作业
B
DE
C
A 组 复习与三角形有关的线段:
2.如图:
A
(3)若AF =CF,BF 与
31.八年级数学三角形(单元小结)(解析版)

第十一章三角形单元总结【思维导图】【知识要点】知识点一三角形的概念三角形的概念 :由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
三角形特性三角形用符号“∆”表示,顶点是A、B、C的三角形记作“∆ABC”,读作“三角形ABC”。
三角形按边分类等腰三角形:有两条边相等的三角形叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的夹角叫做底角。
等边三角形:底边与腰相等的等腰三角形叫做等边三角形,即三边都相等。
三角形三边的关系(重点)(1)三角形的任意两边之和大于第三边。
三角形的任意两边之差小于第三边。
(这两个条件满足其中一个即可)用数学表达式表达就是:记三角形三边长分别是a,b,c,则a+b>c或c-b<a。
(2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b三角形的分类三角形按边的关系分类如下:三角形按角的关系分类如下:三角形的稳定性三角形具有稳定性四边形及多边形不具有稳定性要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了。
考查题型一三角形的分类典例1(2020·朔州市期末)已知△ABC的一个外角为70°,则△ABC一定是()A.锐角三角形B.直角三角形C.钝角三角形D.锐角三角形或钝角三角形【答案】C【详解】∵△ABC的一个外角为70°,∴与它相邻的内角的度数为110°,∴该三角形一定是钝角三角形,故选:C.变式1-1(2020·温州市期中)在△ABC中,若∠A:∠B:∠C=1:3:5,则△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.形状不确定【答案】C【分析】根据∠A:∠B:∠C=1:3:5,可设∠A=x°,∠B=3x°,∠C=5x°,再根据三角形内角和为180°可得方程x+3x+5x=180,解方程算出x的值,即可判断出△ABC的形状.【详解】解:∵∠A:∠B:∠C=1:3:5,∴设∠A=x°,∠B=3x°,∠C=5x°,∴x+3x+5x=180,解得:x=20,∴∠C=5×20°=100°,∴△ABC是钝角三角形.故选:C.变式1-2(2019·定西市期中)若△ABC中,A:B:C1:2:4∠∠∠=,则△ABC一定是()A.锐角三角形B.钝角三角形C.直角三角形D.任意三角形【答案】B【分析】根据三角形内角和180︒,求出最大角∠C,直接判断即可.【详解】解:∵∠A:∠B:∠C=1:2:4.∴设∠A=x°,则∠B=2x°,∠C=4x°,根据三角形内角和定理得到:x+2x+4x=180,解得:x=1807.则∠C=4×1807= 7207°,则△ABC 是钝角三角形. 故选B. 考查题型二 三角形的稳定性典例2(2019·唐山市期中)下列图形具有稳定性的是( )A .B .C .D .【答案】A【分析】根据三角形具有稳定性,四边形具有不稳定性进行判断即可得.【详解】A 、具有稳定性,符合题意;B 、不具有稳定性,故不符合题意;C 、不具有稳定性,故不符合题意;D 、不具有稳定性,故不符合题意,故选A .变式2-1(2020·安阳市期末)王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ).A .0根B .1根C .2根D .3根【答案】B【解析】三角形具有稳定性,连接一条对角线,即可得到两个三角形,故选B变式2-2(2020·乌鲁木齐市期末)为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )A .两点之间,线段最短B .垂线段最短C .三角形具有稳定性D .两直线平行,内错角相等 【答案】C【解析】试题分析:三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.解:这样做的道理是三角形具有稳定性.故选:C考查题型三 三角形的三边关系典例3(2019·宜兴市期中)下列各组线段不能组成三角形的是 ( )A .4cm 、4cm 、5cmB .4cm 、6cm 、11cmC .4cm 、5cm 、6cmD .5cm 、12cm 、13cm【答案】B【分析】根据三角形的任意两边之和大于第三边对各选项分析判断后利用排除法求解.【详解】A 、4485+=>,∴445cm cm cm 、、能组成三角形,故本选项错误; B 、461011+=<,∴4611cm cm cm 、、不能组成三角形,故本选项正确; C 、,∴456cm cm cm 、、能组成三角形,故本选项错误;D 、5121713+=>,∴51213cm cm cm 、、能组成三角形,故本选项错误. 故选:B .变式3-1(2019·邯郸市期中)已知a 、b 、c 是△ABC 的三条边长,化简|a +b -c|-|c -a -b|的结果为( ) A .2a +2b -2cB .2a +2bC .2cD .0 【答案】D【解析】试题解析:∵a 、b 、c 为△ABC 的三条边长,∴a+b-c >0,c-a-b <0,∴原式=a+b-c+(c-a-b )=0.故选D .变式3-2(2019·平顶山市期末)已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( ) A .1B .2C .8D .11【答案】C【分析】根据三角形两边之和大于第三边,两边之差小于第三边可确定出第三边的范围,据此根据选项即可判断.【详解】设第三边长为x ,则有7-3<x<7+3,即4<x<10,观察只有C 选项符合,故选C.变式3-3(2020·驻马店市期末)已知x ,y 满足40x -+=,则以x ,y 的值为两边长的等腰三角形的周长是( )A .20或16B .20C .16D .以上答案都不对 【答案】B【分析】先根据非负数的性质列式求出x 、y 的值,再分4是腰长与底边两种情况讨论求解.【详解】解:根据题意得,4-x=0,y-8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故选B.知识点二 与三角形有关的线段三角形的高:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
人教版八年级下册物理精品教学课件 第十一章 功和机械能 小结与复习

例10
在如图所示,甲、乙两个质量不同的小球,从相同高度静止 释放,甲球下落过程中经过P、Q两点,忽略空气阻力,下 列说法正确的是( B ) A.着地瞬间两球的动能相等 B.甲球在P点和Q点的机械能相等 C.释放瞬间两球的重力势能相等 D.从释放到着地,两球所受重力做的功相等
例11
在某运动员做蹦极运动,如图甲所示,从高处O点开始下落,A点是
例1
如一位同学正在进行投掷实心球的训练。以下情境中,他对 球做功的是( C )
A.手拿球静止
B.手托球水平匀速直线移动
C.将球举起
D.抛出后的球在空中继续运动
例2
李红同学的教室在教学楼的3楼,如果每层楼高3 m,李红
的体重为500 N,则李红要从地面走到教室,她需要克服自 身重力做功___3__0_0_0___J。
__W____ ,其他常用功率单位是___千__瓦____。单位换算:1kW=
__1_0_0__0__W。
3.推导公式:P=
W t
=
Fs t
=Fv (v 的单位必须是m/s)。
例4
用起重机将质量为5t的集装箱匀速提升10m,若集装箱上升 的速度为0.5m/s,则上升过程中起重机的拉力对集装箱做功 的功率是__2_._5_×__1_0_4_W;若上升过程中起重机以20kW的恒定 功率将集装箱匀速提升,则该过程需要___2_5____s。(g取10 N/kg)
(3)不做功的三种情况:
示意图 没有力,有距离 有力,没有距离
有力,也有距离
特点 有力有距离,力的方 物体受力,但静止 物体在水平方向不受力,
向与距离的方向垂直
因惯性而动
举例
人提水桶水平前进, 提水桶的力和水桶的 重力均不做功
第十一章 一元一次不等式(小结思考)(课件)七年级数学下册(苏科版)

B. ac>bc
a<b,c<0
ac>bc
C.a+c>b+c
b>a,c<0
b+c>a+c
D.a+b<c+b
a>c,b>0
a+b>c+b
c<0<a<b
c
O
a
b
知识结构
概念
一
元
一
次
不
等
式
定界点
定方向
画数轴
(三要素) (空心与实点)(大向右,小向左)
性质
不等式表示
不等式的解集
表示
不等式所有解的集合. 方法
利用一元一次不等式(组)解决实际问题
(2) 青少年活动中心决定再购进上述四种图书,总费用不超过32000元.
如果《西游记》比《三国演义》每本售价多10元,《水浒传》比《红楼
梦》每本售价少10元,要使先后购进的四大名著刚好配套(四大名著各
一本为一套),那么这次最多购买《西游记》多少本?
解:(2) 《三国演义》每本售价为60-10=50(元),
合并同类项,得-5x≥-20,
系数化为1,得x≤4,
因为x是正整数,所以x为1,2,3,4,
(+)
−
故x取正整数1,2,3,4时,代数式3-
的值不小于代数式 的值.
巩固练习
4.已知2-a和3-2a的值的符号相反,求a的取值范围.
注意:分类讨论,有两种可能:
−>
或
− <
+ >
(2)
<
2020年八年级数学上册第十一章小结与复习

7.如图,△ABC 中,AD 是 BC 边上的高,AE、BF 分别是∠BAC、∠ABC 的平分线,∠BAC=50°, ∠ABC=60°,则∠EAD+∠ACD=( A ) A.75° B.80° C.85° D.90°
8.(2019-2020·石台县期末)如图,在△ABC 中,AD 是高,AE 是角平分线,AF 是中线,则下列说法中 错误的是( C ) A.BF=CF B.∠C+∠CAD=90° C.∠BAF=∠CAF D.S△ABC=2S△ABF
快速对答案
1B
2C
3D
4 2a-10
5
详细答案 点击题序
6C
提示:点击 进入习题
7A
8C
9
详细答案 点击题序
10 A
11 B
12 D
快速对答案
13 30° 10°
14 50°
详细答案
15 点击题序
详细答案
16 点击题序 17 C
18 45
提示:点击
19 60
20
详细答案 点击题序
进入习题
1.(2019·淮安中考)下列长度的 3 根小木棒不能搭成 三角形的是( B ) A.2 cm,3 cm,4 cm B.1 cm,2 cm,3 cm C.3 cm,4 cm,5 cm D.4 cm,5 cm,6 cm
2.(2019·抚顺中考)若一个等腰三角形的两边长分别 为 2,4,则第三边的长为( C ) A.2 B.3 C.4 D.2 或 4
3.(2019-2020·南昌期中)有四根长度分别为 3,4, 5,x(x 为正整数)的木棒,从中任取三根,首尾顺次 相接都能组成一个三角形,则组成的三角形的周长
A.最小值是 11 B.最小值是 12 C.最大值是 14 D.最大值是 15
人教版数学八年级上册第十一章复习小结:三角形

第十一章三角形复习小结教学目标:1、回忆本章知识,形本钱章知识构造.2、总结本章解题规律,进展跟踪训练.重点:归纳本章知识构造,进展跟踪训练.难点:总结本章解题规律.教学过程:一、回忆本章知识,形本钱章知识构造二、双基训练:⒈在活动课上,小红有两根长为4cm,8cm的小木棒,现打算拼一个等腰三角形,那么小红应取的第三根小木棒的长应为8 cm.⒉⊿ABC中,假设∠A∶∠B∶∠C=1∶2∶3,那么△ABC是直角三角形.⒊三角形中至少有一个角不小于60 °;没有对角线的多边形是三角形;一个多边形中,锐角最多有三个;一个四边形截去一个角后可以得到的多边形是三角形或四边形或五边形.⒋一个多边形的每个外角都是30°,那么它是十二边形,其内角和是1800°.⒌一个多边形的每个内角都相等,且比它的一个外角大100°,那么边数n=9 .⒍如图⑴,在直角△ABD中,∠D=90°,C为BD上一点,那么x可能是〔B〕A、10B、20C、30D、40⒎如图⑵有两个正方形和一个等边三角形,那么图中度数为30°的角有〔D〕A、1个B、2个C、3个D、4个⒏一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成其中三个分别为正三角形、正四边形、正六边形,那么另一个为〔B〕A、正三边形B、正四边形C、正五边形D、正六边形三、例题解析:例1.等腰三角形一腰上的中线将周长分为6和15两局部,求此三角形的腰长. 解:如图等腰△ABC中,AB=AC,BD是腰AC上的中线,x设AB=AC=x ,BC=y 那么AD=DC=2①当AB+AD=6 , BC+CD=15时,即:x +2x =6,y +2x =15 解得x =4, y =13 ∵4+4<13∴此时不能组成三角形,故x =4, y =13不合题意,舍去.②当AB +AD =15 , BC +CD =6时,即:x +2x =15,y +2x =6 解得x =10, y =1∵10+1>10∴10、10、1能构成三角形.∴此三角形的腰长为10.例2.如图⑶一个四边形ABCD 模板,设计要求AD 与BC 的夹角应为30°,CD与BA 的夹角应为20°.现在已测得∠A =80°,∠B =70°,∠C =90°,请问:这块模板是否合格?并说明理由.解:这块模板合格.理由:延长AD 、BC 相交于点E,延长BA 、CD 相交于点F在△ABE 中∵∠EAB =80°,∠B =70°∴∠E =180°―∠EAB―∠B =30°在△CFB 中∵∠FCB =90°,∠B =70°∴∠F =180°―∠FCB―∠B =20°∴这块模板合格.例3. ⊿ABC 中,⑴如图⑷,∠DBC 和∠ECB 的角平分线相交于点O ;⑵如图⑸,∠ABC 的角平分线BD 和∠ACE 的角平分线相交于点O ;如图⑹,∠CBD 的角平分线BO 和∠BCE 的角平分线CO 相交于点0,试猜测∠A 与∠D 的关系,并选择其中一个进展证明.提示:⑴∠BOC =180°-〔∠2+∠3〕=180°-〔∠1+∠4〕=180°-〔∠5+∠6+∠7+∠8〕=180°-〔∠BAC +∠BOC 〕=90°-2BAC ∠ ⑵∠A =322∠-∠=2O ∠⑶∠BOC =180°-2ABC ACB ∠+∠ =180°-1802A -∠=90°+2A ∠.三、稳固练习: 1.有四条线段,长度分别是12cm,10cm,8cm,4cm,选其中的三条组成三角形,那么可组成 3 个不同的三角形.2.如果等腰三角形的两边长为5cm 和9cm ,那么三角形周长为19cm 或23cm .3.△ABC 中,假设∠A ∶∠B ∶∠C=3∶4∶7,那么△ABC 是 直角 三角形.4.一个n 边形的每个内角都相等,且比它的一个外角大60°,那么边数n = 6 .5..三角形最长边等于10,另两条边的长分别为x 和4,周长为C ,那么x 和C 的取值范围分别是 6<x≤10 ,20<C≤246.如图⑺,AB ∥CE, ∠C =37°,∠A =114°,那么∠F 的度数为 77°.7.如图⑻所示,△ABC 中AB =AC ,请你添加一个条件....AD 平分∠EAC 〔不唯一〕,使得AD ∥BC.8.如图⑼,D 、E 是边AC 的三等分点假设△ABC 的面积为12㎝2,那么△BDC 的面积是8 ㎝2.9.如图⑽,∠1+∠2+∠3+∠4的度数是300°.10.一个多边形的内角和是1980°,那么它的边数是_13 _,它的外角和是360 ° ,共有__65__条对角线.11.一个正多边形,它的一个外角等于与它相邻的内角的15,那么这个多边形是〔 D 〕A 、五边形B 、八边形C 、九边形D 、十二边形12.以下说法不正确的选项是〔 D 〕A 、任意形状的一些三角形可镶嵌地面B、用形状大小完全一样的六边形可镶嵌地面C、用形状大小完全一样的任意四边形可镶嵌地面D、用任意一种多边形可镶嵌地面13.用两个正三角形与下面的假设干个〔B〕可以进展平面镶嵌.A、正方形B、正六边形C、正八边形D、正十二边形14.如图⑾,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,那么∠A、∠1、∠2之间的关系是〔B〕A、∠A=∠1-∠2B、2∠A=∠1-∠2C、3∠A=2∠1-∠2D、3∠A=2〔∠2-∠1〕15.如图⑿,∠1+∠2=180°,DG∥AC,求证:∠A=∠DFE.证明:∵∠1+∠2=180°,∠1+∠DFE=180°∴∠2=∠DFE∴AB∥EF∴∠A=∠3又∵DG∥AC∴∠3=∠DFE ∴∠A=∠DFE.16.如图⒀, △ABC中,点D在AC上,且∠ABC=∠C=∠BDC, ∠ABD=∠A,求∠A的度数.解:设∠ABD=∠A=x°∵∠BDC=∠ABD+∠A∴∠ABC=∠C=∠BDC=2x°∵∠A+∠ABC+∠C=180°∴x°+2x°+2x°=180°∴x=36,∴∠A=36°17.如图⒁,D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.解:∵DF⊥AB∴∠AFE=90°又∵∠CEF =∠AFE +∠A,∠CEF =∠ECD +∠D∴∠AFE +∠A =∠ECD +∠D又∵∠A =35°,∠D =42°∴90°+35°=∠ECD +42°∴∠ECD =83°,即∠ACD =83°.18.如图⒂,△ABC 中,∠ACB =90°,CD 是AB 边上的高,BE 是AC 边上的中线,AB =10cm,BC =8cm,AC =6cm.⑴求CD 的长;⑵求△ABE 的面积.解:⑴∵S △ABC =12(AC×BC)=12(AB×CD) ∴12(6×8)=12(10×CD) ∴CD = 4.8(cm) .⑵∵BE 是AC 边上的中线∴S △ABE =12S △ABC =12 (682)=12(cm 2). 19.如图⒂,∠xoy =90°,点A 、B 分别在射线ox,oy 上移动,BE 是∠ABy 的平分线,BE 的反向延长线与∠OAB 的平分线相交于点C ,试问∠C 的大小是否随点A 、B 的移动而发生变化?如果保持不变,求出∠C 的大小,如果随点A 、B 的移动而发生变化,请求出变化范围.解:∠C 的大小保持不变.∵BE 是∠ABy 的平分线∴∠3=∠2=12∠ABy 又∵AC 平分∠OAB∴∠1=12∠OAB ∴∠C =∠3-∠1=12∠ABy -12∠OAB =12 (∠ABy -∠OAB)=12∠xoy 又∵∠xoy =90°∴∠C =45°.。
人教版高中物理必修第3册 第十一章 电路及其应用 章末小结与素养评价
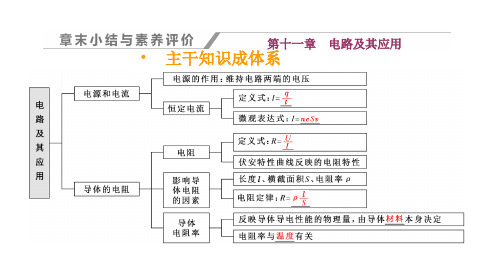
•(1) 根 据 实 验 室 中 已 有 如 下 的 实 验 仪 器 , 设 计 了 如 图 117乙所示的电路图。 •A.干电池两节(每节电动势约1.5 V); •B.待测二极管; •C.电流表(量程40 mA,内阻约几欧); •D.电流表(量S程5 mA,内阻RA=20 Ω); •E.滑动变阻器(阻值范围为0~10 Ω); •F.电阻箱(最大阻值为999 Ω); •G.导线、开关若干。 •则图乙中电流表A1应选择________,电流表A2应选择 ________。(填仪器前的字母)
• 2.电路分析与计算的解题思路 • (1)明确各电路元件的串、并联关系以及电流表、 电压表测量的对象,分析电路结构。
• (2)根据题目已知条件确定是从电路的整体还是从 某一部分电路入手进行分析,要从串、并联电路的特 点出发找出各段电路之间的电流、电压关系,选用相 应规律或公式建立方程。
• (3)注意接在电路中的电流表和电压表是否是理想 电表,如果是非理想电表,则应注意其内阻的大小;
即1I=R+ERA+EρSx, 则由图像可得:R+ERA=a; EρS=b-c a, 则 RA=aE-R; 解得:ρ=b-caSE=b-a4cπd2E。 答案:(1)0.755(0.754~0.756 均正确) (2)③b-a4cπd2E aE-R
• 5.(2021·焦作检测)二极管具有单向导电性,电路符 号是“ ”。实验小组想通过实验描绘某种型号的 二极管正向导通时的伏安特性曲线,并从这种型号二 极管说明书上得到其伏安特性曲线如图11-7甲所示。
R0+R RU~U R0U+R~UR
0~U 0~UR
典例2 (2021 年 1 月新高考 8 省联考·广东卷节选)某学习小组探究 LED 灯的伏安特性曲线。
人教版物理八年级章末复习学案(第十一章 功和机械能)

章末复习(第十一章功和机械能)一、功1.如果一个力作用在物体上,物体在这个力的方向上移动了一段距离,就说这个力对物体做了功。
做功包含两个必要因素:一是,二是。
不做功的三种情况: 、、。
2.计算:在物理学中,功等于的乘积;公式:。
3.单位:功的单位是,它有一个专门的名称叫做,简称,符号是;1 N·m=1 J。
二、功率4.物理意义:功率是表示物体做功的物理量。
功率大,说明做功,单位时间内做的功。
5.定义:与之比叫做功率,用符号表示。
6.定义式:。
公式推导:P===Fv。
7.单位:功率的国际单位是,简称,符号是。
工程技术上常用的功率单位是。
两单位间的关系是。
8.爬楼功率的测量(1)实验器材:。
(2)需要测量的物理量:。
(3)设计实验:①用体重计测出人的质量,记作m;②用皮卷尺测出所爬楼层的高度,记作h;③用停表测出爬楼所用的时间,记作t。
(4)功率表达式:。
三、机械能9.能量:物体能够,我们就说这个物体具有能量。
能量的单位是。
一个物体能够做的功越,表示这个物体的能量越。
10.动能(1)定义:物体由于而具有的能,叫做动能。
(2)决定因素:动能的大小由物体的和决定;质量越大,速度越大,物体的动能就。
11.重力势能(1)定义:在地球表面附近,物体由于所具有的能,叫做重力势能。
(2)决定因素:重力势能的大小由 和 决定;质量越大,位置越高,物体的重力势能就 。
12.弹性势能:物体由于发生 而具有的能,叫做弹性势能。
弹性势能的大小与物体的材料和弹性形变程度有关。
13.机械能(1)定义: 和 统称为机械能。
(2)大量研究结果表明,如果只有动能和势能相互转化,机械能的总和 ,或者说,机械能是 的。
1.辨析动能和势能能量种类 概念特点决定因素 共同特点动能物体由于运动而具有的能一切运动的物体都具有动能质量、速度具有能的物体都能够对外做功势能重力势能在地球表面附近,物体由于受到重力并处在一定高度时所具有的能一切受到重力且被举高的物体都具有重力势能质量、高度弹性 势能物体由于发生弹性形变而具有的能一切发生弹性形变的物体都具有弹性势能材料、弹性形 变程度2.功与功率的比较命题点1 做功的必要条件如图所示,运动员将杠铃举起的过程中,对杠铃 ,将杠铃举在头顶静止不动时,对杠铃 (前两空均选填“做功”或“不做功”)。
电工电子技术基础第十一章

第二节 滤波电路
二、LC 平滑滤波器
1.工作原理:LC 平滑滤波器的电路与工作波形如图所示。
滤波电容 C 的选择条件:能使它在 50 Hz(或100 Hz)频 率时的容抗相对于电感 L 的感抗小的多。
第二节 滤波电路
2.参数选择 滤波电容 L的选择条件:L 选择越大,滤波效果越好,通 常取值在几亨到几十亨。
第三节 稳压电路
一、硅稳压二极管的工作特性 二、工作原理
第三节 稳压电路
稳压电路:当电网电压波动或负载发生变化时,输出稳定 电压的电路。
实验 11 - 1 硅稳压二极管特性实验 1.按图所示电路安装实验线路。
2.记录实验结果分析归纳。
第三节 稳压电路
一、硅稳压二极管的工作特性
1.硅稳压二极管:具有稳压特点,是晶体管稳压电路的基 本元件,是特殊的二极管。符号:
导通条件而导通,由于晶闸管正向压降很小,电源电压几乎全 部加到负载上,即
uL = u2
第一节 整流电路
③ 在 < t < 期间,尽管 uG 在晶闸管导通以后立即消
失,但晶闸管仍然保持导通,因此,在这期间,负载电压 uL 基本与二次电压 u2 保持相等。
④ 当 t = 时,U2 = 0,晶闸管自行关断。
5.将示波器与直流电压表接在点 8 和 6 点间,用 2.2 k 电位器作为电路负载。用电流表测量输出电流。
第四节 直流稳压电源
6.调节自耦调压器,使输入电压在 10% 的范围内调整, 即分别使 Ui = 200 V 和 Ui = 240 V ,测量相应的输出电压。
7.关掉电源、拆掉电路。对实验结果进行分析和归纳总结 (1)结合 3、5、7、8 的波形变化,说明各部分作用。 (2)输入电压调整时,输出电压为什么可以稳定。 (3)稳压管工作时有何要求(反接、限流、稳压值的选 择)。
11第十一章损伤、中毒病人的护理-护士考点串讲讲解(推荐文档)

2015年全国护士执业资格考试 考前冲刺串讲
第十一章 损伤、中毒病人的护理
2015年全国护士执业资格考试 考前冲刺串讲
第一节 创伤病人的护理
第十一章 损伤、中毒病人的护理
创伤的分类 创伤病人的护理措施
考试重点
扭挫了(扭伤、挫伤)、 挤爆(挤压伤、爆震伤)了
历年考题
例:患者男,20岁。因工程塌方被石板压迫4小时,伤肢严重肿胀,组织广泛坏死。该损伤属于 A.扭伤 B.挤压伤 C.挫伤 D.冲击伤 E.撕裂伤
√
历年考题
例:患者女,50岁。一氧化碳中毒2小时入院。患者深昏迷,呼吸规则,血碳氧血红蛋白(COHb)55%。为促进一氧化碳的排出,最佳的措施是 A.应用呼吸机 B.高压氧舱治疗 C.间断高浓度给氧 D.持续低流量给氧 E.应用呼吸兴奋剂
√
小结
煤气中毒,脑先受损; 樱桃红色,典型体征; 碳氧测定,最能确诊; 一旦发生,脱离环境; 导管给氧,八至十升 ; 清醒以后,休息两周 ; 以免发生,迟发脑病。
√
Ⅰ度烧伤:伤及表皮浅层浅Ⅱ度烧伤:伤及表皮的生发层和真皮乳头层疼痛剧烈深Ⅱ度烧伤:伤及真皮层。痛觉迟钝Ⅲ度烧伤:痛觉消失
历年考题
例:男性,30岁,体重70kg,烧伤后4h送至医院。右上肢水肿明显,剧烈疼痛,有较大水疱,双下肢皮肤焦黄,触之不痛,如皮革样。该病人的烧伤深度为 A.右上肢浅Ⅱ度,双下肢Ⅲ度B.右上肢深Ⅱ度,双下肢Ⅲ度 C.右上肢浅Ⅱ度,双下肢深Ⅱ度D.右上肢与双下肢均为深Ⅱ度 E.右上肢浅Ⅲ度,双下肢深Ⅱ度
护理措施-急救
抢救生命,先抢救危及生命的伤情。 禁食、胃肠减压 对有内脏脱出者不可回纳腹腔以免污染,可用消毒或清洁碗盖住脱出内脏
护理措施-内脏损伤的护理
八年级数学上册 第11章 数的开方章末复习课件

章末复习(fùxí)
第一页,共十三页。
知识结构
第二页,共十三页。
释疑 解 (shìyí) 惑
1.如何利用(lìyòng)平方根的概念解题?
在利用(lìyòng)平方根的概念解题时,主要涉及平方根的 性质:正数有两个平方根,且它们互为相反数;以及平 方根的非负性:被开方数为非负数,算术平方根也为非 负数。
内容 总结 (nèiróng)
章末复习。例1 已知某数的平方根是a+3及2a-12,求这个数。解:根据题意可得,a+3+2a-12=0.。 ∴a+3=6,2a-12=-6.。=-32-1-3=-36。解关于x的方程(fāngchéng)(a+2)x+b2=a-1。即a=-3,b=。解:由题意, 得m-n=2,。m-2n+3=3,即m=2n.。∴m=4,n=2.。课堂小结
例3 计算:( 2 ) 3( 4 ) 23( 4 ) 3 ( 1) 23 27
解:原式=-8×|-4| +(-4)×
1
2
Байду номын сангаас-3
4
=-32-1-3=-36
第六页,共十三页。
典例精析
例1 如图所示,数轴上表示 3 的点是
。
分析:由于1<3<4,故1< <3 2,故这样的
点在表示1和2的点之间,故选C。
第七页,共十三页。
B=m2n3 4m6n1是4m+6n-1的立方根,求B-A
的立方根。 解:由题意,得m-n=2,
即m=n+2;m-2n+3=3,即m=2n.
∴m=4,n=2. ∴A= 16 =4,B=3 27 =3。
种子和果实的成熟生理

思考讨论
本章小结 考核要点
相关连接
第十一章植物的成熟和衰老生理
第一节 种子和果实的成熟生理
一、种子成熟时的生理生化变化
教学内容 ห้องสมุดไป่ตู้学目标
2.蛋白质的变化 2.蛋白质的变化 3.脂肪的变化 3.脂肪的变化
酸价—中和1克油脂中游离脂肪酸所需KOH 中和1克油脂中游离脂肪酸所需KOH
第一节 种子和果实的成熟生理
一、种子成熟时的生理生化变化
教学内容 教学目标 重点难点 课堂讲授
种子形成初期 呼吸作用: 呼吸作用: 旺盛 代 谢: 强 有 机 物:小分子可溶态 水 分: GA: GA: IAA: IAA: ABA: ABA: 多
溶胶 递增 递增 原生质胶体: 原生质胶体:
种子成熟 渐低 渐弱
细胞分裂,子房膨大;胚形成,核变硬;子房 细胞分裂,子房膨大;胚形成,核变硬; 速增
思考讨论
本章小结 考核要点
相关连接
返回
上页
下页
节末
退出
第十一章植物的成熟和衰老生理
第一节 种子和果实的成熟生理
二、果实的生长和成熟时的生理生化变化
教学内容 教学目标 重点难点 课堂讲授
思考讨论
本章小结 考核要点
相关连接
的毫克数。 的毫克数。 碘价-1克油脂能吸收碘当量的克数。 克油脂能吸收碘当量的克数。
重点难点 课堂讲授
思考讨论
4.非丁(Phyrin)的变化 4.非丁(Phyrin)的变化 非丁(Phyrin) (二)其它生理生化变化
1.呼吸速度的变化 1.呼吸速度的变化 2.内源激素的变化 1)。 2.内源激素的变化 (图9-1)。 此外,种子含水量与干物质积累恰好相反, 此外,种子含水量与干物质积累恰好相反, 随着种子的成熟而逐渐降低。 随着种子的成熟而逐渐降低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由图可得对顶角 ∠ACB=∠DCE
感悟提升
图形语言
(公共边 公共角 对顶角)
找条件
(至少有一组 对应边相等)
对应边相等 全等三角形 对应角相等
第四组练习:三角形全等的应用
证明: ∵AC⊥EF,AH⊥FD,
4. AC⊥EF于点C,AH⊥FD于点B, ∠E=90°,AC=FE.求证:AH=FD.
1. 请填出使两个三角形全等的条件,并把条件标注 在图形上. 在△ABC 和△A′B′C′中, _____=_____, _____=_____, _____=_____ , A' ∴△ABC≌△A′B′C′. A
B' B C
C'
感悟提升
对应边相等 全等三角形 平移、翻折、旋转
找条件
(至少有一组 对应边相等)
A'
D
O C
A
B
A
B
2.如图,△ACB≌△A′CB′, ∠BCB′=30°,则∠ACA′的度数为( B ) A.20° B.30° C.35° D.40°
B'
C
第二组练习:全等三角形性质应用
3.如图,OA=OB,OC=OD,∠O=50°, ∠D=35°,则∠AEC等于( A) A.60° B.50° C.45° D.30°
1. 如图AB=DC,AC=BD. 求证: ∠A=∠D. 证明:在△ABC 和△DCB中,
A
D
AB=DC,
AC=BD, BC=CB(公共边),
O
B C
∴ △ABC≌△DCB, ∴∠A=∠D.
由图可得公共边BC=BC
第四组练习:三角形全等的应用
2. 如图OD=OC,OA=OB. 求证:AD=BC. 证明: 在△ODA 和△OCB中, O OD=OC,
1. △ABC是等腰三角形,D、E分别是腰AB 及AC延长线上的一点,且BD=CE,连接DE交底BC于 点G. 求证:GD=GE.
A
思考:GD和GE不在两个全等三角形 中,如何证明相等呢?
D B M C G E
解题思路:过点D作DM∥CE,构 造等腰△DMB,再得出 △DMG≌△ECG,即得出结论.
∴BE=CF.
感悟提升
图形语言 (公共边,公 共角,对顶角)
对 应 边 相 等
全等三角形
边相等 (等角对等边 ,角平分线性 质定理,线段 中点)
角相等 (垂直,平行,角 平分线,同(等) 角的余(补)角相 等)
找条件
(至少有一组 对应边相等)
平移、翻折、旋转
对 应 角 相 等
第五组练习:综合运用
5.在△ABC中,AD平分∠BAC, BD=CD,DE⊥AB于点E, DF⊥AC于点F.求证:BE=CF.
DE⊥AB,DF⊥AC, ∴DE=DF. ∵ DE⊥AB,DF⊥AC,
∴△BED和△BED是直角三角形. 在Rt△BED和Rt△CFD中, BD=CD, DE=DF, ∴ Rt△BED≌Rt△CFD.
O B
A
D E C
第二组练习:全等三角形性质应用 ( 选 做 题 ) 4. 如 图 , 在 Rt△ABC 中 , ∠ACB=90°,AC=4,BC=3,把Rt△ABC绕点A逆时 针旋转60°,得到△ADE,问△ABD的形状;旋 转90°呢? A
E
B
C
D
GSP选做题
答案:等边三角形;等腰直角三角形
第三组练习:三角形全等的判定
第十一章
全等三角形
第十一章 章末小结
知识梳理
线段相等
定义:线段中点 基本图形: 三角形 等腰三角形 全等 三角形 定义:平分线
角相等
基本图形:三角形
等腰三角形 全等 三角形
第一组练习:全等三角形的有关概念的应用
1. 把△ABC沿AC翻折得到△ADC,若∠B=85°, 则∠D= 85 ° A . A D G B
第三组练习:三角形全等的判定
3. 已知:如图AC、BD相交于O,OA=OC,请你添 加一个条件,使△AOB≌△COD并说明理由.
△AOB≌ △COD
D C O
S
A
B
A
S
OA=OC ∠DOC=∠AOB OD=OB
还有其他添法吗?
∠C=∠A(ASA)或∠D=∠B(AAS)
第四组练习:三角形全等的应用
课外作业
1. 教材P27第8、9题. (选做题)2.已知:如图,AB、CD互相平分于点O, 过点O作直线交AD、BC于点F、E.求证:OF=OE.
C
E B
O
A
F
D
对应角相等
第三组练习:三角形全等的判定
2.(2011十堰)工人师傅常用角尺平分一个任意角. 作法如下:如图,∠AOB是一个任意角,在边OA, OB上分别取OM=ON,移动角尺,使角尺两边相同的 刻度分别与M,N重合.过角尺顶点C作射线OC.由 此作法得△MOC≌△NOC的依据是( B ) A.AAS B.SAS C.ASA D.SSS
B
D E
A C
∠O=∠O(公共角), OA=OB,
∴ △ODA ≌△OCB,
∴AD=BC.
由图可得公共角∠o=∠o
第四组练习:三角形全等的应用
3. 如图AC=DC,BC=EC. 求证:AB∥ED.
证明: 在△ACB和△DCE中,
B
AC=DC,
A
C E
D
∠ACB=∠DCE(对顶角), BC=EC,
∴ △ACB ≌△DCE,
D
B
E
C
F
C 2. △ABC沿BC平移得到△DEF,若BC=10,
EC=4,则CF= 6 .
第一组练习:全等三角形的有关概念的应用
3. △ABC≌ △ADE,∠C=∠E,若∠BAC=75°, ∠DAC =40°,则∠CAE = 35° .
A E
B
D
C
第二组练习:全等三角形性质应用
1.△ABC≌ △BAD,A和B、C和D是对应点,如果 BD=5 cm,AD=4 cm,AB=6 cm,那么BC的长是(C ) A.6cm B.5cm C.4cm D.无法确定
感悟提升
图形语言 (公共边,公 共角,对顶角)
构造三角形
对 应 边 相 等
全等三角形
边相等 (等角对等边 ,角平分线性 质定理,线段 中点)
角相等 (垂直,平行,角 平分线,同(等) 角的余(补)
平移、翻折、旋转
对 应 角 相 等
畅所欲言
这节课中, 有什么收获 ? 还有什么疑惑呢?
∴∠ABG=∠FCG= 90°. ∵ ∠FGC=∠AGB, ∴ ∠A=∠F.
∵ AC⊥EF, ∴∠ACH=90°.
A B G F C H E D
在△ACH和△FED中, ∠A=∠F, AC=FE, ∠A=∠F,
∴ △ACH≌△FED,
AH=FD .
第四组练习:三角形全等的应用
证明: ∵AD平分∠BAC,
