高二段寒假数学作业3

合集下载

高二数学理科寒假作业

高二年级上学期理科数学寒假作业（完卷时间：120分钟满分：150分）一、选择题(在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内．每题5分，共计50分．）1.下列两变量中具有相关关系的是（）A.正方体的体积与边长；B.匀速行驶的车辆的行驶距离与时间；C.人的身高与体重；D.人的身高与视力2.某初级中学领导采用系统抽样方法，从该校预备年级全体800名学生中抽50名学生做牙齿健康检查。

现将800名学生从1到800进行编号，求得间隔数8001650k==，即每16人抽取一个人。

在1~16中随机抽取一个数，如果抽到的是7，则从33 ~ 48这16个数中应取的数是（）A．40．B．39． C．38． D．37．3．命题“若一个数是负数,则它的平方是正数”的否命题是（）A．“若一个数是正数,则它的平方是负数”B．“若一个数是正数,则它的平方不是正数”C．“若一个数不是负数,则它的平方不是正数”D．“若一个数不是负数,则它的平方是负数”4．若某程序框图如图所示，则输出的p的值是（）A． 21 B．26 C． 30 D．555．已知命题265:xxp≥-，命题2|1:|>+xq，则p是q的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件6．现有男、女学生共8人，从男生中选2人，从女生中选1人分别参加数学、物理、化学三科竞赛，共有90种不同方案，那么男、女生人数分别是A．男生2人女生6人B．男生3人女生5人C．男生5人女生3人D．男生6人女生2人.7．已知椭圆14222=+ayx与双曲线1222=-yax有相同的焦点，则a的值是（）A．1 B．2 C．3 D. 48.在正方形ABCD内任取点P，则使APB∠大于90的概率是（）A．8πB．4πC．2πD．16π9.中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4,2），则它的离心率为（）A10.如图，正方体ABCD－A1B1C1D1的棱长为1，点M在棱AB上，且AM＝13，点P是平面ABCD上的动点，且动点P到直线A1D1的（第4题图）1A距离与点P 到点M 的距离的平方差为1，那么动点P 的轨迹（） A ．圆 B ．椭圆 C ．双曲线 D ．抛物线二、填空题（请把答案填在题中横线上，每题4分，共计20分．） 11．抛物线212x y =的焦点到其准线的距离为 . 12. 如右图所示，在一个边长为2的正方形中随机撒入200粒豆子，恰有120粒落在阴影区域内，则该阴影部分的面积约为 . 13．从1,2,3,4,5这5个数中任取两个,则这两个数正好相差1的概率是________.14．在平行六面体1111ABCD A B C D -中，化简1()AB AD DD BC ++-的结果为______；15. 已知椭圆2211612x y +=，其弦AB 的中点为M ，若直线AB 和OM 的斜率都存在，则两条直线的斜率之积等于（O 为坐标原点）______；三、解答题（共6个小题,共80分.解答应写出文字说明、证明过程或演算步骤.）16．(本小题满分13分)已知命题p ：方程2212x y m +=表示焦点在x 轴上的椭圆；命题q ：方程01)2(442=+-+x m x 无实根，若()p q ∧⌝为真命题，求m 的取值范围。

2014-2015高二数学寒假作业(双基)

2014-2015高二数学寒假作业必修1—5（双基）（有问题可加QQ 群：309030193 进行咨询求解）（数学1必修）第一章（上）集合一、选择题1．下列各项中，不可以组成集合的是（） A ．所有的正数 B ．等于2的数 C ．接近于0的数 D ．不等于0的偶数 2．下列四个集合中，是空集的是（） A ．}33|{=+x x B ．},,|),{(22R y x x y y x ∈-=C ．}0|{2≤x x D ．},01|{2R x x x x ∈=+- 3．下列表示图形中的阴影部分的是（）A ．()()A CBC B ．()()AB AC C ．()()A B B CD ．()A B C4．下面有四个命题：（1）集合N 中最小的数是1；（2）若a -不属于N ，则a 属于N ；（3）若,,N b N a ∈∈则b a +的最小值为2；（4）x x212=+的解可表示为{}1,1；其中正确命题的个数为（） A ．0个 B ．1个 C ．2个 D ．3个 5．若集合{},,M a b c =中的元素是△ABC 的三边长，则△ABC 一定不是（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形 6．若全集{}{}0,1,2,32U UC A ==且，则集合A 的真子集共有（）A ．3个B ．5个C ．7个D ．8个二、填空题1．用符号“∈”或“∉”填空（1）0______N , 5______N,16______N（2）1______,_______,______2R Q Q e C Q π-（e 是个无理数）（3{}|,,x x a a Q b Q=+∈∈2. 若集合{}|6,A x x x N =≤∈，{|}B x x =是非质数，C AB =，则C 的非空子集的个数为。

3．若集合{}|37A x x =≤<，{}|210B x x =<<，则A B =_____________． 4．设集合{32}A x x =-≤≤,{2121}B x k x k =-≤≤+,且A B ⊇，则实数k 的取值范围是。

高二年级假期数学作业

高二年级假期数学作业（文科）1. 已知方程112522=-+-m ymx表示焦点在Y 轴上的椭圆,则实数m 的范围是 .2. 已知方程222=+ky x 表示焦点在Y 轴上的椭圆,则实数k 的范围是 .3. 方程231y x -=所表示的曲线是4. 如果方程222=+ky x 表示焦点在y 轴上的椭圆，实数k 的取值范围1. 已知动圆P 过定点)0,3(-A ，并且在定圆64)3(:22=+-y x B 的内部与其相内切，动圆圆心P 的轨迹方程 .2. 一动圆与定圆032422=-++y y x 内切且过定点)2,0(A ，动圆圆心P 的轨迹方程3. 已知圆4)3(:221=++y x C ,圆100)3(:222=+-y x C ，动圆P 与1C 外切，与2C 内切，动圆圆心P 的轨迹方程4. 已知)0,21(-A ，B 是圆4)21(:22=+-y x F （F 为圆心）上一动点,线段AB 的垂直平分线交BF 于P ,则动点P 的轨迹方程为 5. 已知ABC ∆三边AB 、BC 、AC 的长成等差数列，且,CA AB >点B 、C 的坐标)0,1(-、)0,1(，点A 的轨迹方程6. 一条线段AB 的长为a 2，两端点分别在x 轴、y 轴上滑动，点M 在线段AB 上，且2:1:=MB AM ,点M 的轨迹方程7. 已知椭圆的焦点坐标是)25,0(±，直线023:=--y x l 被椭圆截得线段中点的横坐标为21，椭圆方程8. 若ABC ∆的两个顶点坐标分别是)6,0(B 和)6,0(-C ，另两边AB 、AC 的斜率的乘积是94-，顶点A 的轨迹方程为9. 已知圆122=+y x ，从这个圆上任意一点向轴引垂线段，则线段的中点的轨迹方程是 10. 已知椭圆1452222=+yx，A 、B 分别是长轴的左右两个端点，P 为椭圆上一个动点，AP 中点的轨迹方程1．过椭圆)0(12222>>=+b a by ax 的左焦点1F 作x 轴的垂线交椭圆于点P ，F2为右焦点，若︒=∠6021PF F ，则椭圆的离心率为 2．在平面直角坐标系中，椭圆)0(12222>>=+b a by ax 的焦距为2，以O 圆心，a 为半径作圆，过点)0,(2ca作圆的两切线互相垂直，则离心率e ＝。

高二数学寒假作业练习题及答案(Word版)

高二数学寒假作业练习题及答案（2021最新版）作者：______编写日期：2021年__月__日A.y=x3B.y=|x|+1C.y=-x2+1D.y=2-|x|2.若f(x)=，则f(x)的定义域为()A.B.C.D.(0，+∞)3.设函数f(x)(xR)满足f(-x)=f(x)，f(x+2)=f(x)，则y=f(x)的图象可能是()图2-14.函数f(x)=(a>0且a≠1)是R上的减函数，则a的取值范围是()A.(0,1)B.C.D.1.已知函数f(x)=则f=()A.B.eC.-D.-e2.设函数f(x)定义在实数集上，它的图象关于直线x=1对称，且当x≥1时，f(x)=2x-x，则有()A.f0，且a≠1)，则函数f(x)=loga(x+1)的图象大致是()图2-25.定义在R上的偶函数f(x)满足：对任意x1，x2[0，+∞)，且x1≠x2都有>0，则()A.f(3)1的解集为()A.(-1,0)(0，e)B.(-∞，-1)(e，+∞)C.(-1,0)(e，+∞)D.(-∞，1)(e，+∞)4.已知函数f(x)是定义在R上的奇函数，其最小正周期为3，且x时，f(x)=log(1-x)，则f(2010)+f(2021)=()A.1B.2C.-1D.-21.函数y=的图象可能是()图2-42.定义在R上的函数f(x)满足f(-x)=-f(x)，f(x-2)=f(x+2)，且x(-1,0)时，f(x)=2x+，则f(log220)=()A.1B.C.-1D.-3.定义两种运算：ab=，ab=，则f(x)=是()A.奇函数B.偶函数C.既奇又偶函数D.非奇非偶函数4.已知函数f(x)=|lgx|，若02的解集为()A.(2，+∞)B.(2，+∞)C.(，+∞)D.6.f(x)=x2-2x，g(x)=ax+2(a>0)，对x1∈[-1,2]，x0∈[-1,2]，使g(x1)=f(x0)，则a的取值范围是()A.B.C.[3，+∞)D.(0,3]7.函数y=f(cosx)的定义域为(kZ)，则函数y=f(x)的定义域为________.8.已知定义在R上的函数y=f(x)满足条件f=-f(x)，且函数y=f 为奇函数，给出以下四个命：(1)函数f(x)是周期函数;(2)函数f(x)的图象关于点对称;(3)函数f(x)为R上的偶函数;(4)函数f(x)为R上的单调函数.其中真命的序号为________.(写出所有真命的序号)专集训(二)A【基础演练】1.B【解析】是偶函数的是选项B、C、D中的函数，但在(0，+∞)上单调递增的函数只有选项B中的函数.2.A【解析】根据意得log(2x+1)>0，即01，解得x>e;当x1，解得-10时，y=lnx，当x或log4x2或02等价于不等式f(|log4x|)>2=f，即|log4x|>，即log4x>或log4x2或00，所以a的取值范围是.7.【解析】由于函数y=f(cosx)的定义域是(kZ)，所以u=cosx 的值域是，所以函数y=f(x)的定义域是.8.(1)(2)(3)【解析】由f(x)=f(x+3)f(x)为周期函数;又y=f为奇函数，所以y=f图象关于(0,0)对称;y=f向左平移个单位得y=f(x)的图象，原来的原点(0,0)变为，所以f(x)的图象关于点对称.又y=f 为奇函数，所以f=-f，故f=-f=-f(-x)f(-x)=f(x)，所以f(x)为偶函数;又f(x)为R上的偶函数，不可能为R上的单调函数.【篇二】1.(2021·浙江高考)已知i是虚数单位，则(-1+i)(2-i)=()A.-3+iB.-1+3iC.-3+3iD.-1+i解析：选B(-1+i)(2-i)=-1+3i.2.(2021·北京高考)在复平面内，复数i(2-i)对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解析：选Az=i(2-i)=2i-i2=1+2i，复数z在复平面内的对应点为(1,2)，在第一象限.3.若(x-i)i=y+2i，x，yR，则复数x+yi=()A.-2+iB.2+iC.1-2iD.1+2i解析：选B由(x-i)i=y+2i，得xi+1=y+2i.x，yR，x=2，y=1，故x+yi=2+i.4.(2021·新课标全国卷)若复数z满足(3-4i)z=|4+3i|，则z的虚部为()A.-4B.-C.4D.解析：选D因为|4+3i|==5，所以已知等式为(3-4i)z=5，即z=====+i，所以复数z的虚部为.5.(2021·陕西高考)设z是复数，则下列命题中的假命题是()A.若z2≥0，则z是实数B.若z2<0，则z是虚数C.若z是虚数，则z2≥0D.若z是纯虚数，则z2<0解析：选C设z=a+bi(a，bR)，则z2=a2-b2+2abi，由z2≥0，得则b=0，故选项A为真，同理选项B为真;而选项D为真，选项C 为假.故选C.。

高二数学寒假作业

高二数学寒假作业篇一：高二数学假期作业(2)高二数学假期作业（2）第Ⅰ卷（选择题，共60分）一、选择题：本大题共12分，每小题5分，共60分．1．若函数f(某)在某＝1处的导数为3，则f(某)的解析式可以为A．f(某)＝(某－1)2＋3(某－1)B．f(某)＝2(某－1)C．f(某)＝2(某－1)2D．f(某)＝某－12．(某)10的展开式中某6y4项的系数是A．840B．－840C．210D．－2103．一个学生能够通过某种英语听力测试的概率是得通过的概率是A．，他连续测试2次，那么其中恰有一次获2D．14B．13C．12344．已知曲线y＝co某，其中某∈[0，A．1B．23π]，则该曲线与坐标轴围成的面积等于25C．D．325．一位母亲纪录了儿子39岁的身高的数据（略），她根据这些数据建立的身高y（cm）与年龄某的回归模型为y＝7.19某＋73.93，用这个模型预测这个孩子10岁时的身高，则正确的叙述是A．身高一定是145.83cmC．身高在145.83cm以上6．若复数B．身高在145.83cm左右D．身高在145.83cm以下a3i（a∈R，i为虚数单位）是纯虚数，则实数a的值为12iA．－2B．4C．－6D．67．若z∈C且|z＋2－2i|＝1，则|z－2－2i|的最小值等于A．2B．3C．4D．58．通过随机询问250名不同性别的大学生在购买食物时是否看营养说明书，得到如下2某2联A．95%以上认为无关B．90%95%认为有关C．95%99.9%认为有关D．99.9%以上认为有关9．从4位男教师和3位女教师中选出3位教师，派往郊区3所学校支教，每校1人，要求这3位教师中男、女教师都要有，则不同的选派方案有A．210种B．186种C．180种D．90种10．若A，B，C，D，E，F六个不同元素排成一列，要求A不排在两端，且B、C相邻，则不同的排法共有A．72种B．96种C．120种D．144种11．(某2＋2某＋1)d某＝()．A．4B．13C．12D．3412．从一副不含大小王的52张扑克牌中不放回地抽取2次，每次抽1张，已知第1次抽到A，那么第2次也抽到A的概率为()．A．B．13C．12D．117第Ⅱ卷（非选择题，共74分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题卡指定位置上．13．在数列{an}中，a1＝3，且an1＝a2，则数列{an}的通项公式an＝_____．n（n为正整数）14．若(2某－1)7＝a7某7＋a6某6＋…＋a1某＋a0，则a7＋a5＋a3＋a1＝_____________．15．某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号，每次可以任挂1面、2面或3面，并且不同的顺序表示不同的信号，一共可以表示___________种不同的信号．16．函数y＝in3某＋co3某在[－，]上的最大值是________________．44三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．17．（本小题满分12分）n2(n1)2用数学归纳法证明：当n为正整数时，1＋2＋3＋……＋n＝．433318．（本小题满分12分）某年级的联欢会上设计了一个摸奖游戏，在一个不透明的口袋中装有10个红球和20个白球，这些球除颜色外完全相同，一次从中摸出5个球，至少摸到3个红球就中奖，求中奖概率．根据工资待遇的差异情况，你愿意选择哪家单位？请说明你的理由．20．（本小题满分12分）先阅读下面的文字，再按要求解答．如图，在一个田字形地块的A、B、C、D四个区域中栽种观赏植物，要求同一区域种同一种植物，相邻两区域（A与D，B与C不相邻）种不同的植物，现有四种不同的植物可供选择，问不同的种植方案有多少种？AB某学生给出如下的解答：CD解：完成四个区域种植植物这件事，可分4步，第一步：在区域A种植物，有C14种方法；第二步：在区域B种植与区域A不同的植物，有C13种方法第三步：在区域D种植与区域B不同的植物，有C13种方法第四步：在区域C种植与区域A、D均不同的植物，有C12种方法根据分步计数原理，共有C14C3C3C2＝72（种）答：共有72种不同的种植方案．问题：（Ⅰ）请你判断上述的解答是否正确，并说明理由；（Ⅱ）请写出你解答本题的过程．为了研究不同的给药方式（口服与注射）和药的效果（有效与无效）是否有关，进行了相22．（本小题满分14分）已知函数f(某)＝(某2－2某)ek某（k∈R，e为自然对数的底数）在(和∞)上递增，在[上递减．（Ⅰ）求实数k的值；（Ⅱ）求函数f(某)在区间[0，m]上的最大值和最小值．根据193个病人的数据，能否作出药的效果与给药方式有关的结论？请说明理由．高二数学假期作业（2）参考答案二、填空题：每小题4分，共16分．13．3214．109415．1516．1三、解答题：共74分．n1122217．证明：（1）当n＝1时，左边＝1，右边＝＝1，4∴等式成立．································································································2分（2）假设当n＝k时，等式成立，即k2(k1)21＋2＋3＋……＋k ＝．··································································4分43333那么，当n＝k＋1时，有k2(k1)21＋2＋3＋……＋k＋(k＋1)＝＋(k＋1)3．········································6分422(k1)2(k2)22k2k4k4＝(k＋1)(＋k＋1)＝(k＋1)＝444(k1)[(k1)1]2＝．··················································································9分433333这就是说，当n＝k＋1时，等式也成立．···························································10分根据（1）和（2），可知对n∈N某等式成立．·······················································12分18．解：设摸出红球的个数为某，则某服从超几何分布，其中N＝30，M＝10，n＝5．············································································4分于是中奖的概率为P(某≥3)＝P(某＝3)＋P(某＝4)＋P(某＝5) (6)分353454555C10C30C10C30C10C30101010＝＋＋································································9分555C30C30C30≈0.191．······································································································12分19．解：根据月工资的分布列，可得E某1＝1200某0.4＋1400某0.3＋1600某0.2＋1800某0.1＝1400．··································································································2分22D某1＝(1200－1400)某0.4＋(1400－1400)某0.3＋(1600－1400)2某0.2＋(1800－1400)2某0.1＝40000···································································································4分E某2＝1000某0.4＋1400某0.3＋1800某0.2＋2200某0.1＝1400·····································································································6分D某2＝(1000－1400)2某0.4＋(1400－1400)2某0.3篇二：2022高二数学下册寒假作业答案D.4某-3y+7=08.过点的直线中,被截得最长弦所在的直线方程为()A.B.C.D.9.(2022年四川高考)圆的圆心坐标是10.圆和的公共弦所在直线方程为____.11.(2022年天津高考)已知圆的圆心是直线与轴的交点，且圆与直线相切，则圆的方程为.12(2022山东高考)已知圆过点，且圆心在轴的正半轴上，直线被该圆所截得的弦长为，则圆的标准方程为____________13.求过点P(6，-4)且被圆截得长为的弦所在的直线方程.14、已知圆C的方程为某2+y2=4.(1)直线l过点P(1,2)，且与圆C交于A、B两点，若|AB|=23，求直线l的方程;(2)圆C上一动点M(某0，y0)，ON=(0，y0)，若向量OQ=OM+ON，求动点Q的轨迹方程人的结构就是相互支撑，众人的事业需要每个人的参与。

成都七中高二数学寒假作业文科班

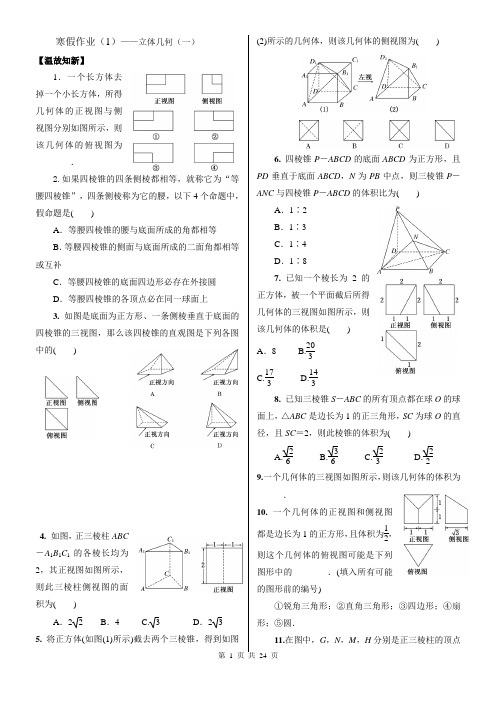
寒假作业（1）——立体几何（一）【温故知新】1．一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为________．2.如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是()A．等腰四棱锥的腰与底面所成的角都相等B．等腰四棱锥的侧面与底面所成的二面角都相等或互补C．等腰四棱锥的底面四边形必存在外接圆D．等腰四棱锥的各顶点必在同一球面上3.如图是底面为正方形、一条侧棱垂直于底面的四棱锥的三视图，那么该四棱锥的直观图是下列各图中的()4.如图，正三棱柱ABC－A1B1C1的各棱长均为2，其正视图如图所示，则此三棱柱侧视图的面积为()A．22B．4 C. 3 D．2 35.将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的侧视图为()6.四棱锥P－ABCD的底面ABCD为正方形，且PD垂直于底面ABCD，N为PB中点，则三棱锥P－ANC与四棱锥P－ABCD的体积比为()A．1∶2B．1∶3C．1∶4D．1∶87.已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是()A．8 B.203C.173 D.1438.已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为()A.26 B.36 C.23 D.229.一个几何体的三视图如图所示，则该几何体的体积为______．10.一个几何体的正视图和侧视图都是边长为1的正方形，且体积为12，则这个几何体的俯视图可能是下列图形中的________．(填入所有可能的图形前的编号)①锐角三角形；②直角三角形；③四边形；④扇形；⑤圆．11.在图中，G，N，M，H分别是正三棱柱的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有________．(填上所有正确答案的序号)12.已知m，n，l为不同的直线，α，β为不同的平面，有下面四个命题：①m，n为异面直线，过空间任一点P，一定能作一条直线l与m，n都相交．②m，n为异面直线，过空间任一点P，一定存在一个与直线m，n都平行的平面．③α⊥β，α∩β＝l，m⊂α，n⊂β，m，n与l都斜交，则m与n一定不垂直；④m，n是α内两相交直线，则α与β相交的充要条件是m，n至少有一条与β相交．则四个结论中正确的个数为()A．1B．213. 已知正方体ABCD－A1B1C1D1中，E，F分别为BB1，CC1的中点，那么异面直线AE与D1F所成角的余弦值为________．14.已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．(1)画出该三棱锥的直观图；(2)求出侧视图的面积．【拓展提升】15.若两条异面直线所成的角为60°，则称这对异面直线为“黄金异面直线对”，在连接正方体各顶点的所有直线中，“黄金异面直线对”共有________对．【体验高考】16.设四面体的六条棱的长分别为1,1,1,1，2和a，且长为a的棱与长为2的棱异面，则a的取值范围是()A．(0，2) B．(0，3)C．(1，2) D．(1，3)寒假作业（2）——立体几何（二）【温故知新】1．已知三个命题：①若点P 不在平面α内，A 、B 、C 三点都在平面α内，则P 、A 、B 、C 四点不在同一平面内；②两两相交的三条直线在同一平面内；③两组对边分别相等的四边形是平行四边形．其中正确命题的个数是 ( )A ．0B ．1C ．2D ．32.如图，α∩β＝l ，A 、B ∈α，C ∈β，且C ∉l ，直线AB ∩l ＝M ，过A 、B 、C 三点的平面记作γ，则γ与β的交线必通过 ( ) A ．点AB ．点BC ．点C 但不过点MD ．点C 和点M3.如图，在四面体ABCD 中，若截面PQMN 是正方形，则在下列命题中，错误的为 ( )A ．AC ⊥BDB ．AC ∥截面PQMN C ．AC ＝BDD ．异面直线PM 与BD 所成的角为45°4．在正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为棱AA 1、CC 1的中点，则在空间中与三条直线A 1D 1、EF 、CD 都相交的直线 ( )A ．不存在B ．有且只有两条C ．有且只有三条D ．有无数条5．如图，M 是正方体ABCD －A 1B 1C 1D 1的棱DD 1的中点，给出下列四个命题：①过M 点有且只有一条直线与直线AB ，B 1C 1都相交；②过M 点有且只有一条直线与直线AB ，B 1C 1都垂直；③过M 点有且只有一个平面与直线AB ，B 1C 1都相交；④过M 点有且只有一个平面与直线AB ，B 1C 1都平行．其中真命题是 ( ) A ．②③④B ．①③④C ．①②④D ．①②③6．将正方形ABCD 沿对角线BD 折起，使平面ABD ⊥平面CBD ，E 是CD 的中点，则异面直线AE 、BC 所成角的正切值为 ( )A. 2B.22C ．2 D.127．如图，G 、H 、M 、N 分别是三棱柱的顶点或所在棱的中点，则表示直线GH 与MN 是异面直线的图形有________．8．下列命题中正确的是________．①若△ABC 在平面α外，它的三条边所在的直线分别交平面α于P 、Q 、R ，则P 、Q 、R 三点共线；②若三条直线a 、b 、c 互相平行且分别交直线l 于A 、B 、C 三点，则这四条直线共面；③空间中不共面的五个点一定能确定10个平面； ④若a 不平行于平面α，且a ⊄α，则α内的所有直线与a 异面．9．已知正方体ABCD －A 1B 1C 1D 1中，E 为C 1D 1的中点，则异面直线AE与BC 所成角的余弦值为________．10.如图所示，在三棱锥C －ABD 中，E ，F 分别是AC 和BD 的中点，若CD ＝2AB ＝4，EF ⊥AB ，则EF 与CD 所成的角是________．11．如图所示，已知E、F分别是正方体ABCD－A1B1C1D1的棱AA1和棱CC1的中点．试判断四边形EBFD1的形状．【拓展提升】12.如图，已知：E、F、G、H分别是正方体ABCD －A1B1C1D1的棱AB、BC、CC1、C1D1的中点，证明：FE、HG、DC三线共点．【体验高考】13．正方形ABCD中，点E，F分别在AB，CD 上，且AE＝2EB，CF＝2FD，将直角梯形AEFD沿EF 折起到A′EFD′的位置，使点A′在平面ABCD上的射影G恰好落在BC上．(1)判断直线AA′与DD′的位置关系，并证明；(2)证明平面A′AE⊥平面A′BC.寒假作业（3）——立体几何（三）1．下列条件中，能作为两平面平行的充分条件的是()A．一个平面内的一条直线平行于另一个平面B．一个平面内的两条直线平行于另一个平面C．一个平面内有无数条直线平行于另一个平面D．一个平面内任何一条直线都平行于另一个平面2．已知直线a，b，平面α，则以下三个命题：①若a∥b，b⊂α，则a∥α；②若a∥b，a∥α，则b∥α；③若a∥α，b∥α，则a∥b.其中真命题的个数是()A．0B．1 C．2 D．33．若一直线上有相异三个点A，B，C到平面α的距离相等，那么直线l与平面α的位置关系是() A．l∥αB．l⊥αC．l与α相交且不垂直D．l∥α或l⊂α4.已知直线m⊥平面α，直线n⊂平面β，则下列命题正确的是()A．若n∥α，则α∥βB．若α⊥β，则m∥nC．若m⊥n，则α∥βD．若α∥β，则m⊥n 5．平面α∥平面β的一个充分条件是()A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α6.如图，正方体ABCD－A1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线()A．不存在B．有1条C．有2条D．有无数条7．平面α∥平面β，a⊂α，b⊂β，则直线a，b的位置关系是________．8．在正方体ABCD－A1B1C1D1中，E是DD1的中点，则BD1与平面ACE的位置关系为________．9.设a，b为空间的两条直线，α，β为空间的两个平面，给出下列命题：①若a∥α，a∥β，则α∥β；②若a⊥α，a⊥β，则α∥β；③若a∥α，b∥α，则a∥b；④若a⊥α，b⊥α，则a∥b.上述命题中，所有真命题的序号是________．10．已知平面α∥β，P∉α且P∉β，过点P的直线m与α，β分别交于A.C，过点P的直线n与α，β分别交于B，D，且P A＝6，AC＝9，PD＝8则BD的长为________．11.如图，在棱长为2的正方体ABCD－A1B1C1D1中，E，F分别是BD，BB1的中点．(1)求证：EF∥平面A1B1CD；(2)求证：EF⊥AD1.【拓展提升】12.如图，矩形AMND所在的平面与直角梯形MBCN所在的平面互相垂直，MB∥NC，MN⊥MB.(1)求证：平面AMB∥平面DNC；(2)若MC⊥CB，求证：BC⊥AC. 【体验高考】13.如图，直三棱柱ABC－A′B′C′，∠BAC ＝90°，AB＝AC＝2，AA′＝1，点M，N分别为A′B 和B′C′的中点．(1)证明：MN∥平面A′ACC′；(2)求三棱锥A′－MNC的体积．(锥体体积公式V ＝13Sh，其中S为底面面积，h为高)寒假作业（4）——立体几何（四）【温故知新】1．已知平面α，β，直线l，若α⊥β，α∩β＝l，则()A．垂直于平面β的平面一定平行于平面αB．垂直于直线l的直线一定垂直于平面αC．垂直于平面β的平面一定平行于直线lD．垂直于直线l的平面一定与平面α、β都垂直2.如图，O为正方体ABCD－A1B1C1D1的底面ABCD的中心，则下列直线中与B1O垂直的是() A．A1D B．AA1C．A1D1D．A1C13．已知α，β是两个不同的平面，m，n是两条不重合的直线，则下列命题中正确的是()A．若m∥α，α∩β＝n，则m∥nB．若m⊥α，m⊥n，则n∥αC．若m⊥α，n⊥β，α⊥β，则m⊥nD．若α⊥β，α∩β＝n，m⊥n，则m⊥β4. 设a，b是两条不同的直线，α，β是两个不同的平面，则下列四个命题：①若a⊥b，a⊥α，b⊄α，则b∥α；②若a∥α，a ⊥β，则α⊥β；③若a⊥β，α⊥β，则a∥α或a⊂α；④若a⊥b，a⊥α，b⊥β，则α⊥β.其中正确命题的个数为()A．1B．2 C．3 D．45．给出命题：(1)在空间里，垂直于同一平面的两个平面平行；(2)设l，m是不同的直线，α是一个平面，若l⊥α，l∥m，则m⊥α；(3)已知α，β表示两个不同平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；(4)a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一个平行．其中正确命题个数是()A．0 B．1 C．2 D．36.如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在() A．直线AB上B．直线BC上C．直线AC上D．△ABC内部7.如图，已知P A⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．8．如图所示，直线P A垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面P AC的距离等于线段BC的长．其中正确的是() A．①②B．①②③C．①D．②③9.如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A －BCD，则在三棱锥A－BCD中，下面命题正确的是()A．平面ABD⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ADC⊥平面ABC10.点P在正方体ABCD－A1B1C1D1的面对角线BC1上运动，给出下列四个命题：①三棱锥A－D1PC的体积不变；②A1P∥平面ACD1；③DP⊥BC1；④平面PDB1⊥平面ACD1.其中正确的命题序号是________．11.如图所示，已知P A⊥矩形ABCD所在平面，M，N分别是AB，PC的中点．(1)求证：MN⊥CD；(2)若∠PDA＝45°，求证：MN⊥平面PCD.【拓展提升】12.如图，在直三棱柱ABC－A1B1C1中，A1B1＝A1C1，D，E分别是棱BC，CC1上的点(点D不同于点C)，且AD⊥DE，F为B1C1的中点．求证：(1)平面ADE⊥平面BCC1B1；(2)直线A1F∥平面ADE. 【体验高考】13.如图所示，在四棱锥P－ABCD中，AB⊥平面P AD，AB∥CD，PD＝AD，E是PB的中点，F是DC上的点且DF＝12AB，PH为△P AD中AD边上的高．(1)证明：PH⊥平面ABCD；(2)若PH＝1，AD＝2，FC＝1，求三棱锥E－BCF 的体积；(3)证明：EF⊥平面P AB.寒假作业（5）——立体几何（五）【温故知新】1．某几何体的三视图如图所示，该几何体的体积是( )A ．8 B.83C ．4 D.432．已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且AB ＝3，BC ＝2，则棱锥O －ABCD 的体积为( ) A.51 B ．351 C ．251D ．6513．如图是一个几何体的三视图，则它的表面积为( )A ．4π B.154π C ．5πD.174π 4．用若干个大小相同，棱长为1的正方体摆成一个立体模型，其三视图如图所示，则此立体模型的表面积为( )A ．24B ．23C ．22D ．21 5．若一个几何体的三视图如下图所示，则此几何体的体积为( )A.112B ．5 C.92D ．46.如图，正方体ABCD －A ′B ′C ′D ′的棱长为4，动点E ，F 在棱AB 上，且EF ＝2，动点Q 在棱D ′C ′上，则三棱锥A ′－EFQ 的体积( )A ．与点E ，F 位置有关B ．与点Q 位置有关C ．与点E ，F ，Q 位置都有关D ．与点E ，F ，Q 位置均无关，是定值7．如图所示，已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成，则该多面体的体积是________．8．若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为________．9．在三棱锥A －BCD 中，AB ＝CD ＝6，AC ＝BD ＝AD ＝BC ＝5，则该三棱锥的外接球的表面积为________．10．如图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝AD ＝3 cm ，AA 1＝2 cm ，则四棱锥A －BB 1D 1D 的体积为________cm 3.11.如图，把边长为2的正六边形ABCDEF 沿对角线BE 折起，使AC ＝6.(1)求证：面ABEF ⊥面BCDE ； (2)求五面体ABCDEF 的体积．【拓展提升】12．如图，在四棱锥P －ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB＝4，CD＝2，侧面P AD是边长为2的等边三角形，且与底面ABCD垂直，E为P A的中点．(1)求证：DE∥平面PBC；(2)求三棱锥A－PBC的体积．【体验高考】13．一个空间几何体的三视图及部分数据如图所示，其正视图、俯视图均为矩形，侧视图为直角三角形．(1)请画出该几何体的直观图，并求出它的体积；(2)证明：A1C⊥平面AB1C1.寒假作业（6）——线性规划【温故知新】1.如图所示的平面区域(阴影部分)，用不等式表示为 A ．2x －y －3＜0 B ．2x －y －3＞0 C ．2x －y －3≤0D ．2x －y －3≥02. 已知点(－3，－1)和点(4，－6)在直线3x －2y －a ＝0的两侧，则a 的取值范围为( )A ．(－24,7)B ．(－7,24)C ．(－∞，－7)∪(24，＋∞)D ．(－∞，－24)∪(7，＋∞)3. 已知实数x 、y 满足⎩⎪⎨⎪⎧x ≥1，y ≤2，x －y ≤0，则此不等式组表示的平面区域的面积是( )A.12B.14 C ．1 D.184．若x ，y 满足约束条件⎩⎪⎨⎪⎧x ≥0，x ＋2y ≥3，2x ＋y ≤3则z ＝x －y 的最小值是( )A ．－3B ．0 C.32D ．35. 若直线y ＝2x 上存在点(x ，y )满足约束条件⎩⎪⎨⎪⎧x ＋y －3≤0，x －2y －3≤0，x ≥m ，则实数m 的最大值为( ) A ．－1 B ．1 C.32D ．26. 已知点Q (5,4)，动点P (x ，y )满足⎩⎪⎨⎪⎧2x －y ＋2≥0，x ＋y －2≤0，y －1≥0，则|PQ |的最小值为( )A ．5 B.43 C ．2D ．77.写出能表示图中阴影部分的二元一次不等式组是__________．8. 若点P (m,3)到直线4x －3y ＋1＝0的距离为4，且点P 在不等式2x ＋y ＜3表示的平面区域内，则m ＝________.9. 设变量x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋2y ≥2，2x ＋y ≤4，4x －y ≥－1，则目标函数z ＝3x －y 的取值范围是 10．设z ＝2x ＋y ，其中x ，y 满足⎩⎪⎨⎪⎧x ＋y ≥0，x －y ≤0，0≤y ≤k ，若z 的最大值为6，则k 的值为________；11. 画出不等式组⎩⎪⎨⎪⎧x －y ＋5≥0，x ＋y ≥0，x ≤3表示的平面区域，并回答下列问题：(1)指出x ，y 的取值范围；(2)平面区域内有多少个整点？【拓展提升】12. 变量x 、y 满足⎩⎪⎨⎪⎧x －4y ＋3≤0，3x ＋5y －25≤0，x ≥1.(1)设z ＝yx ，求z 的最小值；(2)设z ＝x 2＋y 2，求z 的取值范围．【体验高考】13.某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车．某天需送往A地至少72吨的货物，派用的每辆车需满载且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人，运送一次可得利润350元．该公司合理计划当天派用两类卡车的车辆数，可得最大利润z＝()A．4 650元B．4 700元C．4 900元D．5 000元寒假作业（7）——算法初步【预习新知】一、阅读必修3教材第一章第一单元《算法与程序框图》，回答下列问题：1、你对“算法”的理解。

2015-2016高二数学(理)寒假作业

)
A． , l , m l B． m, , C． , , m D． n , n , m 5．如图，AB 为圆 O 的直径，点 C 在圆周上（异于点 A，B），直线 PA 垂直于圆 O 所在的平面，点 M 为线段 PB 的中点．有以下四个命题： ①PA∥平面 MOB； ②OC⊥平面 PAC； ③MO∥平面 PAC； ④平面 PAC⊥平面 PBC．其中正确的命题是（） A．①② B．①③ C．③④ D．②④ 6．如图，在斜三棱柱 ABC－A1B1C1 的底面△ABC 中，∠A＝90° ，且 BC1⊥AC，过 C1 作 C1H⊥底面 ABC，垂足为 H，则点 H 在（） A．直线 AC 上 B．直线 AB 上 C．直线 BC 上 D．△ABC 内部 7．如图，在空间四边形 ABCD 中，点 E , H 分别是边 AB, AD 的中点，
F ,G 分别是边 BC,CD 上的点，且
CF CG 2 ＝＝，则（） CB CD 3
A． EF 与 GH 互相平行 B． EF 与 GH 异面 C． EF 与 GH 的交点 M 可能在直线 AC 上，也可能不在直线 AC 上 D． EF 与 GH 的交点 M 一定在直线 AC 上 8. 正四面体 ABCD 的棱长为 1，其中线段 AB / / 平面，E，F 分别是线段 AD 和 BC 的中点，当正四面体绕以 AB 为轴旋转时，线段 EF 在平面上的射影 E1F1 长的范围是（ A.[0，） B.[
O1 ABCD 的外接球的表面积为（
A． 9 B． 324
） C． 81 D．
243 2
）
6．如果一个正四面体（各个面都是正三角形）的体积为 9 cm3 ，则其表面积的值为（ A． 18 3cm2 B． 18cm2 C． 12 3cm2 ） D． 12cm2

陕西省宁强县天津高级中学高二数学假期作业试题(三) 理新人教A版【会员独享】

陕西省宁强县天津高级中学高二数学假期作业试题（三）理新人教A 版【会员独享】一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的．1. 复数(m2 – 3m) + mi ()m ∈R 是纯虚数，则实数m 的值是（）A ．3B ．0C ．0或3D ．0或1或32. 函数2()4f x x =的导函数是（）A ．'()2f x x =B ．'()4f x x =C ．'()8f x x =D ．'()16f x x =3. 下列等于1的积分是（）A ．10xdx ⎰B ．10(1)x dx +⎰C ．dx ⎰101D ．dx ⎰1021 4. 设m ∈N*，且m ＜25，则(25－m)(26－m)…(30－m)等于（） A ．625m A - B ．2530m m A -- C ．630m A - D ．530m A - 5. 西大附中数学组有实习老师共5名，现将他们分配到高二年级的1、2、3三个班实习，每班至少1名，最多2名，则不同的分配方案有（）A ．30种B ．90种C ．180种D ．270种6. 函数3()31f x x x =-+在闭区间 [– 3，0] 上的最大值、最小值分别是（）A ．1，− 1B ．1，− 17C ．3，− 17D ．9，− 1977. 现有男、女学生共7人，从男生中选1人，从女生中选2人分别参加数学、物理、化学三科竞赛，共有108种不同方案，那么男、女生人数分别是（）A ．男生4人，女生3人B ．男生3人，女生4人C ．男生2人，女生5人D ．男生5人，女生2人. 8. 设322()3(1)1f x kx k x k =+--+在区间（0，3）是增函数，则k 的取值范围是（）A ．0<kB ．01k <≤C ．1k ≥D ．1k ≤9. 函数333()(1)(2)(100)f x x x x =+++在1x =-处的导数值为（）A ．0B ．100!C ．3·99！D ．3·100！10. 跳格游戏：如图，人从格子外只能进入第1个格子，在格子中每次可向前跳1格或2格，那么人从格外跳到第8个格子的方法种数为（）A ．8种B ．13种C ．21种D ．34种二、填空题：本大题共5小题，每小题5分，共2511．已知复数Z 满足(1)1i Z +=-，则复数Z = ______________．12. 6人站成一排，甲、乙、丙3个人不能都站在一起的排法种数为____________．13.已知5025001250(23)x a a x a x a x =++++，其中01250a a a a ，，，，是常数，计算220245013549()()a a a a a a a a ++++-++++=______________．14. ()f x 是定义在(0)+∞，上的非负可导函数，且满足()'()0xf x f x -≥，对任意正数m ，n 若m n ≥，则()mf n 与()nf m 的大小关系是()mf n ______()nf m （请用≤，≥，或=）15. 求曲线x x x y 223++-=与x 轴所围成的图形的面积为______________．三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．16. (本小题满分13分)现有4个同学去看电影，他们坐在了同一排，且一排有6个座位．问：所有可能的坐法有多少种？此4人中甲，乙两人相邻的坐法有多少种？所有空位不相邻的坐法有多少种？（结果均用数字作答）17. (本小题满分13分)已知322()3(1)1f x x ax bx a a x =+++>=-在时的极值为0．求常数a ，b 的值；求()f x 的单调区间．18.(本小题满分13分) 一个暗箱里放着6个黑球、4个白球．（每个球的大小和质量均相同）不放回地依次取出2个球，若第1次取出的是白球，求第2次取到黑球的概率；有放回地依次取出2个球，求两球颜色不同的概率；有放回地依次取出3个球，求至少取到两个白球的概率．19.(本小题满分12分)已知函数32()3(1)(36)1f x mx m x m x =-++++，其中0m m ∈<R ，，若m = – 2，求()y f x =在（2，–3）处的切线方程；当[]11x ∈-，时，函数()y f x =的图象上任意一点的切线斜率恒大于3 m ，求m 的取值范围．20.(本小题满分12分)已知函数()ln ||(0)f x x x =≠，函数()'()(0)'()a g x f x x f x =+≠．0x ≠时，求函数()y g x =的表达式；若a > 0，函数()y g x =在(0)+∞，上的最小值是2，求a 的值；在 (2) 的条件下，求直线2736y x =+与函数()y g x =的图象所围成图形的面积．21.(本小题满分12分) 已知函数2()(0)22mx mf x m x -=+>．若()ln 1f x x m ≥+-在[1)+∞，上恒成立，求m 取值范围；证明：2 ln2 + 3 ln3+…+ n lnn 3223512n n n+-≤（*n ∈N ）．宁强县天津中学高二数学（理科）作业（三）答案一、选择题1．A 2．C 3．C 4．C 5．B 6．C 7．B 8．C 9．C 10．C. 二、填空题11．12i Z -+= 12．576种 13．1 14．≤ 15．3712三、解答题16．解：(1)46360A = 4分(2)2325120A A = 8分(3)4245240A C = 13分17．解：(1) 由题易知'2(1)360(1)130f a b f a b a ⎧-=-+=⎪⎨-=-+-+=⎪⎩解得a = 2，b = 9. 6分(2) f (x) = x3 + 6 x 2 + 9 x + 4，'2()3129f x x x =++由），）和（，增区间为（∞+∞>1-3--0)('x f），减区间为（1-3-0)('<x f 13分18．解：(1) 32 4分 (2) 2512 ······························ 8分 (3) 12544 ····························· 13分 19．解：（1）易知12)2('-==f k 又过（2，-3）2112+-=∴x y························· 5分 (2) 由已知得()3f x m '>，即22(1)20mx m x -++> ··········· 6分又0m <所以222(1)0x m x m m -++<即[]222(1)0,1,1x m x x m m-++<∈-① 设212()2(1)g x x x m m=-++，其函数开口向上，由题意知①式恒成立， · 8分所以22(1)0120(1)010g m m g ⎧-<+++<⎧⎪⇒⎨⎨<⎩⎪-<⎩解之得 43m -<又0m < ························ 11分所以403m -<< 即m 的取值范围为4,03⎛⎫- ⎪⎝⎭··················· 12分 20．解：(1) ∵()ln f x x =，∴当0x >时，()ln f x x =; 当0x <时，()ln()f x x =-∴当0x >时，1()f x x '=; 当0x <时，11()(1)f x x x'=⋅-=-. ∴当0x ≠时，函数1()g x ax x=+ ················· 4分 (2) ∵由⑴知当0x >时，1()g x ax x=+ ， ∴当0,0a x >>时，()2g x a ≥当且仅当1x a=时取等号. ∴函数()y g x =在(0,)+∞上的最小值是a ，由已知221a a ⇒= ∴依题1a =.(3) 由27361y x y x x ⎧=+⎪⎪⎨⎪=+⎪⎩解得2121322,51326x x y y ⎧==⎧⎪⎪⎪⎨⎨=⎪⎪=⎩⎪⎩∴直线2736y x =+与函数()y g x =的图象所围成图形的面积 232271()()36S x x dx x ⎡⎤=+-+⎢⎥⎣⎦⎰=74ln 243- ············· 12分 21．解：令2()ln 1022mx m g x x m x -=--+-≤在[1,)x ∈+∞上恒成立 '2212(1)(2)()222m m x mx m g x x x x ---+-=-+= ················ 4分 (1) 当2111m -<-≤时，即1m ≥时 '()0g x ≤在[1,)+∞恒成立．()g x ∴在其上递减．max (1)0g g =≤∴原式成立．当211m->即0<m<1时 max 2(1)0,(1)(1)0g g g g m==->= ∴不能恒成立．综上：1m ≥ ··························· 9分(2) 由 (1) 取m=1有lnx 11()2x x≤- 21ln 2x x x -∴≤令x=n 21ln 2n n n -∴≤ 22212ln 23ln3....ln [23..1]2n n n n ∴+++≤++++- 222(1)(21)12 (6)n n n n +++++=∴化简证得原不等式成立．。

知心慧学高二数学寒假作业

知心慧学高二数学寒假作业Hello, I will generate a coherent English-Chinese article for you, with each English sentence followed by its Chinese translation, in the format of an article. Here is the "Intelligent and Insightful Learning: Math Homework for Sophomore Winter Vacation":The winter vacation is a golden opportunity for students to consolidate their academic knowledge and prepare for the upcoming semester. (寒假是学生们巩固知识、准备新学期学习的黄金时期。

) Sophomore students in high school are facing the challenge of advancing to more complex mathematical concepts. (高二的学生们正面临着学习更复杂数学概念的挑战。

)"Knowledgeable and Insightful Learning" is a platform that provides targeted homework assignments to help students master key mathematical concepts. (“知心慧学”是一个平台，提供有针对性的作业，帮助学生掌握数学核心概念。

)This winter vacation, the math homework assigns a variety of exercises to cover different topics such as algebra, geometry, and trigonometry. (这个寒假，数学作业布置了各种练习题，涵盖代数、几何、三角学等不同主题。

高二数学寒假作业：(二)(Word版含答案)

高二数学寒假作业（二）一、选择题，每小题只有一项是正确的。

1.“1x >”是“11x<”的（） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.命题“Z x ∈，使022≤++m x x ”的否定是（） A.Z x ∈，使m x x ++22＞0 B. 不存在Z x ∈，使m x x ++22＞0 C. Z x ∈，使022≤++m x x D. Z x ∈，使m x x ++22＞03.在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是（）A. 1B. 2C. 4．若a 、b 、c b a R >∈,，则下列不等式成立的是A ．b a 11< B ．22b a > C ．1122+>+c b c a D ．||||c b c a > 5.已知A （1，－2，11），B （4，2，3），C （6，－1，4）为三角形的三个顶点，则ABC ∆是A. 直角三角形B. 钝角三角形C. 锐角三角形D. 等腰三角形6.已知(121)-，，A 关于面xOy 的对称点为B ，而B 关于x 轴的对称点为C ，则BC =（）Ａ．(0)，4，2 Ｂ．(0)，4，0 Ｃ．(042)--，，Ｄ．(2)，0，-27.已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为30°的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是（）A ．B ．C ．)+∞D ． )+∞ 8.已知双曲线22221x y a b-=的一个焦点与抛物线214x y =的焦点重合，且双曲线的渐近线方程为2y x =±，则该双曲线的方程为（）A 、224515y x -= B 、22154x y -= C 、22154y x -= D 、225514y x -= 9.设直线l ：y ＝2x ＋2，若l 与椭圆2214y x +=的交点为A 、B ，点P 为椭圆上的动点，则使△PAB1的点P 的个数为（）A 、0B 、1C 、2D 、3二、填空题10.”）使（“01ax 1,1-x 2≥-∈∃为真命题，则a 的取值范围是____▲______. 11.等比数列{}n a 的各项均为正数，且1651=a a ，则 2122232425log +log +log +log +log =a a a a a ________ 。

【原创】山东省菏泽市2014-2015学年高二上学期寒假作业(三)数学Word版含答案

【原创】2015高二数学寒假作业（三）一、选择题1、已知平面α 的一个法向量)41,12,(--=y x a ，又)2,21,3(),1,2,1(-=-=c b 且c b ,在α 内，则a ＝( )A ．)41,2653,529(---B ．)41,5227,529(---C ．)41,261,529(--D ．)41,2653,5227(---2、若直线l 1，l 2的方向向量分别为)23,1,21(),3,2,1(21---==v v ，则l 1，l 2的位置关系是( )A ．垂直B ．重合C ．平行D ．平行或重合3、正三棱柱ABC —A 1B 1C 1的所有棱长相等，AC 1与面BB 1C 1C 所成角的余弦值为（）4、如图所示，PA ＝PB ＝PC ，且它们所成的角均为60°，则二面角B －PA －C 的余弦值是( ) A ．21 B ．31C ．33D ．235、如图，正三棱柱ABC －A 1B 1C 1的各棱长都是2，E 、F 分别是AB 、A 1C 1的中点，则EF 的长是( )A ．2 B. 3 C.5D.76、已知平面α∥平面β，直线l Ìα，α与β之间的距离为d ，有下列四个命题： ①β内有且仅有一条直线与l 的距离为d ； ②β 内所有的直线与l 的距离都等于d ； ③β内有无数条直线与l 的距离为d ； ④β内所有直线与α的距离都等于d . 其中真命题是( ) A ．① B ．② C ．①与④ D ．③与④二、填空7、在底面是直角梯形的四棱锥P －ABCD 中，侧棱P A ⊥底面ABCD ，BC ∥AD ，∠ABC ＝90°，P A ＝AB ＝BC ＝2，AD ＝1，则AD 到平面PBC 的距离为________．8、若P 是△ABC 所在平面外一点，而△PBC 和△ABC 都是边长为2的正三角形，PA ＝6，则二面角P －BC －A 的大小是______．9、已知)1,1,2(),2,0,1(==AC AB ，则平面ABC 的一个法向量为____________． 10．已知正方体ABCD －A 1B 1C 1D 1中，点P 为线段DD 1上任意一点，则在正方体的所有棱中与平面ABP 平行的共有______条.三、解答题11、如图，在平行六面体ABCD-A 1B 1C 1D 1中，点M 是线段A 1D 的中点，点N 在线段C 1D 1上，且D 1N=13D 1C 1，∠A 1AD=∠A 1AB=60°, ∠BAD=90°，AB=AD=AA 1=1. (1)求满足1MN xAB yAD zAA =++u u u r u u u r u u u u r u u u u r的实数x 、y 、z 的值.(2)求AC1的长.12、抛物线的顶点在原点，它的准线过双22221(0,0)y x a b a b-=>>曲线的一个焦点，并与双曲线的实轴垂直，已知抛物线与双曲线的交点为)6,23(，求抛物线的方程和双曲线的方程.13、已知关于x 的一元二次方程 (m ∈Z) ① mx 2－4x ＋4＝0,② x 2－4mx ＋4m 2－4m －5＝0，求方程①和②都有整数解的充要条件.【原创】2015高二数学寒假作业（三）参考答案一、选择题 1~6 CDBCCD 二、填空 7、 2 8、90°9、(－2，3，1) 10．(2)(3)(4) 三、解答题11、证明：（1）111112MN AN AM AA A D DN AD =-=++-uuu r uuu u r uuu u r uuuu r uuuur uuu u r uuu r11111()32111,22311,.32A A A D A B A A A D A A A D A B x y z =++-+=++\===uuu u r uuu r uuu r uuu u r uuu r uuu u r uuu r uuu r （2）∵1||||||1,0AB AD AA AB AD ====u u u r u u u r u u u u r u u u r u u u rg, 11221122211111,2||()2()1132(0)522|| 5.A B A A A A A D A C A B A D A A A B A D A A A B A D A B A A A D A A A C ==\=++=+++++=+++=\=uuu r uuu u r uuu u r uuu r g g uuuu r uuu r uuu r uuu u r uuu r uuu r uuu u r uuu r uuu r uuu r uuu u r uuu r uuu u r g g g uuuu r12、解：由题意可知，抛物线的焦点在x 轴，又由于过点)6,23(，所以可设其方程为)0(22〉=p px y p 36=∴ ∴p =2 所以所求的抛物线方程为x y 42=所以所求双曲线的一个焦点为（1，0），所以c =1，设所求的双曲线方程为112222=--∴a y a x而点)6,23(在双曲线上，所以116)23(2222=--a a 解得412=a所以所求的双曲线方程为134422=-y x13、方程①有实根的充要条件是,04416≥⨯⨯-=∆m 解得m ≤1方程②有实根的充要条件是0)544(41622≥---=∆m m m ，解得.45-≥m ,.145Z m m ∈≤≤-∴而故m=－1或m=0或m=1. 当m=－1时，①方程无整数解. 当m=0时，②无整数解；当m=1时，①②都有整数.从而①②都有整数解m=1.反之，m=1①②都有整数解. ∴①②都有整数解的充要条件是m=1.。

V0008,本学年华师一附中高二上学期学生寒假作业(选择题,填空题各30题,解答题30题,共90题,分10天完成

高二上学期寒假作业（ 2011年元月）教材必修（3），选修2-3内容. 共90题，分10天完成. 每天3道选择题，3道填空题，3道解答题共9道题.一、选择题1. 设随机变量ξ服从(2,)B p ，随机变量η服从(3,)B p ,若5(1)9P ξ≥=，则(1)P η≥= ( ) A.2327B.2027C.1927D.16272. 为预防和控制甲流感，某学校医务室欲将23支相同的温度计分发到高三年级10个班级中，要求分发到每个班级的温度计不少于2支，则不同的分发方式共有 ( )A.120种B.175种C.220种D.820种3. 如图，用四种不同颜色给图中的A,B,C,D,E,F 六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法用 ( ) （A ）288种（B ）264种（C ）240种（D ）168种4.随机变量12+=ξη，则η的数学期望为（）A.1.1B.3.2C.11kD.22k+15. 已知423401234(12)x a a x a x a x a x -=++++，则2202413()()a a a a a ++-+的值是（） A ．1 B ．16 C ．41 D ．816. 从6名团员中选出4人分别担任书记、副书记、宣传委员、组织委员四项职务，若其中甲、乙不能担任书记，则不同的任职方案种数是（）A ．280B ．240C ．180D ．96 7. 暑期学校组织学生参加社会实践活动，语文科目、数学科目、外语科目小组个数分别占总数的12、13、16，甲、乙、丙三同学独立地参加任意一个小组的活动，则他们选择的科目互不相同的概率是（） A ．136B ．112C ．16D ．35368. 集合{(,)||1|}A x y y x =≥-,集合{(,)|||6}B x y y x =<-+，先后掷两颗骰子，掷第一颗骰子得点数为a ,掷第二颗骰子得点数为b ,则(,)a b A B ∈ 的概率等于（）A.14B.29C.736D.11369. 某旅馆有1个三人间，2个两人间可用，有三个成年人带两个小孩来投宿，小孩不宜单独住一间（必须有成人陪同），且不要求房间里都住有人，则不同的安排住宿的方法有（）A.60种B.62种C.64种D.66种 10. 44)1()1(x x +-的展开式中x 的系数是（）A ．4-B ．3-C ．3D ．411. 将A 、B 、C 、D 四个球放入编号为1、2、3的三个盒子中，若每个盒子中至少放一个球且A 、B 两个球不能放在同一盒子中，则不同的放法有（）A ．15B ．18C ．30D ．3612.已知n⎛⎝的展开式中的各项系数之和大于8，小于32，则展开式中系数最大的项是（） A4 B． C．4 D4或413. 设ξ是离散型随机变量，32)(1==x p ξ，31)(2==x p ξ，且21x x <，若34=ξE ，92=ξD ，则21x x +的值为（）A ．35 B ．37 C ．3 D ．31114. 代数式)))321432154321+++++++++c c b b b b a a a a a （（（的展开式的项数有（） A ．12 B ．13 C ．60 D ．360 15. 现有5双不同颜色的手套（每双手套的两只颜色相同），从中任取3只，若取出的3只手套颜色各不相同，则这样的取法有多少种？（）A. 480B. 360C.120D.8016. 把3个相同的小球放入4个不同的盒子中，每个盒子最多放2个小球，则不同方法有（）A. 16B. 24C. 64D. 8117. 某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（）A ．13B ．37C ．67D ．5618. 从0、1、2、3、4、5、6中任取出两个奇数和两个偶数，可组成没有重复数字的四位数有（）A.72个B.378个C.432个D.840个 19. 一批产品抽50件测试，其净重介于13克与19克之间，将测试结果按如下方式分成六组：第一组，净重大于等于13克且小于14克；第二组，净重大于等于14克且小于15克；……第六组，净重大于等于18克且小于19克．如图是按上述分组方法得到的频率分布直方图．设净重小于17克的产品数占抽取数的百分比为x ，净重大于等于15克且小于17克的产品数为y ，则从频率分布直方图中可分析出x 和y 分别为（）A ．0.9,35B ．0.9,45C ． 0.1,35D ．0.1,45 20. 电子钟一天显示的时间是从00∶00到23∶59，每一时刻都由四个数字组成，则一天中任一时刻显示的四个数字之和为23的概率为（）0.30.30.10.00.00.0A ．1801 B ．2881 C ．3601 D ．480121. 在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”。

高二数学寒假作业(理科)

第1天月日星期学习导航:1. 理解不等式关系及其在数轴上的表示,能用作差法比较两个数(式)的大小,在比较两数的大小时,能应用配方法,分解因式法,分类讨论法等数学方法;2. 理解并掌握不等式的性质及证明过程,能利用不等式的性质证明一些比较简单的不等式;3. 能利用不等式的性质求某些变量或代数式的范围.能用不等式的性质解决一些实际问题. 1. 已知,,,R c b a ∈下面推理正确的是( ) A 22bm am b a 〉⇒〉 B b a c b c a 〉⇒〉 C b a ab b a 110,33〈⇒〉〉 D ba ab b a 110,22〈⇒〉〉 2.若,0log log 44〈〈b a 则( )A 10〈〈〈b aB 10〈〈〈a bC 1〉〉b aD 1〉〉a b 3.下列大小关系正确的是( ) A 3.044.03log 34.0〈〈 B 4.03.0433log 4.0〈〈 C 4.033.0434.0log 〈〈 D 34.03.044.03log 〈〈 4.现给出下列三个不等式(1) a a 212〉+; (2) )23(222--〉+b a b a ;(3)22222)())((bd ac d c b a +〉++其中恒成立的不等式共有( )个Ａ０Ｂ１Ｃ２Ｄ３５已知方程02=++b ax x 的两根为21,x x ，命题2,1:x x p 都大于２，命题,4:21〉+x x q 则命题p 和命题q 的关系是（）Ａ q p ⇒ Ｂ q p ⇐Ｃq p ⇔Ｄq p ≠〉６．若对任意的,R x ∈不等式ax x ≥恒成立，则实数a 的取值范围是（）Ａ1〈-a Ｂ1≤a Ｃ1〈a Ｄ1≥a7．若),lg(lg ,lg ,)(lg ,10122x c b a x x x ===〈〈则c b a ,,的大小顺序是_________________8．若βα,满足22πβαπ〈〈〈-，则βα-2的取值范围是________________9．在（1）若b a 〉，则b a 11〈；（2）若22bc ac 〉，则b a 〉；（3）若0,0〈〈〈〈d c b a ，则bd ac 〉；（4）若b a 〈，则xa xb a b ++〈，这四个命题中，正确的命题序号是_________________10．已知,0≠ab 比较)1)(1(+-++b a b a 与1)(22+-b a 的大小11．设0〉a 且,0,1〉≠t a 比较ta log 21与21log +t a 的大小12．已知,6024,3420〈〈〈〈b a 求abb a b a ,,-+的范围13．已知b a ,满足,30,42≤-≤≤+≤b a b a 求ab 的范围14若实数c b a ,,,满足: 44;64322+-=-+-=+a a c b a a c b 试确定c b a ,,大小关系15现有甲乙两家旅行社对家庭旅游提出优惠方案。

高二寒假作业数学必修1知识点,练习题及答案

高二上数学寒假作业必修1数学知识点.练习题第一章、集合与函数概念 §1.1.1、集合1、把研究的对象统称为元素，把一些元素组成的总体叫做集合。

集合三要素：确定性、互异性、无序性。

2、只要构成两个集合的元素是一样的，就称这两个集合相等。

3、常见集合：正整数集合：*N 或+N ，整数集合：Z ，有理数集合：Q ，实数集合：R .4、集合的表示方法：列举法、描述法. §1.1.2、集合间的基本关系1、一般地，对于两个集合A 、B ，如果集合A 中任意一个元素都是集合B 中的元素，则称集合A 是集合B 的子集。

记作B A ⊆. 2、如果集合B A ⊆，但存在元素B x ∈，且A x ∉，则称集合A 是集合B 的真子集.记作：A B.3、把不含任何元素的集合叫做空集.记作：∅.并规定：空集合是任何集合的子集.4、如果集合A 中含有n 个元素，则集合A 有n2个子集.§1.1.3、集合间的基本运算 1、一般地，由所有属于集合A 或集合B 的元素组成的集合，称为集合A 与B 的并集.记作：B A . 2、一般地，由属于集合A 且属于集合B 的所有元素组成的集合，称为A 与B 的交集.记作：B A . 3、全集、补集？{|,}UC A x x U x U =∈∉且 §1.2.1、函数的概念1、设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有惟一确定的数()x f 和它对应，那么就称B A f →:为集合A 到集合B 的一个函数，记作：()A x x f y ∈=,.2、一个函数的构成要素为：定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，则称这两个函数相等. §1.2.2、函数的表示法1、函数的三种表示方法：解析法、图象法、列表法. §1.3.1、单调性与最大（小）值1、注意函数单调性证明的一般格式：解：设[]b a x x ,,21∈且21x x <，则：()()21x f x f -=… §1.3.2、奇偶性1、一般地，如果对于函数()x f 的定义域内任意一个x ，都有()()x f x f =-，那么就称函数()x f 为偶函数.偶函数图象关于y 轴对称.2、一般地，如果对于函数()x f 的定义域内任意一个x ，都有()()x f x f -=-，那么就称函数()x f 为奇函数.奇函数图象关于原点对称. 第二章、基本初等函数（Ⅰ） §2.1.1、指数与指数幂的运算1、一般地，如果a x n=，那么x 叫做a 的n 次方根。

2012-2013年高二数学(文)寒假作业

2012-2013年山东省宁阳二中高二数学（文）寒假作业1，解三角形练习题一、选择题：1. △ABC 中，sin 2A =sin 2B +sin 2C ，则△ABC 为( )直角三角形 B 等腰直角三角形 C 等边三角形 D 等腰三角形2. 在△ABC 中，c=3，B=300，则a 等于（）A ．B ．CD ．2 3. 不解三角形，下列判断中正确的是（）A ．a=7，b=14，A=300有两解B ．a=30，b=25，A=1500有一解C ．a=6，b=9，A=450有两解D ．a=9，c=10，B=600无解 4. 已知△ABC 的周长为9，且4:2:3sin :sin :sin =C B A ，则cosC 的值为（）A ．41-B ．41 C ．32- D ．32 5. 在△ABC 中，A ＝60°，b ＝1，其面积为3，则C B A cb a s i n s i n s i n ++++等于( )A ．33B ．3392 C ．338D ．239 6. 在△ABC 中，AB ＝5，BC ＝7，AC ＝8，则AB ²AC 的值为( ) A ．79 B ．69 C ．5D ．-57.关于x 的方程02cos cos cos 22=-⋅⋅-CB A x x 有一个根为1，则△ABC 一定是（）A ．等腰三角形B ．直角三角形C ．锐角三角形D ．钝角三角形8. 设m 、m +1、m+2是钝角三角形的三边长，则实数m 的取值范围是( ) A.0＜m ＜3B.1＜m ＜3C.3＜m ＜4D.4＜m ＜69. △ABC 中，若c=ab b a ++22，则角C 的度数是( ) A.60°B.120°C.60°或120°D.45°10. 在△ABC 中，若b=22,a=2，且三角形有解，则A 的取值范围是( ) A.0°＜A ＜30° B.0°＜A ≤45° C.0°＜A ＜90° D.30°＜A ＜60° 11.在△ABC 中，A B B A 22s i n t a n s i n t a n ⋅=⋅，那么△ABC 一定是（） A ．锐角三角形 B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形12. 如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为（）(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定二、填空题13.在△ABC 中，有等式：①asinA=bsinB ；②asinB=bsinA ；③acosB=bcosA ；④sin sin sin a b cA B C+=+. 其中恒成立的等式序号为______________ 14. 在等腰三角形 ABC 中，已知sinA ∶sinB=1∶2，底边BC=10，则△ABC 的周长是。

江苏省盐城中学2012-2013学年高二寒假作业反馈练习数学

高二年级寒假反馈练习数学试题（2013.02）命题：袁琴杨生涛审题：徐文陈建一、填空题：1.已知复数34z i =-，则||z = ▲ .2.已知向量,a b 满足||1,||3a b == ，,a b 之间的夹角为060，则()a a b ⋅+= ▲ .3.若命题“2,(1)10x R x a x ∃∈+-+<”是假命题，则实数a 的取值范围是 ▲ .4.在等差数列}{n a 中，已知1a ＝1，前5项和5S =35, 则8a 的值是 ▲ .5.工厂生产了某种产品3000件，它们来自甲、乙、丙三条生产线．为检查这批产品的质量，决定采用分层抽样的方法进行抽样．若从甲、乙、丙三条生产线抽取的个数分别为a ，b ，c ，且a ，b ，c 构成等差数列，则乙生产线生产了 ▲ 件产品．6.执行右图算法框图,若输入20a =,12b =,则输出的值为 ▲ .7.双曲线x 2－y24＝1的渐近线被圆x 2＋y 2－6x －2y ＋1＝0所截得的弦长为 ▲ ．8.已知直线⊥l 平面α，直线⊂m 平面β，则下列四个命题：①m l ⊥⇒βα//；②m l //⇒⊥βα；③βα⊥⇒m l //；④βα//⇒⊥m l 其中正确命题的序号是 ▲ ．9.已知函数f(x)＝mx 2＋lnx －2x 在定义域内单调递增，则实数m 的取值范围是 ▲ .10.求值：00sin 40(tan 103)-= ▲ .11.已知函数22log (1),0,()2,0.x x f x x x x +>⎧=⎨--≤⎩ 若函数()()g x f x m =-有3个零点，则实数m 的取值范围是 ▲ .12.若对满足条件)0,0(3>>=++y x xy y x 的任意y x ,，01)()(2≥++-+y x a y x 恒成立，开始结束输入a ,ba ＞b输出aa ←a ×bYN 第6题则实数a 的取值范围是 ▲ . 13.已知椭圆)0(12222>>=+b a by ax 的左焦点1F ，O 为坐标原点，点P 在椭圆上，点Q 在椭圆的右准线上，若12PQ F O = ，11111(F P F OF Q F P F O λλ=+）(>0)｜｜｜｜，则椭圆的离心率为 ▲ .14.对于函数()x f ，若区间[]()b a b a M <=,，使得(){}M M x x f y y =∈=,，则称区间M 为函数()x f 的一个“稳定区间”，下列4个函数：①()x e x f =，②()3x x f =， ③()x x f 2cosπ=，④ ()1ln +=x x f ；其中存在“稳定区间”的函数的有 ▲ .（填写序号）二、解答题：15. 已知||2,||2x y ≤≤，点P 的坐标为(,).x y（1）求当,x y ∈R 时，P 满足22(2)(2)4x y -+-≤的概率；（2）求当,x y ∈Z 时，P 满足22(2)(2)4x y -+-≤的概率．16.在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，向量)sin ,2cos 2(C C m -=，)sin 2,2(cosC C n =，且.n m ⊥（1）求角C 的大小；（2）若2222c b a +=，求A tan 的值.17.据市场调查，某商场的一种商品在过去的一个月内（以30天计）销售价格()f t （元）与时间t （天）的函数关系近似满足()100(1)k f t t=+（k 为正常数），日销售量()g t （件）与时间t （天）的函数关系近似满足()125|25|g t t =--，且第25天的销售金额为13000元.（1）试写出该商品的日销售金额()w t 关于时间(130,)t t t N ≤≤∈的函数关系式；（2）该商品的日销售金额()w t 的最小值是多少？18.如图，已知椭圆2222:1x y C ab+=(0)a b >>的左顶点，右焦点分别为,A F ，右准线为m .圆D ：02322=--++y x y x .（1）若圆D 过,A F 两点，求椭圆C 的方程；（2）若直线m 上不存在点Q ，使AFQ ∆为等腰三角形，求椭圆离心率的取值范围；（3）在（1）的条件下，若直线m 与x 轴的交点为K ，将直线m 绕K 顺时针旋转4π得直线l ，动点P在直线l 上，过P 作圆D 的两条切线，切点分别为M 、N ，求弦长MN 的最小值.19.已知数列{}n a 中，21a =，前n 项和为S n ，且1()2n n n a a S -=．（1）求1a ；（2）证明数列{}n a 为等差数列，并写出其通项公式；（3）设1lg 3n n na b +=，试问是否存在正整数p ，q(其中1<p<q)，使1b ，p b ，q b 成等比数列？若存在，求出所有满足条件的数组(p ，q)；若不存在，说明理由．xymDKFA20. 已知定义在实数集上的函数*(),n n f x x n N =∈，其导函数记为'()n f x ，且满足2221212121()()[()]f x f x f x a x x x x -'+-=-，12,,a x x 为常数，12x x ≠．（1）试求a 的值；（2）记函数13()()ln ()F x b f x f x =⋅-，(]0,x e ∈，若()F x 的最小值为6，求实数b 的值；（3）对于（2）中的b ，设函数()()3x bg x =，1122(,),(,)A x y B x y （12x x <）是函数()g x 图象上两点，若21021'()y y g x x x -=-，试判断012,,x x x 的大小，并加以证明．数学试题（2013.02）一、填空题：1.已知复数34z i =-，则||z = ▲ . 52.已知向量,a b 满足||1,||3a b == ，,a b 之间的夹角为060，则()a a b ⋅+ = ▲ . 253.若命题“2,(1)10x R x a x ∃∈+-+<”是假命题，则实数a 的取值范围是 ▲ . [－1.3]4.在等差数列}{n a 中，已知1a ＝1，前5项和5S =35, 则8a 的值是 ▲ .225.工厂生产了某种产品3000件，它们来自甲、乙、丙三条生产线．为检查这批产品的质量，决定采用分层抽样的方法进行抽样．若从甲、乙、丙三条生产线抽取的个数分别为a ，b ，c ，且a ，b ，c 构成等差数列，则乙生产线生产了 ▲ 件产品．10006.执行右图算法框图,若输入20a =,12b =,则输出的值为 ▲ .5167双曲线x 2－y 24＝1的渐近线被圆x 2＋y 2－6x －2y ＋1＝0所截得的弦长为 ▲ ．48.已知直线⊥l 平面α，直线⊂m 平面β，则下列四个命题：①m l ⊥⇒βα//；②m l //⇒⊥βα；③βα⊥⇒m l //；④βα//⇒⊥m l开始结束输入a ,ba ＞b输出aa ←a ×bYN 第5题其中正确命题的序号是 ▲ ．①③9.已知函数f(x)＝mx 2＋lnx －2x 在定义域内单调递增，则实数m 的取值范围是 ▲ .12m ≥10.求值：00sin 40(tan 103)-= ▲ . －111..已知函数22log (1),0,()2,0.x x f x x x x +>⎧=⎨--≤⎩ 若函数()()g x f x m =-有3个零点，则实数m 的取值范围是 ▲ . (0,1)12.若对满足条件)0,0(3>>=++y x xy y x 的任意y x ,，01)()(2≥++-+y x a y x 恒成立，则实数a 的取值范围是 ▲ . 37(,]6-∞13.已知椭圆)0(12222>>=+b a by ax 的左焦点1F ，O 为坐标原点，点P 在椭圆上，点Q 在椭圆的右准线上，若12PQ F O = ，11111(|F P F OF Q F P F O λλ=+）(>0)｜｜｜，则椭圆的离心率为 ▲ .512-14.对于函数()x f ，若区间[]()b a b a M <=,，使得(){}M M x x f y y =∈=,，则称区间M 为函数()x f 的一个“稳定区间”，下列4个函数：①()xe xf =，②()3x x f =，③()x x f 2cosπ=，④ ()1ln +=x x f ；其中存在“稳定区间”的函数的有 ▲ ②③三、解答题：15. 已知||2,||2x y ≤≤，点P 的坐标为(,).x y（1）求当,x y ∈R 时，P 满足22(2)(2)4x y -+-≤的概率；16π（2）求当,x y ∈Z 时，P 满足22(2)(2)4x y -+-≤的概率．62516.在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，向量)sin ,2cos 2(C C m -=，)sin 2,2(cosC C n =，且.n m ⊥（3）求角C 的大小；3π（2）若2222c b a +=，求A tan 的值. 33-17.据市场调查，某商场的一种商品在过去的一个月内（以30天计）销售价格()f t （元）与时间t （天）的函数关系近似满足()100(1)k f t t=+（k 为正常数），日销售量()g t （件）与时间t （天）的函数关系近似满足()125|25|g t t =--，且第25天的销售金额为13000元.（1）试写出该商品的日销售金额()w t 关于时间(130,)t t t N ≤≤∈的函数关系式；（2）该商品的日销售金额()w t 的最小值是多少？解：（1）由题意,得(25)(25)13000f g ⋅=,即100(1)1251300025k +⋅=,解得1k =1()()()100(1)(125|25|)w t f t g t t t=⋅=+--=100100(101)(125,)150(2530,)100(149)t t t N t t t N t t ⎧++⎪≤<∈⎪⎨≤≤∈⎪+-⎪⎩（2）①当125t ≤<时,因为10020t t+≥,所以当10t =时,()w t 有最小值12100②当2530t ≤≤时,∵150t t-在[25,30]上递减,∴当30t =时,()w t 有最小值12400∵12100〈12400，∴当10t =时，该商品的日销售金额()w t 取得最小值为1210018.如图，已知椭圆2222:1x y C ab+=(0)a b >>的左顶点，右焦点分别为,A F ，右准线为m .圆D ：02322=--++y x y x .（1）若圆D 过,A F 两点，求椭圆C 的方程；（2）若直线m 上不存在点Q ，使AFQ ∆为等腰三角形，求椭圆离心率的取值范围；（3）在（1）的条件下，若直线m 与x 轴的交点为K ，将直线m 绕K 顺时针旋转4π得直线l ，动点P 在直线l 上，过P 作圆D 的两条切线，切点分别为M 、N ，求弦长MN 的最小值.18．解：（1）圆02322=--++y x y x 与x 轴交点坐标为，(2,0)A -，(0,1)F ，故2,1a c ==，所以3b =，xymDKFA椭圆方程是：22143xy+=（2）设直线m 与x 轴的交点是Q ，依题意FQ FA ≥，即2ac a c c-≥+,22aa c c≥+,12a c ca ≥+,112e e≥+,2210e e +-≤ 102e <≤（3）直线l 的方程是40x y --=，圆D 的圆心是13(,)22，半径是322，设MN 与PD 相交于H ，则H 是MN 的中点，且P M ⊥MD ，222222221M D M P M D PD M D M D M N N H M D PDPDPD⋅⋅-==⋅=⋅=⋅-当且仅当P D 最小时，MN 有最小值，P D 最小值即是点D 到直线l 的距离是26=d ，所以MN 的最小值是263。

2014-2015学年高二数学寒假作业(3)(Word版,含答案)

高二数学寒假作业（三）一、选择题，每小题只有一项是正确的。

1.在等差数列{a n }中，若,23=a ,85=a ，则9a 等于 ( )A ．16B ．18C ．20D ．222.已知一等比数列的前三项依次为33,22,++x x x ，那么2113-是此数列的第（）项 A ．2 B ．4 C ．6 D ．8 3.下列不等式中，与不等式023≥--x x 同解的是（）（A ）()()023≥--x x （B ）()()023>--x x（C ）032≥--x x （D ）()02lg ≤-x4.已知,a b 为非零实数，且a b <，则下列不等式中恒成立的序号是（）①22a b <；②22ab a b < ；③2211ab a b <；④b a a b <；⑤3223a b a b < A ．①⑤ B ．②④ C ．③④ D ．③⑤5.已知()()1,0,0,0,1,1A B -,OA OB λ+与OB 的夹角为60°，则λ的值为（）A.D. 6.已知向量)0,1,1(=，)2,0,1(-=，且k +与-2互相垂直，则k 的值是（）A ．1B ．57C ．53D ．51 7.在平行六面体ABCD －A 1B 1C 1D 1中，M 为AC 与BD 的交点，若11B A ＝a ，11D A ＝b ，A 1＝c ，则下列向量中与M B 1相等的向量是( )A.－12a ＋12b ＋c B. 12a －12b ＋c C. 12a ＋12b ＋c D.－12a －12b ＋c 8.设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F ，且和 y 轴交于点A ,若OAF ∆(O 为坐标原点)的面积为4，则抛物线方程为( ).A.24y x =±B.28y x =±C. 24y x = D.28y x =9.命题“对任意x R ∈都有21x ≥”的否定是A.对任意x R ∈，都有21x <B.不存在x R ∈，使得21x <C.存在0x R ∈，使得201x ≥D.存在0x R ∈，使得201x < 二、填空题10.空间中点M （—1，—2，3）关于x 轴的对称点坐标是11.已知x ＞2，则y ＝21-+x x 的最小值是________． 12.已知等比数列{}n a ,若11=a ，45=a ，则3a =13.数列 121, 241, 381, 4161, 5321, …, n n 21, 的前n 项之和等于．三、计算题14.（12分）如图1－1，在△ABC 中，∠ABC ＝90°，AB BC ＝1，P 为△ABC 内一点，∠BPC ＝90°.(1)若PB ＝12，求PA ； (2)若∠APB ＝150°，求tan ∠PBA.图1－115．（本题12分）顶点在原点，焦点在x 轴上的抛物线，被直线21y x =+ 求抛物线方程。

高二数学假期作业及答案

1．已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧x －y －1≥0，x ＋y －3≥0，3x ＋y －11≤0，则z ＝2y ＋1x －1的取值范围是( ) A ．[－2，3] B.⎣⎡⎦⎤－13，3 C.⎣⎡⎦⎤－13，52 D.⎣⎡⎦⎤52，3 2.在正项等比数列{a n }中，log 2a 3＋log 2a 6＋log 2a 9＝3，则a 1a 11＝________．3..在等比数列{a n }中，a 3，a 15是方程x 2－6x ＋8＝0的根，则a 1a 17a 9的值为( ) A ．2 2 B ．4C ．－22或2 2D ．－4或44．已知x ，y 满足不等式组⎩⎪⎨⎪⎧x ≥0，x －y ≤0，4x ＋3y ≤14，设(x ＋2)2＋(y ＋1)2的最小值为ω，则函数f (t )＝sin ⎝⎛⎭⎫ωt ＋π6的最小正周期为( ) A.2π3B ．π C.π2 D.2π55．已知等比数列{a n }的各项均为正数，a 1＝1，公比为q .等差数列{b n }中，b 1＝3，且{b n }的前n 项和为S n ，a 3＋S 3＝27，q ＝S 2a 2. (1)求{a n }与{b n }的通项公式；(2)设数列{c n }满足c n ＝32S n，求{c n }的前n 项和T n . 6．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，满足2a sin A ＝(2sin B －3sin C )b ＋(2sin C －3sin B )c .(1)求角A 的大小；(2)若a ＝2，b ＝23，求△ABC 的面积．1.解析：选B 作出不等式组所表示的平面区域如图中阴影部分所示，由题意可知，z ＝2y ＋1x －1＝2·y ＋12x －1，它表示平面区域内的点(x ，y )与定点M ⎝⎛⎭⎫1，－12的连线的斜率的2倍．由图可知，当点(x ，y )位于点C 时，直线的斜率取得最小值－16；当点(x ，y )位于点A 时，直线的斜率取得最大值32.故z ＝2y ＋1x －1的取值范围是⎣⎡⎦⎤－13，3，选B. 2.解析：∵在正项等比数列{a n }中，log 2a 3＋log 2a 6＋log 2a 9＝3，∴log 2(a 3a 6a 9)＝log 2a 36＝3，∴a 6＝2，∴a 1a 11＝a 26＝4.答案：43..解析：选A ∵a 3，a 15是方程x 2－6x ＋8＝0的根，∴a 3a 15＝8，a 3＋a 15＝6，因此a 3，a 15均为正，由等比数列的性质知，a 1a 17＝a 29＝a 3a 15＝8，∴a 9＝22，a 1a 17a 9＝22，故选A. 4．解析：选D 由不等式组⎩⎪⎨⎪⎧x ≥0，x －y ≤0，4x ＋3y ≤14作出可行域如图中阴影部分所示，(x ＋2)2＋(y ＋1)2的几何意义为可行域内的点与定点C (－2，－1)之间的距离的平方，其最小值为5，故f (t )＝sin ⎝⎛⎭⎫5t ＋π6，其最小正周期T ＝2π5，故选D. 5．解：(1)设数列{b n }的公差为d ，∵a 3＋S 3＝27，q ＝S 2a 2， ∴q 2＋3d ＝18，6＋d ＝q 2，联立方程可得q ＝3，d ＝3，∴a n ＝3n －1，b n ＝3n . (2)由(1)知S n ＝n （3＋3n ）2，c n ＝32S n ＝32·23·1n （n ＋1）＝1n －1n ＋1， ∴T n ＝1－12＋12－13＋13－14＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1. 6．解：(1)由已知及正弦定理可得 2a 2＝(2b －3c )b ＋(2c －3b )c ，整理得b 2＋c 2－a 2＝3bc ，所以cos A ＝32.又A ∈(0，π)，故A ＝π6.(2)由正弦定理asin A ＝bsin B ，a ＝2，b ＝23，A ＝π6，得sin B ＝32.又B ∈⎝⎛⎭⎫0，5π6，故B ＝π3或2π3.若B ＝π3，则C ＝π2，于是S △ABC ＝12ab ＝23；若B ＝2π3，则C ＝π6，于是S △ABC ＝12ab sin C ＝ 3.。

高二高考期间数学家庭作业(三)

高二高考期间数学家庭作业（三）《导数及其应用》单元精要整合一、单项选择题：1、若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则000()()limh f x h f x h h→+--的值为( )A.0()f x 'B.02()f x 'C.02()f x '-D.02、一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是( )A.7米/秒B.6米/秒C.5米/秒D.8米/秒 3、曲线x x y 43-=在点(1,3)-处的切线倾斜角为( )A.34π B.2π4、曲线3()2f x x x =+-在0p ( )A.(1,0)B.(2,8)4)- 5、若()sin cos f x x α=-,则()f α'A.cos α B.sin αC.6、若曲线4y x =的一条切线l A.430x y --= B.4x y +-0= 7、对正整数n ,设曲线)1(x x y n -=,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和的公式是( ) A.2n B.22n - C.12n + D.122n +-8、设a ∈R ,函数()e e x xf x a -=+⋅的导函数是()f x ',且()f x '是奇函数.若曲线()y f x =的一条切线的斜率是32,则切点的横坐标为 ( ) A.ln 2 B.ln 2- C.ln 22 D.ln 22-二、填空题：9、已知函数x x x f +-=2)(的图象上的一点)2,1(--A 及临近一点)2,1(y x B ∆+-∆+-则=∆∆xy. 10、曲线32242y x x x =--+在点(1,一3)处的切线方程是___________ 11、在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为 .12、若函数32()1f x x x mx =+++是R 上的单调函数，则实数m 的取值范围是 13、曲线3cos (0)2y x x π=≤≤与坐标轴围成的面积是 14、已知函数2)(23-=+++=x c bx ax x x f 在处取得极值，并且它的图象与直线33+-=x y 在点（1，0）处相切，15、已知函数)(x f 是定义在R 不等式()0f x >的解集是 . 三、解答题：16. 已知曲线 y = x 3+ x －2 在点 P 0 第三象限,⑴求P 0的坐标; ⑵若直线17. 已知函数32()(1)48(2)f x ax a x a x b =+-+-+的图象关于原点成中心对称, 试判断()f x 在区间[]4,4-上的单调性,并证明你的结论.18. 设函数())(0)f x ϕϕπ=+<<,且()()f x f x '+为奇函数.(1)求ϕ的值;(2)求()'()f x f x +的最值.19. 已知函数()ln f x x =(0)x ≠,函数1()()(0)()g x af x x f x '=+≠' ⑴当0x ≠时,求函数()y g x =的表达式;⑵若0a >,函数()y g x =在(0,)+∞上的最小值是2 ,求a 的值;20. 设函数3()f x ax bx c =++(0)a ≠为奇函数,其图象在点(1,(1))f 处的切线与直线1870x y +-=垂直,导函数'()f x 的最小值为12.(1)求a ,b ,c 的值; (2)设2()()f x g x x=,当0x >时,求()g x 的最小值.21. 已知函数()e x f x kx x =-∈R ，（Ⅰ）若e k =，试确定函数()f x （Ⅱ）若0k >，且对于任意x ∈R （Ⅲ）设函数()()()F x f x f x =+-)*N ．《导数及其应用》单元精要整合答案1.B 000000()()()()limlim 2[]2h h f x h f x h f x h f x h h h →→+--+--=0000()()2lim 2()2h f x h f x h f x h→+--'==.2.C3.A.4.D5.B ()sin ,()sin f x x f αα''==.6.A 与直线480x y +-=垂直的直线l 为40x y m -+=,即4y x =在某一点的导数为4,而34y x '=,所以4y x =在(1,1)处导数为4,此点的切线为430x y --=.7.D ()()11222,:222(2)n n n x y n y n x --='=-++=-+-切线方程为,令0x =,求出切线与y 轴交点的纵坐标为()012n y n =+,所以21n na n =+,则数列1n a n ⎧⎫⎨⎬+⎩⎭的前n 项和()21212nnS -=-8.A '()xxf x e ae-=-,()f x ',有'()x x f x e e -=-,设切点为00(,)x y ,则00'()xf x e =),∴0ln2x =.9 .3x -∆ 2(1)y x -+∆=--+∆ ∴xx x x y ∆-∆+-+∆+--=∆∆)1()1(210. 520x y +-= 易判断点(1,-3)在曲线32242y x x x =--+上,故切线的斜率()211|344|5x x k y x x =='==--=-,∴切线方程为()351y x +=--,即520x y +-=11. (-2,15) 231022y x x '=-=⇒=±,又点P 在第二象限内,∴2x =-,得点P 的坐标为(-2,15)12. 1[,)3+∞ 13. 5214. 68)(23+-+=x x x x f 15. ),1()0,1(+∞- 可得()'()f x f x x>,由导数的定义得,当01x <<时,()(1)()1f x f f x x x->-,又0)1(=f ,()(1)()xf x x f x <-,∴()0f x <;当1x >时,同理得()0f x <.又)(x f 是奇函数,画出它的图象得()0f x >⇒(1,0)(x ∈-+∞. 16. .解:⑴由y =x 3+x －2，得y ′=3x 2+1，由已知得3x 2+1=4，解之得x =±1.当x =1时，y =0;当x =－1时，y =－4.又∵点P 0在第三象限,∴切点P 0的坐标为 (－1,－4).⑵∵直线1l l ⊥,1l 的斜率为4,∴直线l 的斜率为14-,∵l 过切点P 0,点P 0的坐标为(－1,－4)∴直线l 的方程为14(1)4y x +=-+17. 解: 答f (x )在[-4,4]心对称,则f (x )是奇函数,所以a =1,b =0,∴当(4,4)()0x f x '∈-∴<又∵函数(f 递减函数.18. 解:(1)()'()f x f x +=6=又0ϕ<<π,()'()f x f x +是奇函数,∴=ϕ6π.(2)由(1)得()'()f x f x +)=+π=-. ∴()'()f x f x +的最大值为2,最小值为2-. 19. 解:⑴∵()ln f x x =,∴当0x >时,()ln f x x =; 当0x <时, ()ln()f x x =-∴当0x >时,1()f x x '=; 当0x <时,11()(1)f x x x'=⋅-=-. ∴当0x ≠时,函数()ay g x x x ==+.⑵∵由⑴知当0x >时,()ag x x x=+,∴当0,0a x >>时, ()≥g x x =.∴函数()y g x =在(0,)+∞上的最小值是∴依题意得2=∴1a =. 20. 解:(1)∵()f x 为奇函数,∴()()f x f x -=-,即33ax bx c ax bx c --+=---, ∴0c =,又∵2'()3f x ax b =+的最小值为12,∴12b =;又直线1870x y +-=的斜率为∴2a =,12b =,0c =为所求. (2)由(1)得x >时,2()()f x g x x =62()2x x =+≥⋅∴()g x 的最小值为.21. 解：（Ⅰ）由e k =得()f x =由()0f x '>得1x >，故()f x 的单调递增区间是(1)+∞，，由()0f x '<得1x <，故()f x 的单调递减区间是(1)-∞，．（Ⅱ）由()()f x f x -=可知()f x 是偶函数．于是()0f x >对任意x ∈R 成立等价于()0f x >对任意0x ≥成立．由()e 0x f x k '=-=得ln x k =．①当(01]k ∈，时，()e 10(0)x f x k k x '=->->≥．此时()f x 在[0)+∞，上单调递增．故()(0)10f x f =>≥，符合题意．②当(1)k ∈+∞，时，ln 0k >．当x 变化时()()f x f x '，的变化情况如下表：122x ++， 1()(1)e 2.n F n F +>+由此得，21[(1)(2)()][(1)()][(2)(1)][()(1)](e 2)n n F F F n F F n F F n F n F +=->+故12(1)(2)()(e2)n n F F F n n +*>+∈N ，．。

高二数学暑假作业(三)

张家界雨露学校2024年高二年级暑假作业（三）姓名：班级：总分：150分；范围：选择性必修一1.1-1.3一、单选题(每小题5分，共40分）1．若{},,a b c构成空间的一组基底，则下列向量不共面的为（）A．a，a b +，a c+B ．a，b，2a b+C ．a ，- a c ，cD ．b ，a c + ，a b c++2．如图，在三棱柱111ABC A B C -中，1BC =（）A ．1AB AC AA -+B ．1AB AC AA --+ C ．1AB AC AA ++ D ．1AB AC AA -++ 3．已知在四面体O ABC -中，,,3,,1a OA OB OC OM MA N b c ==== 为BC 的中点，若MN xa yb zc =++，则x y z ++=（）A ．3B ．34C ．12D ．134．向量()()2,1,1,1,1,a b x =-= ，若a b ⊥，则x =（）A ．2-B ．1-C ．1D ．05．空间直角坐标系中，点()1,2,3P 关于平面xOy 的对称点是（）A ．()1,2,3--B ．()1,2,3-C ．()1,2,3-D ．()1,2,3-6．由四个棱长为1的正方体组合成的正四棱柱1111ABCD A B C D -（如图所示），点P 是正方形1111D C B A 的中心，则向量1AA AP ⋅=（）A ．1B ．2C ．4D ．87．已知向量(,1,2)m a = ，11(,,1)22b = ，若a ∥b，则实数m =（）A ．12B ．14C ．1D ．28．已知平行六面体1111ABCD A B C D -中，1113,4,5AA BD AD DC AB BC ==⋅-⋅= ，则1cos ,AA BD <>=（）A ．512B ．512-C ．415D ．415-二、多选题（每小题6分，共18分）9．在空间直角坐标系O －xyz 中，以下结论正确的是（）A ．点()1,3,4A -关于x 轴对称的点的坐标为(－1，－3，4)B ．点()1,2,3P -关于xOy 平面对称的点的坐标为(－1，2，－3)C ．点()3,1,5B -关于原点对称的点的坐标为(3，－1，－5)D ．()()1,1,2,1,3,3M N -两点间的距离为310．给出下列命题，其中正确命题有（）A ．空间任意三个不共面的向量都可以作为一个基底B ．已知a b ⊥，则,a b与任何向量都不构成空间的一个基底C ．已知向量//a b，则,a b 与任何向量都不能构成空间的一个基底D ．,,,A B M N 是空间四点，若,,BA BM BN不能构成空间的一个基底，则,,,A B M N 共面11．已知空间单位向量1e ，2e ，3e 两两互相垂直，设1232a e e e =++ ，123b e e e =+- ，1232c e e e =+-，则下列说法正确的有（）A ．a 与b 的夹角为π3B ．()2//c a b+ C ．b ，c 所成角的余弦值为223D ．a ，b，c 其中任意两个都可以作为基底来表示另外一个向量三、填空题(每小题5分，共15分）12．已知4a =，空间向量e为单位向量，23,πa e =，则空间向量a 在向量e方向上投影向量的模为．13．已知(2,1,3),(1,4,2)a b =-=--，c (4,5,)λ=，若,,a b c三向量不能构成空间向量的一组基底，则实数λ的值为.14．已知点()0,0,0O ，()1,2,2A ，()2,1,1B ，()1,0,2P ，点Q 在直线OP 上运动，当QA QB ⋅取得最小值时，点Q 的坐标是．四、解答题（15-19题：13分、15分、15分、17分、17分，共77分）15．如图所示，在正方体1111ABCD A B C D -中，化简向量表达式：(1)AB CD BC DA +++；(2)1111AA B C D D ++ ；16．如图，在平行六面体ABCD ﹣A1B1C1D1中，AB ＝5，AD ＝3，AA1＝4，∠DAB ＝90°，∠BAA1＝∠DAA1＝60°，设AB a = ，AD b = ，1AA c =．(1)用a ，b ，c表示1AC ；(2)求AC1的长．17．四棱柱ABCD A B C D -''''的六个面都是平行四边形，点M 在对角线A B '上，且12A M MB '=，点N 在对角线A C'上，且13A N NC '=．(1)设向量AB a =，AD b=，C AA ='，用a、b、c表示向量D M ' 、D N '；(2)求证：M 、N 、D ¢三点共线．18．设O 为坐标原点，(2,0,2),(1,1,2),(3,0,4)OA OB OC =-=-=-．(1)求cos ,AB AC ；(2)若点P 为直线OC 上一动点，求PA PB ⋅的最小值．19．已知空间中三点()()()2,0,2,1,1,2,3,0,4A B C ----，设a AB = ，b AC =.(1)已知向量ka b + 与b互相垂直，求k 的值;(2)求ABC 的面积.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高二数学寒假作业三
一、选择题：(本大题共10小题，每小题4分，共40分，在每小题给出的四个选择项中,
只有一项是符合题目要求的. )
1、直线13+=x y 的倾斜角的大小是（）
A ． 135°
B ． 120°
C ． 60°
D ． 30° 2、已知点(,1,2)A x B 和点(2,3,4),
且AB =,则实数x 的值是（） A ．43-或 B ．26-或 C ．4-3或 D ．2-6或 3、右图的正方体ABCD D C B A -''''中,异面直线A A '与'BC 所成的角
是（）
A ．︒
30 B ．︒
45 C ．︒
60 D ．︒
90 4、方程22
2
=+ky x 表示焦点在y 轴上的椭圆，则k 的取值范围是（）
A ．),0(+∞
B ．（0，2）
C ．（1，+∞）
D ．（0，1）
5、已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（） A ．,,m n m n αα
若则‖‖‖
B ．,,αγβγαβ⊥⊥若则‖
C ．,,mm αβαβ
若则‖‖‖
D ．,,m n m n
αα⊥⊥若则‖
6、如图，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个圆，那么这
个几何体的侧面积．．．为（） A ．
4
π
B ． 54π
C ． π
D ． 32π
7、圆C 1：9)2(22
2
=++-y x ）（与圆C 2：4)2-(12
2
=++y x ）（的公切线有（）
A ．0条
B ．2条
C ．3条
D ．4条 8、直线093=-+y ax 与直线03=+-b y x 关于原点对称，则
b a ,的值是（）
A ．9,1==b a
B ．9,1-==b a
C
A
B
A C ’
C ．9,1=-=b a
D ．9,1-=-=b a
9、如图所示，平面α⊥平面β，A ∈α，B ∈β，AB 与两平面α、β所成的
角分别为
4π和6
π
，过A 、B 分别作两平面交线的垂线，垂足为A ′、B ′，则AB ∶A ′B ′等于（）
A ．2∶1
B ．3∶1
C ．3∶2
D ．4∶3 10、若直线1x y
a b
+=通过点(cos sin )M αα，，则（） A ．2
2
1a b +≤
B ．2
2
1a b +≥
C ．
22111a b +≤ D ．
2211
1a b
+≥
二、填空题 (本大题共5小题，每小题4分，共20分，把答案填在答题纸上)
11、焦点在x 轴上的椭圆
2214x y m +=的离心率为12
，则m =________________； 12、以点(－2,3)为圆心且与y 轴相切的圆的方程是________________；
13、半径为a 的球放在墙角，同时与两墙面和地面相切，那么球心到墙角顶点的距离为________________；
14、正四棱锥S —AB CD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，则直线BC 与平面PAC 所成的角是________________；
15、在平面直角坐标系xoy 中，已知A B C ∆
顶点)0,3()0,3(C A 和-在椭圆116
2522=+y x 上，则s i n s i n s i n A C
B
+=________________。

三、解答题 (本大题共5小题, 共60分. 解答应写出文字说明、证明过程或演算步骤) 16、如图，在四棱锥P ABCD -中，底面ABCD 是矩形，O 为底面中心，PA ⊥平面ABCD ，
AB AD PA 2==．的中点是PD M
（1）求证：直线MO ∥平面PAB ；（2）求证：平面PCD ⊥平面ABM 。

17、求过两直线013=-+y x 与072=-+y x 的交点，且在两坐标轴上截距互为相反数的直线方程。

18、已知曲线Ｃ：022
2
=+++m x y x （ｍ∈Ｒ） (1) 讨论曲线C 的形状；
(2) 若7-=m ，过点)2,1(-P 的直线与曲线C 交于B A ,两点，且72||=AB ，求直线AB 的
倾斜角α。

19、如图，在棱长为1的正方体ABCD D C B A -1111中，（1）求直线
1B D 与平面11A BC 所成的角；（2）求线A 到面11A BC 的距离。

20、已知椭圆:C )0(12222>>=+b a b
y a x 经过点)1,0(，离心率23
=e
（1）求椭圆C 方程;
（2）设直线1+=my x 与椭圆C 交与B A ,两点，点A 关于x 轴的对称点为D
则当m 变化时，直线DB 与x 轴是否交于一个定点？若是，写出定点坐标，并证明你的结论；若不是，请说明理由。