信息光学苏显渝版PPT窦柳明解读61页PPT
合集下载
信息光学课后习题解答 苏显渝主编 61页PPT文档

2
g1(x) -1 G1() 0
G 2 () H 2 ()1 2 ( 1 ) ( 1 ) 1re (c ) t1 ( 1 ) ( 1 )
3 32
1(1)(1)
6
g2(x)
-1G2()
1 cos2
3
x
1.12 已知一平面波的复振幅表达式为
试计算各自对输入函数 f(x)co 2 sx的响应
g1( x) 和 g2( x)
解: H 1()re(c )t H2()1 3rec(t3)
F ()1(1)(1)
2
G 1 ()H 1 ()1 2 ( 1 ) ( 1 )
re(c)1 t(1 )(1 ) 0
0x2
0
1 x 2
=2 1 x 2
0
其它 2x0
0x2 其它
g(x) 2( x) 2
(3 )co(m x)rbe(x c)t(xn)rec(xt)
com(xb)
n
com (x)b re(c x)t
rect( x)
=
1.6 已知 exp( x2) 的傅里叶变换为 exp(2) 试求
f () 1
h(x-)
0x
g(x)0 xf()h (x)d x1e-(x)d
0
x1e-(x)d 1ex 0
g( x)
g( x0 )
0 x0
x
1.11 有两个线性平移不变系统,它们的原点脉冲响应分别为
h 1(x)sicn (x) 和 h 2(x )sic n (3x )
ex x p 2 ) (?
exp(x2ຫໍສະໝຸດ 22)
g1(x) -1 G1() 0
G 2 () H 2 ()1 2 ( 1 ) ( 1 ) 1re (c ) t1 ( 1 ) ( 1 )
3 32
1(1)(1)
6
g2(x)
-1G2()
1 cos2
3
x
1.12 已知一平面波的复振幅表达式为
试计算各自对输入函数 f(x)co 2 sx的响应
g1( x) 和 g2( x)
解: H 1()re(c )t H2()1 3rec(t3)
F ()1(1)(1)
2
G 1 ()H 1 ()1 2 ( 1 ) ( 1 )
re(c)1 t(1 )(1 ) 0
0x2
0
1 x 2
=2 1 x 2
0
其它 2x0
0x2 其它
g(x) 2( x) 2
(3 )co(m x)rbe(x c)t(xn)rec(xt)
com(xb)
n
com (x)b re(c x)t
rect( x)
=
1.6 已知 exp( x2) 的傅里叶变换为 exp(2) 试求
f () 1
h(x-)
0x
g(x)0 xf()h (x)d x1e-(x)d
0
x1e-(x)d 1ex 0
g( x)
g( x0 )
0 x0
x
1.11 有两个线性平移不变系统,它们的原点脉冲响应分别为
h 1(x)sicn (x) 和 h 2(x )sic n (3x )
ex x p 2 ) (?
exp(x2ຫໍສະໝຸດ 22)
信息光学第五章苏显渝版作者窦柳明

5.2 波前记录与再现
5.2 波前记录与再现
5.2.1 波前记录:
1. 物光波与参考光波干涉形成干涉图
设传播到记录介质面上的物光波波前 和参考光波波前分别为:
O( x, y) O( x, y) exp[ j( x, y)] R( x, y) R( x, y) exp[ j ( x, y)]
1. 再现光波是全息记录时的参考光波,即C(x,y)=R(x,y):
(1) U3 RCO(x, y) R 2 O(x, y) A O
若参考光的强度在记录面上近似为均匀的,则
tH ( x, y) tb ( O 2 RO RO )
tb t0 R 2
为简单,有时写成: tH ( x, y) I( x, y)= R 2 O 2 RO RO
5.2 波前记录与再现
5.2.2 波前再现:
5.1 光学全息概述
波前记录(全息记录):物光波与参考光波干涉的记录过程。
全息图:被某种介质记录下的物光波与参考光波形成的干涉 图。[物光波的振幅和相位信息转化成为干涉图(干涉条纹) 中的条纹衬比度、条纹间距及取向等的空间分布。] 波前再现(全息再现):把全息图作为衍射屏,用符合一定条件 的光波照射全息图,特定方位的衍射波就可以重现原物光波。
U1 :系数的作用仅仅改变照明光波C的振幅,并不改变C的特性。
U2 :C波经历|O (x,y)| 2分布的一张底片的衍射,是一种“噪声”信息;
UI和U2基本上保留了照明光波的特性.这一项称为全息衍射场中的0级波。
U3 :包含有物的相位信息,但还含有附加相位。这一项最有希望
再现物光波;全息图衍射场中的+1级波。
底层:使亲水的乳胶层牢固地粘附于疏水的玻璃片上。
信息光学PPT课件第五章光学全息

)
Uc (x,
y, z)
Ae jkr
U
( x,
y,
z)
U( x, y, z) Ae jkr Aexp jk( x cos y cos z cos )
Uc ( x, y, z) Ae jkr U ( x, y, z)
共轭光波的数学表达式为原光波复振幅的共轭复数。
已知 于是
参考波
R
记录介质上的的总光强为 I( x, y) O( x, y) R( x, y) 2
O
物波
记录介质
O( x, y) 2 R( x, y) 2 R( x, y)O( x, y) R( x, y)O( x, y)
O(x, y) 2 R(x, y) 2 2r(x, y)O0(x, y)cos (x, y) (x, y)
参考波
R
O
物波
记录介质
上图为波前记录的示意图,设传播到记录介质上的物光波前复振幅(对于理 想单色光,其空间的复振幅分布是不随时间变化的)为
O( x, y) Oo ( x, y)exp j ( x, y)
传播到记录介质上的参考光波前复振幅
R( x, y) r( x, y)exp j ( x, y)
全息图片
全息图片
当照明光波与参考光波均为正入射的平面波时,入射到 全息上的相位可取为零。这时U3和U4中的系数均为实 数,无附加相位因子,全息图衍射场中的+1级和-1级光 波严格镜像对称。由共轭光波U4所产生的实像,对观察 者而言,该实像的凹凸与原物体正好相反,因而给人以 某种特殊的感觉,这种像称为赝像。
如何得到三维的图像呢?
如果我们能够用某一种方法把物体光波(其中包含振幅和 相位信息)以某种方式记录下来,则当我们想办法把物光波 再现出来的话,就能再现三维的物体。
信息光学课件

电磁场与麦克斯韦方程
电磁场的基本概念
电磁场是由电场和磁场组成的, 它们之间存在相互作用。
麦克斯韦方程
描述了电磁场变化的四个基本方程 ,包括电场的散射方程、磁场的散 射方程、电场的波动方程和磁场的 波动方程。
电磁场的能量守恒
电磁场在空间中传播时,其能量不 会消失也不会凭空产生,即电磁场 的能量守恒。
将光学传感技术应用于物联网领域,实现智能化 、远程化和自动化的监测和控制。
3
光学传感器的集成与小型化
通过集成和优化光学器件,实现光学传感器的微 型化和便携化,满足不同应用场景的需求。
05 信息光学实验与实践教学 环节设计
实验内容与目标设定
实验内容
信息光学实验包括干涉、衍射、光学 信息处理等基本实验,以及一些综合 性和创新性实验。
信息光学课件
目录
CONTENTS
• 信息光学概述 • 信息光学基础理论 • 信息光学器件与系统 • 信息光学前沿技术与发展趋势 • 信息光学实验与实践教学环节设计 • 信息光学课程评价与总结反思环节设计
01 信息光学概述
信息光学定义与特点
信息光学定义
信息光学是一门研究光学信息的 获取、传输、处理、存储和显示 的科学。
傅里叶变换与信息光学
傅里叶变换
是一种将时域信号转换为频域信号的数学工具,常用于信号处理 和图像处理等领域。
信息光学的基本概念
信息光学是一门研究光波在空间和时间上传递、处理和存储信息的 科学。
信息光学的应用
信息光学在通信、生物医学成像、军事等领域有着广泛的应用,如 光纤通信、光学显微镜、光学雷达等。
03 信息光学器件与系统
光学器件分类与特点
主动光学器件
信息光学第1章1

注意:δ函数的图像,有幅值(是无穷大吗?)
小测试:请在一个坐标系里画出δ(x),δ(x-5), 2δ(x-5)的图像。
在本门课程中,δ(x)函数常常用来表示点光源的功率密 度,由于点光源所占面积趋近于零,所以在x=0点功率密度 趋近于无穷大。
?点光源模型中什么量是有限Байду номын сангаас呢?
?如果可以用δ (x)来建立模型的话,由数学公式看出积分 要是1,这代表什么物理意义?
数学物理模型完全吻合。
δ函数三大性质(会理解(图像),会应用)
(1) 函数的筛选性质---采样完成
x,
0
0
由定义,经变量代换,可直接证明。
x0 , y0
(2) 函数采样性质(与普通函数的乘积性质)---采样准备
h ( x) ( x x0 ) h ( x0 ) ( x x0 )
b. 函数图形
c. 二维三角形函数表达式及图形
, a a a b
d.该函数在日后的学习中 将有重要的位置。目前仅 需需注意,该二维函数图 形的侧面并非平面。并非 所有过定点且垂直于xoy的 平面与之相截都能得到三 角形。
5. sinc函数
a. 表达式
b. 图形
x
x
sin
答复:抽样过程在物理上,是以积分的方式实现的。 x0点处的信号在被仪器 记录前表达为f(x0)δ(x-x0),恰恰是为确保该点信号被仪器记录为f(x0)。过程为:
f ( x0 ) ( x x0 )dx f ( x0 )
f(x0)δ(x-x0)所表达的抽样,意为“被抽样前的准备”,切不可用f(x0)来描述。
rect
x y 1, rect
小测试:请在一个坐标系里画出δ(x),δ(x-5), 2δ(x-5)的图像。
在本门课程中,δ(x)函数常常用来表示点光源的功率密 度,由于点光源所占面积趋近于零,所以在x=0点功率密度 趋近于无穷大。
?点光源模型中什么量是有限Байду номын сангаас呢?
?如果可以用δ (x)来建立模型的话,由数学公式看出积分 要是1,这代表什么物理意义?
数学物理模型完全吻合。
δ函数三大性质(会理解(图像),会应用)
(1) 函数的筛选性质---采样完成
x,
0
0
由定义,经变量代换,可直接证明。
x0 , y0
(2) 函数采样性质(与普通函数的乘积性质)---采样准备
h ( x) ( x x0 ) h ( x0 ) ( x x0 )
b. 函数图形
c. 二维三角形函数表达式及图形
, a a a b
d.该函数在日后的学习中 将有重要的位置。目前仅 需需注意,该二维函数图 形的侧面并非平面。并非 所有过定点且垂直于xoy的 平面与之相截都能得到三 角形。
5. sinc函数
a. 表达式
b. 图形
x
x
sin
答复:抽样过程在物理上,是以积分的方式实现的。 x0点处的信号在被仪器 记录前表达为f(x0)δ(x-x0),恰恰是为确保该点信号被仪器记录为f(x0)。过程为:
f ( x0 ) ( x x0 )dx f ( x0 )
f(x0)δ(x-x0)所表达的抽样,意为“被抽样前的准备”,切不可用f(x0)来描述。
rect
x y 1, rect
信息光学理论与应用(第版)

开关功能:可在某点开启或 关闭另一函数 ,或描述光学 直边(或刀口)的透过率。
图1.1.6 二维阶跃函数
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章
《信息光学》课件
4.符号函数
1 x / a 0
sgn
x a
0 1
x/a0 x/a0
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章
3.阶跃函数
● 一维情形:
1
step
x a
1 / 0
2
其中 a 0
x/ a0 x/ a0 x/ a0
● 二维情形:
f (x, y) step(x)
《信息光学》课件
图1.1.5 一维阶跃函数
x a
rect
y b
1
0
其中
x a, y b 22
其他
a 0,b 0
表示矩孔透过率。
图1.1.2 二维矩形函数
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章
《信息光学》课件
2.sinc函数
● 一维情形:
sinc
《信息光学》课件
上述积分形式表明: 函数可由等振幅的所有频率的
正弦波(用余弦函数表示)来合成,换言之, 函数可
分解成包含所有频率的等振幅的无数正弦波。
4.梳状函数
● 一维情形:
comb
x x0
n
x x0n x0
n
信息光学第七章-光学全息ppt课件
引入一相干参考波,该参考波在H上产生 的复振幅分布为
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
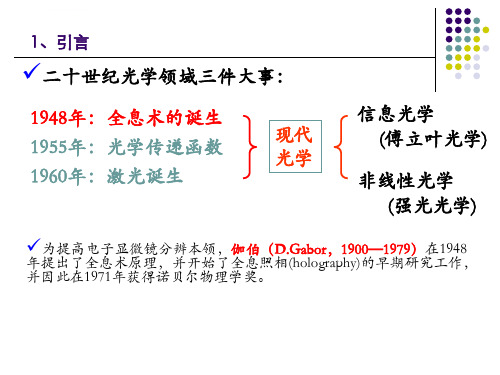
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
信息光学第一章ppt

例: f(x)={
x, 0
0<x<1 其它
求 f (-2x+4)
解1: f(-2x+4)= f[-2(x-2)],包含折叠、压缩、平移
先折叠
再压缩
f(x)
f(-x)
f(-2x)
0 1 x -1 0 x
-1/2 0 x
最后平移
f[-2(x-2)]
0 3/2 x
11
解2: 根据已知条件有
f
(2x
4)
x a/2
其它
应用:单缝透过率、门函数、时间脉冲波形.
标准型:
1 x 1/ 2
rect(x)
0
else
15
y
0
x0
a
x
rect ( x x0 ) a
16
17
18
2 sinc函数 应用:单缝或矩形孔的夫琅和费衍射的振幅分布
强度分布为sinc函数平方
注意归一化和非归一 化的两种表达方法。
xa / 2
原函数f(x)在某点x的值卷积后用某一段(x-a/2, x+a/2) 的积分值来表示, 等价于这段区间的平均值。
50
卷积的运算性质
交换律:f (x) h(x) h(x) f (x) 分配律:[aw(x) bv(x)] h(x) aw(x) h(x) bv(x) h(x) 分配律体现了卷积的线性特性。 结合律:[v(x) w(x)] h(x) v(x) [w(x) h(x)] 可分离变量特性: 如果参与卷积的两个函数是可分离的, 其 二维卷积也是可分离的。(极坐标和直角坐标)
1 a
1 a
当a 0时, (ax)dx lim m (ax)dx lim am (ax)d ax
信息光学原理第2章

2.1 光波的数学描述
2.1.5 复振幅分布的空间频谱(角谱)
利用傅里叶变换对位于单色光场中的xy平面上的复振幅分布进
行傅里叶分析,有
U x, y A fx, fy exp j2 fxx fy y dfxdfy
A fx, fy U x, yexp j2 fxx fy y dxdy
几何光学 (光与宏观物质的作用)
信息光学原理(电子工业出版社) 苏显渝 吕乃光 陈家壁
信息光学是光学和信息科学相结合的新的学科分支。 它研究以光为载体的信息的获取、信息的交换和处 理、信息的传递和传输,是信息科学的一个分支。 信息光学采用线性系统理论、傅里叶分析方法分析 各种光学现象。
第二章
标量衍射理论
cos2 cos2 cos2 1
2.1 光波的数学描述
对于如右图所示 的沿某一确定方向传播的平面波,在xy 平面上的复振幅为:
U x, y, z a exp jkz cos exp jk x cos y cos
a
exp
jkz
1
cos2
cos2
exp
jk
x
cos
y
cos
u x, y, z,t a x, y, zcos 2t x, y, z
其中,v是光波的时间频率;a(x,y,z)和(x,y,z)分别是P点光振动
的振幅和初相位。根据欧拉公式,可将该波函数表示为复指数函数 取实部的形式:
u x, y, z, t Re a x, y, z e j2tx,y,z
参考文献:
(1) W. Lauterborn, T.Kurz, M.Wiesenfeldt, Coherent optics, 北京:世界图书出版社,1998。
《信息光学》课件

信息光学的发展历程
19世纪末至20世纪初
光学显微镜和望远镜等光学仪器的发明和应用,为信息光学的发展 奠定了基础。
20世纪中叶
随着激光技术的出现和发展,信息光学开始进入快速发展阶段。
20世纪末至今
随着计算机技术和光电子技术的不断进步,信息光学在通信、数据 存储、生物医学等领域得到了广泛应用。
信息光学的基本原理
02
信息光学的基本技术
光学全息技术
光学全息技术是一种利用光的干涉和衍射原理来记录和再现 三维物体的技术。通过将物体发出的光波与参考光波干涉, 将干涉图样记录在全息介质上,然后使用合适的照明光波进 行再现,即可得到物体的三维图像。
全息技术可以用于制作全息图、全息显示、全息干涉计量和 全息光学元件等。在科学研究、工业检测、医疗诊断和军事 领域等方面有广泛应用。
光学信息处理技术
光学信息处理技术是指利用光的干涉、衍射和折射等光学现象来进行信息处理的 技术。这种技术具有高速、大容量、并行处理等优点,可以用于图像处理、信号 处理、模式识别和计算机科学等领域。
常见的光学信息处理技术包括傅里叶变换光学、光学图像处理、光学计算和光学 神经网络等。
光学计算技术
光学计算技术是指利用光学方法来实现计算的技术。这种 技术利用了光的并行性和快速性,可以实现高速、高精度 和大容量的计算。
运行,为人工智能领域的发展提供新的动力。
信息光学在未来的应用前景
下一代光通信网络
随着5G、6G等通信技术的发展,信息光学将在构建下一代光通信 网络中发挥关键作用,实现超高速、超大规模的数据传输。
智能感知与物联网
光学传感器和光通信技术将在智能感知和物联网领域发挥重要作用 ,实现更高效、更智能的物联网应用。
信息光学 第三章 苏显渝版 PPT作者窦柳明概要

jk 1 1 1 2 2 P ( x , y )exp x y 2 d0 di f
1 1 1 d0 di f
x0 x i y0 yi exp jk x y dxdy d0 di d 0 d i
程中的丢失、衰减、相移的变化,即研究成像系统的空间频率 传递特性——传递函数,从而做到对系统全面、定量的评价。
第三章 光学成像系统的传递函数
即可以由传递函数全面定量地对系统进行评价。 系统的传递函数可由两种方法获得: (1)由系统的设计数据(材料参数、结构参数等)计算出来: ——叫做传递函数的计算。 (2) 由检测仪器进行测定: ——叫传递函数的测定。
已知物面分布 成像系统 像面分布(复振幅分布和光强分布) 相干叠加(相干光照明) 非相干叠加,即强度叠加 (非相干光照的) 点扩散函数(脉冲响应)
关键是:求点物的像 场分布——点扩散 函数(脉冲响应)
δ( x x0 , y y0 ) 成像系统
小面元组合 (加权函数)
h( x0 , y0 ; xi , yi )
d0
di
3.1 相干照明衍射受限系统的点扩散函数
U 0 ( x 0 , y0 ) ( x 0 , y0 )
Ul U l
U i ( x i , yi ) ( xi , yi )
( x, y )
0 , y0 ) (x
, y0 ) ( x0 2) 求 dUl ,
d0
di
dU l ( x , y; x 0 , y0 )
2 2 x x 2 y y x x y y exp( jkd0 ) 0 0 0 0 0 , y0 ) exp jk dU l ( x, y; x0 x x , y y exp jk 0 0 0 0 2d 0 j d 0 2d0 0
信息光学后答案 苏显渝PPT学习教案

j2
x)dx
2 2 (2 )2
f (x) dx
2 2 (2 )2
0
2
第12页/共116页
1.10设线性平移不变系统的原点响应 为 试计算系统对阶跃函数step(x)的响应 。
h( x) e xp( x)step( x)
解:
h(x) exp( x)step(x) e xp( x)
comb( x)
n
comb( x) rect( x)
rect( x)
=
1.6 已知
exp( x )2
的傅里叶变换为
e xp( x2 ) ?
解:
利用傅里叶变换的坐标缩放性质可求 得答案
试求
exp( 2 )
x2
e
xp(
2
2
)
?
f (ax, by)
1
F( , )
ab a b
第6页/共116页
e xp( x2 )
e xp(
x
2
)
exp( 2 2 )
x 2
e xp(
2
2
)
e
xp
x2
2 2
2
?
2 e xp 2 2 2
2 e xp 2 2 2 2
第7页/共116页
1.7 计算积分
(1) sinc4(x) ? 解:利用广义巴塞伐定理求解
2
2
1 1
2
2
1 3
2
2
其它
G( ) 3 ( ) 1 ( )
4 3/ 2 4 1/ 2
第11页/共116页
1.9 设
f (x) exp( x ), 0 求
f ( x)
工程光学 第二章 郁道银版 PPT作者窦柳明(长沙理工大学)

第二节 理想光学系统的基点和基面
(3)为求物镜的物方焦距f、物方焦点的位置F、物方主点的位 置H,可沿反向光路追迹一条平行于光轴的光线。 利用近轴光线的光路计算公式 平行光线初始坐标为: 逐面计算,其结果为:
l u1 0 h1 10m m i1 h1 / r1
' lF mm, u' 0.121869 ' l ' 70.0183 h h f ' 82.055m m tgU ' u 'l ' l f ' 12.0366 mm
第一节
理想光学系统与共线成像理论
作图法证明: ①已知两对共轭面的位置和放大率
已知:M为理想光学系统 像面O’1与物面O1共轭,其对应放大率为β1 像面O’2 与物面O2共轭,其对应放大率为β2 求: 物空间任意物点O的像点位置O’ B A M O’ B’ A’
第一节
理想光学系统与共线成像理论
作图法证明: ②已知一对共轭面的位置和放大率,以及轴上两对共 轭点的位置
定义:像方焦点、焦平面;像方主点、主平面;像方焦距
A B Q’ F’ H’ E’
像方主平面
像方主点H’:平行于光轴的入射光线AB的延长线,与其出射光 线E’F’反向延长线交于Q’,过Q’作垂直光轴的平面与光轴的交点 H’。 像方主平面:过像方主点H’且垂直于光轴的平面Q’ H’ 。
第二节 理想光学系统的基点和基面
第二章
理想光学系统
第二章
1 第一节 第二节 第三节
理想光学系统
理想光学系统与共线成像理论 理想光学系统的基点与基面 理想光学系统的物像关系
2
3
4
4 5
第四节
