回扣基础规范答题十.docx

合集下载

2020年高考化学二轮复习回扣基础规范答题十一明确规范答题的9种要求

H＋＋CO23－。
⑦HCO－ 3 的水解方程式： HCO－ 3 ＋H2O H3O＋＋CO23－ HCO－ 3 ＋H2O H2CO3＋OH－。
⑧NaHSO4熔化时电离方程式：
NaHSO4===Na＋＋H＋＋SO24－ NaHSO4=熔==化==Na＋＋HSO－ 4 。
⑨NH4Cl固体和消石灰加热制NH3： △
3.方程式的书写一定要符合要求，“答非所问”不给分如：“化学方程式”“离子方程式”“电极方程式”“电解方程式”“水解方程式”“电离方程式”“热化学方程式”。 (1)不配平不给分。 (2)非最小公倍数不给分(电极反应式、热化学方程式除外)。 (3)“△”“↑”“↓”“→”“ ”“电解”“催化剂”“高温”“高压”等均应正确使用，否则扣分。请订正下面的错误： ①在硝化细菌作用下，O2 将 NH＋ 4 氧化为 NO－ 3 ： 2NH＋ 4 ＋5O2===2NO－ 3 ＋4H2O NH＋ 4 ＋2O2硝==化==细==菌= NO－ 3 ＋H2O＋2H＋。
①
＋Cl2 ―F―e→
＋HCl
＋Cl2 ―光―照→
＋HCl 。
②CH3COOH＋C2H5OH―浓―硫 △――酸→CH3COOC2H5＋H2O
CH3COOH＋C2H5OH
浓硫酸 △
CH3COOC2H5＋H2O
。
③C2H4＋Br2―→C2H4Br2 CH2===CH2＋Br2―→
。
④CH3CH2OH=浓1=7H=0=2S=℃=O=4CH2===CH2↑ CH3CH2OH―浓1―7硫―0―℃酸→CH2===CH2↑＋H2O 。
(4)自然界中，硬度最大的是金钢石
纠错金刚石
( 1分 ) ( 0分 ) ( 0分 ) ( 0分 )

反贪污、贿赂考试试题

反贪污、贿赂考试试题1、下列行为那一项不属于贿赂腐败行为（）？［单选题］A、向政府官员提供财物以获得公司业务竞争优势B、向政府行政人员赠送礼物以保有公司正当业务C、公司赠送员工节日礼品（正确答案）D、与商业伙伴一同出游并为其支付费用以获取合作机会2、下列哪一项不属于“利益输送”的情形（）［单选题］A、同业竞争（正确答案）B'统方C、影响第三方独立性D、通过第三方贿赂3、下列哪一项不属于"利益冲突"的情形（）［单选题］A、利用公司信息、渠道等私自获取本属公司的商业机会B、在与本公司存在竞争关系的公开交易公司中持有超过1%的所有权C、利用自己公司职务的便利侵占、盗用公司财产（正确答案＞D、从公司的客户、供应商或竞争对手处取得贷款4、下列哪种商业招待送礼行为不需要经过财务负责人及以上级别的人审批（）［单选题］A、赠送价值688元的礼品给客户B、招待来访客户人均388元的自助餐C、招待客户10人用餐花费2000元（（正确答案）D、宴请上级部门领导用餐开销6888元5、列哪一行为符合政府招待的送礼标准与程序（）［单选题1A、经部门负责人审批，向政府官员赠送价值399元的礼品B、经部门负货人、财务预算审批，并上报合规及总裁'向政府官员赠送价值399元的礼品（正确答案）C、经部门负责人、财务预算审批，并上报合规及总裁，向政府官员赠送价值599元的礼品D、经部门负责人、财务预算审批，向政府官员赠送价值399元的礼品6、下列关于第三方反贿赂的表述，错误的是（）［单选题］A、公司要求公司的第三方遵守公司反贿赂政策以及所适用的法律B、公司要求在与第三方合同中加入反贿赂条款C、公司对原来第三方合同中未添加反贿赂腐败条款的，无需另外签署补充申明（（正确答案）D、对于第三方合同管理有疑问的，可以咨询法务部7'下列关于人事招聘反贿赂腐败管理的表述，正确的是（）［单选题］A、聘用具有特殊背景的人员，必须记录其特殊背景（正确答案）B、聘用具有特殊背景的人员，可以对其优待C、聘用具有特殊背景的人员，不需要对他进行背景调查D、聘用具有特殊背景的人员，有相关疑问时咨询法务部8、下列关于员工违反公司《反贿赂腐败基本政策》（以下简称《政策》）的表述中，错误的是（）［单选题］A、员工违反《政策》，情节产重的公司可以解除劳动合同B、员工违反《政策》-涉嫌犯罪的移送司法机关C、员工违反《政策》，造成经济损失的追究其赔偿责任D^员工违反《政策》，其部门负责人无需承担管理责任（正确答案）9、下列哪一项不属于反贿赂腐败监督管理小组的组成成员（）［单选题］A、法务部B、审计部C、运营部门（正确答案）D'人事部10、下列哪一国家的反贿赂腐败相关法律规范创制了"商业组织预防贿赂失职罪”（）［单选题］A'中国B'德国C、法国D、英国（正确答案）1•公司对招待送礼行为一律禁止。

医院专项整治行动和九项准则实施细则试题

医院专项整治行动和九项准则实施细则试题一、判断题（对的打“让，错的打“X”，每题5分，共10道，共50分）1“红包”回扣专项整治行动的整治内容是“将医务人员在从事诊疗活动过程中，索取或者收受患者及其亲友给予的礼品、礼金、消费卡和有价证券、股权、其他金融产品等财物，以及接受患者及其亲友安排、组织或者支付费用的宴请或者旅游、健身、娱乐等活动安排均界定为‘红包’，全部纳入专项整治范围。

”［判断题］对（正确答案）错2 .严禁工作人员利用职务之便，从开具的药品、检验检查及其他特殊检查等服务中谋取私利。

［判断题］对;错3 .除因需要在医联体内正常转诊外，严禁以谋取个人利益为目的，通过网上或线下途径介绍、引导患者到其他指定医疗机构或场所检查、诊治。

［判断题］对错4 .严禁参加或接受药品、医疗设备、医疗器械、医用卫生材料等医药生产、经营企业及其经销人员安排、组织或者支付费用的宴请、礼品、旅游、学习、考察、健身或其他娱乐休闲等活动安排。

［判断题］对（正确答案）错5 .“红包”回扣专项整治行动整治时间为2024年1月―2024年6月。

［判断题］对（正确答案）错6 .每年对医务人员进行1-2次集体综合考评，重点对医疗质量、诊疗行为、服务态度、劳动纪律、履职职责等方面进行考评，把考评结果与职称晋升、工资绩效、表彰先进和定期考核等直接挂钩，实行医德医风“一票否决”制。

［判断题］对错7 .设置举报箱、公布举报电话，设立院内、院外行风监督员，采取走出去、请进来等方式，充分听取意见和建议，自觉接受人民群众监督。

对违反职业道德和行业纪律的工作人员，一经查实，要严格按照相关规定进行处理。

［判断题］对I错8 .医院确定采购需求前，可通过咨询、论证、问卷调查等方式了解相关产业发展、市场供给、同类采购项目历史成交信息，可能涉及的运行维护、升级更新、备品备件、耗材等后续采购及其他相关情况等，需求调查的对象应具有代表性且不少于3个。

［判断题］对（正确答案）错9 .医院根据医保部门政策调整情况、及时调整医疗服务价格情况，严格执行医疗服务价格政策。

高考化学回扣基础规范答题 (4)

九、背会不失分的化学实验问题(规范解答50条)(一)有关实验操作的问题1．检验离子是否已经沉淀完全的方法规范解答将反应混合液静置，在上层清液中继续滴加沉淀剂××，若不再产生沉淀，则××离子已经沉淀完全，若产生沉淀，则××离子未完全沉淀。

2．过滤时洗涤沉淀的方法规范解答向过滤器中加蒸馏水至没过沉淀，待水自然流下后，重复操作2～3次。

3．检验沉淀是否洗涤干净的方法规范解答以FeCl3溶液与NaOH溶液制得Fe(OH)3沉淀后过滤为例：取最后一次的洗涤液少许置于试管中，加入用硝酸酸化的硝酸银溶液，若有白色沉淀生成，则沉淀未洗涤干净，若无白色沉淀生成，则沉淀已经洗涤干净。

注意要选择一种溶液中浓度较大的、比较容易检验的离子检验，不能检验沉淀本身具有的离子。

4．配制一定物质的量浓度的溶液时定容的操作方法规范解答向容量瓶中加水至离刻度线1～2 cm处，改用胶头滴管滴加，眼睛平视刻度线，滴加水至凹液面的最低点与刻度线相切。

5．读取量气装置中的气体体积的方法规范解答待装置冷却至室温后，先上下移动量筒(或量气管有刻度的一侧)使量筒内外(或量气管的两侧)液面相平，然后使视线与凹液面的最低点相平读取数据。

6．用pH试纸测定溶液的pH的方法规范解答取一小片pH试纸放在洁净干燥的玻璃片或表面皿上，用干燥洁净的玻璃棒蘸取待测液点在试纸的中部，待pH试纸显色后与标准比色卡比色。

7．酸碱中和滴定判断滴定终点的方法规范解答当滴入最后一滴××溶液时，锥形瓶中的溶液由××色变为××色，且半分钟内不再恢复原色，说明已经达到滴定终点。

8．分液的操作方法规范解答将萃取后的分液漏斗放在铁架台的铁圈上静置，待液体分层后打开分液漏斗上口的玻璃塞(或将玻璃塞上的凹槽与分液漏斗上的小孔重合)，使漏斗内外空气相通，小心地旋转分液漏斗的活塞，使下层液体沿烧杯内壁流入烧杯中，待下层液体流出后及时关闭活塞，将上层液体从分液漏斗的上口倒出。

(浙江专版)高中数学回扣验收特训(二)新人教A版必修1

回扣验收特训(二)A. [ —1,2] C. [2 ,+^)1<x <2,故选 B.法二：因为x M — 1，排除A ;取x = 3,贝U 4— 2x = 4— 6=—2< 0，所以x 丰3,排除C 、 D,故选B.则满足f (a ) = 1的实数a 的值为()B. 1 D. 2a w 0,解析：选A 依题意，知满足f (a ) = 1的实数a 必不超过零，于是有2由此解a = 1,得 a =— 1.3. 下列函数中，在区间(1 ,+^)上是增函数的是()1 A. y = — x + 1B . y =- 1 — xC. y =— (x — 1)2D. y = 31—x解析：选B 由题意可知，y = — x + 1与y = 31—x 在定义域上均为减函数， y = —(x — 1)21的对称轴为x = 1，且开口向下，所以在区间(1 ,+^)上是减函数，只有函数 y =在区 1 — x间(1 ,+^)上是增函数.故选 B.4. 函数 f (x ) = x 5 + x 3+ x 的图象()A.关于y 轴对称B .关于直线y = x 对称 C.关于坐标原点对称D.关于直线y = — x 对称解析：选C 易知f (x )是R 上的奇函数，因此图象关于坐标原点对称. 15. 已知 f (x ) = x + -一 1, f (a ) = 2，贝U f ( — a )=()x［回扣验收特训］1 .函数 f (x )=卜4-2x 的定义域为(解析：选B 法要使函数f (x )= —2x 有意义,寸x + 1x +1>0, 则4— 2x > 0,解得―B . ( — 1,2] D. [1 ,+^)2, x >0,2.若函数f (x ) = 2x , x < 0,A. — 1 C.— 2A. —4B.—2C.—1D.—31 解析：选 A T f (x ) = x +-— 1,x1 1f (a ) = a +-一 1 = 2,.•. a +- = 3,' ' aa1 1•. f ( — a ) =— a — — 1 = — a +— 1 = — 3 — 1 = — 4.aa6. 偶函数y =f (x )在区间［0,4］上单调递减，则有()nnA. f ( — 1) > f —> f ( — n) B . f — > f ( — 1) > f ( — n)33nnC. f ( —n ) > f ( — 1) > f jD. f ( — 1) > f ( — n ) > f §解析：选A 函数y = f (x )为偶函数，所以f ( — 1) = f (1) , f ( — n ) = f ( n )，又函数y n n=f ( x )在区间［0,4］上单调递减，所以 f (1) > f 3> f ( n )，则 f ( — 1) >f -3> f (—n ).解析：••• f(x )是偶函数，.••图象关于 y 轴对称.又f (2) = 0,且f (x ) 在［0 ,+^)单调递减，则f (x )的大致图象如图所示，由 f (x — 1) >0,得 —2 v x — 1v 2,即一1vx v 3.答案：(—1,3)&不等式x 2+ 2x —a >0对任意x € ［1 ,)恒成立，则a 的取值范围是 ___________2解析：令 f (x ) = x + 2x , x € ［1 ,+s ), 则f (x ) = (x + 1)2— 1在［1 ,+s )上是增函数， •••当x = 1时f (x )取最小值f (1) = 3. ■/x + 2x — a >0对任意 x € ［1 ,+s )恒成立， •• 3— a >0,即 a <3. 答案：(—a, 3)2x + a , x v 1,9.已知实数a z 0,函数f (x )=若f (1 — a ) = f (1 + a )，则a 的值—x — 2a , x > 1.为 ________ .解析：①当 1 — a v 1, 即卩 a >0 时，此时 a + 1 > 1,由 f (1 — a ) = f (1 + a )，得 2(1 — a )7.已知偶函数f (x )在［0,+s )单调递减,f (2) = 0.若f (x — 1) >0,则x 的取值范围综上所述, 3a =- 4. 答案：-3 410•设函数24+ x f(x) = 4-7.(1)求f (x )的定义域，并判断f (x )的奇偶性; 2⑵求证：f - =- f (2 X ).x解：(1)要使原函数有意义，只需4 — x 2工0,即x 工土 2,所以f (x )的定义域为｛X |X M 土 2｝.因为f (x )的定义域为｛X |X M 土 2｝，所以定义域关于原点对称.又 f ( - X )=若-X 2二~ = 4^笃=f (X )，所以f (X )为偶函数. X 4 X⑵证明：因为f— 2 ,2 2 X - 1' 4―一x1 + X2 2,4+ 2xf(2X) = 4— ~2x 21 - x 2所以 f - =-f (2X).2-x + 2x , x > 0,11.已知奇函数f (X ) = 0, x = 0,2x + mx x < 0.(1)求实数m 的值; ⑵画出函数图象.解：(1)当 x < 0 时，一x > 0,22f ( - x ) —- ( - X ) + 2( - x ) —- x - 2x , 又因为f (X )为奇函数，所以 f ( — x ) =- f (x ) =- x 2- 2x , 所以 f (x ) = X 2 + 2x,所以 m= 2.3+ a =- (1 + a ) — 2a,解得 a =-空(舍去);②当 1-a > 1,即卩 a v 0 时，此时 a + 1 < 1,由 f (1 -a ) = f (1 + a )，得—(1 - a ) - 2a =32(1 + a ) + a ,解得a =-；，符合题意.42—x + 2x, x> 0,(2)由⑴知f(x) = 0, x = 0,2x + 2x, x v 0,函数f(x)的图象如图所示.x12. f(x) = 2是定义在(一1,1)上的奇函数.1 + x(1) 用定义证明f(x)在(一1,1)上是增函数；(2) 解不等式f (t —1) + f(t) v 0.X1 X2 解：(1)证明：设X1 , X2 € ( —1,1)，且X1 V X2,则f(X1)—f(X2) = 2 — 2 =1 + X1 1 + X2X1 1 + X2—X2 1 + x2X1 —X2 1 —X1X21 + x2 1 + x2 = 1 + x2 1 + x2~，因为一1 V X1 V X2 V 1,所以X1 —X2V 0,1 —X1X2> 0 ,所以f(X1)—f(X2)V 0, 即即f ( X1) V f (X2),所以函数f (X)在(一1,1)上是增函数.(2)由函数f (X)是定义在(一1,1)上的奇函数且f(t —1) + f (t) V 0,得f(t —1) V — f (t)—1 V t —1V 1,=f ( —t)，又由(1)可知函数f(x)在(一1,1)上是增函数，所以有一1V —t V 1, ? 0t —1V —t1 1V t V2，所以不等式的解集是t 0V t V2 .。

2021年采购回扣面试如何回答

People are complacent because they have done beautiful things, but the success of things is often due to fluke, rather than pre-designed.简单易用轻享办公（WORD文档/A4打印/可编辑/页眉可删）采购回扣面试如何回答采购回扣是采购工作中常见的一种现象，采购员如何应对采购中的回扣问题？回扣是指卖方从买方支付的商品款项中按一定比例返还给买方的价款。

按照是否采取账外暗中的方式，回扣可以简单分为两种，即“账内明示”的回扣、账外暗中的回扣。

下面详细来了解下。

采购如何应对回扣问题？人们都说作为一个采购师不拿回扣都没人干了，采购师培训讲师解说采购中遇到或是在面试中遇到的“回扣”问题。

不是这个行业的人都知道采购这个职业油水大，更何况是采购的老大，企业的管事者呢。

问心自问：“当了采购师真的不拿回扣吗？能做到吗？”。

企业在对采购人员进行面试时特别重视“回扣”这个问题，因为员工拿回扣意味着采购来的物料质量上的问题，要不就是成本有有问题。

在采购师培训课间导师假定为面试关，问了几个学员这个问题。

有些学员回答的比较虚伪，面试官一听就能听出来，是在回避“回扣”这个问题。

所谓的“以企业为家”那是不可能的，你连家都照顾不好，怎么会不去榨企业的油水呢？在面对一个很普遍的问题，不应该采取回避的方式，应该要实事求是的正面回答问题，要充分表现的'自己的晋升和事业才是重要的，小恩小惠看不上的态度才是正确的。

要给自己找很充分的理由，让面试官觉得回扣对你来说根本不重要。

采购师培训采购师培训课程有俩个回答范例做为参考：1、采购吃回扣的疑问虽然是一个较普及的问题，但同时也是单个的疑问，并不是每个采购员都会吃回扣的。

我以为必定会有这样一类人，他们具有较强的事业心并以公司利益为重，对于这些人来说，事业的成功是其一生的追求，拿回扣就意味着“舍大取小”，而我恰恰就归于这样的人。

【配套课件】技能规范回扣5.8

球的表面积是___3_6_π___．
本解析正三棱锥对棱互相垂直，即 AC⊥SB，
课栏
又 SB∥MN，且 MN⊥AN，∴SB⊥AN，从而
目开
SB⊥平面 SAC.
关 ∴∠BSA＝90°，以 S 为顶点，将三棱锥补成
一个正方体，如图所示，故外接球的直径 2R＝ 3·SA，即
R＝3，
∴S＝4πR2＝36π.
本课
则该直线与此平面平行．
栏目
性质定理：一条直线与一个平面平行，则过这条直线的任
开关
一平面与此平面的交线与该直线平行．
(3)直线与平面垂直的判定定理和性质定理：
判定定理：一条直线与一个平面内的两条相交直线都垂直，
则该直线与此平面垂直．
性质定理：垂直于同一个平面的两条直线平行．
高考要点回扣
第5讲
V 台＝13(S＋ SS′＋S′)h(S、S′为上、下底面面积，h 为高)．
(6)球的表面积和体积
S 球＝4πR2，V 球＝43πR3.
高考要点回扣
第5讲
2．空间直线的位置关系：①相交直线——有且只有一个公共
点．②平行直线——在同一平面内，没有公共点．③异面
本
课直线——不在同一平面内，也没有公共点．
足出发的两个向量，则这两个向量的夹角的大小就是二面角
的平面角的大小．
本课
方法二
通过平面的法向量来求，设二面角的两个面的法向
栏目
量分别为 n1 和 n2，则二面角的大小等于〈n1，n2〉(或 π－〈n1，
开关
n2〉)．
易错警示：(1)求线面角时，得到的是直线方向向量和平面法向量的夹角的余弦，容易错以为是线面角的余弦． (2)求二面角时，两法向量的夹角有可能是二面角的补角，要注意从图中分析．

回扣验收特训(一) 算法初步

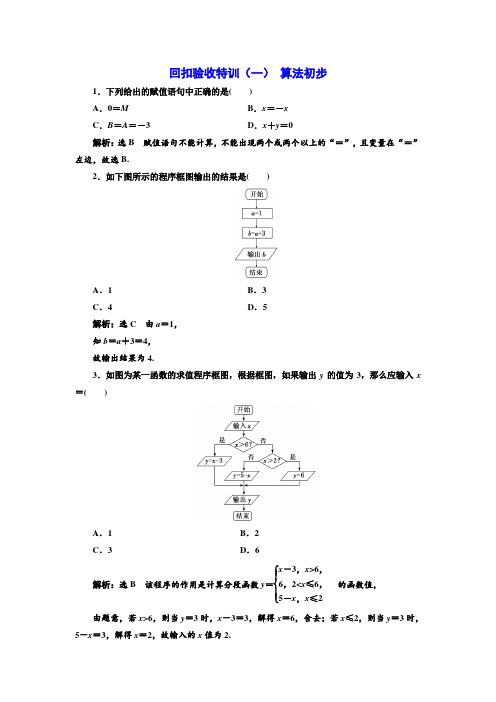
回扣验收特训（一）算法初步1．下列给出的赋值语句中正确的是( ) A ．0＝M B ．x ＝－x C ．B ＝A ＝－3D ．x ＋y ＝0解析：选B 赋值语句不能计算，不能出现两个或两个以上的“＝”，且变量在“＝”左边，故选B.2．如下图所示的程序框图输出的结果是( )A ．1B ．3C ．4D ．5解析：选C 由a ＝1，知b ＝a ＋3＝4，故输出结果为4.3．如图为某一函数的求值程序框图，根据框图，如果输出y 的值为3，那么应输入x ＝( )A ．1B ．2C ．3D ．6解析：选B 该程序的作用是计算分段函数y ＝⎩⎪⎨⎪⎧x －3，x >6，6，2<x ≤6，5－x ，x ≤2的函数值，由题意，若x >6，则当y ＝3时，x －3＝3，解得x ＝6，舍去；若x ≤2，则当y ＝3时，5－x ＝3，解得x ＝2，故输入的x 值为2.4．如图所示的程序框图的功能是()A．求a，b，c中的最大值B．求a，b，c中的最小值C．将a，b，c由小到大排列D．将a，b，c由大到小排列解析：选A逐步分析框图中各图框的功能可知，此程序的功能为求a，b，c中的最大值．故选A.5．高三某班15名学生一次模拟考试成绩用茎叶图表示如图1.执行图2所示的程序框图，若输入的a i(i＝1,2，…，15)分别为这15名学生的考试成绩，则输出的结果为()A．6 B．7C．8 D．9解析：选D由程序框图可知，其统计的是成绩大于或等于110的人数，所以由茎叶图知，成绩大于或等于110的人数为9，因此输出的结果为9.故选D.6．秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例．若输入n，x的值分别为3,2，则输出v 的值为()A．9 B．18C．20 D．35解析：选B由程序框图知，初始值：n＝3，x＝2，v＝1，i＝2，第一次循环：v＝4，i＝1；第二次循环：v＝9，i＝0；第三次循环：v＝18，i＝－1.结束循环，输出当前v的值18.故选B.7．已知某程序框图如图所示，则程序运行结束时输出的结果为________．解析：第一次循环结束时，n＝2，x＝3，y＝1；第二次循环结束时，n＝4，x＝9，y＝3；第三次循环结束时，n＝6，x＝27，y＝3.此时满足n>4，结束循环，输出log y x＝log327＝3.答案：38．已知程序如下，若输出的结果为2 016，则输入的x 的值为________．解析：由算法语句可知，该程序是求函数c ＝⎩⎪⎨⎪⎧2x ＋1，x ≤0，x 2－x ＋2 014，x >0的函数值．由题意知c ＝2 016，若x ≤0，则有2x ＋1＝2 016，解得x ＝1 0152，显然不合题意；若x >0，则有x 2－x ＋2 014＝2 016，即x 2－x －2＝0，解得x ＝－1或x ＝2，显然x ＝－1不合题意，故x ＝2.答案：29．我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n ＝________.解析：第一次循环，得S ＝2；第二次循环，得n ＝2，a ＝12，A ＝2，S ＝92；第三次循环，得n ＝3，a ＝14，A ＝4，S ＝354；第四次循环，得n ＝4，a ＝18，A ＝8，S ＝1358>10，结束循环，输出的n ＝4.答案：410．按下列程序框图来计算：如果输入的x ＝5，则应该运算________次才停止．解析：由题意，该程序按如下步骤运行：经过第一次循环得到x ＝3×5－2＝13，不满足x >200，进入下一步循环；经过第二次循环得到x ＝3×13－2＝37，不满足x >200，进入下一步循环；经过第三次循环得到x ＝3×37－2＝109，不满足x >200，进入下一步循环；经过第四次循环得到x ＝3×109－2＝325，因为325>200，结束循环并输出x 的值．因此，运算进行了4次后，输出x 值而程序停止．故答案为4. 答案：411．定义n ！＝1×2×3×…×n ，画求10！的值的程序框图．解：12．某商场实行优惠措施，若购物金额x 在800元以上(包括800元)，则打8折，若购物金额x 在800元以下500元以上(包括500元)，则打9折；否则不打折．设计算法的程序框图，要求输入购物金额x ，能输出实际交款额．解：本题的实质是求函数y ＝⎩⎪⎨⎪⎧0.8x ，x ≥800，0.9x ，500≤x <800，x ，x <500的值．程序框图如下：。

二轮政治全国通用专题复习基础知识回扣专题8份(8份打包)回扣三试题

回扣三文化生活一、选择题(12个小题，每题4分，共48分)1.(2015·贵州贵阳模拟)2015年春节，中央电视台新闻联播《新春走基层》播出“家风是什么”，引发社会广泛关注。

家风又称门风，是一个家庭或家族的传统风尚或作风，它可以是祖上传下来的一本书、一幅字，也可以是长辈们的一句话。

它是一种无言的教育、无字的典籍、无声的力量。

材料体现了家风()①作为一种精神现象离不开物质载体②作为传统文化促进社会和个人发展③对个人的影响潜移默化且深远持久④营造文化氛围增强家人的精神力量A.①②B.①③C.②④D.③④解析②说法错误，应该是优秀良好的家风才会促进社会和个人发展；④说法错误，优秀良好的家风才能增强精神力量；故选B。

答案 B2.(2015·江西临川模拟)国务院常务会议指出，依靠创新，推进文化创意和实际服务等新型、高端服务业发展，促进与相关产业深度融合，是调整经济结构的重要内容，有利于改善产品和服务品质、满足群众多样化需求，也可以催生新业态、带动就业、推动产业转型升级。

这说明()①文化与政治相互交融的特点日益显著②文化由经济、政治决定，是经济和政治的反映③一定的文化会给予经济以重大影响④文化生产力在现代经济的总体格局中的作用越来越突出A.①②B.③④C.②③D.①④解析此次会议精神，重视了文化与经济相互交融的关系，注重文化对经济的反作用，认识到了文化生产力在现代经济总体格局中的作用，③④说法正确；①②与题意不符。

该题选B。

答案 B3.(2015·山东莱芜模拟)为2014年APEC领导人非正式会议设计制作的特色中式服装11月10日亮相水立方。

该特色中式服装将民族传统、中国风范、领袖气质、东方元素等要素融入其中，承载了中华民族深厚的文化底蕴，表达了中国当代的国家精神和崭新的国家面貌，得到与会者的高度赞誉。

这表明()①文化既是民族的又是世界的②传统文化要与时代精神相结合③文化多样性是民族文化创新的基础④政治是一种最直接的文化传播方式A.①②B.③④C.②③D.①④解析材料未体现文化多样性，③与题意无关；④表述明显错误，排除；依据材料信息，①②表述正确且符合题意，答案A正确。

回扣验收特训(三) 统计案例

回扣验收特训（三）统计案例1．在两个学习基础相当的班级实行某种教学措施的实验，测试结果见下表，则实验效果与教学措施( )A ．有关 C ．关系不明确D ．以上都不正确解析：选A 随机变量K 2的观测值 k ＝100×(48×12－38×2)250×50×86×14≈8.306>6.635，则有99%的把握认为“实验效果与教学措施有关”． 2．下列说法中正确的有：( ) ①若r >0，则x 增大时，y 也相应增大； ②若r <0，则x 增大时，y 也相应增大；③若r ＝1或r ＝－1，则x 与y 的关系完全对应(有函数关系)，在散点图上各个散点均在一条直线上．A ．①②B ．②③C ．①③D ．①②③ 解析：选C 若r >0，表示两个相关变量正相关，x 增大时，y 也相应增大，故①正确．r <0，表示两个变量负相关，x 增大时，y 相应减小，故②错误．|r |越接近1，表示两个变量相关性越高，|r |＝1表示两个变量有确定的关系(即函数关系)，故③正确．3．有下列数据( )A ．y ＝3×2x －1 B ．y ＝log 2x C ．y ＝3xD ．y ＝x 2解析：选A 分别把x ＝1,2,3，代入求值，求最接近y 的值．即为模拟效果最好． 4．若两个变量的残差平方和是325，∑i ＝1n(y i －y )2＝923，则随机误差对预报变量的贡献率约为( )A ．64.8%B ．60%C ．35.2%D ．40%解析：选C 由题意可知随机误差对预报变量的贡献率约为325923≈0.352.5．为了解儿子身高与其父亲身高之间的关系，随机抽取5对父子的身高数据如下：则y 关于x 的线性回归方程为( ) A.y ^＝x －1 B.y ^＝x ＋1 C.y ^＝88＋12xD.y ^＝176 解析：选C 由表中数据可知x ＝176，y ＝176，代入选项知C 正确．6．收集一只棉铃虫的产卵数y 与温度x 的几组数据后发现两个变量有相关关系，并按不同的曲线来拟合y 与x 之间的回归方程，并算出了对应相关指数R 2如下表：则这组数据模型的回归方程的最好选择应是( ) A.y ^＝19.8x －463.7 B.y ^＝e 0.27x －3.84 C.y ^＝0.367x 2－202D.y ^＝(x －0.78)2－1解析：选B 用相关指数R 2来刻画回归效果，R 2的值越大，说明模型的拟合效果越好． 7．某学校对课程《人与自然》的选修情况进行了统计，得到如下数据：那么，在犯错误的概率不超过__________的前提下认为选修《人与自然》与性别有关．解析：K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )＝163.794>10.828，即在犯错误的概率不超过0.001的前提下认为选修《人与自然》与性别有关．答案：0.0018．某研究机构对高中学段学生的记忆能力x 和识图能力y 进行统计分析，得到如下表数据：若y 与x 的回归直线方程y ^＝3x －32，则实数m 的值是________．解析：由题意，x ＝32，y ＝8＋m 4，所以样本中心点坐标为⎝⎛⎭⎫32，8＋m 4，因为回归直线必过样本中心点，y 与x 的回归直线方程为y ^＝3x －32，所以8＋m 4＝3×32－32，所以m ＝4.答案：49．某医疗研究所为了检验某种血清预防感冒的作用，把500名使用过血清的人与另外500名未使用过血清的人一年中的感冒记录作比较，提出假设H 0：“这种血清不能起到预防感冒的作用”，利用2×2列联表计算得k ≈3.918，经查临界值表知P (K 2≥3.841)≈0.05.对此，有以下四个结论：①有95%的把握认为“这种血清能起到预防感冒的作用”； ②若某人未使用该血清，那么他在一年中有95%的可能性得感冒； ③这种血清预防感冒的有效率为95%； ④这种血清预防感冒的有效率为5%. 其中所有正确结论的序号是________．解析：由题意，因为k ≈3.918，P (K 2≥3.841)≈0.05，所以只有①正确，即有95%以上的把握认为这种血清能起到预防感冒的作用．答案：①10．某地最近十年粮食需求量逐年上升，下表是部分统计数据：(1)利用所给数据求年需求量与年份之间的回归直线方程y ＝b x ＋a ； (2)利用(1)中所求出的回归直线方程预测该地2018年的粮食需求量．解：(1)由所给数据看出，年需求量与年份之间是近似直线上升，下面来求回归直线方程，为此对数据预处理如下：对预处理后的数据，容易算得，x ＝0，y ＝3.2，又－4×(－21)＋(－2)×(－11)＋0×0＋2×19＋4×29＝260， (－4)2＋(－2)2＋02＋22＋42＝40，所以b ^＝26040＝6.5，a ^＝y －b ^x ＝3.2.由上述计算结果，知所求回归直线方程为 y ^－257＝b ^(x －2012)＋a ^＝6.5(x －2012)＋3.2，即y ^＝6.5(x －2012)＋260.2.(2)利用回归直线方程，可预测2018年的粮食需求量为 y ^＝6.5(2018－2012)＋260.2＝6.5×6＋260.2＝299.2(万吨)．11．在中学生综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评．某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：表一：男生表二：女生(1)1人测评等级为合格的概率；(2)由表中统计数据填写下面的列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”.参考临界值表：解：(1)设从高一年级男生中抽出m人，则m500＝45500＋400，解得m＝25，则从女生中抽取20人，所以x＝25－15－5＝5，y＝20－15－3＝2.表二中非优秀学生共5人，记测评等级为合格的3人为a，b，c，尚待改进的2人为A，B，则从这5人中任选2人的所有可能结果为(a，b)，(a，c)，(b，c)，(A，B)，(a，A)，(a，B)，(b，A)，(b，B)，(c，A)，(c，B)，共10种．记事件C表示“从表二的非优秀学生中随机选取2人，恰有1人测评等级为合格”，则C的结果为(a，A)，(a，B)，(b，A)，(b，B)，(c，A)，(c，B)，共6种．所以P(C)＝610＝35，故所求概率为35.(2)列联表如下：因为1－0.9＝0.1，P(K2≥2.706)＝0.10，而K2＝45×(15×5－15×10)230×15×25×20＝1.125<2.706，所以没有90%的把握认为“测评结果优秀与性别有关”．。

高中数学回扣验收特训(一)新人教A版必修1

回扣验收特训（一）1．已知集合A ＝{x |2x －3＜3x }，B ＝{x |x ≥2}，则( ) A ．A ⊆B B ．B ⊆A C ．A ⊆∁R BD ．B ⊇∁R A解析：选B A ＝{x |x ＞－3}，B ＝{x |x ≥2}，∴B ⊆A .2．已知集合A ＝{x |x 2－2x ＋a ＞0}，且1∉A ，则实数a 的取值范围是( ) A ．(－∞，1] B ．[1，＋∞) C ．[0，＋∞)D ．(－∞，1)解析：选A 由题意知A ＝{x |x 2－2x ＋a ＞0}，且1∉A ，则1－2＋a ≤0，即实数a 的取值范围是(－∞，1]，故选A.3．已知A ＝{x |x ＋1＞0}，B ＝{－2，－1,0,1}，则(∁R A )∩B ＝( ) A.{}－2，－1 B.{}－2 C ．{－1,0,1}D.{}0，1解析：选A 因为A ＝{x |x ＞－1}，所以∁R A ＝{x |x ≤－1}，所以(∁R A )∩B ＝{－2，－1}． 4．已知集合U ＝R ，集合A ＝{x |x ＜－2或x ＞4}，B ＝{x |－3≤x ≤3}，则(∁U A )∩B ＝( ) A ．{x |－3≤x ≤4} B ．{x |－2≤x ≤3} C ．{x |－3≤x ≤－2或3≤x ≤4} D ．{x |－2≤x ≤4}解析：选B ∁U A ＝{x |－2≤x ≤4}．由图知(∁U A )∩B ＝{x |－2≤x ≤3}．5．已知A ，B 均为集合U ＝{1,3,5,7,9}的子集，且A ∩B ＝{3}，(∁U B )∩A ＝{9}，则A ＝( )A ．{1,3}B ．{3,7,9}C ．{3,5,9}D ．{3,9}解析：选D 因为A ∩B ＝{3}，所以3∈A ，又(∁U B )∩A ＝{9}，所以9∈A .若5∈A ，则5∉B (否则5∈A ∩B )，从而5∈∁U B ，则(∁U B )∩A ＝{5,9}，与题中条件矛盾，故5∉A .同理1∉A,7∉A ，故A ＝{3,9}．6．对于集合M ，N ，定义M －N ＝{x |x ∈M ，且x ∉N }，M ⊕N ＝(M －N )∪(N －M )，设A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥－94，x ∈R，B ＝{x |x ＜0，x ∈R}，则A ⊕B ＝( ) A.⎝ ⎛⎭⎪⎫－94，0B.⎣⎢⎡⎭⎪⎫－94，0C.⎝⎛⎭⎪⎫－∞，－94 ∪[0，＋∞) D.⎝⎛⎦⎥⎤－∞，－94∪(0，＋∞)解析：选C 依题意得A －B ＝{x |x ≥0，x ∈R}，B －A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜－94，x ∈R，故A ⊕B ＝⎝⎛⎭⎪⎫－∞，－94 ∪[0，＋∞)．故选C.7．已知集合M ＝{1，m }，N ＝{n ，log 2n }，若M ＝N ，则(m －n )2 016＝________.解析：由M ＝N 知⎩⎪⎨⎪⎧ n ＝1，log 2n ＝m 或⎩⎪⎨⎪⎧n ＝m ，log 2n ＝1，∴⎩⎪⎨⎪⎧m ＝0，n ＝1或⎩⎪⎨⎪⎧m ＝2，n ＝2.∴(m －n )2 016＝1或0.答案：1或08．已知集合A ＝{x |y ＝x }，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12＜2x＜4，则(∁R A )∩B ＝________. 解析：因为A ＝{x |y ＝x }＝{x |x ≥0}，所以∁R A ＝{x |x ＜0}．又B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12＜2x＜4＝{x |－1＜x ＜2}，所以(∁R A )∩B ＝{x |－1＜x ＜0}．答案：{x |－1＜x ＜0}9．已知全集U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 的恰有两个元素的子集，且满足下列三个条件：①若a 1∈A ，则a 2∈A ；②若a 3∉A ，则a 2∉A ；③若a 3∈A ，则a 4∉A .则集合A ＝________.(用列举法表示)解析：假设a 1∈A ，则a 2∈A ，则由若a 3∉A ，则a 2∉A 可知，a 3∈A ，与题意不符，∴假设不成立；假设a 4∈A ，则a 3∉A ，则a 2∉A ，且a 1∉A ，与题意不符，∴假设不成立，故集合A ＝{a 2，a 3}(经检验知符合题意)．答案：{a 2，a 3}10．已知全集U 为R ，集合A ＝{x |0＜x ≤2}，B ＝{x |x ＜－3或x ＞1}．求：(1)A ∩B ； (2)(∁U A )∩(∁U B )； (3)∁U (A ∪B )．解：∁U A ＝{x |x ≤0或x ＞2}，∁U B ＝{x |－3≤x ≤1}，A ∪B ＝{x |x ＜－3或x ＞0}． (1)A ∩B ＝{x |1＜x ≤2}．(2)(∁U A )∩(∁U B )＝{x |－3≤x ≤0}． (3)∁U (A ∪B )＝{x |－3≤x ≤0}．11．已知集合A ＝{x |x 2－5x ＋6＝0}，B ＝{a,2,2a －1}． (1)求集合A ；(2)若A ⊆B ，求实数a 的值．解：(1)集合A ＝{x |x 2－5x ＋6＝0}＝{x |(x －2)(x －3)＝0}＝{2,3}．(2)若A ⊆B ，即{2,3}⊆{a,2,2a －1}．所以a ＝3，或2a －1＝3.当a ＝3时，2a －1＝5，B ＝{3,2,5}，满足A ⊆B .当2a －1＝3时，a ＝2，集合B 不满足元素的互异性，故舍去．综上，a ＝3.12．设全集I ＝R ，已知集合M ＝{x |(x ＋3)2≤0}，N ＝{x |x 2＋x －6＝0}． (1)求(∁I M )∩N ；(2)记集合A ＝(∁I M )∩N ，已知集合B ＝{x |a －1≤x ≤5－a ，a ∈R}，若A ∪B ＝A ，求实数a 的取值范围．解：(1)∵M ＝{x |(x ＋3)2≤0}＝{－3}，N ＝{x |x 2＋x －6＝0)＝{－3,2}，∴∁I M ＝{x |x ∈R 且x ≠－3}， ∴(∁I M )∩N ＝{2}． (2)A ＝(∁I M )∩N ＝{2}， ∵A ∪B ＝A ，∴B ⊆A ， ∴B ＝∅或B ＝{2}，当B ＝∅时，a －1＞5－a ，得a ＞3；当B ＝{2}时，⎩⎪⎨⎪⎧a －1＝2，5－a ＝2，解得a ＝3，综上所述，所求a 的取值范围为{a |a ≥3}．。

高中高考数学考前回扣回扣8

回扣8计数原理1.分类加法计数原理完成一件事，可以有n类办法，在第一类办法中有m1种方法，在第二类办法中有m2种方法，……，在第n类办法中有m n种方法，那么完成这件事共有N＝m1＋m2＋…＋m n种方法(也称加法原理).2.分步乘法计数原理完成一件事需要经过n个步骤，缺一不可，做第一步有m1种方法，做第二步有m2种方法，……，做第n步有m n种方法，那么完成这件事共有N ＝m1×m2×…×m n种方法(也称乘法原理)3.排列(1)排列的定义：从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列.(2)排列数的定义：从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数，用A m n表示.(3)排列数公式：A m n＝n(n－1)(n－2)…(n－m＋1).(4)全排列：n个不同元素全部取出的一个排列，叫做n个元素的一个全排列，A n n＝n·(n－1)·(n－2)·…·2·1＝n！.排列数公式写成阶乘的形式为A m n＝n！(n－m)！，这里规定0！＝1.4.组合(1)组合的定义：从n个不同元素中取出m(m≤n)个元素合成一组，叫做从n个不同元素中取出m个元素的一个组合.(2)组合数的定义：从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数，叫做从n个不同元素中取出m个元素的组合数，用C m n表示.(3)组合数的计算公式：C m n＝A m nA m m＝n！m！(n－m)！＝n(n－1)(n－2)…(n－m＋1)m！，由于0！＝1，所以C 0n ＝1.(4)组合数的性质：①C m n ＝C n －m n ；②C m n ＋1＝C m n ＋C m －1n . 5.二项式定理(a ＋b )n ＝C 0n a n ＋C 1n a n －1b 1＋…＋C k n an －k b k ＋…＋C n n b n (n ∈N *).这个公式叫做二项式定理，右边的多项式叫做(a ＋b )n 的二项展开式，其中的系数C k n (k ＝0，1，2，…，n )叫做二项式系数.式中的C k n a n －k b k 叫做二项展开式的通项，用T k ＋1表示，即展开式的第k ＋1项：T k ＋1＝C k n an －k b k . 6.二项展开式形式上的特点(1)项数为n ＋1.(2)各项的次数都等于二项式的幂指数n ，即a 与b 的指数的和为n .(3)字母a 按降幂排列，从第一项开始，次数由n 逐项减1直到零；字母b 按升幂排列，从第一项起，次数由零逐项增1直到n .(4)二项式的系数从C 0n ，C 1n ，一直到C n －1n ，C n n .7.二项式系数的性质(1)对称性：与首末两端“等距离”的两个二项式系数相等，即C m n ＝C n －m n .(2)增减性与最大值：二项式系数C k n ，当k <n ＋12时，二项式系数是递增的；当k >n ＋12时，二项式系数是递减的. 当n 是偶数时，那么其展开式中间一项12+n T 的二项式系数最大.当n 是奇数时，那么其展开式中间两项112-+n T 和112++n T 的二项式系数相等且最大.(3)各二项式系数的和(a ＋b )n 的展开式的各个二项式系数的和等于2n ，即C 0n ＋C 1n ＋C 2n ＋…＋C k n＋…＋C n n ＝2n .二项展开式中，偶数项的二项式系数的和等于奇数项的二项式系数的和，即C1n＋C3n＋C5n＋…＝C0n＋C2n＋C4n＋…＝2n－1.1.关于两个计数原理应用的注意事项(1)分类加法和分步乘法计数原理，都是关于做一件事的不同方法的种数的问题，区别在于：分类加法计数原理针对“分类”问题，其中各种方法相互独立，用其中任何一种方法都可以做完这件事；分步乘法计数原理针对“分步”问题，各个步骤相互依存，只有各个步骤都完成了才算完成这件事.(2)混合问题一般是先分类再分步.(3)分类时标准要明确，做到不重复不遗漏.(4)要恰当画出示意图或树状图，使问题的分析更直观、清楚，便于探索规律.2.对于有附加条件的排列、组合应用题，通常从三个途径考虑：(1)以元素为主考虑，即先满足特殊元素的要求，再考虑其他元素；(2)以位置为主考虑，即先满足特殊位置的要求，再考虑其他位置；(3)先不考虑附加条件，计算出排列数或组合数，再减去不合要求的排列数或组合数.3.排列、组合问题的求解方法与技巧(1)特殊元素优先安排；(2)合理分类与准确分步；(3)排列、组合混合问题先选后排；(4)相邻问题捆绑处理；(5)不相邻问题插空处理；(6)定序问题排除法处理；(7)分排问题直排处理；(8)“小集团”排列问题先整体后局部；(9)构造模型；(10)正难则反，等价条件.4.对于二项式定理应用时要注意：(1)区别“项的系数”与“二项式系数”，审题时要仔细.项的系数与a，b有关，可正可负，二项式系数只与n有关，恒为正. (2)运用通项求展开的一些特殊项，通常都是由题意列方程求出k，再求所需的某项；有时需先求n，计算时要注意n和k的取值范围及它们之间的(3)赋值法求展开式中的系数和或部分系数和，常赋的值为0，±1.(4)在化简求值时，注意二项式定理的逆用，要用整体思想看待a 、b .1.用1，2，3三个数字组成一个四位数，规定这三个数必须全部使用，且同一数字不能相邻出现，这样的四位数有( )A.36个B.18个C.9个D.6个答案 B解析利用树状图考察四个数位上填充数字的情况，如：1⎩⎪⎪⎪⎨⎪⎪⎪⎧ 2⎩⎪⎨⎪⎧ 1⎩⎨⎧ 233⎩⎨⎧ 123⎩⎪⎨⎪⎧ 1⎩⎨⎧ 232⎩⎨⎧ 13，共可确定8个四位数，但其中不符合要求的有2个，所以所确定的四位数应有18个，故选B.2.某学习小组男女生共8人，现从男生中选2人，女生中选1人，分别去做3种不同的工作，共有90种不同的选法，则男，女生人数为( )A.2，6B.3，5C.5，3D.6，2答案 B解析设男生人数为n ，则女生人数为8－n ，由题意可知C 2n C 18－n A 33＝90，即C 2n C 18－n ＝15，解得n ＝3，所以男，女生人数为3，5，故选B.3.将甲，乙等5位同学分别保送到北京大学，清华大学，浙江大学三所大学就读，则每所大学至少保送一人的不同保送方法有( )A.150种B.180种C.240种D.540种解析先将5个人分成三组，(3，1，1)或(1，2，2)，分组方法有C 35＋C 15C 24C 222＝25(种)，再将三组全排列有A 33＝6(种)，故总的方法数有25×6＝150(种).4.从5位男教师和4位女教师中选出3位教师，派到3个班担任班主任(每班1位班主任)，要求这3位班主任中男、女教师都要有，则不同的选派方案共有( )A.210种B.420种C.630种D.840种答案 B解析因为要求3位班主任中男、女教师都要有，所以共有两种情况，1男2女或2男1女.若选出的3位教师是1男2女则共有C 15C 24A 33＝180(种)不同的选派方法，若选出的3位教师是2男1女则共有C 25C 14A 33＝240(种)不同的选派方法，所以共有180＋240＝420(种)不同的方案，故选B.5.若二项式(2x ＋a x )7的展开式中1x 3的系数是84，则实数a 等于( ) A.2 B.54 C.1 D.24答案 C解析二项式(2x ＋a x )7的通项公式为T k ＋1＝C k 7(2x )7－k (a x)k ＝C k 727－k a k x 7－2k ，令7－2k ＝－3，得k ＝5.故展开式中1x3的系数是C 5722a 5＝84，解得a ＝1. 6.(x －1)4－4x (x －1)3＋6x 2(x －1)2－4x 3(x －1)＋x 4等于( )A.－1B.1C.(2x －1)4D.(1－2x )5答案 B解析 (x －1)4－4x (x －1)3＋6x 2(x －1)2－4x 3(x －1)＋x 4＝((x －1)－x )4＝1.7.某班准备从甲、乙等七人中选派四人发言，要求甲乙中两人至少有一人参加，那么不同的发言顺序有( )A.30种B.600种C.720种D.840种答案 C解析 A 47－A 45＝720(种).8.如图，花坛内有5个花池，有5种不同颜色的花卉可供栽种，每个花池内只能种一种颜色的花卉，相邻两池的花色不同，则栽种方案的种数为( )A.180B.240C.360D.420答案 D解析若5个花池栽了5种颜色的花卉，方法有A 55种，若5个花池栽了4种颜色的花卉，则2，4两个花池栽同一种颜色的花，或3，5两个花池栽同一种颜色的花，方法有2A 45种；若5个花池栽了3种颜色的花卉，方法有A 35种，所以最多有A 55＋2A 45＋A 35＝420(种).9.(x ＋1ax)5的各项系数和是1 024，则由曲线y ＝x 2和y ＝x a 围成的封闭图形的面积为______.答案 512解析设x ＝1，则各项系数和为(1＋1a )5＝1 024＝45，所以a ＝13，联立⎩⎪⎨⎪⎧ y ＝x2y ＝x 31可得交点坐标分别为(0，0)，(1，1)，所以曲线y ＝x 2和y ＝x 31围成的封闭图形的面积为⎠⎛01(x 31－x 2)d x ＝⎝ ⎛⎭⎪⎫34x 34－13x 3⎪⎪⎪10＝34－13＝512. 10.圆上有10个点，过每三个点画一个圆内接三角形，则一共可以画的三角形个数为______.答案 120解析圆上任意三点都不共线，因此有三角形C310＝120(个).11.一排共有9个座位，现有3人就坐，若他们每两人都不能相邻，每人左右都有空座，而且至多有两个空座，则不同坐法共有________种.答案36解析可先考虑3人已经就座，共有A33＝6(种)，再考虑剩余的6个空位怎么排放，根据要求可产生把6个空位分为1，1，2，2，放置在由已经坐定的3人产生的4个空中，共有C24＝6，所以不同的坐法共有6×6＝36(种).12.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中，有5架舰载机(甲、乙、丙、丁、戊)准备着舰，如果甲、乙两机必须相邻着舰，而丙、丁不能相邻着舰，那么不同的着舰方法有________种.答案24解析先把甲、乙捆绑在一起有A22种情况，然后对甲、乙整体和戊进行排列，有A22种情况，这样产生了三个空位，插入丙、丁，有A23种情况，所以着舰方法共有A22A22A23＝2×2×6＝24(种).13.实验员进行一项实验，先后要实施5个程序(A，B，C，D，E)，其中程序A只能出现在第一步或最后一步，程序C或D在实施时必须相邻，则实验顺序的编排方法共有______种.答案24解析依题意，当A在第一步时，共有A22A33＝12(种)；当A在最后一步时，共有A22A33＝12(种).所以实验的编排方法共有24种.14.用1，2，3，4，5，6组成数字不重复的六位数，满足1不在左右两端，2，4，6三个偶数中有且只有两个偶数相邻，则这样的六位数的个数为________.答案288解析从2，4，6三个偶数中任意选出2个看作一个“整体”，方法有A23＝6(种)，先排3个奇数，有A33＝6(种)，形成了4个空，将“整体”和另一个偶数插在3个奇数形成的4个空中，方法有A24＝12(种).根据分步乘法计数原理求得此时满足条件的六位数共有6×6×12＝432(种).若1排在两端，1的排法有A12A22＝4(种)，形成了3个空，将“整体”和另一个偶数插在3个奇数形成的3个空中，方法有A23＝6(种)，根据分步乘法计数原理求得此时满足条件的六位数共有6×4×6＝144(种)，故满足1不在左右两端，2，4，6三个偶数中有且只有两个偶数相邻，则这样的六位数的个数为432－144＝288(种)。

高中数学回扣验收特训(二)统计新人教B版必修3(2021学年)

2017-2018学年高中数学回扣验收特训(二）统计新人教B版必修３编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望（201７-2018学年高中数学回扣验收特训(二)统计新人教B版必修3)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为20１7-2018学年高中数学回扣验收特训(二)统计新人教B版必修3的全部内容。

回扣验收特训(二）统计1.某全日制大学共有学生５ 6０0人，其中专科生有１ 3０0人、本科生有3 ０00人、研究生有１３０0人，现采用分层抽样的方法抽取2８0人，调查学生利用因特网查找学习资料的情况,则应在专科生、本科生与研究生这三类学生中分别抽取( )A.65人，150人,65人Ｂ.3０人,150人,100人Ｃ.93人,9４人,93人D.80人，１20人，80人解析:选A 抽样比为28０5 600=错误!，所以专科生应抽取错误!×1300=65（人），本科生应抽取错误!×3 00０＝150（人)，研究生应抽取错误!×1 300=６5(人),故选A。

２．某学校为调查学生的学习情况,对学生的课堂笔记进行了抽样调查,已知某班级一共有56名学生,根据学号(００1～056)，用系统抽样的方法抽取一个容量为4的样本,已知00７号、021号、049号在样本中，那么样本中还有一个学生的学号为（）A．01４ﻩ B.028Ｃ.０3５ﻩ D.０４２解析:选 C 由系统抽样的原理知抽样的间隔为＼ｆ(56，4)=１4,故第一组的学号为001~014,所以０0７为第一组内抽取的学号,所以第二组抽取的学号为021；第三组抽取的学号为035；第四组抽取的学号为049。

高考数学回扣专项练回扣练8.docx

回扣练8 计数原理1.将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有________种.2.若从1,2,3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有________种.3.从1,3,5,7,9这五个数中，每次取出两个不同的数分别记为a ，b ，共可得到lg a －lg b 的不同值的个数是________.4.用0,1，…，9十个数字，可以组成有重复数字的三位数的个数为________.5.使⎝⎛⎭⎫3x ＋1x x n (n ∈N *)的展开式中含有常数项的最小的n ＝________. 6.设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m＋1展开式的二项式系数的最大值为b ，若13a ＝7b ，则m ＝________.7.设函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫x －1x 6，x <0，－x ， x ≥0，则当x >0时，f [f (x )]表达式的展开式中常数项为________.所以f [f (x )]表达式的展开式中常数项为(－1)3C 36＝－20. 8.某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排，其中甲、乙两种必须排在一起，而丙、丁两种不能排在一起，不同的排法共有________种.9.10名同学合影，站成了前排3人，后排7人.现摄影师要从后排7人中抽2人站前排，其他人的相对顺序不变，则不同调整方法的种数为__________.10.若⎝⎛⎭⎪⎫x ＋a 3x 8的展开式中，x 4的系数为7，则实数a ＝________.11.将序号分别为1,2,3,4,5的5张参观券全部分给4人，每人至少1张，如果分给同一人的2张参观券连号，那么不同的分法种数是________.12.从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有________种.(用数字作答)13.若⎝⎛⎭⎫2x －1x n 展开式中各项的二项式系数之和为32，则该展开式中含x 3的项的系数为________.14.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中，有5架舰载机(甲、乙、丙、丁、戊)准备着舰，如果甲、乙两机必须相邻着舰，而丙、丁不能相邻着舰，那么不同的着舰方法有________种.15.实验员进行一项实验，先后要实施5个程序(A ，B ，C ，D ，E )，其中程序A 只能出现在第一步或最后一步，程序C 或D 在实施时必须相邻.则实验顺序的编排方法共有________种.答案精析回扣8 计数原理1.12解析分两步：第一步，选派一名教师到甲地，另一名到乙地，共有C 12＝2(种)选派方法；第二步，选派两名学生到甲地，另外两名到乙地，共有C 24＝6(种)选派方法.由分步计数原理得不同的选派方案共有2×6＝12(种).2.66解析满足题设的取法可分为三类：一是四个奇数相加，其和为偶数，在5个奇数1,3,5,7,9中，任意取4个，有C 45＝5(种)；二是两个奇数加两个偶数其和为偶数，在5个奇数中任取2个，再在4个偶数2,4,6,8中任取2个，有C 25·C 24＝60(种)；三是四个偶数相加，其和为偶数，4个偶数的取法有1种，所以满足条件的取法共有5＋60＋1＝66(种).3.18解析由于lg a －lg b ＝lg a b (a >0，b >0)，从1,3,5,7,9中任取两个作为a b 有A 25＝20种，又13与39相同，31与93相同，∴lg a －lg b 的不同值的个数有A 25－2＝20－2＝18. 4.252解析 0,1,2，…，9共能组成9×10×10＝900(个)三位数，其中无重复数字的三位数有9×9×8＝648(个).∴有重复数字的三位数有900－648＝252(个).5.5解析展开式的通项公式T r ＋1＝C r n (3x )n －r ⎝⎛⎭⎫1x x r ， ∴T r ＋1＝3n －r C r n xn －52r ，r ＝0,1,2，…，n . 令n －52r ＝0，n ＝52r ，故最小正整数n ＝5. 6.6解析 (x ＋y )2m 展开式中二项式系数的最大值为C m 2m ，∴a ＝C m 2m .同理，b ＝C m ＋12m ＋1. ∵13a ＝7b ，∴13·C m 2m ＝7·C m ＋12m ＋1. ∴13·(2m )！m ！m ！＝7·(2m ＋1)！(m ＋1)！m ！.∴m ＝6. 7.－20解析当x >0时，f (x )＝－x <0，所以f [f (x )]＝f (－x )＝⎝⎛⎭⎫1x －x 6， T r ＋1＝C r 6x －12(6－r )·(－x 12)r ＝(－1)r C r 6x －3＋r 2＋r 2，由r －3＝0，得r ＝3.所以f [f (x )]表达式的展开式中常数项为(－1)3C 36＝－20.8.24解析甲、乙排在一起，用捆绑法，丙、丁不排在一起，用插空法，不同的排法共有2A 22·A 23＝24(种).9.420解析从后排抽2人的方法种数是C 27；前排的排列方法种数是A 25.由分步计数原理知不同调整方法种数是C 27A 25＝420.10.12解析T r ＋1＝C r 8x 8－r ⎝ ⎛⎭⎪⎫a 3x r ＝a r C r 8x 8－43r ，由8－43r ＝4得r ＝3，由已知条件a 3C 38＝7，则a 3＝18，a ＝12. 11.96解析将5张参观券分成4堆，有2个联号有4种分法，每种分法再分给4人，各有A 44种分法，∴不同的分法种数共有4A 44＝96.12.60解析分三步：第一步，一等奖有C 16种结果；第二步，二等奖有C 25种结果；第三步，三等奖有C 33种结果，故共有C 16·C 25·C 33＝6×10＝60种可能的结果. 13.－80解析 ∵⎝⎛⎭⎫2x －1x n 展开式中各项的二项式系数之和为32，∴2n ＝32，n ＝5.故展开式的通项公式为T r ＋1＝C r 5·25－r ·x 5－r ·(－1)r ·x －r ＝(－1)r ·25－r ·C r 5·x 5－2r .令5－2r ＝3，解得r ＝1，则该展开式中含x3的项的系数为－16×5＝－80，故答案为－80.14.24解析先把甲、乙捆绑在一起有A22种情况，然后对甲、乙整体和戊进行排列，有A22种情况，这样产生了三个空位，插入丙、丁，有A23种情况，所以着舰方法共有A22A22A23＝2×2×2×3＝24(种).15.24解析依题意，当A在第一步时，共有A22A33＝12(种)；当A在最后一步时，共有A22A33＝12(种).所以实验的编排方法共有24种.。

高考数学回扣专项练4.docx

回扣专项练1．(2015·大连模拟)已知等差数列{a n}的公差d<0，若a4·a6＝24，a2＋a8＝10，则该数列的前n项和S n的最大值为( )A．50 B．40 C．45 D．352．已知等差数列{a n}的前n项和为S n，a1＝－11，a5＋a6＝－4，S n取得最小值时n的值为( ) A．6 B．7 C．8 D．93．已知等比数列{a n}的公比为q，记b n＝a m(n－1)＋1＋a m(n－1)＋2＋…＋a m(n－1)＋m，c n＝a m(n－1)＋1·a m(n－1)＋2·…·a m(n－1)＋m (m，n∈N*)，则以下结论一定正确的是( )A．数列{b n}为等差数列，公差为q mB．数列{b n}为等比数列，公比为q2mC．数列{c n}为等比数列，公比为qm2D．数列{c n}为等比数列，公比为qm m4．(2015·德州模拟)定义数列{x n}：x1＝1，x n＋1＝3x3n＋2x2n＋x n；数列{y n}：y n＝11＋2x n＋3x2n；数列{z n}：z n＝2＋3x n1＋2x n＋3x2n；若{y n}的前n项的积为P，{z n}的前n项的和为Q，那么P＋Q等于( )A．1 B．2 C．3 D．不确定5．数列{a n}满足a1＝2，a n＋1＝2a n＋1，b n＝⎪⎪⎪⎪⎪⎪a n＋2a n－1，n∈N*，则数列{b n}的通项公式b n＝________.6．某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵数是前一天的2倍，则需要的最少天数n(n∈N*)等于________．7．设数列a n＝log(n＋1)(n＋2)，n∈N*，定义使a1·a2·a3·…·a k为整数的实数k为中国梦吉祥数，则在[1，2 016]内的所有中国梦吉祥数之和为________.8．设a1，a2，…，a50是从－1、0、1这三个整数中取值的数列，若a1＋a2＋a3＋…＋a50＝9，且(a 1＋1)2＋(a 2＋1)2＋…＋(a 50＋1)2＝107，则a 1，a 2，…，a 50中是数字0的个数为________．9．对于E ＝{a 1，a 2，...，a 100}的子集X ＝{ai 1，ai 2，...，ai k }，定义X 的“特征数列”为x 1，x 2，...，x 100，其中xi 1＝xi 2＝...＝xi k ＝1.其余项均为0，例如：子集{a 2，a 3}的“特征数列”为0,1,1,0,0， 0(1)子集{a 1，a 3，a 5}的“特征数列”的前三项和等于_________________________；(2)若E 的子集P 的“特征数列”p 1，p 2，…，p 100满足p 1＝1，p i ＋p i ＋1＝1,1≤i ≤99；E 的子集Q 的“特征数列”q 1，q 2，…，q 100满足q 1＝1，q j ＋q j ＋1＋q j ＋2＝1,1≤j ≤98，则P ∩Q 的元素个数为________．10．设数列{a n }的前n 项和为S n,4S n ＝a 2n ＋2a n －3，且a 1，a 2，a 3，a 4，…，a 11成等比数列，当n ≥11时，a n >0.(1)求证：当n ≥11时，{a n }成等差数列；(2)求{a n }的前n 项和S n .11.设各项均为正数的数列{a n }的前n 项和为S n ，满足4S n ＝a 2n ＋1－4n －1，n ∈N *，且a 2，a 5，a 14构成等比数列．(1)证明：a 2＝4a 1＋5；(2)求数列{a n }的通项公式；(3)证明：对一切正整数n ，有1a 1a 2＋1a 2a 3＋…＋1a n a n ＋1<12. 12．(2015·深圳模拟)设各项均为正数的数列{a n }的前n 项和为S n ，且S n 满足S 2n －(n 2＋n －3)S n －3(n 2＋n )＝0，n ∈N *.(1)求a 1的值；(2)求数列{a n }的通项公式；(3)证明：对一切正整数n ，有1a 1(a 1＋1)＋1a 2(a 2＋1)＋…＋1a n (a n ＋1)<13.答案精析回扣专项练41．C [∵a 4＋a 6＝a 2＋a 8＝10，a 4·a 6＝24，d <0，∴⎩⎪⎨⎪⎧ a 4＝6，a 6＝4. ∴d ＝a 6－a 46－4＝－1，∴a n ＝a 4＋(n －4)d ＝10－n .∴当n ＝9或10时S n 取到最大值，S 9＝S 10＝45.]2．A [∵a 5＋a 6＝a 1＋a 10＝－11＋a 10＝－4，∴a 10＝7，∴－11＋9d ＝7，∴d ＝2， ∴a 7＝a 10－3d ＝1>0，a 6＝a 10－4d ＝－1<0，故选A.]3．C [显然，{b n }不可能是等比数列；{c n }是等比数列；证明如下：c n ＝a m (n －1)＋1·a m (n －1)＋2…a m (n －1)＋m ，c n ＋1＝a mn ＋1·a mn ＋2…a mn ＋m ，c n ＋1c n ＝a mn ＋1·a mn ＋2…a mn ＋m a m (n －1)＋1·a m (n －1)＋2…a m (n －1)＋m＝q m q m …q m ＝(q m )m ＝qm 2.]4．A [由题设可得：y n ＝x n x n ＋1，所以P ＝y 1y 2…y n ＝x 1x 2·x 2x 3·x 3x 4…x n x n ＋1＝x 1x n ＋1. z n ＝2＋3x n1＋2x n ＋3x 2n＝y n (2＋3x n ) ＝x n (2＋3x n )x n ＋1＝2x n ＋3x 2n x n ＋1＝2x n ＋3x 2n ＋1－1x n ＋1＝1x n －1x n ＋1. 所以Q ＝⎝ ⎛⎭⎪⎫1x 1－1x 2＋⎝ ⎛⎭⎪⎫1x 2－1x 3＋⎝ ⎛⎭⎪⎫1x 3－1x 4＋…＋⎝ ⎛⎭⎪⎫1x n －1x n ＋1＝1x 1－1x n ＋1. 所以P ＋Q ＝x 1x n ＋1＋1x 1－1x n ＋1＝1x n ＋1＋11－1x n ＋1＝1.故选A. 巧解：取n ＝1，可得P ＋Q ＝1，故选A.]5．2n ＋1解析由条件得b n ＋1＝⎪⎪⎪⎪⎪⎪a n ＋1＋2a n ＋1－1＝⎪⎪⎪⎪⎪⎪2a n ＋1＋22a n ＋1－1＝2⎪⎪⎪⎪⎪⎪a n ＋2a n －1＝2b n ，且b 1＝4，所以数列{b n }是首项为4，公比为2的等比数列，则b n ＝4·2n －1＝2n ＋1.6．6 解析每天植树棵数构成等比数列{a n }，其中a 1＝2，q ＝2.则S n ＝a 1(1－q n )1－q＝2(2n －1)≥100，即2n ＋1≥102.∴n ≥6，∴最少天数n ＝6.7．2 026解析 a 1·a 2·a 3·…·a k ＝log 23·log 34·…·log (k ＋1)(k ＋2)＝log 2(k ＋2)，仅当k ＝2n －2时，上式为中国梦吉祥数．其和：21－2＋22－2＋…＋210－2＝2 026.8．11解析 (a 1＋1)2＋(a 2＋1)2＋…＋(a 50＋1)2＝107，则(a 21＋a 22＋…＋a 250)＋2(a 1＋a 2＋…＋a 50)＋50＝107，∴a 21＋a 22＋…＋a 250＝39，故a 1，a 2，…，a 50中数字0的个数为50－39＝11.9．(1)2 (2)17解析 (1)子集{a 1，a 3，a 5}的“特征数列”中共有3个1，其余均为0，该数列为1,0,1,0,1,0,0，…，0.故该数列前3项的和为2.(2)E 的子集P 的“特征数列”p 1，p 2，…，p 100中，由于p 1＝1，p i ＋p i ＋1＝1(1≤i ≤99)，因此集合P 中必含有元素a 1.又当i ＝1时，p 1＋p 2＝1，且p 1＝1，故p 2＝0.同理可求得p 3＝1，p 4＝0，p 5＝1，p 6＝0，….故E 的子集P 的“特征数列”为1,0,1,0,1,0,1,0，…，1,0，即P ＝{a 1，a 3，a 5，a 7，…，a 99}．E 的子集Q 的“特征数列”q 1，q 2，…，q 100中，由于q 1＝1，q j ＋q j ＋1＋q j ＋2＝1(1≤j ≤98)，因此集合Q 中必含有元素a 1.又当j ＝1时，q 1＋q 2＋q 3＝1，当j ＝2时，q 2＋q 3＋q 4＝1，当j ＝3时，q 3＋q 4＋q 5＝1，…，故q 1＝1，q 2＝q 3＝0，q 4＝1，q 5＝q 6＝0，q 7＝1，….所以E 的子集Q 的“特征数列”为1,0,0,1,0,0,1,0,0，…，0,1，即Q ＝{a 1，a 4，a 7，a 10，…，a 100}．因为100＝1＋(n －1)×3，故n ＝34，所以集合Q 中有34个元素，其下标为奇数的有17个．因此P ∩Q ＝{a 1，a 7，a 13，a 19，…，a 97}，共有17个元素．10．(1)证明由4S n ＝a 2n ＋2a n －3,4S n ＋1＝a 2n ＋1＋2a n ＋1－3，得4a n ＋1＝a 2n ＋1－a 2n ＋2a n ＋1－2a n ，(a n ＋1＋a n )(a n ＋1－a n －2)＝0. 当n ≥11时，a n >0，所以a n ＋1－a n ＝2，所以当n ≥11时，{a n }成等差数列．(2)解由4a 1＝a 21＋2a 1－3，得a 1＝3或a 1＝－1. 又a 1，a 2，a 3，a 4，…，a 11成等比数列，所以a n ＋1＋a n ＝0 (n ≤10)，q ＝－1，而a 11>0，所以a 1>0，从而a 1＝3.所以a n ＝⎩⎪⎨⎪⎧ 3(－1)n －1 (1≤n ≤10)，2n －19 (n ≥11)，所以S n ＝⎩⎪⎨⎪⎧ 32[1－(－1)n ](1≤n ≤10)，n 2－18n ＋80(n ≥11).11．(1)证明当n ＝1时，4a 1＝a 22－5，a 22＝4a 1＋5，因为a n >0，所以a 2＝4a 1＋5.(2)解当n ≥2时，4S n －1＝a 2n －4(n －1)－1,4a n ＝4S n －4S n －1＝a 2n ＋1－a 2n －4，a 2n ＋1＝a 2n ＋4a n ＋4＝(a n ＋2)2，因为a n >0，所以a n ＋1＝a n ＋2，当n ≥2时，{a n }是公差d ＝2的等差数列．因为a 2，a 5，a 14构成等比数列，a 25＝a 2·a 14，(a 2＋6)2＝a 2·(a 2＋24)，解得a 2＝3，由(1)可知，4a 1＝a 22－5＝4，a 1＝1，又因为a 2－a 1＝3－1＝2，则{a n }是首项a 1＝1，公差d ＝2的等差数列．数列{a n }的通项公式为a n ＝2n －1.(3)证明1a 1a 2＋1a 2a 3＋…＋1a n a n ＋1 ＝11·3＋13·5＋15·7＋…＋1(2n －1)(2n ＋1)＝12[⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n －1－12n ＋1]＝12⎝⎛⎭⎪⎫1－12n＋1<12.12．(1)解令n＝1代入得a1＝2(负值舍去)．(2)解由S2n－(n2＋n－3)S n－3(n2＋n)＝0，n∈N*得，[S n－(n2＋n)](S n＋3)＝0.又已知各项均为正数，故S n＝n2＋n.当n≥2时，a n＝S n－S n－1＝n2＋n－(n－1)2－(n－1)＝2n，当n＝1时，a1＝2也满足上式，所以a n＝2n，n∈N*.(3)证明∵4k2＋2k－(3k2＋3k)＝k2－k＝k(k－1)≥0，k∈N*，∴4k2＋2k≥3k2＋3k，∴1a k(a k＋1)＝12k(2k＋1)＝14k2＋2k≤13k2＋3k＝13(1k－1k＋1)．∴1a1(a1＋1)＋1a2(a2＋1)＋…＋1a n(a n＋1)≤13(11－12＋12－13＋…＋1n－1n＋1)＝13(1－1n＋1)<13.。

配套课件技能规范回扣(6)

关
∵当 x>0 时，(x2＋1)f′(x)－2xf(x)<0，
∴g′(x)<0，∴g(x)在(0，＋∞)上为减函数．
由题意得 f(1)＝0，∴g(1)＝0，
∴g(x)>0 的解集为(0,1)．
高效抢分练习
第5讲
由题意知 f(x)为奇函数，∴g(x)也为奇函数，
当 x<0 时，g(x)>0 的解集为(－∞，－1)，
g(x)>g(x0)＝0；任取 x1∈(x*，x0)有 g(x1)>0.
又当 x∈(－∞，x1)时，
高效抢分练习
第5讲
易知 g(x)＝ex＋ax2－(e＋f′(x0))x－f(x0)＋x0f′(x0)<ex1＋ax2 －(e＋f′(x0))x－f(x0)＋x0f′(x0)
＝ax2＋bx＋c，
本其中 b＝－(e＋f′(x0))，c＝ex1－f(x0)＋x0f′(x0)．
第5讲
＝2ex0－x0ex0＋x0e-x0 (x0>0)．
则(2t)′＝2e x0－ex0－x0ex0＋e-x0－x0 e-x0
本＝(1－x0)(e x0＋e-x0)．
课栏
因为 ex0＋e-x0>0，所以当 1－x0>0，即 0<x0<1 时，(2t)′>0,2t
目开
在 x0∈(0,1)上单调递增；
栏
目开
所以 f(x)＝ex (x>0)在 P 点的切线 l 的方程为
关 y－e x0＝ex0(x－x0)．
所以 M(0，e x0－x0ex0)．
过 P 点的 l 的垂线方程为 y－ex0＝－e1x0(x－x0)，
所以
N0，e