三维空间立体绘图基本命令与例子
立体图形怎么画

立体图形怎么画立体图形是由三维空间中的几何体构成的,具有长度、宽度和高度三个方向。
常见的立体图形有立方体、长方体、球体、圆锥体、圆柱体等。
在绘制立体图形时,需要遵循一定的规律和技巧,以获得更加真实、精确和美观的效果。
下面将介绍如何绘制常见的立体图形,并提供相关的绘图技巧和实例。
1.立方体的绘制立方体是一种六面体,每个面都是一个正方形。
在绘制立方体时,需要先画定位线,然后绘制正方形的平面,再将他们合成一个六面体。
(1)先画出一个正方形,作为立方体的底面,在底面四个顶点处描绘四个边向上的垂直线,这些线应高出底面边的长度,相交处即为顶部的四个点。
(2)连接底面和顶部,从每个底面上端平行线向上连接,然后向下连接到相应的垂直线,再连接相邻的线段,即得到了一个完整的立方体。
绘制立方体时需要注意以下几点:(1)定位线和平面的尺寸应该相同,以确保立方体的比例正确。
(2)在制作六个正方形时,要保证它们的边缘互相平行,这有助于提高图形的准确性。
(3)在绘制各个面时,应遵循透视原理,即远离我们的面会缩小,而靠近我们的面会增大。
2.长方体的绘制长方体是一种六面体,由两个平行的长方形作为顶部和底部,以及四个矩形作为侧面组成。
与立方体类似,绘制长方体时也需要先绘制定位线和平面。
(1)确定长方体的长度、宽度和高度,以此在画面上虚构出一个长方体的框架。
(2)在底面四个顶点处描绘四个边向上的垂直线,这些线应高出底面边的长度,相交处即为顶部的四个点。
(3)连接底面和顶部,从每个底面上端平行线向上连接,然后向下连接到相应的垂直线,再连接相邻的线段,即得到了一个完整的长方体。
绘制长方体时需要注意以下几点:(1)与立方体相同,定位线和平面的尺寸应该相同,以确保长方体的比例正确。
(2)在制作顶部和底部的两个长方形时,要确保它们的边缘互相平行,这有助于提高图形的准确性。
(3)在绘制矩形时,应遵循透视原理,以确保各个侧面的比例正确。
3.球体的绘制球体是一种三维圆形体,由无数平行的圆形组成,可以绘制出不同的大小和形状。
matlab三维绘图命令和演示

三维绘图1 三维绘图指令2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2) ●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影:contour(peaks, 20);●plot3可画出三度空间中的曲线:t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线:t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);3 三维绘图的主要功能绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色(一)三维线图plot3 ——基本的三维图形指令调用格式:plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。
CAD三维绘图技巧与实例

CAD三维绘图技巧与实例CAD(计算机辅助设计)是一种常用的三维绘图工具,可以用于制作各种建筑、机械、电子等领域的图纸。
在使用CAD软件时,掌握一些绘图技巧可以提高绘图效率和质量。
本文将介绍几种常用的CAD三维绘图技巧,并通过实例演示其应用方法。
一、坐标系的设置和使用在进行三维绘图时,首先需要设置一个合适的坐标系。
在CAD软件中,坐标系可以通过选择一个参考点和两个相交的轴来定义。
在绘图时,我们可以利用坐标系来确定物体的位置和方向。
例如,我们要在CAD中绘制一个立方体。
首先,我们可以通过命令“UCS”打开坐标系设置对话框,选择一个合适的参考点,然后选择两个相交轴。
接下来,我们可以使用命令“rectangle”绘制一个矩形,在矩形绘制过程中,CAD会根据当前的坐标系设置确定矩形的位置和方向。
最后,我们可以使用命令“extrude”将矩形拉伸成立方体。
二、视图的切换和选择在CAD中,我们可以通过切换不同的视图来查看三维模型的不同部分。
常用的视图包括正视图、侧视图、俯视图等。
在进行绘图时,我们可以通过选择合适的视图来进行绘制和编辑。
例如,我们要在CAD中绘制一个汽车模型。
首先,我们可以通过命令“view”选择一个适合的视图。
在选择了视图后,我们可以使用命令“line”绘制汽车的轮廓线。
在绘制过程中,我们可以通过命令“trim”对不需要的线进行修剪,以获得更加精确的轮廓。
最后,我们可以使用命令“extrude”将轮廓线拉伸成实体,然后再对实体进行细节的编辑和调整。
三、复制和镜像在CAD中,复制和镜像是常用的操作,可以减少绘图的重复性工作。
例如,我们要在CAD中绘制一个花瓶模型。
首先,我们可以通过命令“circle”绘制一个底面的圆。
接下来,我们可以使用命令“copy”复制该圆,然后通过命令“move”将复制的圆上移一段距离,得到花瓶的底座。
然后,我们可以通过命令“mirror”沿一个轴镜像复制的圆,得到花瓶的另一半。
基本XYZ立体绘图命令

M ATLAB程式设计与应用3.基本XYZ立体绘图命令在科学目视表示(Scientific visualization)中,三度空间的立体图是一个非常重要的技巧。
本章将介绍MATLAB基本XYZ三度空间的各项绘图命令。
mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵surf(xx, yy, zz); % 画出立体曲面图为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...- 1/3*exp(-(x+1).^2 - y.^2)我们亦可对peaks函数取点,再以各种不同方法进行绘图。
10 三维立体绘图

语法为:view(〔A,E〕) (举例)
例子: az = 180; el = 90; view(az, el);
2 在绘制网状图时,可以使得原来被 遮盖的网格线显现出来。使用: Hidden off/on 开关命令 3 如需要使用图标自由拖动图形观察, 可以使用: Rotate3d on/off 开关命令 4 如果希望曲面图切去某部分以显示 不同效果,可以使用nan(not a number)代替数值矩阵中某部分的 值。这样就会产生镂空的效果。 举例:control.m
举例:surfl_.m
三、几种特殊图形
1 长条图(Bar Graphs) 特别适用于少量且离散的数据。 命令为:bar( )、bar3( ) (举例)
Bar示例1
x = -2.9:0.2:2.9; bar(x,exp(-x.*x),'r')
Bar示例2
Y = round(rand(5,3)*10); subplot(2,2,1) bar(Y,'group') title 'Group' subplot(2,2,2) bar(Y,'stack') title 'Stack' subplot(2,2,3) barh(Y,'stack') title 'Stack' subplot(2,2,4) bar(Y,1.5) title 'Width = 1.5'
2 扇型图(Pie Chart) 命令为:pie()或 pie3() (举例) 每个扇型面积正比于每个元素对于总 和的比值,若x元素总和小于1,则 matlab将其视作面积百分比值,因而 可以画出不完全扇型图。
pie示例
3D建模操作命令大全

3D建模操作命令大全一、常用命令1. `选择`: 用于选择模型中的对象,可通过单击、拖拽或使用选择框进行选择。
2. `移动`: 将选定的对象在3D空间中进行移动。
3. `旋转`: 对选定的对象进行旋转操作。
4. `缩放`: 对选定的对象进行缩放操作,可放大或缩小对象的尺寸。
5. `复制`: 复制选定的对象,生成相同的副本。
6. `删除`: 删除选定的对象。
7. `撤销`: 撤销上一步操作。
8. `重做`: 恢复撤销的操作。
二、建模命令1. `创建`: 创建基本的几何图形,如立方体、圆柱体和球体。
2. `绘制`: 绘制自定义的几何图形,可以使用直线、曲线、多边形等工具。
3. `编辑`: 对已创建的几何图形进行编辑,如修改形状、调整大小等。
4. `连接`: 连接多个几何图形,形成复杂的模型。
5. `镜像`: 在模型中创建镜像副本,对称于参考轴。
6. `填充`: 为模型内部添加填充,使其看起来更加实体。
7. `修剪`: 修剪几何图形的部分区域,使其符合要求。
三、渲染命令1. `材质`: 为模型添加材质,如纹理、颜色和反射属性。
2. `光源`: 在场景中添加光源,调整光源的位置和亮度。
3. `相机`: 调整相机的位置和视角,以获取所需的渲染效果。
4. `渲染`: 进行3D模型的渲染操作,生成最终的图像或动画。
四、导出命令1. `导出`: 将创建的3D模型导出为其他格式的文件,如OBJ、STL等。
2. `打印`: 将3D模型输出为物理实体,通过3D打印机进行打印。
以上仅为部分常用的3D建模操作命令,具体的命令还会根据不同的建模软件而有所差异。
希望本文档对您在3D建模工作中能有所帮助。
04-三维立体绘图

4-1 基本立体绘图指令
示范4-3 :plotxyz011.m
MATLAB 程序设计入门篇:三维立体绘图
4-1 基本立体绘图指令
示范4-4 :plotxyz01.m 使用 linspace 来生成较密集的资料,以便画出 由函数 形成的立体网状图
x = linspace(-2, 2, 25); y = linspace(-2, 2, 25); [xx, yy] = meshgrid(x, y); zz = xx.*exp(-xx.^2-yy.^2); 25×25 的矩阵 mesh(xx, yy, zz); % 在 x 轴 [-2,2] 之间取 25 点 % 在 y 轴 [-2,2] 之间取 25 点 % xx 和 yy 都是 25×25 的矩阵 % 计算函数值,zz 也是 % 画出立体网状图
MATLAB 程序设计入门篇:三维立体绘图
4-1 基本立体绘图指令
整理:基本三维立体绘图指令的列表
類別 曲線圖 指令 plot3, ezplot3 說明 立體曲線圖
surface
低階函數 line3 contour, ezcontour 等高線 contour3
Surf 用到的低階指令
Plot3 用到的低階指令 平面上的等高線 空間中的等高線
MATLAB 程序设计入门篇:三维立体绘图
4-1 基本立体绘图指令
示范4-7:plotxyz04.m
MATLAB 程序设计入门篇:三维立体绘图
4-1 基本立体绘图指令
meshc: meshc 可同时画出网状图与「等高线」 (Contours) 示范4-8:plotxyz05.m
[x, y, z] = peaks; meshc(x, y, z); axis tight;
matlab三维绘图命令和演示
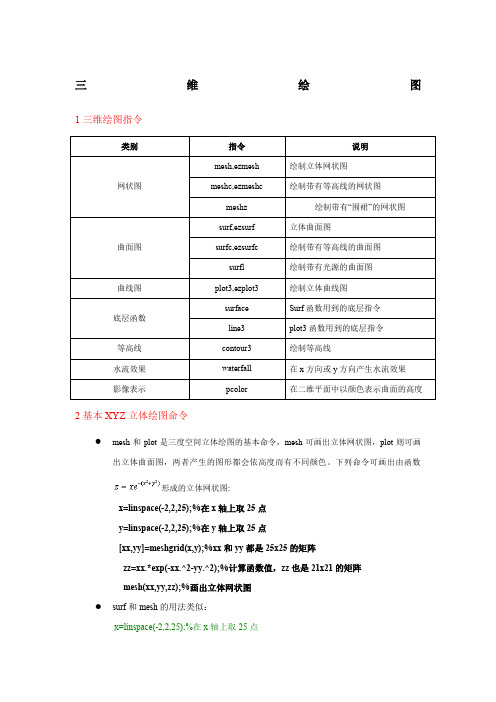
三维绘图1三维绘图指令2基本XYZ 立体绘图命令●mesh 和plot 是三度空间立体绘图的基本命令,mesh 可画出立体网状图,plot 则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2,2,25);%在x 轴上取25点 y=linspace(-2,2,25);%在y 轴上取25点[xx,yy]=meshgrid(x,y);%xx 和yy 都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2);%计算函数值,zz 也是21x21的矩阵 mesh(xx,yy,zz);%画出立体网状图● surf 和mesh 的用法类似:x=linspace(-2,2,25);%在x 轴上取25点y=linspace(-2,2,25);%在y轴上取25点[xx,yy]=meshgrid(x,y);%xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2);%计算函数值,zz也是25x25的矩阵surf(xx,yy,zz);%画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)-10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)-1/3*exp(-(x+1).^2-y.^2)●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks,20);●contour画出曲面等高线在XY平面的投影:contour(peaks,20);●plot3可画出三度空间中的曲线:t=linspace(0,20*pi,501);plot3(t.*sin(t),t.*cos(t),t);亦可同时画出两条三度空间中的曲线:t=linspace(0,10*pi,501);plot3(t.*sin(t),t.*cos(t),t,t.*sin(t),t.*cos(t),-t);3三维绘图的主要功能绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图?绘制三维曲面图、柱面图和球面图?绘制三维多面体并填充颜色(一)三维线图plot3?——?基本的三维图形指令调用格式:plot3(x,y,z)?——?x,y,z是长度相同的向量plot3(X,Y,Z)?——?X,Y,Z是维数相同的矩阵plot3(x,y,z,s)?——?带开关量plot3(x1,y1,z1,’s1’,?x2,y2,z2,’s2’,?…)二维图形的所有基本特性对三维图形全都适用。
matlab三维绘图命令和演示

三维绘图2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2)●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影:contour(peaks, 20);plot3可画出三度空间中的曲线:t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线:t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);三维绘图的主要功能:绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色(一)三维线图plot3 ——基本的三维图形指令调用格式:plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。
AutoCAD三维常用命令

三维建模常用命令一.UCS命令、UCSICON命令用户坐标系(UCS)在三维操作中很有用,当用户在制作3D模型时必须经常在三维空间中旋转UCS到适当的位置,然后根据新的坐标系统来输入点的位置,或是在新的坐标平面上编辑对象,之后再回到世界坐标系。
我们可以设定许多不同的UCS,但只有一个“唯一”的世界坐标。
执行UCSICON命令,选择OR(Origin)把坐标图象移到当前的原点。
二.ZOOM命令在制作3D模型之前可先执行ZOOM命令设定适当的屏幕作图范围。
例如:ZOOM→Center→设定屏幕中心点→设定屏幕视图高度三.VPOINT命令(View/3D Viewpoint/Top… )(View/3D Viewpoint/SW Isometric…)(View/3D Viewpoint/Select… )SW Isometric:西南方向的视图(从左下方观察)SE Isometric:东南方向的视图(从右下方观察)NE Isometric:东北方向的视图(从右上方观察)NW Isometric:西北方向的视图(从左上方观察)用此命令可设定适当的平行投影观测点(角度)。
或者执行VPOINT命令后,系统提示输入视点时直接按回车键,有鼠标动态输入视点。
例如:VPOINT→1,-2,1.5(第四象限上方,即SE)举例1:VPOINT→1,-2,1.5ZOOM→C→0,0→19LINE→-10,0→10,0LINE→0,-10→0,10LINE→0,0,0→0,0,5CIRCLE→0,0→3UCS→X→90 请留意屏幕左下角坐标图象的变化CIRCLE→10,0→3UCS→S→FRONTUCS→Y→90CIRCLE→10,0→3LINETYPE→S→DASHEDLINE→END(点1) →END(点2) →END(点3) →CUCS→S→RIGHTUCS→3→END(点1) →END(点2) →END(点3)UCSICON→ORLINETYPE→S→BYLAYERCIRCLE→0,0→3UCS→V(保持原点不动而以当前屏幕的观察方向来定出新的坐标系统) UCS→O→END(点3)(把坐标原点移到新的位置)CIRCLE→0,0→3UCS→OB→点取最左端的圆(以得到与该图元一致的坐标系统)UCS→R→FRONT(取回原来储存的坐标系统)UCS→WUCSICON→NCHPROP→选取前面画的五个圆→T→1HIDE四.VPORTS命令此命令把作图屏幕分割成数个窗口,在这些窗口中设定不同的观察角度(如平面、正立面、侧立面、等角透视等),如此才能够清楚地掌握整个模型,并且选择适当的窗口来进行编辑。
第十三章三维作图基础知识

第十三章三维作图基础知识一、使用视点(vpoint)观察模型1.命令激活方法:vpoint下拉菜单:视图----三维视图----视点快捷方式:-VP2.功能:确定观察三维对象的视点3.操作方法:-VP回车①指定视点②旋转③显示坐标球和三角架(默认)罗盘是地球的二维表示。
中心点代表北极(0,0,1)内圆弧表示赤道,外圆弧表示南极(0,0,-1)内圆之内:上半球,,内圆与外圆之间:下半球注意:(1).设置的视点的效果为轴测投影图,而不是透视投影图,其投影方向为视点与坐标原点的连线方向。
(2).视点只指明方向,不指定距离(3).视点一旦设定后,直到改变为止。
三维坐标中的特殊视点表视点视图视点视图0,0,1 俯视图-1,-1,0 左前俯视图0,0,-1 仰视图1,1,1 右后俯视图0,-1,0 前视图-1,1,1 左后俯视图0,1,0 后视图1,-1,-1 右前仰视图1,0,0 右视图-1,-1,-1 左前仰视图-1,0,0 左视图1,1,-1 右后仰视图1,-1,1 右前俯视图–1,1,-1 左后仰视图二、快速确定特殊视点1、激活命令的方法:下拉菜单:视图----三维视图---各特殊视点的选项2.功能:快速确定特殊视点3.操作:视图----三维视图三、.三维动态观察器1、激活命令的方法:下拉菜单:视图---三维动态观察器快捷方式:3DO2、功能:在当前视图中动态地,交互地观察模型3、操作:3DO回车轨道的中心称为目标点。
被观察的目标点是固定不动的,而视点可以绕目标点在三维空间转动。
四、用户坐标系(UCS)通过不断的创建新的坐标系,使三维作图变得二维作图一样容易。
在一个图形文件中可以创建无数个UCS,但只有一个是当前坐标系1.命令激活方式下拉菜单:工具---新建UCS工具栏:右击工具栏UCS2.功能:创建用户坐标系3.操作UCS回车:①新建(N)②移动(M)③正交(G)④上一个(P)⑤恢复(R)⑥保存(S)⑦删除(D)⑧应用(A)⑨?⑩世界(W)N回车:①Z轴(ZA)②三点(3)③对象(OB)④面(F)⑤视图(V)X/Y/Z五、3D空间中的高度和厚度高度:某个对象的底部到当前USE的XOY平面的垂直距离。
(整理)AutoCAD三维常用命令.

三维建模常用命令一.UCS命令、UCSICON命令用户坐标系(UCS)在三维操作中很有用,当用户在制作3D模型时必须经常在三维空间中旋转UCS到适当的位置,然后根据新的坐标系统来输入点的位置,或是在新的坐标平面上编辑对象,之后再回到世界坐标系。
我们可以设定许多不同的UCS,但只有一个“唯一”的世界坐标。
执行UCSICON命令,选择OR(Origin)把坐标图象移到当前的原点。
二.ZOOM命令在制作3D模型之前可先执行ZOOM命令设定适当的屏幕作图范围。
例如:ZOOM→Center→设定屏幕中心点→设定屏幕视图高度三.VPOINT命令(View/3D Viewpoint/Top… )(View/3D Viewpoint/SW Isometric…)(View/3D Viewpoint/Select… )SW Isometric:西南方向的视图(从左下方观察)SE Isometric:东南方向的视图(从右下方观察)NE Isometric:东北方向的视图(从右上方观察)NW Isometric:西北方向的视图(从左上方观察)用此命令可设定适当的平行投影观测点(角度)。
或者执行VPOINT命令后,系统提示输入视点时直接按回车键,有鼠标动态输入视点。
例如:VPOINT→1,-2,1.5(第四象限上方,即SE)举例1:VPOINT→1,-2,1.5ZOOM→C→0,0→19LINE→-10,0→10,0LINE→0,-10→0,10LINE→0,0,0→0,0,5CIRCLE→0,0→3UCS→X→90 请留意屏幕左下角坐标图象的变化CIRCLE→10,0→3UCS→S→FRONTUCS→Y→90CIRCLE→10,0→3LINETYPE→S→DASHEDLINE→END(点1) →END(点2) →END(点3) →CUCS→S→RIGHTUCS→3→END(点1) →END(点2) →END(点3)UCSICON→ORLINETYPE→S→BYLAYERCIRCLE→0,0→3UCS→V(保持原点不动而以当前屏幕的观察方向来定出新的坐标系统) UCS→O→END(点3)(把坐标原点移到新的位置)CIRCLE→0,0→3UCS→OB→点取最左端的圆(以得到与该图元一致的坐标系统)UCS→R→FRONT(取回原来储存的坐标系统)UCS→WUCSICON→NCHPROP→选取前面画的五个圆→T→1HIDE四.VPORTS命令此命令把作图屏幕分割成数个窗口,在这些窗口中设定不同的观察角度(如平面、正立面、侧立面、等角透视等),如此才能够清楚地掌握整个模型,并且选择适当的窗口来进行编辑。
matlab三维绘图命令和演示
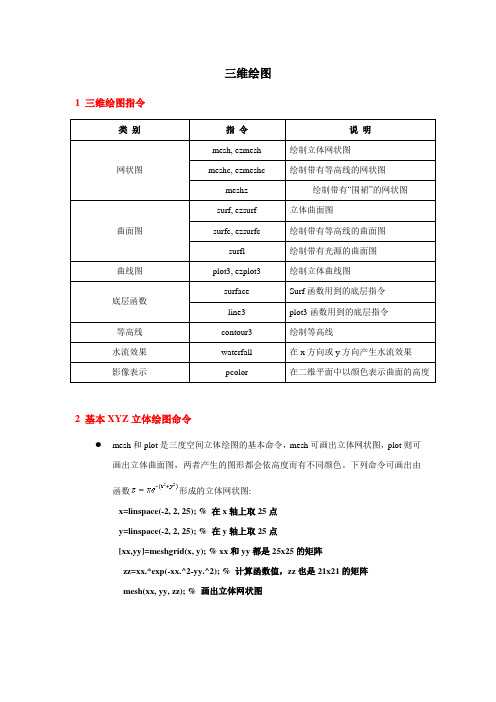
三维绘图1 三维绘图指令2 基本XYZ立体绘图命令mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) -1/3*exp(-(x+1).^2 - y.^2)●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影:contour(peaks, 20);plot3可画出三度空间中的曲线:t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线:t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);3 三维绘图的主要功能绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色(一)三维线图plot3 ——基本的三维图形指令调用格式:plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,‟s1‟,x2,y2,z2,‟s2‟,…)二维图形的所有基本特性对三维图形全都适用。
AutoCAD三维常用命令

三维建模常用命令一.UCS命令、UCSICON命令用户坐标系(UCS)在三维操作中很有用,当用户在制作3D模型时必须经常在三维空间中旋转UCS到适当的位置,然后根据新的坐标系统来输入点的位置,或是在新的坐标平面上编辑对象,之后再回到世界坐标系。
我们可以设定许多不同的UCS,但只有一个“唯一”的世界坐标。
执行UCSICON命令,选择OR(Origin)把坐标图象移到当前的原点。
二.ZOOM命令在制作3D模型之前可先执行ZOOM命令设定适当的屏幕作图范围。
例如:ZOOM→Center→设定屏幕中心点→设定屏幕视图高度三.VPOINT命令(View/3D Viewpoint/Top… )(View/3D Viewpoint/SW Isometric…)(View/3D Viewpoint/Select… )SW Isometric:西南方向的视图(从左下方观察)SE Isometric:东南方向的视图(从右下方观察)NE Isometric:东北方向的视图(从右上方观察)NW Isometric:西北方向的视图(从左上方观察)用此命令可设定适当的平行投影观测点(角度)。
或者执行VPOINT命令后,系统提示输入视点时直接按回车键,有鼠标动态输入视点。
例如:VPOINT→1,-2,1.5(第四象限上方,即SE)举例1:VPOINT→1,-2,1.5ZOOM→C→0,0→19LINE→-10,0→10,0LINE→0,-10→0,10LINE→0,0,0→0,0,5CIRCLE→0,0→3UCS→X→90 请留意屏幕左下角坐标图象的变化CIRCLE→10,0→3UCS→S→FRONTUCS→Y→90CIRCLE→10,0→3LINETYPE→S→DASHEDLINE→END(点1) →END(点2) →END(点3) →CUCS→S→RIGHTUCS→3→END(点1) →END(点2) →END(点3)UCSICON→ORLINETYPE→S→BYLAYERCIRCLE→0,0→3UCS→V(保持原点不动而以当前屏幕的观察方向来定出新的坐标系统) UCS→O→END(点3)(把坐标原点移到新的位置)CIRCLE→0,0→3UCS→OB→点取最左端的圆(以得到与该图元一致的坐标系统)UCS→R→FRONT(取回原来储存的坐标系统)UCS→WUCSICON→NCHPROP→选取前面画的五个圆→T→1HIDE四.VPORTS命令此命令把作图屏幕分割成数个窗口,在这些窗口中设定不同的观察角度(如平面、正立面、侧立面、等角透视等),如此才能够清楚地掌握整个模型,并且选择适当的窗口来进行编辑。
三立体维图绘制

先制作一个圆形“底板” 先按“shit”拖放拿出一 个同心圆,确保是正圆。 或调整同心圆“大小和位 置”,让“高度”和“宽 度”相等即可。
•
•
用“空心弧”画出一段圆环, 调整其“大小和位置”,确保 其“高度”和“宽度”与前面 做出的同心圆相同 把圆环与同心圆对齐,拖动调 整顶点至所需大小
•
• •
• •
如下图,设置圆环的深度—— “厚度”。 如果想再美观一点,可设置 “顶端宽度”,使圆环顶面边 缘出现些许弧度
• •
再下来是个性化每一段圆环了。 选择其中一段圆环,在“形状 填充”里选择颜色和渐变效果。
•
设置与表面颜色相近的线条色
•
设置与表面颜色相近的深度颜 色和轮廓线色
• •
相同地,设置好其它几个圆弧。 现在的图形应该基本可用,如 果想有其它效果,还可调整表 面材料和照明效果,如下图所 产生的金属反光效果。
• •
最后,根据表达的需要,细调 旋转和透视。 随着旋转和透视的变化,圆环 表面的照明效果会发生变化, 有时需返回“三维格式”调整 “照明”
• •
这个饼图也是用类似手法制作。 绿色饼块是利用“厚度”和 “离地高度”调整所得。
如法炮制,根据需要用“空心 弧”画出几段圆环,并细心调 整成所需比例,并与同心圆底 板重合。 开始做同心圆是为了调整方便, 检查每段圆环是否对齐。 调整过程中可按“A可组合成一个 图形。 先前做的同心圆底板可删除。
•
如下图,设置圆环的Y轴旋转和 透视。
三维常用命令

一.拉伸 EXTRUDE(使二维变成三维实体)-ext
1.下拉菜单 DRAW(绘图)-SOLIDS(实体)-EXTRUDE(拉伸) 2.命令 EXTRUDE(EXT)
1)沿着Z轴拉伸
2)PATH按路径拉伸
注意:
1)物体与路径不能共面(针对路径拉伸)
2)物体与路径不能平行(针对路径拉伸)
3)路径不能过于直徒或者形过大(路径不能有曲率过大的地方)
4)形状一定要封闭(面域),路径可以封闭,也可以不封闭
二.创建旋转曲面
1.REVSURF (REVOLVED SURFACE)
菜单:绘图---曲面---旋转曲面
将旋转对象绕轴旋转,生成旋转曲面
第一步:要有形对象和轴对象
第二步:旋转角度
2.在旋转曲面时,旋转出来的物体不够圆滑怎么办?
我们首先要设定旋转方向的分段数SURFTAB1,
SURFTAB2。
三维图形

№2三维图形1. 基本绘图命令三维图形绘制中常用的基本绘图命令有函数plot3、网图函数、及着色图等。
①plot3函数plot3函数是函数plot函数的三维扩展,其调用格式如下:plot3(x,y,z,s) 它与plot函数相比,只是增加了一个维数而已,调用方法一样。
例1:绘制三维螺旋线。
x=0:pi/50:10*pi;y=sin(x);z=cos(x);plot3(x,y,z);例2:绘制参数为矩阵的三维图。
[x,y]=meshgrid(-2:0.1:2,-2:0.1:3);%生成网格点。
z=x.*exp(-x.^2-y.^2);plot3(x,y,z);②网图函数MATLAB语言对于网格的处理方法是:将xy平面按指定方式分隔成平面网格,然后根据程序中给定的方式计算第三维变量的值(即z的值)与对应的xy平面的坐标构成三维点元素,根据由此得到的(x,z)和(y,z)计算各平面的曲线,彼此相连就构成了网格图。
MATLAB 语言提供了一系列的网图函数(如下表所示)。
函数meshgrid成平面网格,该平面网格可以用来绘制三维曲面,具体调用格式如下:[X,Y]=meshgrid(x,y) 这里,x和y为给定的向量,一方面可以用来定义网格划分区域;另一方面也可以用来定义网格划分方法。
矩阵X和Y则是网格划分后的数据矩阵,如例2所示。
函数mesh是用来绘制三维的网图,具体调用格式如下:mesh(X,Y,Z,C)用于绘制四个矩阵变量的彩色网格面图形。
观测点可由函数view定义,坐标轴可由axis函数定义,颜色由C设置,也可由函数colormap实现。
缺省参数C时,C=Z,即网图高度正比于图高。
当X和Y为两个向量时,要求length(X)=n,length(Y)=m,且[m,n]=size(Z)。
这种情况下,网格的顶点为(X(j),Y(i),Z(i,j))的三倍。
注意:X对应于Z的列,而Y对应于Z的行,mesh(Z)和mesh(Z,C)使用x=1:n及y=1:m。
三维绘图的基本操作7

三维绘图的基本操作7。
1 三维线图指令plot3【 * 例 7。
2 三维网线图和曲面图7。
2 网线图、曲面图基本指令格式【 * 例 7。
7.3 三维绘图的基本操作7.3.1 三维线图指令plot3【 * 例 7.3.1 -1 】简单例题。
t=(0:0.02:2)*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z,'b-',x,y,z,'bd'),view([-82,58]),box on,legend(' 链 ',' 宝石 ')图 7.3.1 -1 宝石项链7.3.2 三维网线图和曲面图7.3.2.2 网线图、曲面图基本指令格式【 * 例 7.3.2 .2-1 】用曲面图表现函数。
clf,x=-4:4;y=x;[X,Y]=meshgrid(x,y); % 生成 x-y 坐标“格点”矩阵Z=X.^2+Y.^2; % 计算格点上的函数值surf(X,Y,Z);hold on,colormap(hot)stem3(X,Y,Z,'bo') % 用来表现在格点上计算函数值图 7.3.2 .2-1 曲面图和格点7.3.3 透视、镂空和裁切7.3.3.1 图形的透视【 * 例 7.3.3 .1-1 】透视演示[X0,Y0,Z0]=sphere(30); % 产生单位球面的三维坐标X=2*X0;Y=2*Y0;Z=2*Z0; % 产生半径为 2 的球面的三维坐标clf,surf(X0,Y0,Z0); % 画单位球面shading interp % 采用插补明暗处理hold on,mesh(X,Y,Z),colormap(hot),hold off % 采用 hot 色图hidden off % 产生透视效果axis equal,axis off % 不显示坐标轴图 7.3.3 .1-1 剔透玲珑球7.3.3.2 图形的镂空【 * 例 7.3.3 .2-1 】演示:如何利用“非数” NaN ,对图形进行剪切处理。
第六章 三维空间绘图

2
繪製三維的網格圖
3
利用mesh() 繪製三維的網格圖
4
mesh() 的使用範例
>> xx=[2 3 4;2 3 4;2 3 4;2 3 4] xx = 2 3 4 2 3 4 2 3 4 2 3 4 >> yy=[3 3 3;2 2 2;1 1 1;0 0 0] yy = 3 3 3 2 2 2 1 1 1 0 0 0 >> zz=[8 8 9;8 8 9;7 7 7;7 7 6] zz = 8 8 9 8 8 9 7 7 7 7 7 6
f ( x, y ) 3(1 x) 2 e x
2
( y 1)2
2 2 x 2 2 1 10 x 3 y 5 e x y e ( x 1) y 3 5
12
Peaks的語法
>> peaks; z=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)... -10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)... -1/3*exp(-(x+1).^2-y.^2) >> [xx,yy,zz]=peaks(32); >> surfc(xx,yy,zz);
z ( x y )e
2 2 x2 y2
, 5 x 5, 5 y 5
• 請以實線、紅色、圓形200個資料點繪製下 列函數的圖形。
cos 4t sin 3t [ , , t ], 0 t 6 2t 1 t 1
28
>> peaks(24);
13
空間曲線繪圖
>> t=linspace(0,30,120); >> plot3(t.*sin(t),t.*cos(t),t,'-ro');
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M ATLAB程式设计与应用
3.基本XYZ立体绘图命令
在科学目视表示(Scientific visualization)中,三度空间的立体图是一个非常重要的技巧。
本章将介绍MATLAB基本XYZ三度空间的各项绘图命令。
mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot 则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画
出由函数形成的立体网状图:
x=linspace(-2, 2, 25); % 在x轴上取25点
y=linspace(-2, 2, 25); % 在y轴上取25点
[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵
zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵
mesh(xx, yy, zz); % 画出立体网状图
surf和mesh的用法类似:
x=linspace(-2, 2, 25); % 在x轴上取25点
y=linspace(-2, 2, 25); % 在y轴上取25点
[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵
zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵
surf(xx, yy, zz); % 画出立体曲面图
为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:
要画出此函数的最快方法即是直接键入peaks:
peaks
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2)
我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:
[x,y,z]=peaks;
meshz(x,y,z);
axis([-infinf -infinf -infinf]);
waterfall可在x方向或y方向产生水流效果:
[x,y,z]=peaks;
waterfall(x,y,z);
axis([-infinf -infinf -infinf]);
下列命令产生在y方向的水流效果:[x,y,z]=peaks;
waterfall(x',y',z');
axis([-infinf -infinf -infinf]);
meshc同时画出网状图与等高线:[x,y,z]=peaks;
meshc(x,y,z);
axis([-infinf -infinf -infinf]);
surfc同时画出曲面图与等高线:
[x,y,z]=peaks;
surfc(x,y,z);
axis([-infinf -infinf -infinf]);
contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);
axis([-infinf -infinf -infinf]);
contour画出曲面等高线在XY平面的投影:contour(peaks, 20);
plot3可画出三度空间中的曲线:
t=linspace(0,20*pi, 501);
plot3(t.*sin(t), t.*cos(t), t);
亦可同时画出两条三度空间中的曲线:
t=linspace(0, 10*pi, 501);
plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);
返回。
