六年级奥数题:圆和组合图形(B)[1]
六年级圆和组合图形奥数题

圆和组合图形(1)姓名 一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴部分面积是 平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.6.如右图,阴影部分的面积为2平方厘米,面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.平方厘米. 10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知:AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米). 3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米). 5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). 7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72. 8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘⌒⌒米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米). 13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米). 14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级圆和组合图形奥数题
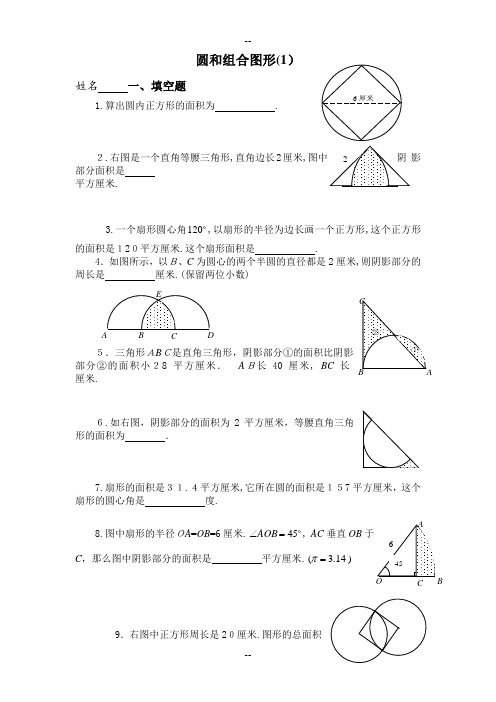
圆和组合图形(1)姓名 一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中影部分面积是 平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形AB C部分②的面积小28平方厘米. A B长40厘米, BC 厘米.6.如右图,阴影部分的面积为2形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),平方厘米.二、解答题11. ABC 是等腰直角三角形. D是半圆周的中点BC 是半圆的直径,已知: AB =B C=10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米). 3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE =BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米). 5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形A BC的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形A BC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72. 8. 5.13.三角形AC O是一个等腰直角三角形,将AO看作底边,A O边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米). 9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形B EDO 的面积再加上圆面积的41. 三角形A ED 的面积是21)210()21010(⨯÷⨯÷+面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米). 13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米). 14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米.故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级圆和组合图形奥数题

圆和组合图形(1)姓名一.填空题1.算出圆内正方形的面积为.2.右图是一个直角等腰三角形,直角边长2厘米,影部分面积是 平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是.4.如图所示,以B .C 为圆心的两个半圆的直径都是2厘米,则暗影部分的周长是厘米.(保留两位小数)ABC 是直角三角形,影部分①的面积比暗影部分②的面积小28平方厘米. A B 长40厘米, BC 长厘米.6.如右图,暗影部分的面积为2平方厘米,的面积为.7.扇形的面积是31.4平方厘米,它地点圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB ,AC 那么图中暗影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),平方厘米.二.解答题11.ABC 是等腰直角三角形. D 点,BC 是半圆的直径,已知:AB =BC =10,那么暗影部分的面积是若干?( 12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(暗影部分的面积)是若干平方厘米?13.如图,已知圆心是O ,半径r =9厘米,21∠=∠那么暗影部分的面积是若干平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个极点,它们的公共点是该正方形的中间.假如每个圆的半径都是1厘米,那么暗影部分的总面积是若干平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形组成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米). 2. 1.14平方厘米.由图示可知,图中暗影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知前提可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE .CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是暗影部分周长为09.312045.1=+⨯(厘米). 5. 32.8厘米.从图中可以看出暗影部分①加上空白部分的面积是半圆的面积,暗影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6.13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中暗影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为⌒⌒1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而暗影部分面积为14.13-9=5.13(平方厘米). 9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中暗影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出帮助线,则暗影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故暗影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 暗影部分面积为55)56(=⨯-(平方厘米). 13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以朋分成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故暗影部分面积为四个圆面积之和与两个空白面积之和的差,即为8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级奥数题-圆及组合图形

六年级奥数题-圆及组合图形(含分析答案解析)(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆和组合图形(后面有答案分析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28 厘米.2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.4510.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.二、解答题11. ABC, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少(圆周率14.3=π)12.如图,半圆S 1的面积是平方厘米,圆S 2的面积是平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O,半径r=9厘米,15=∠,那么阴影部分的面积是多∠1=2少平方厘米?π.3(≈的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.⌒ ⌒半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). 7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. .三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为=(平方厘米).9. .由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为厘米,直径为5厘米.阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级奥数题圆及组合图形(含分析答案解析)
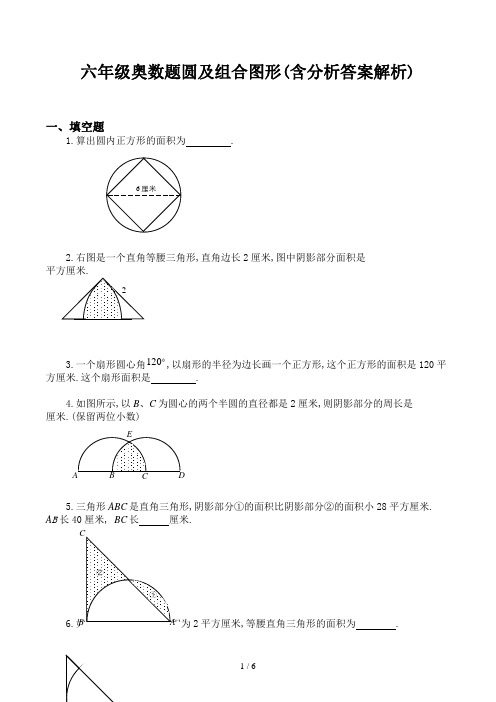
六年级奥数题圆及组合图形(含分析答案解析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米..2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.二、解答题11. ABC , BC 是半圆的直径,已知:AB =BC =10,14.3=π)4512.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米. 半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.⌒ ⌒将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米). 11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米.阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为 221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米.故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级圆和组合图形奥数题

圆和组合图形(1姓名一、填空题1.算出圆内正方形的面积为.2.右图是一个直角等腰三角形,厘米,图中暗影部分面积是平方厘米.120以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是.4.如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则暗影部分的周长是厘米.(保存两位小数)ABC是直角三形,暗影部分①的面积比暗影部分②的面积小28平方厘米. AB40厘米, BC长厘米.6.如右图,暗影部分的面积为2平方厘米,腰直角三角形的面积为.7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.OA=OB=6厘米.45=∠AOB AC垂直OB于C,么图中暗影部分的面积是平方厘米9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),积的和是平方厘米. 二、解答题11.ABC 是等腰直角三角形. D 是半圆周的中点,BC 是半圆的直径,已知:AB =BC =10,那么暗影部分的面积是多少?(12.如图,半圆S1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(暗影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米1521=∠=∠那么暗影部分的面积是多少平方厘米14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中间.如果每个圆的半径都是1厘米,那么暗影部分的总面积是多少平方厘米?———————————————答 案—————————————————————— 1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,平方厘米).2. 平方厘米.由图示可知,图中暗影部分面积为两个圆心角为45平方厘米).3. 平方厘米.平方厘米).4. 厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为60=∠=∠BCEEBC .厘米).因而暗厘米). 5. 厘米.从图中可以看出暗影部分①加上空白部分的面积是半圆的面积,暗影部分②加上空白部分的面积是三角形ABC ①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC厘米). .将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,平方厘米). ⌒ ⌒7.72360728. .三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO厘米),故三角形ACO 的面积为平方厘米).平方厘米),从而暗影部分面积为-(平方厘米). 9. .由正方形周长是20厘米,可得正方形边长也就是圆的半厘米).面积,即平方厘米).10. 90平方厘米.图中暗影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即 (平方厘米).11. 如图作出辅助线,则暗影部分的面积为三角形AED 的面积减去正方形BEDO三角形AED正方形面积是故暗影部分面积为:.12. 由已知半圆S1的面积是平方厘米得半径的平方为平方厘米),故半径为3厘米,直径为6厘米.又因圆S2的面积为方厘米,所以S2半径的平方为平方厘米),因而它的半径为厘米,直径为5厘米.平方厘米).13. 因OA=OB,故三角形OAB为等腰三角形,即∠-=∠AOBOBA,=∠=2150⨯180151=15,⨯-∠BOC360==150=1502∠AOC,因而60扇形面积为平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为平方厘米).正方形内空白部分面积为4方形面积之差,即平方厘米),.故暗影部分面积为四个圆面积之和与两个空白面积之和的差,即为平方厘米).。
六年级圆和组合图形奥数题

圆和组合图形(1)姓名 一、填空题1.算出圆内正方形的面积为 .》2.右图是一个直角等腰三角形,直角边长2厘米,部分面积是 平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.— 6.如右图,阴影部分的面积为2平方厘米,面积为 .7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于那么图中阴影部分的面积是 平方厘米.)14.3(=π/9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积平方厘米. (二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知:AB =BC =10,那么阴影部分的面积是多少(圆周率14.3=π) ~12.如图,半圆S 1的面积是平方厘米,圆S 2的面积是平方厘米.那么长方形(阴影部分的面积)是多少平方厘米 $13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米)14.3(≈π>14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米、————————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米). 3. 平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 厘米.:边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米). 5. 厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有⌒⌒282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ¥ 7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72. 8. .三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为=(平方厘米).9. .由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米. ¥图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米). 14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级奥数圆与组合图形

第一讲:圆与组合图形一、训练目标知识传递:运用整体代换法、旋转、平移、等积变形、及等腰直角三角形的特殊性来解题。
能力强化:分析能力、综合能力、观察能力、操作能力。
思想方法:转化思想、比较思想、恒等思想。
二、知识与方法归纳数量代换法。
有些图形,数量关系比较隐蔽,可以利用题中数量间的关系,相互代换,求出其中一个数量,把未知条件转化成已知条件。
旋转平移变形法。
面积的大小具有恒定性,有时图形的位置或方向不利于解题,可以把某一部分能力旋转平移来使条件之间有关联,从而为解题创造条件。
等积变形法。
在三角形中,如果两个三角形(或平行四边形)等底等高,则这两个三角形(或平行四边形)面积相等。
除去这两个图形的公共部分,则它们剩余部分面积相等。
我们经常要用到这种思想方法。
等腰直角三角形的特殊性。
在等腰直角三角形中,两直角边相等。
斜边上的高等于斜边的一半。
斜边上的高所在的直线恰好是等腰直角三角形的对称轴。
三、经典例题类型5 利用R2代换例1、已知正方形ABCD的对角线AC长为10厘米,求阴影部分的面积。
例2、如图,已知阴影部分的面积为30平方厘米,求圆环的面积。
类型6 利用等腰直角三角形的特殊性求面积例3、如图,已知等腰直角三角形ABC的面积为12平方厘米,求阴影部分的面积。
类型7 利用平移与旋转来求面积例4、如图是个对称图形,求阴影部分的面积。
类型8 利用等积变形求面积例5、如图,已知大正方形边长为10分米,求阴影部分的面积。
类型9 动手操作题例6、如图,一只狗被一根12米长的绳子栓在一建筑物的墙角上,这个建筑是边长为9米的等边三角形,狗不能进入建筑物内活动。
求狗所能活动到的地面部分的面积。
(本题中将狗看作一个可移动的点)三、内化训练1、圆内有一最大的正方形,已知圆的面积是平方厘米,请计算四个弓形的面积之和。
2、如图,已知三角形ABC为等腰直角三角形,BC为圆的直径且 BC=12厘米,求阴影部分的面积。
3、已知正方形的边长为10厘米,求阴影部分的面积。
(完整word版)六年级奥数练习(阴影面积).doc

.六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少2. 右图是一个直角等腰三角形 , 直角边长 2 厘米 , 图中阴影部分面积是多少平方厘米 .23.一个扇形圆心角 120 ,以扇形的半径为边长画一个正方形 , 这个正方形的面积是 120 平方厘米 . 这个扇形面积是多少?4. 右图中三角形是等腰直角三角形, 阴影部分的面积是( 平方厘米 ).5.三角形 ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小 28 平方厘米 . AB长 40 厘米 , BC长厘米 .6.如右图 , 阴影部分的面积为 2 平方厘米 , 等腰直角三角形的面积为.7.扇形的面积是 31.4 平方厘米 , 它所在圆的面积是 157平方厘米 , 这个扇形的圆心角是度.8. 图中扇形的半径OA=OB=6厘米.AOB 45 ,AC垂直 OB于 C,那么图中阴影部分的面积是平方厘米. (3.14 ) 9.右图中正方形周长是 20 厘米 . 图形的总面积是平方厘米 .10.在右图中 ( 单位 : 厘米 ), 两个阴影部分面积的和是平方厘米 .11212.如图 , 半圆S1的面积是 14.13 平方厘米 , 圆S2的面积是19.625 平方厘米 . 那么长方形 ( 阴影部分的面积 ) 是多少平方厘米 ?13. 如图 , 已知圆心是, 半径r =9 厘米, 1215 ,O那么阴影部分的面积是多少平方厘米? ( 3.14 )13、如图 , 求阴影部分的面积.21 2 14、大圆的半径比小圆的半径长 6 厘米 , 且大圆半径是小圆半径的 4 倍. 大圆的面积比小圆的面积大平方厘米 .15、在一个半径是 4.5 厘米的圆中挖去两个直径都是 2 厘米的圆 . 剩下的图形的面积是平方厘米 .( 取 3.14, 结果精确到 1 平方厘米 )16、如图所求 , 圆的周长是16.4 厘米 , 圆的面积与长方形的面积正好相等. 图中阴影部分的周长是厘米.( 3.14).19、已知右图中大正方形边长是 6 厘米 , 中间小17.下图中正方形部分是一个水池,其余部分是草坪,正方形边长是 4 厘米 . 求阴影部分的面积 .已知正方形的面积是 300 平方米,草坪的面积是多少平方米?17、已知 : ABCD是正方形 ,ED=DA=AF=2 厘米 , 阴影部分的面积是.C BGE D A F20. 如图 { 图在下面 } 两个连在一起的轮轴,已知小轮的半径是 3 分米,当这个小轮转 3 圈时,大轮正好转一圈,21.3 只蜜蜂分别沿着阴影部分的边缘飞 1 次,那只蜜蜂飞过的路线最长?( 3 个正方形的边长都为4m)18、如图 : 阴影部分的面积是多少 ?四分之一大圆22的半径为 r .( 计算时圆周率取)23. 将半径分别是 3 厘米和 2 厘米的两个半圆如图放置,求阴影部分的周长24. 求阴影部分的面积.3、下图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各25. 一个圆环外直径是内直径的二分之三倍,圆环面积分成两段,其中长的一段是短的 2倍。
六年级奥数题-圆及组合图形(含分析答案解析)

六年级奥数题-圆及组合图形(含分析答案解析)work Information Technology Company.2020YEAR圆和组合图形(后面有答案分析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).⌒ ⌒5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米. 半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). 7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级奥数题-圆及组合图形(含分析答案解析)

圆和组合图形(后面有答案分析)一、填空题1._______________________________ 算出圆内正方形的面积为2._______________________________________________________________ 右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 __________________3.一个扇形圆心角120。
,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米•这个扇形面积是 _______________ .4•如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是____________ 厘米.(保留两位小数)5.____________________________ 三角形力%是直角三角形,阴影部分①的而积比阴影部分②的面积小28 平方厘米.长40厘米,%长厘米.6.如右图,阴影部分的而积为2平方厘米,等腰直角三角形的面积7.扇形的而积是31.4平方厘米,它所在圆的而积是157平方厘米,这个扇形的圆心角是__________ 度.8.图中扇形的半径OA=O^6厘米.ZAOB = 45°, AC垂直OB亍G那么图中阴影部分的而积是__________ 平方厘米.(” =3・14)A9._______________________________________________ 右图中正方形周长是20厘米.图形的总面积是_____________________________________ 平方厘米.10.___________________________________________________ 在右图中(单位:厘米),两个阴影部分面积的和是 _____________________________ 平方厘米.二、解答题11.力%是等腰直角三角形.Q是半圆周的中点,%是半圆的直径,已知: AABMO,那么阴影部分的面积是多少?(圆周率∕r = 3.14)12.如图,半圆S的面积是14.13平方厘米,圆S的而积是19.625平方厘米. 那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是Q半径尸9厘米,Z1 = Z2 = 15‰那么阴影部分的而积是多少平方厘米?(龙心3・14)14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总而积是多少平方厘米?1.18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成•三角形底为6厘米,高为3厘米,故正方形而积为6×3×1×2 = 18(平 2方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45。
(完整版)六年级奥数图形问题精选
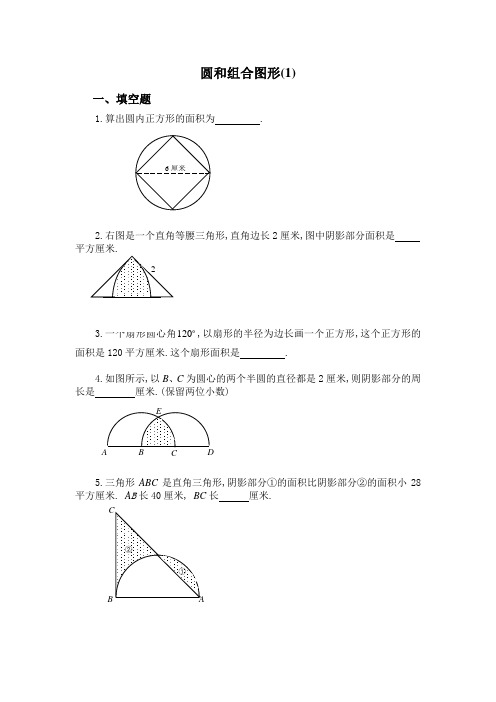
圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28长 厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米.将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米). ⌒⌒7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为:22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米. 又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA , 同理150=∠AOC ,于是602150360=⨯-=∠BOC . 扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解1.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.⌒花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米.如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r,则①的面积为:72227224122r rr r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=Sx ,解得S=6.D14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).面积计算(三)专题简析:对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
(完整)六年级奥数题:圆和组合图形(含分析答案)
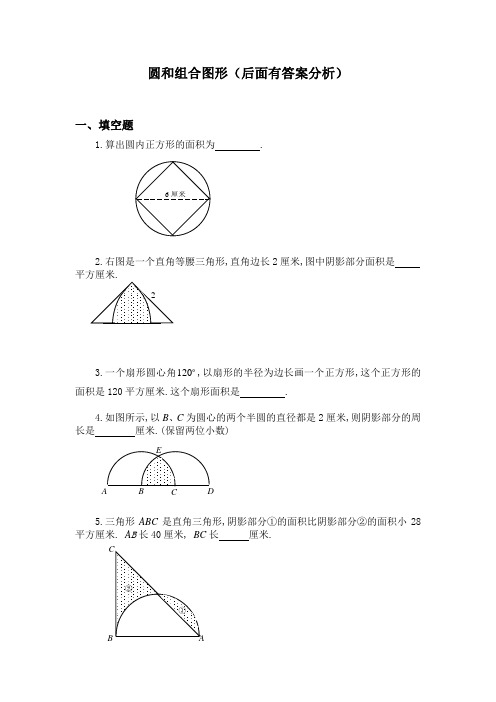
圆和组合图形(后面有答案分析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平⌒ ⌒方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为 221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
六年级奥数题:圆和组合图形(B)[1]
![六年级奥数题:圆和组合图形(B)[1]](https://img.taocdn.com/s3/m/55a3c068ff00bed5b9f31def.png)
陆老师奥数培训讲义圆和组合图形(六年级)例1】.如图,阴影部分的面积是多少?例,且大圆半径是小圆半径的4倍.大圆例】2厘米的圆.剩下的图形1平方厘米) ,阴影部分的面积是 (平方厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π 练习题1.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是多少平方厘米?.2.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是多少平方厘米.?3.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是多少平方厘米?.4.ADB 的面积的311倍,那么,CAB ∠是多少度./? 5.以圆弧为分界线的甲、乙两部分的面积差(大减小例 3,宽为2的长方形面积,为6例2. 大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米). 例3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).例4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).例5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米). 练习题1. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米). 又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠, 又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米). 2. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).3. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米). 4. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60. 5. 0.14.⌒扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为12214.3-÷厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r . 12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为:323204221)24(414)220(4222+=⨯⨯+⨯-⨯-⨯-+⨯πππ二、解答题11.如图:阴影部分的面积是多少四分之一大圆的半径为r .(计算时圆周率取722) 6厘米,中间小正方.求阴影部分的面积. S 的圆放在桌上,桌面被圆2S +2,并且重合的两块是等面a 过两个圆心A 、B , 如果直线a 下9,求圆面积S 的值.14.2厘米的圆板,从平面上1BC 、CD 滚到2的位置,如果AB 、BCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十二、圆和组合图形(2)
一、填空题
1.如图,阴影部分的面积是 .
2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.
3.在一个半径是
4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)
4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).
5.如图所求,圆的周长是1
6.4厘米,圆的面积与
长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π
6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .
7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.
8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .
9.图中,
3
11倍,那么,CAB
∠是 度.
10.厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)
二、解答题 11.如图:
阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取
7
22)
12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.影部分的面积.
13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值. 2
14.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?
练习1
1、 如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2、 如图18-3所示,AE=ED ,DC =1
3 BD ,S △ABC =21平方厘米。
求阴影部分的面积。
3、 如图18-4所示,DE =1
2
AE ,BD =2DC ,S △EBD =5平方厘米。
求三角形ABC 的面积。
练习2
1、 两条对角线把梯形ABCD 分割成四个三角形,(如图18-6所示),已知两个三角形的面积,求另两
个三角形的面积是多少? 2、 已知AO =1
3
OC ,求梯形ABCD 的面积(如图18-7所示)。
3、 已知三角形AOB 的面积为15平方厘米,线段OB 的长度为OD 的3倍。
求梯形ABCD 的面积。
(如
图18-8所示)。
B
D 18-2
C D
C D 18-
4 C 18-6 C
18-7 18-8
答 案 1. 6.
两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.
2. 188.4.
小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大
4.18814.3)28(22=⨯-(平方厘米).
3. 57.
305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).
4. 10.26.
从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即
26.1062
1
)26(14.322=⨯-
÷⨯(平方厘米).
5. 20.5.
设圆的半径为r ,则圆面积即长方形面积为2
r π,故长方形的长为r DC π=.
阴影部分周长r r r r r r AD BA BC DC ππππ24
524
1)(⨯=⨯+-++=+++=
5.204.164
5
=⨯=
(厘米). 6. 6
5
48
(平方厘米). 如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD
的面积为502100=÷(平方厘米).
又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠, 又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为
61
261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为6
5
4861150=-(平方厘米).
7. 19.1416.
花瓣图形的结构是正方形的面积,加上四个4
3
圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是
⌒
1416.191642
1
144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).
8. 2.43平方厘米.
如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即
43.2360
45
214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘
9. 60.
设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有
222
1
311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.
10. 0.14.
扇形面积为14.341214.32
=⨯
⨯(平方厘米),甲部分面积为43.0214.321
22=÷-⨯(平方厘米),乙部分面积为57.04
1
22214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).
11. 如图,小正方形的边长为
2
r
,则①的面积为: 7
222722412
2
r r r r =
⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为2
22
4
17272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,
部分面积为
2
7
2r .
12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于1024262
2
=÷-÷(平方厘米). 13.
设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-
x S ,于是有23
184+-=S x ,解得S=6.
14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:
)420(46
14)220(2212
2-+⨯⨯+⨯-+⨯⨯ππ
07.2283
23
204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).
D。
