2017-2018学年安徽省六安市舒城中学高一下学期第一次统考(开学考试)物理试题PDF版
安徽省六安市舒城中学2017-2018学年高一下学期第一次统考语文试题

【题文】阅读下面的材料,根据自己的感悟和联想,写一篇不少于800字的文章。
了解别人不易,认识自己更难。
所以古希腊德尔菲神庙门楣上镌刻着这样的神谕:“认识你自己!”古希腊哲学家苏格拉底常用这句话来教育弟子。
中国古代哲学家老子亦在《道德经》中告诫人们:“知人者智,自知者明。
”可见认识自己很重要,会使你更明智。
要求:①选好角度,自定立意;②自拟题目;③除诗歌外,不限文体;④文体特征明显。
【答案】认识自己在古希腊巴那斯山如口处的巨石上,镌刻着这样几个大字“认识你自己”,许多古希腊的哲学家认为人类的最高智慧就是认识自己,就像一个人为了爱他人而那个人和他的真正需要一样,人必须认识自己、了解自己,以便理解自己生命的意义、自我的价值和真正的快乐是什么,并认识怎样才能实现这些需要。
走在繁华的大街,看着人们匆匆的走来又匆匆的离去,我不禁要感慨人生的漫长与复杂,人们本来是在同一个起点,为了不同的目标,他们各奔东西。
大部分的人都是在追名逐利,认为名和利就是快乐幸福。
其实,他们并没有真正属于自己的目标,都以社会的价值观作为自己的价值观。
静下心来想一想,难道名利真是我们真心想要的吗?我们的真正目标是什么如果连最基本的东西都没弄清楚而一味沉湎于名利中,仿佛是一艘小船在大海中不断搜寻,当船上载满金钱的时候,夜幕已经降临,其他的船益远去,而自己的那块彼岸仍然很远,旺盛的精力消耗殆尽,唯一能做的就是独守着一堆无用的珍宝,梦想着彼岸的景色。
作为一名学生,我们更应该认识自己,知道自己该做什么,不该做什么。
摆脱浮躁的思绪,让自己独有的优越条件充分发挥。
然而,还是有些青年盲目的跟风,而当曾经风行一时的东西不在流行时,他们才恍然大悟,原来自己的青春早已一去不复返,而自己仍然两手空空。
认真想一下,在你的生命中,最重要、最值得追寻的到底是什么?你有没有坚定的去追寻?人应该找回自己,活出自己想要的生命。
人生就像一出戏,在自己生命的舞台上,我们是制片,是导演,更是主角。
【配套K12】安徽省六安市2017-2018学年高一英语下学期第一次统考(开学考试)试题

舒城中学2017—2018学年度第二学期第一次统考高一英语(时间:120分钟分值:150分)第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What’s the relationship between the two speakers?A. Boss and secretary.B. Husband and wife.C. Teacher and student.2. What is the man doing?A. Asking for permission.B. Asking for help.C. Asking the way.3. What does the man mean?A. The car is too expensive.B. The car is worth its price.C. The car isn’t of good quality.4. Who bought the piano?A. The woman’s father.B. The man’s father.C. The woman.5. What can we learn from the conversation?A. The woman is a close friend of the man.B. The woman is tired of her work.C. The woman is seeing a doctor.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
安徽省六安一中2017-2018学年高一下学期开学数学试卷 Word版含解析
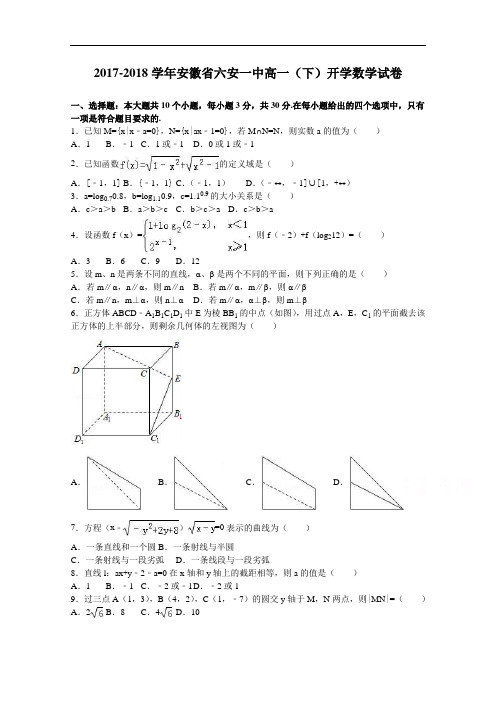
2017-2018学年安徽省六安一中高一(下)开学数学试卷一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知M={x|x﹣a=0},N={x|ax﹣1=0},若M∩N=N,则实数a的值为()A.1 B.﹣1 C.1或﹣1 D.0或1或﹣12.已知函数的定义域是()A.[﹣1,1] B.{﹣1,1} C.(﹣1,1)D.(﹣∞,﹣1]∪[1,+∞)3.a=log0.70.8,b=log1.10.9,c=1.10.9的大小关系是()A.c>a>b B.a>b>c C.b>c>a D.c>b>a4.设函数f(x)=,则f(﹣2)+f(log212)=()A.3 B.6 C.9 D.125.设m、n是两条不同的直线,α、β是两个不同的平面,则下列正确的是()A.若m∥α,n∥α,则m∥n B.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β6.正方体ABCD﹣A1B1C1D1中E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为()A.B.C.D.7.方程(x﹣)=0表示的曲线为()A.一条直线和一个圆 B.一条射线与半圆C.一条射线与一段劣弧D.一条线段与一段劣弧8.直线l:ax+y﹣2﹣a=0在x轴和y轴上的截距相等,则a的值是()A.1 B.﹣1 C.﹣2或﹣1 D.﹣2或19.过三点A(1,3),B(4,2),C(1,﹣7)的圆交y轴于M,N两点,则|MN|=()A.2B.8 C.4D.1010.对于平面直角坐标系内任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“折线距离”:d(A,B)=|x2﹣x1|+|y2﹣y1|.则下列正确的是()①若A(﹣1,3),B(1,0),则;②若A为定点,B为动点,且满足d(A,B)=1,则B点的轨迹是一个圆;③若点C在线段AB上,则d(A,C)+d(C,B)=d(A,B).A.①②B.②C.③D.①②③二、填空题(每题4分,满分16分,将答案填在答题纸上)11.若函数f(x)=xln(x+)为偶函数,则a=.12.设函数f(x)=,则函数的零点个数为个.13.在长方体ABCD﹣A1B1C1D1中,M、N分别是棱BB1、B1C1的中点,若∠CMN=90°,则异面直线AD1与DM所成的角为.14.求函数的最小值为.三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤.)15.已知点A(﹣3,﹣1)和点B(5,5).(Ⅰ)求过点A且与直线AB垂直的直线l的一般式方程;(Ⅱ)求以线段AB为直径的圆C的标准方程.16.已知函数f(x)对一切实数x,y都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.(1)求f(0);(2)求f(x)的解析式;(3)当x∈[0,]时,f(x+3)<2x+a恒成立,求a的范围.17.如图,直三棱柱ABC﹣A′B′C′,∠BAC=90°,,AA′=1,点M,N分别为A′B 和B′C′的中点.(Ⅰ)证明:MN∥平面A′ACC′;(Ⅱ)求三棱锥A′﹣MNC的体积.(椎体体积公式V=Sh,其中S为底面面积,h为高)18.如图,在四棱锥P﹣ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(1)证明BE⊥DC;(2)求二面角E﹣AB﹣P的值;(3)求直线BE与平面PBD所成角的正弦值.19.设直线l1:y=k1x+1,l2:y=k2x﹣1,其中实数k1,k2满足k1k2+1=0.(1)证明:直线l1与l2相交;(2)试用解析几何的方法证明:直线l1与l2的交点到原点距离为定值;(3)设原点到l1与l2的距离分别为d1和d2,求d1+d2的最大值.2015-2016学年安徽省六安一中高一(下)开学数学试卷参考答案与试题解析一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知M={x|x﹣a=0},N={x|ax﹣1=0},若M∩N=N,则实数a的值为()A.1 B.﹣1 C.1或﹣1 D.0或1或﹣1【考点】交集及其运算.【分析】根据题意,M={a},若M∩N=N,则N⊆M,对N是不是空集进行分2种情况讨论,分别求出符合条件的a的值,综合可得答案.【解答】解:根据题意,分析可得,M是x﹣a=0的解集,而x﹣a=0⇒x=a;故M={a},若M∩N=N,则N⊆M,①N=∅,则a=0;②N≠∅,则有N={},必有=a,解可得,a=±1;综合可得,a=0,1,﹣1;故选D.2.已知函数的定义域是()A.[﹣1,1] B.{﹣1,1} C.(﹣1,1)D.(﹣∞,﹣1]∪[1,+∞)【考点】函数的定义域及其求法.【分析】由函数解析式可得,通过解不等式组可得x的范围,即得函数的定义域.【解答】解:∵,∴,∴1≤x2≤1∴x2=1即x=±1∴函数的定义域为:{﹣1,1}故选B3.a=log0.70.8,b=log1.10.9,c=1.10.9的大小关系是()A.c>a>b B.a>b>c C.b>c>a D.c>b>a【考点】指数函数的图象与性质.【分析】由指数函数,对数函数的单调性,确定0<a=log0.70.8<1,b=log1.10.9<0,c=1.10.9>1.【解答】解:0<a=log0.70.8<1,b=log1.10.9<0,c=1.10.9>1.故选A.4.设函数f(x)=,则f(﹣2)+f(log212)=()A.3 B.6 C.9 D.12【考点】函数的值.【分析】先求f(﹣2)=1+log2(2+2)=1+2=3,再由对数恒等式,求得f(log212)=6,进而得到所求和.【解答】解:函数f(x)=,即有f(﹣2)=1+log2(2+2)=1+2=3,f(log212)==12×=6,则有f(﹣2)+f(log212)=3+6=9.故选C.5.设m、n是两条不同的直线,α、β是两个不同的平面,则下列正确的是()A.若m∥α,n∥α,则m∥n B.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β【考点】空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.【分析】用直线与平面平行的性质定理判断A的正误;用直线与平面平行的性质定理判断B 的正误;用线面垂直的判定定理判断C的正误;通过面面垂直的判定定理进行判断D的正误.【解答】解:A、m∥α,n∥α,则m∥n,m与n可能相交也可能异面,所以A不正确;B、m∥α,m∥β,则α∥β,还有α与β可能相交,所以B不正确;C、m∥n,m⊥α,则n⊥α,满足直线与平面垂直的性质定理,故C正确.D、m∥α,α⊥β,则m⊥β,也可能m∥β,也可能m∩β=A,所以D不正确;故选C.6.正方体ABCD﹣A1B1C1D1中E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为()A.B.C.D.【考点】简单空间图形的三视图.【分析】根据剩余几何体的直观图即可得到平面的左视图.【解答】解:过点A,E,C1的平面截去该正方体的上半部分后,剩余部分的直观图如图:则该几何体的左视图为C.故选:C.7.方程(x﹣)=0表示的曲线为()A.一条直线和一个圆 B.一条射线与半圆C.一条射线与一段劣弧D.一条线段与一段劣弧【考点】曲线与方程.【分析】根据(x﹣)=0,可得x=或=0,从而可得结论.【解答】解:∵(x﹣)=0,∴x=或=0(﹣2≤y≤4),∴x2+(y﹣1)2=9(x≥0)或x=y(﹣2≤y≤4).故选D.8.直线l:ax+y﹣2﹣a=0在x轴和y轴上的截距相等,则a的值是()A.1 B.﹣1 C.﹣2或﹣1 D.﹣2或1【考点】直线的截距式方程.【分析】先求出直线在两个坐标轴上的截距,由在两个坐标轴上的截距相等解方程求得a的值.【解答】解:由直线的方程:ax+y﹣2﹣a=0得,此直线在x轴和y轴上的截距分别为和2+a,由=2+a,得a=1 或a=﹣2,故选D.9.过三点A(1,3),B(4,2),C(1,﹣7)的圆交y轴于M,N两点,则|MN|=()A.2B.8 C.4D.10【考点】两点间的距离公式.【分析】设圆的方程为x2+y2+Dx+Ey+F=0,代入点的坐标,求出D,E,F,令x=0,即可得出结论.【解答】解:设圆的方程为x2+y2+Dx+Ey+F=0,则,∴D=﹣2,E=4,F=﹣20,∴x2+y2﹣2x+4y﹣20=0,令x=0,可得y2+4y﹣20=0,∴y=﹣2±2,∴|MN|=4.故选:C.10.对于平面直角坐标系内任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“折线距离”:d(A,B)=|x2﹣x1|+|y2﹣y1|.则下列正确的是()①若A(﹣1,3),B(1,0),则;②若A为定点,B为动点,且满足d(A,B)=1,则B点的轨迹是一个圆;③若点C在线段AB上,则d(A,C)+d(C,B)=d(A,B).A.①②B.②C.③D.①②③【考点】的真假判断与应用.【分析】利用“折线距离”:d(A,B)=|x2﹣x1|+|y2﹣y1|,逐一判断①②③即可得到答案.【解答】解:①∵A(﹣1,3),B(1,0),则d(A,B)=|1﹣(﹣1)|+|0﹣3|=2+5=5,故①错误;②不妨令点A为坐标原点,B(x,y),则d(A,B)=|x|+|y|=1,B点的轨迹是一个正方形,而不是圆,故②错误;③设直角坐标平面内的任意两点A(x1,y1),B(x2,y2),设C点坐标为(x0,y0),∵点C在线段AB上,∴x0在x1、x2之间,y0在y1、y2之间,不妨令x1<x0<x2,y1<y0<y2,则d(A,C)+d(C,B)=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|=x0﹣x1+y0﹣y1+x2﹣x0+y2﹣y0=x2﹣x1+y2﹣y1=|x2﹣x1|+|y2﹣y1|=d(A,B)成立,故③正确.∴正确的是③.故选:C.二、填空题(每题4分,满分16分,将答案填在答题纸上)11.若函数f(x)=xln(x+)为偶函数,则a=1.【考点】函数奇偶性的性质.【分析】由题意可得,f(﹣x)=f(x),代入根据对数的运算性质即可求解.【解答】解:∵f(x)=xln(x+)为偶函数,∴f(﹣x)=f(x),∴(﹣x)ln(﹣x+)=xln(x+),∴﹣ln(﹣x+)=ln(x+),∴ln(﹣x+)+ln(x+)=0,∴ln(+x)(﹣x)=0,∴lna=0,∴a=1.故答案为:1.12.设函数f(x)=,则函数的零点个数为3个.【考点】函数零点的判定定理.【分析】问题等价于函数y=f(x)与函数y=﹣图象的公共点个数,作出函数的图象可得.【解答】解:函数的零点个数等价于函数y=f(x)与函数y=﹣图象的公共点个数,作出它们的图象可得公共点个数为3,故答案为:313.在长方体ABCD﹣A1B1C1D1中,M、N分别是棱BB1、B1C1的中点,若∠CMN=90°,则异面直线AD1与DM所成的角为90°.【考点】异面直线及其所成的角.【分析】先连BC1,则BC1∥AD1,则异面直线AD1与DM所成的角转化为直线BC1与DM 所成的角.结合M、N分别是棱BB1、B1C1的中点及三垂线定理得出直线BC1与DM所成的角90°,从而求得异面直线AD1与DM所成的角.【解答】解:连BC1,则BC1∥AD1则异面直线AD1与DM所成的角为直线BC1与DM所成的角.∵M、N分别是棱BB1、B1C1的中点∴BC1∥MN,∵∠CMN=90°,∴直线BC1⊥MC,又MC是斜线DM在平面BCC1B1上的射影,∴DM⊥BC1,直线BC1与DM所成的角90°,则异面直线AD1与DM所成的角为90°.故答案为:90°.14.求函数的最小值为5.【考点】函数的最值及其几何意义.【分析】根据其几何意义即可求出答案.【解答】解:函数=+=+表示x轴上动点P(x,0)到A(4,1)和B(0,﹣2)的距离和,当P为AB与x轴的交点时,函数取最小值|AB|==5,故答案为:5三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤.)15.已知点A(﹣3,﹣1)和点B(5,5).(Ⅰ)求过点A且与直线AB垂直的直线l的一般式方程;(Ⅱ)求以线段AB为直径的圆C的标准方程.【考点】圆的标准方程.【分析】(Ⅰ)求出过点A且与直线AB垂直的直线l的斜率,根据点斜式得直线l的方程,整理得直线l的一般式方程;(Ⅱ)确定圆心坐标与半径,即可求以线段AB为直径的圆C的标准方程.【解答】解:(Ⅰ)由条件知,则根据点斜式得直线l的方程为,整理得直线l的一般式方程为4x+3y+15=0.…(Ⅱ)由题意得C(1,2),故以线段AB为直径的圆C的标准方程为(x﹣1)2+(y﹣2)2=25.…16.已知函数f(x)对一切实数x,y都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.(1)求f(0);(2)求f(x)的解析式;(3)当x∈[0,]时,f(x+3)<2x+a恒成立,求a的范围.【考点】抽象函数及其应用.【分析】(1)令x=1,y=0得f(0)的方程,解方程即可得出;(2)y=0,可得f(x)的方程,即可解出f(x)的解析式;(3)f(x+3)<2x+a可化为a>x2+5x在x∈[0,]恒成立,转化为a>(x2+5x)max,求最值即可.【解答】解:(1)令x=1,y=0得f(1+0)﹣f(0)=2,又f(1)=0,可得f(0)=﹣2,(2)令y=0,可得f (x )﹣f (0)=x (x +1), 所以f (x )=x 2+x ﹣2,(3)x ∈[0,]时,f (x +3)<2x +a 恒成立,即x ∈[0,]时,a >x 2+5x +10恒成立. ∴a >(x 2+5x +10)max ,因为x 2+5x +10在[0,]单调增,所以最大值为.所以a 的范围是a >.17.如图,直三棱柱ABC ﹣A ′B ′C ′,∠BAC=90°,,AA ′=1,点M ,N 分别为A ′B和B ′C ′的中点.(Ⅰ)证明:MN ∥平面A ′ACC ′; (Ⅱ)求三棱锥A ′﹣MNC 的体积.(椎体体积公式V=Sh ,其中S 为底面面积,h 为高)【考点】直线与平面平行的判定;棱柱的结构特征;棱柱、棱锥、棱台的体积. 【分析】(Ⅰ)证法一,连接AB ′,AC ′,通过证明MN ∥AC ′证明MN ∥平面A ′ACC ′.证法二,通过证出MP ∥AA ′,PN ∥A ′C ′.证出MP ∥平面A ′ACC ′,PN ∥平面A ′ACC ′,即能证明平面MPN ∥平面A ′ACC ′后证明MN ∥平面A ′ACC ′.(Ⅱ)解法一,连接BN ,则V A ′﹣MNC =V N ﹣A ′MC =V N ﹣A ′BC =V A ′﹣NBC =.解法二,V A ′﹣MNC =V A ′﹣NBC ﹣V M ﹣NBC =V A ′﹣NBC =.【解答】(Ⅰ)(证法一)连接AB ′,AC ′,由已知∠BAC=90°,AB=AC ,三棱柱ABC ﹣A ′B ′C ′为直三棱柱,所以M 为AB ′的中点,又因为N 为B ′C ′中点,所以MN ∥AC ′,又MN ⊄平面A ′ACC ′,AC ′⊂平面A ′ACC ′,所以MN ∥平面A ′ACC ′; (证法二)取A ′B ′中点,连接MP ,NP .而M ,N 分别为AB ′,B ′C ′中点,所以MP ∥AA ′,PN ∥A ′C ′.所以MP ∥平面A ′ACC ′,PN ∥平面A ′ACC ′;又MP ∩PN=P ,所以平面MPN ∥平面A ′ACC ′,而MN ⊂平面MPN ,所以MN ∥平面A ′ACC ′; (Ⅱ)(解法一)连接BN ,由题意A ′N ⊥B ′C ′,平面A ′B ′C ′∩平面B ′BCC ′=B ′C ′,所以A ′N ⊥平面NBC ,又A ′N=B ′C ′=1,故V A ′﹣MNC =V N ﹣A ′MC =V N ﹣A ′BC =V A ′﹣NBC =. (解法二)V A ′﹣MNC =V A ′﹣NBC ﹣V M ﹣NBC =V A ′﹣NBC =.18.如图,在四棱锥P ﹣ABCD 中,PA ⊥ABCD ,AD ⊥AB ,AB ∥DC ,AD=DC=AP=2,AB=1,点E 为棱PC 的中点. (1)证明BE ⊥DC ;(2)求二面角E ﹣AB ﹣P 的值;(3)求直线BE 与平面PBD 所成角的正弦值.【考点】直线与平面所成的角;空间中直线与直线之间的位置关系;二面角的平面角及求法.【分析】(1)如图所示,建立空间直角坐标系,只要证明=0,即可得出⊥.(2)设平面ABE 的法向量为=(x ,y ,z ),利用,可得取,取平面PAB 的法向量为=(1,0,0),设二面角E ﹣AB ﹣P 的平面角为θ,利用cos =即可得出.(3)=(﹣2,﹣1,0),=(0,﹣1,2),设平面PBD 的法向量为=(x ,y ,z ),利用,即可得出,设直线BE 与平面PBD 所成角的为α,利用sin α=|cos |=即可得出.【解答】(1)证明:如图所示,建立空间直角坐标系, A (0,0,0),B (0,1,0),P (0,0,2),C (﹣2,2,0),D (﹣2,0,0),E (﹣1,1,1),∴=(﹣1,0,1),=(0,2,0),∴=0,∴⊥, ∴BE ⊥DC .(2)解: =(0,1,0),设平面ABE 的法向量为=(x ,y ,z ),则,即,取=(1,0,1),取平面PAB 的法向量为=(1,0,0), 设二面角E ﹣AB ﹣P 的平面角为θ,cos===,由图可知:二面角E ﹣AB ﹣P 的平面角θ为锐角, ∴.(3)解:=(﹣2,﹣1,0),=(0,﹣1,2),设平面PBD 的法向量为=(x ,y ,z ),则,化为,取=(1,﹣2,﹣1),设直线BE 与平面PBD 所成角的为α,则sin α=|cos|===.19.设直线l1:y=k1x+1,l2:y=k2x﹣1,其中实数k1,k2满足k1k2+1=0.(1)证明:直线l1与l2相交;(2)试用解析几何的方法证明:直线l1与l2的交点到原点距离为定值;(3)设原点到l1与l2的距离分别为d1和d2,求d1+d2的最大值.【考点】过两条直线交点的直线系方程.【分析】(1)假设l1与l2平行,有k1=k2,代入k1k2+1=0,得k12+1=0,这与k1为实数的事实相矛盾,故l1与l2相交.(2)由(1)知k1≠k2,联立方程组求得交点坐标,然后由两点间的距离公式求得直线l1与l2的交点到原点距离为定值;(3)利用点到直线的距离和不等式的性质进行解答.【解答】证明:(1)反证法:假设l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+1=0,得k12+1=0,这与k1为实数的事实相矛盾,∴k1≠k2,故l1与l2相交.(2)由(1)知k1≠k2,由方程组解得交点P的坐标(x,y)为,而x2+y2=+===1.即l1与l2的交点到原点距离为1.解:(3)d1+d2=+=+=+====,当|k1|=1即k1=±1时,d1+d2的最大值是.2016年11月2日。
安徽省六安市舒城中学高一下学期第一次统考(开学考试)

舒城中学2017—2018学年度第二学期第一次统考高一英语命题:审题:(时间:120分钟分值:150分)第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What’s the relationship between the two speaker s?A. Boss and secretary.B. Husband and wife.C. Teacher and student.2. What is the man doing?A. Asking for permission.B. Asking for help.C. Asking the way.3. What does the man mean?A. The car is too expensive.B. The car is worth its price.C. The car isn’t of good quality.4. Who bought the piano?A. The woman’s father.B. The man’s father.C. The woman.5. What can we learn from the conversation?A. The woman is a close friend of the man.B. The woman is tired of her work.C. The woman is seeing a doctor.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
高一英语下学期第一次统考(开学考试)试题

舒城中学2017—2018学年度第二学期第一次统考高一英语(时间:120分钟分值:150分)第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What’s the relationship between the two speakers?A. Boss and secretary.B. Husband and wife.C. Teacher and student.2. What is the man doing?A. Asking for permission.B. Asking for help.C. Asking the way.3. What does the man mean?A. The car is too expensive.B. The car is worth its price.C. The car isn’t of good quality.4. Who bought the piano?A. The woman’s father.B. The man’s father.C. The woman.5. What can we learn from the conversation?A. The woman is a close friend of the man.B. The woman is tired of her work.C. The woman is seeing a doctor.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
安徽省六安市舒城中学2017-2018学年高一下学期历史第一次统考(开学考试)试卷(解析版)

安徽省六安市舒城中学2017-2018学年高一下学期历史第一次统考(开学考试)试卷一、单选题1.王国维《殷周制度论》载:“立子以贵不以长,立嫡以长不以贤者,乃传子法之精髓,由传子之制而嫡庶之制生焉。
夫舍弟而传子者,所以息争也。
”材料表明宗法制()A. 注重任人唯贤,维护贵族政治B. 约束兄弟子女,追求政治平等C. 维护等级关系,强化封建专制D. 强调尊卑有序,稳定社会秩序【答案】D【考点】商周时期的政治制度【解析】【分析】本题主要考查宗法制的知识,旨在考查学生运用所学知识解决问题的能力。
宗法制强调贵贱有序,稳定统治秩序,这与“立子以贵不以长,立嫡以长不以贤者”相符,故D项正确。
AB不符合材料的信息,排除;C和封建专制时间不符,排除C。
故答案为D【点评】本题考查阅读材料分析材料的能力,由材料“立子以贵不以长,立嫡以长不以贤者,乃传子法之精髓,”结合所学即可得出结论难度适中。
2.《左传·昭公二十六年》载:“昔武王克殷,成王靖四方,康王息民,并建母弟,以藩屏周”。
材料描述的是()A. 禅让制B. 世袭制C. 宗法制D. 分封制【答案】D【考点】商周时期的政治制度【解析】【分析】D由材料“昔武王克殷,成王靖四方,康王息民,并建母弟,以藩屏周”,反映的是西周时期的分封制;A是我国古代原始社会后期民主推选部落或部落联盟首领的制度,排除;C材料没有世界按血缘等级分配政治权力,排除C;B材料的主旨不是王位在一家一姓中传承,排除B。
故答案为D。
【点评】本题考查学生阅读材料分析问题的能力,昔武王克殷,以藩屏周是关键信息。
3.到了秦.汉统一,由封建转为郡县,古人称“化家为国”,一切贵族家庭都倒下了,只有一个家却变成了国家。
这里“化家为国”指的是()A.分封制的瓦解B.郡县制的实行C.封建制度的确立D.郡国并行制的实施【答案】B【考点】秦中央集权制度的形成【解析】【分析】材料中说秦汉统一之后出现了“化家为国”的现象,也就是原有的家族体系转换为统一的国家体系,这是典型的分封制度向郡县制的转化,所以强调的是郡县制的实行,本题选择B选项。
安徽省六安市舒城中学2017-2018学年高一下学期第一次

舒城中学2017—2018学年度第二学期第一次统考高一文数(时间120分钟,满分150分)命题: 审题:一、选择题(本题共12小题,每小题5分,共60分) 1.函数f (x )+lg (2-x-1)的定义域为( )A .(-5,+∞)B .[-5,+∞)C .(-5,0)D .(-2,0)2.已知O 、A 、B 是平面上的三个点,直线AB 上有一点C ,满足2AC +CB =0,则OC 等于( )A .2OA -OB B .-OA +2OB C.23OA -13OB D .-13OA +23OB 3.已知OA =(2,3),OB =(-3,y ),且OA ⊥OB ,则y 等于( ) A .2 B .-2 C.12D .-124.若e 1,e 2是平面内夹角为60°的两个单位向量,则向量a =2e 1+e 2与b =-3e 1+2e 2的夹角为( )A .30°B .60°C .90°D .120°5.函数f (x )=cos 2x +6cos 2x π⎛⎫- ⎪⎝⎭的最大值为( ) A .4 B .5 C .6D .76.如图,在△ABC 中,AD ⊥AB ,BC BD ,|AD |=1,则AC ·AD =( )A .B .7.已知p >q >1,0<a <1,则下列各式中正确的是( ) A .a p >a q B .p a <q a C .a -p >a -qD .p -a >q -a8.已知函数y =f (x )是定义在R 上的偶函数,当x ≤0时,y =f (x )是减函数,若|x 1|<|x 2|,则( )A .f (x 1)-f (x 2)<0B .f (x 1)-f (x 2)>0C .f (x 1)+f (x 2)<0D .f (x 1)+f (x 2)>09.已知向量OA =(2,2),OB =(4,1),在x 轴上有一点P ,使AP ·BP 有最小值,则点P 的坐标是( )A .(-3,0)B .(2,0)C .(3,0)D .(4,0)10.如图,函数f (x )的图象为折线ACB ,则不等式f (x )≥log 2(x +1)的解集是()A .{x |-1<x ≤0}B .{x |-1≤x ≤1}C .{x |-1<x ≤1}D .{x |-1<x ≤2}11.如图是函数f (x )=A ·cos(2π3x +φ)-1(A >0,|φ|<π2)的图象的一部分,则f (2 017)=()A .0B .2D .112..对于函数f (x ),若∀a ,b ,c ∈R ,f (a ),f (b ),f (c )为某一三角形的三边长,则称f (x )为“可构造三角形函数”,已知函数f (x )=是“可构造三角形函数”,则实数t 的取值范围是( )A .[0,+∞)B .[0,1]C .[1,2]D .二、填空题(本大题共4小题,每小题5分,共20分) 13.函数yx 的值域为________.14.要得到函数y =13sin(2x +π8)的图象,只需将函数y =13sin 2x 的图象________个单位. 15.如图,在矩形ABCD 中,AB,BC =2,点E 为BC 的中点,点F 在边CD 上,若AB ·AF,则AE ·BF 的值是________.16.已知函数f (x )=221,03,0ax x x ax x ⎧++≤⎨->⎩有3个零点,则实数a 的取值范围是________.三、解答题(本大题共6小题,解答时应写出文字说明、证明过程或演算步骤) 17.已知全集为实数集R ,集合A ={x |y},B ={x |log 2x >1}.(1)求A ∩B ,(∁R B )∪A ;(2)已知集合C ={x |1<x <a },若C ⊆A ,求实数a 的取值范围.18.设函数f (x )的定义域为(-3,3),满足f (-x )=-f (x ),且对任意x ,y ,都有f (x )-f (y )=f (x -y ),当x <0时,f (x )>0,f (1)=-2.(1)求f (2)的值;(2)判断f (x )的单调性,并证明;(3)若函数g (x )=f (x -1)+f (3-2x ),求不等式g (x )≤0的解集.19.(1)已知a =4,b =3,(2a -3b )·(2a +b )=61,求a 与b 的夹角;(2)设OA =(2,5),OB =(3,1),OC =(6,3),在OC 上是否存在点M ,使MA ⊥MB ?若存在,求出点M 的坐标;若不存在,请说明理由.20.函数f (x )=cos(πx +φ) (0<φ<π2)的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f 13x ⎛⎫+ ⎪⎝⎭,求函数g (x )在区间11,23⎡⎤-⎢⎥⎣⎦上的最大值和最小值.21.对于函数f (x )=a -2b x +1(a ∈R ,b >0,且b ≠1).(1)探索函数y =f (x )的单调性;(2)求实数a 的值,使函数y =f (x )为奇函数;(3)在(2)的条件下,令b =2,求使f (x )=m (x ∈[0,1])有解的实数m 的取值范围.舒城中学2017-2018学年高一第二学期入学考试试卷数学(文科)(时间120分钟,满分150分)命题: 审题:一、选择题(本题共12小题,每小题5分,共60分) 1.函数f (x )=-2x +5+lg (2-x -1)的定义域为( ) A .(-5,+∞) B .[-5,+∞) C .(-5,0)D .(-2,0)2.已知O 、A 、B 是平面上的三个点,直线AB 上有一点C ,满足2AC +CB =0,则OC 等于( )A .2OA -OB B .-OA +2OB C.23OA -13OB D .-13OA +23OB3.已知OA =(2,3),OB =(-3,y ),且OA ⊥OB ,则y 等于( ) A .2 B .-2 C.12D .-124.若e 1,e 2是平面内夹角为60°的两个单位向量,则向量a =2e 1+e 2与b =-3e 1+2e 2的夹角为( )A .30°B .60°C .90°D .120°5.函数f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x 的最大值为( )A .4B .5C .6D .76.如图,在△ABC 中,AD ⊥AB ,BC =3BD ,|AD |=1,则AC ·AD =( )A.2 3 B.3 3C.32D. 37.已知p>q>1,0<a<1,则下列各式中正确的是( )A.a p>a q B.p a<q aC.a-p>a-q D.p-a>q-a8.已知函数y=f(x)是定义在R上的偶函数,当x≤0时,y=f(x)是减函数,若|x1|<|x2|,则( )A.f(x1)-f(x2)<0B.f(x1)-f(x2)>0C.f(x1)+f(x2)<0D.f(x1)+f(x2)>09.已知向量OA=(2,2),OB=(4,1),在x轴上有一点P,使AP·BP有最小值,则点P的坐标是( )A.(-3,0) B.(2,0)C.(3,0) D.(4,0)10.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )A.{x|-1<x≤0} B.{x|-1≤x≤1}C.{x|-1<x≤1} D.{x|-1<x≤2}11.如图是函数f(x)=A·cos(2π3x+φ)-1(A>0,|φ|<π2)的图象的一部分,则f(2 017)=( )A .0B .2 C.32D .112..对于函数f (x ),若∀a ,b ,c ∈R ,f (a ),f (b ),f (c )为某一三角形的三边长,则称f (x )为“可构造三角形函数”,已知函数f (x )=是“可构造三角形函数”,则实数t 的取值范围是( ) A .[0,+∞) B .[0,1] C .[1,2] D .二、填空题(本大题共4小题,每小题5分,共20分) 13.函数y =1-2x +x 的值域为________. 答案:(]-∞,114.要得到函数y =13sin(2x +π8)的图象,只需将函数y =13sin 2x 的图象________个单位.答案:向左平移π1615.如图,在矩形ABCD 中,AB =2,BC =2,点E 为BC 的中点,点F 在边CD 上,若AB ·AF =2,则AE ·BF 的值是________.答案: 216.已知函数f (x )=⎩⎨⎧ax 2+2x +1,x ≤0,ax -3,x >0有3个零点,则实数a 的取值范围是________.答案:(0,1)三、解答题(本大题共6小题,解答时应写出文字说明、证明过程或演算步骤)17.已知全集为实数集R,集合A={x|y=x-1+3-x},B={x|log2x >1}.(1)求A∩B,(∁R B)∪A;(2)已知集合C={x|1<x<a},若C⊆A,求实数a的取值范围.解:(1)由已知得A={x|1≤x≤3},x>1}={x|x>2},B={x|log2所以A∩B={x|2<x≤3},B)∪A={x|x≤2}∪{x|1≤x≤3}={x|x≤3}.(∁R18.设函数f(x)的定义域为(-3,3),满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.(1)求f(2)的值;(2)判断f(x)的单调性,并证明;(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.解:(1)在f(x)-f(y)=f(x-y)中,令x=2,y=1,代入得:f(2)-f(1)=f(1),所以f(2)=2f(1)=-4.(2)f(x)在(-3,3)上单调递减.证明如下:设-3<x1<x2<3,则x1-x2<0,所以f(x1)-f(x2)=f(x1-x2)>0,即f(x1)>f(x2),所以f(x)在(-3,3)上单调递减.(3)由g(x)≤0得f(x-1)+f(3-2x)≤0,所以f(x-1)≤-f(3-2x).又f(x)满足f(-x)=-f(x),所以f(x-1)≤f(2x-3),又f(x)在(-3,3)上单调递减,所以⎩⎨⎧-3<x -1<3,-3<2x -3<3,x -1≥2x -3,解得0<x ≤2,故不等式g (x )≤0的解集是(0,2].19.(1)已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61,求a 与b 的夹角; (2)设OA =(2,5),OB =(3,1),OC =(6,3),在OC 上是否存在点M ,使MA ⊥MB ?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)(2a -3b )·(2a +b )=4a 2-4a ·b -3b 2=61. ∵|a |=4,|b |=3, ∴a ·b =-6,∴cos θ=a ·b |a ||b |=-64×3=-12,∴θ=120°.(2)假设存在点M ,且OM =λOC =(6λ,3λ)(0<λ≤1), ∴MA =(2-6λ,5-3λ),MB =(3-6λ,1-3λ), ∴(2-6λ)×(3-6λ)+(5-3λ)(1-3λ)=0, ∴45λ2-48λ+11=0,得λ=13或λ=1115.∴OM =(2,1)或OM =⎝ ⎛⎭⎪⎫225,115.∴存在M (2,1)或M ⎝ ⎛⎭⎪⎫225,115满足题意.20.函数f (x )=cos(πx +φ)0<φ<π2的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f ⎝ ⎛⎭⎪⎫x +13,求函数g (x )在区间⎣⎢⎡⎦⎥⎤-12,13上的最大值和最小值.解:(1)由题图得f (0)=32,所以cos φ=32,因为0<φ<π2,故φ=π6.由于f (x )的最小正周期等于2,所以由题图可知1<x 0<2,故7π6<πx 0+π6<13π6, 由f (x 0)=32得cos ⎝ ⎛⎭⎪⎫πx 0+π6=32,所以πx 0+π6=11π6,故x 0=53. (2)因为f ⎝ ⎛⎭⎪⎫x +13=cos⎣⎢⎡⎦⎥⎤π⎝ ⎛⎭⎪⎫x +13+π6 =cos⎝ ⎛⎭⎪⎫πx +π2=-sin πx , 所以g (x )=f (x )+f⎝ ⎛⎭⎪⎫x +13 =cos⎝ ⎛⎭⎪⎫πx +π6-sin πx =cos πx cos π6-sin πx sin π6-sin πx =32cos πx -32sin πx =3sin ⎝ ⎛⎭⎪⎫π6-πx . 当x ∈⎣⎢⎡⎦⎥⎤-12,13时,-π6≤π6-πx ≤2π3.所以-12≤sin ⎝ ⎛⎭⎪⎫π6-πx ≤1,故当π6-πx =π2,即x =-13时,g (x )取得最大值3;当π6-πx =-π6,即 x =13时,g (x )取得最小值-32. 21.对于函数f (x )=a -2b x+1(a ∈R ,b >0,且b ≠1). (1)探索函数y =f (x )的单调性;(2)求实数a 的值,使函数y =f (x )为奇函数;(3)在(2)的条件下,令b =2,求使f (x )=m (x ∈[0,1])有解的实数m 的取值范围.解:(1)函数f (x )的定义域为R ,设x 1<x 2,则f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫a -2bx 1+1-⎝⎛⎭⎪⎫a -2bx 2+1=2bx 1-bx 2bx 1+1bx 2+1.当b >1时,由x 1<x 2, 得bx 1<bx 2,从而bx 1-bx 2<0,于是f (x 1)-f (x 2)<0,所以f (x 1)<f (x 2), 此时函数f (x )在R 上是单调增函数; 当0<b <1时,由x 1<x 2, 得bx 1>bx 2,从而bx 1-bx 2>0,于是f (x 1)-f (x 2)>0,所以f (x 1)>f (x 2), 此时函数f (x )在R 上是单调减函数.(2)函数f (x )的定义域为R ,由f (0)=0得a =1. 当a =1时,f (x )=1-2b x +1=b x -1b x +1,f (-x )=1-2b -x +1=b -x -1b -x +1=1-b x1+b x .满足条件f (-x )=-f (x ), 故a =1时,函数f (x )为奇函数. (3)f (x )=1-22x +1, ∵x ∈[0,1],∴2x ∈[1,2],2x +1∈[2,3], 22x +1∈⎣⎢⎡⎦⎥⎤23,1,∴f (x )∈⎣⎢⎡⎦⎥⎤0,13,要使f (x )=m (x ∈[0,1])有解,则0≤m ≤13,即实数m 的取值范围为⎣⎢⎡⎦⎥⎤0,13.。
安徽省六安市高一生物下学期第一次统考(开学考试)试题

舒城中学2017-2018学年度第二学期第一次统考高一生物时间:100分钟分值:100分一、选择题(共40小题,每小题1.5分,共60分)1.下列有关生命系统的叙述正确的是 ( ) A.生命系统中各生物体均具有多种组织、器官和系统B.生物圈是地球上最基本的生命系统和最大的生态系统C.肌肉细胞里的蛋白质和核酸属于生命系统的分子层次D.H1N1流感病毒不属于生命系统,但其增殖离不开活细胞2.下列关于显微镜的使用不.正确的是()A.观察切片时,先低倍后高倍是因为低倍镜下易找到观察的目标B.换用高倍镜后视野将变暗,为提高亮度,可放大光圈或换平面镜为凹面镜采光C.低倍镜下视野的右上角有一不清晰物像,此时应换用高倍镜并调节细准焦螺旋观察D.观察质壁分离时不需用高倍镜,因为洋葱鳞片叶表皮细胞较大3.科学家在利用无土栽培法培养一些名贵花卉时,培养液中添加了多种必需化学元素,其配方如下:其中花卉根细胞吸收最少的离子是()A.Mg2+B.SO42-C.Zn2+D.H2PO42-4.在生物组织中还原糖、脂肪、蛋白质的鉴定实验中,对实验材料选择的叙述,错误的是( ) A.甘蔗茎的薄壁组织、甜菜的块根等,都含有较多的糖且近于白色,因此可以用于进行还原糖的鉴定B.花生种子含脂肪多且子叶肥厚,是用于脂肪鉴定的理想材料C.大豆种子蛋白质含量高,是进行蛋白质鉴定的理想植物组织材料D.鸡蛋清含蛋白质多,是进行蛋白质鉴定的理想动物材料5.若某蛋白质的相对分子质量为10972,在合成这个蛋白质分子的过程中脱水量为1728,假设氨基酸的平均相对分子质量为127,则组成该蛋白质分子的肽链有()A.4条B.3条 C.2条 D.1条6.某多肽,经测定其分子为C21H x O y N4S2(无二硫键)。
已知该多肽是由下列氨基酸中的几种作为原料合成的:苯丙氨酸(C9H11NO2)、天冬氨酸(C4H7NO4)、亮氨酸(C6H13NO2)、丙氨酸(C3H6NO2)、半胱氨酸(C3H7NO2S),下列有关叙述不正确的()A.该多肽水解后形成3种氨基酸B.该多肽中氢原子数和氧原子数分别为32和5C.该多肽中不止1个羧基D.该多肽中有3个肽键7.植物细胞的细胞质内含有的糖类和核酸主要是()A. 糖原和DNAB.淀粉和DNAC.糖原和RNAD. 淀粉和RNA8.根据概念图,下列叙述正确的是()A.①表示的碱基有5种B.②表示核糖C.④表示核糖核苷酸D.④表示脱氧核糖核苷酸9.生命科学研究中常用图示表示微观物质的结构,图中1~3分别表示植物细胞中常见的三种有机物,则图中1~3可分别表示 ( )A.多肽、RNA、淀粉B.DNA、RNA、纤维素C.DNA、蛋白质、糖原D.蛋白质、核酸、糖原10.在DNA分子的一条链中,连接两个相邻碱基A和T的化学结构是 ( ) A.脱氧核糖—磷酸—脱氧核糖B.核糖—磷酸—核糖C.磷酸—脱氧核糖—磷酸D.氢键11.生物体内含Zn2+的酶最多,有70多种酶的活性与Zn2+有关,缺乏Zn2+生物就无法正常生活,这说明无机盐 ( ) A.对维持生物体的生命活动有重要作用B.对维持细胞形态有重要作用C.对维持酸碱平衡有重要作用D.对调节细胞内的浓度有重要作用12.利用电子显微镜观察试样甲、乙、丙的细胞结构,观察到细胞结构a~e具有下列特征:a、b、c均由双层膜构成,其中a的膜上具有小孔,而b、c没有小孔;细胞分裂时,从d的周围发出丝状物;e由几个囊状结构重叠而成。
安徽省六安市第一中学2017-2018学年高一英语下学期开学考试试题(扫描版,含答案)

百度文库是百度发布的供网友在线分享文档的平台。
百度文库的文档由百度用户上传,需要经过百度的审核才能发布,百度自身不编辑或修改用户上传的文档内容。
网友可以在线阅读和下载这些文档。
百度文库的文档包括教学资料、考试题库、专业资料、公文写作、法律文件等多个领域的资料。
百度用户上传文档可以得到一定的积分,下载有标价的文档则需要消耗积分。
当前平台支持主流的doc(.docx)、.ppt(.pptx)、.xls(.xlsx)、.pot、.pps、.vsd、.rtf、.wps、.et、.dps、.pdf、.txt 文件格式。
本文档仅用于百度文库的上传使用。
高一下学期第一次统考(开学考试)试题(理)

安徽省六安市舒城中学2017-2018学年高一下学期第一次统考(开学考试)数学试题(理)一、选择题1.若非空集合{}{}161|,531|≤≤=-≤≤+=x x Y a x a x X ,则使得)(Y X X ⊆成立 的所有a 的集合是 ( )A.{}70|≤≤a aB.{}73|≤≤a aC.{}|7a a ≤D.∅ 2.观察下列各式;,,3906255,781255,156255,312558765 ====则20185的末四位数字是( )A.3125B.5625 C .0625 D.81253.已知函数)2sin()(ϕ+=x x f 满足)()(a f x f ≤对x ∀∈R 恒成立,则函数 ( )A.)(a x f - 一定为奇函数B.)(a x f -一定为偶函数C.)(a x f +一定为奇函数D.)(a x f +一定为偶函数4.已知C B A ,,是平面上不共线的三点,O 为该平面内一点,且||||||==,动点P 满足1[(1)(1)(12)],3OP OA OB OC λλλλ=-+-++∈R ,则点P 的轨迹一定经过ABC ∆ 的( )A.内心B.垂心C.重心D.外心 5.已知函数[]x x f x x ,21212)(-+=表示不超过x 的最大整数,则函数[][])()(x f x f y -+= 的值域为( ) A.{}0 B.{}0,1-C.{}1,0,1-D.{}0,2- 6. 40tan 50cos 4-=( ) A.2 B. 232+ C .3 D.122-7.设θ为两个非零向量b a ,的夹角.已知对任意实数||,a t b t +的最小值为1.则 ( )A.若θ确定,则||a 唯一确定B.若θ确定,则||b 唯一确定C.若||a 确定,则θ唯一确定D.若||b 确定,则θ唯一确定 8.已知函数21()e (0)2x f x x x =+-<与)ln()(2a x x x g ++=的图像上存在关于y 轴对 称的点,则a 的取值范围是( )A.(-∞B.⎛-∞ ⎝ C.⎛ ⎝ D.⎛ ⎝9.已知函数x x x f 2sin cos )(=,下列结论中错误的是 ( )A.)(x f y =的图像关于点(π,0)对称B.)(x f y =的图像关于直线π2x =对称 C.)(x f y =的最大值为23 D.)(x f y =既是奇函数又是周期函数10.已知平面凸四边形ABCD ,其中)1,3(),3,1(-==BD AC ,则CD AB •的取值范围 是 ( )A.()2,0B.(]4,0C.[)0,2-D.[)0,4- 11.已知函数211()2(ee )x xf x x x a --+=-++有唯一零点,则a = ( ) A.21- B.31 C.21 D.1 12.三个数π,,0,2a b c ⎛⎫∈ ⎪⎝⎭,且满足条件:c c b b a a ===)cos(sin ,)sin(cos ,cos .则它们 的大小关系是 ( )A.b a c >>B.a c b >>C.c b a >>D.b c a >> 二、填空题13.设xx x x f lg lg lg 811411211)(+++++=,则=+)1()(x f x f . 14.已知21,),6,0(),0,3(e e B A -为单位向量,若213e e +=,则2e 在1e 方向上的投 影为 .15.已知[)0,2πθ∈,且有)cos (sin 7sin cos 221010θθθθ->-,则θ的取值范围 是 .16.设π0,2x ⎛⎫∈ ⎪⎝⎭,函数x x x f 2sin 14cos 3)(++=的最大值为 .三、解答题17.如图,在xOy 平面上,点(1,0)A ,点B 在单位圆上,AOB θ∠=(0θπ<<).(1)若点34(,)55B -,求tan()4πθ+的值; (2)若OA OB OC +=,1813OB OC ⋅=,求cos()3πθ-.18.已知二次函数f (x )=x 2+bx +c (b ,c ∈R ).(1)若f (-1)=f (2),且不等式x ≤f (x )≤2|x -1|+1对x ∈恒成立,求函数f (x )的解析式;(2)若c <0,且函数f (x )在上有两个零点,求2b +c 的取值范围.19.已知向量)cos ,(sin x x a =, )sin ,(sin x x b =, )0,1(-=c .(1)若π3x =,求向量a , c 的夹角θ;(2)若3ππ,84x ⎡⎤∈-⎢⎥⎣⎦,函数x f •=λ)(的最大值为12,求实数λ的值.20. 已知a ∈R ,函数21()log ()f x a x=+. (1)当5a =时,解不等式()0f x >;(2)若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素,求a 的 取值范围;(3)设0a >,若对任意1[,1]2t ∈,函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围.21.用向量方法解题:如图所示,在ABC ∆中,点F E D ,,分别是边AC BC AB ,,的三等分 点,且BE EC 2=,FC AF AD BD 2,2==,设AE 与CD 交于P 点,AE 与BF 交于Q点,BF 与CD 交于R 点.若1=∆ABC S ,求PQR S ∆.22.(1)已知函数))((D x x f y ∈=,))((D x x g y ∈=在D 上都是单调递减函数,且对 0)(,0)(,>>∈∀x g x f D x ,试判断函数)()(x g x f y =在D 上的单调性并加以证明;(2)求函数()F x x =⎥⎦⎤⎢⎣⎡45,41上的最小值.。
安徽省六安市舒城中学17—18学年下学期高一第一次统考(开学考试)数学(文)试题(答案不完整)

舒城中学2017—2018学年度第二学期第一次统考高一文数(时间120分钟,满分150分)命题: 审题:一、选择题(本题共12小题,每小题5分,共60分) 1.函数f (x )+lg (2-x-1)的定义域为( )A .(-5,+∞)B .[-5,+∞)C .(-5,0)D .(-2,0)2.已知O 、A 、B 是平面上的三个点,直线AB 上有一点C ,满足2AC +CB =0,则OC 等于( )A .2OA -OB B .-OA +2OB C.23OA -13OB D .-13OA +23OB 3.已知OA =(2,3),OB =(-3,y ),且OA ⊥OB ,则y 等于( ) A .2 B .-2 C.12D .-124.若e 1,e 2是平面内夹角为60°的两个单位向量,则向量a =2e 1+e 2与b =-3e 1+2e 2的夹角为( )A .30°B .60°C .90°D .120°5.函数f (x )=cos 2x +6cos 2x π⎛⎫- ⎪⎝⎭的最大值为( ) A .4 B .5 C .6D .76.如图,在△ABC 中,AD ⊥AB ,BC BD ,|AD |=1,则AC ·AD =( )A .B .7.已知p >q >1,0<a <1,则下列各式中正确的是( ) A .a p >a q B .p a <q a C .a -p >a -qD .p -a >q -a8.已知函数y =f (x )是定义在R 上的偶函数,当x ≤0时,y =f (x )是减函数,若|x 1|<|x 2|,则( )A .f (x 1)-f (x 2)<0B .f (x 1)-f (x 2)>0C .f (x 1)+f (x 2)<0D .f (x 1)+f (x 2)>09.已知向量OA =(2,2),OB =(4,1),在x 轴上有一点P ,使AP ·BP 有最小值,则点P 的坐标是( )A .(-3,0)B .(2,0)C .(3,0)D .(4,0)10.如图,函数f (x )的图象为折线ACB ,则不等式f (x )≥log 2(x +1)的解集是()A .{x |-1<x ≤0}B .{x |-1≤x ≤1}C .{x |-1<x ≤1}D .{x |-1<x ≤2}11.如图是函数f (x )=A ·cos(2π3x +φ)-1(A >0,|φ|<π2)的图象的一部分,则f (2 017)=()A .0B .2D .112..对于函数f (x ),若∀a ,b ,c ∈R ,f (a ),f (b ),f (c )为某一三角形的三边长,则称f (x )为“可构造三角形函数”,已知函数f (x )=是“可构造三角形函数”,则实数t 的取值范围是( )A .[0,+∞)B .[0,1]C .[1,2]D .二、填空题(本大题共4小题,每小题5分,共20分) 13.函数yx 的值域为________.14.要得到函数y =13sin(2x +π8)的图象,只需将函数y =13sin 2x 的图象________个单位. 15.如图,在矩形ABCD 中,AB,BC =2,点E 为BC 的中点,点F 在边CD 上,若AB ·AF,则AE ·BF 的值是________.16.已知函数f (x )=221,03,0ax x x ax x ⎧++≤⎨->⎩有3个零点,则实数a 的取值范围是________.三、解答题(本大题共6小题,解答时应写出文字说明、证明过程或演算步骤) 17.已知全集为实数集R ,集合A ={x |y},B ={x |log 2x >1}.(1)求A ∩B ,(∁R B )∪A ;(2)已知集合C ={x |1<x <a },若C ⊆A ,求实数a 的取值范围.18.设函数f (x )的定义域为(-3,3),满足f (-x )=-f (x ),且对任意x ,y ,都有f (x )-f (y )=f (x -y ),当x <0时,f (x )>0,f (1)=-2.(1)求f (2)的值;(2)判断f (x )的单调性,并证明;(3)若函数g (x )=f (x -1)+f (3-2x ),求不等式g (x )≤0的解集.19.(1)已知a =4,b =3,(2a -3b )·(2a +b )=61,求a 与b 的夹角;(2)设OA =(2,5),OB =(3,1),OC =(6,3),在OC 上是否存在点M ,使MA ⊥MB ?若存在,求出点M 的坐标;若不存在,请说明理由.20.函数f (x )=cos(πx +φ) (0<φ<π2)的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f 13x ⎛⎫+ ⎪⎝⎭,求函数g (x )在区间11,23⎡⎤-⎢⎥⎣⎦上的最大值和最小值.21.对于函数f (x )=a -2b x +1(a ∈R ,b >0,且b ≠1).(1)探索函数y =f (x )的单调性;(2)求实数a 的值,使函数y =f (x )为奇函数;(3)在(2)的条件下,令b =2,求使f (x )=m (x ∈[0,1])有解的实数m 的取值范围.舒城中学2017-2018学年高一第二学期入学考试试卷数学(文科)(时间120分钟,满分150分) 命题: 审题:一、选择题(本题共12小题,每小题5分,共60分) 1.函数f (x )=-2x +5+lg (2-x -1)的定义域为( ) A .(-5,+∞) B .[-5,+∞) C .(-5,0)D .(-2,0)2.已知O 、A 、B 是平面上的三个点,直线AB 上有一点C ,满足2AC +CB =0,则OC 等于( )A .2OA -OB B .-OA +2OB C.23OA -13OB D .-13OA +23OB3.已知OA =(2,3),OB =(-3,y ),且OA ⊥OB ,则y 等于( ) A .2 B .-2 C.12D .-124.若e 1,e 2是平面内夹角为60°的两个单位向量,则向量a =2e 1+e 2与b =-3e 1+2e 2的夹角为( )A .30°B .60°C .90°D .120°5.函数f (x )=cos 2x +6cos ⎝⎛⎭⎫π2-x 的最大值为( )A .4B .5C .6D .76.如图,在△ABC 中,AD ⊥AB ,BC =3BD ,|AD |=1,则AC ·AD =( )A .2 3B .3 3 C.32D. 37.已知p >q >1,0<a <1,则下列各式中正确的是( ) A .a p >a q B .p a <q a C .a -p >a -qD .p -a >q -a8.已知函数y =f (x )是定义在R 上的偶函数,当x ≤0时,y =f (x )是减函数,若|x 1|<|x 2|,则( )A .f (x 1)-f (x 2)<0B .f (x 1)-f (x 2)>0C .f (x 1)+f (x 2)<0D .f (x 1)+f (x 2)>09.已知向量OA =(2,2),OB =(4,1),在x 轴上有一点P ,使AP ·BP 有最小值,则点P 的坐标是( )A .(-3,0)B .(2,0)C .(3,0)D .(4,0)10.如图,函数f (x )的图象为折线ACB ,则不等式f (x )≥log 2(x +1)的解集是( )A .{x |-1<x ≤0}B .{x |-1≤x ≤1}C .{x |-1<x ≤1}D .{x |-1<x ≤2}11.如图是函数f (x )=A ·cos(2π3x +φ)-1(A >0,|φ|<π2)的图象的一部分,则f (2 017)=( )A .0B .2 C.32D .112..对于函数f (x ),若∀a ,b ,c ∈R ,f (a ),f (b ),f (c )为某一三角形的三边长,则称f (x )为“可构造三角形函数”,已知函数f (x )=是“可构造三角形函数”,则实数t 的取值范围是( )A .[0,+∞)B .[0,1]C .[1,2]D .二、填空题(本大题共4小题,每小题5分,共20分) 13.函数y =1-2x +x 的值域为________. 答案:(]-∞,114.要得到函数y =13sin(2x +π8)的图象,只需将函数y =13sin 2x 的图象________个单位.答案:向左平移π1615.如图,在矩形ABCD 中,AB =2,BC =2,点E 为BC 的中点,点F 在边CD 上,若AB ·AF =2,则AE ·BF 的值是________.答案: 216.已知函数f (x )=⎩⎪⎨⎪⎧ax 2+2x +1,x ≤0,ax -3,x >0有3个零点,则实数a 的取值范围是________.答案:(0,1)三、解答题(本大题共6小题,解答时应写出文字说明、证明过程或演算步骤) 17.已知全集为实数集R ,集合A ={x |y =x -1+3-x },B ={x |log 2x >1}. (1)求A ∩B ,(∁R B )∪A ;(2)已知集合C ={x |1<x <a },若C ⊆A ,求实数a 的取值范围. 解:(1)由已知得A ={x |1≤x ≤3}, B ={x |log 2x >1}={x |x >2}, 所以A ∩B ={x |2<x ≤3},(∁R B )∪A ={x |x ≤2}∪{x |1≤x ≤3}={x |x ≤3}.18.设函数f (x )的定义域为(-3,3),满足f (-x )=-f (x ),且对任意x ,y ,都有f (x )-f (y )=f (x -y ),当x <0时,f (x )>0,f (1)=-2.(1)求f (2)的值;(2)判断f (x )的单调性,并证明;(3)若函数g (x )=f (x -1)+f (3-2x ),求不等式g (x )≤0的解集. 解:(1)在f (x )-f (y )=f (x -y )中,令x =2,y =1,代入得:f (2)-f (1)=f (1),所以f (2)=2f (1)=-4. (2)f (x )在(-3,3)上单调递减.证明如下: 设-3<x 1<x 2<3,则x 1-x 2<0, 所以f (x 1)-f (x 2)=f (x 1-x 2)>0, 即f (x 1)>f (x 2),所以f (x )在(-3,3)上单调递减. (3)由g (x )≤0得f (x -1)+f (3-2x )≤0, 所以f (x -1)≤-f (3-2x ). 又f (x )满足f (-x )=-f (x ), 所以f (x -1)≤f (2x -3), 又f (x )在(-3,3)上单调递减, 所以⎩⎪⎨⎪⎧-3<x -1<3,-3<2x -3<3,x -1≥2x -3,解得0<x ≤2,故不等式g (x )≤0的解集是(0,2].19.(1)已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61,求a 与b 的夹角;(2)设OA =(2,5),OB =(3,1),OC =(6,3),在OC 上是否存在点M ,使MA ⊥MB ?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)(2a -3b )·(2a +b )=4a 2-4a ·b -3b 2=61. ∵|a |=4,|b |=3, ∴a ·b =-6,∴cos θ=a ·b |a ||b |=-64×3=-12,∴θ=120°.(2)假设存在点M ,且OM =λOC =(6λ,3λ)(0<λ≤1), ∴MA =(2-6λ,5-3λ),MB =(3-6λ,1-3λ), ∴(2-6λ)×(3-6λ)+(5-3λ)(1-3λ)=0, ∴45λ2-48λ+11=0,得λ=13或λ=1115.∴OM =(2,1)或OM =⎝⎛⎭⎫225,115.∴存在M (2,1)或M ⎝⎛⎭⎫225,115满足题意.20.函数f (x )=cos(πx +φ)0<φ<π2的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f ⎝⎛⎭⎫x +13,求函数g (x )在区间⎣⎡⎦⎤-12,13上的最大值和最小值. 解:(1)由题图得f (0)=32,所以cos φ=32, 因为0<φ<π2,故φ=π6.由于f (x )的最小正周期等于2,所以由题图可知1<x 0<2,故7π6<πx 0+π6<13π6,由f (x 0)=32得cos ⎝⎛⎭⎫πx 0+π6=32, 所以πx 0+π6=11π6,故x 0=53.(2)因为f ⎝⎛⎭⎫x +13=cos ⎣⎡⎦⎤π⎝⎛⎭⎫x +13+π6 =cos ⎝⎛⎭⎫πx +π2=-sin πx ,所以g (x )=f (x )+f ⎝⎛⎭⎫x +13 =cos ⎝⎛⎭⎫πx +π6-sin πx=cos πx cos π6-sin πx sin π6 -sin πx=32cos πx -32sin πx =3sin ⎝⎛⎭⎫π6-πx . 当x ∈⎣⎡⎦⎤-12,13时,-π6≤π6-πx ≤2π3. 所以-12≤sin ⎝⎛⎭⎫π6-πx ≤1,故当π6-πx =π2,即x =-13时,g (x )取得最大值3;当π6-πx =-π6,即x =13时,g (x )取得最小值-32. 21.对于函数f (x )=a -2b x +1(a ∈R ,b >0,且b ≠1).(1)探索函数y =f (x )的单调性;(2)求实数a 的值,使函数y =f (x )为奇函数;(3)在(2)的条件下,令b =2,求使f (x )=m (x ∈[0,1])有解的实数m 的取值范围. 解:(1)函数f (x )的定义域为R ,设x 1<x 2,则f (x 1)-f (x 2)=⎝⎛⎭⎫a -2bx 1+1-⎝⎛⎭⎫a -2bx 2+1=2bx 1-bx 2bx 1+1bx 2+1.当b >1时,由x 1<x 2, 得bx 1<bx 2,从而bx 1-bx 2<0, 于是f (x 1)-f (x 2)<0,所以f (x 1)<f (x 2), 此时函数f (x )在R 上是单调增函数; 当0<b <1时,由x 1<x 2, 得bx 1>bx 2,从而bx 1-bx 2>0, 于是f (x 1)-f (x 2)>0,所以f (x 1)>f (x 2), 此时函数f (x )在R 上是单调减函数. (2)函数f (x )的定义域为R ,由f (0)=0得a =1. 当a =1时,f (x )=1-2b x +1=b x -1b x +1,f (-x )=1-2b -x +1=b -x -1b -x +1=1-b x 1+b x.满足条件f (-x )=-f (x ), 故a =1时,函数f (x )为奇函数. (3)f (x )=1-22x +1,∵x ∈[0,1],∴2x ∈[1,2],2x +1∈[2,3], 22x+1∈⎣⎡⎦⎤23,1, ∴f (x )∈⎣⎡⎦⎤0,13, 要使f (x )=m (x ∈[0,1])有解,则0≤m ≤13,即实数m 的取值范围为⎣⎡⎦⎤0,13.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年安徽省六安市舒城中学高一下学期第一次统考(开学考试)物理试题(总分:100分时间:100分钟)(提示:本卷多为寒假作业仿真题,忌抄袭答案;实验题、计算题应规范作答)一、单项选择题(只有一个正确选项4×8=32分)1.一个质点做方向不变的直线运动,加速度的方向始终与速度方向相同,但加速度大小逐渐减小直至为零,在此过程中()A.速度逐渐减小,当加速度减小到零时,速度达到最小值B.位移逐渐减小,当加速度减小到零时,位移达到最小值C.位移逐渐增大,当加速度减小到零时,位移将不再增大D.速度逐渐增大,当加速度减小到零时,速度达到最大值2.关于曲线运动,下列说法中正确的是()A.物体在变力作用下一定做曲线运动B.若物体的速度方向和加速度方向总在同一直线上,则该物体可能做曲线运动C.做曲线运动的物体,其速度可能不变D.物体作曲线运动时合力不可能为零3.如下图所示,在两块相同的竖直木块之间,有质量均为m的4块相同的砖,用两个大小均为F的水平力压木板,使砖静止不动,则第2块砖对第1块砖的摩擦力大小为()A.0 B.mgC.mg/2 D.mg/44.如下图甲所示为杂技表演的安全网示意图,网绳的结构为正方格形,O、a、b、c、d…等为网绳的结点.安全网水平张紧后,若质量为m=50kg的运动员从高处落下,并恰好落在O点上.该处下凹至最低点时,网绳dOe、bOg均成120°向上的张角,如下图乙所示,此时O点受到的向下的冲击力大小为F=1200N,则这时O点周围每根网绳承受的力的大小为(g=10 m / s2 )()A.600N B.500NC. 1700ND. 850N5. 如下图所示,在光滑水平面上叠放着A、B两物体,已知m A=6kg、m B=2 kg,A、B间动摩擦因数μ=0.2,现用水平力F向右拉A,g取10 m/s2,(已知最大静摩擦力等于滑动摩擦力) 则: ()A.当拉力F<12 N时,A静止不动B.当拉力F=12 N时,A相对B滑动C.当拉力F=10 N时,B受A的摩擦力等于10 ND.当拉力F=60 N时,B受A的摩擦力等于12 N6.如图所示,质量为M的斜劈形物体放在水平地面上,质量为m的粗糙物块以某一初速度沿劈的斜面向上滑,至速度为零后又加速返回,而物体M始终保持静止,则在物块m上、下滑动的整个过程中()A.地面对物体M的摩擦力一直向左B.物块m对物体M的摩擦力没有改变C.地面对物体M的支持力总等于(M+m)gD.物块m上、下滑动时的加速度大小相同7.如图所示:一玻璃筒中注满清水,水中放一软木做成的小圆柱体R(圆柱体的直径略小于玻璃管的直径,轻重大小适宜,使它在水中能匀速上浮)。
将玻璃管的开口端用胶塞塞进(图甲)。
现将玻璃管倒置(图乙),在软塞上升的同时,将玻璃管水平向右由一定的初速度做减速运动,观察木塞的运动,将会看到它斜向右上方运动,经过一段时间,玻璃管移向图丙中虚线所在位置,软木塞恰好运动到玻璃管的顶端,在图丁四个图中,能正确反映木塞运动轨迹的是:()8.如图所示,倾角为θ的传送带沿逆时针方向以加速度a加速传动时,小物体A与传送带相对静止,重力加速度为g.则()A.只有a>g sinθ,A才受沿传送带向上的静摩擦力作用B.无论a为多大,A都受沿传送带向上的静摩擦力作用C.只有a=g sinθ,A才受沿传送带向上的静摩擦力作用D.只有a<g sinθ,A才受沿传送带向上的静摩擦力作用二、多项选择题(4×4=16分,多选或错选不得分,选不全得一半分)9.关于平抛运动,下列说法正确的是()A.平抛运动是匀变速曲线运动B.平抛运动中速度的变化△V与竖直方向速度的变化△Vy 相等C.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动D.自一定高度向水平地面平抛小铁球,其落地时间只与抛出点的高度有关10.如图所示,倾角为θ=370的光滑直角斜面ABC放在水平面上,劲度系数分别为k1=200N/m、k2=100N/m的两个轻弹簧沿斜面悬挂着,两弹簧之间有一质量为m1=4kg的重物,最下端挂一质量为m2=2kg的重物,此时两重物处于平衡状态,现把斜面ABC绕A点缓慢地顺时针旋转90°后,重新达到平衡,(sin37°=0.6,cos37°=0.8,取g=10 m / s2)则:A . k1始终处于伸长状态 B. k2最后处于压缩状态C. m1沿斜面移动了42cmD. m2沿斜面移动了70cm11.如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它以a=2m/s2的加速度匀加速地向上提起重物.已知重物的质量m=30 kg,人的质量M=50 kg,g取10 m/s2.试求:A .人对绳子的拉力为300N B人对地面的压力为140NC.轻杆BC的张力为3603ND.水平细绳AB的张力为2403N12.受水平外力F作用的物体,在粗糙水平面上作直线运动,其v-t图线如下图所示,则()A.在0~t1秒内,外力F大小可能不断增大B.在t1时刻,外力F一定不为零C.在t1~t2秒内,外力F大小可能不断减小D.在t1~t2秒内,外力F大小可能不断增大三、实验题(2+12=14分)13.在物理必修一“互成角度的两个共点力的合成”的实验中,采取下列哪些措施可减小实验误差. (填序号)A.同一次实验过程中,O点位置允许变动B.实验中,弹簧秤必须保持与木板平行,读数时视线要正对弹簧秤刻度C.拉橡皮条的细绳要稍长些D.实验前,先把所用的两个弹簧秤的钩子相互钩住,平放在桌子上,向相反的方向拉动,检查读数是否相同E.实验中,可以先将其中一个弹簧秤沿某一方向拉到最大量程,然后只需调节另一弹簧秤的大小和方向,把橡皮条另一端拉到O点14.某同学设计了如图所示的装置,利用米尺、秒表、轻绳、轻滑轮、轨道、小车、托盘和砝码等器材来测定小车和轨道间的动摩擦因数μ.小车和托盘上分别放有若干砝码,小车质量为M,小车上砝码总质量为m′,托盘和盘中砝码的总质量为m.实验中,小车在水平轨道上从A到B做初速为零的匀加速直线运动,重力加速度g取10 m/s2.(1)为计算小车的加速度a,须测出它在A、B间运动的物理量________与________,进而计算小车对应的加速度值。
(2)根据牛顿运动定律得到a与m的关系式为:a= (用M、m′、m、μ、g表示)(3)他想通过多次改变m,并测出相应的a值,并利用上式来计算μ.若要求a是m的一次函数,必须使上式中的________保持不变。
操作方法是实验中应将从托盘中取出的砝码放置于_________.(4)利用测得的多组对应的a、m值,按照(3)中的要求,给出一种较准确的测μ值的方法。
四、计算题(8+8+10+12=38分)15.在竖直的井底,将一物块以V0=24 m/s的初速度竖直地向上抛出,物块经过井口时被人接住,在被人接住前1 s内物块的位移大小是15 m,不计空气阻力,g取10 m/s2,求此竖直井的深度.16.如图,某一小球以V0=10m/s的速度水平抛出,在落地之前经过空中A.B 两点,在A点小球的速度与水平方向的夹角为45°,在B点小球的速度与水平方向的夹角为60°,空气阻力忽略不计,g=10m/s2,求:(1)小球在B点的速度大小(2)A.B两点间水平距离X AB的值17.一弹簧一端固定在倾角为37°光滑斜面的底端,另一端拴接质量m1=4 kg的物块P,Q为一与P不粘连的重物,已知Q的质量m2=8 kg,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止,如图所示.现给Q施加一个方向始终沿斜面向上的拉力F,使它从静止开始沿斜面向上做匀加速运动,已知在运动过程中拉力F的最小值为48N.(sin37°=0.6,cos37°=0.8,g取10 m/s2) 求:(1)力F的最大值(2)物块P、Q刚分离时,重物Q的速度多大?18.如图所示,传送带沿逆时针方向以速度v0=2 m / s匀速运动,两皮带轮A、B之间的距离L=8.2 m,皮带绷紧与水平方向的夹角θ=37°。
将一可视为质点的小物块无初速地从上端放到传送带上,已知物块与传送带间的动摩擦因数μ=0.5,物块在与皮带相对滑动时能在皮带上留下白色痕迹。
(sin37°=0.6,cos37°=0.8,取g=10 m / s2)求:物块在带上传送过程中,(1)运动时间t的值。
(2)物块相对传送带的位移△X的大小。
(3)白色痕迹的长度S值高一物理参考答案一、单项选择题(4×8=32分)二、多项选择题(4×4=16分,多选或错选不得分,选不全得一半分)三、实验题:(2+12=14分) 13、 BCD14、(1) 位移x 、 时间t (2)a=()()1g g M m m m μμ++'-+(3、 小车 (4) 作出a_-m 的函数图像为一次函数,利用斜率求出μ四、计算题(8+8+10+12=38分)(请写出必要的解题过程) 15.解:设物块从抛出到被人接住历时为t ,以竖直向上为正方向; (1)当最后一秒位移方向向上时有2211((1)(1)1522o o V t gt V t g t -----= 得:t =1.4s物块上升至最高点需用时:2.4oo V t s g== ∴竖井深度为:h=212o V t gt -=23.8m ————4分(2) 当最后一秒位移方向向下时有2211((1)(1)1522o o V t gt V t g t -----=-得:t =4.4s物块从最高点下落至井口且最后1s 内位移为15m 用时为t 1,则221111(1)1522gt g t m --= 得t 1=2s 物块上升至井口用时t 2=0.4sh=22212o V t gt -=8.8m ————4分16、(8′)解:0220(1)60,=10320(2)45,=1031)3103//3/,((1)2B y B y B x B B y Bx Ay A y Ax B y A y AB O VB tag V V V V V Vtag m sm s m sA B V V V V s x V t t m g ---==+==------=•=---==---分小球通过点运动时间为:分在点:得在A 点:得分17、(10′)解:,(1)从受力角度看,两物体分离的条件是两物体间的正压力为0,从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等。
