6.备课资料(1.3 算法案例)
2019-2020年高中数学必修三1.3《算法案例(复习)》word教案

2019-2020年高中数学必修三1.3《算法案例(复习)》word教案一、教学目标1、知识与技能(1)明确算法的含义,熟悉算法的三种基本结构:顺序、条件和循环,以及基本的算法语句。
(2)能熟练运用辗转相除法与更相减损术、秦九韶算法、排序、进位制等典型的算法知识解决同类问题。
2、过程与方法在复习旧知识的过程中把知识系统化,通过模仿、操作、探索,经历设计程序框图表达解决问题的过程。
在具体问题的解决过程中进一步理解程序框图的三种基本逻辑结构:顺序、条件分支、循环。
3、情态与价值观算法内容反映了时代的特点,同时也是中国数学课程内容的新特色。
中国古代数学以算法为主要特征,取得了举世公认的伟大成就。
现代信息技术的发展使算法重新焕发了前所未有的生机和活力,算法进入中学数学课程,既反映了时代的要求,也是中国古代数学思想在一个新的层次上的复兴,也就成为了中国数学课程的一个新的特色。
二、教学重难点重点:算法的基本知识与算法对应的程序框图的设计难点:与算法对应的程序框图的设计及算法程序的编写三、学法与教学用具学法:利用实例让学生体会基本的算法思想,提高逻辑思维能力,对比信息技术课程中的程序语言的学习和程序设计,了解数学算法与信息技术上的区别。
通过案例的运用,引导学生体会算法的核心是一般意义上的解决问题策略的具体化。
面临一个问题时,在分析、思考后获得了解决它的基本思路(解题策略),将这种思路具体化、条理化,用适当的方式表达出来(画出程序框图,转化为程序语句)。
教学用具:电脑,计算器,图形计算器四、教学设计(一)、本章的知识结构(二)、知识梳理(1)四种基本的程序框终端框(起止框)输入.输出框处理框判断框(2)三种基本逻辑结构顺序结构条件结构循环结构(3)基本算法语句(一)输入语句单个变量多个变量(二)输出语句(三)赋值语句(四)条件语句IF-THEN-ELSE 格式当计算机执行上述语句时,首先对IF 后的条件进行判断,如果条件符合,就执行THEN 后的语句1,否则执行ELSE 后的语句2。
高中数学 1.3算法案例精品教案 新人教A版必修3

1.3算法案例第三、四课时 秦九韶算法与排序(1)教学目标(a )知识与技能1.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
2.掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序,进而能设计冒泡排序法的程序框图及程序,理解数学算法与计算机算法的区别,理解计算机对数学的辅助作用。
(b )过程与方法模仿秦九韶计算方法,体会古人计算构思的巧妙。
能根据排序法中的直接插入排序法与冒泡排序法的步骤,了解数学计算转换为计算机计算的途径,从而探究计算机算法与数学算法的区别,体会计算机对数学学习的辅助作用。
(c )情态与价值通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
通过对排序法的学习,领会数学计算与计算机计算的区别,充分认识信息技术对数学的促进。
(2)教学重难点重点:1.秦九韶算法的特点2.两种排序法的排序步骤及计算机程序设计难点:1.秦九韶算法的先进性理解2.排序法的计算机程序设计(3)学法与教学用具学法:1.探究秦九韶算法对比一般计算方法中计算次数的改变,体会科学的计算。
2.模仿排序法中数字排序的步骤,理解计算机计算的一般步骤,领会数学计算在计算机上实施的要求。
教学用具:电脑,计算器,图形计算器(4)教学设想(一)创设情景,揭示课题我们已经学过了多项式的计算,下面我们计算一下多项式1)(2345+++++=x x x x x x f 当5=x 时的值,并统计所做的计算的种类及计算次数。
根据我们的计算统计可以得出我们共需要10次乘法运算,5次加法运算。
我们把多项式变形为:1)))1(1(1()(2+++++=x x x x x x f 再统计一下计算当5=x 时的值时需要的计算次数,可以得出仅需4次乘法和5次加法运算即可得出结果。
显然少了6次乘法运算。
这种算法就叫秦九韶算法。
(二)研探新知1.秦九韶计算多项式的方法01210123120132211012211)))((())(()()(a a x a x a x a a x a x a x a x a a x a x a x a x a a x a x a x a x a x f n n n n n n n n n n n n n n n n n n n +++++==+++++=+++++=+++++=--------------例1 已知一个5次多项式为8.07.16.25.325)(2345-+-++=x x x x x x f 用秦九韶算法求这个多项式当5=x 时的值。
高中数学 (1.3 算法案例)示范教案 新人教A版必修3

课题:书法---写字基本知识课型:新授课教学目标:1、初步掌握书写的姿势,了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点:基本笔画的书写。
难点:运笔的技法。
教学过程:一、了解书法的发展史及字体的分类:1、介绍我国书法的发展的历史。
2、介绍基本书体:颜、柳、赵、欧体,分类出示范本,边欣赏边讲解。
二、讲解书写的基本知识和要求:1、书写姿势:做到“三个一”:一拳、一尺、一寸(师及时指正)2、了解钢笔的性能:笔头富有弹性;选择出水顺畅的钢笔;及时地清洗钢笔;选择易溶解的钢笔墨水,一般要固定使用,不能参合使用。
换用墨水时,要清洗干净;不能将钢笔摔到地上,以免笔头折断。
三、基本笔画书写1、基本笔画包括:横、撇、竖、捺、点等。
2、教师边书写边讲解。
3、学生练习,教师指导。
(姿势正确)4、运笔的技法:起笔按,后稍提笔,在运笔的过程中要求做到平稳、流畅,末尾处回锋收笔或轻轻提笔,一个笔画的书写要求一气呵成。
在运笔中靠指力的轻重达到笔画粗细变化的效果,以求字的美观、大气。
5、学生练习,教师指导。
(发现问题及时指正)四、作业:完成一张基本笔画的练习。
板书设计:写字基本知识、一拳、一尺、一寸我的思考:通过导入让学生了解我国悠久的历史文化,激发学生学习兴趣。
这是书写的起步,让学生了解书写工具及保养的基本常识。
基本笔画书写是整个字书写的基础,必须认真书写。
课后反思:学生书写的姿势还有待进一步提高,要加强训练,基本笔画也要加强训练。
课题:书写练习1课型:新授课教学目标:1、教会学生正确书写“杏花春雨江南”6个字。
2、使学生理解“杏花春雨江南”的意思,并用钢笔写出符合要求的的字。
重点:正确书写6个字。
难点:注意字的结构和笔画的书写。
教学过程:一、小结课堂内容,评价上次作业。
二、讲解新课:1、检查学生书写姿势和执笔动作(要求做到“三个一”)。
2、书写方法是:写一个字看一眼黑板。
(老师读,学生读,加深理解。
高中数学人教A版必修3《1.3算法案例》教案4

领悟十进制,二进制的特点,了解计算机的电路与二进制的联系,进一步认识到计算机与数学的联系。
教学重点
各进位制表示数的方法及各进位制之间的转换
教学难点
除k去余法的理解以及各进位制之间转换的程序框图的设计
教学方法
在学习各种进位制特点的同时探讨进位制表示数与十进制表示数的区别与联系,熟悉各种进位制表示数的方法,从而理解十进制转换为各种进位制的除k去余法。
教学过程:
批注
活动一:创设情景,揭示课题(5分钟)
问题1:(一)创设情景,揭示课题
我们常见的数字都是十进制的,但是并不是生活中的每一种数字都是十进制的.比如时间和角度的单位用六十进位制,电子计算机用的是二进制.那么什么是进位制?不同的进位制之间又又什么联系呢?
活动二:步入新知,师生交流(20分钟)
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制。现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
Байду номын сангаас必修三
《1.3算法案例》教学案
课题:案例3进位制第个教案
课型:新授课年月日
教
学
目
标
1.知识与技能
了解各种进位制与十进制之间转换的规律,会利用各种进位制与十进制之间的联系进行各种进位制之间的转换。
2.过程与方法
学习各种进位制转换成十进制的计算方法,研究十进制转换为各种进位制的除k去余法,并理解其中的数学规律。
上述方法也可以推广为把十进制化为k进制数的算法,这种算法成为除k取余法.
当数字较小时,也可直接利用各进位制表示数的特点,都是以幂的形式来表示各位数字,比如2*103表示千位数字是2,所以可以直接求出各位数字.即把89转换为二进制数时,直接观察得出89与64最接近故89=64*1+25
高中数学必修三1.3算法案例-辗转相除法
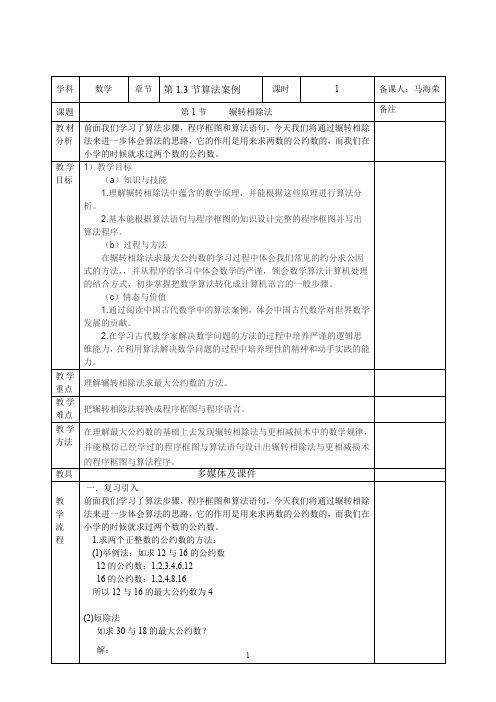
1734=816×2+102
816=102×8
2)再求102与1343的最大公约数
1343=102×13+17
102=17×6
所以17为102与1343的最大公约数
所以17为1734、816、1343这三个数的最大公约数
板
书
设
计
第1.3节算法案例-----辗转相除法
............................... ................................... ...............
课后作业
P45练习:1.
P48习题1.3A组:1.
课
后
反
思
1.辗转相除法的思想2.辗转相除法算法框图3.例题讲解
................................ ................................... ...............
............................... ................................... ...............
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
(b)过程与方法
在辗转相除法求最大公约数的学习过程中体会我们常见的约分求公因式的方法,,并从程序的学习中体会数学的严谨,领会数学算法计算机处理的结合方式,初步掌握把数学算法转化成计算机语言的一般步骤。
(c)情态与价值
1.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
PRINT m
END
课堂练习:1.求两数4081与20723的最大公约数.
1.3 算法案例

①以除法为主. ②两个整数差值较大时运算次数 较少.
①以减法为主. ②两个整数的差值较大时,运算次数 较多. ③相减,两数相等得结果.
③相除余数为零时得结果
④相减前要做是否都是偶数的判断
联 系
①都是求两个正整数的最大公约数的方法. ②二者的实质都是递推的过程.
③二者都要用循环结构来实现
3.秦九韶算法 (1)概念:求多项式 f(x)=anxn+an-1xn-1+…+a1x+a0 的值时,常用秦九韶算 法,这种算法的运算次数较少,是多项式求值比较先进的算法,其实质是转
名师点拨秦九韶算法有以下几个优点:
(1)大大减少了乘法的次数,使计算量减小.在计算机上做一次乘法所需要 的时间是做加法、减法的几倍到十几倍,减少做乘法的次数也就加快了计算的 速度;
(2)规律性强,便于利用循环语句来实现算法; (3)避免了对自变量 x 单独做幂的计算,每次都是计算一个一次多项式的 值,从而可以提高计算的精度.
v2=v1x+an-2, v3=v2x+an-3, ……
vn=vn-1x+a0.
(2)算法步骤: 第一步,输入多项式的次数 n、最高次项的系数 an 和 x 的值. 第二步,将 v 的值初始化为 an,将 i 的值初始化为 n-1. 第三步,输入 i 次项的系数 ai. 第四步,v=vx+ai,i=i-1. 第五步,判断 i 是否大于或等于 0.若是,则返回第三步;否则,输出多项式的 值 v.
是否都是偶数.若是,用 2 约简;若不是,执行第二步.第二步,以较大的数减去 较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操 作,直到所得的数相等为止,则这个数或这个数与约简的数的乘积就是所求 的最大公约数.
1.3算法案例(适用)ppt

2021/3/2
秦九韶算法的基本思想 思考1:对于多项式f(x)=x5+x4+x3+x2+x+1,求
f(5)的值. 分析:把5代入多项式,若先计算各项的值,
2021/3/2
思考4:辗转相除直到何时结束? 主要运用的是哪种算法结构?
辗转相除法是一个反复执行直到余数等于0停止的步骤, 这实际上是一个循环结构
辗转相除法求两个数的最大公约数,其算法可以描述如下: ① 输入两个正整数m和n; ② 求余数r:计算m除以n,将所得余数存放到变量r中; ③更新被除数和余数:m=n,n=r。
第二步:以较大的数减去较小的数,接着把差 与较小的数比较,并以大数减小数.继续这个操作, 直到所得的数相等为止,则这个等数或这个数与约 简的数的乘积就是所求的最大公约数.
2021/3/2
例1:用更相减损术求98与63的最大公约数.
因为63不是偶数,所以98-源自3=35,63-35=28,
35-28=7,
2021/3/2
思考3:注意到8251=6105×1+2146,那么8251 与6105这两个数的公约数和6105与2146的公约数有 什么关系?
我们发现6105=2146×2+1813,同理,6105与 2146的公约数和2146与1813的公约数相等.
思考4:重复上述操作,你能得到8251与6105这 两个数的最大公约数吗? 8251=6105×1+2146, 1813=333×5+148,
得:18和24最大公约数是:2×3=6
短除法
想一想,如何求8251与6105的最大公约数?
2021/3/2
思考2:对于8251与6105这两个数,它们的最大 公约数是多少?你是怎样得到的?
1. 3算法案例(教、教案)

1.3算法案例【教案目标】:1.理解辗转相除法与更相减损术中蕴含的数学原理,并能根据这些原理进行算法分析。
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
【教案重难点】:重点:理解辗转相除法与更相减损术求最大公约数的方法。
难点:把辗转相除法与更相减损术的方法转换成程序框图与程序语言。
【教案过程】:情境导入:1.教师首先提出问题:在初中,我们已经学过求最大公约数的知识,你能求出18与30的公约数吗?2.接着教师进一步提出问题,我们都是利用找公约数的方法来求最大公约数,如果公约数比较大而且根据我们的观察又不能得到一些公约数,我们又应该怎样求它们的最大公约数?比如求8251与6105的最大公约数?这就是我们这一堂课所要探讨的内容。
b5E2RGbCAP 新知探究:1.辗转相除法例1 求两个正数8251和6105的最大公约数。
<分析:8251与6105两数都比较大,而且没有明显的公约数,如能把它们都变小一点,根据已有的知识即可求出最大公约数)p1EanqFDPw解:8251=6105×1+2146显然8251的最大公约数也必是2146的约数,同样6105与2146的公约数也必是8251的约数,所以8251与6105的最大公约数也是6105与2146的最大公约数。
DXDiTa9E3d6105=2146×2+18132146=1813×1+3331813=333×5+148333=148×2+37148=37×4+0则37为8251与6105的最大公约数。
以上我们求最大公约数的方法就是辗转相除法。
也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的。
利用辗转相除法求最大公约数的步骤如下:RTCrpUDGiT第一步:用较大的数m除以较小的数n得到一个商q0和一个余数r0;第二步:若r0=0,则n为m,n的最大公约数;若r0≠0,则用除数n除以余数r0得到一个商q1和一个余数r1;5PCzVD7HxA 第三步:若r1=0,则r1为m,n的最大公约数;若r1≠0,则用除数r0除以余数r1得到一个商q2和一个余数r2;jLBHrnAILg……依次计算直至rn=0,此时所得到的rn-1即为所求的最大公约数。
1.3算法案例优秀课件

点评:秦九韶算法是求一元多项式的值的 一种方法.
它的特点是:把求一个n次多项式的值转化 为求n个一次多项式的值,通过这种转化,把运算 的次数由至多n(n+1)/2次乘法运算和n次加法 运算,减少为n次乘法运算和n次加法运算,大大 提高了运算效率.
v1=anx+an-1,
v2=v1x+an-2,
v3=v2x+an-3, ……, vn=vn-1x+a0.
[问题3]能否探索更好的算法,来解决任意多 项式的求值问题? 秦九韶《数书九章》. f(x)=2x5-5x4-4x3+3x2-6x+7 v0=2 =(2x4-5x3-4x2+3x-6)x+7 v1=v0x-5=2×5-5=5 =((2x3-5x2-4x+3)x-6)x+7 v2=v1x-4=5×5-4=21 =(((2x2-5x-4)x+3)x-6)x+7 v3=v2x+3=21×5+3=108 =((((2x-5)x-4)x+3)x-6)x+7 v4=v3x-6=108×5-6=534
PRINT f
END
点评:上述算法一共做了15次乘法运算,5次加法 运算.优点是简单,易懂;缺点是不通用,不能解 决任意多项式求值问题,而且计算效率不高. n次多项式至多n(n+1)/2次乘法运算和n次加法运算
[问题2]有没有更高效的算法?
分析:计算x的幂时,可以利用前面的计算结 果,以减少计算量,
89=44×2+1,
可以用2连续去除89
=(22×2+0)×2+1
或所得商(一直到商为 0为止),然后取余数
=((11×2+0)×2+0)×2+1 ---除2取余法.
课件6:1.3 算法案例 第一课时

和 n 次加法运算.
(2)秦九韶算法程序框图: 以 5 次多项式 f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0 当 x=
x0 时为例,如图.
一 求两个数的最大公约数 【例 1】 分别用辗转相除法和更相减损术逐步列出求 (1)98 和 63; (2)8251 和 6105 的最大公约数的步骤,你有什么发现?对
更相减损术 S1 98-63=35, S2 63-35=28, S3 35-28=7, S4 28-7=21, S5 21-7=14, S6 14-7=7, 故 98 和 63 的最大公约数为 7.
(2)求 8 251 和 6 105 的最大公约数的步骤: 辗转相除法 S1 8 251=6 105×1+2 146, S2 6 105=2 146×2+1 813, S3 2 146=1 813×1+333, S4 1 813=333×5+148, S5 333=148×2+37, S6 148=37×4, 所以,8 251 和 6 105 的最大公约数为 37.
优劣作出评判. 【分析】 辗转相除法是做两个数的带余除法,更相减损
术是做两个数的减法.
解:(1)求 98 和 63 的最大公约数的步骤: 辗转相除法 S1 98=63 ×1+35, S2 63=35 ×1+28, S3 35=28×1+7, S4 28=4 ×7, 所以,98 和 63 的最大公约数为 7.
更相减损术求最大公约数的程序设计:
INPUT “a,b=”;a,b WHILE a<>b
IF a>b THEN a=a-b
ELSE b=b-a
END IF WEND PRINT a END
3.秦九韶算法 (1)秦九韶算法过程分析: 设 Pn(x)=anxn+an-1xn-1+…+a1x+a0,将其改写为 Pn(x)=(anxn-1+an-1xn-2+…+a1)x+a0 =… =((anxn-2+an-1xn-3+…+a2)x+a1)x+a0 =(…((anx+an-1)x+an-2)x+…+a1)x+a0
1.3 算法案例

互动探究
3.将本例(1)中的二进制数101 101(2)转化为三进制数.
解:101 101(2)=1×25+0×24+1×23+1×22+0×21+1×20= 45,
∴45=1 200(3).
栏目 导引
第一章
算法初步
方法感悟
1 .求两个正数的最大公约数,当两数差别较大时,用辗转
相除法,当两数差别不大时,用更相减损术较快.
第一章
算法初步
1.3 算法案例
第一章
算法初步
学习导航
学习目标 重点难点 ― → 算法思想 ― ― → 算法用途 案例 ― 重点:引导学生理解算法思想. 难点:学生对算法应用的掌握.
体会 了解
栏目 导引
第一章
算法初步
新知初探思维启动
1.辗转相除法
所谓辗转相除法,就是对于任意给定的两个正整数,用较大
栏目 导引
第一章
算法初步
2.更相减损术
更相减损术是我国古代数学专著《九章算术》中介绍的任意
一种求两个正整数最大公约数的方法.其基本过程是:对于 给定的两个正整数,判断它们是否都是偶数.若是,用2约简; 较大数减去较小的数 ,接着把所得的____ 差 与 若不是,则用____________________ 较小的数 比较,并以大数减小数.继续这个操作,直到所 __________ 相等 为止,则这个数(等数)或这个数与约简的数的 得的数______ 乘积就是所求的最大公约数.
栏目 导引
第一章
算法初步
想一想 2.实际应用更相减损术时要做的第一步工作是什么? 提示:先判断 a, b是否全为偶数,若是,则先都除以 2 再 进行.
栏目 导引
第一章
算法初步
6.示范教案(1.3 算法案例)

1.3 算法案例整体设计教学分析在学生学习了算法的初步知识,理解了表示算法的算法步骤、程序框图和程序三种不同方式以后,再结合典型算法案例,让学生经历设计算法解决问题的全过程,体验算法在解决问题中的重要作用,体会算法的基本思想,提高逻辑思维能力,发展有条理地思考与数学表达能力.三维目标1.理解算法案例的算法步骤和程序框图.2.引导学生得出自己设计的算法程序.3. 体会算法的基本思想,提高逻辑思维能力,发展有条理地思考与数学表达能力.重点难点教学重点:引导学生得出自己设计的算法步骤、程序框图和算法程序.教学难点:体会算法的基本思想,提高逻辑思维能力,发展有条理地思考与数学表达能力. 课时安排3课时教学过程第1课时案例1 辗转相除法与更相减损术导入新课思路1(情境导入)大家喜欢打乒乓球吧,由于东、西方文化及身体条件的不同,西方人喜欢横握拍打球,东方人喜欢直握拍打球,对于同一个问题,东、西方人处理问题方式是有所不同的.在小学,我们学过求两个正整数的最大公约数的方法:先用两个数公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来. 当两个数公有的质因数较大时(如8 251与6 105),使用上述方法求最大公约数就比较困难.下面我们介绍两种不同的算法——辗转相除法与更相减损术,由此可以体会东、西方文化的差异.思路2(直接导入)前面我们学习了算法步骤、程序框图和算法语句.今天我们将通过辗转相除法与更相减损术来进一步体会算法的思想.推进新课新知探究提出问题(1)怎样用短除法求最大公约数?(2)怎样用穷举法(也叫枚举法)求最大公约数?(3)怎样用辗转相除法求最大公约数?(4)怎样用更相减损术求最大公约数?讨论结果:(1)短除法求两个正整数的最大公约数的步骤:先用两个数公有的质因数连续去除,一直除到所得的商是两个互质数为止,然后把所有的除数连乘起来.(2)穷举法(也叫枚举法)穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数.(3)辗转相除法辗转相除法求两个数的最大公约数,其算法步骤可以描述如下:第一步,给定两个正整数m,n.第二步,求余数r:计算m除以n,将所得余数存放到变量r中.第三步,更新被除数和余数:m=n,n=r.第四步,判断余数r是否为0.若余数为0,则输出结果;否则转向第二步继续循环执行.如此循环,直到得到结果为止. 这种算法是由欧几里得在公元前300年左右首先提出的,因而又叫欧几里得算法.(4)更相减损术我国早期也有解决求最大公约数问题的算法,就是更相减损术. 《九章算术》是中国古代的数学专著,其中的“更相减损术”也可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”翻译为现代语言如下:第一步,任意给定两个正整数,判断它们是否都是偶数,若是,用2约简;若不是,执行第二步.第二步,以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作,直到所得的数相等为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.应用示例例1 用辗转相除法求8 251与6 105的最大公约数,写出算法分析,画出程序框图,写出算法程序.解:用两数中较大的数除以较小的数,求得商和余数:8 251=6 105×1+2 146.由此可得,6 105与2 146的公约数也是8 251与6 105的公约数,反过来,8 251与6 105的公约数也是6 105与2 146的公约数,所以它们的最大公约数相等.对6 105与2 146重复上述步骤:6 105=2 146×2+1 813.同理,2 146与1 813的最大公约数也是6 105与2 146的最大公约数.继续重复上述步骤:2 146=1 813×1+333,1 813=333×5+148,333=148×2+37,148=37×4.最后的除数37是148和37的最大公约数,也就是8 251与6 105的最大公约数.这就是辗转相除法.由除法的性质可以知道,对于任意两个正整数,上述除法步骤总可以在有限步之后完成,从而总可以用辗转相除法求出两个正整数的最大公约数.算法分析:从上面的例子可以看出,辗转相除法中包含重复操作的步骤,因此可以用循环结构来构造算法.算法步骤如下:第一步,给定两个正整数m,n.第二步,计算m除以n所得的余数为r.第三步,m=n,n=r.第四步,若r=0,则m,n的最大公约数等于m;否则,返回第二步.程序框图如下图:程序:INPUT m,nDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND点评:从教学实践看,有些学生不能理解算法中的转化过程,例如:求8 251与6 105的最大公约数,为什么可以转化为求6 105与2 146的公约数.因为8 251=6 105×1+2 146,可以化为8 251-6 105×1=2 164,所以公约数能够整除等式两边的数,即6 105与2 146的公约数也是8 251与6 105的公约数.变式训练你能用当型循环结构构造算法,求两个正整数的最大公约数吗?试画出程序框图和程序.解:当型循环结构的程序框图如下图:程序:INPUT m,nr=1WHILE r>0r=m MOD nm=nn=rWENDPRINT mEND例2 用更相减损术求98与63的最大公约数.解:由于63不是偶数,把98和63以大数减小数,并辗转相减,如下图所示.98-63=3563-35=2835-28=728-7=2121-7=1414-7=7所以,98和63的最大公约数等于7.点评:更相减损术与辗转相除法的比较:尽管两种算法分别来源于东、西方古代数学名著,但是二者的算理却是相似的,有异曲同工之妙.主要区别在于辗转相除法进行的是除法运算,即辗转相除;而更相减损术进行的是减法运算,即辗转相减,但是实质都是一个不断的递归过程.变式训练用辗转相除法或者更相减损术求三个数324,243,135的最大公约数.解:324=243×1+81,243=81×3+0,则324与243的最大公约数为81.又135=81×1+54,81=54×1+27,54=27×2+0,则81 与135的最大公约数为27.所以,三个数324、243、135的最大公约数为27.另法:324-243=81,243-81=162,162-81=81,则324与243的最大公约数为81.135-81=54,81-54=27,54-27=27,则81与135的最大公约数为27.所以,三个数324、243.135的最大公约数为27.例3 (1)用辗转相除法求123和48的最大公约数.(2)用更相减损术求80和36的最大公约数.解:(1)辗转相除法求最大公约数的过程如下:123=2×48+27,48=1×27+21,27=1×21+6,21=3×6+3,6=2×3+0,最后6能被3整除,得123和48的最大公约数为3.(2)我们将80作为大数,36作为小数,因为80和36都是偶数,要除公因数2.80÷2=40,36÷2=18.40和18都是偶数,要除公因数2.40÷2=20,18÷2=9.下面来求20与9的最大公约数,20-9=11,11-9=2,9-2=7,7-2=5,5-2=3,3-2=1,2-1=1,可得80和36的最大公约数为22×1=4.点评:对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等.变式训练分别用辗转相除法和更相减损术求1 734,816的最大公约数.解:辗转相除法:1 734=816×2+102,816=102×8(余0),∴1 734与816的最大公约数是102.更相减损术:因为两数皆为偶数,首先除以2得到867,408,再求867与408的最大公约数.867-408=459,459-408=51,408-51=357,357-51=306,306-51=255,255-51=204,204-51=153,153-51=102,102-51=51.∴1 734与816的最大公约数是51×2=102.利用更相减损术可另解:1 734-816=918,918-816=102,816-102=714,714-102=612,612-102=510,510-102=408,408-102=306,306-102=204,204-102=102.∴1 734与816的最大公约数是102.知能训练求319,377,116的最大公约数.解:377=319×1+58,319=58×5+29,58=29×2.∴377与319的最大公约数为29,再求29与116的最大公约数.116=29×4.∴29与116的最大公约数为29.∴377,319,116的最大公约数为29.拓展提升试写出利用更相减损术求两个正整数的最大公约数的程序.解:更相减损术程序:INPUT “m,n=”;m,nWHILE m<>nIF m>n THENm=m-nELSEm=n-mEND IFWENDPRINT mEND课堂小结(1)用辗转相除法求最大公约数.(2)用更相减损术求最大公约数.思想方法:递归思想.作业分别用辗转相除法和更相减损术求261,319的最大公约数.分析:本题主要考查辗转相除法和更相减损术及其应用.使用辗转相除法可依据m=nq+r,反复执行,直到r=0为止;用更相减损术就是根据m-n=r,反复执行,直到n=r为止.解:辗转相除法:319=261×1+58,261=58×4+29,58=29×2.∴319与261的最大公约数是29.更相减损术:319-261=58,261-58=203,203-58=145,145-58=87,87-58=29,58-29=29,∴319与261的最大公约数是29.设计感想数学不仅是一门科学,也是一种文化,本节的引入从东、西方文化的不同开始,逐步向学生渗透数学文化.从知识方面主要学习用两种方法求两个正整数的最大公约数,从思想方法方面,主要学习递归思想.本节设置精彩例题,不仅让学生学到知识,而且让学生进一步体会算法的思想,培养学生的爱国主义情操.第2课时案例2 秦九韶算法导入新课思路1(情境导入)大家都喜欢吃苹果吧,我们吃苹果都是从外到里一口一口的吃,而虫子却是先钻到苹果里面从里到外一口一口的吃,由此看来处理同一个问题的方法多种多样.怎样求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值呢?方法也是多种多样的,今天我们开始学习秦九韶算法.思路2(直接导入)前面我们学习了辗转相除法与更相减损术,今天我们开始学习秦九韶算法.推进新课新知探究提出问题(1)求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值有哪些方法?比较它们的特点.(2)什么是秦九韶算法?(3)怎样评价一个算法的好坏?讨论结果:(1)怎样求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值呢?一个自然的做法就是把5代入多项式f(x),计算各项的值,然后把它们加起来,这时,我们一共做了1+2+3+4=10次乘法运算,5次加法运算.另一种做法是先计算x2的值,然后依次计算x2·x,(x2·x)·x,((x2·x)·x)·x的值,这样每次都可以利用上一次计算的结果,这时,我们一共做了4次乘法运算,5次加法运算.第二种做法与第一种做法相比,乘法的运算次数减少了,因而能够提高运算效率,对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以采用第二种做法,计算机能更快地得到结果.(2)上面问题有没有更有效的算法呢?我国南宋时期的数学家秦九韶(约1202~1261)在他的著作《数书九章》中提出了下面的算法:把一个n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0改写成如下形式:f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+ a0=((a n x n-2+a n-1x n-3+…+a2)x+a1)x+a0=…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0.求多项式的值时,首先计算最内层括号内一次多项式的值,即v1=a n x+a n-1,然后由内向外逐层计算一次多项式的值,即v2=v1x+a n-2,v3=v2x+a n-3,…v n=v n-1x+a0,这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.上述方法称为秦九韶算法.直到今天,这种算法仍是多项式求值比较先进的算法.(3)计算机的一个很重要的特点就是运算速度快,但即便如此,算法好坏的一个重要标志仍然是运算的次数.如果一个算法从理论上需要超出计算机允许范围内的运算次数,那么这样的算法就只能是一个理论的算法.应用示例例1 已知一个5次多项式为f (x )=5x 5+2x 4+3.5x 3-2.6x 2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.解:根据秦九韶算法,把多项式改写成如下形式:f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8,按照从内到外的顺序,依次计算一次多项式当x=5时的值:v 0=5;v 1=5×5+2=27;v 2=27×5+3.5=138.5;v 3=138.5×5-2.6=689.9;v 4=689.9×5+1.7=3 451.2;v 5=3 415.2×5-0.8=17 255.2;所以,当x=5时,多项式的值等于17 255.2.算法分析:观察上述秦九韶算法中的n 个一次式,可见v k 的计算要用到v k-1的值,若令v 0=a n ,我们可以得到下面的公式:⎩⎨⎧=+==--).,,2,1(,10n k a x v v a v k n k kn 这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.算法步骤如下:第一步,输入多项式次数n 、最高次的系数a n 和x 的值.第二步,将v 的值初始化为a n ,将i 的值初始化为n-1.第三步,输入i 次项的系数a i .第四步,v=vx+a i ,i=i-1.第五步,判断i 是否大于或等于0.若是,则返回第三步;否则,输出多项式的值v. 程序框图如下图:程序:INPUT “n=”;nINPUT “an=”;aINPUT “x=”;xv=ai=n-1WHILE i>=0PRINT “i=”;iINPUT “ai=”;av=v*x+ai=i-1WENDPRINT vEND点评:本题是古老算法与现代计算机语言的完美结合,详尽介绍了思想方法、算法步骤、程序框图和算法语句,是一个典型的算法案例.变式训练请以5次多项式函数为例说明秦九韶算法,并画出程序框图.解:设f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0首先,让我们以5次多项式一步步地进行改写:f(x)=(a5x4+a4x3+a3x2+a2x+a1)x+a0=((a5x3+a4x2+ a3x+a2)x+a1)x+a0=(((a5x2+a4x+ a3)x+a2)x+a1)x+a0=((((a5x+a4)x+ a3)x+a2)x+a1)x+a0.上面的分层计算,只用了小括号,计算时,首先计算最内层的括号,然后由里向外逐层计算,直到最外层的括号,然后加上常数项即可.程序框图如下图:例2 已知n次多项式P n(x)=a0x n+a1x n-1+…+a n-1x+a n,如果在一种算法中,计算k x0(k=2,3,4,…,n)的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要__________次运算.下面给出一种减少运算次数的算法:P0(x)=a0,P k+1(x)=xP k(x)+a k+1(k=0,1,2,…,n-1).利用该算法,计算P3(x0)的值共需要6次运算,计算P10(x0)的值共需要___________次运算.答案:65 20点评:秦九韶算法适用一般的多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0的求值问题.直接法乘法运算的次数最多可到达2)1(nn,加法最多n次.秦九韶算法通过转化把乘法运算的次数减少到最多n次,加法最多n次.例3 已知多项式函数f(x)=2x5-5x4-4x3+3x2-6x+7,求当x=5时的函数的值. 解析:把多项式变形为:f(x)=2x5-5x4-4x3+3x2-6x+7=((((2x-5)x-4)x+3)x-6)x+7.计算的过程可以列表表示为:最后的系数2 677即为所求的值.算法过程:v0=2;v1=2×5-5=5;v2=5×5-4=21;v3=21×5+3=108;v4=108×5-6=534;v5=534×5+7=2 677.点评:如果多项式函数中有缺项的话,要以系数为0的项补齐后再计算.知能训练当x=2时,用秦九韶算法求多项式f(x)=3x5+8x4-3x3+5x2+12x-6的值.解法一:根据秦九韶算法,把多项式改写成如下形式:f(x)=((((3x+8)x-3)x+5)x+12)x-6.按照从内到外的顺序,依次计算一次多项式当x=2时的值.v0=3;v1=v0×2+8=3×2+8=14;v2=v1×2-3=14×2-3=25;v3=v2×2+5=25×2+5=55;v4=v3×2+12=55×2+12=122;v5=v4×2-6=122×2-6=238.∴当x=2时,多项式的值为238.解法二:f(x)=((((3x+8)x-3)x+5)x+12)x-6,则f(2)=((((3×2+8)×2-3)×2+5)×2+12)×2-6=238.拓展提升用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3时的值.解:f(x)=((((((7x+6)+5)x+4)x+3)x+2)x+1)xv0=7;v1=7×3+6=27;v2=27×3+5=86;v3=86×3+4=262;v4=262×3+3=789;v5=789×3+2=2 369;v6=2 369×3+1=7 108;v7=7 108×3+0=21 324.∴f(3)=21 324.课堂小结1.秦九韶算法的方法和步骤.2.秦九韶算法的计算机程序框图.作业已知函数f(x)=x3-2x2-5x+8,求f(9)的值.解:f(x)=x3-2x2-5x+8=(x2-2x-5)x+8=((x-2)x-5)x+8∴f(9)=((9-2)×9-5)×9+8=530.设计感想古老的算法散发浓郁的现代气息,这是一节充满智慧的课.本节主要介绍了秦九韶算法.通过对秦九韶算法的学习,对算法本身有哪些进一步的认识?教师引导学生思考、讨论、概括,小结时要关注如下几点:(1)算法具有通用的特点,可以解决一类问题;(2)解决同一类问题,可以有不同的算法,但计算的效率是不同的,应该选择高效的算法;(3)算法的种类虽多,但三种逻辑结构可以有效地表达各种算法等等.第3课时案例3 进位制导入新课情境导入在日常生活中,我们最熟悉、最常用的是十进制,据说这与古人曾以手指计数有关,爱好天文学的古人也曾经采用七进制、十二进制、六十进制,至今我们仍然使用一周七天、一年十二个月、一小时六十分的历法.今天我们来学习一下进位制.推进新课新知探究提出问题(1)你都了解哪些进位制?(2)举出常见的进位制.(3)思考非十进制数转换为十进制数的转化方法.(4)思考十进制数转换成非十进制数及非十进制之间的转换方法.活动:先让学生思考或讨论后再回答,经教师提示、点拨,对回答正确的学生及时表扬,对回答不准确的学生提示引导考虑问题的思路.讨论结果:(1)进位制是人们为了计数和运算方便而约定的计数系统,约定满二进一,就是二进制;满十进一,就是十进制;满十二进一,就是十二进制;满六十进一,就是六十进制等等.也就是说:“满几进一”就是几进制,几进制的基数(都是大于1的整数)就是几.(2)在日常生活中,我们最熟悉、最常用的是十进制,据说这与古人曾以手指计数有关,爱好天文学的古人也曾经采用七进制、十二进制、六十进制,至今我们仍然使用一周七天、一年十二个月、一小时六十分的历法.(3)十进制使用0~9十个数字.计数时,几个数字排成一行,从右起,第一位是个位,个位上的数字是几,就表示几个一;第二位是十位,十位上的数字是几,就表示几个十;接着依次是百位、千位、万位……例如:十进制数3 721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一.于是,我们得到下面的式子:3 721=3×103+7×102+2×101+1×100.与十进制类似,其他的进位制也可以按照位置原则计数.由于每一种进位制的基数不同,所用的数字个数也不同.如二进制用0和1两个数字,七进制用0~6七个数字.一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式a n a n-1…a1a0(k)(0<a n<k,0≤a n-1,…,a1,a0<k).其他进位制的数也可以表示成不同位上数字与基数的幂的乘积之和的形式,如110 011(2)=1×25+1×24+0×23+0×22+1×21+1×20,7 342(8)=7×83+3×82+4×81+2×80.非十进制数转换为十进制数比较简单,只要计算下面的式子值即可:a n a n-1…a1a0(k)=a n×k n+a n-1×k n-1+…+a1×k+a0.第一步:从左到右依次取出k进制数a n a n-1…a1a0(k)各位上的数字,乘以相应的k的幂,k的幂从n开始取值,每次递减1,递减到0,即a n×k n,a n-1×k n-1,…,a1×k,a0×k0;第二步:把所得到的乘积加起来,所得的结果就是相应的十进制数.(4)关于进位制的转换,教科书上以十进制和二进制之间的转换为例讲解,并推广到十进制和其他进制之间的转换.这样做的原因是,计算机是以二进制的形式进行存储和计算数据的,而一般我们传输给计算机的数据是十进制数据,因此计算机必须先将十进制数转换为二进制数,再处理,显然运算后首次得到的结果为二进制数,同时计算机又把运算结果由二进制数转换成十进制数输出.1°十进制数转换成非十进制数把十进制数转换为二进制数,教科书上提供了“除2取余法”,我们可以类比得到十进制数转换成k进制数的算法“除k取余法”.2°非十进制之间的转换一个自然的想法是利用十进制作为桥梁.教科书上提供了一个二进制数据与16进制数据之间的互化的方法,也就是先由二进制数转化为十进制数,再由十进制数转化成为16进制数. 应用示例思路1例1 把二进制数110 011(2)化为十进制数.解:110 011(2)=1×25+1×24+0×23+0×22+1×21+1×20=1×32+1×16+1×2+1=51.点评:先把二进制数写成不同位上数字与2的幂的乘积之和的形式,再按照十进制的运算规则计算出结果.变式训练设计一个算法,把k进制数a(共有n位)化为十进制数b.算法分析:从例1的计算过程可以看出,计算k进制数a的右数第i位数字a i与k i-1的乘积a i·k i-1,再将其累加,这是一个重复操作的步骤.所以,可以用循环结构来构造算法.算法步骤如下:第一步,输入a,k和n的值.第二步,将b的值初始化为0,i的值初始化为1.第三步,b=b+a i·k i-1,i=i+1.第四步,判断i>n是否成立.若是,则执行第五步;否则,返回第三步.第五步,输出b的值.程序框图如下图:程序:INPUT “a,k,n=”;a,k,nb=0i=1t=a MOD 10DOb=b+t*k^(i-1)a=a\\10t=a MOD 10i=i+1LOOP UNTIL i>nPRINT bEND例2 把89化为二进制数.解:根据二进制数“满二进一”的原则,可以用2连续去除89或所得商,然后取余数.具体计算方法如下:因为89=2×44+1,44=2×22+0,22=2×11+0,11=2×5+1,5=2×2+1,2=2×1+0,1=2×0+1,所以89=2×(2×(2×(2×(2×2+1)+1)+0)+0)+1=2×(2×(2×(2×(22+1)+1)+0)+0)+1=…=1×26+0×25+1×24+1×23+0×22+0×21+1×20=1 011 001(2).这种算法叫做除2取余法,还可以用下面的除法算式表示:把上式中各步所得的余数从下到上排列,得到89=1 011 001(2).上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.变式训练设计一个程序,实现“除k取余法”.算法分析:从例2的计算过程可以看出如下的规律:若十制数a除以k所得商是q0,余数是r0,即a=k·q0+r0,则r0是a的k进制数的右数第1位数.若q0除以k所得的商是q1,余数是r1,即q0=k·q1+r1,则r1是a的k进制数的左数第2位数.……若q n-1除以k所得的商是0,余数是r n,即q n-1=r n,则r n是a的k进制数的左数第1位数.这样,我们可以得到算法步骤如下:第一步,给定十进制正整数a和转化后的数的基数k.第二步,求出a除以k所得的商q,余数r.第三步,把得到的余数依次从右到左排列.第四步,若q≠0,则a=q,返回第二步;否则,输出全部余数r排列得到的k进制数.程序框图如下图:程序:INPUT “a,k=”;a,kb=0i=0DOq=a\\kr=a MOD kb=b+r*10^ii=i+1a=qLOOP UNTIL q=0PRINT bEND思路2例1 将8进制数314 706(8)化为十进制数,并编写出一个实现算法的程序.解:314 706(8)=3×85+1×84+4×83+7×82+0×81+6×80=104 902.所以,化为十进制数是104 902.点评:利用把k进制数转化为十进制数的一般方法就可以把8进制数314 706(8)化为十进制数.例2 把十进制数89化为三进制数,并写出程序语句.解:具体的计算方法如下:89=3×29+2,29=3×9+2,9=3×3+0,3=3×1+0,1=3×0+1,所以:89(10)=10 022(3).点评:根据三进制数满三进一的原则,可以用3连续去除89及其所得的商,然后按倒序的顺序取出余数组成数据即可.知能训练将十进制数34转化为二进制数.分析:把一个十进制数转换成二进制数,用2反复去除这个十进制数,直到商为0,所得余数(从下往上读)就是所求.解:即34(10)=100 010(2)拓展提升把1 234(5)分别转化为十进制数和八进制数.解:1 234(5)=1×53+2×52+3×5+4=194.则1 234(5)=302(8)所以,1 234(5)=194=302(8)点评:本题主要考查进位制以及不同进位制数的互化.五进制数直接利用公式就可以转化为十进制数;五进制数和八进制数之间需要借助于十进制数来转化.课堂小结(1)理解算法与进位制的关系.(2)熟练掌握各种进位制之间转化.作业习题1.3A组3、4.设计感想计算机是以二进制的形式进行存储和计算数据的,而一般我们传输给计算机的数据是十进制数据,因此计算机必须先将十进制数转换为二进制数,再处理,显然运算后首次得到的结果为二进制数,同时,计算机又把运算结果由二进制数转换成十进制数输出.因此学好进位制是非常必要的,另外,进位制也是高考的重点,本节设置了多种题型供学生训练,所以这节课非常实用.。
1.3 算法案例

1.3 算法案例一、知识点归纳与讲解1、辗转相除法与更相减损术(1)辗转相除法所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。
若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
(1)算法步骤:第一步:输入两个正整数m ,n (m>n).第二步:计算m除以n所得的余数r.第三步:m=n,n=r.第四步:若r=0,则m,n的最大公约数等于m,否则转到第二步.第五步:输出最大公约数m.(2)程序框图:(3)程序(2)更相减损术所谓更相减损术,就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
事实上分两步完成,第一步:任意给定两个正整数;判断他们是否都是偶数。
若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。
继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
(1)算法步骤第一步:输入两个正整数a,b;第二步:若a不等于b ,则执行第三步;否则转到第五步;第三步:把a-b的差赋予r;第四步:如果b>r, 那么把b 赋给a,把r 赋给b;否则把r 赋给a ;返回第二步; 第五步:输出最大公约数b.(2)程序框图 (3)程序说明:辗转相除法和更相减损术的区别与联系:(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.辗转相除法和更相减损术本质均是将两数逐步分解成某一数的倍数加上余数,直至余数等于0为止,之所以一个为除(即乘),一个减(即加),是因为“乘”运算原本由“加”运算变化而来,更相减损术对于求多于两个数的最大公约数问题,更具有优越性。
学案6:1.3 算法案例

1.3算法案例1.问题导航(1)什么叫辗转相除法?(2)什么叫更相减损术?(3)辗转相除法与更相减损术的区别是什么?(4)什么是秦九韶算法?(5)学习了十进制,知道十进制是使用0~9十个数字,那么二进制、五进制、七进制分别使用哪些数字?读后验收1.辗转相除法与更相减损术(1)辗转相除法:又叫欧几里得算法,是一种求两个正整数的最大公约数的古老而有效的算法.(2)更相减损术:我国古代数学专著《九章算术》中介绍的一种求两个正整数的最大公约数的算法.2.秦九韶算法功能它是一种用于计算一元n次多项式的值的方法改写后的形式f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+a0=((a n x n-2+a n-1x n-3+…+a2)x+a1)x+a0=…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0计算方法从括号最内层开始,由内向外逐层计算v1=a n x+a n-1,v2=v1x+a n-2,v3=v2x+a n-3,v n=v n-1x+a0,…这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.3.进位制(1)进位制进位制是人们为了计数和运算方便而约定的记数系统,“满几进一”就是几进制,几进制的基数就是几.(2)其他进位制与十进制间的转化①其他进位制化成十进制其他进位制的数化成十进制时,表示成不同位上数字与基数的幂的乘积之和的形式.②十进制化成k进制的方法——“除k取余法”.自我测评1.用更相减损术求294和84的最大公约数时,需做减法运算的次数是() A.2B.3C.4 D.52.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是()A.6,6 B.5,6C.5,5 D.6,53.完成下列进位制之间的转化.(1)1 034(7)=________(10);(2)119(10)=________(6).4.当所给的多项式按x的降幂排列“缺项”时,用秦九韶算法改写多项式时,应注意什么?名师点津1.对于任何一个数,我们可以用不同的进位制来表示.2.表示各种进位制数一般在数字右下角加注来表示,如111 001(2)表示二进制数,34(5)表示5进制数.3.电子计算机一般都使用二进制.4.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用.5.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的M进制数.6.利用秦九韶算法可以减少计算次数提高计算效率.题型探究探究一求最大公约数例1 用辗转相除法求612与468的最大公约数,并用更相减损术检验所得结果.方法归纳(1)利用辗转相除法求给定的两个数的最大公约数,即利用带余除法,用数对中较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的数对,再利用带余除法,直到大数被小数除尽,则这时的较小数就是原来两个数的最大公约数.(2)利用更相减损术求两个正整数的最大公约数的一般步骤是:首先判断两个正整数是否都是偶数.若是,用2约简,也可以不除以2,直接求最大公约数,这样不影响最后结果.跟踪训练1.(1)1 624与899的最大公约数是________.(2)用辗转相除法求80和36的最大公约数,并用更相减损术检验所得结果.探究二秦九韶算法及其应用例2 用秦九韶算法写出当x=3时f(x)=2x5-4x3+3x2-5x+1的值.方法归纳利用秦九韶算法将f(x)改写成如下形式f(x)=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0,其计算步骤为:先计算v1=a n x+a n-1,再计算v2=v1x+a n-2,每次都是把上一次的结果乘以x 再与下一个系数相加,其计算量为乘法n次,加法n次.跟踪训练2.利用秦九韶算法求多项式f(x)=3x6+12x5+8x4-3.5x3+7.2x2+5x-13当x=6时的值,写出详细步骤.探究三进位制例3 (1)把二进制数101 101(2)化为十进制数;(2)把十进制数458转化为四进制数.方法归纳(1)将k进制转化为十进制的方法是:先将这个k进制数写成各个数位上的数字与k的幂的乘积之和的形式,再按照十进制的运算规则计算出结果.(2)十进制转化为k进制,采用除k取余法,也就是除基数,倒取余.跟踪训练3.(1)二进制数算式1 010(2)+10(2)的值是()A.1 011(2)B.1 100(2)C.1 101(2)D.1 000(2)(2)下列各组数中最小的数是()A.1 111(2)B.210(6)C.1 000(4)D.101(8)易错警示因忽略零系数项而致误例4 利用秦九韶算法求多项式f(x)=x6-5x5+6x4+x2+3x+2当x=-2时的值为() A.320 B.-160C.-320 D.300跟踪训练4.(1)用秦九韶算法计算多项式f(x)=12+35x-8x2+6x4+5x5+3x6在x=-4时的值时,v3的值为()A.-144 B.-136C.-57 D.34(2)已知多项式f(x)=3x5+8x4-3x3+5x2+12x-6,则f(2)=________.当堂检测1.下列关于利用更相减损术求156和72的最大公约数的说法中正确的是() A.都是偶数必须约简B.可以约简,也可以不约简C.第一步作差为156-72=84;第二步作差为72-84=-12D.以上都不对2.用辗转相除法计算294与84的最大公约数时,需要做的除法次数是() A.1 B.2C.3 D.43.二进制数1 101 111(2)化成十进制数是________.4.若k进制数123(k)与十进制数38相等,则k=________.参考答案1.【解析】选C.294-84=210,210-84=126,126-84=42,84-42=42,共做4次减法运算.【答案】C2.【答案】A3.【解析】(1)1 034(7)=1×73+0×72+3×7+4×70=368.(2)∴119(10)=315(6).【答案】(1)368(2)3154.解:所缺的项写成系数为零的形式,即写成0·x n的形式.例1解:用辗转相除法:612=468×1+144,468=144×3+36,144=36×4,即612和468的最大公约数是36.用更相减损术检验:612和468为偶数,两次用2约简得153和117,153-117=36,117-36=81,81-36=45,45-36=9,36-9=27,27-9=18,18-9=9,所以612和468的最大公约数为9×2×2=36.跟踪训练1. (1)【解析】1 624=899×1+725,899=725×1+174,725=174×4+29,174=29×6,故1 624与899的最大公约数是29.【答案】29(2)解:辗转相除法:80=36×2+8,36=8×4+4,8=4×2+0.故80和36的最大公约数是4.用更相减损术检验:80-36=44,44-36=8,36-8=28,28-8=20,20-8=12,12-8=4,8-4=4,∴80和36的最大公约数是4.例2 解:∵f(x)=((((2x+0)x-4)x+3)x-5)x+1,v0=2,v1=2×3+0=6,v2=6×3-4=14,v3=14×3+3=45,v4=45×3-5=130,v5=130×3+1=391,所以f(3)=391.跟踪训练2.解:f(x)=(((((3x+12)x+8)x-3.5)x+7.2)x+5)x-13.v0=3,v1=v0×6+12=30,v2=v1×6+8=188,v3=v2×6-3.5=1 124.5,v4=v3×6+7.2=6 754.2,v5=v4×6+5=40 530.2,v6=v5×6-13=243 168.2.所以f(6)=243 168.2.例3 解:(1) 101 101(2)=1×25+0×24+1×23+1×22+0×21+1×20=32+8+4+1=45,所以二进制数101 101(2)转化为十进制数为45.(2)458=13 022(4).跟踪训练3.【解析】(1)选B.二进制数的加法是逢二进一,所以选B.【答案】B(2)【解析】选A.统一化为十进制数为1 111(2)=15;210(6)=78;1 000(4)=64;101(8)=65.【答案】A例4 【解析】将多项式变式为f(x)=(((((x-5)x+6)x+0)x+1)x+3)x+2,v0=1,v1=-2+(-5)=-7,v2=-7×(-2)+6=20,v3=20×(-2)+0=-40,v4=-40×(-2)+1=81,v5=81×(-2)+3=-159,v6=-159×(-2)+2=320.【答案】A[错因与防范](1)考虑x=-2而认为多项式的值为负值.(2)易忽略多项式中系数为0的项,致使多项式改写不正确.(3)解题时注意多项式变形后有几次乘法和几次加法.(4)要注意所给多项式的项数,特别是系数为0的项跟踪训练4 .(1)【解析】选B.根据秦九韶算法多项式可化为f(x)=(((((3x+5)x+6)x+0)x-8)x+35)x+12.由内向外计算v0=3;v1=3×(-4)+5=-7;v2=-7×(-4)+6=34;v3=34×(-4)+0=-136.【答案】B(2)【解析】根据秦九韶算法,把多项式改写成如下形式:f(x)=((((3x+8)x-3)x+5)x+12)x-6.按照从内到外的顺序,依次计算一次多项式当x=2时的值.v0=3,v1=3×2+8=14,v2=14×2-3=25,v3=25×2+5=55,v4=55×2+12=122,v5=122×2-6=238,所以当x=2时,多项式的值为238.【答案】2381.【解析】选B.约简是为了使运算更加简捷,故不一定要约简,A错.C中第二步应为84-72=12,故选B.【答案】B2.【解析】选B.294=84×3+42,84=42×2,至此公约数已求出.【答案】B3.【解析】1 101 111(2)=1×20+1×21+1×22+1×23+0×24+1×25+1×26=111.【答案】1114.【解析】由k进制数123可知k≥4.下面可用验证法:若k=4,则38(10)=212(4),不合题意;若k=5,则38(10)=123(5)成立,所以k=5.【答案】5。
1.3 算法案例

配人教版 数学 必修3
对于B:因为124(5)=1×52+2×51+4×50=39≠62,所以 B错误.
对于C:因为110(2)=1×22+1×21+0×20=6, 10(3)=1×31+0×30=3,6>3,所以C正确. 对于D:因为32(4)=3×41+2×40=14, 23(6)=2×61+3×60=15,14≠15. 所以D错误.故选C.
【解析】f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)x,所 以有
v0=7; v1=7×3+6=27;
配人教版 数学 必修3
v2=27×3+5=86; v3=86×3+4=262; v4=262×3+3=789; v5=789×3+2=2 369; v6=2 369×3+1=7 108; v7=7 108×3=21 324. 故当x=3时,多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+ x的值为21 324.
配人教版 数学 必修3
3.用辗转相除法求294和84的最大公约数时,需要做除法
的次数是( )
A.1
B.2
C.3
D.4
【答案】B
【解析】本题考查辗转相除法的过程.294=84×3+42,84
=42×2,故选B.
配人教版 数学 必修3
4.以下各数有可能是五进制数的是( )
A.15
B.106
C.731
配人教版 数学 必修3 再把十进制数 458 化为六进制数.
458=2 042(6). 故 13 022(4)=2 042(6).
配人教版 数学 必修3
不同进位制之间数的大小比较时忽略转化致误
【示例】下列结论正确的是( )
A.88(9)<210(6) C.110(2)>10(3) 【错解】A或B
