fx-4800P曲线计算
“第1章 绪论”CASIOfx-4800P计算程序

“第1章 绪论”CASIOfx-4800P 计算程序§1.1 参考椭球元素计算测量中,高程的基准面是大地水准面,地表某点距离大地水准面的垂直距离称为该点的高程H ;大地坐标系的基准是参考椭球,用大地经度L 和大地纬度B 表示点在参考椭球表面的位置,用大地方位角A 表示球面上边长的方向。
定义参考椭球大小的元素值为:a ——长半轴b ——短半轴f ——扁率 aba f −=e ——第一偏心率 2222a b a e −=e ′ ——第二偏心率 2222b b a e −=c ——极曲率半径 ba c 2=我国采用过的两个参考椭球元素值以及GPS 测量使用的参考椭球元素值列于表1-1。
表1-1 参考椭球元素值坐标系名称 1954北京坐标系 1980西安坐标系 WGS-84坐标系(GPS 用)参考椭球名称 克拉索夫斯基椭球 IUGG —1975椭球 IUGG —1979椭球a 6378245 6378140 6378137b6356863.01877 6356755.28815 6356752.31424066 f 1:298.3 1:298.257 1:298.2572235632e 0.006693421622966 0.006694384999588 0.006694379990132e ′ 0.006738525414684 0.006739501819473 0.00673949674227 c6399698.90178 6399596.65199 6399593.62601(1) 数学模型通过参考椭球面上任一点的法线,可以作无数个法截面,法截面与参考椭球面的交线称为法截线,球面上不同纬度及方向法截弧线的曲率半径是不相同的。
1) 子午圈曲率半径M通过参考椭球旋转轴南北极的法截面(也称子午面)与参考椭球面相截形成的闭合圈称为子午圈,其曲率半径M 的计算公式为:3Vc M =(1-1) 式中21η+=V(1-2) B e cos ′=η(1-3)2) 卯酉圈曲率半径N与该点子午面相垂直的法截面与参考椭球面相截形成的闭合圈称为卯酉圈,其曲率半径N 的计算公式为:Vc N =(1-4)3) 平均曲率半径R2V c MN R == (1-5)由于V >1,所以有M R N >>。
卡西欧F4800计算编程公式

P=L^2÷6R-L^4÷336R^3-R(1-cos(90L÷πR))
Q=E^2÷6R-E^4÷336R^3-R(1-cos(90E÷πR))
D=(P-Q)I÷2 : F=(P+Q+2R)I÷2
M=F+M-D:Q=F+N+D
|PC|^2=(y+3)^2+1=y^2+6y+10=(y+3)^2+1>=1 (在y=-3时取得最小值1)
|PB|-|PC|=√(y^2+4)-√(y^2+6y+10)
当|PB|=|PC|时能取得最小值0,不能取得最大值,最小时y=-1
(3)
平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,所以MN两点关于x=1对称
起点 第一回旋线终点
或
圆曲线起点 圆曲线
中点 圆曲线终点
或
第二回旋线起点 第二回旋线
终点
R1
Ry
R2 Ls1
Ly
Ls2 T1
D=Z[W-1]+ScosP
F=Z[W+Z+1]+SsinP:Goto6
Lb1 3
I=S-S^5÷40R^2÷L^2+S^9÷3456R^4÷L^4
J=Q(S^3÷6RL-S^7÷336R^3÷L^3)
P=P+A+90QS^2÷πRL:Goto5
Lb1 4
M=90(2S+L)÷πR
Z[1]“YH”=M+πRAbs F÷180▲
4800公路测量放样计算程序

4800公路测量放样计算程序CASIO fx-4800P计算器程序DA DI——N E (公路弯道坐标计算)K“JD”:R:S“LS”:F“PJ——L-R+”:A“ZH——N”:B“ZH——E”:C“JD——N”:D“JD——E”M“ZH”=K-(R+S2÷(24R))tan(Abs F÷2)-S÷2+S^3÷(240R2)▲N“HY”=M+S▲O“QZ”=M+(πRAbs F÷180+S)÷2▲Z[1]“YH”=M+πRAbs F÷180▲Q“HZ”= Z[1]+S▲T=K-M▲L=Q-M▲E=(R+S2÷(24R))÷cos(F÷2)-R▲Lb1 0:{G}:G“ZHUANG HAO”:G<O==>Z=G-M≠=>Z=Q-G:△{U}:U“I——B OUT+IN-”Z<S+0.005==>H=tan-1(24Z2S2R2-Z^6)÷(48Z^3R^3-6Z^4SR)):V=Z-Z^5÷(40S2R2)+Usin H:W=Z^3÷(6SR)-Z ^7÷(336Z^3R^3)-Ucos H:≠=>H=180(Z-S÷2)÷(πR):V=Rsin H+S÷2-S^3÷(240R2)+Usin H:W=R-Rcos H+S2÷(24R)-Ucos H:△F<0==>G<O==>X=V:Y=W:≠=>X=T+Tcos F-Vcos F-Wsin Abs F:Y=Tsin Abs F -Vsin Abs F+Wcos F:△≠=>G<O==>X=V:Y=-W:≠=>X=T+Tcos F-Vcos F-Wsin Abs F:Y=Vsin Abs F-Tsin Abs F-Wcos F:△△C=A==>D≥B==>P=90:≠=>P=270:△≠=>C<A==>P= tan-1((D-B)÷(C-A))+180:≠=>P= tan-1((D-B)÷(C-A)):△△I“COM——N”=A+√(X2+Y2)cos(P-tan-1(Y÷X))▲J“COM——E”=B+√(X2+Y2)sin(P-tan-1(Y÷X))▲G=G+20Goto 0程序运行输入:JD?——交点桩号R?——圆曲线半径LS?——缓和曲线长度PJ——L-R+?——偏角右偏为正ZH——N?——ZH点N坐标ZH——E?——ZH点E坐标JD——N?——JD点N坐标JD——E?——JD点E坐标输出:ZH= ——ZH点桩号HY= ——HY点桩号QZ= ——QZ点桩号YH= ——YH点桩号HZ= ——HZ点桩号T= ——切线长L= ——曲线长E= ——外矢距再输入:ZHUANG HAO?——输入任一点桩号I——B OUT+IN-?——距中线距离(外侧为正)再输出:COM——N= ——计算出N坐标COM——E= ——计算出E坐标以此循环——再输入——再输出程序中各字母所代表的含义:A——ZH点N坐标B——ZH点E坐标C——JD点N坐标D——JD点E坐标E——外矢距F——偏角(右偏为正)G——弯道内任一点桩号H——弯道内任一点切线角I——计算出的N坐标J——计算出的E坐标K——交点桩号L——曲线长M——ZH点桩号N——HY点桩号O——QZ点桩号P——ZH--JD方位角Q——HZ点桩号R——圆曲线半径S——缓和曲线长度T——切线长U——距中线距离(外侧为正)V——支距W——支距X——弯道内坐标Y——弯道内坐标Z——任一点曲线长度Z[1]——YH点桩号。
非对称缓和曲线坐标计算程序

非对称缓和曲线坐标计算程序CASIO fx-4800P QXZB曲线坐标计算CASIO4800 QXZB可计算不等缓和曲线、圆曲线上的任意中、边桩坐标:该程序适用于计算器 CASIO fx-4800P,可计算与线路中心成任意夹角的缓和曲线、圆曲线中、边桩坐标及待测点方位角和距离。
1、DK(JD)?输入交点桩号2、X(JD)?输入交点坐标X3、Y(JD)?输入交点坐标Y4、T1?输入第一切线长(如果只有一条切线两者都输入一致)5、T2?输入第二切线长(如果只有一条切线两者都输入一致)6、FWJ?输入直线方位角(ZH→JD)7、A?输入转角:左转为负,右转为正8、R?输入圆曲线半径9、LS1?输入第一缓和曲线长(如果只有一条缓和曲线两者都输入一致)10、LY?输入圆曲线长(L-LS1-LS2)11、LS2?输入第二缓和曲线长(如果只有一条缓和曲线两者都输入一致)12、X(ZJD)?输入置镜点坐标X13、Y(ZJD)?输入置镜点坐标Y14、JSDK?输入前视点里程15、PL?输入偏距16、PA?输入偏角程序下载地址:/blog/post/QXZB-4800.html评价答案好:18不好:1原创:18非原创:0菲メ帆ぅ回答采纳率:52.8% 2010-06-02 17:37满意答案好评率:57%(for Casio-fx4850)扩展变量操作(15个):Defm 15←┚ ( O为字母、0为数字)J-PQX (平面数据输入,自行切换到J-JSMS)Defm 15←┚A“JD” B“JDX” C“JDY” F“FWJ” O“A0:Z-,Y+” RE“LS1” K“LS2”:E<1=>E=1E-9⊿K<1=>K=1E-9⊿Z[1]=EE÷24R-E∧4÷2688RRR:Z[2]=E÷2-EEE÷240RR:X=(EE-KK)÷24R÷sin Abs O :“T1=”:Z[3]=(R+Z[1])tan(Abs O÷2)+Z[2]-X◢“T2=”:Z[4]=(R+KK÷24R-K∧4÷2688RRR)tan(Abs O ÷2)+K÷2-KKK÷240RR+X◢“L=”:L=Abs OπR÷180+(E+K)÷2◢J=tan-1((R+Z[1])÷(Z[3]-Z[2]):“E=”:X=(R+Z[1])÷sin J-R◢X=A-Z[3]:Y=X+E:E<1=>“ZY=”:X◢≠=> “ZH=”:X◢“HY=”:Y◢⊿ “QZ=”:Y =X+(L-K-E)÷2+E◢Y=X+L-K:X=X+L:K<1=> “YZ=”:X◢≠=> “YH=”:Y◢“HZ=”:X◢⊿Prog“J-JSMS” ←┚J-JSMS(放样模式主程序)“1-ZS, FY,3-FS”: Lb1 0:{Z}: Z“MS”≤2=>Goto 1: ≠=> Z≤4=> Goto2⊿⊿←┚Lb1 1 :Q“X-YIQI”S“Y-YIQI”T“X-HOUSI”U“Y-HOUSI”:{PDW}:P“F=”D“BZ=”W“BJ=”: Prog“JP”: Prog“FY”: Goto 1←┚Lb1 2 :{XYW}:XYW“BJ”: Prog“JF”: “P=”: P◢“BZ=”: D◢JP(平曲线正算子程序)Fixm←┚Lb1 1 :J=F:X= B-Z[3]cos F :Y= C-Z[3]sin F :G=E←┚P≤A-Z[3]=>I=A-Z[3]-P:M=-I:N=0:H=F+W:Goto 5←┚≠=>P≤A-Z[3]+E=>I=P-A+Z[3]:H=90II÷REπ:O<0=>H=-H⊿H=H+W+F:Goto 3←┚≠=>P≤A-Z[3]+L-K=>I=P-A+Z[3]-E:Goto 4: ≠=>Goto 2⊿⊿←┚Lb1 2 :X= B+Z[4]cos(F+O :Y= C+Z[4]sin(F+O :J=F+O+180:G=K←┚P≤A-Z[3]+L=>I=A-Z[3]+L-P:H=90II÷RKπ:O>0=>H=-H⊿H=H+J+W+180:Goto 3 ←┚≠=>I=P-A+Z[3]-L:M=-I:N=0:H=J+W+180:Goto 5 ←┚Lb1 3 :M=I-I∧5÷40RRGG:N=III÷6GR-I∧7÷336RRRGGG:Goto 5 ←┚Lb1 4 :H=(E+2I)×90÷πR:M=R sin H+Z[2]:N=R(1-cos H)+Z[1]:O<0=>H=-H⊿H=J+H+W: Goto 5←┚Lb1 5 :P≤A-Z[3]+L-K=> O<0=>N=-N⊿≠=>O>0=>N=-N⊿⊿Goto 6←┚Lb1 6 :X =X+M cos J-N sin J+D cos H:Y =Y+M sin J+N cos J+D sin H“X=”: X ◢。
4800计算器曲线计算程序

线路测设坐标计算程序(Casio fx-4800p)在铁路、公路工程勘测和施工测量中,相对复杂的线路测设工作占了很大比重,且传统线路测设公式已不能满足现代化曲线测设的需要。
为此,笔者根据工程测量的特点,严格定义了坐标系,推导了线路测设的通用计算公式。
该公式不但可以计算单交点平曲线坐标,同时还可以计算复曲线坐标,如不完整缓和曲线等。
根据该公式,笔者编写了Casio fx-4800p 计算器上的单交点平曲线中桩、边桩坐标计算程序。
该程序可以判断已知数据输入的正确性,并可限制输入的测设点里程。
在程序编制过程中,已考虑了零溢出问题。
一.使用说明1.起动名为“ZXZB”的计算程序。
2.输入已知数据:X(QD)—起点纵坐标(EXE)Y(QD)—起点横坐标(EXE)X(JD)—交点纵坐标(EXE)Y(JD)—交点横坐标(EXE)S(JD)—交点里程(EXE)X(ZD)—终点纵坐标(EXE)Y(ZD)—终点横坐标(EXE)RY —圆曲线半径(EXE)L1 —前缓和曲线长度(EXE)RS —前缓和曲线起始半径(0表示无穷大)(EXE)L2 —后缓和曲线长度(EXE)RE —后缓和曲线结束半径(0表示无穷大)(EXE)S(HZ1) —起点缓直点里程(EXE)S(ZH1) —交点直缓点里程(EXE)S(HZ2) —交点缓直点里程(EXE)S(ZH2) —终点直缓点里程(EXE)S? —测设点里程(EXE)X=*** —显示测设点纵坐标(EXE)Y=*** —显示测设点横坐标(EXE)I? —边桩距(左负右正)(EXE)XB=*** —显示边桩纵坐标(EXE)YB=*** —显示边桩横坐标(EXE)I? —输入0结束边桩计算,继续下一测设点计算。
二.计算举例1.已知数据:X(QD)=2175.199 Y(QD)=1015.467X(JD)=2000 Y(JD)=2000S(JD)=6000X(ZD)=2621.088 Y(ZD)=2783.741RY=600L1=220 RS=5800L2=180 RE=3300S(HZ1)=5200 S(ZH1)=5631.047S(HZ2)=6311.047 S(ZH2)=67002.求:各测设点中桩坐标及左边桩10M、右边桩20M坐标3.计算结果三.源程序清单ZXZB1. Defm 15:Rad:Norm↙2. A"X(QD)":B"Y(QD)":C"X(JD)":D"Y(JD)":Z"S(JD)":E"X(ZD)":F"Y(ZD)":N"RY"↙3. Q"L1":R"RS":V"L2":W"RE":G"S(HZ1)":H"S(ZH1)":K"S(HZ2)":L"S(ZH2)":Fixm↙4. O=H+Q:P=K-V:M=Pol (C-A,D-B):T=J:Z[3]=J: Z[1]=C+Rec (Z-H,J+π):Z[2]=D+J↙5. M=Pol(E-C,F-D):Z [12]=J:T=J-T:Abs T>π=>T>π=>T=T-2π: ≠>T=T+2π△△↙6. T>0=>Z[13]=1:≠>Z[13]=-1△↙7. R=0=>Z[14]=0:≠>Z[14]=QN÷(R-N)△↙8. W=0=>Z[15]=0:≠>Z[15]=VN÷(W-N)△↙9.Q=0=>I=0:≠>I=(2QZ[14]+Q²) ÷2÷N÷( Z[14]+Q)△↙10.V=0=>J=0:≠>J=(2V(Z[15]+V)-V²)÷2÷N÷( Z[15]+V)△↙11.Z[6]=Z[3]+I Z[13]: Z[9]=Z[12]-JZ[13] ↙12.T=Abs T-I-J:J=TN:Abs(P-O-J)>0.05=>"ERROR"▲Goto 1△↙13.M=Q:Prog "ZHD":Z[4]=X:Z[5]=Y:M=J:Porg "HYD":Z[7]=X:Z[8]=Y:M=V:Prog "YHD": Z[10]=X:Z[11]=Y↙14.Prog "ZXZS"↙15.Lbl 1:0:"":Pause 0ZXZS1.Rad:Norm:Fixm2.Lbl 2:{S}:S<G=>"RANGE OUT"▲Goto 5△↙3.S>L=>"RANGE OUT"▲Goto 5△↙4.S<H=>M=Z[3]:X=Z[1]+Rec(S-H,M):Y=Z[2]+J:Goto 3△↙5.S<O=>M=S-H:Prog "ZHD":Goto 3△↙6.S<P=>M=S-O:Prog "HYD":Goto 3△↙7.S<K=>M=S-P:Prog "YHD":Goto 3△↙8.M=Z[12]:X=Z[10]+Rec(S-K,M):Y=Z[11]+J↙9.Lbl 3:I"X"=Int (1000X+0.5)÷1000▲J"Y"=Int(1000Y+0.5)÷1000▲10.Lb1 4:I=0:{I}:I>0=>Goto 2△↙11.T=X+Rec(I,M+π÷2):U=Y+J:T"XB"=Int (1000T+0.5)÷1000▲U"YB"=Int(1000U+0.5)÷1000▲Goto 4↙12.Lbl 5:0:"":Pause 0ZHD1.Fixm:M<0.001=>T=0:U=0:M=Z[3]:Goto 6△↙2.I=Z[14]:X=N(I+Q):Y=Z[13]:T=M-(20I²+15IM+3M²)M^3÷120÷X²:T=T+((1008I+1680M)I^3+1080I²M²+(315I+35M)M^3)M^5÷120960÷X^4↙3.U=((70I+84M)I²+(35I+5M)M²)M^4÷1680÷X^3:U=(3I+M)M²÷6÷X-U:U=U+((3696I+7920M)I^4+(6930I+3080M)I²M²+(693I+63M)M^4)M^6÷2661120÷X^5:U=UY↙4.M=(2IM+M²)÷2÷X:I=Z[3]:M=I+MY↙5.Lbl 6:X=Z[1]+Tcos I-Usin I:Y=Z[2]+Tsin I+Ucos IHYD1.Fixm:M=M÷N:I=Z[6]:Y=Z[13]:T=Nsin M:U=(N-Ncos M)Y:M=I+MY2.X=Z[4]+Tcos I-Usin I:Y=Z[5]+Tsin I+Ucos IYHD1.Fixm:M<0.001=>T=0:U=0:M=Z[9]:Goto 7△↙2.I=Z[15] +V:X=NI:Y=Z[13]:T=M-(20I²-15IM+3M²)M^3÷120÷X²:T=T+((1008I-1680M)I^3+1080I²M²-(315I-35M)M^3)M^5÷120960÷X^4↙3.U=((70I-84M)I²+(35I-5M)M²)M^4÷1680÷X^3:U=(3I-M)M²÷6÷X-U:U=U+((3696I-7920M)I^4+(6930I-3080M)I²M²+(693I-63M)M^4)M^6÷2661120÷X^5:U=UY↙4.M=(2IM-M²)÷2÷X:I=Z[9]:M=I+MY↙5.Lbl 7:X=Z[7]+Tcos I-Usin I:Y=Z[8]+Tsin I+UCos I注: 1.由于本计算器程序容量为4500步,本程序只能计算单交点平曲线;2.当已知数据输入存在错误时,程序能够自动判断错误后退出;3.当输入的测设点里程超出范围时,计算自动终止;4.编制程序过程中已经考虑了零溢出问题。
测量程序

CASIO fx-4800测量程序1. 已知凸曲线半径R、切线长T、两切线交点里程K及高程H、切线纵坡P,求凸曲线上任意点里程X处高程 Y(SU QU XIAN T)X“LI CHENG”P“ZONG PO”K“JDX”TRA=K-T÷√(P2+1)×P÷Abs(P)B=H- T÷√(P2+1)×P÷Abs(P)Y“Y ZHONG”=B+(X-A)×P-(X-A)2÷2÷RT——竖曲线切线长R——竖曲线半径H——竖曲线交点处高程K——竖曲线交点里程P——竖曲线纵坡A——竖曲线切点里程2.已知凹曲线半径R、切线长T、两切线交点里程K及高程H、切线纵坡P,求凹曲线上任意点里程X处高程 Y (SU QU XIAN A)X“LI CHENG”P“ZONG PO”K“JDX”TRA=K+T÷√(P2+1)×P÷Abs(P)B=H+ T÷√(P2+1)×P÷Abs(P)Y“Y ZHONG”=B+(X-A)×P-(X-A)2÷2÷RX——竖曲线任意点里程T——竖曲线切线长R——竖曲线半径H——竖曲线交点处高程K——竖曲线交点里程P——竖曲线纵坡3.已知圆曲线起点、终点坐标及起点、终点处里程,半径R,求圆曲线上任意点里程O处坐标 X、Y (Y——Y)O“LX”Z“IF L Z=1;IF R Z=-1”P“L0”V“L1”U“X0”S“Y0”T“X1”Q“Y1”RA=Z×SIN(90×(O-P)÷(π×R))COS(TAN-1((Q-S)÷(T-U))+Z×90×(U-O)÷π÷R)×R:X=A+UB= Z×SIN(90×(O-P)÷(π×R))SIN(TAN-1((Q-S)÷(T-U))+Z×90×(U-O)÷π÷R)×R:Y=B+UO——圆曲线上任意点里程P——圆曲线起点里程V——圆曲线终点里程Z——左偏Z=1 右偏Z=-1U——平曲线起点X坐标S——平曲线起点Y坐标T——平曲线终点X坐标Q——平曲线终点Y坐标R——平曲线半径X——圆曲线上任意点X坐标4.已知前点、中点坐标,顺时针角度K,中点至后点距离S,求后点坐标 X、Y (QIANZHON HOU)A“X0”B“Y0”C“X1”D“Y1”K“SHUN JIAO”S“JU LI”POL((C-A),(D-B))T=J+KX=A+S×COS(T)Y=B+S×SIN(T)A——中点X坐标B——中点Y坐标C——前点X坐标D——前点Y坐标5. 已知前点、后点坐标,中点至前点距离Q,中点至后点距离R,顺时针角度V,求中点坐标X、Y(QIANGOU ZHONG)Q“QIAN JU LI”R“HOU JULI”V“SHUN JIAO” A“X0”B“Y0”C“X1”D“Y1”POL((C-A),(D-B))L=SIN-1(R÷I×SIN(V))X=A+Q×COS(L+J)Y=B+Q×SIN(L+J)A——前点X坐标B——前点Y坐标6. 已知两点坐标,求两点间距离、方位角(LIAN DIAN)A“X0”B“Y0”C“X1”D“Y1”POL((C-A),(D-B))A——中点X坐标B——中点Y坐标C——前点X坐标D——前点Y坐标7.平面放样,已知中点前点放样点坐标,求中点至放样点距离S、顺时针角度K(FANGYANG P)A“X0”B“Y0”C“X1”D“Y1”XYPOL((C-A),(D-B)):R=JPOL((X-A),(Y-B))K“SHUN JIAO”=J-RS“JU LI”=I8.已知起点、终点两点坐标,起点终点连线为直线、起点里程L0、求两点间任意点里程N处坐标X、Y (Z——Z)N“Lx” A“X0”B“Y0”L“L0”C“X1”D“Y1”POL((C-A),(D-B))X=A+(N-L)×COSJY=B+(N-L)×SINJN——任意点里程A——起点X坐标B——起点Y坐标L——起点里程C——终点X坐标D——终点Y坐标X——任意点X坐标Y——任意点Y坐标9.已知扩大基础上两墩柱坐标、扩大基础长O、宽P,求扩大基础四角点坐标(KDJC ZUOBIAO)A“X0”B“Y0”C“X1”D“Y1”O“LA”P“LB”POL((C-A),(D-B))Q=√(((O-I)÷2)2+(P÷2)2)P=√((P÷2)2+(O-(O-I)÷2)2)S=SIN-1(P÷2÷Q)T=SIN-1(P÷2÷R)E“XA”=A+Q×COS(J+180-S)F“YA”=B+Q×SIN(J+180-S)G“XB”=A+Q×COS(J+180+S)H“YB”=B+Q×SIN(J+180+S)K“XC”=A+R×COS(J-T)L“YC”=B+R×SIN(J-T)M“XD”=A+R×COS(J+T)N“YD”=B+R×SIN(J+T)A——墩柱1 X坐标B——墩柱1 Y坐标C——墩柱2 X坐标D——墩柱2 Y坐标O——扩大基础长边长度P——扩大基础短边长度E——扩大基础A角点X坐标G——扩大基础B角点X坐标 H——扩大基础B角点Y坐标 K——扩大基础C角点X坐标 L——扩大基础C角点Y坐标M——扩大基础D角点X坐标。
单条曲线坐标计算程序(新) 卡西欧4800计算器

单条曲线坐标计算程序(casio fx-4800P)(只限于对称型综合曲线使用)包含1个主程序和2个子程序1、主程序: “QU-XIAN”O“JDLC”:A“JDX”:B“JDY”:R:G“L0”:Z“ZUAN-JIAO”:H“FANG-XIANG”:V“Z-1,Y+1”LbL 1{S,M}G>0=>Prog“ZH-Y-HZ”:≠=>Prog“YY”⊿U<360=>U:≠=>U=U-360⊿E=X+cos(U-90)×MF=Y+sin(U-90)×MK=X+cos(U+90)×MP=Y+sin(U+90)×MX◢Y◢E“ZX”◢F“ZY”◢K“YX”◢P“YY”◢U“HUANG-XIANG”◢Goto 12、子程序:“ZH-Y-HZ”T=(R+G2÷24R)tg(Z÷2)+G÷2-G3÷240R2L=R(Z-G÷R×180÷π)×π÷180+2GC=O-TD=C+GI=C+L-GN=C+LE=A+Tcos(H+180)F=B+Tsin(H+180)K=E+cos(H+VG2÷6÷R÷G×180÷π)×(G-G5÷90÷(RG)2)P=F+sin(H+VG2÷6÷R÷G×180÷π)×(G-G5÷90÷(RG)2)Q=A+cos(H+VZ)×TW=B+sin(H+VZ)×TS<c=>L=C-S:X=A+cos(H+180)×(T+L):Y=B+sin(H+180)×(T+L):U=H⊿S>C=>L=S-C:J=H+VL2÷6÷R÷G×180÷π:L=L-L^5÷90÷(RG)2:X=E+cosJ ×L: Y=F+sinJ×L:U=H+3V(S-C)2÷6÷R÷G×180÷π⊿S>D=>L=S-D:J=H+VG÷R×90÷π+90VL÷π÷R:L=2R×sin(90L÷R÷π):X=K+cosJ×L:Y=P+sinJ×L:U=H+VG÷R×90÷π+V×180(S-D)÷π÷R⊿S>I=>L=N-S:J=H+VZ-VL2÷6÷R÷G×180÷π:L=L-L^5÷90÷(RG)2:X=Q+cosJ×(-L): Y=W+sinJ×(-L):U=H+VZ-3V(N-S)2÷6÷R÷G×180÷π⊿S>N=>L=S-N:J=H+VZ:X=A+cosJ×(T+L):Y=B+sinJ×(T+L):U=J⊿3、子程序:“YY”T=Rtg(Z÷2)L=RZ×π÷180C= O-TN=C+LE=A+Tcos(H+180)F=B+Tsin(H+180)S<C=>L=C-S:X=A+cos(H+180)×(T+L):Y=B+sin(H+180)×(T+L):U=H⊿S>C=>L=S-C:J=H+90VL÷πR:X=E+cosJ×(2Rsin(90L÷πR)):Y=F+sinJ×(2Rsin(90L÷πR)):U=H+180VL÷πR⊿S>N=>L=S-N:J=H+VZ:X=A+cosJ×(T+L):Y=B+sinJ×(T+L):U=J⊿使用说明:JDLC--------------交点里程JDX---------------交点X坐标JDY---------------交点Y坐标R-----------------圆曲线半径L0----------------缓和曲线长ZUAN-JIAO---------线路转角FANG-XIANG--------ZH(ZY)方向角V“Z-1,Y+1”-----系数,左转输“-1”,右转输“+1”S-----------------待求点桩号M-----------------边桩距离显示计算结果:X、Y--------------- 待求点中桩坐标ZX、ZY--------------待求点左边桩坐标YX、YY--------------待求点右边桩坐标HUANG-XIANG---------待求点方向角匝道上回旋线元任意点坐标计算程序(casio fx-4800P)文件名:ZA DAO HUANC :O :LbL 1{S,J,W}H=1=>M=0△R=0=>G=0:≠=>G=C ÷R △ I=G+S-K H=2=>M=C ÷RD:G=C ÷R:I=G-S+K △ V=1=>L=M+S-K △ V=-1=>L=M-S+K △ T=O-90VM 2÷C ÷π:A=L-M-(L^5-M^5)÷40C 2+(L^9-M^9)÷3456C^4-(L^13-M^13)÷599040C^6:B=(L^3-M^3)÷6C-(L^7-M^7)÷336C^3+(L^11-M^11)÷42240C^5-(L^15-M^15) ÷9676800C^7: U=X+V ACosT-BSinT ◢Z=Y+V ASinT+BCosT ◢P=O+Abs(G 2-I 2) ÷2C×180÷π×DP<360=>P ◢≠=>P=P-360◢△E=U+JCos(P-90) ◢F=Z+JSin(P-90) ◢N=U+WCos(P+90) ◢Q=Z+WSin(P+90) ◢Goto 1一、 使用说明C ——为回旋线曲率半径变化率,C=A 2=RL 0O ——为(ZH 、YH )方向角S ——回旋上待求点里程K ——回旋线起算点(ZH 、YH )里程X 、Y ——起算点(ZH 、YH )的横、纵坐标U 、Z ——待求点横、纵坐标P ——待求点方向角J 、W ——待求点左、右边桩距离E 、F ——待算点左边桩横、纵坐标N 、Q ——待算点右边桩横、纵坐标D ——线路转向判断值,左转为“-1”,右转为“+1”二、 注意事项H ——缓和曲线类型判断值,第一缓和曲线为“1”,第二缓和曲线为“2”(起算点半径为无穷大为第一缓和曲线,起算点为YH 点时为第二缓和曲线)V ——曲率半径大小比较值,曲率半径ρ由大变小为“+1”,反之为“-1”,线路左转时,曲率半径ρ要带负号进行比较R ——起算点(ZH 、YH )的半径值,不需输入正负号,在ZH 时,半径为∞(无穷大),此时半径输入0 。
CASIO-fx4800程序

CASIO-fx4800程序本人自网络上进行整理,谢谢大家支持!!!!CASIO-fx4800p 1 KWX Lbl1:{ABC}:Z[5]=A:Z[6]=B:Z[7]=C:Lbl2:Prog“ZBJX”:Abs(Z[5]-X)<0.001ÞG oto 4∆ Pol(Z[5]-X,Z[6]-Y):K=K+Icos(J-V):U=U-Isin(J-V):Goto2:Lbl4:Prog“SQX”:A=Z[7]-H:A$0ÞL=AbsU -1.5A-13:¹ÞL=AbsU-1.0A-15∆ Ky A+0.75y Uy Ay Goto 1¿ 2 ZBJX Fixm:{K}:Lbl 0:{K}:K:K# $ÞW:C: D:A:B:R:S∆ P=S2/24R-S4/2688R3:Q=S/2-S3/240R2:T=(R+P)tg(AbsA/2)+Q:L=pRAbsA/180:E=W-T:F= E+L¿ K#EÞL=W-K:X=C+Lcos(B-180):Y=D+Lsin(B-180):V=B:Goto 1∆ K#E+SÞL=K-E:X=L-L5/40R2S2: Y=L3-6RS-L7/336R3S3:Pol(T-X,Y):X=C+Icos(B-180-AbsAJ/A):Y=D+Isin(B-180- AbsAJ/A):V=B+90L2Ab sA/ApRS:Goto 1∆ K#FÞL=K-E-S:I=(S/2+L)×180/pR:X=T-RsinI-Q:Y=R(1-cosI)+P:V=IAbsA/A+B:Pol(X, Y):X=C+Icos(B-180-JAbsA/A):Y=D+ Isin(B-180-JAbsA/A):Goto 1∆ K#F+SÞL=F+S-K:X=T-L+L5/40R2S 2:Y=L3/6RS-L7/336R3S3:Pol(X,Y):X=C+Icos(B+A+JAbsA/A):Y=D+ Isin(B+A+JAbsA/A):V=B+A-90L2A bsA/ApRS:Goto 1∆ K>F+SÞL=K+T-S-F:X=C+Lcos(A+B):Y=D+Lsin(A+B):V=A+B:Goto 1∆ Lbl 1:X=X+ Ucos(V-090):Y=Y+Usin(V-090)¿ O=V¿ 3 SQX Fixm:{K}:K#$ÞG:C:R:E:F∆ W=F-E:T=Abs(RW/2):K<G-TÞH=C-E(G-K)∆ K$G-TÞH=C-E(G-K)+(K+T-G)2AbsW/2RW∆ K$GÞH=C-F(G-K)+(K-G-T)2AbsW/2RW∆K$G+TÞH=C-F(G-K)∆¿ 4 HGHXP {KU}:K:U=U:Prog“ZBJX”:Prog:“SQX”:Xy Yy H¿ 备注:1(KWX)中,A、B、C为某点的坐标X,Y,Z;K 桩号;L 当L=0时处于开挖线位置;A 高程;A+0.75 测点高程+路面厚度;U 距中线距离。
公路曲线中桩边桩坐标fx4800P计算程序

公路曲线中桩边桩坐标fx4800P计算程序在快速发展的公路建设事业中,使用GPS坐标控制系统的高等级公路日渐增多,并且,随着高精度的测量设备的广泛采用,其他等级公路也开始普遍应用坐标控制。
使用坐标控制的公路项目,有着线型流畅、行车速度快而舒适、环境优美等特点,这些都来源于高质量的设计与施工,卡西欧fx-4800p计算器由于其轻便、精度高、易于操作,能够解决设计、施工当中很多的实际困难,因此,倍受公路工程技术人员的青睐。
本人通过在高速公路多年的施工经验,编写了许多公路测量实用程序,如常用的中桩边桩计算程序,匝道坐标计算程序,施工放样程序,换带程序等等。
下面把公路中常用的中桩边桩计算程序介绍给大家,希望本程序能够对公路测量同行有所帮助.。
1 程序清单:LbI 0:Defm 6↙″CURVE MODE″:{M}:M″0:T1=T2,1:T1≠T2″↙M=0=>Goto 7:≠>M=1=>Goto 8:≠>Goto 0⊿⊿↙LbI 7:{ABCDEFGR}↙A″ZHD″:B″HZD″:C″XJD″:D″YJD″:E″ELPHA″:F″PJ:Z(-),Y(+)″:G″L0″:R↙T=(R+G2÷(24R)-G ÷(2688R ))tan(AbsF÷2)+0.5G-G ÷(240R2) ↙U=G:V=T: Goto 1↙LbI 8:{ABCDEFGUTVR}↙A″ZHD″:B″HZD″:C″XJD″:D″YJD″:E″ELPHA″:F″PJ:Z(-),Y(+)″:G″L01″:U″L0 2″:T″T1″:V″T2″: R↙LbI 1:{H}:H″DQD″↙H≥B=>M=1: ≠>H>B-U=>M=2: ≠>H≥A+G=>M=3: ≠>H≥A=>M=4: ≠>HM=5⊿⊿⊿⊿⊿↙M≤2=>L=Abs(H-B): ≠>L=Abs(H-A)⊿↙M=1=>Z[1]=L: ≠>M=2=>Z[1]=√((L-L ÷(40R2U2)+L ÷(3456R U ))2+(L ÷(6RU)- L ÷(336R U )+ L÷(42240R U ))2): ≠>M=3=>Z[1]=√((G-G ÷(40R2)+G ÷(3456R ))2+(G2÷(6R)-G ÷(336R )+G ÷(42240R ))2):≠>M=4=>Z[1]=√((L-L ÷(40R2G2)+L÷(3456R G ))2+ (L ÷(6RG)- L ÷(336R G )+ L÷(42240R G ))2): ≠>M=5=>Z[1]=L⊿⊿⊿⊿⊿↙M≤2=>Z[2]=C+Vcos(E+F): Z[3]=D+Vsin(E+F): ≠>Z[2]=C+Tcos(E+180): Z[3]=D+Tsin(E+180) ⊿↙M=1=>Z[4]=E+F:≠>M=2=>Z[4]=E+F+180:≠>M=5=>Z[4]=E+ 180:≠>Z[4]=E ⊿⊿⊿↙N=F÷AbsF↙M=1=>I=0:≠>M=2=>I=-N(30L2÷(ΠRU)):≠>M=3=>I=N(30G÷(ΠR)):≠>M=4=>I=N(30L2÷(ΠR G)):≠>M=5=>I=0⊿⊿⊿⊿⊿↙Z[4]=Z[4]+I↙Z[5]=Z[2]+Z[1]cosZ[4]↙Z[6]=Z[3]+Z[1]sinZ[4]↙M≠3=>Goto 3⊿↙LbI 2:P=90L÷(ΠR):Q=90(L-G)÷(ΠR)↙Z[5]= Z[5]+2RsinQcos(E+NP)↙Z[6]= Z[6]+2RsinQsin(E+NP)↙LbI 3↙X″X(ZX)″=Z[5]◢Y″Y(ZX)″=Z[6]◢LbI 4↙M=3=>I=90N(2L-G) ÷(ΠR): ≠>I=3I⊿↙M=1=>P=E+F: ≠>M=2=>P=E+F+180: ≠>M=5=>P=E+180: ≠>P=E⊿⊿⊿↙P=P+I-90:Q=P+180↙M=2=>X=P-90: ≠>M=5=>X=P+180: ≠>X=Q-90⊿⊿↙XX=X+360: ≠>X>360=>X=X-360⊿⊿↙X″QXFWJ(Z-Y)″=X◢{SW}:S″SZ ″: W″SY ″:AbsS+AbsW=0=>Goto 1⊿↙M=2=>Goto 5: ≠>M=5=>Goto 5: ≠>Goto 6⊿⊿↙LbI 5:S=-S:W=-W↙LbI 6↙X″X(Z)″=Z[5]+ScosP◢Y″Y(Z)″=Z[6]+SsinP◢X″X(Y)″=Z[5]+WcosQ◢Y″Y(Y)″=Z[6]+WsinQ◢Goto 1↙2 程序参数说明:开始运行程序时选择曲线类型(CURVE MODE),0为等切线曲线,1为不等长切线曲线。
CASIOfx-4800P 路线计算(偏角法对称型)

CASIO fx-4800P 路线放样计算程序(偏角法对称型计算)程序说明:1、本程序是计算对称型圆曲线中、边桩坐标。
2、程序所占内存2400步左右。
3、本程序单个交点输入。
4、程序运行计算时有五大桩号提示。
L1 DegL2 Defm 19L3 Fixm 程序菜单1-设站,2-数据输入,3-路线坐标计算,4-设新点L4 Lbl 0L5 {A}:A”SZ-1,INPUT.SJ-2,LXFY-3,XD-4”L6 A=1=> Goto 1L7 A=2=> Goto 2L8 A=3=> Goto 3L9 A=4=> Goto BL10 Goto 0 输入站点与后视点坐标L11 Lbl 1L12 {BCDE}:B”ZDX”:C”ZDY”:D”HDX”:E:”HDY”L13 Pol(D-B,E-C)L14 Z[1]”HD”=I◢L15 J>0=>Z[2]”HA”=J◢≠>Z[2]”HA”=360+J◢L13 Goto 0 交点要素数据输入L14 Lbl 2L15 {FGHIKLMNRP}:F”JD1X”:G”JD2Y”:H”JDX”:K”JDY”:L”JD2X”:M”JD2Y”:N”JDLC”:R”JDR”:P”JDLS1”L16 Pol(H-F,K-G)L17 J>0=>Z[3]”1=>0”=J◢≠>Z[3]”1=>0”=360+J◢L18 Pol(L-H,M-K)L19 J>0=>Z[4]”0=>2”=J◢≠>Z[4]”0=>2”=360+J◢Z[3]+180>360=>Z[18]=Z[3]-180 计算交点转角和判断是左角还是右角Z[3]+180<360=>Z[18]=Z[3]+180Z[18]<Z[4]=>Z[19]=Abs(Z[18]+360-Z[4]])Z[18]>Z[4]=>Z[19]=Abs(Z[18]-Z[4])Z[19]>180=>U=1:O=Z[19]-180Z[19]<180=>U=-1:O=180-Z[19]L20 Z[5]=90P/R/πL21 Z[6]=(R+P^2/24/R)Tan(O/2)+(P/2-P^3/240/R^2) 切线长L22 Z[7]= πON/180+P 曲线长L23 Z[8]= πR(O-2Z[5])/180 圆曲线长L24 Z[13]=N-Z[6] ZH点L25 Z[14]=Z[13]+P HY点L26 Z[15]=Z[14]+Z[8]/2 QZ点L27 Z[16]=Z[14]+Z[8] YH点L28 Z[17]=Z[16]+P HZ点L29 Goto 0 路线计算输入里程桩号L30 Lbl 3L31 {S}:S”INPUT LC”L32 S<Z[13]+10=>S>Z[13]-10=>Goto C ZH点L33 P≠0=>S<Z[14]+10=>S>Z[14]-10=>Goto D YH点L34 S<Z[15]+10=>S>Z[15]-10=>Goto E QZ点L35 P≠0=>S<Z[16]+10=>S>Z[16]-10=>Goto F HY点L36 S<Z[17]+10=>S>Z[17]-10=>Goto G HZ点L37 S>Z[13]=>S≤Z[14]=>T=S-Z[13]:Goto 4 ZH点至HY点段L38 S>Z[14]=>S<Z[16]=>T=S-Z[14]:Goto 6 HY点至YH点段L39 S≥Z[16]=>S<Z[17]=>T=Z[17]-S: Goto 4 YH点至ZH点段L40 S≤Z[13]=>Goto 8 ZH点前直线段L41 S≥Z[17]=>Goto 9 HZ点后直线段L42 Goto 0 计算缓和段长偏角L43 Lbl 4L44 P≠0=>Z[9]=30T^2/π/R/PL45 P≠0=>Z[10]=√((T-T^5/(40R^2P^2))^2+(T^3/6RP)^2)L46 P≠0=>S≥Z[13]=>S≤Z[14]=>Goto 5 ZH点至HY点段L47 P≠0=>S≥Z[16]=>S≤Z[17]=>Goto 7 YH点至HZ点段L48 S>Z[14]=>S<Z[16]=>T=S-Z[14]:Goto 6 HY点至YH点段L49 S≤Z[13]=>Goto 8L50 S≥Z[17]=>Goto 9L48 Goto 0 计算ZH点至YH点段中线坐标L51 Lbl 5L52 U=1=>V=Z[3]-Z[9]:Z[11]”H1”=Z[3]-3Z[9] ◢U=-1=>V=Z[3]+Z[9]:Z[11]”H1”=Z[3]+3Z[9] ◢L53 Rec(Z[10],V)L54 X=H+Z[6]COS(180+Z[3])+IL55 Y=K+Z[6]SIN(180+Z[3])+JL56 Goto A 计算圆曲线段中线坐标L57 Lbl 6L58 Z[9]=90T/π/RL59 U=1=>V=Z[3]-Z[5]-Z[9]:Z[12]=Z[3]-Z[5]/3:Z[11]”YQ”=Z[3]-Z[5]-2Z[9] ◢U=-1=>V=Z[3]+Z[5]+Z[9]:Z[12]=Z[3]+Z[5]/3:Z[11]”YQ”=Z[3]+Z[5]+2Z[9] ◢L60 Rec(ABS(2RSinZ[9]),V)L61 X=H+Z[6]Cos(180+Z[3])+ √((P-P^3/40/R^2)^2+(P^2/6/R)^2)CosZ[12]+IL62 Y=K+Z[6]Sin(180+Z[3])+ √((P-P^3/40/R^2)^2+(P^2/6/R)^2)SinZ[12]+JL63 Goto A 计算YH点至HZ点段坐标L64 Lbl 7L65 U=1=>V=Z[4]+180+Z[9]:Z[11]”H2”=Z[4]+3Z[9] ◢U=-1=>V=Z[4]+180-Z[9]:Z[11]”H2”=Z[4]-3Z[9] ◢L66 Rec(Z[10],V)L67 X=H+Z[6]CosZ[4]+IL68 Y=K+Z[6]SinZ[4]+JL69 Goto A 计算ZH点前直线坐标L70 Lbl 8L71 Z[11]=Z[3]L72 Rec(N-S,Z[3])L73 X=H-IL74 Y=K-JL75 Goto A 计算HZ点后直线坐标L76 Lbl 9L77 Z[11]=Z[4]L78 Rec(S-N+2Z[6]-Z[7],Z[4])L79 X=H+IL80 Y=K+jL81 Goto A 计算边桩坐标与站点到计算点的平距和方位角L82 Lbl AL83 {W}:W”INPUT FX”L84 X”X”=X+WCos(90+Z[11]) ◢L85 Y”Y”=Y+WSin(90+Z[11]) ◢L86 Pol(X-B,Y-C)L87 I”HD”=I◢L88 J>0=>J”HA”=J◢≠>J”HA”=360+J◢L89 {A}:A”Cont.FY-3,EXT-4”L90 A=3=>Goto 3L91 A=4=>Goto 0 计算新点的坐标L92 Lbl bL93 {O}:O”XD.HD”:{Z}:Z”XD.HA”L94 Rec(O,Z)L95 X”XP”=B+I◢L96 Y”YP”=C+J◢L97 Goto 0 ZH点L98 Lbl CL99 P=0=>Z[13]”ZYD”=Z[13] ◢P≠0=>Z[13]”ZHD”=Z[13] ◢L100 {A}:A”WuDZ-1,NO-3”L101 A=1=>S=Z[13]: T=S-Z[13]:Goto 4L102 A=3⇒S<Z[13]⇒Goto 8≠> T=S-Z[13]:Goto 4L103 Lbl D YH点L104 Z[14]”HYD”=Z[14] ◢L105 {A}:A”WuDZ-1,NO-3”L106 A=1=>S=Z[14]:T=S-Z[13]:Goto 4L107 A=3=> T=S-Z[13]:Goto 4L108 Lbl E QZ点L109 Z[15]”QZD”=Z[15] ◢L110 {A}:A”WuDZ-1,NO-3”L111 A=1=>S=Z[15]:T=S-Z[14]:Goto 6L112 A=3=> T=S-Z[14]:Goto 6L113 Lbl F YH点L114 Z[16]”YHD”=Z[16] ◢L115 {A}:A”WuDZ-1,NO-3”L116 A=1=>S=Z[16]:T=Z[17]-S:Goto 4L117 A=3=> T=Z[17]-S:Goto 4L118 Lbl G HZ点L119 P=0=>Z[17]”YZD”=Z[17] ◢P≠0=>Z[17]”HZD”=Z[17] ◢L120 {A}:A”WuDZ-1,NO-3”L121 A=1=>S=Z[17]:T=Z[17]-S:Goto 4L122 A=3=>T=Z[17]-S:Goto 4。
CASIO_fx-4800P常用测量程序

一、QXFY 辛甫森公式放样程序1. U“X0”:V“Y0”2. A“XA”:B“Y A”:C“CA”:D“1÷RA”:E“1÷RB”:F“KA”:G“KB”3. Lb1 1:{HLR}:H“KI”:L“JJ”:R“DZ+Y-”4. H>G Goto 15. H<F Goto 16. P=(E-D) ÷Abs(G-F):Q=Abs(H –F):Z=P×Q:T=D+Z7. W=C+(Z+2D)Q×90÷π8. M=C+(Z÷4+2D)Q×22.5÷π:N=C+(3Z÷4+2D)Q×67.5÷π:K=C+(Z÷2+2D)Q×45÷π9. X=A+Q(cosC+4(cosM+cosN)+2cosK+cosW)÷12+Rcos(W-L)10. Y=B+Q(sinC+4(sinM+sinN)+2sinK+sinW) ÷12+ Rsin (W-L)11. Pol((X-U),(Y-V))J≤0J=J+360J“FWJ”12. I“S”13. Goto 1程序显示说明:须输入参数:X0:置镜点X (对应变量U)Y0:置镜点Y (对应变量V)XA:曲线起算点X (对应变量A)Y A:曲线起算点Y (对应变量B)CA:曲线起算点切线方位角(对应变量C) 1÷RA:1÷半径,即起算点曲率,右偏为正左偏为负(对应变量D)1÷RB:1÷半径,即曲终点曲率,右偏为正左偏为负(对应变量E)KA:起算点里程(对应变量F)KB:曲终点里程(对应变量G)KI:待求点里程(对应变量H)JJ:夹角(与前进方向切线方位角夹角,向右为正)(对应变量L)D“Z+Y-”:偏距,左正右负(对应变量R)计算结果: W: 待求点切线方位角(对应变量W) X:计算点x (对应变量X)Y:计算点y (对应变量Y)FWJ:放样方位角(对应变量J)S:放样距离(对应变量I)K BX 0Y 0本程序依据复化辛甫森公式计算原理改进而成,特点是把曲线按曲率变化点分成若干计算单元单独计算,不论直线(曲率为0)、圆曲线(曲率为1/R )、卵形曲线,只要按曲率变化点分解弄清变化点曲率半径,右偏左偏曲线由曲率的正负号分别,既可求得该计算单元内任意里程中桩及斜交或正交的边桩。
卡西欧4800P计算器测量程序集共10页

福建林业职业技术学院工程系土木工程室高国兴CASIO fx-4500PA计算中桩、边桩坐标程序直线、圆曲线中桩及左、右边桩计算程序fx-4800p=”:C“Xθ=”:D“Yθ=”:E“Wθ=”:N=Ans:R“R=”:L“Lμo=”:K“D=”:M“JμoQ=9θL÷(πR):S=2RsinQ :O =C+Scos(N-Q)◢P=D+Ssin(N-Q)◢W=E-2Q◢X=O+Kcos(N-2Q-M)◢Y=P+Ksin(N-2Q-M)◢注:Xθ=起算点坐标Yθ=起算点坐标Wθ=起算点方位角R=曲线半径,线路前进方向,左+,右-直线R为无穷大=置镜点到待求点距离LμoD左、右边距离=前进方向左(+90),右(-90)JμoO=中桩坐标P=中桩坐标W=待求点方位角X=左、右边桩坐标Y=左、右边桩坐标缓和曲线中桩及左、右边桩计算程序Fx-4800pC“Xθ=”:D“Yθ=”:E“Wθ=”:N=Ans:R“R=”:F“Lθ=”:=”:K“D=”:M“Jμo=”←L“LμoU=L-L^5÷(40R2F2):V=L^3÷(6RF)-L^7÷(336R^3F^3):Q=tan-1(V÷U):S=√(U2+V2)←B=9θL2÷(πRF):O=C+Scos(N-Q)◢P=D+Ssin(N-Q)◢W=E-B◢X=O+Kcos(N-B-M)◢Y=P+Ksin(N-B-M)◢注:Xθ=起算点坐标Yθ=起算点坐标Wθ=起算点方位角R=曲线半径,线路前进方向,左+,右-Lθ=缓和曲线长=置镜点到待求点距离LμoD左、右待求距离=前进方向左(+90),右(-90)JμoO=中桩坐标P=中桩坐标W=待求点方位角X=左、右边桩坐标Y=左、右边桩坐标放样程序fx-4800pRLI“XZ”:W:“YZ”:G“XH”:H“YH”←B=H-W ←C=G-I ←Prog“P”:U=A←K=√(B2+C2)←C=X“X-”-I←B=Y“Y-”-W←Prog“P”←L“L”=√(B2+C2)◢V=A-U:V<θ==>V=V+36θ⊿V “V=”◢PA=tan-1(B÷C)←B≥θ==> C≥θ==> A=A:≠=> C<θ==> A=A+18θ⊿⊿≠=> B<θ==> C≥θ==> A=A+36θ: ≠=>C<θ==>A= A+18θ⊿⊿⊿←XZ、YZ—置镜点X、Y坐标;XH、YH—后视点坐标;X-、Y-—前视点坐标;输出:R=水平角、L=置镜点至前视点水平距离。
CASIO-fx4800P型计算器连续计算线路高程、坐标

CASIO-fx4800P型计算器连续计算线路高程、坐标及放样程序【简述】为了适应现场快速、准确、灵活的放样要求,作者根据线路施工测量特点,运用计算器的编程功能,使整条线路的施工测量计算数据能连续快速的计算,只要把整条线路各个交点处的计算要素输入子程序中,你便拥有整条线路的“数据库”。
在忙碌的施工现场,你不必携带大量的施工图和资料来查找平面、纵断面的设计要素,更不必担心设计要素的输入错误,从而使得计算和放样轻松、方便、快捷。
【计算范围】坐标部分包括:各等级公路和高速路的直线段、圆曲线段、加对称缓和曲线的圆曲线段中、边桩坐标及放样计算。
高程部分包括:各等级公路和高速路的直线段、竖曲线段、缓和超高段中、边桩高程及放样计算。
一、坐标及放样程序【起算数据】:交点里程桩号、交点坐标、前直线方位角、交点转角、圆曲线半径、缓和曲线长(一)主程序:XYFY2Fix4M"Xc=":P"Yc=" '如须放样输入测站坐标值,否则输入0Lbl0{HS}:H"K0+0":S"B=(-B,0,B)":Prog"A" '变量输入和声明S=0=>E=0:≠>E=90 '求边桩坐标时的偏角值判定L=πRN÷180+V '含有缓曲线的曲线总长T=(V÷2-V^3÷(240R^2))+(R+(V^2÷(24R)-V^4÷(2688R^3)))tan(N÷2) '切线长A=Q-T:B=A+V:D=A+L:C=D-V 'A-ZH(ZY)点桩号,B-HY点桩号,C-YH点桩号,D-HZ(YZ)点桩号Rec(T,F+180) '求ZH(ZY)点的坐标增量Z[1]=W+I:Z[2]=K+J 'ZH(ZY)点坐标值Rec(T,F+GN) '求HZ(YZ)点的坐标增量Z[3]=W+I:Z[4]=K+J 'HZ(YZ)点的坐标值Lbl1U=S÷(Abs(S+10E-19)):S=AbsS '左右偏角每件判定H<A=>Goto2: ≠> '第一直线上坐标计算判定H<B=>Goto3: ≠> '第一缓和曲线上坐标计算判定H<C=>Goto4: ≠> '净圆曲线上坐标计算判定H<D=>Goto5: ≠> Goto6⊿⊿⊿⊿ '第二缓和曲线和第二直线上坐标计算判定Lbl2Rec(Q-H,F+180) '第一直线上中桩坐标增量计算X=W+I:Y=K+J '中桩坐标值计算Rec(S,F+180-(180-E)U) '第一直线上与中桩同一断面的边桩增量计算X=X+I:Y=Y+J '边桩坐标值计算S=SU '边长条件判定Goto8Lbl3 '进入第一缓曲线段计算Z=H-A '待求点至ZH点的距离O=90Z^2÷(πRV) '所求点缓曲线对应的圆心角X=Z-Z^5÷(40R^2V^2)+Z^9÷(3456R^4V^4) '缓曲线上ZH点至待求的支距X坐标Z=Z^3÷(6RV)-Z^7÷(336R^3V^3)+Z^11÷(42240R^5V^5) '缓曲线上ZH点至待求点的支距Y坐标Lbl7Rec(X,F)X=Z[1]+I:Y=Z[2]+JRec(Z,F+90G) '把中桩支距坐标转换成测量统一坐标X=X+I:Y=Y+JRec(S,F+O G+EU) '曲线边桩坐标增量计算X=X+I:Y=Y+J '坐标计算结果S=SU '边长条件Goto8Lbl4 '进入主圆计算部分Z=H-A-V÷2 '曲线上待求点到HY点的里程O=180Z÷(Rπ) '待求点方位角所对应的圆心角X=Rsin O+(V÷2-V^3÷(240R^2))Z=R(1-cos O)+(V^2÷(24R)-V^4÷(2688R^3)) '主圆部分待求点支距坐标XY Goto7Lbl5 '进入第二缓和曲线计算Z=D-H '曲线上待求点到HZ点的里程O=90Z^2÷(πRV) '待求点方位角所对应的圆心角X=Z-Z^5÷(40Z R^2V^2)+^9÷(3456R^4V^4)Z=Z^3÷(6RV)-Z^7÷(336R^3V^3)+Z^11÷(42240R^5V^5) '待求点支距坐标XY Rec(X,F+GN+180)X=Z[3]+I:Y=Z[4]+J '把中桩支距坐标转换成测量统一坐标Rec(Z,F+GN+180-90G)X=X+I:Y=Y+JRec(S,F+GN+180-O G-(180-E)U) '曲线边桩坐标增量计算X=X+I:Y=Y+J '坐标计算结果S=SUGoto8Lbl6 '进入第二直线段计算部分Rec(H-D+T,F+GN) '中桩坐标增量计算X=W+I:Y=K+J '中桩坐标计算结果Rec(S,F+GN+EU) '边桩坐标增量计算X=X+I:Y=Y+J '边桩坐标计算结果S=SUGoto8Lbl8X=X◢ '显示坐标计算结果Y=Y◢M≠0=>Goto9: ≠>Goto0 ⊿Lbl9 '进入放样部分计算Pol(X-M,Y-P) '增量计算J<0=>J=J+360: ≠>J=J ⊿J"A"=Int J+0.01Int(60Frac J)+0.006Frac(60Frac J) ◢ '方位角计算结果(此显示值为度分秒格式)I"L"=I◢ '极距计算结果Goto0∙(二)子程序:AH≤ZY2(ZH2)=>Q=JD1:W=X1:K=Y1:R=R1:F=F0:N=N1:V=Ls1:G=1(-1):=>H≤ZY3(ZH3)=>Q=JD2:W=X2:K=Y2:R=R2:F=F1:N=N2:V=Ls2:G=1(-1):=>H≤ZY4(ZH4)=>Q=JD3:W=X3:K=Y3:R=R3:F=F2:N=N3:V=Ls3:G=1(-1):=>H≤ZY5(ZH5)=>Q=JD4:W=X4:K=Y4:R=R4:F=F3:N=N4:V=Ls4:G=1(-1):=>……………………………H≤ZY n+1(ZH n+1)=>Q=JD n:W=X n:K=Y n:R=R n:F=F n-1:N=N n:V=Ls n:G=1(-1)注:H—待求点桩号ZY n+1(ZH n+1)—后曲线起点桩号 Q—本曲线交点桩号 W—本曲线交点X坐标K—本曲线交点Y坐标 R—本曲线内圆曲线半径 F—前直线方位角 N—本交点转角V—本曲线内缓和曲线长 G—线路转向符,左转角-1,右转角为+1二、高程及放样程序【起算数据】:变坡点桩号A、变坡点高程B、前后纵坡C D、竖曲半径R、横坡度F、最大超高横坡度G、ZH点桩号、YH点桩号、HZ点桩号、施工层厚度N、视线高W (一)主程序:GCFYW"SXG=":N '常量输入(视线高程、施工层厚度)Lbl 1{LО}:L"K0+0":О"B=" :Prog"B" '变量输入及声明K=C-D '坡度差及竖曲线偏角K>0=>J=-1:≠>J=1⊿ '凹凸竖曲线判断条件T=Abs(RK)÷2 '竖曲线切线长,如需显示则在后面加上◢H=A-T '竖曲线起点ZY桩号,如需显示则在后面加上◢X=A+T '竖曲线终点YZ桩号,如需显示则在后面加上◢M=L-A '待求点至变坡点的距离L≤H=>P=B+MC-N-W: ≠> '前纵坡直线段中桩高程计算L≤A=>P=B+MC+J(T-AbsM)2÷(2R)-N-W: ≠> '前纵坡竖曲线中桩高程计算L≤X=>P=B+MD+J(T-AbsM)2÷(2R)-N-W: ≠> '后纵坡竖曲线中桩高程计算L>X=>P=B+MD-N-W⊿⊿⊿⊿⊿ '后纵坡直线段中桩高程计算E=0=>Goto 2 '直线部分中、边桩计算判断条件≠>L≤E=> Goto 2 '直线部分中、边桩计算判断条件≠>L>V=> Goto 2 '直线部分中、边桩计算判断条件≠>L>E=> Goto 3 '前缓曲超高部分中、边桩计算判断条件≠> L>U=> Goto 4⊿⊿⊿⊿ '后缓曲超高部分中、边桩计算判断条件Lbl 2O=0=>Z“H”=AbsP◢'显示直线部分中、边桩高程计算结果≠>Y“HB”=Abs(P-OF)◢不需放样显示高程,否则显示放样水准尺计数⊿Goto 1Lbl 3S=(L-E)(F+G)÷(V-U)-F '前缓曲线超高横坡度计算S≤F=> Goto 5:≠>S≤G=> Goto 6 '超高起点(终点)至零界面、零界面至全超高及全超高≠> Goto 7 ⊿⊿ 部分的计算判断条件Lbl 4S=(V-L)(F+G)÷(V-U)-F '后缓曲线超高横坡度计算S≤F=> Goto 5:≠>S≤G=> Goto 6 '超高起点(终点)至超高变坡零界面、零界面至全≠> Goto 7 ⊿⊿ 超高、全超高部分计算判断条件Lbl 5O=0=>Z“H1”=AbsP◢'超高起点(终点)至超高变坡零界面中、边桩高程≠>Y“H-D1”=Abs(P-OF)◢计算结果显示Q“H-G1”=Abs(P+OS)◢⊿Goto 1Lbl 6O=0=>Z“H2”=AbsP◢'超高变坡零界面至全超高中、边桩高程≠>Y“H-D2”=Abs(P-OS)◢计算结果显示Q“H-G2”=Abs(P+OS)◢⊿Goto 1Lbl 7O=0=>Z“H3”=AbsP◢'全超高中、边桩高程计算结果显示≠>Y“H-D3”=Abs(P-OG)◢Q“H-G3”=Abs(P+OG)◢⊿Goto 1∙∙注:W“SXG”-视线高N-施工层厚度L"K0+0"-待求点桩号О"B="-中桩至边桩距离(二)子程序:BL≤ZY2=>A=JD1:B=H1:C=I0:D=I1: R=R1:F=I h:E=ZH1:U=YH1:V=HZ1:G=I max1 :≠>L≤ZY3=>A=JD2:B=H2:C=I1:D=I2: R=R2:F=I h:E=ZH2:U=YH2:V=HZ2:G=I max2 :≠>L≤ZY4=>A=JD3:B=H3:C=I2:D=I3: R=R3:F=I h:E=ZH3:U=YH3:V=HZ3:G=I max3 :≠>L≤ZY4=>A=JD3:B=H3:C=I2:D=I3: R=R3:F=I h:E=ZH3:U=YH3:V=HZ3:G=I max3 :≠> ……………………L≤ZY n+1=>A=JD n:B=H n:C=I n-1:D=I n: R=R n:F=I h:E=ZH n:U=YH n:V=HZ n:G=I maxn注:ZY N+1:-下一个竖曲线起点桩号(如:变坡点2的计算范围为前竖曲线终点YZ1至后竖曲线起点ZY3,则在程序中“L≤ZY3”就应输入ZY3的里程桩。
巧用卡西欧FX—4800 P计算器快速精确测放竖曲线
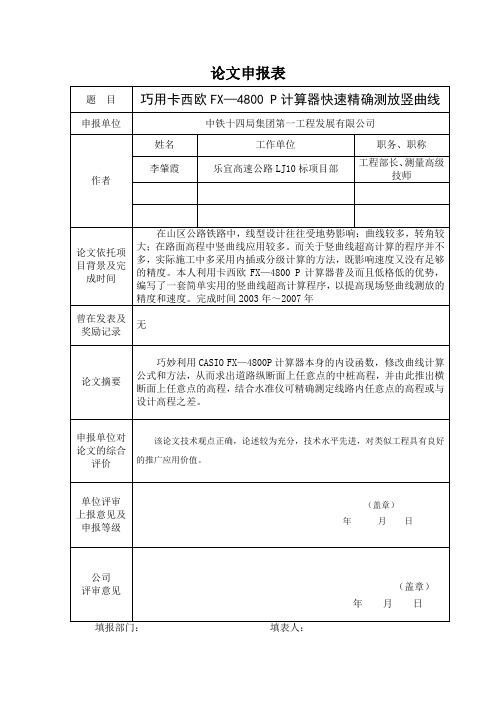
论文申报表巧用卡西欧FX—4800 P计算器快速精确测放竖曲线李肇霞【摘要】巧妙利用CASIO FX—4800P计算器本身的内设函数,修改曲线计算公式和方法,从而求出道路纵断面上任意点的中桩高程,并由此推出横断面上任意点的高程,结合水准仪可精确测定线路内任意点的高程或与设计高程之差。
【关键词】自动;快速;精确;任意测定;1前言近年来在高等级公路铁路建设中对道路的质量要求越来越高,尤其是对线路纵断面的要求。
设计院为了提高道路的行车质量,不断优化线路纵断面,在许多高速公路中竖曲线占路线总长的比例都在80%以上,竖曲线的数量已远远超过平面曲线。
在实际施工中如何快速准确地确定线路的高程是测量放样工作中的一大难题。
竖曲线上各点高程的计算程序设计,要在PC—1500袖珍计算机或计算机上完成程序设计比较容易,但要在FX—4800P计算器上完成线路各点的高程的计算是比较繁琐的。
FX—4800P计算器变量只有26个,各种函数也受到限制。
但是考虑到FX—4800P计算器使用比较普及,价格低,为了充分发挥现有设备的作用,本文介绍了一套简单实用的新程序,供同行们参考使用。
2 fx-4800P的特点从所周知,CASIO fx -4500PA编程函数计算器早在20世纪80年代就已经在我国工程界得到了广泛的应用,fx -4800P是比fx -4500PA更高一个级别的产品,它采用硬翻盖设计,除了具有fx -4500PA的全部功能以外,还主要改进了下列特性:2.1 具有16列×4行显示屏(fx -4500PA只有12列×2行),可以显示更多的信息,这对于编写与修改程序特别方便。
2.2 在程序区域中最多可以存储4500字节的程序与数据(fx -4500PA只能存储1103字节)。
2.3 求方程的数值解。
例如可以求方程2X2+6X-9=0的数值解。
2.4 复数计算功能,例如可以进行下列复数表达式的运算√(3+4i)=1.27201965+0.786151378i2.5 一、二次微分计算,例如_d_(x3+4x2+x-6)∣x=3 = 52dx_d2_(x3+4x2+x-6)∣x=3 = 26dx22.6 求和计算,例如6∑(K2-3K+5)=55K=22.7 fx -4800P是使用15位的尾数进行内部计算,但小数位最多只能显示9位数字。
卡西欧fx-4800P编程

一、本人编写整段曲线坐标程序一则。
可作为参考,从ZH-HY-YH-HZ可一次性计算出中心或切点方向或法线方法等坐标,当只有圆曲线时,L0输入0,只计算单圆周曲线。
示意图无法粘贴。
若有问题请回复。
本程序经调试计算准确。
缓和曲线、圆曲线计算程序A“JDX”:B“JDY”:C“R”:D“L0”:J“HR”:F“T”:G“QD”:H“ZD”:I“Z,Y,-,+”:T“E”:I>0=>Z=1:≠=>Z= -1:△LB1 1:{K,L,M}:K“ZHUANG”:L“L1”:M“L2”:K<G+D=>N“Li”=K-G:Y=1:E=J:GOTO 2:≠=>K≤H-D=> GOTO 3:≠=>N=H-K:E=J+I-180:Y=-1: GOTO 2:△△Lb1 2:O“X0”=A-COS E×F:P“Y0”=B-SIN E×F:Q=N-N^5÷(40×C2×D2):R=N^3÷(6×C×D):S=TAN-1(R÷Q)×YZ:U=Y Z N2×90÷(ДCD)+E:K ≤G+D=>U=U-90:≠=>U=U+90:△V=U+90:W“X1”=O+COS(E+S)×√(Q2+R2)+COS U×L+COS V×M▲X“Y1”=P+SIN(E+S)×√(Q2+R2)+SIN U×L+SIN V×M▲GOTO 1:Lb1 3:O=J+Z(0.5×Abs I+90):P“X0”=Cos O×(C+T)+A:Q“Y0”=Sin O×(C+T)+B:R=O-180-Z((H-G)-2D)×90÷Д÷C:S=(K-(G+D))×180÷Д÷C:U=R+ZS:W“X1”=P+COS U×(C+ZL)+COS(U+Z×90)×M▲X“Y1”=Q+SIN U×(C+ZL)+ SIN(U+Z×90)×M▲GOTO 1说明:JDX:交点X坐标 JDY:交点Y坐标R:半径 L0:缓和曲线长 HR:前进方位角T:切线长 QD:起点桩号 ZD:终点桩号Z,Y,-,+:偏角,左为负,右为正E:外矢距ZHUANG:待求点桩号L1:待求点法线方向距离,左侧为正,右侧为负,求中桩坐标时为0L2:待求点切线方向距离,左侧为正,右侧为负,求中桩坐标时为0本程序用于计算缓和曲线圆曲线缓和曲线缓和曲线为对称型缓和曲线,若无缓和曲线,计算单圆曲线时L0输入0卡西欧4800计算全站仪坐标程序!这个是我月个朋友编写的“卡西欧4800计算全站仪坐标程序”一共是5个程序。
CASIO fx4800P曲线任意里程中边桩坐标正反算程序

Y0 ?线元起点的Y坐标
S0 ?线元起点里程
F0 ?线元起点切线方位角
LS ?线元长度
R0 ?线元起点曲率半径
RN ?线元止点曲率半径
Q ? 线 元左右偏标志(左偏Q=-1,右偏Q=1,直线段Q=0)
S=700 Z= 5 计算得 XS=19823.25398 YS=28503.95084
S=780 Z=-5 计算得 XS=19785.25749 YS=28575.02270
S=780 Z=0 计算得 XS=19781.15561 YS=28572.16358
X=19742.686 Y=28652.914 计算得 S=870.0003175 Z=- 0.00041814
X=19737.837 Y=28651.697 计算得 S=870.0002748 Z= 4.999808656
X=19741.5912 Y=28722.0580 计算得 S=939.9999786 Z= -5.123024937 80.0000016 Z= 4.99999578
X=19747.536 Y=28654.131 计算得 S=870.0001137 Z= -4.99941049
919.527 19736.072 28701.893 91 17 30.63 80.285 221.75 9579.228 -1
999.812 19744.038 28781.659 80 40 50.00 100.000 1E45 1E45 0
WD)+90:X=X+ZcosF:Y=Y+ZsinF
3. 反算子程序(SUB2)
T=G-90:W=Abs((Y-V)cosT-(X-U)sinT):Z=0:Lbl 0:Prog "SUB1":L=T+QEW(C+
利用卡西欧fx-4800P计算器编程求解曲线与曲线交点

利用卡西欧fx-4800P计算器编程求解曲线与曲线交点
王景海
【期刊名称】《铁道勘察》
【年(卷),期】2008(034)006
【摘要】首先讨论了用二分法求解工程测量中曲线与曲线交点的具体算法,然后在卡西欧fx-4800p 计算器上编程实现该算法,最后结合实际工程给出了算例.
【总页数】3页(P15-17)
【作者】王景海
【作者单位】北京四方工程建设监理有限责任公司,北京,100039
【正文语种】中文
【中图分类】U2
【相关文献】
1.利用CASIO编程计算器进行直线与缓和曲线交点坐标的精确计算 [J], 高振玲
2.基于卡西欧5800计算器单交点非对称曲线坐标正反算程序设计 [J], 孙亚奇
3.单曲线边桩坐标在卡西欧计算器的编程计算 [J], 王立平
4.利用CASIO编程计算器进行圆曲线与缓和曲线交点坐标的精确计算 [J], 高振玲;马俊福
5.单曲线边桩坐标在卡西欧计算器的编程计算 [J], 王立平
因版权原因,仅展示原文概要,查看原文内容请购买。
