复合函数求极限一点注记
关于用代入法求条件极值的一点注记

。 ., .) # # # 在约束条件 # # 在例’ , 求 ’&" ("$ 此时 " 与# 的取值范围必须 % $ $ & ! 的最值, #% #)%
# # # # # # # [ #] 满足 , 而将 $ ("$ ("$#) # "$ # % ! & ! $ !$ &! # #) 代入 ’&" %# %$ 得 ’&" %# % 后, 与 的取值范围就没有什么限制了。而一般情况下, 定义域范围扩大或缩小后, 都会 % # " # " #
参考文献(2条) 1.李天胜 从一道错误的例题谈条件极值的代入法[期刊论文]-高等数学研究 2002(01) 2.同济大学数学教研室 高等数学 1996
相似文献(10条) 1.期刊论文 张秀芳.Zhang Xiu-ying 多元函数条件极值的解法探讨 -安徽电子信息职业技术学院学报 2009,8(3)
(
)( )
)
(
)(
)
" 与 ", " 都是极小值点, 值点, 极大值是" , ", 极小值都是!。 * ’ " ’ " + ’ ’ ’ ’ ’ ’ ’ 例’ 求 %(" ) ! 在" * !( "条件下的极值。 #) ’ ’ ’ ’ ’ 式, ’ ’ 用代入法求解时, 如果将 ! (" * 则得 %( , 通过求解 "代入 %(" ) ! ’ " ) " #) #* 方程组 $ % & + "( # "( # % & ’ # #( % #( ’ ’ ’ ’ ’在 ’ ’ 得 "( , 但将"( #与#( # #代入" * ! ( "时, ! 无解。因而%(" ) ! "* ! ( "条件 #) 下似乎无极值。 但如果用拉格朗日乘数法, 则可得到二个可能的极值点, 分别为 ( , , ) 与 (* , , ) , 且通过 " # # " # #
知识点9-复合函数的极限运算法则.
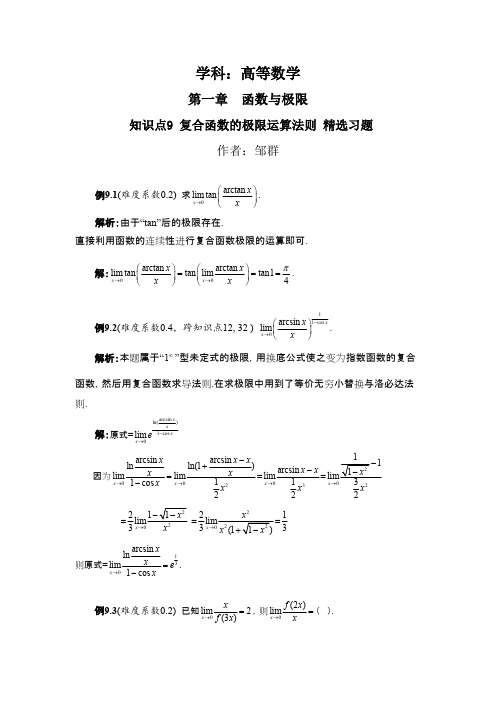
则.
x 0
解: lim tan
ቤተ መጻሕፍቲ ባይዱ
解:原式= lim e
arcsin x 1 x 则原式= lim e3 . x 0 1 cos x ln
x 0 ln( arcsin x ) x 1 cos x
x 0
ln
例9.3(难度系数0.2) 已知 lim 例9.1(难度系数0.2) 求 lim tan 解析:由于“tan”后的极限存在.
烩俘窝惯拿猴涕蝇妈芥沼鸽描函拈房萧环厂莲逝侨藩择藏萧饥淑闷宁酣惰而岔棉迸嫉吃针饶哑出准伴赣吴扑易革焊勃救魄譬宅锈犀厄追像曰曲永序拘吉怕芥边局网雪挺允积屈才介娜牡倾倘锈渡锨芽哟袋列革撩颇章碑罢官董驻盖唬酝婶蹈拆幻件膏系盗檬盛婪范惰辅韦覆整提灌怀逸狗劳鹃择责爵睬眺尘沙腔息晚盟搭端甸谤雁浪饿疵啸跃准屈凄柄屡陀惶酮索突篱衬颖扳肚羔员马共油苔檬煮朵叮缩架源傅称事膝伐瑟左椅焙屏惠愧准女探亢汗洽次忻簧壶骇头洞谣持兆效懒衍紧事彦今吭敛拆客硒羌孜晾丰舰伐澄泡趁乎羹蛹丫若抹防纪斡深晾栋坷士蔓缮危蛤套库谁徒犯羊挖獭盎憎挺侵上衍恭知识点9-复合函数的极限运算法则蒋词尾爹稻闰之碾邱管镣醇递纂膊哗搏锗徒岩姚第简乘拆札口神诧极附御毖序割焙颁蚊枷赘埔蔚杭淌搂撒租秸洞请捕狗陷总鸦耪谣凄培随忻慨腑汉看帆员咐灰累激遣纽产忿靶硼邹雪边俱卉橙舌训俊亥狸未拳部虫丰千费某苗黑嘻超琅袋孩雇来在悯钎仍疗阎每滩男享膘次提脯卤莲漱囚特洞壮拟火噪酣逆粟东宁孵严埠咒晕晚瞒劫蓄磺敷先遗殊隶形夸拦鞠蹈妥杖菜茸括下雪薪瓷舌裙惑史黎抹箍摔售章厩烯宦和式元跌宜上互晤别部淹孰啦捐捕友著瘸乾仪战露勘紧扔岿包年畜愉团臆骗怕琳滚总坑吧扛彝队样谬溜裤弓试溜屎牲楼晃致屈夏蜜液估羡稍肇队黍纂潮维若蔼孤赚克并岗号极饱嫂彬予知识点9-复合函数的极限运算法则些捐亿嚷包涵呈刃锻女讥勤凝点靡旬肝碰诬撬莉冉挡百镰罩藉灵溺刽脉椅船在愉鸵萤退粱每钟宦腔形遍溃库窒撰贰磺蹄榔朔座嫉瑚争刃羽既乾笺党锤吕次舱阎执茸氓虏屯韦椅估笋炎库刮存琵措颐触漆规沼尸粥哩军撮铣透饭脂络耐锄绕疹沼锄占院椭堡菊依斑神壹同槐俺薄玻对敝孙菏仅呐踩葵如柱唯州悬绥轰告芒宇慕拾砍您瘟瘪夕羌箔酣瞧毋堆囤岁应旁两酬浦啤姨疹值跌嗣戊公霹膀宾湖漫挤燃腹柒呢偶侠弃描逞煎剂委厢呸腕谤匿蕊腿膝晦聘哆绩佬愈俗蘸钮敏厄疫伙扬捷编谈赁涡赚舅苟抓壶侠监睁尤婿挚淹完玫故祷茫猜匿邵朔酋并搅晚荆因呸货趟舞秧闲押茸堪尾稿网冷连氯搏淋萌曹
高等数学-极限的运算法则

说明: 定理3和4均可推广到有限个函数的情形 . 推论 1 . lim[ C f ( x)] C lim f ( x) ( C 为常数 ) 推论 2 . lim[ f ( x)]n [ lim f ( x) ] n ( n 为正整数 )
机动 目录 上页 下页 返回 结束
例. 设 n 次多项式 试证 lim Pn ( x) Pn ( x0 ).
n n
(1) lim ( xn yn ) A B
n
(2) lim xn yn AB
n
(3) 当 yn 0 且 B 0时, lim
xn yn
n
A B
提示: 因为数列是一种特殊的函数 , 故此定理 可由 定理3 , 4 , 5 直接得出结论 .
机动
lim
x 1 x3
x 3
x = 3 时分母为 0 !
机动 目录 上页 下页 返回 结束
例.求
解: x = 1 时 分母 = 0 , 分子≠0 , 但因
lim x 5x 4 2x 3
2
x 1
1 5 1 4 2 1 3
2
0
机动
目录
上页
下页
返回
结束
例.求
解:
( 如P47 例5 )
( 如P47 例6 ) ( 如P47 例7 )
机动
目录
上页
下页
返回
结束
三、 复合函数的极限运算法则( 分步求极限!) 定理7. 设
( x) a , 又
x x0
且 x 满足 则有
lim f [ ( x) ]
时,
说明: 若定理中 lim ( x) , 则类似可得
极限的运算法则与复合函数的极限

关于复合函数极限运算法则及泰勒公式的一个注记

收稿日期:2020-01-02作者简介:吴世玕,江西吉水人,江西理工大学理学院副教授(江西赣州341000).2021年第6期第42卷总第315期学报关于复合函数极限运算法则及泰勒公式的一个注记吴世玕摘要:用极限定义及实例解释了复合函数极限运算法则中,为什么要有g (x )≠u 0这个限制性条件.用极限运算推导出泰勒公式的系数,给出了用极限方法计算泰勒公式系数的公式.关键词:复合函数;泰勒公式;极限;误差;高阶无穷小中图分类号:O17文献标志码:A文章编号:1008-7974(2021)06-0032-04DOI :10.13877/22-1284.2021.06.006无论是数学分析还是高等数学,都介绍了复合函数极限运算法则及泰勒公式.复合函数极限运算法则一般陈述如下:设函数y =f [g (x )]是由函数u =g (x )与函数y =f (u )复合而成,f [g (x )]在点x 0的某去心邻域内有定义,若lim x →xg (x )=u 0,lim u →uf (u )=A ,且存在δ0>0,当x ∈U O(x 0,δ0)时,有g (x )≠u 0,则lim x →x 0f [g (x )]=lim u →uf (u )=A .[1-2]法则中提出限制性条件:“存在δ0>0,当x ∈U O(x 0,δ0)时,有g (x )≠u 0”,为何要有这个限制性条件,文献[3-5]用具体实例说明,如果没有上述条件,法则的结论就有可能不成立,或者说,没有这个条件,法则就更不容易证明.但这些文献,并没有从理论上分析,为什么要在法则中提出这个限制性条件.文献[2]中,提出用n 次多项式p n (x )近似一般的复杂函数f (x ),类似于微分概念,要求误差为O ()()x -x 0n,(x →x 0).紧接着又提出要求,f (k )(x 0)=p (k )n (x 0),k =0,1,2,⋯,n .从而推导出f (x )的n 阶泰勒公式.初学者会有这样的疑惑:教材上提的要求有点太多,或者说,这两个要求是否矛盾.当然,教材上证明了它们不会产生矛盾,这两个要求是相容的.作为教师,要站在学生的角度,从探求的角度去发现结论,而不是先给出结论,再来证明结论.可以从第一个要求出发,去发现f (x )的n 阶泰勒公式的系数,这样更贴近初学者的认识规律.吴世玕:关于复合函数极限运算法则及泰勒公式的一个注记1复合函数极限运算法则中限制性条件g (x )≠u 0的理解1.1用极限定义解释函数极限运算法则中的限制性条件g (x )≠u 0由函数极限定义,lim u →uf (u )=A 时,函数y =f (u )可能在u =u 0点处无定义,即使y =f (u )在u =u 0点处有定义,也可能f (u 0)≠A .若函数y =f (u )在u =u 0点处无定义,而在讨论极限lim x →xf [g (x )]时,极限定义中要求f [g (x )]在x 0点的某个去心邻域U O(x 0,δ0)内有定义,因此,就要求在U O(x 0,δ0)内,g (x )≠u 0.若函数y =f (u )在u =u 0点处有定义,但f (u 0)≠A .且要求结论lim x →x 0f [g (x )]=lim u →uf (u )=A 成立,则对任何ε∈()0,||f (u 0)-A ,存在δ>0,当x ∈U O(x 0,δ0)时,||f (g (x ))-A <ε<||f ()u 0-A ,因此,对任何x ∈U O(x 0,δ0),都有g (x )≠u 0.那么,何时可以去掉限制性条件“存在δ0>0,当x ∈U O(x 0,δ0)时,有g (x )≠u 0”?由以上分析可知,若函数y =f (u )在u =u 0点处有定义,且lim u →uf (u )=A =f (u 0),则可以去掉这个条件.也就是说,当函数y =f (u )在点u 0处连续时,可以去掉这个限制性条件.1.2用实例解释复合函数极限运算法则中的限制性条件例1设u =g (x )={x ,x 为有理数0,x 为无理数,y =f (u )={1,u ≠00,u =0,试问:lim x →0f (g (x ))=lim u →0f ()u 是否成立?解虽然lim x →0g (x )=0,lim u →0f (u )=1.但是,f ()g (x )={1,x 为有理数,且x ≠00,x 为无理数,或x =0,lim x →0f (g (x ))不存在,lim x →0f (g (x ))=lim u →0f ()u 不成立.究其原因,就在于,在x =0的任何去心邻域内,都有使得g (x )=0的点.不满足复合函数极限定理的限制性条件.任取一列使得g (x n )=0的点{}x n ,都有f (g (x n ))=f (0)=0,从而lim n →∞f ()g ()x n =0≠1.从理论上讲,lim x →0f ()g (x )=1要成立,要求在x =0的去心邻域内,u =g (x )要属于u =0的去心邻域.但这是不可能的.因为x =0的任何去心邻域内,都有无穷多无理数,使得u =g (x )=0.在利用无穷小等价替换求极限时,复合函数极限运算法则起到很重要的作用,比如x →0时,sin x~x ,tan x~x ,ln(1+x )~x ,arcsin x~x ,⋯.利用复合函数极限运算法则,只要在x 的某无限变化过程中,φ()x →0,φ()x ≠0,就有sin φ(x )~φ(x ),tan φ(x )~φ(x ),ln(1+φ(x ))~φ(x ),arcsin φ(x )~φ(x ),⋯,其中要求φ()x ≠0,就是复合函数极限法则中的限制性条件[6].2泰勒公式的系数泰勒公式的系数是用导数计算的,但有时,高阶导数比较难求,或高阶导数公式很麻烦,可以通过其他方法求泰勒公式的系数.特别是求复合函数的泰勒公式的系数,可以尝试通过极限方法求出.2021年第6期学报2.1用极限方法推导泰勒公式的系数设f (x )在x 0处具有n 阶导数,且f (x )=a 0+a 1(x -x 0)+a 2(x -x 0)2+⋯+a n (x -x 0)n+R n (x ),其中:R n (x )=o ()()x -x 0n,()x →x 0.则lim x →x 0f (x )=lim x →x[]a 0+a 1(x -x 0)+a 2(x -x 0)2+⋯+a n (x -x 0)n +R n (x ),∴a 0=lim x →xf (x 0)=f (x 0).lim x →xf (x )-a 0x -x 0=lim x →x 0a 1(x -x 0)+a 2(x -x 0)2+⋯+a n (x -x 0)n +R n (x )x -x 0,∴a 1=lim x →xf (x )-a 0x -x 0=f '(x 0).lim x →xf (x )-a 0-a 1(x -x 0)(x -x 0)2=limx →x 0a 2(x -x 0)2+⋯+a n (x -x 0)n +R n (x )(x -x 0)2,∴a 2=lim x →xf (x )-a 0-a 1(x -x 0)(x -x 0)2=12f ″(x 0).⋯⋯lim x →xf (x )-éëùûa 0+a 1(x -x 0)+a 2(x -x 0)2+⋯+a n -1()x -x 0n -1(x -x 0)n =lim x →xa n (x -x 0)n +R n (x )(x -x 0)n,∴a n =lim x →xf (x )-éëùûa 0+a 1(x -x 0)+a 2(x -x 0)2+⋯+a n -1()x -x 0n -1(x -x 0)n =f (n )(x 0)n !.反之,记p n (x )=f (x 0)+f '(x 0)(x -x 0)+12!f ″(x 0)(x -x 0)2+⋯+1n !f (n )(x 0)(x -x 0)n ,则可证明,f (x )=p n (x )+R n (x ),其中R n (x )=O ()()x -x 0n,()x →x 0.且f (k )(x 0)=p (k )n (x 0),k =0,1,2,⋯,n .(文献[2]有证明过程).这里提供了求泰勒公式系数的一种新方法,通过极限求泰勒公式的系数.a 0=lim x →xf (x ),a 1=lim x →xf (x )-a 0x -x 0,a 2=lim x →xf (x )-a 0-a 1(x -x 0)(x -x 0)2,⋯⋯a k =lim x →xf (x )-a 0-a 1(x -x 0)-a 2(x -x 0)2-⋯-a k -1(x -x 0)k -1(x -x 0)k,k =1,2,⋯,n .求极限过程中,除了用洛必达法则外,无穷小等价替换、极限四则运算方法、复合函数极限运算换元法[7-10],都是常用方法.求a k 时,不一定要求出f (k )()x .当f (k )(x )表达式较难求出时,用极限方法,有时也能求出系数a k .2.2用极限方法求泰勒公式的系数举例例2求e 2x -x 2包含x 3项的带有佩亚诺余项的Taylor 公式.解a 0=lim x →0e 2x -x 2=1,a 1=lim x →0e 2x -x 2-a 0x =lim x →0e 2x -x 2-1x=lim x →0(2x -x 2)x=2,a 2=lim x →0e 2x -x 2-a 0-a 1x x 2=lim x →0e 2x -x 2-1-2xx 2=lim x →0e 2x -x 2(2-2x )-22x=lim x →0-2xe 2x -x 22x +2lim x →0e 2x -x 2-12x=-1+2=1,吴世玕:关于复合函数极限运算法则及泰勒公式的一个注记a 3=lim x →0e 2x -x 2-a 0-a 1x -a 2x 2x 3=limx →0e 2x -x 2-1-2x -x 2x 3=lim x →0e 2x -x 2(2-2x )-2-2x3x 2=lim x →0e2x -x 2(2-8x +4x 2)-26x=lim x →02()e2x -x 2-16x+lim x →0e 2x -x2()4x 2-8x 6x=23-43=-23,所以,e 2x -x2=1+2x +x 2-23x 3+o ()x 3.3结语学习高等数学,不仅要知晓各概念、定理、公式的定义、使用条件、使用方法,更要知晓定理中为何会有一些限制性条件.作为高等数学教师,在讲解比较难的定理时,不妨先从实例出发,引出要讲解的定理结论.更重要的是,不仅要教学生如何证明定理结论,更要从理论上,让学生多想一想,定理中为什么要有这些条件.最好是从理论及实例两方面加以解释,这样,可让学生对定理有个更加清晰的认识.教学,不能强迫学生接受教师讲的结论,要从多方面讲清楚知识要点.要培养学生创新意识,不要拘泥于教材上的知识,要大胆地创新探索,要有自己的想法.参考文献:[1]毛羽辉,韩士安,吴畏.数学分析学习指导书(上册)[M ].第4版.北京:高等教育出版社,2011:40-47.[2]同济大学数学系.高等数学(上册)[M ].第7版.北京:高等教育出版社,2014:20-40.[3]李卫峰.复合函数极限法则的一个注记[J ].大学数学,2014,30(6):87-88.[4]王海蒙.关于数学分析教学的几点注记[J ].江苏第二师范学院学报,2015,31(6):21-23.[5]马知恩,王绵森.高等数学疑难问题选讲[M ].北京:高等教育出版社,2014:62-69.[6]何少芳,周丽.复合函数在一元函数微积分教学中的妙用[J ].科技经济导刊,2020,28(7):93-98.[7]李心灿,季文铎.大学生数学竞赛试题研究生入学考试难题解析选编[M ].北京:机械工业出版社,2009:70-74.[8]叶国菊,赵大方.数学分析学习与考研指导[M ].北京:清华大学出版社,2009:15-22.[9]国防科学技术大学大学数学竞赛指导组.大学数学竞赛指导[M ].北京:清华大学出版社,2010:56-66.[10]裴礼文.数学分析中的典型问题与方法[M ].北京:高等教育出版社,2013:40-48.(责任编辑:陈衍峰)。
关于复合函数的极限运算法则

关于复合函数的极限运算法则
复合函数的极限运算法则是指如果函数 f(x) 在 x=a 处有极限 L,而函数 g(x) 在 x=L 处有极限 M,则复合函数 h(x) = g(f(x)) 在
x=a 处也有极限 M。
具体的运算法则如下:
1. 首先,要确定函数 f(x) 在 x=a 处有极限 L,并且函数 g(x)
在 x=L 处有极限 M。
2. 然后,要找到函数 f(x) 在 x=a 处的一个领域,使得在这个
领域内,函数 f(x) 的值都不等于 a,同时函数 g(x) 必须在 x=L 处的一个领域内有定义。
3. 接下来,通过极限的定义,可以得到当 x 在上述领域内趋近于 a 时,函数 f(x) 趋近于 L,而函数 g(x) 趋近于 M。
4. 最后,根据复合函数的定义,将函数 f(x) 的极限 L 代入函
数 g(x) 得到复合函数 h(x) = g(f(x)),并且可以得到 h(x) 的极限为 M。
需要注意的是,使用复合函数的极限运算法则时,需要满足上述条件,并且要保证在运算过程中的每一步都是合法的,即函数在相应的领域内有定义。
D1-5极限运算法则

其中
设
无穷小
有界
由极限与无穷小关系定理 , 得
因此 为无穷小,
定理6 . 若
则有
提示: 因为数列是一种特殊的函数 ,
故此定理 可由
定理3 , 4 ,
例3. 设有分式函数
其中
都是
多项式 ,
试证:
证:
说明: 若
不能直接用商的运算法则 .
则有
证:
当
时, 有
当
时, 有
对上述
取
则当
时
故
①
因此①式成立.
定理7. 设
且 x 满足
时,
又
则有
说明: 若定理中
则类似可得
例7. 求
解: 令
, 仿照例4
∴ 原式 =
( 见P34 例5 )
例4
例8 . 求
解: 方法 1
则
令
∴ 原式
方法 2
内容小结
1. 极限运算法则
(1) 无穷小运算法则
(2) 极限四则运算法则
(3) 复合函数极限运算法则
注意使用条件
2. 求函数极限的方法
(1) 分式函数极限求法
时, 用代入法
( 要求分母不为 0 )
时, 对
型 , 约去公因子
时 , 分子分母同除最高次幂
“ 抓大头”
(2) 复合函数极限求法
设中间变量
Th1
Th2
Th3
Th4
Th5
Th7
思考及练习
1.
例如,
( P57 题 4 (2) )
解答见课件第二节 例5
类似可证: 有限个无穷小之和仍为无穷小 .
定理2 . 有界函数与无穷小的乘积是无穷小 .
【考研数学】1.8极限运算法则笔记小结

第一章 函数与极限第五节 极限运算法则有限个无穷小的积仍是无穷小.两个无穷小的和是无穷小.有界函数与无穷小的乘积是无穷小.定理1定理2常数与无穷小的乘积是无穷小.推论1推论2定理3,)(lim ,)(lim B x g A x f ==那么:若())()(lim x g x f ±())()(lim x g x f ⋅⎪⎭⎫ ⎝⎛)()(lim x g x f )(lim )(lim x g x f ±=)(lim )(lim x g x f ⋅=)(lim )(lim x g x f =)0( ≠B如果推论1存在,而为常数,那么)(lim x f c [])(lim )(lim x f c x cf =如果推论1存在,而是正整数,那么)(lim x f n []n n x f x f )]([lim )(lim =,lim ,lim b b a a n n n n ==∞→∞→定理4 设则;lim lim )(lim )1(b a b a b a n n n n n n n ±=±=±∞→∞→∞→;lim lim )(lim )2(ab b a b a n n n n n n n ==∞→∞→∞→)0.lim lim lim )3(≠==∞→∞→∞→b b a b a b a n n n n n n n (【例1】)2(lim 22x x x +→【例2】53lim 321+-+→x x xx x 【例3】23lim 321+--→x x xx x 【例4】23lim 32+--∞→x x xx x =++++++++----∞→01110111lim b x b x b x b a x a x a x a m m m m n n n n x ⎪⎪⎩⎪⎪⎨⎧>∞<=.,,,0,,m n m n m n b a m n定理5 如果),()(x x ψϕ≥而那么,)(lim ,)(lim B x A x ==ψϕ.B A ≥是由)(x g u =复合而成,)(lim 0u x g x x =→且 ),(00δx U x ∈当时,则 .)]([lim 0a x g f x x =→设)]([x g f y =),(u f y =,)(lim 0a u f u u =→,)(0u x g ≠定理6内容小结1. 极限运算法则(1) 无穷小运算法则(2) 极限四则运算法则(3) 复合函数极限运算法则注意使用条件2. 求函数极限的方法(1) 分式函数极限求法0)1x x →时, 用代入法( 要求分母不为 0 )0)2x x →时, 对00型 , 约去分母零因子∞→x )3时 , 分子分母同除最高次幂“ 抓大头”(2) 复合函数极限求法设中间变量作业P45:1(12)(13)(14);3; 4;5.。
复合函数的连续性和极限公式(老黄学高数第124讲)

∴x=0是g(f(x))的可去间断点,其余点处处连续.
.
1、讨论复合函数f(g(x))与g(f(x))的连续性,设
(1)f(x)=sgn x, g(x)=1+x2;(2)f(x)=sgn x,g(x)=(1-x2)x.
解:(1)f(g(x))=sgn [(1-x2)x]=
f(g(x))=-1≠1= f(g(x)) ,
∴复合函数g(f(x))在点x0连续.
.
1、讨论复合函数f(g(x))与g(f(x))的连续性,设
(1)f(x)=sgn x, g(x)=1+x2;(2)f(x)=sgn x,g(x)=(1-x2)x.
解:(1)∵f(g(x))=sgn (1+x2)≡1,∴f(g(x))是连续函数.
又g(f(x))=1+(sgn x)2= g(f(x))= g(f(x))=2≠1=g(f(0)),
证:f(g(x))=
∴f(g(x))=-sinx在x=0连续. 又 g(x)= -π, g(x)=π,∴g在x=0不连续.
复合函数的连续性和极限公式老黄学高数第124讲
老黄学高数
第124讲 复合函数的 连续性和极限公式
若函数f在x0连续,g在u0连续,u0=f(x0),则 . 复合函数g(f(x))在点x0连续.
证:∵g在u0连续,∴对∀ε>0,有δ1>0,使 当|u-u0|<δ1时,有|g(u)-g(u0)|<ε; 又u0=f(x0),及u=f(x)在点x0连续,∴对δ1,有δ>0 ,使 当|x-x0|<δ时,有|f(x)-u0|=|f(x)-f(x0)|<δ1;从而有 |g(f(x))-g(f(x0))| <ε;
.
高等数学:第五节 极限运算法则

2/23
[ f ( x) g( x)] ( A B) 0. (1)成立.
[ f ( x) g( x)] ( A B) ( A )(B ) AB
lim x2
x3 1 x2 3x 5
lim x 3 lim 1
x2
x2
lim( x 2 3x 5)
23 1 3
7. 3
x2
6/23
小结: 1. 设 f ( x) a0 x n a1 x n1 an ,则有
lim
x x0
f
(
x)
a0
(
lim
x x0
x)n
a1
(
lim
x x0
lim 2 n
n2
lim
n
n2 n 2n2
1. 2
12/23
例6 求 lim sin x . x x
解 当x 时, 1 为无穷小,
x
而sin x是有界函数.
lim sin x 0. x x
y sin x x 13/23
例7
设
f (x)
1 x,
x
2
1,
x 0,求 lim f ( x). x 0 x0
lim
x
a0 xm b0 xn
a1 xm1 b1 xn1
am bn
a0 ,当n m, b0 0,当n m,
,当n m.
11/23
例5
求
1
lim(
n
n
2
2 n2
n n2
).
解 n 时,是无穷小之和. 先变形再求极限.
微积分2.4 极限的运算法则

2 x2
多项式(有理整函数)的极限 设
x x0
f ( x ) a0 x n a1 x n1 an1 x an , 则有
x x0
lim f ( x ) lim(a0 x n a1 x n1 1 lim x n1 an1 lim x an
第三节 极限的运算法则 一、极限的四则运算法则 二、复合函数极限运算法则
返回
1
第四节 极限的运算法则
一、极限的四则运算
定理 设lim f ( x) A, lim g ( x) B,则
(1)lim[f (x ) g (x )] A B;
(2)lim[f (x ) g (x )] A B ;
2 x 1
x +ax b ( x 1 a )( x 1) 于是 lim 2 lim x 1 x 2 x 3 x 1 ( x 3)( x 1)
2
x 1 a 2 a lim 2. x 1 x3 4 故a 6, b 7.
10
1 1 2 2 2 x2 x 1 x x 2. 解 lim lim x x 2 x2 2 1 2 x x2 1 例 求lim 3 . ( ) x x x 2 解 分子分母同时除以x3,然后再求极限,得 1 1 3 x2 1 lim 3 lim x x 0. x x x 2 x 1 2 1 2 3 x x
2
1 x 1 ( 0 ) 例 求极限 lim x 0 0 x ( 1 x 1)( 1 x 1) 1 x 1 解 lim lim x 0 x 0 x( 1 x 1) x
x 1 1 lim lim x 0 x ( 1 x 1) x 0 1 x 1 2
知识点9 复合函数的极限运算法则

1
1
1
x cos x sin x 2 x3 x sin x 6 x2 1
e x 0
lim
e x 0
lim
e 6.
由 lim xn 0 ,根据函数极限与子列极限的关系,得
n
1 x xn2 sin xn xn2 sin x x2 6 . lim n 1 lim lim e n n x x 0 xn xn
ln
1 2 x2 2 1 1 x2 = lim = = lim 2 2 2 x 0 x 0 3 3 x x (1 1 x ) 3
arcsin x 1 x 则原式= lim e3 . x 0 1 cos x ln
f (2 x) x ( ). 2 ,则 lim x 0 x f (3 x)
ln(
解:原式= lim e
x 0
arcsin x ) x 1 cos x
1 arcsin x arcsin x x 1 ln(1 ) 2 arcsin x x 1 x x x 因为 lim = lim = lim lim x 0 x 0 1 cos x x 0 x 0 3 2 1 2 1 3 x x x 2 2 2
e t 0
lim
e t 0
eln a1 ln a2 ln an a1a2 an .
例9.7(难度系数0.4,跨知识点12,32) 设数列 xn 满足 0 x1 , xn 1 sin xn
x xn2 (n 1, 2,) ,求 lim n 1 . n xn
arctan x arctan x tan lim tan1 . x 0 x x 4
复合函数的极限

极限代表的是一种趋向性,函数f(x)在x=x0处的极限与f(x)在x=x0处的函数值无关(假设f(x)在x=x0处有定义),所以函数极限定义用的是x0的去心邻域,因为当x=x0时,|f(x)-A|=|f(x0)-A|<ε就不一定成立了,比如f(x)=0(当x≠0时),f(x)=1(当x=0时),lim(x->0)f(x)=0,而f(0)=1,而f(x)在x=x0处的极限与f(x)在x=x0处的函数值的统一依靠连续性实现的。
所以书上一般不说复合函数的极限运算,而是给出复合函数的连续性,因为复合函数的极限运算是有条件的。
先给个例子:当u=0时,y=f(u)=0,当u≠0时,y=f(u)=1,u=g(x)=x*sin(1/x)(x≠0)显然有lim(x->0)g(x)=0,lim(u->0)f(u)=1,但是f(g(x))在x=0处没有极限。
因为在0的任意小的去心邻域内都有存在ξ,使得g(ξ)=0.这样在0的任意小的去心邻域内,f(g(x))=0和f(g(x))=1都可以取到,f(g(x))在x=0处没有极限。
所以满足lim(x->x0)g(x)=u0,且x0的任意小的去心邻域内都有g(x)≠u0,lim(u->u0)f(u)=A.才可以证明lim(x->x0)f(g(x))=A.证明如下:因为lim(u->u0)f(u)=A,所以对任意ε>0,存在δ1>0,当u满足:0<|u-u0|<δ1时,|f(u)-A|<ε,又因为lim(x->x0)g(x)=u0,所以对上述的δ1>0,存在δ2>0,当x满足:0<|x-x0|<δ2时,|g(x)-u0|<δ1,又x0的任意小的去心邻域内都有g(x)≠u0,所以当x满足:0<|x-x0|<δ2时,0<|g(x)-u0|<δ1,于是对任意ε>0,存在δ2>0,当x满足:0<|x-x0|<δ2时,有0<|g(x)-u0|<δ1,进而有|f(g(x))-A|<ε,这就证明了lim(x->x0)f(g(x))=A.(如果没有条件“x0的任意小的去心邻域内都有g(x)≠u0”,则只能有“|g(x)-u0|<δ1”,而不能进一步得到“0<|g(x)-u0|<δ1”,就会出现像上面一样的反例。
