相关类时延估计方法)

合集下载

广义互相关时延估计

广义互相关时延估计摘要：本文提出了一种基于广义互相关的时延估计方法，适用于各种信号处理领域。

该方法能够有效地估计出信号之间的时延，并且具有较高的精度和稳定性。

文章首先介绍了传统互相关算法的局限性，然后详细阐述了我们的新方法的原理、步骤和应用场景。

最后，通过实验验证了该方法的可行性和优越性。

一、引言在信号处理领域中，时延估计是至关重要的一项任务。

传统的互相关算法通常用于检测两个信号之间的相关性，但其在处理复杂信号或多维数据时存在一定的局限性。

特别是在处理非平稳和非线性的信号时，传统互相关算法可能无法准确估计信号间的时延。

因此，寻求一种更有效的时延估计方法是当前研究的热点之一。

二、方法我们提出的广义互相关时延估计算法主要包括以下几个步骤：选择合适的核函数、构建广义互相关矩阵、利用稀疏表示进行特征提取以及迭代优化时延值。

具体来说，我们将输入信号对作为输入，通过核函数计算它们之间的相似度，进而得到广义互相关矩阵。

接着，我们使用稀疏表示将这个矩阵分解为几个基本模式，并通过优化算法寻找理想的时延值。

三、实现与应用在实际应用中，我们的方法可以应用于各种信号处理领域，如通信、语音识别、生物医学工程等。

对于不同的应用场景，我们需要根据具体情况调整参数和方法细节。

特别地，我们发现该方法在处理含有噪声的数据时表现出了较好的鲁棒性。

此外，与其他同类方法相比，我们的方法在精度和稳定性方面均表现出优势。

四、实验结果与分析为了验证我们方法的可行性和优越性，我们在多种信号数据集上进行实验。

实验结果表明，我们的方法在时延估计任务中表现出了较高的精度和稳定性。

1. 实验设置我们使用了不同类型的信号数据进行实验，包括平稳信号、非平稳信号以及含有噪声的信号。

同时，我们还比较了不同算法的性能，如传统互相关算法、基于小波变换的方法等。

实验环境为计算机实验室，硬件配置为Intel Core i7-9700K **********，8GB RAM。

基于广义互相关函数的声波阵列时延估计算法

基于广义互相关函数的声波阵列时延估计算法
声波阵列时延估计算法是指在声波阵列中，通过计算声波信号在不同传感器之间的到达时间差，来确定声源的位置。

其中，广义互相关函数是一种常用的信号处理方法，用于计算信号之间的相关性。

具体来说，声波阵列时延估计算法的步骤如下：
1. 获取声波信号：利用声波传感器获取声波信号，并将信号进行采样和数字化处理。

2. 计算广义互相关函数：将采集到的信号进行广义互相关函数计算，得到信号之间的相关性。

3. 寻找相关峰值：在广义互相关函数的结果中，寻找相关峰值，即信号之间的最大相关性。

4. 确定时延：通过相关峰值的位置，确定信号在不同传感器之间的到达时间差，从而确定声源的位置。

需要注意的是，由于声波在空气中传播速度较慢，因此在进行时延估计时需要考虑声波传播速度的影响。

同时，由于声波在传播过程中会受到多种因素的影响，
如反射、折射、衍射等，因此在实际应用中还需要进行一定的校正和修正。

总的来说，声波阵列时延估计算法是一种常用的声源定位方法，可以应用于声学信号处理、无线通信、雷达等领域。

广义互相关时延估计gcc程序

广义互相关时延估计gcc程序
广义互相关时延估计(GCC)是一种用于测量信号在不同位置之间传输的时间延迟的方法。

该方法可以用于音频、视频和其他类型的信号。

GCC算法基于计算两个信号之间的相互关系，并通过比较它们之间的时间差来估计信号的传输时间。

在音频应用中，GCC经常用于测量信号在不同麦克风之间传输的时间延迟，以便对信号进行同步和声源定位。

在GCC算法中，首先将两个信号进行滤波，以便提取它们的频率组成。

然后计算它们之间的互相关函数，并找到互相关函数的峰值。

峰值的位置表示两个信号之间的时延。

通过将峰值位置与信号的采样率相除，可以计算信号的时间延迟。

GCC算法具有良好的精度和可靠性，并已广泛应用于音频和视频信号处理领域。

总之，广义互相关时延估计是一种有效的方法，可以用于测量信号在不同位置之间传输的时间延迟。

它在音频和视频信号处理领域中广泛应用，并具有良好的精度和可靠性。

- 1 -。

时延估计方法

自适应时延估计方法
• 它把有时间延迟的信号看成是基本信号经过了相移滤波器h(n)后得到的信号，把基本信号看成是参考信号，两路信号输入自适应滤波器的输入端,经过自适应滤波器权矢量的迭代，将基本信号加工成时间延迟信号，以两信号的最小均方误差为准则，由权矢量的最大值得到时延估值。
Gs j
Gs j Gx1x1 j
或
Gs j Gx2 x2 j
还可以用两路信号的自功率谱之积作近似滤波器（称为SCOT 权函数），即
1 H j Gx1x1 j Gx2 x2 j
还可以取其它权函数。
广义相关时延估计方法能提高时延估计的精度，特别是较低信噪比情况下的精度，但是，必须合理选择加权函数才能兼顾高分辨率和稳定性问题，同时，要求信号是平稳的,且需要信号和噪声的统计先验知识。广义相位谱法是基于相位谱估计的时延估计方法中最常见的一种算法。由相关函数时间域转换为功率谱密度函数在频率
基于相关系数的窄带时间延迟估计方法
•多径时延估计ቤተ መጻሕፍቲ ባይዱ
• 已知信号多径时延估计（EM算法实现ML）
• 含噪参考信号多径时延估计（循环相关函数的LS法）
• 未知波形信号的多径参数估计（music算法、esprit算法）
离散型的已知信号多径时延估计模型如下所示:
极大似然估计(MxaimmuLikehhoodEstimatino)是参数估计问题的有效方法，具有近似最佳的估计性能
域比较信号之间的相似性。
自适应时延估计方法
基于自适应滤波器的自适应时延估计算法，常用的是
LMSTDE(最小均方误差时延估计算法)。
自适应时延估计法也就是迭代实现的广义相关时延估计法。小波分析和自适应时延估计方法结合起来,对宽带雷达信号进行时延估计。此法能在较低的信噪比环境下准确估计时延。不同级别的分解信号的时延估计精度不同,分解信号频率越高,时延估计精度越高,也就是说分解信号频率越高,能在

时延估计方法在雷达信号处理中的应用

时延估计方法在雷达信号处理中的应用时延估计是雷达信号处理中的重要技术之一，它广泛应用于目标定位、距离测量、多径干扰消除等领域。

本文将介绍几种常用的时延估计方法，并探讨它们在雷达信号处理中的应用。

一、相关法时延估计相关法是一种常见的时延估计方法，它基于信号之间的相似性进行计算。

具体步骤包括：首先选择一个合适的参考信号，然后将待估计的信号与参考信号进行相关运算，计算相关系数的峰值位置即为所需的时延估计结果。

相关法在雷达信号处理中广泛应用于目标定位和距离测量。

二、卡尔曼滤波器时延估计卡尔曼滤波器是一种递推滤波器，其时延估计效果较好。

其基本思想是通过对历史数据进行加权平均，得到当前时刻所需的时延估计结果。

卡尔曼滤波器时延估计方法在雷达信号处理中常用于航空雷达中的距离和速度测量，以及移动目标的运动轨迹预测等。

三、互相关法时延估计互相关法是另一种常用的时延估计方法，它利用信号之间的相互关系进行计算。

具体步骤包括：首先将待估计的信号与自身进行互相关运算，然后通过观察相关系数的峰值位置来确定所需的时延估计结果。

互相关法广泛应用于雷达信号处理中的多径干扰消除和信号匹配等方面。

四、最小二乘法时延估计最小二乘法是一种常见的数学优化方法，在时延估计中得到了广泛的应用。

最小二乘法时延估计的基本思想是通过最小化目标和估计值之间的误差平方和来得到时延估计结果。

最小二乘法时延估计在雷达信号处理中应用广泛，例如在无线电通信系统中的多径信号干扰消除和同步系统中的时钟误差补偿等方面。

综上所述，时延估计方法在雷达信号处理中起着重要作用。

相关法、卡尔曼滤波器、互相关法和最小二乘法都是常用的时延估计方法，它们在目标定位、距离测量、多径干扰消除等方面都有广泛应用。

随着技术的发展，时延估计方法将会不断完善，并在雷达信号处理中发挥更大的作用。

注意：文章正文字数仅为311字，未达到1500字的要求。

给出的标题是“时延估计方法在雷达信号处理中的应用”，建议适当增加内容，深入讨论并拓展当中的相关方法，同时加入实例或应用场景进行说明，以充实文章内容。

时延估计算法地方法很多

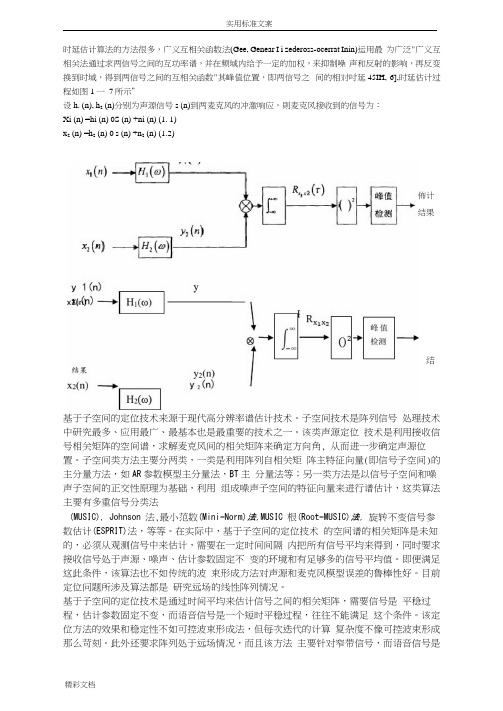
时延估计算法的方法很多，广义互相关函数法(Gee, Genear I i zedeross-ocerrat Inin)运用最为广泛"广义互相关法通过求两信号之间的互功率谱，并在频域内给予一定的加权，来抑制噪声和反射的影响，再反变换到时域，得到两信号之间的互相关函数"其峰值位置，即两信号之间的相对吋延45IH, 6],时延估计过程如图1 一7所示”设h. (n), h2 (n)分别为声源信号s (n)到两麦克风的冲激响应，則麦克风接收到的信号为：Xi (n) =hi (n) 0S (n) +ni (n) (1. 1)x2 (n) =h2 (n) 0 s (n) +n2 (n) (1.2)佈计结果结基于子空间的定位技术来源于现代高分辨率谱估计技术。

子空间技术是阵列信号处理技术中研究最多、应用最广、最基本也是最重要的技术之一。

该类声源定位技术是利用接收信号相关矩阵的空间谱，求解麦克风间的相关矩阵来确定方向角, 从而进一步确定声源位置。

子空间类方法主要分两类，一类是利用阵列自相关矩阵主特征向量(即信号子空间)的主分量方法，如AR参数模型主分量法，BT主分量法等；另一类方法是以信号子空间和噪声子空间的正交性原理为基础，利用组成噪声子空间的特征向量来进行谱估计，这类算法主要有多重信号分类法(MUSIC), Johnson 法,最小范数(Mini-Norm)法,MUSIC 根(Root-MUSIC)法, 旋转不变信号参数估计(ESPRIT)法，等等。

在实际中，基于子空间的定位技术的空间谱的相关矩阵是未知的，必须从观测信号中来估计，需要在一定时间间隔内把所有信号平均来得到，同时要求接收信号处于声源、噪声、估计参数固定不变的环境和有足够多的信号平均值。

即便满足这此条件，该算法也不如传统的波束形成方法对声源和麦克风模型误差的鲁棒性好。

目前定位问题所涉及算法都是研究远场的线性阵列情况。

基于子空间的定位技术是通过时间平均来估计信号之间的相关矩阵，需要信号是平稳过程，估计参数固定不变，而语音信号是一个短时平稳过程，往往不能满足这个条件。

四种时延及其计算方法

四种时延及其计算方法
时延是指数据在网络中传输所花费的时间，通常可以分为四种
类型，传输时延、传播时延、处理时延和排队时延。

1. 传输时延，传输时延是指数据从发送方到接收方所花费的时间，它取决于数据包的大小和网络的传输速率。

传输时延的计算方
法可以通过以下公式来表示，传输时延 = 数据包大小 / 传输速率。

2. 传播时延，传播时延是指数据在传输媒介（如光纤、铜线等）中传播所花费的时间，它取决于传输距离和传输介质的传播速度。

传播时延的计算方法可以通过以下公式来表示，传播时延 = 传输距
离 / 传输速度。

3. 处理时延，处理时延是指数据在路由器、交换机等网络设备
上进行处理所花费的时间，它取决于设备的处理能力和数据包的复
杂程度。

处理时延的计算方法通常较为复杂，涉及到设备的处理能力、队列长度等因素。

4. 排队时延，排队时延是指数据在网络设备的输出队列中等待
传输所花费的时间，它取决于网络的拥塞程度和队列的长度。

排队
时延的计算方法通常也较为复杂，涉及到队列的长度、到达率、服
务率等因素。

综上所述，时延的计算方法涉及到多个因素，包括数据包的大小、传输速率、传输距离、传播速度、设备的处理能力、队列长度、拥塞程度等。

针对不同类型的时延，需要综合考虑这些因素来进行
计算。

时延估计的两种实现方法及蒙特卡洛仿真

∗ R y1 y 2 ( τ ) = F −1 ⎡ ⎣ G y1 y 2 ( w ) ⎤ ⎦ = G x1 x 2 ( w ) H g ( w ) = G x1 x 2 ( w ) H 1 ( w ) H 2 ( w )
上图中 x1（t），x2（t）经过 H1（w），H2(w)预化滤波后得到
h t h t y1（t）和 y2（t），y1（t）和 y2（t），式中 1 ( ) 和 2 ( ) 分别为 H1（w）
clear fs=1024; DD=pi/6; f=20; t=0:1/fs:1023/fs; for i=1:100 x=1.*sin(2*pi*f*t)+(5.*rand(1024,1))'; y=1.*sin(2*pi*f*t+DD)+(5.*rand(1024,1))'; X=fft(x,1024); Y=fft(y,1024); psd=csd(x,y); d=sum(f*atan(imag(max(psd))/real(max(psd))))/sum(f); d=d*180/pi; subplot(2,2,1),plot(x);title('x1(t)'); subplot(2,2,3),plot(abs(X),'r');title('x1(t)µÄÆµÆ×'); subplot(2,2,2),plot(y);title('x2(t)'); subplot(2,2,4),plot(abs(Y),'g');title('x2(t)µÄÆµÆ×'); ys(i)=d; yt(i)=30; %text(1,d+1,'{ÏàÎ»²î}=60')

实验三时延问题估计

实验三时延问题估计一、时延问题理论介绍时间延迟估计可分为两大类：主动时延估计和被动时延估计。

雷达或主动声纳系统是主动时延估计的典型例子，雷达或主动声纳发出电磁波或声波搜寻目标，当这些信号达到目标后，其中一部分信号反射回雷达或声纳的接收系统。

根据信号发出时刻与返回时刻的时间差（即时间延迟），就可以确定反射信号的目标的方位、距离和速度等参量。

被动时延估计系统不主动发出信号，而是接收目标发出的电磁波或声波去搜索目标。

时延估计所要解决的基本问题为：准确、迅速地估计和测定接收器或接收器阵列接收到的同源信号之间的时间延迟。

由于在接受现场可能存在各种噪声和干扰，接收到的目标信号往往淹没于噪声和干扰之中，因此，对带通噪声信号进行时延估计要排除噪声和干扰的影响，提高接收信号的信噪比。

二、蒙特卡洛方法简介蒙特卡罗(Monte Carlo) 方法, 又称随机抽样法，统计试验法或随机模拟法，是一种用计算机模拟随机现象，通过仿真试验得到实验数据，再进行分析推断，得到某些现象的规律或某些问题的求解的方法。

蒙特卡罗方法的基本思想是：为了求解数学、物理、工程技术或生产管理等方面的问题，首先建立一个与求解有关的概率模型或随机过程，使它的参数等于所求问题的解，然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征,最后给出所求解的近似值。

概率统计是蒙特卡罗方法的理论基础，其手段是随机抽样或随机变量抽样。

对于那些难以进行的或条件不满足的试验而言是一种极好的替代方法。

蒙特卡罗方法能够比较逼真地描述事物的特点及物理实验过程，解决一些数值方法难以解决的问题，很少受几何条件限制，收敛速度与问题的维数无关。

例如在许多工程、通讯、金融等技术问题中，所研究的控制过程往往不可避免地伴有随机因素，若要从理论上很好地揭示实际规律，必须把这些因素考虑进去。

理想化的方法是在相同条件下进行大量重复试验，采集试验数据，再对数据进行统计分析，得出其规律。

但是这样需要耗费大量的人力、物力、财力，尤其当一个试验周期很长或是一个破坏性的试验时,通过试验采集数据几乎无法进行，此时蒙特卡罗方法就是最简单、经济、实用的方法。

基于EMD分解重构的互相关时延估计方法

程中ＩＭＦ分量的选取问题，设计了一种基于皮尔逊（Ｐｅａｒｓｏｎ）相关系数的选取方法，选取ＩＭＦ分量进行
重构消噪并结合互相关的时延估计方法，构成了基于ＥＭＤ分解重构的互相关时延估计方法。通过对实际采集的声信号进行仿真实验，验证了该方法的有效性。关键词：被动声定位技术；时延估计；ＥＭＤ分解重构算法；皮尔逊相关系数
中图分类号：ＴＰ３９１文献标识码：Ａ文章编号：１０００—８８２９（２０１３）０７— ００４５— ０４
Ｃｒｏｓｓ－ＣｏｒｒｅｌａｔｉｏｎＤｅｌａｙＥｓｔｉｍａｔｉｏｎＭｅｔｈｏｄＢａｓｅｄｏｎＥＭＤ
ｃｏｍｍｏｎｃｏｒｒｅｌａｔｉｏｎｍｅｔｈｏｄ，ＩＭＦｒｅｃｏｎｓｔｒｕｃｔｉｏｎａｎｄｎｏｉｓｅｅｌｉｍｉｎａｔｉｏｎａｒｅａｐｐｌｉｅｄｉｎｔｈｅｅｓｔｉｍａｔｉｏｎｏｆａｃｏｕｓｔｉｃ
ｍａｔｉｏｎｍｅｔｈｏｄｂａｓｅｄｏｎＥＭＤｄｅｃｏｍｐｏｓｉｔｉｏｎａｎｄｒｅｃｏｎｓｔｕｃｒｔｉｏｎｌｇａｏｒｉｔｈｍｉｓｐｕｔｆｏｒｗａｒｄｂｙｓｅｌｅｃｔｉｎｇＩＭＦｃｏｍ— ｐｏｎｅｎｔｓｏｒｆｒｅｃｏｎｓｔｕｃｒｔｉｎｇａｎｄｄｅｎｏｉｓｉｎｇ，ａｎｄｃｏｍｂｉｎｉｎｇｗｉｔｈｔｈｅｃｒｏｓｓ－ｃｏｒｅｌａｔｉｏｎｔｉｍｅｄｅｌａｙｅｓｔｉｍａｔｉｏｎｍｅｔｈ — ｏｄ．Ｔｈｅｖａｌｉｄｉｔｙｏｆｔｈｉｓｍｅｔｈｏｄｉｓｐｒｏｖｅｄｂｙｓｉｍｕｌａｔｉｏｎｅｘｐｅｉｒｍｅｎｔｏｎｔｈｅａｃｔｕａｌｃｏｌｌｅｃｔｅｄａｃｏｕｓｔｉｃｓｉｇｎａ１．

基于广义互相关各类加权时延估计

基于广义互相关各类加权时延估计下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!基于广义互相关各类加权时延估计引言随着通信技术的不断发展和普及，对于时延估计的需求也日益增加。

matlab 时延估计算法

matlab 时延估计算法
Matlab中有多种时延估计算法可用，具体选择哪种算法取决于需要解决的问题和
数据的特点。

以下是几种常见的时延估计算法：
1. 互相关法（Cross-Correlation Method）：通过计算信号之间的互相关性来估计
时延。

使用`xcorr`函数可以实现。

2. 相位差法（Phase Difference Method）：通过计算信号的相位差来估计时延。

可
以使用`angle`函数计算信号的相位差。

3. 激励波形匹配法（Excitation Signal Matching Method）：通过比较输入信号和
输出信号之间的差异来估计时延。

可以使用最小二乘法或其他优化算法来实现。

4. 均方差法（Mean Square Error Method）：通过最小化输入信号和输出信号之间
的均方差来估计时延。

可以使用`mean`和`sqrt`函数计算均方差。

5. 互信息法（Mutual Information Method）：通过计算信号之间的互信息来估计时延。

可以使用`mutualinfo`函数实现。

以上是一些常见的时延估计算法，实际应用中可能还有其他算法可供选择。

具体
选择哪种算法应根据实际情况来确定，包括信号特性、计算复杂度和精度要求等。

【doc】时间延迟估计的基本原理和方法

时间延迟估计的基本原理和方法●储问计第11卷笫3期海/7,键再洋技术TECHN0L0GY时间延迟估计的基本原理和方法邱天爽(大连理工大学)乎V o1.11.No.3Sept,1992摘舅术文综述时间延迟估计的基本原理和基率方法.包括相关法和广义相关法,观谱法和广义双谱法,相位谱法H广义相位谱洼,自适应信号处理法等,并对各种估计方法的性能进行了分析比较.1概述时伺延迟通常是指接收陈列中的不同接收器所接收到的同源信号之间的时间差.这个时间差是由于不同接收器在陈列中所处的空间位置决定的.时间延迟估计就是指采用各种参数估计和信号处理的理论和方法,对上述时阉延迟进行估计和测定,从而进一步确定或估计其它有关参数.时间延迟估计是七十年代中期以后迅速发展起来的一个数字信号处理的重要领域,它是由被动定位技术的发展脱颖而出酊.在雷达,声纳,地球物理,海洋技术和生物医学工程等领域都有重要龅应用【l",并促进了谆些学科的发展.目标定位技术是时间延迟估计(简称TDE)理论和方法的主要应用领域和来源.目标定位问题是雷达,声纳,地震测量等技术的基本问题.目标定位的方法可以分为两太类,即主动方法和被动方法.主动定位方薅是由测定者发出信号并接收被测目标返回的信号,并由此信号进行定位常达就是一种主动定位系统被动定位则不发出探渊信号,———～1■———三一而仅接收由被测目标发出的信号,并由此进//,行目标定位.被动声纳就是一种被动定位系//f,;声撼统与主动定位方法相比,被动定位方法的l,—7,:/主要优点是无需发射能量,且具有隐蔽性,?/?膏肆这对于军事丰钉生物医学上的应用?是有意义走的本文仅讨论有关被动定位问题中的时间—,—————————,——'苎竺和苎量曼.关于主动图多珞传输示章图定位问癍讨论请觅文献(2o). '……'一海洋技术第1i卷在三维空间中,例如在海洋中,目标所发生的声音(作为信号源)可以经过多条路径(信道)而到达接收器,如图1所示.通常.假定信号在信道中的无色散球面渡的方式传播"".为了简化分析和研究,常常将信号源和接收器考虑在同一个平面中,从而将问题化简为二维定位问题.这样.在二维空间中,球面渡退化为柱面渡.若与接收器阵列相比,信源的位置很远,则可以认为信源发出的信号为一柱面波.图2给出了一个最基本的双基元被动定位系统:图中,A,B为两个相距为三的接收器,S为被测目标.即信B.源发出的信号是以平面波的形式在信道中传输的.设A.B接收到的信号分别为.()和.(f).如下式所示:i(f)=s(f)+n()(1a)图双基死被动定位系统.(f)=4..(f—D)+打.(f)(1b)式中.(f)是目标信号.口为衰减常数.为便于计算.不妨设口=1.D是由于目标信号传输距离不同所产生的时间延迟.n(f)和"(})是接收器A.B所接收到的噪声.通常.假定信号和噪声均为高斯分布的平稳随机过程,且互不相关.由三角形AABG的几何关系可知:BG=ABCOSABG=一ABcOS口(2由于ABeL,BG=c?D,其中c为声速.D是(1)式中的时延参数,因此,目标的方位角为:口=aTCCOS(-BG/.4B)=arccos(一c?DIL)(3)由(3)式可知.上为两接收器之间的距离.C为声速.均为可测量的量,因此,目标定位问题的关键是时间延迟D的估计.海水中声速的经验公式如(4)式所示;c=1,150+4.21T--0087T+1.14Cs-85)+O175p(4)式中.C为声速,单位为m/s;T为水温,单位为℃;s为水的盐度.以千分比计;P为水的静压力,单位为大气压.常用的水中声速平均值为1500m/s"".图3三基元被动系统如果要同时测量目标的距离和方法,则需三个相间一定?距离的接收器组成一个线阵,如图3所示:目标的距离和方位角分别为il:月:尘二(兰㈩n,cD_cD,1,0—一一—一,一…f型!1(6)"I—————一I【6)式中.DD,-分别为接收器接收到的目标倩号之间的相对时延,当上{《月时,cD.{《t砜.●第3期时间延迟估计的基本原理和方法H=aveeos(--cD/L2)()式(7)与式(3)相同.因此.只要测量出时延D,就可以确定目标的距离和方法,即实现目标的定位.另一方而.若信号源和接收器之问存在相对运动的话,还可以通过时延估计而得到相对运动的速度.综上所述,被动系统的目标定位问题,归根结底是一个相问一定距离的两接收器信号的时间延迟的估计问题.时延估计的精度越高,定位的误差就越小"".2时间延迟估计的理论基础根据观测数据对一个量或几个量进行定量推断就是估计问题"".时间延迟估计是根据不同位置接收器所接收到的瞬源信号来估计其中所包含的时延信息.基本估计理论,相关理论,谱『占计理论,自适应理论和付里叶变换的原理构成了时间延迟估计的理论基础.2.t基本估计理论对于确定的被动定位系统而言,时间延迟D是一个确定的量.但是由于信道中存在干扰和噪声,因此接收器所收到的信号或称之为观灞数据是随机的.这样,由观渊所得到的估计值必然存在估计误差.同样,信号的随机性决定了必须采用统计的方法来进行时间延迟的估计.常用的基本估计方法有最小二乘估计.线性最小方差估计,最小方差估计,贝叶斯债计.最大后验估计.最大似然估计及最小误差熵估计等.在时间延迟估计中,人们常常报时间延迟D看作确定而未知的量,故常采用最大似然估计方法来处理….这是因为在被动定位的条件下,用最大似然估计方法进行时延估计具有无偏,有效和一致三种性质.从这个意义上来说,最大似然估计是一种最佳估计''".'2.2相关理论f相关理论是在时域中考察信号之间相似程度的理论.平稳随机过程的自相关和互相关函数定义如下:月..(f)=丑[.(f)(f—f)],(8)月,..(f)=L((})(f—f))(9)在时间延迟估计中,利用相关函数进行两接收信号相似性的比较.相似性最大即相关函数取极大值时的时间延迟,则作为真实时延估计值.2.5谱估计理论所谓谱估计,就是根据过程的先验知识,建立近似实际过程的模型,并利用观铡数据和自相关函数来估计假设的模型参数….由于随机过程的功率谱是其自相关函数的付里叶变换,因此从原理上来说...由相关法解决的时延估计.同样可以由谱估计的方珐来解,决,,,自相关函数及其付里吐变换功率谱有两个局阻№第一,白相关函数仪包含过程的振幅信帛,面包审相位情阜.而时延问羁是和J用相位信粤的.讳二,呆用自担关蓐数时.海带技柬第11卷通常假设实际观测到的数据是由正态自噪声激励的最小相位系统产生的但在实际中.这个条件不一定总能满足.这样使用观测数据的自相关函数或其功率谱就得不到信号的全部信息".目前,时间延迟的谱估计法是采用双谱和相位谱来进行的.2.4自适应信号处理理论自适应信号处理的特点是它可以自动地调节滤波器自身的参数.在设计滤波器时,只图4自适应信号处理示意图需很少或根本不需要任何关于信号和噪声的先验知识.自适应滤波器的实现大致与维纳滤波器同样筒单,而性能却同卡尔曼滤波器一样好.自适应滤波器是工作于闭环(反馈)状态的图4】给出了自适应信号处理的原理框图"":当输入信号为平稳随机序列时.自适应算法应调节权系数,使Y(")与d(≈)的均方误差E(e.)]最小.自适应信号处理具有多种形式可以完成不同的功能.在时闻延迟估计中,自适应信号处理以两种形式被应用.第一种形式是利用自适应滤波器消除信号中伴随的噪声然后再进行相关等时延估计.…第二种形式是直接利用自适应算法来估计时间延迟参数"".2.5付里叶变换的原理和方法付里叶变换是信号处理领域的一种十分有用的工具.尤其是快速付里叶变换的出现,使在频率域进行快速信号处理成为现实.下式给出了有限时宽序列的离散付里叶变换(DFT)式:N一1)=三x()exp(-y(2~rkn/N)]0≤≤N-1(1Oa)'Ⅳ1()青()expC~I(2,Ⅳ)]O<n-<<N一1(105)在时阊延迟估计问题中.付里叶变换是一个十分有用的工具.例如进行噪声处理.相关计算港估计和自适应信号处理,都可以利用FFT算法来加快计算速度.?3时间延迟估计的基本方法时间延迟估计的方法大体上可以分为四种.即相关法,双谱法,相位谱法和自适应法.5.1柜关时延估计和广义租关时延估计法相关估计法是最根本时廷估计方法.这种方法是利用(1)式中两个接收信号()和,(})的互相关函数来估计时祠延迟的(1)式中两信号的互相关函数为:.(f)=F((}).(}一f))=曰O:--D)(II)式中.—D)为信号s(})的相关函数.由相关函数的性质曰(9)≥1曰(f)l,可知当————————....●第5期时间延迟估计的基本原理和方法f=D时,只(f)达到最大值计算两接收信号z(f)和x.(f)的互相关函数,并求出求峰值出现的时刻,则其峰值时刻即为所要求的时间延迟D当互相关函数的主极大峰很尖锐时,容易比较准确地求得扳大点的位置.然而在实际应用中,出于噪声的影响,互相关函数的主极大峰常常比较平坦.这样就很难判断出极大点的准确位置.从而使时间延迟的估计产生较大的误差.为了提高时间延迟估计的精度.又提出了广义相关法.在广义相关时延估计中.两个输入信号(f)和(f)先经过预滤波.然后再求互相关函数图5给出了广义互相关时延估计的原理框图.图5广义相关时延估计法原理框图台信号x(f)和(f)先经过预滤波器日(,)和日.(,)进行预滤波,变为y()和y,(}),然后再对y(f)和y(t)求互相关函数,并经峰值检测确定时延估计值D.实际上.互相关函数….(f)和广义互相关函数….(f)常常是由对互功率谱的估计而求得的.互功率谱的估计可由下式得到^G..(,)=F.(,)F(1)/r(12)式中,F(,)和F(,)分别为接收信号(})和.(f)的频谱,T为观测时问,表示复共轭"".这样,求广义互相关函数时对信号的预滤波就相当于对互功率诺G...(,)进行加窗运算.即:G,.,(,)="(,)?.(,)(13)式中G.t:(,)表示广义互功率谱,(,)为加窗函数(,)的作用是尽量加宽信号和信噪比大的频率成分,以改善时延估计的精度.对广义互功率谱进行付里叶反变换,则得到广义相关函数r∞(f)=1(,)-G(,)exp(,2,f)?(14)经过峰值检测,即可得到较基本互相关法更为精确的时延估计表l给出了几种域佳和次最佳加窗函数.表1给出广义相关时延估计的几种加窗函数表1名称基奉互相兆加宙匝数删(,)1海洋技术第11卷名称Roth冲鼗响应SCOT(平滑相干变换)RFL~T(相位变换)EckartI————!ML馥HT加商匝数丽…G,J】',)力_,)哪).IG|JI去丽1其中.1r..(,)l为振幅平方相干函数在时延估计中,上述加窗函数均的未知,只能用它们的估计值来代替5.2双谱时延估计和广义双谱时延估计法将(1)式的两接收信号(f)和(t)离散化,则得到其离散的序列:.(i)=()+(f)f=1,2.一一-Ⅳ(15a).(f)=(i-D)+(i)i一1.2.…Ⅳ(15b)(f)与.()之间的相似性可以用三阶矩或双谱来度量.由于零均值平稳正态序列的三阶矩为零.故可以消除正态噪声的影响,而且有较佳的性能"".{.(f))的双谱为;B.tt(,m)t(m,)xp(一J(.+mt)]=日.(,∞.)(16){()}和{x.(z)}的互双谱为:口t:(--.)=翠厅,t(J,,,)exp[一,(甜+国)]?=日.(J,)?exp[一mD].(17)比较(16)式和(17)式,可见占.t.,.(co.∞:)和日z.t(∞.∞.)只差一个因子?~xp(-抽D).它包含了时间延迟D的信息.即:p(_D)(18)___.p卜'L将(18)式做付里叶反变换,褥∞)=去等1)_e)(19)当u(O出现峰值时,即为所要估计的时间延迟.比较(19)式神(14可见每用与)艄作●第3期时间延迟估计的基本原理和方法用是相似的.为了提高双谱时延估计的精度,对{}进行加窗处理,再进行付里叶反变换,得:u(})=j『—:c.c.]2上lB(∞a)u吼(20)这种将u,(j)峰值出现的时刻作为时延估值的方法称为广义双谱时延估计法.据报道,广义双谱时延估计的方差小于基本双谱时延估计的方差".因此,广义双谱时延估计是提高时延估计精度的有效方法.5.5相位谱时延估计和广义相位谱时延估计法相位谱时延估计法是一种直接利用互功率谱,即利用时延和相位函数之间的关系而直接得到时延估值的方法"".由相位数据估计时延的方法如下::::且(21)——rI～式中,,.t(,t)是平滑后的相位谱函数估计值,B是.自回归线的斜率.,一是频率相位谱法是基于FFT变换的.因此计算简单不过,当信号的功率谱曲线有较大的渡动时,时延估计的精度显着下降.为了克服这一缺点,提出了广义相位谱时延估计法"",即对相位谱函数求斜率时给予一定的加权平均,使最终得到的时延估计更为精确,式(22)为广义相位谱时延估计的计算式:里(22)理论分析和计算机模拟都证明,采用广义相位谱法进行时延估计,具有较强的抗干扰能力,且其估计方差可达到克拉美罗下界.-5.4自适应时延估计法自适应时延估计法是一种基于自适应信号处理技术的时延估计方法.这种方法又可以进一步区分为两种形式,即前置消噪法和直接自适应法.前置消噪法的一个例子是在广义相关器之前加上前置自适应滤渡器,用于消除接收信号(})和(f)中包含的噪声.据报道,当外界干扰噪声比较强烈时,采用前置消噪自适应时延估计,可以极大地减小估计的方差0.直接自适应法则是利用自适应信号处理技术,直接或间接地估计出时延参数.所谓直接估计就是直接自适应地修改时延参数而进行估计.所谓间接估计则是通过自适应地修改系统参数来估计时间延迟的.囹6给出了利用最小均方(LMS)算法进行直接自适应时延估计的原理框图.海洋拄术第11卷图e.LMS自遗应时廷估计器的原理图两接收信号(f)和x.(f)经离散亿后形成(^)和()分别作为自适应噪声抵消系统的参考输入和基本输入,()(=0,I,…m)表示自适应滤波器的加权系数.且按照最小均方准则来.进行调整.这相当于在参考输入端的信号,()上插入了一段延迟.以保证()和x.()的最大的相关性当选代收敛时,权系数峰值所在的权序号就是时延估计值.这种估计方法的方差略高于克拉美罗下界但对于缺乏信号和噪声的先验知识的应用情况是一种有效的方法.4各种时延估计方法的性能比较总的来说,上述四种时延估计方法各有优缺点,很难说哪～种方法是全面优越的.不过各种广义方法要比基本方法的估计椿度要高.4.1关千估计精度广义相关法采用最大似然加窗函数时,其估计方差可达到克拉美罗下界",是一种最优的估计方法.广义相位谱估计法采羽OptimumCol,eFenceFunction作为加窗函数时,其估计方差也可达到克拉美罗下界".,也是一种最优估计.自适应时延估计方法可以产生与广义相关法相同舶最小方差而逼近壳拉美罗下界"".4.2美千计算复杂度一般来说,各种方法的广义算法均比基本舅法复杂一些.对于广义相关法和广义相位谱法来说=者都是时延的最大似然估计.前者的计算需要用FFT将时域信号变换到频率域,在完成广义互谱估计之后,再刚lFFT返回到时域.而后者则仅需用FFT变换到频域,无需存变回到时域,并省去了峰值检测和向插运算,直接就得到了时延忭汁.第3期时间延迟估计的基本原理和方法4.5关于限橱条件相关法和双谱法部要求被测目标没有或仅有缓r恒昀移动,且在有限的观察时间T 内,信号和噪声的统计特性保持不变.自适应方法比较适用于对信号和噪声的先验统计知识缺乏了解的情况,若考虑了先验知识,则估计方差会显着减小.广义相位谱法具有较强的抗干扰能力,适用于信嗓比较低的情况.时间延迟估计是信处理学科的一个十分活跃的领域,十几年来,人们对此领域的关注和研究一直长盛不衰.从1981年至l990午,IEEE国际声学,语声和信号处理学术会议(ICASSP)论文集中关于时延估计的论文平均每年为1嫦,由此可见一斑关于时问延迟估计理论和方l法的研究,对于雷达,声纳等军事领域的研究工件,对于地震学,水声学,空气声学,核反应堆故障诊断.地下传输管线泄精的检测定位等科学和工业领域的研究工作,都有着重要的意义和价值.可以预见,在如此广泛的应用背景推动下,时延估计的理论,方法和技术一定会得到迅速发展本文得到大连理工大学王宏禹教授的指导,谨此致酣参考文献1C.H.Kaapp,G.C.Carter,TheGeneralizedCorrelationMethodforEstimationof rimeDelay,IEEETrans.V oI.ASSP_24,No.4,PP.320—327,1979.2G.C.Ca~tar,TimeDelayEstimationforPassiveSonarSignalProcessing, IEEETrans.V oI.ASSP-29,No.3,PP.463—470,1981.3E.J.Hannah,P.J.Thomsom,TimeDeIayEstimation,JOurnalofTimeSeriesAaalysis,V o1.9,No.1,PP.21-33,I988.4A.H.Quazi,AnOvarviewonthe1.imeDelayEstimation,IEEETrans.V o1. ASSP-29,No.3,Pp.527-533,l081.5J.O.Smith,B,FriedlanderAdaptlveMultlpathDelay.Estimatlon,IEEETrans.V oI.Assp一33,No4,PP.g12~822,1985.6F.A.Reed,P.L.Fe~ntuch,N.】.Betshad.TimeDelayEstimationUsingthe LMSAdapticeFilter—StaticBehavior,IEEETransV oI.ASSP-29.No.3,PP56【-57i,I9g1.,7A.Fertner,A.Sjolund,ComparisonofV ariousTimeDelayEstimationMethod byComputerSimulation,IEEETrans.V o1.ASSP-34,No.5,PP.1329—1330,1986. 8G.C.Carter,P.B.Abraham,EstimationofSourceMotionfromTimeDelayand TimeCompressionMeasurement,J.Aconst.Soc..Am.63(3),Mar,PP.830—832, 1980.9J.Krotik,MEizenman,S.Pasupathy,TimeDelayEstimatloaViaGenerallzed CorrelationwithAdaptiveSpatialPrefiltering.ICASSP,86,PP.35.20.卜4,i986.海洋技术第i1巷IO钱玉美.广义双谱时延估计,CCSP一88.PP.1233—1239.i988.1lJKrollk.M.Eizenman,S.Pasupathy,AdaptiveoftheLMSAdaptiveLine EnhancerinTimeDelayEstimation,IcASSPs85,PP.46.7.I-4,J986.12D.H.Y oun,N.Ahmed,ComparisonofTwoAdaptiveMethodforTimeDelay Estimation,ICASSPt83,PP.883-886,J983.J3J.Krokik.M.Joy.S.Pasapathy.M.Eixenman,AComparativeStudyofthe. LMSAdaptiveFilterV ersusGeneral/zedCorrelationMethodforTimeDelayEstimation,ICASSW84PP.15.11.I-4,1984.14王宏禹,随机数字信号处理,科学出版社,J988..15王宏禹,现代谱估计.东南大学出版社,I990.J6郏兆宁,向大威,7K声信号被动检测与参数估计理论,科学出板社.J983.17C.F.Cowan.P.M.Grant.AdaptlveFiIters(中译本),复旦大学出板社,1990.18钱玉美,从噪声中提取信号灼时延信息.第四届全国镦弱信号检测学术会议论文集.PP.52-57,1986.J9Z.Zheng.H.Z.Qiang,theGeneralizedPhaseSpeetrumMethodfOrTimeDelay EstimaLion.IcASSP~84,PP.46.2.卜4,1984.2OR.A.Aires,TargetPositionEstimationinRadarandSonar.andGeneralized AmbiguityAnalysisforMaximumLikelihoodParameterEstimation,Proc.IEEE,V o1.67.No.6.PP.920—930,1979.2l声纳与水下观测,上海科学技术出板社.22周概容.概率论与数理统计,高等教育出信社.J984.23A.V.奥本诲姆,致字信号处理.科学出板社.1990.24侯朝焕.实用FFT信号处理技术,海洋出板社,1990.25F.A.Reed,P.L.Feintuch,N.J.Bershad.TimeDelayEstimationUsingtheLMSAdaptiveFiIter--DynamicBehavior,IEEETrans,V o1.ASSP一29,No.3,PP.671—576,l981.TheBasicprincipleAndMethodofTimedelayEstimationQiu~ianshuang(Dalia,~Univ.eNq.,Technology)'Aht矗tThepapcrglvesacomprehensivodescriptionofthebasicpr;ncipleandmethodoftime—delayestlmatlon.ine1udingcorr~latlogmethodand generalizedcorretatio/1double—spectrummethodandgeneralizeddoub1一espectrum,phase—spectrtlmmethodandgeneralizedphase-spectrlio1.as we11asadaptiveaigna1PrOCessing,Thecharacteristicsofthedifferent methodsareaIsoai2alysed8ndcol22口ared。

时延估计的两种实现方法及蒙特卡洛仿真

国防科学技术大学电子科学与工程学院《随机信号分析与处理》课程论文这里做了 100 次仿真估计估计均值为 44.9731，随着次数增加估计值更加接近 45。

相关函数估计的实现采用相同的信号，进行估计，对信号进行匹配滤波处理仿真结果如下可见信号经过皮匹配滤波后瞬时信噪比得以提高，便于提高时延国防科学技术大学电子科学与工程学院《随机信号分析与处理》课程论文的检测。

不同信噪比将影响信号的估计精度，信噪比越大时延估计越精确我们通过匹配滤波可以提高信号的瞬时信噪比进而提高信号的检测精度，在信噪比在-9db 下的估计误差为 7.1615e-004，提高信噪比，在信噪比为 5db国防科学技术大学电子科学与工程学院《随机信号分析与处理》课程论文下的估计误差为 2.6042e-004，可见仿真可以实现较高精度的检测。

参考文献 1、唐娟等。

不同环境下的时延估计算法及其仿真研究，计量学报，2001 2、江南，黄建国等。

基于互相关函数的频域实现时延估计器，计量学报，25 卷第四期，2004 3、陆军、钱裕美。

自适应多目标时延估计器。

数据采集与处理，第四期 4、侯子江，麦克风阵列时延估计算法的研究（研究生论文）附录程序代码： clearfs=1024; DD=pi/6; f=20; t=0:1/fs:1023/fs; for i=1:100x=1.*sin(2*pi*f*t+(5.*rand(1024,1'; y=1.*sin(2*pi*f*t+DD+(5.*rand(1024,1';X=fft(x,1024; Y=fft(y,1024; psd=csd(x,y;d=sum(f*atan(imag(max(psd/real(max(psd/sum(f; d=d*180/pi;subplot(2,2,1,plot(x;title('x1(t'; subplot(2,2,3,plot(abs(X,'r';title('x1(tµÄÆµÆ×'; subplot(2,2,2,plot(y;title('x2(t'; subplot(2,2,4,plot(abs(Y,'g';title('x2(tµÄÆµÆ×'; ys(i=d; yt(i=30; %text(1,d+1,'{ÏàÎ»²î}=60'国防科学技术大学电子科学与工程学院《随机信号分析与处理》课程论文 end figure plot(ys,'*'; hold on plot(yt,'r'; rr=mean(ys; figure for i=1:100 R=xcorr(x,y; plot(R; [t,j(i]=max(R; end D=abs((mean(j-fs/fs; Dl=DD/(2*pi*f; abs(D-Dlh1=5.*sin(2*pi*f*(1023/fs-t; h2=5.*sin(2*pi*f*(1023/fs-t+DD; Fh1=fft(h1; Fh2=fft(h2; x0=ifft(X.*Fh1; y0=ifft(Y.*Fh2; x00=conv(x,h1; y00=conv(y,h2; for i=1:100R0=xcorr(x00,y00; [n,p(i]=max(R0; end D0=abs((mean(p-fs/fs; Dl0=DD/(2*pi*f;abs(D0-Dl0 hold on plot(R0,'r';title('ÐÅºÅµÄÏà¹Øº¯Êý ÐÅÔë±ÈÎª-9db';。

广义相关时延估计算法的自适应实现形式

广义相关时延估计算法的自适应实现形式
Adaptive Realizing Form of Generalized Correlation Al gori thm for Time Delay Esti mation
行鸿彦1 , 赵守国1 , 邸继征2, 刘照泉1 , 万明习1
( 1. 西安交通大学电子与信息工程学院生物医电系 , 陕西西安 710049; 2. 山西师范大学数学系 , 山西临汾 041004)
/ G x 1x2( f ) [ 1 -
r 12 ( f )
2
].
1. 2 Roth 处理器 Rot h 处理器是 Rot h [ 7] 其权函数是或
R
( f ) = 1/ G x 1 x 1 ( f ) ( f ) = 1/ G x 2 x 2 ( f )
( 8)
R
其中 , G x 1 x 1 ( f ) 是 x 1 的自相关谱密度. 那么 x 1( t ) , x 2( t ) 经过预滤波的信号 y 1 和 y 2 的互相关函数的估值为
∫
∞
自适应滤波器的参数是在迭代过程中根据墓中最优化准则不断调整或不断跟踪动态输入环境 , 最 ( 4) 终达到最优化. 基于自适应信号处理技术的时延估计法, 即用自适应滤波器来替代广义相关法的预滤 ( 5) ( 6) 波器或直接实现自适应的广义相关时延估计. 其特点是不需预先知道输入信号、噪声的先验知识 . 由自适应滤波器理论
( 1)
作者简介 : 行鸿彦 ( 1962-) , 男 , 山西新绛人 , 副教授 , 在读博士生 , 主要从事数字信号处理 , 小波分析等方面研究 .
— 48 — 其中: s ( t ) 为源信号即发射信号 ;

相关类时延估计方法)

广义互相关时延估计

基于广义互相关函数的声波阵列时延估计算法

广义互相关时延估计gcc程序

时延估计方法

时延估计方法在雷达信号处理中的应用

时延估计算法地方法很多

四种时延及其计算方法

时延估计的两种实现方法及蒙特卡洛仿真