神木中学高一训练案10月11日

合集下载

神木中学高一训练案10月1日

明)
(2)当氯水中不再产生气泡时，某学生欲检验该反应所产生的气体，则该同学可采取的合理操作是
(说明：氯水有一定腐蚀性，操作时需戴橡胶手套)
A．NaOHB．NaClC．Ca(OH)2D．Na2CO3
5、A( HCl) B(Cl2) C(Ca(ClO)2) D(HClO) E(CO2)上述变化不能直接实现的是（）
A．A→BB．B→CC．C→DD．D→E
6、漂白粉在空气中容易变质的原因是（）
A．CaCl2易吸收空气中的水分B．Ca(ClO)2易与盐酸反应
A．硝酸银溶液B．酚酞溶液C．紫色蕊溶液D．饱和食盐水
11、下列说法正确的是（）
A．漂白粉比较稳定，可以露置于空气中B．漂白粉在漂白时，一定要加适量盐酸
C．Cl2具有漂白性，能使湿润的有色布条褪色D．进行铜在氯气中燃烧的实验，集气瓶内应铺一层细沙
12、漂粉精是用Cl2与反应来制取的制取反应方程式为_____________漂粉精是(填纯净物、混合物)，其有效成分为(化学式).Cl2和漂粉精用于漂白物体是因为在一定条件下产生之故.
C．Ca(ClO)2见光易分解D．Ca(ClO)2易与空气中的CO2和水作用
7、市场上销售的“84”消毒液，其商品标识上有如下叙述：①本品为无色溶液，呈碱性②使用时加水稀释③
可对餐具、衣物进行消毒，可漂白浅色衣服则其有效成份可能是（）
A．Cl2B．SO2C．NaClOD．KMnO4
8、下列物质的水溶液不具有漂白性的是（）
1、Cl2是有毒的，曾被法西斯制成毒气弹用于侵略战争。当这种毒气弹顺风爆炸时，通常可用的防御办法是（）
A．人畜应躲到低洼的地方去B．可用烧碱溶液浸湿软布蒙面
C．可用肥皂水或尿液浸湿软布蒙面D．人畜应多饮水

神木高中测试题及答案

神木高中测试题及答案一、选择题（每题2分，共20分）1. 神木高中位于哪个国家？A. 中国B. 美国C. 英国D. 日本答案：A2. 神木高中的校训是什么？A. 勤奋、求实、创新B. 团结、紧张、严肃、活泼C. 诚信、勤奋、博学、笃行D. 爱国、进步、民主、科学答案：C3. 神木高中的校徽颜色是？A. 红色B. 蓝色C. 绿色D. 黄色答案：B4. 神木高中的图书馆藏书量超过多少册？A. 5万册B. 10万册C. 15万册D. 20万册答案：B5. 神木高中的校庆日是每年的哪一天？A. 5月1日B. 10月1日C. 12月1日D. 1月1日答案：C6. 神木高中的体育设施包括以下哪些？A. 足球场B. 篮球场C. 游泳池D. 所有以上答案：D7. 神木高中的学生会主席是谁？A. 张三B. 李四C. 王五D. 赵六答案：B8. 神木高中的校歌是由谁创作的？A. 王老师B. 李老师C. 张老师D. 刘老师答案：A9. 神木高中的毕业典礼通常在哪个季节举行？A. 春季B. 夏季C. 秋季D. 冬季答案：B10. 神木高中的学生社团数量是多少？A. 20个B. 30个C. 40个D. 50个答案：C二、填空题（每题2分，共10分）1. 神木高中的校训是________、________、________、________。

答案：诚信、勤奋、博学、笃行2. 神木高中的校徽上的主要图案是________。

答案：一本书3. 神木高中的校庆日是每年的________月________日。

答案：12月1日4. 神木高中的学生会主席李四是________系的学生。

答案：物理5. 神木高中的图书馆每周开放________天。

答案：7三、简答题（每题10分，共30分）1. 请简述神木高中的历史背景。

答案：神木高中成立于1950年，是本市历史悠久的学府之一，以其优秀的教学质量和丰富的校园文化著称。

2. 神木高中的教育理念是什么？答案：神木高中秉持“以人为本，全面发展”的教育理念，致力于培养学生的综合素质和创新能力。

直线的两点式方程(重难点突破)原卷版

2.2.2 直线的两点式方程知识点一：直线的两点式方程经过两点),(),,(222111y x P y x P (其中2121,y y x x ≠≠)的直线方程为1112122121(,)y y x x x x y y y y x x --=≠≠--，称这个方程为直线的两点式方程，简称两点式.知识点诠释：1.这个方程由直线上两点确定；2.当直线没有斜率(21x x =)或斜率为)(021y y =时，不能用两点式求出它的方程.),(),,(222111y x P y x P 选择的顺序无关.4．在应用两点式求直线方程时，往往把分式形式1112122121(,)y y x x x x y y y y x x --=≠≠--通过交叉相乘转化为整式形式121211()()()()y y x x y y x x --=--，从而得到的方程中，包含了12x x =或12y y =的情况，但此转化过程不是一个等价的转化过程，不能因此忽略由1x 、2x 和1y 、2y 是否相等引起的讨论．要避免讨论，可直接假设两点式的整式形式．知识点二：直线的截距式方程若直线l 与x 轴的交点为()0A a ，，与y 轴的交点为()0,B b ，其中0,0≠≠b a ，则过AB 两点的直线方程为1=+bya x ，这个方程称为直线的截距式方程.a 叫做直线在x 轴上的截距，b 叫做直线在y 轴上的截距.知识点诠释：0,0≠≠b a ，即截距式方程不能表示过原点的直线以及不能表示与坐标轴平行的直线.2.求直线在坐标轴上的截距的方法：令x =0得直线在y 轴上的截距；令y = 0得直线在x 轴上的截距.重难点题型(一)、直线的两点式方程（2）．（2022·全国·高二课时练习）过点()1,1A -与点(),4B m （m ∈R ）的直线的方程为______．（2019·全国高一专题练习）过点()1,3A --，()2,4B 的直线方程是A ．314321y x --=-- B ．314321y x ++=++ C ．423412y x --=-- D ．332143y x ++=++（2022秋·山东日照·高二校考阶段练习）（多选题）下面说法中错误的是（）重难点题型(二)、直线的截距式方程A ．0,0a b >>B ．0,0a b ><C ．0,0a b <>D ．0,0a b <<（2022秋·新疆塔城·高二乌苏市第一中学校考阶段练习）经过点()1,1M 且在两轴上截距相等的直线方程是（）A ．2x y +=B ．1x y +=C ．1x =或1y =D ．2x y +=或x y =（2022秋·河南郑州·高三郑州外国语学校校考阶段练习）已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数=a .重难点题型(三)、冲刺满分（压轴题）例3、（2022秋·江苏淮安·高二校联考期中）已知ABC 三个顶点是()()()4,4,4,0,2,0A B C -. (1)求AB 边中线CD 所在直线方程； (2)求AB 边上的高线所在方程；（2021春·陕西榆林·高一陕西省神木中学校考阶段练习）已知三角形三顶点()()()0,1,2,0,2,0A B C -，求：(1)AC 边上的高所在的直线方程； (2)AB 边的中线所在的直线方程.例4、（2022秋·天津宁河·高二天津市宁河区芦台第一中学校考阶段练习）设直线l的方程为+++-=∈Ra x y a a(1)20()(1)若l在两坐标轴上的截距相等，求直线的方程.(2)若l不经过第二象限，求实数a的取值范围.△的面积为S，求S的最小值并求此时直线l (3)若直线l交x轴正半轴于点A，交y轴负半轴于点B，AOB的方程.（2022秋·江苏连云港·高二校考阶段练习）设k为实数，若直线l的方程为()12240k x y k+-++=，根据下列条件分别确定k的值：(1)直线l的斜率为2；(2)直线l与两坐标轴在第二象限围成的三角形面积为12.。

陕西省神木中学高一语文下学期第一次月考试题(无答案)

陕西省神木中学2013—2014学年度第二学期第一次月考高一语文试卷注意事项：本试卷分为第I卷（选择题）和第Ⅱ卷（非选择题）两部分，选择题答案用2B铅笔在机读卡上填涂，非选择题答案用0.5mm黑色中性笔写在答题纸上。

将有关考生信息按要求在机读卡和答题纸上填涂清楚。

考试结束后，只收机读卡和答题纸。

试卷满分150分，考试时间120分钟。

第I卷（选择题共42分）一、（42分，每小题3分）1．下列各组词语中，加点字读音都正确的一项是（）A．怯弱（qiè）纨绔（kù）弓弦（xián）敛气屏声（bǐng）B．拓片（tà）负疚（jiù）悚然（sǒng）沸反盈天（fú）C．吞噬（shì）脊髓（suǐ）戏谑（xuè）韬光养晦（huì）D．石栈（jiàn）朔漠（shuò）迁谪（zhé）群山万壑（hè）2．下列各句中，加点的词语使用恰当的一项是（）A.会议开始时气氛有些沉闷，多亏张教授抛砖引玉的一番话，大家的发言才活跃起来。

B. 这次活动承蒙贵公司慷慨解囊，热情相助，取得了圆满成功，他日有托，本人定当投桃报李，鼎力相助。

C.实事求是地说，我也算够民主了，说虚怀若谷也不为过，现在的博主数以千记，相信大家对博客都有自己的看法，众口难调，还是顺其自然吧。

D. 在对人的个性与自由严重束缚的贾府中,有着鲜明反抗意识的晴雯必然首当其冲地成为统治阶级迫害的对象。

3．列句子中句意明确，没有语病的一句是（）A．在张大爷住院治疗一段时间后，感到体力和思维都大不如以前了。

B．蔡校长说：“李虎对张林的批评是有充分准备的，我相信他们会处理好这件事。

”C．“低保政策”体现了党和政府对困难群众的关爱，但要把关爱落到实处，却远不是划几条标准那么简单。

D．山东大学积极采取措施，培养新入校的大学生，力争在较短时间内解决史学界后继乏人的状况。

2020-2021学年陕西省神木中学高一下学期第二次月考生物试题

2020-2021学年陕西省神木中学高一下学期第二次月考生物试题1. 2020年11月28日，“奋斗者”号完成万米深潜海试验任务并顺利返航，体现了我国自主研发深海装备技术的突破和进步。

潜水器在深海发现了水滴鱼、盲虾等，还有大量的微生物。

下列相关分析错误的是（）A．水滴鱼细胞中的RNA主要位于细胞质中B．盲虾细胞内含有自由水和结合水C．盲虾细胞中含量最多的有机物是蛋白质D．水滴鱼细胞膜中主要成分是脂肪和蛋白质2.下图是某化合物的结构式。

关于该化合物的叙述，正确的是（）A．该化合物中含1个游离的氨基和1个游离的羧基B．由于②④⑥的不同，该化合物由3种氨基酸组成C．上图含有③和⑤两个肽键，因此该化合物为二肽D．因该化合物含3个氨基酸，若彻底水解该化合物分子，则共需要3个水分子3.如图①～④为几种细胞器的示意图，下列叙述错误的是（）A．叶片表皮细胞不能同时找到①②③④四种细胞器B．在高倍光学显微镜下观察不到①③的双层膜结构C．①和③可以发生能量的转换，②和④进行脂质的合成D．分泌淀粉酶的唾液腺细胞中的②④比肌细胞的多4.人肝细胞合成的脂肪以VLDL（脂肪与蛋白质复合物）形式分泌出细胞外。

VLDL分泌出细胞外的方式是（）A．自由扩散B．协助扩散C．主动运输D．胞吐5.某同学将紫色洋葱鳞片叶外表皮细胞置于溶液Z中，观察细胞失水量的变化情况，其结果如图所示。

下列相关叙述正确的是（）A．溶液Z是一定浓度的蔗糖溶液B．甲点时失水量最大，吸水能力最强C．甲点时溶液Z的溶质开始进入细胞，并开始吸水D．甲→乙液泡紫色变淡，乙点后细胞吸水涨破6.下图表示生物体内发生的两个化学反应，①②③④表示化学键，下列相关叙述不正确的是（）A．细胞中的吸能反应一般与ATP合成的反应相联系B．ATP分子水解时，图中所示的化学键④最易断裂C．图中酶1和酶2的化学本质相同，但是二者的种类不同D．ATP与ADP相互转化的能量供应机制，体现了生物界的统一性7.如图为生物体内葡萄糖分解代谢过程的图解。

陕西省榆林市神木中学2020-2021学年高一上学期第三次月考数学试题

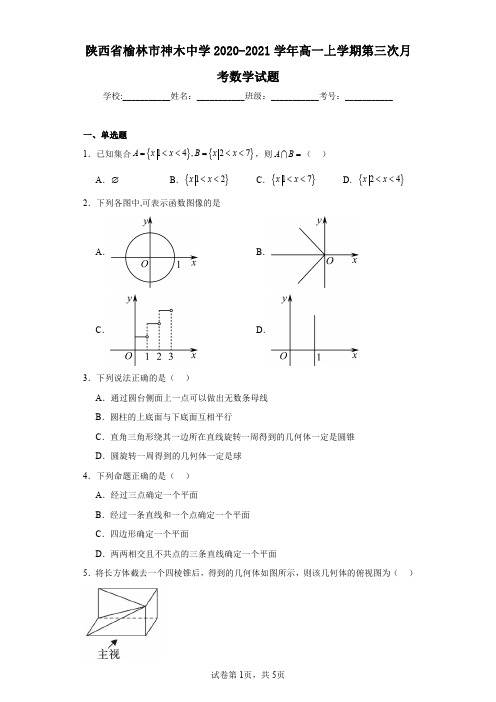
陕西省榆林市神木中学2020-2021学年高一上学期第三次月考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题．．．．．下列说法正确的是（）．通过圆台侧面上一点可以做出无数条母线．圆柱的上底面与下底面互相平行．直角三角形绕其一边所在直线旋转一周得到的几何体一定是圆锥．圆旋转一周得到的几何体一定是球．下列命题正确的是（）．经过三点确定一个平面．经过一条直线和一个点确定一个平面．四边形确定一个平面．两两相交且不共点的三条直线确定一个平面．将长方体截去一个四棱锥后，得到的几何体如图所示，则该几何体的俯视图为（．．．．lα二、填空题14．已知圆锥的底面半径为15．一个西瓜切3刀，最多能切出16．我国古代数学名著《九章算术》中将正四棱锥称为方锥．已知半球内有一个方锥，方锥的底面内接于半球的底面，方锥的顶点在半球的球面上，若方锥的体积为半球的表面积为三、解答题17．设函数()()()22log 4log 32f x x x =+--．(1)求函数()f x 的定义域；(2)当()0f x >时，求x 的取值范围．18．如图，在正方体1AC 中，E 为1BB 上不同于1B B ，的任一点，1111,AB A E F B C C E G ⋂=⋂=，求证：(1)求证：E ，F ，G ，H 四点共面；(2)设EG 与FH 交于点P ，求证：20．如图，在四棱锥P ABCD -,,ABCD PA AD E ⊥和F 分别是(1)PA ⊥底面ABCD ；(2)平面//BEF 平面PAD ．21．在如图所示的直三棱柱(1)求证：平面11CA B ⊥平面(2)求三棱锥11B A B C -的体积．22．已知二次函数()f x 满足(1)求函数()f x 的解析式；(2)设函数()()g x mx f x =-，若函数()g x 存在两个零点1x 和()212x x x <，使得区间()12,x x 内恰好存在两个整数点，求实数m 的取值范围．。

陕西省榆林市神木市第四中学2023-2024学年高一下学期第三次检测考试数学试题(含解析)

神木四中2023~2024学年度第二学期高一第三次检测考试数学全卷满分150分，考试时间120分钟.注意事项：1.答题前，先将自己的姓名､准考证号填写在试卷和答题卡上，并将条形码粘贴在答题卡上的指定位置.2.请按题号顺序在答题卡上各题目的答题区域内作答，写在试卷､草稿纸和答题卡上的非答题区域均无效.3.选择题用2B 铅笔在答题卡上把所选答案的标号涂黑；非选择题用黑色签字笔在答题卡上作答；字体工整，笔迹清楚.4.考试结束后，请将试卷和答题卡一并上交.5.本卷主要考查内容：必修第二册第六章､第七章.一､单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设点是正三角形的中心，则向量是（）A.相同的向量B.模相等的向量C.共线向量D.共起点的向量2.若，则（）A. B.1 C.2 D.43.在中，，则（）4.平面内顺次连接所组成的图形是（）A.平行四边形B.直角梯形C.等腰梯形D.以上都不对5.欧拉恒等式（为虚部单位，为自然对数的底数）被称为数学中最奇妙的公式.它是复分析中欧拉公式的特例：当自变量时，，得.根据欧拉公式，复数的虚部为（）O ABC ,,AO BO CO i i z z =+zz =12ABC 2,120AB AC C === sin A =()()()()1,1,2,0,0,2,2,0A B C D --i πe 10+=i e i e cos isin x x x =+πx =i πe cos πisin π1=+=-i πe 10+=2023π4eB.C.6.已知平面向量满足，且的夹角为（）A.B. C. D.7.如图，在中，为的中点，则（）A. B. C. D.8.如图，某市人民广场正中央有一座铁塔，为了测量塔高，小胡同学先在塔的正西方点处测得塔顶的仰角为，然后从点处沿南偏东方向前进140米到达点处，在处测得塔顶的仰角为，则铁塔的高度是（）A.70米B.80米C.90米D.100米二､多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.已知为虚数单位，复数，则（）A.的共轭复数为B.C.为实数D.在复平面内对应的点在第一象限10.已知向量满足，则下列说法正确的是（）A.B.C. D.向量的夹角为,a b 1a b == 2a b += ,a b π6π3π22π3ABC 4,AB DB P = CD BP = 1142AB AC -+ 1143AB AC -+ 5182AB AC -+ 5183AB AC -+ AB C 45 C 30 D D 30 AB i 1212i,2i z z =+=-1z 12i -+12z z =12z z +12z z ⋅,,a b c ()()()31,3,3,1,2,2a b a b c +=--=-=- b = a c⊥ a ∥c ,a b π411.若是平面内两个不共线的向量，则下列说法不正确的是（）A.可以表示平面内的所有向量B.对于平面中的任一向量，使的实数有无数多对C.均为实数，且向量与共线，则有且只有一个实数，使D.若存在实数，使，则12.在中，内角所对的边分别为，其中，且，则下列说法正确的是（）A.B.C.若为边的中点，则的最大值为3D.若为锐角三角形，则其周长的取值范围为三､填空题：本题共4小题，每小题5分，共20分.13.已知复数是纯虚数，其中为虚数单位，则实数的值为__________.14.已知向量，则与向量平行的单位向量为__________.15.在中，内角的对边分别为，若，且的面积为，则的外接圆的面积为__________.16.在平行四边形中，是直线上的一点，且，若，则__________.四､解答题：本题共6小题，共70分.解答应写出必要的文字说明､证明过程及演算步骤.17.（本小题满分10分）已知复数满足：是实数，的共轭复数在复平面内对应的点在第四象限.（1）求；（2）若，求的值.18.（本小题满分12分）12,e e α()12,e e λμλμ+∈R ααa 12a e e λμ=+,λμ1122,,,λμλμ1112e e λμ+ 2122e e λμ+λ()11122122e e e e λμλλμ+=+ ,λμ120e e λμ+= 0λμ==ABC ,,A B C ,,a b c a =2212b c bc +-=π3A =ABC D BC AD ABC (6+()()2232310i z m m m m =-+++-i m ()3,6a = a ABC ,,A B C ,,a b c 4c =ABC 222a b c +-ABC ABCD E BD AE BD ⊥18AE AC ⋅= AE = z 2i z -z z z z ()2i ,z z a b a b +=-∈R ,a b已知向量，且.（1）求的值；（2）求向量与的夹角的余弦值.19.（本小题满分12分）在中，内角的对边分别为，向量且.（1）求角；（2）若，求内切圆的半径.20.（本小题满分12分）如图，在等腰三角形中，是线段上的动点（异于端点），.（1）若是边的中点，求的值；（2）当的位置.21.（本小题满分12分）在中，内角的对边分别为，且.（1）求角；（2）若为锐角三角形，是线段的中点，求的长的取值范围.22.（本小题满分12分）在平面四边形中（在的两侧），.（1）若；（2）若，求四边形的面积的最大值.()()()2,4,,1,1,2a b m c === ()2a b c -⊥ m a b - 23b c - ABC ,,A B C ,,a b c )(),,3cos ,sin m b n A B == m ∥n A 2a c ==ABC ABC 30,AB AC BAC F ∠=== AC 3BC BE = F AC AE BF ⋅ AE BF ⋅= F ABC ,,A B C ,,a b c sin sin sin sin b a C A c B A--=+B ABC 2,AC D =AC BD ABCD ,B D AC 1,120AD CD ADC ∠=== 90,DAB BC ∠== ABC ∠2AB BC =ABCD神木四中2023~2024学年度第二学期高一第三次检测考试·数学参考答案､提示及评分细则1.B 是正的中心，向量分别是以三角形的中心和顶点为起点和终点的向量，到三个顶点的距离相等，但向量不是相同向量，也不是共线向量，也不是起点相同的向量.故选B.2.A ，故选A.3.B ，由余弦定理可得：，解得：，或-3（舍去），由正弦定理可得：.故选B.4.B 因为，则，，所以四边形为直角梯形.故选B.5.C ，则虚部为.故选C.6.D ，设夹角为，又.故选D.7.C 由题意知.故选C.8.A 设塔的高度为，在中，因为，所以；在中，因为，所以；在中，，根据余弦定理可得，即，解得或（舍去）.故选A.9.BD 因为的共轭复数为，所以A 不正确；因为，所以B 正确；因为，所以不正确；O ABC ,,OA OB OCO ∴AO BO CO == ,,AO BO CO ()()()i i 1i 1i 1i 1i 1,i 1i 1i 12222z zz +--+====⋅=--+2,120AB AC C === ∴2222cos AB BC AC BC AC C =+-⋅2230BC BC +-=∴1BC =∴sin sin BC C A AB ⋅==()()()()1,1,2,2,2,2,3,1AB DC BC DA =-=-=--= 2,,DC AB AB BC CD BC =⊥⊥ BC AD ≠ABCD 2023πi 42023π2023π77πe cosisin cos πisin 4444=+=+=2222|2|3,443a b a b a a b b +=∴+=+⋅+= ,a b 1,14cos 43,cos 2θθθ++==-[]2π0,π,3θθ∈∴=()11111113514242422482BP BD DP AB DC AB AC AD AB AC AB AB AC =+=-+=-+-=-+-⋅=-+ AB h Rt ABC 45ACB ∠= BC h =Rt ABD 30ADB ∠= BD =BCD 60,,BCD BC h BD ∠=== 2222cos60BD BC CD BC CD =+-⋅ 2221)14021402h h =+-⨯⨯70h =140h =-112i z =+12i z =-1z ===1212i 2i 3i z z +=++-=+C因为，点的坐标在第一象限，所以D正确.10.AC因为，所以，所以，所以A正确；，故B错误；因为，所以，故C正确；，所以.故D错误.故选AC.11.BC由题意可知：可以看成一组基底向量，根据平面向量基本定理可知：A，D正确，B不正确；对于C，当时，则，此时任意实数均有，故C不正确.故选BC.12.ACD由题意可知，利用余弦定理得，因为，所以，故A正确；由上述可知，的面积，且易知，解出，当且仅当时取等号，此时，故B错误；在和中，对和利用余弦定理，，化简后有，由上述知，的最大值为12，因此最大为3，故C正确；利用正弦定理，，则，于是的周长，由于是锐角三角形，因此解出，则，故D正确.故选ACD.()()1212i2i43iz z⋅=+-=+()4,3()()31,3,3,1a b a b+=--=-()()1,1,2,0a b=-=2a=b=()12124a c⋅=-⨯+⨯-=-≠()()12120-⨯--⨯=a∥ccos,a ba ba b⋅===⋅3π,4a b=12,e e1212λλμμ====11122122e e e eλμλμ+=+=λ()11122122e e e eλμλλμ+=+2222212b c b c a bc+-=+-=2221cos22b c aAbc+-== ()0,πA∈π3A=ABC1sin2S bc A==2212212b c bc bc+-=-…12bc…b c==S==ABDACDADB∠ADC∠22222222BD AD AB CD AD ACBD AD CD AD+-+-=-⋅⋅232bcAD=+bc AD4sin sin sinb c aB C A===4sin,4sinb Bc C==ABCπ4sin4sin6L B C B⎛⎫=++=++⎪⎝⎭π0,2π0,2BC⎧<<⎪⎪⎨⎪<<⎪⎩ππ62B<<(6L∈+13.1 则.14.或因为，所以平行的单.15. 因为的面积为，所以，即，又，所以，设的外接圆的半径为，所以，解得，所以的外接圆的面积为.16.3记，又，所以，所以，解得.17.解：（1）设复数，是实数，得，，又在第四象限，，；（2）由（1）得：，，.18.解：（1）因为，且，所以，解得；（2）因为，所以，2212,320,25,3100m m m m m m m m ⎧==⎧-+=⎪⇒⎨⎨≠≠-+-≠⎪⎩⎩或且1m =⎛ ⎝()3,6a = a == a =⎛= ⎝17π4ABC 222a b c +-2221sin 2a b c ab C +-=1sin cos 4C C =22sin cos 1,sin 0C C C +=>sin C =ABC r 2sin c r C ==r =ABC 217ππ4r =AC BD O ⋂=AE BD ⊥0AE EO ⋅= ()222222218AE AC AE AO AE AE EO AE AE EO AE ⋅=⋅=⋅+=+⋅== 3AE = ()i ,z m n m n =+∈R ()2i 2i z m n -=+-20,2n n -==1z m ===±z 0,0,1m n m ∴>>∴=12i z ∴=+2212i,12i,(12i)34i z z z =+=-=+=-+212i 34i 22i z z ∴+=--+=-+2,2,22,a ab b =-⎧∴∴=-=-⎨-=⎩()()()22,42,122,2a b m m -=-=- ()2a bc -⊥ ()222220a b c m -⋅=-+⨯= 3m =()()()()()()2,43,11,3,2323,131,23,4a b b c -=-=--=-=- ()()()()35,23313415a b c a b b c -=-=-⋅-=⨯-+⨯-=-所以19.解：（1）因为向量与，，又，所以，又，所以；（2）由余弦定理得，所以，解得或（舍），所以的面积设内切圆的半径为，所以，解得.20.解：（1）由题意知，由于是边的中点，因此，因此；（2）不妨设，因此，1.，解出，故是线段靠近处的四等分点.21.解：（1）因为，由正弦定理得，所以，由余弦定理得，又，所以；（2）因为，所以.因为是线段的中点，所以，()()23cos ,2323a b b c a b b c a b b c -⋅---===-- ),m b = ()3cos ,sin n A B = sin 3cos 0B b A -=sin 3sin cos 0A B B A -=sin 0B ≠3cos 0A A -=tan A =()0,πA ∈π3A =2222cos a b c cb A =+-22722b b =+-3b =1b =-ABC 1sin 2S bc A ==ABC r ()(112322S a b c r r =++=⨯+=r =2133AE AB AC =+ F AC 12BF BA AC =+ 22211213||332362AE BF AB AC AB AC AB AC ⎛⎫⎛⎫⋅=+⋅-+=-+=- ⎪ ⎪⎝⎭⎝⎭(),0,1AF AC λλ=∈ BF AB AC λ=-+ ()2221221||2(233333AE BF AB AC AB AC AB AC AB AC λλλλλ-⎛⎫⋅=+⋅-+=-++⋅=-++- ⎪⎝⎭ )12λ=+--=14λ=F AC A sin sin sin sin b a C A c B A --=+b a c a c b a --=+222a c b ac +-=2221cos 222a cb ac B ac ac +-===()0,πB ∈π3B =222a c b ac +-=224a c ac +=+D AC ()12BD BA BC =+所以，由正弦定理得，所以，又为锐角三角形，所以解得，所以，所以，所以，所以，即的长的取值范围是.22.解：（1）在中，由余弦定理得，即因为，所以，又，所以.在中，由正项定理得，所以又，所以，所以；（2）设，所以.在中，由余弦定理得.所以的面积，()()22221111242BD BA BC a c ac ac ⎡⎤=+=++=+⎢⎥⎣⎦2πsin sin sin sin 3a b c A B C ====,a A c C ==16π8π4sin sin sin 233363ac A C A A A ⎛⎫⎛⎫==+=-+ ⎪ ⎪⎝⎭⎝⎭ABC π0,22ππ0,32A A ⎧<<⎪⎪⎨⎪<-<⎪⎩ππ62A <<ππ5π2666A <-<8,43ac ⎛⎤∈ ⎥⎝⎦27,33BD ⎛⎤∈ ⎥⎝⎦BD ∈BD DAC 2222cos 3AC DA DC DA DC ADC ∠=+-⋅=AC =1,120AD CD ADC ∠=== 30DAC ∠= 90DAB ∠= 60BAC BAD DAC ∠∠∠=-= ABC sin sin AC BC ABC BAC∠∠=sin sin AC BAC ABC BC∠∠===BC AC =>=60ABC ∠< 45ABC ∠= (0)BC m m =>2BA m =ABC 222222224353cos 244BA BC AC m m m ABC BA BC m m∠+-+--===⋅ABC 11sin 222S BA BC ABC m ∠=⋅=⋅=所以，此时，又的面积，所以四边形的面积的最大值为max 1S =253m =DAC 1sin 2DAC S DA DC ADC ∠=⋅= ABCD max 1DAC S S +=。

2024-2025学年陕西省榆林市神木市第七中学高一上学期期中考试物理试题

2024-2025学年陕西省榆林市神木市第七中学高一上学期期中考试物理试题1.在物理学的重大发现中科学家们创造了许多物理思想与研究方法，高一上学期同学们学习了理想实验法、控制变量法、极限思想法、建立物理模型法、类比法和科学假说法等等，以下关于所用物理学研究方法的叙述正确的是（）A．根据速度定义式，当非常小时，就可以用表示物体在时刻的瞬时速度，这是应用了平均值法B．在不需要考虑物体本身的大小和形状时，忽略物体的大小和形状，用质点代替物体的方法，采用了等效替代的思想C．伽利略的理想实验是一个纯思维实验，其正确性应接受实践的检验D．在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看做匀速直线运动，然后把各小段的位移相加。

这里采用了微元法2.巴黎奥运会田径比赛于2024年8月1日至11日举行，关于运动会上有关运动的描述，下列说法正确的是（）A．开幕式中升奥运会会旗时，观察到会旗冉冉升起，观察者是以“会旗”为参考系的B．在田径比赛中，跑步运动员的比赛成绩是一个时间间隔C．在自行车比赛中，车速度越大其加速度越大，车的速度减小其加速度一定减小D．田径运动员通过一段路程其位移不可能为零，位移的大小永远不等于路程3. 2024年4月12日，中国海警2502舰艇编队在我钓鱼岛领海内巡航.这是中国海警依法开展的维权巡航活动.钓鱼岛自古就是我国固有领土，位置距福州市某港直线距离为。

若我国海警船从福州市某港出发去钓鱼岛巡航，到达钓鱼岛时航行了，历时，则下列说法中正确的是（）A．该海警船位移大小是，路程是B．该海警船往返一次位移大小是C．该海警船航行了，历时，平均速度大小为D．该过程海警船的路程小于位移的大小4.壁球是在用墙壁围起场地内，按照一定规则，两人相互交替用拍子击打对手击在墙壁上反弹球的一项竞技体育运动。

壁球以大小为的水平速度垂直碰撞墙壁，与墙碰撞后，沿着水平方向以大小为的速度反向弹回，已知壁球与墙壁接触的时间，那么壁球与墙壁接触过程的平均加速度的大小和方向分别为（）A．，反弹方向B．，反弹方向C．，碰墙方向D．，碰墙方向5.某快递公司推出了用无人机配送快递的方法，某次配送时无人机从地面由静止开始竖直向上飞行，运动的图像如图所示，以竖直向上为正方向，下列说法正确的是（）A．无人机在第末开始改变速度方向做减速运动B．无人机在末至末竖直向下做减速运动C．在前运动过程中，第末无人机离地面最高D．无人机在前内的位移大小为6.埃菲尔铁塔矗立在法国巴黎的战神广场，是世界著名建筑，也是法国文化象征之一，巴黎城市地标之一、某人将小球由塔的顶端静止释放，经测量可知小球着地前1s的位移为释放后1s位移的15倍，忽略空气阻力，重力加速度g取10m/s2。

专题训练：速度、加速度和图像综合问题-[初升高衔接]2023-2024学年新高(002)

专题训练：速度、加速度和图像综合问题一、单选题1．（2023春·黑龙江鸡西·高一校考期中）某学生在百米赛跑中，已知他在起跑瞬时的速度为4m/s，经过10s到达终点时的瞬时速度为8m/s，则该学生在整个运动过程的平均速度大小是（）A．4m/s B．6m/s C．8m/s D．10m/s2．（2023春·四川绵阳·高一四川省绵阳南山中学校考期中）高度差一定的两点间可以搭建无数条光滑的曲线轨道，让相同小球从起点端静止向下滑落，其中有一条曲线轨道的小球是最先到达终点端，这条曲线我们称之为最速降线。

如图所示，6个轨道起始端和终点端高度差相同，其中轨道3满足最速降线，6个相同的小球同时从起始端静止释放最后都到达终点端的整个过程中，不计一切阻力，下列说法正确的是（）A．从轨道1滑下的小球位移最小B．从轨道3滑下的小球平均速度最小C．从轨道3滑下的小球重力的平均功率最大D．各小球滑到终点时的重力的瞬时功率相同3．（2023春·湖北恩施·高一校联考期中）2022年2月20日，北京冬奥会圆满结束。

中国代表团斩获15枚奖牌，位居奖牌榜第三位，以谷爱凌、苏翊鸣为代表的优秀运动员更是在各自项目上为国争光，取得了历史性突破。

下列关于某些冬奥会比赛项目的说法正确的是（）A．在花样滑冰比赛中研究运动员的转体动作时，可以把运动员看成质点B．在钢架雪车项目中，雪车最高时速能达到140km/h，140km/h指的是平均速率C．在跳台滑雪比赛中，研究运动员的飞行轨迹不可以把运动员看成质点D．冰壶比赛中，冰壶脱手后向前继续运动是因为惯性图所示的两个4．（2023春·广东广州·高一校联考期中）在某校举办的趣味运动会上，甲、乙两位同学形成了如v t运动过程（图中各段均为直线，甲做匀速运动），甲的图像和乙的图像所围成的面积为0S，则在0~1t时间内，下列说法正确的是（）A．甲的位移大小为0SB．乙的位移大小为0SSC．乙匀加速的位移为02vD．乙全程的平均速度为035．（2023秋·安徽蚌埠·高一统考期末）下列关于汽车运动的描述，不可能发生的是（）A．汽车在某一时刻速度很大，而加速度为0B．汽车的加速度方向与速度方向相反C．汽车速度变化量很大，而加速度较小D．汽车加速度很大，而速度变化很慢6．（2023秋·高一课时练习）一物体自原点开始在x轴上运动，其初速度v0<0，加速度a<0，若加速度不断减小直至为零，则（）A．物体的速度不断减小，位移不断减小B．物体的速度不断增大，位移不断减小C．当a=0时，速度达到最大D．当a=0时，速度达到最大，位移达到最大7．（2022秋·陕西渭南·高一白水县白水中学校考期末）在直线运动中，下列有关物体运动的说法中正确（）A．速度大的物体其加速度也一定大B．物体的速度变化大其加速度也一定大C．速度变化越快其加速度也越大D．加速度为负值则一定做减速运动8．（2021秋·河北秦皇岛·高一校考阶段练习）下列关于速度、加速度的描述中，正确的是（）A．物体的速度为零时，加速度也为零B．物体的速度变化越慢，加速度越大C．加速度在数值上等于单位时间内速度的变化量D．物体的速度变化量越大，加速度越大9．（2022秋·高一课时练习）如图所示，汽车向右沿直线运动，原来的速度是v1，经过一小段时间之后，速度变为v 2，v ∆表示速度的变化量。

神木中学高一数学第一次月考试题

神木中学高一数学第一次月考试题（满分150分，时间120分）一、选择题：共10小题，在每小题给出的四个选项中，只有一项是符合题目要求的．（每小题5分，共50分）1.下列命题正确的个数是（）①0AB BA += ； ②00AB ⋅= ； ③AB AC BC -= ； ④00AB ⋅=A 、1B 、2C 、3D 、42.在ΔABC 中,若060,43=∠==BAC ,则=⋅ （）A 、6B 、4C 、-6D 、-43.已知(1,2)a = ,(2,3)b x =-且a ∥b ,则x = （）A 、－3B 、34-C 、0D 、344．与向量(12,5)d =平行的单位向量（）A ．)5,1312(B ．)135,1312(--C ．)135,1312(或 )135,1312(--D ．)135,1312(±±5、下列命题中： ①若0a b ⋅= ,则0a = 或0b = ; ②若不平行的两个非零向量a ,b满足a b = ,则()()0a b a b +⋅-=; ③若a 与b 平行,则a b a b ⋅=⋅ ； ④若a ∥b ,b ∥c ,则a ∥c;其中真命题的个数是（）A 、1B 、2C 、3D 、4 6.若)()(),1,2(),4,3(b a b x a b a -⊥+-==且,则实数x= （） A 、23 B 、223 C 、323 D 、423 7．若32041||-=-，5||,4||==b a ，则b a 与的数量积为（） A ．102 B ．－103 C ．103 D ．108、若向量(1,1)a = ,(1,1)b =- ,(1,2)c =-,则c 等于（）A 、1322a b -+B 、1322a b -C 、3122a b -D 、3122a b -+9．在△ABC 中，D 、E 、F 分别BC 、CA 、AB 的中点，点M 是△ABC 的重心，则 MA MB MC +-等于（）A ．B ．4C ．4D ．410．已知向量)sin ,(cos θθ=,向量)1,3(-=则|2|-的最大值，最小值分别是（）A ．0,24B ．24,4C ．16,0D ．4,0 二、填空题：(每小题5分，共25分） 11.已知===x x a 则,13,5(12．非零向量||||||,+==满足，则b a ,的夹角为 .13.已知向量(,12),(4,5),(,10)OA k OB OC k ===-，且A 、B 、C 三点共线，则k= .14．设E D ，分别是ABC ∆的边BC AB ，上的点,AB AD 21=,BC BE 32=,若21λλ+= (21λλ，为实数),则21λλ+的值为__________.15.若平面向量与向量)2,1(-=的夹角是o 180，且53||=，则= .三、解答题：（共6小题，总分75分）解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）如图,ABCD 是一个梯形,//=, M 、N 分别是,的中点,已知=a ,=b ,试用→→b ,a 表示,DC BC和.MN17．（本小题满分12分）已知(1,2)a =,)2,3(-=b ,当k 为何值时，（1）ka b + 与3a b - 垂直？（2）k a + b 与3a -b 平行？平行时它们是同向还是反向？ABNMDC18、（本小题满分12分）在平面直角坐标系xOy 中，点A(－1,－2)、B(2,3)， C(－2,－1)。

陕西省榆林市神木中学2020-2021学年高一上学期第一次测试数学试题

A．等腰三角形
B．锐角三角形
C．直角三角形
D．钝角三角形
8．若关于 x 的方程 x2 bx c 0 的两根分别为 2, 1，则 b c （）
A．－1
B．1
C．－3
D．3
9．若函数 y f x 的定义域为 M x 2 x 2 ，值域为 N y 0 y 2 ，则函数
试卷第 1 页，共 4 页
陕西省榆林市神木中学 2020-2021 学年高一上学期第一次测试数学试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列结论不． 2 Ï R
2．设集合 A {2,3,5,7}, B {1,2,3,5,8} ，则 A B （）
D． 1Z
A． {1, 3, 5, 7}
B． {2, 3}
C． {2, 3, 5}
D．{1, 2,3,5,7,8}
3．已知关于 x 的方程 x2 2x m 0 有两个不相等的实数根，则（）
A． m 1
B． m £ 1
C． m 1
D． m 1
4．在下列图像中，表示函数图像的可能是（）
A．
2
，
[3]
3,
5 2
2
，则
f
(x)
的值域是
A．（0，1）
B． (0,1]
C．[0,1)
D．[0,1]
12．某中学的学生积极参加体育锻炼，其中有 1440 名学生喜欢足球或游泳，900 名学
生喜欢足球，1230 名学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生人数为（）
A．630
B．690
C．840

2024-2025学年陕西省榆林市神木市府谷中学高一(上)第一次调研数学试卷(含答案)

2024-2025学年陕西省榆林市神木市府谷中学高一（上）第一次调研数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合M ={x|x >3}，N ={x|x >2}，则M 与N 的关系可用Venn 图表示为( )A. B.C. D.2.已知集合A ={x| x +1<2},B ={x|1<x <3}，则A ∩(∁R B)=( )A. {x|x ≤1}B. {x|−1≤x ≤3}C. {x|−1≤x ≤1}D. {x|0<x <3}3.下列说法正确的是( )A. 若a >b >0，则ac >bcB. 若a >b ，则|a|>|b|C. 若a <b <0，则a 2>abD. 若a >b >c ，则a b >a +c b +c 4.“a 2>1”是“1a >0”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.已知关于x 的不等式ax 2+bx +c >0的解集为{x|−2<x <7}，其中a ，b ，c 为常数，则不等式cx 2+bx +a⩽0的解集是( )A. {x|−12⩽x⩽17}B. {x|x⩽−17或x⩾12}C. {x|x⩽−12或x⩾17} D. {x|−17⩽x⩽12}6.某中学的学生积极参加体育锻炼，其中有95%的学生喜欢篮球或羽毛球，60%的学生喜欢篮球，82%的学生喜欢羽毛球，则该中学既喜欢篮球又喜欢羽毛球的学生数占该校学生总数的比例是( )A. 63%B. 55%C. 47%D. 42%7.已知集合M={(1,0)}，则下列与M相等的集合个数为( ) ①{(x,y)|{x−y=1,x+y=1}②{(x,y)|y=x−1+1−x}③{x|x=(−1)n−12,n∈N}④{x|−1<x<2,x∈N}A. 0B. 1C. 2D. 38.若正数x,y满足xy−2x−y=0，则x+y2的最小值是( )A. 2B. 22C. 4D. 42二、多选题：本题共3小题，共18分。