六年级数学思维能力拓展专题突破系列(一)数论专题(中)
小升初六年级全册数学思维训练PDF版

小升初六年级全册数学思维训练PDF版目录第1讲图解法解题(一) (1)第2讲图解法解题(二) (4)第3讲长方体和正方体(一) (8)第4讲长方体和正方体(二) (12)第5讲分数简便运算(一) (15)第6讲分数简便运算(二) (19)第7讲分数简便运算(三) (22)第8讲分数简便运算(四) (26)第9讲巧用比解应用题(一) (29)第10讲巧用比解应用题(二) (33)第11讲巧用比解应用题(三) (37)第12讲对应法解题 (41)第13讲转化单位一(一) (44)第14讲转化单位一(二) (49)第15讲倒推法解题(一) (53)第16讲分数百分数应用题 (57)第17讲假设法解题(一) (60)第18讲假设法解题(二) (63)第19讲设数代入法(一) (66)第20讲设数代入法(二) (70)第21讲工程问题(一) (73)第22讲工程问题(二) (77)第23讲较复杂的百分数应用题 (81)第24讲成本和利润 (84)第25讲浓度问题 (87)第26讲假设法解题练习 (90)第27讲较复杂的行程问题 (94)第28讲圆柱和圆锥 (97)第29讲用比例解题 (105)第30讲不定方程 (109)应用题综合练习 (112)综合练习(一) (120)综合练习(二) (124)综合练习(三) (127)六年级数学思维训练第1讲图解法解题(一)例1:有甲乙两个车间,如果从甲车间调10人到乙车间,则两个车间的人数正好相等;如果从乙车间调20人到甲车间,则甲车间的人数恰好是乙车间的3倍,原来两个车间各有多少人?例2:甲乙两数的和是52,甲数的3倍与乙数的5倍的和是202。
求甲乙两数各是多少?例3:某学校运来两堆煤,第一堆比第二堆多40吨,两堆各用去30吨后,剩下的第一堆煤是第二堆煤的3倍。
求两堆煤原来各多少吨?-1-关注每一个孩子的成长让每一位学生都有进步例4:甲油库原存油是乙油库的6倍,若两油库各增加60吨后,则甲库的存量是乙库的3倍。
六年级数学思维能力拓展专题突破系列(一)数论专题(下)

六年级数学思维能力拓展专题突破系列(一)数论专题(下)------余数定理(一)熟悉余数的基本定义和性质并能应用解题1.余数的定义是什么?2.余数的性质是什么?3.熟练解余数和问题例题1:被除数,除数,商与余数之和是463,已知商是8,余数是16,求除数。
例题2:被除数,除数,商与余数之和是2143,已知商是33,余数是52,求被除数和除数。
例题3:两数相除,商是499,余数是3,被除数最小是几?例题4:用108除一个数余100,如果改用36除这个数,那么余数是几?例题5:1111除以一个两位数,余数是66,求这个两位数。
(即该课程的课后测试)1、被除数,除数,商与余数之和是2151,已知商是37,余数是50,求除数。
2、被除数,除数,商与余数之和是2329,已知商是46,余数是37,求被除数和除数。
3、两数相除,商是511,余数是7,被除数最小是几?4、用108除一个数余99,如果改用27除这个数,那么余数是几?5、1111除以一个两位数,余数是33,求这个两位数。
1、解:设除数为a,则由余数性质得被除数为37a+50。
依题意,37a+50+a+37+50=2151,则38a=2014,得a=53。
2、解:设除数为a,则由余数性质得被除数为46a+37。
依题意,46a+37+a+46+37=2329,则47a=2209,得a=47,所以除数为47,被除数为46a+37=2199。
3、解:设除数为a,则被除数为511a+7。
由余数性质,除数要大于余数,所以a>7,则a最小为8,被除数最小为511×8+7=4095。
4、解:设这个数为a,且a除以108商为b,则由余数性质知a=108b+99。
改用27除a,因为108是27 的倍数,所以a除以27的余数就是99除以27的余数,则余数为18。
5、解:设这个两位数为n,则1111-33=1078是n 的倍数。
将1078分解质因数得1078=2×72×11,1078的两位约数有11,14,22,49,77,98,但是由余数性质知n>33,所以这个只可能为49或者77或者98。
(尖子生题库)数与形-2023六年级数学思维拓展(通用版)含答案含答案

(尖子生题库)专题16数与形的解题技巧2023六年级数学思维拓展奥数培优讲义(通用版)通过不同事物的某些相似性逆向类推出其他的相似性的方法,叫做逆向类推法。
解答数形结合问题时,先仔细观察算式的特点,找出其中隐含的规律,再解答。
数与形是数学中的两个最古老、也是最基本的研究对象,它们在一定条件下可以相互转化。
数与形是有联系的,这个联系称之为数形结合,或形数结合。
数形结合的思想,其实质是将抽象的数学语言与直观的图像结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化。
数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷。
顶点处。
应选( )。
A .673,左下B .674,上C .673,右下D .674,左下2.用白色和灰色小正方形按下面规律排成大正方形。
……第一幅第二幅第三幅第五幅图一共用了()个灰色小正方形。
A.19 B.21 C.25 D.363.下图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护话题的电话最多,共70个。
则本周“百姓热线”共接到热线电话有()。
A.350个B.200个C.180个D.150个4.观察数列的排列规律,然后从四个选项中选出你认为最合理的一项,来填补空缺项:1 2 4 8 16()A.32 B.24 C.64 D.205.仔细分析,后面的第10个方框里有()个点。
A.36 B.37 C.38 D.406.与1+3+5+7+9+5+3+1得数相同的算式是()。
A.42B.52+32C.52-327.如图的每个正方形中的四个数之间都有相同的规律,请根据此规律,计算出m的值是()。
A.86 B.74 C.52.中。
A.60 B.50 C.46 D.4517.观察下列图形:第1个图形有6根小棒,第2个图形有11根小棒,第3个图形有16根小棒……,第10个图形有()根小棒。
六年级上册拓展思维练习题

六年级上册拓展思维练习题一、数学思维练习题1. 小明有3只黄球,4只蓝球,5只红球,他随机从中选择1只球,那么他至少要取出多少只球才能确保得到3只颜色都不同的球?2. 有一行数字:1, 7, 9, 4, 2, 8, 6。
将数字中的偶数和奇数分别从小到大排列,然后将两部分数字连接起来,得到一个新的数。
a) 这个新数是多少?b) 如果将数字中的质数和非质数分别从小到大排列,然后连接起来,得到另一个新的数,这个新数是多少?3. 有一个正方形4 x 4的棋盘,其中有一些格子是黑色的。
每次可以选择一个格子,将其颜色改变(黑色变为白色,白色变为黑色)。
经过若干次操作后,最多可以使棋盘上只有一个格子是黑色,请问最少需要经过多少次操作?4. 将1至9的数字填入九宫格中,每行、每列和每个九宫格内的数字均不重复。
5. 用四个9,可以得到1至100之间的哪些数字?二、语文思维练习题1. 请根据以下提示,写出一个故事:提示:王小明是一位聪明的小学生,有一天,他在上学路上捡到一颗奇怪的石头。
王小明收集了一些小石头,通过观察,请问他是如何判断哪些小石头是宝石?2. 请用下面的词语组成一个连贯的短文:(狼吞虎咽、疾驰、庆祝、焚烧、舒缓、挣扎、难堪、微弱)3. 小华是一个勤奋的学生,她的爷爷经营了一家老字号的餐馆。
请你以“小华和她的爷爷”为题,写一篇小短文,介绍小华是如何帮助她的爷爷管理餐馆的?三、科学思维练习题1. 有一种动物,它的一种特征是拥有两对翅膀,它的一种特征是它只能在夜间活动。
你知道是什么动物吗?2. 请解释以下科学现象:为什么水会从地底下的井里涌出来?(考虑重力、压力等因素)3. 小明想要种一片草地,他从种子开始,一直照顾到长出绿茵茵的草地。
请列举出小明在整个过程中需要进行的步骤。
4. 请解释以下科学概念:静止摩擦力和滚动摩擦力有何不同?四、综合思维练习题1. 提示:请用下面的文字,写一篇关于“友情”的短文。
(温暖,忠诚,支持,互相帮助,难过,困难,分享,欢乐)2. 小明参加了学校的足球队比赛,但是他的队伍落后了对手。
六年级数学专题思维训练—数论综合(含答案及解析)

六年级数学专题思维训练—数论综合1 公元前后,居住在墨西哥东部尤卡坦半岛的玛雅人的记数法是二十进制,他们基本的数字符号仅有两个:“.”和“一”,“.”来自玉米、豆子或卵石的形状,表示1;“一”是豆荚的形状,表示5.用这两个符号的上、下排列,组成了1~19各个数字(如下图所示).2 一个五位数恰好等于它各位数字和的2007倍,则这个五位数是——.3 (1)从1到3998这3998个自然数中,有多少个数能被4整除?(2)从1到3998这3998个自然数中,有多少个数的各位数字之和能被4整除?4 如下图所示,摆放2×2的“4宫格”要用12根火柴棒;摆放3×3的“9宫格”要用24根火柴棒.小明用1300根火柴棒,恰好摆放成一个m×m的“m-宫格”,问m =?4宫格 9宫格5 二十多位小朋友围成一圈做游戏,他们依顺时针顺序从小赵报1开始连续报数,但7的倍数或带有数字7的数都要跳过去不报;报错的人表演一个节目.小明是第一个报错的人,当他右边的同学报90时他错报了91.如果他第一次报数报的是19,那么这群小朋友共有——人.6 从1至9这九个数字中挑出六个不同的数填在下图的六个圆圈内,使任意相邻两个圆圈内数字之和都是质数,那么最多能找出种不同的挑法来(六个数字相同、排列次序不同的都算同一种).7 能被3整除且至少有一个数字是6的四位数有 个8 不大于2009的自然数中,被3整除且恰有一个数码是6的有 个9 试说明,将1+21+31+。
+401的和写成一个最简分数nm 时,m 不会是5的倍数10 数89之数码和为17.请问1、2、3、…、2008这2008个数之数码和的总和为多少?11 21ab 是一个四位数,由四个阿拉伯数字a 、b ,1,2组成的其他23个四位数的和等于 90669,求a 和6的值.12 N是一个各位数字互不相等的自然数,它能被它的每个数字整除.N的最大值是13 在3和5之间插入6、30、20这三个数,得到3、6、30、20、5这样一串数.其中每相邻两个数的和可以整除它们的积(例如,3_』-6=9,9可以整除3×6;再如,6__-30=36,36可以整除6×30).请你在4与3这两数之间的三个空中各填入一个非零的整数,使得其中每相邻两个数的和可以整除它们的积.4、_ ___、____、____、314 N为自然数,且N+l、N+2、…、N+9与690都有大于1的公因数.N的最小值为15 写一个首位数字比末位数字大2的n位数(n大于或等于3)A,交换首位数字和末尾数字,得n位数B,A、B相减(大数减小数),所得的差为n位数C,把C的首位数字和末尾数字互换得D,C和D的和是S,不论写怎样的符合要求的数A,所得S都是一个常数K的倍数,则K的最大值是参考答案及解析1 公元前后,居住在墨西哥东部尤卡坦半岛的玛雅人的记数法是二十进制,他们基本的数字符号仅有两个:“.”和“一”,“.”来自玉米、豆子或卵石的形状,表示1;“一”是豆荚的形状,表示5.用这两个符号的上、下排列,组成了1~19各个数字(如下图所示).【答案】68097【分析】17+4×20+10×202+8×203=680972 一个五位数恰好等于它各位数字和的2007倍,则这个五位数是——.【答案】36126或54189【分析】这个五位数为abcde,由题意abcde= 2007 (a+b+c+d +e)由于9¦ 2007,可得9¦abcde,则有9¦(a+b+c+d+e), 2007×9=18063,这个五位数是18063的倍数,只可能为:18063,36126,54189,7225290315.经检验,36126和54189符合题意.3 (1)从1到3998这3998个自然数中,有多少个数能被4整除?(2)从1到3998这3998个自然数中,有多少个数的各位数字之和能被4整除?【答案】 (1)999个,(2)999个.【分析】(l)由于每连续4个自然数中必有一个能被4整除,3998÷4=999……2.因此从1到3998这3998个自然数中能被4整除的一共有999个‘(2)为了方便,将0到3999这4000个整数都看成四位数abcd(不是四位则在前面补零,如12=0012).由于b.c,d各有10种数字可任意选择,而且当b.c.d选定后.为满足a+b+c+d 能被4整除,千位数字“必唯一确定.事实上,若b+c+d=4K时,则a=o;若b+c+d=4K+l 时.则a=3 :若b+c+d=4K+2时,则a=2;若b+C+d=4K+3,则a=1.(K为整数)综上所述,在o到3999这4000个整数中有1×10 ×10×10=1000(个)数的各位数字之和能被4整除.因此,从1到3998这3998个自然数中有1ooo-1=999(个)数的各位数字之和能被4整除,4 如下图所示,摆放2×2的“4宫格”要用12根火柴棒;摆放3×3的“9宫格”要用24根火柴棒.小明用1300根火柴棒,恰好摆放成一个m×m的“m-宫格”,问m =?76田4宫格 9宫格【答案】25【分析】m2向的火柴棒有m+1列,每列有m根,也共有m(m+1)根.所以,摆放”,m2宫格”共用了2m( m+1) 根火柴棒.由2m(m+ l) =1300,得到m(m+1)=650=2×52×13=25×26.因此m=25 .5 二十多位小朋友围成一圈做游戏,他们依顺时针顺序从小赵报1开始连续报数,但7的倍数或带有数字7的数都要跳过去不报;报错的人表演一个节目.小明是第一个报错的人,当他右边的同学报90时他错报了91.如果他第一次报数报的是19,那么这群小朋友共有——人.【答案】24【分析】情况一:..跳过去不报”指一个小朋友报了6,下一个小朋友不报数而是拍手.再下一个小朋友报8.此时,每个人应当轮到的数和上一次轮到的数(报出来或者拍手跳过)之间的差等于总人数.小明本次应当拍手,而不是报出91.所以”总人数是91—19=72的约数.有72.36.24,18,……,其中是“二十多”的只有24.情况二:,.跳过去不报”指一个小朋友报了6,下一个小朋友直接报8.此时.把所有i 的倍数和带有数字7的数去掉之后,剩余的数排成一列,每个人应当轮到的数和上一次轮到的数在这个数列中的位置号之差等于总人数.从19到90这72个数中,含有数字7的有27,37,47,57,67,70到79.87.共16个.是i 的倍数且不含有数字7的有21,28,35,42,49,56,63,84共8令,所以排除掉之后剩下48个.总人数应当是48的约数,有48,24,16,……,其中是“二十多”的也只有24。
小学数学思维拓展(六年级)电子文档

第一讲分数的巧算(1)例:计算:练习1:计算:练习2:计算:第二讲分数的巧算(2)例:计算:练习1:计算:练习2:计算:第三讲分数的巧算(3)例:计算:练习1:计算:练习2:计算:第四讲分数的巧算(4)例:计算:练习1:计算:练习2:计算:第五讲比较分数大小(1)例:比较和的大小。
练习1:比较的大小。
练习2:比较的大小。
第六讲比较分数大小(2)例:比较的大小。
练习1:比较的大小。
练习2:比较的大小。
第七讲比较分数大小(3)例:比较的大小。
练习1:比较的大小。
练习2:比较的大小。
第八讲比较分数大小(4)例:比较的大小。
练习1:比较的大小。
练习2:比较的大小。
第九讲按比例分配问题(1)例:两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积比是3:1,而另一个瓶子中酒精与水的体积比是4:1,若把两瓶酒精溶液混合,求混合液中酒精与水的体积之比?练习1:有两瓶同样重的盐水,甲瓶盐水中盐与水重量的比是1:8,乙瓶盐水中盐与水重量的比是1:5。
现将两瓶盐水并在一起,求混合后的盐水中盐与水重量的比是多少?练习2:一块合金内铜和锌的比是2:3,现在再加入8克锌,共得新合金58克,求新合金内铜和锌的比?第十讲按比例分配问题(2)例:一个长方体的棱长总和是252厘米,它的长、宽、高之比是4:3:2,长方体的表面积是多少平方厘米?练习1:一个长方形的长与宽之比是18:5,如果长减少13厘米,宽增加13厘米,则面积增加338平方厘米,原长方形面积是多少平方厘米?练习2:等腰三角形的一个顶角与一个底角的比是5:2,它的顶角和底角各是多少度?第十一讲按比例分配问题(3)例:甲、乙、丙三箱苹果共重60千克,如果从甲、乙两箱中各取出3千克苹果放入丙箱中,则甲、乙、丙三箱苹果的重量比是1:2:3,甲、乙、丙三箱苹果原来各重多少千克?练习1:大、小两桶油共重270千克,大桶里的油被用去20千克后,剩下的油与小桶里的油重量比是3:2,求大桶里原来装有多少千克油?练习2:一条路全长120千米,分成上坡、平路、下坡三段,各段路程长之比依次是1:2:3,某人骑自行车走各段路程所用时间之比依次是4:5:6,已知此人骑自行车上坡的速度是每小时10千米,求此人骑自行车走完全程需用多少小时?第十二讲按比例分配问题(4)例:六年级有140名同学被分成三组进行植树活动,已知第一组和第二组人数的比是2:3,第二组和第三组人数的比是4:5,这三个小组各有多少人?练习1:光明小学六年级学生人数与五年级学生人数的比是9:10,五年级学生人数与四年级学生人数的比是5:7,已知这三个学年共有学生330人,六年级有学生多少人?练习2:六(1)班去年男女生人数的比是3:4,今年又转来3名男生,这时男女生人数的比是5:6,六(1)班今年有学生多少人?第十三讲按比例分配问题(5)例:甲、乙、丙三人的水果糖比例是9:4:2,甲给了丙30块水果糖,乙也给了丙一些水果糖,比例变为2:1:1,问乙给了丙几块水果糖?练习1:将一堆玻璃球全部分给甲、乙、丙三个小朋友。
六年级数学小升初专题训练-第3节-数论拓展人教新课标含答案

第3节:数论拓展模块一:数位问题我们通常使用的是十进制计数法,其特点是“满十进一”。
.这样,数字0?9可以组成无穷无尽、千变万化的数。
数字的数值、数位的变化,决定不同的数.同一个数字,由于它在所写的数里的位置不同,所表示的数也不同.也就是说,每一个数字除了本身的值以外,还有一个“位置值。
例如“5”,写在个位上,就表示 5个一;写在十位上,就表示5个十;写在百位上,就表示5个百,等等。
根据以上原则,我们可以将数写成另一种形式,例如:926表示9个百,2个十,6个一,即926=9×100+2×10+6×1。
11.3表示1个十,1个一,3个0.1,即11.3=1×10+1×1+3×0.1。
有时,我们也用字母代替阿拉伯数字表示数,如:abc表示a个百,b个十,c个一。
其中,a可以是1?9中的数字,不能是0;b和c是0?9中的数字。
【例1】有一个小数,先把它的小数点向左移动2004位后,再向右移动2005位,结果是40.3,原来的小数是。
【例2】小李在某个三位数的最左边添上了一个数字1,得到一个新的四位数,且这个数是原数的9倍,那么原来的三位数是。
【例3】一个三位数,三个数位上的数字和为16,百位上的数字比十位上的数字小1,个位上的数字比十位上的数字大2,则十位上的数字是()A.4B.5C.61.有这样的一类三位数:个位和百位上的数字交换后仍然是这个数,这样的三位数共有()个。
A.10B.9C.902.—个两位数,它个位上的数字是m,十位上的数字是n,用含有字母的式子表示这个两位数是()A.mn B.10m n C.10n m3.一个数的小数点向右移动一位后比原来的数大25.2,原数是。
4.一个两位数,个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,则原来的两位数为()。
A.54B.27C.72D.455.—个自然数各个数位上的数之和是16,而且各数位上的数字都不相同。
【思维拓展】数学六年级思维拓展之经典应用题(附答案)必考知识点

六年级思维拓展之经典应用题1.甲乙两个小朋友各有一袋糖,每袋糖不到20粒。
如果甲给乙一定数量的糖后,甲的糖就是乙的糖粒数的2倍;如果乙给甲同样数量的糖后。
甲的糖就是乙的糖粒数的3倍。
那么甲乙两个小朋友共有多少粒。
2.在期末考试,哥哥的数学成绩比语文高7分,弟弟的数学成绩是语文的67又知道弟弟的数学成绩比哥哥的数学成绩的5高4分,总成绩比哥哥低3分,那6么弟弟的语文成绩是多少分?3.5个空瓶可以换1瓶汽水,某班同学喝了161瓶汽水。
其中有一些是用喝剩下的空瓶换来的,那么他们至少要买多少瓶汽水?4.老师在黑板上写了十三个自然数,让同学们计算它们的平均数,要求保留两位小数,王林算得答案是12.43,老师说最后一个数字错了,那么正确的答案是()。
A12.42B12.44C12.46D12.475.有8只盒子,每只盒内放有同一种笔。
8只盒子所装笔的支数分别为17支、23支、33支、36支、38支、42支、49支、51支。
在这些笔中,圆珠笔的支数是钢笔支数的2倍,钢笔支数是铅笔支数的1,只有1只盒里放的是水彩笔。
3这盒水彩笔共有多少支?6.A、B、C、D、E在一次满分为100分的考试中,得分都是大于91的整数,如果A、B、C的平均分为95分,B、C、D的平均分为94分,A是第一名,E 是第三名得96分,那么D的得分是多少?7.小明爷爷的年龄是一个二位数,将此二位数的数字交换得到的数就是小明爸爸的年龄,又知道他们的年龄的差是小明年龄的4倍,求小明的年龄。
8.爸爸、哥哥、妹妹三人现在的年龄和是64岁。
当爸爸的年龄是哥哥年龄的3倍时,妹妹是9岁;当哥哥的年龄是妹妹年龄的2倍时,爸爸是34岁。
现在三个人的年龄各是多少岁?9.某市居民自来水收费标准如下:每户每月用水4吨以下,每吨1.80元;当超过4吨时,超过部分每吨3.00元。
某月甲乙两户共交水费26.40元,用水量之比为5:3,问:甲乙两户各应交水费多少元?10.食堂买来5只羊,每次取出两只合称一次重量,得到10种不同重量(单位:千克):47,50,51,52,53,54,55,57,58,59。
2021年六年级数学思维训练:数论综合一

2021年六年级数学思维训练:数论综合一一、兴趣篇1.如果某整数同时具备如下3条性质:①这个数与1的差是质数;②这个数除以2税金的商也就是质数;③这个数除以9税金的余数就是5.那么我们称这个整数为幸运数.求出所有的两位幸运数.2.一个五位数8□25□,空格中的数未知,请问:(1)如果该数能被72整除,这个五位数是多少?(2)如果该数能被55整除,这个五位数是多少?3.在大于5000的自然数中,能够被11相乘,并且数字和为13的数,共计个.4.一个各位数字均不以0的三位数能够被8相乘,将其百位数字、十位数字和个位数字分别抛掉后可以获得三个两位数(比如,按此方法由247将获得47、27、24).未知这些两位数中一个就是5的倍数,另一个就是6的倍数,除了一个就是7的倍数.原来的三位数就是多少?5.26460的所有约数中,6的倍数存有多少个?与6互质的存有多少个?6.一个自然数n共有9个约数,而n1恰有8个约数,满足条件的自然数中,最小的和第二小的分别是多少?7.一个自然数,它的最小的约数和次大的约数的和就是111,这个自然数就是.8.存有一个算式6×5×4×3×2×l.小明在上式中把一些“×”改成“÷”,计算结果还是自然数,那么这个自然数最轻就是多少?9.一个两位数分别除以7、8、9,所得余数的和为20.问:这个两位数是多少?10.信息在战争中就是非常关键的,它常以密文的方式传输.对方能够以获取密文却很难晓得截获密文的密码,这样就达至保密的促进作用.有一天我军查获了敌军的一串密文:a3788421c,字母则表示还没被截获出的数字.如果晓得密码满足用户如下条件:①密文由三个三位数连在一起组成,每个三位数的三个数字互不相同;②三个三位数除以12所得到的余数是三个互不相同的质数;③三个字母表示的数字互不相同且不全是奇数.你能破解此密文吗?二、答疑题(共12小题,满分0分后)11.已知×是495的倍数,其中a、b、c分别代表不同的数字.请问:三位数是多少? 12.11个已连续两位数乘积的末4位都就是0,那么这11个数的总和最轻就是多少?13.有一个算式9×8×7×6×5×4×3×2×l.小明在上式中把一些“×”换成“÷”,计算结果还是自然数,那么这个自然数最小是多少?14.存有15十一位同学,每位同学都存有个编号,他们的编号就是1号至15号.1号同学写下了一个自然数,2号说道:“这个数能被2相乘”,3号接着说道:“这个数能被3相乘”…依此下去,每位同学都说道,这个数能被他的编号数相乘.1号一一并作了检验:只有两个同学(他们的编号就是已连续的)说道得不对,其余同学都对.问:(1)说的不对的两位同学他们的编号是哪两个连续的自然数?(2)如果1号同学写下的自然数就是一个五位数,那么这个自然数为多少?第1页(共28页)15.存有2021盏灯,分别对应编号为1至2021的2021个控制器.现在存有1至2021的2021个人去按动这些控制器.未知第1个人按的控制器的编号就是1的倍数(也就是说他把所有控制器都按了一遍),第2个人按的控制器的编号就是2的倍数,第3个人按的控制器的编号就是3的倍数.依此搞下去,第2021个人按的控制器的编号就是2021的倍数,如果刚开始的时候,灯全系列就是亮着的,那么这2021个人按瘤果,除了多少盏灯就是亮着的?16.狐狸和黄鼠狼展开弹跳比赛,狐狸每次Cheese一次.比赛途中,从起点已经开始内要米,黄鼠狼每次跳米,它们每秒钟都只米设有一个陷井,当它们之中有一个掉进陷井时,另一个冲了多少米?17.一个偶数恰有6个约数不是3的倍数,恰有8个约数不是5的倍数.请问:这个偶数是多少?18.一个合数,其最小的两个约数之和为1164.谋所有满足要求的合数.19.未知a 与b就是两个正整数,且a>b.答:(1)如果它们的最小公倍数是36,那么这两个正整数有多少种情况?(2)如果它们的最小公倍数是120,那么这两个正整数有多少种情况?20.未知a与b的最大公约数就是14,a与c的最轻公倍数就是350,b与c的最轻公倍数也就是350.满足用户上述条件的正整数a、b、c共计多少组?21.已知两个连续的两位数除以5的余数之和是5,除以6的余数之和是5,除以7的余数之和是1.求这两个两位数.22.在一个圆圈上存有几十个孔(没100个),例如图.小明像是玩玩象棋那样,从a孔启程沿着逆时针方向,内要几个孔跳一步,期望一圈以后能够冲返回a孔.他先试着内要2孔跳一步,结果就可以冲到b孔.他又打声内要4孔跳一步,也就可以冲到b 孔.最后他内要6孔跳一步,刚好冲返回a孔.你晓得这个圆圈上共计多少个孔吗?三、解答题(共8小题,满分0分)23.存有6个互不相同且不以0的自然数,其中任一5个数的和都就是7的倍数,任一4个数的和都就是6的倍数.答:这6个数的和最轻就是多少?24.设n=301×302×…×2021×2021,答:(1)n的末尾一共会出现多少个连续的数字“0”?(2)用n不断除以12,直至结果无法被12相乘年才,一共可以除以多少次12?25.老师告诉贝贝和晶晶一个小于5000的四位数,这个四位数是5的倍数.贝贝计算出它与5!的最小公倍数,晶晶计算出它与10!的最大公约数,结果发现贝贝的计算结果恰好是晶晶的5倍.锖问:这个四位数是多少?26.一个正整数,它分别加之75和48以后都不是120的倍数,但这两个和的乘积却能够被120相乘.这个正整数最轻就是多少?27.a、b、c是三个非零自然数.a和b的最小公倍数是300,c和a、c和b的最大公约数都是20,且a>b>c.请问:满足条件的a、b、c共有多少组?28.存有一类三位数,它们除以2、3、4、5、6所获得的余数互不相同(可以含0).这样的三位数中最轻的三个就是多少?第2页(共28页)29.存有一个自然数除以15、17、19所获得的商与余数之和都成正比,并且商和余数都大于1,那么这个自然数就是多少?30.有4个互不相同的三位数,它们的首位数字相同,并且它们的和能被它们之中的3个数整除,请写出这4个数.第3页(共28页)参考答案与试题解析一、兴趣篇1.如果某整数同时具备如下3条性质:①这个数与1的差是质数;②这个数除以2税金的商也就是质数;③这个数除以9税金的余数就是5.那么我们称这个整数为幸运数.求出所有的两位幸运数.【分析】先找到满足用户(3)的这个数除以9的余数就是5,即为找到大于100的9的倍数乘以5即可,然后再从(3)中找到满足用户(1)的即为这个数与1的高就是质数,最后在从满足用户(1)的数中找到满足用户(2)的这个数除以2税金的商也就是质数,据此答疑.【解答】解:100以内9的倍数有:9、18、27、36、45、54、63、72、80、81、90、99,满足(3)这个数除以9的余数是5:14、23、32、41、50、59、68、77、86、95满足(1)这个数与1的差是质数:14、32、68满足(2)这个数除以2所得的商也是质数:14答:这个幸运数是14.2.一个五位数8□25□,空格中的数未明,答:(1)如果该数能被72相乘,这个五位数就是多少?(2)如果该数能被55相乘,这个五位数就是多少?【分析】(1)因为72=8×9,根据被8或9相乘数的特征分析深入探讨得出结论答案即可;(2)因为55=5×11,根据被8或9相乘数的特征分析深入探讨得出结论答案即可.【答疑】求解:(1)因为72=8×9,所以8+□+2+5+□=15+2×□能被9整除,符合条件的只有6,而256恰好能被8整除,所以这个五位数为86256.(2)因为55=5×11,所以能被5整除,末尾只能是5和0,8+□+2(5+□)=5+□□能被11整除,当末尾是5时,没有答案;当末尾是0时,这个五位数为85250.3.在小于5000的自然数中,能被11整除,并且数字和为13的数,共有18个.【分析】能够被11相乘的数的性质:把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别提出来,Ploudalm它们的差,如果这个高就是11的倍数(包含0),那么,原来这个数就一定能够被11相乘.结合题意,只有两种情况:①奇数位数字和=12,偶数位数字和=1.②奇数位数字和=1,偶数位数字和=12.【答疑】求解:①奇数位数字和=12,偶数位数字和=1,为3190,3091,4180,4081共4种可能将.第4页(共28页)②奇数位数字和=1,偶数位数字和=12.为1309,1408,1507,1606,1705,1804,1903;319,418,517,616,715,814,913共14种可能将.共4+14=18种.故答案为:18.4.一个各位数字均不为0的三位数能被8整除,将其百位数字、十位数字和个位数字分别划去后可以得到三个两位数(例如,按此方法由247将得到47、27、24).已知这些两位数中一个是5的倍数,另一个是6的倍数,还有一个是7的倍数.原来的三位数是多少?【分析】设这个三位数的百位数为a,十位数字为b,个位数字为c,根据被8整除数的特征和被5、6、7整除的数的特征分析探讨得出答案即可.【答疑】求解:设立这个三位数的百位数为a,十位数字为b,个位数字为c,因为三位数能被8整除,所以c为非0偶数,三个两位数中ab,bc,ac中bc与ac 均为以c结尾的数字,而c为非0偶数,所以能是5的倍数的就只能是ab了,所以b=5,因为三位数能被8整除,所以设100a+10×5+c=8k(k为整数),得c+50=4(25a+2k)为4的倍数,所以c只能为2或6,当c=2时,bc=52既不是6的倍数也不是7的倍数,所以c=6,bc=56是7的倍数,所以ac是6的倍数,所以a是6,所以原来的三位数是656.5.26460的所有约数中,6的倍数存有多少个?与6互质的存有多少个?【分析】首先将26460分解质因数,再进一步根据约数和的计算方法,找出含有6的质因数和不含6的质因数的数的个数即可.232【解答】解:26460=2×3×5×7,26460所有约数中6的倍数的数,Loupe26460÷6=4410的所有约数224410=2×3×5×7,故约数个数为(1+1)(2+1)(1+1)(2+1)=36个,也就是6的倍数存有36个;与6互质,即约数中不含质因子2和32即所求为5×7=245的所有约数,故与6互质的有(1+1)(2+1)=6个,也就是与6互质的有6个.6.一个自然数n共计9个约数,而n1恰存有8个约数,满足条件的自然数中,最轻的和第二大的分别是多少?【分析】因为9=3×3=9×1,所以可以把n看做只有一个质因数或两个质因数,进一步从最小的质因数考虑,逐步探讨得出答案即可.【解答】解:根据约数个数公式可知:n①当n=a,即n只有一个质因数时,n+1=9,所以n=8,8这样最小的n=2=256,n1=255=3×5×17,恰好存有(1+1)×(1+1)×(1+1)=8个约数,合乎题意;nm②当n=a×b,即n存有两个质因数时,(n+1)(m+1)=9,所以n=m=2,第5页(共28页)。
六年级趣味数学思维拓展题50道及答案

六年级趣味数学思维拓展题50道及答案(1) 【和倍问题】一人看见山上有一群羊,他自言自语道:“我如果有这些羊,再加上这些羊,然后加上这些羊的一半,又加上这些羊一半的一半,最后再加上我家里的那一只,一共有100只羊”,山上的羊群共有__________只.(2) 【行程问题】米老鼠从A 到B ,唐老鸭从B 到A ,米老鼠与唐老鸭行走速度之比是65∶,如下图所示:M 是A ,B 的中点,离M 点26千米的C 点有一个魔鬼,谁从它处经过就要减速25%,离M 点4千米的D 点有一个仙人,谁从它处经过就能加速25%.现在米老鼠与唐老鸭同时出发,同时到达,那么A 与B 之间的距离是__________千米.(3) 【空瓶换饮料】牛奶和李子果酱被装在同样的瓶子里出售,同时商店还开展回收此类空瓶的业务.每5个空瓶可以换1瓶牛奶,每10个空瓶可以换1瓶李子果酱.小强从地窖里找到了60个空瓶,拿到商店去换物品.他每次只换回一瓶牛奶,或一瓶李子果酱,并且等把换到的牛奶或李子果酱都吃掉后,再拿空瓶去换物品.在进行了若干次交换之后,他手中只剩下了1个空瓶.问:他一共进行了__________次交换.(4) 【行程问题】A ,B 两地相距90米,包子从A 地到B 地需要30秒,菠萝从B 地到A 地需要15秒,现在包子和菠萝从A ,B 两地同时相对而行,相遇时包子与B 地的距离是多少米?(5) 【约数与倍数】有一个电子钟,每走9分钟亮一次灯,每到整点响一次铃.中午12点整,电子钟响铃又亮灯.问:下一次既响铃又亮灯是几点钟?(6)【行程问题】老师教同学们做游戏:在一个周长为114米的圆形跑道上,两个同学从一条直径的两端同时出发沿圆周开始跑,1秒钟后他们都调头跑,再过3秒他们又调头跑,依次照1,3,5……分别都调头而跑,每秒两人分别跑5.5米和3.5米,那么经过几秒,他们初次相遇?(7)【行程问题】南辕与北辙两位先生对于自己的目的地s城的方向各执一词,于是两人都按照自己的想法驾车同时分别往南和往北驶去,二人的速度分别为50千米/时,60千米/时,那么北辙先生出发5小时他们相距多少千米?.(8)【递推数列】每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有_________对兔子.(9)【间隔问题】在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成10等份,第二种刻度线把木棍分成12等份,第三种刻度线把木棍分成15等份,如果沿每条刻度线把木棍锯断,木棍总共被锯成多少段?(10)【空瓶换饮料】师生共52人外出春游,到达后,班主任要给每人买一瓶矿泉水,给了班长买矿泉水的钱.班长到商店后,发现商店正在进行促销活动,规定每5个空瓶可换1瓶矿泉水.班长只要买______瓶矿泉水,就可以保证每人一瓶.(11) 【年龄问题】大雪后的一天,小明和爸爸共同步测一个圆形花圃的周长.他俩的起点和走的方向完全相同,小明的平均步长是54厘米,爸爸的平均步长是72厘米,由于两人的脚印有重合,并且他们走了一圈后都回到起点,这时雪地上只留下60个脚印,这个花圃的周长是多少厘米?(12) 【图形面积】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.(13) 【比例问题】一位牧羊人赶着一群羊去放牧,跑出一只公羊后,他数了数羊的只数,发现剩下的羊中,公羊与母羊的只数比是9:7;过了一会儿跑走的公羊又回到羊群,却又跑走了一只母羊,牧羊人又数了数羊的只数,发现公羊与母羊的只数比是7:5.这群羊原来有多少只?(14) 【最不利原则】一排椅子只有15个座位,部分座位已有人就座,乐乐来后一看,他无论坐在哪个座位,都将与已就座的人相邻.问:在乐乐之前已就座的最少有几人?(15) 【最不利原则】六年级2班有50名学生,报名去春游的有28人,结果春游那天来了32人,其中肯定有些人改变主意了(报名了没来,没报名,却来了),那么,F B A最多有______人改变主意了.(16)【列方程解应用题】某日停电,房间里燃起了长,短两根蜡烛,它们燃烧速度是—样的.开始时长蜡烛是短蜡烛长度的2倍,当送电后吹灭蜡烛,发现此时长蜡烛是短蜡烛长度的3倍.短蜡烛燃烧掉的长度是5厘米.问原来两根蜡烛各有多长?(17)【排列组合】五个人互相传球,由甲开始发球,并作为第一次传球,经过4次传球后,球仍回到甲手中.问:共有_________种传球方式.(18)【行程问题】在一条长12米的电线上,黄甲虫在8:20从右端以每分钟15厘米的速度向左端爬去,8:30红甲虫和蓝甲虫从左端分别以每分钟13厘米和11厘米的速度向右端爬去,红甲虫在什么时刻恰好在蓝甲虫和黄甲虫的中间?(19)【行程问题】小淘气乘正在下降的自动扶梯下楼,如果他一级一级的走下去,从扶梯的上端走到下端需要走36级.如果小淘气沿原自动扶梯从下端走到上端(很危险哦,不要效仿!),需要用下楼时5倍的速度走60级才能走到上端.请问这个自动扶梯在静止不动时有多少级?(20)【比较大小】编号为1,2,3的三只蚂蚁分别举起重量为115127,302333,439488克的重物.问:金、银、铜牌应分别发给几号蚂蚁____________________________.(21)【约数与倍数】有一群猴子正要分56个桃子.每只猴子可以分到同样个数的桃子.这时,又窜来4只猴子.只好重新分配,但要使每只猴子分到同样个数的桃子,必须扔掉一个桃子.则最后每只猴子分到桃子___个.(22)【图形面积】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?(23)【不定方程】实验小学的五年级学生租车去野外开展“走向大自然,热爱大自然”活动,所有的学生和老师共306人恰好坐满了5辆大巴车和3辆中巴车,已知每辆中巴车的载客人数在20人到25人之间,求每辆大巴车的载客人数.(24)【还原问题】刚打完篮球,冬冬觉得非常渴,就拿起一大瓶矿泉水狂喝.他第一口就喝了整瓶水的一半,第二口又喝了剩下的13,第三口则喝了剩下的14,第四口再喝剩下的15,第五口喝了剩下的16.此时瓶子里还剩0.5升矿泉水,那么最开始瓶子里有___________升矿泉水.(25)【还原问题】有18块砖,哥哥和弟弟争着去搬.弟弟抢在前面,刚摆好砖,哥哥赶到了.哥哥看弟弟搬得太多,就抢过一半.弟弟不肯,又从哥哥那儿抢走一半,这时爸爸走过来,他从哥哥那拿走一半少2块,从弟弟那儿拿走一半多2块,结果是爸爸比哥哥多搬了3块,哥哥比弟弟多搬了3块.问最初弟弟准备搬多少块?(26)【还原问题】3个探险家结伴去原始森林探险,路上觉得十分乏味就聚在一起玩牌.第一局,甲输给了乙和丙,使他们每人的钱数都翻了一番.第二局,甲和乙一起赢了,这样他们俩钱袋里面的钱也都翻了倍.第三局,甲和丙又赢了,这样他们俩钱袋里的钱都翻了一倍.结果,这3位探险家每人都赢了两局而输掉了一局,最后3人手中的钱是完全一样的.细心的甲数了数他钱袋里的钱发现他自己输掉了100元.你能推算出来甲,乙,丙3人刚开始各有多少钱吗?(27)【盈亏问题】养猪专业户王大伯说:“如果卖掉75头猪,那么饲料可维持20天,如果买进100头猪,那么饲料只能维持15天.”问:王大伯一共养了多少头猪?(28)【和倍问题】少年宫手工组的小朋友们做工艺品“猪娃娃”.每个人先各做一个纸“猪娃娃”;接着每2个人合做一个泥“猪娃娃”;然后每3个人合做一个布“猪娃娃”;最后每4个人合做一个电动“猪娃娃”.这样下来,一共做了100个“猪娃娃”,由此可知手工组共有________个小朋友.(29)【不定方程】在一次活动中,丹丹和冬冬到射击室打靶,回来后见到同学“小博士”,他们让“小博士”猜他们各命中多少次.“小博士”让丹丹把自己命中的次数乘以5,让冬冬把自己命中的次数乘以4,再把两个得数加起来告诉他,丹丹和冬冬算了一下是31,“小博士”正确地说出了他们各自命中的次数.你知道丹丹和冬冬各命中几次吗?(30)【行程问题】一个圆的圆周长为1.26米,两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行.这两只蚂蚁每秒钟分别爬行5.5厘米和3.5厘米,在运动过程中它们不断地调头.如果把出发算作第零次调头,那么相邻两次调头的时间间隔顺次是1秒,3秒,5秒,……,即是一个由连续奇数组成的数列.问它们相遇时,已爬行的时间是多少秒?(31)【不定方程】小明玩套圈游戏,套中小鸡一次得9分,套中小猴得5分,套中小狗得2分.小明共套了10次,每次都套中了,每个小玩具都至少被套中一次,小明套10次共得61分.问:小明至多套中小鸡几次?(32)【行程问题】游乐场的溜冰滑道如下图.溜冰车上坡每分行400米,下坡每分行600米.已知从A点到B点需3.7分,从B点到A点只需2.5分.问:AC比BC 长多少米?(33)【最不利原则】一排椅子只有15个座位,部分座位已有人就座,乐乐来后一看,他无论坐在哪个座位,都将与已就座的人相邻.问:在乐乐之前已就座的最少有几人?(34)【行程问题】从花城到太阳城的公路长12公里.在该路的2千米处有个铁道路口,是每关闭3分钟又开放3分钟的.还有在第4千米及第6千米有交通灯,每亮2分钟红灯后就亮3分钟绿灯.小糊涂驾驶电动车从花城到太阳城,出发时道口刚刚关闭,而那两处交通灯也都刚刚切换成红灯.已知电动车速度是常数,小糊涂既不刹车也不加速,那么在不违反交通规则的情况下,他到达太阳城最快需要多少分钟?<<<,游戏时将(35)【不定方程】三张卡片上分另标有p,q,r数码(整数)且0p q r三张卡片随意分发给A,B,C三个人,每人各一张,根据每个人得到卡片上的数码数分别给他们记分,如此重复游戏若干轮,结果A,B,C三人得分总数分别为20,10,9.已知B在最后一轮的得分是r,那么⑴在第一轮得分是q的是谁?⑴p,q,r分别是?(36)【容斥原理】老师出了200道题让小明,小华,小强三人做.三人每人都做对了120道,且每道题都有人做对.如果把三人都做对的称为简单题,只有一人做对的称为难题,那么难题比简单题多__________道.(37)【行程问题】甲,乙两人分别从相距35.8千米的两地出发,相向而行.甲每小时行4千米,但每行30分钟就休息5分钟;乙每小时行12千米,则经过________小时________分的时候两人相遇.(38)【行程问题】孙悟空在花果山,猪八戒在高老庄,花果山和高老庄中间有条流沙河,一天,他们约好在流沙河见面,孙悟空的速度是200千米/小时.猪八戒的速度是150千米/小时,他们同时出发2小时后还相距500千米,则花果山和高老庄之间的距离是多少千米?(39)【新定义】称一个两头(首位与末尾)都是1的数为“两头蛇数”.一个四位数的“两头蛇数”去掉两头,得到一个两位数,它恰好是这个“两头蛇数”的约数.这个“两头蛇数”是_________________.(写出所有可能)(40)【和差问题】有18块砖,哥哥和弟弟争着去搬.弟弟抢在前面,刚摆好砖,哥哥赶到了.哥哥看弟弟搬得太多,就抢过一半.弟弟不肯,又从哥哥那儿抢走一半,这时爸爸走过来,他从哥哥那拿走一半少2块,从弟弟那儿拿走一半多2块,结果是爸爸比哥哥多搬了3块,哥哥比弟弟多搬了3块.问最初弟弟准备搬多少块?(41) 【统筹规划】A,B 两个粮店分别有70吨和60吨大米,甲,乙,丙三个居民点分别需要30吨,40吨和50吨大米.从A,B 两粮店每运1吨大米到三个居民点的运费如右图所示:如何调运才能使运费最少.(42) 【行程问题】龟,兔进行1000米的赛跑.小兔斜眼瞅瞅乌龟,心想:“我小兔每分钟能跑100米,而你乌龟每分钟只能跑10米,哪是我的对手.”比赛开始后,当小兔跑到全程的一半时,发现把乌龟甩得老远,便毫不介意地躺在旁边睡着了.当乌龟跑到距终点还有40米时,小兔醒了,拔腿就跑.请同学们解答两个问题:它们谁胜利了?为什么?(43) 【统筹规划】下图是A,B,C,D,E 五个村之间的道路示意图,○中数字是各村要上学的学生人数,道路上的数表示两村之间的距离(单位:千米).现在要在五村之中选一个村建立一所小学.为使所有学生到学校的总距离最短,试确定最合理的方案.到站运费/元发站甲乙AB 030400丙302053丙10732B A 乙甲发站运费/元到站500米终点起点E D C B A 54235035202040(44)【游戏与策略】如图,在55 方格的A格中有一只爬虫,它每次总是只朝上下左右四个方向爬到相邻方格中.那么它能否不重复地爬遍每个方格再回到A格中?A(45)【图形面积】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?(46)【行程问题】猎狗发现前方150米处有一只兔子正在逃跑,拔腿就追.兔子逃跑的速度是每秒14米,猎狗追赶的速度是每秒18米.在兔子前方520米处是一片灌木丛,如果兔子能钻进灌木丛,猎狗就捉不到它了.猎狗究竟能不能抓住兔子呢?(47)【统筹规划】一条直街上有5栋楼,从左到右编号为1,2,3,4,5,相邻两楼的距离都是50米.第1号楼有1名职工在A厂上班,第2号楼有2名职工在A厂上班……,第5号楼有5名职工在A厂上班.A厂计划在直街上建一通勤车站接送这5栋楼的职工上下班,为使这些职工到通勤车站所走的路程之和最小,车站应建在距1号楼__________米处.(48)【倍数问题】有几个同学想称一下体重,可是秤的秤砣不齐,只能称50千克以上的重量,他们只好每人都和其他人合称一次,共得到以下10个数据(单位:千克):75,78,79,80,81,82,83,84,86,88.问:⑴有几名同学?⑴他们的重量各是多少千克?(49)甲,乙两人要到沙漠中探险,他们每天向沙漠深处走20千米,已知每人最多可携带一个人24天的食物和水.⑴如果不准将部分食物存放在途中,问其中一人最远可以深人沙漠多少千米(当然要求二人最后返回出发点)?⑴如果可以将部分食物存放于途中以备返回时取用,情况又怎样呢?(50)【统筹规划】有一家五口人要在夜晚过一座独木桥.他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟.当时正是初一夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指.所幸的是他们有一盏油灯,同时可以有两个人借助灯光过桥.但要命的灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢.六年级趣味数学思维拓展题50道答案(1)36(2)A,B两地相距92千米(3)11次交换(4)包子距B地的距离是60米(5)3点钟(6)1秒483(7)550千米(8)144(9)28段(10)42瓶(11)2160厘米(12)17(13)这群羊原来有49只(14)5人.任意相邻的3张座位上至少要坐一人.(15)40人(16)原短蜡烛长10厘米,原长蜡烛长20厘米(17)52(18) 9:05(19) 54级(20) 2,1,3(21) 5(22) 24(23) 大巴车的载客人数为48人(24) 3升(25) 4块(26) 刚开始时甲有260元,乙有80元,丙有140元.(27) 600头(28) 48人(29) 丹丹命中了3次,冬冬命中了4次(30) 49秒(31) 小明至多套中小鸡5次(32) 1440米(33) 5人.任意相邻的3张座位上至少要坐一人.(34) 24分钟(35) ⑴第一轮得q 分的是C ⑴1p =,4q =,8r =(36)40道题(37)2小时19分(38)1200千米(39)所有可能的数为1111,1131,1771,1911(40)4块(41)560元(42)100米(43)D点(44)不可能(45)448(46)追不上(47)4号楼(48)5名同学,他们的体重分别为37千克,38千克,41千克,43千克,45千克.(49)360千米(50)首先姐姐跟弟弟一起过,用时3分钟,姐姐再回去送油灯,用时3分钟,老爷爷跟爸爸一起过河,用时12分钟,弟弟将灯送回去,用时1分钟,弟弟和母亲一起过,用时6分钟,弟弟送灯过河,用时1分钟,最后与姐姐一起过河,用时3分钟.一共用时:3312161329++++++=(分钟).最后能够安全全部过河。
六年级奥数学练习试卷思维培训资料 数论一

小升初名校真题专项测试-----计算测试时间:15分钟 姓名_________ 测试成绩_________1、++=__。
(05年首师附考试题) 21121212022121212113131313212121505 【解】:周期性数字,每个数约分后为+++=1 21121221521132、一个自然数除以2的商是一个自然数的平方,而除以3的商是一个自然数的立方,符合条件的最小的自然数是 . (06年西城实验中学)【解】:除以2是平方数,意味着这个自然数是平方数的2倍,除以3的商是一个自然数的立方,意味着这个自然数是立方数的3倍,所以满足条件的最小自然数是6483、如果在一个两位数的两个数字之间添写一个零,那么所得的三位数是原来的数的9倍,问这个两位数是__。
(05年101中学入学测试题)【解】:设原来数为ab ,这样后来的数为a0b,把数字展开我们可得:100a+b=9×(10a+b),所以我们可以知道5a=4b,所以a=4,b=5,所以原来的两位数为45。
4、129后面补上一个两位数,使它他能被95整除,请问补上的两位数是__。
(江苏“小数杯”)【解】:在129后面补上00,这样12900÷95=135…75,所以商应该是136×95=12920。
5、下列数不是八进制数的是 。
A 、125 B 、126 C 、127 D 、128 (人大附英语实验班测试题)【解】:八进制数是由除以8的余数得来的,不可能出现8,所以答案是D 。
6、求1×2×3×4×……×100的积的末尾共有多少个0?(首师附培训结业测试,第一届迎春杯试题)【解】:就看能分解出几个质因数5,可见能分解出一个5的数即5倍数有:[]=20个,能分解出两5100个5的数即25的倍数有:[]=4个,所有总共有20+4=24个。
251007、甲、乙、丙代表互不相同的3个正整数,并且满足:甲×甲=乙+乙=丙×135.那么甲最小是____。
六年级下册数学试题-思维能力训练:数论中的组合(解析版PDF)全国通用

+ 数论中的组合9本讲内容数论中的最值数论中的计数构造与论证前铺知识数字谜中的最值——五年级秋季第11讲(第9级下)同余——五年级春季第4讲(第10级下)后续知识最值问题综合——六年级暑假第14讲(第11级上)数论中的规律——六年级秋季第5讲(第11级上)1.由5个不同的数字组成的五位数是5的倍数,这样的五位数最小为_________.【答案】102352.由5个不同的数字组成的五位数是3的倍数,这样的五位数最大为_________.【答案】 987633.1~50的自然数中,是2的倍数或5的倍数有_______个.【答案】30个(1)一个各个数位互不相同的六位数能被9整除,这个数最大是多少?最小是多少?(2)一个各个数位互不相同的六位数能被1、2、3、4、5、6整除,这个数最大是多少? 最小是多少?【分析】 两道题都是极端假设和局部调整(1)法一:(试除法)最大:满足条件的六位数最大为987654,98765493÷ ,再调整987654-3=987651.最小:满足条件的六位数最小为102345,10234596÷ ,调整,102348即为9的倍数.法二:最大:除个位之外的最大五位数为98765,加上个位后能被9整除,故个位最大为1,所以满足条件的六位数最大为987651.最小:除个位之外的最小五位数为10234,加上个位后能被9整除,故个位最小为8,所以,满足条件的六位数最小为102348.(2)法一:(试除法)最大:满足条件的最大六位数为987654. [1,2,3,4,5,6]60=,9876546054÷ ,987600是60的倍数,再局部调整987600-60=987540.最小:满足条件的最小六位数为102345. [1,2,3,4,5,6]60=,1023456045÷ ,调整,102360为9的倍数,但有重复数字,枚举得最小为123480.法二:最大:987650,9876506050÷ ,987600是60的倍数,再局部调整987600-60=987540.最小:123450,1234506030÷ ,调整,123480即为所求.一个各位数字互不相同的四位数能被6、7、8整除,这个数最大是多少?【分析】[]6,7,8=168,极端分析,98765168149÷ ,98765149=98616-满足条件.(1)与6互质的最小的合数是多少?(2)45乘以一个数字a 变成了一个完全平方数,那么a 的最小值是多少?【分析】 (1)由于要与6互质,则这个合数中的质因数不能包括2与3,因此这个合数最小的质因数是5,因此这个合数是5的倍数,且倍数中不含质因数2和3,只有25是与6互质的最小的合数.(2)将45分解质因数245=35⨯,由于完全平方数的性质“奇因偶指”,所以,a 最小是5解决数论中的最值问题思想方法:极端分析和局部调整.即先假设一个最大或者最小的,如果不满足条件,再局部调整.数论中的最值数论计数问题常见的方法有:枚举法:分类有序,不重不漏;加乘原理:加法分类,类类独立;乘法分步,步步相关;排列组合:排列有序,组合无序;周期和容斥原理.大于2009的自然数中,被57除后,商和余数相等的数有多少个?【分析】 根据题意,设这样的数被59除后商和余数都是(57)a a <,这个数可表示为5758a a a ⨯+=,因此582009a >,易得a 至少为35,所以满足题意的数共有56-35+1=22(个).(1)从1、2、3、4、5、6这些数中,任取两个数,使其和不能被3整除,则有_______种取法.(2)从1~9这9个数码中取出3个,使它们的和是3的倍数,则不同取法有_______种.【分析】 (1)24210⨯+= .(2)分情况讨论.第一种,3个数都是3的倍数,有1种情况.第二种,3个数除以3都余1,有1种情况.第三种3个数除以3都余2,有1种情况.第四种,一个除以3余1,一个除以3余2,一个是3的倍数,有:3×3×3=27种情况所以,一共有1+1+1+27=30种不同取法.从自然数1~40中任意选取两个数,使得所选取的两个数的和为偶数,有多少种取法?【分析】2个数的和为偶数,即能被2整除,可以分为两类: 第一类:两奇数的和为偶数:1~40中有20个奇数,20个中选2个,有20×19÷2=190(种)取法; 第一类:两偶数的和为偶数:1~40中有20个偶数,20个中选2个,有20×19÷2=190(种)取法; 根据加法原理,共有190190=380+(种)取法.(1)N 是一个各位数字互不相等的三位数,它能被它的每个数字整除.N 的最大值是.(2)N 是一个各位数字互不相等的四位数,它能被它的每个数字整除.N 的最大值是.【分析】 极端分析与局部调整.(1)936.(2)9864.数论中的计数综合容斥原理模块50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;先让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?【分析】方法Ⅰ:枚举,把1—50编号写下来,4的倍数:编号4,8,12,……,48,标记一下;6的倍数:编号6,12,18,……,48,标记一下;面向老师的同学是没有转过的和转动两次的,共有38人;方法Ⅱ:找周期,[]4,6=12,12个人一周期, 1,2,3,4,5,6,7,8,9,10,11,12,其中4,8,12转一次,6,12再转一次,12个人面向老师的有9人,501242÷=周期个,面向老师:492=38⨯+人方法Ⅲ:容斥原理,转0次的同学:50505050[][][344612--+=,转2次的同学:50[412=,所以面向老师的一共有38人.注意所求的不仅是没转过的,还有转了2次的.【铺垫】求在1至100的自然数中能被3或7整除的数的个数.【分析】100100100 [[][]43 3721+-=.【拓展】体育课上,260名学生面向老师站成一行,按老师口令,从左到右报数:1,2,3,…,260,然后,老师让所报的数是4的倍数的同学向后转,接着又让所报的数是5的倍数的同学向后转,最后让所报的数是6的倍数的同学向后转,现在面向老师的学生有________人.【分析】转0次:260260260260260260260260[[[][][][][]138 45620123060 ---+++-=转2次:260260260260 [[][]3[]30 20123060++-⨯=注意所求的不仅是没转过的,还有转了2次的. 所以面向老师的168人.在1至1000的自然数中,既不能被5整除,又不能被7整除尽的数有多少个?【分析】100010001000[][][]3145735+-= ,1000‐314=686.1.数论最值问题采取极端分析与局部调整相结合.2.数论计数问题采取枚举,加乘原理,排列组合,容斥原理等方法.1.在628后面补上3个数字,组成一个六位数,使它能分别被2,4,9整除,且使这个数尽可能大.则这个六位数是________.【分析】628992. 2.在所有各位数字互不相同的五位数中,能被45整除的数最小是多少?【分析】由于该数各位数字均互不相同,又能被45整除,则数字和为9的倍数,且末位为0或者5.由于0+1+2+3+4=10大于9,则数字和应该为18.为了使其尽量小,先满足首位取1,再考虑千位取0,则个位必须为5,此时五位数为105ab ,数字和为:618a b ++=,所以最小3,9a b ==,则这个五位数为103953.大于100的整数中,被13除后商与余数相同数有多少个?【分析】1001379÷= ,因此大于100的整数中,被13除后商与余数相同的数分别有1388⨯+、……131212⨯+,共有5个.4.从1、2、3、4、5、6这些数中,任取两个数,使其和能被3整除,则有_______种取法.【分析】枚举,12+,15+,24+,36+,45+,共5种5.100名同学面向老师站成一排报数,老师令报3的倍数的同学向后转,报5的倍数的同学再向后转,现在面向老师的同学有_____名.【分析】 转的同学:100100100473535⎡⎤⎡⎤⎡⎤+-=⎢⎥⎢⎥⎢⎥⨯⎣⎦⎣⎦⎣⎦个没转的同学:100-47=53. 转两次的:100635⎡⎤=⎢⎥⨯⎣⎦. 面向老师的:53+6=59.1.四个完全一样的直角三角形和一个小正方形拼成一个大正方形(如图),如果小正方形面积是1 平方米,大正方形面积是5平方米,那么直角三角形中,较短的直角边长度是多少米?【分析】 记直线三角形的两条直角边a 、b (a b >),有222()15a b a b ⎧-=⎪⎨+=⎪⎩,可得21a b =⎧⎨=⎩. 最短的直角边长是1米.2.丁丁和玲玲两人摘苹果,丁丁说:“把我摘的苹果给玲玲7个,玲玲摘的苹果的个数就是我的2倍.”玲玲说:“把我摘的苹果给丁丁7个,他的苹果个数就和我的一样多了.”问丁丁和玲玲各摘了多少个苹果?【分析】设丁丁摘了x 个苹果,由题意得: 772(7)7x x ++=--14221x x +=-35x =.即丁丁摘了35个苹果,而玲玲的苹果个数为357749++=(个).3.学而思学员根据下列条件从A 、B 、C 、D 、E 五个地方选定参观地点,最多能去的地方是_____和_____两地.⑴若去A 地也必须去B 地.⑵B 、C 两地最多去一地.⑶D 、E 两地至少去一地.⑷C 、D 两地都去或者都不去.⑸若去E 地,一定要去A 、D 两地.【分析】假设去了E 地,根据条件(5)也去了A 和D ,根据条件(1)去了A 就一定要去B , 根据条件(2)不能去C 地,从而去了D 却没有去C ,这与条件(4)矛盾,所以没有去E ,根据条件(3),一定去了D ,根据条件(4),也一定去了C ,根据条件(2)去了C 就不能再去B ,根据条件(1)一定没有去A.所以,只去了C 和D.请同学们算一算,你的出生年月日的数字和+某年年龄+那一年的年份数字和,得到一个结果,那么在2020年之前有多少个这样的和是质数(比如大宽在2004年1月2日出生,1岁时对应2005年,那么那一年和为9+1+7=17满足条件).。
小学教育ppt课件教案数论思维训练的概念扩展与举一反三

创新问题设计
01
结合生活实际和数学知识,设计具有挑战性和创新性的问题,
激发学生的探索欲望。
问题பைடு நூலகம்战
02
鼓励学生独立思考、尝试解决问题,培养学生的挑战精神和解
决问题的能力。
应对策略
03
针对学生在解决问题过程中遇到的困难和挑战,提供有效的指
导和帮助,引导学生寻找解决问题的突破口。
跨学科综合应用案例分析
演绎证明过程展示及启示
演绎证明过程
演绎证明是一种从已知的事实和规则出 发,通过逻辑推理得出新结论的证明方 法。在数论中,演绎证明常用于证明定 理和推论。
VS
启示
演绎证明过程展示了数学思维的严谨性和 逻辑性。它告诉我们,在数学中,任何一 个结论都必须经过严格的证明才能被接受 。同时,演绎证明也启示我们在解决数学 问题时,要善于运用已知的知识和方法, 通过逻辑推理得出新的结论。
分数、小数和百分数的定义
分数表示部分与整体的关系,小数表示十进制分数,百分数表示 百分比。
相互转化
探讨分数、小数和百分数之间的相互转化方法,如分数与小数的互 化、百分数与小数或分数的互化等。
应用举例
通过举例说明分数、小数和百分数在日常生活和数学中的应用,如 折扣计算、比例分配等。
代数表达式及方程解法示例
归纳分类思想在数论中体现
归纳分类思想
归纳分类是一种重要的数学思维方法,它通过对问题的分析和归纳,将问题分类并找出各类问题的共 性和规律,从而简化问题的解决过程。
在数论中体现
在数论中,归纳分类思想常用于对整数性质的研究。例如,通过对整数的归纳分类,可以得出整数的 奇偶性、整除性等性质。同时,归纳分类思想也常用于解决数论中的计数问题,如通过分类讨论来求 解某些特定条件下的整数个数等。
小阶6合一思维拓展课程-【学生】六年级秋季课后巩固13

1130=15×6=( ).A .15−16 B .15+16 C .13−110 D .13+110 2.计算:11×2+12×3+13×4+14×5+15×6+16×7+17×8+18×9+19×10=( ).A 190 B 110 C 910 D 11103.16+112+120+130+142+156=( ). A 14 B 38 C 12 D 584.11×3+13×5+15×7+⋯+123×25=( ). A 2425B 1825C 1225D 6255.计算 5+65×6−6+76×7+7+87×8−8+98×9+9+109×10=( ). A 15 B 310 C 25 D 126.1235+1556+45+78+57=( ). A 2 B 3 C 4 D 5第1讲分数裂项(一)7.计算:11×2+12×3+13×4+14×5+15×6=( ).A .12 B .56 C .1 D .768.计算:16+112+120+130+142+156+172+190=( ).A 15 B 310 C 25 D 129.计算:41×3−83×5+125×7−167×9+209×11−2411×13=( ). A 1 B 34 C 1213 D 141310.计算:12×4+14×6+16×8+....+198×100=( ). A 1100 B 49100 C 1200 D 492001.计算:25×(11×3+13×5+15×7+⋯+123×25)= .2.计算:(18+124+148+180+1120+1168+1224+1288)×128 = .第2讲分数裂项(二)3.乐乐老师为了检验大家的计算能力,举办了一场计算大比拼比赛,获得胜利的队伍将获得多米诺骨牌一份,大家跃跃欲试,心里盘算着,计算还不容易,纷纷报名参加!牛牛第一个报名.1 2+16+215+235+477=.4.2008118+2009154+20101108+20111180+20121270=.5.计算:12+13+130+131+141+2051+10119+26120+38123+27124=.6.240×39+239×38+⋯+26×5+25×4=.7.计算:(13+115+135+163+199+1143)×2015=.8.计算:11×4+14×7+17×10+⋅⋅⋅⋅⋅⋅+197×100=.9.2644×8+2648×12+26412×16+⋯+264124×128+264128×132=.10.计算:12×4×6+14×6×8+16×8×10+⋯+196×98×100=.1.书的总册数一定,每包的册数和包数().A.成正比例B.成反比例C.不成比例D.宝宝不会做2.正方形的边长和面积().A.成正比例B.成反比例C.不成比例D.宝宝不会做3.豆豆和沐沐,一起去超市买可乐,可乐的价钱相同.若豆豆买了12瓶,沐沐买了16瓶,那豆豆与沐沐所花的钱数比为().第3讲比例应用题进阶A.3:4B.4:3C.2:3D.3:24. 小魏与贝拉去商店采购糖果,小魏买的都是奶糖,贝拉买的都是水果糖,并且两人花的钱数一样多.假如奶糖与水果糖的单价比为3:2,那小魏与贝拉买的数量之比是( ). A.3:4 B.4:3 C.2:3 D.3:25. 康师傅加工一批零件.如果他的工作效率提高14,那么提高前后的工作时间之比是( ).A.3:4B.4:3C.4:5D.5:46. 甲乙两人同时加工一批零件,已知甲乙工作效率比是3∶5,完成任务时,乙比甲多加工120个零件,这批零件共有( )个. A.300 B.360 C.420 D.4807. 加工一个零件,甲要2分钟,乙要4分钟,丙要5分钟.同时加工一批零件,最后三人同时完成各自任务.若甲比多乙加工200个零件,那丙加工了( )个零件. A.160 B.360 C.480 D.10008甲、乙两数的比是2:7,已知甲是108,则乙数是( ).A. 54B. 2167C. 378D. 9569.甲、乙、丙三人各自独立完成同一件工作,效率比是2:3:4,则三人完成工作所用的时间比是( ).A.2:3:4B.4:3:2C.1:2:3D. 6:4:310.豆豆拿着妈妈给的钱去买苹果,平时每斤苹果5元钱,今天由于打折促销,苹果价格变为每斤4元钱,于是豆豆多买了2斤苹果.妈妈给了豆豆( )元钱.A. 40B. 60C. 80D. 1001.如图,三角形ABC 中,D 、E 分别是AB 、AC 上的点,AD =1,DB =5,AE =3,EC =4;已知三角形ADE 的面积为1,则三角形ABC 的面积为( ).A. 203 B. 14 C. 28 D. 422.如下图,三角形ABC 中,D 、E 分别是AB 、AC 上的点,AB =2AD ,AC =3AE ;三角形ABC 的面积是120平方厘米,则三角形ADE 面积为( ).A. 20B. 30C. 40D. 50EDCBA EDCBA第4讲 相似模型3.如图,已知AE =13AC ,CD =14BC ,BF =15AB ,则三角形DEF 的面积三角形ABC 的面积的值为( ).A. 14 B. 13 C. 512 D. 124.如图,在平行四边形ABCD 中,E 为AB 的中点,AF =2CF ,三角形AFE(图中阴影部分)的面积为8平方厘米.则平行四边形的面积是( )平方厘米.A. 24B. 36C. 48D. 605.如图,三角形ABC 中,E 是AC 上的点,D 是BA 延长线上的点,AE =1,AD =2,EC =3,AB =4;如果三角形ABC 的面积是12,则三角形ADE 的面积是( ).A. 1B. 1.5C. 2D. 2.56.如图,已知三角形ABC 面积为1,分别延长AB 、BC 、CA 至D 、E 、F ,使BD =AB ,CE =BC ,AF =AC ,则三角形DEF 的面积为( ).图20-14ECDABF ECA. 4B. 7C. 10D. 137.如下图,已知AB =4AD ,AC =5AE ,已知S △ABC =100,则三角形ADE 的面积为( ).A. 5B. 6C. 8D. 108.如下图,已知DB =2AD ,EC =3AE ,已知S △ADE =10,则三角形ABC 的面积为( ).A. 60B. 80C. 90D. 1209.如图,三角形ABC 的面积为1,其中AB:BE =1:3,BC:CD =1:2,三角形BDE 的面积是( ).FECB A 1EDCBA EDCBAA. 8B. 9C. 10D. 1210.如图,AD =13AB ,BE =14BC ,FC =15AC .如果三角形DEF 的面积是50平方厘米,那么三角形ABC 的面积是( )平方厘米.A. 80B. 100C. 120D. 1501.如图,DC 平行于AB ,AC 和DB 交于点O ,AB:DC=3:2,则DO:OB=( ).A .2:3B .3:2C .4:9D .9:4EDCBAA BCDEF第5讲 蝴蝶模型A BCDO2. 如图,梯形ABCD 中,DC 平行AB ,且AB:DC=2:1,请问图中4块小三角形的面积比,即S 1:S 2:S 3:S 4是( ).A .1:2:2:4B .1:2:4:2C .1:4:4:16D .1:4:16:43. 如图,在梯形ABCD 中,三角形BCO 的面积是18平方厘米,三角形OCD 的面积是12平方厘米,那么梯形ABCD 的面积是( )平方厘米.A .36B .42C .48D .504. 如图是一个平行四边形花圃设计图,已知红花占地40平方米,黄花占地60平方米,BD 是对角线,与CE 交于O 点,则草坪ABOE 的面积为( )平方米.红花40黄花60白花草坪OABDCEA BCDO S 1 S 2S 3S 4ADB COA .100B .110C .120D .1305.如图,DC 平行于AB ,AC 和DB 交于点O ,DO 长4厘米,OB 长10厘米,AO 长15厘米,那么OC 长( )厘米.A .5B .6C .7D .86.如图,在梯形ABCD 中,三角形BCO 的面积是9平方厘米,三角形OCD 的面积是6平方厘米,那么梯形ABCD 的面积是( )平方厘米.A .25B .27C .28D .307.如图,平行四边形ABCD 的面积是120,DE =13AD ,AC 与BE 的交点为F ,那么图中阴影部分面积是( ).A .36B .40C .44D .48ABCDOADB CO8.如图所示,BD 、CF 将长方形ABCD 分成4块,三角形DEF 的面积是4平方厘米,三角形CED 的面积是6平方厘米.则四边形ABEF 的面积是( )平方厘米.A .9B .10C .11D .129.如图,正方形ABCD 中,E 是BC 边的中点,AE 与BC 相交于G 点,三角形BEG 的面积为1平方厘米,则正方形ABCD 面积是( )平方厘米.A .10B .12C .14D .1610.如图,阴影部分面积为2,那么正六边形面积为( ).A .12B .14C .16D .1864FEDCBA G EDCBA1.在ΔABC 中,BD:DC =3:2,三角形AOB 的面积是12,则三角形AOC 的面积是( ).A 、6B 、8C 、12D 、182.如图,在三角形ABC 中,D 、E 、F 分别是BC 、CA 、AB 上的点,AD 、BE 、CF 相交于一点O ,AF:FB =1:2,BD:DC =4:3,则CE:EA =( ).A 、2:3B 、3:2C 、3:4D 、4:33.如图,ΔABC 中,CD =2DB ,CE =4EA ,AD 与BE 相交于点O ,连接CO . (1)在燕尾ABOC 中,S ΔABO :S ΔACO =( ). A 、1:2 B 、2:1 C 、1:4 D 、4:1(2)在燕尾BCOA 中,S ΔBCO :S ΔBAO =( ).ABCDOOFED CBA 第6讲 燕尾模型A 、1:2B 、2:1C 、1:4D 、4:14.如图,三角形ABC 中,D 是BC 中点,E 是AC 中点,AD 和BE 相交于点O .已知三角形AOB 的面积是10平方厘米,请问三角形ABC 的面积是( )平方厘米.A 、25B 、30C 、35D 、405.如图,四边形ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于点G ,则四边形AGCD 的面积是( )平方厘米.A 、48B 、72C 、96D 、108OEDCBAOEAGFE DCBA6.如图,在三角形ABC 中,三角形AEO 的面积是1,三角形ABO 的面积是2,三角形BOD 的面积是3,则四边形DCEO 的面积是( ).A 、15B 、18C 、21D 、247.如图,已知三角形ABE 的面积是12平方厘米,三角形ACE 的面积是24平方厘米,三角形BCE 的面积是12平方厘米.三角形BDE 的面积是( )平方厘米.A .3B .4C .5D .68.如图,三角形AOB 与三角形AOC 的面积比是3:2,且BD =36,则CD 的长是( ).A .60B .54C .36D .249.如图,在三角形ABC 中,D 、E 、F 分别是BC 、CA 、AB 上的点,AD 、BE 、CF 相交于一点O ,AF:FB =2:3,AE:EC =4:5,则BD:DC 的比为( ).E DCBA2412BA .5:6B .6:5C .3:4D .4:310.三角形ABC 中,C 是直角,已知AC =2,CD =2,CB =3,AM =BM ,那么三角形AMN (阴影部分)的面积为( ).A .0.2B .0.3C .0.4D .0.51.一个正方体的平面展开图如如图所示,将它折叠成正方体后,“主”字对面的字是( )A .富B .强C .自D .由OFEDCBA ABCDM N第7讲 立体图形展开图2.如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开,成为一个平面图形,则展开图可以是()A.B.C.D.3.商店包装牛奶的纸箱是一个长方体,图是这个纸箱的展开图.这个纸箱的体积是()立方厘米.A.无法计算B.576 C.192 D.2884.有一些大小相同的正方体木块堆成一堆,从上面看是图a,从正面看是图b,从左面看是图c,这堆小木块至少有()块.A.16B.17C.18D. 195.如图,是一个由若干个小正方体组成的几何体的主视图和左视图,则该几何体最多可由多少个小正方体组合而成?()A.12个B.13个C.14个D.15个6.如图是一个正方体的展开图,原正方体中两个相对面上的数字相加的和都是10,A应该是()A.8 B.7 C.6 D.07.如图,这个正方体的上半部分是阴影,下半部分是白色的,下面四幅图中,是这个正方体的展开图的是()A.B.C.D.8.下面是一个长方体的展开图,它的体积是()立方厘米.(单位:厘米)A.77 B.105 C.142 D.2319.一仓库里堆放着若干个完全相同的正方体货箱,这堆货箱的三视图如图所示,这堆正方体货箱共有()个.A.7B.8C.9D. 1110.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有()A.3个B.5个C.7个D.9个1.有一座时钟现在显示上午10点整.问:( )分钟后,分针与时针第一次重合. A .50 B .54611 C .60 D .655112.九点多时候有两次时针和分针夹角为60度,这两次之间相隔( )分钟. A .10 B .101011C .20D .219113.6点多的某个时刻,数字6恰好在时针和分针的正中央,即两针的位置正好关于数字6对称,这时是6点( )分.A .27311B .32811C .27913D .324134.沐沐从2点多开始玩游戏,开始时记下了时针和分针的位置,3点多时候玩完恰好发现时针和分针调换了位置,那么他玩了( )分钟的游戏. A .27913B .55513C .60D .655115.小源的手表比家里的闹钟走得要快一些.这天中午12点时,小源把手表和闹钟校准,但当闹钟走到下午1点时,手表显示的时间是1点5分.请问:当闹钟显示当天下午5点的时候,手表显示的时间是( ).A .5点20分B .5点25分C .5点27311分 D .5点30分第8讲 时钟问题(一)6.小明每天晚上7点要看新闻联播,问此时分针和时针的夹角为( )度.A .120B .130C .140D .1507.现在是3点,再过( )分时针与分针第一次重合.A .131113B .15C .16411D .208.5点多的某个时刻,两针的位置正好关于数字5对称,这时是5点( )分.A .23113B .25C .27311D .279139.小红上午8点多钟开始做作业时,时针与分针正好重合在一起.10点多钟做完时,时针与分针正好又重合在一起.小红做作业用了( ).A .1小时B .1小时55513分C .2小时D .2小时101011分10.贝拉的手表比家里的闹钟走得要快一些.这天中午12点时,贝拉把手表和闹钟校准,但当闹钟走到下午1点时,手表显示的时间是1点5分.请问:当手表显示当天下午6点半的时候,闹钟显示的时间是( ).A .6点B .6点5分C .6点55分D .7点第9讲时钟问题(二)1.6点钟以后,经过多少分钟,分针与时针第一次成180度?2.小明在9点与10点之间开始解一道数学题,当时手表的时针和分针第一次在同一条直线.当小明解完这道题时,时针和分针刚好也在同一条直线上且没到10点.请问:小明解这道题用了多少分钟?3.雯雯在晚上7点与8点之间看了一集动画片,动画片开始时分针与时针正好成一条直线,动画片结束时两针正好重合.这集动画片一共播放了多长时间?4.一天晚上,小刚同学熬夜写作业,写到凌晨2点多时,实在不行了,倒在床上就开始呼呼大睡.睡觉前他看了一下闹钟,发现了一件有趣的事情,时钟上的时针和分针正好重合在了一起.早晨8点多时,小刚被闹钟闹醒.他看了一下闹钟,又发现了一件有意思的事—一此时时钟上的时针和分针正好张开成一条直线,小刚睡了多少小时?5.小华与妈妈上午8点多钟外出,临出门时他一看钟,时针与分针是重合的,下午2点多钟回到家,一进门看到时针与分针方向相反,正巧成一条直线,他们外出了小时.6.西成高铁开通后,张老师一家从西安北站乘高铁去成都,11点多出发,下午2点多可以到达,张老师看表发现,出发时时针和分针正好成一个平角,到达时时针和分针正好成直角,列车运行小时.7.2时到3时之间时针和分针在“2”的两边,并且两针所形成的射线到“2”的距离相等.问这时是2时多少分?8.田田晚上去超市买东西,到的时候是7点24分,买完出来的时候仍然是7点多,且分针和时针所夹的角度与到超市时相同.请问:田田出来的时候是7点几分?买东西一共花了多少分钟?9.某人下午六时多外出买东西,出门时看手表,发现表的时针和分针的夹角为110°,七时前回家时又看手表,发现时针和分针的夹角仍是110°.那么此人外出多少分钟?10.现在是六点钟整,至少过多久,分针和时针会分布在数字“6”的两边,关于数字“6”对称?第10讲物不知数1.有一盒乒乓球,每次8个8个地数,10个10个地数,12个12个地数,最后总是剩下3个.这盒乒乓球至少有()个.A.43 B.63 C.83 D.1232.厨房买来一些鸡蛋,总数不到100个,3个3个地数余2个,4个4个地数余3个,5个5个地数余4个.这些鸡蛋一共有()个.A.59 B.60 C.61 D.1193.五(1)班开展数学课外活动,每组6人余3人,每组7人余3人,每组8人余5人.五一班有()人.A.39 B.42 C.45 D.484.一筐橘子,三三数之余一,五五数之余四,七七数之余二,筐里最少有()个橘子.A.79 B.80 C.81 D.1605.一些方便面采用两种包装,每16袋装一箱或24袋装一箱都正好装完而且没有剩余,这些方便面最少有()袋.A.32 B.48 C.64 D.736.一批零件平均分给3个、5个、7个师傅做都剩1个,这批零件在200~250之间,请问这批零件有()个.A.211 B.209 C.106 D.1047.五年级的学生排队做操,如果10人一行则余2人,如果12人一行则余4人,如果16人一行则余8人,那么五年级最少有()人.A.232 B.235 C.240 D.2488.某小学的六年级有一百多名学生.若按三人一行排队,则多出一人;若按五人一行排队,则多出二人;若按七人一行排队,则多出一人.该年级的人数是().A.127 B.125 C.123 D.121−之间,将他们分成若干组,如果3人一组余1人,5人一组余2人,7人一9.某校人数在300400组余3人.则该校()人.A.365 B.366 C.367 D.368−个之10.东东家有一些鸡蛋,5个5个数多3个, 8个8个多5个,已知这些鸡蛋在130150间.东东家有()个鸡蛋.A.131 B.133 C.135 D.137第11讲浓度问题(一)1.一瓶浓度为7%的盐水1000克,那么含盐()克.A.7 B.70 C.700 D.70002.把50克糖放入450克水中,这时糖水的浓度为()% .A.10 B.11.11 C.15 D.203.一杯浓度为20%的酒精溶液,如果含水160克,那么含酒精()克.A.32 B.40 C.64 D.804.现有浓度为30%的糖水80克,加入80克浓度为20%的糖水,混合后浓度是()%. A.15 B.20 C.25 D.505.要将200克浓度为10%的盐水浓度稀释为4%,需要加水()克.A.200 B.300 C.400 D.5006.含糖20%的糖水36千克,要制成含糖45%的糖水,需蒸发掉水()千克.A.6 B.10 C.15 D.207.有800克10%的盐水,要使浓度提高为20%,那么需要加盐()克.A.80 B.100 C.120 D.1508.现有浓度为10%的糖水20千克,在该溶液中再加入()千克浓度为30%的糖水,可以得到浓度为22%的糖水.A.10 B.20 C.30 D.409.现有浓度为30%的糖水80千克,从中蒸发掉20千克水后浓度是()%.A.30 B.35 C.40 D.4510.两种钢分别含镍5%和40%,要得到140吨含镍30%的钢,需要含镍5%的钢和含镍40%的钢各()吨.A.5%的20吨,40%的120吨 B.5%的40吨,40%的100吨C.5%的60吨,40%的80吨 D.5%的80吨,40%的60吨第12讲浓度问题(二)1.甲种酒精溶液中有纯酒精2千克,水8千克;乙种酒精溶液中有纯酒精9千克,水6千克;要配制成浓度为45%的酒精溶液16千克,问两种酒精溶液各需多少千克?2.两个杯中分别装有40%与10%的盐水,倒在一起后混合的盐水含盐30%.若再加入300克20%的盐水,则含盐量变为25%,那么原来40%的盐水有多少克.3.甲瓶盐水浓度是12%,乙瓶盐水度是32%,当两瓶盐水混合时,盐水浓度为20%,如果把两瓶盐水各取出10升,再把剩下的盐水混合,这时盐水浓度为19%.乙瓶原来盐水有多少升.4.现在有浓度为36%的盐水若干,加入一定数量的水后稀释成浓度为30%的盐水,如果再稀释为24%的盐水,还需要加入的水是第一次加入水数量的几倍?5.有甲、乙、丙三瓶糖水,含糖量分别为30%,25%,24%,其中甲瓶中有30kg,先将甲、乙两溶液混合,浓度变为28%;再将丙瓶中的糖水倒入混合液中,浓度变为26%,问丙瓶原有多少千克糖水?6.配制浓度为25%的糖水1000克,需用浓度为22%和27%的糖水各多少千克?7.把浓度为30%、40%和50%的某溶液混合在一起,得到浓度为36%的溶液50升.已知浓度为30%的溶液用量是浓度为50%的溶液用量的3倍,浓度为30%的溶液的用量是多少升?8.丁丁的桌上放着一瓶25克纯酒精,丁丁先倒出5克,然后又往里面加入了5克的水后摇匀,这时溶液浓度是多少?接着他又倒出5克,加入5克水,此时溶液浓度变为多少?9.牛牛的桌前是浓度为20%的盐水100克,牛牛向里面加入了质量相同的盐和水后,变成了浓度为30%的盐水,请问:牛牛加了多少克的盐?10.田田的桌子上放着几杯盐水,她先将其中两杯浓度为40%和10%的混合在一起后,浓度变为30%,再加入300克20%的盐水,浓度变为25%,那么原来40%的那杯盐水有多少克呢?1.把正六边形分成面积相等、形状相同的十二部分,以下方法正确的有( )个.A. 1个B.2个C.3个D.4个2.已知正六边形面积为100,A 、B 、C 、D 、E 、F 分别为所在边中点,则阴影六角星的面积为( ).F E D CB A第13讲 特殊图形A .25B .50C .75D .1003.如图,阴影部分的面积为10,那么正六边形ABCDEF 的面积是( ). A .40 B .50 C .60 D .704.如图,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若三角形PBC 、三角形PEF 的面积为4与6,则正六边形ABCDEF 的面积为( ). A .30 B .40 C .50 D .605.如图,正八边形的面积是120平方厘米,问:正八边形中的阴影部分的面积是( )平方厘米.A .20B .30C .40D .60C6.下图这个十二边形的面积为2018,其中每个三角形均为等边三角形.则阴影部分的面积是().A.504.5 B.1009 C.1513.5 D.20187.如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形.则阴影面积是()平方厘米.A.12 B.16 C.18 D.208.如图,阴影部分的面积为30,那么正六边形ABCDEF 的面积是( ). A .90 B .100 C .110 D .1209.如图,正八边形中的阴影部分的面积是125平方厘米,则正八边形的面积是( )平方厘米. A .175 B .200 C .225 D .25010.如图,在一个正十二边形内,做三个小正方形以及六个等边三角形,如果阴影部分面积的面积是2019,那么正十二边形的面积是( ). A .2019 B .3033 C .4038 D .5045F第14讲比例解行程1.上坡的路程和下坡的路程相等,一辆汽车上坡速度与下坡速度之比是3:5,这辆汽车上坡与下坡用的时间比应是( ) .A.5:8 B.5:3 C.3:5 D.3:82.大海、贝拉练习跑步,两人的速度比是7:6,相同的时间内,贝拉跑了840米,大海跑了( )米.A.640 B.720 C.980 D.10903.甲乙两人的速度比为2:5,两人同时出发,行走的时间比为3:4,则甲、乙走的路程比为( ).A.3:10 B.8:15 C.2:5 D.3:44.从甲地到乙地,若速度提高0.2倍,则时间少用1小时,则原计划用( )小时.A .5B .6C .10D .125.甲、乙两个城市相距若干千米,一列客车与一列货车同时从两个城市相向开出,客车与货车速度比是11:9,相遇时客车比货车多行60千米. 甲、乙两市相距( )千米. A .270B .330C .540D .6006.甲、乙两班学生到离校39千米的博物馆参观,但只有一辆汽车,一次只能乘坐一个班的学生.为了尽快到达博物馆,两个班商定,由甲班先坐车,乙班先步行,同时出发,甲班学生在途中某地下车后步行去博物馆,汽车则从某地立即返回去接在途中步行的乙班学生.如果甲、乙两班学生步行速度相同,汽车速度是他们步行速度的10倍,那么汽车应在距博物馆( )千米处返回接乙班学生,才能使两班同时到达博物馆.A .6B .7C .8D .97.星期天早晨,哥哥和弟弟都要到奶奶家去.弟弟先走10分钟,哥哥出发20分钟后追上了弟弟.如果哥哥每分钟多走10米,出发15分钟后就可以追上弟弟.则弟弟每分钟走( )米. A .60B .70C .80D .908.甲、乙两车的速度比是4:7,两车同时从两地出发相向而行,相遇时甲车比乙车少走30千米.两地相距( )千米. A .40B .70C .110D .140A B C D9.两列火车同时从两个城市相向开出,相遇时甲车比乙车多行40千米,甲乙两车的速度比为5:3.则两城之间的距离是()千米.A.60 B.100 C.120 D.16010.A、B两个连队同时分别从营地出发前往目的地进行演习,A连有卡车可以装载正好一个连的人员,为了让两个连队的士兵同时尽快到达目的地,A连士兵坐车出发一定时间后下车让卡车回去接B连的士兵,两营的士兵恰好同时到达目的地,已知营地与目的地之间的距离为32千米,士兵行军速度为8千米/小时,卡车行驶速度为40千米/小时,则两营士兵到达目的地一共要( ). A.0.8小时B.1.2小时C.1.6小时D.2小时第15讲经济问题1.某商品成本是300元,售出后获得利润30元,则该商品的利润率是()%.A.5 B.9 C.10 D.152.商场中某件新款衣服的成本是500元,商家期望获得20%的利润率,则商家需要将该新款衣服的定价定为()元.A.400 B.500 C.550 D.6003.某商品售价是800元,赔了20%,售出这件商品,该商店赔了()元.A.80 B.120 C.160 D.2004.商场以1000元定价某手提包,因价格太高无人购买,决定按定价的80%出售,则该手提包的售价是()元.A.80 B.800 C.1000 D.12005.商场中某一种商品成本是100元,原计划按50%的利润率定价,后来考虑到定价太高,结果按定价的八折出售,则该商品的售价是()元.A.80 B.100 C.120 D.1506.一种商品,甲店的进货价比乙店的进货价便宜10%,甲店按20%的利润率来定价,乙店按15%的利润率来定价,甲店的定价比乙店的定价便宜11.2元,则乙店的进货价是()元.A.40 B.80 C.120 D.1607.甲乙两种商品的单价和为100元,因季节变化,甲商品降价10%,乙商品提价5%,调价后,甲乙两种商品的单价之和比原单价之和提高了2%,甲乙两种商品现在的单价分别为().A.甲20元,乙80元 B.甲80元,乙20元C.甲18元,乙84元 D.甲84元,乙18元8.一种成本为1600元的商品,定价2000元,则这种商品的利润率为()% .A.25 B.50 C.75 D.1009.一种商品的定价是1200元,后来打八折促销,则促销价是()元.A.800 B.880 C.960 D.100010.语文辅导书的利润率是20%,数学辅导书的利润率是30%,校长花了3000元购进这两种辅导书,之后卖出获利780元,则其中语文辅导书的总进价是()元.A.1200 B.1500 C.1800 D.2200第16讲圆柱与圆锥初步1.一个圆柱体的底面直径是4分米,高是5分米,它的侧面积是()平方分米,表面积是()平方分米.(π取3.14)A.31.4,87.92 B.31.4,163.28 C.62.8,87.92 D.62.8,163.282.一个圆柱体的底面直径是4分米,高是5分米,它的体积是()立方分米.(π取3.14)A .62.8B .125.6C .188.4D .251.23.有一个圆柱体零件,高10厘米,底面直径是8厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见下图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂( )平方厘米.(结果保留π)A .132πB .164πC .196πD .228π4.一个圆柱的高增加3分米,侧面积就增加56.52平方分米,它的体积增加( )立方分米.(π取3.14)A .56.52B .65.94C .75.36D .84.785.下面圆锥的体积为( )立方厘米.(单位:cm )(π取3.14)1215154A.21.98 B.251.2 C.282.6 D.3146.在一个高10厘米,底面半径为3厘米的圆柱的上下底面个挖去一个尽可能大的圆锥,那么挖去的体积是()立方厘米. (π取3.14)A.31.4 B.64.8 C.94.2 D.125.67.如图,有一个圆柱和一个圆锥,它们的高和底面直径标在图上(单位:厘米).则圆柱的体积是圆锥体积的()倍.A.8 B.16 C.24 D.328.一个圆柱的底面半径是4厘米,高是10厘米,它的体积是()立方厘米.(π取3)A.120 B.240 C.480 D.9609.有一个圆柱,如果高增加1厘米,则表面积增加6.28平方厘米.如果该圆柱高10厘米,则其体积是( )立方厘米.(π取3.14)A .31.4B .62.8C .94.2D .125.610.一个圆锥的底面半径为2厘米,高为6厘米,那么它的底面积是( )平方厘米,体积是( )立方厘米. (π取3.14)A .6.28,25.12B .12.56,25.12C .6.28,75.36D .12.56,75.361.德国人使用二十进制,那么“”写成二十进制的数是( ).A .(123)20B .(132)20C .(231)20D .(321)202.二十进制中的“”在十进制中代表( )个. A .231 B .261 C .461 D .8613.如果人类的祖先每只手有七个手指头,计数方式同例题1,那么十进制的45个在这里应该表示为( ).A .B .C .第17讲 进位制D .4.把下列各数转化为十进制数:(463)8=( );A .299B .303C .307D .3115.把下列各数转化为十进制数:(245)7=( ).A .131B .133C .135D .1376.把十进制的65转化成五进制数,结果为( );A .225B .230C .235D .2407.把十进制的65转化成八进制数,结果为( ).A .101B .103C .105D .1078.计算:(101101)2+(10111)2=( )2;A .(1000000)2B .(1000100)2C .(1001000)2D .(1010000)29.计算:(101101)2−(10111)2=()2.A.(10100)2 B.(10011)2 C.(10101)2 D.(10110)210.计算:(101)2×(1011)2=()2A.(101010)2 B.(110111)2C.(111011)2D.(111101)21.计算:11×3+13×5+15×7+⋯+199×101=.2.计算:21×3+23×5+⋯+251×53=.第18讲学期大总结3.甲容器中有6%的盐水200克,乙容器中有10%的盐水80克.往甲、乙两容器中分别倒入等量的水,使两个容器中的浓度一样.每个容器应倒入水克.4.在A×B=C中,当A一定时,B和C成比例;当C一定时,A和B成比例.5.小明在2点多钟时开始做奥数题.当他做完时已经3点多钟,此时的时针和分针与开始做题时正好交换了位置,小明做题用了分钟.6.如图,长方形ACDF中,AC=3BC,FD=3FE,阴影部分的面积为30,△AFG的面积为.7. 下图中三角形ABC面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积.8.有A,B两个容器,如图,先把A容器装满水,然后将水倒入B容器,B容器中水的深度是多少厘米?( π取3.14)9.一列专为武汉疫区提供防护物资的货车和另一列载着医护人员的客车同时从相距1200千米的两地相对开出,经过3小时两车相遇,客车与货车的速度比是3:2,货车的速度是每小时多少千米?10. 商店按批发价购进一批皮球,成本价每个0.15元,零售价每个0.25元,当卖到只剩20个皮球时,卖得的钱除去全部成本已获利10元,这批皮球共多少个?计算:(10101)2÷(11)2=()2.A.(101)2 B.(110)2C.(111)2D.(1000)2【答案】C.【分析】(10101)2÷(11)2=(111)2.计算:(101)2×(1011)2=()2A.(101010)2 B.(110111)2C.(111011)2D.(111101)2【答案】B.【分析】(101)2×(1011)2=(110111)2.。
学会利用数学思维解决数论问题

学会利用数学思维解决数论问题数论是数学的一个重要分支,它研究整数的性质和规律。
在解决数论问题时,数学思维起着至关重要的作用。
本文将介绍一些利用数学思维解决数论问题的方法和技巧。
一、质数的判断与性质在数论中,质数是一个重要的概念。
我们知道,质数是只能被1和自身整除的自然数。
要判断一个数是否为质数,可以利用数学思维中的试除法。
即将待判断的数依次除以从2开始的自然数,并观察余数是否为0,若余数为0,则不是质数;若余数都不为0,最后确定为质数。
质数的性质也是数论中的重要内容。
其中一个著名的结论是:任意大于1的自然数,都可以唯一地分解成质数的乘积。
这个性质也被称为质因数分解定理。
利用数学的归纳思维,可以证明这个定理。
二、最大公约数和最小公倍数最大公约数和最小公倍数也是数论中常见的问题。
假设有两个数a 和b,求它们的最大公约数(GCD)和最小公倍数(LCM)。
数学思维告诉我们,可以利用辗转相除法来解决这个问题。
辗转相除法的基本思路是,用较大的数除以较小的数,再用除数除以余数,一直循环直到余数为0。
此时,除数即为最大公约数。
而最小公倍数则可以通过最大公约数和两数之积的关系得到。
三、同余模运算同余模运算是数论中的重要概念,在解决数论问题时经常会用到。
对于整数a、b和正整数n,如果其差a-b可以被n整除,则称a与b关于模n同余,记作a≡b (mod n)。
同余模运算具有以下性质:(1) 若a≡b (mod n),则a+c≡b+c (mod n);(2) 若a≡b (mod n),则ac≡bc (mod n)。
利用这些性质,可以简化数论问题的求解过程。
四、费马小定理和欧拉定理费马小定理是数论中的重要定理,它给出了用于计算模质数下的指数的快速方法。
费马小定理的表述为:若p为质数,a为不被p整除的整数,则a^(p-1) ≡ 1 (mod p)。
这个定理在密码学领域有广泛应用。
欧拉定理是费马小定理的推广。
它给出了更一般情况下计算模整数的指数的方法。
小学数学六年级上册思维拓展精选练习题

小学数学六年级上册思维拓展精选练习题填空题部分1、一根绳长12 米,剪去它的 23 后,比原来短了( )米。
2、一个正方形的周长是54米,它的边长是( )米,边长与周长的比值是( )。
3、甲、乙两桶油共重15千克,从甲桶里取出 15 ,从乙桶也取出 15,共取出( )千克。
4、已知A × 23 =B × 67 =×C =D ÷56 ,其中A 、B 、C 、D 是非0自然数,把四个字母从大到小排列是:( )﹥( )﹥( )﹥( )。
5、一个减法算式中,减数是差的 27,被减数与差的比是( )。
6、从学校走到电影院,甲用8分钟,乙用10分钟,甲和乙的速度比是( )。
A .8:10B .10:8C .4:5D .5:47、甲仓存粮18吨,从甲仓运3吨放入乙仓,两仓存粮同样多,原来甲仓比乙仓多( )。
A .3吨B .12C . 13D .238、如果一个正方形周长和一个圆周长相等,那么这个正方形和圆的面积比是( )∶( )。
9、工程队3天完成了一项工程的81,完成全项工程的一半需( )天。
10、判断:一个非0自然数,把它增加101以后再减少101,这个数大小没变。
………( ) 11、把920米平均分成3份,每份是( )米,每份占9米的( )。
12、一桶油,第一次用去14 ,正好是5升,第二次用去这桶油的12 ,第二次用去( )升。
13、栽一批苹果树,成活率是95%,为了保证成活380棵,至少要栽( )棵苹果树。
14、把一根长96厘米的铁丝焊成一个高是4厘米,底面的长与宽的比是3:2的长方体框架,这个框架的长是( )厘米,宽是( )厘米。
15、判断:黄师傅加工了101个零件,全部合格,合格率为101%。
…( ) 16、选择:爸爸今年a 岁,比小明大b 岁,再过5年,爸爸和小明相差( )A .a B. b C. a-b D. b+517、在200克盐水中,盐与水的比为1:24,又放入4克盐后,盐与水的比为( ):( ) 18、选择:甲数的54是24,乙数的43是24,甲数与乙数的比较( )。
数与形-数学思维拓展2023六年级上册含答案
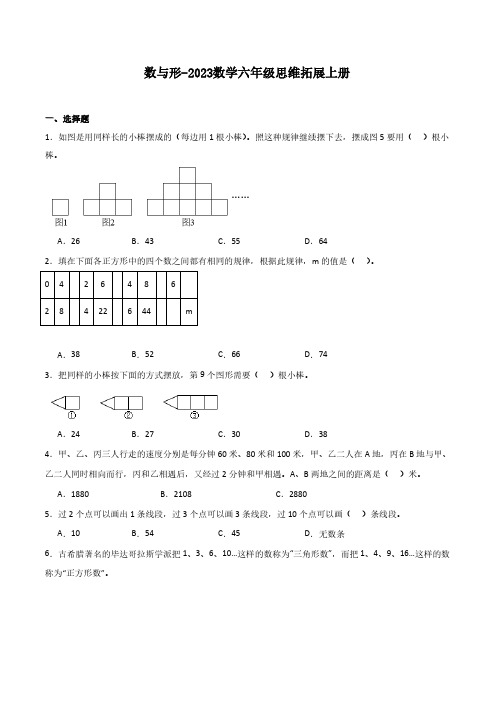
数与形-2023数学六年级思维拓展上册一、选择题1.如图是用同样长的小棒摆成的(每边用1根小棒)。
照这种规律继续摆下去,摆成图5要用()根小棒。
A.26 B.43 C.55 D.642.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是()。
0 4 2 6 4 8 62 8 4 22 6 44 mA.38 B.52 C.66 D.74A.24 B.27 C.30 D.384.甲、乙、丙三人行走的速度分别是每分钟60米、80米和100米,甲、乙二人在A地,丙在B地与甲、乙二人同时相向而行,丙和乙相遇后,又经过2分钟和甲相遇。
A、B两地之间的距离是()米。
A.1880 B.2108 C.28805.过2个点可以画出1条线段,过3个点可以画3条线段,过10个点可以画()条线段。
A.10 B.54 C.45 D.无数条6.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”。
从上图中可以发现: 任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和,例如4=1+3。
把“正方形数”36写成两个相邻的“三角形数”之和,正确的是( )。
A .36=10+26B .36=12+24C .36=15+21D .36=16+20二、填空题7.如下图:从图( )可知2222a b a ab b +=++()成立(填序号)。
在图③中,a 是15cm ,b 是10cm , 8.1111124864−−−−−= ( )。
9.用同样大小的黑色五角星按如图的方式摆图案,按照这样的规律摆下去,摆第黑色五角星,摆第10个图案需要( )个黑色五角星。
10.用小棒按照如下图方式摆图形,摆第五个图形需要( )根小棒,根小棒。
……三、解答题16.如果数字1、2、3、4、5、6分别用下图表示:那么左下图表示的数字是(),在右下图中画出表示62的图。
2023-2024学年六年级数学小升初思维拓展培优讲义(通用版)(尖子生培优讲义)复杂和差倍问题(知

复杂和差倍问题(一)和倍问题:已知两个数的和及两个数的倍数关系,求这两个数各是多少的应用题叫做和倍问题和倍问题的关键就是求出1倍数:和÷(倍数+1)=1倍数1倍數×倍数=几倍数(二)差倍问题:已知两个数的差及两个数的倍数关系,求这两个数各是多少的应用题叫做差倍问题解决差倍问题的关键就是求出1倍数和“差”是多少:差÷(倍数-1)=1倍数1倍數×倍数=几倍数(三)和差问题:已有两个数的和及两个数的差,求这两个数各是多少的应用题叫做和差问题和差公式:(和-差)÷2=小数(和+差)÷2=大数解答和差问题的关键在于若干个不相等的数的问题化为相等的数的问题。
1.某车间男工人数是女工人数的2倍,若调走21个男工,那么女工人数是男工人数的略不计).问剩余部分的铝管至少是多少厘米?4.一盒咖啡中有若干袋,一包方糖中有若干块.小唐喝前两盒咖啡时每袋咖啡都放3块方糖,结果共用了1包方糖和第2包中的24块;小唐喝后三盒咖啡时每袋咖啡都只放1块方糖,最后第3包方糖还剩下36块,那么每盒咖啡有多少袋?5.甲现在的年龄是乙过去某一时刻年龄的2倍,那时甲正好是乙现在这样大,当乙到了甲现在的年龄时,甲与乙年龄之和为63,那么现在甲、乙年龄分别是多少岁?6.有若干盒卡片分给一些小朋友,如果只分一盒,每人至少可以得到7张;如果每人分8张卡片,则还缺少5张.现在把所有卡片都分完,每人分到60张,而且还多出4张.问:共有多少个小朋友?7.小白兔和小灰兔各有若干只.如果5只小白兔和3只小灰兔放到一个笼子中,小白恰好放完,小灰兔还多12只.那么小白兔和小灰兔共有多少只?8.抽干一口井,在无渗水的情况下,用甲抽水机要20分钟,用乙抽水机要30分钟.现因井底渗水,且每分钟渗水量相等,用两台抽水机合抽18分钟正好抽干.如果单独用甲抽水机抽水,多少分钟把水抽干?9.一个人用140元买了一件外衣、一顶帽子和一双鞋.外衣比帽子贵90元,外衣和帽子共比鞋贵120元.一双鞋多少元?10.1年前父母的年龄和是兄弟二人年龄和的7倍;4年后,父母的年龄和是兄弟二人年龄和的4倍.已知爸爸比妈妈大2岁,妈妈今年几岁?11.幼儿园有三个班,甲班比乙班多4人,乙班比丙班多4人,老师给小孩分枣,甲班每个小孩比乙班每个小孩少分3个枣,乙班每个小孩比丙班每个小孩少分5个枣,结果16.一家三口人,父亲与儿子年龄加起来是51岁,母亲与儿子年龄加起来是47岁,父亲、母亲、儿子三人年龄加起来是87岁,问:父亲、母亲、儿子的年龄各是多少?17.某小学有学生975人.全校男生人数是六年级学生人数的4倍少23人,全校女生人数是六年级学生人数的3倍多11人.问全校有男、女生各多少人?18.父子年龄之和是45岁,再过5年,父亲的年龄正好是儿子的4倍,父子今年各多少岁?19.一堆围棋子,黑子的个数是白子的3倍,每次拿5枚黑子,2枚白子,拿了若干次后,白子拿完,还剩11枚黑子.这堆棋子中,共有白子多少?20.三个小组共有180人,一、二两个小组人数之和比第三小组多20人,第一小组比第二小组少2人,求第一小组的人数.26.甲、乙、丙三人,平均体重63千克,甲与乙的平均体重比丙的体重多3千克,甲比丙重2千克,求乙的体重.27.今年彬彬的年龄是表弟年龄的4倍,20年后,彬彬的年龄比表弟的年龄的2倍少l2岁,今年彬彬、表弟各多少岁?28.一群蚂蚁搬家,蚁洞内原来存放着一些食物,第一次运出的比原来的一半少80克,第二次运出的比剩下的一半多50克,第三次运出的比再剩下的一半多20克,这时蚁洞内还剩250克食物,蚁洞内原来有多少克食物?29.一次口算比赛共20道题,做对一道题得5分,做错一道题倒扣5分,不做不得分也不扣分.东东在比赛中每道题都做了,最后考了60分.你知道东东做对了几道题吗?30.甲仓所存面粉是乙仓的3倍,从甲仓运走8500千克,从乙仓运走500千克后,两仓所40.有两堆棋子,第一堆有87个,第二堆有69个.那么从第一堆拿多少个棋子到第二堆,就能使第二堆棋子数是第一堆的3倍.参考答案:设甲所带的钱数为5份,则甲和乙都还剩份,所以每份是(元),则甲原来带了(元),乙原来带了(元).84,6074÷,说明卡片的盒数是即如果我们在每盒中加58盒共加40张,即每人需要退出4张,其中要有是我们一开始借来的要还出去,即要退出只小白兔和3只小灰兔装一个笼子,小白兔恰好装完,小灰兔还多【详解】,所以每分钟的渗水量是,甲抽水单独抽完水45分钟.【详解】将父母看成一个人,年龄每年增加2岁,兄弟看成一个人每年增加2岁,设父母1+=年,兄弟年龄年前年龄和是7份,那么1年前兄弟二人的年龄就是1份,后来过了145-÷-=,是1份加10,4倍就是4份加40,父母年龄是7份加10,所以1份就是(4010)(73)10所以1年前父母和是70,妈妈年龄,妈妈今年35岁.我们可以得到方程:x+1+3=.【详解】17.男生541人 女生434人【详解】解:设六年级学生人数是“1份”,那么男生是4份-23人,女生是3份+11人,全校是7份-(23-11)人.每份是(975+12)÷7=141(人) 男生人数:141×4-23=541(人) 女生人数:975-541=434(人) 答:有男生541人、女生434人. 18.父亲39岁,儿子6岁【详解】再过5年,父子俩一共长了10岁,那时他们的年龄之和是4510=55+(岁),由于父亲的年龄是儿子的4倍,因而55岁相当于儿子年龄的41=5+倍,可以先求出儿子5年后的年龄,再求出他们父子今年的年龄.5年后的年龄和为:455255+⨯=(岁) 5年后儿子的年龄:554111÷+=()(岁)儿子今年的年龄:1156-=(岁),父亲今年的年龄:45639-=(岁) 19.22【详解】由于原来黑子的个数是白子的3倍,假如拿的时候每次拿6枚黑子和2枚白子,则当白子拿完的时候黑子也恰好拿完,而现在每次拿5枚黑子,比每次拿6枚少拿1枚,最后还剩下11枚黑子,所以共拿了11次,这堆棋子中共有白子21122⨯=枚. 20.49人【详解】先将一、二小组视为整体,记为A 组,则A 组与第三组的人数之和为180人,A 组比第三组多20人,则A 组有(180+20)÷2=100人,第三组有(180-20)÷2=80人. 而A 组为第一、二两个小组人数之和为100人,第一小组比第二小组少2人. 那么第一小组有(100-2)÷2=49人. 21.6天【详解】若干天后,乙油库存油:(112-80)÷(2-1)=32(吨) 天数:(80-32)÷8 =48÷8 =6(天)答:6天后甲油库剩下的油是乙油库剩下油的2倍. 22.甲9岁,乙3岁30.12000 4000【详解】由上图可以看出如果乙仓不运出粮食,甲仓运出8500-500=8000(公斤)粮食,正好相当于乙仓的2倍,可以通过这种对应关系求出乙仓存面粉的公斤数,再求甲仓存面粉的公斤数.8500-500=8000(公斤)8000÷2=4000(公斤)4000×3=12000(公斤)答:甲仓原有面粉12000公斤,乙仓原有面粉4000公斤.31.70吨175吨【详解】大米:(60+45+35)÷(3-1)=70(吨)面粉:70+60+45=175(吨)答:原来有大米70吨,面粉175吨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学思维能力拓展专题突破系列(一)数论专题(中)------奇偶问题(一)熟练解翻硬币问题与求和问题1.翻硬币问题如何解?2.求和问题如何解?3.写出规范简洁的解答过程例题1:有三枚五分硬币,国徽面朝上放桌上,规定每次必定翻两枚,若干次之后,能否全部变为国徽面朝下?例题2:桌上放有77枚正面朝下的硬币,第1次翻动77枚,第2次翻动其中的76枚,第3次翻动其中的75枚……第77次翻动其中的1枚。
按这样的方法翻动硬币,能否使桌上所有的77枚硬币都正面朝上?说明你的理由。
例题3:小华买了一本共有96张练习纸的练习本,并依次将它的各面编号(1~192)。
小丽从该练习本中撕下其中25张纸,并将写在它们上面的50个编号相加。
试问,小丽所加得的和数能否为2000?例题4:有98个孩子,每人胸前有一个号码,号码从1到98各不相同。
试问:能否将这些孩子排成若干排,使每排中都有一个孩子的号码数等于同排中其余孩子号码数的和?并说明理由。
(即是课程的课后测试)1、从三个1、三个3、三个5、三个7、三个9这15个数字中能否选出5个数,使它们的和等于30?为什么?2、任意取出1234个连续自然数,它们的总和是奇数还是偶数?3、一串数排成一行,它们的规律是:前两个数都是1,从第三个数开始,每一个数都是前两个数的和。
如下所示:1,1,2,3,5,8,13,21,34,55,…试问:这串数的前100个数(包括第100个数)中,有多少个偶数?4、能不能将1010写成10个连续自然数之和?如果能,把它写出来;如果不能,说明理由。
5、能否将1至25这25个自然数分成若干组,使得每一组中的最大数都等于组内其余各数的和?1、解:不能。
因为这15个数都是奇数,从中选出5个数,5个奇数的和还是奇数,不可能为30。
2、解:奇数。
从最小开始两个分一组,可以分成1234÷2=617组,每一组里都是相邻两个数,相邻两个数的和是奇数,617个奇数的和还是奇数。
3、解:我们找这列数的奇偶性规律。
依次为:奇、奇、偶、奇、奇、偶、奇、奇、偶、……。
每三个一循环,每个循环里有一个偶数,所以前100个里有33个偶数。
4、解:不能。
因为任意10个连续自然数,从最小开始每两个分一组,正好分成5组,每组里都是相邻两个数。
而相邻两个数的和是奇数,所以任意10个连续自然数的和等于5个奇数的和,还是奇数。
1010是偶数,所以不可能写成10个连续自然数之和。
5、解:不能。
因为如果可以,则每一组所有数的和是最大数的2倍,这一组总和是个偶数,若干个偶数的和还是偶数。
而1+2+3+……+25=325是一个奇数,矛盾。
所以不可能。
六年级数学思维能力拓展专题突破系列(一)数论专题(中)------奇偶问题(二)熟练解奇偶问题及其相关问题1.什么是奇偶问题?2.奇偶问题如何与其他知识点相结合?3.熟悉知识点并能熟练解题例题1:设标有A,B,C,D,E,F,G的7盏灯顺次排成一行,每盏灯安装一个开关。
现在A,C,D,G这4盏灯亮着,其余3盏灯没亮。
小华从灯A开始顺次拉动开关,即从A到G,再从A开始顺次拉动开关,他这样拉动了2011次开关后,哪些灯亮着?例题2:在黑板上写上1,2,…,2011,只要黑板上还有两个或两个以上的数就擦去其中的任意两个数a,b,并写上a-b(其中a≥b)。
问:最后黑板上剩下的是奇数还是偶数?例题3:俱乐部里只有两种人:一是老实人,永远说真话;一是骗子,永远说假话。
某天俱乐部全体成员围成一圈,每个老实人两旁都是骗子,每个骗子两旁都是老实人。
外来一人问俱乐部的张三:“俱乐部共有多少人?”张三答:“45人。
”另一个成员李四说:“张三是老实人。
”李四是老实人还是骗子?例题4:现有足够多的苹果、梨、桔子三种水果,最少要分成多少堆(每堆都有苹果、梨和桔子三种水果),才能保证找得到这样的两堆,把这两堆合并后这三种水果的个数都是偶数?(即是课程的课后测试)1、有20个1升的容器,分别盛有1,2,3,…,20立方厘米水。
允许由容器A向容器B倒进与B容器内相同的水(在A中的水不少于B中水的条件下)。
问:在若干次倒水以后能否使其中11个容器中各有11立方厘米的水?2、围棋盘上有19×19个交叉点,现在放满了黑子与白子,且黑子与白子相间地放,并使黑子(或白子)的上、下、左、右的交叉点上放着白子(或黑子)。
问:能否把黑子全移到原来的白子的位置上,而白子也全移到原来黑子的位置上?3、某市五年级99名同学参加数学竞赛,竞赛题共30道,评分标准是基础分15分,答对一道加5分,不答记1分,答错一道倒扣1分。
问:所有参赛同学得分总和是奇数还是偶数?4、任意交换某个三位数的数字顺序得到一个新的三位数,原三位数与新三位数之和能否等于999?5、有30枚2分硬币和8枚5分硬币,5角以内共有49种不同的币值,哪几种币值不能由上面38枚硬币组成?1、解:不可能。
首先,A倒给B后B中水必定是偶数立方厘米,所以B不可能是11立方厘米。
另外,有11立方厘米水的容器只能由原来装着大于或者等于11立方厘米水的容器倒掉多余部分得来,比如A是12立方厘米水的容器而B是1立方厘米水的容器,A倒1立方厘米水给B得到。
但是大于或者等于11立方厘米的只有10个,所以不可能有11个容器中各有11立方厘米。
2、解:不能。
因为19×19=361,所以要么黑子比白子多一个,要么白子比黑子多一个,不可能把黑子全移到原来的白子的位置上,同时白子也全移到原来黑子的位置上。
3、解:奇数。
30题全答对得15+5×30=165分是奇数,答错一道就总分减去6分,不答一道就总分减去4分,无论怎样,总分必定是奇数。
99个奇数的和还是奇数。
4、解:不能。
两数和为999,各位数相加时必定没有向上进位,又因为新三位数与原三位数只是三个数字的排列顺序不同,所以把两个三位数的个位、十位、百位数字加在一起一定是偶数,而9+9+9=27是奇数,矛盾。
5、解:当币值为偶数时,可以用若干枚2分硬币组成;当币值为奇数时,除1分和3分这两种币值外,其余的都可以用1枚5分和若干枚2分硬币组成,所以5角以下的不同币值,只有1分和3分这两种币值不能由题目给出的硬币组成。
六年级数学思维能力拓展专题突破系列(一)数论专题(中)------完全平方数掌握完全平方数性质并能熟练解题1.完全平方数分解质因数有什么特点?2.完全平方数约数个数有什么特点?3.熟练应用性质解题例题1:一个三位数是个完全平方数,它的前两位数也是完全平方数,个位也是完全平方数,符合条件的全部三位数的和是多少?例题2:一个非零自然数与2940的积是完全平方数,那么这个数最小是多少?例题3:在1到2007之间的自然数中,恰有奇数个约数的数的总和是多少?例题4:一个自然数减去45及加上44都仍是完全平方数,求此数。
例题5:有一个自然数,它与168的和恰好等于某个数的平方;它与100的和恰好等于另一个数的平方,这个数是多少?(即是课程的课后测试)1、自然数N是一个两位数,它是一个完全平方数,且N的个位数字与十位数字都是完全平方数,这样的自然数有多少个?2、一个两位数与它的反序数(个位数字与十位数字交换)的和是一个完全平方数,求这样的两位数。
3、求一个能被180整除的最小完全平方数。
4、一个非零自然数与46305的积是完全平方数,那么这个数最小是多少?5、一个自然数如果加上60,则为一个完全平方数,如果加上43,则为另一个完全平方数,求这个自然数。
1. 解:(法一)设自然数N为十位和个位分别为a和b,则a只能在1、4、9中选,b 只能在0、1、4、9中选。
组成的两位数中,是完全平方数的只有一个49。
(法二)两位数的完全平方数有16、25、36、49、64、81,其中,只有49符合题意。
2. 解:设这个两位数的十位和个位数字分别为a和b,则10a+b+10b+a=11a+11b=11(a+b)是一个完全平方数,必有a+b等于11、44、99、……;又a+b最多只有9+9=18,所以只能有a+b=11。
这样的两位数有92、83、74、65、56、47、38、29。
3. 解:由,这个完全平方数是180的倍数,分解质因数的次数必定为偶数次,所以至少为180的5倍,即这个最小完全平方数为180×5=900。
4. 解:设此数为a,由,要使乘积是完全平方数,则乘积的分解质因数形式中每个因数必须为偶数次,这样,a分解质因数后必须至少有一个3、一个5、一个7,所以a最小为3×5×7=105。
5. 解:设这个自然数为a,加上60后得到A的平方,加上43后得到B的平方,则有,两式相减得。
又因为17是质数,所以必定有A+B=17,A-B=1,得A=9,B=8,代入得a=21,所以这个数为21。
六年级数学思维能力拓展专题突破系列(一)数论专题(中)------位值原理熟悉位值原理并熟练解题1.位值原理是什么?2.一般位值原理如何出题?如何分情况解决?3.位值原理证明题一般解题步骤是什么?例题1:一个两位数,各位数字的和的5倍比原数大4,求这个两位数。
例题2:某三位数是其各位数字之和的23倍,求这个三位数。
例题3:有一个两位数,如果把数码1加写在它的前面,那么可得到一个三位数,如果把1加写在它的后面,那么也可以得到一个三位数,而且这两个三位数相差414,求原来的两位数。
例题4:从1~9九个数字中取出三个,用这三个数可组成六个不同的三位数。
若这六个三位数之和是3774,则这六个三位数中最小的可能是几?最大的可能是几?例题5:证明:一个三位数减去它的各个数位的数字之和后,必能被9整除。
(即是课程的课后测试)1、求一个三位数,它等于抹去它的首位数字之后剩下的两位数的4倍与25之差。
2、有一个三位数,把它的个位数移到百位上,百位和十位上的数码相应后移一位成了一个新的三位数,原三位数的2倍恰好比新三位数大1,求原来的三位数。
3、将一个四位数的数字顺序颠倒过来,得到一个新的四位数(这个数也叫原数的反序数),新数比原数大8802。
求原来的四位数。
4、用1,9,8三张数字卡片可以组成若干个不同的三位数,所有这些三位数的平均值是多少?5、证明:一个三位数与它的反序数(数字顺序颠倒)的差,必能被99整除。
1.解:设这个三位数为,依题意得,即,得,因为。
当a=1时,非整数解;当a=2时,b=7,c=5。
综上知,这个三位数为275。
2.解:设这个三位数为,依题意得,即,得190a+19b=98c+1,左边是19的倍数,所以右边也是19的倍数,得c=6,代入得a=3,b=1,所以原来三位数是316。
3.解:设原来四位数为,依题意得,得999d+90c=90b+999a+8802,即111d+10c=10b+111a+978,因为111d+10c最多为999+90=1089,a最少为1,所以a=1,此时111a+978=1089,所以b只能等于0。
