二叉树练习A
二叉树练习题及答案

二叉树练习题及答案一、选择题1.关于二叉树的下列说法正确的是(B )A.二叉树的度为2 B.二叉树的度可以小于2C.每一个结点的度都为2 D .至少有一个结点的度为2 2.在树中,若结点A有4个兄弟,而且B是A的双亲,则B的度为(C )A.3 B.4C.5 D .63.若一棵完全二叉树中某结点无左孩子,则该结点一定是(D )A.度为1的结点B.度为2的结点C.分支结点 D .叶子结点4.深度为k的完全二叉树至多有(C )个结点,至少有( B )个结点。
A.2k-1-1 B.2k-1C.2k-1 D .2k5.在具有200个结点的完全二叉树中,设根结点的层次编号为1,则层次编号为60的结点,其左孩子结点的层次编号为(C 2i ),右孩子结点的层次编号为( D 2i+1),双亲结点的层次编号为(60/2=30 A )。
A.30 B.60C.120 D .1216.一棵具有124个叶子结点的完全二叉树,最多有(B )个结点。
A.247 B.248C.249 D .250二、填空题1.树中任意结点允许有零个或多个孩子结点,除根结点外,其余结点有且仅有一个双亲结点。
2.若一棵树的广义表表示法为A(B(E,F),C(G(H,I,J,K),L),D(M (N))),则该树的度为 4 ,树的深度为 4 ,树中叶子结点的个数为8 。
3.若树T中度为1、2、3、4的结点个数分别为4、3、2、2,则T中叶子结点的个数为14 。
n=n0+n1+n2+n3+n4=n0+4+3+2+2=n0+11n=1+孩子=1+4+6+6+8+25n0+11=25n0=144.一棵具有n个结点的二叉树,若它有m个叶子结点,则该二叉树中度为1的结点个数是n-2m+1 。
5.深度为k(k>0)的二叉树至多有2k -1 个结点,第i层上至多有2i-1个结点。
6.已知二叉树有52个叶子结点,度为1的结点个数为30,则总结点个数为133 。
二叉树例题

二叉树例题摘要:一、二叉树的基本概念1.二叉树的定义2.二叉树的特点3.二叉树的重要性质二、二叉树的重要操作1.插入节点2.删除节点3.遍历二叉树3.1 前序遍历3.2 中序遍历3.3 后序遍历三、二叉树的应用场景1.数据结构2.算法设计3.文件系统正文:一、二叉树的基本概念1.二叉树定义:二叉树是一种特殊的树形数据结构,其中每个节点最多有两个子节点,通常分别称为左子节点和右子节点。
由于每个节点最多有两个子节点,因此二叉树具有很好的分支特性,可以实现高效的数据查找、插入和删除操作。
2.二叉树特点:二叉树具有以下特点:a.每个节点最多有两个子节点,分别称为左子节点和右子节点。
b.所有节点的左子节点和右子节点分别有序排列。
c.所有叶子节点(即没有子节点的节点)都位于同一层。
3.二叉树的重要性质:二叉树具有以下两个重要性质:a.完全二叉树:若设二叉树的深度为h,除第h层外,其它各层的节点数都达到最大值,且第h层所有节点都连续集中在最左边,则称该二叉树为完全二叉树。
b.满二叉树:若设二叉树的深度为h,且除第h层外,其它各层的节点数都达到最大值,则称该二叉树为满二叉树。
满二叉树的每个节点都有两个子节点。
二、二叉树的重要操作1.插入节点:在二叉树中插入一个新节点,可以分为以下几种情况:a.插入叶子节点:直接将新节点作为叶子节点插入到指定位置。
b.插入非叶子节点:将新节点插入到合适的位置,使树的结构保持平衡。
2.删除节点:在二叉树中删除一个节点,可以分为以下几种情况:a.删除叶子节点:直接删除叶子节点。
b.删除非叶子节点:找到待删除节点的替代节点,将其替代节点与待删除节点断开连接,然后删除替代节点。
3.遍历二叉树:遍历二叉树是访问二叉树中所有节点的过程,通常有前序遍历、中序遍历和后序遍历三种方式。
3.1 前序遍历:先访问根节点,然后遍历左子树,最后遍历右子树。
3.2 中序遍历:先遍历左子树,然后访问根节点,最后遍历右子树。
二叉树的习题

几个关于二叉树的算法知一个完全二叉树的深度为4第最低层的有5个叶子结点问有多少个叶子结点?1*任何一棵完全二叉树都满足总结点由一个满二叉树+底层结点数2*一棵完全二叉树都满足总结点数n/2=叶子结点n03*由一个工式得(2^n-1-2^n-n1+1)‘n为第几层,n1表示为总结点数’‘如果知道总结点数可以算底层的叶子结点数’如果是算第倒数第二层可以就直接用(2^n-1+1)’就可以直接得到该层的结点数。
设总结点为n低层叶子结点为n4,第三层的叶子结点为n3 由3*可以得到倒数第二层的结点数,再加上书已知的叶子结点就可以得到总结点。
再用2*就能算出所有的叶子结点。
图p125页已知中序和后序求前序后序为a b c d e f g h中序为a c b d h g e f前序根左右中序左根右后序 左右根可得 h 是根结点是h 所以a b c d 是左子树的结点而g e f 是右子树的结点由后序可得d 是左子树的根,a b c 都是左子树上左面的结点根据后充可得a b c 的顺序a 在c 的前面说明工是左子结点,b 在c 的后面是右子结点同时有后充也可以说明这是左子树,右子树可得h 是右子绔的根结点,根据后充g 前面没有结点,e f 是右子树右面的结点,在根据中充可得是e 在f 的前面,用后充也可验证。
*哈夫曼树完全是由n0 和n2构成的没有n1的结点。
*哈夫曼树和完全二叉树不一样在于完全二叉树有度为1的结点。
已知一个高度为7的完全二叉树至少有多少个结点一棵完全二叉树由一棵满二叉树和底层叶子结点构成构cf a b dhg e成已知高度为7可得到第6层以上是一棵满二叉树可得63个结点又说是一棵完全二叉树和至少有可得七层有一个结点所以可得64个结点.。
二叉树算法题

二叉树算法题
题目一:二叉树的深度
给定一个二叉树,找出其最大深度。
示例:
输入:
# 定义二叉树节点
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
# 创建二叉树
root = TreeNode(3)
root.left = TreeNode(9)
root.right = TreeNode(20)
root.right.left = TreeNode(15)
root.right.right = TreeNode(7)
输出:
4
解释:二叉树的深度为4,分别是 [3], [9, 20], [15, 7] 和 []。
提示:递归深度优先搜索 (DFS) 是一个有效的解决方案。
对于每个节点,我们可以递归地计算其左子树和右子树的深度,然后返回最大的深度。
为了避免重复计算,我们可以使用一个队列来存储已访问的节点。
在计算深度的过程中,我们需要跟踪当前的深度。
当我们到达一个节点的深度时,我们就可以从队列中删除它,因为我们不需要再次计算它。
为了避免进入无限循环,我们需要在算法中使用一个变量来记录访问过的节点数量,如果超过了树中的节点数量,我们可以提前返回结果。
数据结构二叉树习题含答案

第6章树与二叉树1.选择题(1)把一棵树转换为二叉树后,这棵二叉树得形态就是().A。
唯一得B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子(2)由3个结点可以构造出多少种不同得二叉树?()A。
2B.3 C。
4D。
5(3)一棵完全二叉树上有1001个结点,其中叶子结点得个数就是()。
A。
250 B.500 C.254 D.501(4)一个具有1025个结点得二叉树得高h为( ).A。
11 B。
10 C.11至1025之间 D。
10至1024之间(5)深度为h得满m叉树得第k层有( )个结点。
(1=〈k=<h)A。
m k-1 B。
mk-1 C.m h-1 D。
m h—1(6)利用二叉链表存储树,则根结点得右指针就是()。
A.指向最左孩子 B.指向最右孩子 C。
空D.非空(7)对二叉树得结点从1开始进行连续编号,要求每个结点得编号大于其左、右孩子得编号,同一结点得左右孩子中,其左孩子得编号小于其右孩子得编号,可采用( )遍历实现编号。
A。
先序B、中序 C、后序D、从根开始按层次遍历(8)若二叉树采用二叉链表存储结构,要交换其所有分支结点左、右子树得位置,利用()遍历方法最合适。
A.前序 B.中序 C。
后序 D。
按层次(9)在下列存储形式中,()不就是树得存储形式?A.双亲表示法 B.孩子链表表示法 C.孩子兄弟表示法D.顺序存储表示法(10)一棵非空得二叉树得先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足( )。
A.所有得结点均无左孩子B.所有得结点均无右孩子C.只有一个叶子结点 D.就是任意一棵二叉树(11)某二叉树得前序序列与后序序列正好相反,则该二叉树一定就是( )得二叉树。
A。
空或只有一个结点 B.任一结点无左子树C.高度等于其结点数 D.任一结点无右子树(12)若X就是二叉中序线索树中一个有左孩子得结点,且X不为根,则X得前驱为( )。
A.X得双亲 B。
二叉树练习题及答案

一、选择题1.关于二叉树的下列说法正确的是(B )A.二叉树的度为2 B.二叉树的度可以小于2C.每一个结点的度都为2 D .至少有一个结点的度为2 2.在树中,若结点A有4个兄弟,而且B是A的双亲,则B的度为(C )A.3 B.4C.5 D .63.若一棵完全二叉树中某结点无左孩子,则该结点一定是(D )A.度为1的结点B.度为2的结点C.分支结点 D .叶子结点4.深度为k的完全二叉树至多有(C )个结点,至少有( B )个结点。
A.2k-1-1 B.2k-1C.2k-1 D .2k5.在具有200个结点的完全二叉树中,设根结点的层次编号为1,则层次编号为60的结点,其左孩子结点的层次编号为( C 2i ),右孩子结点的层次编号为( D 2i+1),双亲结点的层次编号为(60/2=30 A )。
A.30 B.60C.120 D .1216.一棵具有124个叶子结点的完全二叉树,最多有(B )个结点。
A.247 B.248C.249 D .250二、填空题1.树中任意结点允许有零个或多个孩子结点,除根结点外,其余结点有且仅有一个双亲结点。
2.若一棵树的广义表表示法为A(B(E,F),C(G(H,I,J,K),L),D(M (N))),则该树的度为 4 ,树的深度为 4 ,树中叶子结点的个数为8 。
3.若树T中度为1、2、3、4的结点个数分别为4、3、2、2,则T中叶子结点的个数为14 。
n=n0+n1+n2+n3+n4=n0+4+3+2+2=n0+11n=1+孩子=1+4+6+6+8+25n0+11=25n0=144.一棵具有n个结点的二叉树,若它有m个叶子结点,则该二叉树中度为1的结点个数是n-2m+1 。
5.深度为k(k>0)的二叉树至多有2k -1 个结点,第i层上至多有2i-1个结点。
6.已知二叉树有52个叶子结点,度为1的结点个数为30,则总结点个数为133 。
7.已知二叉树中有30个叶子结点,则二叉树的总结点个数至少是30+29+0=59 。
二叉树练习

2、求各树的前序序列和后序序列 、
(a)的前序序列:ABCDEF 后序序列:BDEFCA (b)的前序序列:GHIJK 后序序列:IJKHG (c)的前序序列:LMPQRNO 后序序列:QRPMNOL
(1)已知一棵二叉树的前序序列和中序序列分别为ABDGHCEFI和 (1)已知一棵二叉树的前序序列和中序序列分别为ABDGHCEFI和 已知一棵二叉树的前序序列和中序序列分别为ABDGHCEFI GDHBAECIF,请画出此二叉树。 GDHBAECIF,请画出此若二叉树中各结点的值均不相同,则由二叉树的前序序列和中 序序列,或由其后序序列和中序序列均能唯一地确定一棵二叉树, 序序列,或由其后序序列和中序序列均能唯一地确定一棵二叉树, 但由前序序列和后序序列却不一定能唯一地确定一棵二叉树。 但由前序序列和后序序列却不一定能唯一地确定一棵二叉树。
A \ C / / \ D E F / \ / G H I / B
2)已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG和 2)已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG和 已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG DECBHGFA, DECBHGFA,请画出此二叉树
分别写出图下图)所示各二叉树的前序、中序和后序序列。 分别写出图下图 所示各二叉树的前序、中序和后序序列。 所示各二叉树的前序
(a) (b) (c) (d)
前序序列:12345 前序序列:12345
中序序列:24531 中序序列:13542
后序序列:54321 后序序列:54321
前序序列:12357864 中序序列:17583524 后序序列:78563421 前序序列:124735689 中序序列:742153896 后序序列742589631
树-二叉树习题

一、单项选择1.二叉树是非线性数据结构,所以()A、它不能用顺序存储结构存储B、它不能用链式存储结构存储C、顺序存储结构和链式存储结构都能存储D、顺序存储结构和链式存储结构都不能存储参考答案 C2.把一棵树转换为二叉树后,这棵二叉树的形态是()A、唯一的B、有多种C、有多种,但根结点都没有左孩子D、有多种,但根结点都没有右孩子参考答案 A 3.已知一棵二叉树前序遍历和中序遍历分别为ABDEGCFH和DBGEACHF,则该二叉树的后序遍历为()。
A)GEDHFBCA B)DGEBHFCAC)ABCDEFGH D)ACBFEDHG参考答案 B 4.从二叉搜索树中查找一个元素时,其时间复杂度大致为( )。
A. O(n)B. O(1)C. O(log2n)D. O(n2)参考答案 C 5.将一棵有100个结点的完全二叉树从根这一层开始,每一层从左到右依次对接点编号,根为1,则编号为49的结点的左孩子编号为( ) 。
A.98 B.99 C.50 D.48参考答案 A 6. 高度k的二叉树的最大结点数为( ).A.2k-1 B.2K+1 C.2K-1 D. 2k+1参考答案 A 9.在一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为:()A.15 B.16 C.17 D.47参考答案 B 10.如果T1是由有序数T转换而来的二叉树,那么T中结点的后序遍历序列就是T1结点的()遍序序列A.前序 B.中序 C.后序 D.层次参考答案 B 11.如图所示T2是由森林T1转换而来的二叉树,那么森林T1有()叶结点。
A.4 B.5 C.6 D.7参考答案 C 12.有n个叶子结点的哈弗曼树的结点总数是()A.不确定 B.2n C.2n+1 D.2n-1参考答案 D 二、填空题1.对于一棵具有n个结点的二叉树,一个结点的编号为i(1≤i≤n),若它有左孩子则左孩子结点的编号为________,若它有右孩子,则右孩子结点的编号为________,若它有双亲,则双亲结点的编号为________。
二叉树练习A

二叉树练习A树的概念和存储结构:1、对于一棵具有n个结点的树,其中所有度之和等于( )A. nB. n-1C. n-2D.n+12、一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数是( )A. 41B.81C.113D.1223、树最适合用来表示()A. 有序数据元素B.无序数据元素C.元素之间具有层次关系的数据D.元素之间无联系的数据4、以下存储结构中,不是树的存储结构的是()A.双亲存储结构B.孩子兄弟链接存储结构C.孩子链存储结构D.顺序存储结构5、对于一棵具有n个结点、度为4的树来说,()A.树的高度至多是n-3B.树的高度至多是n-4C.第i层上至多有4(i-1)个结点D.至少在某一层上正好有4个结点6、度为4、高度为h的树,则()A.至少有h=3个结点B.至多有4h-1个结点C.至多有4h个结点D.至少有h+4个结点7、假定一棵度为3的树种结点数位50,则其最小高度为()A.3B.4C.5D.6二、综合应用题1、若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的叶子结点的个数是多少?总结点个数是多少?2、已知一棵度为4的树中,其度为0、1、2、3的结点数分别为14、4、3、2,求该树的结点总数n和度为4的结点个数,并给出推导过程。
3、已知一棵度为m的树中,有n1个度为1的结点,有n2个度为2的结点,…,有n m个度为m的结点,问该树有多少个叶子结点?4、含n个结点的度为3的树,最小高度是多少?5、对于含有n个结点的度为m的树,回答以下问题:(1)采用孩子链存储结构时,其中空指针域的个数有多少?(2)采用孩子兄弟链存储结构时,其中空指针域的个数有多少?二叉树的概念和性质一、选择题:1、二叉树和度为2的树相同之处包括( )A. 每个结点都有一个或两个孩子结点B. 至少有一个根结点C. 至少有一个度为2的结点D. 每个结点至多只有一个双亲结点2、按照二叉树的定义,具有3个结点的二叉树有()种。
数据结构二叉树练习题
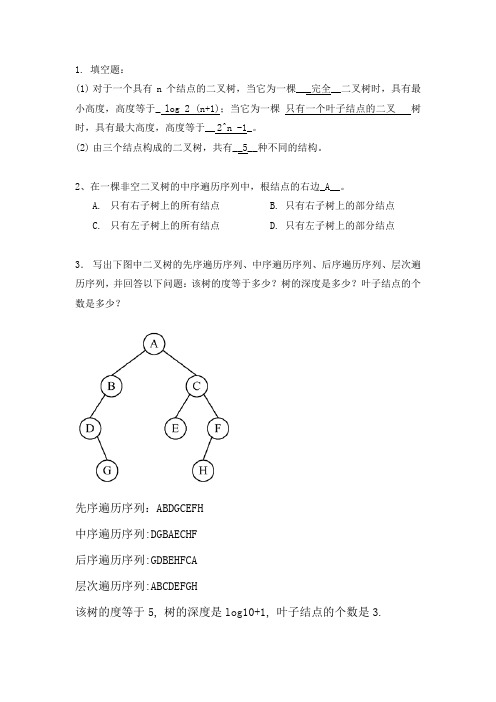
1. 填空题:
(1) 对于一个具有n个结点的二叉树,当它为一棵___完全__二叉树时,具有最小高度,高度等于_log 2 (n+1);当它为一棵只有一个叶子结点的二叉树时,具有最大高度,高度等于__2^n -1_。
(2) 由三个结点构成的二叉树,共有__5__种不同的结构。
2、在一棵非空二叉树的中序遍历序列中,根结点的右边_A__。
A. 只有右子树上的所有结点
B. 只有右子树上的部分结点
C. 只有左子树上的所有结点
D. 只有左子树上的部分结点
3.写出下图中二叉树的先序遍历序列、中序遍历序列、后序遍历序列、层次遍历序列,并回答以下问题:该树的度等于多少?树的深度是多少?叶子结点的个数是多少?
先序遍历序列:ABDGCEFH
中序遍历序列:DGBAECHF
后序遍历序列:GDBEHFCA
层次遍历序列:ABCDEFGH
该树的度等于5,树的深度是log10+1,叶子结点的个数是3.
4.已知一棵二叉树的中根和后根遍历序列如下,画出该二叉树。
中根遍历序列:C D B E G A H F I J K
后根遍历序列:D C E G B F H K J I A。
数据结构二叉树习题含答案

2.1 创建一颗二叉树创建一颗二叉树,可以创建先序二叉树,中序二叉树,后序二叉树。
我们在创建的时候为了方便,不妨用‘#’表示空节点,这时如果先序序列是:6 4 2 3 # # # # 5 1 # # 7 # #,那么创建的二叉树如下:下面是创建二叉树的完整代码:穿件一颗二叉树,返回二叉树的根2.2 二叉树的遍历二叉树的遍历分为:先序遍历,中序遍历和后序遍历,这三种遍历的写法是很相似的,利用递归程序完成也是灰常简单的:2.3 层次遍历层次遍历也是二叉树遍历的一种方式,二叉树的层次遍历更像是一种广度优先搜索(BFS)。
因此二叉树的层次遍历利用队列来完成是最好不过啦,当然不是说利用别的数据结构不能完成。
2.4 求二叉树中叶子节点的个数树中的叶子节点的个数= 左子树中叶子节点的个数+ 右子树中叶子节点的个数。
利用递归代码也是相当的简单,2.5 求二叉树的高度求二叉树的高度也是非常简单,不用多说:树的高度= max(左子树的高度,右子树的高度) + 12.6 交换二叉树的左右儿子交换二叉树的左右儿子,可以先交换根节点的左右儿子节点,然后递归以左右儿子节点为根节点继续进行交换。
树中的操作有先天的递归性。
2.7 判断一个节点是否在一颗子树中可以和当前根节点相等,也可以在左子树或者右子树中。
2.8 求两个节点的最近公共祖先求两个节点的公共祖先可以用到上面的:判断一个节点是否在一颗子树中。
(1)如果两个节点同时在根节点的右子树中,则最近公共祖先一定在根节点的右子树中。
(2)如果两个节点同时在根节点的左子树中,则最近公共祖先一定在根节点的左子树中。
(3)如果两个节点一个在根节点的右子树中,一个在根节点的左子树中,则最近公共祖先一定是根节点。
当然,要注意的是:可能一个节点pNode1在以另一个节点pNode2为根的子树中,这时pNode2就是这两个节点的最近公共祖先了。
显然这也是一个递归的过程啦:可以看到这种做法,进行了大量的重复搜素,其实有另外一种做法,那就是存储找到这两个节点的过程中经过的所有节点到两个容器中,然后遍历这两个容器,第一个不同的节点的父节点就是我们要找的节点啦。
二叉树常见选择题和知识点

二叉树是数据结构中的一种重要类型,常见于编程面试和计算机科学课程的考试中。
以下是一些关于二叉树的常见选择题和相关知识点:
1. 基本概念:
-什么是二叉树?
-什么是二叉搜索树(BST)?
-什么是平衡二叉树(A VL树)?
2. 二叉树遍历:
-先序遍历、中序遍历、后序遍历的定义和区别。
-给定一个二叉树的先序遍历和中序遍历结果,如何构建这棵树?
3. 二叉搜索树的性质:
-二叉搜索树的定义和性质。
-如何判断一个二叉树是否是二叉搜索树?
4. 二叉树的深度和节点计数:
-二叉树的深度是指什么?如何计算二叉树的深度?
-如何统计一个二叉树中的节点数量?
5. 平衡二叉树:
-什么是平衡二叉树?
- A VL树是如何维护平衡性的?
6. 堆和优先队列:
-什么是二叉堆?
-如何用二叉堆实现优先队列?
7. 哈夫曼树:
-什么是哈夫曼树?
-如何构建哈夫曼树?
8. 二叉树的应用:
-二叉树在数据库中的应用。
-二叉树在文件系统中的应用。
9. 二叉树的扩展:
-什么是二叉树的Morris遍历?
-什么是线索二叉树?
以上只是一些例子,实际上,关于二叉树的选择题和知识点还有很多。
在学习和准备面试时,建议对每个知识点进行深入理解,同时通过实际的编程练习加深对二叉树的掌握。
数据结构二叉树习题

14选择题 6 填空题
1.由三个结点可以构造出多少种不同的二叉树( C ) 。
A)3
B)4
C)5
D)6
2.在一棵深度为k的完全二叉树中,所含结点个数不小于( D )。
A)2k
B) 2k+1
C)2k-1
D) 2k-1
至少有多少个结点:k-1层全满, k层只有一个结点
2k-1-1+1=2k-1
5.在一棵二叉树中,假定度为2的结点数为5个,度 为1的结点数为6个,则叶子结点数为( 6 )个。
6.如图所示,该二叉树的中序遍历序列是 (ABCDEGF ) 。
后序遍历:
中序遍历:
dabec
debac
左子右树子树
前序遍历: c e d ba
c e db
a
14.下列关于二叉树的说法正确的是( C ) 。
A)一颗二叉树中的结点个数大于0
B)二叉树中任何一个结点要么是叶子,要么恰有两个子女
C)一棵二叉树中叶子结点的个数等于度为2的结点个数加1
D)二叉树中任何一个结点的左子树和右子树上的结点个数 一定相等。
性质2:k-1层的结点总数(最多)
3.如图所示的4棵二叉树中,( A )不是完全二叉树。
(A)
(B)
(C)
(D)
4.对于任何一棵二叉树,如果其终端结点数为n0,度为
2的结点数为n2,则n0=(
)。
A. n2-1 B. n2+1
C. n2
D. n2-2
5.树中所有结点的度等于所有结点数加( C )
中序遍历:
ABDGCFK
DGBAFCK
左子树
右子树
后序遍历:
二叉树练习题答案

一、下面是有关二叉树的叙述,请判断正误(∨)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
( X )2.二叉树中每个结点的两棵子树的高度差等于1。
(∨)3.二叉树中每个结点的两棵子树是有序的。
( X )4.二叉树中每个结点有两棵非空子树或有两棵空子树。
( X)5.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
( X )6.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
( X )7.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i-1个结点。
(∨)8.用二叉链表法存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
( X )9. 具有12个结点的完全二叉树有5个度为2的结点。
二、填空1.由3个结点所构成的二叉树有 5 种形态。
2. 一棵深度为6的满二叉树有 26-33 个分支结点和 32 个叶子。
3.一棵具有257个结点的完全二叉树,它的深度为 9 。
4. 设一棵完全二叉树具有1000个结点,则此完全二叉树有500 个叶子结点,有 499 个度为2的结点,有 1 个结点只有非空左子树,有 0 个结点只有非空右子树。
(分析:完全二叉树中三种节点个数n0,n1,n2,其中n1为0或1;n0=n2+1;总节点个数N=n0+n1+n2=n0+n1+n0-1=2*n0-1+n1.由此推出当完全二叉树中节点个数为偶数时n1为1,否则为0,则可计算本题)5. 二叉树的基本组成部分是:根(N)、左子树(L)和右子树(R)。
因而二叉树的遍历次序有六种。
最常用的是三种:前序法(即按N L R次序),后序法(即按 LRN 次序)和中序法(也称对称序法,即按L N R次序)。
这三种方法相互之间有关联。
若已知一棵二叉树的前序序列是BEFCGDH,中序序列是FEBGCHD,则它的后序序列必是 FEGHDCB 。
6. 用5个权值{3, 2, 4, 5, 1}构造的哈夫曼(Huffman)树的带权路径长度是 (1+2)*3+3*2+(4+5)*2= 33 。
二叉树练习

二叉树习题1.画出具有3个结点的二叉树的所有不同形态。
2.画出具有2个结点的三叉树的所有不同形态。
3.画出具有3个结点的二层三叉树的所有不同形态。
4.深度为5的二叉树至多有【】个结点。
(A)13 (B)32 (C)31 (D)105.在下面4棵二叉树中,【】不是完全二叉树。
(A) (B) (C) (D)6.在任意一个二叉树中,叶子结点数等于度为2的结点数加1?7.将一棵有100个结点的完全二叉树从根这一层开始,每一层从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为【】。
8.二叉树的先序遍历序列中,任意一个结点均处于其子女结点的前面?9.在一个非空二叉树的中序遍历序列中,根结点的右边【】。
(A)只有右子树的所有结点 (B) 只有右子树的部分结点(C)只有左子树的所有结点(D) 只有左子树的部分结点10.下图是一棵二叉树的顺序存储结构,构造二叉树,写出其先序遍历、中序遍11.一棵二叉树的中序序列为ABCDEFGHIJK,先序序列为EBADCFHGIKJ,求对应的二叉树。
12.由相同权值的一组叶子结点所构成的二叉树具有不同的形态和不同的带权路径长度,其中哈夫曼树的带权路径长度最小,(1)试用权值分别为3,9,6,2,8的叶子结点构造3棵二叉树,其中一棵须为哈夫曼树(2)计算哈夫曼树的带权路径长度(3)试解释为何哈夫曼树常被称作最优二叉树或最佳判定树。
(要求:构造二叉树只需画出二叉树即可,不要求过程;求解带权路径长度时需写出计算过程)。
(7分)13.假设用于通信的电文仅由5个字母a ,b ,c ,d ,e 组成,字母在电文中出现的频率分别为1,2,3,3,4,试求解各字母的哈夫曼编码。
(HUFFMAN算法简单提示:进行n-1次合并,即选取当前根结点权值最小的两棵二叉树进行合并,最小为左,次小为右,权值相同时先扫描到的为最小。
哈夫曼编码左分支为0,右分支为1。
)。
二叉树练习

a b c e d h g i j f
题每题7分 四.算法填空题(前3题每题 分,第4题10分) 算法填空题( 题每题 题 分
1.下列算法实现二叉树中序遍历的非递归算法,请在空白处填入正确的C语句或表达式。 下列算法实现二叉树中序遍历的非递归算法,请在空白处填入正确的 语句或表达式 语句或表达式。 下列算法实现二叉树中序遍历的非递归算法 void inorder(BiTreeNode *T) { BiTreeNode *stack[maxsize], *p=T; //设立栈,存放指针 设立栈, 设立栈 int top=0; //栈顶标记,top==0为空 栈顶标记, 栈顶标记 为空 do p!=NULL { while ( ) //扫描左子树,非空则进栈 扫描左子树, 扫描左子树 { stack[top]=p; top++; ; } p=p->leftChild if(top>0) { Top-; ; p=stack[top]; printf(p->data); //访问结点的值 访问结点的值 ; p=p->rightChild } } while ( p!=NULL || top!=0 ) }
C 6.在高度为h的完全二叉树中, .在高度为 的完全二叉树中 的完全二叉树中, 。 A.度为 的结点都在第 层上 的结点都在第h层上 B.第i(1≤i<h)层上结点的度都为 层上结点的度都为2 .度为0的结点都在第 . < 层上结点的度都为 C.第i(1≤i<h)层上有 i-1个结点 层上有2 D.不存在度为 的结点 . < 层上有 .不存在度为1 C最 7.二叉树若用顺序存储结构(数组)存放,则下列四种运算中的 .二叉树若用顺序存储结构(数组)存放, 容易实现。 容易实现。 A.先序遍历二叉树 B.判断两个结点是不是在同一层上 . . C.层次遍历二叉树 D.根据结点的值查找其存储位置 . . 8. 一棵树可转换成为与其对应的二叉树,则下面叙述正确的是 A 。 一棵树可转换成为与其对应的二叉树, A.树的先根遍历序列与其对应的二叉树的先序遍历相同 . B.树的后根遍历序列与其对应的二叉树的后序遍历相同 . C.树的先根遍历序列与其对应的二叉树的中序遍历相同 . D.以上都不对 .
二叉树性质练习题

8.若一棵二叉树中度为l的结点个数是3,度为2的结点个数是4,则该二叉树叶子结点的个数是()A.4B.5C.7D.8若根结点的层数为1,则具有n个结点的二叉树的最大高度是( )A.nB.C. n+1D.n/2在一棵度为3的树中,度为3的结点个数为2,度为2 的结点个数为1,则度为0的结点个数为( )A.4 B.5 C.6 D.7已知一棵含50个结点的二叉树中只有一个叶子结点,则该树中度为1的结点个数为()A. 0B. 1C. 48D. 49除第一层外,满二叉树中每一层结点个数是上一层结点个数的()A.1/2倍B.1倍C.2倍D.3倍.已知一棵完全二叉树有64个叶子结点,则该树可能达到的最大深度为()A.7 B.8C.9 D.10高度为5的完全二叉树中含有的结点数至少为( )A.16B.17C.31D.32有64个结点的完全二叉树的深度为( )(根的层次为1)。
A. 8B. 7C. 6D. 58.若一棵二叉树有11个叶子结点,则该二叉树中度为2的结点个数是()A.10 B.11C.12 D.不确定的二叉树中第5层上的结点个数最多为( )A.8B.15C.16D.32若一棵二叉树中度为l的结点个数是3,度为2的结点个数是4,则该二叉树叶子结点的个数是()A.4B.5C.7D.8.一棵含18个结点的二叉树的高度至少为( )A.3B.4C.5D.6下列陈述中正确的是( )A.二叉树是度为2的有序树B.二叉树中结点只有一个孩子时无左右之分C.二叉树中必有度为2的结点D.二叉树中最多只有两棵子树,并且有左右之分假设一棵完全二叉树含1000个结点,则其中度为2的结点数为___________。
任意一棵完全二叉树中,度为1的结点数最多为________。
已知一棵完全二叉树中共有768结点,则该树中共有个叶子结点。
在含100个结点的完全二叉树中,叶子结点的个数为___________。
已知完全二叉树T的第5层只有7个结点,则该树共有____________个叶子结点。
排序二叉树例题

排序二叉树例题摘要:一、排序二叉树的概念与特点1.定义与组成2.特点与性质二、排序二叉树的基本操作1.插入操作2.删除操作3.查找操作三、排序二叉树的应用场景与优势1.快速排序算法2.归并排序算法3.优势与局限性四、排序二叉树的例题解析1.题目一2.题目二3.题目三正文:一、排序二叉树的概念与特点排序二叉树,又称有序二叉树,是一种特殊的二叉树结构。
它的每个节点具有以下性质:1.若左子树不为空,则左子树上所有节点的值均小于根节点的值;2.若右子树不为空,则右子树上所有节点的值均大于根节点的值;3.左、右子树也分别为排序二叉树。
排序二叉树具有以下特点:1.每个节点最多只有两个子节点,即左子节点和右子节点;2.树中所有节点的左子树和右子树也分别为排序二叉树;3.排序二叉树是一种递归结构,可以通过对子树的排序构建出整个排序二叉树。
二、排序二叉树的基本操作1.插入操作在排序二叉树中插入一个新节点,需要按照以下步骤进行:1) 首先将新节点作为根节点,构建一个空的排序二叉树;2) 然后将新节点与原树中的根节点进行比较,将新节点插入到正确的位置;3) 最后对插入后的树进行调整,使其重新满足排序二叉树的性质。
2.删除操作在排序二叉树中删除一个节点,需要按照以下步骤进行:1) 找到待删除节点在树中的位置,将其删除;2) 对删除节点后的子树进行调整,使其重新满足排序二叉树的性质。
3.查找操作在排序二叉树中查找某个节点,可以通过递归遍历树的方式进行。
具体查找方法包括二分查找、顺序查找等。
三、排序二叉树的应用场景与优势1.快速排序算法快速排序算法是一种基于排序二叉树的高效排序算法。
它通过选取一个基准值,将数组分为两部分,左边的元素均小于基准值,右边的元素均大于基准值,然后对左右两部分分别进行快速排序。
快速排序的时间复杂度为O(nlogn)。
2.归并排序算法归并排序算法也是一种基于排序二叉树的高效排序算法。
它通过将数组不断拆分为子数组,然后对子数组进行排序,最后将排序好的子数组合并成一个有序数组。
二叉树习题及答案

1.设一棵完全二叉树共有699个结点,则在该二叉树中的叶子结点数?1根据“二叉树的第i层至多有2^(i − 1)个结点;深度为k的二叉树至多有2^k − 1个结点(根结点的深度为1)”这个性质:因为2^9-1 < 699 < 2^10-1 ,所以这个完全二叉树的深度是10,前9层是一个满二叉树,这样的话,前九层的结点就有2^9-1=511个;而第九层的结点数是2^(9-1)=256 所以第十层的叶子结点数是699-511=188个;现在来算第九层的叶子结点个数。
由于第十层的叶子结点是从第九层延伸的,所以应该去掉第九层中还有子树的结点。
因为第十层有188个,所以应该去掉第九层中的188/2=94个;所以,第九层的叶子结点个数是256-94=162,加上第十层有188个,最后结果是350个2完全二叉树:若二叉树中最多只有最下面两层的结点的度可以小于2,并且最下面一层的结点(叶结点)都依次排列在该层最左边的位置上,这样的二叉树为完全二叉树。
比如图:完全二叉树除叶结点层外的所有结点数(叶结点层以上所有结点数)为奇数,此题中,699是奇数,叶结点层以上的所有结点数为保证是奇数,则叶结点数必是偶数,这样我们可以立即选出答案为B!如果完全二叉树的叶结点都排满了,则是满二叉树,易得满二叉树的叶结点数是其以上所有层结点数+1比如图:此题的其实是一棵满二叉树,我们根据以上性质,699+1=700,700/2=350,即叶结点数为350,叶结点层以上所有结点数为350-1=349。
3完全二叉树中,只存在度为2的结点和度为0的结点,而二叉树的性质中有一条是:n0=n2+1;n0指度为0的结点,即叶子结点,n2指度为2的结点,所以2n2+1=699 n2=349;n0=3502.在一棵二叉树上第5层的结点数最多是多少一棵二叉树,如果每个结点都是是满的,那么会满足2^(k-1)1。
所以第5层至多有2^(5-1)=16个结点!3.在深度为5的满二叉树中,叶子结点的个数为答案是16 ~ 叶子结点就是没有后件的结点~ 说白了~ 就是二叉树的最后一层~ 深度为K的二叉树~ 最多有2^k-1个结点~ 最多有2^(k-1)个结点~ 所以此题~ 最多有2^5-1=31个结点~ 最多有2^(5-1)=16个叶子结点~4.某二叉树中度为2的结点有18个,则该二叉树中有几个叶子结点?结点的度是指树中每个结点具有的子树个数或者说是后继结点数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、对于一棵具有n个结点的树,其中所有度之和等于( )
A. n
B. n-1
C. n-2
D.n+1
2、一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数是( )
A. 41
B.81
C.113
D.122
3、二叉树和度为2的树相同之处包括( )
A. 每个结点都有一个或两个孩子结点
B. 至少有一个根结点
C. 至少有一个度为2的结点
D. 每个结点至多只有一个双亲结点
4、假设一棵二叉树的结点个数为50,则它的最小高度是( )
A. 4
B. 5
C.6
D. 7
5、若一棵二叉树具有10个度为2的结点,5个度为1的结点,则叶子结点个数为( )
A. 9
B. 11
C.15
D.不确定
6、设高度为h的二叉树只有度为0和度为2的结点,则此类二叉树所包含的结点数至少为( )
A.2h
B.2h-1
C.2h+1
D.h+1
7、一个具有1025个结点的二叉树的高h为( )
A.11
B.10
C.11-025
D.12-1024
8、设二叉树有2n个结点,则m<n,不可能存在____的结点
A.n个度为0
B.2m个度为0
C.2m个度为1
D. 2m个度为2
9、若一个完全二叉树的结点个数为100,则第60个结点的度为____
A. 0
B.1
C.2
D. 不确定
10、将一棵有100个结点的完全二叉树从根这一层开始,每一层从左到右依次对结点进行编号,根结点编号为1,则编号最大的分支结点的编号为____
A. 48
B.49
C.50
D. 51
11、一棵完全二叉树上有1001个结点,其中,叶子节点的个数是____
A. 250
B.254
C.501
D. 505
12、高度为h的完全二叉树最少有____个结点
A.2h
B. 2h +1
C. 2h -1
D. 2h -1
13、一棵有124个叶子结点的完全二叉树,最多有____个结点
A.247
B. 248
C. 249
D. 250
14、一棵含有k个叶子结点且没有单分支的完全二叉树,其高度为_____
15、已知一棵完全二叉树的第6层(设根为第一层)有8个叶子结点,则该完全二叉树的结点个数最多是_______
A.39
B. 52
C. 111
D. 119
16、对于完全二叉树中的任一结点,若其右分枝下的子孙最大层次为h,则其左分支下的子孙的最大层次为_______
A.h
B. h+1
C. h或h+1
D. 任意
17、以下说法中,____是正确的。
A 在完全二叉树中,叶子结点的双亲的左兄弟(如果存在)一定不是叶子结点
B 任何一棵二叉树,叶子结点个数为度为2的结点数减1,即n0=n2-1
C 二叉树不适合顺序存储结构
D 节点按完全二叉树层序编号的二叉树中,第i个节点的左孩子的编号为2i
18、一棵满二叉树中共有n个节点,其中有m个叶子节点,高度为h,则____
A.n=h+m
B. h+m=2n
C. m=h-1
D. n=2h-1
19、在一棵二叉树中度为0的节点个数为k,度为1的节点个数为m,则该二叉树采用二叉链存储结构时,有____个指针指向孩子节点
A.k
B.m
C. 2k+m-2
D. 2k+m
20、一棵有n个节点的二叉树采用二叉链存储结点,其中空指针数为_____
A .n B. n+1 C.n-1 D.2n。
