练习册ch5-ch6答案(2010修订)

合集下载

环境科学导论09级关键知识点-201012

环境科学导论10级考试题Ch1绪论Ch2生态学绪论Ch3人口问题与环境Ch4当前全球性的环境问题Ch5我国主要的环境污染问题Ch6自然资源的生态保护Ch7生物安全与外来生物入侵Ch8能源、粮食与环境Ch9我国环境保护法规与对策Ch10可持续发展和循环经济一、选择题：Ch11、人类的环境以人类为（ A ），就有别于其他生物的环境，它包括社会环境和自然环境两部分。

A．中心事物B．社会环境C．生物环境D．研究重点2、自然环境是人类赖以生存和发展的各种自然因素的总和，就是通常所称的（ D ）。

Ａ．中心事物Ｂ．地质环境Ｃ．宇宙环境Ｄ．自然界3、水俣病的成因是人由于食用鱼、贝，而使机体中富集了（ D ）。

A．镉B．多氯联苯C．砷化合物D．甲基汞4、引起骨痛病的重金属污染物是（ D ）。

A．Zn B．Hg C．Pb D．Cd5、下列属于次生环境问题的是（ B ）。

A．海啸B．全球温室效应C．火山喷发D．水旱灾害6、环境质量的好坏取决于环境要素中（ C ）。

A．环境要素的平均状况B．最优状态的要素C．最差状态的要素D．环境诸要素的总和Ch27、种群是指某特定时间，栖居在某个自然区域内的（ C ）的组合。

Ａ．不同个体Ｂ．生物群落Ｃ．同种个体Ｄ．生态位8、群落是指不同种的（ B ）有规律的集合体。

Ａ．细菌Ｂ．种群Ｃ．食物链Ｄ．动物9、一个营养级上生存的生物量有一个极限，它取决于（ A ）的数量。

这个事实适用于人类。

因而人类应该限制自己的数量。

Ａ．前一个营养级Ｂ．下一个营养级Ｃ．生态效率Ｄ．分解率10、某些有毒物质在沿（ A ）传递过程中其毒物沿营养级增高而富集，毒性增强。

许多公害病就是这样引起的。

Ａ．食物链Ｂ．生态系统Ｃ．生态位Ｄ．生态金字塔11、生产者能把环境中的无机物制造成（ A ），不仅供自身生长发育的需要，同时也是其他生物类群及人类的需要。

Ａ．有机物Ｂ．无机物Ｃ．营养物Ｄ．蛋白质12、全世界几十亿人口，加上不计其数的动物和微生物都是直接和间接靠（ D ）养活。

Ch6 微型计算机原理与接口技术答案

能。 I/O端口的编址方式通常有两种：一是与内存单元统一编址，二是独立编址。8088/8086系统采用I/O端口独立编址方式。 6.2 试比较4种基本输入输出方法的特点。（不要求）解：在微型计算机系统中，主机与外设之间的数据传送有4种基本的输入输出方式：无条件传送方式、查询工作方式、中断工作方式、直接存储器存取(DMA)方式。它们各自具有以下特点：（1）无条件传送方式适合与简单的、慢速的、随时处于“准备好”接收或发送数据的外部设备，数据交换与指令的执行同步，控制方式简单。（2）查询工作方式针对并不随时“准备好”、且满足一定状态才能实现数据的输入/输出的简单外部设备，其控制方式也比较简单，当CPU的效率比较低。（3）中断工作方式是由外部设备作为主动的一方，在需要时向CPU提出工作请求，CPU在满足响应条件时响应该请求并执行相应的中断处理程序。这种工作方式使CPU的效率提高，但控制方式相对较复杂。（4）DMA方式适合于高速外设，是4种基本输入/输出方式中速度最高的一种。
解：16位地址信号通过译码电路与74LS244芯片连接。其连接如下图所示。
74LS244
...
…
IOR
A 15
A 13
A 12
A 11
系
A 10
统
A9
总
A8
线
A2
A 14
A7
A6
A5 A4 A3
A A
01
DB
≥1 ≥1
&
D0
I0
I1 D7
. . .
E1 I7
E2
2
www.khd课后a答w案.网com
断点的逆过程。即CPU会自动地将堆栈内保存的断点信息弹出到IP、CS和FLAG中，保证被中断的程序从断点处继续往下执行。 6.11 CPU满足什么条件能够响应可屏蔽中断？

复尔凯肠内营养输注用品系列

注
破管道引起营养液泄漏。
系
统
注意事项
经典
问题及解决办法:
的肠
导丝拔出困难
内
原因：
营养
（1）拔管方向错误
输注
（2）拔管手势错误
系
（3）营养管皱折
统
拔管方向错误
经典的肠内营养输注系统
曹子昂, 上海第二医科大学附属仁济医院胸外科
拔管手势错误
经典的肠内营养输注系统
系
统
产品特性
经
典的
容易护理:
肠
– 通用的喂养管连接口：
内营
与管饲输注器及各种注射器相匹配
养
– 不透X光：
输注
X线下容易看见以确认管道位置
系
统
产品特性
经典
安全舒适
的
– 可在体内保留42天：
肠内
聚氨酯材质生物相容性好，对机体无明显刺激，
营
减少各种并发症
养
– 管径可供选择，适应不同患者：
注
系
包装规格：10根/盒
统
有效期：5年(从灭菌日算起)
如何肠内管饲喂养一个患者 ...
经典的肠内营养输注系统
… 当可选方法有限时?
有些患者：
经典
有下列危险情况增加的患者:
的肠
– 返流
内营
– 呕吐
养
– 大脑损伤后胃肠痉挛
输
注
重症胰腺炎
系
统
鼻胃管的局限性
经
典
的
肠
–无法安全地实施肠内营养
经
CAS

ch5物化练习题答案

第五章相平衡练习题答案1. 答：(D)2. 答：(C)3. 答：（B）4. [答] (A)5. [答] (D)R = S - N = 5 - 3 = 2 ( S为物质种数，N为元素数)C= S - R - R' = 5 - 2 - 0 = 3Φ=4 ( 三固，一气)f = C+ 2 -Φ= 3 + 2 - 4 = 16. [答] (C) S= 4C= S - R - R' = 4 - 1 - 2 = 1f*= C+ 1 -Φ= 1 + 1 - 2 = 07. [答] (C)S = 6 , R = 4 , R' = 0,C= 6 - 4 - 0 = 2f* = 2 -Φ+ 1 = 3 -Φ= 0 , Φ= 38. [答] (C)S = 5 , R = 3 , R' = 0,C= 5 - 3 = 2f*= 2 -Φ+ 1 = 0, 最大的Φ= 3 , 除去硫酸水溶液与冰还可有一种硫酸水含物与之共存。

9. [答] (A)(1) 入塔前，物种数S = 3 ，独立组与数C= 3(2) 已达平衡C= S - R - R' = 3 - 1 - 0 = 2(3) 只充 NH3气入塔并达平衡C= S - R - R' = 3 - 1 - 1 = 1因 2NH3 U N2+ 3H2R = 1又 [H2] = 3[N2] R' = 110. [答] (A)C= C- R - R' = 5 - 2 - 0 = 311. [答] (C)S = n + 1 , R = 0 , R' = 0又C= n + 1，Φ=2 f = C + 3 -Φ = n + 1 + 3 - 2 = n + 212. [答] (C)CH3COOH + C2H5OH = CH3COOC2H5+ H2OC= S - R - R' = 4 - 1 - 1 = 2f = C+ 2 - Φ= 2 + 2 - 2 = 213. [答] (C)f = C+ 3 - Φ = 2 + 3 - 2 = 314. [答] (C)15. [答] (B)C= S - R - R' = 3 - 0 - 0 = 3f= C- Φ+ 1 = 3 - 2 + 1 = 216. [答] (B)f = C+ 2 - Φ = 2 + 2 - 3 = 117. [答] (B)C= 2 ( 蔗糖，水 ) ,Φ = 2 ( 蔗糖溶液，纯水)f = C + 3 - Φ = 2 + 3 - 2 = 3 , f*= 2在渗透平衡的体系中，有二个平衡压力，即p(纯水)和p(糖水)所以,相律应写成：f + Φ = C+ 318. [答] (A)恒沸混合物与化合物不同，没有确定的组成。

概论论与数理统计课本答案CH6 ans

概率论第六章习题解答习题6.11．求下列总体分布中参数的矩估计：（1）21,01,(;)0,,x x f x θθθ+−≤≤⎧=⎨⎩其他其中θ < 1；（2）f (x ; p ) = p (1 − p ) x − 1，x = 1, 2, …；其中0 < p < 1；（3）1211221e ,,(;,)0,,x x f x θθθθθθ−−⎧⎪≥=⎨⎪⎩其他其中−∞ < θ 1 < +∞，θ 2 > 0．解：（1）因11320021211E()(21)d ()323226X x x x x x θθθθθθθ−−=+−=+=+=+∫，有θ = 6 E (X ) − 3，故θ 的矩估计为ˆ63X θ=−；（2）因1121111d d d 11E()(1)d d d 1(1)x x x x x x x x q X x p p p x qp q p q p p q q q q p q ∞∞∞∞−−====⎛⎞=⋅−=⋅=====⎜⎟−−⎝⎠∑∑∑∑，故1E()p X =，p 的矩估计为1ˆpX=；（3）因∫∫∫∞+−−+∞−−∞+−−∞+−−+−=−⋅=⋅=121121121121d eede)1(d e1)(E 2θθθθθθθθθθθθθx x x x x X x x x x212121121eeθθθθθθθθθ+=−−=+∞−−+∞−−x x x ，且∫∫∫∞+−−+∞−−∞+−−∞+−−⋅+−=−⋅=⋅=121121121121d 2eede)1(d e1)(E 22222θθθθθθθθθθθθθx x x x x x X x x x x22212122122222)(E 2d e12e121121θθθθθθθθθθθθθθ++=+=⋅+−=∫∞+−−+∞−−X x x x x x ，则2222122212122)(22)](E [)(E )(D θθθθθθθ=+−++=−=X X X ，即)(D 2X =θ，)(D )(E 1X X −=θ，故θ 1和θ 2的矩估计为n S X −=1ˆθ，nS =2ˆθ． 2．求下列总体分布中参数的极大似然估计：（1）f (x ; θ ) = θ (1 − θ ) x − 1，x = 1, 2, …；其中0 < θ < 1；（2）λλλ−=e !);(x x f x，x = 0, 1, 2, …；其中λ > 0；（3）222)(ln 2eπ21),;(σµσσµ−−=x xx f ，x = 0；其中−∞ < µ < +∞，σ > 0．解：（1）nx nx x x n ni i n x f x f x f L −−−−∑−=−−⋅−===121)1()1()1()1();();();()(11121θθθθθθθθθθθθ""，即)1ln()(ln )(ln 1θθθ−−∑+==n x n L ni i ，令011)(1d )(ln d 1=−−⋅−∑+⋅==θθθθn x n L n i i ，得xx nni i11==∑=θ，故θ 的极大似然估计为X1ˆ=θ；（2）λλλλλλλλλλλλn n x n x x x n x x x x x x x f x f x f L ni in−−−−∑=⋅===e !!!e !e !e !);();();()(212121121"""，即λλλn x x x x L n ni i −−⋅∑==)!!!ln(ln )(ln 211"，令01d )(ln d 1=−⋅∑==n x L n i i λλλ，得x x n ni i ==∑=11λ，故λ 的极大似然估计为X =λˆ；（3）),;(),;(),;(),(222212σµσµσµσµn x f x f x f L "=212222222212)(ln 212)(ln 2)(ln 22)(ln 1e)π2(1eπ21eπ21eπ21σµσµσµσµσσσσ∑===−−−−−−−−ni i n x nnx nx x x x x x x x ""，即21221222)(ln )ln()ln π2(ln 2),(ln σµσσµ∑−−−+−==ni i n x x x x nL "，令0ln 2)1()(ln 2),(ln 21212=−∑=∑−⋅−−=∂∂==σµσµµσµn x x L ni i ni i ，得∑==ni i x n 1ln 1µ，再令02)(ln 12),(ln 412222=∑−+⋅−=∂∂=σµσσσµni i x n L ，得∑−==n i i x n 122)(ln 1µσ，故µ和σ 2的极大似然估计为∑==n i i X n 1ln 1ˆµ，∑−===∧∑n i n i i i X n X n 1212)ln 1(ln 1σ． 3．设总体X 的密度函数为⎩⎨⎧<<+=,,0,10,)1();(其他x x x f θθθ求参数θ 的极大似然估计与矩法估计，并看看它们是否一致？今获得样本观测值为0.4, 0.7, 0.27, 0.55,0.68, 0.31, 0.45, 0.83．试分别求θ 的极大似然估计值与矩估计值．解：因121212()(;)(;)(;)(1)(1)(1)(1)()n n n n L f x f x f x x x x x x x θθθθθθθθθθθθ==+⋅++=+"""，即ln L (θ ) = n ln (θ + 1) + θ ln (x 1 x 2 … x n )，令12d ln ()1ln()0d 1n L n x x x θθθ=⋅+=+"，则12111ln()ln nn ii nnx x x x θ==−−=−−∑"，故θ 的极大似然估计为1ˆ1ln nii nX θ==−−∑；因1211E()(1)d (1)22xX x x x θθθθθθθ++=⋅+=+⋅=++∫，有2E()11E()X X θ−=−，故θ 的矩法估计为21ˆ1X Xθ−=−；显然参数θ 的极大似然估计与矩法估计不一致；又因样本观测值为0.4, 0.7, 0.27, 0.55, 0.68, 0.31, 0.45, 0.83，有1(0.40.70.83)0.523758x =+++="，故θ 的极大似然估计值为8ˆ10.3982ln 0.4ln 0.7ln 0.83θ=−−=+++"，θ 的矩估计值为20.523751ˆ0.099710.52375θ×−==−．习题6.21．设容量为3的随机样本X 1 , X 2 , X 3取自概率密度函数为1,0,(;)0,,x f x θθθ−⎧<<⎪=⎨⎪⎩其他的总体．证明1(1)ˆ4X θ=和2(3)ˆ43X θ=都是θ 的无偏估计量．证：总体X 的分布函数为0,0,(;),0,1,,x x F x x x θθθθ<⎧⎪⎪=≤<⎨⎪≥⎪⎩则容量为3的样本的最小顺序统计量X (1) 的分布函数和密度函数为33(1)0,0,(;)1[1(;)]11,0,1,,x x F x F x x x θθθθθ<⎧⎪⎪⎛⎞=−−=−−≤<⎨⎜⎟⎝⎠⎪⎪≥⎩23(1)(1)3(),0,(;)(;)0,x x f x F x θθθθθ⎧−<<⎪′==⎨⎪⎩其他且最大顺序统计量X (3) 的分布函数和密度函数为33(3)0,0,(;)[(;)],0,1,,x x F x F x x x θθθθθ<⎧⎪⎪⎛⎞==≤<⎨⎜⎟⎝⎠⎪⎪≥⎩23(3)(3)3,0,(;)(;)0,x x f x F x θθθθ⎧<<⎪′==⎨⎪⎩其他得234222321(1)33300031212ˆE()4E()4()d (2+)d 2+234x x x X x x x x x x x θθθθθθθθθθθθθ⎛⎞==⋅−=−=−=⎜⎟⎝⎠∫∫，2432(3)33300044344ˆE()E()d d 334x x X x x x x θθθθθθθ==⋅==⋅=∫∫，故1(1)ˆ4X θ=和2(3)ˆ43X θ=都是θ 的无偏估计量． 2．设总体X 服从伯努利分布B (1, p )，p 为未知参数（0 < p < 1）．样本X 1 , …, X n 来自于X ．（1）证明：当n = 1时，p 2不存在无偏估计；（2）若n ≥ 2，求p 2的一个无偏估计量．解：（1）当n = 1时，样本X 1的概率分布为101~1X p p ⎛⎞⎜⎟−⎝⎠，则任何统计量T = T (X 1)的数学期望为E (T ) = T (0) ⋅ (1 − p ) + T (1) ⋅ p = T (0) + [T (1) − T (0)] ⋅ p ≠ p 2，故当n = 1时，p 2不存在无偏估计；（2）若n ≥ 2，有样本均值11n i i X X n ==∑，样本方差2211()1n i i S X X n ==−−∑，则E()E()X X p ==，22E()D()(1)S X p p p p ==−=−，即222E()E()E()X S X S p −=−=，故2X S −是p 2的一个无偏估计量．3．设从均值为µ ，方差为σ 2（> 0）的总体X 中分别抽取容量为n 1 , n 2的两个独立样本，样本均值分别为1X 和2X ．试证：对于任意满足条件a + b = 1的常数a 和b ，12ˆaX bX µ=+都是µ 的无偏估计，并确定a 、b 使方差ˆD()µ达到最小．解：因12E()E()X X µ==，211D()X n σ=，222D()X n σ=，有12ˆE()E()E()()a X b X a b a b µµµµ=+=+=+，故当a + b = 1时，ˆE()µµ=，12ˆaX bX µ=+都是µ 的无偏估计；又22222222222121112121212()2(1)ˆD()D()D()(1)n n a n a n a a a X b X a a n n n n n n σσµσ⎡⎤+−+−=+=⋅+−⋅=+=⎢⎥⎣⎦，令212112ˆ2()2d D()0d n n a n a n n µσ+−==，得112n a n n =+，且2212212ˆ2()d D()0d n n n n a µσ+=>，故当112n a n n =+，2121n b a n n =−=+时，方差ˆD()µ达到最小． 4．设X 1 , X 2 , X 3 , X 4是来自均值为θ 的指数分布的样本，其中θ 未知．证明下列三个估计量1123411()()36T X X X X =+++，212341(6543)10T X X X X =+−+，T 3 = 2 X 1 − X 2 + 3 X 3 − 3 X 4 ，均为θ的无偏估计量，并说明上述估计量中哪个最有效．证：因总体X 服从均值为θ 的指数分布，即X ~ e (1/θ )，有E (X ) = θ ，D (X ) = θ 2 ，则112341111E()[E()E()][E()E()]()()3636T X X X X θθθθθ=+++=+++=，2123411E()[6E()5E()4E()3E()](6543)1010T X X X X θθθθθ=+−+=+−+=，E (T 3) = 2 E (X 1) − E (X 2) + 3 E (X 3) − 3 E(X 4) = 2θ − θ + 3θ − 3θ = θ ，故T 1 , T 2 , T 3均为θ 的无偏估计量；又222221123411115D()[D()D()][D()D()]()()93693618T X X X X θθθθθ=+++=+++=， 22222212341143D()[36D()25D()16D()9D()](3625169)10010050T X X X X θθθθθ=+++=+++=，D (T 3) = 4 D (X 1) + D (X 2) + 9 D (X 3) + 9 D (X 4) = 4θ 2 + θ 2 + 9θ 2 + 9θ 2 = 23θ 2 ，显然D (T 1) < D (T 2) < D (T 3)，故T 1最有效，T 2其次，T 3最差．5．设ˆθ是参数θ 的无偏估计量，且ˆD()0θ>，试证：2ˆ()θ不是θ 2的无偏估计量．证：因ˆθ是参数θ 的无偏估计量，即ˆE()θθ=，有2222ˆˆˆˆE[()]()[E()]()D D θθθθθθ=+=+>，故2ˆ()θ不是θ 2的无偏估计量．习题6.31．随机地从一批零件中抽取10个，测得其长度（单位：cm ）为：2.13, 2.14, 2.12, 2.13, 2.11, 2.15, 2.14, 2.13, 2.12, 2.13．假设该批零件的长度服从正态分布N (µ , σ 2)，试求总体均值µ 的置信系数为95%的置信区间：（1）若已知σ = 0.01；（2）若σ 未知．解：（1）单个正态总体，已知σ ，估计µ ，总体均值µ 的点估计为X，枢轴量为~(0,1)X U N =，置信系数1 − α = 0.95，置信区间为/2/2(X u u αα−+，因1(2.13 2.14 2.13) 2.1310x =+++="，σ = 0.01，n = 10，u 0.025 = 1.96，故µ 的置信系数95%的置信区间为(2.13 1.96 2.13 1.96(2.1238,2.1362)−+=；（2）单个正态总体，未知σ ，估计µ ，总体均值µ 的点估计为X，枢轴量为~(1)X T t n =−，置信系数1 − α = 0.95，置信区间为/2/2((1)(1)X t n t n αα−−+−，因1(2.13 2.14 2.13) 2.1310x =+++="， 222221[(2.13 2.13)(2.14 2.13)(2.13 2.13)]0.01159s =−+−++−="，n = 10，t 0.025 (9) = 2.2622，故µ 的95%置信区间为(2.13 2.2622 2.13 2.2622(2.1217,2.1383)−+=．2．为估计制造某件产品所需的单件平均工时（单位：小时），现制造了五件，记录所需工时为：10.5, 11, 11.2, 12.5, 12.8．设制造单件产品所需工时服从正态分布，试求单件平均工时的置信系数95%的置信区间．解：单个正态总体，未知σ ，估计µ ，总体均值µ 的点估计为X，枢轴量为~(1)X T t n =−，置信系数1 − α = 0.95，置信区间为/2/2((1)(1)X t n t n αα−−+−，因1(10.51112.8)11.65x =+++="，222221[(10.511.6)(1111.6)(12.811.6)]0.99754s =−+−++−="，n = 5，t 0.025 (4) = 2.7764，故µ 的95%置信区间为(11.6 2.7764 2.7764(10.3615,12.8385)−+=．3．设有两台机床用来生产规格相同的铝合金薄板．随机选取每台机床轧制的产品若干张，测得它们的厚度（单位：cm ）如下：机器I ：0.243, 0.238, 0.248, 0.245, 0.236, 0.241, 0.239，机器II ：0.261, 0.254, 0.255, 0.257, 0.253, 0.250，设两台机床所生产的薄板的厚度服从方差相等的正态分布．试给出两台机床生产的铝合金薄板平均厚度差的置信系数为95%的置信区间．解：两个正态总体，未知22,x y σσ（但22x yσσ=），估计µ x −µ y ，均值差µ x −µ y 的点估计为X Y −，枢轴量为()()~(2)X Y T t n m µµ−−−=+−，置信系数1 − α = 0.95，置信区间为(，因1(0.2430.2380.239)0.24147x =+++="，1(0.2610.2540.250)0.2556y =+++="， 222221[(0.2430.2414)(0.2380.2414)(0.2390.2414)]0.00426x s =−+−++−="，222221[(0.2610.255)(0.2540.255)(0.2500.255)]0.00375ys =−+−++−="， n = 7，m = 6，t 0.025 (11) = 2.2010，故µ 的95%置信区间为(0.24140.255 2.2010(0.0185,0.0087)−±=−−．4．由容量为15，取自正态总体N (µ , σ 2)的随机样本算得23.2, 4.24x s ==，确定σ 2和σ 的置信系数90%的置信区间．解：单个正态总体，估计σ 2，总体方差σ 2的点估计为S 2，枢轴量为2222(1)~(1)n S n χχσ−=−，置信系数1 − α = 0.90，置信区间为2222/21/2(1)(1)(,)(1)(1)n S n S n n ααχχ−−−−−，因s 2 = 4.24，n = 15，20.05(14)23.685χ=，20.95(14) 6.571χ=，故σ 2的90%置信区间为14 4.2414 4.24(,(2.5062,9.0336)23.685 6.571××=； σ 的90%置信区间为(1.5831,3.0056)=．5．设有两个化验员A 和B 独立对某种聚合物中的含氯量用同一种方法各做了10次测定，其测定值的方差分别为220.512,0.665ABs s ==．假定各自的测定值均服从正态分布，方差分别为2Aσ和2Bσ，求22ABσσ的置信系数为0.90的置信区间．解：两个正态总体，估计22A B σσ，方差比22A Bσσ的点估计为22A B S S ，枢轴量为2222~(1,1)A AB B S F F n m S σσ=−−，置信系数1 − α = 0.90，置信区间为2222/22222/21/2/2111(,)(,(1,1))(1,1)(1,1)(1,1)A A A A B B B BS S S S F m n F n m F n m F n m S S S S αααα−⋅⋅=⋅⋅−−−−−−−−，因220.512,0.665A B s s ==，n = 10，m = 10，F 0.05 (9, 9) = 3.18，故22A Bσσ的置信系数为0.90的置信区间为0.51210.512(, 3.18)(0.2421,2.4484)0.665 3.180.665××=．6．设枪弹的速度（单位：米/秒）服从正态分布．为了比较两种枪弹的速度，在相同的条件下进行了速度测定．算得数据如下：枪弹甲：m = 110，2810x =，s x = 121.41；枪弹乙：n = 100，2682y =，s x = 105.06．试求这两种枪弹的平均速度之差的置信系数近似为95%的置信区间．解：两个正态总体，未知22,x yσσ（大样本），估计µ x −µ y ，均值差µ x −µ y 的点估计为X Y −，大样本情形下枢轴量为()()~(0,1)X Y T N µµ−−−=，置信系数1 − α = 0.95，置信区间为(，因m = 110，2810x =，s x = 121.41，n = 100，2682y =，s x = 105.06，u 0.025 = 1.96，故µ x −µ y 的95%置信区间为(28102682 1.96(97.36,158.64)−±=．复习题六1．设X 1 , …, X n 为来自总体X 的样本，X 的概率密度函数为22(),0,(;)0,,x x f x θθθθ⎧−<<⎪=⎨⎪⎩其他其中θ（> 0）是未知参数．试求参数θ 的矩估计量．解：因3323222002212E()()d ()()23233X x x x x x θθθθθθθθθθ=⋅−=−=−=∫，有θ = 3 E (X )，故θ 的矩估计为ˆX θ=．注：此题有误，密度函数非零取值范围应为0 < x < θ ．2．伯莱托（Pareto ）分布是常用于研究收入的模型，其分布函数为⎪⎩⎪⎨⎧<≥⎟⎠⎞⎜⎝⎛−=,,0,,1),;(111212θθθθθθx x x x F 其中θ 1 > 0，θ 2 > 0．若随机样本X 1 , …, X n 取自该分布，求θ 1与θ 2的极大似然估计量．解：伯莱托分布的密度函数为⎪⎩⎪⎨⎧<≥⋅=′=+,,0,,),;(),;(11112212122θθθθθθθθθθx x x x F x f则1211211212121112212122112122222222)(),;(),;(),;(),(++++=⋅==θθθθθθθθθθθθθθθθθθθθθθθθn n nnn x x x x x x x f x f x f L """，即ln L (θ 1, θ 2) = n ln θ 2 + n θ 2 ln θ 1 − (θ 2 + 1) ln (x 1 x 2 …x n )，显然θ 1越大，ln L (θ 1, θ 2) 就越大，且x i ≥ θ 1，故θ 1的极大似然估计量为)1(11},,min{ˆX X X n =="θ；令0)ln(ln 1),(ln 2112221=−+⋅=∂∂n x x x n n L "θθθθθ，得111212ln ln 11ln )ln(θθθ−=−=∑=ni i n x n n x x x n "，故θ 2的极大似然估计量为)1(12ln ln 11ˆX X n ni i −=∑=θ．3．设总体X 的概率密度为2231/224πe ,0,(;)0,0,xx x f x x ααα−−−⎧⎪>=⎨≤⎪⎩ 试求参数α 的矩估计和极大似然估计，并证明矩估计量是无偏的．解：因222231/2211/2200E()4πe d 2π(1)de xxX x x x x αααα+∞+∞−−−−−−=⋅=⋅−∫∫22222211/2211/221/21/2002πe2πe d()0(2πe )2πx x x x x ααααααα+∞+∞+∞−−−−−−−−−=−+=+−=∫，故α=，α的矩估计为ˆXα=；因2222221231/2231/2231/221212()(;)(;)(;)4πe4πe4πenx x x n n L f x f x f x x x x αααααααααα−−−−−−−−−==⋅""2213/22124π()eni i x n n n n x x x αα=−−−∑="，即212211ln ()ln 43ln ln π2ln()2nn i i n L n n x x x x ααα==−−+−∑"，令231d ln ()1230d n i i L n x αααα==−⋅+=∑，得α=，故α的极大似然估计为ˆα= 4．设总体X 的密度函数为||1(;)e ,2x f x x λλ−−=−∞<<+∞，试求参数λ（−∞ < λ < +∞）的极大似然估计量．解：112||||||||121111()(;)(;)(;)e e e e 2222ni n i x x x x n n L f x f x f x λλλλλλλλ=−−−−−−−−∑==⋅=""，即1ln ()ln 2||ni i L n x λλ==−−−∑，设顺序统计量为x (1) , x (2) , …, x (n )，并且记x (0)为−∞，x (n + 1)为+∞，不妨设x (k ) ≤ λ < x (k + 1)，k = 0, 1, …, n − 1, n ，则1111ln ()ln 2()()ln 2()kn k ni i i i i i k i i k L n x x n k x x n k λλλλλ==+==+=−−−−−=−−+−+−∑∑∑∑11ln 2(2)kni i i i k n n k x x λ==+=−+−+−∑∑，若2n k <，有n − 2k < 0，ln L (λ )关于λ 单调增加，若2nk >，有n − 2k < 0，ln L (λ )关于λ 单调减少，当n 为偶数时，取2nk =，ln L (λ )在()()221n n x x λ+≤<时达到最大，（由连续性知()21n x λ=时也达到最大），故当n 为偶数时，λ 的极大似然估计量ˆλ为区间()()221[,]n n X X+上的任何值；当n 为奇数时，取12n k −=，ln L (λ )在()()1122n n x x λ−+≤<时单调增加，取12n k +=，ln L (λ )在()()1322n n x x λ++≤<时单调减少，即ln L (λ ) 在()12n x λ+=时达到最大，故当n 为奇数时，λ 的极大似然估计量()12ˆn X λ+=．5．设总体X ~ N (µ , σ 2)，X 1 , …, X n 是X 的样本，X 为样本均值，求常数c 和d ，使∑−=+−1121)(n i i i X X c 与∑=−ni i X X d 1||分别为σ 2和σ 的无偏估计．解：因E (X i ) = µ ，2222)](E [)(D )(E µσ+=+=i i i X X X ，则∑∑∑−=++−=++−=+−+=−+=⎥⎦⎤⎢⎣⎡−1112211112211121)](E )(E 2)(E )(E [)2(E )(E n i i i i i n i i i i i n i i i X X X X c X X X X c X X c221122222)1(22)1(]2)()[(σσµµσµσ−=⋅−⋅=−+++=∑−=n c n c c n i ，故当)1(21−=n c 时，21121)(E σ=⎥⎦⎤⎢⎣⎡−∑−=+n i i i X X c ，∑−=+−−1121)()1(21n i i i X X n 为σ 2的无偏估计；因∑∑≠=−−=−=−ij j i n j j i i X n X n n X n X X X 1111，有i X X −服从正态分布，且E()E()E()0i i X X X X µµ−=−=−=，22222(1)1(1)11D()D()D()(1)i i jj i n n n X X X X n n n n n n σσ≠−−−−=+=+⋅−=∑，则21~(0,)i n X X N n σ−−~(0,1)X N ，记X Y =Y ~ N (0, 1)，则22222200E(||)||d 2d 2y y y Y y yy y+∞−−−+∞+∞−∞===−=∫∫即E(||)i X X −=，11E(||)E(||)n ni i i i d X X d X X d n ==−=−=⋅∑∑，故当d =时，1E ||ni i d X Xσ=⎡⎤−=⎢⎥⎣⎦∑1||n i X X =−为σ 的无偏估计．。

语文9下配套练习册答案第二单元

5 孔乙己一、l．(1)kSn (2)dub (3)shi (4)sh] (5)tui (6)zhdn2．(1)荤 (2)羼 (3)疤 (4)蘸 (5)惋 (6)舀 3．呐喊鲁迅周树人文学思想革命4．略。

5．B二、6．(1)虚荣心十足、四体不勤、死要面子、自欺欺人、迂腐可笑，但又心地善良等。

(2)动作、神态、外貌、语言等描写。

(3)使故事显得真实亲切；使情节集中，内容简要；增加悲凉的意味。

(4)小说反映了封建文化和封建教育对读书人的毒害，控诉了科举制度的罪恶。

(也可有其他说法。

) 7．(1)①脸上的伤疤。

②经常偷人家的财物。

(2)①一个“排”字表现了孔乙己根本不把对方放在眼里，显示了孔乙己摆阔气、内心得意的心理。

②写出了孔乙己额上青筋暴起似乎历历可数的形象，逼真地表现了孔乙己当时窘迫的神情。

(3)“窃”和“偷”是同义词，意思相同，只不过前者是文言，后者是白话。

孑L乙己为了面子，为了维持读书人．的“清高”而狡辩，这是泊欺欺人，强词夺理。

(4)示例：①穿长衫的都不会站着喝酒。

②站着喝酒的都不会是穿长衫的。

③孔乙己是站着喝酒而又穿长衫的。

④像孑L乙己这样的穿着和喝酒方式在这个酒店里仅有他一人。

(5)略。

8．(1)肖像描写：他脸上黑而且瘦，已经不成样子；穿一件破夹袄，盘着两腿，下面垫一个蒲包，用草绳在肩上挂住。

作用：与前面的肖像描写形成对比，突出了孔乙己更加悲惨的境况，揭露了丁举人的罪恶，为孔乙己的悲剧结局作铺垫。

(2)①中秋过后的一个下午②咸亨酒店③孔乙己、掌柜、“我”④孔乙己到酒店最后一次喝酒。

(3)与前文的“排”出九文大钱形成对比，说明孔乙己衣袋里已剩钱不多；用手探取，描写出了孔乙己穷困不堪的可怜神态，表明孔乙己已经走到穷途末路了。

(4)渲染悲凉气氛，’预示孔乙己悲剧的必然来临。

(5)直接原因是他的偷窃，根本原因是封建科举制度的摧残，封建制度的腐朽和黑暗，以及当时社会的冷摸。

(6)这些变化说明了封建制度不但毒害了孔己已Y的想叼基，‘l雨且摧残了俺的肉体，l更深刻地揭示了孔乙己受封建教育毒害之深。

(整理)集成电路设计习题答案1-5章

CH11．按规模划分，集成电路的发展已经经历了哪几代？它的发展遵循了一条业界著名的定律，请说出是什么定律？晶体管-分立元件-SSI-MSI-LSI-VLSI-ULSI-GSI-SOC。

MOORE定律2．什么是无生产线集成电路设计？列出无生产线集成电路设计的特点和环境。

拥有设计人才和技术，但不拥有生产线。

特点：电路设计，工艺制造，封装分立运行。

环境：IC产业生产能力剩余，人们需要更多的功能芯片设计3．多项目晶圆（MPW）技术的特点是什么？对发展集成电路设计有什么意义？MPW：把几到几十种工艺上兼容的芯片拼装到一个宏芯片上，然后以步行的方式排列到一到多个晶圆上。

意义：降低成本。

4．集成电路设计需要哪四个方面的知识？系统，电路，工具，工艺方面的知识CH21．为什么硅材料在集成电路技术中起着举足轻重的作用 ?原材料来源丰富，技术成熟，硅基产品价格低廉2．GaAs和InP材料各有哪些特点? P10,11 3．怎样的条件下金属与半导体形成欧姆接触？怎样的条件下金属与半导体形成肖特基接触？接触区半导体重掺杂可实现欧姆接触，金属与掺杂半导体接触形成肖特基接触4．说出多晶硅在CMOS工艺中的作用。

P13 5．列出你知道的异质半导体材料系统。

GaAs/AlGaAs, InP/ InGaAs, Si/SiGe, 6．SOI材料是怎样形成的，有什么特点?SOI绝缘体上硅，可以通过氧隔离或者晶片粘结技术完成。

特点：电极与衬底之间寄生电容大大减少，器件速度更快，功率更低7. 肖特基接触和欧姆型接触各有什么特点？肖特基接触：阻挡层具有类似PN结的伏安特性。

欧姆型接触：载流子可以容易地利用量子遂穿效应相应自由传输。

8. 简述双极型晶体管和MOS晶体管的工作原理。

P19,21CH31．写出晶体外延的意义，列出三种外延生长方法，并比较各自的优缺点。

意义：用同质材料形成具有不同掺杂种类及浓度而具有不同性能的晶体层。

外延方法:液态生长，气相外延生长，金属有机物气相外延生长2．写出掩膜在IC制造过程中的作用，比较整版掩膜和单片掩膜的区别，列举三种掩膜的制造方法。

ch6习题及答案

ch6习题及答案习题6解答判断题：1.二叉树中每个结点有两个子女结点，而对一般的树则无此限制，因此二叉树是树的特殊情形。

( ╳ )2.二叉树就是结点度为2的树。

( ╳ )( (哈工大2000年研究生试题)3.二叉树中不存在度大于2的结点，当某个结点只有一棵子树时无所谓左、右子树之分。

( ╳ ) (陕西省1998年自考试题)4.当k≥1时，高度为k的二叉树至多有21 k个结点。

( ╳ )5.完全二叉树的某结点若无左孩子，则它必是叶结点。

(√)(中科院软件所1997年研究生试题)6.用一维数组存放二叉树时，总是以前序遍历顺序存储结点。

( ╳ )7.若有一个结点是某二叉树子树的中序遍历序列中的最后一个结点，则它必是该子树的前序遍历序列中的最后一个结点。

( ╳ )8.存在这样的二叉树，对它采用任何次序的遍历，结果相同。

(√)(哈工大2000年研究生试题)9.中序线索二叉树的优点之一是便于在中序下查找前驱结点和后继结点。

(√)10.将一棵树转换成二叉树后，根结点没有左子树，( ╳ )(北邮1999年研究生试题。

)11.由树转换成二叉树，其根结点的右子树总是空的。

(√)12.前序遍历森林和前序遍历与该森林对应的二叉树其结果不同。

( ╳ )13.在叶子数目和权值相同的所有二叉树中，最优二叉树一定是完全二叉树。

( ╳ )14.在哈夫曼编码中，当两个字符出现的频率相同时，其编码也相同，对于这种情况应作特殊处理。

( ╳ )15.霍夫曼树一定是满二叉树。

( ╳ )16.树的度是树内各结点的度之和。

( ╳ )17.由二叉树的结点构成的集合可以是空集合。

(√)18.一棵树中的叶子结点数一定等于与其对应的二叉树中的叶子结点数。

( ╳ )选择题：19.树最适合用来表示( C )。

A．有序数据元素 B. 无序数据元素C．元素之间具有分支层次关系的数据 D. 元素之间无联系的数据20.如果结点A有3个兄弟，而且B是A的双亲，则B的度是( D )。

李晓峰__通信原理习题答案-CH6

习题61. 对模拟信号()sin(200)/200m t t t π=进行抽样。

试问：（1）无失真恢复所要求的最小抽样频率为多少？（2）在用最小抽样频率抽样时，1分钟有多少抽样值。

解：(1) 由表2.1.2，有()(),0Ff BSa Bt rect B Bπ←−→>()sin(200)sin(200)200200200t t m t B ttππππ===，()200200f f Mf rect rect B B ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭∴100H f H z=∴无失真最小抽样频率2200S H f f H z==(2) 一分钟抽样值的数目为60200*6012000S f ⨯==个2. 已知信号()mt 的频谱为：()1,100010000,ff H z Mf⎧-<⎪=⎨⎪⎩其他(1) 假设以1500H z 的速率对它进行抽样，试画出已抽样信号()S m t 频谱图。

(2) 若用3000S f H z =的速率抽样，重做(1)小题解：(1)()()()n S Sn m t m t t T δ∞=-∞=-∑()()()()11SS Sk kSSM f Mf fkf M fkf T T δ∞=-∞=⨯-=-∑∑（2）)Hz3. 4. 5.6. 求下面中频信号最小抽样频率 (1)中心频率为60MHz ，带宽为5MHz (2)中心频率为30MHz ，带宽为6.5MHz (3)中心频率为70MHz ，带宽为2MHz解：带通抽样定理：H f 是B 的整数倍时，取2S f B =无混叠。

H f 不是B 的整数倍时，设带通信号的上截止频率为H f ，下截止频率为L f ，则其带宽H L B f f =-，此时无混叠的采样所需要的最低频率S f 应满足：()2121S HL k k f f f B n n ⎛⎫⎛⎫=-+=+ ⎪ ⎪⎝⎭⎝⎭()HH H H L H Lf f f n k n f f B f f ⎢⎥⎢⎥===-⎢⎥⎢⎥--⎣⎦⎣⎦n 是H f B 是整数部分，k是Hf B 的小数部分。

数据结构Ch6习题答案

、选择题:
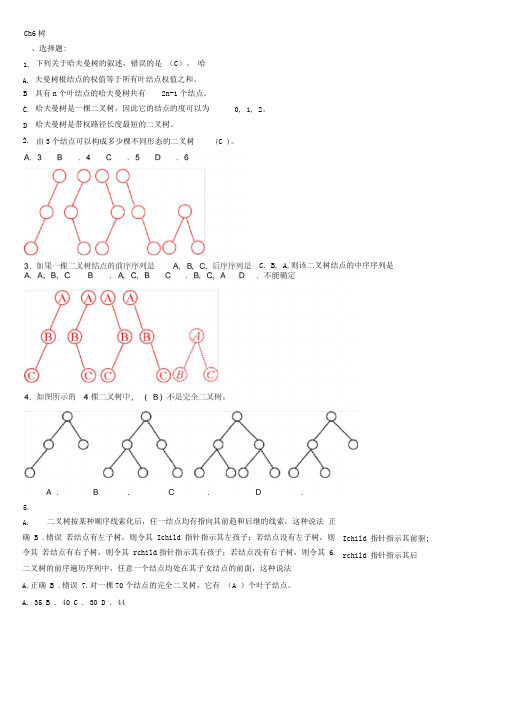
下列关于哈夫曼树的叙述，错误的是（C）。哈夫曼树根结点的权值等于所有叶结点权值之和。
B.
具有n个叶结点的哈夫曼树共有2n-1个结点。
C.
D.
哈夫曼树是一棵二叉树，因此它的结点的度可以为哈夫曼树是带权路径长度最短的二叉树。
0, 1,2。
由3个结点可以构成多少棵不同形态的二叉树
2.
(C)。
n在m前的条件是（C）。
.n在m左方D . n是m子孙
15 .将一棵有100个结点的完全二叉树从上到下
,从左到右依次对结点进行编号，根结点的编号为 49的结点的左孩子编
号为（A）。
A.98B .99C .50D
48
16.某二叉树的前序和后序序列正好相反，则该二叉树
)、>1=1/
定是(
B）二叉树。
A.空或只有一个结点
C, B, A,则该二叉树结点的中序序列是
二叉树按某种顺序线索化后，任一结点均有指向其前趋和后继的线索，这种说法正确B.错误若结点有左子树，则令其Ichild指针指示其左孩子；若结点没有左子树，则令其若结点有右子树，则令其rchild指针指示其右孩子；若结点没有右子树，则令其 6.二叉树的前序遍历序列中，任意一个结点均处在其子女结点的前面，这种说法
A.正确B.错误 7.对一棵70个结点的完全二叉树，它有（A）个叶子结点。
A.35B .40C .30D .44
&设一棵二叉树中，度为
第1层;
第2层:
第』层:
A.10B .11
n0=n2+1
9•假定根结点的层次为
0,
A.3B .4C
假定根结点的层次为
10.若一棵二叉树中,

CH6压电式传感器(含答案)《传感器与检测技术(第2版)》习题及解答.docx

第6章压电式传感器一、单项选择题1、对石英晶体，下列说法正确的是（）0A.沿光轴方向施加作用力，不会产生压电效应，也没有电荷产生。

B.沿光轴方向施加作用力，不会产生压电效应，但会有电荷产生。

C.沿光轴方向施加作用力，会产生压电效应，但没有电荷产生。

D.沿光轴方向施加作用力，会产生压电效应，也会有电荷产生。

2、石英晶体和压电陶瓷的压电效应对比正确的是（）A.压电陶瓷比石英晶体的压电效应明显，稳定性也比石英晶体好B.压电陶瓷比石英晶体的压电效应明显，稳定性不如石英晶体好C.石英晶体比压电陶瓷的压电效应明显，稳定性也比压电陶瓷好D.石英晶体比压电陶瓷的压电效应明显，稳定性不如压电陶瓷好3、两个压电元件相并联与单片时相比说法正确的是（）A.并联时输出电压不变，输出电容是单片时的一半B.并联时输出电压不变，电荷量增加了 2倍C.并联时电荷量增加了 2倍，输出电容为单片时2倍D.并联时电荷量增加了一倍，输出电容为单片时的2倍4、两个压电元件相串联与单片时相比说法正确的是（）A.串联时输出电压不变，电荷量与单片时相同B.串联时输出电压增大一倍，电荷量与单片时相同C.串联时电荷量增大一倍，电容量不变D.串联时电荷量增大一倍，电容量为单片时的一半5、用于厚度测量的压电陶瓷器件利用了（）原理。

A.磁阻效应B.压阻效应C.正压电效应D.逆压电效应6、压电陶瓷传感器与压电石英晶体传感器的比较是（）。

A.前者比后者灵敏度高B.后者比前者灵敏度高C.前者比后者性能稳定性好D.前者机械强度比后者的好7、压电石英晶体表面上产生的电荷密度与（）。

A.晶体厚度成反比C.作用在晶片上的压力成正比8、压电式传感器目前多用于测量（A.静态的力或压力C.位移B.晶体面积成正比D.剩余极化强调成正比）oB.动态的力或压力D.温度A.不产生压电效应B. 产生逆向压电效应C. 产生横向压电效应D. 产生纵向压电效应关于压电式传感器中压电元件的连接，以下说法正确的是（二、多项选择题1、压电晶体式传感器其测量电路常采用（）。

CH6-指针练习题及答案

第六章指针练习题及答案一、填空题1、定义int a[]={1,2,3,4,5,6},*p=a;语句printf("%d",（*++p）++);的输出结果是（）。

2、以下程序的执行结果是（）。

main(){ char s[]="abcdefg"; char *p;p=s; printf("ch=%c\n",*(p+5)); }3、以下程序的执行结果是（）。

main(){ int a[][={1,2,3,4,5,6};for(p=&a[5];p>=a;p--) printf("%d",*P);printf("\n"); }4、以下程序的执行结果是（）。

main(){ int a[12]={1,2,3,4,5,6,7,8,9,10,11,12},*p[4],i;for(i=0;i<4;i++)p[i]=&a[i*3];printf("%d\n",p[3][2]);}5、设包含如下程序的文件名为myprog.c，编译后键入命令：myprog one two three，则执行结果是（）。

main(int argc,char *argv[]){ int i;for(i=1;i<argc;i++)printf("%s%c",argv[i],(i<argc-1)?":');}6、下面程序的运行结果是（）char s[80],*sp="HELLO!";sp=strcpy(s,sp); s[0]='h'; puts(s);7、下面程序段的运行结果是（）char *s1="AbcdEf",*s2="aB";s1++; t=(strcmp(s1,s2)>0); printf("%d\n",t);8、下面程序段的运行结果是（）char str[]="abc\0def\0ghi"; char *p=str; printf("%s",p+5)9、若有以下定义和语句：int a[4]={0,1,2,3},*p; p=&a[1]; 则++(*p)的值是（）。

ch6习题及答案

ch6习题及答案习题6解答判断题：1.二叉树中每个结点有两个子女结点，而对一般的树则无此限制，因此二叉树是树的特殊情形。

( ╳ )2.二叉树就是结点度为2的树。

( ╳ )( (哈工大2000年研究生试题)3.二叉树中不存在度大于2的结点，当某个结点只有一棵子树时无所谓左、右子树之分。

( ╳ ) (陕西省1998年自考试题)4.当k≥1时，高度为k的二叉树至多有21 k个结点。

( ╳ )5.完全二叉树的某结点若无左孩子，则它必是叶结点。

(√)(中科院软件所1997年研究生试题)6.用一维数组存放二叉树时，总是以前序遍历顺序存储结点。

( ╳ )7.若有一个结点是某二叉树子树的中序遍历序列中的最后一个结点，则它必是该子树的前序遍历序列中的最后一个结点。

( ╳ )8.存在这样的二叉树，对它采用任何次序的遍历，结果相同。

(√)(哈工大2000年研究生试题)9.中序线索二叉树的优点之一是便于在中序下查找前驱结点和后继结点。

(√)10.将一棵树转换成二叉树后，根结点没有左子树，( ╳ )(北邮1999年研究生试题。

)11.由树转换成二叉树，其根结点的右子树总是空的。

(√)12.前序遍历森林和前序遍历与该森林对应的二叉树其结果不同。

( ╳ )13.在叶子数目和权值相同的所有二叉树中，最优二叉树一定是完全二叉树。

( ╳ )14.在哈夫曼编码中，当两个字符出现的频率相同时，其编码也相同，对于这种情况应作特殊处理。

( ╳ )15.霍夫曼树一定是满二叉树。

( ╳ )16.树的度是树内各结点的度之和。

( ╳ )17.由二叉树的结点构成的集合可以是空集合。

(√)18.一棵树中的叶子结点数一定等于与其对应的二叉树中的叶子结点数。

( ╳ )选择题：19.树最适合用来表示( C )。

5升六英语答案.doc

Test for Grade FiveName ______ Class __________ Level ______ I.Look and choose.(找出不同类的一项)(10%) ( )(1) behind inside outside evening( )(2) asleep awake quite hide()(3) fluffy soft shiny lady( )(4) mine youhisour s( X5)tieetrtrainstrawberry( )(6) lunch box felt pen crayon notebook ( )(7)pi neappie durian plum shadow( )(8)flat block building mountain( )(9)biscuit panda lizard tiger( )(10)touch smell hear earII.Look and write.(根据要求写单词)(10%)(1) ________________________ children(单数)_ )child(2)foot(复数) _ feet ___(3) ________________________ make(现在分词)_making ____________________________ (4)go(第三人称单数)_goes_(5)he(名词性物主代词)_his_ (6)my(名词性物主代词)—mine_ (7)lady(复数)—ladies ____ ( 8)touch(同类词)_ smell(9)behind(同类词)—inside _ (10) shiny(同类词)_SUNNY ____III.Think and choose.(选择正确答案)(40%)(A )(1)_ Js the boy's shadow? It is long.A. WhereB.HowC.What(A )(2)______ is the block? It is in fornt of the library.A.WhereB.WhatC.Who(B )(3)_____ is behind the sofa? The ball.A.WhoB.WhatC.Where(B )(4)Which umbrella do you like, the red one_ the black one?A. andB. orC. but(A ”5) _____ that lady? She's our English teacher.A. Who'sB. WhoseC.How( B )(6)ls this a pear or an apple? ________ a pear.A.Yes, it'sB. It'sC.Yes( B )(7) ____ walk on the grass.A.Can'tB.Don't C,Not(A )(8)Do you want ______ hammers?No, the big one please.A. bothB. theC./( B )(9)The baby is_B ____ . Please be quiet.A.sleepB.sleepingC. awake(B )(10)Have you got plums?Sorry, I haven't got __ plums.A. any,anyB. some, anyC. any,some()(11) Is this parcel ______ ?No, it's not ___ . It's ___ .A. yours, mine, hersB. hers, yours, mineC. hers, mine, yours( A )(12)Look! The cat is waging _____ face.A. itsB.it'sC.it(A )(13)Put some beans or rice_ the cup.A. inB. toC. of( a )(14)l_ able to taste ______ my tongue.A. am,withB.is, withC.am, to(A )(15)Be __ ! The train is coming.A.carefulB.careC.quiet(C )(16) My new bike is _____ t he door. I can't see it.A. aboveB. inC. outside( C )(17) I can taste coffee with my _______ .A. handsB. earsC.tongue(B )(18)May I use ____ car? Sorry. _______ i s not there.A.yours,oursB.your,oursC. yours, our(B )(19)Draw a cat and a dog _______ the paper.A. inB. onC.at(A )(20)Give _____ a ruler, please. A. me B. IC.myIV.Think and write.(根据首字母填入所缺单词)(10%)(1 )ls the boy's shadow l_oog ___ or s_hort ____ ?(2) Tve got two balls. Do you want the r_ed_one or thebjue ____ one?(3) The shoes are n and n ____ .(4) My quilt is s __ and f ____ .(5) The ice-cream is c_ool __ a nd s_oft ___ .V.Read and match.(为下列问题和回答配对)(10%)(1 )Where are my books? d A.They're Danny's.⑵What has he got? c B.To the library.(3) Where are you going? b C. He's got some water.(4) What are you doing? e D.On the desk.(5) Whose lunch boxes are these? a E. Tm running.VI.Read and judge.(阅读短文，理解后作答)(20%)(1)I have a cat. She is black and white. Her name is Kitty.She has a long tail and small ears. Her tail is black, but her ears are white. Her nose is white, too. She has a basket. She sleeps in her basket. She gets up in the evening. She goes out at night. She catches mice at night. Kitty likes fish and milk. She eats fish every day. She drinks milk every day. Kitty does not like dogs and they do not like her. Kitty likes me and I like her. I often play with her after school.（错）1. Kitty is a pretty girl.（对）2. Kitty is a black and white cat.（错）3. Kitty sleeps in bed at night.（错）4. Kitty and the dogs are good friends.（对）5. Kitty has fish and milk every day.（2）Today is Saturday. Ifs a fine day. Mr. White is in the park with his family. Mr. and Mrs. White have two sons. Their names are Ben And Jerry. They are students. The boys have a sister, Alice. Alice is only three. Now Ben and Jerry are playing ball games with their father. Alice is siting on the grass with her mother. She has a toy panda in her hand. What a happy family! （ A ）1. How many people are there in Mr. White's family?A. FourB. FiveC. Six（ A ） 2. Are Ben and Jerry schoolboys?A. Yes, they are.B. No, they aren't.C. Sorry, I don't know.（ C ） 3. How many children do Mr. and Mrs. White have? (C ) 4. What's in Alice's hand?A. A kiteB. A puppetC. A toy panda( B ) 5. What's Mr. White doing now?A. Playing computer games.B. Playing ball games.C. Walking in the park.。

CH5应用题参考答案

CH5 应用题参考答案1旋转型设备上信息的优化分布能减少为若干个I/O服务的总时间。

设磁鼓上分为20个区，每区存放一个记录，磁鼓旋转一周需20毫秒，读出每个记录平均需用1毫秒，读出后经2毫秒处理，再继续处理下一个记录。

在不知当前磁鼓位置的情况下：（1）顺序存放记录1、……，记录20时，试计算读出并处理20个记录的总时间；（2）给出优先分布20个记录的一种方案，使得所花的总处理时间减少，且计算出这个方案所花的总时间。

答：定位第1个记录需10ms。

读出第1个记录，处理花2ms，这时已到了第4个记录，再转过18个记录(花18ms)才能找到记录2，所以，读出并处理20个记录的总时间：10+3+(1+2+18)×19=13+21×19=412ms如果给出优先分布20个记录的方案为：1，8，15，2，9，16，3，10，17，4，11，18，5，12，19，6，13，20，7，14。

当读出第1个记录，花2ms处理后，恰好就可以处理记录2，省去了寻找下一个记录的时间，读出并处理20个记录的总时间：10+3+3×19=13+247=260ms2现有如下请求队列：8，18，27，129，110，186，78，147，41，10，64，12；试用查找时间最短优先算法计算处理所有请求移动的总柱面数。

假设磁头当前位置下在磁道100。

答：处理次序为：100-110-129-147-186-78-64-41-27-18-12-10-8。

移动的总柱面数：264。

3上题中，分别按升序和降序移动，讨论电梯调度算法计算处理所有存取请求移动的总柱面数。

答：升序移动次序为：100-110-129-147-186-78-64-41-27-18-12-10-8。

移动的总柱面数：264。

降序移动次序为：100-78-64-41-27-18-12-10-8-110-129-147-186。

移动的总柱面数：270。

练习册ch5-ch6答案(2010修订)

环境科学导论09级关键知识点-201012

Ch6 微型计算机原理与接口技术 答案

复尔凯肠内营养输注用品系列

ch5物化练习题答案

概论论与数理统计课本答案CH6 ans

语文9下配套练习册答案第二单元

(整理)集成电路设计习题答案1-5章

ch6习题及答案

李晓峰__通信原理习题答案-CH6

数据结构Ch6习题答案

CH6压电式传感器(含答案)《传感器与检测技术(第2版)》习题及解答.docx

CH6-指针练习题及答案

ch6习题及答案

5升六英语答案.doc

CH5应用题参考答案

Ch6 微型计算机原理与接口技术答案